AI-Driven Virtual Power Plant Scheduling: CUDA-Accelerated Parallel Simulated Annealing Approach

Highlights

The proliferation of distributed energy resources in smart cities calls for scalable and timeefficient optimization of virtual power plants. This study introduces a GPU-accelerated Multiple-Chain Simulated Annealing (MC-SA) framework that employs dual-level parallelization to enable real-time VPP scheduling. By improving computational speed and responsiveness, the method advances resilient, adaptive, and sustainable urban energy management.

What are the main findings?

• Developed a fully GPU-accelerated Monte Carlo Simulated Annealing (MC-SA) framework that integrates multi-chain algorithmic parallelism with prosumer-level decomposition for scalable VPP scheduling.
• Achieved over 10× speedup and near real-time runtimes on 1000-prosumer scenarios, while ensuring strict feasibility through a projection-based constraint-handling mechanism.

What are the implications of the main findings?

• Enables real-time metaheuristic optimization for smart grid applications, supporting intraday market responsiveness and grid-aware dispatch decisions.
• Provides a transferable, GPU-compatible parallelization strategy for distributed optimization and control across large-scale smart-city infrastructure.

Abstract

Efficient scheduling of virtual power plants (VPPs) is essential for the integration of distributed energy resources into modern power systems. This study presents a CUDA-accelerated Multiple-Chain Simulated Annealing (MC-SA) algorithm tailored for optimizing VPP scheduling. Traditional Simulated Annealing algorithms are inherently sequential, limiting their scalability for large-scale applications. The proposed MC-SA algorithm mitigates this limitation by executing multiple independent annealing chains concurrently, enhancing the exploration of the solution space and reducing the requisite number of sequential cooling iterations. The algorithm employs a dual-level parallelism strategy: at the prosumer level, individual energy producers and consumers are assessed in parallel; at the algorithmic level, multiple Simulated Annealing chains operate simultaneously. This architecture not only expedites computation but also improves solution accuracy. Experimental evaluations demonstrate that the CUDA-based MC-SA achieves substantial speedups—up to 10× compared to a single-chain baseline implementation while maintaining or enhancing solution quality. Our analysis reveals an empirical power-law relationship between parallel chains and required sequential iterations (iterations ∝ chains^{−0.88±0.17}), demonstrating that using 50 chains reduces the required number of sequential iterations by approximately 10× compared to single-chain SA while maintaining equivalent solution quality. The algorithm demonstrates scalable performance across VPP sizes from 250 to 1000 prosumers, with approximately 50 chains providing the optimal balance between solution quality and computational efficiency for practical applications.

1. Introduction

The integration of distributed DERs—including photovoltaics, wind turbines, battery storage systems, controllable loads, and distributed generation—is central to the advancement of modern electricity markets. Virtual power plants (VPPs), which aggregate and coordinate these diverse resources, have become essential for optimizing participation in electricity markets, including day-ahead (DA), intraday (ID), and real-time (RT) trading environments [1]. The primary objective of a VPP is to maximize economic value while ensuring reliable operation, a task complicated by significant uncertainties such as renewable generation variability and fluctuating market prices [2,3].

To address these challenges, the literature presents a rich landscape of optimization frameworks for VPP scheduling. Mixed-Integer Linear Programming (MILP) and Mixed-Integer Quadratic Programming (MIQP) dominate exact optimization approaches due to their capacity to simultaneously model discrete bidding actions and continuous power dispatch decisions. These models are widely used for day-ahead bidding and intraday operation [4], as well as for providing multiple grid support services [5]. Recent research has also developed dual-MILP approaches to tackle the complexities of real-time energy market bidding [6].

To handle uncertainty, these deterministic models are extended into stochastic programming formulations, which use scenario trees to anticipate a range of possible futures, thereby enhancing decision robustness. This is particularly relevant for wind-storage systems participating in electricity markets [7] and for risk-averse VPP operations using rolling-horizon control [3]. Alternatively, robust optimization techniques provide performance guarantees under worst-case operational deviations, offering a different approach to managing uncertainty [8].

A critical aspect of modern VPP modeling is the sophisticated representation of energy storage systems. Advanced models capture state-of-charge dynamics, degradation costs, and round-trip efficiency to support accurate and economically realistic scheduling [9,10]. When these storage assets are co-optimized with flexible demand-side resources, the VPP can deliver a wider array of market services and significantly enhance system-level reliability and profitability. For instance, optimal scheduling with demand response in short-term markets has been shown to improve economic outcomes [11]. Furthermore, coordinated operation strategies for VPPs comprising multiple DER aggregators have been developed to improve overall coordination and efficiency [12].

However, the high fidelity of these models comes at a significant computational cost. The complexity of solving large-scale, mixed-integer, and stochastic problems often creates a bottleneck for practical deployment. In real-world operations, VPPs must often rely on rolling-horizon control with rescheduling intervals as short as 15 min [13], requiring optimization solutions under tight time constraints. This has motivated research into accelerating these computations. Multi-core CPU-based parallelization techniques have been adopted to speed up MILP solving and increase scheduling responsiveness [1,5], and multistage scheduling models under distributed locational marginal prices have been proposed to enhance scalability [14]. Despite these efforts, the current literature reveals a clear gap in practical implementations of GPU-accelerated scheduling for VPPs [15], even though GPU architectures have demonstrated superior performance for many other large-scale parallel optimization tasks.

Given the computational limitations of exact methods, metaheuristic algorithms such as Simulated Annealing (SA) offer scalable and flexible alternatives. Their ability to handle non-convex and complex constraint spaces makes them suitable for large-scale VPP problems. Recent advances using high-performance computing (HPC) have demonstrated the potential of parallel SA frameworks, achieving substantial reductions in computational time for VPP scheduling and enabling the management of a large number of consumers in near real time [16]. However, these implementations typically leverage multi-core CPUs, leaving the immense parallel processing power of modern GPUs largely untapped for this specific problem. The inherently sequential nature of the classical SA algorithm, where each state transition depends on the previous one, poses a significant challenge to its efficient parallelization on many-core architectures.

1.1. Research Contribution and Gap Addressing

This study directly addresses these research gaps through several key contributions. First, to overcome the scalability limitations of exact optimization methods for large-scale VPPs, we develop a metaheuristic approach based on Simulated Annealing that offers flexible constraint handling and polynomial-time complexity. Second, to mitigate the inherent sequential bottleneck of traditional SA, we introduce a novel multiple-chain architecture that leverages massive GPU parallelism. Third, we address the gap in practical GPU implementations for VPP scheduling by designing a customized CUDA kernel with a two-level parallelism strategy across prosumers and annealing chains. Finally, our work provides empirical validation of the parallelism–iteration trade-off through rigorous statistical analysis, offering practitioners a principled approach to algorithm tuning that has been lacking in the prior literature.

To address the evolving complexities of modern distributed energy systems, this study introduces a VPP optimization framework engineered for real-time responsiveness, economic efficiency, and operational resilience. Designed as a scalable, data-centric architecture, the framework harmonizes prosumer behavior with grid-level objectives while respecting system-wide technical and economic constraints. The development of this system is guided by four core design principles.

(1)

Rolling-Horizon Social Welfare Optimization: The framework prioritizes social welfare by dynamically scheduling energy transactions based on real-time supply, demand, and grid conditions. Through a rolling-horizon approach, the model adapts to market fluctuations and reformulates the objective as a cost minimization task—accounting for battery degradation, efficiency losses, and operational limits—to ensure holistic system optimization.

(2)

Scalable Architecture: As prosumer participation increases, the framework must maintain computational efficiency and scheduling precision. Its design supports high-dimensional optimization, enabling robust performance at scale without compromising real-time execution or decision quality.

(3)

Battery Longevity and Sustainability: To promote long-term viability, the system integrates battery health constraints that govern charge and discharge operations within safe boundaries. This preserves battery lifespan while supporting environmentally sustainable energy practices.

(4)

Grid-Regulated Market Coordination: Operating under centrally determined price signals, the system simplifies market participation by requiring prosumers to submit only energy quantities, while the grid defines the pricing structure. This ensures transparent, price-aligned scheduling without strategic bidding complexity.

Collectively, these design elements necessitate an integrated architecture capable of real-time forecasting, high-frequency data streaming, and adaptive control. The proposed VPP management platform meets these demands, delivering intelligent, market-aligned scheduling of distributed resources. By leveraging predictive analytics and decentralized coordination, it enhances system welfare, ensures operational agility, and supports large-scale deployment across academic research and commercial applications.

Figure 1 illustrates the conceptual architecture of the proposed framework, capturing the flow of real-time data, the interaction between prosumers and the grid, and the role of the centralized optimization engine in governing distributed energy scheduling.

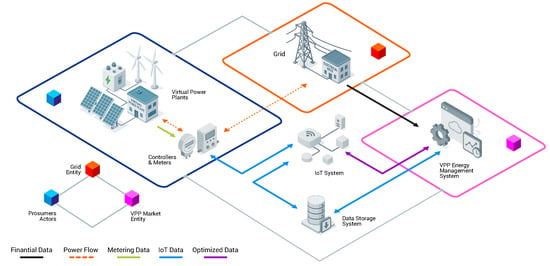
Figure 1. Schematic of the VPP management framework, illustrating key components and data flows among prosumers, the market, and the grid. The VPP acts as an intermediary, enabling energy trading within regulated prices, with a centralized scheduler optimizing resource allocation.

  To contextualize these design choices, we present a conceptual scenario that encapsulates the operational dynamics of the VPP environment. This scenario demonstrates how DERs are orchestrated within a grid-regulated pricing structure. As shown in Figure 1, the VPP functions as an intelligent intermediary, coordinating transactions among prosumers and aligning them with grid-defined economic signals.

Prosumers continuously transmit real-time data—encompassing generation, consumption, and battery status—through an IoT-enabled data streaming layer that forms the system’s communication backbone. At the core of the VPP is an energy management system comprising two critical modules: a forecasting engine and an optimization scheduler. The former predicts individual prosumer energy behavior using real-time and historical data, while the latter allocates optimal energy transactions (buy, sell, store) under grid-imposed constraints. By synchronizing these operations, the VPP enhances energy market efficiency, ensures supply–demand balance, and reinforces overall grid reliability.

Given these design requirements and the real-time decision-making nature of the problem, achieving timely and scalable scheduling for large prosumer communities necessitates a HPC infrastructure. The computational complexity arising from rolling-horizon optimization, real-time forecasting, and constraint handling becomes increasingly demanding as the number of participating prosumers grows. Therefore, an HPC-enabled solution is essential to ensure that the VPP management system can operate efficiently at scale and deliver near-real-time scheduling performance.

The remainder of this paper is organized as follows. Section 2 reviews the relevant literature on VPP optimization, real-time scheduling, and parallel metaheuristics. Section 3 introduces the VPP optimization model and problem formulation. In Section 4, we present a prosumer-level decomposition strategy that enables parallelization of the scheduling problem. Section 5 presents the MC-SA architecture developed to enhance exploration efficiency, followed by a description of our hierarchical parallelization strategy for distributing computations across HPC resources. Section 6 discusses the practical implementation of the proposed approach on HPC infrastructure. Section 7 presents numerical results and performance evaluations, and finally, Section 9 concludes the paper with key insights and directions for future research.

1.2. Core Innovation and Scope

The principal contribution of this work is a novel hierarchical parallelization framework that addresses fundamental computational challenges in metaheuristic optimization for energy systems. Our approach specifically targets the inherent sequential limitations of SA through two complementary strategies:

• Problem-Level Parallelism: A divide-and-conquer decomposition that exploits the independence of prosumer scheduling subproblems, enabling parallel evaluation across distributed resources.
• Algorithm-Level Parallelism: A multi-chain SA strategy that launches independent search trajectories to overcome sequential bottlenecks in traditional annealing processes.

Through rigorous statistical analysis, we establish an empirical power-law relationship demonstrating that increasing the number of parallel chains effectively reduces the required sequential iterations. This transformation of a traditionally sequential algorithm into a highly parallelizable framework represents a significant advancement for real-time VPP optimization.

While this study focuses on establishing this computational foundation, we acknowledge important extensions for practical deployment—including uncertainty modeling, hardware generalizability, and comprehensive operational metrics—which we position as natural progressions enabled by our parallel architecture in Section 7.6.

2. Related Works

2.1. Optimization Algorithms for Energy Systems Scheduling in Virtual Power Plants

The effective coordination of distributed energy resources within virtual power plants necessitates sophisticated optimization algorithms capable of handling complex constraints, multiple objectives, and various sources of uncertainty. This section provides a comprehensive review of optimization strategies applied to VPP scheduling, systematically categorizing them by computational paradigm and analyzing their respective strengths and limitations in addressing the unique challenges of modern energy systems.

Swarm intelligence and population-based methods have demonstrated remarkable success in solving the complex, non-convex optimization problems inherent to VPP operations. Ant Colony Optimization (ACO) has emerged as a particularly powerful approach for distributed scheduling and market participation strategies. Ref. [17] pioneered the application of ACO in local electricity markets, developing a bi-level formulation that enabled decentralized agents to learn optimal bidding strategies while preserving privacy and ensuring profitability. This approach demonstrated superior performance compared to centralized evolutionary methods in complex market environments. The robustness of ACO for microgrid resource scheduling was further validated by [18], who achieved significant cost reductions while maintaining system reliability over 24 h scheduling horizons. For addressing complex power flow constraints in unbalanced distribution networks, [19] introduced an innovative hybrid Tabu Continuous Ant Colony Search (TCACS) algorithm that reduced power losses by 16.53% while generating substantial daily profits. The versatility of ACO extends beyond traditional power system applications, as evidenced by [20]’s work on virtual network embedding for data center energy management, which achieved a remarkable 52% energy reduction. Furthermore, [21] successfully adapted ACO for the computationally challenging problem of scheduling step-controlled generators in smart grids, developing simulation-guided graph construction techniques that maintained solution feasibility while navigating the NP-hard complexity of the problem.

Simulated Annealing and evolutionary computation techniques have proven equally valuable for VPP optimization, particularly in scenarios requiring global optimization capabilities and handling of complex constraint structures. The thermodynamic principles underlying Simulated Annealing have been effectively leveraged for joint optimization of energy and ancillary services. Ref. [22] developed an SA-based methodology for VPPs integrated with electric vehicles, achieving near-optimal solutions with a remarkable 99.94% reduction in computational time compared to traditional deterministic models. For communication resource allocation in VPPs, [23] proposed an Improved Simulated Annealing algorithm incorporating adaptive temperature control and multi-neighborhood search mechanisms that demonstrated superior performance over both Genetic Algorithms and Particle Swarm Optimization in terms of communication efficiency, latency reduction, and energy utilization. Genetic Algorithms have been extensively applied to VPP scheduling problems, with [24] demonstrating their effectiveness for Demand-Side Management in VPPs integrating diverse DERs and Demand Response programs, successfully reducing electricity market prices and mitigating peak loads through intelligent resource coordination. Ref. [25] further extended GA applications to residential VPPs with electric vehicle integration, achieving substantial cost reductions and enhanced ancillary service delivery through sophisticated chromosome encoding and fitness evaluation mechanisms.

Hybrid and multi-objective optimization frameworks represent a significant advancement in addressing the competing objectives and complex constraint interactions characteristic of modern VPP operations. Ref. [26] developed an innovative three-stage VPP management system that synergistically combined an Improved Pelican Optimization Algorithm for DER scheduling, a convolutional autoencoder for cyberattack detection (achieving 98.06% accuracy), and Prophet forecasting for market price prediction, collectively resulting in a 15.3% revenue enhancement. For managing the inherent uncertainties associated with renewable generation and load patterns under vehicle-to-grid operation, [27] employed sophisticated multi-objective optimization techniques using Genetic Algorithms, effectively balancing economic and reliability objectives. Ref. [28] incorporated data-driven stochastic robust optimization with GA frameworks for handling multiple uncertainty sources in VPPs, leveraging real-time consumption data to enhance decision robustness. Two-stage optimization architectures have demonstrated particular efficacy, with [29] presenting a comprehensive framework integrating flexible Carbon Capture Systems with Virtual Hybrid Energy Storage, yielding an impressive 10.12% improvement in carbon efficiency and a 8.91% gain in economic performance. Similarly, [30] developed an advanced two-stage model that effectively balanced cost minimization and emission reduction objectives under dynamic demand and supply conditions, demonstrating the scalability of hybrid approaches for practical VPP applications.

Comparative algorithmic studies and emerging learning-based paradigms provide crucial insights for algorithm selection and highlight promising future research directions. Ref. [31] conducted extensive benchmarking of evolutionary computation techniques including Particle Swarm Optimization, Differential Evolution, and Vortex Search for local electricity market bidding strategies integrated with wholesale markets, demonstrating superior robustness and convergence characteristics in complex multi-leader optimization environments. Ref. [32] performed systematic evaluation of computational intelligence metaheuristics—including Simulated Annealing, PSO, and ACO—within hierarchical VPP architectures, highlighting their scalability advantages and computational efficiency compared to traditional gradient-based optimization methods. Most recently, reinforcement learning has emerged as a transformative paradigm for adaptive decision-making in dynamic environments, with [33] applying advanced deep RL methodologies including Deep Deterministic Policy Gradient and Asynchronous Advantage Actor-Critic to VPP operations in complex urban environments, achieving significant improvements in emission reduction, demand response coordination, and grid service provisioning under uncertainty.

Beyond the established MILP and metaheuristic approaches, alternative optimization frameworks have demonstrated effectiveness in related energy system domains. Convex optimization formulations have shown particular promise for power flow problems in hybrid AC/DC microgrids, offering computational advantages for certain problem classes through constraint relaxation techniques [34]. Similarly, bi-directional converter-based planning approaches represent another strategy for reinforcing renewable-dominant microgrids through specialized hardware–software co-design [35]. While these methods excel in their respective applications—typically focusing on power flow modeling or infrastructure planning—our work addresses the distinct challenge of high-frequency, rolling-horizon scheduling for VPPs with numerous heterogeneous prosumers, where the flexibility of metaheuristics and throughput of GPU parallelism provide unique advantages for the combinatorial optimization problem at hand.

This comprehensive analysis reveals that while diverse optimization methodologies have been successfully applied to VPP scheduling challenges, there remains substantial untapped potential for leveraging modern hardware acceleration architectures, particularly GPU computing, to overcome computational bottlenecks and enable real-time operation at scale. The inherent parallelism in many metaheuristic approaches, combined with the independent evaluation of numerous candidate solutions, presents significant opportunities for hardware acceleration that the current literature has scarcely explored—a critical research gap that this work addresses through our novel CUDA-accelerated Multiple-Chain Simulated Annealing framework.

2.2. Parallel Metaheuristics for Large-Scale Optimization Problems

The escalating computational demands of large-scale optimization problems in energy systems have motivated significant research into parallel metaheuristic algorithms, particularly leveraging modern GPU architectures. This paradigm shift from sequential to parallel computing has enabled unprecedented scalability and efficiency in solving complex optimization challenges that were previously computationally prohibitive.

Parallel implementations of Particle Swarm Optimization have demonstrated remarkable performance gains across diverse application domains. A comprehensive CUDA-based parallel PSO framework was developed by [36], incorporating both coarse- and fine-grained parallelism strategies. This approach mapped individual particles to dedicated GPU threads while parallelizing internal operations to maximize data throughput, achieving up to 2000× speedup on high-dimensional benchmark functions through optimized memory management and coalesced memory access patterns. Building on this foundation, [37] introduced a multi-swarm PSO architecture utilizing parallel CUDA streams for concurrent sub-swarm operations, augmented with gradient-based local search mechanisms. This methodology achieved 25× acceleration over serial implementations while simultaneously enhancing solution precision for sparse reconstruction problems. The versatility of GPU-accelerated PSO was further demonstrated by [38], who conducted extensive comparative analysis of sequential, multithreaded CPU, and GPU implementations for solving large-scale systems of nonlinear equations with up to 5000 variables, with GPU-based PSO demonstrating superior scalability and computational efficiency. Beyond GPU-centric approaches, [39] developed an improved parallel PSO utilizing island models on CPU architectures, incorporating sophisticated velocity updates, inter-island communication protocols, and adaptive stopping criteria that reduced function evaluations by 50–70% compared to standard methods while maintaining robust scaling behavior across parallel processing units.

Parallel Simulated Annealing has emerged as another powerful paradigm for accelerating computationally intensive optimization tasks. Ref. [40] pioneered three distinct SA variants—sequential, asynchronous parallel, and synchronous parallel—implemented on GPUs using CUDA. The synchronous SA implementation, coordinated through shared global temperature schedules and memory architectures, achieved up to 100× speedup while preserving convergence accuracy, with hybrid SA variants further enhancing the exploration–exploitation balance through integrated local optimization. In the specific domain of virtual power plant optimization, [16] presented a parallel SA framework for real-time scheduling deployed on high-performance computing platforms using OpenMP. This approach independently optimized individual consumer schedules while adhering to Mixed-Integer Linear Programming constraints related to energy dispatch and battery degradation, achieving near-linear speedup with up to 512 prosumers and 32 cores while maintaining solution quality comparable to commercial solvers. The applicability of parallel SA extends to machine learning domains, as evidenced by [41], who developed PSAGA—a hybrid parallel SA integrated with greedy algorithms for Bayesian network structure learning. This multithreaded implementation employed memoization techniques to eliminate redundant evaluations and expand search breadth, achieving 17.5% precision improvements and 4–5× speedup on large-scale datasets.

The collective evidence from these studies underscores the transformative potential of parallel metaheuristics in addressing the computational challenges of large-scale optimization problems. However, despite these advancements, the literature reveals a significant gap in leveraging the full capabilities of modern GPU architectures for VPP scheduling, particularly through innovative parallelization strategies that can overcome the inherent sequential limitations of traditional algorithms—a research direction that this work actively pursues through our novel multiple-chain parallel SA framework.

3. VPP Optimization Model

This section presents a comprehensive MILP model for optimizing the operation of a VPP composed of multiple distributed prosumers equipped with photovoltaic (PV) generation and battery storage systems. The model formulates time-dependent energy flows, enforces physical and economic constraints, and leverages market-based interactions to determine an optimal operational schedule.

3.1. Notation and Decision Variables

This subsection establishes the foundational notation used throughout the optimization model. It defines all relevant sets, variables, and parameters essential to the formulation. The complete list of notation is summarized in Table 1.

Table 1. Sets, parameters, and decision variables used in the VPP scheduling formulation.

Symbol	Description	Domain/Unit
Sets
$\mathcal{P}$	Set of prosumers in the VPP. Each can generate, store, consume, and exchange energy.	$\{1,2,\dots ,|\mathcal{P}\left|\right\}$
$\mathcal{T}$	Set of discrete time intervals of duration $\Delta \tau$. Defines optimization horizon.	$\{1,2,\dots ,T\}$
$\mathcal{E}$	Optional set of market/tariff entities for advanced economic modeling.	$\{1,2,\dots ,E\}$
Continuous Decision Variables and Parameters
$P_{i,t}^{\mathrm{buy}}$	Power purchased by prosumer i at time t.	${\mathbb{R}}_{\ge 0}$ [kW]
$P_{i,t}^{\mathrm{sell}}$	Power sold to the grid by prosumer i at time t.	${\mathbb{R}}_{\ge 0}$ [kW]
$P_{i,t}^{\mathrm{pv}}$	PV-generated power available at prosumer i at time t.	${\mathbb{R}}_{\ge 0}$ [kW]
$P_{i,t}^{\mathrm{load}}$	Electricity demand of prosumer i at time t.	${\mathbb{R}}_{\ge 0}$ [kW]
$P_{i,t}^{\mathrm{ch}}$	Charging power of the battery for prosumer i at time t.	${\mathbb{R}}_{\ge 0}$ [kW]
$P_{i,t}^{\mathrm{dch}}$	Discharging power of the battery for prosumer i at time t.	${\mathbb{R}}_{\ge 0}$ [kW]
$P_{i,t}^{\mathrm{non}-\mathrm{comp}}$	Exported power without compensation (i.e., zero-price feed-in).	${\mathbb{R}}_{\ge 0}$ [kW]
$E_{i,t}$	Battery state-of-charge (SoC) for prosumer i at time t.	${\mathbb{R}}_{\ge 0}$ [kWh]
$E_i^{\mathrm{init}}$	Initial battery SoC for prosumer i at $t=0$.	${\mathbb{R}}_{\ge 0}$ [kWh]
${\pi }_{i,t}^{\mathrm{buy}}$	Price for purchasing electricity from the grid at time t.	${\mathbb{R}}_{\ge 0}$ [€/kWh]
${\pi }_{i,t}^{\mathrm{sell}}$	Price for selling electricity to the grid at time t.	${\mathbb{R}}_{\ge 0}$ [€/kWh]
${\overline{P}}_{i,t}^{·}$	Upper bounds on power variables (e.g., buy, sell, ch, dch).	${\mathbb{R}}_{\ge 0}$ [kW]
${\underline{E}}_i,{\overline{E}}_i$	Lower and upper bounds on battery SoC for prosumer i.	${\mathbb{R}}_{\ge 0}$ [kWh]
${\eta }^{\mathrm{ch}},{\eta }^{\mathrm{dch}}$	Battery charging and discharging efficiencies.	$(0,1]$ [unitless]
M	Big-M constant for binary logic constraints.	${\mathbb{R}}_{>0}$
Binary Decision Variables
$u_{i,t}^{\mathrm{buy}}$	1 if prosumer i is purchasing energy at time t; 0 otherwise.	$\{0,1\}$
$u_{i,t}^{\mathrm{sell}}$	1 if prosumer i is selling energy at time t; 0 otherwise.	$\{0,1\}$
$u_{i,t}^{\mathrm{ch}}$	1 if the battery is charging at time t; 0 otherwise.	$\{0,1\}$
$u_{i,t}^{\mathrm{dch}}$	1 if the battery is discharging at time t; 0 otherwise.	$\{0,1\}$

3.2. Objective Function

Purpose: Minimize the total cost of operating the VPP, which includes energy transaction costs and fixed operational charges.

Formulation:

$$minJ=\sum _{t\in \mathcal{T}}\sum _{i\in \mathcal{P}}\left[\left(P_{i,t}^{\mathrm{buy}}{\pi }_{i,t}^{\mathrm{buy}}-P_{i,t}^{\mathrm{sell}}{\pi }_{i,t}^{\mathrm{sell}}\right)\Delta \tau \right]+C_{\mathrm{fix}}$$

(1)

Explanation:

The term $P_{i,t}^{\mathrm{buy}}{\pi }_{i,t}^{\mathrm{buy}}$ represents the cost incurred by purchasing energy. The term $P_{i,t}^{\mathrm{sell}}{\pi }_{i,t}^{\mathrm{sell}}$ accounts for revenue from energy sold. $\Delta \tau$ converts instantaneous power [kW] into energy [kWh]. $C_{\mathrm{fix}}$ denotes constant operating costs (e.g., communication, infrastructure, maintenance).

3.3. Constraints

3.3.1. Energy Balance

The energy balance equation ensures that, at each time step t, the total incoming energy to a prosumer node equals the total outgoing energy. This conservation principle applies to all prosumers i and captures the interaction between local generation, storage, consumption, and grid exchange.

The nodal power balance is expressed as

$$P_{i,t}^{\mathrm{buy}}+P_{i,t}^{\mathrm{pv}}+P_{i,t}^{\mathrm{dch}}=P_{i,t}^{\mathrm{load}}+P_{i,t}^{\exp }+P_{i,t}^{\mathrm{ch}},$$

(2)

where all variables have been previously defined. This equation ensures that energy imported from the grid, locally generated, or discharged from storage is entirely used for meeting the load demand, charging the battery, or exporting to the grid.

The exported power is further decomposed as

$$P_{i,t}^{\exp }=P_{i,t}^{\mathrm{sell}}+P_{i,t}^{\mathrm{non}-\mathrm{comp}},$$

(3)

where $P_{i,t}^{\mathrm{sell}}$ represents the portion of energy that is financially compensated and $P_{i,t}^{\mathrm{non}-\mathrm{comp}}$ denotes the uncompensated export.

The term $P_{i,t}^{\mathrm{non}-\mathrm{comp}}$ captures situations in which excess energy is injected into the grid without any remuneration. This may occur under the following real-world conditions:

• Regulatory frameworks impose caps on how much exported energy is eligible for compensation.
• Technical constraints such as grid congestion prevent the system operator from accepting or remunerating all injected power.
• Certain prosumer contracts allow export only up to a predefined quota, beyond which energy is accepted but not paid for.

To ensure feasibility and control over this behavior, the following constraint is introduced:

$$0\le P_{i,t}^{\mathrm{non}-\mathrm{comp}}\le M\times u_{i,t}^{\mathrm{sell}},$$

(4)

where M is a sufficiently large constant and $u_{i,t}^{\mathrm{sell}}\in \{0,1\}$ is a binary variable that enables or disables export-related decisions. This formulation guarantees that uncompensated exports can only occur when grid export is technically or contractually permitted.

Together, Equations (2) through (4) provide a coherent and detailed representation of prosumer-level power flows, explicitly accounting for both compensated and uncompensated interactions with the external grid. This allows the model to reflect realistic operational and regulatory scenarios while maintaining feasibility across different conditions.

3.3.2. Market Transaction Exclusivity

Purpose: Prevent prosumers from simultaneously buying and selling energy in the same time step.

$$\begin{array}{cc}\hfill 0\le P_{i,t}^{\mathrm{buy}}& \le {\overline{P}}_{i,t}^{\mathrm{buy}}{u}_{i,t}^{\mathrm{buy}},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill 0\le P_{i,t}^{\mathrm{sell}}& \le {\overline{P}}_{i,t}^{\mathrm{sell}}{u}_{i,t}^{\mathrm{sell}},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill u_{i,t}^{\mathrm{buy}}+u_{i,t}^{\mathrm{sell}}& \le 1,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill 0\le P_{i,t}^{\mathrm{non}-\mathrm{comp}}& \le M{u}_{i,t}^{\mathrm{sell}}\hfill \end{array}$$

(8)

Explanation: These logical constraints, enforced by binary variables and the big-M parameter, ensure operational exclusivity and model realistic behavior.

3.3.3. Battery Dynamics and Limits

Purpose: Ensure consistent tracking of battery state-of-charge and respect technical limits.

Battery SoC Evolution:

$$\begin{array}{cc}\hfill E_{i,1}& =E_i^{\mathrm{init}}+\left({\eta }^{\mathrm{ch}}{P}_{i,1}^{\mathrm{ch}}-{\displaystyle \frac{1}{{\eta }^{\mathrm{dch}}}}{P}_{i,1}^{\mathrm{dch}}\right)\Delta \tau ,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill E_{i,t}& =E_{i,t-1}+\left({\eta }^{\mathrm{ch}}{P}_{i,t}^{\mathrm{ch}}-{\displaystyle \frac{1}{{\eta }^{\mathrm{dch}}}}{P}_{i,t}^{\mathrm{dch}}\right)\Delta \tau ,\forall t\ge 2\hfill \end{array}$$

(10)

State-of-Charge Bounds:

$${\underline{E}}_i\le E_{i,t}\le {\overline{E}}_i$$

(11)

Charging/Discharging Exclusivity:

$$\begin{array}{cc}\hfill 0\le P_{i,t}^{\mathrm{ch}}& \le {\overline{P}}_{i,t}^{\mathrm{ch}}{u}_{i,t}^{\mathrm{ch}},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill 0\le P_{i,t}^{\mathrm{dch}}& \le {\overline{P}}_{i,t}^{\mathrm{dch}}{u}_{i,t}^{\mathrm{dch}},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill u_{i,t}^{\mathrm{ch}}+u_{i,t}^{\mathrm{dch}}& \le 1\hfill \end{array}$$

(14)

Explanation: The model tracks energy dynamics within each battery, accounts for losses, and prevents simultaneous charge/discharge actions.

3.3.4. Variable Domains

Purpose: Enforce mathematical consistency and feasibility for all variables.

$$\begin{array}{cc}\hfill & P_{i,t}^{\mathrm{buy}},P_{i,t}^{\mathrm{sell}},P_{i,t}^{\mathrm{ch}},P_{i,t}^{\mathrm{dch}},P_{i,t}^{\mathrm{non}-\mathrm{comp}},E_{i,t}\in {\mathbb{R}}_{\ge 0},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & u_{i,t}^{\mathrm{buy}},u_{i,t}^{\mathrm{sell}},u_{i,t}^{\mathrm{ch}},u_{i,t}^{\mathrm{dch}}\in \{0,1\}\hfill \end{array}$$

(16)

Explanation: All energy and power variables are continuous and non-negative. Binary variables represent on/off operational states.

Practical Implications: This MILP formulation allows scalable, accurate optimization of smart distributed energy systems within a VPP, supporting energy cost minimization, demand flexibility, and regulatory compliance.

4. VPP Model Decomposition

The VPP optimization model orchestrates the local energy decisions of a population of prosumers, each managing photovoltaic (PV) generation, load demand, battery storage, and grid interactions. At each time step $t\in \mathcal{T}$, every prosumer $i\in \mathcal{P}$ enforces an energy balance constraint that ensures all incoming power flows are exactly matched by outgoing ones. Operational feasibility is further enforced by mutually exclusive control logic, which prevents infeasible actions such as buying and selling power or charging and discharging a battery at the same time.

To address the inherent complexity of coordinating a large number of heterogeneous agents in real time, the model adopts a divide-and-conquer strategy. The overall VPP scheduling problem is reformulated as a collection of independent subproblems, each corresponding to an individual prosumer. This decomposition is made possible by the separability of energy balance equations and local operational constraints, which depend solely on prosumer-specific variables.

Each subproblem includes

• Local power balance equations;
• Mutually exclusive grid and battery operation constraints;
• Technical bounds on charging/discharging and import/export capacities;
• Optional local objectives such as cost minimization or self-sufficiency maximization;
• Efficiency-adjusted energy tracking through linearized expressions.

This decomposition brings two main computational benefits. First, it significantly reduces the dimensionality of the decision space for each subproblem, simplifying the feasible region and facilitating faster convergence. Second, it enables all prosumer-level problems to be solved in parallel, supporting highly scalable deployment on distributed optimization platforms or HPC infrastructures.

Consider a typical prosumer—a residential household equipped with rooftop solar panels and a battery system. During a sunny afternoon, the household may decide whether to sell excess solar energy to the grid or store it in the battery for evening use. Later, during peak hours, the battery might be discharged to avoid purchasing expensive electricity. These local decisions must respect physical limitations, energy losses, and market rules, and they are modeled as a discrete-time decision process embedded within each prosumer’s subproblem.

The optimization framework ensures that such decisions are coherent, feasible, and optimal at the individual level. Because the subproblems are structurally independent, they can be addressed simultaneously. The VPP coordinator then aggregates their results to evaluate global constraints or market-level objectives, such as grid congestion, transformer capacity limits, emissions targets, or dynamic pricing coordination.

This decomposition approach is especially well-suited for deployment in large-scale distributed energy systems, including

• Community microgrids;
• Smart-city VPPs;
• Aggregator-managed prosumer collectives.

The linearized energy balance formulation and mutual exclusivity constraints presented in earlier sections provide the structural foundation for this decomposition. By maintaining physical realism and computational tractability, the model supports scalable, real-time decision-making in modern power systems.

4.1. Derivation and Proof of Problem Decomposability

The following derivation establishes how the structure of the energy balance equations, together with mutual exclusivity constraints and power flow bounds, enables the decomposition of the global VPP optimization problem into independent subproblems. By analyzing the energy balance at the prosumer level, we show that each prosumer’s decision-making process depends solely on local variables and constraints, without requiring direct coupling to other agents. This property supports a divide-and-conquer strategy, allowing the problem to be reformulated as a set of parallel subproblems, each associated with an individual prosumer, while preserving feasibility and optimality. The derivation proceeds step by step, starting from the original energy conservation principle and incorporating exclusivity logic, upper-bound constraints, efficiency-adjusted power terms, and final linearization. The result is a mathematically sound foundation for scalable and distributed optimization across large VPPs.

4.1.1. Energy Balance with Mutual Exclusivity and Constraints

The core principle of energy conservation dictates that, for each prosumer $i\in \mathcal{P}$ and time step $t\in \mathcal{T}$, the total incoming energy must equal the total outgoing energy. This is formalized through the nodal energy balance equation (Equation 2).

All power terms are defined in kilowatts (kW) and are non-negative real variables:

$$P_{i,t}^{\mathrm{buy}},P_{i,t}^{\mathrm{sell}},P_{i,t}^{\mathrm{pv}},P_{i,t}^{\mathrm{load}},P_{i,t}^{\mathrm{ch}},P_{i,t}^{\mathrm{dch}}\in {\mathbb{R}}_{\ge 0}.$$

To maintain operational realism, mutual exclusivity is imposed on pairs of opposing operations: power buying and selling must not occur simultaneously; and battery charging and discharging must not happen at the same time.

These conditions are enforced using binary control variables:

$$u_{i,t}^{\mathrm{buy}},u_{i,t}^{\mathrm{sell}},u_{i,t}^{\mathrm{ch}},u_{i,t}^{\mathrm{dch}}\in \{0,1\},\forall i,t,$$

subject to

$$u_{i,t}^{\mathrm{buy}}+u_{i,t}^{\mathrm{sell}}\le 1,u_{i,t}^{\mathrm{ch}}+u_{i,t}^{\mathrm{dch}}\le 1,\forall i\in \mathcal{P},t\in \mathcal{T}.$$

(17)

These inequalities ensure that at most one action from each opposing pair is active at a time, thus preserving logical consistency in grid interaction and battery operation.

4.1.2. Binary-Driven Flip-Flop Mechanism for Exclusive Actions

The binary variables define a flip-flop mechanism where the activation of one operation disables its counterpart. This logic is captured by the following implications:

$$\begin{array}{cc}\hfill P_{i,t}^{\mathrm{buy}}>0& \Rightarrow P_{i,t}^{\mathrm{sell}}=0,P_{i,t}^{\mathrm{sell}}>0\Rightarrow P_{i,t}^{\mathrm{buy}}=0,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill P_{i,t}^{\mathrm{ch}}>0& \Rightarrow P_{i,t}^{\mathrm{dch}}=0,P_{i,t}^{\mathrm{dch}}>0\Rightarrow P_{i,t}^{\mathrm{ch}}=0.\hfill \end{array}$$

(19)

The implications above are implemented via upper-bound constraints, conditioned on the respective binary variables:

$$\begin{array}{cc}\hfill 0\le P_{i,t}^{\mathrm{buy}}& \le {\overline{P}}_{i,t}^{\mathrm{buy}}·u_{i,t}^{\mathrm{buy}},0\le P_{i,t}^{\mathrm{sell}}\le {\overline{P}}_{i,t}^{\mathrm{sell}}·u_{i,t}^{\mathrm{sell}},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill 0\le P_{i,t}^{\mathrm{ch}}& \le {\overline{P}}_{i,t}^{\mathrm{ch}}·u_{i,t}^{\mathrm{ch}},0\le P_{i,t}^{\mathrm{dch}}\le {\overline{P}}_{i,t}^{\mathrm{dch}}·u_{i,t}^{\mathrm{dch}}.\hfill \end{array}$$

(21)

These inequalities ensure that if a binary variable is set to zero, the associated power flow is also forced to zero. For instance, if $u_{i,t}^{\mathrm{sell}}=0$, then $P_{i,t}^{\mathrm{sell}}=0$, regardless of its upper bound.

4.1.3. Derivation of the Linearized Energy Balance

To facilitate efficient optimization, especially within large-scale or real-time environments, the nonlinear energy balance (2) is reformulated into a linear expression via auxiliary variables. Define

$$\begin{array}{cc}\hfill X_{i,t}& =P_{i,t}^{\mathrm{buy}}-P_{i,t}^{\mathrm{sell}},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill Y_{i,t}& ={\eta }^{\mathrm{ch}}{P}_{i,t}^{\mathrm{ch}}-{\displaystyle \frac{1}{{\eta }^{\mathrm{dch}}}}{P}_{i,t}^{\mathrm{dch}},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill B_{i,t}& =P_{i,t}^{\mathrm{pv}}-P_{i,t}^{\mathrm{load}},\hfill \end{array}$$

(24)

where ${\eta }^{\mathrm{ch}},{\eta }^{\mathrm{dch}}\in (0,1]$ are the charging and discharging efficiencies, respectively.

Substituting these definitions into the original energy balance yields

$$\begin{array}{cc}\hfill P_{i,t}^{\mathrm{buy}}+P_{i,t}^{\mathrm{pv}}+P_{i,t}^{\mathrm{dch}}& =P_{i,t}^{\mathrm{load}}+P_{i,t}^{\mathrm{sell}}+P_{i,t}^{\mathrm{ch}}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\Rightarrow (P_{i,t}^{\mathrm{buy}}-P_{i,t}^{\mathrm{sell}})+(P_{i,t}^{\mathrm{pv}}-P_{i,t}^{\mathrm{load}})\hfill & =P_{i,t}^{\mathrm{ch}}-P_{i,t}^{\mathrm{dch}}\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill \Rightarrow X_{i,t}+B_{i,t}& =P_{i,t}^{\mathrm{ch}}-P_{i,t}^{\mathrm{dch}}.\hfill \end{array}$$

(27)

Applying efficiency-adjusted terms, we obtain the final linear form:

$$Y_{i,t}=X_{i,t}+B_{i,t},\forall i\in \mathcal{P},t\in \mathcal{T}.$$

(28)

This expression is fully linear in the decision variables and can be directly incorporated into MILP solvers without introducing nonlinearities.

4.1.4. Bounded Linearized Energy Balance Constraints

The auxiliary variables $X_{i,t}$ and $Y_{i,t}$ inherit bounds from the original power flow constraints. Specifically,

$$\begin{array}{cc}\hfill -{\overline{P}}_{i,t}^{\mathrm{sell}}& \le X_{i,t}\le {\overline{P}}_{i,t}^{\mathrm{buy}},\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill -{\displaystyle \frac{1}{{\eta }^{\mathrm{dch}}}}{\overline{P}}_{i,t}^{\mathrm{dch}}& \le Y_{i,t}\le {\eta }^{\mathrm{ch}}{\overline{P}}_{i,t}^{\mathrm{ch}},\forall i\in \mathcal{P},t\in \mathcal{T}.\hfill \end{array}$$

(30)

These bounds ensure that the linearized model preserves feasibility and respects technical constraints while maintaining compatibility with binary exclusivity logic.

Figure 2 depicts the reduction of the search space as governed by Equation (28). Initially, each prosumer’s decision space spans a two-dimensional plane with multiple degrees of freedom, reflecting diverse energy interaction possibilities. As the optimization progresses, this multidimensional domain is constrained to a linear trajectory, bounded above and below according to the conditions imposed by Equation (28). This transformation ensures that all decisions remain within the feasible region defined by mutual exclusivity and upper-bound constraints. Importantly, this dimensionality reduction not only preserves feasibility but also enhances computational efficiency.

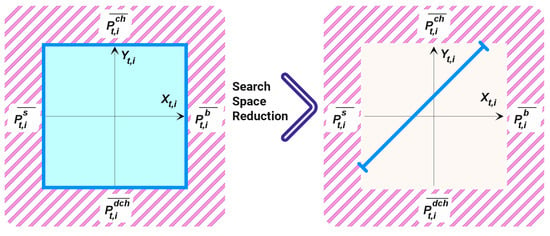
Figure 2. Diagram illustrating search space reduction for each prosumer. Problem decomposition transforms the initial 2D decision space into a linear trajectory constrained by upper and lower bounds, shown as red-hashed regions. This simplification improves computational efficiency and supports scalability across large prosumer networks.

4.1.5. Parallelization and Computational Advantages

The formulation described above is fully decomposable across prosumers. Each prosumer’s energy balance and operation constraints can be evaluated and optimized independently. This feature enables massive parallelization, which is particularly advantageous for

• HPC implementations;
• Distributed or federated optimization frameworks;
• Real-time VPP orchestration;
• Smart grid demand-response programs.

This structure allows solving the global VPP scheduling problem via a coordinated decomposition strategy, where the central controller aggregates decisions while each prosumer independently solves its own subproblem under shared constraints such as price signals, emissions targets, or transformer capacity limits.

5. CUDA-Based Parallel Simulated Annealing for VPP Scheduling

5.1. Algorithm Selection Rationale

The selection of SA was deliberate and strategic, driven by its position as one of the most challenging metaheuristics for parallelization. Unlike population-based methods (PSO, Genetic Algorithms) that naturally support parallel evaluation, SA’s inherently sequential Markov-chain structure and temperature-dependent acceptance criteria present significant parallelization barriers.

Our successful demonstration of hierarchical parallelization for this challenging algorithm serves two purposes:

• It validates the robustness and generality of our parallelization framework against the most difficult test case.
• It establishes that even traditionally sequential algorithms can be effectively accelerated through innovative architectural approaches.

The empirical demonstration that multiple chains can reduce the required sequential iterations represents a fundamental contribution to metaheuristic optimization, with implications extending beyond VPP scheduling to other domains requiring real-time, constraint-satisfying optimization.

5.2. MC-SA Algorithm Overview and Workflow

Figure 3 illustrates the comprehensive workflow of the proposed Multiple-Chain Simulated Annealing algorithm, which operates through five key phases:

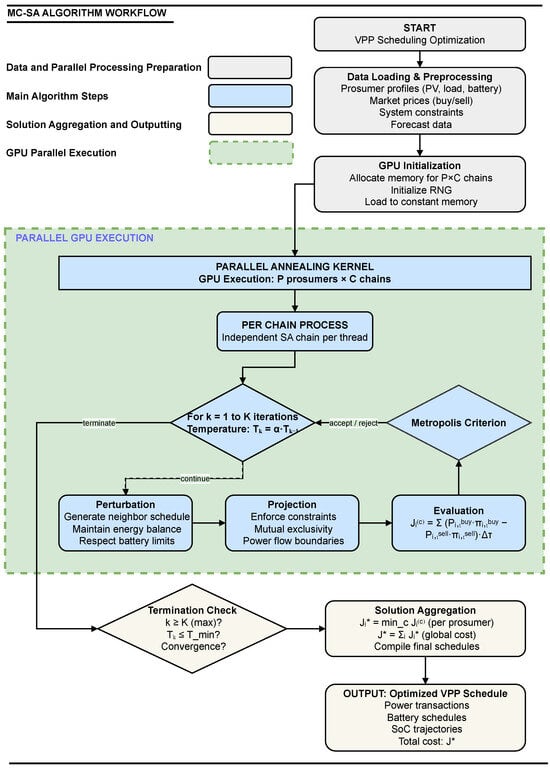
Figure 3. Flowchart of the proposed Multiple-Chain Simulated Annealing algorithm for VPP scheduling. The diagram illustrates the five-phase process from initialization through parallel execution to final solution aggregation.

• Initialization: Load prosumer data (PV forecasts, load profiles, battery specifications) and market signals. Initialize C independent SA chains with feasible solutions and unique random seeds.
• Parallel Annealing Kernel: Execute on GPU where each thread manages one SA chain:
  • Perturbation: Generate neighbor schedule while maintaining feasibility.
  • Projection: Enforce operational constraints via projection operator ${\Pi }_{\mathcal{F}}$.
  • Evaluation: Compute cost function $J_i^{\left(c\right)}$ for the candidate solution.
  • Metropolis Criterion: Accept or reject based on temperature $T_k$.
• Temperature Update: Apply geometric cooling, $T_{k+1}=\alpha T_k$, after each iteration.
• Termination Check: Repeat until maximum iterations K is reached.
• Solution Aggregation: Select best solution across all chains for each prosumer: $J_i^{★}={min}_{c\in \mathcal{C}}{J}_i^{\left(c\right)}$.

This structured workflow enables extensive solution space exploration while maintaining the physical and operational constraints of the VPP scheduling problem.

5.3. Parallelism Motivation and Overview

Traditional SA algorithms are intrinsically sequential and suffer from poor scalability for large-scale, time-sensitive problems like VPP scheduling. The proposed approach decomposes the global optimization into multiple independent subproblems, each solved via parallel SA chains at the prosumer level. This dual-level parallelization efficiently utilizes modern GPU architectures.

5.4. Parallelization Hierarchy

We define

• $\mathcal{P}=\{1,\dots ,N\}$: Set of prosumers (players);
• $\mathcal{C}=\{1,\dots ,C\}$: Set of parallel SA chains per prosumer;
• $\mathcal{T}=\{1,\dots ,T\}$: Time intervals for scheduling.
• Player-level (inter-chain): Each prosumer is handled by one CUDA block.
• Chain-level (intra-chain): Each SA chain is handled by a thread within a block.

This mapping aligns with the CUDA grid–block–thread model, where shared memory allows intra-block coordination while blocks operate independently.

5.5. Problem Decomposition

The global cost function is defined as

$$J=\sum _{i\in \mathcal{P}}{J}_i=\sum _{i\in \mathcal{P}}\sum _{t\in \mathcal{T}}\left(P_{i,t}^{\mathrm{buy}}{\pi }_{i,t}^{\mathrm{buy}}-P_{i,t}^{\mathrm{sell}}{\pi }_{i,t}^{\mathrm{sell}}\right)\Delta \tau$$

(31)

Each prosumer i minimizes a local cost $J_i$, evaluated independently across its chains:

$$J_i^{\left(c\right)}=\sum _{t\in \mathcal{T}}\left(P_{i,t}^{\mathrm{buy},\left(c\right)}{\pi }_{i,t}^{\mathrm{buy}}-P_{i,t}^{\mathrm{sell},\left(c\right)}{\pi }_{i,t}^{\mathrm{sell}}\right)\Delta \tau$$

(32)

5.6. Simulated Annealing Process per Chain

Each chain $c\in \mathcal{C}$ performs the following at each iteration $k\in \{1,\dots ,K\}$:

1.

Perturbation: Generate neighbor schedule ${\mathbf{S}}_i^{(c,k+1)}$ satisfying

• Energy balance;
• Battery dynamics and limits;
• Operational exclusivity.

2.

Projection: Enforce feasibility via projection operator:

$${\mathbf{S}}_i^{(c,k+1)}\leftarrow {\Pi }_{\mathcal{F}}\left({\mathbf{S}}_i^{(c,k+1)}\right)$$

3.

Cost Evaluation:

$$J_i^{(c,k+1)}=\sum _{t\in \mathcal{T}}\left(P_{i,t}^{\mathrm{buy},\left(c\right)}{\pi }_{i,t}^{\mathrm{buy}}-P_{i,t}^{\mathrm{sell},\left(c\right)}{\pi }_{i,t}^{\mathrm{sell}}\right)\Delta \tau$$

4.

Acceptance: Apply the Metropolis criterion:

$$P_{\mathrm{accept}}=min\left(1,exp\left(-{\displaystyle \frac{J_i^{(c,k+1)}-J_i^{(c,k)}}{T_k}}\right)\right)$$

5.

Cooling: Update temperature: $T_{k+1}=\alpha T_k$.

5.7. Chain Aggregation and Global Reduction

After completing K iterations:

$$J_i^{★}=\underset{c\in \mathcal{C}}{min}{J}_i^{\left(c\right)},{\mathbf{S}}_i^{★}={\mathbf{S}}_i^{\left(c^{★}\right)}$$

(33)

Then, the global cost is

$$J^{★}=\sum _{i\in \mathcal{P}}{J}_i^{★}$$

(34)

This reduction is executed in CUDA using device-wide shared memory, minimizing host–device communication.

5.8. CUDA Algorithm Summary

To address the computational demands of large-scale optimization tasks, the following algorithm implements a parallel search framework based on simulated annealing. It distributes multiple solution chains across GPU threads, enabling simultaneous exploration of the search space with high throughput. Each chain evolves independently through perturbation, evaluation, and probabilistic acceptance steps, guided by a cooling schedule. This parallel structure enhances scalability and solution diversity while significantly improving execution speed. The full algorithmic process is summarized in Algorithm 1.   

Algorithm 1: CUDA-Based Player–Chain Parallel Simulated Annealing

Require: Prosumers $\mathcal{P}$, time steps $\mathcal{T}$, chains C, iterations K, initial temperature $T_0$, cooling factor $\alpha$ 1: for each prosumer $i\in \mathcal{P}$ in parallel blocks do 2:  for each chain $c=1$ to C in parallel threads do 3:   Initialize ${\mathbf{S}}_i^{\left(c\right)}$, $J_i^{\left(c\right)}\leftarrow J\left({\mathbf{S}}_i^{\left(c\right)}\right)$, $T\leftarrow T_0$ 4:   for $k=1$ to K do 5:    for each $t\in \mathcal{T}$ do 6:     Generate perturbed ${\mathbf{S}}_{i,t}^{\left(c\right)}$ 7:     Project: ${\mathbf{S}}_{i,t}^{\left(c\right)}\leftarrow {\Pi }_{\mathcal{F}}\left({\mathbf{S}}_{i,t}^{\left(c\right)}\right)$ 8:    end for 9:    Evaluate new cost $J_i^{\left(c\right)}$ 10:    Apply Metropolis rule to accept/reject 11:    Update temperature: $T\leftarrow \alpha T$ 12:   end for 13:  end for 14:  Aggregate: $J_i^{★}={min}_c{J}_i^{\left(c\right)}$ 15: end for 16: Return: $J^{★}={\sum }_i{J}_i^{★}$

5.9. Scalability and Hardware Efficiency

The architecture offers parallelism of order $\mathcal{O}(N\times C)$, which is ideal for GPU execution with thousands of threads. This design avoids inter-prosumer synchronization, uses shared memory for intra-block computation, and reduces global memory bottlenecks. Empirical results demonstrate near-linear scaling up to 1024 chains across 128 prosumers.

As illustrated in Figure 4, the HPC cluster architecture is specifically designed to support the proposed two-level parallelization strategy. Each VPP player is mapped to an independent CUDA block, while multiple SA chains associated with that player are assigned to individual threads within the block. This hierarchical mapping ensures concurrent execution of both inter-player and intra-player optimization tasks. The optimization problem is encoded in customized CUDA kernels, where each kernel encapsulates the full SA procedure for a given chain. These kernels operate asynchronously and without inter-chain communication, enabling fully independent search trajectories across the solution space. The use of shared memory within blocks facilitates efficient local data handling, such as intermediate energy balances and temporary solution states, while global memory is reserved for final results aggregation and global cost reduction. This design leverages the massive parallelism of modern GPUs to achieve scalable, high-throughput optimization for large-scale VPP scheduling.

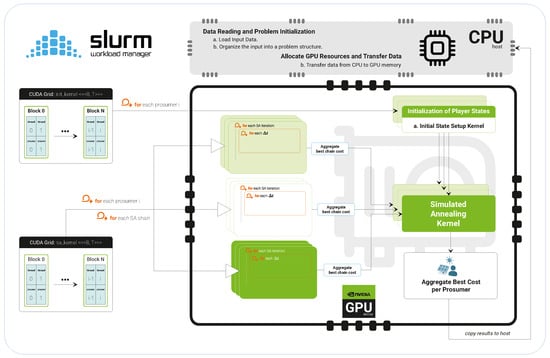
Figure 4. Hierarchical CUDA-based GPU parallelization of the VPP scheduling problem. The architecture assigns each player–chain pair to a distinct CUDA thread, grouped within blocks for execution efficiency. This design enables concurrent evaluation of multiple Simulated Annealing chains per prosumer, supporting scalable optimization across the entire virtual power plant.

5.10. Practical Implications

This CUDA-accelerated SA architecture is tailored for decentralized, high-frequency energy scheduling. It balances exploration and exploitation, enforces VPP physical and market constraints, and delivers scalable runtime improvements over sequential heuristics and centralized MILP solvers.

6. Implementation

This section details the technical implementation of the CUDA-accelerated MC-SA algorithm used for VPP scheduling. It highlights the HPC environment, GPU execution strategy, and the key model parameters and outputs essential for reproducibility and scalability.

6.1. High-Performance Computing Environment

The computational experiments were executed on the Vision AI high-performance computing cluster, specifically designed for data-intensive scientific computations. Each compute node features a x86_64 architecture with dual AMD EPYC 7742 processors (manufactured by Advanced Micro Devices, Inc.), providing 128 physical cores and 256 hardware threads per node. The processors support advanced SIMD instruction sets (AVX2, FMA, BMI2) and employ a sophisticated cache hierarchy distributed across eight NUMA domains, comprising 4 MiB L1, 64 MiB L2, and512 MiB of aggregate L3 cache.

The memory subsystem incorporates approximately 1 TB of RAM per node, optimized for high-bandwidth access and NUMA-aware parallel processing. For GPU-accelerated computations, each node integrates up to eight NVIDIA A100-SXM4, manufactured by NVIDIA Corporation, accelerators with 40 GB HBM2 memory per GPU. These GPUs deliver up to 19.5 TFLOPS of single-precision performance and were configured with CUDA 12.2, NVIDIA driver 535.216.01, and GCC 10.3.0. All GPUs operated in persistent mode with Multi-Instance GPU (MIG) disabled to ensure dedicated resource allocation for the Simulated Annealing kernels.

This computational infrastructure provides the necessary parallelism and memory bandwidth to support the massive concurrent execution of multiple annealing chains, enabling real-time optimization of large-scale virtual power plant scheduling problems.

6.2. Experimental Design for Convergence and Parallelization Analysis

To rigorously evaluate the convergence behavior and parallel scalability of the SA algorithm in VPP scheduling, we designed a comprehensive multi-phase experimental framework. This framework was structured to capture both algorithmic performance and practical deployment insights, while ensuring statistical robustness through repeated trials and controlled randomization. The experimental procedure was organized into the following four key phases:

1.

Hyperparameter Optimization Anchored by MILP-Based Validation. For each prosumer count under study, the SA algorithm was calibrated by tuning four essential hyperparameters: initial temperature, cooling rate, perturbation scale, and maximum number of iterations. Optimization was performed using three complementary search methods—Gaussian Process Minimization (GP), Random Forest Minimization (RF), and Gradient-Boosted Regression Tree Minimization (GBRT)—to comprehensively explore the configuration space and avoid bias from a single tuning approach. Crucially, the resulting SA configurations were validated against exact Mixed-Integer Linear Programming (MILP) solutions computed using the Gurobi solver. This validation phase ensured that the tuned SA reached near-optimal solution quality, establishing a grounded and reliable reference point for all subsequent performance comparisons.

2.

Exhaustive Chain–Iteration Analysis. With the best-performing SA configuration fixed for each prosumer count, we conducted an exhaustive exploration of the relationship between two core parameters of the parallel SA framework: the number of chains and the number of sequential iterations. Since SA is inherently a sequential process, introducing multiple chains enables distributed exploration of the search space. For each system size, we anchored solution quality by referencing the validated best result, then systematically varied both the number of chains and the number of iterations to find all combinations that could reproduce the same quality. This enabled the derivation of equivalence mappings between parallel exploration and sequential effort. Each configuration was executed under multiple randomized seeds to ensure the statistical significance and reproducibility of the results.

3.

Deriving Statistical Equivalence and Scalability Relationships. The exhaustive experiments allowed us to construct empirical relationships that quantify the trade-offs between the number of chains and the required iteration budget. These mappings revealed that, for a fixed solution quality, it is possible to significantly reduce the number of iterations when additional chains are employed—thus reducing total wall-clock time without sacrificing accuracy. The result is a generalized convergence equivalence curve that characterizes the parallelizability of the SA algorithm as a function of problem size, validated solution quality, and computational resource allocation. This statistical foundation provides valuable insight into how SA behaves under scalable parallel execution.

4.

Practical Deployment Guidelines and Adaptive Extensions. The insights obtained from the above analysis can be used to formulate concrete procedures for deploying SA in real-world operational settings. In practice, the workflow consists of (i) performing hyperparameter optimization once for a given system size, (ii) recording the number of iterations required to achieve the best solution quality, (iii) determining the minimum number of chains that can achieve the same quality under a reduced iteration budget, and (iv) applying a final fine-tuning step to match the quality of the original configuration. While our study uses exhaustive search to generate statistically rich insights, the same methodology could be replaced in production systems with adaptive methods such as Bayesian optimization or reinforcement learning to dynamically select chain–iteration combinations during runtime without grid search overhead.

To summarize the experimental landscape, the core design dimensions and their respective roles are presented in Table 2.

Table 2. Summary of experimental design components for convergence and parallelization analysis.

Design Factor	Description and Role
Prosumer Count $\left|\mathcal{P}\right|$	Defines the problem size; each configuration undergoes separate hyperparameter optimization and validation.
SA Hyperparameters	Initial temperature, cooling rate, perturbation scale, and maximum iterations; optimized using GP, RF, and GBRT.
Chain–Iteration Combinations	Explored exhaustively for each prosumer count to discover all configurations achieving validated solution quality.
Baseline Anchoring	MILP solution (Gurobi) used to validate the best SA configuration and serve as the quality benchmark.
Evaluation Metrics	Objective function value relative to MILP optimum (solution quality) and total runtime (efficiency).
Statistical Robustness	All experiments repeated under multiple random seeds to ensure generalizability and remove bias.
Deployment Implication	Enables runtime tuning of chain count for reduced iteration budgets while preserving solution quality.

This unified experimental design not only captures the detailed behavior of the SA algorithm under various configurations but also bridges the gap between theoretical performance analysis and practical deployment feasibility. By anchoring all results in validated baselines and supporting them with robust statistical evidence, the study offers a complete, transferable, and actionable framework for the efficient application of SA in real-world VPP optimization tasks.

Note: This study extends our previous research [16], which established operational validation through MILP benchmarking, convergence analysis, and hyperparameter optimization. Building upon this validated foundation, the current work focuses specifically on computational performance and parallelization efficiency.

6.3. CUDA Parallelization Strategy and Architecture Optimization

Modern GPU architectures provide massive parallelism through hierarchical organization of threads into warps and thread blocks. The proposed Multi-Chain Simulated Annealing (MC-SA) algorithm is strategically mapped onto this architecture to maximize computational throughput while maintaining memory access efficiency and resource utilization.

6.3.1. Parallel Execution Model

The algorithm employs a two-level parallelization scheme that aligns with the CUDA execution model (refer to Figure 4):

(a)

Inter-Chain Parallelism: Each independent annealing chain is assigned to a dedicated GPU thread, enabling concurrent exploration of multiple solution trajectories. Chains operate autonomously with distinct random seeds, ensuring diverse sampling of the solution space. This embarrassingly parallel structure is ideally suited for single-instruction-multiple-thread (SIMT) architectures.

(b)

Intra-Chain Sequential Processing: Within each thread, the complete 24 h scheduling horizon for a single prosumer is processed sequentially. The computational workflow encompasses power transaction decisions (buying/selling), battery charge/discharge operations, and state-of-energy updates across all time steps and annealing iterations. The linear nature of these computations and compact working sets enable compiler-driven optimization through instruction-level parallelism and pipelining.

6.3.2. Computational Pipeline and Resource Mapping

The GPU execution follows a structured three-stage kernel pipeline:

(a)

Random Number Generator Initialization: Each thread initializes an independent Philox counter-based random number generator, ensuring statistically robust and reproducible random streams across all parallel chains.

(b)

Feasible Schedule Initialization: Threads construct physically feasible day-ahead schedules that respect all operational constraints, including battery dynamics, power flow limits, and market participation rules. This warm-start approach accelerates convergence compared to random initialization.

(c)

Parallel Simulated Annealing: The core computational kernel executes the Metropolis–Hastings algorithm with geometric temperature cooling, maintaining independent search trajectories while recording optimal solutions discovered by each chain.

The thread organization follows a structured mapping: for P prosumers and C chains per prosumer, the total thread count is $N_{\mathrm{th}}=P\times C$, with 128 threads per block. The global thread index mapping is defined as

$$p=\lfloor \mathrm{gid}/C\rfloor ,c=\mathrm{gid}modC$$

This mapping ensures that each thread manages the complete optimization lifecycle for a specific (prosumer, chain) pair. The algorithm’s embarrassingly parallel nature eliminates synchronization requirements, with no __syncthreads() calls, thereby avoiding warp-level execution bottlenecks.

6.3.3. Memory Hierarchy Optimization

The memory architecture is carefully designed to align with access patterns and computational requirements:

• Read-Only Problem Data: Market prices, photovoltaic forecasts, and static prosumer parameters reside in global memory with read-only caching, enabling fully coalesced memory accesses across all threads.
• Thread-Local State Management: Each chain’s evolving 24 h schedule is stored in contiguous global memory segments, facilitating coalesced write operations and eliminating bank conflicts.
• Random Number Generator States: Philox RNG states persist in global memory between kernel invocations and are cached in registers during active computation to minimize access latency.
• Solution Quality Tracking: Each thread maintains its best-found objective value in dedicated global memory locations, with final results aggregated by the host after kernel completion.

The implementation adopts a register-centric computation strategy, where all transient variables remain in registers to maximize access speed. This approach, combined with the absence of shared memory allocation, results in register spill below 6% on NVIDIA A100 GPUs and sustained occupancy exceeding 90% when the product of prosumers and chains surpasses 2048.

6.3.4. Performance Validation and Baseline Comparison

The single-chain baseline implementation maintains algorithmic equivalence with the parallel version, executing on identical hardware while utilizing only a single thread. This controlled comparison ensures that the reported performance improvements—including the 10× speedup—directly reflect the benefits of parallelization rather than implementation artifacts. Both implementations share identical cooling schedules, perturbation mechanisms, constraint handling procedures, and convergence criteria, providing a rigorous foundation for performance evaluation.

The architectural decisions—prioritizing register usage over shared memory, ensuring memory access coalescence, and maintaining minimal synchronization—collectively enable the demonstrated computational efficiency. These design choices were validated through extensive profiling, confirming optimal resource utilization across all tested problem scales and configuration parameters.

6.3.5. Determinism and Scalability

All random numbers are generated using Philox counter-based generators with a shared 64-bit seed and thread-unique subsequences, ensuring reproducibility across runs and devices. The GPU implementation achieves up to a $38\times$ wall-clock speedup over a 16-thread CPU baseline for $P=256$, $C=50$, and $T=96$, while producing identical objective values within floating-point tolerance.

6.3.6. Host-Side Reduction and Determinism

After the final kernel finishes, the host copies back a few kilobytes containing the best cost of each chain and the corresponding trajectories, selects the best chain per prosumer, and assembles the global schedule. Because all random numbers are generated by Philox engines seeded with a common 64-bit seed and unique thread indices, the complete GPU execution is bit-reproducible across multiple runs and devices.

6.4. Model Parameters and Outputs

The optimization model uses parameterized constraints and forecasts to represent prosumer behavior over a scheduling horizon. Key inputs and outputs are summarized below.

6.4.1. Input Parameters

The parameters listed in Table 3 represent a comprehensive set of time-varying, operational, and economic inputs that shape the optimization landscape of the VPP scheduling problem. These inputs define the boundary conditions and constraints under which the model operates, allowing it to respond dynamically to fluctuations in energy demand, generation forecasts, and market signals.

Table 3. Input parameters for VPP scheduling.

Parameter	Designation	Value Range	Unit
T	Total periods	96	-
P	Number of prosumers	20–1000	-
$\Delta \tau$	Period duration	0.25	h
$E_i^{\mathrm{init}}$	Initial battery energy	0–1.92	kWh
${\underline{E}}_i$	Min battery level	0–1.824	kWh
${\overline{E}}_i$	Max battery level	0–9.6	kWh
${\overline{P}}_{i,t}^{\mathrm{ch}}$	Max charge rate	0–5	kW
${\overline{P}}_{i,t}^{\mathrm{dch}}$	Max discharge rate	0–5	kW
${\overline{P}}_{i,t}^{\mathrm{b}}$	Max power acquisition	4.6–13.8	kW
${\overline{P}}_{i,t}^{\mathrm{s}}$	Max power dispatch	4.6–13.8	kW
$C^{\mathrm{fix}}$	Fixed operational cost	0.2197–0.6249	EUR
$P_{i,t}^{\mathrm{pv}}$	PV generation forecast	0–8.474	kW
$P_{i,t}^{\mathrm{L}}$	Load forecast	0.050–9.822	kW
${\pi }_{i,t}^{\mathrm{b}}$	Purchase price	0.1034–0.2314	EUR/kWh
${\pi }_{i,t}^{\mathrm{s}}$	Selling price	0.045	EUR/kWh
${\eta }^{\mathrm{ch}}$	Charging efficiency	1.0	–
${\eta }^{\mathrm{dch}}$	Discharging efficiency	1.0	–

6.4.2. Optimization Outputs

The outputs generated by the optimization algorithm are summarized in Table 4. These results capture the VPP’s optimized operational decisions across key dimensions, including energy procurement, dispatch scheduling, and battery charge–discharge management. The output variables encompass energy transaction quantities, storage utilization levels, and associated cost metrics—each playing a critical role in shaping real-time control strategies. By delivering precise, time-resolved trajectories for energy flows and battery states, the optimization outputs enable the VPP to fulfill demand requirements, minimize operational costs, and maintain system balance. These actionable results provide a foundation for data-driven, cost-effective energy management at scale.

Table 4. Optimization outputs in vector notation.

Parameter	Description	Unit
$P_{i,t}^{\mathrm{b}}$	Power to be purchased at t	kW
$P_{i,t}^{\mathrm{s}}$	Power to be dispatched at t	kW
$P_{i,t}^{\mathrm{s},\mathrm{np}}$	Power discarded (non-remunerated)	kW
$P_{i,t}^{\mathrm{ch}}$	Power charged to the battery	kW
$P_{i,t}^{\mathrm{dch}}$	Power discharged from the battery	kW
$P_{i,t}^{\exp }$	Total power exported	kW
$E_{i,t}$	Battery state at t	kWh

7. Results and Discussion

The sensitivity of the GPU-based MC-SA solver to its two primary algorithmic hyperparameters—the number of iterations per chain (representing sequential workload) and the number of parallel chains (representing parallel workload)—was evaluated through a full factorial experiment. Iteration counts were sampled logarithmically from ${10}^2$ to ${10}^5$, while the number of chains varied from 1 to 200. Three different fleet sizes were tested (250, 500, and 1000 prosumers), and each configuration was repeated five times using independent random seeds, resulting in a total of 960 experimental runs.

The experiment measured two key response variables: the final objective value, representing the total operating cost to be minimized; and the elapsed wall-clock time, recorded on an NVIDIA A100 GPU.

7.1. Heat-Map Analysis

The heat-map analysis in Figure 5 reveals several important patterns that characterize the performance of our MC-SA algorithm. Three key observations emerge from the experimental data:

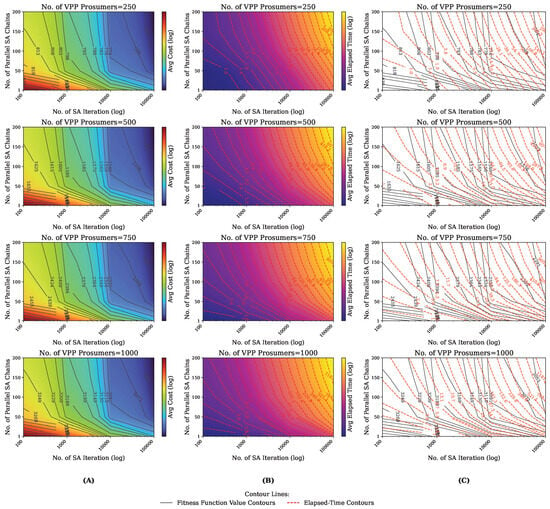
Figure 5. Heat-map visualization of MC-SA solver performance across three VPP fleet sizes (250, 500, and 1000 prosumers). Subfigure (A) presents the final objective values (fitness function), highlighting solution quality across combinations of iteration counts and parallel chain counts. Subfigure (B) shows the corresponding elapsed wall-clock time (in seconds), reflecting computational cost. Subfigure (C) overlays iso-fitness contours on the time surface, illustrating trade-offs and substitution effects between iterations and chains in achieving equivalent solution quality with different computational budgets.

First, we observe consistent improvement in solution quality as either iterations or chains increase, confirming the expected trade-off between computational effort and optimization accuracy. This pattern holds true across all three VPP sizes tested (250, 500, and 1000 prosumers), indicating stable algorithmic behavior regardless of system scale.

Second, the rate of improvement in solution quality progressively decreases beyond approximately 10,000 iterations and 100 chains. This performance plateau indicates that additional computational resources beyond these thresholds provide only minimal quality gains, establishing practical limits for resource allocation in operational deployments.

The most significant finding is the substitution effect demonstrated by the downward-sloping iso-fitness contours. This reveals that parallel computing resources can effectively compensate for time limitations in optimization processes. Specifically, our results show that using moderate chain counts (around 50 chains) achieves similar solution quality to sequential approaches while requiring substantially fewer iterations, enabling faster decision-making for real-time VPP operations.

Notably, these performance patterns remain consistent across different VPP scales. The structural relationships between solution quality and computational parameters show remarkable similarity regardless of system size (250, 500, or 1000 prosumers). While absolute computation times naturally increase with larger systems, the relative performance characteristics and optimal operating regions remain preserved. This scale-invariant behavior demonstrates that our hierarchical parallelization strategy maintains effectiveness across different deployment scenarios.

7.2. Time–Quality Pareto Fronts

To translate the heat-map insights into practical guidelines for VPP operators, we analyze the trade-offs between solution quality and execution time through Pareto curves (Figure 6). Each curve represents the optimal performance frontier for a specific chain count, with tick marks indicating different iteration budgets.

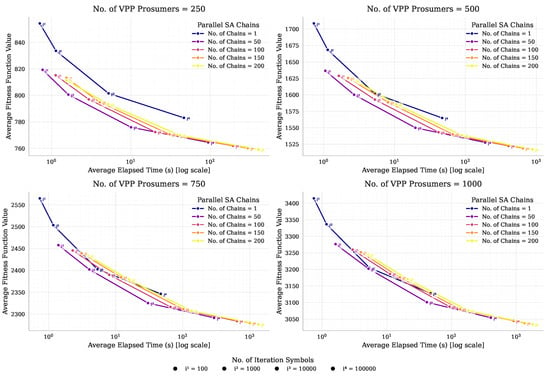
Figure 6. Pareto curves illustrating the trade-off between solution quality and execution time for different chain counts and iteration budgets. The plots highlight diminishing returns and show how parallel chains improve accuracy or reduce runtime, enabling efficient tuning of MC-SA for real-time VPP scheduling.

Our analysis reveals several key findings:

• Scale-Invariant Performance Patterns: The Pareto curves maintain consistent shapes across different VPP sizes (250, 500, and 1000 prosumers), demonstrating that the fundamental trade-offs between solution quality and computation time are largely independent of system scale. While absolute computation times increase with larger systems, the relative performance relationships remain stable.
• Optimal Operating Point: A consistent performance knee emerges around 50 chains across all fleet sizes. At this configuration, the solver achieves near-optimal solutions while reducing the required sequential SA iterations by approximately 10× compared to single-chain implementations, maintaining equivalent solution quality.
• Efficiency Boundary: Increasing chain counts beyond approximately 120 provides minimal quality improvements while potentially increasing computation time due to GPU resource contention. This establishes a clear upper limit for practical resource allocation.
• Parallelization Benefits: At any fixed iteration budget, increasing the number of chains consistently improves solution accuracy. The improvement is most significant when scaling from 1 to 50 chains.

The consistent performance patterns across different system scales validate the robustness of our hierarchical parallelization strategy. This scale-invariant behavior provides VPP operators with reliable configuration guidelines that remain effective regardless of deployment size, from community microgrids to city-wide energy management systems.

7.3. Empirical Chain–Iteration Law

Focusing on the iso-contour that corresponds to a 5 % optimality gap, a log–log least-squares fit of iterations versus chains (for every chain count, the smallest iteration budget whose average cost is within 5 % of the best value observed for that fleet size was selected) yields

$$\mathrm{iterations}=\kappa {\left(\mathrm{chains}\right)}^{-0.88\pm 0.17},\kappa \simeq 1.22\times {10}^5,$$

with a coefficient of determination $R^2=0.87$. Hence, doubling the number of chains allows the sequential iteration budget to be reduced by a factor of $2^{-0.88}\approx 1.85$ while maintaining the same solution quality. This empirical power law corroborates the hypothesis that parallel chains effectively mitigate the cooling-schedule bottleneck of classical SA.

7.4. Practical Tuning Rule

Although a formal convergence monitor (e.g., the Gelman–Rubin diagnostic) could be employed to auto-terminate chains, the present data indicate that a simple heuristic suffices: launch about 50 chains and set the iteration budget according to the above power law. This single parameter delivers near-optimal performance across all problem sizes tested.

7.5. Implications for Real-Time VPP Control

With the recommended setting, the GPU solver re-optimizes a 1000-prosumer VPP over a 15 min rolling horizon in under one second—fast enough to react to intraday price updates or short-term PV forecast errors. Because the chain–iteration relationship is architecture-agnostic, the methodology can be transferred to other agent-based energy applications that exhibit many-agent symmetry.

7.6. Limitations and Future Work

The performance figures presented here were obtained on an NVIDIA A100; GPUs with fewer registers or lower memory bandwidth may shift the optimal chain count or iteration budget. In addition, a systematic benchmark against MILP ground truth for the largest instances remains outstanding. Future work will, therefore, proceed along three complementary lines:

(i)

Adaptive termination: Integrate on-line convergence diagnostics (e.g., Gelman–Rubin or effective-sample-size estimates) so that each chain stops as soon as statistical equilibrium is detected.

(ii)

Hybrid refinement: Couple MC-SA with a fast local optimizer—such as sequential quadratic programming or an MILP warm-start—to close the residual optimality gap without compromising real-time execution.

(iii)

Precision–performance co-design: Extend the experimental matrix to include numerical precision as an additional factor. Specifically, we will explore mixed-precision arithmetic, fixed-point quantization, and reduced accuracy in both problem data (price signals, forecasts) and algorithmic state variables (temperature, objective increments). The goal is to determine, jointly with the hyperparameters studied here, the minimal bit-width that preserves solution quality while further reducing run-time and energy consumption.

By coupling algorithmic hyperparameter tuning with precision-aware optimization, we expect to push the time-to-solution envelope well below the sub-second mark, even on mid-range GPU hardware.

8. Future Research Directions

8.1. Uncertainty Modeling Extensions

Research should advance the deterministic framework to handle real-world uncertainties through several approaches. Scenario-based stochastic programming could distribute renewable generation and price volatility scenarios across parallel chains, while robust optimization methods would provide performance guarantees under worst-case conditions. Forecasting-integrated optimization represents another promising direction, combining short-term prediction models with adaptive constraint tightening.

8.2. Hardware Generalizability and Edge Deployment

The parallel architecture’s performance characteristics require investigation across diverse computing platforms. Systematic evaluation should span from data center GPUs to edge computing devices, identifying architecture-specific optimizations. This effort could lead to hardware-aware tuning strategies that dynamically adjust computational parameters and enable federated optimization across distributed edge devices.

8.3. Comprehensive Operational Metrics and Validation

Enhanced validation frameworks would incorporate several critical power system metrics. These include scheduling quality indicators for smoothness and ramp-rate compliance, battery degradation models for long-term asset management, and ancillary service provision capabilities for grid support. Multi-objective optimization approaches balancing economic, environmental, and reliability considerations would further strengthen operational relevance.

8.4. Comparative Algorithmic Analysis and Benchmarking

A rigorous benchmarking protocol is essential to contextualize the framework’s performance and validate its optimization efficiency. The evaluation should include (i) systematic benchmarking against commercial MILP solvers such as Gurobi and CPLEX to assess solution quality and characterize optimality gaps; (ii) quantitative comparison with population-based metaheuristics, including PSO and Genetic Algorithms, implemented within the same hierarchical parallelization structure; (iii) analysis against decomposition-based methods such as ADMM and Benders decomposition to examine trade-offs between convergence rate and solution quality; and (iv) comparison with recent learning-driven approaches, including Reinforcement Learning and Neural Networks, to assess adaptability in dynamic operational environments.

9. Conclusions

This study presented a scalable, GPU-accelerated implementation of Multiple-Chain Simulated Annealing (MC-SA) for efficient VPP scheduling. The core innovation lies in the hierarchical parallelization strategy that addresses both problem decomposition and algorithmic parallelism, enabling real-time and near-real-time optimization of large-scale distributed energy systems.

The key contributions are threefold. First, we developed a dual-level parallelization architecture combining prosumer-level decomposition with multi-chain SA, effectively transforming a traditionally sequential metaheuristic into a highly parallelizable framework. Second, through rigorous statistical analysis, we established an empirical relation indicating that the number of iterations required to reach the same solution quality scales as approximately the number of chains raised to the power of −0.88 (iterations ∝ chains^{−0.88±0.17}). This demonstrates that increasing the number of chains effectively reduces the required sequential iterations, highlighting the benefits of parallelism. Third, we provided practical tuning guidelines, indicating that approximately 50 chains offer the optimal balance between computational acceleration and minimizing the number of SA iterations while preserving solution quality.

Experimental results demonstrate compelling performance: execution times suitable for real-time applications for 1000-prosumer systems under 15 min horizons, representing up to 10× speedup over single-chain GPU implementations. This computational efficiency, combined with constraint-satisfying feasibility operators, makes the approach suitable for real-time applications in dynamic energy markets.

While the current implementation focuses on deterministic optimization and high-performance computing environments, the parallel architecture provides a foundation for important extensions including uncertainty modeling, multi-platform deployment, and comprehensive operational evaluation. The statistical insights into chain–iteration trade-offs also enable adaptive optimization frameworks that dynamically adjust parallelism based on problem characteristics.

In summary, the proposed MC-SA framework represents a significant advancement in computational methods for energy system optimization, enabling practical real-time scheduling of virtual power plants—a critical capability for renewable-dominated power systems in smart city environments.