Optical Diagnostics Applications to Laboratory Astrophysical Research

Abstract

Laboratory astrophysics is an emerging interdisciplinary field bridging high-energy-density plasma physics and astrophysics. Optical diagnostic techniques offer high spatiotemporal resolution and the unique capability for simultaneous multi-field measurements. These attributes make them indispensable for deciphering extreme plasma dynamics in laboratory astrophysics. This review systematically elaborates on the physical principles and inversion methodologies of key optical diagnostics, including Nomarski interferometry, shadowgraphy, and Faraday rotation. Highlighting frontier progress by our team, we showcase the application of these techniques in analyzing jet collimation mechanisms, turbulent magnetic reconnection, collisionless shocks, and particle acceleration. Future trajectories for optical diagnostic development are also discussed.

1. Introduction

Astrophysics seeks to unravel the fundamental laws governing cosmic evolution, from stellar birth to galactic dynamics. However, traditional observational approaches are often constrained by immense distances, protracted timescales, and the inherent uncontrollability of cosmic environments, limiting our ability to probe localized physical processes in detail. The advent of high-power laser facilities has opened a new frontier by enabling the controlled recreation of extreme astrophysical conditions in the laboratory. These laser-driven experiments offer unique advantages including proximity, transient duration, controllability, and repeatability [1] providing a powerful platform for quantitatively validating theoretical models and elucidating underlying microscopic mechanisms [2].

Laboratory astrophysics emerged in the 1990s, spurred by the recognition of profound physical similarities between laser-produced plasmas and key astrophysical phenomena, such as radiation transport, hydrodynamic instabilities, and magnetic reconnection [3]. Notable achievements include resolving the pulsation mechanism of Cepheid variable stars through precision opacity measurements [4], understanding stellar formation dynamics [5], analyzing Rayleigh–Taylor instability evolution in supernova remnants [6], probing X-ray source structures in solar flare loops [7], investigating kink instabilities in the Crab Nebula jet [8], clarifying magnetic field generation in the interstellar medium [9], and detecting thermonuclear reactions analogous to those in stellar cores [10]. A central goal of laboratory astrophysics is to uncover the physical principles governing matter under extreme plasma conditions—environments marked by ultra-high temperatures ($\mathrm{keV}$), immense pressures ($\mathrm{Gbar}$), and strong self-generated magnetic fields ($\mathrm{MG}$). Accurate physical modeling of these systems is critical to the precise resolution of multiscale parameters, including density gradients, magnetic field topology, and particle energy distributions. However, the transient nature (nanosecond to picosecond timescales) and intense gradients typical of such environments pose significant challenges for conventional diagnostics.

In this context, optical diagnostics have become indispensable tools. Techniques such as shadowgraphy, Nomarski interferometry, and Faraday rotation provide high spatio-temporal resolution and enable synchronous inversion of multiple physical fields—capabilities essential for dissecting key processes such as radiation transport, shock evolution, and magnetic reconnection [11,12,13,14,15,16]. For example, Sano et al. [17] combined optical shadowgraphy with B-dot probes to capture shock-driven growth of the Richtmyer-Meshkov instability and turbulent amplification of weak seed magnetic fields, confirming the role of this mechanism in interstellar field enhancement. Kuramitsu et al. [16] used Nomarski interferometry and self-emission imaging to reveal electron-scale magnetic reconnection and jet propagation at the electron Alfvén velocity under magnetization. Revet et al. [18] applied interferometry and X-ray spectroscopy to quantify how large-scale magnetic fields redirect astrophysical jets, demonstrating the effect of field inclination on collimation.

Although previous studies have demonstrated individual applications of these optical methods, a systematic framework integrating them as a combined diagnostic system and critically evaluating their synergistic potential has been lacking. This review aims to fill that gap by elaborating the principles, performance, and inversion methods of key optical diagnostics and, more importantly, showcasing how their integrated application has advanced our understanding of astrophysical jet collimation, turbulent reconnection, collisionless shocks, and particle acceleration. Finally, we discuss current limitations and outline future pathways—including tomography and AI-enhanced inversion—that promise to transform optical diagnostics from a tool for phenomenological simulation into a robust platform for microscopic mechanism analysis.

2. Optical Diagnostic System

2.1. Optical Diagnostic Setup

The diagnostic configurations and experiments described herein were primarily conducted using the Shenguang-II (SG-II) laser facility located at the Shanghai Institute of Optics and Fine Mechanics, China. Figure 1a,b schematically illustrate the optical diagnostic layout relative to the target chamber. The background pressure within the target chamber was maintained at $P_0\sim {10}^{-2}$ $\mathrm{Pa}$. The SG-II facility delivers eight beams, each with an energy $E_0\sim 250\mathrm{J}$, a wavelength of 351 $\mathrm{nm}$, and a pulse duration of 1 $\mathrm{ns}$. As depicted in Figure 1, a counterfoil target configuration was employed, utilizing a pair of copper foils separated by 4.5 $\mathrm{mm}$. The eight drive beams were symmetrically split into two groups and simultaneously focused onto the opposing surfaces of the foils, achieving a focal spot diameter of 150 $\mathsf{\mu }$m. The expanding plasma flows interact near the midplane between the foils. A ninth probe laser beam, with a wavelength of 527 $\mathrm{nm}$ and a duration of 30 $\mathrm{ps}$, was directed transversely through the interaction region to serve as the diagnostic probe. This probe enabled three distinct optical diagnostics: Nomarski interferometry, shadowgraphy, and Faraday rotation. The temporal evolution of the plasma within the interaction region was captured by varying the relative delay time between the main drive beams and the probe beam. Representative images obtained from these diagnostics are shown in Figure 1c (interferogram), Figure 1d (Faraday rotation image), and Figure 1f (shadowgraphy).

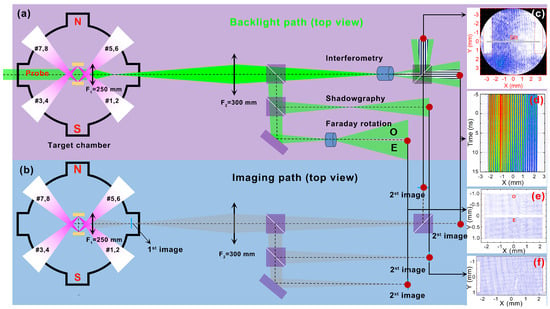
Figure 1. Schematic view of the experimental setup. (a,b): Shadowgraphy, Nomarski interferometry, and Faraday rotation diagnostics all employ two-stage imaging. The green beam represents the probe light, while the purple beams represent the drive light. The temporal evolution of the plasma is acquired by varying the relative delay time between the probe and drive beams. Representative images obtained from the diagnostics are shown: (c) interferogram, (d) Faraday rotation image, (e,f) Shadowgraphy.

2.2. Principles of Optical Diagnosis

Figure 2 illustrates the schematic principles of data analysis for the three diagnostics. After traversing the plasma, the probe light undergoes changes in phase, polarization state, and intensity. The Nomarski interferometer, constructed based on the variation of optical phase, can provide the distribution of electron number density and velocity. The Faraday rotation, established on the basis of the variation of optical polarization, can measure the distribution of magnetic field strength along the direction of the probe light. Shadowgraphy is highly sensitive to the second spatial derivative of electron density and can reveal the spatial profile of plasma outflow. The measurement principles of these three optical diagnostics will be detailed in the following section.

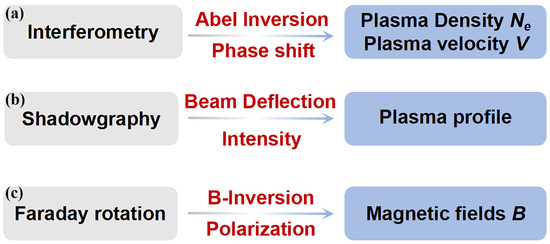
Figure 2. Schematic diagram of data analysis principles for the three core optical diagnostics. (a) Nomarski Interferometry: Measures the phase shift of the probe beam to reconstruct the line-integrated electron density, which is then inverted (e.g., via Abel inversion) to obtain the local density distribution, $n_e$, and the plasma flow velocity. (b) Shadowgraphy: Sensitive to the second spatial derivative of the electron density, it visualizes plasma density gradients and outlines the overall plasma profile through beam deflection-induced intensity variations. (c) Faraday Rotation: Measures the polarization rotation of the probe beam, which is proportional to the path-integrated product of electron density and the axial magnetic field component, $\int n_e{B}_{\Vert }dl$, enabling the inference of magnetic field strength and topology.

2.2.1. Nomarski Interferometer

Nomarski interferometry employs a strictly equal-path interference scheme. For experiments involving nanosecond-scale laser pulses, the temporal coherence requirement is readily satisfied, making spatial coherence the primary consideration for high-quality interferogram formation. Assuming the probe laser is initially horizontally linearly polarized, a front polarizer (acting as the polarizer) is rotated by ${45}^{\circ }$ relative to the horizontal axis. After passing through the plasma region, the probe light is relayed through primary and secondary imaging lenses onto a CCD camera. Emerging from the secondary imaging lens as a spherical wave, the light passes through a Wollaston prism positioned near the lens’s focal point. The prism splits the wave into two beams with orthogonal polarizations: the ordinary (o) and the extraordinary (e). A final polarizer (analyzer), oriented perpendicularly to the initial polarizer, is placed before the final image plane. Interference fringes are thus formed on the image plane. The fringe width can be adjusted by altering the position of the Wollaston prism relative to the secondary imaging lens.

Nomarski interferometry primarily retrieves the electron density distribution and the propagation velocity of the plasma. The relationship between electron density and fringe shift is derived as follows:

$$\int n_{e}dl=2D{n}_c\lambda$$

(1)

where $n_c$ is the critical density ($n_c\sim 3.94\times {10}^{21}$ cm⁻³), D is the displacement of the stripes, and $\lambda$ is the probe wavelength. Both are known constants for a given probe laser. Utilizing this equation, the two-dimensional electron density distribution perpendicular to the probe beam path can be obtained via Abel inversion, applicable where the electron density $n_e\ll n_c$. Furthermore, the average plasma velocity ($v=D/t$) is determined from the fringe displacement observed at different relative delay times.

2.2.2. Shadowgraphy

Shadowgraphy employs short-pulsed laser probes directed through a target plasma region to capture plasma morphology directly. The receiving device is a scientific-grade CCD camera, enabling the capture of transient plasma evolution at millimeter spatial scales and nanosecond temporal resolutions. Research establishes that shadowgraphy imaging primarily depends on the probe laser intensity and the refractive index distribution within the plasma region. When the probe laser traverses the plasma under vacuum conditions, probe rays undergo deflection, inducing intensity variations at the imaging plane. The deflection angles ($\alpha$ and $\beta$ representing the angles in the x- and y-directions, respectively) are proportional to the gradient of the refractive index ($\eta$) within the observed plasma region, expressed as:

$$\alpha ={\displaystyle \frac{\partial }{\partial x}}\int ndl,\beta ={\displaystyle \frac{\partial }{\partial y}}\int ndl$$

(2)

The relative change in intensity (I) at the imaging plane compared to the incident probe intensity ($I_T$) is proportional to the divergence (gradient) of the deflection angles, expanded as:

$${\displaystyle \frac{I-I_T}{I_T}}={\displaystyle \frac{\partial \alpha }{\partial x}}+{\displaystyle \frac{\partial \beta }{\partial y}}={\displaystyle \frac{{\partial }^2}{\partial x^2}}\int ndl+{\displaystyle \frac{{\partial }^2}{\partial y^2}}\int ndl={\nabla }^2\int ndl$$

(3)

Consequently, the resultant shadowgram is proportional to the second-order spatial derivative of the refractive index. High-resolution shadowgraphy images are obtained only when refractive index gradients exhibit significant spatial variation (i.e., non-uniform plasma density structures are present).

2.2.3. Faraday Rotation

When a linearly polarized optical probe traverses a magnetized plasma medium, its plane of polarization undergoes rotation about the axis defined by the local magnetic field vector. The presence of a magnetic field within the plasma implies that the scattering process depends not only on the electron density but also intrinsically on the magnetic field configuration. To enable single-shot diagnostics of the probe beam’s polarization state change, a Wollaston prism is employed experimentally to split the beam into two orthogonally polarized components. These components ordinary (O) and extraordinary (E) are imaged non-interferometrically onto the same CCD detector. This configuration is functionally analogous to a Nomarski interferometer but operates without beam coherence, facilitating spatially separated imaging of each polarization component. This optical design permits direct pixel-by-pixel comparison of intensity variations between the two images, thereby enabling quantitative determination of the Faraday rotation angle for the probe beam.

A Wollaston prism resolves the probe beam, which has undergone Faraday rotation, into its ordinary (O) and extraordinary (E) polarization components. A square aperture positioned at the primary image plane ensures that the modulated intensity distributions of both the O-ray ($I_O$) and E-ray ($I_E$) are captured across the full field of view by a scientific-grade CCD camera. The Faraday rotation angle ($\phi$) is calculated by inverting the measured intensity ratio of the images, satisfying the relation $\phi ={\displaystyle \frac{1}{2}}{sin}^{-1}\left({\displaystyle \frac{I_0-I_E}{I_0+I_E}}\right)$. Furthermore, $\phi$ is related to the magnetic field strength (B) via: $\phi ={\displaystyle \frac{e}{2m_{e}c{n}_c}}\int n_e{B}_z·dl=2.6\times {10}^{-17}\lambda \int n_e{B}_z·dl$, where $n_e$ is the electron density and $\lambda =527 \mathrm{nm}$ is the probe wavelength. The derived component $B_z$ represents the magnetic field projection parallel to the probe beam propagation direction.

The capabilities of these diagnostics are accompanied by inherent limitations tied to their fundamental principles and implementation. All three techniques share a temporal resolution dictated by the probe laser pulse duration, typically in the picosecond-to-nanosecond range, and a spatial resolution at the micrometer scale, primarily limited by diffraction and imaging system quality. Specific systematic errors must be considered: Nomarski interferometry relies on the assumption of axial symmetry for robust Abel inversion, and its accuracy degrades in the presence of complex, asymmetric structures. Shadowgraphy is highly sensitive to the second derivative of density, making its signal challenging to quantify absolutely in strongly inhomogeneous plasmas where ray bending becomes significant. Faraday rotation provides a path-integrated measurement of the magnetic field, requiring inversion techniques to localize the field source and inherently mixing contributions from all plasma regions along the line of sight. Acknowledging these constraints is crucial for the accurate interpretation of the experimental data presented in subsequent sections.

3. Typical Applications in Laboratory Astrophysics

3.1. Study on the Formation and Evolution of Collimated Jets

Astrophysical jets are highly collimated, supersonic plasma outflows ejected from various astrophysical systems. They are ubiquitously observed in diverse environments, including young stellar objects (YSOs), planetary nebulae, active galactic nuclei (AGNs), and gamma-ray bursts [19,20,21,22]. The triggering mechanisms and collimation processes of these jets remain central topics in astrophysics. While radiative cooling, magnetic fields, and the surrounding interstellar medium (ISM) are currently regarded as key factors influencing jet collimation, the precise details remain unresolved [23,24,25]. Given the inherent complexity of jet evolution and the limitations imposed by finite observation times and viewing angles for specific astrophysical jets, high-power laser facilities have emerged in recent years as vital tools for complementing astrophysical observations and theoretical modeling.

Here, Yuan et al. [26] utilized the SG-II laser facility to irradiate C-shaped targets, generating colliding plasma flows. We employed a combined diagnostic approach using Nomarski interferometer and shadowgraphy imaging to diagnose the jet formation and evolution dynamics in real-time, as illustrated in Figure 3. Specifically, CH (plastic) targets and high-Z Au (gold) targets were used to investigate the effect of differing radiative cooling efficiencies on plasma propagation.

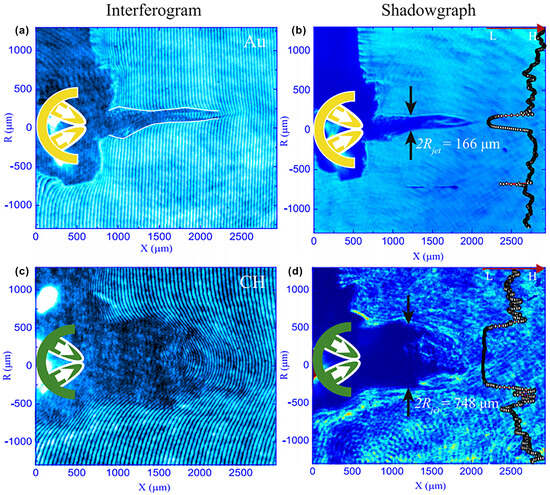
Figure 3. Experimental jets generated by Au and CH targets at 3 ns. The first row shows (a) the interferogram and (b) the shadowgraph of the Au-jet. The second row shows (c) the interferogram and (d) the shadowgraph of CH-jet [26].

The experiments reveal a striking contrast: The Au target, exhibiting strong radiative cooling, produced a highly collimated jet with a characteristic velocity of $(6.1\pm 0.6)\times {10}^5\mathrm{m}/\mathrm{s}$, a narrow radius of ∼83 $\mathsf{\mu }$m, and a high aspect ratio of $\sim 22$ (Figure 3a,b). In stark contrast, the CH target produced a significantly diffused outflow with a radius of ∼374 $\mathsf{\mu }$m and a much lower aspect ratio of ∼7 (Figure 3c,d). This pronounced morphological disparity provides direct experimental evidence that radiative cooling is the core physical mechanism responsible for maintaining tight collimation in the Au jet. The radiative cooling power ($J_{\mathrm{rad}}\propto Z^2{T}^{1/2}{n}^2$) causes the thermal radial expansion of the gold plasma to be counteracted by a strong density collapse effect, thereby enabling the Au jet to maintain a stable, narrow radius during propagation. Conversely, the CH outflow, lacking efficient cooling, exhibits dynamics dominated by thermal pressure, resulting in rapid radial expansion (expansion velocity $v\sim$ 122 km/s). This work demonstrates for the first time in a laboratory setting that the combined effects of radiative cooling and the photoionized ambient medium are dominant in achieving and sustaining jet collimation.

3.2. Study on Turbulent Magnetic Reconnection

Turbulent magnetic reconnection represents a fundamental mechanism for magnetic energy dissipation in plasmas. Its dissipation region is characterized by fragmented current sheets containing multiple reconnection sites, exhibiting phenomena such as splitting, disruption, and the acceleration of energetic electrons and ions. This process is ubiquitously observed in astrophysical plasma environments, including the solar atmosphere and Earth’s magnetosphere [27,28,29,30,31]. Previously, direct in situ probing of the fragmented current sheet structures and turbulent cascade processes inherent to turbulent reconnection has proven exceptionally challenging.

Ping et al. [32] have achieved the first laboratory realization of laser-driven turbulent magnetic reconnection using the SG-II facility. As depicted in Figure 4a, four symmetrically incident laser beams irradiated two parallel Al foil targets separated by 600 $\mathsf{\mu }$m. This setup generated oppositely directed toroidal magnetic fields via the Biermann battery effect. Employing 60 ps green probe laser shadowgraphy ($\lambda$ = 0.531 $\mathsf{\mu }$m) combined with Fourier power spectrum analysis, the experiment captured, for the first time in a laboratory setting, the turbulent fragmentation of the current sheet (Figure 4b,c). Under strong driving conditions (Case I: 200 $\mathsf{\mu }$m focal spot separation), the current sheet exhibited significantly enhanced density fluctuations. Its power spectrum manifested dual power-law scaling: ${\alpha }_1=-3/2$ in the fluid regime ($k{d}_i<1$) and ${\alpha }_2=-7/3$ in the inertial range of ions ($k{d}_i>1$) (Figure 4d). Under weak drive conditions (Case II: 400 $\mathsf{\mu }$m separation), the corresponding spectral indices were ${\alpha }_1=-4/3$ and ${\alpha }_2=-3$ (Figure 4e). This spectral evolution, consistent with turbulent spectra observed in the heliosphere, confirms that strong driving enhances the turbulent cascade. Crucially, the variation in spectral indices is directly linked to magnetic island formation resulting from current sheet fragmentation. These findings provide critical insights into energy dissipation, the origins of high-energy particles, and acceleration mechanisms in solar flares.

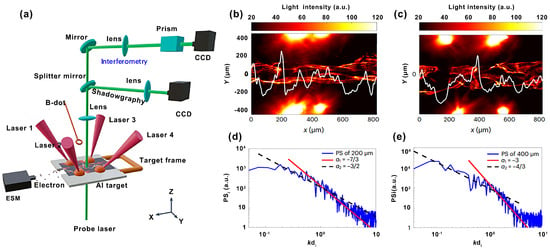
Figure 4. Laser-driven turbulent magnetic reconnection experiments. (a), The experimental set-up. (b,c), Optical shadowgraphy results at the delay time of 1 ns for cases I (b) and II (c). (d,e), Power spectra of the average light intensity, PSi [32].

3.3. Experimental Observation of Electrostatic Shock Wave Pairs

Collisionless shocks represent a remarkable phenomenon in space and astrophysical plasmas, where supersonic flows generate electromagnetic fields via instabilities, enabling particle acceleration to cosmic-ray energies. Despite abundant astrophysical observations, understanding these microscopic processes remains a fundamental challenge. Yuan et al. [33] investigated the formation and evolution of counter-propagating electrostatic shocks using laser-driven, symmetric copper (Cu) foils. Figure 5 present characteristic interferograms and the corresponding electron density distributions within the interaction region at $t=6\mathrm{ns}$ and $t=10\mathrm{ns}$, respectively. At $t=6\mathrm{ns}$ (Figure 5a,c), the two colliding plasma streams (initial density $n_e\sim 1\times {10}^{19}{\mathrm{cm}}^{-3}$, relative velocity $2v\sim 7.5\times {10}^7 \mathrm{cm}/\mathrm{s}$) undergo mutual penetration near the center ($x\sim$ 2560 $\mathsf{\mu }$m), forming an overlapping double-shock structure. The peak density reaches $5.2\times {10}^{19}{\mathrm{cm}}^{-3}$, significantly exceeding the free-stream superposition expectation ($2\times {10}^{19}{\mathrm{cm}}^{-3}$), yielding a density jump ratio of 2.6. The shock transition width of 450 $\mathsf{\mu }$m is substantially smaller than the ion mean free path (${\lambda }_{mfp}$ = 16–500 mm), confirming the collisionless nature of the shocks. By t = 10 ns (Figure 5b,d), the shock pair separates and propagates along the $\pm x$-direction. The peak density increases to 6.2–6.5 $\times {10}^{19}{\mathrm{cm}}^{-3}$, the transition region broadens to ∼700 $\mathsf{\mu }$m, and the average propagation velocity is $v_s\sim 2.7\times {10}^6\mathrm{cm}/\mathrm{s}$, corresponding to a Mach number $M\in 3\sim 5$.

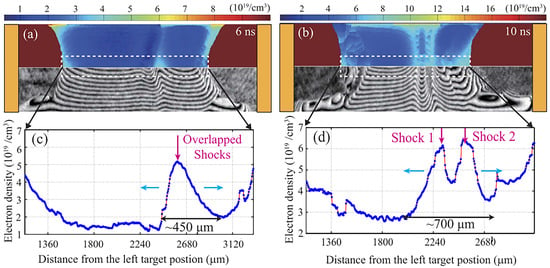
Figure 5. Experimental characterization of counter-propagating collisionless shocks. (a,b) Electron density maps (upper panels), obtained from interferograms via Abel inversion at 6 $\mathrm{ns}$ and 10 $\mathrm{ns}$, reveal the formation and evolution of a double-shock structure. (c,d) are the corresponding electron density profile plotted along the flow direction. The pink arrows and blue arrows represent the shocks position and the propagation directions, respectively.The corresponding lineouts (lower panels) of electron density (blue solid lines) are fitted (black curves) to quantitatively determine the key shock parameters: the density jump ratio (indicating compression strength and shock Mach number) and the shock transition width (a signature of the collisionless mechanism, as it is much smaller than the classical ion mean free path) [33].

Theoretical analysis identifies these shocks as electrostatically dominated. Applying the electrostatic shock width model by Park et al. [34] with experimental parameters ($T_e\sim$ 300–420 e, $A_Z=64$) yields a calculated width $L_{ES}\sim$ 600–800 $\mathsf{\mu }$m, agreeing well with measurements (450–700 $\mathsf{\mu }$m). Conversely, the characteristic width for an electromagnetic (Weibel-type) shock ($L_{EM}\sim 15\mathrm{mm}$) far exceeds the target separation (4.5 $\mathrm{mm}$, effectively excluding its dominance. This work reports the first laboratory observation of stably propagating, counter-propagating collisionless shocks. It reveals the formation dynamics of electrostatic shock pairs in symmetric flow systems, providing a critical experimental counterpart to astrophysical shocks, such as the double-shock structures observed in supernova remnants.

3.4. Electron Stochastic Acceleration in Kinetic Turbulent Plasmas

The origin of high-energy charged particles in the universe remains a fundamental unsolved problem, long challenging astrophysicists and recognized as one of Science’s 125 pivotal questions [35,36,37,38,39]. While astronomical observations combined with simulations have provided insights into particle acceleration mechanisms—including magnetic reconnection acceleration [40,41,42], diffusive shock acceleration [43,44], and stochastic acceleration [45,46] and recent experiments have confirmed electron acceleration via processes like magnetic reconnection and collisionless shock formation [47,48], laboratory identification of stochastic acceleration as a viable mechanism has remained elusive, particularly due to challenges in generating collisionless, turbulent plasmas.

Addressing this, Yuan et al. [49] report the first direct laboratory observation of turbulent magnetic field evolution dynamics driven by the Weibel instability, employing polarization-sensitive Faraday rotation diagnostics combined with shadowgraphy imaging. The experiment, conducted on the Shenguang-II laser facility, utilized two symmetrically incident laser beams ($\lambda$ = 351 nm, 1 $\mathrm{kJ}$ per beam) to ablate a lithium deuteride (LiD) powder target, generating interpenetrating plasma flows (separation: 3.2 mm) with a Mach number 6. Faraday rotation measurements (Figure 6e) reveals, the magnetic field exhibits a regular filamentary structure, with a peak path-integrated field strength ($\int B_{\Vert }dl$) of 0.75 $\mathrm{MG}·\mathrm{mm}$ during the linear phase (t = 1 ns). By the nonlinear phase ($t=3\mathrm{ns}$), adjacent current filaments merge and kink (Figure 6f), evolving into magnetic island-like structures with spatial scales of 300∼400 $\mathsf{\mu }$m, signifying a transition to a turbulent magnetic topology. Synchronized shadowgraphy captured the transverse growth of current filaments (Figure 6c,d). Fourier power spectrum analysis confirmed that the power spectrum of this disordered structure closely aligns with kinetic-scale turbulent spectra. Theoretical simulations indicate that the observed energetic electrons arise primarily from turbulent stochastic acceleration: Thermal electrons gain energy through multiple collisions (scattering events) with magnetic islands within the turbulent plasma. This work represents the first laboratory recreation of a kinetic-scale turbulent environment analogous to the transition phase preceding shock formation in supernova remnants. It provides critical experimental evidence for the turbulence-dominated stochastic acceleration mechanism, directly addressing the long-standing challenge of understanding the microphysical basis of particle acceleration in turbulent astrophysical plasmas.

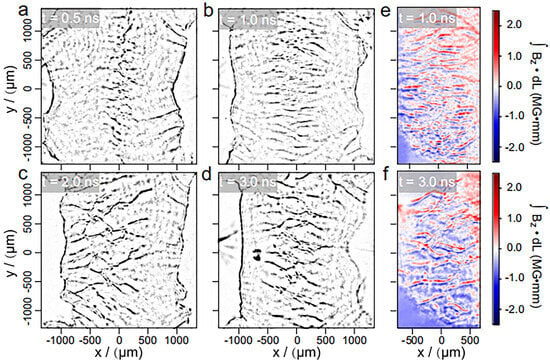
Figure 6. Experiment demonstrating the evolution of Weibel instability. Filaments in (a–d) measured using shadowgraphy represent the information of plasma density, and in (e,f) measured using the Faraday method represent the path-integrated magnetic field strength [49].

3.5. Kelvin Helmholtz Instability

The Kelvin-Helmholtz (KH) instability, a fundamental fluid instability, is ubiquitous in space and astrophysical plasmas. Its evolution in environments such as Earth’s magnetopause is significantly regulated by magnetic fields. However, the kinetic evolution of the magnetized KH instability has long lacked experimental validation, hindering our understanding of mass and energy transport processes in solar wind-magnetosphere coupling [50,51,52].

Using the SG-II laser facility, Sun et al. [53,54] conducted pioneering experiments investigating the effect of an external magnetic field on the KH instability. Four nanosecond laser beams (total energy: 1 $\mathrm{kJ}$, $\lambda =351\mathrm{nm}$, intensity $I\sim {10}^{15}\mathrm{W}/{\mathrm{cm}}^2$) irradiated a 10 $\mathsf{\mu }$m thick CH foil, generating a high-velocity plasma flow ($v\sim 100\mathrm{km}/\mathrm{s}$). This flow interacted with a periodically modulated aluminum layer (amplitude: 25 $\mathsf{\mu }$m, wavelength: 75 $\mathsf{\mu }$m), forming a velocity shear layer that subsequently developed the KH instability. A 4000 $\mathrm{G}$ permanent magnetic field was applied perpendicular to the plasma propagation direction (Z-axis), simulating the magnetopause’s perpendicular field configuration. Synchronous shadowgraphy and Nomarski interferometer measurements captured the evolution of the KH vortex. Figure 7a–c show side-view shadowgraphs taken at delay times of 4 $\mathrm{ns}$, 5 $\mathrm{ns}$, and 6 $\mathrm{ns}$ under an external magnetic field of 4000 $\mathrm{G}$. At 4 ns, the KH instability is initiated by ionization and begins to deform by 5 $\mathrm{ns}$, eventually forming a distinct Kelvin–Helmholtz vortex by 6 $\mathrm{ns}$, representing the linear evolutionary stage of the KH instability. Notably, the presence of the magnetic field induces bifurcations in the flow behind the target, with two large forked jets appearing around the interaction region, as highlighted in the yellow frames. In contrast, Figure 7d–f present the case without an external magnetic field. A large jet is observed around the interaction region, but its shape differs significantly from that in the magnetized case, with no obvious bifurcation. This indicates that the applied magnetic field alters the trajectory of electrons and affects the motion of the plasma outflow. Plasma outflow velocities are approximately 286.7 $\mathrm{km}/\mathrm{s}$ and 337 $\mathrm{km}/\mathrm{s}$ at 4 $\mathrm{ns}$ and 6 $\mathrm{ns}$, respectively, slightly lower than those observed in the magnetized case. The corresponding FLASH simulations indicate that compression of the plasma flow amplifies the external field from 4000 $\mathrm{G}$ to 20,000 $\mathrm{G}$ (2 $\mathrm{T}$). The amplified magnetic field persistently compresses the plasma, displacing the flow 150 $\mathsf{\mu }$m in the +Z direction. This displacement attenuates the shear layer of velocity, thus suppressing the development of KH instability. This work presents the first laboratory realization and comprehensive optical diagnosis of magnetized KH instability evolution spanning linear to nonlinear regimes. The experimental results align with observations from the Magnetospheric Multiscale (MMS) mission satellites and are critical to understanding solar wind-magnetosphere interactions and energy dissipation during geomagnetic storms.

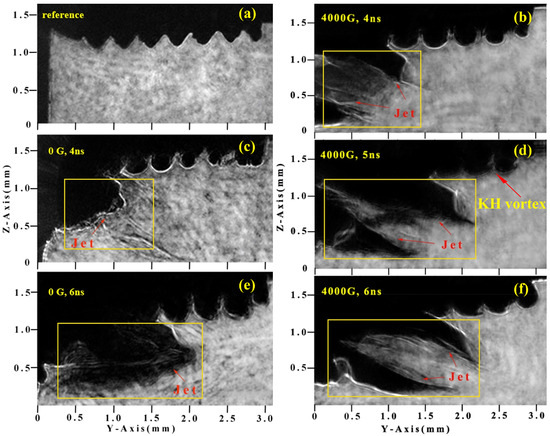
Figure 7. Experimental observation of magnetized Kelvin-Helmholtz (KH) instability. Side-view shadowgraphy images compare the evolution of the KH instability (a,c,e) without and (b,d,f) with an externally applied magnetic field. The direct comparison clearly demonstrates the significant suppression of KH vortex growth, and highlighting its stabilizing role in shear flow dynamics [54].

3.6. Laboratory Investigations of Wakefield Acceleration Mechanisms

In recent years, plasma wakefield acceleration has been recognized as one of the potential mechanisms explaining the origin of ultra-high-energy cosmic rays (UHECRs). Chen et al. first proposed that wakefields excited by Alfvén shocks in relativistic plasma flows can generate power-law energy spectra through stochastic acceleration processes, thus offering an efficient bottom-up acceleration mechanism for UHECRs [55]. This mechanism avoids the synchrotron radiation losses that challenge traditional Fermi acceleration at high energies, and its rectilinear acceleration trajectory makes it particularly suitable for interpreting observed extreme energy events. Subsequently, Chen et al. further introduced a magnetic wave-driven wakefield accelerator (MPWA) model, in which magnetic waves (such as whistler waves) generate longitudinal electric fields via the ponderomotive force in magnetized plasmas, enabling efficient particle acceleration [56]. This model is applicable not only to astrophysical environments but also provides a theoretical basis for novel accelerator designs in laboratory settings. In terms of experimental validation, Kaganovich et al. demonstrated the first all-optical two-stage laser wakefield acceleration. Using a 2 $\mathrm{TW}$ laser pulse to generate $\sim 1\mathrm{MeV}$ electron beams in nitrogen gas and injecting them into a wakefield excited by a 10 $\mathrm{TW}$ laser in helium, they successfully boosted electron energies beyond 20 $\mathrm{MeV}$ [57]. This experiment confirmed the feasibility of wakefield acceleration. As noted by Takabe et al. in their review, laser-driven plasmas in the laboratory allow for ground-based simulations of cosmic ray acceleration mechanisms, particularly the reproduction of UHECR power-law spectra via wakefield acceleration [58]. These studies not only advance the field of laboratory astrophysics but also open up new experimental pathways for understanding extreme cosmic phenomena.

4. Challenges and Future Perspectives

Despite the significant successes achieved, the current suite of optical diagnostics faces several technical challenges that must be addressed to further advance laboratory astrophysics. First, reconstruction of three-dimensional magnetic field topologies remains a primary obstacle. Conventional Faraday rotation only probes the line-of-sight magnetic field component ($B_{\Vert }$), preventing complete characterization of the turbulent magnetic energy cascade. Future efforts should focus on developing magnetic tomography techniques, potentially by combining multiangle Faraday rotation measurements with advanced inversion algorithms. Second, strong gradients in plasma density can severely distort the optical path, compromising the quantitative accuracy of shadowgraphy and interferometry. The development of adaptive optics or computational phase-retrieval methods may mitigate these effects. Finally, the joint inversion of multiple physical parameters (e.g., density, temperature, and magnetic field) from a single set of diagnostic data requires more sophisticated and optimized algorithms. The integration of artificial intelligence and machine learning approaches holds great promise for handling this complexity, enabling faster and more accurate multi-physical field reconstructions from large and noisy experimental datasets. Overcoming these challenges will be crucial for pushing optical diagnostics towards the ultimate goal of providing a holistic, multi-dimensional view of extreme plasma phenomena in the laboratory.

5. Conclusions

This paper systematically elaborates on the pivotal role of optical diagnostic technologies in laboratory astrophysics research. By developing a synergistic diagnostic system incorporating Nomarski interferometer, shadowgraphy, and Faraday rotation, we have achieved simultaneous multiphysical field inversion of extreme plasma parameters (electron density gradient, plasma profile, magnetic field strength, velocity field) with spatiotemporal resolution reaching the picosecond and micrometer scales. Using the SG-II laser facility, we have obtained the following innovative results: (1) Jet Collimation Mechanism Analysis: Through comparative Au/CH double-target experiments, the radiative cooling effect ($J_{\mathrm{rad}}\propto Z^2{T}^{1/2}{n}^2$) was quantitatively demonstrated for the first time as the key factor maintaining the high collimation (aspect ratio $> 22$) of astrophysical jets, resolving the cooling efficiency controversy in theoretical models. (2) Turbulent Magnetic Reconnection Dynamics: Fragmented current sheet structures and dual-power-law energy spectra were captured, revealing the governing influence of drive strength on turbulent cascade processes. (3) Experimental collisionless shock calibration: Stable electrostatic shock propagation (Mach number $M\in$ 3∼5) was observed in symmetric flow systems. The measured shock width (400∼700 $\mathsf{\mu }$m) is in excellent agreement with the predictions of the Park model, effectively ruling out an electromagnetic shock-dominated mechanism. (4) Validation of Turbulent Stochastic Acceleration: By reconstructing the evolution of Weibel turbulence magnetic fields via Faraday rotation, the collision-dominated stochastic electron acceleration process within magnetic islands was experimentally confirmed for the first time, providing new evidence for the origin of cosmic high-energy particles. (5) Magnetohydrodynamic Instability Control: A external magnetic field was found to suppress the growth of KH vortices through shear layer compression, clarifying the physical constraints on energy transport at magnetopause boundaries.

However, the current optical diagnostic system still faces several technical challenges. First, in 3D Field Reconstruction, existing Faraday rotation techniques only invert the axial magnetic field component, hindering the reconstruction of three-dimensional turbulent magnetic field topologies and resulting in incomplete validation of magnetic energy cascade models. The second, in complexity of Multi-Physical-Field Coupling, refractive-index discontinuities in strongly gradient plasmas induce optical path distortions, degrading the quantitative accuracy of shadowgraphy. Furthermore, algorithms for the joint inversion of density and magnetic fields require significant optimization. To address these challenges, future advancements in optical diagnostic technologies require breakthroughs in areas such as magnetic topology tomography reconstruction and artificial intelligence-enhanced inversion techniques.