Generalization of Napoleon–Barlotti Theorem

Abstract

The Napoleon–Barlotti theorem belongs to the family of theorems related to the Petr–Douglas–Neumann theorem. The Napoleon–Barlotti theorem states: On the sides of an affine-regular n-gon construct regular n-gons. Then the centers of these regular n-gons form a regular n-gon. In the paper we give a generalization of this theorem.

1. Introduction

The Napoleon–Barlotti theorem (NBT) [1,2] is related to the Petr–Douglas–Neumann theorem [3,4,5,6,7]. It states that if one erects regular n-gons on the sides of an affine regular n-gon, then their centers form a regular n-gon. The special case of NBT is Thébault’s theorem [8]: If one erects squares on the sides of a parallelogram ($ABCD$), all either outside or inside of the parallelogram, then their centers form another square. See also Van Aubel theorem [9] and its generalization by J.R. Silvester [10].

In the paper, we prove a more general theorem, of which NBT is a special case.

Theorem 1.

Consider an arbitrary n-gon $ABC\dots XY$ and a fixed point $P.$ Construct an affine image $A^{\prime }{B}^{\prime }{C}^{\prime }\dots X^{\prime }{Y}^{\prime }$ of the n-gon and an affine image $P^{\prime }$ of $P.$ Next, construct mutually similar n-gons on the sides of the affine polygon $A^{\prime }{B}^{\prime }{C}^{\prime }\dots X^{\prime }{Y}^{\prime }$ such that

$$ABC\dots XY\sim A^{\prime }{B}^{\prime }{C}_1{D}_1\dots X_1{Y}_1\sim A_2{B}^{\prime }{C}^{\prime }\dots X_2{Y}_2\sim \dots \sim A^{\prime }{B}_n{C}_n\dots X_n{Y}^{\prime },$$

where the similarities, except the first one, are all direct (the first similarity may be direct or indirect). Therefore, there are only two ways to construct these n polygons. Let us construct points $P_1,P_2,\dots ,P_n$ that have the same relative position with respect to the vertices of polygons with indices $1,2,\dots ,n$ as the point P with respect to the polygon $ABC\dots XY$. Finally, construct feet of perpendiculars $Z_1,Z_2,\dots ,Z_n$ dropped from the point P to the sides $AB,BC,\dots ,XY,YA$ of the original polygon. Then, the similarity

$$Z_1{Z}_2\dots Z_n\sim P_1{P}_2\dots P_n$$

holds. Moreover, this similarity has the same coefficient regardless of the choice of the point P. The position of the point $P^{\prime }$ relative to the polygon $P_1{P}_2\dots P_n$ is the same as the position of the point P relative to the polygon $Z_1{Z}_2\dots Z_n.$

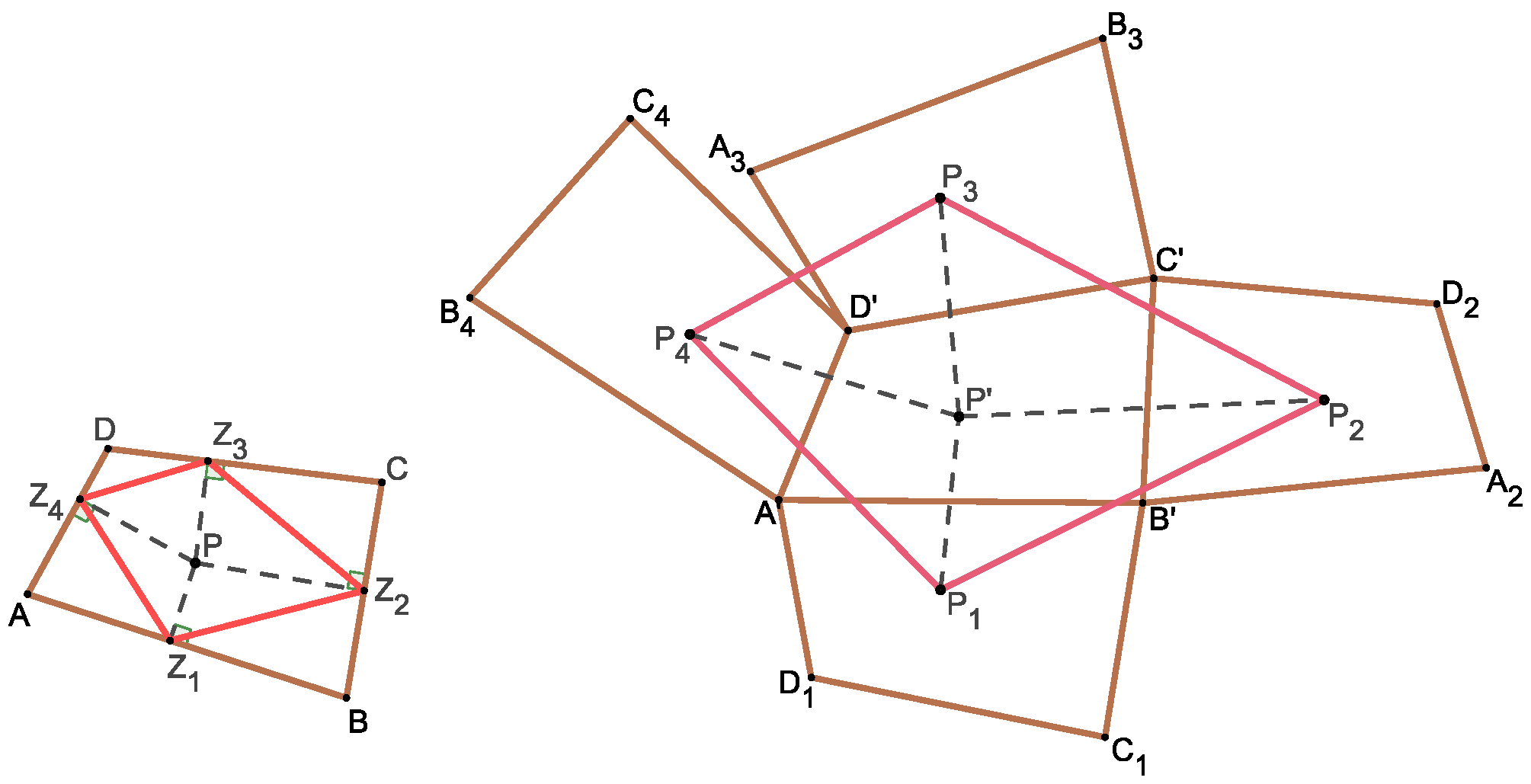
The theorem applied to a quadrilateral $ABCD$ is illustrated in Figure 1. It is obvious that NBT is a special case of Theorem 1, since the feet $Z_1,Z_2,\dots ,Z_n$ of the perpendiculars that dropped from the center of a regular n-gon to its sides form a regular n-gon.

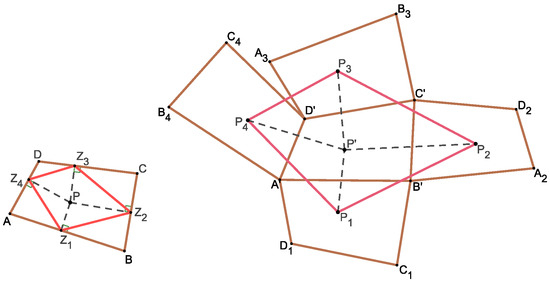
Figure 1. Theorem 1 for a square. The position of the point P with respect to the quadrilateral $Z_1{Z}_2{Z}_3{Z}_4$ is same as the position of $P^{\prime }$ with respect to $P_1{P}_2{P}_3{P}_4$.

The proof will be carried out in three steps: first, we prove Theorem 1 for an arbitrary triangle (Section 2, Theorem 2); then, we show that the validity of the theorem for a triangle can be used to prove that a certain mapping is a similarity (Section 3, Theorem 3). A direct consequence of this fact is the validity of Theorem 1 (Section 3).

2. Step One: Proof of Theorem 1 for an Arbitrary Triangle

Theorem 2.

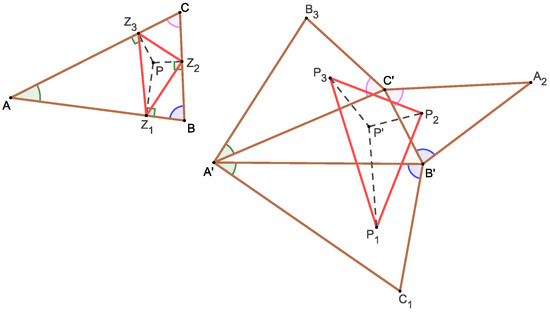
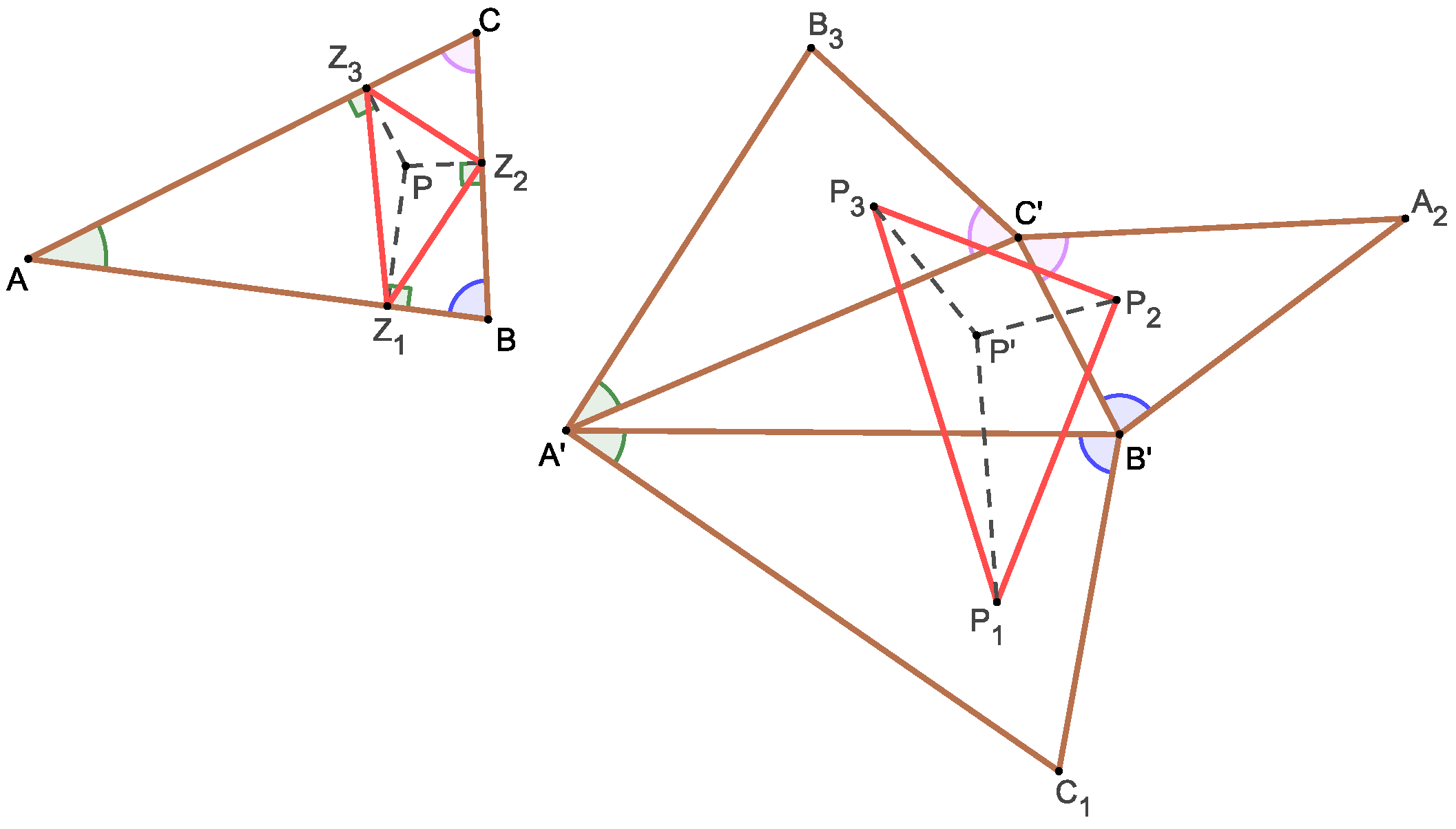
Consider an arbitrary triangle $ABC$ and a point P. Construct an affine image $A^{\prime }{B}^{\prime }{C}^{\prime }$ of the triangle $ABC$ and an affine image $P^{\prime }$ of the point P. Construct mutually similar triangles on the sides $A^{\prime }{B}^{\prime },B^{\prime }{C}^{\prime },C^{\prime }{A}^{\prime }$ such that (Figure 2)

$$ABC\sim A^{\prime }{B}^{\prime }{C}_1\sim A_2{B}^{\prime }{C}^{\prime }\sim A^{\prime }{B}_3{C}^{\prime },$$

where the last three triangles are related to each other by direct similarity. Therefore, either none of the triangles overlap with triangle $A^{\prime }{B}^{\prime }{C}^{\prime }$ or they have a non-empty intersection. Let points $P_1,P_2,P_3$ have the same relative position with respect to the triangles $A^{\prime }{B}^{\prime }{C}_1$, $A_2{B}^{\prime }{C}^{\prime }$, $A^{\prime }{B}_3{C}^{\prime }$ as is the position of the point P with respect to the triangle $ABC$. Finally, let us denote that $Z_1,Z_2,Z_3$ feet of perpendiculars dropped from the point P to the sides $AB,BC,CA$, respectively. Then, the similarity

$$▵Z_1{Z}_2{Z}_3\sim ▵P_1{P}_2{P}_3$$

holds, where the similarity coefficient does not depend on the position of the point P.

Figure 2. Theorem 1 for a triangle. The position of the point P with respect to the triangle $Z_1{Z}_2{Z}_3$ is the same as the position of $P^{\prime }$ with respect to triangle $P_1{P}_2{P}_3$.

Moreover, the position of the point P with respect to the triangle $Z_1{Z}_2{Z}_3$ is the same as the position of the point $P^{\prime }$ with respect to the triangle $P_1{P}_2{P}_3.$

Proof. 

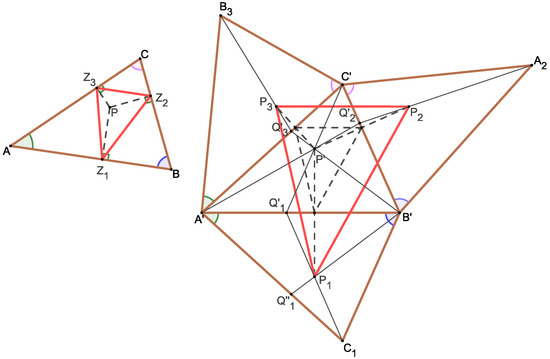
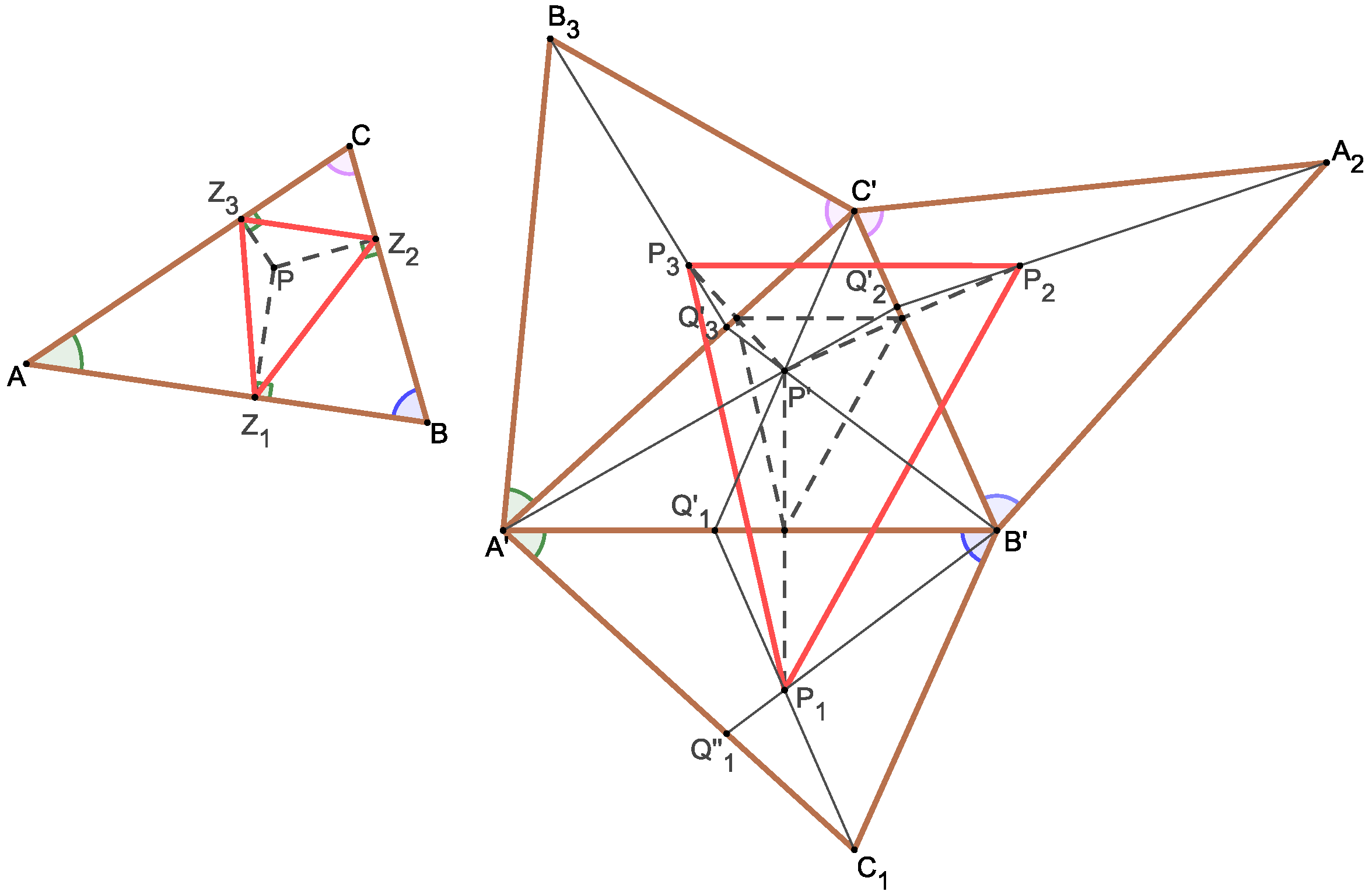
(For an alternative proof of this special case, see Theorem 2 in [11]). Let us start with a simple observation: if the triangles $ABC$ and $A^{\prime }{B}^{\prime }{C}^{\prime }$ are similar, then the statement of the theorem is obviously true (Figure 3), since, in this case, the points $P_1,P_2,P_3$ are reflections of the point $P^{\prime }$ over sides $A^{\prime }{B}^{\prime },B^{\prime }{C}^{\prime },C^{\prime }{A}^{\prime }$, and therefore, the pedal triangle of the point $P^{\prime }$ with respect to the triangle $A^{\prime }{B}^{\prime }{C}^{\prime }$ is similar to the triangle $P_1{P}_2{P}_3$ with the ratio of 1:2. However, the pedal triangle is similar to the triangle $Z_1{Z}_2{Z}_3$ with a ratio of 1:k, where k is the coefficient of the similarity between triangles $A^{\prime }{B}^{\prime }{C}^{\prime }$ and $ABC.$ Thus, the similarity coefficient of triangles $Z_1{Z}_2{Z}_3$ and $P_1{P}_2{P}_3$ is k:2.

Figure 3. This figure refers to two facts: (i) Theorem 1 holds if triangles $ABC$ and $A^{\prime }{B}^{\prime }{C}^{\prime }$ are similar, and (ii) lines $Q_1^{\prime }{C}^{\prime },Q_2^{\prime }{A}^{\prime }$ and $Q_3^{\prime }{B}^{\prime }$ intersect in the affine image $P^{\prime }$ of the point $P,$ whether the triangles are similar or not.

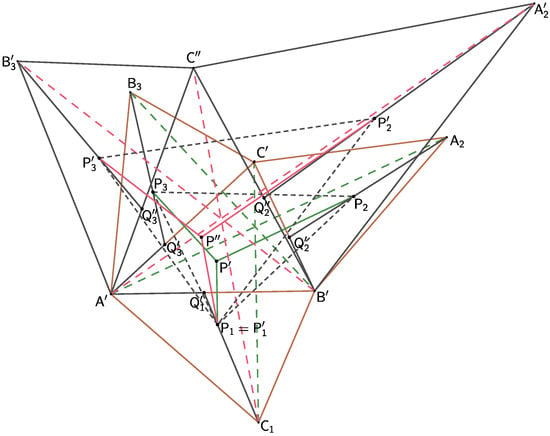
Let us now leave the assumption that triangles $A^{\prime }{B}^{\prime }{C}^{\prime }$ and $ABC$ are similar. Denote $Q_1^{\prime },Q_2^{\prime }$, and $Q_3^{\prime }$ as the intersections of lines $C_1{P}_1,A_2{P}_2$, and $B_3{P}_3$ with lines $A^{\prime }{B}^{\prime },B^{\prime }{C}^{\prime }$, and $C^{\prime }{A}^{\prime }$ (Figure 3). We will show that lines $Q_1^{\prime }{C}^{\prime },Q_2^{\prime }{A}^{\prime }$, and $Q_3^{\prime }{B}^{\prime }$ intersect at the point $P^{\prime }.$

Let $Q_1^{″}$ be the intersection of lines $B^{\prime }{P}_1$ and $A^{\prime }{C}_1$. Now, consider the affinity that transforms the triangle $A^{\prime }{B}^{\prime }{C}_1$ to the triangle $A^{\prime }{B}^{\prime }{C}^{\prime }.$ This affinity maps the point $P_1$ onto $P^{\prime },$ the point $Q_1^{\prime }$ onto itself, and the point $Q_1^{″}$ onto $Q_3^{\prime },$ since

$${\displaystyle \frac{|A^{\prime }{Q}_1^{″}|}{|Q_1^{″}{C}_1|}}={\displaystyle \frac{|A^{\prime }{Q}_3^{\prime }|}{|Q_3^{\prime }{C}^{\prime }|}}.$$

It is due to the fact that the triangles $A^{\prime }{B}^{\prime }{C}_1$ and $A^{\prime }{B}_3{C}^{\prime }$ are similar, and points $P_1$ and $P_3$ have the same relative position with respect to their vertices. Therefore, the line $B^{\prime }{Q}_3^{\prime }$ passes through the point $P^{\prime }.$

Similarly, the line $A^{\prime }{Q}_2^{\prime }$ passes through the point $P^{\prime }$. Moreover, the properties of the affine mapping imply that $C^{\prime }{C}_1\Vert P^{\prime }{P}_1$ and

$${\displaystyle \frac{|Q_1^{\prime }{P}_1|}{|Q_1^{\prime }{C}_1|}}={\displaystyle \frac{|P_1{P}^{\prime }|}{|C_1{C}^{\prime }|}}.$$

The symmetry implies

$$A^{\prime }{A}_2\Vert P^{\prime }{P}_2,{\displaystyle \frac{|Q_2^{\prime }{P}_2|}{|Q_2^{\prime }{A}_2|}}={\displaystyle \frac{|P_2{P}^{\prime }|}{|A_2{A}^{\prime }|}}$$

and

$$B^{\prime }{B}_3\Vert P^{\prime }{P}_3,{\displaystyle \frac{|Q_3^{\prime }{P}_3|}{|Q_3^{\prime }{B}_3|}}={\displaystyle \frac{|P_3{P}^{\prime }|}{|B_3{B}^{\prime }|}}$$

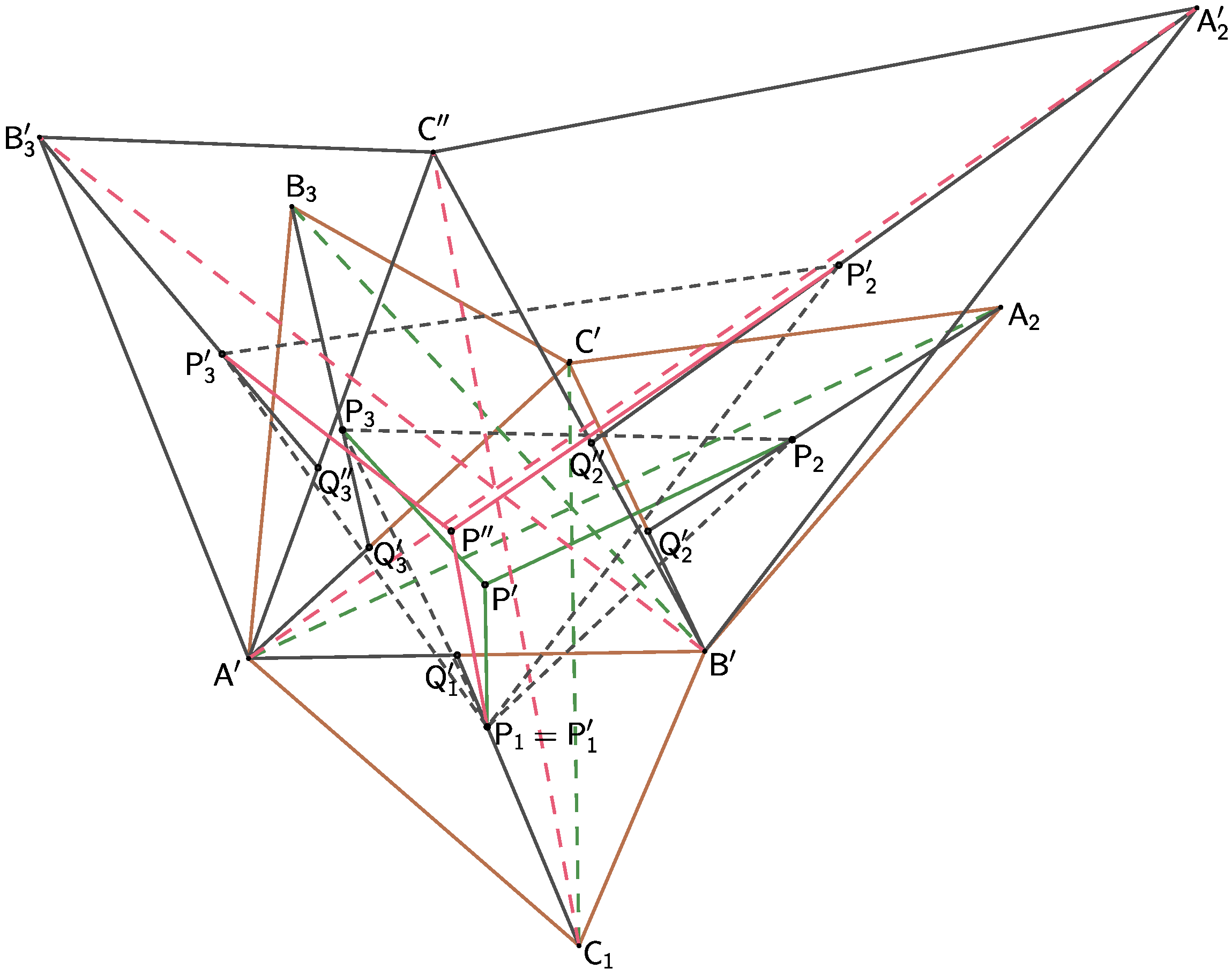
(Figure 4).

Figure 4. For the similar triangle $A^{\prime }{B}^{\prime }{C}^{\prime }$, Theorem 1 holds. It follows that this theorem holds for any triangle $A^{\prime }{B}^{\prime }{C}^{″}$.

Based on the findings that Theorem 1 holds for similar triangles $ABC\sim A^{\prime }{B}^{\prime }{C}^{\prime }$ and that the lines $Q_1^{\prime }{C}^{\prime }$, $Q_2^{\prime }{A}^{\prime }$, and $Q_3^{\prime }{B}^{\prime }$ intersect in the affine image $P^{\prime }$ of the point P for arbitrary triangles $ABC$ and $A^{\prime }{B}^{\prime }{C}^{\prime }$, we now prove the validity of the theorem in its entirety. We will consider triangle $ABC,$ then triangle $A^{\prime }{B}^{\prime }{C}^{\prime }$, which, as noted above, will be similar to the triangle $ABC,$, and finally an arbitrary triangle $A^{\prime }{B}^{\prime }{C}^{″},$ for which we will show that the theorem is also true.

All new points in the configuration of triangle $A^{\prime }{B}^{\prime }{C}^{″}$ are distinguished from points in the original configuration of the similar triangle $A^{\prime }{B}^{\prime }{C}^{\prime }$ by adding a dash $Q_3^{\prime }\leftrightarrow Q_3^{″},P_3\leftrightarrow P_3^{\prime },B_3\leftrightarrow B_3^{\prime },P^{\prime }\leftrightarrow P^{″},\dots$ (Figure 4).

We know that the line $P^{″}{P}_3^{\prime }$ is parallel to the line $B^{\prime }{B}_3^{\prime }$, and the line $P^{\prime }{P}_3$ is parallel to the line $B^{\prime }{B}_3.$ Furthermore,

$${\displaystyle \frac{|P^{″}{P}_3^{\prime }|}{|B^{\prime }{B}_3^{\prime }|}}={\displaystyle \frac{|Q_3^{″}{B}_3^{\prime }|}{|Q_3^{″}{P}_3^{\prime }|}}={\displaystyle \frac{|Q_3^{\prime }{B}_3|}{|Q_3^{\prime }{P}_3|}}={\displaystyle \frac{|P^{\prime }{P}_3|}{|B^{\prime }{B}_3|}}.$$

Therefore,

$${\displaystyle \frac{|P^{″}{P}_3^{\prime }|}{|P^{\prime }{P}_3|}}={\displaystyle \frac{|B^{\prime }{B}_3^{\prime }|}{|B^{\prime }{B}_3|}}.$$

By analogy, we arrive at the equalities

$${\displaystyle \frac{|P^{″}{P}_2^{\prime }|}{|P^{\prime }{P}_2|}}={\displaystyle \frac{|A^{\prime }{A}_2^{\prime }|}{|A^{\prime }{A}_2|}},{\displaystyle \frac{|P^{″}{P}_1|}{|P^{\prime }{P}_1|}}={\displaystyle \frac{|C^{″}{C}_1|}{|C^{\prime }{C}_1|}}$$

and parallelism of segments

$$P^{″}{P}_2^{\prime }\Vert A^{\prime }{A}_2^{\prime },P^{\prime }{P}_2\Vert A^{\prime }{A}_2,P^{″}{P}_1\Vert C_1{C}^{″},P^{\prime }{P}_1\Vert C^{\prime }{C}_1.$$

Thus, to prove that the pattern formed by the points $P^{\prime },P_1,P_2,P_3$ is similar to the pattern formed by the points $P^{″},P_1,P_2^{\prime },P_3^{\prime },$ it is sufficient to show that the pairs of segments $(C^{\prime }{C}_1,C^{″}{C}_1)$, $(B^{\prime }{B}_3,B^{\prime }{B}_3^{\prime })$, and $(A^{\prime }{A}_2,A^{\prime }{A}_2^{\prime })$ are in the same ratio and make the same angle. In other words, it is enough to prove the similarity of the triangles

$$▵B_3^{\prime }{B}^{\prime }{B}_3\sim ▵C^{″}{C}_1{C}^{\prime }\sim ▵A_2^{\prime }{A}^{\prime }{A}_2.$$

(1)

It is sufficient to prove only the first similarity; the second one follows from symmetry. The similarity of triangles

$$▵C_1{A}^{\prime }{C}^{″}\sim ▵B^{\prime }{A}^{\prime }{B}_3^{\prime }$$

(2)

follows from the fact that they have the same angle at the vertex $A^{\prime }$ and due to the similarity

$$▵A^{\prime }{B}^{\prime }{C}_1\sim ▵A^{\prime }{B}_3^{\prime }{C}^{″}$$

the equality of ratios

$${\displaystyle \frac{|A^{\prime }{B}^{\prime }|}{|A^{\prime }{C}_1|}}={\displaystyle \frac{|A^{\prime }{B}_3^{\prime }|}{|A^{\prime }{C}^{″}|}}$$

is valid.

By analogy, we arrive at the similarity

$$▵C_1{A}^{\prime }{C}^{\prime }\sim ▵B^{\prime }{A}^{\prime }{B}_3.$$

(3)

Since both similarities (2) and (3) are direct, (1) follows.

It remains to show that the similarity coefficient of the triangle $P_1{P}_2^{\prime }{P}_3^{\prime }$ and the pedal triangle of the point P does not depend on the position of the point $P.$ We know that this is true for $▵P_1{P}_2{P}_3,$ but the similarity of triangles $P_1{P}_2^{\prime }{P}_3^{\prime }$ and $P_1{P}_2{P}_3$ is determined by the coefficient

$$s={\displaystyle \frac{|P_1{P}^{″}|}{|P_1{P}^{\prime }|}}$$

(4)

which is fixed by the affinity converting the triangle $A^{\prime }{B}^{\prime }{C}_1$ into the triangle $A^{\prime }{B}^{\prime }{C}^{″}.$

Since the triangle $A^{\prime }{B}^{\prime }{C}_1$ is determined by its side $A^{\prime }{B}^{\prime }$ and the original triangle $ABC,$ we can conclude the following: Given triangles $ABC$ and $A^{\prime }{B}^{\prime }{C}^{″},$ the affinity and ratio (4) are determined uniquely, and therefore, the similarity coefficients of triangles $Z_1{Z}_2{Z}_3$ and $P_1{P}_2{P}_3$ are the same for all points $P.$ □

3. Step Two: Generalization of Theorem 1 to an Arbitrary n-gon

As shown in the previous step, the mapping between the points

$$P,Z_1,Z_2,Z_3\to P^{\prime },P_1,P_2,P_3$$

is a similarity. For the next considerations, we will identify the triangle $ABC$ with the triangle $A^{\prime }{B}^{\prime }{C}_1.$ We define the mapping $M\left(P_1\right)$ as follows.

Let an affinity F be given by an axis $g,$ a point $P_1$, and its image $P^{\prime }.$ Consider all triangles $A^{\prime }{B}^{\prime }{C}_1$ and $A^{\prime }{B}^{\prime }{C}^{\prime }$ related to the given affinity F. That is, all sides $A^{\prime }{B}^{\prime }$ of the variable triangles lie on the given axis g. Now, we fix the point $P_1.$ Denote the foot of the perpendicular from $P_1$ to the g-axis by $Z_1$ and the feet of perpendiculars to other sides of any $▵A^{\prime }{B}^{\prime }{C}_1$ by $Z_2,Z_3,\dots ,Z_n$ with n given by the number of triangles taken into account.

For arbitrary triangles $A^{\prime }{B}^{\prime }{C}_1$ and $A^{\prime }{B}^{\prime }{C}^{\prime }$ related to the given affinity, construct triangles $A_2{B}^{\prime }{C}^{\prime }$ and $A^{\prime }{B}_3{C}^{\prime }$ to be directly similar to the triangle $A^{\prime }{B}^{\prime }{C}_1.$ Let points $P_2$ and $P_3$ be in the same relative position with respect to these triangles as the point $P_1$ is with respect to the triangle $A^{\prime }{B}^{\prime }{C}_1.$ As proven in Theorem 2, there is a similar mapping that transforms the points

$$P_1,Z_1,Z_2,Z_3,Z_4,\dots$$

to the points

$$P^{\prime },P_1,P_2,P_3,P_4,\dots .$$

Let us emphasize that this mapping is the same for all points $Z_n,$ because, for any triple, it is a similar mapping

$$P_1,Z_1,Z_X,Z_Y\to P^{\prime },P_1,P_X,P_Y$$

(5)

with a common coefficient (4). In accordance with the current notation, we rewrite this coefficient in the following form:

$$s={\displaystyle \frac{|P_1{P}^{\prime }|}{2|P_1{Z}_1|}}.$$

The coefficient $2s$ is constant for a given affinity. The points $P_1,Z_1$ and their images $P^{\prime },P_1$ are fixed by the assumption. The similarity is therefore either direct or indirect, but it cannot alternate; otherwise, we would get into a contradiction with the relation (5).

Note: Direct or indirect similarity depends on affinity, presumably on whether the point and its image lie on the same side or on opposite sides of the axis. We will not consider this question here.

Let us summarize the previous considerations in a theorem:

Theorem 3.

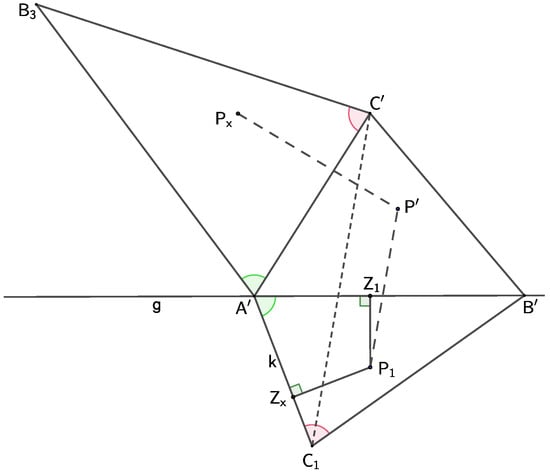
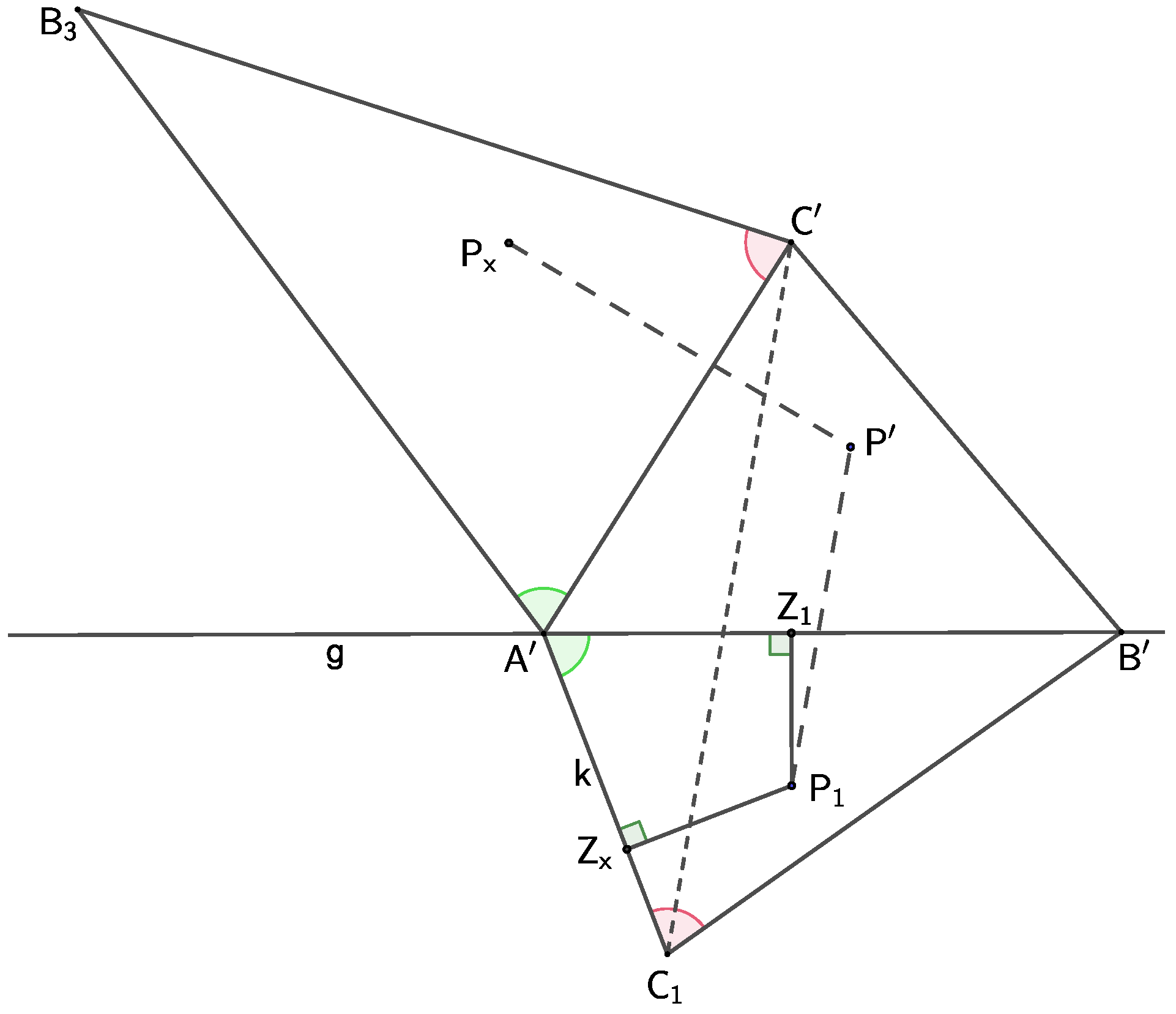
Consider the affinity F and its axis $g.$ Given a point $P_1$ and its image $P^{\prime }$ in the affinity $F,$ let the mapping $M\left(P_1\right)$ assign to each point $Z_X$ a point $P_X$ by the following algorithm (Figure 5):

Figure 5. Mapping $M\left(P_1\right)$. The affinity F and the point $P_1$ are given. Then, the construction procedure is a similarity.

• Construct a perpendicular k to the segment $P_1{Z}_X$ passing through the point $Z_X.$ Let it intersect the axis g at the point $A^{\prime }$ (or $B^{\prime }$).
• Choose any point $C_1$ on the line k and any point $B^{\prime }$ (or $A^{\prime }$) on the axis $g.$ It determines $▵A^{\prime }{B}^{\prime }{C}_1.$
• Construct the affine image $A^{\prime }{B}^{\prime }{C}^{\prime }$ of the $▵A^{\prime }{B}^{\prime }{C}_1.$
• Construct $▵A^{\prime }{B}_3{C}^{\prime }$ (or $A_2{B}^{\prime }{C}^{\prime }$) directly similar to the $▵A^{\prime }{B}^{\prime }{C}_1.$
• Construct the point $P_X$ in the same relative position with respect to $▵A^{\prime }{B}_3{C}^{\prime }$ as the position of the point $P_1$ with respect to $▵A^{\prime }{B}^{\prime }{C}_1.$
• Definition: the image of the point $Z_1$ (the foot of the perpendicular from $P_1$ to the line g) is the point $P_1.$

The mapping $M\left(P_1\right)$ between points

$$P_1,Z_1,Z_2,Z_3,Z_4,\dots \to P^{\prime },P_1,P_2,P_3,P_4,\dots$$

defined in this way is a similarity. Moreover, no matter which point $P_1$ we choose, assuming a fixed affinity, the similarity coefficient given by

$$k={\displaystyle \frac{|P_1{P}^{\prime }|}{|P_1{Z}_1|}}$$

is constant, as implied by the affine-mapping property.

4. Step Three: Final Completion of Theorem 1

The proof of Theorem 1 is a corollary of Theorem 3. This is because the affinity F between the polygons $A^{\prime }{B}^{\prime }{C}_1{D}_1\dots X_1{Y}_1$ and $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }\dots X^{\prime }{Y}^{\prime }$ is given, and every point $P_2,P_3,\dots P_n$ can be constructed using the point $P_1$ by the algorithm described in Theorem 3. Therefore, the mapping $M\left(P_1\right)$ is a similarity. As is obvious, the pedal polygon of the point $P_1$ with respect to the polygon $A^{\prime }{B}^{\prime }{C}_1{D}_1\dots X_1{Y}_1$ is similar to the pedal polygon of the point P with respect to the original polygon $ABCD\dots XY.$ The theorem is proven for an arbitrary n-gon.

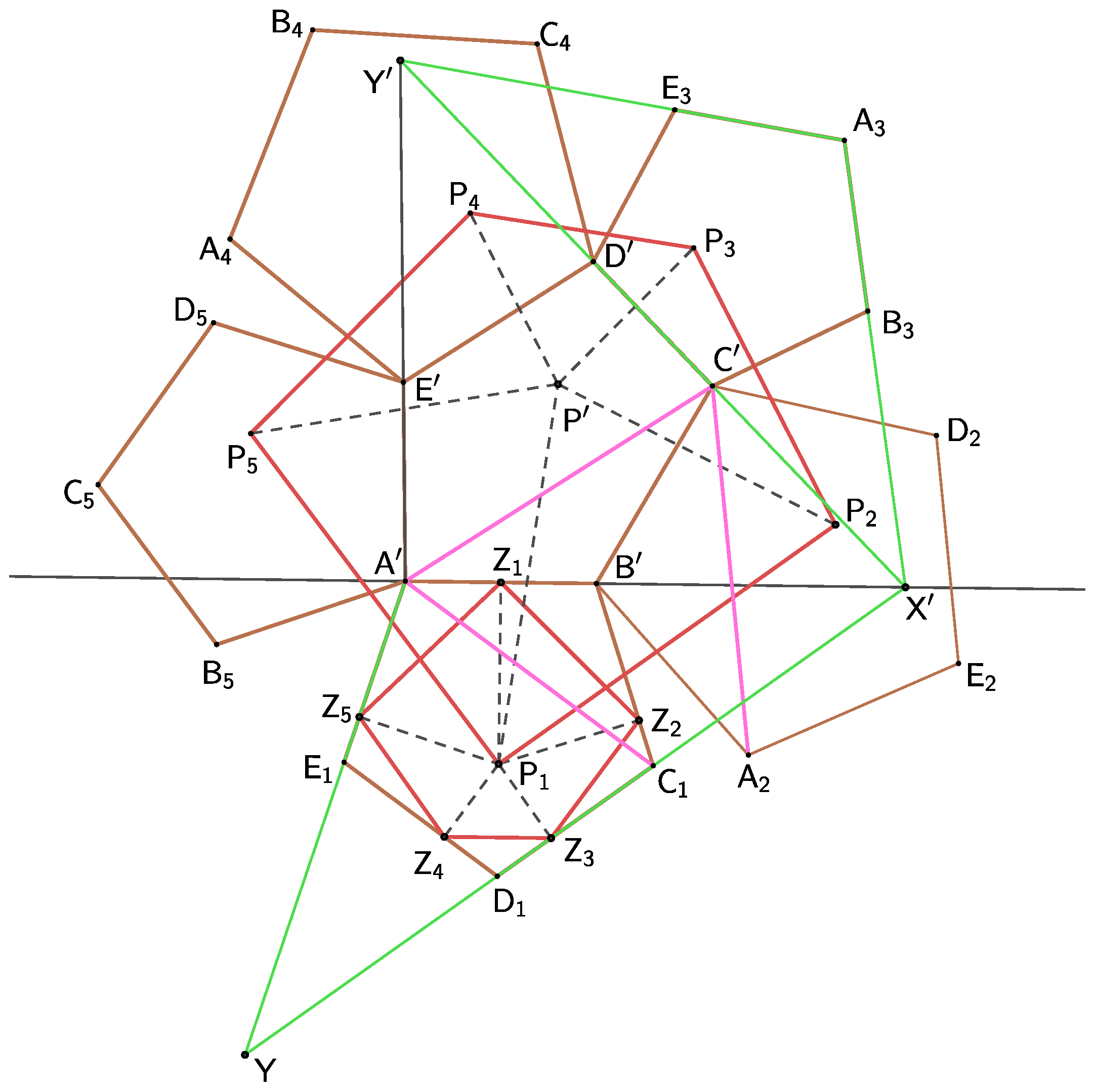
Let us show a concrete example for a regular pentagon and an arbitrary point $P_1.$

Example 1.

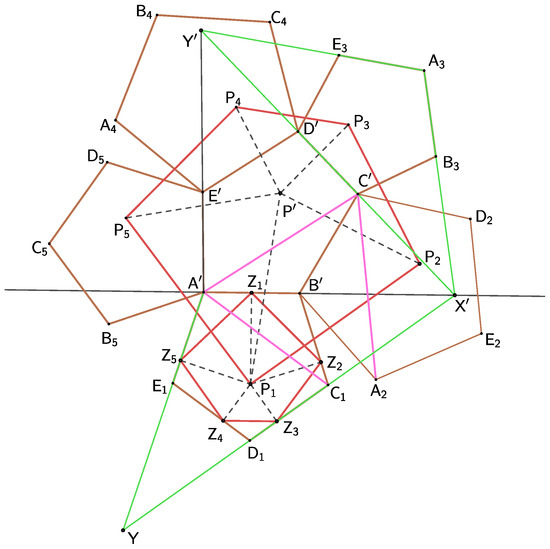
Consider a regular pentagon $A^{\prime }{B}^{\prime }{C}_1{D}_1{E}_1$ and its affine image $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }{E}^{\prime }$. Let the affine axis be the line $A^{\prime }{B}^{\prime }$ (Figure 6). Next, consider a point $P_1$ and feet $Z_1,Z_2,Z_3,Z_4,Z_5$ of perpendiculars dropped from $P_1$ to the sides $A^{\prime }{B}^{\prime },B^{\prime }{C}_1,$$C_1{D}_1,D_1{E}_1$, and $E_1{A}^{\prime }$, respectively.

Figure 6. Theorem 1 for a regular pentagon $A^{\prime }{B}^{\prime }{C}_1{D}_1{E}_1$ and its affine image $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }{E}^{\prime }{F}^{\prime }.$ The points $P_2,P_3,\dots ,P_5$ can be constructed in two equivalent ways: as points with the same relative position with respect to their actual pentagon or using the algorithm described in Theorem 3.

The construction of the point $P_2$ corresponding to the pentagon $A_2{B}^{\prime }{C}^{\prime }{D}_2{E}_2$ is carried out as follows: consider $▵A^{\prime }{B}^{\prime }{C}_1$ and point $P_1,$ then consider the affine image $A^{\prime }{B}^{\prime }{C}^{\prime }$ of the triangle, and then construct the $▵A_2{B}^{\prime }{C}^{\prime }$ and the point $P_2,$ which has the same relative position with respect to $▵A_2{B}^{\prime }{C}^{\prime }$ as point $P_1$ has to $▵A^{\prime }{B}^{\prime }{C}_1$. However, it is the mapping $M\left(P_1\right)$ defined in Theorem 3 that maps the point $Z_2$ to the point $P_2.$

By analogy, consider the pentagon $A_3{B}_3{C}^{\prime }{D}^{\prime }{E}_3$ and its corresponding point $P_3.$ It is the same point that we obtain by the following procedure. By extending the segments $C_1{D}_1$ and $E_1{A}^{\prime }$, we get $▵A^{\prime }{X}^{\prime }Y.$ Let the point $X^{\prime }$ lie on the axis. In the same way, by extending the segments $A^{\prime }{E}^{\prime }$ and $C^{\prime }{D}^{\prime },$ we achieve the $▵A^{\prime }{X}^{\prime }{Y}^{\prime }.$ The point $Z_3$ is the foot of the perpendicular dropped from the point $P_1$ to the line $X^{\prime }Y$. Now, construct the $▵A_3{X}^{\prime }{Y}^{\prime }$ to be directly similar to the $▵A^{\prime }{X}^{\prime }Y,$ and its corresponding point $P_3^{\prime }.$ It is not difficult to verify that $P_3^{\prime }=P_3.$ We have arrived at the same map $M\left(P_1\right)$ (affinity is the same); now, map the point $Z_3$ to the point $P_3.$ We can therefore conclude that the pedal polygon $Z_1{Z}_2{Z}_3{Z}_4{Z}_5$ is similar to the polygon $P_1{P}_2{P}_3{P}_4{P}_5.$

The Napoleon-Barlotti theorem is a direct consequence of Theorem 1.

5. Conclusions

In this article we have proven a theorem of which the Napoleon–Barlotti theorem is a special case.

Note that most theorems belonging to the family of the Petr–Douglas–Neumann theorems are proven by algebraic methods. In this paper, we proved NBT and its generalization for arbitrary n using classical geometry. Although this classical geometric proof may seem rather long, we hope that this approach will enrich the proof techniques for this family of theorems.