Abstract
In this paper, we propose a class of elementary plane geometry problems closely related to the title of this paper. Here, a circle is the one-dimensional curve bounding a disk. For any non-negative integer, a circle is called n-enclosing if it contains exactly n lattice points on the -plane in its interior. In this paper, we are mainly interested in when the largest n-enclosing circle exists and what the largest radius is. We study the small integer cases by hand and extend to all with the aid of a computer. We find that frequently such a circle does not exist, e.g., when . We then show a few general results on these circles including some regularities among their radii and an easy criterion to determine exactly when the largest n-enclosing circles exist. Further, from numerical evidence, we conjecture that the set of integers whose largest enclosing circles exist is infinite, and so is its complementary in the set of non-negative integers. Throughout this paper, we present more mysteries/problems/conjectures than answers/solutions/theorems. In particular, we list many conjectures and some unsolved problems including possible higher-dimensional generalizations at the end of the last two sections.
MSC:
52C05; 52A10; 52C15; 52C25; 52C26; 52C35
1. Introduction
There are many naive-looking number theory problems, such as the twin prime conjecture and the Goldbach conjecture, whose solutions are extremely difficult and remain unsolved until this day. Many geometry problems have also fascinated human kind for millennia, e.g., the Pythagorean theorem, known to Babylonians well before Pythagoras and named “Gou-Gu theorem” in the East, and the much deeper Poincare conjecture on sphere packing, one of the Millennium Prize Problems.
In this paper, we propose to study a class of seemingly naive plane geometry problems concerning circles and lattice points on the -plane. Here, a circle means the one-dimensional circumference of a disk and a lattice point is a point on the -plane with integer coordinates.
We first recall a famous result of H. Steinhaus first stated as Problem 24 on page 17 of his book [1] (also see [2,3]) and then answered on page 84.
Theorem 1.
For every positive integer n, there exists a circle of area n enclosing exactly n lattice points in its interior.
In fact, the original problem did not have the condition on the area. Honsberger [4] (p. 118) further strengthened it by restricting the area to be n. Several years earlier, Schinzel [5] showed that for every positive integer n, there exists a circle on the plane having exactly n lattice points on its circumference, which was given the name Schinzel circle. Also see [4] (p. 118). For any circle of radius r centered at the origin, it is well known that the number of lattice points in the interior and on the boundary is given by
See, e.g., Refs. [6] or [7] (Equation (8). The sequence is the sequence [A000328] on the OEIS website [8]. By considering the area one can see that the number is close to for large r. In particular, one may find the following estimate credited to Gauss in Hardy’s book [9] (p. 67):
We will present a related result in Theorem 9 with a short proof. Incidentally, the error bound for can be further improved which turns out to be a significant problem having close connection with analytic number theory and therefore has attracted quite some work throughout the past century. See [7,10,11,12,13,14,15,16,17].
In another direction, we found the following as Problem 634 on p. 57 of [18]:
What is the radius of the largest circle that you can draw on graph paper that encloses
To answer the above questions it is intuitively helpful to draw the pictures using some computer software so that the radii of the circles can be varied continuously. We have used Geogebra heavily in our experiments.
To generalize the above questions we need to introduce some terminology. We call a non-negative integer nmaximally circlable (The word “circlable” does not really exist in English. Perhaps a more precise version should be maximally enclosable by a circle. But the acronym MEBAC is still too long compared to MC), if there exists a largest circle enclosing exactly n lattice points in its interior. Otherwise n is called non-maximally circlable (non-MC). Since such circles might not be unique what we mean by “largest” is the largest radius of these circles. For brevity, we will often drop “exactly” and “in its interior” in the rest of the paper.
For convenience, we fix the key triangle as the triangle with vertices at , , and , including both its interior and its boundary. If n is MC then we let be a largest circle enclosing n lattice points with its center O, called an MC-circle of n, and let be its radius, called the MC-radius of n. By translations horizontally and vertically, we see that O can be moved to the unit square in the first quadrant adjacent to the origin. By rotating around the center of this square, we may further assume O is in the south-east sub-square of this unit square. Then a reflection about the line can send O to if it is not already there. We call the operations as above rigid motions of the lattice system (i.e., isometries keeping the grid invariant) (It is easy to see that all grid invariant isometries are given by translations by integer values, reflections about integers or half integer or integers, and rotations by multiples of around a lattice point or around the center of a unit square). Therefore, every MC-circle of n can be transformed to with .
For convenience, we call a set of n lattice points a MC-set of n if an MC-circle of n encloses them. A circle is called a lattice circle if it has at least three lattice points on its circumference. From overwhelming evidence, we formulate the following conjectures.
Conjecture 1.
For any MC integer n, both the configuration of the MC-set and the MC-circle of n are unique up to rigid motions of the lattice system.
We want to caution the reader that for a fixed integer n there may be different n-enclosing lattice circles with different configurations of the n-lattice points even under rigid motions. But most of these circles are not the MC-circle of n. See, e.g., the two 89-enclosing circleson page 16.
Key Notation and Terminology. Throughout the paper, we adopt the convention that means n is MC and is its MC-radius. On the other hand, the notation means n is non-MC and is the least upper bound of the radii of all the n-enclosing circle. This is a little mouthful and therefore we will use the acronym LUBOR of n in the rest of the paper. We also emphasize that the notation and are always reserved for this purpose. When we say “enclose” we always mean to contain inside but not on the boundary/circumference.
We will primarily focus on the following questions in this paper.
Main Problem 1.
Let n be a non-negative integer.
- (1)
- When is n MC? When is n non-MC? Are there good criteria?
- (2)
- How to determine MC-radius of n if n is MC?
- (3)
- How to determine LUBOR of n if n is non-MC?
- (4)
- Is there a largest n-enclosing lattice circle?
We will answer Main Problem 1(1)–(4) for all . In this range, we also find that the answer to Main Problem 1(4) is affirmative for all but cannot confirm this in general at present. However, we can show that the MC-circles of n are all lattice circles in Theorem 4.
For examples, we will prove in Theorem 2 that which means the largest circle enclosing four lattice points exists and its radius is . It is quite obvious that four lattice points form an MC-set of four if and only if they form a unit square, which confirms Conjecture 1.
In Theorem 3, we will prove that and , i.e., the largest circles enclosing five or six lattice points do not exist and their LUBOR are both . This phenomenon relating the LUBOR of a non-MC number to some MC-radius of a smaller MC number should continue to hold for other non-MC numbers. We will confirm this in Theorem 7 which provides a satisfactory answer to Main Problem 1(3).
Concerning the relations between different MC-radii and the LUBORs, we have the following main results.
Main Theorem 1.
Let be the positive sequence of MC-radii (for MC n) and LUBORs (for non-MC n). Then we have the following:
- (1)
- (=Theorem 5) is a non-decreasing sequence.
- (2)
- (=Theorem 7) Suppose are two consecutive MC numbers and n is non-MC such that . Then , namely, is the LUBOR for all such non-MC n immediately following k.
- (3)
- (=Corollary 2) Suppose , k is an MC number and all the numbers between k and n (exclusive) are non-MC. Then the radius of the largest n-enclosing lattice circle is strictly smaller than if and only if n is non-MC.
We now briefly describe the content of this paper. We start with small integers in the next section and provide a few essential ideas to be used in the general case. In Section 3, we state a few general results including those in the Main Theorem, which provide the foundation for our computer computation in Section 5.
Section 4 focuses on two special classes of lattice circles which likely will include infinitely many MC-circles. Most of our computational results are then presented in Section 5 which completely solves Main Problems 1 for all . We then conclude the paper with a brief summary and some further problems for possible future research at the end of the last two sections.
2. Small Numbers: n ≤ 18
We can treat the cases with through pure geometric argument.
Theorem 2.
The MC-radii , , , , and .
Proof.
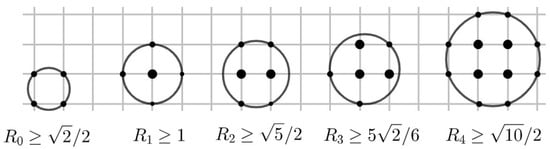
We give detailed proofs of these cases because, although they are simple, they reflect most of the main ideas one can use to prove the general MC cases.
First, the circles in Figure 1 imply the lower bounds of for . Now we need to show the opposite inequalities so that are equal to these values, respectively.

Figure 1.
The largest circles enclosing zero to four lattice points.
. Let O be the center of a circle whose radius . We now show that it must enclose at least one lattice point, which implies that and so . Indeed, as we explained in the introduction we may assume as shown in the picture  . Then the lower right corner point is at most away from O and therefore must lie in the interior of the circle O of radius .
. Then the lower right corner point is at most away from O and therefore must lie in the interior of the circle O of radius .
 . Then the lower right corner point is at most away from O and therefore must lie in the interior of the circle O of radius .
. Then the lower right corner point is at most away from O and therefore must lie in the interior of the circle O of radius .. Let be the center of a circle whose radius . We now show that it must enclose at least two lattice points, which implies that and so . By the picture  , the bottom two vertices and are at most 1 unit away from O and therefore must lie in the interior of the circle O of radius .
, the bottom two vertices and are at most 1 unit away from O and therefore must lie in the interior of the circle O of radius .
 , the bottom two vertices and are at most 1 unit away from O and therefore must lie in the interior of the circle O of radius .
, the bottom two vertices and are at most 1 unit away from O and therefore must lie in the interior of the circle O of radius .. Let be the center of a circle whose radius . We now show that it must enclose at least three lattice points, which implies that and so . By the picture  the bottom two lattice vertices and already lie in the interior of the circle O of radius . Further, the upper right corner point of the square is at most away from O and therefore must lie in the interior of the circle O of radius .
the bottom two lattice vertices and already lie in the interior of the circle O of radius . Further, the upper right corner point of the square is at most away from O and therefore must lie in the interior of the circle O of radius .
 the bottom two lattice vertices and already lie in the interior of the circle O of radius . Further, the upper right corner point of the square is at most away from O and therefore must lie in the interior of the circle O of radius .
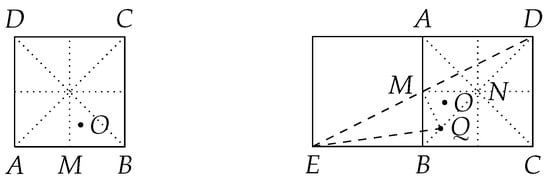
the bottom two lattice vertices and already lie in the interior of the circle O of radius . Further, the upper right corner point of the square is at most away from O and therefore must lie in the interior of the circle O of radius .. Let be the center of a circle whose radius . We now show that it must enclose at least four lattice points, which implies that . Continuing the argument in the case of we may assume the left picture in Figure 2 in which the three lattice points A, B and C are already in the interior of the circle O.

Figure 2.
Circles with radius must enclose at least four lattice points.
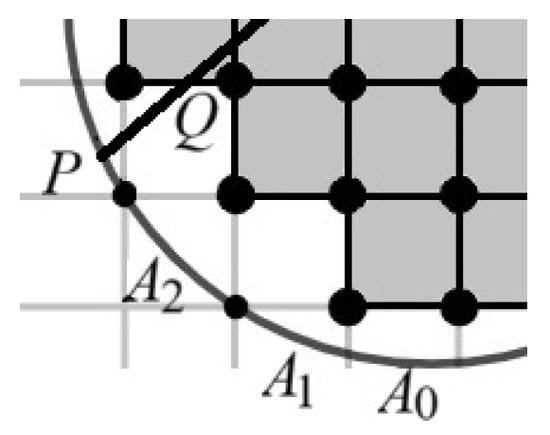
Let N be the center of . To save space, we rotate the picture clockwise by 90°. Now mark the point Q on so that as shown by the right picture in Figure 2. Then and divides into two smaller triangles. If O is in then
If O is in then
So the fourth point, either D or E, lies in the interior of the circle O of radius .
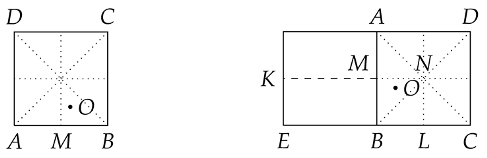
. This case turns out to be easy because of the apparent symmetry. Let be the center of a circle whose radius . Since it is easy to see that all the four corners of the unit square must lie in the interior of the circle. Let N be the center of and rotate the square clockwise by 90° to save space.

Then
since O is in the rectangle with diagonal . Hence five lattice points A, B, C, D and E are all in the interior of the circle O. □
Moving on to the next case, we will see that the largest circle enclosing exactly five lattice points does not exist. Namely, 5 is the first non-MC number. We now give detailed proof of this case which contains basically all the main ideas one may use to prove the general non-MC cases. We first prove the following two lemmas.
Lemma 1.
Every circle of radius must enclose exactly four lattice points or at least seven lattice points. For any real number , every circle of radius r must enclose at least seven lattice points.
Proof.
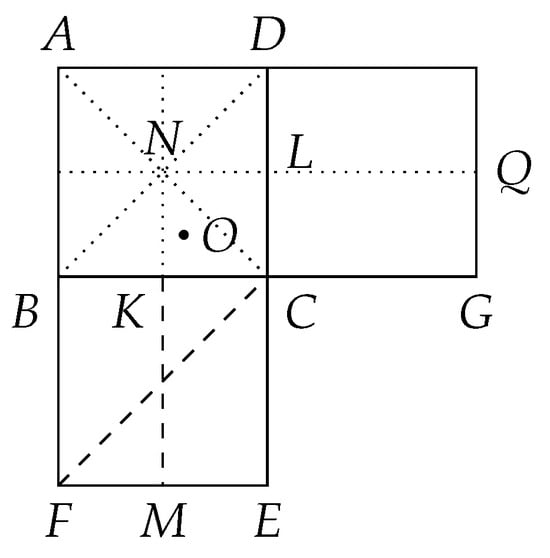
Let be the center of a circle whose radius . If and then clearly the circle encloses exactly four lattice points as shown in Figure 1. If but then clearly the circle encloses at least 12 lattice points.
Now we assume and . Then the circle encloses all the four corners of the unit square since . We now show it encloses at least three more lattice points. We now add two adjacent unit squares as shown in the picture of Figure 3.

Figure 3.
Circles with radius whose center is not at the center of any unit square must enclose at least seven lattice points.
Since , we have
since O is in the rectangle with diagonal and in the rectangle with diagonal . Further, in the right triangle
Thus the three lattice points G, E and F, together with and D, are all in the interior of the circle O. This completes the proof of the lemma. □
To prove the next lemma, we need borrow some ideas from calculus involving the concepts of limit and continuity.
Lemma 2.
There exists a small such that for any real number , there is a circle of radius r enclosing exactly five lattice points and a circle of radius r enclosing exactly six lattice points.
Proof.
The proof uses essentially the same idea as the one for Theorem 5 in the next section. One can also just use that theorem instead of this ad hoc lemma to prove Theorem 3. □
By combining the above two lemmas we achieve the following result immediately.
Theorem 3.
We have for .
Proof.
Lemma 1 implies that for , while Lemma 2 (or Theorem 5 more precisely) shows that , whence the claim in the theorem. □
We can mimic the ideas used in the proof of Theorems 2 and 3 to deal with the cases, say, , by hand. We summarize our computation in Table 1. The interested reader may find all the details in an extended version of this paper with the same title at arxiv.org/abs/2505.06234.

Table 1.
Radii of largest n-enclosing circle for MC n, or its least upper bound for non-MC n.
3. Some General Results
In this section, we will provide a few general statements concerning the MC (resp. non-MC) numbers and their corresponding MC-radii (resp. LUBORs). They will provide us a theoretical foundation for our computer search to be carried out in the next section. Recall that a lattice circle has at least three lattice points on its circumference.
Theorem 4.
If n is MC then its MC-circle must be a lattice circle.
Proof.
Indeed, if has at most two lattice points on its circumference then we can continuously increase its size while keeping both these point on and the number of interior lattice points unchanged. This contradicts the maximality of . □
Theorem 5.
Let be the positive sequence of MC-radii (for MC n) and LUBORs (for non-MC n). Then is a non-decreasing sequence.
Proof.
We prove that for any integer .
Choose to be the largest n-enclosing circle if n is MC by Theorem 4 and let . If n is non-MC then let be any circle of radius such that encloses n points. In the latter case, by continuously deforming while keeping r non-decreasing we may assume contains at least one lattice point A on its circumference. Indeed, if there is no lattice point on then let A be one of the lattice points outside that is closest to the center of the circle with the radial distance to its boundary equal to d. Next, we enlarge the radius of by and then move the circle towards A by so that A lies on the circumference of while the number of interior lattice points is unchange. This is possible since the smallest distance of any point outside is at least d, and an increasing of radius by followed by a move of the circle center by a distance will not touch the point unless the final move is directly towards it.
We next show that we can deform by an infinitesimal amount and then move it to include one more point in its interior.
Let A be a lattice point on . While keeping A on the circumference of we may pull the center O of towards A by an infinitesimal amount so that A becomes the only lattice point on the new circle and the number of lattice points inside is still equal to n. A tiny perturbation of center of towards A while keeping the same radius unchanged will now include A in its interior.
The above argument implies that by the definition of either as an MC-radius or a LUBOR. Since if n is MC and but can be arbitrarily close to if n is non-MC, by taking we arrive at the desired conclusion . □
Theorem 6.
Let n be non-MC and let be its LUBOR. Then there is a lattice circle centered at with radius and a sequence of circles centered at of radius () enclosing the same set of n lattice points such that the limit .
Proof.
By rigid motions, we may assume without loss of generality that all circles we consider have centers in . It is clear that there are infinitely many n-enclosing circles by continuity argument. By the definition of , there exists a sequence of such circles whose radii approach in the limit. Moreover, there are only finitely many different configurations of n lattice point sets inside these circles. Therefore, there is a subsequence of infinitely many such circles whose radii approach in the limit and which contain the same set of n lattice points. Suppose on the contrary the radius circle is not a lattice circle, then the same argument as used in the proof of Theorem 4 implies that is not an upper bound of the radii of all n-enclosing circles, which contradicts the assumption. □
Remark 1.
Notice that the circle in Theorem 6 cannot be lattice circles for all sufficiently large j by discreteness of lattice circles. And the circle must not be the largest n-enclosing lattice circle; otherwise, it would contradicts the condition that n is non-MC.
The next corollary quickly follows from Theorems 4 and 6.
Corollary 1.
For every non-negative integer n, either as an MC-radius or as a LUBOR, is the radius of some lattice circle.
Theorem 7.
Suppose are two consecutive MC numbers and n is non-MC such that . Then , namely, is the LUBOR for all such non-MC n immediately following k.
Proof.
Let be a non-MC given as in the theorem, . We now prove the theorem by induction on j.
If , by definition of the LUBOR , if then there is some such that a circle of radius r encloses exactly n lattice points. By Theorem 6, is the radius of some lattice circle and there is a sequence of circles enclosing the same set S of n lattice points with radii . Notice that in the limit the circle cannot enclose any other points than S but it might lose some in S to its boundary. Therefore, the number of lattice points in , say m, must be no more than n. Since n is non-MC, cannot contain exactly n-points, that is, . Thus its radius by the definition of and Theorem 5. But by the same theorem as and therefore .
Suppose and suppose . Then by the same argument as above we see that for some . By induction assumption and Theorem 5, we see immediately that . As we already know by Theorem 5 since , we must have . This completes the proof of the theorem. □
Corollary 2.
Suppose and k is an MC number and all the numbers between k and n (exclusive) are non-MC. Then the radius of the largest n-enclosing lattice circle is strictly smaller than if and only if n is non-MC.
Proof.
Suppose C is the largest n-enclosing lattice circle with radius r. If n is MC then C is an MC-circle of n and therefore its radius by Theorem 5. On the other hand, if n is non-MC then by Theorem 7. □
Definition 1.
For any MC number n, the length of the longest consecutive non-MC number sequence immediately following n is called its impacting index, denoted by . We call an MC number strong if .
Example 1.
For example, 4 is a strong MC number with since both 5 and 6 are non-MC but 7 is MC. We have seen in Theorem 7 that strong MC numbers play the pivotal role in determining the LUBORs of non-MC numbers.
4. Two Special Classes of n-Enclosing Circles
4.1. First Special Class
For any positive integer k, we may define the unique circle that goes through the following points: , Suppose encloses exactly lattice points, then is a possible candidate for the largest -enclosing circle. If is indeed the largest -enclosing circle then is MC and
We have already seen this is true when and in the case in Theorem 2. We depicted these circles (and many others) in Figure 5 for , on page 12.
In general, it is not hard to see that
To compare these values, we have the Table 2:

Table 2.
First special class of circles with apparent symmetric lattice points on each boundary.
4.2. Second Special Class
For any positive integer k, we can mimic the first class by letting be the circle centered at containing the eight lattice points . Suppose encloses exactly lattice points, then is a possible candidate for the largest -enclosing circle. If is indeed the largest -enclosing circle then is MC and
Similar to the first class in Section 4.1, we have
To compare these values, we have the following table:
Among all the ’s in Table 3 with the following are all strong MC: . We will present their MC-circle symmetry in Figure 5 on page 12.

Table 3.
Second special class of circles with apparent symmetric lattice points on each boundary.
Notice that the sequence is [A000328] on the OEIS website [8]. This is equivalent to saying that when we shrink the circle to radius k while holding the center unchanged, no interior points are moved outside. Indeed, if lattice point satisfies if and only if .
4.3. Some Observations of the Two Special Classes
Recall that an MC number is said to be strong if it is followed immediately by a non-MC number. We noticed that there are many MC numbers in the two classes in Section 4.1 and Section 4.2, and some are even strong ones.
The first class of special circles seem to contain only MC numbers. We find the second class contain only two non-MC numbers 5 and 317 in the table. However, these two classes seem to behave very differently. While each () is the largest -enclosing circle, most of the ’s are not. Among the first 18 numbers, is the largest -enclosing circle only for . From this, it seems that as k becomes bigger, it is more likely that is the largest -enclosing circle. In view of the apparent symmetries among the lattice points on the circles and , we make for following conjecture.
Conjecture 2.
Let and be defined as in Section 4.1 and Section 4.2. Then
- (1)
- The special class of numbers contain only MC numbers, and the strong numbers among them form a subset of positive density.
- (2)
- The special class of numbers contain infinitely many MC numbers, and the strong numbers among them form a subset of positive density.
Due to lack of more evidence, we also would like to know the answer to the following question.
Problem 1.
Are there any other non-MC number beside 5 and 317 in the sequence ?
5. Complete Classification of n ≤ 1000
When n gets larger and larger, it becomes more and more difficult to find the exact values of . However, we have the following theoretical results to help us delegate the main computation to an algebra system such MAPLE or Mathematica. The first one is an analogous formula of (1) for the number of interior points inside a circle of radius r.
Theorem 8.
For any circle of radius r centered at the origin, the number of interior lattice points is given by
Proof.
It is clear that the number of interior lattice points on the x- or y-axes is
since if r is an integer while is the integer part of r otherwise. Suppose now is in the interior of the circle with . Then they must satisfy and , whence the summands in (3). □
Theorem 9.
Let n be a non-negative integer. Suppose is the MC-radius or the LUBOR of n. Then
Proof.
By Steinhaus’ Theorem 1, there exists a circle of area n which encloses exactly n lattice points in its interior. Since its radius must be bounded above by we get . Note the equality cannot hold as is transcendental while is a rational or a quadratic algebraic number as a radius of some lattice circle by Theorems 4 and 6.
The other direction follows from Gauss’ bound (2) easily. For completeness, we now provide a quick proof as follows.
The cases are clearly true. Suppose . Let be the MC-circle of n with radius if n is MC. If n is non-MC let be an n-enclosing circle of radius where r can be made arbitrarily close to by Theorem 6. Let us shade a lattice square if its lower left corner is an interior point of . Then the shaded area is exactly n. We now show that we we reduce the radius of by any while fixing the center of , then all of the circumference will lie in the shaded area.
Indeed, the circumference of is cut into arc pieces by the lattice squares with at least one corner lattice point contained inside . Then each piece not already in the shaded area must have one of the three forms (by applying some rigid motions if necessary) shown in Figure 4: is bounded by j lattice points on two sides (). Let P be any point on such a piece and C the center of . Let Q be the intersection of line with the boundary of the shaded area. Then clearly and therefore . Taking we get . However, the inequality cannot hold since is algebraic while is clearly transcendental.

Figure 4.
Three arc pieces , , of the circumference of represent all possible such pieces cut out by lattice squares.
This completes the proof of the theorem. □
Remark 2.
The sequence is the sequence A051132 on the OEIS website [8]. The difference sequence [A046109] provides the number of lattice points on the circumference of the circle with radius r centered at 0, where is defined by (1).
Given any bound M, we now may use the following algorithm to determine if is MC or non-MC and then find its MC-radius or LUBOR.
- Step 1.
- For each , compute all the radius of n-enclosing lattice circles, and then find the large radius, call it .
- Step 2.
- Start with the MC number 0. For each , suppose we have already determined the cases . Suppose , k is an MC number and all the numbers between k and n (exclusive) are non-MC. Then we can determine n by Main Theorem 1(3) (=Corollary 2): n is MC if and only if . Moreover, if n is MC and if n is non-MC.
Using the above algorithm, we have found the following MC integers with MAPLE:
We can also confirm the rest of the integers are all non-MC:
Furthermore, we can even determine exactly for all .
Essentially the same information can be found for all in Figure 5. They show all the strong numbers as well as all the non-MC numbers in this range.
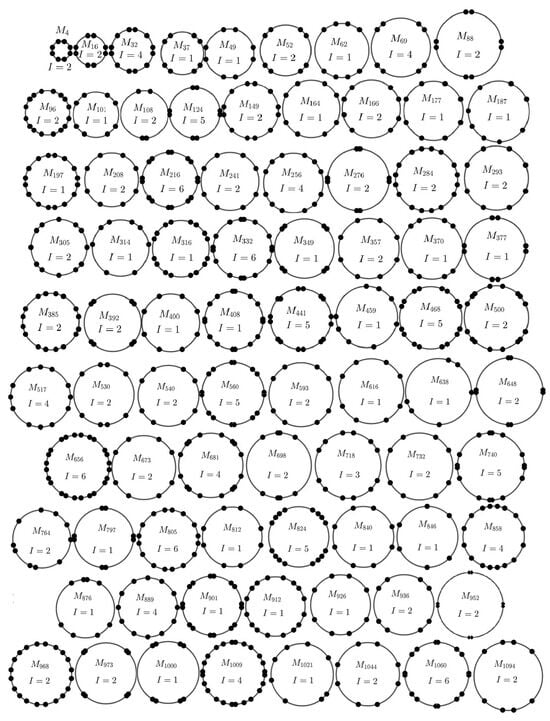
Figure 5.
All strong MC numbers with their impacting indices.
From the evidence we found in the range , we make the following conjectures. All the symmetries mentioned below are mirror symmetries keeping the lattice system invariant.
Conjecture 3.
We have
- (1)
- For all MC numbers we have .
- (2)
- For every non-MC , there exists a largest n-enclosing lattice circle.
- (3)
- Let and let be the radius of the largest n-enclosing lattice circle if it exists and otherwise. Then the numbers in are pairwise distinct.
- (4)
- There are arbitrary long consecutive MC integer sequences.
- (5)
- There are arbitrary long consecutive non-MC integer sequences, namely, the impacting indices are unbounded.
- (6)
- The density of MC integers among non-negative integers is greater than 80%.
- (7)
- The density of non-MC integers among non-negative integers is positive, but less than 20%.
- (8)
- There are infinitely many strong MC numbers, with a positive density among all MC numbers.
- (9)
- Every MC-circle of strong MC number has at least six lattice points on its circumference.
- (10)
- For the majority of the MC numbers, the lattice points on the circumference of its MC-circle have at least one mirror symmetry. This density should be over 50%.
- (11)
- There are infinitely many MC numbers n such that has exactly three lattice points on its circumference which have no lattice invariant mirror symmetry. For the vast majority of all such n’s (with density > 98%), the lattice points form a scalene triangle.
- (12)
- There are very few MC numbers n whose MC-circle has four lattice points without any mirror symmetry, the density should be <2%.
- (13)
- The lattice points on the circumference of every MC-circle of strong MC n have at least one mirror symmetry.
- (14)
- Less than 10% of the MC-circles of strong n among all strong MC-circles have slant axes of symmetry.
- (15)
- Around 20% of the MC-circles among all MC-circles have slant axes of symmetry.
- (16)
- Less than 10% of the MC-circles of strong n among all strong MC-circles have only one horizontal or vertical axis of symmetry.
- (17)
- More than 20% of the MC-circles among all MC-circles have only one horizontal or vertical axis of symmetry.
- (18)
- More than 80% of the MC-circles of strong n among all strong MC-circles have at least two axes of symmetry.
- (19)
- Less than 15% of the MC-circles among all MC-circles have at least two axes of symmetry.
By computer search, we have the following data to support the above conjecture.
- (1)
- For all MC numbers (the actual range we computed) we have .
- (2)
- For every , there is a largest n-enclosing lattice circle among all n-enclosing lattice circle.
- (3)
- This holds for all . In particular, it implies the proceeding conjecture which is equivalent to saying unless .
- (4)
- The 32 consecutive numbers from 410 to 441, inclusive, are all MC.
- (5)
- This may have the weakest support. The largest impacting inex we found so far is 6.
- (6)
- There are 911 MC integers in the range , about 83%. Table 4 shows their distributions over the 100-long intervals:
 Table 4. The distribution of MC integers .
Table 4. The distribution of MC integers . - (7)
- There are 189 non-MC integers in the range , about 17%. Table 5 shows their distribution over the 100-long intervals.
 Table 5. The distribution of non-MC integers .
Table 5. The distribution of non-MC integers . - (8)
- In the range , there are 80 strong ones among the 911 MC numbers. Hence, strong ones count about 7.3% among all non-negative integer, and about 8.8% among all MC numbers. Table 6 shows their distribution over the 100-long intervals.
 Table 6. The distribution of non-MC integers .
Table 6. The distribution of non-MC integers . - (9)
- Notice that and are the only two MC-circles of strong MC numbers with six lattice points on their circumference while all the others have at least eight.
- (10)
- The symmetry property seems to hold for the majority of MC-circles. There are 529 such ’s for all . The density of such MC numbers among all MC numbers should be around 59%. Table 7 shows their distribution over the 100-long intervals.
 Table 7. The distribution of symmetric , .
Table 7. The distribution of symmetric , . - (11)
- For , there are 373 MC numbers whose MC-circle has only three lattice points on its circumference which form a scalene triangle, or an isosceles triangle whose axis of mirror symmetry is not lattice invariant (the latter case is extremely rare since we only found one such MC number: 585). This occurs first at whose MC-circle has only three lattice points on its circumference: . The triangle is clearly scalene and therefore no lattice invariant symmetry can exist. Table 8 shows their distribution over the 100-long intervals. The density of such n’s seems to be around 34% among all non-negative integers and 41% among all MC numbers.
 Table 8. The distribution of asymmetric with 3 boundary lattice points, .
Table 8. The distribution of asymmetric with 3 boundary lattice points, . - (12)
- There are only 10 MC numbers such that contains four lattice points without any lattice invariant mirror symmetry: 66, 352, 422, 706, 731, 760, 908, 940, 1019, 1024. The density of such n’s seems to be around 1% among all non-negative integers. We want to point out that the four lattice points sometime form an isosceles trapezoid, i.e., are equipped with mirror symmetries. This holds for the last six numbers in the above list. However, the axes of symmetry are neither horizontal, nor vertical, nor slant with 45°. Hence, such symmetries are not lattice invariant.
- (13)
- All the symmetries of strong MC-circles are evident from the pictures in Figure 5.
- (14)
- There are only three strong MC numbers whose MC-circles have 45° slant symmetry. The density of such MC numbers among all the strong ones is only about 4%.
- (15)
- Among the 911 MC numbers , there are 176 ’s with 45° slant symmetry. Table 9 shows their distribution over the 100-long intervals. The density of such n’s seems to be around 16% among all non-negative integers and around 19% among all MC numbers.
 Table 9. The distribution of ’s with 45° slant symmetry, .
Table 9. The distribution of ’s with 45° slant symmetry, . - (16)
- Among the 80 strong MC numbers , only the following have only one horizontal/vertical symmetry: 108, 314, 846, and 876, only about 5%.
- (17)
- Among the 911 MC numbers , there are 229 ’s with only one horizontal/vertical symmetry. Table 10 shows their distribution over the 100-long intervals. The density of such n’s seems to be around 23% among all non-negative integers and around 25% among all MC numbers.
 Table 10. The distribution of ’s with only one horizontal/vertical symmetry, .
Table 10. The distribution of ’s with only one horizontal/vertical symmetry, . - (18)
- More than 80% of the MC-circles of strong have at least two axes of symmetry. The exact density is 71/80 in this range.
- (19)
- Among the 911 MC numbers , there are 123 ’s with at least two axes symmetry. Table 11 shows their distribution over the 100-long intervals. The density of such n’s seems to be around 11% among all non-negative integers and around 14% among all MC numbers.
 Table 11. The distribution of ’s with at least two axes symmetry, .
Table 11. The distribution of ’s with at least two axes symmetry, .
We further remark that the two special classes of circles and with quite strong symmetries in Section 4 seem to contain mostly MC numbers and many are actually strong ones.
However, case shows that an n-enclosing lattice circle with strong symmetry does not always guarantee it is an MC-circle of n. See Figure 6. In fact, 89 is non-MC and therefore even the largest lattice circle on the right of Figure 6 is not a largest 89-enclosing circle since such a circle does not exist.
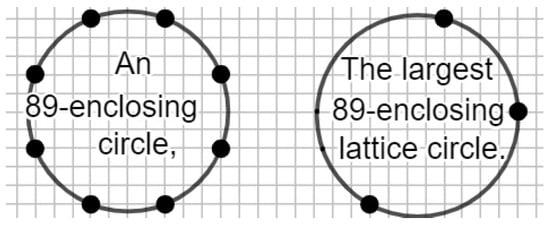
Figure 6.
A circle with strong symmetry may not be a largest enclosing circle. And a largest enclosing lattice circle may not be a largest enclosing circle.
6. Concluding Remarks and Further Research Problems
We have demonstrated in this paper that the naive-looking question “What is the largest circle containing n lattice points in the interior?” has a very delicate answer. For each we can solve the problem by hand and for each we can solve the problem with the aid of a computer. In theory, via our approach we can determine all the MC and non-MC integers n with a precise computation of the largest radius of all the lattice circles enclosing exactly n lattice points, which can be achieved with a finite amount of computation.
The radius sequence is not always increasing. However, whenever a drop after occurs there are some associated non-MC numbers. Moreover, the largest strictly increasing subsequence is conjectured to correspond exactly to all the MC numbers while the LUBOR of any non-MC n is proved to be given by the largest radius in the sequence before . When we only consider the largest lattice n-enclosing circles, is the only number less than 1100 such that with both n and are non-MC numbers.
There are some obvious patterns and symmetries concerning the MC-circles of n, particularly the strong ones, namely, those with trailing non-MC numbers. In Conjecture 3, we have listed numerous observations which we believe should hold in general.
There are a few related research problems which deserve some attention.
Problems 1.
(1) We may consider the question of finding the smallest n-enclosing circles. This problem is closely related to the concept we developed in this paper. For example, we may define similarly the minimal-enclosing numbers and non-minimal-enclosing numbers.
- (2)
- We may consider the question of finding the smallest/largest circles containing n lattice points in the interior and on the boundary. The answers will be drastically different.
- (3)
- We may consider higher-dimension analogs of these questions. For example, what is the largest/smallest sphere in three-dimensional space that encloses exactly n lattice points lattice points in the interior and/not on the boundary.
- (4)
- More generally, as Steinhaus’ Theorem 1 has been generalized to any Hilbert space X in [19,20], we wonder when the largest n-enclosing open balls exist for a quasi-finite set (see [20] (p. 129) for the definition). Do we have similar results in this setting?
Note that Kulikowski [21] showed that for every positive integer n, there is a three-dimensional sphere which has exactly n lattice points on its surface. This is related to Problem 1(3).
Funding
This research was funded by the Jacobs Prize from The Bishop’s School.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares there are no conflicts of interest.
List of Acronyms and Key Terminology
| MC number | maximally circlable number, i.e., a non-negative number n such that |
| there is a largest circle to contain n lattice points in the interior | |
| Non-MC number | non-maximally circlable number, circle as above does not exist |
| MC-circle of n | the largest circle to contain n lattice points in the interior |
| MC-radius of n | the radius of MC-circle of n |
| MC-set of n | a set of n lattice points that are enclosed by an MC-circle of n |
References
- Steinhaus, H. One Hundred Problems in Elementary Mathematics; Basic Book Inc.: New York, NY, USA, 1964. [Google Scholar]
- Sierpinski, W. Sur quelques problèmes concernant les points aux coordonnées entières. L’Enseignement Math. Ser. 2 1958, 4, 25–31. [Google Scholar]
- Sierpinski, W.; de Sur un problème, H. Steinhaus concernant les ensembles de points sur le plan. Fund. Math. 1958, 46, 191–194. [Google Scholar]
- Honsberger, R. Circles, Squares, and Lattice Points, Chapter 11. In Mathematical Gems I: The Dolciani Mathematical Expositions; Mathematical Association of America: Washington, DC, USA, 1973; pp. 117–127. [Google Scholar]
- Schinzel, A. Sur l’existence d’un cercle passant par un nombre donné de points aux coordonnées entières. L’Enseignement Math. Ser. 2 1958, 4, 71–72. [Google Scholar]
- Hilbert, D.; Cohn-Vossen, S. Geometry and the Imagination; Nemenyi, P., Translator; American Mathematical Society: Providence, RI, USA, 1999; pp. 33–35. [Google Scholar]
- Fraser, W.; Gotlieb, C. A calculation of the number of lattice points in the circle and sphere. Math. Comp. 1962, 16, 282–290. [Google Scholar] [CrossRef]
- Sloane, N.J.A. The On-Line Encyclopedia of Integer Sequences. Available online: http://oeis.org (accessed on 24 May 2025).
- Hardy, G.H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed.; Chelsea Publishing Company: New York, NY, USA, 1999. [Google Scholar]
- Hua, L.K. The lattice-points in a circle. Quart. J. Math. Oxford Ser. 1942, 13, 18–29. [Google Scholar] [CrossRef]
- Chen, J.-R. The lattice-points in a circle. Sci. Sinica 1963, 12, 633–649. [Google Scholar]
- Keller, H.B.; Swenson, J.R. Experiments on the Lattice Problem of Gauss. Math. Comput. 1963, 17, 223–230. [Google Scholar] [CrossRef]
- Iwaniec, H.; Mozzochi, C.J. On the divisor and circle problem. J. Number Theory 1988, 29, 60–93. [Google Scholar] [CrossRef]
- Huxley, M.N. Exponential sums and lattice points (and Corrigenda). Proc. Lond. Math. Soc. 1990, 60, 471–502, Erratum in Proc. Lond. Math. Soc. 1993, 66, 70. [Google Scholar]
- Huxley, M.N. Exponential sums and lattice points (and Corrigenda) II. Proc. Lond. Math. Soc. 1993, 66, 279–301. [Google Scholar]
- Huxley, M.N. Exponential sums and lattice points (and Corrigenda) III. Proc. Lond. Math. Soc. 2003, 87, 591–609. [Google Scholar]
- Cilleruello, J. The distribution of lattice points on circles. J. Number Theory 1993, 43, 198–202. [Google Scholar] [CrossRef]
- Mathematics 2. Mathematics Department, Phillips Exeter Academy, August 2024. Available online: https://exeter.edu/app/uploads/2024/08/Math2_2024_printed.pdf (accessed on 14 March 2025).
- Kania, T.; Kochanek, T. Steinhaus’ lattice-point problem for Banach spaces. J. Math. Anal. Appl. 2017, 446, 1219–1229. [Google Scholar] [CrossRef]
- Zwoleński, P. Some generalization of Steinhaus’ lattice points problem. Colloq. Math. 2011, 123, 129–132. [Google Scholar] [CrossRef]
- Kulikowski, T. Sur l’existence d’une sphère passant par un nombre donné aux coordonnées entièes. L’Enseignement Math. Ser. 2 1959, 5, 89–90. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).