The Multiple Utility of Kelvin’s Inversion

Abstract

Inversion with respect to a unit sphere is a powerful tool when dealing with many problems in Mathematics. This inversion preserves harmonicity in ${\mathbb{R}}^2,$ but it does not in ${\mathbb{R}}^n,$ for $n>2.$ Lord Kelvin overcame this problem by defining a new (at the time) inversion, the so-called Kelvin’s inversion (or transformation). This inversion has many good properties, making it extremely useful in each case where the geometry of the original problem raises issues. But by using Kelvin’s inversion, these issues are transformed into easier ones, due to a simpler geometry. In this review paper, we study Kelvin’s inversion, deploying its basic properties. Moreover, we present some applications, where its use enables scientists to solve difficult problems in scattering, electrostaticity, thermoelasticity, potential theory and bioengineering.

1. Introduction

Inversion with respect to a unit sphere is a map $\mathbf{x}\to {\mathbf{x}}^{*},$ where $\mathbf{x},{\mathbf{x}}^{*}\in {\mathbb{R}}^n,n\in \mathbb{N}$ and

$${\mathbf{x}}^{*}=\left\{\begin{array}{cc}{\displaystyle \frac{\mathbf{x}}{{\left|\mathbf{x}\right|}^2}},\hfill & \mathbf{x}\ne \mathbf{0},\infty \hfill \\ 0,\hfill & \mathbf{x}=\infty \hfill \\ \infty ,\hfill & \mathbf{x}=0\hfill \end{array}\right..$$

(1)

It is a conformal map which is used mainly to append ∞ to ${\mathbb{R}}^n$ [1]. This inversion preserves the family of the spheres and hyperplanes in ${\mathbb{R}}^n,$ but unfortunately, it does not preserve harmonicity when $n>2.$

In 1845, William Thomson (Lord Kelvin) overcame this issue. In a letter to Liouville, he presented an inversion with respect to a sphere [2]. Practically, he expanded Green’s idea [3], providing a method for solving boundary value problems (BVPs) with partial differential equations (PDEs) [4], which is known as Kelvin’s inversion (or transformation). Its main advantage is that it transforms a harmonic function to a function which, if divided by the Euclidean distance, is also harmonic. Two years later, he published another paper using his inversion in order to calculate the surface charge density of a conductor shaped as a spherical bowl [5]. Lord Kelvin summarized his work in [4].

The advantage of this method is that when the solution of a BVP in the interior of a domain is known, then the solution of an equivalent BVP in the exterior of a domain can be derived and vice versa. This is an important transformation when the inverted problem creates a domain with simpler geometry, something which is not certain. Kelvin’s inversion transforms a biharmonic function to a function which, if multiplied by the Euclidean distance, is also biharmonic [6]. Moreover, it transforms a stream or a bistream function to a function which, if multiplied by the Euclidean distance or the Euclidean distance on the third power, is also a stream or a bistream function [6], respectively.

This method has been used by many researchers in order to solve problems in various scientific fields, such as in acoustic scattering by non-convex bodies, where the method was used to calculate the capacity of a class of convex bodies [7] and in low-frequency acoustic scattering by a hard scatterer [8]. Kelvin’s inversion has been applied to solving the external Dirichlet or Neumann problem in a non-convex body [9,10] using the Fokas method [11,12], problems in electrostaticity [13,14,15] or in thermoelasticity [16], and blood’s plasma flow past a red blood cell [17].

Theoretical results of the Kelvin’s inversion have also been derived. The R-separation and the R-semiseparation of Stokes’ operators in the inverted spheroidal coordinate systems were proved, and the complete set of the corresponding eigenfunctions and generalized eigenfunctions was obtained [18]. The effect of Kelvin’s inversion has been studied in the following operators: the Weinstein operator [19]; the Grushin operator [20]; Laplace’s biharmonic operator; the Stokes stream operator; and Stokes bistream operator [6]. Kelvin’s inversion has also drawn the attention of researchers with regard to the following areas: multi-harmonic polynomials [21]; a-harmonic functions [22]; Grushin equation [23]; and harmonic polynomials on the Heisenberg group [24].

Furthermore, Kelvin’s inversion has applications in numerical analysis. Nabizadeh et al. [25] developed a method using Kelvin’s transformation to numerically solve Poisson, Laplace, and Helmholtz equations. They applied the method in Poisson or Laplace equations using the finite difference method, finite element method, the Monte Carlo method and specifically in the walk of spheres. They compared the results obtained using the walk of spheres with the Russian roulette method, and also the walk of spheres with Kelvin’s inversion, proving the advantage when the domain is infinite. Moreover, they proved two theorems for the method employing the aforementioned equations.

The structure of this manuscript is as follows: in Section 2, we present Kelvin’s inversion, its definition, basic properties, and formulas. In this section, we also prove the lemmas and the theorems that are not presented (as far as we know) in a published paper or book. Moreover, in Section 3, some applications in many scientific fields are shown, while in Section 4, a discussion on the inversion is conducted.

2. Kelvin’s Inversion

2.1. Definition and Properties of Kelvin’s Inversion

Definition 1. 

If $\mathbf{r}\ne \mathbf{0}$ is a vector in ${\mathbb{R}}^3$, and $a>0$ is the radius of a sphere, Kelvin’s inversion $K:{\mathbb{R}}^3\to {\mathbb{R}}^3,$ defines a vector ${\mathbf{r}}^{\prime }$ via the relation

$$K\left(\mathbf{r}\right):={\mathbf{r}}^{\prime }={\displaystyle \frac{a^2}{r^2}}\mathbf{r},$$

(2)

where $r=\left|\mathbf{r}\right|$ and ${\mathbf{r}}^{\prime }\in {\mathbb{R}}^3.$ The center of the sphere is called the center of inversion.

Comment: Kelvin’s inversion is generally defined in ${\mathbb{R}}^n$ [4], but since this transformation does not depend on $n,$ in this paper, only the cases where $n=2,$ and $n=3$ will be studied.

From (2), it is easy to verify that

$${\mathbf{r}}^{\prime }//\mathbf{r},$$

(3)

$$\mathbf{r}·{\mathbf{r}}^{\prime }=a^2,$$

(4)

$$r{r}^{\prime }=a^2,$$

(5)

where $r=\left|\mathbf{r}\right|,$ $r^{\prime }=\left|{\mathbf{r}}^{\prime }\right|.$ The geometric interpretation of (3) is that the inversion leaves all the directions of the position vectors’ invariant.

From the definition of Kelvin’s inversion, it is easy to prove the following lemma.

Lemma 1. 

Let ${\mathbf{r}}^{\prime }$ be the inverse vector of $\mathbf{r}$ derived from Kelvin’s inversion, $K$, with respect to a sphere of radius $a>0$ and $r^{\prime }=\left|{\mathbf{r}}^{\prime }\right|.$

(a) 

Kelvin’s inversion is its own inverse, which means that

$$\mathbf{r}={\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }.$$

(6)

(b) 

If $b\in {\mathbb{R}}^{*}$ is a constant, it stands that

$$K\left(b\mathbf{r}\right)={\displaystyle \frac{1}{b}}K\left(\mathbf{r}\right).$$

(7)

(c) 

The unit vectors of $\mathbf{r},{\mathbf{r}}^{\prime }$ are the same, i.e.,

$$\widehat{{\mathbf{r}}^{\prime }}=\widehat{\mathbf{r}}.$$

(8)

Proof. 

Let ${\mathbf{r}}^{\prime },{\mathbf{r}}^{″}$ be the inverse vectors of $\mathbf{r},{\mathbf{r}}^{\prime }$ from Kelvin’s inversion with respect to a sphere of radius $a,$ respectively.

(a) 

Then,

$${\mathbf{r}}^{″}={\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }={\displaystyle \frac{a^2}{r^{\prime 2}}}{\displaystyle \frac{a^2}{r^2}}\mathbf{r}\stackrel{\left(4\right)}{=}\mathbf{r}$$

and therefore,

$$\mathbf{r}={\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }.$$

(9)

(b) 

Moreover,

$$K\left(b\mathbf{r}\right)={\displaystyle \frac{a^2}{{\left|b\mathbf{r}\right|}^2}}\left(b\mathbf{r}\right)={\displaystyle \frac{a^2}{b^2{r}^2}}\left(b\mathbf{r}\right)={\displaystyle \frac{1}{b}}{\displaystyle \frac{a^2}{r^2}}\mathbf{r}={\displaystyle \frac{1}{b}}K\left(\mathbf{r}\right).$$

(c) 

Finally,

$$\widehat{{\mathbf{r}}^{\prime }}={\displaystyle \frac{{\mathbf{r}}^{\prime }}{r^{\prime }}}={\displaystyle \frac{{\displaystyle \frac{a^2}{r^2}}\mathbf{r}}{r^{\prime }}}={\displaystyle \frac{a^2}{r^2{r}^{\prime }}}\mathbf{r}\stackrel{\left(4\right)}{=}{\displaystyle \frac{\mathbf{r}}{r}}=\widehat{\mathbf{r}}.$$

□

Moreover, the transformation satisfies the following proposition.

Proposition 1. 

Kelvin’s inversion, K has the following properties:

• It is a radial transformation (i.e., the transformation is based on its distance from a point);
• It is a non-linear transformation since

  $$K(a_1\mathbf{u}+a_2\mathbf{v})\ne a_{1}K\left(\mathbf{u}\right)+a_{2}K\left(\mathbf{v}\right),a_1,a_2\in \mathbb{R};$$
• It acts on every direction $\mathbf{r}$ as an one-to-one inversion;
• It maps points near to the center of the sphere to infinity and vice versa;
• It maps a point near and inside the sphere of inversion to a point near the sphere of inversion but outside of it and vice versa (Figure 1).

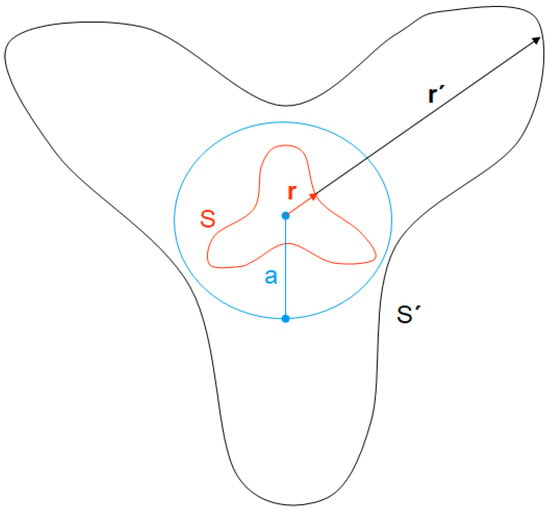
Figure 1. Kelvin’s inversion in 2D, where S is mapped to S’ with respect to the circle of radius a.

The basic properties of Kelvin’s inversion are stated below.

Theorem 1. 

Kelvin’s inversion

(a) 

Preserves the angle between two vectors;

(b) 

Inverts spheres to spheres (as we consider a sphere with infinity radius, i.e., a plane);

(c) 

Inverts planes to spheres passing through the center of inversion and vice versa.

Proof. 

Let ${\mathbf{r}}^{\prime },{\mathbf{r}}_{\mathbf{1}}^{\prime },{\mathbf{r}}_{\mathbf{2}}^{\prime }\in {\mathbb{R}}^3$ be the inverted vectors through Kelvin’s inversion with respect to a sphere with radius a of the vectors $\mathbf{r},{\mathbf{r}}_{\mathbf{1}},{\mathbf{r}}_{\mathbf{2}}\in {\mathbb{R}}^3,$ respectively; so

$${\mathbf{r}}^{\prime }={\displaystyle \frac{a^2}{r^2}}\mathbf{r},{\mathbf{r}}_{\mathbf{1}}^{\prime }={\displaystyle \frac{a^2}{r_1^2}}{\mathbf{r}}_{\mathbf{1}},{\mathbf{r}}_{\mathbf{2}}^{\prime }={\displaystyle \frac{a^2}{r_2^2}}{\mathbf{r}}_{\mathbf{2}}.$$

(a) 

Let $\theta ,{\theta }^{\prime }\in [0,\pi )$ be the angles between the vectors ${\mathbf{r}}_{\mathbf{1}},{\mathbf{r}}_{\mathbf{2}}$ and ${\mathbf{r}}_{\mathbf{1}}^{\prime },{\mathbf{r}}_{\mathbf{2}}^{\prime },$ respectively. Therefore,

$$cos\left({\theta }^{\prime }\right)={\displaystyle \frac{{\mathbf{r}}_{\mathbf{1}}^{\prime }·{\mathbf{r}}_{\mathbf{2}}^{\prime }}{r_1^{\prime }{r}_2^{\prime }}}={\displaystyle \frac{{\displaystyle \frac{a^2}{r_1^2}}{\mathbf{r}}_{\mathbf{1}}·{\displaystyle \frac{a^2}{r_2^2}}{\mathbf{r}}_{\mathbf{2}}}{{\displaystyle \frac{a^2}{r_1}}{\displaystyle \frac{a^2}{r_2}}}}\stackrel{\left(4\right)}{=}{\displaystyle \frac{{\mathbf{r}}_{\mathbf{1}}·{\mathbf{r}}_{\mathbf{2}}}{r_1{r}_2}}=cos\left(\theta \right),$$

deriving that $\theta ={\theta }^{\prime }$ since $\theta ,{\theta }^{\prime }\in [0,\pi ).$

(b) 

If $\mathbf{r}$ is a vector corresponding to a sphere of radius $b>0,$ then

$$r=\left|\mathbf{r}\right|=b,r^{\prime }={\displaystyle \frac{a^2}{r}}={\displaystyle \frac{a^2}{b}},$$

reflecting the fact that the inverted vector ${\mathbf{r}}^{\prime }$ corresponds to a sphere of radius ${\displaystyle \frac{a^2}{b}}.$

The proof of the reverse proposition is similar.

(c) 

Let $|\mathbf{r}-{\mathbf{r}}_{\mathbf{0}}|=r_0$ with $|{\mathbf{r}}_{\mathbf{0}}|=r_0$ be the equation of the sphere passing through the point $(0,0,0).$ Then, using spherical coordinates [26], we derive

$$\mathbf{r}=\left(r_0+r_{0}sin\left(\theta \right)cos\left(\varphi \right),r_{0}sin\left(\theta \right)sin\left(\varphi \right),r_{0}cos\left(\theta \right)\right)$$

and

$$\begin{array}{cc}\hfill r^2={\left|\mathbf{r}\right|}^2=& r_0^2\left(1+2sin\left(\theta \right)cos\left(\varphi \right)+{sin}^2\left(\theta \right){cos}^2\left(\varphi \right)+{sin}^2\left(\theta \right)si{n}^2\left(\varphi \right)+{cos}^2\left(\theta \right)\right)\hfill \\ \hfill =& 2r_0^2\left(1+sin\left(\theta \right)cos\left(\varphi \right)\right).\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill {\mathbf{r}}^{\prime }=& \left({\displaystyle \frac{a^2{r}_0+a^2{r}_{0}sin\left(\theta \right)cos\left(\varphi \right)}{2r_0^2(1+sin\left(\theta \right)cos\left(\varphi \right))}},{\displaystyle \frac{a^2{r}_{0}sin\left(\theta \right)sin\left(\varphi \right)}{2r_0^2(1+sin\left(\theta \right)cos\left(\varphi \right))}},{\displaystyle \frac{a^2{r}_{0}cos\left(\theta \right)}{2r_0^2(1+sin\left(\theta \right)cos\left(\varphi \right))}}\right)\hfill \\ \hfill =& \left({\displaystyle \frac{a^2}{2r_0}},{\displaystyle \frac{a^2{r}_{0}sin\left(\theta \right)sin\left(\varphi \right)}{2r_0^2(1+sin\left(\theta \right)cos\left(\varphi \right))}},{\displaystyle \frac{a^2{r}_{0}cos\left(\theta \right)}{2r_0^2(1+sin\left(\theta \right)cos\left(\varphi \right))}}\right),\hfill \end{array}$$

which proves that the image of vector $\mathbf{r}$ belongs to the plane with equation $x={\displaystyle \frac{a^2}{2r_0}}.$ The proof of the inverse proposition is similar (Figure 2).

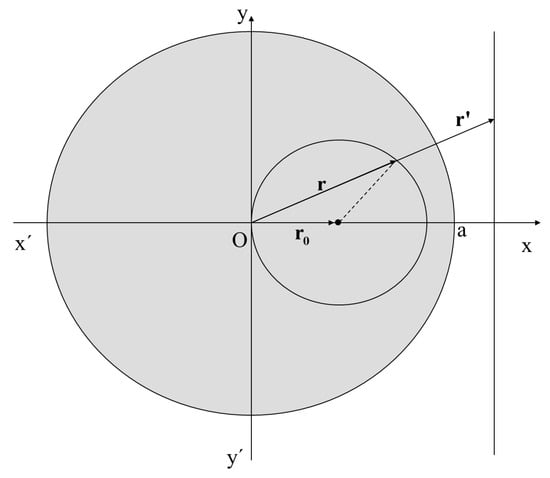Figure 2. Invert a plane with respect to a sphere.

□

Lemma 2. 

If $\mathbf{r}\in \Omega \subseteq {\mathbb{R}}^3$ is the position vector with magnitude $r=\left|\mathbf{r}\right|;$ ${\mathbf{r}}^{\prime }\in {\Omega }^{\prime }\subseteq {\mathbb{R}}^3$ is the vector under Kelvin’s inversion with respect to a sphere of radius $a>0$ with magnitude $r^{\prime }=\left|{\mathbf{r}}^{\prime }\right|;$ $ds$ and $d{s}^{\prime }$ are the infinitesimal areas on $\partial \Omega$ and $\partial {\Omega }^{\prime },$ respectively; and $dV$ and $d{V}^{\prime }$ are the infinitesimal volumes on Ω and ${\Omega }^{\prime },$ respectively, then

$${\displaystyle \frac{ds}{r^2}}={\displaystyle \frac{d{s}^{\prime }}{r^{\prime 2}}}.$$

(10)

$${\displaystyle \frac{dV}{r^3}}={\displaystyle \frac{d{V}^{\prime }}{r^{\prime 3}}}.$$

(11)

Proof. 

$${\displaystyle \frac{d{s}^{\prime }}{r^{\prime 2}}}={\displaystyle \frac{d{x}^{\prime }d{y}^{\prime }}{r^{\prime 2}}}={\displaystyle \frac{{\displaystyle \frac{a^2}{r^2}}dx{\displaystyle \frac{a^2}{r^2}}dy}{{\displaystyle \frac{a^4}{r^2}}}}={\displaystyle \frac{dxdy}{r^2}}={\displaystyle \frac{ds}{r^2}},$$

$${\displaystyle \frac{d{V}^{\prime }}{r^{\prime 3}}}={\displaystyle \frac{d{x}^{\prime }d{y}^{\prime }d{z}^{\prime }}{r^{\prime 3}}}={\displaystyle \frac{{\displaystyle \frac{a^2}{r^2}}dx{\displaystyle \frac{a^2}{r^2}}dy{\displaystyle \frac{a^2}{r^2}}dz}{{\displaystyle \frac{a^6}{r^3}}}}={\displaystyle \frac{dxdydz}{r^3}}={\displaystyle \frac{dV}{r^3}}.$$

□

Lemma 3. 

If ${\mathbf{r}}_{\mathbf{1}}, {\mathbf{r}}_{\mathbf{2}},\in \Omega \subseteq {\mathbb{R}}^3$ and ${\mathbf{r}}_{\mathbf{1}}^{\prime }, {\mathbf{r}}_{\mathbf{2}}^{\prime }\in {\Omega }^{\prime }\subseteq {\mathbb{R}}^3$ are the vectors under Kelvin’s inversion with respect to a sphere of radius $a>0,$ respectively, with magnitudes, $r_i=\left|{\mathbf{r}}_{\mathbf{i}}\right|,i=1,2,$ $r_i^{\prime }=\left|{\mathbf{r}}_{\mathbf{i}}^{\prime }\right|,i=1,2,$ then

$$|{\mathbf{r}}_{\mathbf{2}}^{\prime }-{\mathbf{r}}_{\mathbf{1}}^{\prime }|={\displaystyle \frac{a^2}{r_1{r}_2}}|{\mathbf{r}}_{\mathbf{2}}-{\mathbf{r}}_{\mathbf{1}}|.$$

(12)

Proof. 

Since

$$\begin{array}{cc}\hfill |{\mathbf{r}}_{\mathbf{2}}^{\prime }-{\mathbf{r}}_{\mathbf{1}}^{\prime }{|}^2& ={\left|{\displaystyle \frac{a^2}{r_2^2}}{\mathbf{r}}_{\mathbf{2}}-{\displaystyle \frac{a^2}{r_1^2}}{\mathbf{r}}_{\mathbf{1}}\right|}^2=\hfill \\ \hfill & ={\left|{\displaystyle \frac{a^2}{r_1{r}_2}}\left({\displaystyle \frac{r_1}{r_2}}{\mathbf{r}}_{\mathbf{2}}-{\displaystyle \frac{r_2}{r_1}}{\mathbf{r}}_{\mathbf{1}}\right)\right|}^2=\hfill \\ \hfill & ={\displaystyle \frac{a^4}{r_1^2{r}_2^2}}{\left|{\displaystyle \frac{r_1}{r_2}}{\mathbf{r}}_{\mathbf{2}}-{\displaystyle \frac{r_2}{r_1}}{\mathbf{r}}_{\mathbf{1}}\right|}^2=\hfill \\ \hfill & ={\displaystyle \frac{a^4}{r_1^2{r}_2^2}}\left({\displaystyle \frac{r_1^2}{r_2^2}}{{\mathbf{r}}_{\mathbf{2}}}^2+{\displaystyle \frac{r_2^2}{r_1^2}}{{\mathbf{r}}_{\mathbf{1}}}^2-2{\displaystyle \frac{r_1{r}_2}{r_1{r}_2}}{\mathbf{r}}_{\mathbf{1}}{\mathbf{r}}_{\mathbf{2}}\right)=\hfill \\ \hfill & ={\displaystyle \frac{a^4}{r_1^2{r}_2^2}}\left(r_1^2+r_2^2-2{\mathbf{r}}_{\mathbf{1}}{\mathbf{r}}_{\mathbf{2}}\right)={\displaystyle \frac{a^4}{r_1^2{r}_2^2}}{|{\mathbf{r}}_{\mathbf{2}}-{\mathbf{r}}_{\mathbf{1}}|}^2,\hfill \end{array}$$

we derive

$$|{\mathbf{r}}_{\mathbf{2}}^{\prime }-{\mathbf{r}}_{\mathbf{1}}^{\prime }|={\displaystyle \frac{a^2}{r_1{r}_2}}|{\mathbf{r}}_{\mathbf{2}}-{\mathbf{r}}_{\mathbf{1}}|.$$

□

Some basic formulas employing Kelvin’s inversion [6] are given in the following theorem.

Theorem 2. 

If $\widehat{\mathbf{n}}$ and ${\widehat{\mathbf{n}}}^{\prime }$ are the outward normal unit vectors from Ω and ${\Omega }^{\prime },$ respectively; $\widehat{\mathbf{r}}$ is the unit vector in the direction of $\mathbf{r};$ $\tilde{\mathbb{I}}$ is the unit dyadic; and ⊗ is the tensor product, then

$${\widehat{\mathbf{n}}}^{\prime }=\left(2\widehat{\mathbf{r}}\otimes \widehat{\mathbf{r}}-\tilde{\mathbb{I}}\right)·\widehat{\mathbf{n}},$$

(13)

$$\widehat{\mathbf{n}}=\left(2\widehat{\mathbf{r}}\otimes \widehat{\mathbf{r}}-\tilde{\mathbb{I}}\right)·{\widehat{\mathbf{n}}}^{\prime },$$

(14)

$${\displaystyle \frac{\partial }{\partial n}}=-{\displaystyle \frac{r^{\prime 2}}{a^2}}{\displaystyle \frac{\partial }{\partial n^{\prime }}}.$$

(15)

Proof. 

For the proof, see [6]. □

2.2. Kelvin’s Inversion in Coordinate Systems

Kelvin’s inversion can be applied in a coordinate system, deriving interesting coordinate surfaces. For instance, if we apply the inversion to a prolate spheroid, which is a coordinate surface of the prolate spheroidal coordinate system (Figure 3), we derive an inverted prolate spheroid [26], which is a coordinate surface of the inverted prolate spheroidal coordinate system (Figure 4). In Figure 5, the prolate spheroid, the sphere of inversion, and the corresponding inverted prolate spheroid are presented.

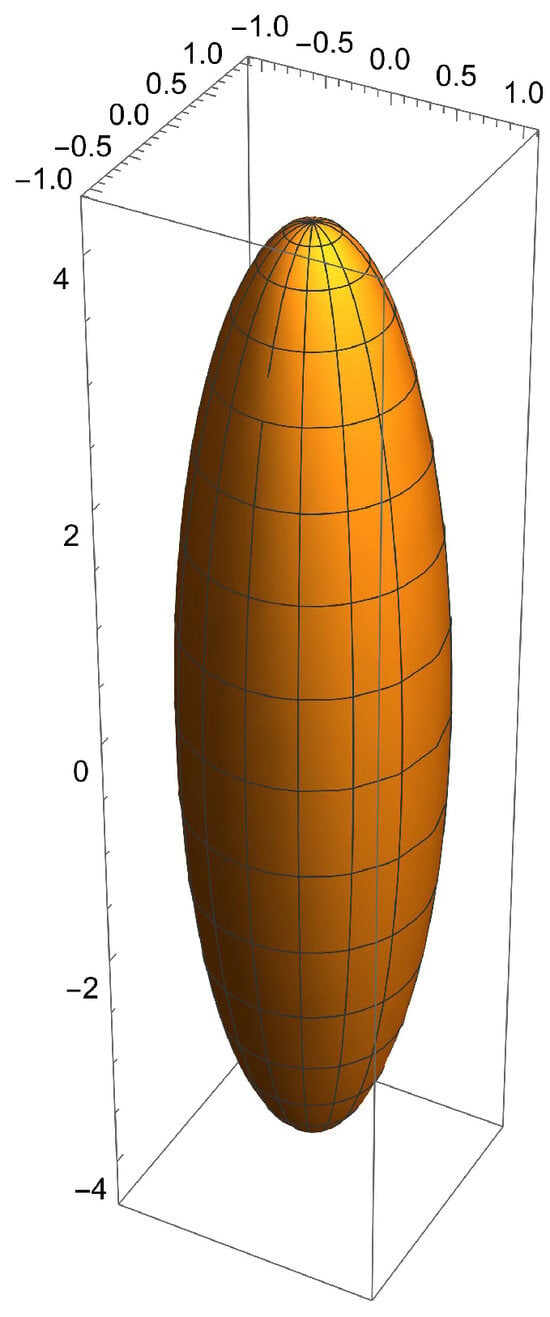
Figure 3. Prolate spheroid.

Figure 4. Inverted prolate spheroid.

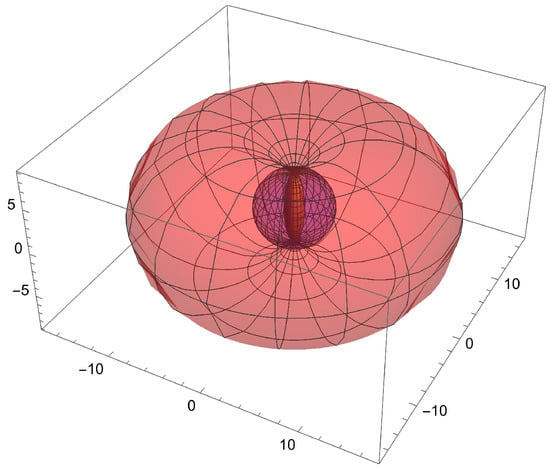
Figure 5. Prolate spheroid, sphere of inversion and inverted prolate spheroid.

In the case of an axisymmetric coordinate system, the following lemma is valid [27].

Lemma 4. 

If $(q_1,q_2,\phi ),$ $\phi \in [0,2\pi )$ is an axisymmetric system of coordinates with metric coefficients $h_1,h_2$ and a radial cylindrical coordinate ϖ, and $(q_1^{\prime },q_2^{\prime },\phi )$ is the corresponding inverted system of coordinates with metric coefficients $h_1^{\prime },h_2^{\prime }$ and a radial cylindrical coordinate ${\varpi }^{\prime }$, then

$$h_1^{\prime }={\displaystyle \frac{1}{r^2}}{h}_1,$$

(16)

$$h_2^{\prime }={\displaystyle \frac{1}{r^2}}{h}_2,$$

(17)

$${\varpi }^{\prime }=r^2\varpi ,$$

(18)

where r is the Euclidean distance of the coordinate system $(q_1,q_2,\phi ).$

Proof. 

For the proof, see [27]. □

2.3. Kelvin’s Inversion in Potential Theory

The effect of Kelvin’s inversion in the Laplace’s operator or the Laplace’s biharmonic operator is given below [6].

Theorem 3. 

If $u\left(\mathbf{r}\right)$ is a smooth enough function in Ω, and ${\Omega }^{\prime }$ is the image of Ω through Kelvin’s inversion, then

$$\nabla u\left(\mathbf{r}\right)={\displaystyle \frac{r^{\prime 2}}{a^2}}\left({\nabla }^{\prime }-2\widehat{\mathbf{r}}{\displaystyle \frac{\partial }{\partial r^{\prime }}}\right)u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right),\mathbf{r}\in \Omega ,{\mathbf{r}}^{\prime }\in {\Omega }^{\prime },$$

(19)

where ∇ is the gradient in $\Omega ,$ ${\nabla }^{\prime }$ is the gradient in ${\Omega }^{\prime },$ ${\mathbf{r}}^{\prime }$ is the inverted vector of $\mathbf{r}$ with respect to a sphere of radius a, and $\widehat{\mathbf{r}}$ is the corresponding unit vector of $\mathbf{r}.$

Proof. 

For the proof, see [6]. □

Theorem 4. 

If $u\left(\mathbf{r}\right)$ is a smooth enough function in Ω and ${\Omega }^{\prime }$ is the image of Ω through Kelvin’s inversion, then

$$\Delta u\left(\mathbf{r}\right)={\displaystyle \frac{r^{\prime 5}}{a^5}}{\Delta }^{\prime }\left[{\displaystyle \frac{a}{r^{\prime }}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)\right],\mathbf{r}\in \Omega ,{\mathbf{r}}^{\prime }\in {\Omega }^{\prime },$$

(20)

$${\Delta }^{2}u\left(\mathbf{r}\right)={\displaystyle \frac{r^{\prime 7}}{a^7}}{\Delta }^{\prime 2}\left[{\displaystyle \frac{r^{\prime }}{a}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)\right],\mathbf{r}\in \Omega ,{\mathbf{r}}^{\prime }\in {\Omega }^{\prime },$$

(21)

where Δ is Laplace’s operator in $\Omega ,$ ${\Delta }^{\prime }$ is Laplace’s operator in ${\Omega }^{\prime },$ ${\Delta }^2=\Delta \circ \Delta ,$ ${\Delta }^{\prime 2}={\Delta }^{\prime }\circ {\Delta }^{\prime },$ ${\mathbf{r}}^{\prime }$ is the inverted vector of $\mathbf{r}$ with respect to a sphere of radius a, and $r=\left|\mathbf{r}\right|,$ $r^{\prime }=\left|{\mathbf{r}}^{\prime }\right|.$

Proof. 

For the proof, see [6]. □

Lemma 5. 

From the previous theorem, it is easy to conclude that

• If function $u\left(\mathbf{r}\right)$ is a harmonic function in $\Omega ,$ then function ${\displaystyle \frac{1}{r^{\prime }}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)$ is a harmonic function in ${\Omega }^{\prime };$
• If function $u\left(\mathbf{r}\right)$ is a smooth enough biharmonic function in $\Omega ,$ then function $r^{\prime }u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)$ is a biharmonic function in ${\Omega }^{\prime }.$

Proof. 

• Since $u\left(\mathbf{r}\right)$ is a harmonic function in $\Omega ,$ then $\Delta u\left(\mathbf{r}\right)=0$, and from (20), we derive

$${\displaystyle \frac{r^{\prime 5}}{a^5}}{\Delta }^{\prime }\left[{\displaystyle \frac{a}{r^{\prime }}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)\right]=0\iff {\Delta }^{\prime }\left[{\displaystyle \frac{a}{r^{\prime }}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)\right]=0,$$

which means that ${\displaystyle \frac{1}{r^{\prime }}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)$ is a harmonic function in ${\Omega }^{\prime }.$

• Since $u\left(\mathbf{r}\right)$ is a biharmonic function in $\Omega ,$ then $\Delta u\left(\mathbf{r}\right)=0$, and from (21), we derive

$${\displaystyle \frac{r^{\prime 7}}{a^7}}{\Delta }^{\prime 2}\left[{\displaystyle \frac{r^{\prime }}{a}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)\right]=0\iff {\Delta }^{\prime 2}\left[{\displaystyle \frac{r^{\prime }}{a}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)\right]=0,$$

which means that $r^{\prime }u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)$ is a biharmonic function in ${\Omega }^{\prime }.$

□

Liouville [28] proved that Kelvin’s inversion is the only transformation in ${\mathbb{R}}^3$, which preserves angles and harmonicity.

2.4. Kelvin’s Inversion in Stokes Flow

Stokes flow is the flow where the viscous forces dominate over the inertial ones [29,30]. In case of an axisymmetric flow, a fourth-order partial differential equation (PDE) describes the flow through a function called the stream function [31]. If $(q_1,q_2,\phi )$ is the axisymmetric system of coordinates with metric coefficients $h_1,h_2,$ and a radial cylindrical coordinate $\varpi$, and $\psi (q_1,q_2,\phi )$ is the stream function, then the PDE which must be satisfied is

$$E^4\psi (q_1,q_2,\phi )=0,$$

where $E^4=E^2\circ E^2$, and the operator $E^2$ is defined as

$$E^2=h_1{h}_2\varpi \left[{\displaystyle \frac{\partial }{\partial q_1}}\left({\displaystyle \frac{h_1}{h_2\varpi }}{\displaystyle \frac{\partial }{\partial q_1}}\right)+{\displaystyle \frac{\partial }{\partial q_2}}\left({\displaystyle \frac{h_2}{h_1\varpi }}{\displaystyle \frac{\partial }{\partial q_2}}\right)\right].$$

(22)

The effect of Kelvin’s inversion on Stokes’ operator, $E^2,$ or on Stokes’ bistream operator, $E^4,$ are given below [6].

Theorem 5. 

If $u\left(\mathbf{r}\right)$ is a smooth enough function in Ω and ${\Omega }^{\prime }$ is the image of Ω through Kelvin’s inversion, then

$$E^{2}u\left(\mathbf{r}\right)={\displaystyle \frac{r^{\prime 3}}{a^3}}{E}^{\prime 2}\left[{\displaystyle \frac{r^{\prime }}{a}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)\right],\mathbf{r}\in \Omega ,{\mathbf{r}}^{\prime }\in {\Omega }^{\prime },$$

(23)

$$E^{4}u\left(\mathbf{r}\right)={\displaystyle \frac{r^{\prime 5}}{a^5}}{E}^{\prime 4}\left[{\displaystyle \frac{r^{\prime 3}}{a^3}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)\right],\mathbf{r}\in \Omega ,{\mathbf{r}}^{\prime }\in {\Omega }^{\prime },$$

(24)

where $E^2$ is the Stokes operator in $\Omega ,$ $E^{\prime 2}$ is the Stokes operator in ${\Omega }^{\prime },$ $E^4=E^2\circ E^2,$ $E^{\prime 4}=E^{\prime 2}\circ E^{\prime 2},$ ${\mathbf{r}}^{\prime }$ is the inverted vector of $\mathbf{r}$ with respect to a sphere of radius a, and $r=\left|\mathbf{r}\right|,$ $r^{\prime }=\left|{\mathbf{r}}^{\prime }\right|.$

Proof. 

For the proof, see [6]. □

Lemma 6. 

The above theorem implies that

• If $u\left(\mathbf{r}\right)$ is a smooth enough stream function in $\Omega ,$ then $r^{\prime }u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)$ is a stream function in ${\Omega }^{\prime };$
• If $u\left(\mathbf{r}\right)$ is a smooth enough bistream function in $\Omega ,$ then $r^{\prime 3}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)$ is a bistream function in ${\Omega }^{\prime }.$

Proof. 

• Since $u\left(\mathbf{r}\right)$ is a stream function in $\Omega ,$ then $E^{2}u\left(\mathbf{r}\right)=0$, and from (23), we derive that

$$E^{\prime 2}\left[{\displaystyle \frac{r^{\prime }}{a}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)\right]=0,$$

which means that $r^{\prime }u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)$ is a stream function in ${\Omega }^{\prime }.$

• Since $u\left(\mathbf{r}\right)$ is a bistream function in $\Omega ,$ then $E^{4}u\left(\mathbf{r}\right)=0$, and from (24), we derive that

$$E^{\prime 4}\left[{\displaystyle \frac{r^{\prime 3}}{a^3}}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)\right]=0,$$

concluding that $r^{\prime 3}u\left({\displaystyle \frac{a^2}{r^{\prime 2}}}{\mathbf{r}}^{\prime }\right)$ is a bistream function in ${\Omega }^{\prime }.$

□

3. Applications

In this section, some applications of Kelvin’s inversion will be presented. For more applications, the anxious reader can refer to [32,33,34].

3.1. Scattering

3.1.1. Capacity and Rayleigh Scattering

Dassios and Kleinman [7] calculated the capacity $C^{\prime }$ of an inverse prolate or oblate spheroid with the surface $S^{\prime }.$ The exterior potential problem is

$$\left\{\begin{array}{c}{\Delta }^{\prime }{u}^{\prime }=0,in{V}^{\prime },\hfill \\ u^{\prime }=1,on{S}^{\prime },\hfill \\ u^{\prime }=O\left({\displaystyle \frac{1}{r^{\prime }}}\right),as{r}^{\prime }\to +\infty ,\hfill \end{array}\right.$$

(25)

where $V^{\prime }$ is the exterior of the inverted spheroid and ${\Delta }^{\prime }$ is Laplace’s operator expressed in the inverted coordinate system.

The capacity of the surface $S^{\prime }$ is then calculated by the relation

$$C^{\prime }=-{\displaystyle \frac{1}{4\pi }}{\int }_{S^{\prime }}{\displaystyle \frac{\partial u^{\prime }}{\partial n^{\prime }}}d{S}^{\prime },$$

(26)

where ${\displaystyle \frac{\partial }{\partial {\eta }^{\prime }}}$ is the outward normal unit derivative on $S^{\prime }.$

By inverting problem (25) using Kelvin’s transformation, they derived the following interior problem:

$$\left\{\begin{array}{c}\Delta u=0,inV,\hfill \\ u={\displaystyle \frac{1}{r}},onS,\hfill \end{array}\right.$$

(27)

and the capacity is now calculated via the relation

$$C^{\prime }=\underset{r\to 0^{+}}{lim}u\left(\mathbf{r}\right),$$

(28)

where S is the surface of the spheroid, V is the interior of the spheroid, and $\Delta$ is Laplace’s operator expressed in the coordinate system.

By applying the inverted spheroidal coordinate system (prolate or oblate), the capacity is obtained, and thus, the low-frequency scattering of a plane wave from an acoustically soft boundary is calculated as the series expansion employing Legendre functions of the first and the second kind [35].

3.1.2. Low-Frequency Acoustic Scattering

Gintides and Kyriaki [8] studied the low-frequency acoustic scattering by a hard inverse-prolate spheroid. The boundary of the scatterer is denoted with $S^{\prime }$ and its exterior with $V^{\prime }.$ The unknown function is $\psi \left({\mathbf{r}}^{\prime }\right),$ expressing the excess pressure field in acoustics; thus, the problem at hand is defined as

$$\left\{\begin{array}{c}({\Delta }^{\prime 2}+k^2)\psi \left({\mathbf{r}}^{\prime }\right)=0,{\mathbf{r}}^{\prime }\in V^{\prime },\hfill \\ {\displaystyle \frac{\partial }{\partial {\eta }^{\prime }}\psi \left({\mathbf{r}}^{\prime }\right)=0,{\mathbf{r}}^{\prime }\in S^{\prime },}\hfill \\ {\displaystyle \underset{r^{\prime }\to +\infty }{lim}{\int }_{S_{r^{\prime }}}{\left|\frac{\partial u}{\partial r^{\prime }}-iku\right|}^{2}d{S}^{\prime }=0,}\hfill \end{array}\right.$$

(29)

where k is the wave number, ${\displaystyle \frac{\partial }{\partial {\eta }^{\prime }}}$ is the outward normal unit derivative on $S^{\prime },$ $S_{r^{\prime }}$ is a sphere of radius $r^{\prime }$ with a center $(0,0,0),$ k is the observation vector, and

$$\psi \left({\mathbf{r}}^{\prime }\right)=e^{i\mathbf{k}·{\mathbf{r}}^{\prime }}+u\left({\mathbf{r}}^{\prime }\right).$$

(30)

They expressed the unknown field as a series expansion of ${\varphi }_n\left({\mathbf{r}}^{\prime }\right)$ and later, every function ${\varphi }_n\left({\mathbf{r}}^{\prime }\right)$ as a sum of an unknown function, $U_n^{\prime }\left({\mathbf{r}}^{\prime }\right)$, and a known one, $P_n\left({\mathbf{r}}^{\prime }\right).$

Therefore, from (29), the functions $U_n^{\prime }\left({\mathbf{r}}^{\prime }\right)$ satisfy the following problem:

$$\left\{\begin{array}{c}{\Delta }^{\prime }{U}_n^{\prime }\left({\mathbf{r}}^{\prime }\right)=0,{\mathbf{r}}^{\prime }\in V^{\prime },\hfill \\ {\displaystyle \frac{\partial }{\partial {\eta }^{\prime }}{U}_n^{\prime }\left({\mathbf{r}}^{\prime }\right)=-\frac{\partial }{\partial {\eta }^{\prime }}{P}_n\left({\mathbf{r}}^{\prime }\right),{\mathbf{r}}^{\prime }\in S^{\prime },}\hfill \\ {\displaystyle U_n^{\prime }\left({\mathbf{r}}^{\prime }\right)=O\left(\frac{1}{r^{\prime 2}}\right),r^{\prime }\to +\infty .}\hfill \end{array}\right.$$

(31)

In order to overcome the difficulties resulting from (31), they used Kelvin’s inversion, translating an exterior of the inverted prolate scatterer problem in an interior to a prolate spheroid, which was easier to handle, deriving a zeroth and a first-order frequency approximation of their problem using associated Legendre functions of the first kind [35].

3.2. Electrostaticity

3.2.1. Conducting Torus

Cade [15] investigated a conducting torus, which was freely influenced (or charged) by an external field, improving his previous work where the torus was influenced by a field parallel to its rotational axis. In order to obtain the charge density $\sigma ,$ the capacity C, and the total charge $Q,$ Kelvin’s inversion was implemented, transforming the external problem into an internal one.

Cade assumed a torus formed by rotating a circle of radius $a,$ with a center $(b,0,c),$ $0<a<b$, around the z-axis, and a sphere of inversion with a center K on the z-axis and a radius R, such that it does not contain or intersect the torus. Therefore, the inverted torus is a torus inside the inversion sphere (Figure 6), where its generating circle has radius $a^{\prime },$ center $(b^{\prime },0,c^{\prime }),$ $0<a^{\prime }<b^{\prime }$, and

$$a^{\prime }={\displaystyle \frac{a{R}^2}{b^2+c^2-a^2}},b^{\prime }={\displaystyle \frac{b{R}^2}{b^2+c^2-a^2}},c^{\prime }={\displaystyle \frac{c{R}^2}{b^2+c^2-a^2}},$$

(32)

resulting in

$${\displaystyle \frac{a^{\prime }}{b^{\prime }}}={\displaystyle \frac{a}{b}},{\displaystyle \frac{a^{\prime }}{c^{\prime }}}={\displaystyle \frac{a}{c}}.$$

(33)

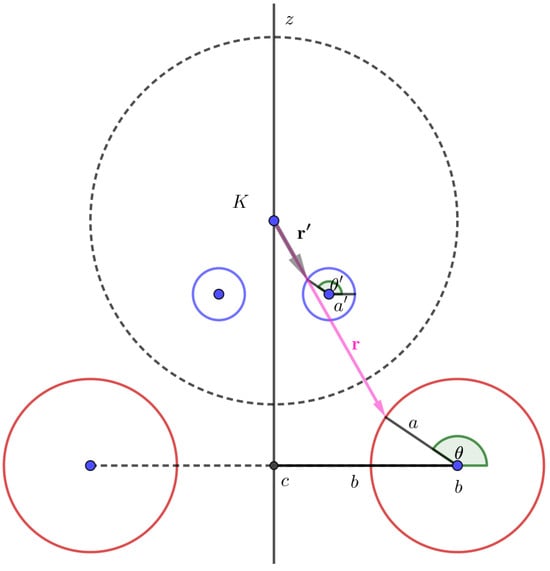
Figure 6. Conducting torus in 2D.

Assuming that the torus inside is a surface of a freely charged conductor with potential $V_0,$ Kelvin’s inversion enables its replacement by the outside surface of a torus at zero potential, influenced by a point charge equal to $-R{V}_0$ at the origin. If ${\sigma }^{\prime }$ is the charge density inside the inverted torus, then

$$\sigma \left(\theta \right)={\displaystyle \frac{R^3}{r^3}}{\sigma }^{\prime }\left({\theta }^{\prime }\right),$$

(34)

where r is the Euclidian distance and $\theta ,{\theta }^{\prime }\in [0,2\pi ]$ are the angles between a parallel to axis the $x^{\prime }x$ and the radius of the torus, corresponding to the point and its inverse with respect to the inversion, respectively (Figure 6).

Using (34), Cade obtained the charge density, the capacity, and the total charge, taking into account previous known results, obtained using the perturbation method to the second order of $a/b$ for these quantities.

3.2.2. Dielectric-Coated Conducting Sphere

Pyati [13] studied the problem of a conducting sphere of radius $a>0$ with a concentric dielectric coating sphere of radius $b>0,$ where $a<b,$ under the influence of a primary electrostatic field ${\varphi }_0,$ which is due to a unit point charge placed at $r_0\ge b$ along the z axis (Figure 7).

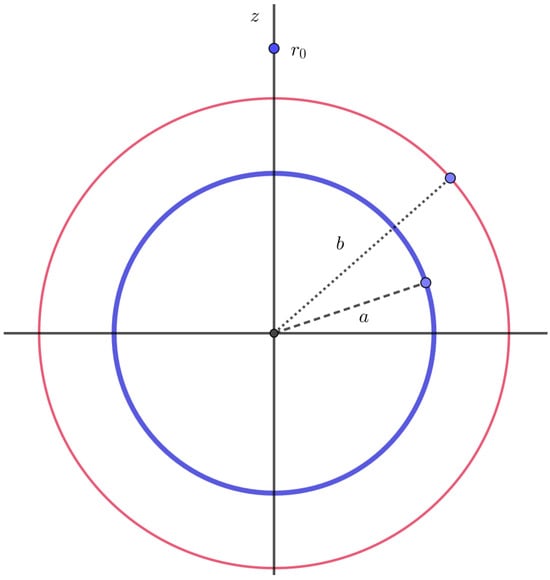
Figure 7. Dielectric-coated conducted sphere in 2D.

The appropriate coordinate system [26] is the spherical one $(r,\theta ,\phi ),$ but the problem has azimuthal symmetry and the surfaces depend only on $r.$ Therefore, only the radial coordinate is embedded in the solution. If ${\varphi }_i\left(r\right)$ and ${\varphi }_e\left(r\right)$ are the potentials to be determined where $a\le r\le b$ and $r\ge b,$ respectively, then we have

$${\varphi }_i\left(r\right)={\varphi }_0\left(r\right)+{\varphi }_2\left(r\right),a\le r\le b,$$

(35)

$${\varphi }_e\left(r\right)={\varphi }_0\left(r\right)+{\varphi }_1\left(r\right),r\ge b,$$

(36)

where ${\varphi }_1\left(r\right)$ and ${\varphi }_2\left(r\right)$ are the perturbations caused by the dielectric-coated sphere. The imposed boundary conditions are

$${\varphi }_i\left(a\right)=0,$$

(37)

$${\varphi }_i\left(b\right)={\varphi }_e\left(b\right),$$

(38)

$${\displaystyle \frac{\partial {\varphi }_e}{\partial r}}{|}_{r=b}=K{\displaystyle \frac{\partial {\varphi }_i}{\partial r}}{|}_{r=b},$$

(39)

where K is the dielectric constant of the coating.

Expressing ${\varphi }_0\left(r\right)$ in spherical harmonics, the task was to obtain ${\varphi }_1\left(r\right)$ and ${\varphi }_2\left(r\right).$ In order to achieve this, they used the principle that, in this coordinate system, if ${\varphi }_0\left(r\right)$ is a harmonic function, then functions

$${\displaystyle \frac{R}{r}}{\varphi }_0\left({\displaystyle \frac{R^2}{r}}\right),{\displaystyle \frac{1}{r}}{\int }_0^{R}t{\varphi }_0\left({\displaystyle \frac{t^2}{r}}\right)dt,{\displaystyle \frac{R}{r}}{\int }_0^{1}f\left(t\right){\varphi }_0\left({\displaystyle \frac{t{R}^2}{r}}\right)dt$$

(40)

are also harmonic, where $R>0$ is the radius of the sphere of Kelvin’s transformation and $f\left(t\right)$ is an arbitrary function.

Taking into advantage (40) and assuming specific forms of ${\varphi }_1\left(r\right)$ and ${\varphi }_2\left(r\right)$, which satisfied Laplace’s equation and the first two BCs, the remaining task was to determine the unknowns from the third BC.

This approach delivers results which converge faster than the well-known straightforward obtained solution.

3.2.3. Multipoles

Amaral et al. [14] studied the inverse multipoles in electrostatistics using Kelvin’s inversion. They used the inversed Poisson equation via the relation

$${\nabla }^2\Phi \left(\mathbf{r}\right)=-{\displaystyle \frac{1}{{ϵ}_0}}\rho \left(\mathbf{r}\right)\iff {\nabla }^{\prime 2}{\Phi }^{\prime }\left({\mathbf{r}}^{\prime }\right)=-{\displaystyle \frac{1}{{ϵ}_0}}{\rho }^{\prime }\left({\mathbf{r}}^{\prime }\right),$$

(41)

where the primes denote the inverse quantities from Kelvin’s inversion. Taking into account the multipole expansion for the potential $\Phi \left(\mathbf{r}\right)$ as a series using spherical harmonics and the integral for the spherical multipole moments, they derived the corresponding potential, the spherical multipole moments, and the electric field in the inverted regime and, therefore, the solution to the problem at hand. First, they applied the derived formulas in a spherical shell and in eccentric spheres. The other two of their applications deserve special reference: the case where the spherical cells pass through the origin (Kelvin’s inversion maps these spheres to planes) and the case of a torus without opening (Kelvin’s inversion maps these toruses to infinite cylinders).

3.3. Thermoelasticity

Chao and Wu [16] studied the problem of circular elastic inclusion bonded to a material matrix, which was subjected to arbitrary thermal loading.

They used the complex variable method to express the potential, and therefore the temperature T, and the heat flux $Q,$ using the relations

$$T=Re\left[g^{\prime }\left(z\right)\right],Q=-kIm\left[g^{\prime }\left(z\right)\right],z\in \mathbb{C},$$

(42)

where k is the heat conductivity and $g\left(z\right)$ is the potential to be derived.

Kelvin’s inversion can be used with complex variables, since a complex number is mapped to a vector in the complex plane and vice versa. Therefore, if $z\in \mathbb{C},$ the region $\left|z\right|<a,a>0,$ is mapped to the region $\left|z\right|>a,$ translating the internal problem (circular inclusion) into an external one (material matrix). For instance, if $u,v$ are the real and the imaginary parts of a holomorphic function $f,$ expressed in polar coordinates [26], i.e.,

$$f\left(z\right)=u(r,\theta )+iv(r,\theta ),r\ge 0,\theta \in [0,2\pi ],$$

then

$$\overline{f\left(z\right)}=\overline{f\left({\displaystyle \frac{a^2}{\overline{z}}}\right)}=\overline{u\left({\displaystyle \frac{a^2}{r}},\theta \right)+iv\left({\displaystyle \frac{a^2}{r}},\theta \right)}=u^{\prime }(r,\theta )-i{v}^{\prime }(r,\theta ),$$

where the primes denote the inverted quantities via Kelvin’s inversion.

They studied two cases depending on the singularities, when all are in the material matrix or all in the inclusion. Moreover, the heat flux was assumed uniform at infinity (in the material matrix) or inside the inclusion or in a half-plane.

3.4. Potential Theory

Baganis and Hadjinicolaou used Kelvin’s inversion to study a problem in potential theory in a 2D non-convex domain using Dirichlet [9] or Neumann [10] boundary conditions. The non-convex body (its boundary is denoted with $\partial V^{\prime }$) has a trefoil shape (Figure 8) and the exterior of the body (denoted as $V^{\prime }\subseteq {\mathbb{R}}^2$) is the domain in which the solution had to be derived. If $q(x,y),(x,y)\in V^{\prime }$ is the unknown potential, the equation which has to be satisfied is

$$\Delta q(x,y)=0,(x,y)\in V^{\prime },$$

(43)

with the Dirichlet boundary condition

$$q(x,y)=f(x,y),(x,y)\in \partial V^{\prime },$$

(44)

or the Neumann boundary condition

$${\displaystyle \frac{\partial q(x,y)}{\partial n^{\prime }}}=f(x,y),(x,y)\in \partial V^{\prime },$$

(45)

where ${\displaystyle \frac{\partial }{\partial n^{\prime }}}$ is the outward normal unit derivative on $\partial V^{\prime }.$

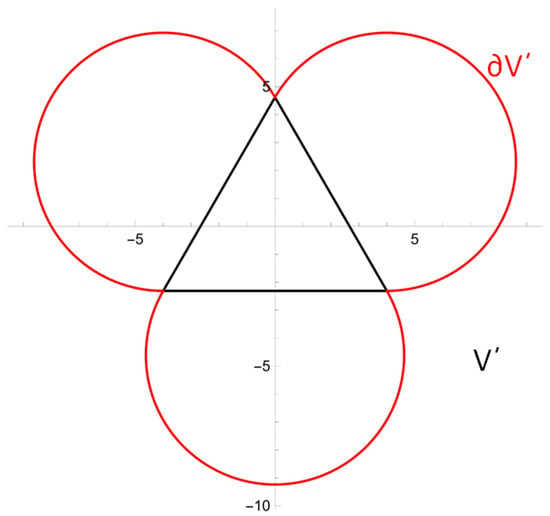
Figure 8. A trefoil and its inverted equilateral triangle.

Using Kelvin’s inversion, the trefoil is transformed in an equilateral triangle and the domain $V^{\prime }$ into the interior of the triangle. Applying the Fokas method [12] and the results from [36], the solution of the inverted problem is obtained, and thus also the potential $q(x,y).$

3.5. Bioengineering

In order to study blood’s plasma flow past a red blood cell (RBC) in capillaries, Dassios et al. [17] used an inverted prolate spheroid as an RBC, and due to the physical requirements of the model, they assumed Stokes flow [31].

If $V^{\prime }$ is the fluid domain, $\partial V^{\prime }$ is the RBC’s surface, U is the uniform velocity of plasma flow (Figure 9), $E^{\prime 2}$ is the Stokes operator in the inverse prolate coordinate system, $E^{\prime 4}=E^{\prime 2}\circ E^{\prime 2},$ ${\mathbf{r}}^{\prime }$ is the position vector, and ${\psi }_a\left({\mathbf{r}}^{\prime }\right)$ is the stream function, then the problem is defined via the relations

$$\left\{\begin{array}{c}{E}^{\prime 4}{\psi }_a\left({\mathbf{r}}^{\prime }\right)=0,{\mathbf{r}}^{\prime }\in V^{\prime },\hfill \\ {\psi }_a\left({\mathbf{r}}^{\prime }\right)=0,{\mathbf{r}}^{\prime }\in \partial V^{\prime },\hfill \\ {\displaystyle \frac{\partial {\psi }_a\left({\mathbf{r}}^{\prime }\right)}{\partial n^{\prime }}}=0,{\mathbf{r}}^{\prime }\in \partial V^{\prime },\hfill \\ {\psi }_a\left({\mathbf{r}}^{\prime }\right)\to {\displaystyle \frac{1}{2}}{\varpi }^{2}U,r^{\prime }\to +\infty ,\hfill \end{array}\right.$$

(46)

where ${\varpi }^{\prime }$ is the radial cylindrical coordinate of the coordinate system and ${\displaystyle \frac{\partial }{\partial n^{\prime }}}$ is the outward normal unit derivative on $\partial V^{\prime }.$ Expressing this problem in the inverse prolate spheroidal coordinates proved that it is very difficult to satisfy the far-field condition. The use of Kelvin’s inversion had a significant impact, since the corresponding interior problem in the prolate coordinate system $(\tau ,\zeta ,\varphi ),$ $\tau \ge 1,$ $-1\le \zeta \le 1,$ $0\le \varphi <2\pi$ is

$$\left\{\begin{array}{c}{E}^4\psi (\tau ,\zeta )=0,\hfill \\ \psi ({\tau }_0,\zeta )=0,\hfill \\ {\displaystyle \frac{\partial \psi (\tau ,\zeta )}{\partial \tau }}{|}_{\tau ={\tau }_0}=0,\hfill \\ \psi (\tau ,\zeta )\to {\displaystyle \frac{c(1-{\zeta }^2)({\tau }^2-1)U}{2\sqrt{{\tau }^2+{\zeta }^2-1}}}(\tau ,\zeta )\to (1,0),\hfill \end{array}\right.$$

(47)

where the equation $\tau ={\tau }_0$ expresses the surface of the prolate spheroid.

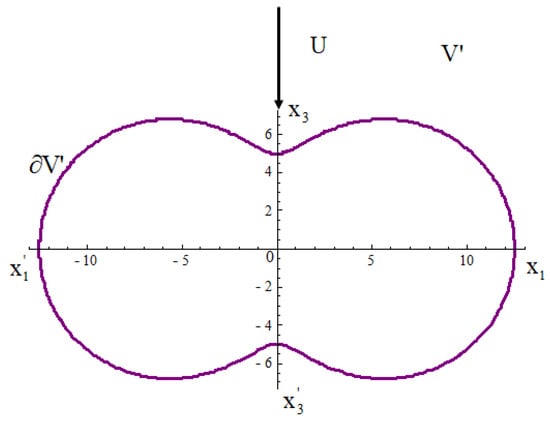
Figure 9. Blood’s plasma flow past an RBC in 2D.

The solution of Stokes flow in the prolate spheroidal coordinate system is

$$\psi (\tau ,\zeta )=g_0\left(\tau \right)G_0\left(\zeta \right)+g_1\left(\tau \right)G_1\left(\zeta \right)+\sum _{n=2}^{+\infty }[g_n\left(\tau \right)G_n\left(\zeta \right)+h_n\left(\tau \right)H_n\left(\zeta \right)],$$

(48)

where $G_n,H_n$ are Gegenbauer functions of the first and the second kind [35], respectively, and $g_n,h_n$ are linear combinations of the functions $G_n,H_n.$

Moreover, the inverted far-field condition from (47) can be written as the stream function in Equation (48), and upon applying orthogonality arguments with respect to $\zeta ,$ the first set of the unknown constants were derived. In order to calculate the remaining unknown constants, the boundary conditions of (47) were employed, as well as the reduction of the obtained stream function to the previous known result of the stream function in the spherical coordinates. Therefore, the solution to the interior problem was derived:

$$\psi (\tau ,\zeta )=\sum _{n=1}^{+\infty }[A_{2n}{G}_{2n}\left(\tau \right)+E_{2n}{G}_{2n+2}\left(\tau \right)]G_{2n}\left(\zeta \right),$$

(49)

where $A_{2n},E_{2n}$ are constants, and using Kelvin’s transformation, the stream function in the exterior domain is

$${\psi }_a\left({\mathbf{r}}^{\prime }\right)={\displaystyle \frac{\psi (\tau ,\zeta )}{c^3{\sqrt{{\tau }^2+{\zeta }^2-1}}^3}}.$$

(50)

This work provided a useful way in order to solve the sedimentation of an RBC in blood’s plasma, the translation of two aggregated low-density lipoproteins within blood’s plasma, and blood’s plasma flow past a swarm of RBCs [37].

4. Discussion

Kelvin’s inversion is a transformation that maps a point to another one with respect to a sphere. Its usefulness is that it can transform the interior of a surface to the exterior of another surface and vice versa [38,39]. Hence, the solution of an exterior (or interior) problem can be obtained when the solution of the corresponding inverted one is known or can be easily derived, providing a powerful tool when targeting difficult problems. Whenever the geometry of the inverted surface is simpler to handle, the use of Kelvin’s inversion is an interesting option. Taking into account that it preserves harmonicity, its use in boundary value problems with partial differential equations provide solutions in cases where the straightforward methods do not. Kelvin’s inversion have been under continuous study, revealing significant properties. These properties have been used in science fields in order to solve various problems. In this paper, we summarized the basic properties of Kelvin’s transformation and presented some of its many applications in scattering, electrostaticity, thermoelasticity, potential theory, and bioengineering, highlighting its usefulness and usability when solving BVPs.