Revisiting Probabilistic Metric Spaces

Abstract

The field of probabilistic metric spaces has an intrinsic interest based on a blend of ideas drawn from metric space theory and probability theory. The goal of the present paper is to introduce and study new ideas in this field. In general terms, we investigate the following concepts: linearly ordered families of distances and associated continuity properties, geometric properties of distances, finite range weak probabilistic metric spaces, generalized Menger spaces, and a categorical framework for weak probabilistic metric spaces. Hopefully, the results will contribute to the foundations of the subject.

1. Introduction

1.1. Preliminary Remarks

The original and primary source on probabilistic metric spaces is [1]. Current research in the field appears to fall into three basic areas: (i) foundational topics [2,3,4,5], (ii) fixed point theory [6,7,8], and (iii) models for applications [9,10]. The primary emphasis in current research seems to be on area (ii). We discuss this topic further in the section on Discussion and Future Work. The admittedly lofty aim of the present paper is to rejuvenate the foundations of the subject by reexamining the original concepts before most research was devoted to Menger spaces and triangle functions.

1.2. Organization

The main body of the paper consists of three sections. Section 2 presents background material on weak probabilistic metric spaces (WPMSs) and introduces the notions of finite range WPMSs and linearly ordered families of distances. Section 3 presents results on constructing Menger spaces and approximating them by finite range Menger spaces, as well as characterizing the generalized Menger spaces. Section 4 introduces a categorical framework for WPMSs and establishes several key properties of the category WP. It also shows that the Menger spaces are a reflective subcategory of WP. Section 5 discusses the potential contributions of the work. There is also an Appendix A devoted to an overview of distance-spaces that includes several results used in other sections of the paper.

1.3. Conventions

We use the symbol □ to denote the end of proofs. The symbol N (resp. Z or R) denotes the natural numbers (resp. integers or real numbers), N⁺ = N\{0}, and R⁺ = [0, +∞). The symbol I denotes [0, 1]. For each x ∈ R, ⌊x⌋ (resp. ⌈x⌉) denotes the largest integer ≤ x (resp. smallest integer ≥ x). For a set S, id_S: S ⟶ S denotes the identity mapping, and for each A ⊆ S, χ_A: S ⟶ {0, 1} (resp. incl_A: A ⟶ S) denotes the characteristic function of A (resp. the inclusion mapping). The symbol P(S) denotes the power-set of S and P_F⁺(S) denotes the family of non-empty finite subsets of S. Given sets S and T, S ∪_d T denotes their disjoint union, F(S, T) is the family of mappings S ⟶ T, and for each t ∈ T, const_t: S ⟶ T is the constant mapping at t. A mapping φ: R⁺⟶ R⁺ is a modulus of continuity if φ is non-decreasing and φ(0+) = φ(0) = 0.

2. Weak Probabilistic Metric Spaces

2.1. Background

Here we present the notion of a weak probabilistic metric space, the associated family of distances, and several examples. The reader familiar with these ideas can skip to Section 2.2.

Define the set of distribution functions

Δ = {F: R ⟶ I | F is left-continuous, non-decreasing, inf(F) = 0, and sup(F) = 1}

and let ≦ denote the point-wise order on Δ. The symbol H denotes the member of Δ defined by H(x) = 0 if x ≤ 0 and H(x) = 1 if x > 0. Let Δ⁺ = {F ∈ Δ | F(0) = 0}. If F ∈ Δ⁺, then F(x) = 0 for each x < 0, so we can assume that R⁺ is the domain of each member of Δ⁺.

A weak probabilistic metric space (WPMS) consists of a set S and F = {F_pq | p, q ∈ S} ⊆ Δ⁺ that satisfies the following properties:

(w₁) For each p ∈ S, F_pp = H.

(w₂) For each p, q ∈ S, F_pq = F_qp.

(w₃) For each distinct p, q, r ∈ S and x, y ∈ R⁺, F_pq(x) = F_qr(y) = 1 ⟹ F_pr(x + y) = 1.

The standard interpretation is that for p, q ∈ S and x ∈ R⁺, F_pq(x) is the probability that the distance from p to q is less than x. For example, F_pq(0) = 0 implies a zero probability that the distance between points p and q is less than 0. Property (w₃) postulates a probabilistic triangle inequality: if the probability that the distance from p to q is less than x and the probability that the distance from q to r is less than y, then the probability that the distance from p to r is less than x + y. We note that (w₃) always holds if p, q, and r are not distinct; for instance, if p = q, then F_pr(y) = 1, so since F_pr is non-decreasing, F_pr(x + y) = 1.

The property (w₁) is a weaker version of the following property:

(w₁′) For each p, q ∈ S, F_pq = H ⇔ p = q.

Otherwise, our definition of a WPMS agrees with the one used in ([1], 1.4.2). (Section 3.1). In the sequel, a pair (S, F) denotes a WPMS. Frequently, we also use the alternate representation (S, F), where F: S × S ⟶ Δ⁺ is defined by F(p, q) = F_pq.

We distinguish the following types of WPMSs. If (S, F) is a WPMS and (w₁′) holds, then we say that (S, F) is a WPMS⁺. We say that a WPMS (S, F) is trivial if for each p, q ∈ S, F_pq = H. More generally, we say that a WPMS (S, F) is special if for each p, q ∈ S, F_pq⁻¹(1) ≠ ∅.

Example 2.1.1.

The WPMS (S, G) determined by a pseudometric space (S, γ) ([1], 1.2.5).

For p, q ∈ S, define G_pq: R⁺ ⟶ I by G_pq(x) = H(x − γ(p, q)). Using the standard interpretation, the probability is zero that the distance from p to q is less than γ(p, q).

Since the motivation for a WPMS is to model a probabilistic situation, it is natural to use a distribution function to define the members of F. The next example illustrates this idea.

Example 2.1.2.

The 1-simple WPMS (S, A, γ, Φ) based on a pseudometric space (S, γ) and a fixed distribution function Φ ∈ Δ⁺\{H} ([1], 8.6.1). For p, q ∈ S, define A_pq: R⁺ ⟶ I by

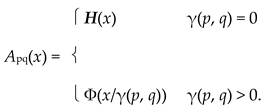If γ(p, q) = 0, then the probability is one that the distance from p to q is less than any positive number. If γ(p, q) > 0, then the probability that the distance from p to q is less than x is determined by the choice of Φ. In the same manner, we can define an α-simple WPMS (S, A, γ, Φ, α) for each 0 < α < 1 by using Φ(x/γ(p, q)^α) in place of Φ(x/γ(p, q)).

Example 2.1.3.

For a distinct pair p, q ∈ S = R⁺, define F_pq: R⁺ ⟶ I by

where a_pq = | p − q |. Also, for each p ∈ S, let F_pp = H. Then (R⁺, F) is a special WPMS.

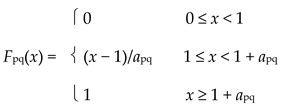Example 2.1.4.

For each p, q ∈ R satisfying | p − q | < 1, define f_pq: R⁺ ⟶ I by

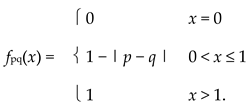Also, for each p, q ∈ R, define F_pq: R⁺ ⟶ I by

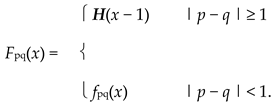Then (R, F) is a WPMS⁺.

There is a natural way to associate distances with a WPMS. For each F ∈ Δ⁺, define the non-decreasing mapping F^{^}: (0, 1] ⟶ [0, +∞] by F^{^}(t) = sup(X(t)), where X(t) = {x ∈ R⁺ | F(x) < t} ([1], Section 4.4). Since F(0) = 0, X(t) ≠ ∅ for each t > 0 and if t < 1, then X(t) is also bounded since sup(F) = 1, so F^{^}(t) is well-defined. If F⁻¹(1) ≠ ∅, then F^{^}(1) is also well-defined.

Given a WPMS (S, F) and 0 < t < 1, define ω_t: S × S ⟶ R⁺ by

ω_t(p, q) = F_pq^{^}(t) = sup{x ∈ R⁺ | F_pq(x) < t}

and define the extended real-valued mapping ω₁: S × S ⟶ [0, +∞] by ω₁(p, q) = F_pq^{^}(1).

The ω_t’s correspond to the d_c’s introduced in ([1], 8.2.3). For each 0 < t < 1, ω_t is a distance, i.e., for each p, q ∈ S, ω_t(p, p) = 0 and ω_t(p, q) = ω_t(q, p) (Appendix A.1). In general, ω_t is not a semi-metric; that is, ω_t(p, q) = 0 can occur for distinct p and q.

Given a WPMS (S, F), let

Ω_F = {ω_t | 0 < t < 1}

denote the set of well-defined distances. Notice that Ω_F is a linearly ordered family of distances: if 0 < s < t < 1, then ω_s ≤ ω_t.

For an α-simple space (S, A, γ, Φ, α) (Example 2.1.2), ω_t = Φ^{^}(t)γ^α for each 0 < t ≤ 1 and in Example 2.1.3, ω_t(p, q) = 1 + ta_pq for distinct p, q ∈ S and 0 < t < 1. Notice that in both cases, each ω_t is a pseudometric. In the following example, the distances are not pseudometrics.

Example 2.1.5.

For each p, q ∈ R⁺, define F_pq: R⁺ ⟶ I by

F_pq(x) = [H(x − | p − q |) + H(x − | p² − q² |)]/2.

Then (R⁺, F) is a special WPMS⁺. As an illustration, if 0 < a = | p − q | < b = | p² − q² |, then

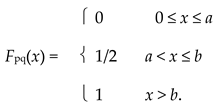The distances fall into two groups: where e₁ and e₂ are defined by e₁(p, q) = min{a, b} and e₂(p, q) = max{a, b}, respectively. The mapping e₂ is a metric, but e₁ is not a pseudometric since the triangle inequality does not hold. In fact, we can make an even stronger statement. For n ∈ N⁺, let x_n = n + 1/n, y_n = n, and z_n = -n + 1/n². Then e₁(x_n, y_n) + e₁(y_n, z_n) = 3/n − 1/n⁴ ⟶ 0 as n ⟶ +∞, but e₁(x_n, z_n) = 2 + 1/n² + 2/n − 1/n⁴ > 2 for each n. Therefore, (R⁺, e₁) does not satisfy the condition (wtc) discussed in Section 3.3.

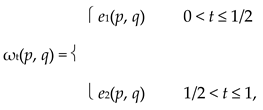2.2. Preliminary Results

In this subsection, we present some basic results that provide further background for the reader as well as a basis for subsequent sections. In proofs, we often assume that p, q, r ∈ S and x, y ∈ R⁺ without explicitly mentioning the sets.

The first result summarizes the relationships between the values of the distribution functions and distances. We use it repeatedly in the text. The proof is elementary, but we include part of it to familiarize the reader with the notation.

Lemma 2.2.1.

The following statements hold for each WPMS (S, F) and 0 < t ≤ 1.

(a)

ω_t(p, q) < x ⟹ Fpq(x) ≥ t.

(b)

Fpq(x) > t ⟹ ωt(p, q) < x.

(c)

Fpq(x) ≥ t ⟹  ωt(p, q) ≤ x and ωu(p, q) < x for  each 0 < u < t.

Proof. 

(b): Suppose y = ω_t(p, q) ≥ x. By the left-continuity of F_pq, for each ε > 0, there is y_ε < y such that F_pq(y) − F_pq(y_ε) < ε. Hence, F_pq(y_ε) ≤ t, so F_pq(y) < t + ε. Since the inequality holds for each ε > 0, F_pq(y) ≤ t. Therefore, F_pq(x) ≤ t since F_pq is non-decreasing. □

To check when a member of Ω_F is a pseudometric, it is useful to introduce the following predicate. Given a WPMS (S, F) and 0 < t ≤ 1, define

(&_t): ∀p, q, r ∈ S, ∀x, y ∈ R⁺ · F_pq(x) ≥ t and F_qr(y) ≥ t ⟹ F_pr(x + y) ≥ t.

It follows from property (w₃) that (&₁) always holds. The next result is implicit in the literature.

Prop 2.2.1.

Suppose (S, F) is a WPMS and 0 < t < 1.

(a)

If (&_t) holds, then ω_t is a pseudometric.

(b)

If ω_s is a pseudometric for each 0 < s < t,  then (&_t) holds.

Proof. 

(a): Let ε > 0 and choose x, y such that ω_t(p, q) < x < ω_t(p, q) + ε/2 and ω_t(q, r) < y < ω_t(q, r) + ε/2.

By Lemma 2.2.1(a), F_pq(x) ≥ t and F_qr(y) ≥ t, so by (&_t), F_pr(x + y) ≥ t. Hence, by Lemma 2.2.1(c), ω_t(p, r) ≤ x + y. Therefore, ω_t(p, r) < ω_t(p, q) + ω_t(q, r) + ε for each ε > 0, so ω_t satisfies the triangle inequality.

(b): If (&_t) does not hold, then there exists p, q, r, x, and y such that F_pq(x) ≥ F_qr(y) ≥ t > F_pr(x + y). Choose F_pr(x + y) < s < t. By Lemma 2.2.1(b), ω_s(p, q) < x and ω_s(q, r) < y. Since F_pr(x + y) < s, by Lemma 2.2.1(a), x + y ≤ ω_s(p, r). Therefore, ω_s(p, q) + ω_s(q, r) < x + y ≤ ω_s(p, r) shows that ω_s does not satisfy the triangle inequality. □

The reader can see from the previous proof that Lemma 2.2.1 might need to be used repeatedly. Therefore, in future proofs, we only use it implicitly.

The following elementary result complements the preceding result.

Lemma 2.2.2.

The following statements are equivalent for a WPMS (S, F).

(a)

(S, F) is special.

(b)

ω₁ is a real-valued mapping.

(c)

ω₁ is a pseudometric.

Proof. 

The implication (a) ⟹ (b) follows from the definition.

(b) ⟹ (c): Let x = ω₁(p, q) and y = ω₁(q, r). By definition, F_pq(x + ε/2) = 1 and F_qr(y + ε/2) = 1 for each ε > 0, so by (w₃), F_pr(x + y + ε) = 1. Hence, ω₁(p, r) ≤ x + y + ε for each ε > 0, so ω₁ satisfies the triangle inequality.

(c) ⟹ (a): Since ω₁(p, q) is finite, F_pq(ω₁(p, q) + 1) = 1. Hence, (S, F) is special. □

The next two results present conditions that are equivalent to Ω_F being a family of pseudometrics and metrics, respectively.

Prop 2.2.2.

The following statements are equivalent for a WPMS (S, F).

(a)

For each 0 < t < 1, ω_t is a pseudometric.

(b)

For each 0 < t < 1, (&_t) holds.

(c)

For each p, q, r ∈ S and x, y ∈ R⁺, F_pr(x + y) ≥ min{F_pq(x), F_qr(y)}.

Proof. 

The implication (c) ⟹ (a) follows from Prop 2.2.1(a) since (c) implies that each (&_t) holds. The implication (a) ⟹ (b) follows from Prop 2.2.1(b).

(b) ⟹ (c): Let s = F_pq(x) and t = F_qr(y). Clearly, if s = 0 or t = 0, then the inequality in (c) holds. Otherwise, if s ≤ t, then by (&_s), F_pr(x + y) ≥ s = min{s, t}. If s > t, then F_pr(x + y) ≥ t = min{s, t} follows from (&_t). □

The following result is not used in the rest of the paper, but it is a natural companion to the previous proposition.

Prop 2.2.3.

The following statements are equivalent for a WPMS (S, F).

(a)

For each 0 < t < 1, ω_t is a metric.

(b)

(i) For each p ≠ q, F_pq is right-continuous at 0.

(ii) For each p, q, r ∈ S and x, y ∈ R⁺, F_pr(x + y) ≥ min{F_pq(x), F_qr(y)}.

Proof. 

(a) ⟹ (b): Suppose p ≠ q and let n ∈ N\{0, 1}. Since ω_1/n(p, q) > 0, there is 0 < ε_n < 1/n such that ε_n < ω_1/n(p, q). Hence, F_pq(ε_n) ≤ 1/n. Therefore, F_pq(0+) = lim_h⟶0+F_pq(h) = 0, which establishes (i). Condition (ii) follows from Prop 2.2.2.

(b) ⟹ (a): By Prop 2.2.2 and (ii), each ω_t is a pseudometric. Assume that p ≠ q and ω_t(p, q) = 0 for some 0 < t < 1. Then each F_pq(1/n) ≥ t, so F_pq is not right-continuous at 0, which contradicts (i). □

We note that right continuity can be characterized by using the interplay between distances and distributions. Given a WPMS (S, F), for each x ∈ R⁺ and p, q ∈ S, define the predicate

(#_x,p,q) ≡ 0 < t ≤ 1 and ω_t(p, q) = x ⟹ F_pq(x) = t.

Then (S, F) satisfies (#_x,p,q) if and only if F_pq is right-continuous at x. We leave this statement for the reader’s consideration.

The condition stated in ([5], (IV)) is equivalent to (&_t) and the equivalence of parts (a) and (b) in Prop 2.2.2 and Prop 2.2.3 is proved in ([5], Lemma 1 and Theorem 1). Also, Prop 2.2.2(a) is proved in ([1], 8.2.3) and Prop 2.2.3 is essentially established in ([11], Theorems 9 and 10).

2.3. Reconstruction and Representation

The first result shows that for any WPMS (S, F), we can always reconstruct the family F = {F_pq} from Ω_F.

Prop 2.3.1.

For each WPMS (S, F), p, q  ∈ S, and x ∈ R⁺, F_pq(x) = sup{0 < t < 1 | ω_t(p, q) < x}, where Ω_F = {ω_t}.

Proof. 

For the proof, we suppress the pairs (p, q) and subscripts pq.

Let x ∈ R⁺ and T = {0 < t < 1 | ω_t < x}. Define v = 0 if T = ∅ and v = sup(T) if T ≠ ∅. If T = ∅, then ω_t ≥ x for each 0 < t < 1, so F(x) ≤ t for each 0 < t < 1. Hence, F(x) = v. If T ≠ ∅, then for each t ∈ T, F(x) ≥ t. Hence, v ≤ F(x). If v < F(x), choose v < r < F(x). Then ω_r < x, so r ∈ T. Hence, v ≥ r, which is a contradiction. Therefore, v = F(x). □

We remark that the following definition of ω_t is used in ([5], (I)): ω_t(p, q) = inf{x | F_pq(x) > t}. Then ([5], (III)) asserts that F_pq(x) = sup{t | ω_t(p, q) < x}.

Next, we present the first new idea in the paper. We say that a WPMS (S, F) has finite range if Rng(F) = ∪{Rng(F_pq) | p, q ∈ S} is a finite set. For this type of WPMS, we can establish the following representation theorem. Also, we will revisit these types of WPMSs in Section 3.2.

Theorem 2.3.1.

Assume that the WPMS (S, F) has the finite range Rng(F) = {t_i | 0 ≤ i ≤ n}, where t₀ = 0 < t₁ < … < t_n = 1 and Ω_F = {ω_t}. Then the following statements hold:

(a)

Ω_F = {ω_t(i) | 1 ≤ i ≤ n} and | Ω_F | = n.

(b)

For each p, q ∈ S and x ∈ R⁺, F_pq(x) = ∑{(t_i+1 − t_i)H(x − ω_t(i+1)(p, q)) | 0 ≤ i < n}.

Proof. 

In various places, we write t(i) in place of t_i.

(a): Given 0 < t ≤ 1, choose 1 ≤ i ≤ n such that t_i−1 < t ≤ t_i. Then for p, q ∈ S,

ω_t(p, q) = sup{x | F_pq(x) < t} = sup{x | F_pq(x) < t_i} = ω_t(i)(p, q).

This establishes ω_t = ω_t(i). Let 1 ≤ i < n and choose p, q, and y such that F_pq(y) = t_i. Then z = ω_t(i+1)(p, q) ≥ y. Since F_pq is left-continuous, there exists 0 < x < y such that F_pq(x) = t_i. If ω_t(i)(p, q) ≥ z, then ω_t(i)(p, q) > x, so F_pq(x) < t_i, which gives a contradiction. Therefore, we have ω_t(i)(p, q) < z = ω_t(i+1)(p, q). It follows that | Ω_F | = n.

(b): For each p, q ∈ S, define G_pq by G_pq(x) = ∑{(t_i+1 − t_i)H(x − ω_t(i+1)(p, q)) | 0 ≤ i < n}.

(1)

(S, G) is a WPMS.

[Each G_pq ∈ Δ⁺ since H is left-continuous and G_pq(x) = 1 for x > ω₁(p, q). It is easy to show that (w₁) and (w₂) hold. Suppose G_pq(x) = G_qr(y) = 1. Since (S, F) is special, by Lemma 2.2.2, ω₁ is a pseudometric. Then by definition, x > ω₁(p, q) and y > ω₁(q, r), so x + y > ω₁(p, r). Therefore, G_pr(x + y) = 1, so (w₃) holds.]

Let Ω_G = {ν_t}.

(2)

ν_t = ω_t for each 0 < t ≤ 1.

[Let p, q ∈ S and choose 1 ≤ i ≤ n such that t_i−1 < t ≤ t_i. Since {ω_t} is linearly ordered, by definition, Rng(G) ⊆ {t_i | 0 ≤ i ≤ n}. Hence, ν_t(p, q) = sup{x | G_pq(x) < t} = sup{x | G_pq(x) < t_i} = ν_t(i)(p, q). By definition, if G_pq(x) ≤ t_i−1, then x ≤ ω_t(i)(p, q), so ν_t(i)(p, q) = sup{x | G_pq(x) < t_i} ≤ ω_t(i)(p, q). If F_pq(x) < t_i, then x ≤ ω_t(i)(p, q), so G_pq(x) < t_i. Therefore,

ω_t(i)(p, q) = sup{x | F_pq(x) < t_i} ≤ sup{x | G_pq(x) < t_i} = ν_t(i)(p, q).

This establishes ω_t(i) = ν_t(i).]

Since (S, F) is a WPMS and by (1), (S, G) is a WPMS, it follows from (2) and Prop 2.3.1 that F = G. □

The WPMS (S, F) in Example 2.1.5 illustrates Theorem 2.3.1 since

F_pq(x) = [H(x − | p − q |) + H(x − | p² − q² |)]/2 = [H(x − e₁(a, b)) + H(x − e₂(a, b))]/2.

In this case, | Ω_F | = {e₁, e₂} and Rng(e₁) = Rng(e₂) = R⁺. Therefore, even for a WPMS with a finite range, the distances may not have finite ranges. In fact, Example 3.1.1 shows that the distances can have the values {0, 1} without the WPMS itself having a finite range.

The following result is an easy consequence of the previous theorem that fits nicely with one’s intuition. We can view it as a “0-1 law”: if the probability is 0 or 1 that the distance from p to q is less than some value, then the distance is described by a unique pseudometric.

Corollary 2.3.1.

The following statements are equivalent for a WPMS (S, F).

(a)

Rng(F) = {0, 1}.

(b)

(S, F) is determined by a pseudometric.

(c)

Ω_F = {ω₁} and ω₁ is a pseudometric.

(d)

| Ω_F| = 1.

Proof. 

(a) ⟹ (b): By Theorem 2.3.1, F_pq(x) = H(x − ω₁(p, q)) for each p, q ∈ S and x ∈ R⁺. Since (S, F) is special, by Lemma 2.2.2, ω₁ is a pseudometric.

(b) ⟹ (c): Suppose F_pq(x) = H(x − ω(p, q)) for a pseudometric ω and each p, q ∈ S and x ∈ R⁺. Then for each 0 < t ≤ 1, ω_t(p, q) = sup{x | F_pq(x) < t} = sup{x | x ≤ ω(p, q)} = ω(p, q).

Clearly, (c) ⟹ (d).

¬(a) ⟹ ¬(d): If 0 < F_pq(x) < 1 for some p, q ∈ S and x ∈ R⁺, choose 0 < s < F_pq(x) < t < 1. Then ω_s(p, q) < x ≤ ω_t(p, q) shows that ω_s ≠ ω_t. Hence, | Ω_F | > 1. □

2.4. Linearly Ordered Families

Here, we present the second new idea in the paper—the application of linearly ordered families of distances. For clarity, we are referring to a family Ω = {ρ_t | 0 < t < 1} of distances defined on a set S that satisfies ρ_s ≤ ρ_t for each 0 < s < t < 1. We say that Ω satisfies the left-continuity property (lcp) (resp. right-continuity property (rcp)) if ρ_t = sup{ρ_s | 0 < s < t} (resp. ρ_t = inf{ρ_s | t < s < 1} for each 0 < t < 1.

Prop 2.4.1.

The following statements hold for a WPMS (S, F).

(a)

The family Ω_F = {ω_t | 0 < t < 1} satisfies (lcp) and if (S, F) is a special WPMS, then ω₁ = sup{ω_t | 0 < t < 1}.

(b)

The family Ω_F satisfies (rcp) if and only if (#): for each distinct pair p, q ∈ S, F_pq is strictly increasing on F_pq⁻¹(0, 1).

Proof. 

(a): Let 0 < t < 1. For p, q ∈ S and ε > 0, there is x ∈ R⁺ such that ω_t(p, q) − ε < x and F_pq(x) < t. If F_pq(x) < s < t, then ω_s(p, q) ≥ x > ω_t(p, q) − ε. Therefore, ω_t = sup{ω_s | 0 < s < t}. If (S, F) is special, then by Lemma 2.2.2, ω₁ is real-valued, so by a similar argument, we can establish that ω₁ = sup{ω_t | 0 < t < 1}.

(b): Suppose Ω_F satisfies (rcp) and p, q ∈ S is a distinct pair. Suppose 0 < F_pq(x) = F_pq(y) = t < 1 for some 0 ≤ x < y. If t < s < 1, then ω_s(p, q) ≥ y and ω_t(p, q) ≤ x, so ω_t(p, q) < inf{ω_s(p, q) | t < s < 1}, which is a contradiction. Therefore, (#) holds. Conversely, if (#) holds and (rcp) does not, then a = ω_t(p, q) < b = inf{ω_s(p, q) | t < s < 1} for some p and q. By the definition of ω_t, F_pq(x) ≥ t for each a < x and for each x < b and t < s < 1, F_pq(x) < s, so F_pq(x) ≤ t. Therefore, F_pq(x) = t for each a < x < b, which is a contradiction. Hence, (rcp) holds. □

The following example describes linearly ordered families of pseudometrics that do not satisfy the (lcp) and (rcp) conditions, respectively.

Example 2.4.1. 

(1)

¬(lcp)

For each n ∈ N and 0 ≤ i < 2ⁿ, let

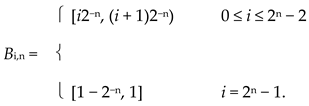Each π_n = {B_i,n | 0 ≤ i < 2ⁿ} is a partition of I and π_n+1 < π_n. Define the pseudometric d_n on I by d_n(p, q) = 0 if p, q ∈ B_i,n for some i and d_n(p, q) = 1 otherwise. For each 0 < t < 1, let ρ_t = d_k, where k = ⌊t/(1 − t)⌋ and let a_k = k/(k + 1) for k ∈ N. Then ρ_t = d_k if and only if a_k ≤ t < a_k+1. Suppose 0 < s < t < 1. If s ∈ [a_m, a_m+1) and t ∈ [a_n, a_n+1), where m < n, then ρ_s = d_m and ρ_t = d_n. Since π_n < π_m, ρ_s ≤ ρ_t, so Ω = {ρ_t} is a linearly ordered family. However, ρ_1/2 = d₁ is not the supremum of the family {ρ_t | 0 < t < 1/2} = {d₀}, so (lcp) does not hold.

(2)

¬(rcp)

For each distinct pair p, q ∈ I, define F_pq: R⁺⟶ I by and let F_pp = H. Then (I, F) is a WPMS and for each 0 < t ≤ 1,

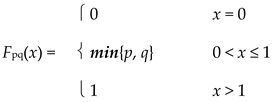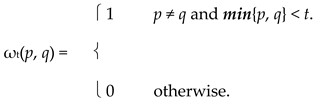If p = 1/2 and q = 3/4, then F_pq = 1/2 on F_pq⁻¹(0, 1), so by Prop 2.4.1(b), (rcp) does not hold. Alternately, ω_1/4(1/4, 3/4) = 0, but ω_s(1/4, 3/4) = 1 for each 1/4 < s < 1, so (rcp) does not hold.

The characterization stated in Prop 2.4.1(b) suggests yet another unexplored property. We say that a WPMS (S, F) satisfies the collective increasing property (cip) if for each 0 ≤ x < y, there exists p, q ∈ S such that F_pq(x) < F_pq(y). We can characterize this property by using the following set: given a WPMS (S, F), the spectrum of F is spec(F) = ∪{spec(ω_t) | 0 < t < 1}, where Ω_F = {ω_t} and spec(ω_t) = {ω_t(p, q) | p, q ∈ S}.

The next result shows that the property (cip) is equivalent to a density criterion.

Prop 2.4.2.

A WPMS (S, F) satisfies (cip) if and only if spec(F) is a dense subset of R⁺.

Proof. 

Suppose (S, F) satisfies (cip). Let 0 ≤ x < y and let x < a < b < y. By definition, there is p, q ∈ S such that F_pq(a) < F_pq(b). Choose F_pq(a) < t < F_pq(b). Then 0 < t < 1 and x < a ≤ ω_t(p, q) < b, so spec(F) is dense in R⁺. Conversely, suppose spec(F) is dense in R⁺ and let 0 ≤ x < y. By assumption, there is 0 < t < 1 and p, q ∈ S such that x < ω_t(p, q) < y. Then F_pq(x) < t ≤ F_pq(y), so (cip) holds. □

Because of the similar definitions, we can ask if (rcp) implies (cip). However, this is not the case. In Example 2.1.3, for distinct p and q, F_pq is strictly increasing on F_pq⁻¹(0, 1) = (1, 1 + a_pq), so by Prop 2.4.1(b), (rcp) holds. However, since each ω_t(p, q) = 1 + ta_pq, spec(F) ⊆ {0} ∪ [1, +∞), so by Prop 2.4.2, (cip) does not hold.

The next result shows that we can easily modify a linearly ordered family of pseudometrics so that (lcp) holds. We leave the proof to the reader.

Lemma 2.4.1.

Let Ω = {ρ_t | 0 < t < 1} be a linearly ordered family of distances (resp. pseudometrics) on a set S and for each 0 < t < 1, define  ρ′_t = sup{ρ_s | 0 < s < t}. Then Ω′ = {ρ_t′} is a linearly ordered family of distances (resp. pseudometrics) on S that satisfies (lcp) and  ρ_t′ ≤  ρ_t for each t.

Other authors have shown that a WPMS can be reconstructed from its family of distances, but the following question does not seem to have been addressed. What conditions on a family of distances guarantee that it has the form Ω_F for some WPMS (S, F)? Based on Prop 2.4.1(a), (lcp) is a necessary condition and as we noted earlier, Ω_F is a linearly ordered family. The next result shows how to construct a special WPMS from a linearly ordered family of distances. A companion result for Menger spaces is presented in Section 3.2.

Theorem 2.4.1.

Let Ω = {ρ_t | 0 < t ≤ 1} be a linearly ordered family of distances on a set S that satisfies the following conditions:

(a)

ρ₁ is a pseudometric and ρ₁ = sup{ρ_t | 0 < t < 1}.

(b)

If p, q ∈ S and ρ₁(p, q) > 0, then ρ_t(p, q) < ρ₁(p, q) for each 0 < t < 1.

Then there is a special WPMS (S, F) such that ω₁ = ρ₁ and ω_t ≤ ρ_t for each 0 < t < 1, where Ω_F = {ω_t}. If Ω also satisfies (lcp), then ω_t = ρ_t for each 0 < t < 1.

Proof. 

For p, q ∈ S and x ∈ R⁺, let T_pq(x) = {0 < t < 1 | ρ_t(p, q) < x} and define F_pq: R⁺ ⟶ I by

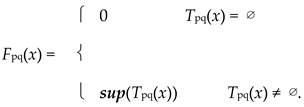(1)

Each F_pq belongs to Δ⁺ and F_pq⁻¹(1) ≠ ∅.

[Since T_pq(0) = ∅, F_pq(0) = 0. If x > 0, then T_pp(x) = (0, 1), so F_pp(x) = 1. Therefore, F_pp = H. Suppose p, q ∈ S is a distinct pair and let g = F_pq. It is routine to show that g(0) = 0 and g is non-decreasing. Also, by definition, g(ρ₁(p, q) + 1) = 1, so sup(g) = 1. Let x > 0 and let {x_n} be a sequence in (0, x) such that x_n ⟶ x. Let t = g(x). If t = 0, then g(x_n) = 0 since g is non-decreasing, so lim_n ⟶+∞g(x_n) = g(x). If t > 0, choose 0 < ε < t. Since t = sup{0 < s < 1 | ρ_s(p, q) < x}, there exists t − ε < s < 1 such that ρ_s(p, q) < x. Then ρ_t−ε(p, q) ≤ ρ_s(p, q) < x_n for sufficiently large n, so g(x_n) ≥ t − ε. Hence, lim_n ⟶+∞g(x_n) = g(x). Therefore, g is left-continuous.]

(2)

(S, F) is a special WPMS.

[It is routine to show that (w₁) and (w₂) hold. Suppose F_pq(x) = F_qr(y) = 1 for distinct p, q, r ∈ S and x, y ∈ R⁺. Then x > 0 and y > 0 and since Ω is linearly ordered, T_pq(x) = T_qr(y) = (0, 1). By (a), ρ₁(p, q) = sup{ρ_t(p, q)} ≤ x and, similarly, ρ₁(q, r) ≤ y, so ρ₁(p, r) ≤ x + y. If ρ₁(p, r) = 0, then each ρ_t(p, r) = 0, so T_pr(x + y) = (0, 1) since x + y > 0. If ρ₁(p, r) > 0, then it follows from (b) that ρ_t(p, r) < ρ₁(p, r) ≤ x + y for each 0 < t < 1, so T_pr(x + y) = (0, 1). Hence, in either case, F_pr(x + y) = 1, so (w₃) holds. Then by (1), (S, F) is a special WPMS.]

Assume that Ω_F = {ω_t}. For the rest of the proof, we suppress the pair (p, q) and subscript pq.

(3)

For each 0 < t < 1, ω_t ≤ ρ_t and ω₁ = ρ₁.

[Given ε > 0, choose x > ω_t − ε such that F(x) < t. Then t ∉ T(x), so ρ_t ≥ x. Therefore, ω_t ≤ ρ_t. If x > ω₁, then F(x) = 1, so T(x) = (0, 1). Hence, ρ_t < x for each 0 < t < 1, so by (a), ρ₁ ≤ x. This establishes ρ₁ ≤ ω₁. By (2) and Prop 2.4.1(a), ω₁ = sup{ω_t} ≤ sup{ρ_t} = ρ₁, so ω₁ = ρ₁.]

(4)

If Ω satisfies (lcp), then ω_t = ρ_t for each 0 < t < 1.

[If ω_t < ρ_t for some 0 < t < 1, then since Ω satisfies (lcp), there is 0 < u < t such that ω_t < ρ_u. Hence, t ≤ F(ρ_u), so F(ρ_u) = sup{0 < s < 1 | ρ_s < ρ_u} > 0. Since Ω is linearly ordered, if ρ_s < ρ_u, then s < u. Hence, F(ρ_u) ≤ u, which is a contradiction. Therefore, ω_t = ρ_t.] □

Condition (b) in the previous result is only used to show that (S, F) satisfies (w₃), so it may not be necessary. It was chosen because it seemed like the simplest condition to add to establish the result. Other assumptions can be made without altering the conclusion. For example, if ρ₁ satisfies (a) and (b′): ρ₁(p, r) < ρ₁(p, q) + ρ₁(q, r) for distinct p, q, r ∈ S, then in the proof of statement (2), ρ₁(p, r) < ρ₁(p, q) + ρ₁(q, r) ≤ x + y, so ρ₁(p, r) < x + y. Therefore, F_pr(x + y) = 1.

Theorem 2.4.1 is suggested by Prop 2.3.1 and by the work on metrically generated spaces and E-spaces ([1], Section 1.7 and Section 9.2, [12]). The latter topic involves using a probability space and a family of metrics as a base space without referring to a linear order.

The following example illustrates the construction used in Theorem 2.4.1.

Example 2.4.2.

For each 0 < t ≤ 1, define the distance ρ_t on (0, 1) by ρ_t(p, q) = | p − q |^2/(t+1). Then Ω = {ρ_t | 0 < t ≤ 1} satisfies the conditions in Theorem 2.4.1 and (lcp) holds, so ω_t = ρ_t for each 0 < t ≤ 1. Therefore, (S, F) is a special WPMS with the following distributions: for 0 < p < q < 1,

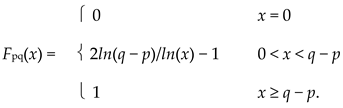3. Menger Spaces

In this section, we discuss the families of Menger spaces and generalized Menger spaces.

3.1. Definitions and Examples

Various conditions can be imposed on a WPMS (S, F) that reflect the properties found in standard examples. One well-known condition has the following form: there is a mapping T: I × I ⟶ I such that the following condition holds:

(T) For each p, q, r ∈ S and x, y ∈ R⁺, F_pr(x + y) ≥ T(F_pq(x), F_qr(y)).

The mapping T is called a norm and other requirements are usually imposed. For instance, T is a t-norm ([1], 5.6.1) if it is commutative, associative, and satisfies the following conditions: (i) for a ∈ I, T(a, 1) = a and (ii) for a, b, c, d ∈ I, a ≤ c and b ≤ d ⟹ T(a, b) ≤ T(c, d). The standard examples of t-norms are Min(a, b) = min{a, b}, Π(a, b) = ab, and T_m(a, b) = max{a + b − 1, 0} ([1], 11.1.1).

We say that a WPMS (S, F) is a Menger space under T ([1], 8.1.4) if T is a t-norm satisfying (T). If (S, F) is a Menger space under Min, then we simply refer to (S, F) as a Menger space. This is a non-standard use of the term that is appropriate for our purposes. We note that if T is a t-norm satisfying (T), then T ≤ Min, so each Menger space is a Menger space under T.

Based on Prop 2.2.2, a WPMS (S, F) is a Menger space if and only if Ω_F consists of pseudometrics; the sufficiency is noted [1], 8.2.3). The WPMSs in Examples 2.1.1 and 2.1.2 are Menger spaces. In Example 2.1.5, some distances are not pseudometrics, so the WPMS is not a Menger space. Here is another example of a Menger space.

Example 3.1.1.

For distinct p, q ∈ I, define F_pq: R⁺⟶ I by

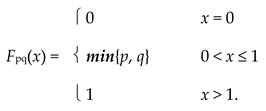Then (S, F) is a Menger space and for each 0 < t ≤ 1,

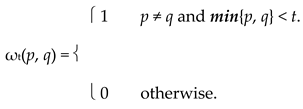3.2. Main Results

The first result is the promised companion to Theorem 2.4.1.

Theorem 3.2.1.

Let Ω = {ρ_t | 0 < t < 1} be a linearly ordered family of pseudometrics on a set S.

(a)

There is a Menger space (S, G) such that ω_t ≤ ρ_t for each 0 < t < 1, where Ω_G = {ω_t}.

(b)

(S, G) is a special WPMS ⇔ sup{ρ_t(p, q) | 0 < t < 1} < +∞ for each p, q ∈ S. In this case, ρ₁ is a pseudometric and ω₁ ≤ ρ₁ = sup{ρ_t}.

(c)

The family Ω satisfies (lcp) ⇔ ω_t = ρ_t for 0 < t < 1. In this case, if (S, G) is special, then ω₁ = ρ₁.

Proof. 

(a): For each p, q ∈ S and x ∈ R⁺, let T_pq(x) = {0 < t < 1 | ρ_t(p, q) < x} and define G_pq: R⁺ ⟶ I by

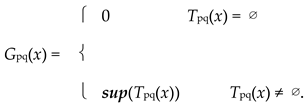(1)

Each G_pq belongs to Δ⁺.

[Since G_pq(ρ_t(p, q) + 1) ≥ t for each 0 < t < 1, sup(G_pq) = 1. Now the rest of the proof used to establish statement (1) in Theorem 2.4.1 shows that G_pq belongs to Δ⁺.]

(2)

(S, G) is a Menger space.

[It is routine to show that (w₁) and (w₂) hold. Suppose 0 < s = G_pq(x) ≤ t = G_qr(y) for p, q, r ∈ S and x, y ∈ R⁺. Given 0 < ε < s, choose s − ε < s′ < s such that ρ_s′(p, q) < x and t − ε < t′ < t such that ρ_t′(q, r) < y. If s′ ≤ t′, then ρ_s′(p, r) ≤ ρ_s′(p, q) + ρ_t′(q, r) < x + y, so G_pr(x + y) ≥ s′ > s − ε. Similarly, if t′ ≤ s′, then G_pr(x + y) ≥ t′ > t − ε ≥ s − ε. Hence, G_pr(x + y) ≥ s = min{G_pq(x), G_qr(y)}, so by (1), (S, G) is a Menger space.]

(3)

For each 0 < t < 1, ω_t ≤ ρ_t.

[The same argument used to prove (3) in Theorem 2.4.1 establishes the statement.]

It follows from (2) and Prop 2.2.2 that each member of Ω_G = {ω_t} is a pseudometric.

(b): Let p, q ∈ S. If (S, G) is special, then G_pq(x) = 1 for some x ∈ R⁺, so sup{ρ_t(p, q)} ≤ x. Conversely, if y = sup{ρ_t(p, q)} < +∞, then G_pq(y + 1) = 1, so (S, G) is special. In addition, if sup{ρ_t(p, q)} < +∞, then by Prop 2.4.1(a), ρ₁ = sup{ρ_t} is a pseudometric on S.

If G_pq(x) < 1 for p, q ∈ S and x ∈ R⁺, then ρ₁(p, q) ≥ ρ_t(p, q) ≥ x for each G_pq(x) < t < 1, so ω₁ ≤ ρ₁.

(c): If ω_t = ρ_t for each 0 < t < 1, then by (2) and Prop 2.4.1(a), Ω satisfies (lcp). Conversely, suppose Ω satisfies (lcp). If ω_t(p, q) < ρ_t(p, q) for some 0 < t < 1 and p, q ∈ S, choose u < t that satisfies ω_t(p, q) < x = ρ_u(p, q). Then t ≤ G_pq(x). Since Ω is linearly ordered, if ρ_s(p, q) < x, then s < u, so G_pq(x) ≤ u. This is a contradiction, so ω_t = ρ_t for each 0 < t < 1.

If (S, G) is special, then by Prop 2.4.1(a) and part (b), ω₁ = sup{ω_t} = sup{ρ_t} = ρ₁. □

Based on a summary of [13], a result similar to Theorem 3.2.1(b) seems to be established, but I cannot give an exact statement since I have not seen the paper. The following examples illustrate the construction used in the previous result.

Example 3.2.1.

In Example 2.4.1(1), for distinct p, q ∈ I, the distribution function in the corresponding Menger space is

where n is the largest integer such that p and q belong to the same member of π_n. By Theorem 3.2.1(a), ω_t ≤ ρ_t for each 0 < t < 1, where Ω_G = {ω_t}. Since Ω = {ρ_t} does not satisfy (lcp) and Ω_G does satisfy (lcp), ω_t < ρ_t for some t. For example, ω_1/2(0, 1/2) = 0 and ρ_1/2(0, 1/2) = 1.

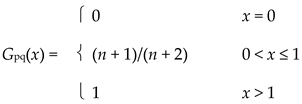Example 3.2.2.

For each 0 < t < 1, define the distance ρ_t on I by ρ_t(p, q) = | p − q |^1−t. Then Ω = {ρ_t} is a linearly ordered family of pseudometrics satisfying (lcp). If 0 < a = | p − q | < 1, then

and

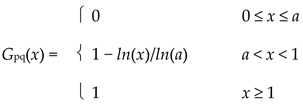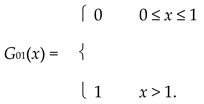The WPMS (I, G) is the Menger space referred to in Theorem 3.2.1 that satisfies Ω = Ω_G.

In Theorem 2.3.1, we presented a representation result for WPMSs with finite range. Here, we show that the Menger spaces satisfying this condition can be used to approximate any Menger space. We begin with the following preliminary result.

Lemma 3.2.1.

Let (S, F) be a WPMS and V = {v₀, …, v_n}, where v₀ = 0 < v₁ < … < v_n = 1. For each p, q ∈ S, define F^V_pq: R⁺ ⟶ I by F^V_pq(x) = min{v ∈ V | F_pq(x) ≤ v}. Then the following statements hold:

(a)

For p, q ∈ S, F^V_pq ∈ Δ⁺ and F^V_pq⁻¹(1) ≠ ∅.

(b)

(S, F^V) satisfies (w₁) and (w₂).

(c)

For p, q ∈ S, F_pq ≤ F^V_pq and || F^V_pq − F_pq ||_∞ ≤ max{v_k+1 − v_k | 0 ≤ k < n}.

(d)

For 0 < t ≤ 1, define ω^V_t: S × S ⟶ R⁺ by

ω^V_t(p, q) = sup{x ∈ R⁺ | F^V_pq(x) < t}.

Then ω^V_t is a distance and ω^V₁ is a pseudometric.

Proof. 

Let p, q ∈ S and let G = F^V_pq. For x ∈ R⁺, let A(p, q, x) = {v ∈ V | F_pq(x) ≤ v}.

(a): Since 1 ∈ V, G is well-defined. Since F_pq(0) = 0, G(0) = 0. Since sup(F_pq) = 1, there is x such that F_pq(x) > v_n−1, so G(x) = 1. Since F_pq is non-decreasing, if x ≤ y, then A(p, q, y) ⊆ A(p, q, x), so G(x) ≤ G(y). Let x > 0 and suppose G(x) = v_k. If k = 0, then G(x) = 0, so G(p) = 0 for 0 < p < x. Hence, G is left-continuous at x. If k > 0, then v_k−1 < F_pq(x) ≤ v_k. Since F_pq is left-continuous, there exists 0 < h < x such that v_k−1 < F_pq(x − h). Therefore, G(p) = v_k for each x − h < p < x, so G is left-continuous at x. This shows that G ∈ Δ⁺.

(b): If p = q and x > 0, then by (w₁) for (S, F), G(x) = min(A(p, p, x)) = min{v ∈ V | H(x) ≤ v} = 1. Hence, since G(0) = 0, G = H, so (w₁) holds. Since (S, F) satisfies (w₂), for p, q ∈ S and x ∈ R⁺, A(p, q, x) = A(q, p, x), so F^V_pq = F^V_qp. Hence, (w₂) holds.

(c): If G(x) = v_k, then F_pq(x) ≤ v_k, so F_pq ≤ G. If k = 0, then G(x) = 0 = F_pq(x). Otherwise, k > 0, so v_k−1 < F_pq(x) and G(x) − F_pq(x) < v_k − v_k−1. Hence, || F^V_pq − F_pq ||_∞ ≤ max{v_k+1 − v_k}.

(d): It follows from part (b) that each ω^V_t is a distance. Also, by part (a), ω^V₁ is well-defined, so by Lemma 2.2.2, it is a pseudometric. □

We say that a WPMS (S, F) can be approximated by a family W of WPMSs if for each ε > 0, there exists (S, G) ∈ W such || F_pq − G_pq ||_∞ < ε for each p, q ∈ S. Now we can establish the following result.

Theorem 3.2.2.

Each Menger space can be approximated by the family of special Menger spaces with a finite range.

Proof. 

Let (S, F) be a Menger space and suppose V = {v₀, …, v_n} with v₀ = 0 < v₁ < … < v_n = 1.

(1)

(S, F^V) is a special Menger space with a finite range.

[Let p, q, r ∈ S, x, y ∈ R⁺, G = F^V_pq, and H = F^V_qr. Suppose G(x) = v_k and H(y) = v_m with k ≤ m. If k = 0, then min{G(x), H(y)} = 0. If k > 0, then G(x) > v_k−1 and H(y) > v_m−1, so F_pq(x + y) > v_k−1. Hence, F^V_pq(x + y) ≥ v_k = min{G(x), H(y)}. A similar argument works if m < k. Therefore, (S, F^V) satisfies condition (T) for T = Min, so by Lemma 3.2.1(a)(b), it is a special Menger space.

Given ε > 0, let V = {k/n | 0 ≤ k ≤ n}, where n ∈ N⁺ satisfies 1/n < ε. Therefore, for each p, q ∈ S, || F^V_pq − F_pq ||_∞ ≤ 1/n by Lemma 3.2.1(c). □

To establish Theorem 3.2.2, (S, F) must be a Menger space. Otherwise, there exists p, q, r ∈ S and x, y ∈ R⁺ such that a = F_pr(x + y) < b = F_pq(x) ≤ F_qr(y). Let V = {0, (a + b)/2, 1}. Then F^V_pq(x) = F^V_qr(y) = 1, but F^V_pr(x + y) ≤ (a + b)/2, so (S, F^V) does not satisfy (w₃).

3.3. Geometric Conditions

The Menger spaces are characterized among WPMSs by the fact that each associated distance is a pseudometric. This is the gold standard. However, before the definition of a metric space was codified, other properties of distances were studied [14,15,16,17]. In particular one largely forgotten property of a distance-space (S, d) is the following weak triangle condition:

(wtc) ≡ ∀ε > 0 ∃δ > 0 ∀x, y, z ∈ M · d(x, z) < δ and d(z, y) < δ ⟹ d(x, y) < ε.

Clearly, each pseudometric satisfies (wtc), but in Example 2.1.5, some distances do not satisfy it. Also, in Example 4.2.1(1), (R, F) is a WPMS⁺ and for each 0 < t ≤ 1,

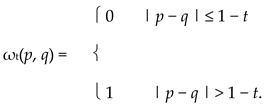Given 0 < t < 1, let p = 0, q = 1 − t, and r = 2(1 − t). Then ω_t(p, q) = ω_t(q, r) = 0, but ω_t(p, r) = 1. Therefore, no member of Ω_F satisfies (wtc). On the other hand, in Example 2.4.2, the (wtc) property holds for each distance.

The importance of the (wtc) property is demonstrated by Theorem A.3.1: if a distance-space (S, d) satisfies (wtc), then d is uniformly equivalent to a pseudometric on S. More generally, other special properties of distances may be useful for the classification of WPMSs. For purposes of comparison, we have included a second (wpc) property in Appendix A.3.

3.4. Generalized Menger Spaces

Now we present the third new idea in the paper. Much study has been devoted to the study of Menger spaces, but it seems that a natural generalization has not received much attention. Consider a WPMS that satisfies the following weaker version of (T), where T = Min:

(M′) ∀ε > 0 ∃δ > 0 ∀p, q, r ∈ S · F_pr(ε) ≥ min{F_pq(δ), F_qr(δ)}.

In this case, we say that (S, F) is a generalized Menger space. If (S, F) is a Menger space, then (M′) holds since F_pr(ε) ≥ min{F_pq(ε/2), F_qr(ε/2)} for each ε > 0.

The next result gives several characterizations of generalized Menger spaces.

Theorem 3.4.1.

The following conditions are equivalent for a WPMS (S, F).

(a)

(M′) holds.

(b)

There is a right-continuous modulus of continuity φ such that for p, q, r ∈ S and 0 < t < 1,

ω_t(p, r) < φ(max{ω_t(p, q), ω_t(q, r)}).

(c)

There is a right-continuous modulus of continuity φ such that F_{pr °} φ ≥ min{F_pq, F_qr} for p, q, r ∈ S.

(d)

Ω_F satisfies (equi-wtc): for each ε > 0, there exists δ > 0 such that for each 0 < t < 1 and p, q, r ∈ S, ω_t(p, r) < δ and ω_t(q, r) < δ ⟹ ω_t(p, q) < ε.

Proof. 

(a) ⟹ (b): In the definition of (M′), δ depends only on ε, so the proof of (a) ⟹ (b) in Theorem A.3.1 shows that there is a non-decreasing mapping τ: (0, +∞) ⟶ (0, +∞) that satisfies the following conditions:

(ec₁) For each p, q, r ∈ S and 0 < t < 1, if ω_t(p, q) < x and ω_t(q, r) < x, then ω_t(p, r) < τ(x).

(ec₂) τ(0+) = 0.

Define the mapping φ: R⁺ ⟶ R⁺ by φ(x) = τ(x+). Since τ is non-decreasing, φ is non-decreasing and an elementary argument shows that φ is right-continuous. Hence, by (ec₂), φ(0+) = φ(0) = 0, so φ is a modulus of continuity that satisfies (ec₁). Let p, q, r ∈ S, 0 < t < 1, and assume that ω_t(p, q) ≤ ω_t(q, r). By (ec₁), if ω_t(q, r) < x, then ω_t(p, r) < τ(x) ≤ φ(x). Hence, by the right-continuity of φ, ω_t(p, r) ≤ φ(ω_t(q, r)).

(b) ⟹ (c): Let x ∈ R⁺ and assume that s = F_pq(x) ≤ t = F_qr(x). Then ω_s(q, r) ≤ ω_t(q, r) ≤ x and ω_s(p, q) ≤ x, so ω_s(p, r) < φ(max{ω_s(p, q), ω_s(q, r)}) ≤ φ(x). Hence, F_pr(φ(x)) ≥ s.

(c) ⟹ (d): Since φ(0+) = φ(0) = 0, given ε > 0, there is δ > 0 such that φ(δ) < ε/2. Suppose ω_t(p, q) < δ and ω_t(q, r) < δ for some 0 < t < 1. Then F_pq(δ) ≥ t and F_qr(δ) ≥ t, so by (c), we obtain F_pr(ε/2) ≥ F_pr(φ(δ)) ≥ t. Hence, ω_t(p, r) ≤ ε/2 < ε. Therefore, Ω_F satisfies (equi-wtc).

(d) ⟹ (a): Let ε > 0 and choose δ > 0 such that the conclusion in (d) holds. Let p, q, r ∈ S and suppose α = F_pq(δ/2) ≤ β = F_qr(δ/2). If α = 0, then F_pr(ε) ≥ min{α, β}. If α = 1, then β = 1. Let 0 < t < 1. Then F_pq(δ/2) = F_qr(δ/2) > t, so ω_t(q, r) < δ and ω_t(q, r) < δ. Hence, ω_t(p, r) < ε, so F_pr(ε) ≥ t. Since t is arbitrary, F_pr(ε) = 1, so F_pr(ε) ≥ min{α, β}. If 0 < α < 1, then ω_α(p, q) < δ and ω_α(q, r) < δ, so ω_α(p, r) < ε. Hence, F_pr(ε) ≥ α = min{α, β}. This establishes (M′). □

In Example 2.1.5, ω_t does not satisfy (wtc) for 0 < t ≤ 1/2, so by the previous result, the WPMS is not a generalized Menger space. The following example also shows that a generalized Menger space may not be a Menger space.

Example 3.4.1.

We reuse Example 2.4.2. For 0 < t ≤ 1, the distance ρ_t on (0, 1) is defined by ρ_t(p, q) = | p − q |^2/(t+1) and (S, F) is a special WPMS.

We claim that Ω = {ρ_t} is an (equi-wtc) family. For 0 < ε < 1, let δ = ε/4 and let p, q, and r be distinct points in (0, 1). Let a = | p − q |, b = | q − r |, and c = | p − r |. For 0 < t < 1, let y = 2/(t + 1), and suppose a^y < δ and b^y < δ. If c = a + b, then c^y < (2δ^1/y)^y = 2^yδ = 2^y−2ε < ε. If c = a − b, then c^y < a^y < ε and, similarly, if c = b − a, then c^y < b^y < ε. By Theorem 3.4.1, (S, F) satisfies (M′). Choose 0 < t < 1 and let p = 1/4, q = 1/2, r = 3/4, and y = 2/(t + 1). Then ρ_t(p, q) = ρ_t(q, r) = (1/4)^y, so ρ_t(p, q) + ρ_t(q, r) = 2(1/4)^y = 2^1−2y and ρ_t(p, r) = 2^−y. Since y > 1, 2^−y > 2^1−2y, so ρ_t is not a pseudometric. Hence, by Prop 2.2.2, (S, F) is not a Menger space.

The following result shows that each generalized Menger space has a closely associated Menger space.

Theorem 3.4.2.

If a WPMS (S, F) satisfies (M′), then there is a Menger space (S, G) and right-continuous moduli of continuity f and g such that the following statements hold for p, q ∈ S and 0 < t < 1, where Ω_F = {ω_t} and Ω_G = {σ_t}:

(a)

σ_t(p, q) < δ < 1/8 ⟹ ω_t(p, q) < f(δ).

(b)

ω_t(p, q) < δ < 1 ⟹ σ_t(p, q) < g(δ).

In terms of distribution functions, for 0 < δ < 1/8, G_pq(δ) ≤ F_pq(f(δ)) and F_pq(δ) ≤ G_pq(g(δ)).

Proof. 

The proof is essentially the same as the proof of (b) ⟹ (c) in Theorem A.3.1 except that we use the regular écart φ from Theorem 3.4.1. In statements (1) and (2), ω denotes one of the mappings ω_t. Their proofs follow the proof of Theorem A.3.1. Recall from Appendix A.1 that if d is a distance on S, then S(d, r) = S_d(r) = {S_d(x, r) | x ∈ S} for each r > 0, where S_d(x, r) = {y ∈ S | d(x, y) < r}.

(1)

For each x ∈ M and r > 0, St(x, S_ω(r)) ⊆ S_ω(x, φ(r)).

(2)

There is a decreasing sequence {ε_k} ⊆ (0, 1] converging to 0 with ε₀ = ε₁ = 1 such that φ(ε_k+1) < ε_k and S_ω(ε_k+1) <^* S_ω(ε_k) for each k > 0.

For each 0 < t < 1, let A_0,t = {S} and A_k,t = S(ω_t, ε_k) for k > 0. By (2), each {A_k,t} is a normal sequence. Define μ_t: S × S ⟶ R by μ_t(p, q) = inf{2^−k | q ∈ St(p, A_k,t)} and let ρ_t be the corresponding path-metric based on Prop A.2.2(i). If 0 < s < t < 1, then A_k,t < A_k,s for each k since ω_s ≤ ω_t. Therefore, μ_s ≤ μ_t, so ρ_s ≤ ρ_t.

Define f: R⁺ ⟶ R⁺ by

and define h: R⁺ ⟶ N⁺ by

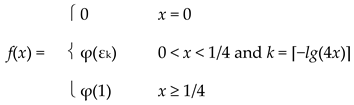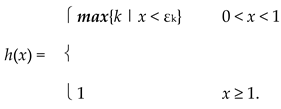Define g: R⁺ ⟶ R⁺ by g(0) = 0 and g(x) = x + 2^−h(x) if x > 0. One can verify that f and g are right-continuous moduli of continuity.

(3)

(i)ρ_t(p, q) < δ < 1/4 ⟹ ω_t(p, q) < f(δ).

(ii) ω_t(p, q) < δ < 1 ⟹ ρ_t(p, q) < g(δ).

[(i): By Prop A.2.2(ii), ρ_t ≤ μ_t ≤ 2ρ_t, so we obtain μ_t(p, q) < 2δ < 1. Let k = ⌈−lg(2δ)⌉. Then 2^−k−1 ≤ 2δ < 2^−k, so μ_t(p, q) ≤ 2^−k. Since q ∈ St(p, A_k,t) = St(p, S_ω(t)(ε_k)), it follows from (1) that ω_t(p, q) < φ(ε_k) = f(δ).

(ii): Let k = h(δ). Since δ < ε_k, it follows that ω_t(p, q) < ε_k, so we have q ∈ St(p, A_k,t). Therefore, ρ_t(p, q) ≤ μ_t(p, q) ≤ 2^−k < g(δ).]

For each 0 < t < 1, let μ′_t = sup{μ_s | 0 < s < t} and ρ′_t = sup{ρ_s | 0 < s < t}. Then μ′_t ≤ μ_t, ρ′_t ≤ ρ_t, and by Lemma 2.4.1, {ρ′_t} is a linearly ordered family of pseudometrics satisfying (lcp). Therefore, by Theorem 3.2.1(a)(c), there is a Menger space (S, G) with σ_t = ρ′_t for each t, where Ω_G = {σ_t}.

(4)

For each 0 < t < 1, μ_t ≤ 2μ′_t and ρ_t ≤ 2ρ′_t.

[Assume that μ′_t(p, q) = 2^−k and choose 0 < s′ < t such that μ_s′(p, q) > 2^−k−1. Let s′ < s < t. Then μ_s(p, q) = 2^−k, so q ∈ St(p, A_k,s). Hence, by (1), ω_s(p, q) ≤ φ(ε_k). By Prop 2.4.1(a), the family {ω_t} satisfies (lcp), so by (2), ω_t(p, q) ≤ φ(ε_k) < ε_k−1. Therefore, μ_t(p, q) ≤ 2^1−k = 2μ′_t(p, q). This establishes the first statement. The second statement follows from the first one and the definition of a path-metric.]

(5)

(i)σ_t(p, q) < δ < 1/8 ⟹ ω_t(p, q) < f(δ)

(ii) ω_t(p, q) < δ < 1 ⟹ σ_t(p, q) < g(δ).

[(i): By (4), ρ_t(p, q) ≤ 2σ_t(p, q) < 2δ < 1/4, so by (3)(i), ω_t(p, q) < f(δ).

(ii): By (3)(ii), σ_t(p, q) ≤ ρ_t(p, q) < g(δ).]

To verify the final statement, assume that G_pq(δ) > F_pq(f(δ)) and choose G_pq(δ) > t > F_pq(f(δ)). Then σ_t(p, q) < δ, so by (5)(i), ω_t(p, q) < f(δ). Hence, F_pq(f(δ)) ≥ t, which is a contradiction. Therefore, G_pq(δ) ≤ F_pq(f(δ)). The other statement is established similarly.] □

4. Operations on WPMSs

4.1. The Category WP

In this section, we introduce the fourth new idea in the paper—a categorical framework for WPMSs and accompanying operations. The idea has been touched on in [4,18], where a generalized notion of probabilistic metric spaces is introduced in the context of quantales.

The reader is referred to [19] for general categorical notions. Let | WP | denote the family of WPMSs. For (S, F) and (T, G) in | WP |, a morphism [f]: (S, F) ⟶ (T, G) is a mapping f: S ⟶ T such that F_pq ≦ G_f(p)f(q) for each p, q ∈ S, where ≦ denotes the point-wise order on Δ⁺. The symbol WP((S, F), (T, G)) denotes the family of morphisms from (S, F) to (T, G). The composition of morphisms [f]: (S, F) ⟶ (T, G) and [g]: (T, G) ⟶ (V, K) is the morphism [g _° f]: (S, F) ⟶ (V, K). Also, [id_S] is the identity morphism for each WPMS (S, F), so WP is a category.

The first result characterizes the morphisms in WP in terms of the families of distances.

Lemma 4.1.1.

The following statements are equivalent for WPMSs (S, F) and (T, G) and a mapping f: S ⟶ T, where Ω_F = {ω_t} and Ω_G = {ρ_t}.

(a)

[f]: (S, F) ⟶ (T, G) is a WP-morphism.

(b)

For each 0 < t < 1, f: (S, ω_t) ⟶ (T, ρ_t) is a non-expansive mapping.

Proof. 

¬(b) ⟹ ¬(a): Choose t, p, and q such that ω_t(p, q) < ρ_t(f(p), f(q)). Let ω_t(p, q) < x < ρ_t(f(p), f(q)). Therefore, G_f(p)f(q)(x) < t ≤ F_pq(x), so ¬(a) holds.

¬(a) ⟹ ¬(b): Choose p, q, and x such that G_f(p)f(q)(x) < F_pq(x) and let G_f(p)f(q)(x) < t < F_pq(x). Then ω_t(p, q) < x ≤ ρ_t(f(p), f(q)). Hence, ω_t(p, q) < ρ_t(f(p), f(q)), so ¬(b) holds. □

Corollary 4.1.1.

The following statements are equivalent for WPMSs (S, F) and (T, G) and a mapping h: S ⟶ T, where Ω_F = {ω_t} and Ω_G = {ρ_t}.

(a)

[h]: (S, F) ⟶ (T, G) is a WP-isomorphism.

(b)

h is a bijection and F_pq = G_h(p)h(q) for each p, q ∈ S.

(c)

For each 0 < t < 1, h: (S, ω_t) ⟶ (T, ρ_t) is a surjective isometry.

Proof. 

The equivalence of (a) and (b) follows from the definition of a WP-isomorphism. The equivalence of (a) and (c) follows from Lemma 4.1.1. □

We note that the notion of isomorphic WPMS’s is the same as the idea of isometric WPMS’s found in ([1], 8.1.2).

The next result lists some elementary facts about the category WP. The proof is left to the reader.

Lemma 4.1.2.

The following statements hold for WPMSs (S, F) and (T, G).

(a)

The monomorphisms (resp. epimorphisms) in WP are exactly the morphisms that are injections (resp. surjections) on the base sets.

(b)

For each t ∈ T, const_t: S ⟶ T defines a WP-morphism [const_t]: (S, F) ⟶ (T, G).

(c)

Let H ⊆ S and F_H = F_|H×H. Then (H, F_H) is a WPMS and incl_H: H ⟶ S defines a WP-morphism [incl_H]: (H, F_H) ⟶ (S, F).

In the literature, both countable products and arbitrary products of WPMSs have been studied. In our setting, we can characterize when products exist.

For a set W = {(S_i, F_i) | i ∈ I} ⊆ | WP |, let S = ΠS_i and define the mapping F: S × S ⟶ F(R⁺, I) by F(p, q) = inf{F_i(p_i, q_i) | i ∈ I}. Then the following statements hold:

(1)

For each p, q ∈ S, F_pq(0) = 0, Rng(F_pq) ⊆ I, and F_pq is non-decreasing. (This follows since each F_i(p_i, q_i) ∈ Δ⁺.)

(2)

(S, F) satisfies (w₁)–(w₃). (Clearly, (w₁) and (w₂) hold. If F_pq(x) = F_qr(y) = 1 for some p, q, r ∈ S and x, y ∈ R⁺, then each F_i(p_i, q_i)(x) = F_i(q_i, r_i)(y) = 1, so F_i(p_i, r_i)(x + y) = 1. Hence, F_pq(x + y) = 1, so (w₃) holds.)

(3)

For each 0 < t < 1, ω_t = sup{ω_i,t}, where Ω_F = {ω_t} and each Ω_F(i) = {ω_i,t}.

It may not be the case that sup(F_pq) = 1 for each p, q ∈ S (Example 4.1.1), so F_pq may not belong to Δ⁺. To remedy this problem, we introduce the following property.

We say that W satisfies the uniform limit property (ulp) if for each ε > 0 and each {p_i, q_i} ⊆ S_i, i ∈ I, there is x ∈ R⁺ such that inf{F_i(p_i, q_i)(x) | i ∈ I} > 1 − ε. Clearly, (ulp) holds if W is a finite family. Also, if W satisfies (ulp), then each F_pq ∈ Δ⁺, so by (1) and (2), (S, F) is a WPMS.

Prop 4.1.1.

The following statements hold for a set W = {(S_i, F_i) | i ∈ I} ⊆ | WP |.

(a)

If W satisfies (ulp), then (S, F) is the product in WP of the members of W. Hence, each finite family of WPMSs has a product in WP.

(b)

If W satisfies (ulp) and W consists of Menger spaces, then (S, F) is a Menger space.

(c)

If W is an infinite set and its product in WP exists, then W satisfies (ulp).

Proof. 

(a): Based on our earlier discussion, (S, F) is a WPMS, where S = ΠS_i and F: S × S ⟶ Δ⁺ is defined by F(p, q) = inf{F_i(p_i, q_i) | i ∈ I}. For each i ∈ I, let π_i: S ⟶ S_i be the standard projection mapping. Since F ≤ F_i, [π_i]: (S, F) ⟶ (S_i, F_i) is a morphism. Let (T, G) be a WPMS and assume that each [f_i]: (T, G) ⟶ (S_i, F_i) is a morphism. Let f: T ⟶ S be the mapping that satisfies π_{i °} f = f_i for each i. Then G(a, b) ≤ F_i(f_i(a), f_i(b)) for each a, b ∈ T and i, so G(a, b) ≤ F(f(a), f(b)). Therefore, [f]: (T, G) ⟶ (S, F) is a morphism. If a morphism [g]: (T, G) ⟶ (S, F) satisfies π_{i °} g = f_i for each i, then clearly, f = g. Hence, (S, F) is the product.

(b): We refer to (2) above. Suppose F(p, r)(x + y) < b = F(p, q)(x) ≤ c = F(q, r)(y) for p, q, r ∈ S and x, y ∈ R⁺. Choose i ∈ I with F_i(p_i, r_i)(x + y) < b. Since b ≤ F_i(p_i, q_i)(x) and c ≤ F_i(q_i, r_i)(y), F_i(p_i, r_i)(x + y) < min{F_i(p_i, q_i)(x), F_i(q_i, r_i)(y)}. This is a contradiction, so (S, F) is a Menger space.

(c): Assume that (T, G) is the product of the family W based on the projection mappings {[σ_i]: (T, G) ⟶ (S_i, F_i)}. If W does not satisfy (ulp), then there is 0 < ε < 1 and {p_i, q_i} ⊆ S_i, i ∈ I, such that inf{F_i(p_i, q_i)(x) | i ∈ I} ≤ δ = 1 − ε for each x ∈ R⁺.

Let ({∗}, H) be the trivial WPMS and for each i, define the morphism [f_i]: ({∗}, H) ⟶ (S_i, F_i) by f_i(∗) = p_i. By assumption, there is a morphism [f]: ({∗}, H) ⟶ (T, G) such that σ_{i °} f = f_i for each i.

Similarly, for each i, define the morphism [g_i]: ({∗}, H) ⟶ (S_i, F_i) by g_i(∗) = q_i. Then there is a morphism [g]: ({∗}, H) ⟶ (T, G) such that σ_{i °} g = g_i for each i. Let s = f(∗) and t = g(∗). Then for each i ∈ I and x ∈ R⁺, G_st(x) ≤ F_i(f_i(∗), g_i(∗))(x) = F_i(p_i, q_i)(x), so sup(G_st) ≤ inf{F_i(p_i, q_i)(x)} ≤ δ, which contradicts the fact that G_st ∈ Δ⁺. Therefore, W satisfies (ulp). □

Many authors have studied products of WPMSs independently of any categorical framework. For example, ([20], Theorem 1) establishes the finite case of Prop 4.1.1(a) and ([21], Proposition 3) “purports” to establish a general product theorem. Here are some additional details about finite products based on the previous construction:

• If (S, F) is the product of a finite family {(S_i, F(i))} of WPMS’s, then ω_t = max{ω_i,t} for each t, where Ω_F = {ω_t} and Ω_F(i) = {ω_i,t} for each i.
• The product of a finite family of Menger spaces is a Menger space. (By Prop 2.2.2, each coordinate distance is a pseudometric, so by the previous remark, each distance in the product is a pseudometric. Hence, by Prop 2.2.2, the product is a Menger space.)
• The product (S, F) of a finite family {(S_i, F_i)} of special WPMS’s is a special WPMS. (For each p, q ∈ S and i, choose x_i such that F_i(p_i, q_i)(x_i) = 1. Then F(p, q)(max{x_i}) = 1.)

The following example shows that the (ulp) property does not hold in general.

Example 4.1.1.

For each n ∈ N⁺, define F_n: [0, n] × [0, n] ⟶ Δ⁺ by F_n(p, q)(x) = H(x − | p − q |).

Each ([0, n], F_n) ∈ | WP_M |, but W = {([0, n], F_n) | n ∈ N⁺} does not satisfy (ulp). To see this, note that for each x ∈ R⁺, inf{F_n(0, n)(x)} = inf{H(x − n)} = 0.

By way of contrast with Prop 4.1.1, we have the following rather dramatic result.

Prop 4.1.2.

No pair of WPMSs has a coproduct in WP.

Proof. 

Let (S, F) and (T, G) be WPMSs and assume that (C, H) is their coproduct in WP based on the morphisms [i]: (S, F) ⟶ (C, H) and [j]: (T, G) ⟶ (C, H). Suppose Ω_H = {ρ_t}. Choose p ∈ S and q ∈ T and let a = i(p) and b = j(q). Let r = ρ_1/2(a, b) + 1. Let D = {0, r} and let K_r0 = K_0r: R⁺ ⟶ I be the characteristic function of (r, +∞). Also, let K₀₀ = K_rr = H. Then (D, K) is a WPMS and Ω_K = {ω_t}, where each ω_t satisfies ω_t(0, r) = r. By Lemma 4.1.2(b), each constant mapping defines a morphism, so there exists a morphism [h]: (C, H) ⟶ (D, K) such that h _° i = const₀ and h _° j = const_r. By Lemma 4.1.1, h: (C, ρ_1/2) ⟶ (D, ω_1/2) is non-expansive, so

ω_1/2(h(a), h(b)) = ω_1/2(0, r) = r ≤ ρ_1/2(a, b) = r − 1,

which is a contradiction. Hence, the coproduct does not exist. □

A result related to Prop 4.1.2 is found in ([22], Proposition 1) stating that the category Met (Section 4.2) has no coproducts. Next, we consider limits in WP.

Prop 4.1.3.

Suppose W = {(S_i, F_i) | i ∈ D} ⊆ | WP |, where (D, ≤) is a directed set, and ({(S_i, F_i) | i ∈ I}, {[f_ij]: (S_j, F_j) ⟶ (S_i, F_i) | i, j ∈ D and i ≤ j}) is an inverse system in WP. If W satisfies (ulp), then the inverse system has an inverse limit in WP.

Proof. 

Let P = ΠS_i and define F: P × P ⟶ Δ⁺ by F(p, q) = inf{F_i(p_i, q_i) | i ∈ I}. By Prop 4.1.1(a), (P, F) is the product of {(S_i, F_i)}. Let S = {s ∈ P | i, j ∈ D and i ≤ j ⟹ f_ij(s_j) = s_i}. By Lemma 4.1.2(c), (S, F_S) is also a WPMS. We claim that ((S, F_S), {[π_i]: (S, F_S) ⟶ (S_i, F_i) | i ∈ D}) is the inverse limit, where each π_i is a projection mapping. If ((T, G), {[φ_i]: (T, G) ⟶ (S_i, F_i) | i ∈ I}) is a source (f_{ij °} φ_j = φ_i for i, j ∈ D satisfying i ≤ j), then φ: T ⟶ S defined by φ(t) = (φ_i(t)) is well-defined and π_{i °} φ = φ_i for each i. By assumption, for u, v ∈ T and i ∈ D, G_uv ≤ F_i(φ_i(u), φ_i(v)), so G_uv ≤ F_S(φ(u), φ(v)). Therefore, [φ]: (T, G) ⟶ (S, F_S) is a WP-morphism. □

Prop 4.1.4.

Each directed system in WP has a direct limit.

Proof. 

Let ({(S_i, F_i) | i ∈ I}, {f_ij: (S_i, F_i) ⟶ (S_j, F_j) | i, j ∈ I and i ≤ j}) be a directed system in WP, where (I, ≤) is a directed set. For each i, j ∈ I, let I(i, j) = {k ∈ I | i ≤ k and j ≤ k}. For each i ∈ I, let S^{^}_i = S_i × {i}, and let S^{^} = ∪{S^{^}_i | i ∈ I}. For each (p, i) ∈ S^{^}_i and (q, j) ∈ S^{^}_j, define (p, i) ~ (q, j) if there is k ∈ I(i, j) such that f_ik(p) = f_jk(q). Then ~ is an equivalence relation on S^{^}.

Let

S = {[(p, i)]: i ∈ I and p ∈ S_i}

denote the set of equivalence classes for ~. Let a = [(p, i)], b = [(q, j)] ∈ S. If a = b, let F_ab = H. If a ≠ b, let

F_ab = sup{F_k(f_ik(p), f_jk(q)) | k ∈ I(i, j)}.

It is easy to show (S, F) is a WPMS. For each i ∈ I, define ψ_i: S_i ⟶ S by ψ_i(p) = [(p, i)].

(1)

Each [ψ_i]: (S_i, F_i) ⟶ (S, F) is a morphism and {[ψ_i]} is a sink for the directed system.

[Let a = [(p, i)], b = [(q, i)] ∈ S, and x ∈ R⁺. If a = b, then F_i(p, q)(x) ≤ 1 = H(x) = F_ab(x). If a ≠ b, then F_i(p, q) ≤ sup{F_k(f_ik(p), f_ik(q)) | i ≤ k} = F_ab(x). If i, j ∈ I and i ≤ j, then f_ij(p) = f_jj(f_ij(p)) for each p ∈ S_i, so (p, i) ~ (f_ij(p), j). Hence, for each p ∈ S_i, ψ_j(f_ij(p)) = [(f_ij(p), j)] = [(p, i)] = ψ_i(p). Therefore, ψ_{j °} f_ij = ψ_i for each i, j ∈ I.]

(2)

((S, F), {[ψ_i]: (S_i, F_i) ⟶ (S, F) | i ∈ I}) is the direct limit of the directed system.

[Let ((T, G), {[φ_i]: (S_i, F_i) ⟶ (T, G) | i ∈ I}) be a sink for the directed system and define the mapping h: S ⟶ T by h([(p, i)]) = φ_i(p). If (p, i) ~ (q, j), then there exists k ∈ I(i, j) such that f_ik(p) = f_jk(q), so φ_i(p) = φ_k(f_ik(p)) = φ_k(f_jk(q)) = φ_j(q). Therefore, h is well-defined and h _° ψ_i = φ_i for each i ∈ I.

We claim that [h]: (S, F) ⟶ (T, G) is a morphism. Let a = [(p, i)], b = [(q, j)] ∈ S. If a = b, then F_ab = H = G_h(a)h(b). Suppose a ≠ b. If k ∈ I(i, j), then since [φ_k] is a morphism,

F_k(f_ik(p), f_jk(q)) ≤ G(φ_k(f_ik(p)), φ_k(f_jk(q))) = G(φ_i(p), φ_j(q)) = G(h(a), h(b)).

Therefore, F_ab ≤ G(h(a), h(b)).] □

Here are two useful examples that illustrate the previous results.

Example 4.1.2.

Each WPMS is the direct limit of the family of finite subspace WPMSs.

Let (S, F) be a WPMS and assume that I ⊆ P_F⁺(S) satisfies S = ∪I and (I, ≤) is a directed set, where ≤ is defined by A ≤ B if A ⊆ B. Let W = {(A, F_A) | A ∈ I} be the family of subspace WPMSs (Lemma 4.1.2(c)) and let F = {[f_AB]: (A, F_A) ⟶ (B, F_B) | A, B ∈ I and A ≤ B}, where each f_AB is the inclusion mapping. Since {W, F} is a directed system, by Prop 4.1.4, {(T, G), {[ψ_A]: A ∈ I} is the direct limit, where T = {[(a, A)]: A ∈ I and a ∈ A} is the set of equivalence classes of ~ and each ψ_A: S ⟶ T is defined by ψ_A(a) = [(a, A)]. Since (a, A) ~ (b, B) if there exists C ∈ I(A, B) such that f_AC(a) = f_BC(b), we have [(a, A)] = {(a, B): a ∈ B ∈ I}.

By Lemma 4.1.2(c), {(S, F), {[incl_A]: (S, F_A) ⟶ (S, F) | A ∈ I} is a sink for the directed system, so there exists a morphism [h]: (T, G) ⟶ (S, F) such that h _° ψ_A = incl_A for each A ∈ I. It is easy to verify that h is a bijection since S = ∪I. Also, G_tt′ = F_h(a)h(b) for each t = [(a, A)] and t′ = [(b, B)], so by Corollary 4.1.1, [h] is an isomorphism. Therefore, (S, F) is the direct limit.

Example 4.1.3.

Each Menger space (S, F) is the inverse limit of special Menger spaces with a finite range.

Let V = {V ∈ P_F⁺([0, 1]) | {0, 1} ⊆ V} and for V, W ∈ V, define V ≤ W if V ⊆ W. Then (V, ≤) is a down-directed set. Statement (1) in Theorem 3.2.2 shows that for each V ∈ V, (S, F^V) is a Menger space with a finite range. Also, by Lemma 3.2.1(c), each π_V = [id_S]: (S, F) ⟶ (S, F^V) is a morphism, so W = {(S, F^V) | V ∈ V} satisfies (ulp). If V, W ∈ V and V ≤ W, then F^W_pq(x) ≤ F^V_pq(x) for each p, q ∈ S and x ∈ R⁺. Therefore, each f_VW = [id_S]: (S, F^W) ⟶ (S, F^V) is a morphism, so (W, {f_VW | V, W ∈ V and V ≤ W}) is an inverse system in WP. Based on the construction in Prop 4.1.3, the inverse limit is (Δ, G), where Δ = {δ ∈ S^V | V, W ∈ V and V ≤ W ⟹ f_VW(δ_W) = δ_V} and G(δ, ξ) = inf{F^V(δ_V, ξ_V) | V ∈ V} for δ, ξ ∈ Δ. Let δ ∈ Δ and let A, B ∈ V. Let V = A ∩ B. Then V ∈ V and δ_A = f_VA(δ_A) = δ_V = f_VB(δ_B) = δ_B, so Δ is the diagonal in S^V, that is,

Δ = {δ ∈ S^V | δ_V = δ_W for each V, W ∈ V}.

Since {(S, F), {π_V | V ∈ V}) is a source for the inverse system, the bijection φ: S ⟶ Δ defined by φ(s)_V = s for each V ∈ V defines a morphism [φ]: (S, F) ⟶ (Δ, G). Let p, q ∈ S and x ∈ R⁺. Then y = F_pq(x) ≤ z = G_φ(p)φ(q)(x) = inf{F^V_pq(x) | V ∈ V}. Choose A ∈ V that contains y. Then z ≤ F^A_pq(x) = y, so F_pq = G_φ(p)φ(q). Hence, by Corollary 4.1.1, [φ] is an isomorphism.

Note that the same conclusion holds by using V = {{0, 1}} ∪ {{0, r, 1}: 0 < r < 1}.

4.2. Subcategories of WP

In this section, we introduce and compare several special subcategories of WP. Here are the categories that we will be using:

Dist—objects are distance-spaces and morphisms are non-expansive mappings.

PMet (resp. Met)—objects are pseudometric (resp. metric) spaces and morphisms are non-expansive mappings.

WP_D—full subcategory of WP based on WPMSs determined by pseudometric spaces.

WP_M—full subcategory of WP based on Menger spaces.

WP_S—full subcategory of WP based on special WPMSs.

The following result describes some relationships between the various categories.

Theorem 4.2.1.

(a)

PMet is a reflective subcategory of Dist.

(b)

PMet and WP_D are isomorphic categories.

(c)

WP_D is a coreflective subcategory of WP_S and the coreflection of a special WPMS (S, F) is the WPMS determined by the pseudometric space (S, ω₁).

(d)

WP_M is a reflective subcategory of WP.

Proof. 

(a): Let (M, ω) be a distance-space. By Prop A.2.1, there is a largest pseudometric d_ω such that d_ω ≤ ω, so r = id_M: (M, ω) ⟶ (M, d_ω) is a non-expansive mapping. Let f: (M, ω) ⟶ (N, σ) be a non-expansive mapping to a pseudometric space and define τ by τ(x, y) = σ(f(x), f(y)). Since σ is a pseudometric, τ is a pseudometric on M satisfying τ ≤ ω, so τ ≤ d_ω. Hence, f: (M, d_ω) ⟶ (N, σ) is a morphism and f _° r = f. Clearly, f is the unique mapping with this property.

(b): For each (S, γ) ∈ | PMet |, let E((S, γ)) = (S, G_γ) (Example 2.1.1) and for each non-expansive mapping g: (S, γ) ⟶ (S′, γ′), where (S′, γ′) ∈ | PMet |, let E(g) = g. By definition, for p, q ∈ S, G_pq(x) = H(x − γ(p, q)). Hence, if G_pq(x) = 1, then x > γ(p, q)) ≥ γ′(g(p), g(q)), so we obtain G′_g(p)g(q)(x) = H(x − γ′(g(p), g(q))) = 1. Therefore, G_pq ≤ G′_g(p)g(q), so E(g) is a morphism. This defines a functor E: PMet ⟶ WP_D.

For each (S, G_γ) ∈ | WP_D |, let F((S, G_γ)) = (S, γ) and for each morphism [h]: (S, G_γ) ⟶ (S′, G_γ′), where (S′, γ′) ∈ | WP_D |, let F(h) = h. Given p, q ∈ S and ε > 0, choose γ(p, q) < x < γ(p, q) + ε. Then G_pq(x) = 1, so G′_h(p)h(q)(x) = 1 since [h] is a morphism. Therefore, x > γ′(h(p), h(q)). Hence, γ(p, q) + ε > γ′(h(p), h(q)) for each ε > 0, so h: (S, γ) ⟶ (S′, γ′) is a non-expansive mapping. This defines a functor F: WP_D ⟶ PMet. Based on the definitions, E _°F (resp. F _° E) is the identity functor on WP_D (resp. PMet), so E is an isomorphism.

(c): If (S, F) is a special WPMS, then by Lemma 2.2.2, γ = ω₁ is a pseudometric. Let (S, G_γ) be the WPMS determined by (S, γ) which belongs to | WP_D |.

(1)

[id_S]: (S, G_γ) ⟶ (S, F) is a morphism.

[Let p, q ∈ S. Since G_pq(x) = H(x − ω₁(p, q)), if x ≤ ω₁(p, q), then G_pq(x) = 0 ≤ F_pq(x). On the other hand, if x > ω₁(p, q), then F_pq(x) = 1, so G_pq(x) ≤ F_pq(x).]

(2)

(S, G_γ) is the coreflection of (S, F) in WP_D.

[Suppose [g]: (M, G_γ′ = {G′_ab})) ⟶ (S, F) is a WP-morphism where the domain WPMS is determined by the pseudometric space (M, γ′). Let a, b ∈ M. Then G′_ab ≤ F_pq, where p = g(a) and q = g(b). If γ′(a, b) < γ(p, q), choose γ′(a, b) < x < γ(p, q). Since x < γ(p, q) = ω₁(p, q), F_pq(x) < 1, but G′_ab(x) = H(x − γ′(a, b)) = 1, so F_pq(x) = 1, which is a contradiction. Hence, γ(p, q) ≤ γ′(a, b), so g is a non-expansive mapping. Therefore, by Lemma 4.1.1, [g]: (M, G_γ′) ⟶ (S, G_γ) is a morphism, which establishes (2).]

(d): Let (S, F) be a WPMS and Ω_F = {ω_t}. By Prop A.2.1, for each 0 < t < 1, the path-metric ρ_t based on ω_t is the largest pseudometric on S satisfying ρ_t ≤ ω_t. Since Ω_F is linearly ordered, Ω = {ρ_t} is also linearly ordered. For each 0 < t < 1, let ρ_t′ = sup{ρ_s | 0 < s < t}. By Lemma 2.4.1, {ρ_t′} is a linearly ordered family of pseudometrics that satisfies (lcp), so by Theorem 3.2.1(a)(c), there is a Menger space (S, G) such that Ω_G = {ρ_t′}. Since each ρ_t′ ≤ ω_t, by Lemma 4.1.1, [id_S]: (S, F) ⟶ (S, G) is a morphism.

(3)

(S, G) is the reflection of (S, F) in WP_M.

Note to editors: the font has changed in the next paragraph…

[Let [f]: (S, F) ⟶ (S^*, F^*) be a WP-morphism to a Menger space, where Ω_F* = {ω_t^*}. By Lemma 4.1.1, for each t, f: (S, ω_t) ⟶ (S^*, ω_t^*) is non-expansive, so ω_t^*(f(p), f(q)) ≤ ω_t(p, q) for p, q ∈ S. Since (S^*, F^*) is a Menger space, by Prop 2.2.2, Ω_F* consists of pseudometrics, so for each t, the equation σ_t(p, q) = ω_t^*(f(p), f(q)) defines a pseudometric σ_t on S satisfying σ_t ≤ ω_t. Hence, by Prop A.2.1, each σ_t ≤ ρ_t. By Prop 2.4.1(a), σ_t = sup{σ_s | 0 < s < t} ≤ sup{ρ_s | 0 < s < t} = ρ_t′. Hence, by Lemma 4.1.1, [f]: (S, G) ⟶ (S^*, F^*) is a morphism. Therefore, [id_S]: (S, F) ⟶ (S, G) is the reflection mapping associated with WP_M.] □

The following example illustrates the reflection into Menger spaces.

Example 4.2.1.

(1)

In Example 2.1.4, (R, F) is not a Menger space and the distances have the following form: for each 0 < t ≤ 1 and p, q ∈ R,

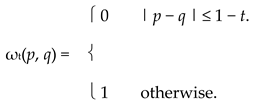Let 0 < t < 1 and ε = 1 − t, and let ρ be a pseudometric satisfying ρ ≤ ω_t. If | p − q | ≤ ε, then ρ(p, q) ≤ ω_t(p, q) = 0, so ρ(p, q) = 0. If | p − q | > ε, choose n satisfying 1/n < ε/| p − q | and let x_k = (1 − k/n)p + (k/n)q for 0 ≤ k ≤ n. For each k, | x_k − x_k+1 | = | p − q |/n < ε, so ω_t(x_k, x_k+1) = 0. Hence, ρ(p, q) ≤ ∑ρ(x_k, x_k+1) ≤ ∑ω_t(x_k, x_k+1) = 0. Therefore, ρ is the zero pseudometric.

The construction used in the proof of Theorem 4.2.1(d) shows that the Menger space reflection of (R, F) is the trivial WPMS (R, {H}).

(2)

In Example 2.1.5, (R⁺, F) is not a Menger space and the distances have the following form: for each 0 < t ≤ 1 and p, q ∈ R⁺,

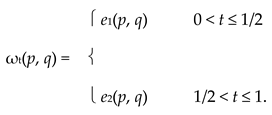By definition, e₁(p, q) = min{a, b} and e₂(p, q) = max{a, b}, where a = | p − q | and b = | p² − q² |. In addition, e₂ is a pseudometric. Let c = 1/2, A = [0, c], and B = (c, +∞). An analysis of cases shows that the largest pseudometric d₁ ≤ e₁ is defined by

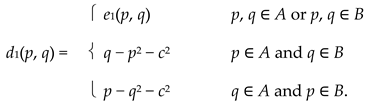The construction used in the proof of Theorem 4.2.1(d) shows that the Menger space reflection (R⁺, G) of (R⁺, F) has the pseudometrics defined by

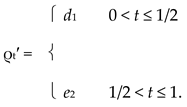The construction is the one used in the proof of Theorem 3.2.1. One can show that if p, q ∈ A or p, q ∈ B, then G_pq = F_pq. However, if p ∈ A and q ∈ B, then

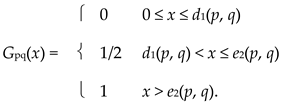For example, if p = 1/4 and q = 1, then a = 3/4 and b = 15/16. Therefore, F_pq(x) = 0 for 0 ≤ x ≤ 3/4 and G_pq(x) = 1/2 for 11/16 < x < 3/4, so F_pq ≠ G_pq.

5. Discussion and Future Work

In some sense, the paper represents a step backwards instead of forwards since it addresses the fundamental issues rather than more contemporary work. However, the results speak for themselves. The most significant ones are (i) the construction of WPMSs from linearly ordered families (Theorems 2.4.1 and 3.2.1), (ii) the introduction of finite range WPMSs and related results (Theorems 2.3.1 and 3.2.2, and Example 4.1.3), (iii) the definition and characterization of generalized Menger spaces (Theorem 3.4.1), and (iv) the presentation of a categorical framework where the Menger spaces are a reflective subcategory (Theorem 4.2.1).

I did not emphasize the point in Section 1.1, but there is a significant amount of recent research on new ideas about distances employed in connection with fixed point theory. The reader is referred to [23,24] for the details. These papers also contain many additional references for the interested reader. Without attempting any summary here, I can say that the work introduces generalized distribution functions on Menger spaces with a t-norm which greatly expands the scope of the subject and potential applications.

Finally, in the text, I mentioned the general problem of classifying WPMSs. The originator of the subject was aware of this issue and proposed interesting ideas in ([25], pp. 441–444) that were used in ([20], Section 3), but have not gained much attention. The geometric properties of distances that we have mentioned may play a role. In my opinion, the classification problem is the most interesting foundational issue. A potential sequel to the present paper may address it in some detail.

Appendix A.1. Distances

We say that a mapping d: M × M ⟶ R⁺ is a distance on a set M if d(x, x) = 0 for each x ∈ M and d(x, y) = d(y, x) for each x, y ∈ M. If d(x, y) > 0 for each distinct pair x, y ∈ M, then d is called a semi-metric. We say that (M, d) is a distance-space (resp. semi-metric space) if d is a distance (resp. semi-metric) on M. Let f: (M, d) ⟶ (N, e) be a mapping between distance-spaces. We say that f is uniformly continuous if for each ε > 0, there exists δ > 0 such that for each x, y ∈ M, d(x, y) < δ ⟹ e(f(x), f(y)) < ε; non-expansive if for x, y ∈ M, e(f(x), f(y)) ≤ d(x, y), and a uniform equivalence if f is a bijection and f and f⁻¹ are uniformly continuous.

Appendix A.2. Covers and Pseudometrics

Let C_X denote the family of covers on a set X. For U, V ∈ C_X, we write U < V if for each U ∈ U, there is V ∈ V such that U ⊆ V. For U ∈ C_X,

U^δ = {St(x, U) | x ∈ X}, where St(x, U) = ∪{U ∈ U | x ∈ U}

U^* = {St(V, U) | V ∈ U}, where St(V, U) = ∪{U ∈ U | U ∩ V ≠ ∅}.

We write U <^δ V if U^δ < V and U <^* V if U^* < V. If U, V, W ∈ C_X, U <^δ V, and V <^δ W; then, U <^* W. A family {U_k | k ∈ N} ⊆ C_X is a normal sequence if U_k+1 <^* U_k for each k.

For a distance space (X, d) and r > 0, S(d, r) = S_d(r) = {S_d(x, r) | x ∈ X} is the cover by open spheres and B_d(r) = {B_d(x, r) | x ∈ X} is the cover by closed spheres, where S_d(x, r) = {y ∈ X | d(x, y) < r} and B_d(x, r) = {y ∈ X | d(x, y) ≤ r}.

Prop A.2.1.

For each distance-space (M, ω), there is a largest pseudometric d_ω on M such that d_ω ≤ ω.

Proof. 

Given x, y ∈ M, we say that P = (x₀, …, x_n) is a path in M from x to y if x = x₀, y = x_n, and each x_k ∈ M. The path-length ω_P is defined by ω_P(x, y) = ∑{ω(x_k, x_k+1) | 0 ≤ k < n}. Then the path-metric d_ω on M is defined by

d_ω(x, y) = inf{ω_P(x, y) | P is a path in M from x to y}.

The reader can verify that d_ω is a pseudometric and if ρ is a pseudometric on M satisfying ρ ≤ ω, then ρ ≤ d_ω. □

The next result states the well-known connection between pseudometrics and normal sequences of covers.

Prop A.2.2.

Let {U_k} be a normal sequence of covers on a set X with U₀ = {X} and let r_k = 2^−k for each k ≥ 0. For each x, y ∈ X, define ω(x, y) = inf{r_k | y ∈ St(x,U_k)}. Then (i) U_k < B_d(2^−k) and S_d(2^−k) < U_k^δ for each k > 0 and (ii) d ≤ ω ≤ 2d, where d = d_ω.

Proof. 

The result (i) is found in ([26], I.14). To prove (ii), we use a statement similar to the one on ([24], page 8, line 22): (#) ≡ d(x, y) < r_k ⟹ y ∈ St(x, U_k+1^*). By (#), if d(x, y) = 0, then y ∈ St(x, U_k) for each k, so ω(x, y) = 0. If d(x, y) > 0, then either (a) d(x, y) = r_k or (b) r_k+1 < d(x, y) < r_k for some k. (a): If k = 0, then ω(x, y) ≤ r₀ = d(x, y); otherwise, by (#), d(x, y) < r_k−1 ⟹ y ∈ St(x, U_k−1). Hence, ω(x, y) ≤ r_k−1 = 2r_k = 2d(x, y). (b): By (#), y ∈ St(x, U_k), so ω(x, y) ≤ r_k = 2r_k+1 < 2d(x, y). □

Appendix A.3. Geometric Conditions

Here are two examples of geometric conditions that can be imposed on a distance-space (M, ω):

• weak polygonal condition

(wpc) ≡ ∀ε > 0 ∃δ > 0 ∀paths P between x, y ∈ M · ω_P < δ ⟹ ω(x, y) < ε

• weak triangle condition

(wtc) ≡ ∀ε > 0 ∃δ > 0 ∀x, y, z ∈ M · ω(x, z) < δ and ω(z, y) < δ ⟹ ω(x, y) < ε.

Clearly, (wpc) implies (wtc), but the converse is false. Corresponding to each condition, there is a theorem that states a uniform equivalence with a pseudometric space. First, we establish the following result.

Prop A.3.1.

A distance-space (M, ω) satisfies (wpc) if and only if id_M: (M, ω) ⟶ (M, d_ω) is a uniform equivalence.

Proof. 

Suppose (M, ω) satisfies (wpc). Given ε > 0, there is δ > 0 such that for any path P from x to y, ω_P < r ⟹ ω(x, y) < ε. If d_ω(x, y) < δ, then there is a path P from x to y with ω_P < δ. Therefore, ω(x, y) < ε, so id_M: (M, d_ω) ⟶ (M, ω) is uniformly continuous. Also, since d_ω ≤ ω, the mapping id_M: (M, ω) ⟶ (M, d_ω) is non-expansive, so id_M is a uniform equivalence. Conversely, suppose id_M: (M, d_ω) ⟶ (M, ω) is uniformly continuous. Given ε > 0, there is δ > 0 such that for x, y ∈ M, d_ω(x, y) < δ ⟹ ω(x, y) < ε. If P is a path between x and y such that ω_P < δ, then d_ω(x, y) ≤ ω_P < δ. Hence, ω(x, y) < ε, so ω satisfies (wpc). □

For the next result, we need to introduce the following notion. We say that a distance-space (M, ω) is a regular écart if there is a non-decreasing mapping φ: [0, +∞) ⟶ (0, +∞) that satisfies

(ec₁) For each x, y, z ∈ M, ω(x, z) < r and ω(y, z) < r ⟹ ω(x, y) < φ(r)

(ec₂) φ(0+) = φ(0) = 0.

Theorem A.3.1.

The following statements are equivalent for a distance-space (M, ω).

(a)

(M, ω) satisfies (wtc).

(b)

(M, ω) is a regular écart.

(c)

There is a path-metric d on M such that id_M: (M, ω) ⟶ (M, d) is a uniform equivalence.

(d)

There is a pseudometric d on M such that id_M: (M, ω) ⟶ (M, d) is a uniform equivalence.

Proof. 

Given ε > 0 and r > 0, define the predicate

P_ω(ε, r) ≡ ∀x, y ∈ M · ω(x, y) ≥ ε ⟹ ∀z ∈ M · ω(x, z) + ω(y, z) ≥ r.

Clearly, (c) ⟹ (d).

(d) ⟹ (a): Let ε > 0 and choose δ > 0 such that d(x, y) < δ ⟹ ω(x, y) < ε. Also, choose r > 0 such that ω(x, y) < r ⟹ d(x, y) < δ/2. Suppose ω(x, y) ≥ ε and let z ∈ M. Then d(x, y) ≥ δ, so without loss of generality, we can assume that d(x, z) ≥ δ/2. Therefore, ω(x, z) + ω(y, z) ≥ ω(x, z) ≥ r. Hence, P_ω(ε, r) holds, so (M, ω) satisfies (wtc).

To make the remaining proof less cluttered, we put the proofs of statements (1)–(4) at the end.

(b) ⟹ (c): By assumption, there is a non-decreasing mapping φ: (0, +∞) ⟶ (0, +∞) that satisfies (ec₁) and (ec₂), so we can assume that φ(0) = 0. Then the following statements hold.

(1)

For each x ∈ M and r > 0, St(x, S_ω(r)) ⊆ S_ω(x, φ(r)).

(2)

There is a decreasing sequence {ε_k} ⊆ (0, 1] converging to 0 with ε₀ = ε₁ = 1 such that φ(ε_k+1) < ε_k and S_ω(ε_k+1) <^* S_ω(ε_k) for each k > 0.

Let {ε_k} be a sequence that satisfies the conditions in (2). Let A₀ = {M} and A_k = S_ω(ε_k) for k > 0. By (2), {A_k} is a normal sequence. Define the distance σ on M by σ(x, y) = inf{2^−k | y ∈ St(x, A_k)} and let d_σ be the induced path-metric. Then by Prop A.2.2(ii), d_σ ≤ σ ≤ 2d_σ, so σ and d_σ are uniformly equivalent.

(3)

ω and σ are uniformly equivalent, so d_σ and ω are uniformly equivalent. Hence, part (c) holds.

(a) ⟹ (b): Without loss of generality, assume that Δ = diam_ω(M) > 0.

Case 1: Δ = +∞ or Δ < +∞ and Rng(ω) ⊆ [0, Δ).

(4)

(i): If Δ = +∞, then there is a non-decreasing g: (0, +∞) ⟶ (0, +∞) such that P_ω(ε, g(ε)) holds for each ε > 0. (ii) If Δ < +∞ and Rng(ω) ⊆ [0, Δ), then there is a non-decreasing g: (0, Δ) ⟶ (0, Δ] such that P_ω(ε, g(ε)) holds for each 0 < ε < Δ.

Subcase 1: L = lim_{ε ⟶ Δ−}g(ε) = +∞.

For each r > 0, B_r = {ε > 0 | g(ε) ≥ r} ≠ ∅. Define τ: (0, +∞) ⟶ [0, +∞) by τ(r) = inf(B_r). If 0 < r < r′, then B_r′ ⊆ B_r, so τ(r) ≤ τ(r′). Hence, τ is non-decreasing. Define φ: (0, +∞) ⟶ (0, +∞) by φ(r) = τ(2r) + r. Then φ is also non-decreasing.

Suppose x, y ∈ M and ω(x, y) ≥ φ(r) for some r > 0. Let z ∈ M and let s = ω(x, z) + ω(y, z). Since ω(x, y) > τ(2r) = inf(B_2r), there is ε ∈ B_2r such that ω(x, y) > ε. Then by (4), s ≥ g(ε) ≥ 2r, so either ω(x, z) ≥ r or ω(y, z) ≥ r. Hence, φ satisfies (ec₁).

Subcase 2: L = lim_{ε ⟶ Δ−}g(ε) < +∞.

For each 0 < r < L, B_r = {0 < ε < Δ | g(ε) ≥ r} ≠ ∅. Define τ: (0, L) ⟶ [0, Δ) by τ(r) = inf(B_r). As in Subcase 1, τ is non-decreasing, so K = lim_{r ⟶ L−}τ(r) exists and K ≤ Δ. Now define τ on (0, +∞) by assigning τ(r) = K for each r ≥ L. Then τ: (0, +∞) ⟶ (0, Δ] is non-decreasing. Define φ: (0, +∞) ⟶ (0, +∞) by φ(r) = τ(2r) + 4rΔ/L. Then φ is also non-decreasing.

Suppose x, y ∈ M and ω(x, y) ≥ φ(r) for some r > 0. Let z ∈ M and let s = ω(x, z) + ω(y, z). If r ≥ L/2, then ω(x, y) ≥ 4rΔ/L ≥ 2Δ, which is impossible. Since r < L/2, ω(x, y) > τ(2r) = inf(B_2r), so there is ε ∈ B_2r such that ω(x, y) > ε. As in Subcase 1, by (4), either ω(x, z) ≥ r or ω(y, z) ≥ r, so φ satisfies (ec₁).

If a = lim_{n ⟶ +∞}τ(1/n) > 0, choose 0 < x < a. If L < +∞, then for each n > 1/L, x < τ(1/n) = inf(B_1/n), so g(x) < 1/n. Hence, g(x) = 0, which is a contradiction. Hence, a = 0, so φ(0+) = 0. If L = +∞, the same proof works, so in either case, φ satisfies (ec₂).

Case 2: Δ < +∞ and Δ ∈ Rng(ω).

Let M′ = M ∪_d B, where B = (0, Δ + 1) and define ω′: M′ × M′ ⟶ R⁺ by ω′(x, y) = ω(x, y) if x, y ∈ M, ω′(x, y) = | x − y | if x, y ∈ B, and ω′(x, y) = ω′(y, x) = 1 if x ∈ M and y ∈ B. Evidently, diam_ω′(M′) = Δ + 1 and Rng(ω′) ⊆ [0, Δ + 1). By part (a), given ε > 0, choose r > 0 such that P_ω(ε, r) holds. Then P_ω′(ε, min{r, ε, 1}) holds, so (M′, ω′) satisfies (wtc). Hence, by Case 1, (M′, ω′) is a regular écart, so (M, ω) is also a regular écart. □

Proof 

(intermediate statements).

(1)

For each x ∈ M and r > 0, St(x, S_ω(r)) ⊆ S_ω(x, φ(r)).

If x ∈ S_ω(p, r) for some p ∈ M, then ω(x, p) < r and ω(p, y) < r for each y ∈ S_ω(p, r), so by (ec₁), ω(x, y) < φ(r). Hence, St(x, S_ω(r)) ⊆ S_ω(x, φ(r)).

(2)

There is a decreasing sequence {ε_k} ⊆ (0, 1] converging to 0 with ε₀ = ε₁ = 1 such that φ(ε_k+1) < ε_k and S_ω(ε_k+1) <^* S_ω(ε_k) for each k > 0.

Let ε₀ = ε₁ = 1 and suppose ε₁, …, ε_k have been defined for k > 0 such that the two conditions hold. By (ec₂), there is r > 0 such that r < ε_k and φ(r) < ε_k and there is 0 < ε_k+1 < ε_k such that φ(ε_k+1) < r. Then φ(ε_k+1) < ε_k and by (1), S_ω(ε_k+1) <^δ S_ω(φ(ε_k+1)) and S_ω(φ(ε_k+1)) < S_ω(r) <^δ S_ω(φ(r)) < S_ω(ε_k). Hence, by our earlier remarks, S_ω(ε_k+1) <^* S_ω(ε_k).

(3)

σ are uniformly equivalent, so d_σ and ω are uniformly equivalent.

Let x, y ∈ M. If σ(x, y) ≤ 2^−(k+1) for some k ≥ 0, then y ∈ St(x, A_k+1), so there is z ∈ M such that x, y ∈ S_ω(z, ε_k+1). Hence, by (ec₁) and (2), ω(x, y) < φ(ε_k+1) < ε_k. Conversely, if ω(x, y) < ε_k for some k > 1, then y ∈ St(x, A_k), so σ(x, y) ≤ 2^−k.

(4)

(i): If Δ = +∞, then there is a non-decreasing g: (0, +∞) ⟶ (0, +∞) such that P_ω(ε, g(ε)) holds for each ε > 0. (ii) If Δ < +∞ and Rng(ω) ⊆ [0, Δ), then there is a non-decreasing g: (0, Δ) ⟶ (0, Δ] such that P_ω(ε, g(ε)) holds for each 0 < ε < Δ.

By part (a), for each ε > 0, S_ε = {r > 0 | P_ω(ε, r)} ≠ ∅.

(i): Let ε > 0 and choose x, y ∈ M such that ω(x, y) > ε. If r ∈ S_ε, then ω(x, y) + ω(y, y) ≥ r, so S_ε ⊆ (0, ω(x, y)]. Define g: (0, +∞) ⟶ (0, +∞) by g(ε) = sup(S_ε). If 0 < ε < ε′, then S_ε ⊆ S_ε′, so g(ε) ≤ g(ε′). Hence, g is non-decreasing. If x, y ∈ M satisfies ω(x, y) ≥ ε > 0, then for each r ∈ S_ε and z ∈ M, ω(x, z) + ω(y, z) ≥ r. Hence, ω(x, z) + ω(y, z) ≥ g(ε), so P_ω(ε, g(ε)) holds.

(ii): Let 0 < ε < Δ. The argument used in (i) shows that S_ε ⊆ (0, Δ]. Define g: (0, Δ) ⟶ (0, Δ] by g(ε) = sup(S_ε). Then the previous argument shows that each P_ω(ε, g(ε)) holds. □

In [17], the (wtc) property is called Axiom V and the definition of a regular écart is attributed to Fréchet. A regular écart is also referred to as property (V) in [14,15]. We can call Theorem A.3.1 the Chittenden-Wilson Theorem since the equivalence of (a) and (b) is established in ([17], Theorem I), (b) ⟹ (d) is proved in [15], and (d) ⟹ (b) is proved in ([17], Theorem II). Our proof that (a) ⟹ (b) is a modified and more detailed version of the original proof and our proof that (b) ⟹ (c) differs significantly from the original proof.