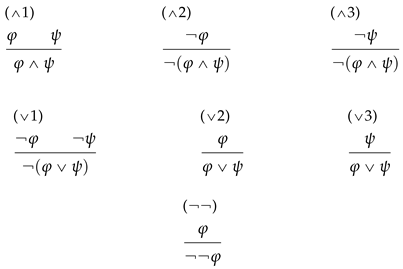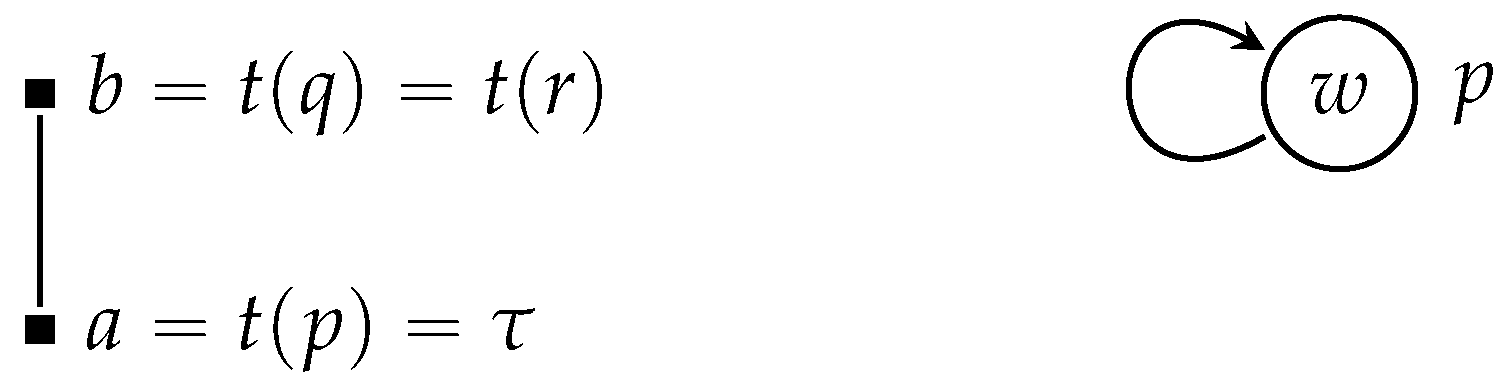Committing to the Truth: The Case of Disjunction

Abstract

If one believes that $2+2=4$, then one also believes that either $2+2=4$ or 971 is a cousin prime number. This follows from doxastic logics based on standard Kripke relational semantics, which validate disjunction introduction for belief. However, this principle does not hold in topic-sensitive semantics. An agent who lacks the concept of a ‘cousin prime number’ may be unable to entertain, and thus unable to believe, any proposition involving that concept. I argue that while disjunction introduction may fail for belief—and for other epistemic states that presuppose belief—it does hold for certain states that do not require belief. In this paper, I focus on the notion of commitment to the truth. Drawing on the concept of logical grounding, I propose formal semantics that preserve the requirement of topic-grasping, but weaken it in a way that allows for a more standard treatment of disjunction.

1. Introduction

Epistemic attitudes are hyperintensional: they do not permit substitution of necessarily equivalent propositions salva veritate. Two propositions are necessarily equivalent when they share the same intension, meaning they are true in exactly the same set of possible worlds. Various logical frameworks have been developed to account for the hyperintensionality of such attitudes. These include logics based on impossible worlds [1,2,3,4], awareness semantics [5,6,7], truthmaker semantics [8,9,10], and topic-sensitive semantics [11]. This paper focuses on the last of these: the topic-sensitive approach.

Topic-sensitive semantics has been successfully applied to model the topic-sensitivity of various epistemic attitudes, including belief [12,13], knowledge [14], and imagination [15,16,17]. Epistemic attitudes—like all propositional attitudes—are mental states. To bear a mental state toward a proposition, one must understand what the proposition is about—that is, its subject matter or topic [18]. To believe $\phi$, one must grasp the concepts involved in $\phi$ (or simply, grasp $\phi$). For instance, to believe the content of the sentence ‘wombats are marsupials’, one must grasp both the concept of ‘wombat’ and the concept of ‘marsupial’. In what follows, I will use the expressions ‘grasping $\phi$’, ‘grasping $\phi$’s topic’, and ‘grasping the concepts involved in $\phi$’ interchangeably.

Imposing a topic-grasping requirement on epistemic attitudes implies that epistemic attitudes are not closed under disjunction introduction. One may believe a proposition $\phi$ without also believing $\phi \vee \psi$, since $\psi$ may add some new topic one does not grasp. One may not even be in a position to believe $\phi \vee \psi$. Consider the following quote by Williamson.

Although the validity of ∨-introduction is closely tied to the meaning of ∨, a perfect logician who knows p may lack the empirical concepts to grasp (understand) the other disjunct q. Since knowing a proposition involves grasping it and grasping a complex proposition involves grasping its constituents, such a logician is in no position to grasp $p\vee q$, and therefore does not know $p\vee q$.

[19] (pp. 282–283)

While Williamson specifically targets knowledge, his argument can naturally be extended to belief, and more generally, to any propositional mental state. Believing that wombats are marsupials does not place one in a position to believe that wombats are either marsupials or ungulates, since one may not grasp the concept of ‘ungulate’. Nonetheless, as Williamson himself emphasizes, the very meaning of ∨ is closely tied to our capacity to perform disjunction introduction. As Hawke [20] (p. 2782) writes, “[d]isjunction introduction is an instance of closure that many […] feel carries particularly acute intuitive weight, so discarding it is a fatal error”. Among these many are Dretske [21] (p. 1009), Hawthorne [22] (pp. 71–73), Holliday [23] (p. 119), Kripke [24] (p. 202), and Nozick [25] (p. 230). As Berto [11] (p. 75) acknowledges, the failure of closure under disjunction introduction may well be the “single hardest thing to swallow” concerning topic-sensitive semantics. There is an intuitive sense in which believing $\phi$ places one in a privileged epistemic position with respect to $\phi \vee \psi$. While belief in $\phi$ may not suffice for being in a position to believe $\phi \vee \psi$, I will argue that it is sufficient to commit one to the truth of $\phi \vee \psi$, regardless of whether one grasps $\psi$.

The paper is structured as follows. In Section 2, I introduce the concept of commitment and argue in Section 3 that by believing $\phi$, one commits oneself to the truth of $\phi \vee \psi$. Section 4 presents topic-sensitive semantics. In Section 5, I introduce the concept of logical grounding—focusing on the grounds of disjunction—and motivate several desiderata. The concept of the minimal topic, which is central to my proposal, is detailed in Section 6 and then employed in Section 7 to propose a new topic-sensitive semantic clause for commitment to the truth. Some logical results are proven in Section 8. I conclude in Section 9.

2. Commitment to the Truth

Belief is often understood, at a basic level, as taking a proposition to be true. However, there are other attitudes that also involve regarding a proposition as true—such as imagining, supposing, and accepting—but these lack the distinctive connection to truth that belief possesses. Unlike these attitudes, belief is typically said to aim at truth. This metaphor has both a descriptive and a normative dimension. Descriptively, belief aims at truth in that belief formation is typically responsive to evidence in a truth-conductive way [26]. Normatively, belief is governed by truth as its standard of correctness: a belief is correct only if the proposition believed is true [27]. In light of this special relationship between belief and truth, to believe $\phi$ is to commit oneself to the truth of $\phi$.

The idea that belief involves a commitment to truth dates back at least to Alston [28] (p. 24), who writes, “in making statements and holding beliefs we commit ourselves to the propositional content’s being true”. Hieronymi [29] (p. 450) expands on this point, explaining that “if I believe p, then I am committed to p as true, that is, I am answerable to questions and criticisms that would be answered by the considerations that bear on whether p”. In believing $\phi$, one commits oneself to its truth, and this commitment renders one epistemically accountable—that is, others are entitled to demand reasons or evidence for my belief, and one is expected to respond with considerations that bear on the truth of $\phi$. Let us explore more in-depth the concept of commitment.

The term commitment can be ambiguous [30] (p. 1172). In one sense, to be committed to something is to be devoted or dedicated to it—for example, saying that someone is committed to volleyball suggests a strong personal investment in the sport. In another sense, however, being committed to something implies occupying a particular normative status. For instance, when I sign a contract, I thereby acquire obligations: I am committed in the sense that I am bound to uphold its terms. It is this latter, normative sense of commitment that I am concerned with here.

As Tebben [30] notes, undertaking a commitment involves limiting one’s options. (See also [31,32] by Tebben for a presentation of these features of commitment.) For example, by signing a contract, I may restrict my actions: if the job requires me to start at 08:00, then I ought not to sleep until 11:00. Of course, I can ignore this requirement, but doing so would be improper. In signing the contract, I become responsible for fulfilling its terms, and I am answerable for having undertaken this responsibility. An interesting related case arises if one believes $\phi$ but does not believe that one believes $\phi$, i.e., one has a first-order belief concerning $\phi$ but lacks the corresponding second-order belief. Is one then criticizable for failing to act as though $\phi$ were true? For present purposes, I treat first-order belief as sufficient for commitment to the truth (and, with it, to action in accordance with that truth). A fuller discussion of how higher-order beliefs interact with commitment is left for future work.

Using Brandom [33]’s terminology, by believing $\phi$, I undertake a cognitive (or doxastic) commitment. Cognitive commitments are functionally analogous to contractual ones: they constrain how I may rightly reason and act. If I believe that $\phi$ is the case, then I ought to reason and act as though $\phi$ is true. While I could behave as if $\phi$ were false, doing so would be epistemically improper. By committing to the truth of $\phi$, I become responsible for treating $\phi$ as true in thought and action, and answerable for having taken on this responsibility.

Being committed to the truth of $\phi$ is to occupy a certain normative position, one that renders me responsible and answerable to questions and criticisms. (Singh [34] argues that this is not what being committed is, but rather a consequence or effect of being committed.) In the following section, I will draw on these normative notions to argue that, in believing $\phi$, one is thereby committed to the truth of $\phi \vee \psi$.

3. Commitment and Disjunctions

By signing a contract, I commit to certain obligations that may not be explicitly stated in the document but are nonetheless required for fulfilling what is explicitly stated. For instance, the contract may not specify that I must wake up before 8 a.m., yet I implicitly commit to doing so if the job requires me to start work at that time. Similarly, when I commit to the truth of a particular proposition, I thereby commit to the truth of other propositions, especially those that stand in logical relation to the original one. Let us begin with an uncontroversial example.

By committing to the truth of $\phi \wedge \psi$, I thereby commit to the truth of $\phi$. If I am required to reason and act as though $\phi \wedge \psi$ is true, I am eo ipso required to reason and act as though $\phi$ is true. Being answerable for $\phi \wedge \psi$ thus entails being answerable for $\phi$. One might object that this simply reflects the fact that if one believes $\phi \wedge \psi$, then one believes $\phi$, and that believing $\phi$ entails being committed to $\phi$. However, I will argue that belief in one proposition can sometimes commit an agent to another proposition, even when the agent does not believe the latter.

Following a helpful comment by a reviewer, I clarify that the scenarios I present are not intended to capture the broader phenomenon of social commitment; my concern here is solely with commitment to the truth and its implications. A comprehensive account of social commitment would require a much wider framework, which lies beyond the scope of this paper. This said, imagine the following scenario.

Flatmates 1. 

Two flatmates, Sam and Andrea, are chatting in the living room. Andrea hears a noise coming from another room and asks, ‘Is Yde in the kitchen?’. Sam, who knows very well that their other flatmate, Yde, is cooking breakfast, replies, ‘Yde is not in the kitchen’.

Sam is behaving wrongly, given his belief state. One notable way of treating a proposition as true is asserting it to others [31] (p. 324). Asserting not-$\phi$, while believing $\phi$ is uncooperative behavior, making Sam liable for it. Now, imagine the following similar scenario.

Flatmates 2. 

Two flatmates, Sam and Andrea, are chatting in the living room. Andrea hears a noise coming from another room and asks, ’Is Yde in the kitchen or the restroom?’. Sam, who knows very well that their other flatmate, Yde, is cooking breakfast, replies, ‘Yde is neither in the kitchen nor in the restroom’.

Nothing makes Sam’s behavior in Flatmates 2 more cooperative than in Flatmates 1. In both cases, Sam is still deceiving Andrea by lying to her. Believing that Yde is in the kitchen commits Sam not only to the truth of ’Yde is in the kitchen’, but also to the truth of ’Yde is either in the kitchen or in the restroom’.

Analogously to the case of conjunction, one might argue that this holds because, in believing that Yde is in the kitchen—and fully grasping the concept of a ‘restroom’—Sam also believes the disjunctive proposition that Yde is either in the kitchen or in the restroom. Since believing $\phi$ entails being committed to the truth of $\phi$, Sam would thereby be committed to the truth of the disjunction. However, it is easy to revise the scenario to show that grasping the second disjunct is not required for such commitment. Consider the following case.

Flatmates 3. 

Two flatmates, Sam and Andrea, are chatting in the living room. Andrea hears some noise coming from another room and asks: ’Is Yde in the kitchen or the morning room?’. Sam does not grasp the concept of ’morning room’ in any shape or form. Sam, who knows very well that their other flatmate, Yde, is cooking breakfast, replies, ’Yde is neither in the kitchen nor in the morning room’.

The fact that, in Flatemates 3, Sam does not grasp the concept of ’morning room’ does not appear to introduce any relevant normative difference compared to Flatemates 2. His behaviour is equally reprehensible in both cases. The commitment extends to the logically related disjunction, even if Sam does not explicitly entertain or grasp the second disjunct.

One can be committed to the truth of a proposition without being in a position to believe it, because commitment to truth is a normative, not a psychological, state [30] (p. 1173). (Tebben [30] draws on this idea to argue that commitment to truth could exist even if eliminative materialism were true, and beliefs did not exist tout court.) Since no particular mental propositional state is required for one to be committed to the truth of $\phi$, it follows that one need not grasp all the concepts involved in $\phi$ to be committed to its truth.

Before moving to the next section, one clarification is in order. I am not arguing that, by believing $\phi$, one is thereby committed to believing $\phi \vee \psi$. Several authors have argued that believing $\phi$ commits one to believe what follows from $\phi$ (see, e.g., Levi [35], Millar [36], Bilgrami [37], Shpall [38], Liberman and Schroeder [39]). This would be problematic for the following reason. If one is committed to believing a proposition, then one ought to believe it. According to the ’ought implies can’ principle, one can be committed to believe $\phi \vee \psi$ only if one is physically and psychologically capable of believing $\phi \vee \psi$, i.e., if one is in a position to believe $\phi \vee \psi$. But if one does not grasp $\psi$, one is not in a position to believe $\phi \vee \psi$. It follows that one cannot be committed to believe $\phi \vee \psi$ if one does not grasp $\psi$. What I am arguing, rather, is that by believing $\phi$, one enters into a specific normative relation with the proposition $\phi \vee \psi$, a relation that does not require being in a position to believe $\phi \vee \psi$.

As a reviewer pointed out, one might raise similar concerns about what one ought to grasp. Must an agent grasp all the concepts involved in $\psi$ for every possible $\psi$? Here too, the ‘ought implies can’ principle comes to the rescue. As bounded agents, we cannot possibly grasp all concepts. Requiring us to do so would therefore be an unreasonable demand, given our human limitations.

In the next section, I introduce topic-sensitive semantics from a formal perspective, showing why, in its current form, it cannot adequately model commitment to the truth. I then propose a straightforward fix to this limitation, whose shortcomings in turn motivate a set of desiderata for a proper formal treatment of commitment to the truth. Building on these desiderata, I draw on the literature on logical grounding to introduce additional formal machinery that refines topic-sensitive semantics in the desired way. Finally, I prove several technical results that establish the main properties of this refined framework and clarify its connection to a corresponding formal account of belief.

4. Topic-Sensitive Semantics

Topic-sensitive semantics is motivated by (i) a theory of topic-sensitive propositional content, inspired by Yablo’s theory of aboutness [18] and Fine’s truthmakers semantics [40,41], and by (ii) topic-sensitivity of propositional mental states such as knowledge, belief, imagination, etc. According to (i), taking propositional contents to be a set of possible worlds does not tell how a sentence is made true. For example, ’Robin is or is not a lawyer’ and ’971 is a cousin prime number’ are true in all possible worlds, but they say different things. To capture this distinction, truth conditions are supplemented with an account of aboutness. The content of a sentence becomes a thick proposition, namely the pair of its intension—the set of possible worlds that make it true—and its subject matter, what it is about. Similarly, according to (ii), propositional mental states are topic-sensitive. An agent can grasp facts about Robin and their job without grasping any concept of number theory. They can, therefore, believe that ’Robin is or is not a lawyer’ without believing that ’971 is a cousin prime number’. Believe that $\phi$ thus requires having information ruling out not-$\phi$ and grasping $\phi$’s topic, what it is about. I will introduce topic-sensitive semantics by roughly following Hawke et al. [14].

I model belief, rather than knowledge, diverging from Hawke et al. [14]. (For topic-sensitive approaches to belief, see [12,13].) Moreover, I simplify the model by not incorporating fragmentation—the idea that an agent’s mind is partitioned into multiple frames—or an information update operator. Since these features are not pertinent to the present discussion, I omit the update operator and assume a non-fragmented mind, i.e., one consisting of a single frame. Additionally, Hawke et al. [14] do not explicitly define an accessibility relation, effectively quantifying over all worlds within a given frame of mind. This amounts to treating the accessibility relation R as an equivalence relation—reflexive, symmetric, and transitive. In contrast, I assume R to be merely serial, which ensures belief consistency. A relation R is serial if, for all w, there exists a v such that $Rwv$. With these adjustments, the model I adopt aligns more closely with the one developed by Rossi and Özgün [42] (noting that their R is reflexive, transitive, and direct), which is itself inspired by Hawke et al. [14].

Let us start by defining the propositional language $\mathcal{L}$ and the modal language ${\mathcal{L}}_{B,C}.$ Let $\mathsf{Prop}=\{p_1,p_2,\dots \}$ be a countable set of propositional variables.

Definition 1 (The language $\mathcal{L}$).

The language $\mathcal{L}$ is defined by the grammar:

$$\phi :=p_i|\neg \phi |(\phi \wedge \phi )|(\phi \vee \phi )$$

Definition 2 (The language ${\mathcal{L}}_{B,C}$).

The language ${\mathcal{L}}_{B,C}$ is defined by the grammar:

$$\phi :=p_i|\neg \phi |(\phi \wedge \phi )\left|(\phi \vee \phi )\right|B\phi |C\psi \mathit{where}\psi \in \mathcal{L}$$

Notice that the operator C ranges only over propositional formulas. The treatment of iterated commitment modalities is left for future work.

Definition 3 (Topic model).

A topic model is a tuple $\mathcal{T}=(T,\oplus ,t,\tau )$, where

• T is a non-empty set of possible topics;
• ⊕: $T\times T\mapsto T$ is an idempotent, commutative, associative operator;
• $\tau \in T$ is a designated topic representing the total topic grasped by the agent;
• $t:\mathsf{Prop}\mapsto T$ is a topic function assigning a topic to each element in $\mathsf{Prop}$.

Let $\mathtt{Var}\left(\phi \right)$ denote the set of propositional variables occurring in $\phi$. The function t extends to the whole language by taking the topic of $\phi$ to be the fusion of the topics of the propositional atoms occurring in it: $t\left(\phi \right)=⨁\left\{t\right(p):p\in \mathtt{Var}(\phi \left)\right\}$. This entails topic-transparency of operators: $t\left(\phi \right)=t(\neg \phi )=t\left(B\phi \right)=t\left(C\right)$ and $t(\phi \wedge \psi )=t(\phi \vee \psi )=t\left(\phi \right)\oplus t\left(\psi \right)$. Topic parthood ⊑ is defined in a standard way: $\forall a,b\in T:a⊑b\mathrm{iff}a\oplus b=b$. I shall use $\overline{)⊑}$ for the negation of ⊑ and ⊏ for strict topic parthood: $\forall a,b\in T:a⊏b\mathrm{iff}a⊑b \mathrm{and} b\overline{)⊑}a$.

It is widely accepted that propositional connectives are topic-transparent [18,43], viz. they have no topic per se. The topic of an interpreted sentence can therefore be understood as the fusion of the topics of its components. It follows that the topic of a disjunction is the fusion of the topic of each disjunct. ‘Wombats are marsupials’ concerns wombats’ place within animal taxonomy, while ‘Wombats are herbivores’ is about their diet. The disjunction of these sentences relates to both wombats’ taxonomy and their diet. The topictransparency of intensional operators is more controversial. See [13] (p. 770) for a possible motivation and [44,45,46] for some recent developments on the topic of intensional operators.

Let us now define a (serial relational) topic-sensitive model and topic-sensitive semantics.

Definition 4 (Topic-sensitive model).

A topic-sensitive model is a tuple $\mathcal{M}=(W,R,V,\mathcal{T})$ where W is a non-empty set of possible worlds, $R\subseteq W^2$ is a binary serial accessibility relation between worlds, $V:\mathsf{Prop}\mapsto 2^W$ is a classical valuation function that assigns to each propositional variable in $\mathsf{Prop}$ a set of possible worlds, $\mathcal{T}$ is a topic model as defined in Definition 3.

The truth of propositional formulas is standard, while $B\phi$ respects the following clause.

$$\begin{array}{ccc}\mathcal{M},w\vDash B\phi \hfill & \mathrm{iff}& (\mathrm{for} \mathrm{all} u\in W,Rwu \mathrm{implies} \mathcal{M}, u\vDash \phi ) \mathrm{and} t\left(\phi \right)⊑\tau \hfill \end{array}$$

(1)

For the sakeof simplicity, I use a monadic operator, similar to the one found in, e.g., [14]. I take both my argument and my approach to be prima facie, mutatis mutandis, applicable to the dyadic topic-sensitive operator found in, e.g., [12]. For a discussion of the varieties of topic-sensitive accounts, see [47] (pp. 3–5).

The truth of a modal formula is defined as the conjunction of two requirements. The first is the standard Hintikkian truth in all epistemically/doxastically accessible possible worlds [48]. This describes an idealized notion of belief, yielding the problem of logical omniscience: one believes every logical consequence of what one believes [49,50]. The problem is alleviated by the second requirement: belief is restricted to formulas that the agent grasps the topic of. Instead of standard Hintikkian clauses, alternative possible-world conditions can be employed in topic-sensitive semantics. For a discussion of this issue, see [42] (pp. 3–4). In any case, as we shall see, the failure of closure under disjunction introduction does not hinge on the choice of possible-world semantics, but rather on the topic-sensitive component of the clause. For instance, Rossi [51] employs a variation of neighborhood-style semantics based on evidence models instead of relational semantics.

Belief is, as Yablo [18,52] argue, immanently closed: one does not believe every proposition that logically follows from one’s beliefs, but only those that both follow from one’s belief and remain on topic with respect to it. Closure under disjunction introduction fails in topic-sensitive semantics because the additional disjunct may introduce a topic alien to the agent. Within this framework, believing a disjunction requires grasping the topic of both disjuncts. This feature is seen as a virtue, aligning with the Williamsonian view that to believe a proposition one must grasp it—and that grasping a complex proposition entails grasping its constituent parts (Section 1). (For some additional thoughts on disjunction in topic-sensitive semantics see [47,53].)

Nonetheless, as I have argued, for non-psychological states—such as the normative state of commitment to the truth—disjunction introduction remains a reasonable principle. The insight that mental states require topic-grasping represents a significant advancement in formal epistemology, enabling important hyperintensional distinctions. We need not throw the baby out with the bathwater. While keeping (1) unchanged, I propose a clause for commitment to the truth according to which full topic-grasping is not necessary for such normative states. To this end, I introduce the concept of a minimal topic—the minimal topic required to be committed to the truth of a proposition—which I define via the notion of logical ground.

5. Some Words on Grounding and Some Desiderata

Grounding is a non-causal dependence relation that describes the “intuitive notion of one thing holding in virtue of another” [54] (p. 37). Some grounding theorists distinguish between different kinds of grounding: logical, conceptual, and metaphysical [55] (p. 21). I shall focus on the former.

The following is a standard principle about the grounds of disjunction: the fact that $\phi$ fully grounds the fact that $\phi \vee \psi$ [56] (p. 567). Where A is a full ground for B iff nothing apart from A is necessary to ground B [54] (p. 50). The thesis follows directly from the classical truth conditions for disjunction and—from what Fine [57] (p. 105) emphasizes—the idea that “the classical truth conditions should provide us with a guide to ground”.

One may suggest the following easy fix: one is committed to the truth of a disjunction iff the modal condition is satisfied and one grasps the topic of at least one of the disjuncts.

$$\begin{array}{cc}\hfill \mathcal{M},w\vDash C(\phi \vee \psi ) \mathrm{i}\mathrm{f}\mathrm{f}& (\mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} u\in W, Rwu \mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s} \mathcal{M}, u\vDash \phi \vee \psi ) \mathrm{and}\hfill \\ \hfill & \left(t\right(\phi )⊑\tau \mathrm{or} t(\phi )⊑\tau )\hfill \end{array}$$

(2)

This clause validates closure under disjunction introduction but faces the following problems.

(P1)

(2) is an ad hoc clause for the commitment to the truth of disjunctions, while we want a general clause able to deal with the commitment to the truth of any propositional formula.

(P2)

(2) is too demanding, as detailed in Example A.

(P3)

(2) generates an undesired mismatch between truth and topic-grasping, as detailed in Example B.

Example A. 

Consider the formula $(p\vee q)\vee r$, a disjunction whose first disjunct is itself a disjunction. According to clause (2), to be committed to the truth of $(p\vee q)\vee r$, one must grasp either the topic of $(p\vee q)$ or the topic of r. However, by the same clause, to be committed to the truth of $(p\vee q)$, it suffices to grasp either the topic of p or the topic of q. Now, suppose an agent grasps $t\left(p\right)$ and believes p (as per (1)), but does not grasp either $t\left(q\right)$ or $t\left(r\right)$. An example of a model satisfying these conditions is ${\mathcal{M}}_1=(W,R,V,\mathcal{T})$, as illustrated in Figure 1, where the set of worlds is $W=\left\{w\right\}$, the accessibility relation is $R=\left\{\right(w,w\left)\right\}$, and the topic model is given by $T=\{a,b\}$, with $a=t\left(p\right)=\tau$ and $b=t\left(q\right)=t\left(r\right)$ such that $\tau ⊏b$. The valuation assigns $V\left(p\right)=\left\{w\right\}$ and $V\left(q\right)=\varnothing$. Given that the agent believes p, they are thereby committed to the truth of $p\vee q$—despite not grasping $t\left(q\right)$. By similar reasoning, they are committed to the truth of $(p\vee q)\vee r$ without grasping $t\left(r\right)$. If closure under disjunction introduction is accepted, then believing p—which requires grasping only $t\left(p\right)$—is sufficient for commitment to the truth of $(p\vee q)\vee r$. No additional topic grasp is required, particularly not $t\left(q\right)$ or $t\left(r\right)$. Thus, clause (2) appears overly demanding in requiring the grasp of $t\left(q\right)$ alongside $t\left(p\right)$ for commitment to $(p\vee q)\vee r$.

Figure 1. Topic-sensitive model ${\mathcal{M}}_1$ for Example A.

Example B. 

Consider the formula $p\vee q$. Assume that for all worlds u such that $Rwu$, we have $\mathcal{M},u\vDash p$ but $\mathcal{M},u⊭q$; that is, p is true and q is false in every world accessible from w. Moreover, suppose that $t\left(p\right)\overline{)⊑}\tau$ while $t\left(q\right)⊑\tau$, meaning the topic of q is grasped, whereas the topic of p is not. An example of a model satisfying these conditions is ${\mathcal{M}}_2=(W,R,V,\mathcal{T})$, depicted in Figure 2, where $W=\left\{w\right\}$, $R=\left\{\right(w,w\left)\right\}$, $T=\{a,b\}$, with $a=t\left(q\right)=\tau$ and $b=t\left(p\right)$ such that $\tau ⊏b$, and $V\left(q\right)=\varnothing$. It follows that ${\mathcal{M}}_2,w\vDash p\vee q$, but this result is problematic. There is no appropriate connection between truth and topic-grasping. The truth of the disjunction at all accessible worlds from w depends solely on the truth of p in those worlds. Yet the agent grasps only the topic of q, not that of p. The grasped topic is irrelevant, since the truth of $p\vee q$ hinges entirely on the topic the agent fails to grasp.

Figure 2. Topic-sensitive model ${\mathcal{M}}_2$ for Example B.

Solving each of these problems—(P1), (P2), and (P3)—constitutes the set of three desiderata for an appropriate modal clause, in addition to the requirement that it validates closure under disjunction introduction. To formulate such a clause, we must first introduce the notion of a minimal topic.

6. Minimal Topic as the Topic of Minimal Grounds

To define what a minimal topic is, I follow Correia [58] in his definition of logical grounding.

Definition 5 (Basic rules for grounding).

The following rules are defined on the propositional language $\mathcal{L}$.

These rules license only inferences from grounding to grounded statements. Since basic grounding rules are a subset of standard natural deduction rules, their application preserves truth. Notice that rules $(\wedge 2)$ and $(\wedge 3)$ are coherent with $(\vee 2)$ and $(\vee 3)$ respectively, fact that by De Morgan laws, $\neg (\phi \wedge \psi )$ is the same as $\neg \phi \vee \neg \psi$. What I say about disjunction holds mutatis mutandis for formulas of the form $\neg (\phi \wedge \psi )$. Similarly, ($\vee 1$) makes sense since $\neg (\phi \vee \psi )$ is the same as $\neg \phi \wedge \neg \psi$. For a discussion about the choice of this set of rules, see [58] (pp. 36–38). We can use them to build rooted trees describing the grounding relation.

Following standard terminology, I call literals propositional atoms and their negations: $\mathsf{Lit}=\mathsf{Prop}\cup \{\neg p:p\in \mathsf{Prop}\}$.

Definition 6 (C-TREE).

Let a C-TREE (complete TREE) be a rooted tree whose nodes are occupied by propositional formulas, and whose transitions are given by the basic rules for grounding, in the sense that (i) leaves and only leaves are occupied by literals, and (ii) every parent node has either one child or two children, in such a way that the principles depicted in the following table are satisfied.

Node occupied by	Number of child(ren)	Child(ren) occupied by
$\phi \wedge \psi$	2	$\phi$     and     $\psi$
$\phi \vee \psi$	1	$\phi$     or     $\psi$
$\neg (\phi \wedge \psi )$	1	$\neg \phi$     or     $\neg \psi$
$\neg (\phi \vee \psi )$	2	$\neg \phi$     and     $\neg \psi$
$\neg \neg \phi$	1	$\phi$

Our condition (i) is stronger than Correia’s, which only says that no parent node is occupied by a literal.

The tree on the left serves as an example of a legal tree in Correia’s work [58] (p. 34). The tree on the right is an expanded version, where every branch terminates in a leaf labeled with a literal. This tree is complete. Henceforth, I will focus exclusively on such complete trees, which I will refer to as C-TREEs. Following Correia, I proceed to define what it means for a tree to be a for a formula and from a set of formulas.

Definition 7 (C-TREE for a formula and from a set of formulas).

A C-TREE is for a formula φ and from a set of formulas Γ when its root is occupied by φ and Γ is the set of all the formulas occupying its leaves.

Since our C-TREEs only allow literals on their leaves, every C-TREE for a formula is from a set of literals. We can now define the minimal ground of a formula.

Definition 8 (Minimal ground).

A set $\Gamma \subseteq \mathsf{Lit}$ is a minimal ground of φ, denoted by $\Gamma ▸\phi$, iff there is a C-TREE such that its root is occupied by φ and Γ is the set of all formulas occupying the leaves of the C-TREE.

I call this a minimal ground since one cannot further expand the C-TREE, and thus cannot find a set of less complex formulas grounding $\phi$. The notion of formula complexity plays a crucial role in the definitions of logical ground provided by Correia [58] and Poggiolesi [59]. For the purposes of this paper, a precise definition of complexity is not essential (these authors offer slightly different accounts). The key requirement is that for a set $\Gamma$ to ground a formula $\phi$, each member of $\Gamma$ must be less complex than $\phi$. Our definition of minimal ground respects this condition since a minimal ground is always a set of literals.

Nonetheless, there is a limiting case where this does not hold: a C-TREE consisting of only one node, which I call a degenerate C-TREE. Consider such a degenerate C-TREE whose root is occupied by the literal p. This root is also the only leaf, so the C-TREE is both from p and for p. By definition, we have $\left\{p\right\}▸p$, yet p has the same complexity as itself. Correia resolves this by excluding degenerate trees, since grounding is typically taken to be an irreflexive relation; nothing can ground itself.

I do not discard degenerate C-TREEs, as doing so would prevent us from modeling commitments to the truth of propositional variables. This is not problematic in our framework, since we are concerned with minimal ground. Importantly, minimality should be understood as minimality relative to a particular environment, in this case, the logical language itself. Once a leaf of a TREE is reached, we have reached the limits of the logical language with respect to grounding. At that point, the best we can do for a literal is to halt further decomposition, preserve its level of complexity, and treat the singleton containing the literal as its minimal ground. Thus, p is the minimal ground of p only in a negative sense: it is minimal due to the lack of a simpler candidate within the language.

Another way to frame this is in terms of truth. Grounding is intimately tied to truth, and truth, in turn, is assigned directly to propositional variables by a valuation. When we arrive at literals, we have reached bedrock—within the language—for truth, and thus also for grounding. A similar line of reasoning applies to topicality: just as truth is directly assigned to propositional variables, so too is subject matter. Accordingly, we should not expect further topical decomposition at the level of literals.

Given the definition of minimal ground, the definition of minimal topic is straightforward.

Definition 9 (Minimal topic).

Take a set $\Gamma \subseteq \mathsf{Lit}$ and a proposition φ such that $\Gamma ▸\phi$. A minimal topic of φ is the topic of $\bigwedge \Gamma$: $t(\bigwedge \Gamma )$.

Since conjunction is topic-transparent, $t(\bigwedge \Gamma )$ is the fusion of the topics of all the formulas in $\Gamma$: $t(\bigwedge \Gamma )=⨁\left\{t\right(\phi ):\phi \in \Gamma \}$. Given the definition of minimal topic, one could put forward the following semantic clause for commitment to the truth.

$$\begin{array}{cc}\hfill \mathcal{M},w\vDash C\phi \mathrm{iff} & (\forall u \in W, \mathit{Rwu} \mathrm{implies} \mathcal{M}, u\vDash \phi ) \mathrm{and}\hfill \\ & \exists \Gamma ▸\phi :t(\bigwedge \Gamma ) ⊑ \tau .\hfill \end{array}$$

(3)

To be committed to the truth of $\phi$, one needs to satisfy two conditions: having information ruling out not-$\phi$ and grasping a minimal topic of $\phi$. (3) validates closure under disjunction introduction and solves (P1) and (P2). Nonetheless, (P3) is not solved since the same disjunction $\psi \vee \chi$ can have two distinct immediate grounds, i.e., $\psi$ or $\chi$. I elaborate on this point in the following section, before putting forward the appropriate modal clause.

7. On the Plurality of Minimal Grounds and the Final Proposal

Given $(\vee 2)$ and $(\vee 3)$, for every parental node occupied by $\psi \vee \chi$, we can generate two TREEs, one having one child node occupied by $\psi$ and the other having one child node occupied by $\chi$. Depending on the choice, we obtain different TREEs and therefore different minimal topics for the same formula. A complex formula can therefore possess several distinct minimal grounds and distinct minimal topics. Example B is still problematic. We need a stricter requirement, connecting the two parts of the semantic clause—the one dealing with truth in a set of possible worlds, and the one dealing with topicality and grounds—more tightly.

To further elaborate, we need to consider the fact that grounding is usually taken to be a factive relation in the following sense: “if a statement is grounded in other statements, then both the grounded statement and the grounding statements must be true” [58] (p. 35). A proper notion of grounding must consider a certain truth assignment. We obtain a stronger definition of minimal grounding involving truth.

Definition 10 (Factive minimal ground).

A set $\Gamma \subseteq \mathsf{Lit}$ is a factive minimal ground of φ with respect to a model $\mathcal{M}$ and a world w, denoted by $\Gamma {▸}^{\mathcal{M},w}\phi$ when $\Gamma ▸\phi$ and $\forall \psi \in \Gamma$: V in $\mathcal{M}$ makes ψ true at w.

When the model $\mathcal{M}$ is clear from context, we will simplify notation and write $\Gamma {▸}^w\phi$ instead of $\Gamma {▸}^{\mathcal{M},w}\phi$. With this in place, we are now in a position to introduce the appropriate modal clause.

$$\begin{array}{ccc}\mathcal{M},w\vDash C\phi \hfill & \mathrm{iff}& \forall u\in W:Rwu \mathrm{implies} (\exists \Gamma {▸}^u\phi :t(\bigwedge \Gamma )⊑\tau )\hfill \end{array}$$

(4)

Notice that $\Gamma$ can be different in each accessible possible world and that the truth of every formula in $\Gamma$ assures the truth of $\phi$ at u: $\phi$ is true in all accessible worlds, and its truth is grounded on the truth of the ’right’ sets of literals, i.e., the ones the agent grasps the topic of. For $C\phi$ to be the case at w, one needs to ’cover topic-wise’ every accessible world from w, as far as the minimal grounds of $\phi$ are concerned. All desiderata are met. Let us consider the following example in order to better understand the meaning of this clause and why it produces an adequate relation between truth and topic-grasping.

Example C. 

Let $\phi :=(p\vee q)\vee r$ (as in Example A). This proposition has three distinct minimal grounds, i.e., $\left\{p\right\}$, $\left\{q\right\}$, and $\left\{r\right\}$. Believing either p or q or r is then sufficient to be committed $(p\vee q)\vee r$. Nonetheless, we may be committed to the truth of a disjunction without believing any of its disjuncts (for instance, when one believes a disjunction without believing any of the disjuncts). Let us consider an example of this kind, by looking at the Kripke model $\mathcal{K}=(W,R,V)$ depicted in Figure 3 such that $W=\{w,u_1,u_2\}$, $R=\{(w,w);(w,u_1);(w,u_2),(u_1,u_1),(u_2,u_2)\}$; $V\left(p\right)=\{w,u_1\}$, and $V\left(q\right)=\{u_1,u_2\}$, $V\left(r\right)=\left\{u_3\right\}$. $R{u}_1{u}_1$ and $R{u}_2{u}_2$ are the case only to satisfy seriality.

Figure 3. Kripke model $\mathcal{K}$ for Example C.

No propositional variable is true in every world accessible from w, and therefore none of them can be believed in w, nor can one be committed to their truth (as per (1) and (4)). However, $\phi$ is true in all such worlds, and thus one can be committed to its truth at w. Let us now determine what the minimal topic required for being committed to the truth of $\phi$ is.

To do so, let us define a function $\mathcal{G}:W\times \mathcal{L}\mapsto 2^{2^{\mathsf{Lit}}}$ which takes a world u and a propositional formula $\psi$ as input and provides the set of factive minimal grounds of $\psi$ with respect to u.

$$\mathcal{G}(u,\psi )=\{\Delta :\Delta {▸}^u\psi \}$$

Let us apply the function $\mathcal{G}$ to $\phi$ at each world in the model.

$$\begin{array}{ccc}\mathcal{G}(w,\phi )& =& \left\{\right\{p\left\}\right\}\\ \mathcal{G}(u_1,\phi )& =& \left\{\right\{p\},\{q\left\}\right\}\\ \mathcal{G}(u_2,\phi )& =& \left\{\right\{q\},\{r\left\}\right\}\end{array}$$

One needs to grasp the topic of the element of at least one factive minimal ground for each world accessible from w. It follows that, in order to be committed to the truth of $(p\vee q)\vee r$ one needs to grasp either $t\left(p\right)\oplus t\left(q\right)$, or $t\left(p\right)\oplus t\left(r\right)$, or $t\left(p\right)\oplus t\left(q\right)\oplus t\left(r\right)$. Let us comment on why these options are viable. Grasping $t\left(p\right)\oplus t\left(q\right)$ is sufficient because p is true in both w and $u_1$ and q in both $u_1$ and $u_2$. By grasping $t\left(p\right)\oplus t\left(q\right)$, one covers topic-wise, every accessible world from w, as far as the minimal grounds of $\phi$ are concerned. The same holds for $t\left(p\right)\oplus t\left(r\right)$ since r is true in $u_2$. A fortiori, the argument holds for $t\left(p\right)\oplus t\left(q\right)\oplus t\left(r\right)$. Notice, however, that grasping $t\left(q\right)\oplus t\left(r\right)$ would not be sufficient, since neither q nor r is true at w. Grasping $t\left(q\right)\oplus t\left(r\right)$ does not cover topic-wise the totality of accessible possible worlds.

The next section presents essential logical results. I first establish the intrinsic link between belief and commitment. Subsequently, I prove that commitment obeys its own unique closure principle. Finally, I demonstrate that this notion is hyperintensional—meaning one can be committed to $\phi$ without being committed to a necessary equivalent $\psi$—and avoids the pitfalls of logical omniscience, as one is not committed to every logical consequence of their commitments.

8. From Belief to Commitment and Ground-Restricted Monotonicity

The notion of commitment to the truth introduced in this paper is the kind that follows from an agent’s belief. As discussed, believing $\phi$ entails being committed to the truth of $\phi$ (Section 2). We begin by formally proving this result, relying on clause (1) for belief and clause (4) for commitment to the truth. To do so, we need to prove a lemma first.

Lemma 1. 

The following is the case for all $\phi \in \mathcal{L}$.

(i)

If $\mathcal{M},w\vDash \phi$ for some $\phi \in \mathcal{L}$, then $\exists \Gamma {▸}^w\phi$.

(ii)

If $\mathcal{M},w⊭\phi$ for some $\phi \in \mathcal{L}$, then $\exists \Gamma {▸}^w\neg \phi$.

Proof. 

We prove this by induction on the structure of $\phi$. I shall refer to the rules of Definition 5.

(p)

Let $\phi :=p$. (i) Assume $\mathcal{M},w\vDash p$. One can construct a degenerate C-TREE to show that $\left\{p\right\}▸p$. We conclude $\left\{p\right\}{▸}^{w}p$. (ii) Assume $\mathcal{M},w⊭p$. Then $\mathcal{M},w\vDash \neg p$. By an analogous reasoning, we obtain $\{\neg p\}{▸}^w\neg p$.

(∧)

Let $\phi :=\alpha \wedge \beta$. (i) Assume $\mathcal{M},w\vDash \alpha \wedge \beta$. Then $\mathcal{M},w\vDash \alpha$ and $\mathcal{M},w\vDash \beta$. By induction hypothesis, $\exists \Delta {▸}^w\alpha$ and $\exists {\Delta }^{\prime }{▸}^w\beta$. This means there is a C-TREE for $\alpha$ from $\Delta$ and a C-TREE for $\beta$ from ${\Delta }^{\prime }$. Given rule ($\wedge 1$), one can construct a C-TREE for $\alpha \wedge \beta$ from $\Delta \cup {\Delta }^{\prime }$. It follows $\exists \Delta ,{\Delta }^{\prime }$ such that $\Delta \cup {\Delta }^{\prime }{▸}^w\alpha \wedge \beta$. (ii) Assume $\mathcal{M},w⊭\alpha \wedge \beta$. Then either $\mathcal{M}⊭\alpha$ or $\mathcal{M}⊭\beta$. By induction hypothesis either $\exists \Delta {▸}^w\neg \alpha$ or $\exists {\Delta }^{\prime }{▸}^w\neg \beta$. This means that there is a C-TREE for $\neg \alpha$ from $\Delta$ and a C-TREE for $\neg \beta$ from ${\Delta }^{\prime }$. Given rule $(\wedge 2)$ and $(\wedge 3)$, one can expand each of such C-TREEs to a C-TREE for $\neg (\alpha \wedge \beta )$ from $\Delta$ and from ${\Delta }^{\prime }$ respectively. It follows that either $\exists \Delta {▸}^w\neg (\alpha \wedge \beta )$ or $\exists {\Delta }^{\prime }{▸}^w\neg (\alpha \wedge \beta )$.

(∨)

Let $\phi :=\alpha \vee \beta$. Similar to the previous, but exploiting ($\vee 2$) and ($\vee 3$) for (i) and $(\vee 1)$ for (ii).

(¬)

Let $\phi :=\neg \alpha$. (i) Assume $\mathcal{M},w\vDash \neg \alpha$. Then $\mathcal{M},w⊭\alpha$. By induction hypothesis, $\exists \Delta {▸}^w\neg \alpha$. (ii) Assume $\mathcal{M},w⊭\neg \alpha$. Then $\mathcal{M},w\vDash \alpha$. By induction hypothesis $\exists \Delta {▸}^w\alpha$. This means there is a C-TREE for $\alpha$ from $\Delta$. By $(\neg \neg )$, one can expand such a C-TREE to a C-TREE for $\neg \neg \alpha$ from $\Delta$. It follows $\exists \Delta {▸}^w\neg \neg \alpha$.

□

Let $\phi \vDash \psi$ mean that for all topic-sensitive models $\mathcal{M}=(W,R,V,\mathcal{T})$ and all $w\in W$: if $\mathcal{M},w\vDash \phi$, then $\mathcal{M},w\vDash \psi$.

Theorem 1. 

For all $\phi \in \mathcal{L},B\phi \vDash C\phi$.

Proof. 

Assume $\mathcal{M},w\vDash B\phi$ for some $\phi \in \mathcal{L}$, i.e., for all u such that $Rwu$: $\mathcal{M},u\vDash \phi$ and $t\left(\phi \right)⊑\tau$. Given Lemma 1, it follows that for all u such that $Rwu$: $\exists \Gamma {▸}^u\phi$. Moreover $t(\bigwedge \Gamma )⊑t\left(\phi \right)⊑\tau$. We conclude $\mathcal{M},w\vDash C\phi$. □

As discussed, topic-sensitive semantics alleviates the problem of logical omniscience (Section 4). A standard way to describe logical omniscience is by the so-called Rule of Monotonicity $\left(RM\right)$, which says that an epistemic state X is closed under classical logical consequence.

$$\left(RM\right):\mathrm{if}\phi \vDash \psi , \mathrm{then} X\phi \vDash X\psi$$

While standard epistemic and doxastic logic validates $\left(RM\right)$, standard topic-sensitive semantics validates a topic-restricted version of the rule, corresponding to immanent closure: X is closed under those classical consequences in which the topic of the conclusion is contained in the topic of the premise (Section 4).

$$\left(R{M}_T\right):\mathrm{if} \phi \vDash \psi \mathrm{and} t\left(\psi \right) ⊑t\left(\phi \right), \mathrm{then} X\phi \vDash X\psi$$

(4) validates $\left(R{M}_G\right)$, a ground-restricted version of the rule.

$$\left(R{M}_G\right):\mathrm{if}\forall \Gamma ▸ \phi : \exists \Delta \subseteq \Gamma \mathrm{such} \mathrm{that}\Delta ▸\psi , \mathrm{then}X\phi \vDash X\psi$$

Theorem 2. 

$\left(R{M}_G\right)$ holds for $X=C$.

Proof. 

Assume $\mathcal{M},w\vDash C\phi$. Then $\forall u\in W,Rwu$ implies $\exists \Theta {▸}^u\phi :t(\bigwedge \Theta )⊑\tau$. Assume $\forall \Gamma ▸\phi :\exists \Delta \subseteq \Gamma$ such that $\Delta ▸\psi$. Then $\exists \Delta \subseteq \Theta$ such that $t(\bigwedge \Delta )⊑t(\bigwedge \Theta )⊑\tau$ and $\forall \chi \in \Delta :\mathcal{M},u\vDash \chi$. Then $\forall u\in W:\mathit{Rwu}\mathrm{implies} \exists \Delta {▸}^u\psi :t(\bigwedge \Delta )⊑\tau$, i.e., $\mathcal{M},w\vDash C\psi$. □

Notice that while $\left(R{M}_G\right)$ holds, it cannot capture all valid instances of $C\phi \vDash C\psi$. For instance, consider the valid consequence $C(p\vee (q\wedge \neg q\left)\right)\vDash Cp$. In this case, we have $\{q,\neg q\}▸p\vee (q\wedge \neg q)$, yet there is no $\Delta \subseteq \{q,\neg q\}$ such that $\Delta ▸p$. This is because $\{q,\neg q\}$ is an incoherent set of literals.

Definition 11 ((In)coherent set of literals).

A set $\Delta \subseteq \mathsf{Lit}$ is coherent if for no $p\in \mathsf{Prop}$: $\{p,\neg p\}\subseteq \Delta$. The set is incoherent otherwise.

No possible world can verify all the members of an incoherent set of literals simultaneously. As a result, commitment to the truth of $p\vee (q\wedge \neg q)$ cannot proceed via an incoherent ground. The only viable ground is the coherent one, $\left\{p\right\}$. In this sense, incoherent grounds can, so to speak, be disregarded. We are now in a position to define $\left(R{M}_G^{*}\right)$, a closure principle capable of handling cases involving incoherent grounds.

$$\left(R{M}_G^{*}\right):\mathrm{if} \mathrm{for} \mathrm{all} \mathrm{coherent}\Gamma ▸\phi :\exists \Delta \subseteq \Gamma \mathrm{such} \mathrm{that} \Delta ▸\psi ,\mathrm{then} X\phi \vDash X\psi$$

Theorem 3. 

$\left(R{M}_G^{*}\right)$ holds for $X=C$.

Proof. 

The structure of the proof is analogous to the one of Theorem 2, but adding the consideration that no incoherent ground can be a factive ground for $\phi$ in some possible world accessible from w, since no possible world can verify all of its elements. □

$\left(R{M}_G^{*}\right)$ does not collapse into $\left(RM\right)$, thereby providing a new, principled strategy for addressing logical omniscience. Moreover, the proposed semantics is hyperintensional. That is, it can distinguish between formulas that are necessarily equivalent. This is to be expected, since the semantics I propose is a variant of topic-sensitive semantics, which is itself hyperintensional. The hyperintensionality of the framework can be illustrated by showing that it invalidates the Rule of Equivalence $\left(RE\right)$, according to which an epistemic state X cannot distinguish between classically equivalent propositions. Let $\phi \vDash \psi$ mean that $\phi \vDash \psi$ and $\psi \vDash \phi$.

$$\left(RE\right):\mathrm{if} \phi \vDash \psi ,\mathrm{then} X\phi \vDash X\psi$$

Notice that showing that $\left(RE\right)$ fails, straightforwardly implies that $\left(RM\right)$ fails as well.

Theorem 4. 

Both (RE) and (RM) fail for $X=C$.

Proof. 

Consider model ${\mathcal{M}}_1$ described in Example A and depicted in Figure 1. $\mathcal{M},w\vDash p\vee \neg p$ and $\mathcal{M},w\vDash q\vee \neg q$. Since both formulas are propositional tautologies, it follows $p\vee \neg p\vDash q\vee \neg q$. However, $\mathcal{M},w\vDash C(p\vee \neg p)$, but $\mathcal{M},w⊭C(q\vee \neg q)$. $\mathcal{M},w\vDash C(p\vee \neg p)$ because $R=\{w,w\}$, $\left\{p\right\}{▸}^{w}p\vee \neg p$, and $t(\bigwedge \{p\left\}\right)=t\left(p\right)=a⊑\tau$. $\mathcal{M},w⊭C(q\vee \neg q)$ because $q\vee \neg q$ has only one minimal topic $t(\bigwedge \{q\left\}\right)=t(\bigwedge \{\neg q\left\}\right)=t\left(q\right)=b$ and $b\overline{)⊑}\tau$. □

9. Conclusions

I have argued that commitment to the truth is closed under disjunction introduction. I proposed a semantic clause for commitment to the truth that preserves the beneficial features of topic-sensitive semantics while modifying its treatment of disjunction. Specifically, only the grasp of the minimal topic of a proposition is required to be committed to its truth. To define this notion of minimal topic, I relied on the concept of logical grounding, which allows us to isolate the minimal parts of a proposition that are truth- and topic-relevant for the purpose of commitment. The resulting connection between truth and topic-grasping has been shown to be both reasonable and effective in avoiding undesirable mismatches. Although the framework was initially motivated by the treatment of disjunction, the modal clause I propose is general and applies to the commitment to the truth of any propositional formula. Finally, I have demonstrated how, within this framework, commitment to the truth is appropriately related to belief and proven some important results concerning hyperintensionality and the failure of logical omniscience.