Fractional Order Thermoelastic Model with Voids in Three-Phase-Lag Thermoelasticity ^†

Abstract

This paper deals with fractional order three-phase-lag (TPL) thermo-elasticity in a micropolar thermoelastic half space medium with voids. The subsequent non-dimensional coupled equations are solved by using the normal mode analysis and eigenvalue approach methods. By doing numerical computations of the physical fields for a substance that resembles a magnesium crystal in the presence of an electromagnetic field, the issue is proven to exist. The effect of the fractional order, the phase lags on the components of temperature, displacement, the stress, and changes in volume fraction field have been depicted graphically. Additionally, a graphic comparison of several types of models employing phase delays and the influence of the magnetic field is displayed.

1. Introduction

Lord and Shulman (1967) [1] derived a new model to overcome the infinite speed of heat transportation which was established by Biot (1956) [2]. The heat equation of this theory is of the wave type, it automatically ensures finite speeds of propagation for heat and elastic waves. Linear model of thermoelasticity is incapable to characterize the behaviour of many new synthetic solids of the elastomer and polymer type. Eringen used the micropolar elasticity term to describe such materials.

Fractional calculus was first used by Abel in the solution of an integral equation that arises in the tautochrone problem. This area has grown rapidly, and applications have been found in several fields, including solid mechanics, geophysics, physics, and mathematical biology. Many mathematical models in the fields of solid mechanics, bio-rheology, non-linear dynamical systems in ecology, and so on, have been successfully modified using fractional calculus. The fractional derivative exhibits non-local properties, and global dependency is among the main reason for its use. Kimmich considered anomalous diffusion and characterised it with the time-fractional diffusion wave equation using the Riemann–Liouville fractional integral. Povstenko [3,4] demonstrated the effect of fractional heat transportation in the presence of thermal stresses. Many authors [5,6,7,8,9] have also discussed fractional calculus in thermoelasticity.

Recently, Tzou [10,11] developed dual-phase-lag heat equation theory by incorporating of two-phase-lags associated with temperature gradient heat flux vector. Two phase lag parameters are related to the fastest effects of thermal inertia. This theory is known as the dual-phase-lag (DPL) model. The later three-phase-lag (TPL) model was developed by Roychoudhury [12].

In the present article, we consider two dimensional problem under TPL heat conduction theory in present of electric and magnetic field. The governing equation are transformed by normal modes. Finally the displacement component and temperature distribution are fixed out analytically from the vector matrix differential equation by eigenvalue method in transformed domain.

2. Basic Equation

The system of governing equations of a rotating micropolar thermoelastic solid is given by [12,13]

$${\sigma }_{ij,j}+F_i=\rho [\ddot{u_i}+{\Omega \times (\Omega \times u)}_i+{(2\Omega \times \dot{u})}_i]$$

(1)

$$m_{ij,i}+{ϵ}_{ijr}{\sigma }_{ir}=J\rho [\ddot{\varphi }+{(\Omega \times \varphi )}_i]$$

(2)

$$\alpha {\psi }_{,ii}-\epsilon \psi -\omega \dot{\psi }-{\beta }^{*}{u}_{i,i}+m\theta =\rho {\epsilon }_1\ddot{\psi }$$

(3)

The components of the force stress and couple stress tensors are

$${\sigma }_{ij}=\lambda u_{r,r}{\delta }_{ij}+\mu (u_{i,j}+u_{j,i})+k(u_{j,i}-{ϵ}_{ijr}{\varphi }_r)-{\beta }^{*}\psi {\delta }_{ij}-{\gamma }_T(\theta +\nu \frac{\partial \theta }{\partial t}){\delta }_{ij}$$

(4)

$$m_{ij}=\alpha {\varphi }_{r,r}{\delta }_{ij}+\beta {\varphi }_{i,j}+\gamma {\varphi }_{j,i}$$

(5)

Fractional order Three-phase-lag Heat conduction without heat source as

$$\left[K^{*}\left(1+\frac{{{\tau }_{\nu }}^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)+K\frac{\partial }{\partial t}\left(1+\frac{{{\tau }_{\theta }}^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\right]{\theta }_{ii}=\left(1+\frac{{{\tau }^{\alpha }}_q}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}+\frac{{{\tau }^{2\alpha }}_q}{2\alpha !}\frac{{\partial }^{2\alpha }}{\partial t^{2\alpha }}\right)(\rho C_E\frac{{\partial }^2\theta }{\partial t^2}+\beta T_0\frac{{\partial }^2}{\partial t^2}\left(e_{kk}\right)+m{T}_0\frac{{\partial }^2\psi }{\partial t^2})$$

(6)

and the strain components are

$$e_{ij}=\frac{1}{2}(u_{i,j}+u_{ji})\mathrm{and}{e}_{kk}=(\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z})$$

(7)

3. Formulation of the Problem

$$\begin{array}{cc}\hfill & (1+{ϵ}_5)\frac{{\partial }^{2}u}{\partial x^2}+(1-a^2+{ϵ}_5)\frac{{\partial }^{2}w}{\partial x\partial z}+a^2\frac{{\partial }^{2}u}{\partial z^2}-{ϵ}_3\frac{\partial {\varphi }_2}{\partial z}-\frac{1}{({ϵ}_1+{ϵ}_2)}(1+v\frac{\partial }{\partial t})\frac{\partial \theta }{\partial x}+{\beta }_1\frac{\partial \psi }{\partial x}\hfill \\ \hfill & =({ϵ}_4+\frac{1}{({ϵ}_1+{ϵ}_2)})\frac{{\partial }^{2}u}{\partial t^2}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & (1+{ϵ}_5)\frac{{\partial }^{2}w}{\partial z^2}+(1-a^2+{ϵ}_5)\frac{{\partial }^{2}u}{\partial x\partial z}+a^2\frac{{\partial }^{2}w}{\partial x^2}-{ϵ}_3\frac{\partial {\varphi }_2}{\partial x}-\frac{1}{({ϵ}_1+{ϵ}_2)}(1+v\frac{\partial }{\partial t})\frac{\partial \theta }{\partial z}+{\beta }_1\frac{\partial \psi }{\partial z}\hfill \\ \hfill & =({ϵ}_4+\frac{1}{({ϵ}_1+{ϵ}_2)})\frac{{\partial }^{2}w}{\partial t^2}\hfill \end{array}$$

(9)

$$\frac{{\partial }^2{\varphi }_2}{\partial x^2}+\frac{{\partial }^2{\varphi }_2}{\partial z^2}-2{ϵ}_7{\varphi }_2+{ϵ}_7(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x})={ϵ}_8\frac{{\partial }^2{\varphi }_2}{\partial t^2}$$

(10)

$$\left[K_1(1+\frac{{{\tau }_v}^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }})+\frac{\partial }{\partial t}(1+\frac{{{\tau }_{\theta }}^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }})\right](\frac{{\partial }^2\theta }{\partial x^2}+\frac{{\partial }^2\theta }{\partial z^2})=p_l\left(\frac{{\partial }^2\theta }{\partial t^2}+{ϵ}_9\frac{{\partial }^2}{\partial t^2}(\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z})+{\beta }_1\frac{{\partial }^2\psi }{\partial t^2}\right)$$

(11)

The components of stress tensor and force tensor are written in the below form:

$${\sigma }_{xx}=({ϵ}_1+{ϵ}_2)\frac{\partial u}{\partial x}+({ϵ}_1-1)\frac{\partial w}{\partial x}-(1+\nu \frac{\partial }{\partial t})\theta$$

(12)

$${\sigma }_{zz}=({ϵ}_1+{ϵ}_2)\frac{\partial w}{\partial z}+({ϵ}_1-1)\frac{\partial u}{\partial x}-(1+\nu \frac{\partial }{\partial t})\theta$$

(13)

$${\sigma }_{xz}=\frac{\partial u}{\partial z}+{ϵ}_2\frac{\partial w}{\partial x}-({ϵ}_2-1){\varphi }_2$$

(14)

$${\sigma }_{zx}=\frac{\partial w}{\partial x}+{ϵ}_2\frac{\partial u}{\partial z}-({ϵ}_2-1){\varphi }_2$$

(15)

$$m_{zy}=\frac{({ϵ}_2-1)}{{ϵ}_4}\frac{\partial {\varphi }_2}{\partial z}$$

(16)

$$m_{xy}=\frac{({ϵ}_2-1)}{{ϵ}_4}\frac{\partial {\varphi }_2}{\partial x}$$

(17)

where ${ϵ}_i,i=1\left(1\right)9$ are given in Appendix A.

To simplify the Equations (1)–(7), we use the non-dimensional variables as below

$$\begin{array}{c}(x^{*},z^{*})=\frac{{\eta }_0}{c_0}(x,z),(t^{*},t_0^{*},{\tau }_0^{*},{\tau }_q^{*},{\tau }_T^{*},{\upsilon }^{*})={\eta }_0(t,t_0,{\tau }_0,{\tau }_q,{\tau }_T,\upsilon ),{\Omega }^{*}=\frac{\Omega }{{\eta }_0}\\ (u^{*},w^{*})=\frac{\rho c_0{\eta }_0}{{\gamma }_T{T}_0}(u,w),{\theta }^{*}=\frac{\theta }{T_0},{\sigma }_{ij}^{*}=\frac{{\sigma }_{ij}}{{\gamma }_T{T}_0},m_{ij}^{*}=\frac{{\eta }_0{m}_{ij}}{c_0{\gamma }_T{T}_0},({\psi }^{*},{\varphi }_2^{*})=\frac{\rho c_0^2}{{\gamma }_T{T}_0}(\psi ,{\varphi }_2).\end{array}$$

(18)

where

$$c_0^2=\frac{\mu }{\rho },\beta =\sqrt{\frac{\lambda +2\mu }{\mu }},{\eta }_0=\frac{\rho c_E{c}_0^2}{k},p_l=\left(1+\frac{{{\tau }^{\alpha }}_q}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}+\frac{{{\tau }^{2\alpha }}_q}{2\alpha !}\frac{{\partial }^{2\alpha }}{\partial t^{2\alpha }}\right).$$

Equations (8)–(17) takes the above form, dropping the * for convenience.

4. Normal Mode Analysis

The decomposition of the solution of the physical variables under consideration has the following form in the normal mode

$$(u,w,\psi ,\theta ,{\varphi }_2,{\sigma }_{jk})(x,z,t)=(\overline{u},\overline{w},\overline{\psi },\overline{\theta },\overline{{\varphi }_2},\overline{{\sigma }_{jk}})\left(x\right)e^{(st+iqz)};$$

(19)

where $\overline{u},\overline{w},\overline{\theta },\overline{{\varphi }_2},\overline{{\sigma }_{jk}},\overline{Q}$ are the amplitudes of the functions, s is a complex constant, $i=\sqrt{-1}$ and q is the wave numbers in the z-direction.

Using above equations we obtain the vector matrix differential equation as

$$\frac{d\overline{z}}{dx}=A\overline{z}$$

(20)

where

$$\overline{z}={(\overline{u},\overline{w},\overline{{\varphi }_2},\overline{\theta },\overline{\psi },\frac{d\overline{u}}{dx},\frac{d\overline{w}}{dx},\frac{d\overline{{\varphi }_2}}{dx},\frac{d\overline{\theta }}{dx},\frac{d\overline{\psi }}{dx})}^T$$

(21)

$$A=\left[\begin{array}{cccccccccc}0& 0& 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 1\\ a_{51}& a_{52}& a_{53}& 0& 0& 0& a_{56}& 0& a_{58}& a_{59}\\ a_{61}& a_{62}& 0& a_{64}& 0& a_{65}& 0& a_{67}& 0& 0\\ a_{71}& 0& a_{73}& 0& 0& 0& a_{76}& a_{77}& 0& 0\\ 0& a_{82}& 0& a_{84}& 0& a_{85}& a_{86}& a_{87}& a_{88}& 0\\ 0& a_{92}& 0& a_{94}& a_{95}& a_{96}& 0& 0& 0& 0\end{array}\right]$$

(22)

and $p_{ls}=\frac{\left(1+\frac{{{\tau }_q}^{\alpha }}{\alpha !}{s}^{\alpha }+\frac{{{\tau }_q}^{2\alpha }}{2\alpha !}{s}^{2\alpha }\right)}{\left[K_1(1+\frac{{{\tau }_v}^{\alpha }}{\alpha !}{s}^{\alpha })+s(1+\frac{{{\tau }_{\theta }}^{\alpha }}{\alpha !}{s}^{\alpha })\right]}$ and all the components of matrix A in Equation (22) are given in Appendix A.

5. Solution

The following equation represents the matrix A’s characteristic equation:

$$det(A-\Lambda I)=0$$

(23)

The eigenvalues of the characteristic Equation (20) are taken in the form $\Lambda =\pm {\Lambda }_i$$(i=1,2,3,4,5)$

The eigen vector $\underset{\sim }{X}$ corresponding to the eigen value $\Lambda$ calculated as

$$\underset{\sim }{X}={\left[\begin{array}{cccccccccc}{\Gamma }_1& {\Gamma }_2& {\Gamma }_3& {\Gamma }_4& {\Gamma }_5& \Lambda {\Gamma }_1& \Lambda {\Gamma }_2& \Lambda {\Gamma }_3& \Lambda {\Gamma }_4& \Lambda {\Gamma }_5\end{array}\right]}^T$$

(24)

where ${\Gamma }_i(i,j=1,2,3,4,5)$ are given in Appendix A. We construct the inverse of the matrix $V=\left(X_1,X_2,X_3,X_4,X_5,X_6,X_7,X_8,X_9,X_{10}\right)={\left(X_{ij}\right)}_{10\times 10},i,j=1\left(1\right)10$ as $V^{-1}=\left({\omega }_{ij}\right),i,j=1,2,3,4,5,6,7,8,9,10$.

Then the solution of the differential Equation (23) is [14,15]

$$\overline{z}=\sum _{j=1}^5{X}_j{y}_j$$

(25)

$$y_r=C_r{e}^{{\lambda }_{r}x}+e^{{\lambda }_{r}x}{\int }_{-\infty }^{\infty }{Q}_r{e}^{-{\lambda }_{r}x}and Q_r=\sum _{j=1}^{10}{\omega }_{rj}{f}_j$$

(26)

where $C_r$ is an arbitrary constant which is to be evaluated using initial and boundary conditions.

$$u=e^{(st+iqy)}\sum _{j=1}^5{X}_{1j}(C_j{e}^{{\Lambda }_{j}x}-\frac{Q_j}{{\Lambda }_j})$$

(27)

$$w=e^{(st+iqy)}\sum _{j=1}^5{X}_{2j}(C_j{e}^{{\Lambda }_{j}x}-\frac{Q_j}{{\Lambda }_j})$$

(28)

$$\theta =e^{(\omega t+iby)}\sum _{j=1}^5{X}_{3j}(C_j{e}^{{\Lambda }_{j}x}-\frac{Q_j}{{\Lambda }_j})$$

(29)

Using Equations (27)–(29) simplifying the above equations we obtain the stress components as follows

$${\sigma }_{zz}=e^{(\omega t+ibz)}\left(\sum _{j=1}^5{C}_j{S}_{1j}\left(x\right)e^{{\Lambda }_{j}x}-M_1\right),{\sigma }_{zx}=e^{(\omega t+ibz)}\left(\sum _{j=1}^5{C}_j{S}_{2j}\left(x\right)e^{{\Lambda }_{j}x}-M_2\right)$$

(30)

$${\sigma }_{xx}=e^{(\omega t+ibz)}\left(\sum _{j=1}^5{C}_j{S}_{4j}\left(x\right)e^{{\Lambda }_{j}x}-M_4\right),{\sigma }_{xz}=e^{(\omega t+ibz)}\left(\sum _{j=1}^5{C}_j{S}_{3j}\left(x\right)e^{{\Lambda }_{j}x}-M_3\right)$$

(31)

$$m_{xy}=e^{(\omega t+ibz)}\left(\sum _{j=1}^5{C}_j{S}_{6j}{e}^{{\Lambda }_{j}x}-M_6\right),m_{zy}=e^{(\omega t+ibz)}\left(\sum _{j=1}^5{C}_j{S}_{5j}{e}^{{\Lambda }_{j}x}-M_5\right)$$

(32)

where $C_j$, $S_{ij}$(x) and $M_k$ (i = 1, 2, 3, 4, 5, 6, 7; j = 1, 2, 3, 4; k = 1, 2, 3, 4, 5, 6, 7) are given in the Appendix A.

6. Discussion

We discuss TPL model in Figure 1, Figure 2, Figure 3 and Figure 4. In Figure 1 the fractional order parameter $\alpha$ has a significant effect on the temperature distribution, where increasing on $\alpha$ causes increasing on and the rate of change of with respect to x also increases when $\alpha$ increases at fixed $t=0.1$.

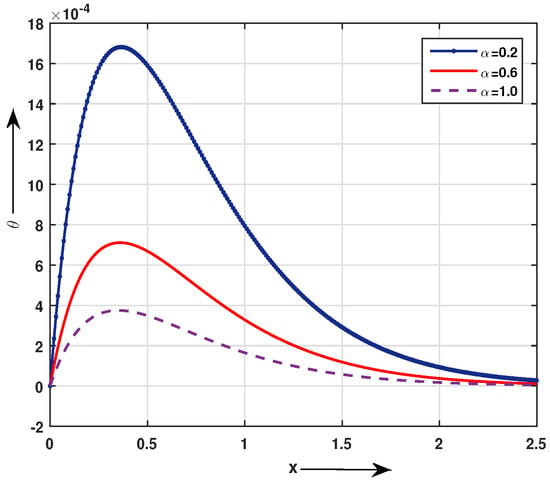
Figure 1. Impact of fractional order parameter on temperature distribution at t = 0.1 and z = 1.

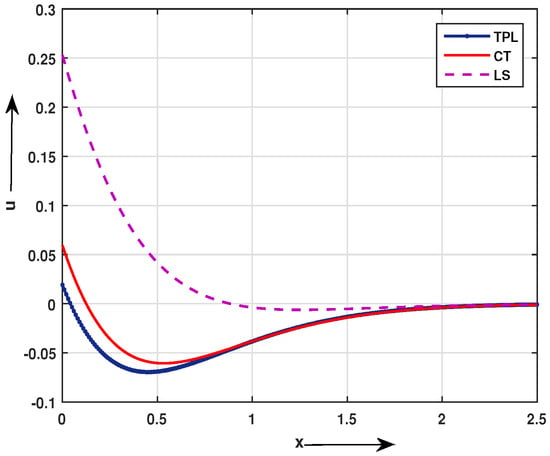
Figure 2. Impact of different thermoelasticity theory on u distribution at t = 0.1 and z = 1.

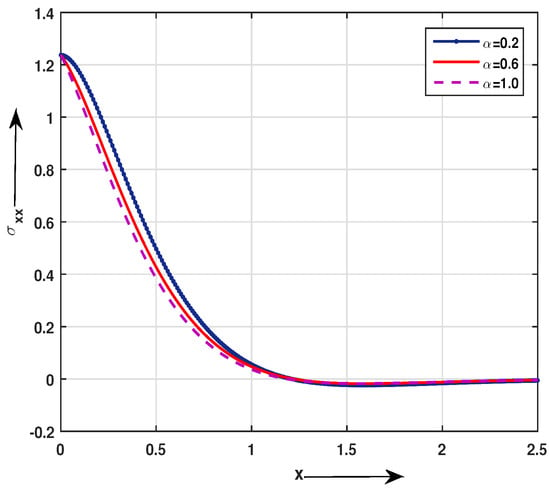
Figure 3. Impact of fractional order parameter on ${\sigma }_{xx}$ distribution at t = 0.1 and z = 1.

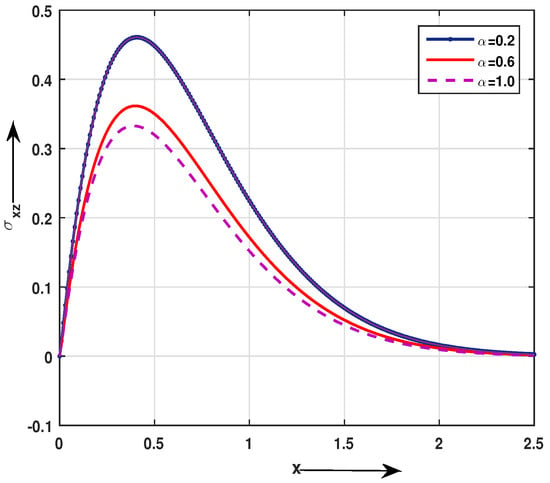
Figure 4. Impact of fractional order parameter on ${\sigma }_{xz}$ distribution at t = 0.1 and z = 1.

In Figure 2, when fractional order $\alpha =1$, time $t=0.1$ are fixed and other constants are same, then u displacement distribution starts with negative values for TPL, LS, CT theory. The u-distribution up to $x=1.2$ for the LS model is greater than for the TPL model and CT model. After $x=1.2$ the result is reversed.

In Figure 3 and Figure 4, the fractional parameter has significant effects on the stress ${\sigma }_{xx}$ and ${\sigma }_{xz}$ distributions. Both starts from zero initially which shows that they satisfy boundary condition. Increasing of fractional parameter $\alpha$ causes decreasing the absolute values of the stresses, and the rate of change of them with respect to x also increase when $\alpha$ increases. For the fixed value of x the stress ${\sigma }_{xz}$ distribution has the lowest value for the fractional parameter $\alpha$ = 0.2 in the range $0\le x\le 1.0$. For $x\ge 1.0$ the distribution gradually increases towards zero.

7. Conclusions

In this work, the effect of the heat source, fractional order and phase lag parameters on the temperature distribution, displacement components, the stress components have been studying for a two-dimensional problem in a half space micro-polar thermoelastic material is considered with the context of the fractional order thermoelasticity theory caring a heat source. We found that, the fractional order parameter has significant effects on all the studied fields and the results supporting the definition of the classification of the thermal conductivity of the materials. We also found significant effects of phase lag parameters.