Fitting Power Spectrum of Scalar Perturbations for Primordial Black Hole Production during Inflation

Abstract

A simple phenomenological fit for the power spectrum of scalar (curvature) perturbations during inflation is proposed to analytically describe slow roll of inflaton and formation of primordial black holes (PBH) in the early universe, in the framework of single-field models. The fit is given by a sum of the power spectrum of slow-roll inflation, needed for a viable description of the cosmic microwave background (CMB) radiation in agreement with Planck/BICEP/Keck measurements, and the log-normal (Gaussian) fit for the power spectrum enhancement (peak) needed for efficient PBH production, in the leading (model-independent) approximation. The T-type $\alpha$-attractor models are used to get the simple CMB power spectrum depending upon the e-folds as the running variable. The location and height of the peak are chosen to yield the PBH masses in the asteroid-size window allowed for the whole (current) dark matter. We find the restrictions on the peak width.

1. Introduction

The inflationary paradigm was initially proposed as a possible solution to the internal problems of the standard (Einstein-Friedmann) cosmology such as the horizon problem, the flatness problem and the problem of initial conditions [1,2]. It was later recognized that inflation in the early universe may be a solution to the structure formation problem also [3]. A major recognition of the inflationary paradigm came with its success in explaining the inhomogeneity and anisotropy of the cosmic microwave background (CMB) radiation [4].

The underlying physics of inflation is still unknown but there is no shortage of theoretical models of inflation. The simplest single-field models of chaotic inflation are based on the quintessence (scalar-tensor gravity) or the modified $F\left(R\right)$-gravity theories. More recently, the quintessence models were further generalized by adding a near-inflection point to the inflaton potential below the inflationary scale, leading to a peak in the power spectrum of scalar perturbations that later collapse to primordial black holes (PBH) [5,6,7,8].1 PBH are also considered as a good (non-particle) candidate for the present dark matter [13,14].

Usually, one begins with a particular inflationary model having a specific scalar potential, and then one numerically derives the power spectrum by using the Mukhanov-Sasaki equation [15,16]. In this paper, we begin with analytic modeling of the power spectrum of scalar (curvature) perturbations for possible PBH production in agreement with CMB measurements. We choose the simplest fit as a sum of the CMB power spectrum in the slow-roll approximation and the log-normal shape of the peak. This allows us to get analytic smooth sewing of both spectra with the minimal number of parameters and a possibility to analytically explore the whole parameter space, which is often difficult in a numerical approach. As regards the CMB power spectrum, we describe it with the help of the T-type $\alpha$-attractor models of inflation [17,18,19] in order to get the simplest form of the spectrum during slow roll. As a result, we find new restrictions on the parameters of PBH production.

Our paper is organized as follows. In Section 2 we briefly review the T-type $\alpha$-attractor models of inflation, which are used as the viable models for CMB in the next Sections. The power spectrum of scalar perturbations during inflation in the slow-roll approximation (relevant to CMB) is derived in Section 3. Section 4 is devoted to our fit of the power spectrum of scalar perturbations for both CMB and PBH production, and the related spectrum of induced gravitational waves (GW). Our conclusion is Section 5.

2. Single-Field Models of Slow-Roll Inflation for CMB

As the simple models of large-single-field inflation, described by the standard quintessence action

$$S[g_{\mu \nu },\varphi ]=\int d^{4}x\sqrt{-g}\left\{\frac{M_{\mathrm{Pl}}^2}{2}R-\frac{1}{2}{g}^{\mu \nu }{\partial }_{\mu }\phi {\partial }_{\nu }\phi -V\left(\phi \right)\right\},$$

(1)

we choose the T-type $\alpha$-attractors [17,18] with the canonical inflaton potential

$$V\left(\phi \right)=V_0{tanh}^2\left(\frac{\phi /M_{\mathrm{Pl}}}{\sqrt{6\alpha }}\right)\equiv V_0{r}^2,r=tanh\frac{\phi /M_{\mathrm{Pl}}}{\sqrt{6\alpha }},$$

(2)

where the constant $V_0$ specifies the scale of inflation, and the $\alpha >0$ is the free parameter of the order one.

This model is a viable model of large-field slow-roll inflation with a nearly flat potential, whose inflationary solution is an attractor describing chaotic inflation, being very close to the Starobinsky model [20] in the case of $\alpha =1$. The CMB tilt of scalar perturbations, predicted by the T-model is given by the simple formula [21]

$$n_s=1-\frac{2}{N_e},$$

(3)

in terms of e-folds $N_e$ as the running variable describing time evolution, $N_e\left(k\right)=ln(k_{\mathrm{final}}/k)$ as the function of scale k [22]. The CMB tensor-to-scalar ratio r is approximately $(N_e\gg 1)$ given by [17,18]

$$r_{\alpha }\approx \frac{12\alpha }{N_e^2},$$

(4)

providing the comfortable theoretical prediction against future measurements of r. Indeed, the current CMB measurements by Planck/BICEP/Keck collaborations [23,24,25] give

$$n_s=0.9649\pm 0.0042(68\%\mathrm{C}.\mathrm{L}.),r<0.036(95\%\mathrm{C}.\mathrm{L}.),$$

(5)

while they are in good agreement with Equations (3) and (4) with the best fit close to $N_e=55$.

The generalization of the simplest T-model potential (2) to the form [17,18]

$$V_{\mathrm{gen}.}\left(\phi \right)=f^2\left(tanh\frac{\phi /M_{\mathrm{Pl}}}{\sqrt{6\alpha }}\right)$$

(6)

with a monotonically increasing (during slow roll) function $f\left(r\right)$, $r=tanh\frac{\phi /M_{\mathrm{Pl}}}{\sqrt{6\alpha }}$, can be used for engineering a near-inflection point in the potential, leading to a peak (enhancement) in the power spectrum of scalar perturbations, needed for PBH formation [26,27].2

In the generalized T-models (6) slow-roll inflation occurs for large positive values of the inflation field $\phi$ with an approximate scalar potential of the E-type [30] as $(M_{\mathrm{Pl}}=1)$

$$V\left(\phi \right)=f_{\infty }^2-4f_{\infty }{f^{\prime }}_{\infty }{e}^{-\sqrt{\frac{2}{3\alpha }}\phi }+\mathcal{O}\left(e^{-2\sqrt{\frac{2}{3\alpha }}\phi }\right),$$

(7)

where we have introduced the parameters $f_{\infty }={\left.f\right|}_{\phi \to \infty }$ and ${f^{\prime }}_{\infty }={\left.{\partial }_{\phi }f\right|}_{\phi \to \infty }$. The constant in front of the second term in Equation (7) can be chosen at will by a constant shift of the inflaton field $\phi$, so that the potential (7) can be simplified to

$$V\left(\phi \right)=V_0\left(1-e^{-\sqrt{\frac{2}{3\alpha }}\phi }\right)+\mathcal{O}\left(e^{-2\sqrt{\frac{2}{3\alpha }}\phi }\right),$$

(8)

which implies Equations (3) and (4).

The $\alpha$-attractors with $\alpha \ne 1$ do not have a simple description on the dual $F\left(R\right)$-gravity side, see e.g., Ref. [31] for details of the correspondence. The Starobinsky function $F\left(R\right)=\frac{M_{\mathrm{Pl}}^2}{2}(R+\frac{R^2}{6m_{\inf .}^2})$ on the modified gravity side arises in the case of $\alpha =1$ and $f\left(r\right)=\sqrt{3}{m}_{\inf .}{M}_{\mathrm{Pl}}r/(r+1)$, where $m_{\inf .}$ is the inflaton (scalaron) mass. In general, the exact dual $F\left(R\right)$ gravity function associated with any inflaton potential V in the model (1) is only known in the parametric (implicit) form, see Equations (2.7) and (2.8) in Ref. [31], as

$$\begin{array}{ccc}\hfill R& =& \hfill \left[\frac{\sqrt{6}}{M_{\mathrm{Pl}}}{V}_{,\phi }+\frac{4V}{M_{Pl}^2}\right]exp\left(\sqrt{\frac{2}{3}}\frac{\phi }{M_{Pl}}\right),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill F& =& \hfill \frac{M_{\mathrm{Pl}}^2}{2}\left[\frac{\sqrt{6}}{M_{\mathrm{Pl}}}{V}_{,\phi }+\frac{2V}{M_{\mathrm{Pl}}^2}\right]exp\left(2\sqrt{\frac{2}{3}}\frac{\phi }{M_{\mathrm{Pl}}}\right).\hfill \end{array}$$

(10)

When $\alpha \ne 1$, or $A\left(R\right)\ne const.$ in the slow-roll approximation with the potential (2), we find that the F-function can be approximated in the form

$$F\left(R\right)=\frac{M_{\mathrm{Pl}}^2}{2}\left[R+A\left(R\right)\frac{R^2}{6m^2}\right]$$

(11)

with the function

$$A\left(R\right)\approx 1-\frac{3}{4}\epsilon ,$$

(12)

where $\epsilon$ is the standard slow-roll parameter

$$\epsilon =\frac{M_{\mathrm{Pl}}^2}{2}{\left(\frac{V_{,\phi }}{V}\right)}^2,$$

(13)

and $R\approx 12H^2\approx 4V/M_{\mathrm{Pl}}^2$ in terms of the Hubble function H and the potential V.

The particular examples of the generalized T-models, suitable for inflation and PBH production, can be obtained by expanding the $f\left(r\right)$-function in Taylor series and tuning the expansion coefficients [26,30].

The slow-roll evolution of inflaton with e-folds N as the running (time) variable is described by the (non-linear) equation of motion, obtained from the standard (Klein-Gordon) equation minimally coupled to gravity in the (spatially flat) universe, when the acceleration term is ignored,

$$\frac{1}{M_{\mathrm{Pl}}^2}{\left(\frac{d\phi }{dN}\right)}^2=\frac{dlnV}{dN}.$$

(14)

This equation has an exact solution in the case of the T-model potential (2), with

$$\phi /M_{\mathrm{Pl}}=\sqrt{2N_0}\mathrm{arcosh}\left(\frac{N}{N_0}\right),N\gg N_0>0,$$

(15)

where the (implicit) integration constant is associated with constant shifts of the field $\phi$. The solution implies

$$\frac{N-N_0}{N+N_0}={tanh}^2\left(\frac{\phi /M_{\mathrm{Pl}}}{\sqrt{6\alpha }}\right),N_0=\frac{3\alpha }{4},$$

(16)

and gives a very simple potential $V\left(N\right)$ of the T-model in the slow-roll approximation,

$$V\left(N\right)=V_0\left(\frac{N-N_0}{N+N_0}\right).$$

(17)

The Hubble function $H\left(N\right)$ is also simply related to the potential $V\left(H\right)$ is the slow-roll approximation via the Friedmann equation

$$H^2\left(N\right)=\frac{V\left(N\right)}{3M_{\mathrm{Pl}}^2}.$$

(18)

The relations between the potential $V\left(N\right)$, the running tensor-to-scalar ratio $r\left(N\right)$ and the slow-roll parameter $\epsilon \left(N\right)$ in the slow-roll approximation are very simple too,

$$r\left(N\right)=16\epsilon \left(N\right)=8\frac{dlnV}{dN}=\frac{12\alpha }{N^2-N_0^2}=\frac{12\alpha }{N^2-{(3\alpha /4)}^2},$$

(19)

leading to a bit more precise formula than Equation (4).

The very simple form (17) of the T-potential $V\left(N\right)$ in the slow-roll approximation is one of the reasons why we choose the T-models as our baseline models in this paper.

3. Power Spectrum of Scalar Perturbations in Slow-Roll Approximation

Primordial scalar perturbations ($\zeta$) and primordial tensor perturbations (primordial gravitational waves g) are defined by a perturbed Friedmann-Lemaitre-Robertson-Walker (FLRW) metric,

$$d{s}^2=d{t}^2-a^2\left(t\right)\left(\delta \_ij+h\_ij\left(\overrightarrow{r}\right)\right)d{x}^{i}d{x}^j,i,j=1,2,3,$$

(20)

where

$$h\_ij\left(\overrightarrow{r}\right)=2\zeta \left(\overrightarrow{r}\right)\delta \_ij+\sum \_a=1,2g^{\left(a\right)}\left(\overrightarrow{r}\right)e^{\left(a\right)}\_ij\left(\overrightarrow{r}\right),H=\frac{da/dt}{a},$$

(21)

in terms of the local basis $e^{\left(a\right)}$ obeying the relations $e_i^{i\left(a\right)}=0$, $g_{,j}^{\left(a\right)}{e}_i^{j\left(a\right)}=0$ and $e_{ij}^{\left(a\right)}{e}^{ij\left(a\right)}=1$.

The primordial spectrum $P_{\zeta }\left(k\right)$ of scalar (density) perturbations is defined by the 2-point correlator of scalar perturbations,

$$⟨{\zeta }^2\left(\overrightarrow{r}\right)⟩=\int dk\frac{P_{\zeta }\left(k\right)}{k}.$$

(22)

The CMB power spectrum can be described by the Harrison-Zeldovich fit

$$P_{\zeta }^{\mathrm{HZ}}\left(k\right)\approx 2.{21}_{-0.08}^{+0.07}\times {10}^{-9}{\left(\frac{k}{k_{*}}\right)}^{n_s-1},$$

(23)

near the pivot scale $k_{*}=0.05{\mathrm{Mpc}}^{-1}$, or in the slow-roll (SR) approximation by

$$P_{\zeta }^{\mathrm{SR}}\left(k\right)\approx P_0{ln}^2\left(\frac{k}{k_{\mathrm{final}}}\right),P_0=const.$$

(24)

The power spectrum $P_{\zeta }\left(N\right)$ is simply related to the potential $V\left(N\right)$ in the slow-roll approximation via the standard relation, see e.g., Refs. [5,29],

$$P_{\zeta }\left(N\right)=\frac{V^2}{12{\pi }^2{M}_{\mathrm{Pl}}^4}{\left(\frac{dV}{dN}\right)}^{-1}.$$

(25)

It also implies

$$1-n_s=\frac{dln{P}_{\zeta }\left(N\right)}{dN}.$$

(26)

In the case of the potential (17), we find very simple equations,

$$P_{\zeta }^{\mathrm{SR}}\left(N\right)=\frac{V_0}{18{\pi }^2{M}_{\mathrm{Pl}}^4\alpha }{(N-N_0)}^2\equiv P_0{(N-N_0)}^2,$$

(27)

and

$$n_s=1-\frac{2}{N-N_0},$$

(28)

where the last equation reproduces Equation (3).

The observed CMB window into inflation does not allow us to reconstruct the full inflaton scalar potential from the power spectrum beyond the slow-roll region. The well-known reconstruction formula, proposed by Hodges and Blumentahl [22] in the form

$$\frac{1}{V\left(N\right)}=-\frac{1}{12{\pi }^2{M}_{\mathrm{Pl}}^4}\int \frac{dN}{P_{\zeta }\left(N\right)},$$

(29)

requires knowing the full power spectrum at different scales and the limits of integration. Moreover, the reconstruction procedure should be based on getting exact solutions to the Mukhanov-Sasaki equation instead of the slow-roll solution in Equation (27), see e.g., Ref. [32] for some examples. It is not our purpose in this paper to reconstruct the inflaton potential beyond its qualitative features. Nevertheless, it may be possible for the CMB region under some additional assumptions, e.g., when assuming a very low value of the tensor-to-scalar ratio r, which implies a small correction $\delta V$ to the constant $V_0$ defining the inflationary scale, i.e., the inflaton potential in the form $V=V_0+\delta V$ with $\left|\delta V\right|\ll V_0$. Then Equation (29) is simplified to

$$\delta V\left(N\right)=\frac{V_0}{12{\pi }^2{M}_{\mathrm{Pl}}^4}\int \frac{dN}{P_{\zeta }\left(N\right)},$$

(30)

while the integration constants merely rescale $V_0$ and shift N. Equation (14) also gets simplified to

$$\frac{V_0}{M_{\mathrm{Pl}}^2}{\left(\frac{d\phi }{dN}\right)}^2=\frac{d\left(\delta V\right)}{dN}.$$

(31)

Then a partial reconstruction of the scalar potential becomes possible from the CMB power spectrum $P_{\zeta }\left(N\right)$ of scalar perturbations without knowing the power spectrum of tensor perturbations, which is also true for the $\alpha$-attractors when the parameter $\alpha$ is small enough, $\alpha \le 1$, with

$$V\left(\phi \right)\approx V_0\left(1-e^{-\sqrt{\frac{2}{3\alpha }}\phi }\right),$$

(32)

as in Equation (8). This is yet another reason for us to take the T-models of $\alpha$-attractors as our baseline models of inflation and generalize their power spectrum of scalar perturbations by adding a peak at higher values of k.

4. Log-Normal Fit for a Peak and GW Spectrum

The log-normal fit is the simplest (Gaussian) description of a peak in the power spectrum, see e.g., Ref. [33]. A power-law ansatz for the peak was considered in Ref. [34]. In this paper we propose another ansatz for the power spectrum, combining the CMB spectrum in the slow-roll approximation with the log-normal fit for the enhancement (peak) of the power spectrum needed for PBH formation at a lower scale,

$${\displaystyle P_{\zeta }\left(k\right)=P_0{ln}^2\left(\frac{k}{k_{\mathrm{final}}}\right)+A\frac{exp{\displaystyle [-\frac{{ln}^2\left(\frac{k}{\phantom{2}{k}_{\mathrm{peak}}}\right)}{2{\sigma }^2}}]}{\sqrt{2\pi }\sigma },}$$

(33)

where $k_{\mathrm{peak}}$ is a position of the peak, $\sigma >0$ is the width of the peak and A is the normalization of the peak amplitude, $A\approx \left(\sqrt{2\pi }\sigma \right)0.01$, needed for efficient PBH production (about ${10}^7$ higher than the CMB amplitude). The normalization factor $P_0$ is given by Equation (27),

$$P_0=\frac{V_0}{18{\pi }^2\alpha M_{\mathrm{Pl}}^4},$$

(34)

see also Equation (24). When $V_0\sim m_{\inf .}^2{M}_{\mathrm{Pl}}^2$, $m_{\inf .}\sim {10}^{-5}{M}_{\mathrm{Pl}}$ and $\alpha \sim 1$, we get $P_0\sim \mathcal{O}\left({10}^{-12}\right)$. The power spectrum (33) can be rewritten, using the e-foldings variable N via the relation

$$dlnk=-dN,$$

(35)

to the simple form

$${\displaystyle P_{\zeta }\left(N\right)=P_0{\left(N-N_0\right)}^2+A\frac{exp{\displaystyle [-\frac{{\left(N-N_{\mathrm{peak}}\right)}^2}{2{\sigma }^2}}]}{\sqrt{2\pi }\sigma }.}$$

(36)

We choose $k_{\mathrm{final}}=e^{N_e}$${\mathrm{Mpc}}^{-1}$$\approx 7.7\times {10}^{23}{\mathrm{Mpc}}^{-1}$.

The PBH masses can be estimated by the relation [9,10,11,12]

$$\frac{M_{\mathrm{PBH}}\left(k\right)}{M_{\odot }}\simeq {10}^{-16}{\left(\frac{k}{{10}^{14}{\mathrm{Mpc}}^{-1}}\right)}^{-2}.$$

(37)

We choose $k_{\mathrm{peak}}$ or $N_{\mathrm{peak}}$ to get $M_{\mathrm{PBH}}$ within the current observational window for PBH as the whole dark matter [9,10,11], i.e., between ${10}^{17}$ g and ${10}^{21}$ g. For example, when $k_{\mathrm{peak}}\approx {10}^{13}{\mathrm{Mpc}}^{-1}$, we get $M_{\mathrm{PBH}}\approx 2\times {10}^{19}$ g. The profile of the power spectrum in given on Figure 1 for some values of $\sigma$.

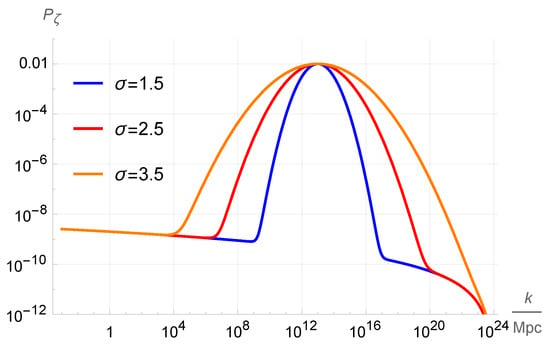
Figure 1. The power spectrum with the parameters $P_0=6.57\times {10}^{-13}$, $k_{\mathrm{peak}}={10}^{13}{\mathrm{Mpc}}^{-1}$, $k_{\mathrm{final}}=7.7\times {10}^{23}$ ${\mathrm{Mpc}}^{-1}$ for $\sigma >1$.

Equations (26) and (36) imply the spectral tilt

$$n_s=1-\frac{2\left(N-N_0\right)-\frac{A\left(N-N_{\mathrm{peak}}\right)e^{-\frac{\left(N-N_{\mathrm{peak}}\right){}^2}{2{\sigma }^2}}}{P_0\sqrt{2\pi }\sigma }}{\frac{A{e}^{-\frac{\left(N-N_{\mathrm{peak}}\right){}^2}{2{\sigma }^2}}}{P_0\sqrt{2\pi }\sigma }+\left(N-N_0\right){}^2}.$$

(38)

It follows from Equation (38) versus Equation (3) that the tilt $n_s$ gets the exponentially small corrections (back reaction) from the peak. To quantitatively evaluate an impact of the back reaction, we introduce the dimensionless parameters for the relative scales,

$${\mu }_L=\frac{k_{\mathrm{left}}-k_{*}}{k_{\mathrm{left}}}\mathrm{and}{\mu }_R=\frac{k_{\mathrm{final}}-k_{\mathrm{right}}}{k_{\mathrm{final}}},$$

(39)

characterizing the separation between the CMB pivot scale $k_{*}$ and the left end $k_{\mathrm{left}}$ of the peak, and the separation between the end of inflation $k_{\mathrm{final}}$ and the right end $k_{\mathrm{right}}$ of the peak, respectively. Since the CMB pivot scale and the PBH scales have to be separated, it implies $k_{*}<k_{\mathrm{left}}$ or ${\mu }_L>0$. The exponential corrections in Equation (38) are negligible when $k_{\mathrm{left}}\ge {10}^3{\mathrm{Mpc}}^{-1}$. On the other hand, the right end of the peak must be within inflation, so that ${\mu }_R>0$. We expect $k_{\mathrm{right}}$ to be close to the end of inflation.3

We illustrate those considerations by our numerical calculations with the results displayed on Figure 2 and Figure 3 for various values of $k_{\mathrm{peak}}$ and $\sigma$ against the observed values of the tilt $n_s$ in Equation (5). The black curves in the ($k_{\mathrm{peak}},\sigma )$-plane correspond to the condition ${\mu }_R=0$. The area above the black curve and the white area are forbidden.

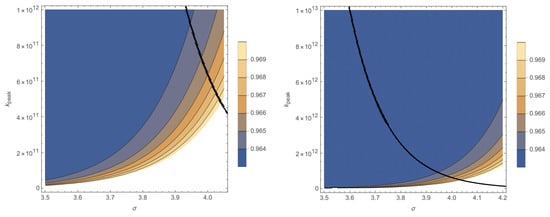
Figure 2. The impact of Equation (38) on the parameters of our model for ${10}^{11}{\mathrm{Mpc}}^{-1}{k}_{\mathrm{peak}}\le {10}^{12}{\mathrm{Mpc}}^{-1}$ (on the left) and for ${10}^{12}{\mathrm{Mpc}}^{-1}\le k_{\mathrm{peak}}\le {10}^{13}{\mathrm{Mpc}}^{-1}$ (on the right) in the $(\sigma ,k_{\mathrm{peak}})$-plane. The (excluded) area above the black curve leads to the right end of the peak after the end of inflation. The other parameters are $P_0=6.57\times {10}^{-13}$ and $k_{\mathrm{final}}=7.7\times {10}^{23}{\mathrm{Mpc}}^{-1}$.

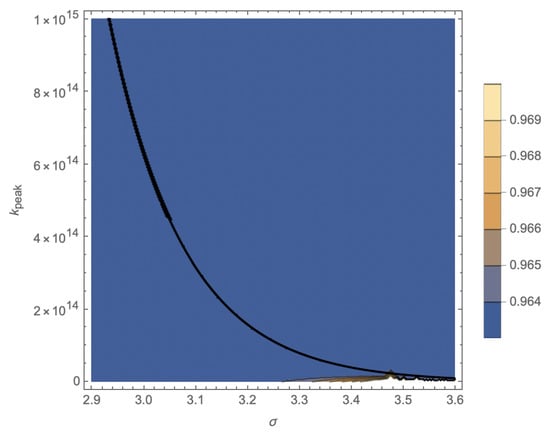
Figure 3. The impact of Equation (38) on the parameters for ${10}^{14}{\mathrm{Mpc}}^{-1}\le k_{\mathrm{peak}}\le {10}^{15}{\mathrm{Mpc}}^{-1}$ in the $(\sigma ,k_{\mathrm{peak}})$-plane. The (excluded) area above the black curve leads to the right end of the peak after the end of inflation. The other parameters are $P_0=6.57\times {10}^{-13}$ and $k_{\mathrm{final}}=7.7\times {10}^{23}{\mathrm{Mpc}}^{-1}$.

For example, when $N_e=55$ and $N_0=3/4$ (or $\alpha =1$), we get $n_s\approx 0.9631$ from Equation (28), whereas we get $n_s\approx 0.9649$ after taking into account the exponential terms in Equation (38) with the parameters $k_{\mathrm{peak}}=6\times {10}^{11}{\mathrm{Mpc}}^{-1}$ and $\sigma =3.945$.

Our analysis allows us to restrict (from above) the possible peak width values $\sigma$ at fixed $k_{\mathrm{peak}}$ and duration of inflation $N_e$ (or $n_s$). We summarize those restrictions in Table 1.4

Table 1. The PBH masses $M_{\mathrm{PBH}}$, the scales $k_{\mathrm{peak}}$ and the upper bounds on $\sigma$.

${\mathit{M}}_{\mathbf{PBH}},\mathbf{g}$	${\mathit{k}}_{\mathbf{peak}},{\mathbf{Mpc}}^{-1}$	$\mathit{\sigma }$
${10}^{21}$	$1.41\times {10}^{12}$	≤3.89
${10}^{20}$	$4.46\times {10}^{12}$	≤3.73
${10}^{19}$	$1.41\times {10}^{13}$	≤3.56
${10}^{18}$	$4.46\times {10}^{13}$	≤3.40
${10}^{17}$	$1.41\times {10}^{14}$	≤3.23

The spectrum of the induced GW can be derived by using the standard formula obtained in the second order with respect to perturbations [36],

$$\begin{array}{c}{\displaystyle {\mathsf{\Omega }}_{GW}\left(k\right)=\frac{{\mathsf{\Omega }}_{r,0}}{32}\underset{0}{\overset{\infty }{\int }}dv\underset{|1-v|}{\overset{1+v}{\int }}du\frac{\mathcal{T}(u,v)}{u^2{v}^2}{P}_{\zeta }\left(vk\right)P_{\zeta }\left(uk\right),}\\ {\displaystyle \mathcal{T}(u,v)=\frac{1}{\phantom{2}4}}{\left[\frac{4v^2-{(1+v^2-u^2)}^2}{4uv}\right]}^2{\left(\frac{u^2+v^2-3}{2uv}\right)}^4[(ln|\frac{3-{(u+v)}^2}{3-{(u-v)}^2}|\\ -\frac{4uv}{u^2+v^2-3}{)}^2+{\pi }^2\mathsf{\Theta }(u+v-\sqrt{3})],\end{array}$$

(40)

where ${\mathsf{\Omega }}_{r,0}=8.6\times {10}^{-5}$. Our numerical results for a wide peak with $\sigma >1$ are displayed on Figure 4.

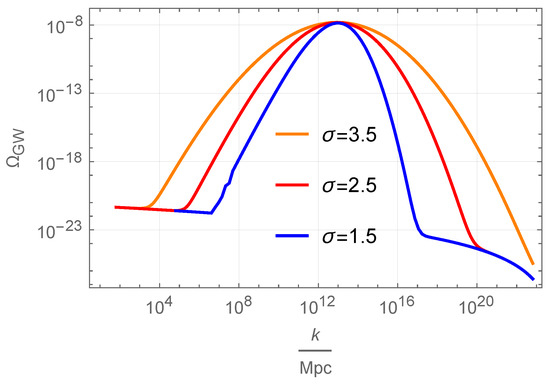
Figure 4. The induced GW spectrum for selected values $\sigma >1$ of a wide peak in the power spectrum, with the parameters $P_0=6.57\times {10}^{-13}$, $k_{\mathrm{peak}}={10}^{13}{\mathrm{Mpc}}^{-1}$ and $k_{\mathrm{final}}=7.7\times {10}^{23}{\mathrm{Mpc}}^{-1}$.

The peak in the GW-spectrum associated with a wide ($\sigma >1$) peak in the power spectrum can be analytically approximated as

$${\mathsf{\Omega }}_{\mathrm{GW},r}^{\left(\mathrm{peak}\right)}\approx 0.125\frac{A^2}{{\sigma }^2}exp\left[\frac{-{ln}^2\left(\frac{k}{k_{\mathrm{peak}}}\right)}{{\sigma }^2}\right]\sim {10}^{-6}{P}_{\zeta }^2\left(k\right).$$

(41)

For comparison, in Figure 5 we give our numerical results for the induced GW spectrum with selected values $\sigma <1$ of a sharp peak in the power spectrum. Then the GW spectrum is not given by a sum of contributions from the peak and the slow-roll, while the simple relation to the power spectrum in Equation (41) is also not valid. Instead, the cross terms in Equation (40) become significant and the shape of the GW spectrum changes, see Figure 5. This phenomenon was also observed in Ref. [37].

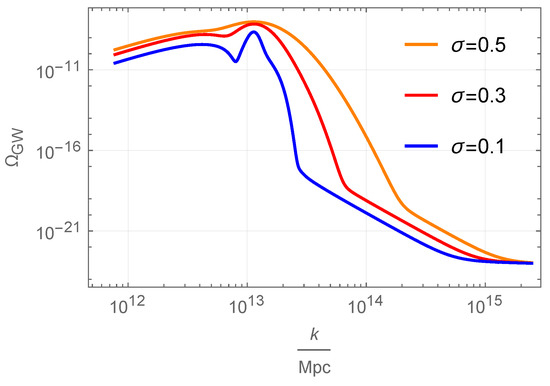
Figure 5. The induced GW spectrum for selected values $\sigma <1$ of a sharp peak in the power spectrum, with the parameters $P_0=6.57\times {10}^{-13}$, $k_{\mathrm{peak}}={10}^{13}{\mathrm{Mpc}}^{-1}$ and $k_{\mathrm{final}}=7.7\times {10}^{23}{\mathrm{Mpc}}^{-1}$.

5. Conclusions

Our investigation in this paper is based on the ansatz (33) for the power spectrum of scalar (curvature) perturbations during inflation. The ansatz is given by a sum of the CMB power spectrum in the slow-roll approximation and the log-normal fit for the power spectrum enhancement (peak) needed for efficient PBH production. The ansatz (33) is very simple, while we use the slow-roll approximation and the T-type $\alpha$-attractor models of inflation in order to justify the first term in Equation (33). The second term in Equation (33) requires the scalar potential in those models to be generalized, e.g., via engineering a near-inflection point and an ultra-slow-roll phase during inflation, see e.g., Refs. [5,6,12,26,27,28,29,30,38,39] for explicit examples. We are aware that the slow-roll approximation is violated during the ultra-slow-roll phase needed for a peak generation, and do not expect that Equation (33) is suitable for a full reconstruction of the inflaton scalar potential. Instead, we take the power spectrum (33) for granted and study its consequences, both analytically and numerically, in the context of CMB and PBH as DM.

Our main results are given in Section 4 including our Figure 1 and Table 1 that summarizes the restrictions on the peak width $\sigma$ from above.