On the Dynamical Instability of Monatomic Fluid Spheres in (N + 1)-Dimensional Spacetime
Abstract
1. Introduction
2. (N + 1)-Dimensional Spacetime of Spherical Symmetry
2.1. Linear Radial Perturbation and the Adiabatic Index
2.2. The Adiabatic Index of an Ideal Monatomic Fluid
2.3. The Pulsation Equation and the Critical Adiabatic Index
2.4. The Effect of Cosmological Constant
3. Homogeneous Fluid Solutions
4. Numerical Results
4.1. Fluid Spheres in (3 + 1) and Higher-Dimensional Spacetime
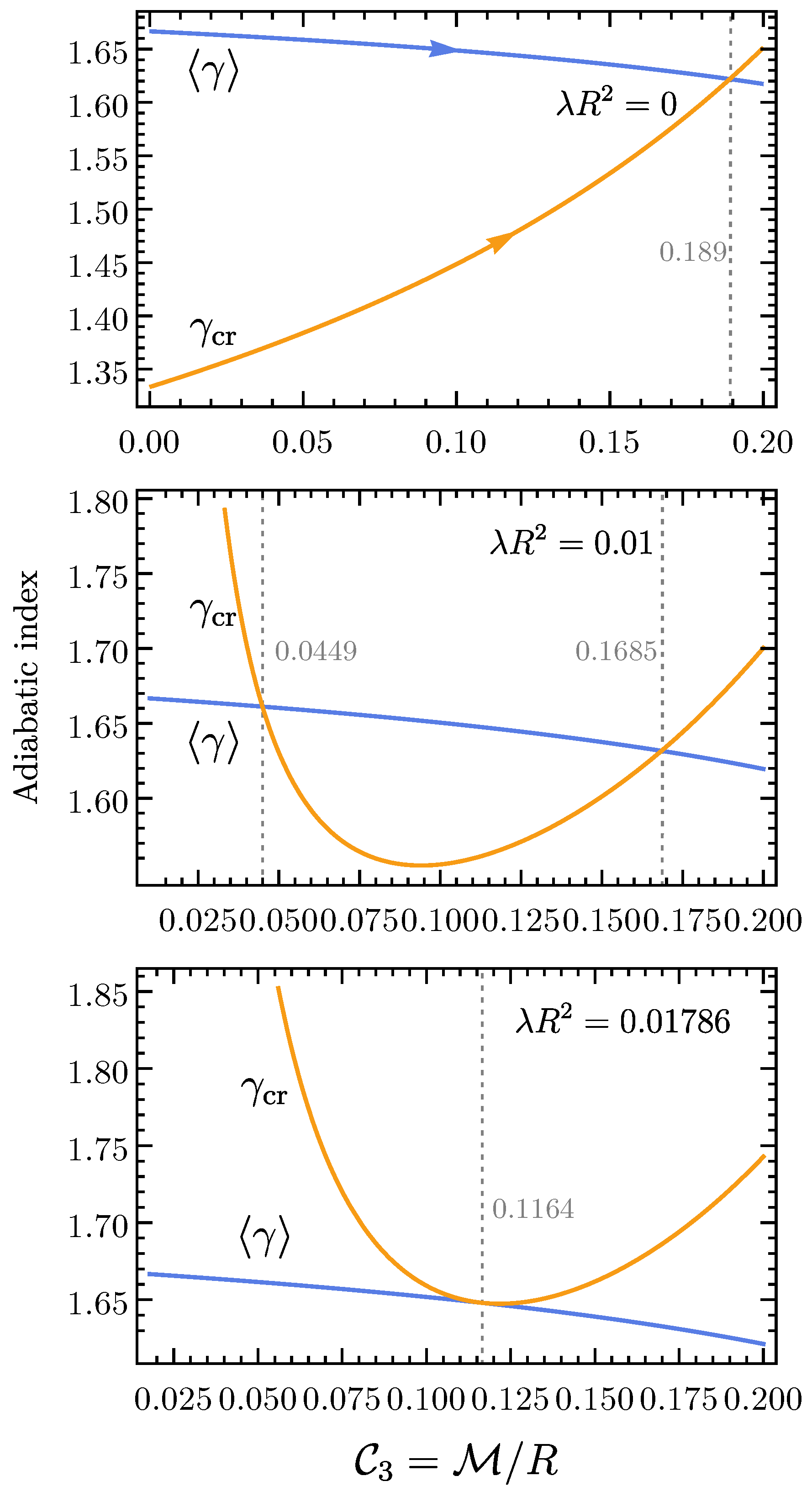
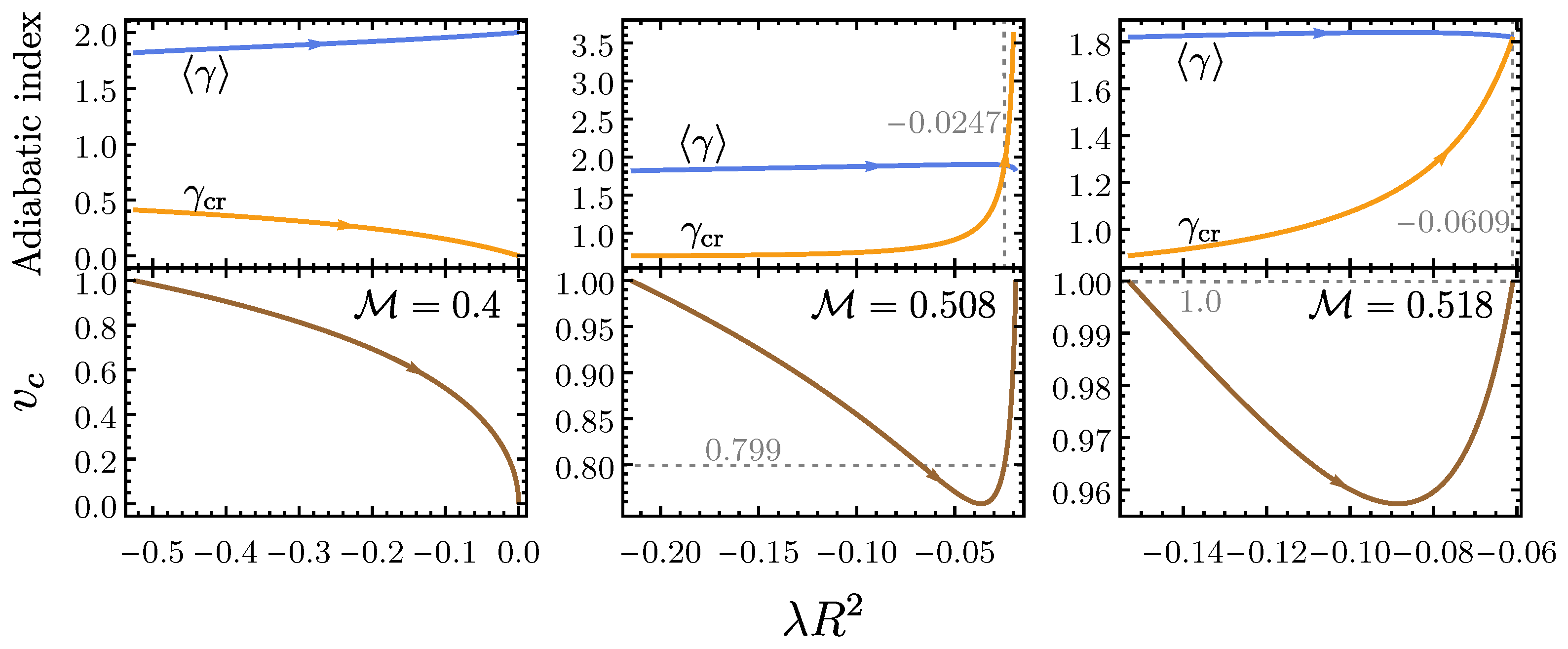
4.2. Fluid Disks in (2 + 1)-Dimensional Spacetime
5. Discussions and Implications
- First law of thermodynamics and equipartition theorem hold;
- Mass–energy dispersion relation is valid;
- Einstein equations hold in (N + 1) dimensions.
- Baby universe emerges from collapsing matter in a black hole;
- Spacetime dimensionality reshuffles in the reign of quantum gravity.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Thermodynamic Identity
Appendix B. Ideal Monatomic Fluid in N-Dimensional Space
Appendix C. The Critical Adiabatic Index in Newtonian Gravity
Appendix D. The Orthogonality Relation and Rayleigh–Ritz Principle
Appendix E. A Rigorous Proof on the Buchdahl Bound
- The energy density is finite and monotonically non-increasing, i.e., ;
- and are positive definite, thus no horizon is present inside the fluid sphere.
Appendix F. Various Tables for N=2
| (Lower/Upper) | (Lower/Upper) | (Lower/Upper) | |
|---|---|---|---|
| / | / | / | |
| / | / | / | |
| / | / | / | |
| / | / | / | |
| / | / | / | |
| / | / | / | |
| / | / | / | |
| 1 |
| 1 |
References
- Ehrenfest, P. In what way does it become manifest in the fundamental laws of physics that space has three dimensions? Proc. Amst. Acad. 1918, 20, 200–209. [Google Scholar]
- Ehrenfest, P. Welche Rolle spielt die Dreidimensionalität des Raumes in den Grundgesetzen der Physik? Ann. Phys. 1920, 366, 440–446. [Google Scholar] [CrossRef]
- Whitrow, G.J. Why Physical Space Has Three Dimensions. Br. J. Philos. Sci. 1955, 6, 13–31. [Google Scholar] [CrossRef]
- Tangherlini, F.R. Schwarzschild field in n dimensions and the dimensionality of space problem. Nuovo Cim. 1963, 27, 636–651. [Google Scholar] [CrossRef]
- Barrow, J.D. Dimensionality. Philos. Trans. R. Soc. Lond. A 1983, 310, 337–346. [Google Scholar] [CrossRef]
- Barrow, J.D.; Tipler, F.J. The Anthropic Cosmological Principle; Oxford University Press: Oxford, UK, 1988. [Google Scholar]
- Caruso, F.; Moreira Xavier, R. On the Physical Problem of Spatial Dimensions: An Alternative Procedure to Stability Arguments. Fund. Sci. 1987, 8, 73–91. [Google Scholar]
- Tegmark, M. On the dimensionality of space-time. Class. Quant. Grav. 1997, 14, L69–L75. [Google Scholar] [CrossRef]
- Momen, A.; Rahman, R. Spacetime Dimensionality from de Sitter Entropy. TSPU Bull. 2014, 12, 186–191. [Google Scholar]
- Gonzalez-Ayala, J.; Cordero, R.; Angulo-Brown, F. Is the (3 + 1)-d nature of the universe a thermodynamic necessity? EPL 2016, 113, 40006. [Google Scholar] [CrossRef]
- Brandenberger, R.H.; Vafa, C. Superstrings in the Early Universe. Nucl. Phys. B 1989, 316, 391–410. [Google Scholar] [CrossRef]
- Greene, B.; Kabat, D.; Marnerides, S. On three dimensions as the preferred dimensionality of space via the Brandenberger-Vafa mechanism. Phys. Rev. D 2013, 88, 043527. [Google Scholar] [CrossRef]
- Durrer, R.; Kunz, M.; Sakellariadou, M. Why do we live in 3 + 1 dimensions? Phys. Lett. B 2005, 614, 125–130. [Google Scholar] [CrossRef]
- Nielsen, H.B.; Rugh, S.E. Why do we live in (3 + 1)-dimensions? In Proceedings of the 26th International Ahrenshoop Symposium on the Theory of Elementary Particles, Buckow, Germany, 27–31 August 1993. [Google Scholar]
- Deser, S. Why does D=4, rather than more (or less)? An Orwellian explanation. Proc. R. Soc. Lond. A 2020, 476, 20190632. [Google Scholar] [CrossRef]
- Carlip, S. Dimension and Dimensional Reduction in Quantum Gravity. Class. Quant. Grav. 2017, 34, 193001. [Google Scholar] [CrossRef]
- Pardo, K.; Fishbach, M.; Holz, D.E.; Spergel, D.N. Limits on the number of spacetime dimensions from GW170817. JCAP 2018, 7, 48. [Google Scholar] [CrossRef]
- Scargill, J.H.C. Can Life Exist in 2 + 1 Dimensions? Phys. Rev. Res. 2020, 2, 013217. [Google Scholar] [CrossRef]
- Ponce de Leon, J.; Cruz, N. Hydrostatic equilibrium of a perfect fluid sphere with exterior higher dimensional Schwarzschild space-time. Gen. Rel. Grav. 2000, 32, 1207–1216. [Google Scholar] [CrossRef]
- Paul, B.C. Relativistic star solutions in higher dimensions. Int. J. Mod. Phys. D 2004, 13, 229–238. [Google Scholar] [CrossRef]
- Zarro, C.A.D. Buchdahl limit for d-dimensional spherical solutions with a cosmological constant. Gen. Rel. Grav. 2009, 41, 453–468. [Google Scholar] [CrossRef]
- Buchdahl, H.A. General Relativistic Fluid Spheres. Phys. Rev. 1959, 116, 1027. [Google Scholar] [CrossRef]
- Goswami, R.; Maharaj, S.D.; Nzioki, A.M. Buchdahl-Bondi limit in modified gravity: Packing extra effective mass in relativistic compact stars. Phys. Rev. D 2015, 92, 064002. [Google Scholar] [CrossRef]
- Feng, W.X.; Geng, C.Q.; Luo, L.W. The Buchdahl stability bound in Eddington-inspired Born-Infeld gravity. Chin. Phys. C 2019, 43, 083107. [Google Scholar] [CrossRef]
- Chakraborty, S.; Dadhich, N. Universality of the Buchdahl sphere. arXiv 2022, arXiv:2204.10734. [Google Scholar]
- Chandrasekhar, S. Dynamical Instability of Gaseous Masses Approaching the Schwarzschild Limit in General Relativity. Phys. Rev. Lett. 1964, 12, 114–116. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Dynamical Instability of Gaseous Masses Approaching the Schwarzschild Limit in General Relativity. Astrophys. J. 1964, 140, 417–433, Erratum in: Astrophys. J. 1964, 140, 1342. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Podurets, M.A. The Evolution of a System of Gravitationally Interacting Point Masses. Sov. Astron. 1966, 9, 742. [Google Scholar]
- Ipser, J.R. A binding-energy criterion for the dynamical stability of spherical stellar systems in general relativity. Astrophys. J. 1980, 238, 1101. [Google Scholar] [CrossRef]
- Günther, S.; Straub, C.; Rein, G. Collisionless equilibria in general relativity: Stable configurations beyond the first binding energy maximum. Astrophys. J. 2021, 918, 48. [Google Scholar] [CrossRef]
- Feng, W.X.; Yu, H.B.; Zhong, Y.M. Dynamical Instability of Collapsed Dark Matter Halos. JCAP 2022, 5, 36. [Google Scholar] [CrossRef]
- Lynden-Bell, D.; Wood, R. The gravo-thermal catastrophe in isothermal spheres and the onset of red-giant structure for stellar systems. Mon. Not. R. Astron. Soc. 1968, 138, 495. [Google Scholar] [CrossRef]
- Spitzer, L. Dynamical Evolution of Globular Clusters; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
- Boehmer, C.G.; Harko, T. Dynamical instability of fluid spheres in the presence of a cosmological constant. Phys. Rev. D 2005, 71, 084026. [Google Scholar] [CrossRef]
- Posada, C.; Hladík, J.; Stuchlík, Z. Dynamical instability of polytropic spheres in spacetimes with a cosmological constant. Phys. Rev. D 2020, 102, 024056. [Google Scholar] [CrossRef]
- Arbañil, J.D.V.; Carvalho, G.A.; Lobato, R.V.; Marinho, R.M.; Malheiro, M. Extra dimensions’ influence on the equilibrium and radial stability of strange quark stars. Phys. Rev. D 2019, 100, 024035. [Google Scholar] [CrossRef]
- Haemmerlé, L. General-relativistic instability in hylotropic supermassive stars. Astron. Astrophys. 2020, 644, A154. [Google Scholar] [CrossRef]
- Feng, W.X.; Yu, H.B.; Zhong, Y.M. Seeding Supermassive Black Holes with Self-Interacting Dark Matter: A Unified Scenario with Baryons. Astrophys. J. Lett. 2021, 914, L26. [Google Scholar] [CrossRef]
- Roupas, Z. Relativistic Gravothermal Instabilities. Class. Quant. Grav. 2015, 32, 135023. [Google Scholar] [CrossRef]
- Roupas, Z.; Chavanis, P.H. Relativistic Gravitational Phase Transitions and Instabilities of the Fermi Gas. Class. Quant. Grav. 2019, 36, 065001. [Google Scholar] [CrossRef]
- Roupas, Z. Relativistic Gravitational Collapse by Thermal Mass. Commun. Theor. Phys. 2021, 73, 015401. [Google Scholar] [CrossRef]
- Cruz, N.; Zanelli, J. Stellar equilibrium in (2 + 1)-dimensions. Class. Quant. Grav. 1995, 12, 975–982. [Google Scholar] [CrossRef]
- Banados, M.; Teitelboim, C.; Zanelli, J. The Black hole in three-dimensional space-time. Phys. Rev. Lett. 1992, 69, 1849–1851. [Google Scholar] [CrossRef]
- Ross, S.F.; Mann, R.B. Gravitationally collapsing dust in (2 + 1)-dimensions. Phys. Rev. D 1993, 47, 3319–3322. [Google Scholar] [CrossRef]
- Pretorius, F.; Choptuik, M.W. Gravitational collapse in (2 + 1)-dimensional AdS space-time. Phys. Rev. D 2000, 62, 124012. [Google Scholar] [CrossRef]
- Husain, V.; Olivier, M. Scalar field collapse in three-dimensional AdS space-time. Class. Quant. Grav. 2001, 18, L1–L10. [Google Scholar] [CrossRef]
- Jałmużna, J.; Gundlach, C.; Chmaj, T. Scalar field critical collapse in 2 + 1 dimensions. Phys. Rev. D 2015, 92, 124044. [Google Scholar] [CrossRef]
- Bourg, P.; Gundlach, C. Critical collapse of a spherically symmetric ultrarelativistic fluid in 2 + 1 dimensions. Phys. Rev. D 2021, 103, 124055. [Google Scholar] [CrossRef]
- Bourg, P.; Gundlach, C. Critical collapse of an axisymmetric ultrarelativistic fluid in 2 + 1 dimensions. Phys. Rev. D 2021, 104, 104017. [Google Scholar] [CrossRef]
- Giddings, S.; Abbott, J.; Kuchar, K. Einstein’s theory in a three-dimensional space-time. Gen. Rel. Grav. 1984, 16, 751–775. [Google Scholar] [CrossRef]
- Ogilvie, G.I. Astrophysical fluid dynamics. J. Plasma Phys. 2016, 82, 205820301. [Google Scholar] [CrossRef]
- Tooper, R.F. Adiabatic Fluid Spheres in General Relativity. Astrophys. J. 1965, 142, 1541. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; John Wiley and Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Axenides, M.; Georgiou, G.; Roupas, Z. Gravothermal Catastrophe with a Cosmological Constant. Phys. Rev. D 2012, 86, 104005. [Google Scholar] [CrossRef]
- Feng, W.X. Gravothermal phase transition, black holes and space dimensionality. Phys. Rev. D 2022, 106, L041501. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum: Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Prat, J.; Hogan, C.; Chang, C.; Frieman, J. Vacuum energy density measured from cosmological data. JCAP 2022, 6, 15. [Google Scholar] [CrossRef]
- Mo, H.; van den Bosch, F.; White, S. Galaxy Formation and Evolution; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Kolb, E.W.; Turner, M.S. The Early Universe; Addison-Wesley Publishing: Boston, MA, USA, 1990; Volume 69. [Google Scholar]
- Deser, S.; Jackiw, R.; ’t Hooft, G. Three-Dimensional Einstein Gravity: Dynamics of Flat Space. Ann. Phys. 1984, 152, 220. [Google Scholar] [CrossRef]
- Deser, S.; Jackiw, R. Three-Dimensional Cosmological Gravity: Dynamics of Constant Curvature. Ann. Phys. 1984, 153, 405–416. [Google Scholar] [CrossRef]
- Banados, M.; Henneaux, M.; Teitelboim, C.; Zanelli, J. Geometry of the (2 + 1) black hole. Phys. Rev. D 1993, 48, 1506–1525, Erratum: Phys. Rev. D 2013, 88, 069902. [Google Scholar] [CrossRef]
- Brown, J.D.; Henneaux, M. Central Charges in the Canonical Realization of Asymptotic Symmetries: An Example from Three-Dimensional Gravity. Commun. Math. Phys. 1986, 104, 207–226. [Google Scholar] [CrossRef]
- Brown, J.D.; Creighton, J.; Mann, R.B. Temperature, energy and heat capacity of asymptotically anti-de Sitter black holes. Phys. Rev. D 1994, 50, 6394–6403. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse: The role of general relativity. Riv. Nuovo Cim. 1969, 1, 252–276. [Google Scholar] [CrossRef]
- Borchers, H.J.; Buchholz, D. The Energy Momentum Spectrum in Local Field Theories With Broken Lorentz Symmetry. Commun. Math. Phys. 1985, 97, 169. [Google Scholar] [CrossRef]
- Woodard, R.P. Ostrogradsky’s theorem on Hamiltonian instability. Scholarpedia 2015, 10, 32243. [Google Scholar] [CrossRef]
- Pathria, R.K. The Universe as a Black Hole. Nature 1972, 240, 298–299. [Google Scholar] [CrossRef]
- Good, I.J. Chinese universes. Phys. Today 1972, 25, 15. [Google Scholar] [CrossRef]
- Easson, D.A.; Brandenberger, R.H. Universe generation from black hole interiors. JHEP 2001, 6, 24. [Google Scholar] [CrossRef]
- Gaztanaga, E.; Fosalba, P. A Peek Outside Our Universe. Symmetry 2022, 14, 285. [Google Scholar] [CrossRef]
- Gaztanaga, E. How the Big Bang Ends Up Inside a Black Hole. Universe 2022, 8, 257. [Google Scholar] [CrossRef]
- Roupas, Z. Detectable universes inside regular black holes. Eur. Phys. J. C 2022, 82, 255. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse and space-time singularities. Phys. Rev. Lett. 1965, 14, 57–59. [Google Scholar] [CrossRef]
- Hawking, S. Occurrence of singularities in open universes. Phys. Rev. Lett. 1965, 15, 689–690. [Google Scholar] [CrossRef]
- Geroch, R.P. Singularities in closed universes. Phys. Rev. Lett. 1966, 17, 445–447. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Hawking, S. The Cosmic black body radiation and the existence of singularities in our universe. Astrophys. J. 1968, 152, 25. [Google Scholar] [CrossRef]
- Garfinkle, D. Numerical simulations of generic singularities. Phys. Rev. Lett. 2004, 93, 161101. [Google Scholar] [CrossRef]
- Frolov, V.P.; Markov, M.A.; Mukhanov, V.F. Black Holes as Possible Sources of Closed and Semiclosed Worlds. Phys. Rev. D 1990, 41, 383. [Google Scholar] [CrossRef]
- Frolov, V.P.; Markov, M.A.; Mukhanov, V.F. Through a black hole into a New Universe? Phys. Lett. B 1989, 216, 272–276. [Google Scholar] [CrossRef]
- Popławski, N.J. Cosmology with torsion: An alternative to cosmic inflation. Phys. Lett. B 2010, 694, 181–185, Erratum in Phys. Lett. B 2011, 701, 672–672. [Google Scholar] [CrossRef]
- Dubovsky, S.; Flauger, R.; Gorbenko, V. Solving the Simplest Theory of Quantum Gravity. JHEP 2012, 9, 133. [Google Scholar] [CrossRef]
- Biswas, T.; Mazumdar, A.; Siegel, W. Bouncing universes in string-inspired gravity. JCAP 2006, 3, 9. [Google Scholar] [CrossRef]
- Biswas, T.; Brandenberger, R.; Mazumdar, A.; Siegel, W. Non-perturbative Gravity, Hagedorn Bounce & CMB. JCAP 2007, 12, 11. [Google Scholar] [CrossRef]
- Dvali, G.R.; Gabadadze, G.; Porrati, M. 4-D gravity on a brane in 5-D Minkowski space. Phys. Lett. B 2000, 485, 208–214. [Google Scholar] [CrossRef]
- Pourhasan, R.; Afshordi, N.; Mann, R.B. Out of the White Hole: A Holographic Origin for the Big Bang. JCAP 2014, 4, 5. [Google Scholar] [CrossRef]
- Brandenberger, R.; Heisenberg, L.; Robnik, J. Non-singular black holes with a zero-shear S-brane. JHEP 2021, 5, 90. [Google Scholar] [CrossRef]
- Linde, A.D.; Zelnikov, M.I. Inflationary Universe With Fluctuating Dimension. Phys. Lett. B 1988, 215, 59–63. [Google Scholar] [CrossRef]
- Smolin, L. The Life of the Cosmos; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Susskind, L. The Anthropic landscape of string theory. arXiv 2003, arXiv:hep-th/0302219. [Google Scholar]
- Linde, A.D. Inflation, quantum cosmology and the anthropic principle. arXiv 2002, arXiv:hep-th/0211048. [Google Scholar]
- Bousso, R.; Polchinski, J. The string theory landscape. Sci. Am. 2004, 291, 78–87. [Google Scholar] [CrossRef]
- Ball, P. Mysterious cosmos. Nature 2004. [Google Scholar] [CrossRef]
- Smolin, L. Scientific alternatives to the anthropic principle. arXiv 2004, arXiv:hep-th/0407213. [Google Scholar]
- Weinberg, S. Anthropic Bound on the Cosmological Constant. Phys. Rev. Lett. 1987, 59, 2607. [Google Scholar] [CrossRef]
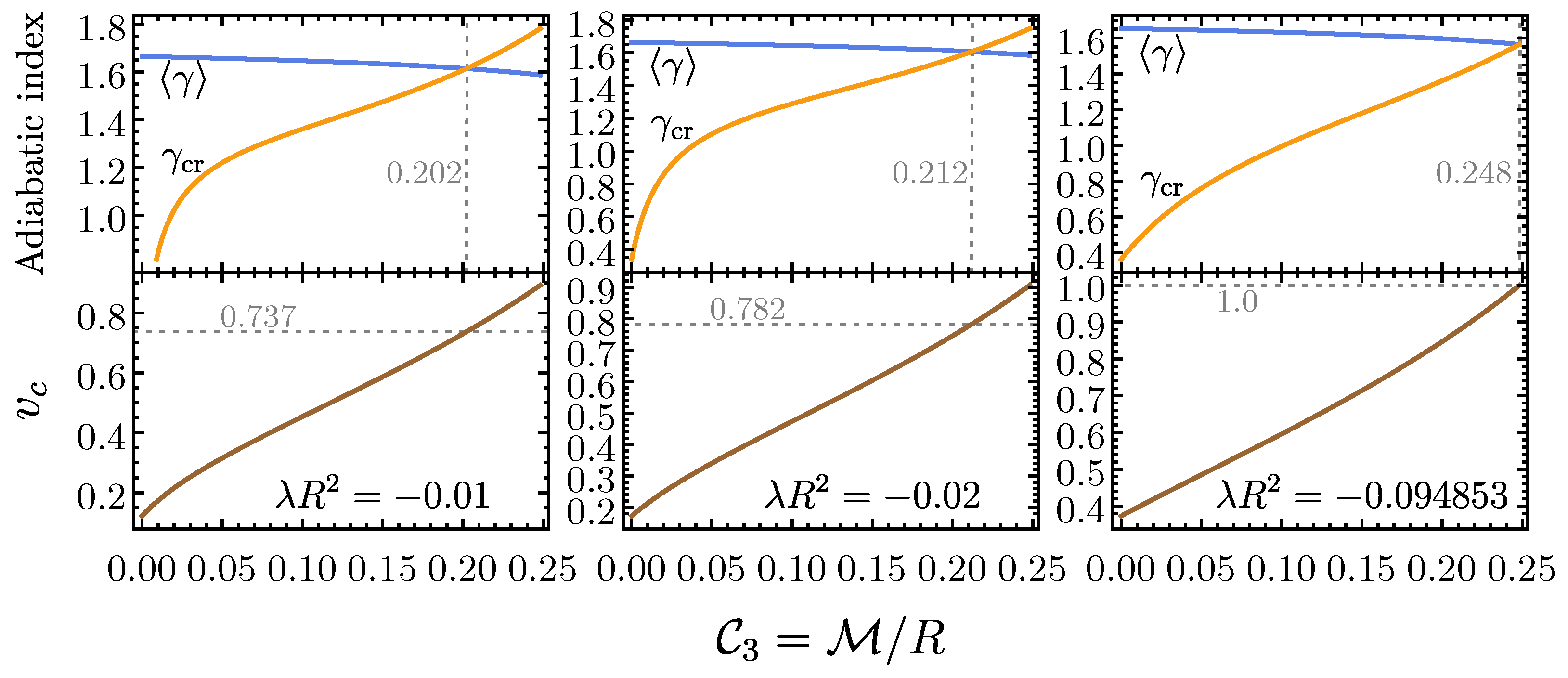

| 0 | |||
| N | |||
|---|---|---|---|
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, W.-X. On the Dynamical Instability of Monatomic Fluid Spheres in (N + 1)-Dimensional Spacetime. Astronomy 2023, 2, 22-46. https://doi.org/10.3390/astronomy2010004
Feng W-X. On the Dynamical Instability of Monatomic Fluid Spheres in (N + 1)-Dimensional Spacetime. Astronomy. 2023; 2(1):22-46. https://doi.org/10.3390/astronomy2010004
Chicago/Turabian StyleFeng, Wei-Xiang. 2023. "On the Dynamical Instability of Monatomic Fluid Spheres in (N + 1)-Dimensional Spacetime" Astronomy 2, no. 1: 22-46. https://doi.org/10.3390/astronomy2010004
APA StyleFeng, W.-X. (2023). On the Dynamical Instability of Monatomic Fluid Spheres in (N + 1)-Dimensional Spacetime. Astronomy, 2(1), 22-46. https://doi.org/10.3390/astronomy2010004






