Structure Functions and Tau Neutrino Cross Section at DUNE Far Detector ^†

Abstract

DUNE’s Argon time-projecting chambers (TPC) detectors will allow us to conduct precise studies about phenomena that have, until now, seemed too challenging to measure, like tau neutrino $\left({\nu }_{\tau }\right)$ interactions. Cross section measurements are needed to understand how accurate our neutrino-nucleus interaction models are and how accurately we can use them to reconstruct neutrino energy. Quasi-elastic scattering (QE), $\Delta$ resonance production (RES), and deep inelastic scattering (DIS) processes are known to provide dominant contributions in the medium and high neutrino energy to the total cross-section of ${\nu }_{\tau }$(N) and ${\overline{\nu }}_{\tau }$(N). These cross-sections have large systematic uncertainties compared to the ones measured for ${\nu }_{\mu }$ and ${\nu }_e$ and their antiparticles. Studies point out that the reason for these differences is due to the model dependence of the ${\nu }_{\tau }$(N) cross-sections in treating the nuclear medium effects described by the nucleon structure functions, $F_{1N,\cdots ,3N}(x,Q^2)$ for ${\nu }_{\mu }$ and ${\nu }_e$. These proceedings show the semi-theoretical and experimental approach to the estimation of the ${\nu }_{\tau }$(N) and ${\overline{\nu }}_{\tau }$(N) cross-sections in DUNE for the DIS region. We will check the contributions of the additional nucleon structure functions $F_{4N}(x,Q^2)$ and $F_{5N}(x,Q^2)$ and their dependence on Q² and Bjorken-x scale.

1. Introduction

The current generation of neutrino experiments have provided a nearly complete description of the three flavor paradigm, but almost all knowledge of the tau neutrino sector is taken from lepton universality for cross sections and the unitarity of the Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix for oscillations (an indirect way); it is critical that these assumptions are tested in a direct way and DUNE will be able to provide the data to analyze and disentangle the last piece of the puzzle, the physics of the tau neutrino.

The DUNE Far Detector (FD), currently under construction, will consist of four 10 kt fiducial mass LArTPC modules located at a baseline of 1285 km from the LBNF neutrino source at the 4850 km level of the Sanford Underground Research Facility in Lead, South Dakota. The long baseline, large detector mass, and intense beam will allow DUNE to measure all three flavor oscillation parameters in a single experiment. While DUNE is optimized to measure ${\nu }_e$ appearance in a ${\nu }_{\mu }$ beam, the broadband beam and long baseline lead to significant ${\nu }_{\tau }$ appearance above the kinematic threshold to produce a $\tau$-lepton, Ref. [1]. DUNE is the only upcoming neutrino experiment expected to be able to collect a larger sample of oscillated ${\nu }_{\tau }$ events from a beam than all previous experiments.

A truthlevel study of ${\nu }_{\tau }$-CC interactions in Ref. [2], where the $\tau$-lepton decayed hadronically, suggests that relatively simple kinematic requirements of events containing at least one ${\pi }^{\pm }$ could confirm ${\nu }_{\tau }$-CC appearance with a significance of $3.1\sigma$ in one year of running in the CP-optimized beam mode or $7.9\sigma$ in one year of running in the tau-optimized beam mode, assuming $1.2$ MW beam power and 40 kt fiducial mass, see Figure 1. This selection corresponds to ∼60% signal efficiency and ∼80% NC background rejection efficiency. The expected counts per year for the CP-optimized neutrino mode are ≈30 ${\overline{\nu }}_{\tau }$ and ≈130 ${\nu }_{\tau }$ and for the tau optimized neutrino mode they are expected to be ≈800 ${\nu }_{\tau }$.

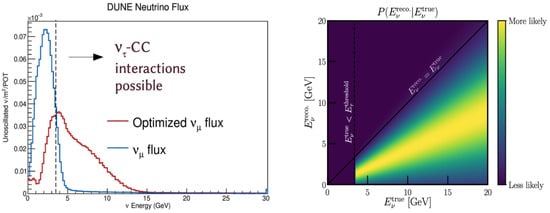
Figure 1. (Left): in blue, CP-optimized beam, here the design requires a 3 horns configuration; in red, tau-optimized beam, the design requires a 2 horns configuration. This is a future upgrade, and it is under investigation. (Right): Migration matrix for hadronically decaying $\tau$ leptons produced via ${\nu }_{\tau }$-CC interactions. The assumed bias is $45\%$ and the resolution is $25\%$. No migration exists below $E_{\nu }^{true}\approx 3.4$ GeV, as the scattering process is kinematically forbidden, Ref. [3].

Quasi-elastic scattering (QE), $\Delta$ resonance production (RES), and deep inelastic scattering (DIS) processes are known to provide dominant contributions at medium and high neutrino energy to the total cross section of ${\nu }_{\tau }$(N) and ${\overline{\nu }}_{\tau }$(N) cross sections. These cross sections have large systematic uncertainties compared to the ones for ${\nu }_{\mu }$ and ${\nu }_e$. Studies point out that the reason for these differences is the model dependence of the ${\nu }_{\tau }$(N) cross sections in treating the nuclear medium effects described by the nucleon structure functions, $F_{1N,...,3N}(x,Q^2)$ for ${\nu }_{\mu }$ and ${\nu }_e$. These nucleon structure functions are used to calculate DIS cross section by including kinematic corrections, but due to the addition of the $\tau$-lepton mass another two additional nucleon structure functions become non-negligible, $F_{4N}(x,Q^2)$ and $F_{5N}(x,Q^2)$.

2. DIS ${\mathbf{\nu }}_{\mathbf{\tau }}$-CC cross Section

Neutrino interactions are a major contributor to systematic uncertainties in oscillation measurements (T2K, NOvA). The measurement of the $E_{\nu }$ and $\nu$-nucleus interactions relies on reconstruction techniques based either on kinematics (T2K, HK) or calorimetric methods (DUNE, NOvA, SBN); both techniques require reliable predictions from the interaction models. Now, it turns out that, when it comes to oscillations, the extraction of the oscillation parameter is biased by the interaction models as well because it is $E_{\nu }$ dependent, see Equation (1). On the other hand, the number of events detected is proportional to such probability, flux, and cross section, which at the same time are $E_{\nu }$-dependent, see Equation (2). Notice that nuclear and hadronic effects are $E_{\nu }$-dependent as well; therefore, obtaining reliable predictions from the interaction models is necessary, and how do we attain access to study those—through cross section measurements.

$$P_{{\nu }_{\alpha }\to {\nu }_{\beta }}=si{n}^{2}2{\theta }_{i}si{n}^2\left({\displaystyle \frac{\Delta m_i^{2}L}{4E_{\nu }}}\right)$$

(1)

$$N_{FD}^{\alpha \to \beta }(E_{\nu },rec)\propto \sum _i{\varphi }_{\alpha }\left(E_{\nu }\right)\times {\sigma }_{\beta }^i\left(E_{\nu }\right)\times P_{{\nu }_{\alpha }\to {\nu }_{\beta }}\times {ϵ}_{\beta }(E_{\nu },E_{\nu ,rec}).$$

(2)

2.1. Tau Neutrino Interactions

Due to the large mass of the ${\tau }^{\pm }$ relative to the $e^{\pm }$ and ${\mu }^{\pm }$, the threshold for this process to occur is $3.5$ GeV (see Figure 1).

Surveys of various decay modes of the tau lepton are dominant in the study of tau neutrino physics, see those branching ratios in Table 1. The leptonic decay channels of the tau are more challenging than their hadronic peers; this happens because the background from CC interactions (${\nu }_e$ and ${\nu }_{\mu }$) is larger than the neutral current (NC) background, and also because the tau decays to charged leptons at approximately half the rate it decays to hadrons.

Table 1. Dominant decay modes of ${\tau }^{-}$. Kaonic decays and others go into the “other” category, Ref [2].

Decay Mode	Branching Ratio (%)
Leptonic	35.2
$e^{-}{\overline{\nu }}_e$${\nu }_{\tau }$	17.3
${\mu }^{-}{\overline{\nu }}_{\mu }$${\nu }_{\tau }$	17.4
Hadronic	64.8
${\pi }^{-}{\pi }^0$${\nu }_{\tau }$	25.5
${\pi }^{-}$${\nu }_{\tau }$	10.8
${\pi }^{-}{\pi }^0{\pi }^0$${\nu }_{\tau }$	9.3
${\pi }^{-}{\pi }^{-}{\pi }^{+}$${\nu }_{\tau }$	9.0
${\pi }^{-}{\pi }^{-}{\pi }^{+}{\pi }^0$${\nu }_{\tau }$	4.5
other	5.7

2.2. Structure Functions

A structure function (SF) characterizes the internal structure of the nucleon; the contributions of the SF to the cross section are functions of the charged lepton mass. In 1975, Albright and Jarlskog [4] pointed out that there are two additional structure functions—$F_4$ and $F_5$—that contribute to the ${\nu }_{\tau }$-CC cross section, a key input to theoretical and experimental analyses of tau neutrino. $F_4$ and $F_5$ are ignored in muon neutrino interactions because of a suppression factor depending on $m_l^2/\left(M_N{E}_{\nu }\right)$, where $M_N$ and $m_l^2$ are the nucleon and lepton mass, respectively. At leading order, in the limit of massless quarks and target, $F_4$ and $F_5$ are:

$$F_4=0and2x{F}_5=F_2,$$

(3)

where x is the Bjorken-x variable. These generalizations of the Callan–Gross relation $F_2=2x{F}_1$ are called the Albright–Jarlskog (AJ) relations.

Neglecting neither the target nucleon mass $M_N$ nor the final state lepton mass $m_{\tau }$, the ${\nu }_{\tau }$ (anti-)neutrino CC differential cross section is represented by a standard set of five structure functions [5]:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d^2{\sigma }_A}{dxdy}}=& {\displaystyle \frac{G_F^2{M}_N{E}_{\nu }}{\pi {\left(1+{\displaystyle \frac{Q^2}{M_W^2}}\right)}^2}}\{\left[y^{2}x+{\displaystyle \frac{m_l^{2}y}{2E_{\nu }{M}_N}}\right]F_{1A}(x,Q^2)\\ & +\left[\left(1-{\displaystyle \frac{m_l^2}{4E_{\nu }^2}}\right)-\left(1+{\displaystyle \frac{M_{N}x}{2E_{\nu }}}\right)y\right]F_{2A}(x,Q^2)\\ & \pm \left[xy\left(1-{\displaystyle \frac{y}{2}}\right)\right]F_{3A}(x,Q^2)+{\displaystyle \frac{m_l^2(m_l^2+Q^2)}{4E_{\nu }^2{M}_N^{2}x}}{F}_{4A}(x,Q^2)\\ & -{\displaystyle \frac{m_l^2}{E_{\nu }{M}_N}}{F}_{5A}(x,Q^2)\},\end{array}$$

(4)

where $x,y,Q^2$ are the standard DIS kinematic variables related through $Q^2=2M_N{E}_{\nu }xy$.

Notice that, in Equation (4), in the limit $m_l^2\to 0$, only $F_1,F_2$ and $F_3$ contribute. Once again, given the higher mass value of the $tau$ lepton, $F_4$ and $F_5$ pointed out by (AJ) relations occur only in heavy lepton $\left(\tau \right)$ scattering and are negligible for ${\nu }_{\mu }$ and ${\nu }_e$, but become important for ${\nu }_{\tau }$ cross section. Notice that $F_4=0$ also holds when the nucleon target is replaced by a lepton target.

Figure 2 (both panels) shows that, in evaluations of the total CC cross section, the naive AJ relations are good approximations to the NLO results. This is true at low energies, where the ${\nu }_{\tau }$ cross section does not probe small-x, and at high energies where $F_4,F_5$ are suppressed, anyway.

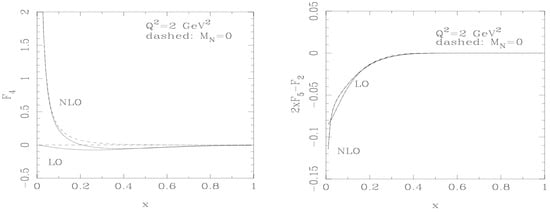
Figure 2. (Left): $F_4$, the LO curve with $M_N=0$ shows that $F_4=0$, at NLO, $F_4\approx 1\%$ of $F_5$; therefore, the AJ relations are good approximations to the NLO result. (Right): $F_5$, at LO, AJ relation is violated, $2x{F}_5-F_2\ne 0$; this is due to the charm quark mass corrections; NLO corrections have an effect primarily at small-x [6].

3. Preliminary Results and Outlook

Following Equation (4), we use the tau-optimized beam flux simulation with the DUNE far detector geometry and Genie 3.0.6 [7]. The cross section for the tau (anti) neutrino for the standard model (SM) prediction and the $F_4=0,F_5=0$ hypothesis is shown in Figure 3, the SM prediction being smaller than the $F_4=0,F_5=0$ hypothesis. From Figure 2, the effect from $F_4$ can be discarded, but what about $F_5$?

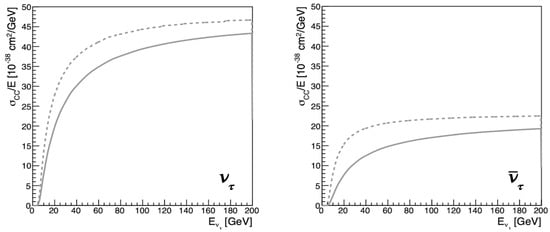
Figure 3. (Left), ${\nu }_{\tau }$ and (right), ${\nu }_{\tau }$-CC cross sections. Notice the difference between the cross sections in the $F_4=0,F_5=0$ hypothesis (dashed line) and the standard model prediction (solid line).

$F_5(x,Q^2)$ Nature

The effect of $F_5$ in the $\left[x,Q^2\right]$ phase space as a function of the number of events can be appreciated in Figure 4. On the left side, we have the SM prediction, and on the right, the case when $F_4=F_5=0$, notice the changes between $x=0.2-0.5$, we can access a higher number of statistics and therefore, to get the chance to study nuclear interactions deeper. Based on what Figure 4 shows, we go to check over the $\left[x,Q^2\right]$ phase space as a function of $F_5$ itself, see Figure 5 (left). At lower x, $F_5$ values are high; notice that below $Q^2=1$, the non-perturbative regime takes place, while above $Q^2=1$ corresponds to the perturbative regime. Figure 5 (right) shows the ratio between having $F_5=0$ or $F_5\ne 0$, the ratio is greater than 1; which is expected since $F_5$ is a subtracted component of the total cross section, see Equation 4; also, it means that there is a chance to disentangle an overall normalization change from a scaling of $F_5$.

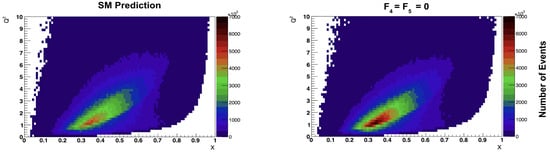
Figure 4. (Left): $F_5(x,Q^2)$ phase space for the SM prediction. (Right): $F_5(x,Q^2)$ phase space for the case when $F_4=F_5=0$, which shows a greater region for nuclear interactions between $x=0.2-0.5$.

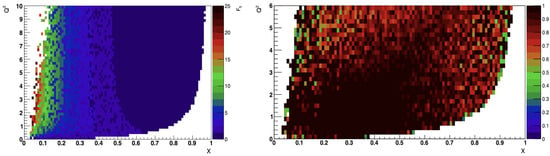
Figure 5. (Left): $F_5(x,Q^2)$ phase space, $F_5$ is sensitive in values for x and $Q^2$ that wrap different interactions models. (Right): the ratio between having $F_5=0$ or $F_5\ne 0$, this ratio is greater than one, meaning that there is a chance to disentangle an overall normalization change from a scaling of $F_5$.

4. Discussion

There are new features that appear in the case of the ${\nu }_{\tau }$A interactions as compared to ${\nu }_e$ and ${\nu }_{\mu }$ interactions that contribute to modifying the cross sections, those are:

• Kinematic changes in $Q^2$ and $E_l$ due to the presence of $m_{\tau }$.
• The contributions due to the additional nucleon structure functions $F_4(x,Q^2)$ and $F_5(x,Q^2)$ in the presence of $m_{\tau }\ne 0$.
• As a function of $Q^2$, there is an enhancement that does not come just from a normalization, but due to the changes in the shape of the presence of $m_{\tau }$.

Tau neutrinos play a central role in testing the lepton flavor universality violation of hints uncovered in flavor physics experiments, and DUNE will provide a unique opportunity to study the connections among neutrino flavors.

In order to obtain a reliable kinematic reconstruction, a machine learning approach is being reviewed, which is currently a technique called panoptic segmentation [8]. Panoptic segmentation combines semantic segmentation, which is the process of assigning a class label to each pixel, and Instance segmentation, which is the task of detecting objects in the image.