Transverse Enhancement, Longitudinal Quenching and Coulomb Sum Rule in e-¹²C and e-¹⁶O Quasielastic Scattering ^†

Abstract

We present a short summary of a phenomenological analysis of all available electron scattering data on ${}^{12}\mathrm{C}$ (about 6600 differential cross-section measurements) and on ${}^{16}\mathrm{O}$ (about 250 measurements) within the framework of the quasielastic (QE) superscaling model (including Pauli blocking). All QE and inelastic cross-section measurements are included down to the lowest momentum transfer 3-vector $\mathbf{q}$ (including photo-production data). We find that there is enhancement of the transverse QE response function ($R_T^{QE}$) and quenching of the QE longitudinal response function ($R_L^{QE}$) at low $\mathbf{q}$ (in addition to Pauli blocking). We extract parameterizations of a $multiplicative$ low $\mathbf{q}$ “longitudinal quenching factor” and an $additive$ “transverse enhancement” contribution. The fit can be used as a proxy to validate the modeling of cross sections in Monte Carlo event generators for electron and neutrino (${\nu }_{e,\mu }$) scattering. Additionally, we find that the excitation of nuclear states contributes significantly (up to 30%) to the Coulomb sum rule $SL\left(\mathbf{q}\right)$. We extract the most accurate determination of $SL\left(\mathbf{q}\right)$ to date and find it to be in disagreement with random phase approximation (RPA) based calculations but in reasonable agreement with recent theoretical calculations, such as “first-principle Green’s function Monte Carlo”.

1. Introduction

We present a short summary of our recent publications which report on a fit [1,2] to all available electron scattering data on ${}^{12}\mathrm{C}$ (about 6600 differential cross section measurements) and ${}^{16}\mathrm{O}$ (about 250 measurements) within the framework of the quasielastic (QE) superscaling model (including Pauli blocking). The cross-section measurements include the available data on QE (down to the lowest momentum transfer $\mathbf{q}$ ($\equiv |\overrightarrow{q}|$), inelastic production, and photoproduction. As the fit provides an accurate description of the data, the fit includes inelastic structure functions and empirical parameters to model both an enhancement of the transverse (T) QE response function $R_T^{QE}$ and quenching of the longitudinal (L) QE response function [3,4] $R_L^{QE}$ at low $\mathbf{q}$. The fit can be used as a proxy to validate the modeling of cross sections in Monte Carlo event generators for electron and neutrino (${\nu }_{e,\mu }$) scattering. The “transverse enhancement” TE($\mathbf{q},\nu$)) of $R_T^{QE}$ and the “quenching factor” $F_{quench}^L\left(\mathbf{q}\right)$ of $R_L^{QE}$ are of great interest to ${\nu }_{e,\mu }$ scattering experiments. The electron-scattering differential cross section can be written as

$$\frac{d^2\sigma }{d\nu d\mathsf{\Omega }}={\sigma }_M[A{R}_L(\mathbf{q},\nu )+B{R}_T(\mathbf{q},\nu )],{\sigma }_M={\alpha }^2{cos}^2(\theta /2)/\left[4E_0^2{sin}^4(\theta /2)\right].$$

(1)

Here, $E_0$ is the incident electron energy, $E^{\prime }$ and $\theta$ are the energy and angle of the final state electron, $\nu =E_0-E^{\prime }$, $A={(Q^2/{\mathbf{q}}^{\mathbf{2}})}^{\mathbf{2}}$, $B={tan}^2(\theta /2)+Q^2/2{\mathbf{q}}^{\mathbf{2}}$, $Q^2$ is the square of the 4-momentum transfer (defined to be positive), and ${\mathbf{q}}^{\mathbf{2}}$ = $Q^2+{\nu }^2$. In the analysis, we also use the invariant hadronic mass $W^2=M_p^2+2M_p\nu -Q^2$.

2. Analysis and Results

The inelastic Coulomb sum rule is the integral of $R_L(\mathbf{q},\nu )d\nu$, excluding the elastic peak and pion production processes. It has contributions from QE scattering and from the electro-excitations of nuclear states. Dividing by the square of the proton electric form factor $G_{Ep}$, we obtain the normalized inelastic Coulomb sum rule $SL\left(\mathbf{q}\right)$. Careful consideration of the nuclear excitations is critical for an accurate extraction of the normalized Coulomb sum rule $SL\left(\mathbf{q}\right)$ at low $\mathbf{q}$, as these states can contribute up to 30%. At high $\mathbf{q}$, it is expected that $S_L\to 1$ because both nuclear excitation form factors and Pauli suppression are small. At small $\mathbf{q}$, it is expected that $S_L\to 0$ because by gauge invariance, the structure function for all inelastic processes must be zero [5] at $\mathbf{q}$ = 0.

In addition to performing a universal fit to all ${}^{12}\mathrm{C}$ and ${}^{16}\mathrm{O}$ electron-scattering data, we also parameterize the measurements of the L and T form factors for the electro-excitation of all nuclear states with excitation energies ($E_x$) less than 50.0 MeV. The contributions of nuclear excitation to $SL\left(\mathbf{q}\right)$ are calculated using the parametrizations of the form factors. The bottom two panels of Figure 1 show the contributions of nuclear excitations to $SL\left(\mathbf{q}\right)$ for ${}^{12}\mathrm{C}$ and ${}^{16}\mathrm{O}$. The contribution of all excitations is largest (≈0.29) at $\mathbf{q}$ = 0.22 GeV. Although the contributions of different $E_x$ regions to $SL\left(\mathbf{q}\right)$ is different for ${}^{12}\mathrm{C}$ and ${}^{16}\mathrm{O}$, the total contribution turns out to be similar for the two nuclei. The top two panels of Figure 1 show comparisons of our fit to some of the $R_L$ measurements by Yamaguchi et al. [6]. The universal fit to the ${}^{12}\mathrm{C}$ data is an update of the 2012 fit by Bosted and Mamyan [7,8] We include all available data down to the lowest q. The QE contribution is modeled by the superscaling approach with Pauli blocking calculated using the Rosenfelder method. The superscaling function extracted from the fit is similar to the superscaling functions of Amaro et al., 2005 [9] and Amaro et al., 2020 [10] and yields similar Pauli suppression.

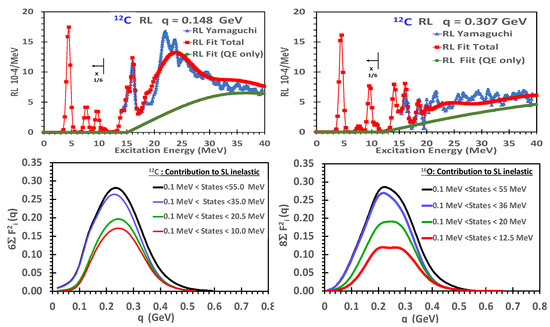
Figure 1. Top two panels: comparison of $R_L(\mathbf{q},\nu )$ extracted from our ${}^{12}\mathrm{C}$ fit to a sample of experimental data [6]. For excitation energies <12 MeV, the values are multiplied by 1/6. Bottom two panels: the contributions of longitudinal nuclear excitations (between 2 and 55 MeV) to the Coulomb sum rule for ${}^{12}\mathrm{C}$ and ${}^{16}\mathrm{O}$.

In modeling the QE response, we use the same scaling function for both $R_L^{QE}(\mathbf{q},\nu )$ and $R_T^{QE}(\mathbf{q},\nu )$ and fit for empirical corrections to the response functions. For $R_T^{QE}$, we extract an additive “transverse enhancement” TE($\mathbf{q},\nu$) contribution (which includes both single nucleon and two nucleon final states, and meson exchange currents (MECs)). TE($\mathbf{q},\nu$) increases $R_T^{QE}$ with the largest fractional contribution around $Q^2$ = 0.3 GeV${}^2$. For $R_L^{QE}$ we extract a multiplicative $\mathbf{q}$-dependent “longitudinal quenching factor”, $F_{quench}\left(\mathbf{q}\right)$, which decreases $R_L^{QE}$ at low $\mathbf{q}$.

Since $\frac{d^2\sigma }{d\mathsf{\Omega }d\nu }$ measurements span a range of $\theta$ and $\mathbf{q}$, parametrizations of both TE($\mathbf{q},\nu$) and $F_{quench}^L\left(\mathbf{q}\right)$ can be extracted. The analysis includes all data for a range of nuclei. However, in this paper, we only include electron scattering data on ${}^1\mathrm{H}$, ${}^2\mathrm{H}$, ${}^{12}\mathrm{C}$ and ${}^{16}\mathrm{O}$. Briefly, the fit includes the following:

• Coulomb corrections using the effective momentum approximation (EMA) in modeling scattering from nuclear targets.
• Updated nuclear elastic+excitation form factors.
• Superscaling $FN\left({\psi }^{\prime }\right)$ parameters are re-extracted, including the broadening parameter $K_F$.
• Parameterizations of the free nucleon form factors are re-derived from all ${}^1\mathrm{H}$ and ${}^2\mathrm{H}$ data.
• Rosenfelder Pauli suppression, which reduces and changes the QE distribution at low $\mathbf{q}$ and $\nu$.
• Updates of fits to inelastic electron scattering data (in the nucleon resonance region and inelastic continuum) for ${}^1\mathrm{H}$ and ${}^2\mathrm{H}$.
• A $\mathbf{q}$-dependent $E_{\mathrm{shift}}^{QE}\left(\mathbf{q}\right)$ parameter accounting for the optical potential of final state nucleons.
• Photo-production data in the nucleon resonance region and inelastic continuum.
• Gaussian Fermi smeared nucleon resonance and inelastic continuum. The $K_F$ (Fermi smearing) parameters for pion production and QE can be different.
• Parametrizations of the medium modifications of both the L and T structure functions responsible for the EMC effect (nuclear dependence of inelastic structure functions). These are applied to the free nucleon cross sections prior to the application of the Fermi smearing.
• Parametizations of TE($\mathbf{q},\nu$) and $F_{quench}^L\left(\mathbf{q}\right)$ as described below.
• QE data at all values of $Q^2$ down to $Q^2$ = 0.01 GeV${}^2$ (which were not included in the Bosted–Mamyan fit).

The average (over $\nu$) Pauli suppression factor for $x<2.5$ ( $x=\mathbf{q}/K_F$, $K_F$ = 0.228 GeV) is described by

$$⟨F_{Pauli}^{This-analysis}\left(\mathbf{q}\right)⟩=\sum _{j=0}^{j=3}{k}_j{\left(x\right)}^j.$$

(2)

For the superscaling function used in this analysis, $k_o$ = 0.3054, $k_1$ = 0.7647, $k_2$ = −0.2768 and $k_3$ = 0.0328. The Pauli suppression factor for $x>2.5$ is 1.0.

Comparisons of the fit to electron scattering $\frac{d^2\sigma }{d\mathsf{\Omega }d\nu }$ measurements at different values of $\theta$ for $\mathbf{q}$ values close to 0.30, 0.38 and 0.57 GeV (corresponding to extractions of $R_L$ and $R_T$ by Jourdan [3,4]) are shown in Figure 2. Shown are the total $\frac{d^2\sigma }{d\mathsf{\Omega }d\nu }$ cross section (solid purple line), the total minus the contribution of nuclear excitations (solid blue), the QE cross section without TE (dashed blue), the TE contribution (solid red), and inelastic pion production (dot-dashed black). The fit is in good agreement with all electron scattering data for both small and large $\theta$.

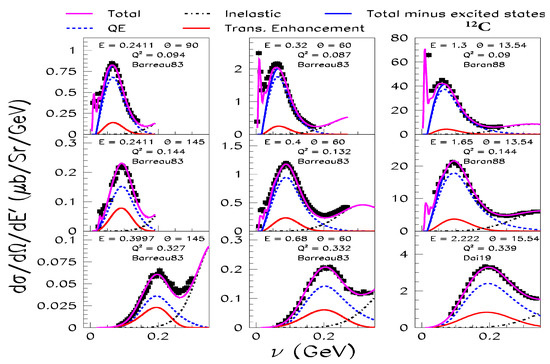
Figure 2. Comparison of the fit to electron scattering $\frac{d^2\sigma }{d\mathsf{\Omega }d\nu }$ measurements at $\mathbf{q}$ values close to 0.30, 0.38 and 0.57 GeV (and different scattering angles). Shown are total $\frac{d^2\sigma }{d\mathsf{\Omega }d\nu }$ (solid purple line), total minus the contribution of the nuclear excitations (solid blue), the QE cross section without TE (dashed blue), the TE($\mathbf{q},\nu$) contribution (solid red) and inelastic pion production (dot-dashed black line).

The extracted QE “longitudinal quenching factor” $F_{quench}^L\left(\mathbf{q}\right)$ is unity for x > 3.75 and zero for x < 0.35. For $0.35<x<3.75$, it is parameterized by

$$\begin{array}{cc}\hfill & F_{quench}^L\left(\mathbf{q}\right)=\frac{{(x-0.2)}^2}{{(x-0.18)}^2}\left[1.0+A_1{(3.75-x)}^{1.5}+A_2{(3.75-x)}^{2.5}+A_3{(3.75-x)}^{3.5}\right],\end{array}$$

(3)

with $A_1$ = −0.13152 $A_2$ = 0.11693, and $A_3$ = −0.03675. The top-left panel of Figure 3 shows the extracted $F_{quench}^L\left(\mathbf{q}\right)$. (black-dotted line). The yellow band includes the statistical (from the fit), parameterization (different functional forms) and a normalization error of 2% (all added in quadrature).

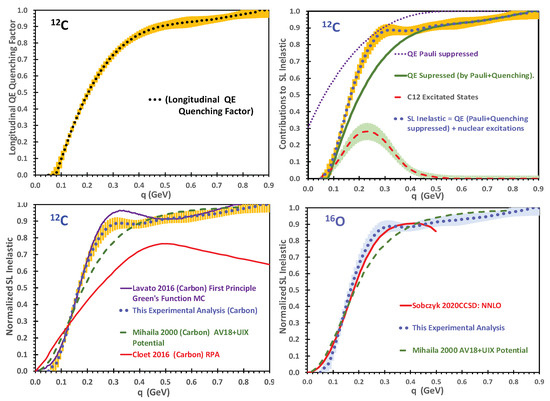
Figure 3. Top left panel: QE “longitudinal quenching factor” (dotted-black line with yellow error band). Top right panel: the various contributions to $SL\left(\mathbf{q}\right)$ for ${}^{12}\mathrm{C}$ (dotted blue with yellow error band) including QE with Pauli suppression only (dotted purple), QE suppressed by both “Pauli” and “longitudinal quenching” (solid green), and the contribution of nuclear excitations (red dashed with green error band). Bottom left panel: $SL\left(\mathbf{q}\right)$ for ${}^{12}\mathrm{C}$ (dotted blue with yellow error band) compared to theoretical calculations including Lovato et al. [11] (solid purple), Mihaila and Heisenberg [12] (dashed green), and RPA Cloet et al. [13] (solid red). Bottom right panel: $SL\left(\mathbf{q}\right)$ for ${}^{16}\mathrm{O}$ (dotted dark blue with light blue error band) compared to theoretical calculations of Sobczyk et al. [14] (red dashed) and Mihaila and Heisenberg [12] (dotted dashed).

If another formalism is used to model QE scattering (e.g., RFG or spectral functions), then the quenching factor for the model $F_{quench}^{model}\left(\mathbf{q}\right)$ is given by

$$\begin{array}{c}\hfill F_{quench}^{L-model}\left(\mathbf{q}\right)=\frac{⟨F_{Pauli}^{This-analysis}\left(\mathbf{q}\right)⟩}{⟨F_{Pauli}^{model}\left(\mathbf{q}\right)⟩}{F}_{quench}^L\left(\mathbf{q}\right).\end{array}$$

(4)

The top right panel of Figure 3 shows the various contributions to the measured $SL\left(\mathbf{q}\right)$ for ${}^{12}\mathrm{C}$ (dotted blue line with yellow error band). Shown are the QE contributions with only Pauli suppression (dotted purple), QE suppressed by both “Pauli suppression” and $F_{quench}^L\left(\mathbf{q}\right)$ labeled as QE total suppression (solid green), and the contribution of nuclear excitations (red dashed line). The green error band is 15% (from the comparison of form factor parameterizations [2] with data) plus 0.01 added in quadrature.

The top right panel of Figure 3 shows the various contributions to the measured $SL\left(\mathbf{q}\right)$ for ${}^{12}\mathrm{C}$ (dotted blue line with yellow error band). Shown are the QE contribution with only Pauli suppression (dotted purple), QE suppressed by both “Pauli Suppression” and $F_{quench}^L\left(\mathbf{q}\right)$ labeled as QE total suppression (solid-green), and the contribution of nuclear excitations (red dashed line). The green error band is 15% plus 0.01 added in quadrature. The left panel on the bottom of Figure 3 shows a comparison of the extracted $SL\left(\mathbf{q}\right)$ for ${}^{12}\mathrm{C}$ (dotted blue curve with yellow error band) to the theoretical calculations. These include the Lovato et al. [11] “first-principle Green’s function Monte Carlo” (GFMC) calculation (solid purple line), Mihaila and Heisenberg [12] coupled-clusters-based calculation (AV18+UIX potential, dashed green), and Cloet et al. [13] RPA calculation (RPA solid red). Our measurement for ${}^{12}\mathrm{C}$ is in disagreement with Cloet et al. [13] RPA and in reasonable agreement with Refs. [11,12], except near $\mathbf{q}\approx$ 0.30 GeV, where the contribution from nuclear excitations is significant.

The bottom right panel of Figure 3 shows $SL\left(\mathbf{q}\right)$ for ${}^{16}\mathrm{O}$ (dotted-blue with green error band) compared to theoretical calculations. These include the Sobczyk et al. [14] “coupled-cluster with singles and doubles (CCSD) ${\mathrm{NNLO}}_{sat}$” (red dashed line), and Ref. [12] coupled-cluster calculation (AV18+UIX potential, dashed green line). The data are in reasonable agreement with the calculations of Refs. [12,14] for ${}^{16}\mathrm{O}$ except near $\mathbf{q}\approx$ 0.30 GeV, where the contribution from nuclear excitations is significant.

The $TE(\mathbf{q},\nu )$ contribution to the QE transverse structure function $F_1(Q^2,\nu )$ for ${}^{12}\mathrm{C}$ is parameterized as a distorted Gaussian centered around $W\approx 0.88$ GeV and a Gaussian at $W\approx 1.2$ GeV with $Q^2$-dependent width and amplitude. $F_1^{MEC}$ = 0 for $\nu <{\nu }_{min}$ (${\nu }_{min}$ = 16.5 MeV). For $\nu >{\nu }_{min}$, it is given by $F_1^{MEC}=max((f_1^A+f_1^B),0.0)$, where

$$\begin{array}{ccc}\hfill f_1^A& =& a_{1}Y·[{(W^2-W_{min}^2)}^{1.5}·e^{-{(W^2-b_1)}^2/2c_1^2}]\hfill \\ \hfill f_1^B& =& a_{2}Y·{(Q^2+q_o^2)}^{1.5}·\left[e^{-{(W^2-b_2)}^2/2c_2^2}\right]\hfill \\ \hfill Y& =& A{e}^{-Q^4/12.715}\frac{{(Q^2+q_0^2)}^2)}{{(0.13380+Q^2)}^{6.90679}}\hfill \\ \hfill a_1& =& 0.091648,a_2=0.10223.W_{min}^2=M_p^2+2M_p{\nu }_{min}-Q^2,\hfill \end{array}$$

(5)

where Q² is in units of GeV${}^2$, M_p is the proton mass, A is the atomic weight, $q_0^2=1.0\times {10}^{-4}$, $b_1$ = 0.77023, $c_1=0.077051+0.26795Q^2$, $b_2$ = 1.275, and $c_2$ = 0.375.

In summary, using all available electron scattering data, we extract parameterizations of the quenching of $R_L^{QE}(\mathbf{q},\nu )$ and the enhancement of $R_T^{QE}(\mathbf{q},\nu )$ over a large range of $\mathbf{q}$ and $\nu$. We obtain the best measurement of the Coulomb sum rule $SL\left(\mathbf{q}\right)$ to date and compare to the theoretical models. The fit can be used as a proxy to validate the modeling of cross sections in Monte Carlo event generators for electron and neutrino (${\nu }_{e,\mu }$) scattering. The contribution of nuclear excitations to $SL\left(\mathbf{q}\right)$ is significant (up to 29%). Theoretical studies show that nuclear excitations are also significant in ${\nu }_{e,\mu }$ scattering [15,16,17]. Therefore, nuclear excitations should be included in both e-N and $\nu$-N MC generators.