Solvability of a Parametric Fractional-Order Integral Equation Using Advance Darbo G-Contraction Theorem

Abstract

The existence of a parametric fractional integral equation and its numerical solution is a big challenge in the field of applied mathematics. For this purpose, we generalize a special type of fixed-point theorems. The intention of this work is to prove fixed-point theorems for the class of $\beta -$G, $\psi -$G contractible operators of Darbo type and demonstrate the usability of obtaining results for solvability of fractional integral equations satisfying some local conditions in Banach space. In this process, some recent results have been generalized. As an application, we establish a set of conditions for the existence of a class of fractional integrals taking the parametric Riemann–Liouville formula. Moreover, we introduce numerical solutions of the class by using the set of fixed points.

1. Introduction

Approximately, a measure of noncompactness is a function demarcated on the class of all nonempty and bounded subsets of a definite metric space where it is identical to zero on the entire class of comparatively compact sets [1]. A survey of theory and applications of measures of noncompactness is presented in [2]. The normal measures of noncompactness are deliberated, and their possessions are associated. Some consequences regarding normal measures of noncompactness in altered spaces are offered. Additionally, the authors introduced some applications of the measure of noncompactness notion to functional equations involving nonlinear integral equations of arbitrary orders, implicit arbitrary integral equations and q-integral equations of arbitrary orders. The measure of noncompactness plays very significant role in the theory of fixed points and applications. The term measures of noncompactness were initially formulated in the elementary paper of Kuratowski [3]. Furthermore, G. Darbo [4] defined condensing operator and established a fixed-point theorem that involved the idea of a measure of noncompactness which is abundant of applications in functional analysis, integral equations differential equations approximation theory (see for example [4]. Owing to numerous applications of fixed-point theory in proving the existence theorems, this theory has been considered to be an evergreen and considered to be indispensable tool in nonlinear analysis. The Darbo fixed-point theorem extends both the Banach and the Schauder fixed-point theorems. In 2012, Wardowski [5] defined F-contraction and generalized Banach contraction principle in various aspects. Furthermore, Jleli et al. [1] define the F-contraction of Darbo type and established a fixed-point theorem.

In our study, we state and prove fixed-point theorems which are generalized Jleli et al. [1] results. Furthermore, as an application, we demonstrate the applicability of our main result in establishing the existence of solutions of an integral equation of fractional order of the form:

$$z\left(t\right)=u\left(t\right)+\frac{g\left(t,x\right)}{\mathsf{\Gamma }\left(\alpha \right)}\underset{0}{\overset{\theta \left(t\right)}{\int }}\frac{h\left(t,\tau ,x\left(t\right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau ,t\in {\mathbb{R}}^{+},\alpha >0,$$

(1)

where $u,g,h$ and $\theta$ satisfies certain conditions.

2. Methods

Let us recall some notations, definitions and theorems which will be used throughout this paper. In what follows E denotes the Banach space with the norm $\parallel .\parallel$ and throughout this article we use the following notations;

We proceed with an axiomatic definition of measure of noncompactness;

Definition 1

(Axiomatic Definition of Measure of Noncompactness [6,7,8]).A function $\sigma :{\mathfrak{M}}_E⟶{\mathbb{R}}_{+}$ is called $\mathit{M}.\mathit{N}.\mathit{C}$ provided it fulfills the following axioms:

(i) 

(Regularity) $\sigma \left(W\right)=0$ if and only if W is relatively compact.

(ii) 

The family $ker\sigma =\{W\in {\mathfrak{M}}_E:\sigma \left(W\right)=0\}$ is a nonempty and $ker\sigma \subseteq {\mathfrak{N}}_E$.

(iii) 

(Monotonic) $W\subset W^{{}^{\prime }}⟹\sigma \left(W\right)\le \sigma \left(W^{{}^{\prime }}\right)$.

(iv) 

(Invariant under closure) $\sigma \left(W\right)=\sigma \left(\overline{W}\right)$.

(v) 

(Invariant under convex hull) $\sigma \left(W\right)=\sigma \left(coW\right)$.

(vi) 

$\sigma \left(\alpha W+(1-\alpha )W^{{}^{\prime }}\right)\le \alpha \sigma \left(W\right)+(1-\alpha )\sigma \left(W^{{}^{\prime }}\right),$ for all $\alpha \in [0,1]$.

(vii) 

(Generalized Cantor’s intersection theorem) If $W_n\in {\mathfrak{M}}_E$ for $n=1,2,\cdots$ is a decreasing sequence of closed subsets of E and $\underset{n\to \infty }{lim}\sigma \left(W_n\right)=0$ then $W_{\infty }={\displaystyle \bigcap _{n=1}^{\infty }}{W}_n$ is nonempty.

The family defined in axiom $\left(i\right)$ is called the kernel of the $\mathit{M}.\mathit{N}.\mathit{C}$ and denoted by $ker\sigma$. In fact, by the virtue of axiom (vi) we have $\sigma \left({\mathsf{\Omega }}_{\infty }\right)\le \sigma \left({\mathsf{\Omega }}_n\right)$ for any n, thus $\sigma \left({\mathsf{\Omega }}_{\infty }\right)=0.$ This yields that ${\mathsf{\Omega }}_{\infty }\in ker\sigma .$

Theorem 1

(Schauder’s fixed-point theorem [9]).Let Ω be the member of the class $\mathit{N}.\mathit{B}.\mathit{C}.\mathit{C}$ of a Banach space E, then every continuous and compact mapping on Ω has at least one fixed point in Ω.

The Darbo’s fixed-point theorem with respect to a $\mathit{M}.\mathit{N}.\mathit{C}$ $\sigma$ can be stated as below.

Theorem 2

(Darbo’s fixed-point theorem [4]).Let Ω be the member of the class $\mathit{N}.\mathit{B}.\mathit{C}.\mathit{C}$ of a Banach space E and T be the continuous self-mapping defined on every nonempty subset W of Ω such that

$$\sigma \left(T\right(W\left)\right)\le \lambda \sigma \left(W\right)$$

for some $\lambda \in [0,1)$. Then T has at least one fixed point in Ω.

Definition 2

($\mathbb{G}$ -function). A function $G:(0,\eta )\to \mathbb{R}$, where $\eta \in {\mathbb{R}}^{+}$ is said to be $\mathbb{G}$ -function if it satisfies the following conditions;

$\left(G_1\right)$

G is non-decreasing;

$\left(G_2\right)$

For each sequence $⟨{\alpha }_n⟩\subset (0,\eta )$ of positive real numbers $\underset{n\to \infty }{lim}{\alpha }_n=0$ if and only if $\underset{n\to \infty }{lim}G\left({\alpha }_n\right)=-\infty$;

$\left(G_3\right)$

There exists $i\in (0,1)$ such that $\underset{q\to \infty }{lim}{q}^{i}F\left(q\right)=0.$

Example 1.

Let $G:(0,\eta )\to \mathbb{R}$ defined as below are examples of $\mathbb{G}$ -functions

1. 

$G\left(s\right)=-\frac{1}{s}$ for all $s\in \mathbb{R}{s}_{+}.$

2. 

$G\left(s\right)=ln\left(s\right)$ for all $t\in {\mathbb{R}}_{+}.$

Definition 3

($\mathbb{S}$ -function). A function $\tau :{\mathbb{R}}_{+}\to \mathbb{R}$ is said to be a $\mathbb{S}$ -function if it satisfies the inequality;

$$\underset{s\to t^{+}}{liminf}\tau \left(s\right)>0,\forall t\in {\mathbb{R}}_{+}.$$

Example 2.

The mapping $\tau :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ described by the rule $\tau \left(t\right)={\left(2t\right)}^{-1}\forall t\in :{\mathbb{R}}_{+}$ is an example of $\mathbb{S}$ -function.

Definition 4

($\mathsf{\Phi }$-function). A function $\varphi :{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ is said to be a Φ-function if it fulfills the following assumptions;

$\left(i\right)$

ϕ is non-decreasing;

$\left(ii\right)$

ϕ is right-continuous on ${\mathbb{R}}_{+}$;

$\left(iii\right)$

$\varphi \left(t\right)<t\forall t\in {\mathbb{R}}_{+}$;

$\left(iv\right)$

$\underset{n\to \infty }{lim}{\varphi }^n\left(t\right)=0$ for each $t\in {\mathbb{R}}_{+}$.

Theorem 3.

Let Ω be the member of the class $\mathit{N}.\mathit{B}.\mathit{C}.\mathit{C}$ and T be the self-mapping defined on Ω. The mapping T is said to be a ϕ-condensing if

$$\sigma \left(T\left(W\right)\right)⩽\varphi \left(\sigma \left(W\right)\right)$$

for some $\varphi \in \mathsf{\Phi }$ and every nonempty subset W of Ω.

Definition 5

(${\mathsf{\Psi }}_{\mu }$-function). A function $\psi :(-\infty ,\mu )\to (-\infty ,\mu )$ is called ${\mathsf{\Psi }}_{\mu }$-function if it satisfies the following conditions:

$\left(i\right)$

ψ is increasing;

$\left(ii\right)$

ψ is right-continuous on $(-\infty ,\mu )$;

$\left(iii\right)$

$\psi \left(t\right)<t\forall t\in (-\infty ,\mu )$;

$\left(iv\right)$

$\underset{n\to \infty }{lim}{\psi }^n\left(t\right)=-\infty$ for each $t\in (-\infty ,\mu )$.

Example 3.

 

(1) 

For every $\mu \in [0,\infty )$, the mapping $\psi :(-\infty ,\mu )\to (-\infty ,\mu ),$ defined by $\psi \left(t\right)=t-f\left(t\right),$ where $f:(-\infty ,\mu )\to {\mathbb{R}}_{+}$ is continuous and non-increasing function is an example of ${\mathsf{\Psi }}_{\mu }$-function.

(2) 

Foe each $\delta <e^{-1},$ let us define ${\psi }_{\delta }:\mathbb{R}\to \mathbb{R}$ by the rule ${\psi }_{\delta }\left(t\right)=\delta e^{-t}$ is an example of ${\mathsf{\Psi }}_{\mu }$-function.

Definition 6

(G-Contraction of Darbo Type [10]).Let Ω be member of the class $\mathit{N}.\mathit{B}.\mathit{C}.\mathit{C}$ and T is continuous self-operator on Ω. The operator T is called Darbo-type G-contraction if $\exists G\in \mathbb{G}$ and $\tau \in \mathbb{S}$ such that

$$\tau \left(\sigma \left(W\right)\right)+G\left(\sigma \left(TW\right)\right)⩽G\left(\sigma \left(W\right)\right),$$

for any nonempty $W\subset \mathsf{\Omega }$ with $\sigma \left(W\right),\sigma \left(TW\right)>0$, where σ is a $\mathit{M}.\mathit{N}.\mathit{C}$ defined in $E.$

Theorem 4

([10]).Let Ω be member of the class $\mathit{N}.\mathit{B}.\mathit{C}.\mathit{C}$ of a Banach space E and T is continuous self-operator on Ω. If T is Darbo-type G-contraction for any nonempty subset $W\subset \mathsf{\Omega }$, then T has a fixed point in the set Ω.

Definition 7

(${\beta }_{\mu }$-function). A function $\beta :(-\infty ,\mu )\to (-\infty ,1)$ is said to be a ${\beta }_{\mu }$-function if it satisfies the condition that $\beta \left(t_n\right)\to 1\Rightarrow t_n\to -\infty .$

Example 4.

The mapping $\beta :(-\infty ,\mu )\to (-\infty ,1),$ defined by

$$\beta \left(t\right)=\left\{\begin{array}{cc}\frac{1}{2}\hfill & ift=0,\hfill \\ \\ 1-\frac{\tau }{t}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

for any $\tau >0$ is an example of ${\beta }_{\mu }$-function.

3. Results

In this section, we establish new fixed-point theorems for self-mappings in the setting of measure of noncompactness. Therefore, to obtain our first theorem, we use the following class of functions.

Definition 8.

Let Ω be member of the class $\mathit{N}.\mathit{B}.\mathit{C}.\mathit{C}$ and T is continuous self-operator on Ω. The operator T on Ω is called Darbo-type $\beta G$-contraction if $\exists G\in \mathbb{G}$ and $\beta \in {\beta }_{\mu }$ and $\mu ={\displaystyle \underset{o<t<\eta }{sup}}G\left(t\right)>\sigma \left(E\right)$ such that;

$$G\left(\sigma \left(TW\right)\right)⩽\beta \left(G\left(\sigma \left(W\right)\right)\right)G\left(\sigma \left(W\right)\right),$$

for any $W\subset \mathsf{\Omega }$ with $\sigma \left(W\right)>0,\sigma \left(TW\right)>0$, where σ is a measure of noncompactness defined in $E.$

Next, we establish the existence of at least one fixed point.

Theorem 5.

Let Ω be member of the class $\mathit{N}.\mathit{B}.\mathit{C}.\mathit{C}$ of a Banach space E and T is Darbo-type $\beta G$-contraction on Ω, for $G\in \mathbb{G}$ and $\beta \in {\beta }_{\mu }$, then T has at least one fixed point in Ω.

Proof. 

The proof begins with the construction of the sequence $⟨W_n⟩$ of nonempty, closed and convex subset of W such that the following relation holds:

$$T{W}_n\subset W_n\subset W_{n-1}\mathrm{for}\mathrm{all}n\in \mathbb{N}$$

Let $W_0=W,$ we construct a sequence $⟨W_n⟩$ by the rule $W_{n+1}=ConvP\left(W_n\right)$ for $n\in \left\{0\right\}\cup \mathbb{N}.$ For $n=0$, we can easily check that $T{W}_0\subset TW\subset W=W_0.$ Now assume that the rule holds for $k=1,2,3,\cdots n.$ Then, by the definition of $⟨W_n⟩$ we deduce that

$$T{W}_n\subset W_n\mathrm{implies}{W}_{n+1}=conv\left(T{A}_n\right)\subset A_n,$$

Therefore $T{W}_{n+1}\subset T{W}_n\subset W_{n+1}.$ If there exist a positive integer $K\in \mathbb{N}$ such that $\sigma \left(W_K\right)=0,$ then $W_K$ is pre-compact set. Since $T\left(W_K\right)\subseteq conv\left(T{W}_K\right)=W_{K+1}\subseteq W_K$, i.e., T is a self-operator on $W_K$. Then Theorem 2.1 concludes that T has a fixed point in $W_K\subset W.$ On the other hand, we assume that $\sigma \left(W_n\right)>0,\forall n\ge 1$ and prove that $\sigma \left(W_n\right)\to 0$ as $n\to +\infty .$ Now using assumption $v)$ of Definition 1 we have,

$$\begin{array}{cc}\hfill G\left(\sigma \left(W_{n+1}\right)\right)& =G\left(\sigma \left(convP{W}_n\right)\right)\hfill \\ \hfill & =G\left(\sigma \left(T{W}_n\right)\right)\hfill \\ \hfill & ⩽\beta \left(G\left(\sigma \left(W_n\right)\right)\right)G\left(\sigma \left(W_n\right)\right)\hfill \end{array}$$

i.e.,

$$G\left(\sigma \left(W_{n+1}\right)\right)\le \beta \left(G\left(\sigma \left(W_n\right)\right)\right)G\left(\sigma \left(W_n\right)\right).$$

(2)

If $G\left(\sigma \left(W_n\right)\right)⩽G\left(\sigma \left(W_{n+1}\right)\right)$ then $\beta \left(G\left(\sigma \left(W_n\right)\right)\right)⩾1,$ which is contradiction. Hence $G\left(\sigma \left(W_{n+1}\right)\right)⩽G\left(\sigma \left(W_n\right)\right)$ for all $n\in \mathbb{N}.$ i.e., $⟨G\left(\sigma \left(W_n\right)\right)⟩$ is decreasing sequence of real numbers. Since the sequence $⟨G\left(\sigma \left(W_n\right)\right)⟩$ decreasing sequence hence it must be bounded above and may or may not be bounded below.

Claim that the sequence $⟨G\left(\sigma \left(W_n\right)\right)⟩$ is unbounded below. We will prove the claim by assuming the contradiction that the sequence $⟨G\left(\sigma \left(W_n\right)\right)⟩$ is bounded below. Since the sequence is decreasing and bounded below hence it has a convergent sub-sequence say $⟨G\left(\sigma \left({W_n}_{{}_k}\right)\right)⟩,$ and a finite real number r such that $⟨G\left(\sigma \left({W_n}_{{}_k}\right)\right)⟩\to r$ as $k\to +\infty .$

$$\frac{G\left(\sigma \left(W_{n_{k+1}}\right)\right)}{G\left(\sigma \left({W_n}_{{}_k}\right)\right)}\le \beta \left(G\left(\sigma \left(W_{n_k}\right)\right)\right)<1$$

which yields,

$$\beta \left(G\left(\sigma \left({W_n}_{{}_k}\right)\right)\right)\to 1ask\to +\infty .$$

Since $\beta \in {\mathsf{\Gamma }}_{\mu }$ we obtain $r=-\infty$ which is a contradiction. This implies that $⟨G\left(\sigma \left(W_n\right)\right)⟩$ unbounded below and so $\underset{n\to +\infty }{lim}G\left(\sigma \left(W_n\right)\right)=-\infty$. So, from $\left(G_2\right)$ of Definition 2 we obtain that $\sigma \left(W_n\right)\to 0$ as $n\to +\infty$. On the flip side, if $⟨G\left(\sigma \left(W_n\right)\right)⟩$ is unbounded then obviously $\sigma \left(W_n\right)\to 0$ as $n\to +\infty$. Hence from $\left(vi\right)$ of the Definition 1, the countable interaction $W_{\infty }={\displaystyle \bigcap _{n=1}^{\infty }}{W}_n$ is a nonempty set which is convex & closed invariant under T and relatively compact. Hence applying Theorem 1 to the set $W_{\infty }={\displaystyle \bigcap _{n=1}^{\infty }}{W}_n$ we obtain desired result. □

Remark 1.

For $\psi \in {\mathsf{\Psi }}_{\mu }$ and $\mu \in [0,\infty )$ define $\beta :(-\infty ,\mu )\to (-\infty ,1)$ by

$$\beta \left(t\right)=\left\{\begin{array}{cc}\frac{1}{2}\hfill & ift=0,\hfill \\ \\ \frac{\psi \left(t\right)}{t}\hfill & otherwise.\hfill \end{array}\right.$$

then β is member of the family ${\beta }_{\mu }.$

Proof. 

Assume that $\beta \left(r_n\right)\to 1$ then $\beta \in {\mathsf{\Gamma }}_{\mu }$ if $r_n\to -\infty .$ Assume the contradiction that $⟨r_n⟩$ is bounded below, hence it has convergent sub-sequence say $⟨r_{n_k}⟩$ such that $r_{n_k}\to r_0$ as $k\to +\infty$, where $r_0$ is some finite real number. Now, since $\psi$ is upper semi-continuous, we obtain;

$$r_0=\underset{k\to \infty }{lim}{r}_{n_k}=\underset{k\to \infty }{lim\; sup}\psi \left(r_{n_k}\right)\le \psi \left(r_0\right).$$

$$\Rightarrow r_0\le \psi \left(r_0\right)$$

which contradicts the condition $\psi \left(t\right)<t$ for $t\in (-\infty ,\mu )$. Hence the sequence $r_n$ is unbounded below, it follows that $\beta \in {\beta }_{\mu }.$ □

Definition 9.

Let Ω be the member of the class $\mathit{N}.\mathit{B}.\mathit{C}.\mathit{C}$ and T is continuous self-operator on Ω. The operator T on Ω is called Darbo-type $\psi G$-contraction if $\exists G\in \mathbb{G}$, $\psi \in {\mathsf{\Psi }}_{\mu }$ and $\mu ={\displaystyle \underset{o<t<\eta }{sup}}G\left(t\right)$ such that

$$G\left(\sigma \left(PW\right)\right)⩽\psi \left(G\left(\sigma \left(W\right)\right)\right),$$

for any $W\subset \mathsf{\Omega }$ with $\sigma \left(W\right)>0,\sigma \left(TW\right)>0$, where σ is a $\mathit{M}.\mathit{N}.\mathit{C}$ defined on $E.$

Next, we establish the existence of unique fixed point.

Theorem 6.

Let Ω be the member of the class $\mathit{N}.\mathit{B}.\mathit{C}.\mathit{C}$ of a Banach space E and T be continuous self-operator on $\mathsf{\Omega }.$ If T is Darbo-type $\psi G$-contraction for $G\in \mathbb{G}$ and $\psi \in {\mathsf{\Psi }}_{\mu }$ then T has a fixed point in Ω.

Proof. 

The proof begins with the construction of the sequence $⟨W_n⟩$ of nonempty, convex & closed subset of W, such that the sequence $⟨W_n⟩$ validate following relation:

$$T{W}_n\subset W_n\subset W_{n-1}\mathrm{for}\mathrm{all}n\in \mathbb{N}$$

Let $W_0=W,$ we construct a sequence $⟨W_n⟩$ by the rule $W_{n+1}=ConvT\left(W_n\right)$ for $n\in \left\{0\right\}\cup \mathbb{N}.$ For $n=0$ we can easily check that $T{W}_0\subset TW\subset W=W_0.$ Now assume that the rule holds for $k=1,2,3,\cdots n.$ Then, by the pattern of $⟨W_n⟩$ we deduce that

$$T{W}_n\subset W_n\mathrm{implies}{W}_{n+1}=conv\left(T{W}_n\right)\subset W_n,$$

Therefore $T{W}_{n+1}\subset T{W}_n\subset W_{n+1}.$ If there exist a positive integer $K\in \mathbb{N}$ such that $\sigma \left(W_K\right)=0,$ then $W_K$ is relatively compact set. Since $T\left(W_K\right)\subset conv\left(T{W}_K\right)=W_{K+1}\subseteq W_K$, i.e., T is a self-operator on $W_K$. Then Theorem 2.1 concludes that T has a fixed point in $W_K\subset W.$

On the flip side, if $\sigma \left(W_n\right)>0,\forall n\ge 1$ then by the axiomatic definition of $M.N.C$ we have,

$$\begin{array}{cc}\hfill G\left(\sigma \left(W_{n+1}\right)\right)& =G\left(\sigma \left(convT{W}_n\right)\right)\hfill \\ \hfill & =G\left(\sigma \left(T{W}_n\right)\right)\hfill \\ \hfill & ⩽\psi \left(G\left(\sigma \left(W_n\right)\right)\right)\hfill \end{array}$$

Hence, we remain with the inequality,

$$G\left(\sigma \left(W_{n+1}\right)\right)\le \psi \left(G\left(\sigma \left(W_n\right)\right)\right)<G\left(\sigma \left(W_n\right)\right)$$

(3)

From Equation (3) we assure that $⟨G\left(\sigma \left(W_n\right)\right)⟩$ is decreasing sequence of real numbers. Since the sequence $⟨G\left(\sigma \left(W_n\right)\right)⟩$ decreasing sequence hence it must be bounded above and may or may not be bounded below.

Claim that the sequence $⟨G\left(\sigma \left(W_n\right)\right)⟩$ is unbounded below. We will prove the claim by assuming the contradiction that the sequence $⟨G\left(\sigma \left(W_n\right)\right)⟩$ is bounded below. Since the sequence is decreasing and bounded below hence it has a convergent sub-sequence say $⟨G\left(\sigma \left({{}_W}_{{}_k}\right)\right)⟩,$ and a finite real number r such that $⟨G\left(\sigma \left({W_n}_{{}_k}\right)\right)⟩\to r$ as $k\to +\infty .$ By Equation (3) we have,

$$G\left(\sigma \left(W_{{\left(n+1\right)}_k}\right)\right)\le \psi \left(G\left(\sigma \left(W_{n_k}\right)\right)\right)<G\left(\sigma \left(W_{n_k}\right)\right),$$

keep in mind that $\psi$ is lower semi-continuous and apply limit as $k\to +\infty$ we obtain,

$$r\le \psi \left(r\right)<r.$$

Since $\psi \left(r\right)<r\forall r\in (-\infty ,\mu )$, hence by the Definition 5 we obtain $r=-\infty$ which a contradiction. This implies that $⟨G\left(\sigma \left(W_n\right)\right)⟩$ unbounded below and so $\underset{n\to +\infty }{lim}G\left(\sigma \left(W_n\right)\right)=-\infty$. So, from $\left(G_2\right)$, we obtain that $\sigma \left(W_n\right)\to 0$ as $n\to +\infty$. On the flip side, if $⟨G\left(\sigma \left(W_n\right)\right)⟩$ is unbounded then obviously $\sigma \left(W_n\right)\to 0$ as $n\to +\infty$. Hence from $\left(vi\right)$ of the Definition 1, the countable intersection $W_{\infty }={\displaystyle \bigcap _{n=1}^{\infty }}{W}_n$ is a nonempty set which is convex & closed invariant under T and relatively compact. Hence applying Theorem 1 to the set $W_{\infty }={\displaystyle \bigcap _{n=1}^{\infty }}{W}_n$ we obtain the desired result. □

Corollary 1

([1]).Let Ω be member of class $\mathit{B}.\mathit{N}.\mathit{C}.\mathit{C}$ of the Banach space E. Let a self-operator T on Ω is of Darbo-type G-contraction if there exist $G\in \mathbb{G}$ and $\tau \in S$ such that

$$\tau \left(\sigma \left(W\right)\right)+G\left(\sigma \left(TW\right)\right)⩽G\left(\sigma \left(W\right)\right),$$

for any $W\subset \mathsf{\Omega }$ with $\sigma \left(W\right),\sigma \left(TW\right)>0$, where σ is a $M.N.C$ defined in $E.$ Then T has a fixed point in the set Ω.

Proof. 

Let us define $\psi \left(t\right)=t-\tau \left(t\right)$ we obtain the required result from Theorem 6 □

Corollary 2.

Let Ω be member of class $\mathit{B}.\mathit{N}.\mathit{C}.\mathit{C}$ of the Banach space E. Let a self-operator T be a of Darbo-type $\psi G$-contraction, where $\psi \in {\mathsf{\Psi }}_{\mu }$ and G is continuous and non-decreasing function. Then for $\varphi \in \mathsf{\Phi }$ such that T is a ϕ-contraction.

Proof. 

Since the function G is monotonic and continuous function, hence $\exists G^{-1}:G\left({\mathbb{R}}_{+}\right)\to {\mathbb{R}}_{+}$ inverse of G, which is also monotonic.

Now using the Definition 9 we can have,

$$\begin{array}{cc}\hfill G\left(\sigma \left(TW\right)\right)& \le \psi \left(G\left(\sigma \left(W\right)\right)\right)\hfill \\ \hfill \Rightarrow \sigma \left(TW\right)& \le G^{-1}\left(\psi \left(G\left(\sigma \left(W\right)\right)\right)\right),\hfill \end{array}$$

Denote $\varphi \left(t\right)=\left(G^{-1}\psi G\right)\left(t\right)$

Notice that

$$\begin{array}{cc}\hfill {\varphi }^n\left(t\right)& ={\left(G^{-1}\psi G\right)}^n\left(t\right)\hfill \\ \hfill & =\left(G^{-1}\psi G.G^{-1}\psi G...G^{-1}\psi G\right)\left(t\right)\hfill \\ \hfill & =G^{-1}{\psi }^{n}G\left(t\right)\hfill \\ \hfill & =G^{-1}\left({\psi }^n\left(G\left(t\right)\right)\right)\to 0\mathrm{as}n\to \infty \hfill \end{array}$$

(4)

For every $W\subset \mathsf{\Omega }$ with $\sigma \left(W\right)\ne 0$, $G\in \mathbb{G}$ and $\psi \in {\mathsf{\Psi }}_{\mu }$, if T is Darbo-type $\psi G$-contraction then for $\varphi \in \mathsf{\Psi },T$ is $\varphi$ contraction. □

4. Discussion

Presently, there are several results available in the literature about study of existence and behavior of solutions of various types of fractional-order integral equations. The fractional-order integral equations have numerous applications in porous media, control theory, rheology, viscoelasticity, elector chemistry, electromagnetism fluid dynamics (see [11,12,13,14]).

In this article, we will use the measures of noncompactness in $BC\left({\mathbb{R}}_{+}\right);$ the space of all bounded and continuous functions defined on ${\mathbb{R}}_{+}$ [7]. Let $z=z\left(t\right)$ be any real valued bounded and continuous function defined on ${\mathbb{R}}_{+}$, then the norm on $BC\left({\mathbb{R}}_{+}\right)$ is defined as;

$${\left|\right|z\left|\right|}_{BC\left({\mathbb{R}}_{+}\right)}=sup\left\{\right|z\left(t\right)|:t\ge 0\}.$$

Let us take $W\ne \varphi$ be subset of the Banach space $BC\left({\mathbb{R}}_{+}\right)$ and fix $ϵ>0$, $M>0$ and $z\in W$. Now, let us recall the term usually known as modulus of continuity of z on $[0,M]$:

$${\omega }^M(z,ϵ)=sup\left\{\right|z\left(t\right)-z\left(s\right)|;t,s\in [0,M],|t-s|\le ϵ\}.$$

The modulus of continuity of W on the interval $[0,M]$ is expressed by the following term,

$${\omega }^M(W,ϵ)=sup\{{\omega }^M(z,ϵ):z\in C\}.$$

Furthermore, we define the term ${\omega }^{\infty }\left(W\right)$ in the following fashion:

$${\omega }^{\infty }\left(W\right)=\underset{M\to +\infty }{lim}{\omega }_0^M\left(W\right)$$

where

$${\omega }_0^M\left(W\right)=\underset{ϵ\to 0}{lim}{\omega }^M(W,ϵ)$$

Next, define the quantity $B\left(W\right)$ as:

$$B\left(W\right)=\underset{n\to \infty }{lim}\left\{\underset{z\in C}{sup}\left\{sup\left\{\left|z\left(t\right)-z\left(s\right)\right|;t,s⩾M\right\}\right\}\right\}$$

(5)

Finally, we will define the quantity which satisfies the axioms of $M.N.C$ in the following manner;

$$\sigma \left(W\right)={\omega }^{\infty }\left(W\right)+B\left(W\right)$$

(6)

We have, $\sigma \left(W\right)={\omega }^{\infty }\left(W\right)+B\left(W\right)$ is the $M.N.C$ in the space $BC\left({\mathbb{R}}_{+}\right)$ and satisfies regularity, monotonically, invariant under closure, invariant under convex hull, generalized Cantor intersection theorem etc. [7].

4.1. Fractional Integral Equation

In this section, we will validate the existence of the solution of fractional ordered integral Equation (1), using the results of Section 2 of this paper. Let us assume that the integral Equation (1) will satisfies the following conditions;

(a)

The function $u\left(t\right)$ is a member of the space $BC\left({\mathbb{R}}^{+}\right)$ which has finite limit at infinity.

(b)

The function $g\left(t,z\right)=g:{\mathbb{R}}^{+}\times \mathbb{R}\to \mathbb{R}$ is continuous and $M_g=max\left\{\left|g\left(t,0\right)\right|:z\in {\mathbb{R}}^{+}\right\}$, moreover there exist continuous function $\rho \left(t\right):{\mathbb{R}}_{+}\to \mathbb{R}$ with $\rho \left(0\right)=0$ such that the following inequality will satisfies;

$$\left|g\left(t,z\right)-g\left(t,y\right)\right|⩽\rho \left(t\right)\left|z-y\right|$$

for all $t\in {\mathbb{R}}_{+}$ and $z,y\in \mathbb{R}$.

(c)

The function $h\left(t,\tau ,z\left(\tau \right)\right)$ is continuous and there exists a non-decreasing and continuous function $\varphi :{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}$ and $\eta :{\mathbb{R}}_{+}\to \mathbb{R}$ such that;

$$\left|h\left(t,\tau ,z\left(\tau \right)\right)\right|⩽\eta \left(t\right)\varphi \left(\left|\right|z\left|\right|\right)$$

for all $t,\tau \in {\mathbb{R}}_{+}$ and $z\in BC\left({\mathbb{R}}_{+}\right).$

(d)

The function $h\left(t,\tau ,z\left(\tau \right)\right)$ is uniformly continuous on ${\mathbb{R}}_{+}\times {\mathbb{R}}_{+}\times \left[-r,r\right]$ for any $r>0$, moreover, for any $t,\tau \in {\mathbb{R}}_{+}$ such that $\tau \le t$ and $z\in BC\left({\mathbb{R}}_{+}\right)$ the following equality hold:

$$\underset{M\to \infty }{lim}\left\{sup\left\{\left|h\left(t,\tau ,z\right)-h\left(s,\tau ,z\right)\right|:t,s\ge M,\tau \in R_{+},\tau \le t,\tau \le s,\left|z\right|\le r\right\}\right\}=0.$$

(e)

The functions $\xi ,\vartheta ,\psi :{\mathbb{R}}_{+}\to \mathbb{R}$ defined as $\xi \left(t\right)=\rho \left(t\right)\eta \left(t\right){\left(\theta \left(t\right)\right)}^{\alpha }$,$\vartheta \left(t\right)=\rho \left(t\right){\left(\theta \left(t\right)\right)}^{\alpha }$ and $\psi \left(t\right)=g\left(t,0\right){\left(\theta \left(t\right)\right)}^{\alpha }$ are bounded on ${\mathbb{R}}_{+}$. The functions $\vartheta$ and $\psi$ are vanishes at infinity.

(f)

There exist a positive number $r_0$ and $\kappa \in {\mathbb{R}}_{+}$ satisfying the inequality

$\left|\left|u\right|\right|\mathsf{\Gamma }\left(\alpha +1\right)+{\varphi }_b\left[{\xi }_{b}r+{\psi }_b\right]⩽r\mathsf{\Gamma }\left(\alpha +1\right)$ and ${\xi }_b\varphi \left(r_0\right)⩽e^{-\kappa }\mathsf{\Gamma }\left(\alpha +1\right)$

where ${\xi }_b=sup\left\{\xi \left(t\right)|t\in {\mathbb{R}}_{+}\right\},{\psi }_b=sup\left\{\psi \left(t\right)|t\in R_{+}\right\}$.

Theorem 7.

Under the assumptions (a)–(f), there exist at least one solution $v=v\left(s\right)$ of Equation (1) in the space $BC\left({\mathbb{R}}_{+}\right)$ converges to a finite limit at infinity.

Proof. 

For the sake of calculations let us define the operators $H,I,$ and T on the Banach space $BC\left({\mathbb{R}}_{+}\right)$ in the following manner;

$$\begin{array}{cc}\hfill \left(Hz\right)\left(t\right)& =g\left(t,z\left(t\right)\right),\hfill \\ \hfill \left(Iz\right)\left(t\right)& =\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{\theta \left(t\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau ,\hfill \\ \hfill \left(Tz\right)\left(t\right)& =f\left(t\right)+\left(Hz\right)\left(t\right)\left(Iz\right)\left(t\right),\hfill \end{array}$$

(7)

for $t\in {\mathbb{R}}_{+}.$ Obviously Equation (1) can be written in the from $z\left(t\right)=\left(Tz\right)\left(t\right).$ We know that $Tz$ is operator on the interval ${\mathbb{R}}_{+}$ for fixed $z\in BC\left({\mathbb{R}}_{+}\right),$ now we prove that $Tz$ is continuous operator on ${\mathbb{R}}_{+}.$

To do this, fix $M>0$ and $ϵ>0.$ Choose the numbers $s,t\in [0,M]$ with $|t-s|\le ϵ.$ For $s<t$ we obtain;

$$\begin{array}{cc}\hfill \left|\left(Iz\right)\left(t\right)-\left(Iz\right)\left(s\right)\right|& =\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\left|{\int }_0^{\theta \left(t\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau -{\int }_0^{\theta \left(s\right)}\frac{h\left(s,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(s\right)-\tau \right)}^{1-\alpha }}d\tau \right|\hfill \\ \hfill & ⩽\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\left|{\int }_0^{\theta \left(t\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau -{\int }_0^{\theta \left(s\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau \right|\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\left|{\int }_0^{\theta \left(s\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau -{\int }_0^{\theta \left(s\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(s\right)-\tau \right)}^{1-\alpha }}d\tau \right|\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\left|{\int }_0^{\theta \left(s\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(s\right)-\tau \right)}^{1-\alpha }}d\tau -{\int }_0^{\theta \left(s\right)}\frac{h\left(s,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(s\right)-\tau \right)}^{1-\alpha }}d\tau \right|\hfill \\ \hfill & \frac{\varphi \left(\left|\right|z\left|\right|\right)\eta \left(t\right)}{\mathsf{\Gamma }\left(\alpha \right)}\left|{\int }_{\theta \left(s\right)}^{\theta \left(t\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau \right|\hfill \\ \hfill & +\frac{\varphi \left(\left|\right|z\left|\right|\right)\eta \left(t\right)}{\mathsf{\Gamma }\left(\alpha \right)}\left|{\int }_0^{\theta \left(s\right)}\left(\frac{1}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}-\frac{1}{{\left(\theta \left(s\right)-\tau \right)}^{1-\alpha }}\right)d\tau \right|\hfill \\ \hfill & +\frac{{\aleph }_{M,}^{\left|\right|z\left|\right|}\left(h\right)}{\mathsf{\Gamma }\left(\alpha \right)}\left|{\int }_0^{\theta \left(s\right)}\frac{1}{{\left(\theta \left(s\right)-\tau \right)}^{1-\alpha }}d\tau \right|\hfill \end{array}$$

(8)

where we denoted

$${\aleph }_{M,ϵ}^K\left(h\right)=sup\left\{\left|h\left(t,\tau ,z\right)-h\left(s,\tau ,z\right)\right|:t,s,\tau \in \left[0,M\right],\left|t-s\right|⩽\epsilon ,z\in \left[K,-K\right]\right\}$$

Next, from the expression (8) we obtain

$$\begin{array}{cc}\hfill \left|\left(Iz\right)\left(t\right)-\left(Iz\right)\left(s\right)\right|& ⩽\frac{\varphi \left(\left|\right|z\left|\right|\right)\eta \left(t\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}\left({\left(\theta \left(t\right)-\theta \left(s\right)\right)}^{\alpha }\right)\hfill \\ \hfill & +\frac{\varphi \left(\left|\right|z\left|\right|\right)\eta \left(t\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}\left({\left(\theta \left(t\right)-\theta \left(s\right)\right)}^{\alpha }+\left(\theta {\left(s\right)}^{\alpha }-\theta {\left(t\right)}^{\alpha }\right)\right)\hfill \\ \hfill & +\frac{{\aleph }_{M,}^{\left|\right|z\left|\right|}\left(g\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}{\left(\theta \left(s\right)\right)}^{\alpha }\hfill \end{array}$$

(9)

Since, ${\aleph }_{M,ϵ}^{\left|\right|z\left|\right|}\left(g\right)\to 0$ as $ϵ\to 0,$ hence we infer that the function $\left(Iz\right)$ is continuous on $[0,M].$ As M is arbitrary, hence we can say that $\left(Iz\right)$ is continuous on ${\mathbb{R}}_{+}$.

Additionally, from the assumption $\left(b\right)$ we deduce the following expression;

$$\begin{array}{cc}\hfill \left|\left(Hz\right)\left(s\right)-\left(Hz\right)\left(t\right)\right|& =\left|g\left(s,z\left(s\right)\right)-g\left(t,z\left(t\right)\right)\right|\hfill \\ \hfill & \le \left|g\left(s,z\left(s\right)\right)-g\left(s,z\left(t\right)\right)\right|+\left|g\left(s,z\left(t\right)\right)-g\left(t,z\left(t\right)\right)\right|\hfill \\ \hfill & ⩽\rho \left(s\right)\left|z\left(t\right)-z\left(s\right)\right|+{\aleph }_{M,ϵ}^{\left|\right|z\left|\right|}\left(q\right)\hfill \end{array}$$

(10)

where

$${\aleph }_{M,ϵ}^{{}_{\delta }}\left(g\right)=sup\left\{\left|g\left(t,z\left(t\right)\right)-g\left(s,z\left(s\right)\right)\right|:t,s\in \left[0,M\right],\left|t-s\right|⩽\epsilon ,z\in \left[-\delta ,\delta \right]\right\}$$

for an arbitrary $\delta >0.$

By the virtue of assumption $\left(c\right)$ we have ${\aleph }_{M,ϵ}^{\left|\right|z\left|\right|}\left(g\right)\to 0$ as $ϵ\to 0.$ Thus, the expression (10) we conclude that $\left(Hz\right)$ is continuous on $[0,M],$ and hence continuous on the interval ${\mathbb{R}}_{+}.$

Hence, representation (7) and assumption (a) implies that $\left(Tz\right)$ is continuous on the interval ${\mathbb{R}}_{+}.$

Furthermore, let us choose $z\in BC\left({\mathbb{R}}_{+}\right)$ and arbitrarily $t,\tau \in {\mathbb{R}}_{+}$, we will derive the following expression;

$$\begin{array}{cc}\hfill \left|\left(Tz\right)\left(t\right)\right|& ⩽\left|u\left(t\right)\right|+\frac{\left|g\left(t,z\left(t\right)\right)\right|}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{\theta \left(t\right)}\frac{\left|h\left(t,\tau ,z\left(\tau \right)\right)\right|}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau \hfill \\ \hfill & ⩽\left|u\left(t\right)\right|+\left(\frac{\left|g\left(t,z\left(t\right)\right)-g\left(t,0\right)+g\left(t,0\right)\right|}{\mathsf{\Gamma }\left(\alpha \right)}\right){\int }_0^{\theta \left(t\right)}\frac{\varphi \left(\left|\right|z\left|\right|\right)\eta \left(t\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau \hfill \\ \hfill & ⩽\left|\left|u\right|\right|+\frac{1}{\mathsf{\Gamma }(\alpha +1)}\left\{\left[\rho \left(t\right)\left|\left|z\right|\right|+g\left(t,0\right)\right]\varphi \left(\left|\right|z\left|\right|\right)\eta \left(t\right)\right\}{\left(\theta \left(t\right)\right)}^{\alpha }\hfill \\ \hfill & ⩽\left|\left|u\right|\right|+\frac{\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }(\alpha +1)}\left[\left(\xi \left(t\right)\left|\left|z\right|\right|+\psi \left(t\right)\right)\right]\hfill \\ \hfill & ⩽\left|\left|u\right|\right|+\frac{\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}\left[{\xi }_b\left|\left|z\right|\right|+{\psi }_b\right]\hfill \end{array}$$

(11)

The above estimation shows that the function $\left(Tz\right)$ is bounded on the interval ${\mathbb{R}}_{+}$. Since The operator $\left(Tz\right)$ is bounded and continuous on ${\mathbb{R}}_{+}$ therefore we conclude that the operator T transforms the space $BC\left({\mathbb{R}}_{+}\right)$ into itself. Moreover, form the assumptions we deduce that there exist number $r_0>0$ such that H maps the ball $B_{r_0}$ into itself.

Next, we will show that the operator T is continuous on the ball $B_{r_0}$.

To do this, let us fix an arbitrary positive number $ϵ$ and choose $z,y\in B_{r_0}$ such that $\left|\left|z-y\right|\right|\le ϵ$. Let us choose an arbitrary $t\in {\mathbb{R}}_{+}$ then we can obtain the following expression by the virtue of assumptions $\left(c\right)\&\left(d\right)$;

$$\begin{array}{cc}\hfill \left|\left(Iz\right)\left(t\right)-\left(Iy\right)\left(t\right)\right|& ⩽|\frac{g\left(t,z\left(t\right)\right)}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{\theta \left(t\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau \hfill \\ & -\frac{g\left(t,y\left(t\right)\right)}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{\theta \left(t\right)}\frac{h\left(t,\tau ,y\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau |\hfill \\ \hfill & ⩽\left|\frac{g\left(t,z\left(t\right)\right)-g\left(t,y\left(t\right)\right)}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{\theta \left(t\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau \right|\hfill \\ \hfill & +\left|\frac{g\left(t,y\left(t\right)\right)}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{\theta \left(t\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)-h\left(t,\tau ,y\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau \right|\hfill \\ \hfill & ⩽\left|\frac{\rho \left(t\right)\left|\right|z-y\left|\right|}{\mathsf{\Gamma }(\alpha +1)}\varphi \left(\left|\right|z\left|\right|\right)\eta \left(t\right){\left(\theta \left(t\right)\right)}^{\alpha }\right|\hfill \\ \hfill & +\left|\frac{g\left(t,y\left(t\right)\right)-g\left(t,0\right)+g\left(t,0\right)}{\mathsf{\Gamma }(\alpha +1)}{\omega }^2\left(h,\epsilon \right){\left(\theta \left(t\right)\right)}^{\alpha }\right|\hfill \\ \hfill & ⩽\left|\frac{\rho \left(t\right)\left|\right|z-y\left|\right|}{\mathsf{\Gamma }(\alpha +1)}\varphi \left(\left|\right|z\left|\right|\right)\eta \left(t\right){\left(\theta \left(t\right)\right)}^{\alpha }\right|\hfill \\ \hfill & +\left|\frac{\rho \left(t\right)\left|\right|z\left|\right|+g\left(t,0\right)}{\mathsf{\Gamma }(\alpha +1)}{\omega }^2\left(h,\epsilon \right){\left(\theta \left(t\right)\right)}^{\alpha }\right|\hfill \\ \hfill & ⩽\frac{\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }(\alpha +1)}\left(\xi \left(t\right)\left|\right|z-y\left|\right|\right)\hfill \\ \hfill & +\frac{{\omega }^2\left(h,\epsilon \right)}{\mathsf{\Gamma }(\alpha +1)}\left(\rho \left(t\right){\left(\theta \left(t\right)\right)}^{\alpha }\left|\right|z\left|\right|+g\left(t,0\right){\left(\theta \left(t\right)\right)}^{\alpha }\right)\hfill \\ \hfill & ⩽\frac{\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }(\alpha +1)}\left(\xi \left(t\right)\left|\right|z-y\left|\right|\right)+\frac{{\omega }^2\left(h,\epsilon \right)}{\mathsf{\Gamma }(\alpha +1)}\left(\beta \left(t\right)\left|\right|z\left|\right|+\psi \left(t\right)\right)\hfill \end{array}$$

(12)

where

$${\omega }^2\left(h,\epsilon \right)=sup\left\{\left|h\left(t,\tau ,z\left(\tau \right)\right)-h\left(t,\tau ,y\left(\tau \right)\right)\right|:t,\tau \in {\mathbb{R}}_{+},z,y\in \mathbb{R},\left|\right|z-y\left|\right|\le \epsilon \right\}.$$

From assumption (e), it follows that ${\omega }^2\left(h,\epsilon \right)\to 0$ as $\epsilon \to 0.$

From Equations (7)–(9) we conclude that $\left(Iz\right)$ is continuous on the ball $B_{r_0}.$ The operator $Iz$ is continuous and bounded on the ball $B_{r_0}$ which implies that the operator I transform the ball $B_{r_0}$ into itself.

Let us fix an arbitrary nonempty subset W of the ball $B_{r_0}$. Choose $z\in W$ and fix the positive numbers M and $ϵ$ such that $t,s\in [0,M]$ and $|t-s|\le ϵ.$ Then from the above estimated expressions (7)–(10) we obtain

$$\begin{array}{cc}\hfill \left|\left(Tz\right)\left(t\right)-\left(Tz\right)\left(s\right)\right|& ⩽{\aleph }_M^{\left|\right|z\left|\right|}\left(u\right)+\left|\left(Hz\right)\left(t\right)\left(Iz\right)\left(t\right)-\left(Hz\right)\left(s\right)\left(Iz\right)\left(s\right)\right|\hfill \\ \hfill & ⩽{\aleph }_M^{\left|\right|z\left|\right|}\left(u\right)+\left|\left(Hz\right)\left(t\right)\right|\left|\left(Iz\right)\left(t\right)-\left(Iz\right)\left(s\right)\right|+\left|\left(Iz\right)\left(s\right)\right|\left|\left(Hz\right)\left(t\right)-\left(Hz\right)\left(s\right)\right|\hfill \\ \hfill & ⩽{\aleph }_M^{\left|\right|z\left|\right|}\left(u\right)+\left(\rho \left(t\right)\left|\right|z\left|\right|+g\left(s,0\right)\right)\{\frac{\eta \left(t\right)\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}({\left(\theta \left(t\right)-\theta \left(s\right)\right)}^{\alpha }\hfill \\ \hfill & +\frac{\eta \left(t\right)\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}\left({\left(\theta \left(t\right)-\theta \left(s\right)\right)}^{\alpha }+\left(\theta {\left(s\right)}^{\alpha }-\theta {\left(t\right)}^{\alpha }\right)\right))+\frac{{\aleph }_M^{\left|\right|z\left|\right|}\left(h\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}{\left(\theta \left(s\right)\right)}^{\alpha }\}\hfill \\ \hfill & +\frac{\eta \left(s\right)\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}{\left(\theta \left(s\right)\right)}^{\alpha }\left(\rho \left(s\right)\left|z\left(t\right)-z\left(s\right)\right|+{\aleph }_M^{\left|\right|z\left|\right|}\left(g\right)\right)\hfill \end{array}$$

(13)

Applying the supreme to both sides we obtain

$$\begin{array}{cc}\hfill {\omega }^M\left(Tz,\epsilon \right)& ⩽{\aleph }_M^{\left|\right|z\left|\right|}\left(u\right)+\left(\widehat{\rho }\left(M\right)\left|\right|z\left|\right|+\widehat{g}\left(M,0\right)\right)\left(\frac{{\aleph }_M^{\left|\right|z\left|\right|}\left(h\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}\varphi \left(\left|\right|z\left|\right|\right)\widehat{\eta }\left(M\right){\left(\widehat{\theta }\left(M\right)\right)}^{\alpha }\right)\hfill \\ \hfill & +\frac{\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}{\left(\widehat{\theta }\left(M\right)\right)}^{\alpha }\widehat{\eta }\left(M\right)\left(\widehat{\rho }\left(M\right){\omega }^M\left(z,\epsilon \right)+{\aleph }_M^{\left|\right|z\left|\right|}\left(g\right)\right)\hfill \end{array}$$

(14)

Applying $\epsilon \to 0$ we obtain

$${{\omega }_0}^M\left(Tz\right)⩽\frac{\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}{\left(\widehat{\theta }\left(M\right)\right)}^{\alpha }\widehat{\eta }\left(M\right)\widehat{\rho }\left(M\right)\left({{\omega }_0}^M\left(z\right)\right)$$

At length as $M\to \infty$ we have with the following expression,

$${\omega }^{\infty }\left(Tz\right)⩽\frac{\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }\left(\alpha +1\right)}{\xi }_b\left({\omega }^{\infty }\left(z\right)\right)$$

(15)

In what follows let us take a nonempty set $W\subset B{r}_0$. Then, for arbitrary $t\in {\mathbb{R}}_{+}$ and $z,y\in BC\left({\mathbb{R}}_{+}\right)$ such that $\left|\right|z-y\left|\right|\le ϵ$ using the assumptions $\left(b\right),\left(c\right)\&\left(e\right)$ we can derive the following expression,

$$\begin{array}{cc}\hfill \left|\left(Tz\right)\left(t\right)-\left(Ty\right)\left(t\right)\right|& ⩽|\frac{g\left(t,z\left(t\right)\right)}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{\theta \left(t\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau \hfill \\ & -\frac{g\left(t,y\left(t\right)\right)}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{\theta \left(t\right)}\frac{h\left(t,\tau ,y\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau |\hfill \\ \hfill & ⩽\left|\frac{g\left(t,z\left(t\right)\right)-g\left(t,y\left(t\right)\right)}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{\theta \left(t\right)}\frac{h\left(t,\tau ,x\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau \right|\hfill \\ \hfill & +\left|\frac{g\left(t,y\left(t\right)\right)}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{\theta \left(t\right)}\frac{h\left(t,\tau ,z\left(\tau \right)\right)-h\left(t,\tau ,y\left(\tau \right)\right)}{{\left(\theta \left(t\right)-\tau \right)}^{1-\alpha }}d\tau \right|\hfill \\ \hfill & ⩽\left|\frac{\rho \left(t\right)\left|\right|z-y\left|\right|}{\mathsf{\Gamma }(\alpha +1)}\eta \left(t\right)\varphi \left(\left|\right|z\left|\right|\right){\left(\theta \left(t\right)\right)}^{\alpha }\right|\hfill \\ \hfill & +\left|\frac{g\left(t,y\left(t\right)\right)-g\left(t,0\right)+g\left(t,0\right)}{\mathsf{\Gamma }(\alpha +1)}{\omega }^2\left(h,\epsilon \right){\left(\theta \left(s\right)\right)}^{\alpha }\right|\hfill \\ \hfill & ⩽\left|\frac{\rho \left(t\right)\left|\right|z-y\left|\right|}{\mathsf{\Gamma }(\alpha +1)}\varphi \left(\left|\right|z\left|\right|\right)\eta \left(t\right){\left(\theta \left(t\right)\right)}^{\alpha }\right|\hfill \\ \hfill & +\left|\frac{\rho \left(t\right)\left|\right|z\left|\right|+g\left(t,0\right)}{\mathsf{\Gamma }(\alpha +1)}{\omega }^2\left(h,\epsilon \right){\left(\theta \left(t\right)\right)}^{\alpha }\right|\hfill \\ \hfill & ⩽\frac{\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }\alpha +1}\left(\xi \left(t\right)\left|\right|z-y\left|\right|\right)\hfill \\ \hfill & +\frac{{\omega }^2\left(h,\epsilon \right)}{\mathsf{\Gamma }(\alpha +1)}\left(\rho \left(t\right){\left(\theta \left(t\right)\right)}^{\alpha }\left|\right|z\left|\right|+g\left(t,0\right){\left(\theta \left(t\right)\right)}^{\alpha }\right)\hfill \\ \hfill & ⩽\frac{\varphi \left(\left|\right|z\left|\right|\right)}{\mathsf{\Gamma }(\alpha +1)}\left(\xi \left(s\right)\left|\right|z-y\left|\right|\right)+\frac{{\omega }^2\left(h,\epsilon \right)}{\mathsf{\Gamma }(\alpha +1)}\left(\vartheta \left(t\right)\left|\right|z\left|\right|+\psi \left(t\right)\right)\hfill \end{array}$$

Hence, we can easily deduce the following inequality,

$$diam(TW)⩽\frac{\varphi \left(\left|\right|v\left|\right|\right)}{\mathsf{\Gamma }\alpha +1}{\xi }_b\left(diam\left(W\right)\right)$$

Hence, from assumption $\left(f\right)$ and expression (5) we can deduce the following inequality,

$$B(TW)⩽\frac{\varphi \left(\left|\right|v\left|\right|\right)}{\mathsf{\Gamma }(\alpha +1)}{\xi }_b\left(B\left(W\right)\right)$$

(16)

From Equations (6), (15) and (16) we obtain

$$\begin{array}{cc}\hfill \sigma \left(TW\right)& ={\omega }^{\infty }(TW)+B(TW)\hfill \\ \hfill & ⩽\frac{\varphi \left(\left|\right|v\left|\right|\right)}{\mathsf{\Gamma }(\alpha +1)}{\xi }_b\left({\omega }^{\infty }\right(W))+\frac{\varphi \left(\left|\right|v\left|\right|\right)}{\mathsf{\Gamma }(\alpha +1)}{\xi }_b\left(B\left(W\right)\right)\hfill \\ \hfill & ⩽\frac{\varphi \left(\left|\right|v\left|\right|\right)}{\mathsf{\Gamma }(\alpha +1)}{\xi }_b\sigma \left(W\right)\hfill \end{array}$$

(17)

By the virtue of assumption $\left(f\right)$ and properties of functions $G\&\psi$ we derive the following expression,

$$G\left(\sigma \left(TW\right)\right)⩽\psi \left(G\left(\sigma \left(W\right)\right)\right)$$

(18)

where $G:(0,\eta )\to \mathbb{R}$ by $G\left(y\right)=ln\left(y\right)$ and $\psi :\left(-\infty ,0\right)\to \left(-\infty ,0\right)$ by $\psi \left(w\right)=w-\tau$. Linking the expression (18) with Theorem 6 of Section 2 and assuming the properties of $G\&\psi$ we obtain the desired result. In the view of the definition of measure of noncompactness we conclude that the solution of an integral Equation (1) has a finite limit at infinity. □

Now we will discuss an illustrative example for the obtained result.

4.2. Numerical Example

Consider the following fractional-order integral equation in the Banach space $BC\left({\mathbb{R}}_{+}\right)$;

$$z\left(s\right)=\frac{s^2}{s^2+1}+\frac{1}{1+s^3}\frac{arctan\left(a+z\left(s\right)\right)}{\mathsf{\Gamma }\left(\alpha \right)}\underset{0}{\overset{s}{\int }}\frac{\left({\tau }^2{s}^2{e}^{-s}{\left(z\left(s\right)\right)}^2+\frac{s^4}{{\tau }^{\frac{1}{4}}+1}sin\left({z\left(s\right)}^2\right)\right)}{{\left(s-\tau \right)}^{1-\alpha }}d\tau .$$

(19)

$$\left(\alpha \in (0,1],s\in BC\left({\mathbb{R}}_{+}\right)\right)$$

Suppose that $\alpha =1/4$ then we obtain

$$z\left(s\right)=\frac{s^2}{s^2+1}+\frac{1}{1+s^3}\frac{arctan\left(a+z\left(s\right)\right)}{\mathsf{\Gamma }(1/4)}\underset{0}{\overset{s}{\int }}\frac{\left({\tau }^2{s}^2{e}^{-s}{\left(z\left(s\right)\right)}^2+\frac{s^4}{{\tau }^{\frac{1}{4}}+1}sin\left({z\left(s\right)}^2\right)\right)}{{\left(s-\tau \right)}^{1-\frac{1}{4}}}d\tau ,$$

(20)

where $s\in {\mathbb{R}}_{+},\&a\in \mathbb{R}-\left\{0\right\}.$

Notice that the integral Equation (20) is particular case of integral Equation (1).

Indeed, if we replace $\alpha =\frac{1}{4}$ and

$$\begin{array}{cc}\hfill u\left(s\right)& =\frac{as}{s^2+1}\hfill \end{array}$$

$$\begin{array}{cc}\hfill g\left(s,z\left(s\right)\right)& =\frac{1}{1+s^6}arctan\left(\left|a\right|+v\left(s\right)\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill h\left(s,t,z\left(t\right)\right)& =t^2{s}^2{e}^{-s}{z}^2+\left(\frac{s^4}{t^{\frac{1}{4}}+1}\right)sin\left(z^2\right).\hfill \end{array}$$

(21)

In fact, we have functions $u\left(s\right)=\frac{as}{s^2+1}$ and $g\left(s,z\left(s\right)\right)=\frac{1}{1+s^6}arctan\left(\left|a\right|+z\left(s\right)\right)$ satisfies assumption (a) and (b). The function $g\left(s,z\left(s\right)\right)$ satisfies assumption (b) with $\rho \left(s\right)=\frac{1}{1+s^6}$ and $g\left(s,0\right)=\frac{1}{1+s^6}arctan\left(\left|a\right|\right).$ The function

$$h\left(s,t,z\left(t\right)\right)=t^2{s}^2{e}^{-s}{z}^2+\left(\frac{s^4}{t^{\frac{1}{4}}+1}\right)sin\left(z^2\right)$$

satisfies the assumption (c) with $\eta \left(s\right)=s^4{e}^{-s}+\frac{s^4}{s^{\frac{1}{4}}+1}$ and $\varphi \left(r\right)=r^2.$

Now to show the functions $\xi ,\vartheta ,\psi$ satisfies the assumption $\left(e\right)$ we have the following expressions,

$$\xi \left(s\right)=\left(\frac{s^4.e^{-s}}{s^4+1}+\frac{s^4{\left(s\right)}^{\frac{1}{4}}}{\left(s^{\frac{1}{4}}+1\right)s^4+1}\right),\vartheta \left(s\right)=\frac{s^{\frac{1}{4}}}{1+s^4},\psi \left(s\right)=\frac{s^{\frac{1}{4}}}{1+s^6}arctan\left(s\right).$$

It has been easily seen that all the above-defined functions are bounded on ${\mathbb{R}}_{+}$ among them $\psi ,\vartheta$ vanishes at infinity i.e., $\underset{s\to \infty }{lim}\psi \left(s\right)=\underset{s\to \infty }{lim}\vartheta \left(s\right)=0.$ So all the conditions of Theorem 7 are satisfied by the integral Equation (20). Hence, the integral equation admits at least one solution in the space $BC\left({\mathbb{R}}_{+}\right)$.

To find the set of fixed points of Equation (20), using (c), we have the approximated solution for $a=1$

$$z\left(s\right)={\displaystyle \frac{2.93379s^{1/4}z\left(s\right)arctan(z\left(s\right)+1)}{s^3+1}}+{\displaystyle \frac{s^2}{s^2+1}}.$$

A calculation implies that the set of fixed points $fi{x}_{\alpha }(a,s)$ is

$$fi{x}_{1/4}(1,s)=\{s_1=0,s_2=0.188507,s_3=1.35044\}.$$

For $\alpha =1/2,$ we have the solution formula

$$z\left(s\right)={\displaystyle \frac{1.46689\sqrt{s}z\left(s\right)arctan(z\left(s\right)+1)}{s^3+1}}+{\displaystyle \frac{s^2}{s^2+1}}.$$

A computation yields that the set of fixed points is

$$fi{x}_{1/2}(1,s)=\{s_1=0,s_2=0.304319,s_3=1.42606\}.$$

Finally, we consider $\alpha =3/4$ and $a=1,$ then we obtain the solution

$$z\left(s\right)={\displaystyle \frac{1.41421s^{3/4}z\left(s\right)arctan(z\left(s\right)+1)}{s^3+1}}+{\displaystyle \frac{s^2}{s^2+1}};$$

consequently, the set of fixed point is as follows:

$$fi{x}_{3/4}(1,s)=\{s_1=0,s_2=0.411379,s_3=1.47203\}.$$

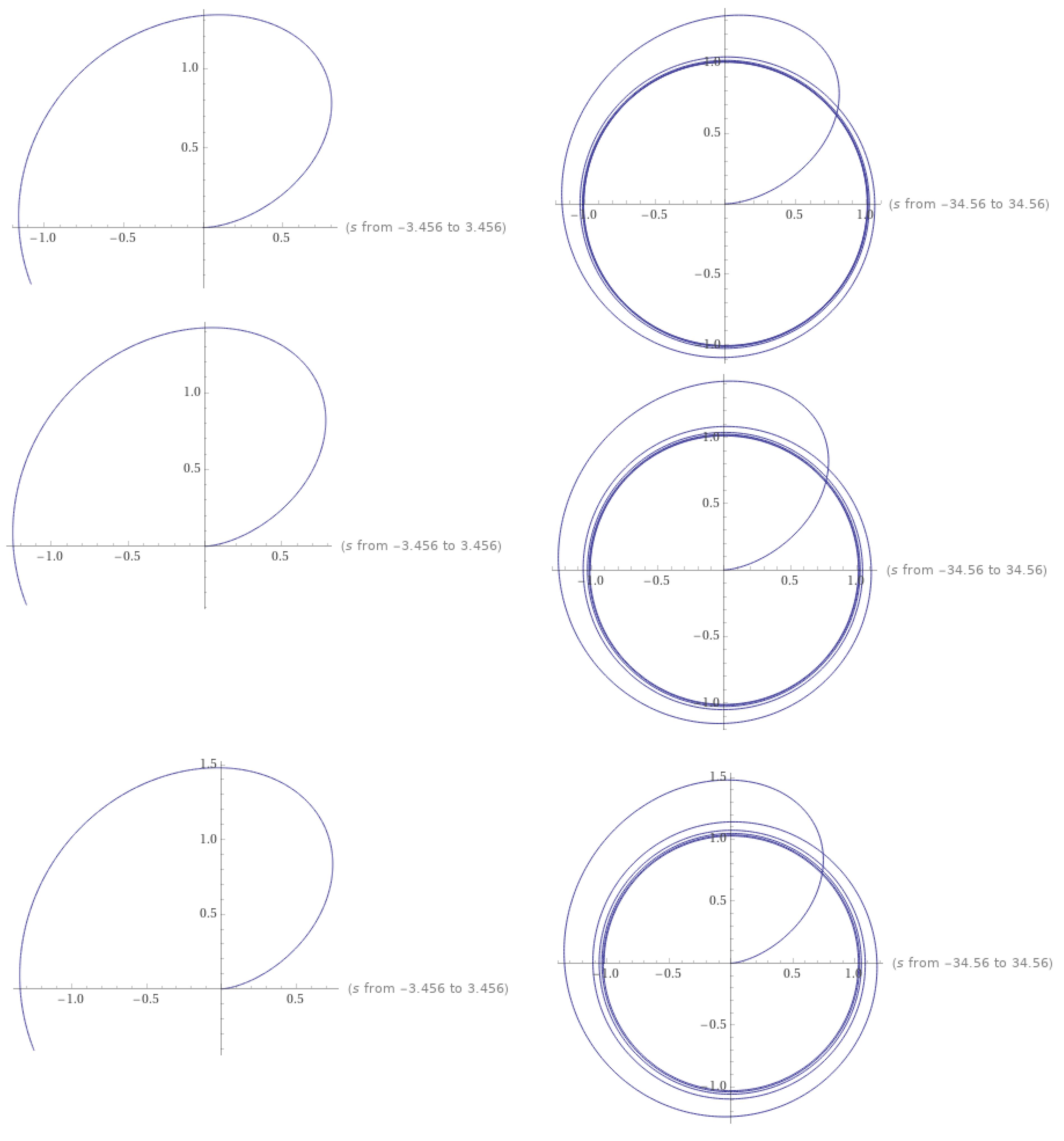
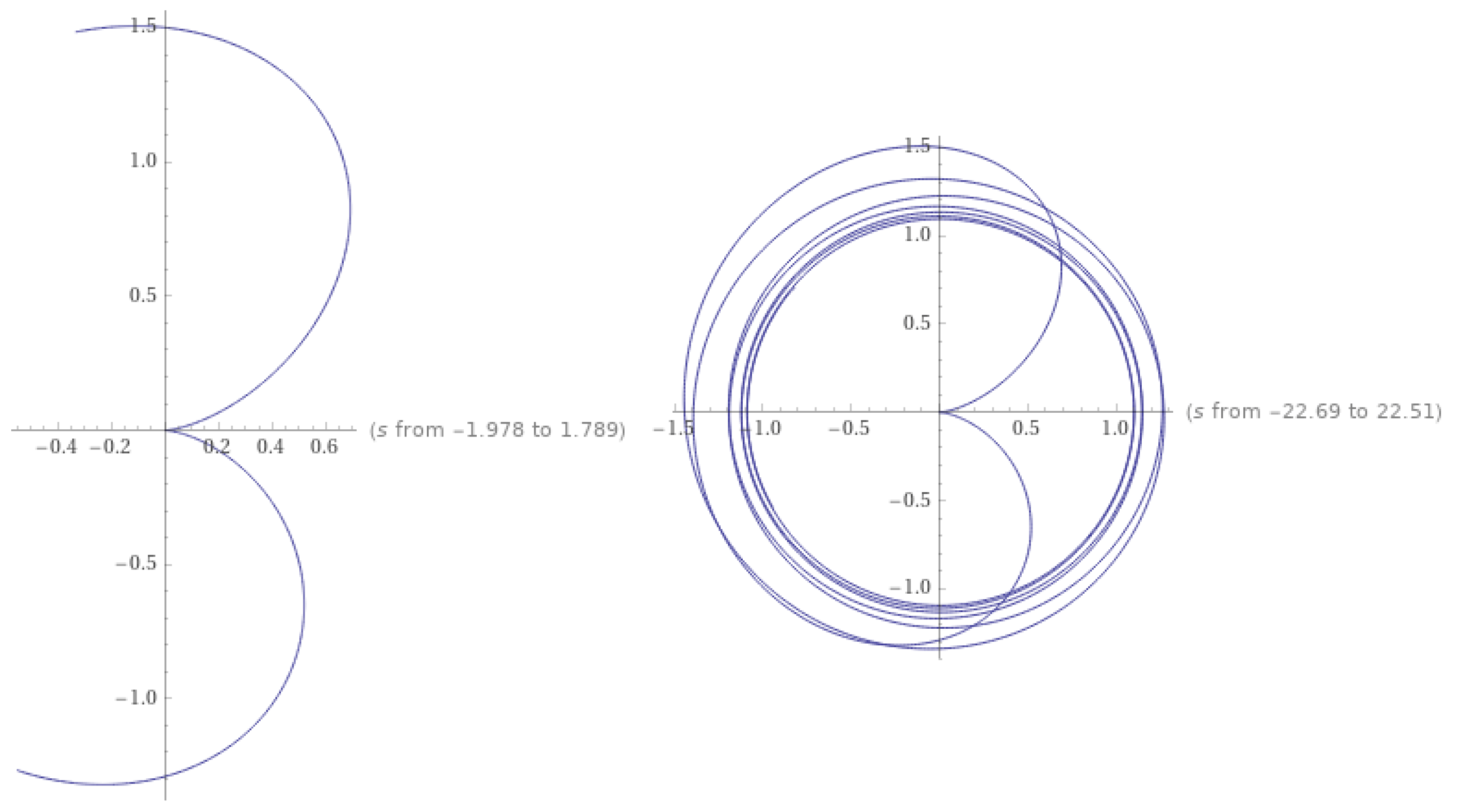
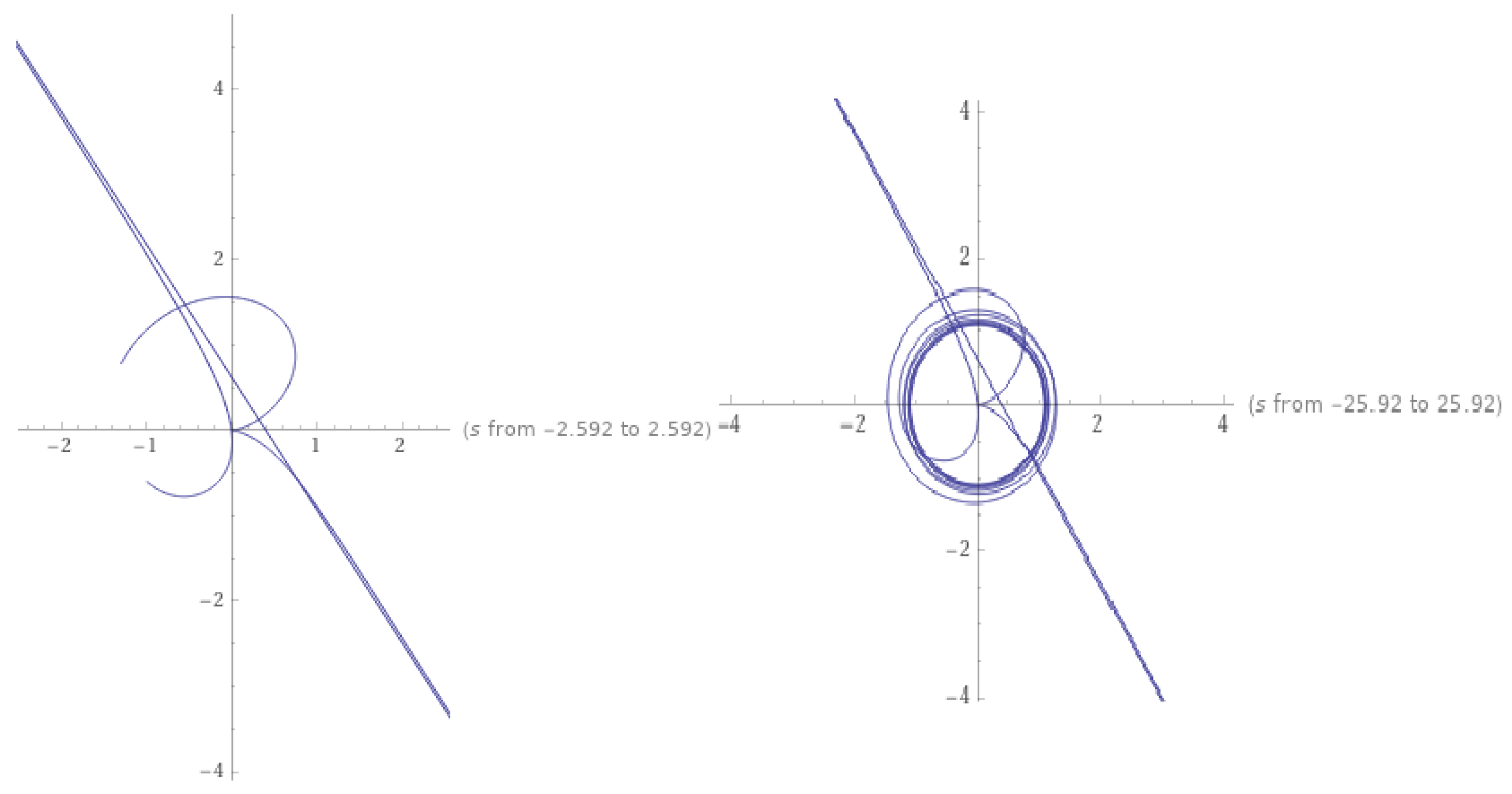
Figure 1 shows the stable periodicity solutions of the integral equation $z\left(s\right)$ depending on the fixed points. Figure 2 indicates the solution for the ordinary case when $\alpha =1$ and $a=1.$ In this case, we obtain

$$z\left(s\right)={\displaystyle \frac{1.3sz\left(s\right)arctan\left(z\right(s)+1)}{s^3+1}}+{\displaystyle \frac{s^2}{s^2+1}}$$

and

$$fi{x}_1(1,s)=\{s_1=0,s_2=0.513503,s_3=1.50813\}.$$

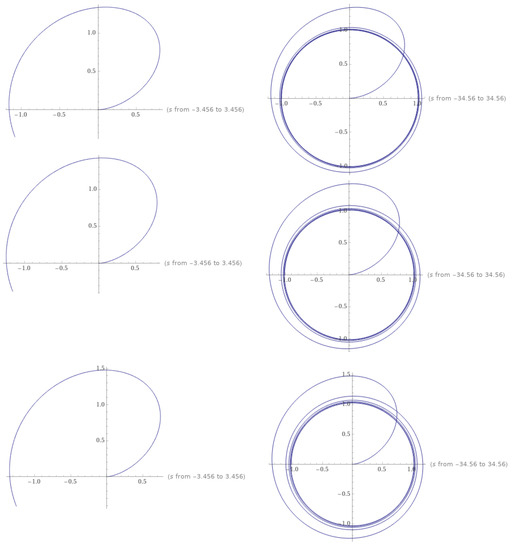
Figure 1. The stable periodicity solution of $z\left(s\right)$ based on the set of fixed points when $\alpha =1/4,1/2,3/4$ respectively.

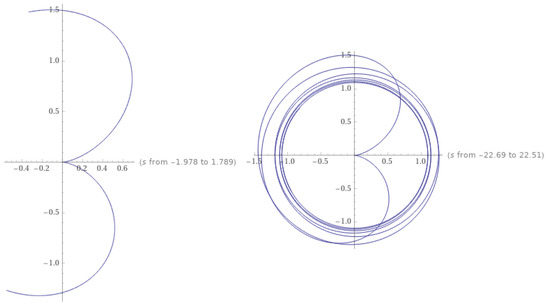
Figure 2. The stable periodicity solution of $z\left(s\right)$ based on the set of fixed points when $\alpha =1$ and $a=1$.

Figure 3 represents the solution for the ordinary case when $\alpha =1$ and $a=2.$ In this case, we have

$$z\left(s\right)={\displaystyle \frac{1.3sz\left(s\right)arctan\left(z\right(s)+2)}{s^3+1}}+{\displaystyle \frac{s^2}{s^2+1}}$$

and

$$fi{x}_1(2,s)=\{s_1=0,s_2=0.436612,s_3=1.58647\}.$$

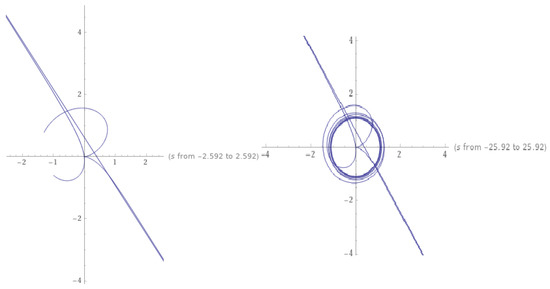
Figure 3. The solution of $z\left(s\right)$ based on the set of fixed points when $\alpha =1$ and $a=2$.

4.3. Convergence to the Fixed Point

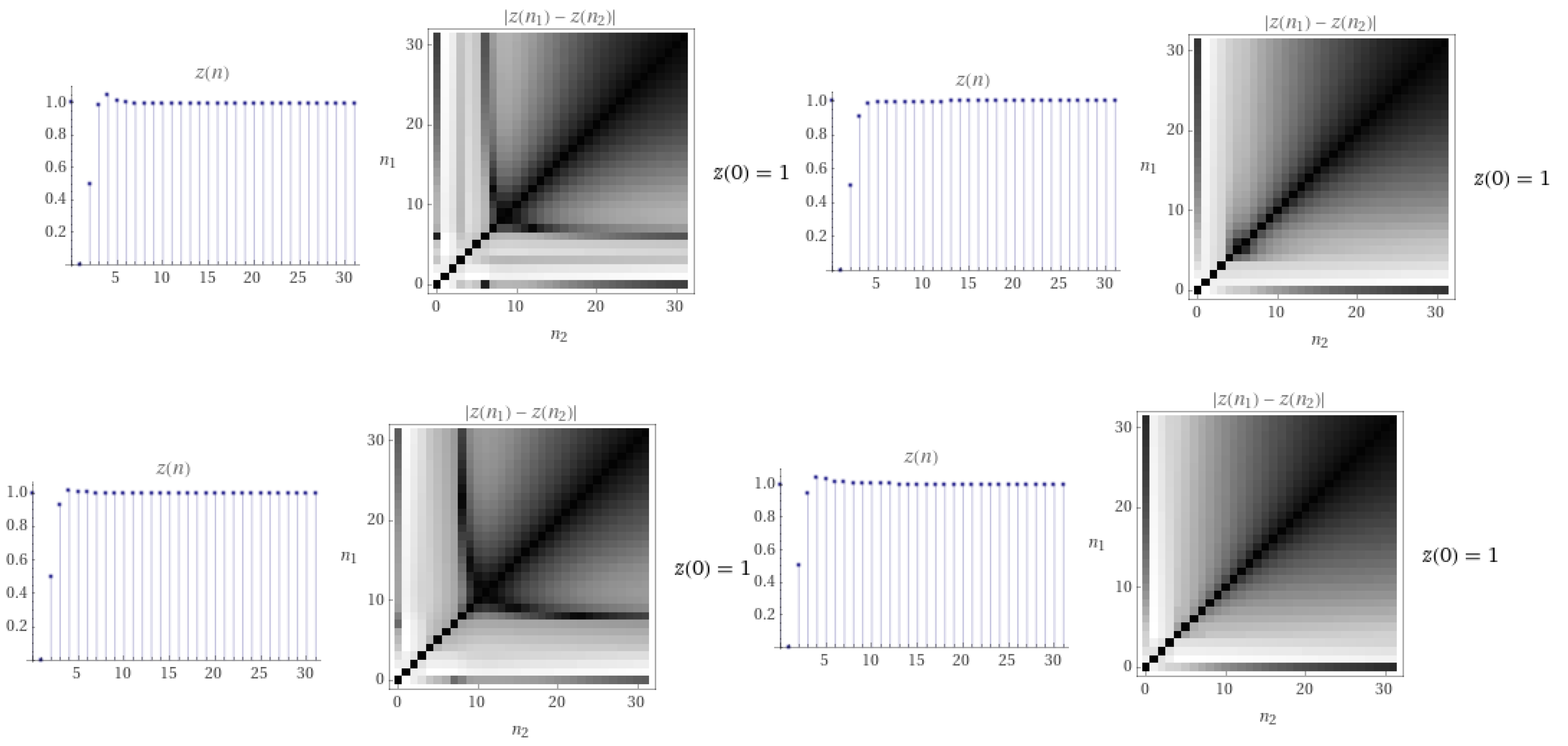
In this place, we iterate the solution of the integral Equation (19). We start with $\alpha =1/4,$ the iteration solution imposes (see Figure 4)

$$\begin{array}{cc}\hfill z(n+1)& ={\displaystyle \frac{2.9n^{1/4}z\left(n\right)arctan(z\left(n\right)+1)}{n^3+1}}+{\displaystyle \frac{n^2}{1+n^2}}\hfill \\ \hfill & ={\displaystyle \frac{n^{1/4}\left(n^{7/4}+n^{19/4}+2.9n^{2}z\left(n\right)arctan(z\left(n\right)+1)+2.9z\left(n\right)arctan(z\left(n\right)+1)\right)}{(n^2+1)(n^3+1)}}.\hfill \end{array}$$

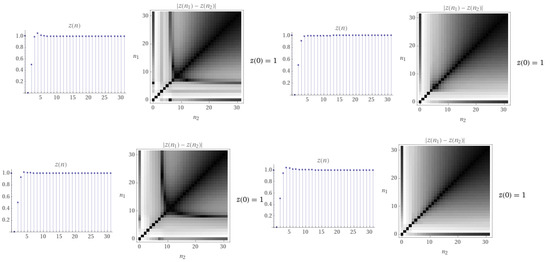
Figure 4. The iteration solution of $z\left(n\right)$ for $\alpha =1/4,1/2,3/4,1$ respectively.

For $\alpha =1/2$ we obtain the iteration solution

$$\begin{array}{cc}\hfill z(n+1)& ={\displaystyle \frac{1.4n^{1/2}z\left(n\right)arctan(z\left(n\right)+1)}{n^3+1}}+{\displaystyle \frac{n^2}{1+n^2}}\hfill \\ \hfill & ={\displaystyle \frac{n^{1/2}\left(n^{9/2}+n^{3/2}+1.4n^{2}z\left(n\right)arctan(z\left(n\right)+1)+1.4z\left(n\right)arctan(z\left(n\right)+1)\right)}{(n^2+1)(n^3+1)}}.\hfill \end{array}$$

Moreover, for $\alpha =3/4$ we obtain

$$\begin{array}{cc}\hfill z(n+1)& ={\displaystyle \frac{1.4n^{3/4}z\left(n\right)arctan(z\left(n\right)+1)}{n^3+1}}+{\displaystyle \frac{n^2}{1+n^2}}\hfill \\ \hfill & ={\displaystyle \frac{n^{3/4}\left(n^{5/4}+n^{17/4}+1.4n^{2}z\left(n\right)arctan(z\left(n\right)+1)+1.4z\left(n\right)arctan(z\left(n\right)+1)\right)}{(n^2+1)(n^3+1)}}.\hfill \end{array}$$

Finally, we assume that $\alpha =1$ then we have

$$\begin{array}{cc}\hfill z(n+1)& ={\displaystyle \frac{1.3nz\left(n\right)arctan\left(z\right(n)+1)}{n^3+1}}+{\displaystyle \frac{n^2}{1+n^2}}\hfill \\ \hfill & ={\displaystyle \frac{n\left(n^4+1.3n^{2}z\left(n\right)arctan(z\left(n\right)+1)+1.3z\left(n\right)arctan(z\left(n\right)+1)\right)}{(n^2+1)(n^3+1)}}.\hfill \end{array}$$

Table 1 shows the number of iterations and the error, which calculated by $|z\left(n\right)-s_i|,i=1,2,3.$

Table 1. Iteration solution of Equation (19).

$\mathit{\alpha }$	n	0	1	2	3	4	Error = $|\mathit{z}\left(\mathit{n}\right)-{\mathit{s}}_{\mathit{i}}|$
1/4	z(n)	1	0	0.5	0.98829	1.04883	0.301
1/2	z(n)	1	0	0.5	0.908102	0.98557	0.41
3/4	z(n)	1	0	0.5	0.928555	1.01562	0.454
1	z(n)	1	0	0.5	0.941959	1.0437	0.464

5. Conclusions

In our current work, we defined $\beta$G-contraction and $\psi$G-contraction of Darbo type and proved corresponding fixed-point theorems using $M.N.C$. Furthermore, the fixed-point theorem proved in Section 2 is applied to demonstrate the existence of a solution of fractional-order integral equation. At the end, an example is given to validate the result. We indicate that the values of the fixed-point increase whenever the values of $\alpha$ increase in $(0,1].$ Moreover, the set of fixed points imposed the periodicity and stability of the fractional integral Equation (20). All figures are presented with the help of Mathematica 11.2.