Multidimensional Dominance Drawings and Their Applications

Abstract

In a dominance drawing $\Gamma$ of a directed acyclic graph (DAG) G, a vertex v is reachable from a vertex u if, and only if all the coordinates of v are greater than or equal to the coordinates of u in $\Gamma$. Dominance drawings of DAGs are very important in many areas of research. They combine the aspect of drawing a DAG on the grid with the fact that the transitive closure of the DAG is apparently obvious by the dominance relation between grid points associated with the vertices. The smallest number d for which a given DAG G has a d-dimensional dominance drawing is called dominance drawing dimension, and it is NP-hard to compute. In this paper, we present efficient algorithms for computing dominance drawings of G with a number of dimensions respecting theoretical bounds. We first describe a simple algorithm that shows how to compute a dominance drawing of G from its compressed transitive closure. Next, we describe a more complicated algorithm, which is based on the concept of modular decomposition of G, and obtaining dominance drawings with a lower number of dimensions. Finally, we consider the concept of weak dominance, a relaxed version of the dominance, and we discuss interesting experimental results.

1. Introduction

Dominance drawings of directed acyclic graphs (DAGs) are very important in many areas of research, including graph drawing [1], computational geometry [2], and information visualization [3], even in very large databases [4], just to mention a few. They combine the aspect of drawing a DAG on the grid with the fact that the transitive closure of the DAG is apparently obvious by the dominance relation between grid points associated with the vertices. In other words, in a dominance drawing, a vertex v is reachable from a vertex u if, and only if all the coordinates of v are greater than or equal to the coordinates of u in $\Gamma$. Notice that it is not possible to find dominance drawings in two-dimensions for most DAGs. The smallest number d for which a given DAG G has a d-dimensional dominance drawing is called a dominance drawing dimension, and it is NP-hard to compute [5]. We denote by $dd\left(G\right)$ the dominance drawing dimension of G. In this paper, we present algorithms for computing a k-dimensional dominance drawing of G, where $k\ge dd\left(G\right)$. Our algorithms are efficient and based on various decomposition techniques.

An $st$-graph is a DAG with one source s and one sink t. Every DAG can be transformed into an $st$-graph by adding a virtual source and connecting it to all the sources and by adding a virtual sink and connecting all the sinks to it. In this paper, we assume, without loss of generality, that every DAG is an $st$-graph. Let $G=(V,E)$ be an $st$-graph. There are linear-time algorithms for computing two-dimensional dominance drawings of $st$-graphs that are planar ($st$-planar graphs) [6]. For non-planar $st$-graphs, more than two dimensions are usually required. A k-dimensional ($k\ge 1$) drawing of G is a drawing of G having k dimensions that we denote by $D_1,\dots ,D_k$. For every $h\in [1,k]$ and $v\in V$, $D_h\left(v\right)$ is the coordinate in the dimension $D_h$ of v. In a k-dimensional dominance drawing of G, given any two vertices $u,v\in V$, $D_h\left(u\right)\le D_h\left(v\right)$ for every $h\in [1,k]$ if, and only if there exists a directed path connecting u to v in G. In this paper, we assume that every path is a directed path. Hence, from now on we omit the word “directed”.

The minimum k such that there exist a k-dimensional dominance drawing of G (its dominance dimension) is $dd\left(G\right)$. A partially ordered set (poset) is a mathematical formalization of the concept of ordering. Any partially ordered set P can be viewed as a transitive DAG. The dimension of a poset is equivalent to the dominance dimension of the corresponding $st$-graph and the results obtained for $st$-graphs and their dominance drawing dimension transfer directly to partial orders and their dimension, and vice versa (see [5] for a formal definition of poset and dimension of a poset). Hence, it follows that we can talk about the known results for partial orders and for $st$-graphs with no distinction.

Testing whether an $st$-graph has a dominance dimension of two requires linear time [7,8]. In particular, [7] gives a necessary and sufficient condition for the test, and [8] presents the linear-time algorithm. It is NP-complete to decide whether $dd\left(G\right)$ is greater than or equal to 3 [5]. A linear-time algorithm that constructs two-dimensional dominance drawings of upward planar graphs is described in [2] (see also [6]). We report the above results in the following lemma:

Lemma 1.

For any $st$-graph G, it is possible to decide in linear time if $dd\left(G\right)=2$ [7,8], while it is NP-complete to decide if $dd\left(G\right)=k$ for any $k\ge 3$ [5]. If G is upward planar, it is possible to construct a two-dimensional dominance drawing of G in linear time [2].

Given a k-dimensional dominance drawing of a DAG G, it is possible to test the existence of a path connecting any two vertices of G in $O\left(k\right)$ time. DAGs are used to represent information in databases. Computing dominance drawings of such DAGs having a low number of dimensions would be important in practice. Unfortunately, most of the existing algorithms for constructing dominance drawings require the input DAG to have specific properties, for example, to be planar, as stated in Lemma 1. For this reason, a relaxed version of dominance drawing, called weak dominance drawing, was introduced in [9]. The “if and only if” condition of dominance becomes an “if” condition in the weak dominance. This implies that the non-existence of a path between the two vertices is guaranteed by finding a dimension D for which $D\left(u\right)>D\left(v\right)$, but the existence of a path is not guaranteed even if $D\left(u\right)\le D\left(v\right)$ for all dimensions D of $\Gamma$. Hence, there is a falsely implied path (fip) between u and v when there is no path between u and v, even though $D\left(u\right)\le D\left(v\right)$ for every dimension D of $\Gamma$. The existence of fips cannot be excluded since the number of dimensions in a weak dominance drawing is typically significantly less than $dd\left(G\right)$.

Li, Hua, and Zhou considered high-dimensional weak dominance drawings in order to obtain efficient solutions to the reachability query problem [10]. Their experimental results show that their algorithms compute weak dominance drawings using few dimensions and having few fips. Extending their work, Lionakis et al. [11] showed that, for the same families of graphs considered in [10] and by using a number of dimensions similar to the one used in [10], it is possible to compute dominance drawings (i.e., 0 fips).

The technique used in [11] is similar to the one described in Section 2 of this paper. The computational time required to compute dominance drawings in [11] is still higher than the one to compute weak dominance drawings [10]. However, these results suggest that a possible direction for this line of research is to actually use directly dominance drawings instead of weak dominance drawings.

This technique is based on the concept of compressed transitive closure, which is a data structure introduced in [12] that can be used to answer any reachability query in $O\left(1\right)$ and requires $O\left(kn\right)$ space, where k is a parameter less than or equal to n.

In Section 3, we present algorithms that compute dominance drawings with a reduced number of dimensions, k, and show that k is a good upper bound of the dominance dimension number of a DAG. These algorithms are based on a clever decomposition of a DAG denoted by modular decomposition, where a module of a DAG $G=(V,E)$ is a set of vertices M of the G having the same set of predecessor and successors in $V\backslash M$. We also show an interesting family of DAGs for which the number of required dimensions is reduced to a small constant.

Next, we discuss the option of using weak dominance more extensively and close our paper by presenting our conclusions and future research challenges.

2. Compressed Transitive Closure and Dominance Drawings

Let $G=(V,E)$ be an $st$-graph with n vertices and m edges. Two vertices $u,v\in V$ are incomparable if there is no path from u to v or from v to u in G. The width of G, denoted by f, is the cardinality of the largest set $U\subseteq V$ such that, for every $u,v\in U$, u and v are incomparable. Given any $st$-graph G, the following lemma describes well-known relationships between its dominance dimension $dd\left(G\right)$, number of vertices n, and width f.

Lemma 2.

Let G be an $st$-graph, n be its number of vertices, and f be its width. The two following inequalities hold:

(1) 

$dd\left(G\right)\le \frac{n}{2}$ [13,14];

(2) 

$dd\left(G\right)\le f$ [14].

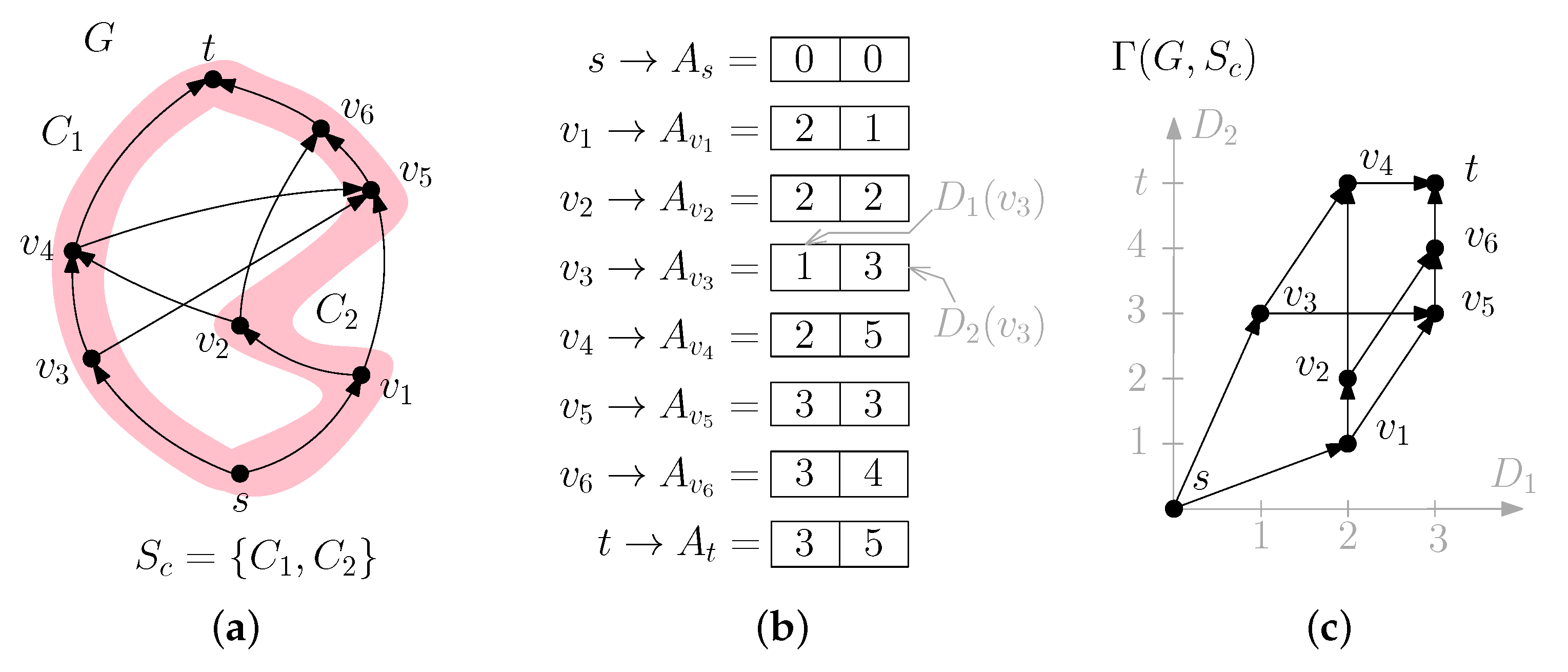
Let s and t be the source and sink of G. A chain of G is an ordered set of vertices $C\subseteq V$ such that, given any two vertices $u,v\in C$, u precedes v in the order of C if, and only if there is a path from u to v in G. See, for example, Figure 1a, where $C_1=\{s,v_3,v_4,t\}$ and $C_2=\{s,v_1,v_2,v_5,v_6,t\}$ are two chains of G.

Definition 1.

A chain cover $S_c$ of G is a set of chains of G having the following two properties:

(a) 

$S_c$ is a partition of $G\backslash \{s,t\}$;

(b) 

s and t are contained in every chain of $S_c$.

An antichain A is a set of vertices such that any pair of vertices $v,w\in A$ is incomparable. Notice that the maximum cardinality of an antichain is equivalent to the width of G. Dilworth [15] proves that the minimum number of chains needed to cover all the vertices of an $st$-graph G is equivalent to the maximum cardinality of the antichain G. We have the following lemma:

Lemma 3.

Let G be an $st$-graph with n vertices and let f be its width. The minimum cardinality of a chain cover of G is f [15]. Additionally, it is possible to compute a chain cover of G with cardinality f in $O\left(f{n}^2\right)$ time [16].

See Figure 1a, where $S_c=\{C_1,C_2\}$ is a chain cover of graph G. Since $f=|S_c|=2$, by Lemma 3 $S_c$ is a chain cover of G with minimum cardinality.

For the rest of this paper, we assume that $G=(V,E)$ is an $st$-graph and we denote by n, m, and f the number of vertices, the number of edges, and the width of G, respectively. By Inequality (2) of Lemma 2, we have $dd\left(G\right)\le f$. In this section, we present a simple and efficient algorithm to compute an f-dimensional dominance drawing of G. We first show how to compute a data structure called the compressed transitive closure of G [12], and then we show that this data structure can be easily used to obtain a dominance drawing.

The compressed transitive closure was presented in [12]. Given a chain cover of G of size k, the compressed transitive closure is a set of n arrays of size k, each one associated to a vertex of G. The compressed transitive closure is an efficient tool for answering reachability queries that has low storage requirements and, as we are going to show later, it can be computed in $O\left(km\right)$ time if a chain cover $S_c$ is given as an input, where k is the cardinality of $S_c$.

As we are going to observe later, the compressed transitive closure can answer any reachability query in $O\left(1\right)$ time, and not $O\left(k\right)$. Similarly, the dominance drawing described in this section can be used to answer any reachability query in $O\left(1\right)$ time. We show that if we see every array of the compressed transitive closure as the coordinates of the corresponding vertex of G in an k-dimensional drawing $\Gamma$ of G, then drawing $\Gamma$ is a dominance drawing of G.

Given a chain cover $S_c$ of cardinality k, computing the compressed transitive closure requires $O\left(km\right)$ time. Since computing $S_c$ having cardinality f requires $O\left(f{n}^2\right)$ time by Lemma 3, we have that it is possible to compute an f-dimensional dominance drawing of any DAG G in $O\left(f{n}^2\right)$ time. To the best of our knowledge, this is the first polynomial-time algorithm to compute a dominance drawing of G in f dimensions.

Let $S_c=\{C_1,\dots ,C_k\}$ be a chain cover of G. As we said before, we show that the compressed transitive closure of G given $S_c$ can be seen as a k-dimensional dominance drawing of G. Before defining the compressed transitive closure, we introduce some notation. By Property (a) of a chain cover, each vertex v of $G\backslash \{s,t\}$ belongs to exactly one chain, say $C_i$, of $S_c$. We denote v by $(i,j)$ meaning that v is the jth vertex of chain $C_i\in S_c$. A similar notation is also used in [12,16]. By Property (b) of a chain cover, s and t belong to every chain of $S_c$, and we define $s=(i,0)$ and $t=(i,|C_i\left|\right)$ for every $i\in [1,k]$. An example is shown in Figure 1a. According to this notation, we have: $v_1=(2,1)$; $v_2=(2,2)$; $v_3=(1,1)$; $v_4=(1,2)$; $v_5=(2,3)$; $v_6=(2,4)$; $s=(1,0)=(2,0)$; $t=(2,5)=(1,3)$.

As we said before, the compressed transitive closure of G given a chain cover $S_c=\{C_1,\dots ,C_k\}$ of G is a data structure that can answer any reachability query in $O\left(1\right)$ time that can be computed in $O\left(km\right)$ time and that requires $O(kn$) space. More precisely, it is a set of n arrays of integers of size k so that every vertex u of G is assigned to the reachability array $A_u$, and the following property holds:

Property 1

(Reachability Property [12]). Let u be any vertex of G and $A_u$ be its reachability array. For any vertex $v=(p,q)$ of G there exists a directed path from u to v if, and only if $A_u\left[p\right]\le q$.

In other words, vertex $u^{\prime }=(p,A_u\left[p\right])$ is the vertex having the lowest position in $C_p$ so that there is a path from u to $u^{\prime }$. Consequently, there is a path from u to a vertex $v\in C_p$ if, and only if the position q of $v=(p,q)$ in $C_p$ is not lower than the position $A_u\left[p\right]$ of $u^{\prime }$ in $C_p$. Notice that if $u=v$, then the directed path exists and it is the empty path and, consequently, $u=(p,q)=(p,A_u\left[p\right])$.

Figure 1b shows the compressed transitive closure of G given the chain cover $S_c=\{C_1,C_2\}$ shown in Figure 1a. Concerning s and t, we have: $s=(1,0)=(2,0)$ and $A_s\left[1\right]=A_s\left[2\right]=0$; $t=(1,3)=(2,5)$, $A_t\left[1\right]=3$, and $A_t\left[2\right]=5$. Regarding the other vertices, for example, vertex $v_1$, we have $v_1=(2,1)$ and $A_{v_1}\left[2\right]=1$. Vertex $v_4$ is the vertex having the lowest position in $C_1$ so that there exists a directed path $\pi =\{(v_1,v_2),(v_2,v_4)\}$ from $v_1$ to $v_4$. Additionally, $v_4=(1,2)$. The value in position 1 of the reachability array of $v_1$ equals the position of $v_4$ in $C_1$ and, consequently, $A_{v_1}\left[1\right]=2$.

We now present the algorithm to compute the compressed transitive closure [12]. The input is an $st$-graph $G=(V,E)$ and a chain cover $S_c=\{C_1,\dots ,C_k\}$ of G. The output is the reachability array $A_u$ for every $u\in V$, that is, the compressed transitive closure of G given $S_c$. The Algorithm 1 has two steps: the Initialization and the Update.

Algorithm 1 Compressed transitive closure computation.

⋆ Input: An $st$-graph $G=(V,E)$ and a chain cover $S_c=\{C_1,\dots ,C_k\}$ of G ⋆ Output: The array $A_v$ for every $v\in V$. Initialization: For any $u=(i,j)\in G$ and $h\in [1,k]$: If $h=i$, v given as $A_u\left[h\right]=v$; else, $A_u\left[h\right]=t$, where t is the sink of G. Update: Compute a topological order T of G. For every $l=n,\dots ,1$: Let $u=(i,j)$ be the vertex so that $T\left(u\right)=l$; Let $u_1,\dots ,u_c$ be the vertices so that $(u,w)\in E$ for any $w\in \{u_1,\dots ,u_c\}$; For every $w\in \{u_1,\dots ,u_c\}$ and every $h\in [1,k]$: $A_u\left[h\right]=min\{A_u\left[h\right],A_w\left[h\right]\}$.

Observe that the above algorithm requires $O\left(kn\right)$ time, since, for every vertex of the graph, you compute k operations. See the Step Update 3. We now show that if we use the reachability array $A_u$ as the coordinates of u in a k-dimensional drawing of G for every vertex u, then we obtain a dominance drawing. See Algorithm 2.

Algorithm 2 CC-Draw (Chain Cover Draw).

⋆ Input: An $st$-graph $G=(V,E)$ and a chain cover $S_c=\{C_1,\dots ,C_k\}$ of G ⋆ Output: A k-dimensional drawing $\Gamma$ of G. • Compute the compressed transitive closure of G given $S_c$. • Compute k-dimensional drawing $\Gamma$ of G having dimensions $D_1,\dots ,D_k$ such that, for every $h\in [1,k]$ and for every $u\in V$, $D_h\left(u\right)=A_u\left[h\right]$.

We denote by $\Gamma (G,S_c)$ the output of Algorithm 1 when G and $S_c$ are given to the algorithm as an input. Refer to Figure 1. Figure 1c depicts the two-dimensional dominance drawing of G computed by using the chain cover $S_c=\{C_1,C_2\}$ depicted in Figure 1a. The compressed transitive closure of G given $S_c$ is depicted in Figure 1b. For example, $A_{v_3}=[1,3]$ and, consequently, $D_1\left(v_3\right)=1$ and $D_2\left(v_3\right)=3$.

Two vertices are placed in the same position in $\Gamma (G,S_c)$ if $D_h\left(u\right)=D_h\left(v\right)$ for every $h\in [1,k]$. In a drawing of a graph, two distinct vertices are never placed in the same position by definition. The following lemma shows that two vertices are never placed in the same position in $\Gamma (G,S_c)$ and that, consequently, $\Gamma (G,S_c)$ is a drawing of G.

Lemma 4.

Let $S_c$ be a chain cover of G and let u and v be any two distinct vertices of G. Vertices u and v are not placed in the same position in $\Gamma (G,S_c)$.

Proof. 

Let $S_c=\{C_1,\dots ,C_l\}$, $u=(i,j)$, and $v=(p,q)$. Suppose first that u and v belong to the same chain, that is, $p=i$. In this case, $u=(i,j)$ and $v=(i,q)$. In addition, $j\ne q$ since u and v are two distinct vertices. We have $D_i\left(u\right)=A_u\left[i\right]=j$ and $D_i\left(v\right)=A_v\left[i\right]=q$. It follows that $D_i\left(u\right)\ne D_i\left(v\right)$ and that, consequently, u and v are not placed in the same position in $\Gamma (G,S_c)$. Suppose that u and v belong to two distinct chains, that is, $p\ne i$. We have $D_i\left(u\right)=A_u\left[i\right]=j$, $D_p\left(u\right)=A_u\left[p\right]$ and $D_i\left(v\right)=A_v\left[i\right]$, $D_p\left(v\right)=A_v\left[p\right]=q$. Consider the two vertices $u^{\prime }=(p,A_u\left[p\right])$ and $v^{\prime }=(i,A_v\left[i\right])$. Suppose by contradiction that the vertices u and v are placed in the same position in $\Gamma (G,S_c)$. In this case, $D_i\left(u\right)=D_i\left(v\right)$ and $D_p\left(u\right)=D_p\left(v\right)$ and, consequently, $j=A_v\left[i\right]$ and $A_u\left[p\right]=q$. Hence, $u^{\prime }=(p,A_u\left[p\right])=(p,q)=v$ and $v^{\prime }=(i,A_v\left[i\right])=(i,j)=u$. By the Reachability Property, $u^{\prime }$ and $v^{\prime }$ are the vertices having the lowest position in $C_p$ and $C_i$ so that there exist a directed path from u to $u^{\prime }$ and from v to $v^{\prime }$, respectively. Since $u=v^{\prime }$ and $v=u^{\prime }$, it follows that there is a path connecting v to u and there is another path connecting u to v. It implies that there must be a cycle that contains v and u in G, which is a contradiction. It follows that u and v are not placed in the same position in $\Gamma (G,S_c)$.    □

Notice that if u and v were placed in the same position, not only $\Gamma (G,S_c)$ could not be considered a drawing of G, but also $\Gamma (G,S_c)$ would not have the property of a dominance drawing. Indeed, in this case $D_h\left(u\right)\le D_h\left(v\right)$ and $D_h\left(v\right)\le D_h\left(u\right)$ for every $h\in [1,k]$ and, consequently, the property of the dominance drawing would imply the existence of a path from u to v and a path from v to u and, consequently, the existence of a cycle in G.

The following theorem shows that drawing $\Gamma (G,S_c)$ is a dominance drawing of G and that it can be computed in $O\left(km\right)$ time.

Theorem 1.

Let G be an $st$-graph with n vertices and m edges and $S_c=\{C_1,\dots ,C_k\}$ be a chain cover of G. We have that $\Gamma (G,S_c)$ is a k-dimensional dominance drawing of G. Additionally, given a chain cover $S_c$, $\Gamma (G,S_c)$ can be computed in $O\left(km\right)$ time.

Proof. 

The fact that computing $\Gamma (G,S_c)$ requires $O\left(km\right)$ time is a direct consequence of the fact that given $S_c$ as input, the compressed transitive closure of G given $S_c$ can be computed in $O\left(km\right)$ [12]. We now prove that $\Gamma (G,S_c)$ is a k-dimensional dominance drawing of G. Let $u=(i,j)$ and $v=(p,q)$ be any two distict vertices of G. By Lemma 4u and v are not placed in the same position in $\Gamma (G,S_c)$. We prove that $D_h\left(u\right)\le D_h\left(v\right)$ for every $h\in [1,k]$ if, and only if there is a path connecting u to v. If $D_h\left(u\right)\le D_h\left(v\right)$ for every $h\in [1,k]$, then $D_p\left(u\right)\le D_p\left(v\right)$. Since $D_p\left(u\right)=A_u\left[p\right]$ and $D_p\left(v\right)=A_v\left[p\right]=q$, we have $A_u\left[p\right]\le q$ and, by the Reachability Property, there is a directed path from u to v. It remains to show that if there exists a directed path from u to v then $D_h\left(u\right)\le D_h\left(v\right)$ for every $h\in [1,k]$. Suppose by contradiction that there exist $h\in [1,k]$ so that $D_h\left(u\right)>D_h\left(v\right)$. Since $D_h\left(v\right)=A_v\left[h\right]$ and $D_h\left(u\right)=A_u\left[h\right]$, we have $A_v\left[h\right]<A_u\left[h\right]$. We denote by $v^{\prime }$ the vertex $(h,A_v\left[h\right])$. Note that by the Reachability Property there is a path connecting v to $v^{\prime }$. Since by hypothesis there is a path from u to v, there is a path connecting u to $v^{\prime }$. On the other hand, since $A_v\left[h\right]<A_u\left[h\right]$, by the Reachability Property we have that there is no path from u to $v^{\prime }$. A contradiction. Hence, $D_h\left(u\right)\le D_h\left(v\right)$ for every $h\in [1,k]$.    □

By Lemma 3 computing $S_c=\{C_1,\dots ,C_k\}$ so that $f=k$ requires $O\left(f{n}^2\right)$ time. Hence, the following theorem is a consequence of Lemma 3 and Theorem 1.

Theorem 2.

Let G be an $st$-graph with n vertices and m edges and let f be its width. It is possible to compute an f-dimensional dominance drawing of G in $O\left(f{n}^2\right)$ time.

3. Transitive Modules and Dominance Drawings

Let G be an $st$-graph. In this section, we first discuss the concept of transitive module of G, which is a module of the transitive graph of G. Second, we present Lemma 5, which shows a bound for $dd\left(G\right)$ not higher than the bounds of Lemma 2. In Section 3.1 we present an algorithm computing dominance drawings respecting the bound of Lemma 5 and in Section 3.2 we discuss its time complexity. The algorithm of Section 2 is simpler than the one described in Section 3.1. On the other hand, as we show in Section 3.3, there exists graph for which the dominance drawings computed by the algorithm of Section 3.1 have $O\left(n\right)$ less dimensions with respect to the dominance drawings computed by the algorithm of Section 2.

A module M of G is a non-empty subset of V such that either $\left|M\right|=1$ or, for any two vertices $v_1,v_2\in M$ and any vertex $u\in V\backslash M$: $(v_1,u)\in E$ if, and only if $(v_2,u)\in E$; $(u,v_1)\in E$ if, and only if $(u,v_2)\in E$. The congruence partition $C_P$ of V is a partition of V into modules. The quotient graph $G/C_P$ is the graph obtained from G by merging the nodes of each module of $C_P$. For a given module $M\in C_P$, we denote by $\mu$ the vertex representing M in $G/C_P$. 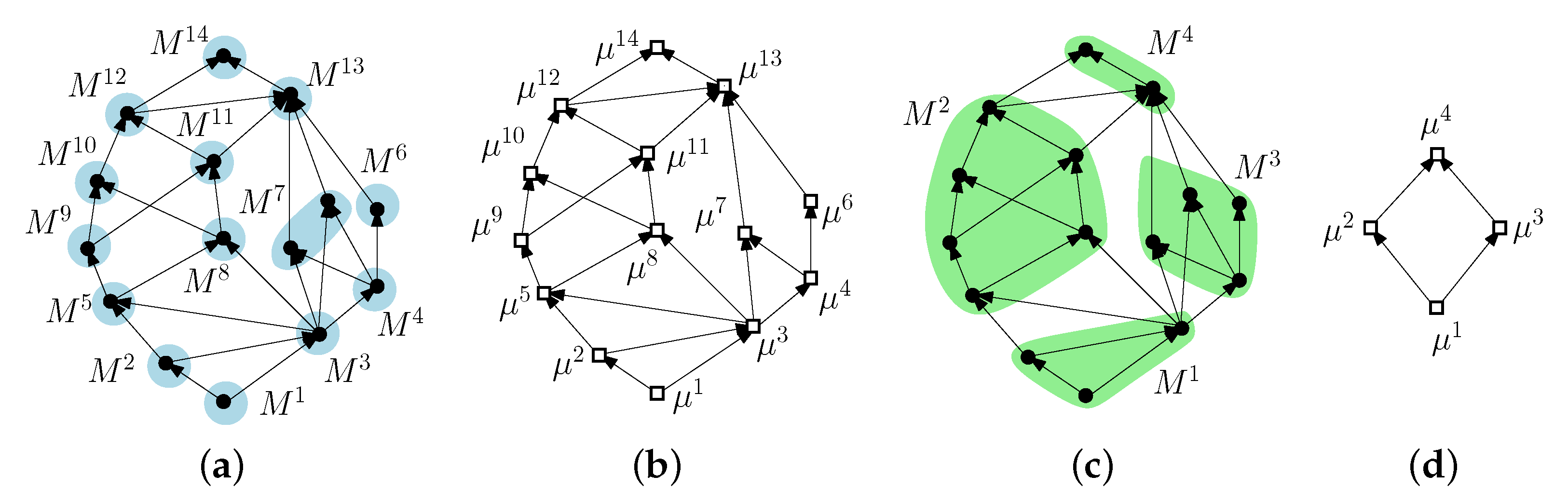Figure 2a shows an $st$-graph G and a congruence partition $C_P=\{M^1,\dots ,M^{14}\}$ of it. Figure 2b shows the quotient graph $G/C_P$.

In this paper, we use the concept of transitive module, transitive congruence partition, and transitive quotient graph of G, defined as a module, a congruence partition, and a quotient graph of the transitive closure graph $G^{*}$ of G. This concept is also used in [17], but there they simply call “module” a transitive module.

Formally, a transitive module $M^{*}$ of G is a non-empty subset of V such that either $|M^{*}|=1$ or, for any two vertices $v_1,v_2\in M^{*}$ and any vertex $u\in V\backslash M^{*}$: there is a path connecting $v_1$ to u if, and only if there is a path connecting $v_2$ to u; there is a path connecting u to $v_1$ if, and only if there is a path connecting u to $v_2$. A transitive congruence partition $C_P^{*}$ of G is a partition of G into transitive modules. The transitive quotient graph $G/C_P^{*}$ is the graph obtained from G by merging the nodes of each transitive module of $C_P^{*}$. For a given module $M^{*}\in C_P^{*}$, we denote by ${\mu }^{*}$ the vertex representing $M^{*}$ in $G/C_P^{*}$.

Notice that every module of G is also a transitive module of G. Hence, the concepts of transitive module, transitive congruence partition, and transitive quotient graphs are a generalization of the concept of module, congruence partition, and quotient graph. For the rest of the paper, since we are going to talk only about transitive modules, transitive congruence partition, and transitive quotient graph, we will omit the symbol “${}^{*}$” in the notation in order to simplify our presentation. Figure 2c shows the $st$-graph G depicted in Figure 2a and a transitive congruence partition $C_P=\{M^1,M^2,M^3,M^4\}$ of G that is not a congruence partition. Figure 2d shows the transitive quotient graph $G/C_P$.

The modular decomposition of G is a tree describing a decomposition of G based into modules of G. The root of the tree is the module $M=V$, containing all the vertices of G, and the leaves of the tree are the singleton modules, where every singleton contains a vertex of G. The children of every non-leaf node M of the tree are the module of G contained in M and that are not contained in any other module contained in M.

The modular decomposition can be computed in $O\left(m\right)$ time and it requires $O\left(n\right)$ time to obtain a congruence partition and the correspondent quotient graph of G from a modular decomposition of G. For further details about modular decomposition see [18]. Computing a transitive congruence partition of G requires $O\left(nm\right)$ time, since we can obtain it by computing a congruence partition of the transitive closure graph of G.

Let $C_P=\{M^1,\dots ,M^h\}$ be a transitive modular decomposition of G and let $G^i=(M^i,E^i)$, where $E^i$ is the subset of edges of E that are incident to two vertices of $M^i$. The congruence dimension of G given $C_P$ is the value $cd(G,C_P)=max\{dd\left(G^1\right),\dots ,$$dd\left(G^h\right),dd(G/C_P)\}$. Since each $G^i$ is a subgraph of G and $G/C_P$ is obtained from G, one might consider that $dd\left(G\right)\ge cd(G,C_P)$. In [19] it is proved that $cd(G,C_P)$ is an upper bound to $dd\left(G\right)$.

Lemma 5.

For every $st$-graph G and any transitive congruence partition $C_P$ of G, the following relation holds: $dd\left(G\right)\le cd(G,C_P)$ [19].

For example, refer to Figure 2c, that depicts a graph G and its transitive congruence partition $C_P=\{M^1,M^2,M^3,M^4\}$. We have that $G/C_P$, $G^1$, $G^3$, and $G^4$ are upward planar and that $G^2$ has width equal to 2. Hence, by Lemma 1 and Inequality (2) of Lemma 2, $dd\left(G^i\right)\le 2$ for every $i\in 1,4$ and $dd(G/C_P)\le 2$. Hence, $cd(G,C_P)=max\{dd\left(G^1\right),\dots ,dd\left(G^4\right),dd(G/C_P)\}\le 2$ and, by Lemma 5, $dd\left(G\right)\le 2$. Since G does not contain a Hamiltonian path, $dd\left(G\right)>1$. It follows that $dd\left(G\right)=2$. Figure 4b shows a two-dimensional dominance drawing of G.

In Section 3.1 we show an algorithm to compute dominance drawings with the bound stated in Lemma 5. More formally, we describe an algorithm to compute a dominance drawing $\Gamma (G,S_{dd})$ of any $st$-graph G having $q=cd(G,C_P)$ dimensions given the set of a q-dimensional dominance drawing $S_{dd}=\{{\Gamma }^0,{\Gamma }^1,\dots ,{\Gamma }^h\}$ of the graphs $G^0,G^1,\dots ,G^h$ associated to a transitive congruence partition $C_P$ of G, where $G^0=G/C_P$. In Section 3.2 we discuss the time complexity of the algorithm.

3.1. Algorithm 2 (Proof of Lemma 5)

Let $C_P=\{M^1,\dots ,M^h\}$ be a transitive congruence partition of G. Assume that, for any two vertices u and v so that $u\in M^j$ and $v\in M^i$, if there is a path connecting u to v in G, then $j\le i$. It is possible to compute a labeling so that the above propriety holds by: Computing a topological sorting T of the vertices of the $st$-graph $G/C_P$ (which is the quotient graph); setting i equal to the topological number of ${\mu }^i$, $T\left({\mu }^i\right)$, for any transitive module $M^i\in C_P$. Note that the two transitive congruence partitions depicted in Figure 2a,c (where the one of (a) is also a congruence partition) have a labeling with this property.

We denote graph $G/C_P$ by $G^0=(V^0,E^0)$. Let $S_{dd}=\{{\Gamma }^0,{\Gamma }^1,\dots ,{\Gamma }^h\}$ be an ordered set of q-dimensional dominance drawings so that, for every $i\in [1,h]$, ${\Gamma }^i$ is a q-dimensional dominance drawing of $G^i$. We prove that given $S_{dd}$, it is possible to obtain a q-dimensional dominance drawing of G. Then, since $dd\left(G^i\right)\le cd(G,C_P)$ for every $i\in [0,h]$ by definition of congruence dimension, the proof of Lemma 5 is a direct consequence of the fact that it is possible to set $q=cd(G,C_P)$. See, for example, Figure 3 that depicts the drawings ${\Gamma }^0,\dots ,{\Gamma }^4$ for the graph depicted in Figure 2c with transitive congruence partition $C_P=\{M^1,\dots ,M^4\}$. The transitive quotient graph $G^0$ is depicted in Figure 2d.

Notice that, given any dominance drawing $\Gamma$ of G with $q^{\prime }<q$ dimensions of a graph, it is possible to obtain a dominance drawing with q dimensions of the graph by adding to $\Gamma$$q-q^{\prime }$ dimensions and by assigning to all the vertices of G the same position in the new dimensions. Hence, the assumption that all the drawings in the set $S_{dd}$ have the same number of dimensions, q, is without loss of generality.

We now show Algorithm 3, which computes a q-dimensional dominance drawing $\Gamma (G,S_{dd})$ of G. The algorithm consists of two steps, presented in detail in Section 3.1.1 and Section 3.1.2. We now give an overview of the algorithm.

Algorithm 3 CP-Draw (Congruence Partition Draw).

⋆ Input: An $st$-graph $G=(V,E)$ and $S_{dd}=\{{\Gamma }^0,{\Gamma }^1,\dots ,{\Gamma }^h\}$ ⋆ Output: A h-dimensional drawing $\Gamma (G,S_{dd})$ of G. Step 1: Compute a q-dimensional drawing ${\overline{\Gamma }}^0$ of $G^0$ (different from ${\Gamma }^0$) having dimensions ${\overline{D}}_1^0,\dots ,{\overline{D}}_q^0$ (see Figure 4a). We denote ${\overline{\Gamma }}^0$ by skeleton drawing (see details in Section 3.1.1). Step 2: Compute a drawing $\Gamma (G,S_{dd})$ (see Figure 4b) by using, for every vertex $v\in M^i$, the coordinates of ${\mu }^i$ in the skeleton drawing ${\overline{\Gamma }}^0$ and of v in ${\Gamma }^i$ in order to set the coordinates of v in $\Gamma (G,S_{dd})$ (see details in Section 3.1.2).

In Section 3.1.2 we prove that $\Gamma (G,S_{dd})$ is a q-dimensional dominance drawing.

3.1.1. Details of Step 1 of Algorithm 2: Preparing the Skeleton Drawing ${\overline{\Gamma }}^0$

We first introduce some notation. Let $D_p^i$ be the $pth$ dimension in drawing ${\Gamma }^i\in S_{dd}$ and $ma{x}_p^i$ a number so that $D_p^i\left(v\right)\le ma{x}_p^i$ for every $v\in G^i$, where $i\in [1,h]$ and $p\in [1,q]$. For every ${\mu }^i\in G^0$, we define the set $U_p^i$ to be the subset of $V^0$ so that, for any ${\mu }^j\in V^0$, ${\mu }^j\in U_p^i$ if, and only if one of the two following cases holds: ($\alpha$) $D_p^0\left({\mu }^j\right)<D_p^0\left({\mu }^i\right)$; ($\beta$) $D_p^0\left({\mu }^j\right)=D_p^0\left({\mu }^i\right)$ and $j<i$ (i.e., ${\mu }^j$ is not reachable from ${\mu }^i$ according to the labeling defined at the beginning of the section). Notice that the two cases never hold for ${\mu }^i$ and that, consequently, ${\mu }^i\notin U_p^i$. Let $shif{t}_p^i={\sum }_{{\mu }^j\in U_p^i}ma{x}_p^j$.

Refer to Figure 3 for an example of the notation $ma{x}_p^i$, $U_p^i$, and $shif{t}_p^i$ defined above. The values $shif{t}_1^i$, for $i\in [1,4]$, are computed as follow.

• i = 1:$U_1^1=\varnothing$, since neither Case ($\alpha$) nor Case ($\beta$) holds for ${\mu }^2$, ${\mu }^3$, and ${\mu }^4$. Hence, $shif{t}_1^1={\sum }_{{\mu }^j\in U_1^1}ma{x}_1^j=0$.
• i = 2:$U_1^2=\left\{{\mu }^1\right\}$, since Case ($\alpha$) holds for ${\mu }^1$ and neither Case ($\alpha$) nor Case ($\beta$) holds for vertices ${\mu }^3$ and ${\mu }^4$. Hence, $shif{t}_1^2={\sum }_{{\mu }^j\in U_1^2}ma{x}_1^j=ma{x}_1^1=1$.
• i = 3:$U_1^3=\{{\mu }^1,{\mu }^2\}$, since Case ($\alpha$) holds for ${\mu }^1$ and ${\mu }^2$ and neither Case ($\alpha$) nor Case ($\beta$) holds for vertex ${\mu }^4$. Hence, $shif{t}_1^3={\sum }_{{\mu }^j\in U_1^3}ma{x}_1^j=ma{x}_1^1+ma{x}_1^2=1+3=4$.
• i = 4:$U_1^4=\{{\mu }^1,{\mu }^2,{\mu }^3\}$, since Case ($\alpha$) holds for ${\mu }^1$ and ${\mu }^2$ and Case ($\beta$) holds for ${\mu }^3$.
  Hence, $shif{t}_1^4={\sum }_{{\mu }^j\in U_1^4}ma{x}_1^j=ma{x}_1^1+ma{x}_1^2+ma{x}_1^3=1+3+2=6$.

Let ${\overline{\Gamma }}^0$ be a q-dimensional drawing of $G^0$ having dimensions ${\overline{D}}_1^0,\dots ,{\overline{D}}_h^0$ so that, for every $i\in [1,h]$ and every $p\in [1,q]$, ${\overline{D}}_p^0\left({\mu }^i\right)=D_p^0\left({\mu }^i\right)+shif{t}_p^i$.

Refer to Figure 4a that depicts the drawing ${\overline{\Gamma }}^0$ given ${\Gamma }^0,{\Gamma }^1,{\Gamma }^2,{\Gamma }^3,{\Gamma }^4$ of Figure 3. Consider dimension ${\overline{D}}_1^0$. Recall that $shif{t}_1^1=0$, $shif{t}_1^2=1$, $shif{t}_1^3=4$ and $shif{t}_1^4=6$, as showed in the illustration of Figure 3 above. We have: ${\overline{D}}_1^0\left({\mu }^1\right)=D_1^0\left({\mu }^1\right)+shif{t}_1^1=0$; ${\overline{D}}_1^0\left({\mu }^2\right)=D_1^0\left({\mu }^2\right)+shif{t}_1^2=1+1=2$; ${\overline{D}}_1^0\left({\mu }^3\right)=D_1^0\left({\mu }^3\right)+shif{t}_1^3=2+4=6$; ${\overline{D}}_1^0\left({\mu }^4\right)=D_1^0\left({\mu }^4\right)+shif{t}_1^4=2+6=8$.

3.1.2. Details of Step 2 of Algorithm 2: Computing a Dominance Drawing $\Gamma (G,S_{dd})$ of $\mathrm{G}$

We construct a q-dimensional drawing $\Gamma (G,S_{dd})$ of G having dimensions $D_1,\dots ,D_q$ as follows: For every vertex $v\in G$, where $v\in M^i$, and for every $p\in [1,q]$, we set $D_p\left(v\right)={\overline{D}}_p^0\left({\mu }^i\right)+D_p^i\left(v\right)$.

Refer to Figure 4b that depicts the drawing $\Gamma (G,S_{dd})$ given ${\Gamma }^0,{\Gamma }^1,{\Gamma }^2,{\Gamma }^3,{\Gamma }^4$ of Figure 3 and ${\overline{\Gamma }}^0$ of Figure 4a. Consider dimension $D_1$ and vertices $a\in M^1$, $b\in M^2$, $c\in M^3$, and $d\in M^4$, also depicted in Figure 3. We have: $D_1\left(a\right)={\overline{D}}_1^0\left({\mu }^1\right)+D_1^1\left(a\right)=0+1=1$; $D_1\left(b\right)={\overline{D}}_1^0\left({\mu }^2\right)+D_1^2\left(b\right)=2+2=4$; $D_1\left(c\right)={\overline{D}}_1^0\left({\mu }^3\right)+D_1^3\left(c\right)=6+1=7$; $D_1\left(d\right)={\overline{D}}_1^0\left({\mu }^4\right)+D_1^4\left(d\right)=8+1=9$;

Figure 4. (a) The skeleton drawing ${\overline{\Gamma }}^0$ given $S_{dd}=\{{\Gamma }^0,\dots ,{\Gamma }^4\}$, where drawings ${\Gamma }^0,\dots ,{\Gamma }^4$ are depicted in Figure 3. (b) The correspondent drawing $\Gamma (G,S_{dd})$.

Figure 4. (a) The skeleton drawing ${\overline{\Gamma }}^0$ given $S_{dd}=\{{\Gamma }^0,\dots ,{\Gamma }^4\}$, where drawings ${\Gamma }^0,\dots ,{\Gamma }^4$ are depicted in Figure 3. (b) The correspondent drawing $\Gamma (G,S_{dd})$.

Notice that, since q can be equal to $cd(G,C_P)$ and since $\Gamma (G,S_{dd})$ is a q-dimensional drawing of G, in order to prove Lemma 5 it is sufficient to show that drawing $\Gamma (G,S_{dd})$ is a dominance drawing of G.

Let u and v be two vertices of G. We prove that there is a path connecting u to v if, and only if $D_p\left(u\right)\le D_p\left(v\right)$ for every $p\in [1,q]$. Suppose $u\in M^j$ and $v\in M^i$, where $j,i\in [1,h]$. We distinguish two cases. In the first case u and v belong to the same transitive module, that is, $i=j$, and in the second case u and v belong to two different transitive modules, that is, $i\ne j$.

In the first case, $i=j$, since ${\Gamma }^i$ is a dominance drawing, we have that there is a path connecting u to v if, and only if $D_p^i\left(u\right)\le D_p^i\left(u\right)$ for every $p\in [1,q]$. We also have that, for every $p\in [1,q]$, $D_p^i\left(u\right)\le D_p^i\left(u\right)$ implies $D_p\left(u\right)\le D_p\left(u\right)$ since $D_p\left(u\right)=c+D_p^i\left(u\right)$ and $D_p\left(v\right)=c+D_p^i\left(v\right)$, where $c={\overline{D}}_p^0\left({\mu }^i\right)$. Hence, there is a path connecting u to v if, and only if $D_p\left(u\right)\le D_p$ for every $p\in [1,q]$.

For the rest of the proof we consider the second case, that is, $i\ne j$. Suppose that there is a path connecting u to v in G. We prove that $D_p\left(u\right)\le D_p\left(v\right)$ for every $p\in [1,q]$. Observe that a path from u to v always implies a path from ${\mu }^j$ to ${\mu }^i$ in $G^0$ and, since ${\Gamma }^0$ is a dominance drawing of $G^0$, we have the following relation:

$$D_p^0\left({\mu }^j\right)\le D_p^0\left({\mu }^i\right).$$

(1)

Since there is a path from ${\mu }^j$ to ${\mu }^i$ then, according to the labeling of the transitive modules based on the topological ordering of $G^0$ introduced at the beginning of the section, we have $j<i$. Relation (1) implies $U_p^j\subseteq U_p^i$. By Relation (1) and $j<i$ we have that either Case ($\alpha$) or Case ($\beta$) holds for ${\mu }^j$ and that ${\mu }^j\in U_p^i$. Hence, $U_p^j\cup \left\{{\mu }^j\right\}\subseteq U_p^i$ and consequently we have the following relation:

$$shif{t}_p^j+ma{x}_p^j\le shif{t}_p^i.$$

(2)

We have $D_p\left(u\right)={\overline{D}}_p^0\left({\mu }^j\right)+D_p^j\left(u\right)=D_p^0\left({\mu }^j\right)+shif{t}_p^j+D_p^j\left(u\right)\le D_p^0\left({\mu }^j\right)+shif{t}_p^j+ma{x}_p^j$, since $ma{x}_p^j$ is by definition the maximum value of a coordinate in the $pth$ dimension of drawing ${\Gamma }^j$. By Relation (1) $D_p^0\left({\mu }^j\right)+shif{t}_p^j+ma{x}_p^j\le D_p^0\left({\mu }^i\right)+shif{t}_p^j+ma{x}_p^j$. By Relation (2) $D_p^0\left({\mu }^i\right)+shif{t}_p^j+ma{x}_p^j\le D_p^0\left({\mu }^i\right)+shif{t}_p^i$. Hence, $D_p\left(u\right)\le D_p^0\left({\mu }^i\right)+shif{t}_p^i={\overline{D}}_p^0\left({\mu }^i\right)\le {\overline{D}}_p^0\left({\mu }^i\right)+D_p^0\left(v\right)=D_p\left(v\right)$. This implies that $D_p\left(u\right)\le D_p\left(v\right)$ for every $p\in [1,q]$.

Suppose that $D_p\left(u\right)\le D_p\left(v\right)$ for every $p\in [1,q]$. We prove that there is a path connecting u to v in G. We first prove the following claim.

Claim 1.

Let u and v be two vertices of G so that $u\in M^j$ and $v\in M^i$. For any $p\in [1,q]$, if $D_p\left(u\right)\le D_p\left(v\right)$ then $D_p^0\left({\mu }^j\right)\le D_p^0\left({\mu }^i\right)$.

Proof. 

We have $D_p\left(u\right)={\overline{D}}_p^0\left({\mu }^j\right)+D_p^j\left(u\right)=D_p^0\left({\mu }^j\right)+shif{t}_p^j+D_p^j\left(u\right)$ and $D_p\left(v\right)={\overline{D}}_p^0\left({\mu }^i\right)+D_p^i\left(v\right)=D_p^0\left({\mu }^i\right)+shif{t}_p^i+D_p^i\left(v\right)$. Hence, since $D_p\left(u\right)\le D_p\left(v\right)$, $D_p^0\left({\mu }^j\right)+shif{t}_p^j+D_p^j\left(u\right)\le D_p^0\left({\mu }^i\right)+shif{t}_p^i+D_p^i\left(v\right)$. Therefore, we have the following relation:

$$D_p^0\left({\mu }^j\right)+shif{t}_p^j-shif{t}_p^i+D_p^j\left(u\right)\le D_p^0\left({\mu }^i\right)+D_p^i\left(v\right).$$

(3)

Suppose for a contradiction that $D_p^0\left({\mu }^j\right)>D_p^0\left({\mu }^i\right)$. It implies $U_p^i\subseteq U_p^j$. Additionally, it implies that Case ($\alpha$) holds for ${\mu }^i$ and that ${\mu }^i\in U_p^j$. We have $U_p^i\cup \left\{{\mu }^i\right\}\subseteq U_p^j$ and consequently $shif{t}_p^i+ma{x}_p^i\le shif{t}_p^j$. It follows that:

$$ma{x}_p^i\le shif{t}_p^j-shif{t}_p^i$$

(4)

Substituting in Relation (3) the result of Relation (4) we have $D_p^0\left({\mu }^j\right)+ma{x}_p^i+D_p^j\left(u\right)\le D_p^0\left({\mu }^i\right)+D_p^i\left(v\right).$ Since $D_p^i\left(v\right)\le ma{x}_p^i$, we have $D_p^0\left({\mu }^j\right)+ma{x}_p^i+D_p^j\left(u\right)\le D_p^0\left({\mu }^i\right)+ma{x}_p^i.$ It follows that $D_p^0\left({\mu }^j\right)+D_p^j\left(u\right)\le D_p^0\left({\mu }^i\right)$ and, consequently, $D_p^0\left({\mu }^j\right)\le D_p^0\left({\mu }^i\right)$, which is a contradiction. It follows that $D_p^0\left({\mu }^j\right)\le D_p^0\left({\mu }^i\right)$. □

In order to conclude the proof of Lemma 5 we present the following argument. Since by hypothesis $D_p\left(u\right)\le D_p\left(v\right)$ for every $p\in [1,q]$, by Lemma 1$D_p^0\left({\mu }^j\right)\le D_p^0\left({\mu }^i\right)$ for every $p\in [1,q]$. Since ${\Gamma }^0$ is a dominance drawing of $G^0$ by hypothesis and since $D_p^0\left({\mu }^j\right)\le D_p^0\left({\mu }^i\right)$ for every $p\in [1,q]$, then there is a path connecting ${\mu }^j$ to ${\mu }^i$ in $G^0$. Therefore, there is a path connecting any vertex of $M^j$ to any vertex of $M^i$ in G and, consequently, there is a path connecting u to v in G.

We proved that for any two vertices u and v of G we have that there is a path from u to v if, and only if $D_p\left(u\right)\le D_p\left(v\right)$ for every $p\in [1,q]$. Hence, drawing $\Gamma (G,S_{dd})$ is a q-dimensional dominance drawing of G. Since q is equal to $cd(G,C_P)$.

3.2. Complexity Analysis

In the previous section we showed an algorithm to compute dominance drawing with the bound stated in Lemma 5. In this section we do a worst-case analysis of the time complexity required to compute the dominance drawing $\Gamma (G,S_{dd})$.

Denote by $O\left(t_1\right)$ the time required to compute the transitive congruence partition $C_P$ of G and by $O\left(t_2\right)$ the time required to compute the set of q-dimensional dominance drawings $S_{dd}=\{{\Gamma }^0,{\Gamma }^1,\dots ,{\Gamma }^h\}$ of graphs $G^0,G^1,\dots ,G^h$. Given $S_{dd}$, it is possible to compute the values $ma{x}_p^i$ and $shif{t}_p^i$ for every $p\in [1,q]$ and every $i\in [1,h]$ in overall $O\left(qn\right)$ time. Hence, the time required to compute $\Gamma \left(S_{dd}\right)$ is $O(t_1+t_2+qn)$. Therefore, we have the following theorem:

Theorem 3.

Let G be any $st$-graph and let $C_P$ be a transitive congruence partition. Let $O\left(t_1\right)$ be the time to compute $C_P$ and $O\left(t_2\right)$ be the time to compute the set of q-dimensional dominance drawings $S_{dd}=\{{\Gamma }^0,{\Gamma }^1,\dots ,{\Gamma }^h\}$, where $q=cd(G,C_P)$. Then, it is possible to compute a q-dimensional dominance drawing of G in $O(t_1+t_2+qn)$ time.

We now give examples of possible values of $t_1$ and $t_2$. Recall that computing a congruence partition requires $O\left(m\right)$ [18]. It is possible to compute a transitive congruence partition $C_P$ in $O\left(nm\right)$ by computing a congruence partition of the transitive closure graph of G. Hence, it is possible to have $t_1=nm$. Let $f^i$ be the width of $G^i$ for every $i\in [0,h]$. If we compute the drawings ${\Gamma }^0,{\Gamma }^1,\dots ,{\Gamma }^h$ by using the algorithm described in Section 2, then, by Theorem 2, $t_2=f^{\prime }{n}^2$, where $f^{\prime }=max\{f^0,\dots ,f^h\}$. Notice that $f^{\prime }\le f$ and that, in this case, by the theorem, it is possible to compute an $f^{\prime }$-dimensional dominance drawing. We have $t_2=n$ if all the graphs $G^0,G^1,\dots ,G^h$ are upward planar [2]. We summarize the result for the special cases described in the above paragraph with the following corollary.

Corollary 1.

It is possible to compute a $f^{\prime }$-dimensional dominance drawing of G in $O(nm+f^{\prime }{n}^2)$ time, where $f^{\prime }\le f$.

3.3. A Comparison between the Algorithms

In this section we show that by using the algorithm described in this section it is possible to compute dominance drawing with $O\left(n\right)$ less dimensions with respect to the ones that we can compute by using the algorithm in Section 2.

Let H be an $st$-graph with n vertices, source s, sink t, and having a transitive congruence partition $C_P=\{M^1,\dots ,M^h\}$, where: $M^1=\left\{s\right\}$; for $i\in [2,h-2]$, $H^i$ is a $3\times 3$ crown graph; $H^{h-1}$ is a set containing $O\left(n\right)$ incomparable vertices. See Figure 5a, where $h=4$.

Let f be the width of H. We have $f=O\left(n\right)$, since $M^{h-1}$ is a set containing $O\left(n\right)$ incomparable vertices. Additionally, it is well known that the $3\times 3$ crown graph has dominance dimension higher than 2, see for example [9]. Therefore, $dd\left(H^i\right)>2$ for every $i\in [2,h-2]$ and $dd\left(H\right)>2$. According to Lemmas 1 and 2 the best-known upper bound for $dd\left(H\right)$ is $\frac{n}{2}$.

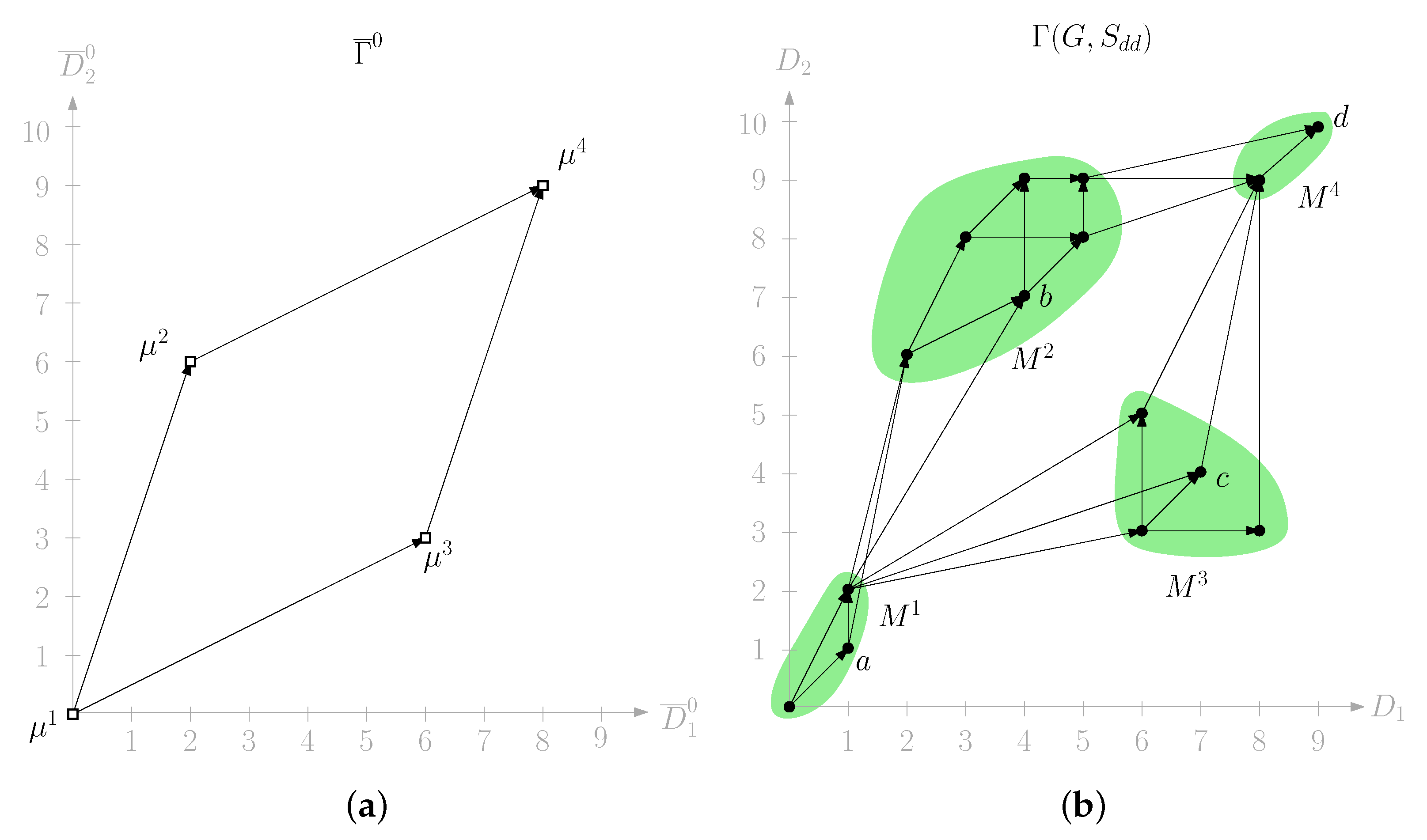
The graphs $H^0,H^1,H^{h-1},H^h$, where $H^0=H/C_P$, are upward planar. Hence, $dd\left(H^i\right)=2$ for every $i\in \{0,1,h-1,h\}$ by Lemma 1. For every $i\in [2,h-2]$, the width of $H^i$ is 3 and, since $dd\left(H^i\right)>2$, we have $dd\left(H^i\right)=3$ by Inequality (2) of Lemma 2. Hence, $cd(H,C_P)=max\{dd\left(H^0\right),\dots ,dd\left(H^h\right)\}=3$. By Lemma 5 and by $dd\left(H\right)>2$ we have $dd\left(H\right)=3$, which is optimum.

It is possible to construct the three-dimensional dominance drawings ${\Gamma }^i$ of $G^i$, for $i\in \{0,1,h-1,h\}$, by Lemma 1 and by adding a third dimension as described at the beginning of Section 3.1. For every $i\in [2,h-2]$, it is possible to construct the three-dimensional dominance drawing ${\Gamma }^i$ of $G^i$ by Theorem 2. Hence, given $C_P$, it is possible to construct $S_{dd}=\{{\Gamma }^0,\dots ,{\Gamma }^h\}$ and the three-dimensional dominance drawing $\Gamma (H,S_{dd})$ of H as described in the proof of Lemma 5. Figure 5b depicts, for every $v\in H$, the values $D_1\left(v\right)$, $D_2\left(v\right)$, $D_3\left(v\right)$ associated to the dimensions $D_1$, $D_2$, and $D_3$ of the drawing $\Gamma (H,S_{dd})$, where graph H is depicted in Figure 5a.

4. A Discussion on Weak Dominance Drawings

In this section we discuss the concept of weak dominance drawings, which is a generalization of the concept of dominance drawing. We point out the reason why it was introduced and we show two recent papers showing that this concept can be very useful in practice.

Given two vertices u and v of a DAG G, checking if there exists a directed path from u to v is denoted by reachability query. The problem of answering efficiently to reachability queries is widely studied in the literature. See, for example [10,17,20]. See also the following two very recent papers [21,22] and see [23] for a survey.

Dominance Drawing is a concept that can be very useful for answering reachability queries, that is, checking the existence of a path connecting two vertices in graph databases.Recall that given a dominance drawing of a DAG G having k dimensions, it is possible to answer to a reachability query very efficiently in $O\left(k\right)$ time by using $O\left(kn\right)$ space. By using some clever strategy, as for the algorithm described in Section 2, the time can also be $O\left(1\right)$, that is, independent of the number of dimensions.

Computing dominance drawings of DAGs having a low number of dimensions would be important in practice. Unfortunately, most of the existing algorithms obtaining dominance drawings require the input DAG to have specific properties, that is, to be planar, as stated in Lemma 1. The algorithms that we presented so far avoid this problem, since no restriction on the input graph is given. On the other hand, the computational time required to compute dominance drawings is still not linear. For example, for the algorithm described in Section 2 computes f-dimensional dominance drawings in $O\left(f{n}^2\right)$ time, where n and f are the number of nodes and the width of G, respectively. When the number of vertices is very large, computing such drawings can be prohibitively expensive. By using heuristics for the computation of (sub-optimal) chain covers we can make the algorithms faster. Another possibility is to relax the concept of dominance. As we are going to observe in the rest of this section, this direction was studied by several authors.

The concept of weak dominance, a relaxed version of dominance, was introduced in [9]. The “if and only if” of dominance becomes an “if” in weak dominance. Namely, in a weak dominance drawing $\Gamma$ of a DAG $G=(V,E)$, two vertices $u,v\in V$ are incomparable in G if there exists two dimensions D and $D^{\prime }$ such that $D\left(u\right)<D\left(v\right)$ and $D^{\prime }\left(v\right)<D^{\prime }\left(u\right)$. Unfortunately, u and v can be incomparable while $D\left(u\right)\le D\left(v\right)$ for any dimension D of $\Gamma$. In this case there is a falsely implied path (fip) between u and v. Clearly, any DAG G admits a k-dimensional weak dominance drawing for any integer k. For example, any topological order of the vertices of G is a one-dimensional weak dominance drawing of G. In [24] it is studied an interesting variation of the weak dominance drawing problem.

Given a weak dominance drawing $\Gamma$, if there are two dimensions D and $D^{\prime }$ of $\Gamma$ such that $D\left(u\right)\le D\left(v\right)$ and $D^{\prime }\left(u\right)\ge D^{\prime }\left(v\right)$, then u and v are incomparable. This computation requires $O\left(k\right)$ time. Otherwise, more expensive computations are needed to check weather there is a path connecting u and v. For example, a Breadth First Search (BFS) would take $O(n+m)$ time per search. Minimizing the number of fips minimizes the number of BFS operations required by the drawing and, consequently, the average time required for a reachability query. Notice that minimizing the number of fips is NP-hard [9,25]. The weak dominance drawings were recently used to construct compact representations of the reachability information in databases [4,10].

Interesting experiments on algorithms computing weak dominance drawings are presented in [4,10]. They show that by using weak dominance drawings, it is possible to answer reachability queries more efficiently with respect to previous results. In [10] they use weak dominance drawing with more than two dimensions in order to have less fips and they show that even by using few dimensions, that is, by using almost linear space, it is possible to improve the results significantly. Extending [10], Lionakis et al. [11] show that, for the same families of graphs considered in [10] and by using a number of dimensions similar to the ones used in [10], it is possible to compute dominance drawings (i.e., 0 fips).

The technique used in [11] is similar to the one described in Section 2 of this paper. The computational time required to compute dominance drawings in [11] is still higher than the one to compute weak dominance drawings [10]. However, these results suggest that a possible direction for this line of research is to actually use directly dominance drawings instead of weak dominance drawings. In fact, in Section 3 we presented algorithms that compute dominance drawings with a reduced number of dimensions with respect to the ones presented in Section 2, and consequently in [10,11].

5. Conclusions and Open Problems

In this paper, we reviewed some mathematical results on dominance drawings of DAGs and their dimension, and presented an efficient algorithm that, for every $st$-graph G with width f, constructs an f-dimensional dominance drawing. As far as we know, these are the most efficient algorithms to construct dominance drawings for any input DAG with a number of dimension that is described by the theoretical bounds.

We used the concept of congruence dimension $cd(G,C_P)$ of G given a transitive congruence partition $C_P$ of G, and we presented an efficient algorithm to compute a dominance drawing of G in $cd(G,C_P)$ dimensions. The congruence dimension $cd(G,C_P)$ of G is a better upper bound of the dominance dimension of G. Indeed, we showed that there exists a family of graphs so that for every graph H of the family the best-known upper bound of $dd\left(H\right)$, according to Hiraguchi’s Theorem (Inequality (1) of Lemma 2), was $\frac{n}{2}$ and we proved that, according to Lemma 5, $dd\left(H\right)=3$.

Notice that the number of dimensions used by a dominance drawing may be large, and the algorithm to compute it requires $O\left(f{n}^2\right)$ time. Therefore, it may be prohibitive for very large data sets as the ones used recently by the database community. There are three ways to approach these problems from theoretical and practical points of view:

• Use a relaxed version of dominance drawing called weak dominance drawing, see [9]. The existence of fips cannot be excluded since the number of dimensions in a weak dominance drawing is typically significantly less than $dd\left(G\right)$. Hence, computing such drawings with few fips is central to any approach involving weak dominance drawings. Recall that minimizing the number of fips is NP-hard [9,25]. Additionally, using more dimensions in a weak dominance drawing reduces the number of fips. It would be interesting to experimentally study this tradeoff.
• Explore heuristics in order to compute dominance drawings of DAGs in “almost linear time”, even if they need a higher number of dimensions. This would be another interesting research direction given the high complexity required by current algorithms.
• Finally, an interesting theoretical open problem is to find algorithms that construct dominance drawings of similar quality as the ones computed by the current algorithms (that require $O\left(f{n}^2\right)$ time) but in less time, or prove a non-trivial lower bound for this construction.