Definition
The displacement micropump with passive check valves is an attractive solution for precise insulin infusion in patients with type I diabetes. Unlike most insulin pumps that push insulin from a cartridge using a piston, a displacement micropump will first pull insulin from the reservoir before infusing it into the patient. This dual sequence introduces new challenges in terms of insulin stability, notably if the reservoir is not pressurized. After an introduction to displacement micropumps and a brief review of the insulin degradation mechanism, micropump design rules are discussed in light of microfluidic theory.
1. Introduction
Diabetes is a chronic metabolic disorder characterized by high blood sugar levels that cause serious damage over time. Type 1 diabetes, also called insulin-dependent diabetes, is a condition in which little or no insulin is produced by the beta-cells of the pancreas. Daily administration of insulin is essential to the survival of people with type 1 diabetes.
Traditionally, insulin is administered by subcutaneous injection using an insulin syringe or pen. Advanced insulin delivery systems include patch pumps which administer fast-acting insulin 24 h a day to meet the body’s needs, via a fine cannula placed subcutaneously. Continuous subcutaneous insulin infusion (CSII) has proven to be effective in diabetes care [1,2,3,4,5,6,7]. These programmable pumps can deliver both basal and bolus doses of insulin. Basal insulin delivery rates are programmed by the physician to meet individual patient needs. Insulin pumps can also deliver bolus insulin to minimize blood glucose deviations after meals. The recent improvement in blood glucose meter accuracy enabled closing the loop thanks to specific algorithms and wireless communication between a continuous glucose meter and the delivery system for one (insulin) or two hormones (insulin and glucagon) [8,9,10,11,12]. Most commercially available insulin pumps feature a piston mechanism connected either to an insulin infusion device or to a cannula patch and occlusion detection system [13,14,15]. The accuracy of bolus and basal rate delivery, in nominal conditions, showed globally good results in agreement with the manufacturers’ specifications [16,17]. Larger deviations are observed at short observation windows (typically less than 1h in basal rate), due to the inherent noise induced by the pumping engine itself and the so-called stick–slip effect of the piston against the internal wall of the insulin container [18,19,20]. Other insulin pump designs have been studied to improve short-term variability of insulin delivery and shorten occlusion detection time [21,22,23,24]. Indeed, insulin delivery systems are designed to detect occlusion, which consists of a partial or complete blockage of insulin delivery, by monitoring the in-line pressure. Occlusion detection is crucial to maintain the blood glucose level in an acceptable range [25]. However, despite improvements in the catheter design to reduce the occurrence of silent occlusion [26], this failure mode remains difficult to detect, especially at low flow rates, as in-line built-in pressure increases slowly over time. Median occlusion detection times (ODT) at 0.1 U/h ranging from 4 h to more than 40 h in commercial insulin pumps were reported [27]. Occlusion may occur shortly after insertion of the infusion set, but generally increases after 2 or 3 days of use. The effect can be related to a kinking of the catheter or the soft cannula, a cannula leakage, the chemical precipitation of insulin, or the fibrin formation at the needle tip [28].
Depending on whether the externally applied energy is converted into fluid kinetic energy, micropumps can be categorized as nonmechanical or mechanical micropumps. These later devices are usually further divided into displacement or dynamic micropumps depending on whether mechanical energy is periodically or continuously transferred to the working fluid [21,29,30,31,32,33,34].
The focus here is on displacement micropumps with flow rectifiers, in which a force is applied periodically to one or more moving boundaries, which in turn exert pressure on the working fluid. Flow rectifying elements are implemented to prevent back-flow and free-flow. Insulin delivery systems with displacement MEMS (micro-electro-mechanical systems) pumps with passive check valves have indeed demonstrated interesting features in terms of occlusion detection and delivery accuracy [23,35,36,37,38,39,40,41]. Numerous actuation mechanisms were associated with this micropump structure, including piezoelectric [40,41,42,43], electrostatic [44,45], ionic conductive polymer film [46], thermopneumatic [47], electromagnetic [48], shape memory alloy [49,50,51], and bimetallic actuators [52].
Such a displacement pump engine is connected to the insulin reservoir and either an infusion set or a cannula that is directly inserted into the skin (patch pump). Sensors can monitor the pressure to detect any events that may induce over- or underdelivery. For basic safety reasons, the pressure relative to the atmosphere in the insulin reservoir is generally zero or slightly negative. During the filling phase of the pumping cycle, a negative pressure is generated in the pumping chamber to open the inlet valve and draw insulin from the reservoir. The fact that the insulin experiences a negative pressure is a significant difference from other insulin delivery systems, except the implantable pump MIP developed by Minimed to infuse U400 insulin via the intraperitoneal route [22]. The pressure of the MIP reservoir is mbar to prevent the risk of overdose induced by leakage and the risk of pocket fill [53,54,55,56]. Most infusion systems are piston pumps that simply push the insulin present into the reservoir to the patient. To illustrate the difference between the two systems, the presence of air in the insulin reservoir is considered. Except in the case of prefilled cartridges, it is difficult to avoid the presence of air, especially if insulin, before being injected into the reservoir, is first extracted from a vial by the patient using a syringe. Air bubbles in a piston pump reservoir can generate an overdose in the event of depressurization (e.g., in an airplane) [22,57]. In the reservoir of a displacement pump with check valves, air can block the valves due to capillary effects and degrade delivery accuracy if air remains in the pumping chamber. The risks for the patient are therefore radically different: over- or underdelivery.
To tackle the challenges of infusing insulin with a displacement pump having check valves, a brief description of the pumping mechanism is first presented, together with an analysis of the link between design, pumping performances, and rapid occlusion detection. The compatibility of this pumping mechanism with the fragile insulin molecule is then reviewed in detail, with a comprehensive analysis of the failure modes. Finally, some insights about the design rules that can be implemented to improve the displacement micropump reliability and thus mitigate the risks associated with this pumping mechanism are presented.
2. Description of a Displacement MEMS Micropump
2.1. Basic Operation
Displacement micropumps with a membrane turned out to be a popular design in drug delivery applications. Such a displacement micropump comprises an actuator, a pumping chamber, a moving membrane, and flow rectification elements such as holes, passive check valves, diffusers, or nozzles [58]. This type of micropump utilizes the reciprocating concept, wherein a cyclic membrane movement is generated by the actuator to alternately increase and reduce the volume of the pumping chamber. For a displacement micropump with ideal flow rectifier elements, the pumping cycle consists of two successive phases:
- The supply phase, wherein the displacement of the membrane induces an increase of the pumping chamber volume; the generated underpressure leads to an opening of the inlet valve and the filling of the pumping chamber cavity with insulin that comes from the non-pressurized reservoir.
- The infusion phase, wherein the displacement of the membrane reduces the pumping chamber volume; the induced overpressure opens the outlet valve and generates a net flow from the pumping chamber toward the patient through the infusion set or the cannula.
The actuation cycle of a displacement micropump with passive check valves is illustrated in Figure 1. The stroke volume is the displaced volume during the infusion phase while the dead volume is the residual volume of the pumping chamber at the end of the infusion phase.
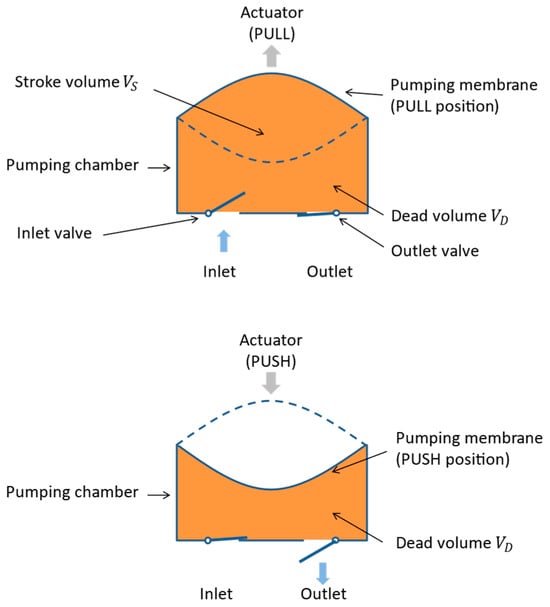
Figure 1.
Schematic views of the membrane of a displacement micropump with passive check valves during the supply phase (top) and the infusion phase (bottom) [59].
2.2. Detailed Structure of a MEMS Micropump
The displacement mechanical pump considered here is a volumetric piezoelectric MEMS micropump associated with two check valves [59,60]. The micropump was designed to deliver 0.2 microliters of insulin per pump stroke (i.e., 0.02 units (U) of U100 insulin), with a maximum error of 3%. The device is made of a stack of wafers bonded together by Au-Au thermocompression or direct bonding: one SOI (silicon-on-insulator) plate in which the moving elements are micromachined (pumping membrane, sensor membranes, and inlet and outlet valves) and two silicon top and cover plates with through holes (see Figure 2). Two square silicon membranes of the pressure sensors are submitted to boron implantation to create piezoresistive strain gauges. The pressure profile measured by the inner detector during a micropump stroke can be used to monitor the valves, pumping membrane, and actuator functions. The outer detector is mainly used to detect out-of-stroke pressure built up in the infusion line. The fluid pathway is shown in Figure 3. The opening thresholds of the valves (i.e., valve pretensions) are typically in the range of 50 to 100 mbar. The flow rate can be programmed to vary from 0 to 2.5 mL/h, considering an aqueous solution of 1 cP (centipoise). As the piezo actuator is overdriven to ensure that the pumping membrane reaches the mechanical stops during the actuation cycle whatever the pressure conditions, the stroke volume is repeatable and insensitive to the variation of viscosity induced by a temperature change.
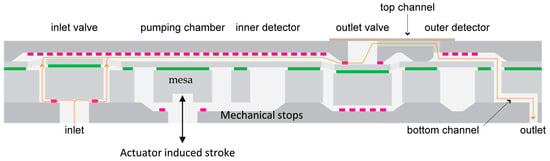
Figure 2.
Schematic cross-section of a MEMS micropump made of an SOI wafer bonded to top and bottom wafers in silicon (in grey). The buried oxide of the SOI wafer is represented by the green layer while the pink rectangles are the anti-bonding pads. The direction of the flow is indicated by the orange arrow. A piezoelectric bender not represented here pushes and pulls the mesa of the pumping membrane via a flexible metal blade. Mechanical stops allow repeatable and accurate pump strokes of 200 nanoliters [40].
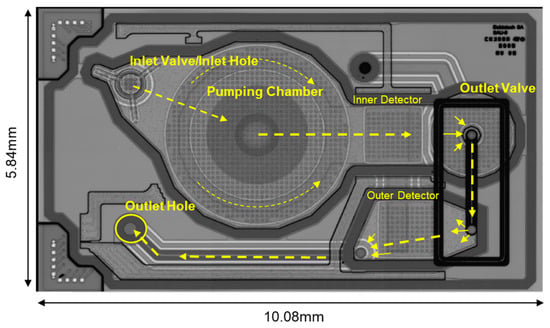
Figure 3.
Top view of the MEMS micropump obtained using IR microscopy. Adapted from [59]. The direction of the insulin flow is indicated by the yellow arrows.
2.3. Micropump Modeling
The dimensioning of the actuator, the valves, the pumping membrane, and the piezoresistive strain gauges can be made using quasi-static conditions. More complex is the determination of the pressure in the different compartments of the micropump during actuation. Analyzing such pressure profiles is crucial to determine whether the micropump is working properly [38,40,59]. Also, the presence of air bubbles in the pumping chamber can significantly impact the delivery accuracy, and a numerical model that can describe the micropump dynamics is desirable.
The simplest option, which exploits the analogy between fluidics and electrical networks, consists of building an electrical equivalent network based on a subdivision of the micropump structure into lumped elements [61].
The analogy can be illustrated as follows. The governing equation of a mechanical system is:
where F, m, v, and are the force, mass, velocity, friction coefficient, and stiffness, respectively. Considering the flow rate through a section S, Equation (1) can be rewritten:
where is the pressure. This later expression is similar to the equation governing an electrical series RLC circuit:
Table 1 shows the correspondence between mechanical and fluidic parameters and their electrical analogs [62]. Applying Kirchhoff’s laws, i.e., flow conservation at any node of the network and no pressure difference along any closed loop, enables the determination of the micropump fluid dynamics during actuation.

Table 1.
Equivalence between mechanical/fluidic and electrical parameters.
This method was considered to design different types of micropumps [23,24,62,63,64,65,66,67,68,69,70]. The different elements of the fluid pathway are replaced by their equivalent electrical elements and the micropump can be simulated using any electrical circuit simulation tool.
Considering the displacement micropump described previously, the general equivalent network is shown in Figure 4. In normal operation, insulin flows from left to right. The pressures in the drug reservoir and infusion site are modeled by voltage sources. Hydrodynamic restrictions and check valves are modeled by fixed and variable resistors, respectively. Displacement of the pumping membrane generates a flow whose electrical equivalent is a controlled current source. Also, the elasticity of structural elements is simulated by capacitors. Inductors are usually not considered when the effects of inertia in the flow can be neglected (at low Re). A more refined model includes variable capacitors that model the air bubble compliance and the vapor pressure of the different insulin excipients. Also, the presence of particulate contamination on the valve seats can be introduced by adding a minimum gap for a valve normally closed.
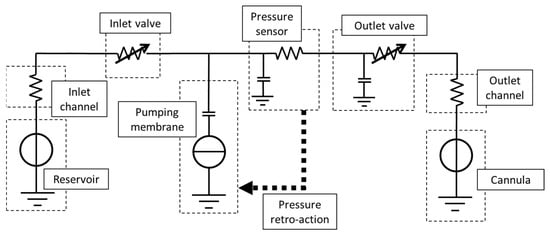
Figure 4.
General electrical equivalent network of a displacement micropump with check valves and pressure sensors. The pressures in the reservoir and injection site are modeled by voltage sources. The flow generated during the actuation of the pumping membrane is modeled as a controlled current source. The different fluidic restrictors, including the valves, are represented by fixed or variable resistors, while the compliant elements are modeled by capacitors. Adapted from [23].
Fluid restrictions usually consist of rectangular channels or rings for radial valves. For a microchannel with a width , a depth , and a length (with and ), the solution of the Navier–Stokes equations is the planar Poiseuille flow, where the hydrodynamic resistance, equal to the pressure drop to flow rate ratio, is:
where η is the dynamic viscosity of the fluid.
The passive check valves consist of cylindrical pillars lying on an annular valve seat. The solution of the Navier–Stokes equations for the radial flow between two parallel disks separated by a distance leads to the following hydrodynamic resistance:
where and are the outer and inner radii of the annular valve seat [23].
The valve opening can be derived from the expression:
where is the valve stiffness obtained through FEM simulations, is the pressure drop across the valve, and S is the cross-section of either the inlet or outlet fluidic port of the micropump. For non-Newtonian fluids, solving the Navier–Stokes equation leads to more complex formulas, which can be found here [71]. Also, many articles and textbooks provide the fluid resistances of various channel cross-sections, see, e.g., [72,73,74,75,76].
The elastic/deformable elements of a micropump are characterized by their pressure-dependent volume deformation or fluid capacitance , defined as follows [63]:
The fluid capacitance can be obtained using an analytical formula for simple geometries or FEM simulations. For a compressible medium of volume V, the fluid capacitance can also be written:
where is the compressibility factor [63]. For air, the capacitance is simply . The capacitance of a square detector membrane, assuming that there is no initial stress, is, for small deflections:
where a and t are the width and thickness of the clamped membrane, while E and are the Young modulus and Poisson’s ratio of the membrane material, respectively [61].
The circular membrane stiffness k, in the linear deformation theory (deflection ), can be approximated by:
where
and is the ratio of mesa and membrane radii.
The coupling between the piezo bender and the membrane with a flexible blade makes the estimation of the overall stiffness difficult (see [59] for the description of a pneumatic method to estimate this value experimentally). For small deflections, it can be assumed that the force generated by the piezo is almost constant during the stroke. Thus, the system can be approximated by a simple membrane with a mesa submitted to a constant force. The detailed analytical formula can be found here to derive the volume change of the pump chamber induced by its deflection [68,77].
If the deformation of the flexible part of the membrane is neglected, a useful formula derived from basic geometrical considerations can be used to approximate this volume change induced by the deflection along the z direction normal to the mesa surface:
The pumping membrane displacement itself is governed by the equilibrium of forces on the pumping membrane, including pressure force, the elastic restoring force of the pumping membrane, elastic force of the mechanical stops, piezo force, and finally the squeeze film force.
This latter force is derived by solving the Navier–Stokes equation for the flow between two flat parallel disks of radius , one disk is fixed (the mechanical stop) while the other one (the moving membrane) moves due to the application of a constant force. The expression of the force, also called Stephan force, is:
where h is the distance between the two disks [78]. This force shall be considered in the numerical model if no specific structures are implemented to reduce this damping effect.
The main outputs of the simulations are the stroke volume, the valve displacements, the estimation of potential free flow and backflow, and the evolution of the pressure inside the pumping chamber during an actuation cycle.
Such an electrical equivalent network is a powerful tool to evaluate, in a design-for-manufacturing approach, the impact of manufacturing tolerances on fluidic performances [23,59]. The effects of single or multiple failure modes on the pressure profiles can also be easily derived to build a detection algorithm able to discriminate valve leakage, air entrance, reservoir overfilling, and occlusion, from any other type of failure modes [40]. A comprehensive review of the various pressure profiles experimentally recorded during air pumping is provided in [59]. This tool can therefore be used to refine the design of the valve, pumping chamber, and actuator to keep the occurrence of these risks at an acceptable level.
3. Specific Factors Influencing the Design of such an Insulin Displacement Micropump
3.1. Insulin Aggregation
The propensity of insulin to form aggregates has been known for almost 100 years [79,80,81]. The formation of insulin fibrils is a physical process driven by the shielding of the hydrophobic domains; the partially unfolded insulin molecules interact to form linear aggregates [82,83]. Factors that affect the fibril formation comprise acidic pH [84], agitation and shear stress [85,86], elevated temperature [87], contact with hydrophobic surfaces [88], and variation in ionic strength [89]. The comprehension of the insulin aggregation mechanisms is crucial to anticipating compatibility with the infusion device [90]. Aggregates of insulin can lead to occlusion of the fluidic pathway [81,82], backflow, and thus, underdelivery, if the fibrils are stuck onto a valve seat or if the fibrils impede the pumping mechanism [39,40], but also free flow and potentially overdelivery if both valves are contaminated and the pressure between the reservoir and infusion line is not balanced [59]. The relevant physical factors that need to be taken into account when designing the displacement micropump are the shear stress control during pumping and the interaction with hydrophobic surfaces, especially air bubbles.
3.2. Shear Stress and Hydrophobic Surfaces
The shear stress of a fluid between two flat plates of surface A separated by a distance y is defined as a unit area amount of force parallel to the plates that is acting on the fluid:
where is the shear stress, F is the drag force applied to a plate, is fluid viscosity, and is the velocity gradient at right angles to the plates. Maximum shear stress occurs when insulin flows through the small valve opening and during the compression of the membrane against the mechanical stops, wherein the fluid is squeezed. Geometrical modifications of the valve seat to shorten the constricted areas wherein high shear is observed is an option that should be considered carefully. A thinner valve seat exhibits a lower hydrodynamic resistance and can lead to larger backflow in the presence of contamination, reducing the pump tolerance to particles. A safer approach to control shear stress in this area consists of tuning the actuation profile to limit the peak of the pulsatile flow rate without affecting the average delivery rate. As the fluidic pathway of a displacement micropump is complex, the tuning of the actuation cycle requires FEM simulations to map the dynamic shear stress.
The squeeze film effect has a negative impact on insulin stability but also delivery accuracy at a fast actuation rate [22,36,40,59]. A classical solution to reduce this effect consists of using small anti-stiction pads that limit the surface of contact between the pumping membrane and the mechanical stops (see the pink pads in Figure 2). As the squeeze film force varies with the fourth power of the radius of the contact surface, according to Equation (13), the use of a multitude of pads reduces the overall squeeze film force by several orders of magnitude. The contact areas that are submitted to maximum shear stress are also automatically reduced and limit the probability of generating aggregates and precipitates. The increased local pressure on the pads can also better crush potential residues and limit the occurrence of underdelivery induced by a limited stroke. Finally, the presence of hydrophobic surfaces can be reduced using a hydrophilic coating or other surface treatments.
3.3. Air Management
3.3.1. Air in the Insulin Reservoir and Air Filter
Air is present in the insulin reservoir due to a combination of factors. As discussed in the introduction, the insulin reservoir is usually maintained at the atmospheric pressure to prevent the risk of free flow. This feature can be obtained by using a flexible or semi-flexible reservoir that is collapsed to limit the initial amount of air. In implantable pumps, the presence of a rigid external casing does not allow a pressure equilibrium between the reservoir and surrounding tissues, thus alternative methods shall be considered to prevent free flow in environmental conditions of high pressures (scuba diving) or after prolonged exposure to low pressure, e.g., during a stay at high altitude [91,92]. The filling, in particular, if this operation is made by the patient, is a second source of air entrance. Degassing from insulin and air permeation through the reservoir membrane also lead to additional air generation in the insulin reservoir [93].
As mentioned in a previous section, the presence of an air interface can lead to the formation of insulin aggregation and fibrils through a complex pathway [83,90]. Body-worn devices are of particular concern due to the combined effect of temperature and shaking. Check-valve micropumps usually come with a filter to prevent the risk of valve leakage or blocking depending on the type of contamination [31]. In the specific case of insulin delivery, the filter protects the valves from reservoir particles, air bubbles, and fibrils of fast-acting insulin analogs within the reservoir [21,22]. The surface of the hydrophilic filter used to prevent air entrance into the pump shall be large enough to allow the complete emptying of the reservoir and to generate a small pressure drop. Its bubble point, defined as the pressure at which air will pass through the wetted membrane filter, is determined using the numerical model of the micropump: its value shall be large enough to prevent air entrance in normal conditions of use and the pore size shall be small enough to prevent valve leakage. The principle of the bubble-point test of a filter is illustrated in Figure 5. This bubble point is defined by:
where P is the bubble-point air pressure (Pa), D the pore diameter (micrometer), the surface tension of the liquid (N/m), and the contact angle between the insulin and the filter material [94]. The membrane filter pore density is finally adjusted to match hydrodynamic resistance requirements. The choice of membrane filter material, like any other material in contact with insulin, shall meet biocompatibility requirements and shall not affect insulin stability and potency.
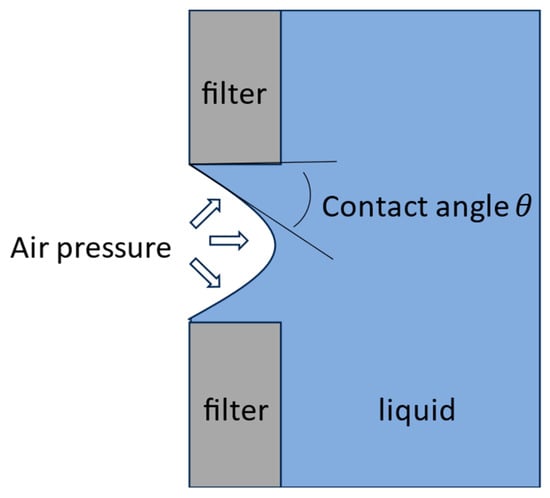
Figure 5.
Principle of the bubble-point test of a hydrophilic filter.
3.3.2. Self-Priming Capability
The compression ratio of the displacement micropump is equal to:
The micropump can be self-priming and bubble tolerant if the compression ratio satisfies specific design rules that notably depend on the pumping rate and valve opening thresholds, also called valve pretensions.
It is assumed that both passive check valves have the same opening threshold , which corresponds to the absolute value of the minimum pressure gradient through the valve to open it. To pump air, the micropump shall first be able to open the valves. The amplitude of the pressure gradient that is generated between the pumping chamber and the inlet and outlet ports shall therefore meet this minimum criterion:
At high actuation frequency, if the compression phase is fast enough to be adiabatic (no heat transfer between the gas and the micropump), then the quantity remains constant (the gas is assumed to be ideal, P is the absolute pressure of the gas in the pumping chamber, V the pumping chamber volume, and the gas adiabatic coefficient equal to 1.4 for air). The micropump can pump air at high frequency if the minimum compression ratio for air satisfies the criterion:
where is the atmospheric pressure [58]. Considering and , the criterion is:
At low actuation frequency, when the gas in the pumping chamber is at thermal equilibrium with the micropump, the compression process is isothermal with . The criterion to pump air becomes:
For and , the criterion at a low actuation rate is:
The criterion derived from the isothermal air compression process can be considered the worst case and therefore taken as input for a robust micropump design. A compression ratio of 1:1.2 and output pressure up to 1.3 bar were reported for MEMS displacement micropumps [40].
The minimum compression ratio for a liquid, considering that the pump is already primed, is:
where is the liquid compressibility. This criterion, thanks to the very low value of (e.g., for water) is easily met whatever the displacement micropump design.
The value of mainly depends on the active area of the valve and its stiffness. Refined models of microvalves can also consider electrostatic and van der Waals forces, solid bridging, hydrogen bonding, and capillary forces [79].
3.3.3. Capillary Adhesion
Different approaches can be considered to prevent valve stiction, including the use of an anti-bonding layer during micromachining, the control of the surface properties and roughness, and the micro-structuration of the valve seat. Coating and surface treatment can indeed lower the adhesion of the valve onto its seat and thus improve the bubble tolerance of the micropump [95].
Capillary force may be a problem if the valve seat surface is large and a meniscus is present on both sides of the valve seat, forming a capillary bridge. The latter can occur in the presence of a large bubble, during drying when the pump is operated at a very low basal rate, or when it is switched off. The presence of air may be the result of an air leak or simple degassing. To operate correctly, the micropump must be able to generate a pressure force on the valve that is sufficiently large to overcome this additional capillary force and thus force the meniscus through the small valve opening [58].
The capillary adhesion that can block an annular valve is illustrated in Figure 6. It is assumed that the liquid wets the surfaces with a contact angle The capillary bridge is characterized by a radius of curvature R and a surface , where w is the width of the valve seat and the distance between the valve symmetry axis and the center of the valve seat. The distance between the two flat surfaces forming the valve is denoted as , with . The Laplace pressure in the liquid is [96,97]:
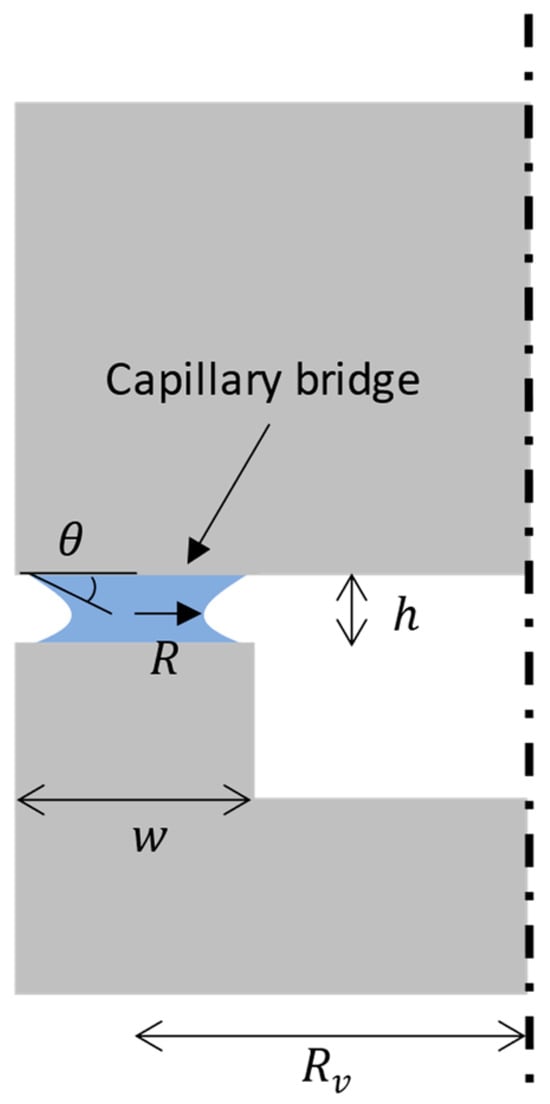
Figure 6.
Capillary adhesion of a schematic annular valve (not to scale). The liquid is represented in blue.
The attractive force between the two surfaces of the valve seat is thus:
For small gap values, this force can be large enough to prevent the opening of the valve. In addition, prolonged contact with a hydrophobic interface such as air when the pump is not activated is a well-known factor that increases the formation of insulin aggregates [81,82], and such gel-like residues or precipitates usually require a purge to remove the obstruction. The use of hydrophobic material to form the valve seat is attractive to prevent stiction during the wafer bonding process and to avoid the capillary valve effect, but on the other hand, the contact of insulin with such hydrophobic surfaces promotes the formation of fibrils, which in turn can lead to valve leakage. Also, hydrophobic surfaces are negatively impacting the self-priming capability of the micropump. Air bubbles become more difficult to purge, which can lead to problems with drug stability [82]. Water, due to its large surface tension of 0.072 N/m, can be considered as the worst case during the dimensioning of the valve and the tests of bubble tolerance.
3.3.4. Valve Pretension
The determination of the valve opening thresholds (or valve pretensions) of a displacement micropump depends on different requirements related to the pumping performance, pumping efficiency, and accuracy considerations. More specifically, in diabetes care, other patient safety considerations need to be taken into account, such as protection against free flow that could lead to a fatal outcome.
By design, the valves shall remain closed when the micropump is not activated. The water column due to external pressure conditions and/or the use of a long infusion line shall not open the valves and thus lead to direct communication between the insulin reservoir and the patient.
Design constraints related to failure detection can also be considered during the dimensioning of the valves. The measurement of the pressure inside the pumping chamber or downstream of the micropump outlet is indeed a powerful tool to monitor the correct functioning of the micropump [40,59]. Tuning the values of the valve pretensions allows for optimized amplitudes of the pressure during an actuation cycle and a better sensitivity of the failure detection algorithm. Valve pretensions of about 50 to 100 mbar, associated with a high compression ratio and a stroke volume of 0.2 µL, enable the reliable and fast detection of any condition affecting pumping accuracy including occlusion, valve leakage, reservoir under- or overpressure, and actuator failure [40,59].
3.3.5. Air in the Pumping Chamber: Underdelivery, Foam, and Cavitation
Hydrophilic surfaces are required to enable the fast and effective priming of the pumping chamber. Indeed, residual air bubbles lower the stroke volume as the compliance (or fluid capacitance) of the pumping chamber increases: a part of the volume displaced by the pumping chamber serves to compress air instead of pushing insulin through the infusion line [40,98]. The expansion of a bubble during actuation can be estimated as follows.
The pressure inside the bubble and in the liquid at the bubble wall are:
and
where is the pressure of non-condensing gas, is the vapor pressure, is the Laplace pressure, is the vapor tension, and R is the bubble radius.
The pressure inside a bubble at equilibrium is:
where is the static pressure in the liquid just outside the bubble wall, and and are the equilibrium bubble radius and volume, respectively. The pressure is calculated using a polytropic law:
where the polytropic index is equal to 1 and Laplace’s coefficient for isothermal and adiabatic bubble expansion. Hence, the relation between the bubble volume and the liquid pressure in the absence of dissipation is [99]:
The presence of insulin excipients such as cresol or meta-cresol shall be considered when estimating the value of the vapor pressure in the bubble.
The design of the pumping chamber must limit areas within which flow during actuation is low, such as a cul-de-sac, as the air trapped in such an area is difficult to remove. Also, a high compression ratio is desirable to improve both priming and bubble purging capability. However, special care shall be taken when setting the actuation speed. A fast pumping membrane motion during the supply phase can generate a large underpressure that in turn leads to potential cavitation, which refers to the formation of a vapor phase within the liquid due to a rapid pressure reduction, and excessive shear stress on the drug molecules [82].
An interesting case occurs indeed when the micropump is perfectly primed. During the actuation, since insulin is considered incompressible, the pressure decreases very quickly and can become negative. This phenomenon can occur when the inlet remains closed (stiction) or when the actuation speed is too fast: in this latter case, the time necessary for the liquid to fill the pumping chamber may be much longer than the actuation voltage ramp. Since the membrane is in equilibrium, that means that the water exerts an attractive force on the membrane and the water is thus under a negative pressure (in tension, or a positive stress state).
By increasing the actuation force on the membrane, the liquid is stretched but this state is metastable: the creation of a bubble can indeed lower the potential energy of the system. However, this process requires overcoming an energy barrier since the liquid–gas transition is discontinuous (first-order transition since the interface between the two phases has a finite energy per unit area, which is equal to the surface tension).
The reversible formation of a vapor bubble of radius R in the liquid requires work to create the liquid/vapor interface equal to
The formation of the bubble volume at the negative pressure p requires the negative work , while filling this volume with a vapor pressure requires a negative work equal to . For large negative pressure p, this latter term can be neglected and the net work to form the bubble is:
At negative pressure, the function has a maximum at the critical radius :
with
A bubble of radius must overcome an energy barrier before it can grow freely while reducing free energy. Bubble expansion stops when the pressure in the liquid rises to the liquid’s vapor pressure [100]. This energy barrier is weak, but relatively very high compared to thermal fluctuations. A liquid can also remain in this metastable state for a very long time at high negative pressures (in a tree, the pressure at the leaf level can reach several bars under zero), and microbubbles usually disappear without reaching the critical size. However, experiments at strongly negative pressures required special preparation to avoid any nucleation sites in the liquid, especially at the interfaces [101]. In practice, this effect is therefore rarely observed.
Pumping insulin at high speed results in the sudden growth of residual air bubbles followed by a partial collapse when insulin enters the pumping chamber during the supply phase. The number of bubbles increases with each actuating cycle until foam is gradually generated, which considerably reduces the dispensing rate. To prevent foaming, the actuation rate can be electronically limited and controlled according to pressure measurements in the pumping chamber [23].
4. Conclusions
A displacement micropump with passive check valves is an attractive solution to infuse insulin. This volumetric micropump, intrinsically insensitive to temperature, external pressure, and viscosity variations, shows impressive delivery accuracy performances that make this technology a good candidate for highly concentrated insulin infusion. However, this type of micropump presents new challenges linked to the management of air bubbles and insulin fibrils. To address this, a set of design rules was proposed and discussed in a design-for-reliability approach. Innovative solutions, including the introduction of new functionalities or additional monitoring systems with dedicated algorithms, need therefore to be implemented to make an effective and safe insulin delivery system based on displacement micropump technology.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The author is an employee of Debiotech SA and declares no conflicts of interest.
References
- Pickup, J.C.; Keen, H.; Parsons, J.A.; Alberti, K.G. Continuous subcutaneous insulin infusion: An approach to achieving normoglycaemia. Br. Med. J. 1978, 1, 204–207. [Google Scholar] [CrossRef] [PubMed]
- Bode, B.W.; Steed, R.D.; Davidson, P.C. Reduction in severe hypoglycemia with long-term continuous subcutaneous insulin infusion in type I diabetes. Diabetes Care 1996, 19, 324–327. [Google Scholar] [CrossRef] [PubMed]
- Lenhard, M.J.; Reeves, G.D. Continuous subcutaneous insulin infusion: A comprehensive review of insulin pump therapy. Arch. Intern. Med. 2001, 161, 2293–2300. [Google Scholar] [CrossRef] [PubMed]
- Misso, M.L.; Egberts, K.J.; Page, M.; O’Connor, D.; Shaw, J. Cochrane review: Continuous subcutaneous insulin infusion (CSII) versus multiple insulin injections for type 1 diabetes mellitus. Evid.-Based Child Health A Cochrane Rev. J. 2010, 5, 1726–1867. [Google Scholar] [CrossRef]
- Bruttomesso, D.; Costa, S.; Baritussio, A. Continuous subcutaneous insulin infusion (CSII) 30 years later: Still the best option for insulin therapy. Diabetes/Metab. Res. Rev. 2009, 25, 99–111. [Google Scholar] [CrossRef] [PubMed]
- Priesterroth, L.; Grammes, J.; Clauter, M.; Kubiak, T. Diabetes technologies in people with type 1 diabetes mellitus and disordered eating: A systematic review on continuous subcutaneous insulin infusion, continuous glucose monitoring and automated insulin delivery. Diabet. Med. 2021, 38, e14581. [Google Scholar] [CrossRef] [PubMed]
- Dos Santos, T.J.; Campos JD, M.D.; Argente, J.; Rodríguez-Artalejo, F. Effectiveness and equity of continuous subcutaneous insulin infusions in pediatric type 1 diabetes: A systematic review and meta-analysis of the literature. Diabetes Res. Clin. Pract. 2021, 172, 108643. [Google Scholar] [CrossRef]
- Steil, G.M.; Panteleon, A.E.; Rebrin, K. Closed-loop insulin delivery—The path to physiological glucose control. Adv. Drug Deliv. Rev. 2004, 56, 125–144. [Google Scholar] [CrossRef]
- Hovorka, R. Closed-loop insulin delivery: From bench to clinical practice. Nat. Rev. Endocrinol. 2011, 7, 385–395. [Google Scholar] [CrossRef]
- Bally, L.; Thabit, H.; Hartnell, S.; Andereggen, E.; Ruan, Y.; Wilinska, M.E.; Evans, M.L.; Wertli, M.M.; Coll, A.P.; Stettler, C.; et al. Closed-loop insulin delivery for glycemic control in noncritical care. N. Engl. J. Med. 2018, 379, 547–556. [Google Scholar] [CrossRef]
- Bergenstal, R.M.; Garg, S.; Weinzimer, S.A.; Buckingham, B.A.; Bode, B.W.; Tamborlane, W.V.; Kaufman, F.R. Safety of a hybrid closed-loop insulin delivery system in patients with type 1 diabetes. JAMA 2016, 316, 1407–1408. [Google Scholar] [CrossRef] [PubMed]
- Tauschmann, M.; Thabit, H.; Bally, L.; Allen, J.M.; Hartnell, S.; Wilinska, M.E.; Ruan, Y.; Sibayan, J.; Kollman, C.; Cheng, P.; et al. Closed-loop insulin delivery in suboptimally controlled type 1 diabetes: A multicentre, 12-week randomised trial. Lancet 2018, 392, 1321–1329. [Google Scholar] [CrossRef] [PubMed]
- Bombaci, B.; Passanisi, S.; Alibrandi, A.; D’Arrigo, G.; Patroniti, S.; Averna, S.; Salzano, G.; Lombardo, F. One-year real-world study on comparison among different continuous subcutaneous insulin infusion devices for the management of pediatric patients with type 1 diabetes: The supremacy of hybrid closed-loop systems. Int. J. Environ. Res. Public Health 2022, 19, 10293. [Google Scholar] [CrossRef]
- Freckmann, G.; Buck, S.; Waldenmaier, D.; Kulzer, B.; Schnell, O.; Gelchsheimer, U.; Ziegler, R.; Heinemann, L. Insulin pump therapy for patients with type 2 diabetes mellitus: Evidence, current barriers, and new technologies. J. Diabetes Sci. Technol. 2021, 15, 901–915. [Google Scholar] [CrossRef] [PubMed]
- Wong, E.Y.; Vadlapatla, R.; Morello, C.M. Diabetes type 1 and type 2—Insulin delivery systems. In Drug Delivery Devices and Therapeutic Systems; Academic Press: New York, NY, USA, 2021; pp. 475–489. [Google Scholar]
- Leelarathna, L.; Roberts, S.A.; Hindle, A.; Markakis, K.; Alam, T.; Chapman, A.; Morris, J.; Urwin, A.; Jinadev, P.; Rutter, M.K. Comparison of different insulin pump makes under routine care conditions in adults with Type 1 diabetes. Diabet. Med. 2017, 34, 1372–1379. [Google Scholar] [CrossRef] [PubMed]
- Freckmann, G.; Kamecke, U.; Waldenmaier, D.; Haug, C.; Ziegler, R. Accuracy of bolus and basal rate delivery of different insulin pump systems. Diabetes Technol. Ther. 2019, 21, 201–208. [Google Scholar] [CrossRef] [PubMed]
- Borot, S.; Franc, S.; Cristante, J.; Penfornis, A.; Benhamou, P.Y.; Guerci, B.; Hanaire, H.; Renard, E.; Reznik, Y.; Simon, C.; et al. Accuracy of a new patch pump based on a microelectromechanical system (MEMS) compared to other commercially available insulin pumps: Results of the first in vitro and in vivo studies. J. Diabetes Sci. Technol. 2014, 8, 1133–1141. [Google Scholar] [CrossRef] [PubMed]
- Bissig, H.; Tschannen, M.; de Huu, M. Traceability of pulsed flow rates consisting of constant delivered volumes at given time interval. Flow Meas. Instrum. 2020, 73, 101729. [Google Scholar] [CrossRef]
- Thornton, J.; Sakhrani, V. How lubricant choice affects dose accuracy in insulin pumps. ONdrugDelivery Mag. 2017, 78, 32–36. [Google Scholar]
- Chappel, E.; Dumont-Fillon, D. Micropumps for drug delivery. In Drug Delivery Devices and Therapeutic Systems; Academic Press: New York, NY, USA, 2021; pp. 31–61. [Google Scholar]
- Chappel, E. Implantable drug delivery devices. In Drug Delivery Devices and Therapeutic Systems; Academic Press: New York, NY, USA, 2021; pp. 129–156. [Google Scholar]
- Fournier, S.; Chappel, E. Modeling of a Piezoelectric MEMS Micropump Dedicated to Insulin Delivery and Experimental Validation Using Integrated Pressure Sensors: Application to Partial Occlusion Management. J. Sens. 2017, 2017, 3719853. [Google Scholar] [CrossRef]
- Chappel, E. Robust alarm design strategy for medical devices: Application to air-in-line detection and occlusion management. Glob. J. Eng. Technol. Adv. 2023, 16, 030–040. [Google Scholar] [CrossRef]
- Cescon, M.; DeSalvo, D.J.; Ly, T.T.; Maahs, D.M.; Messer, L.H.; Buckingham, B.A.; Doyle, F.J., III; Dassau, E. Early detection of infusion set failure during insulin pump therapy in type 1 diabetes. J. Diabetes Sci. Technol. 2016, 10, 1268–1276. [Google Scholar] [CrossRef] [PubMed]
- Gibney, M.; Xue, Z.; Swinney, M.; Bialonczyk, D.; Hirsch, L. Reduced silent occlusions with a novel catheter infusion set (BD FlowSmart): Results from two open-label comparative studies. Diabetes Technol. Ther. 2016, 18, 136–143. [Google Scholar] [CrossRef] [PubMed]
- Freckmann, G.; Kamecke, U.; Waldenmaier, D.; Haug, C.; Ziegler, R. Occlusion detection time in insulin pumps at two different basal rates. J. Diabetes Sci. Technol. 2018, 12, 608–613. [Google Scholar] [CrossRef]
- Deiss, D.; Adolfsson, P.; Alkemade-van Zomeren, M.; Bolli, G.B.; Charpentier, G.; Cobelli, C.; Danne, T.; Girelli, A.; Mueller, H.; Verderese, C.A.; et al. Insulin infusion set use: European perspectives and recommendations. Diabetes Technol. Ther. 2016, 18, 517–524. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.T.; Huang, X.; Chuan, T.K. MEMS-micropumps: A review. J. Fluids Eng. 2002, 124, 384–392. [Google Scholar] [CrossRef]
- Laser, D.J.; Santiago, J.G. A review of micropumps. J. Micromech. Microeng. 2004, 14, R35. [Google Scholar] [CrossRef]
- Woias, P. Micropumps—Past, progress and future prospects. Sens. Actuators B Chem. 2005, 105, 28–38. [Google Scholar] [CrossRef]
- Amirouche, F.; Zhou, Y.; Johnson, T. Current micropump technologies and their biomedical applications. Microsyst. Technol. 2009, 15, 647–666. [Google Scholar] [CrossRef]
- Wang, Y.N.; Fu, L.M. Micropumps and biomedical applications–A review. Microelectron. Eng. 2018, 195, 121–138. [Google Scholar] [CrossRef]
- Bußmann, A.B.; Grünerbel, L.M.; Durasiewicz, C.P.; Thalhofer, T.A.; Wille, A.; Richter, M. Microdosing for drug delivery application—A review. Sens. Actuators A Phys. 2021, 330, 112820. [Google Scholar] [CrossRef]
- Van Lintel HT, G.; van De Pol FC, M.; Bouwstra, S. A piezoelectric micropump based on micromachining of silicon. Sens. Actuators 1988, 15, 153–167. [Google Scholar] [CrossRef]
- Maillefer, D.; Gamper, S.; Frehner, B.; Balmer, P.; Van Lintel, H.; Renaud, P. A high-performance silicon micropump for disposable drug delivery systems. In Proceedings of the Technical Digest. MEMS 2001. 14th IEEE International Conference on Micro Electro Mechanical Systems (Cat. No. 01CH37090), Interlaken, Switzerland, 25 January 2001; pp. 413–417. [Google Scholar]
- Schneeberger, N.; Blondel, A.; Boutaud, B.; Chappel, E.; Maillefer, D.; Schneider, V. Disposable insulin pump-a medical case study. In Proceedings of the DTIP of MEMS & MOEMS, Montreux, Switzerland, 12–14 May 2004; pp. 25–27. [Google Scholar]
- Schneeberger, N.; Allendes, R.; Bianchi, F.; Chappel, E.; Conan, C.; Gamper, S.; Schlund, M. Drug delivery micropump with built-in monitoring. Procedia Chem. 2009, 1, 1339–1342. [Google Scholar] [CrossRef][Green Version]
- Chappel, E.; Mefti, S.; Lettieri, G.L.; Proennecke, S.; Conan, C. High precision innovative micropump for artificial pancreas. In Microfluidics, BioMEMS, and Medical Microsystems XII; San Francisco, USA, 2–4 February 2014; SPIE: Bellingham, WA, USA, 2014; Volume 8976, pp. 279–290. [Google Scholar]
- Dumont-Fillon, D.; Tahriou, H.; Conan, C.; Chappel, E. Insulin micropump with embedded pressure sensors for failure detection and delivery of accurate monitoring. Micromachines 2014, 5, 1161–1172. [Google Scholar] [CrossRef]
- Bußmann, A.; Leistner, H.; Zhou, D.; Wackerle, M.; Congar, Y.; Richter, M.; Hubbuch, J. Piezoelectric silicon micropump for drug delivery applications. Appl. Sci. 2021, 11, 8008. [Google Scholar] [CrossRef]
- Junwu, K.; Zhigang, Y.; Taijiang, P.; Guangming, C.; Boda, W. Design and test of a high-performance piezoelectric micropump for drug delivery. Sens. Actuators A Phys. 2005, 121, 156–161. [Google Scholar] [CrossRef]
- Stehr, M.; Messner, S.; Sandmaier, H.; Zengerle, R. The VAMP—A new device for handling liquids or gases. Sens. Actuators A Phys. 1996, 57, 153–157. [Google Scholar] [CrossRef]
- Zengerle, R.; Ulrich, J.; Kluge, S.; Richter, M.; Richter, A. A bidirectional silicon micropump. Sens. Actuators A Phys. 1995, 50, 81–86. [Google Scholar] [CrossRef]
- Uhlig, S.; Gaudet, M.; Langa, S.; Schimmanz, K.; Conrad, H.; Kaiser, B.; Schenk, H. Electrostatically driven in-plane silicon micropump for modular configuration. Micromachines 2018, 9, 190. [Google Scholar] [CrossRef]
- Guo, S.; Nakamura, T.; Fukuda, T.; Oguro, K. Development of the micro pump using ICPF actuator. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997; Volume 1, pp. 266–271. [Google Scholar]
- Van de Pol FC, M.; Van Lintel HT, G.; Elwenspoek, M.; Fluitman JH, J. A thermopneumatic micropump based on micro-engineering techniques. Sens. Actuators A Phys. 1990, 21, 198–202. [Google Scholar] [CrossRef]
- Böhm, S.; Olthuis, W.; Bergveld, P. A plastic micropump constructed with conventional techniques and materials. Sens. Actuators A Phys. 1999, 77, 223–228. [Google Scholar] [CrossRef]
- Benard, W.L.; Kahn, H.; Heuer, A.H.; Huff, M.A. Thin-film shape-memory alloy actuated micropumps. J. Microelectromech. Syst. 1998, 7, 245–251. [Google Scholar] [CrossRef]
- Makino, E.; Mitsuya, T.; Shibata, T. Fabrication of TiNi shape memory micropump. Sens. Actuators A Phys. 2001, 88, 256–262. [Google Scholar] [CrossRef]
- Xu, D.; Wang, L.; Ding, G.; Zhou, Y.; Yu, A.; Cai, B. Characteristics and fabrication of NiTi/Si diaphragm micropump. Sens. Actuators A Phys. 2001, 93, 87–92. [Google Scholar] [CrossRef]
- Zhan, C.; Lo, T.; Liu, L.; Peihsin, T. A silicon membrane micropump with integrated bimetallic actuator. Chin. J. Electron. 1996, 5, 33. [Google Scholar]
- Renard, E. Continuous intraperitoneal insulin infusion from implantable pumps. In Technological Advances in the Treatment of Type 1 Diabetes; Karger Publishers: 2015; Volume 24, pp. 190–209.
- Renard, E. Implantable insulin delivery pumps. Minim. Invasive Ther. Allied Technol. 2004, 13, 328–335. [Google Scholar] [CrossRef] [PubMed]
- Bally, L.; Thabit, H.; Hovorka, R. Finding the right route for insulin delivery–an overview of implantable pump therapy. Expert Opin. Drug Deliv. 2017, 14, 1103–1111. [Google Scholar] [CrossRef] [PubMed]
- Sefton, M.V. Implantable pumps. Crit. Rev. Biomed. Eng. 1987, 14, 201–240. [Google Scholar]
- King, B.R.; Goss, P.W.; Paterson, M.A.; Crock, P.A.; Anderson, D.G. Changes in altitude cause unintended insulin delivery from insulin pumps: Mechanisms and implications. Diabetes Care 2011, 34, 1932–1933. [Google Scholar] [CrossRef]
- Richter, M.; Linnemann, R.; Woias, P. Robust design of gas and liquid micropumps. Sens. Actuators A Phys. 1998, 68, 480–486. [Google Scholar] [CrossRef]
- Chappel, E. Dry Test Methods for Micropumps. Appl. Sci. 2022, 12, 12258. [Google Scholar] [CrossRef]
- Chappel, E.; Allendes, R.; Bianchi, F.; Calcaterra, G.; Cannehan, F.; Conan, C.; Lefrique, J.; Lettieri, G.L.; Mefti, S.; Noth, A.; et al. Industrialized functional test for insulin micropumps. Procedia Eng. 2011, 25, 795–798. [Google Scholar] [CrossRef]
- Zengerle, R.; Richter, M. Simulation of microfluid systems. J. Micromech. Microeng. 1994, 4, 192. [Google Scholar] [CrossRef]
- Carmona, M.; Marco, S.; Samitier, J.; Morante, J.R. Dynamic simulations of micropumps. J. Micromech. Microeng. 1996, 6, 128. [Google Scholar] [CrossRef]
- Bourouina, T.; Grandchamp, J.P. Modeling micropumps with electrical equivalent networks. J. Micromech. Microeng. 1996, 6, 398. [Google Scholar] [CrossRef]
- Bourouina, T.; Bosseboeuf, A.; Grandchamp, J.P. Design and simulation of an electrostatic micropump for drug-delivery applications. J. Micromech. Microeng. 1997, 7, 186. [Google Scholar] [CrossRef]
- Morganti, E.; Fuduli, I.; Montefusco, A.; Petasecca, M.; U Pignatel, G. SPICE modelling and design optimization of micropumps. Int. J. Environ. Anal. Chem. 2005, 85, 687–698. [Google Scholar] [CrossRef]
- Hsu, Y.C.; Le, N.B. Equivalent electrical network for performance characterization of piezoelectric peristaltic micropump. Microfluid. Nanofluid. 2009, 7, 237–248. [Google Scholar] [CrossRef]
- Bardaweel, H.K. Understanding frequency response of thermal micropumps using electrical network analogy. Can. J. Phys. 2014, 92, 1178–1184. [Google Scholar] [CrossRef]
- Wang, X.Y.; Ma, Y.T.; Yan, G.Y.; Huang, D.; Feng, Z.H. High flow-rate piezoelectric micropump with two fixed ends polydimethylsiloxane valves and compressible spaces. Sens. Actuators A Phys. 2014, 218, 94–104. [Google Scholar] [CrossRef]
- Fournier, S.; Chappel, E. Dynamic simulations of a piezoelectric driven MEMS micropump. Procedia Eng. 2016, 168, 860–863. [Google Scholar] [CrossRef]
- Karmozdi, M.; Afshin, H.; Shafii, M.B. Electrical analogies applied on MMR micropump. Sens. Actuators A Phys. 2020, 301, 111675. [Google Scholar] [CrossRef]
- Cornaggia, L.; Conti, L.; Hannebelle, M.; Gamper, S.; Dumont-Fillon, D.; Van Lintel, H.; Renaud, P.; Chappel, E. Passive flow control valve for protein delivery. Cogent Eng. 2017, 4, 1413923. [Google Scholar] [CrossRef]
- Shah, R.K.; London, A.L. Laminar Flow Forced Convection in Ducts; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Bahrami, M.; Yovanovich, M.M.; Culham, J.R. Pressure drop of fully-developed, laminar flow in microchannels of arbitrary cross-section. In Proceedings of the International Conference on Nanochannels, Microchannels, and Minichannels, Toronto, ON, Canada, 13–15 June 2005; Volume 41855, pp. 269–280. [Google Scholar]
- Bruus, H. Theoretical Microfluidics; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Cottet, J.; Renaud, P. Introduction to microfluidics. In Drug Delivery Devices and Therapeutic Systems; Academic Press: New York, NY, USA, 2021; pp. 3–17. [Google Scholar]
- Young, W.C.; Budynas, R.G.; Sadegh, A.M. Roark’s Formulas for Stress and Strain; McGraw-Hill: New York, NY, USA, 2002; Volume 7, pp. 125–127. [Google Scholar]
- Resch, M.; Scheidl, R. A model for fluid stiction of quickly separating circular plates. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 1540–1556. [Google Scholar] [CrossRef]
- Krogh, A.; Hemmingsen, A.M. The destructive action of heat on insulin solutions. Biochem. J. 1928, 22, 1231. [Google Scholar] [CrossRef] [PubMed]
- Brange, J.; Havelund, S. Insulin pumps and insulin quality—Requirements and problems. Acta Med. Scand. 1983, 213, 135–138. [Google Scholar] [CrossRef] [PubMed]
- Lougheed, W.D.; Woulfe-Flanagan, H.; Clement, J.R.; Albisser, A.M. Insulin aggregation in artificial delivery systems. Diabetologia 1980, 19, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Brange, J.; Andersen, L.; Laursen, E.D.; Meyn, G.; Rasmussen, E. Toward understanding insulin fibrillation. J. Pharm. Sci. 1997, 86, 517–525. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; Shah, M.; Saraogi, I. Molecular aspects of insulin aggregation and various therapeutic interventions. ACS Bio Med Chem Au 2022, 2, 205–221. [Google Scholar] [CrossRef]
- Haas, J.; Vöhringer-Martinez, E.; Bögehold, A.; Matthes, D.; Hensen, U.; Pelah, A.; Abel, B.; Grubmüller, H. Primary steps of pH-dependent insulin aggregation kinetics are governed by conformational flexibility. ChemBioChem 2009, 10, 1816–1822. [Google Scholar] [CrossRef]
- Sluzky, V.; Tamada, J.A.; Klibanov, A.M.; Langer, R. Kinetics of insulin aggregation in aqueous solutions upon agitation in the presence of hydrophobic surfaces. Proc. Natl. Acad. Sci. USA 1991, 88, 9377–9381. [Google Scholar] [CrossRef]
- Sluzky, V.; Klibanov, A.M.; Langer, R. Mechanism of insulin aggregation and stabilization in agitated aqueous solutions. Biotechnol. Bioeng. 1992, 40, 895–903. [Google Scholar] [CrossRef]
- Vilasi, S.; Iannuzzi, C.; Portaccio, M.; Irace, G.; Sirangelo, I. Effect of trehalose on W7FW14F apomyoglobin and insulin fibrillization: New insight into inhibition activity. Biochemistry 2008, 47, 1789–1796. [Google Scholar] [CrossRef] [PubMed]
- Nault, L.; Guo, P.; Jain, B.; Bréchet, Y.; Bruckert, F.; Weidenhaupt, M. Human insulin adsorption kinetics, conformational changes and amyloidal aggregate formation on hydrophobic surfaces. Acta Biomater. 2013, 9, 5070–5079. [Google Scholar] [CrossRef]
- Buell, A.K.; Hung, P.; Salvatella, X.; Welland, M.E.; Dobson, C.M.; Knowles, T.P. Electrostatic effects in filamentous protein aggregation. Biophys. J. 2013, 104, 1116–1126. [Google Scholar] [CrossRef]
- Woods, R.J.; Alarcón, J.; McVey, E.; Pettis, R.J. Intrinsic fibrillation of fast-acting insulin analogs. J. Diabetes Sci. Technol. 2012, 6, 265–276. [Google Scholar] [CrossRef] [PubMed]
- Ryan, S.; Dudley, N.; Green, M.; Pruitt, C.; Jackman, G. Altered mental status at high altitude. Pediatrics 2018, 142, e20173973. [Google Scholar] [CrossRef]
- Dumont-Fillon, D.; Lamaison, D.; Chappel, E. Design and characterization of 3-stack MEMS-based passive flow regulators for implantable and ambulatory infusion pumps. J. Microelectromech. Syst. 2020, 29, 170–181. [Google Scholar] [CrossRef]
- Heinemann, L. Air Bubbles in Insulin Pumps: A Clinically Relevant Issue? J. Diabetes Sci. Technol. 2022, 16, 1351–1355. [Google Scholar] [CrossRef]
- Lindsley, W.G. Filter pore size and aerosol sample collection. In NIOSH Manual of Analytical Methods, 5th Edition. National Institute for Occupational Safety and Health (NIOSH): Atlanta, GA, USA, 2016.
- Maboudian, R.; Howe, R.T. Critical review: Adhesion in surface micromechanical structures. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 1997, 15, 1–20. [Google Scholar] [CrossRef]
- Gennes, P.G.; Brochard-Wyart, F.; Quéré, D. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves; Springer: New York, NY, USA, 2004. [Google Scholar]
- Bhushan, B. Adhesion and stiction: Mechanisms, measurement techniques, and methods for reduction. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2003, 21, 2262–2296. [Google Scholar] [CrossRef]
- Wang, B.; Demuren, A.; Gyuricsko, E.; Hu, H. An experimental study of pulsed micro-flows pertinent to continuous subcutaneous insulin infusion therapy. Exp. Fluids 2011, 51, 65–74. [Google Scholar] [CrossRef]
- Leighton, T.G. The Rayleigh–Plesset equation in terms of volume with explicit shear losses. Ultrasonics 2008, 48, 85–90. [Google Scholar] [CrossRef]
- Fisher, J.C. The fracture of liquids. J. Appl. Phys. 1948, 19, 1062–1067. [Google Scholar] [CrossRef]
- Caupin, F.; Herbert, E. Cavitation in water: A review. C. R. Phys. 2006, 7, 1000–1017. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).