Optimal Sewer Network Design Including Pumping Stations ^†

Abstract

In urban areas with a flat terrain, pumping stations must be included to elevate wastewater and avoid extreme excavation depths. These systems are characterized by high operational costs due to the pump’s power consumption. The present work presents a methodology for the optimal design of sewer networks including pumping stations, whose objective function is to minimize the construction and operation costs of the system. The methodology was tested on three sewer benchmark networks using two cost functions proposed in the literature. In all the sewer benchmarks, the cost achieved in the present work was compared with the best costs reported in the literature.

1. Introduction

The design of an optimal sewer network involves finding the lowest-cost solution. This problem is divided into two subproblems: first, the layout selection phase, the tree structure of the network is determined, which involves selecting the flow direction and type of pipe connection, and second, the hydraulic design phase, which involves defining the diameter and upstream and downstream invert elevation of the pipes. For flat topographies, in which pumping is required to comply with the maximum excavation depth, it is obligatory to consider pumping stations in the optimal design methodology, since the cost of pumping is a significant percentage of the overall cost of a sewer network. Engineers commonly place pumping stations at the end of sewer systems to lift wastewater to the outfall. However, according to a recent study [1], this may not be the most efficient approach. That study found that pumping at the end increases the pumping cost since the pumping flow rate is greater than that in other areas of the network.

2. Methodology

The implementation of pumping stations is proposed in an existing sewer network design methodology that was introduced by Duque et al. [2] and then extended by Saldarriaga et al. [3].

2.1. Layout Section

Duque et al. [2] proposed to solve the layout selection using a mixed-integer programming (MIP) model in which the decision variables represent the flow rate and direction of pipes. Later on, for the layout selection, the three criteria proposed by [3] are employed. Criterion 1 aims to prioritize pipes that align with the direction of the land slope, and to discard from the layout the pipes that are against the slope. Criterion 2 considers both the land slope and the number of outer-branch pipes. However, this criterion also aims to incorporate the energy per unit weight to transport the design flow rate, thus prioritizing pipes with higher head available. Criterion 3 is proposed for flat topographies and aims to minimize the length of the main sewer network series so that the final excavation depth decreases.

2.2. Hydraulic Design

Duque et al. [2] proposed modeling the problem as a directed graph. In this approach, each node represents a specific manhole’s combination of an upstream diameter and an invert elevation, while the arcs depict the feasible joints of nodes, which are the pipes, considering that the downstream diameter must be larger or equal to its upstream diameter to avoid blockages, and the downstream invert elevation must be deeper or equal to its upstream invert elevation to ensure gravity flow.

2.3. Pumping Stations in Sewer Network Design

The methodology outlined here proposes to make a change in the hydraulic design objective function proposed by [2]. It begins by adding a term to the equation that takes pumping stations into consideration (Equation (1)), where $C{T}_{v_i^k,v_j^{k^{\prime }}}$ represents the cost of pipe installation and $C{B}_{v_i^k,v_j^{k^{\prime }}}$ represents the cost of installing a pumping system, to obtain the following:

$$\min \left({{\displaystyle \sum }}_{\left(v_i^k,v_j^{k^{\prime }}\right)\in A_{D1}}C{T}_{v_i^k,v_j^{k^{\prime }}} X_{ij}+{{\displaystyle \sum }}_{\left(v_i^k,v_j^{k^{\prime }}\right)\in A_{D2}}C{B}_{v_i^k,v_j^{k^{\prime }}} Y_{ij}\right)$$

(1)

In this case, $A_{D1}$ represents all pipe combinations along with the depths they can be installed at within the network. $C{T}_{v_i^k,v_j^{k^{\prime }}}$ includes additional properties such as diameter and start and end depth. Additionally, $A_{D2}$ represents the connections within the node for the possible installation of a pumping system. $C{B}_{v_i^k,v_j^{k^{\prime }}}$ has additional properties, such as the required pumping head height at the selected manhole. To model the condition that establishes that only one of the two arcs can be active at a given time, a restriction is added to the model presented in Equation (2). $X_{ij}$ and $Y_{ij}$ represent binary variables taking values of 1 and 0, respectively, depending on whether a pipe is installed or a pump is installed, such that

$$X_{ij}+Y_{ij}\ge 1$$

(2)

3. Case Studies

The networks included as case studies were the following. All three networks were tested under equal hydraulic constraints as presented in Table 1.

Table 1. Implemented sewer networks.

	Moeini [4]	Chicó Sur [2]	Flattened Chicó [2]
Manholes	81	109	109
Pipes	144	160	160
Topography	Flat	Variable	Flat
Pipe length	100 m	Variable	Variable
Total flow rate	Constant	Variable	Variable

Restrictions

Table 2 shows the hydraulic design constraints for the pipes with their conditions.

Table 2. Hydraulic constraints.

Constraint	Value	Condition	Constraint	Value	Condition
Minimum diameter	0.2 m	$\mathrm{Always}$	Minimum velocity	0.7 m/s	$d\le 0.5\mathrm{m}\mathrm{Flow}\mathrm{rate}>0.015{\mathrm{m}}^3/\mathrm{s}$
Maximum filling ratio	0.6	$d\le 0.3\mathrm{m}$		$0.8\mathrm{m}/\mathrm{s}$	$d>0.5\mathrm{m}\mathrm{Flow}\mathrm{rate}>0.015{\mathrm{m}}^3/\mathrm{s}$
	0.7	$0.35\mathrm{m}\le d\le 0.45\mathrm{m}$	Maximum velocity	$5\mathrm{m}/\mathrm{s}$	$\mathrm{Always}$
	0.75	$0.5\mathrm{m}\le d\le 0.9\mathrm{m}$	Minimum gradient	0.003	$\mathrm{Flow}\mathrm{rate}<0.015{\mathrm{m}}^3/\mathrm{s}$
	0.8	$d\ge 1\mathrm{m}$	Minimum depth	1 m	$\mathrm{Always}$

4. Results

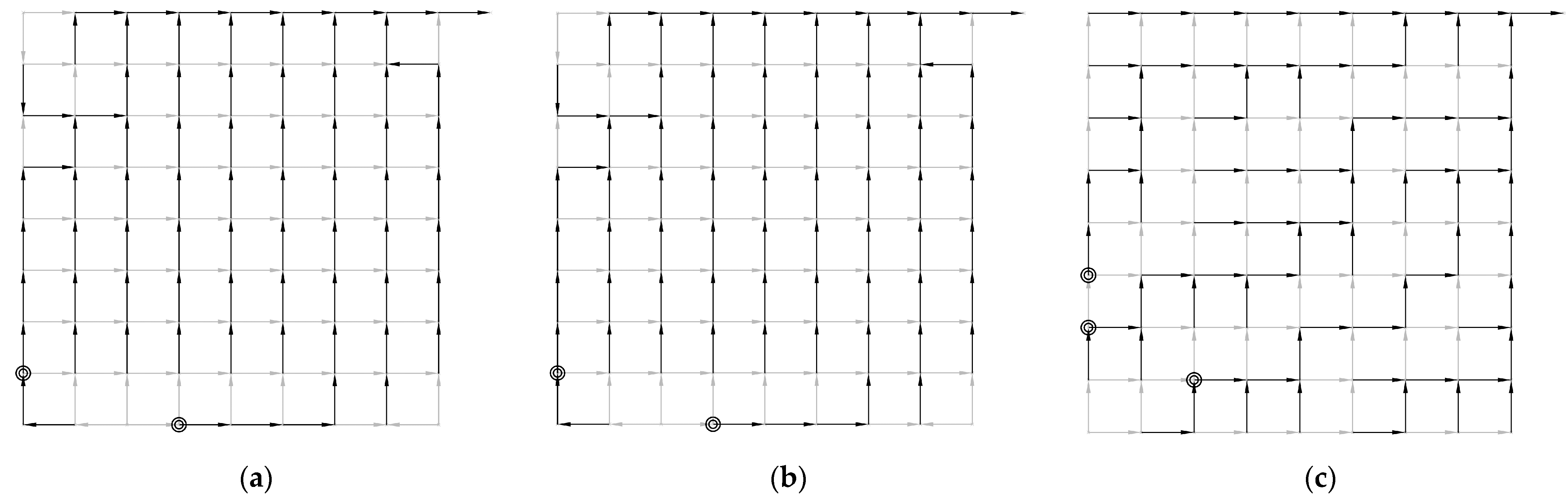
Table 3 shows optimized costs based on the equations presented by Li and Matthew [5]. It is observed that criteria 1 and 2 yield the same value given that a flat topography does not penalize pipe installation costs. Criterion 3 increases the number of continuous pipes, thus increasing the length and depth of the series, which leads to higher costs. In the three considered cases, a clear trend to locate pumping systems in the upstream regions of the network is observed, as detailed in Figure 1. The upstream location of pump systems translates to a diminishing of pumping costs, since these costs are directly correlated to flow rate and depth, both of which are smaller in the upstream regions of the network.

Table 3. Construction costs per criterion for Moeini and Afshar network [4].

Criterion	Construction Cost	Pumps	Location (Manhole)
Criterion 1	JPY 1,506,694.51	2	4, 10
Criterion 2	JPY 1,506,694.51	2	4, 10
Criterion 3	JPY 2,145,321.12	3	12, 19, 28

Figure 1. Scheme of the best design of the benchmark network proposed by [4] obtained from three criteria proposed by [3]. (a) Criterion 1; (b) Criterion 2; (c) Criterion 3.

Table 4 shows the optimized costs for the flattened Chicó Sur network. Due to the topography being flat and the lack of penalties related to pipe costs, criteria 1 and 2 yield the same cost. Criterion 3 yields the minimal construction cost.

Table 4. Construction costs per criterion for flattened Chicó Sur network.

Criterion	Construction Cost	Pumps	Location (Manhole)
Criterion 1	JPY 25,616,939.11	8	3, 8, 20, 24, 27, 28, 42, 44
Criterion 2	JPY 25,616,939.11	8	3, 8, 20, 24, 27, 28, 42, 44
Criterion 3	JPY 1,911,292.69	2	3, 4

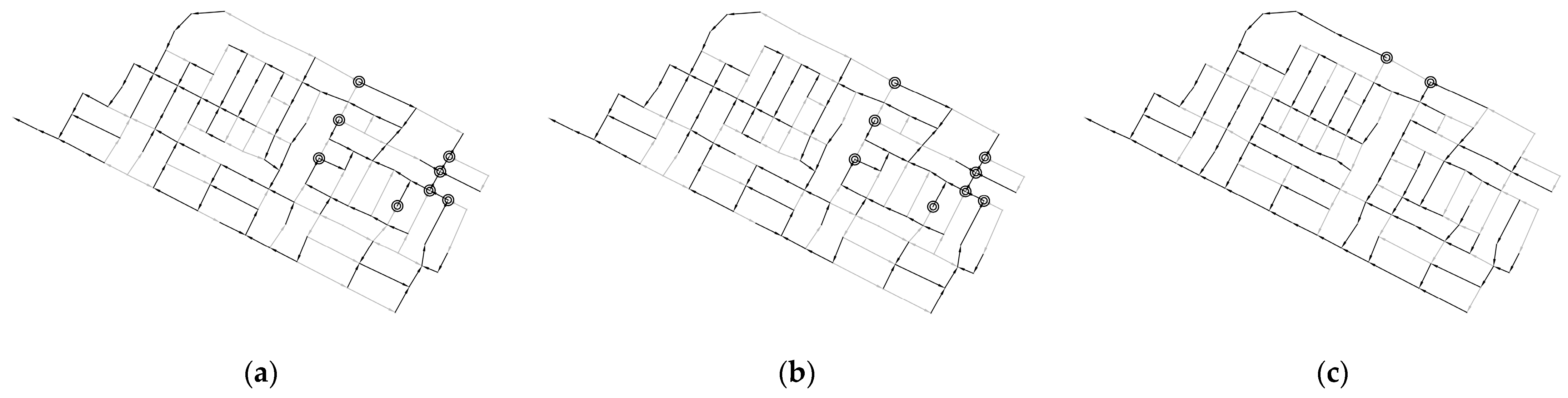
In the three considered cases, it is observed that, under criteria one and two, there is a trend to locate pumping systems in the upstream regions of the network, which in this case increases costs due to more pumps being required. On the other hand, under criterion three, the pump location is more spatially balanced, making more efficient use of energy losses, as presented in Figure 2.

Figure 2. Scheme of the best design of the flattened Chicó Sur benchmark network obtained from three criteria proposed by [3]. (a) Criterion 1; (b) Criterion 2; (c) Criterion 3.

5. Conclusions

A methodology is proposed with the aim to minimize construction costs in sewer networks that include in-line pumping stations, ensuring proper hydraulic performance. The results demonstrate the applicability and efficiency of the methodology in optimized sewer design with in-line pumping stations, in economic terms and while complying with all the hydraulic constraints. The methodology cannot be extended to steep terrain and drop manholes, as these cases result in a loop in the algorithm, thus rendering the Bellman–Ford algorithm inapplicable. Future research on the use of algorithms that allow loops within the graph is required to include drop manholes and other structures.