Identifying the Unknown Parameters of Equivalent Circuit Model for Li-Ion Battery Using Rao-1 Algorithm ^†

Abstract

Accurately estimating the parameters for the equivalent circuit model (ECM) of lithium-ion batteries (LiBs), especially those that are not provided in the manufacturer’s datasheets, is crucial to improving their behavior modeling and our understanding. Therefore, this study focuses on investigating a precise method—the Rao-1 algorithm—for extracting the optimal values of the ECM’s parameters. The primary objective is to minimize the difference between the estimated voltage derived from the ECM and the measured voltage of the battery. To evaluate the effectiveness of this approach, a real-world driving data-based test profile is employed. Moreover, a comparative analysis is conducted against recent state-of-the-art optimization algorithms. The simulation results demonstrate that the employed method is proficient in accurately and relatively quickly estimating the parameters of the ECM and that it surpasses other methods in terms of accuracy.

1. Introduction

Lithium-ion batteries (LiBs) are currently a favored energy storage technology due to their remarkable advantages, including a high energy density, low self-discharge rate, and exceptional cycle life. The availability of an accurate battery model is indispensable for effective battery management systems (BMSs) and other renewable energy systems. Therefore, considerable research has been conducted to formulate sophisticated models aimed at precisely estimating the dynamic behaviors of LiBs [1]. Among the most versatile and accurate approaches capable of accommodating a wide range of battery scenarios and patterns are equivalent circuit models (ECMs) [2,3,4]. However, the process of parameterizing these models is critical to determining the battery’s state of charge (SoC) and state of health (SoH), and it can present several challenges.

Metaheuristic algorithms (MAs), which do not rely heavily on a multitude of designer-provided parameters, often drawing inspiration from the natural behavior of both biological and non-biological sources, are employed as powerful tools to address battery parameter estimation challenges. In this context, researchers have proposed diverse computational techniques to deal with the question of ECM parameter extraction.

As an illustration, in the study in [5], researchers employed the Quantum Particle Swarm Optimization (QPSO) method to fine-tune unknown parameters within a simplified first-order fractional-order model (FOM). Similarly, the authors in [6] utilized the Honey Badger algorithm (HBA) to estimate parameters in a data-driven model for a vanadium redox flow battery. Furthermore, recent advancements in the field of MAs have introduced innovative approaches, including the Artificial Ecosystem Optimizer (AEO) [7], the Cuckoo Search (CS) [8], the Artificial Hummingbird Optimizer Technique (AHOT) [9], the Bald Eagle Search algorithm (BES) [10], and the COOT algorithm (COOT) [11], all of which have been utilized to extract parameters from battery ECMs.

In this study, we aim to investigate the application of the Rao-1 technique for parameter identification in LIB models based on the electrical ECM. In fact, several works have employed the Rao-1 method of estimation of transmission line parameters [12], parameter extraction in photovoltaic cell models [13], and various other research domains. However, to the best of our knowledge, the application of the Rao-1 method for identifying ECM parameters in lithium batteries has not been performed yet.

To assess the efficacy of the Rao-1 methodology, a test profile based on real-world driving data [14] is employed as an optimization framework. Furthermore, a comparative analysis is executed in contrast to contemporary optimization algorithms, specifically, the Arithmetic Optimization Algorithm (AOA) [15], Harris Hawks Optimization (HHO) [16], Leader Harris Hawks Optimization (LHHO) [17] and Chernobyl Disaster Optimizer (CDO) [18]. The simulation outcomes substantiate that the Rao-1 technique excels in its ability to accurately and relatively rapidly estimate parameters inherent to the ECM and that it surpasses alternative methods.

2. Materials and Methods

2.1. Equivalent Circuit Model (ECM) for Li-Ion Battery

In this study, our emphasis revolves around the optimization of parameters within the extended Thevenin model, a model recognized for achieving a good equilibrium between precision and complexity. Illustrated in Figure 1, this model takes the form of a second-order (2RC) model, denoting the presence of two RC branches sequentially aligned with the internal ohmic resistance R₀ and the voltage source (V_oc). The adopted model encompasses a pair of state Equations (1) and (2) and a singular output Equation (3) [19], outlined as follows:

$$\dot{SOC}=-\frac{\eta }{Q_C}{i}_{bat},$$

(1)

$${\dot{v}}_i=-\frac{1}{R_i{C}_i}{v}_i+\frac{1}{C_i}{i}_{bat}$$

(2)

$$v_{bat}=V_{oc}(SOC)-R_0{i}_{bat}-{\sum }_{i=1}^{i=2}{v}_i,$$

(3)

where $SOC$ is the state of charge, Q_C is the battery nominal capacity (Ah), η is the coefficient of charging, $i_{bat}$ is the output/input current, $v_{bat}$ is the terminal voltage, $v_i$ denotes the voltage of the consistent RC branch, $i$ is the branch number, and $R_i$and $C_i$ are the resistance and capacitor of the corresponding RC branch.

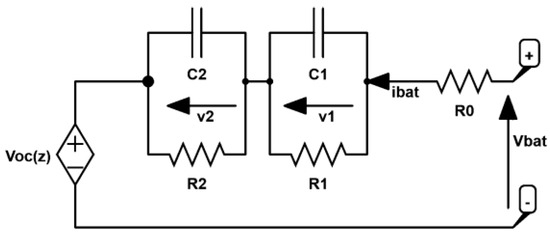
Figure 1. Schematic of the extended Thevenin (second-order) battery model.

For easier use in an optimization algorithm, ordinary differential equations (ODEs) of the 2RC model could be converted from continuous time representation to discrete-time ODEs [20]. Hence, a final discrete-time expression, i.e., Equation (4), will be considered in this paper.

$$v_{bat}\left[k\right]=V_{oc}(SOC\left[k\right])-R_0{i}_{bat}\left[k\right]-\sum _{i=1}^{i=2}{v}_i\left[k\right]$$

(4)

To include the battery dynamics differences between the charging (indicated by “c”) and discharging (indicated by “d”) regimes, Equation (4) was slightly modified, as follows:

$$v_{bat}\left[k\right]=V_{oc}(SOC\left[k\right])-R_{0c}{i}_c\left[k\right]-\sum _{i=1}^{i=2}{v}_{ic}\left[k\right]-R_{0d}{i}_d\left[k\right]-\sum _{i=1}^{i=2}{v}_{id}\left[k\right]$$

(5)

The non-linear relationship between the V_oc and SOC can be expressed as a sixth-order polynomial exponential function [21]:

$$V_{oc}=a_0+a_{1}SOC+a_2{SOC}^2+a_3{SOC}^3+a_4{SOC}^4+a_5{SOC}^5+a_6{SOC}^6$$

(6)

Here, $a_0$ to $a_6$ are the polynomial coefficients.

2.2. Rao-1 Algorithm

The Rao-1 is a simple and recently developed metaphor-less algorithm that does not include any specific or complex parameters and updates the current solutions to converge toward the global solution using the following formula:

$$Y_{i,j}^{new}=Y_{i,j}^t+a_{1,j}\times \left(Y_{b,j}^t-Y_{w,j}^t\right)$$

(7)

where $j\in [1 \mathrm{D}\mathrm{i}\mathrm{m}]$ is the jth dimension (Dim) of the ith solution (noted by $Y_{i,j}^t$) during the current iteration $t$. $a_{1,j}$ is a random number selected from the interval $\left[0 1\right]$. The best and the worst solutions are denoted by $Y_{b,j}^t$ and $Y_{w,j}^t$, respectively. Finally, Equation (7) is used to determine the value of the ith solution in the coming iteration.

$$\left\{\begin{array}{c}{Y}_i^{t+1}=Y_i^{new};if f\left(Y_i^{new}\right)<f\left(Y_i^t\right)\\ Y_i^{t+1}=Y_i^t;else\end{array}\right.$$

(8)

2.3. Objective Function

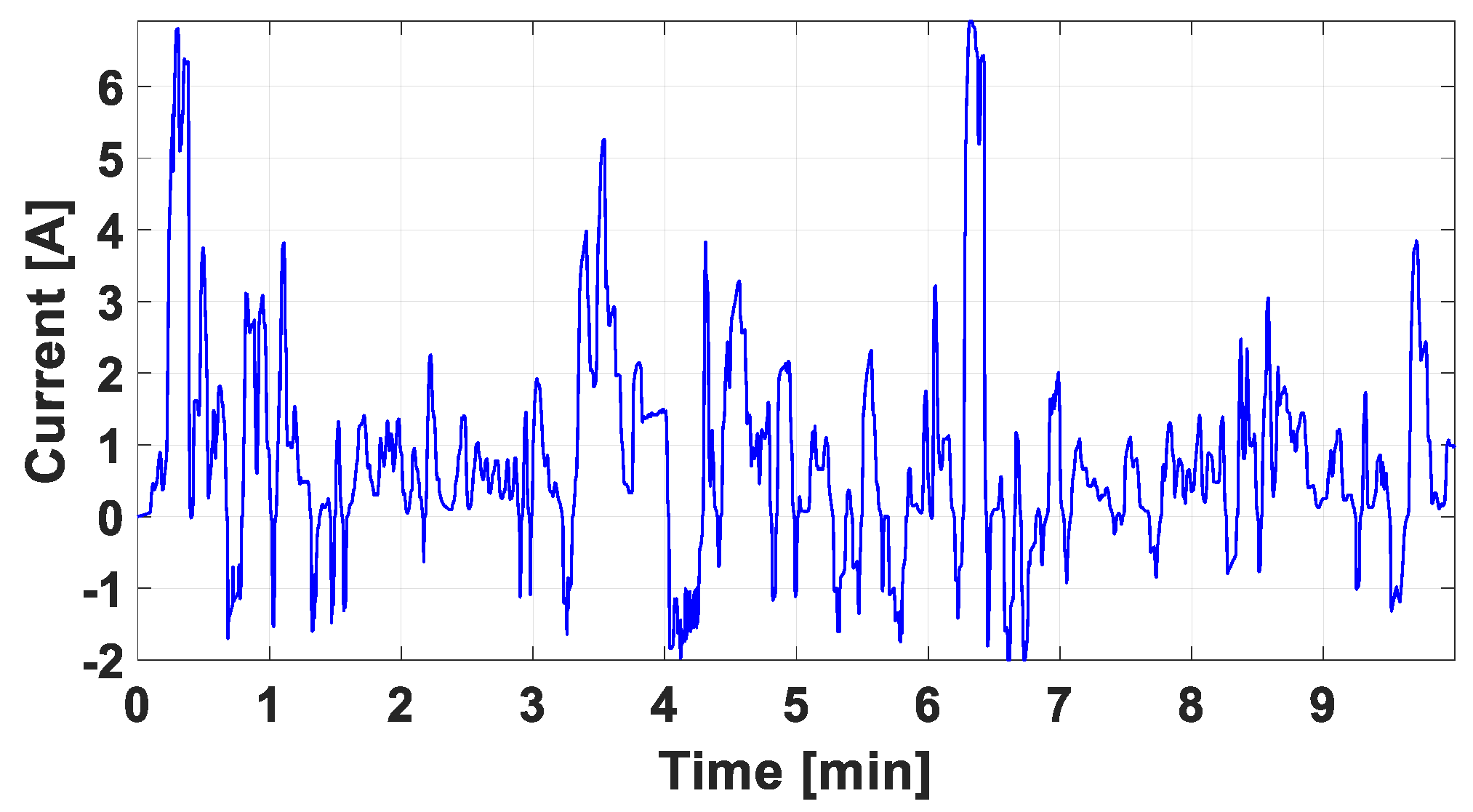
Based on the LiB model described earlier, it can be concluded that different unknown parameters (i.e., ${R_{0c}, R_{1c}, R_{2c}, C_{1c}, C_{2c},R}_{0d}, R_{1d}, R_{2d}, C_{1d}, C_{2d}, a_0$–$a_6$) are involved in the battery model. To closely match the real battery behavior, it is essential to accurately identify these 17 parameters. This identification is based on a real-world driving dataset with the actual current profile depicted in Figure 2 [14]. Hence, Rao-1 is used to estimate and optimize these parameters using this experimental dataset. The root-mean-square error (RMSE) was selected as an objective function to find the proper parameters by effectively minimizing the error between the estimated ${(V}_{est})$ and experimental ${(V}_{exp})$terminal voltages. Consequently, the objective function ${(F}_{RMSE})$ based on the RMSE formula is given by:

$$F_{RMSE}\left(x\right)=Min\left\{\sqrt{\frac{1}{N}{\sum }_{i=1}^N{[V_{exp}\left(i\right)-V_{est}\left(i\right)]}^2}\right\}$$

(9)

Figure 2. Current profile of the real-world driving dataset.

3. Results

In this subsection, we present a succinct summary of the optimization results obtained through the novel Rao-1 technique applied to the studied lithium-ion battery (LiB). The outcomes derived from the Rao-1 algorithm are systematically evaluated alongside the results obtained from four competing algorithms, namely AOA [15], HHO [16], LHHO [17], and CDO [18]. To ensure a fair and consistent comparison, all these techniques have been implemented within the MATLAB software environment (version 2021a), employing identical testing conditions. These conditions include a fixed number of iterations (MaxIt = 100), a consistent population size (PopSize = 30), and the execution of 10 independent runs for each method to uphold the reliability of the comparative analysis.

Table 1 illustrates the achieved parameters, along with their corresponding RMSE values for both the Rao1 approach and its counterpart methods. Remarkably, the lowest RMSE value ($4.3428\times {10}^{-3}$) with a Std of $2.1852\times {10}^{-3}$was accomplished by the Rao1 technique, which proves the good stability and accuracy of this algorithm. Figure 3 illustrates the estimated battery voltage plotted using the best parameters obtained via the Rao-1 method. Clearly, the estimated curve can reduplicate the experimental data with high precision.

Table 1. Optimal parameters acquired via Rao-1 and the other competitive algorithms.

Items	Rao-1	AOA	HHO	LHHO	CDO
$R_{0d}$	2.5911 × 10−2	2.7995 × 10−2	3.2126 × 10−2	2.5178 × 10−2	2.7906 × 10−2
$R_{0c}$	3.5487 × 10−2	2.8551 × 10−2	3.1999 × 10−2	3.9332 × 10−2	2.4125 × 10−2
$R_{1d}$	7.0652 × 10−3	1.0000 × 10−4	1.0076 × 10−4	1.1627 × 10−2	8.6901 × 10−3
$R_{1c}$	1.0000 × 10−1	6.4655 × 10−2	2.9843 × 10−2	5.1134 × 10−2	8.3717 × 10−2
$C_{1d}$	6.2604 × 102	8.8250 × 102	5.7939	7.0488 × 102	9.0000 × 102
$C_{1c}$	3.6262 × 102	9.0000 × 102	3.6243 × 102	8.8082 × 102	2.9654 × 102
$R_{2d}$	4.9927 × 10−2	3.2199 × 10−2	6.5794 × 10−2	1.8990 × 10−2	5.4462 × 10−2
$R_{2c}$	3.6745 × 10−2	3.2037 × 10−2	2.0816 × 10−2	7.9016 × 10−2	5.4139 × 10−2
$C_{2d}$	6.4907 × 103	9.0000 × 103	2.7513 × 103	8.8490 × 103	9.0000 × 103
$C_{2c}$	5.9332 × 103	9.0000 × 103	4.6047 × 103	8.8377 × 103	5.2192 × 103
$a_0$	3.2173	4.0000	3.6869	3.3351	3.2068
$a_1$	1.0000	1.9418 × 10−2	4.2354 × 10−1	8.5170 × 10−1	1.0000
$a_2$	−1.0000 × 10−2	0.0000	−3.8256 × 10−3	−9.9321 × 10−3	0.0000
$a_3$	6.6396 × 10−4	5.5631 × 10−11	7.7382 × 10−4	7.9015 × 10−4	7.7291 × 10−4
$a_4$	−1.0000 × 10−4	0.0000	−7.9211 × 10−5	−3.0875 × 10−5	0.0000
$a_5$	1.0000 × 10−5	4.6992× 10−19	2.1822 × 10−6	3.3216 × 10−6	8.6717 × 10−6
$a_6$	−2.0351 × 10−8	0.0000	−4.3267 × 10−8	−6.8963 × 10−8	−8.3801 × 10−11
Min RMSE	4.3428 × 10−3	1.3183 × 10−2	1.1558 × 10−2	6.1840 × 10−3	5.9515 × 10−3
Std	2.1852 × 10−3	8.3725 × 10−4	6.7700 × 10−3	4.5411 × 10−3	5.6756 × 10−3

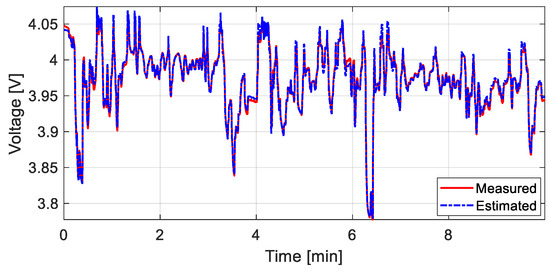
Figure 3. Measured and estimated LIB voltage via the Rao-1 algorithm.

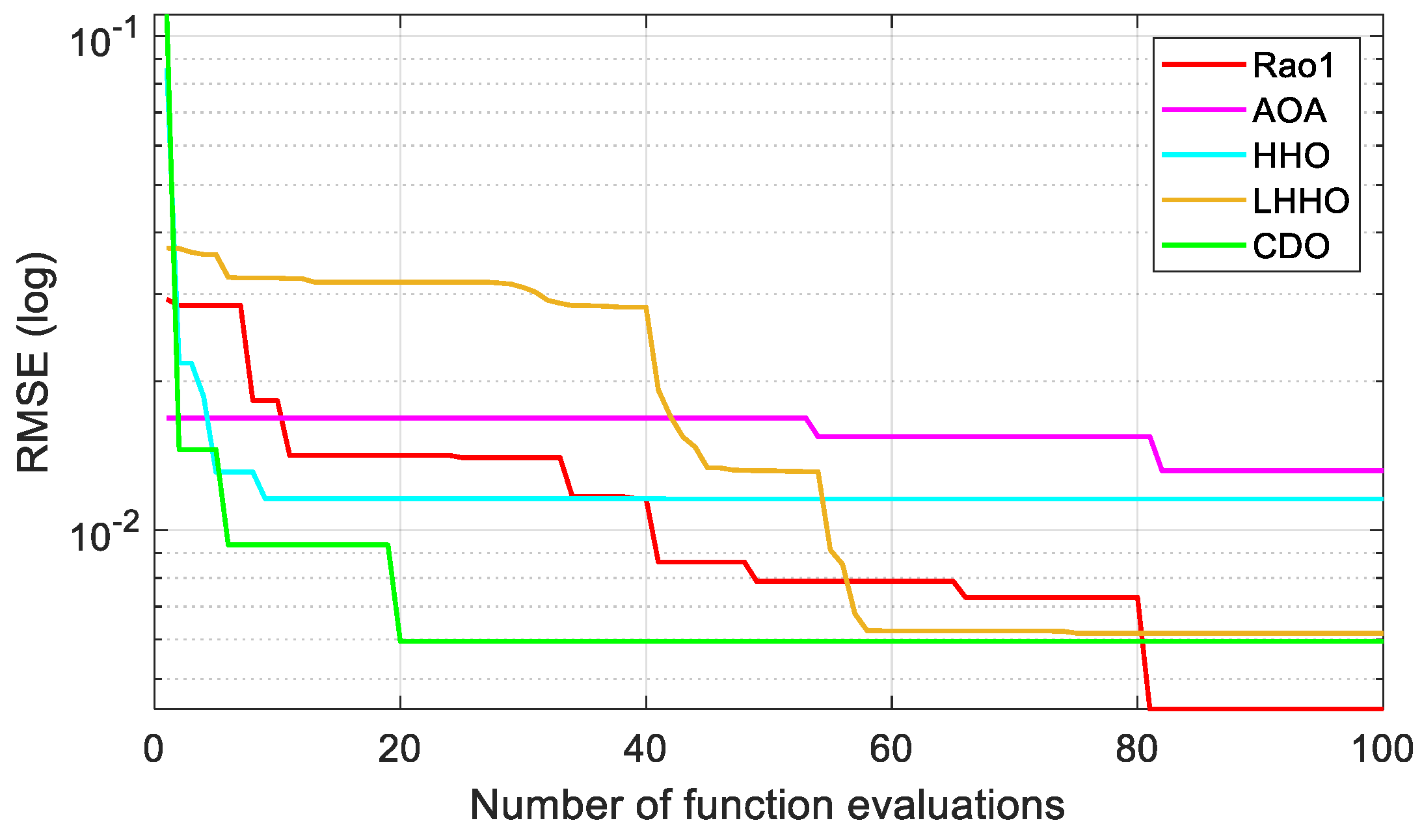
Additionally, a visualization of the convergence curves generated via different algorithms is showcased in Figure 4. Evidently, this illustration further validates the computational effectiveness and accuracy demonstrated by the Rao-1 algorithm, as it attains the optimal RMSE value by the 80th iteration.

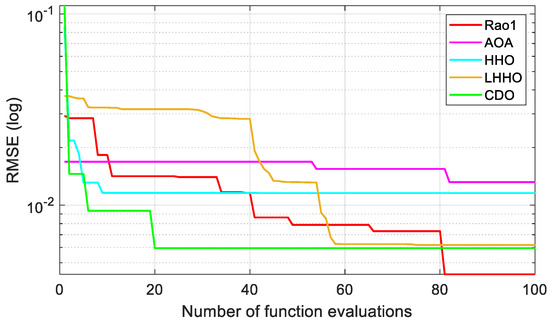
Figure 4. Convergence graphs for all implemented algorithms.

4. Conclusions

The aim of this paper is to evaluate the performance of the newly introduced Rao-1 algorithm in identifying the unknown parameters for battery’s equivalent circuit model. The algorithm is constructed based only on arithmetic operation and do not include any specific or complex parameters. The Rao-1 approach was examined using high-accuracy experimental data, and the achieved results demonstrated the effectiveness and reliability of the proposed method compared to other optimization approaches for the parameter estimation of LiBs. This algorithm accomplished a minimum RMSE with few iteration numbers, $4.3428\times {10}^{-3}$ and Std of $2.1852\times {10}^{-3}$, representing a high accuracy and robustness in predicting the battery voltage comportment. Moreover, with the high closing between the calculated and the real characteristic, the Rao-1 approach can be used as an efficiency tool for battery management systems. As a response to concerns about the potential impact of changing battery parameters on SOC estimation, we have proactively considered strategies to address this challenge. Our research leveraged real-world data to capture the actual operating conditions faced by Li-ion batteries, enhancing the algorithm’s adaptability. Additionally, we recommend the periodic recalibration of the battery model to align it with the evolving characteristics. Continuous monitoring and feedback mechanisms can further enhance accuracy over time. As we move forward, we hope to further explore and refine the Rao-1 algorithm and other prominent metaheuristic algorithms. We also aim to integrate them into battery management systems, taking into account crucial factors such as temperature, aging, and other significant variables. This approach contributes to more efficient and reliable energy storage solutions.