Analytical Modeling of a Transmission Coefficient for Ultrasonic Waves in Human Cancellous Bone ^†

Abstract

This study explores ultrasonic wave propagation in human cancellous bone, treating it as a fluid-saturated elastic medium. The interaction between the structure and fluid during ultrasonic excitation is described using Johnson’s model, modifying Biot’s theory. Biot’s theory predicts fast P1 and slow P2 wave propagation. An analytical transmission coefficient in the frequency domain is derived, accounting for system parameters and excitation frequency. The transmitted signal is calculated by multiplying the incident signal’s spectrum with this coefficient. The study investigates how changing physical and mechanical factors affect the transmission of fast P1 and slow P2 waves through fluid-saturated human cancellous bone, offering insights for medical diagnostics and biomaterial design.

1. Introduction

Osteoporosis, a debilitating medical condition, is characterized by reduced bone density, diminished strength, and increased fragility, transforming bone tissue into a porous, compressible structure resembling a sponge. This condition heightens the risk of fractures, especially at common sites like the spine, hips, ribs, and wrists, due to minor trauma. Structural alterations in osteoporotic trabecular bone involve thinning or disappearance of trabeculae, increasing the spacing between them [1].

Ultrasonic methods play a vital role in detecting and characterizing osteoporosis. Various ultrasound techniques have been developed for trabecular bone assessment, measuring speed of sound and assessing attenuation as functions of frequency, correlating with bone density [2,3]. Other approaches involve parameters related to the speed of sound and longitudinal slow wave propagation within a trabecular bone. Trabecular bone, being a non-homogeneous porous medium, complicates the interaction between ultrasound and bone [4].

Ultrasonic wave propagation complexity in bones arises from factors such as saturating fluid properties [5], solid phase mechanical characteristics [6], anisotropy [7], and macroscopic structural parameters like porosity, tortuosity, and viscous characteristic length [7,8]. Developing a comprehensive theoretical model, such as Biot theory modified by Johnson, is crucial to address this complexity [9,10], aiding the solution of the inverse problem [4,11,12,13] and enabling extraction of bone’s physical and mechanical properties from ultrasonic measurements.

The main objective of this study is to conduct a numerical simulation investigation assessing the sensitivity of key physical parameters, specifically porosity, tortuosity, and viscous characteristic lengths, on ultrasonic wave transmission through a hypothetical sample of human cancellous bone. This research endeavors to enhance our understanding of osteoporosis detection and contribute valuable insights for medical diagnostics and biomaterial design.

2. Theoretical Model

A porous medium can be described as a solid material penetrated by an interconnected network of pores filled with fluid. Within this medium, two continuous entities coexist: the solid matrix and the network of fluid-filled pores. This combination results in a poroelastic medium, characterized by essential properties such as porosity and permeability, and the specific characteristics of its components—the solid and fluid matrices. Within this medium, incident and reflected longitudinal waves, as well as shear waves, can propagate. The sound field within the material can be comprehensively described by considering the amplitudes of these waves.

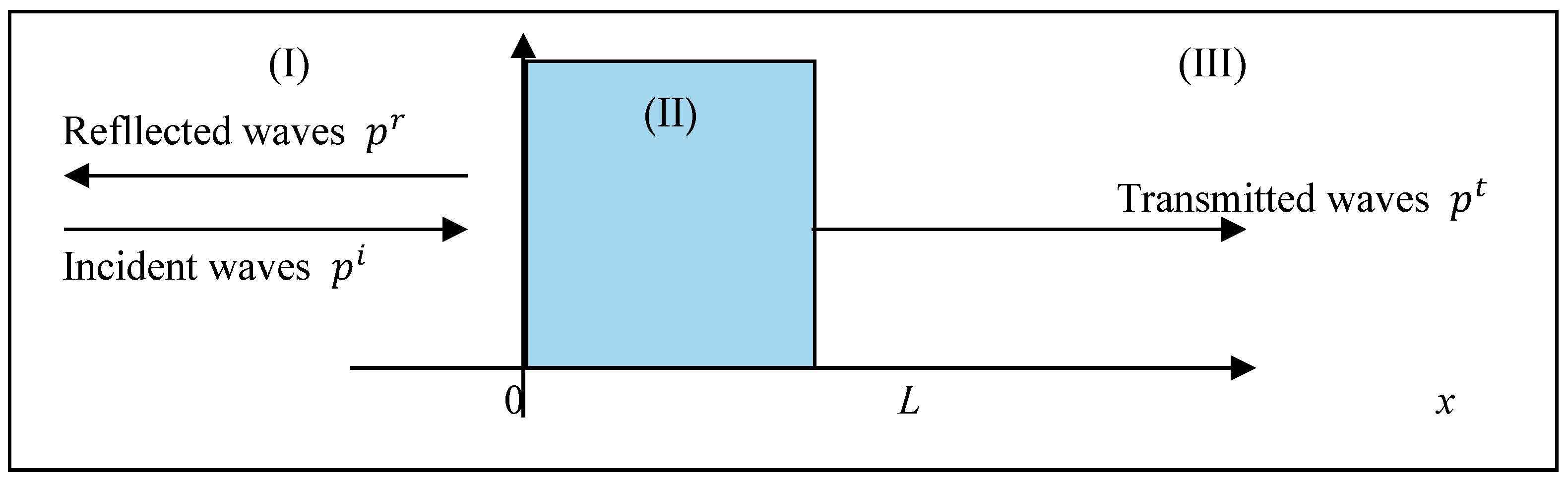
In our analysis, we focus on a monolayer porous medium (as illustrated in Figure 1) comprising a slice of a homogeneous and isotropic porous material characterized by its flexible structure with a thickness denoted as L. This medium occupies a finite space defined within the range $0 \le x \le L$ and is subjected to excitation by a plane acoustic wave with a normal incidence.

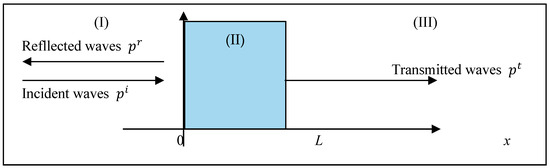
Figure 1. Geometry of the problem at normal incidence.

The theoretical framework we employ draws from the field of dynamic poroelasticity, originally formulated by Biot [9]. This theory provides a comprehensive and general description of the mechanical behavior of such porous media. Biot’s equations are derived from linear elasticity equations governing the solid matrix, Navier–Stokes equations describing the behavior of the viscous fluid, and Darcy’s law, which governs fluid flow within the porous matrix. The equations of motion for both the solid and fluid phases are expressed as follows [8,9,12]:

$${\rho }_{11}\frac{{\partial }^2\overrightarrow{u}}{{\partial t}^2}+{\rho }_{12}\frac{{\partial }^2\overrightarrow{U}}{{\partial t}^2}=P\nabla \left(\nabla ·\overrightarrow{u}\right)+Q\nabla \left(\nabla ·\overrightarrow{U}\right)-N\nabla \wedge \left(\nabla \wedge \overrightarrow{u}\right)$$

(1)

$${\rho }_{12}\frac{{\partial }^2\overrightarrow{u}}{{\partial t}^2}+{\rho }_{22}\frac{{\partial }^2\overrightarrow{U}}{{\partial t}^2}=Q\nabla \left(\nabla ·\overrightarrow{u}\right)+R\nabla \left(\nabla ·\overrightarrow{U}\right)$$

(2)

$\overrightarrow{u}$ and $\overrightarrow{U}$ represent the displacements of the solid and fluid phases, respectively. The parameters ${\rho }_{nm}$ (with n = 1, 2 and m = 1, 2) are known as “mass coefficients” and are linked to the densities of the solid ${\rho }_s$ and fluid ${\rho }_f$ phases through the relationships ${\rho }_{11}=\left(1-\varphi \right){\rho }_s-{\rho }_{12}$, and ${\rho }_{22}=\phi {\rho }_f-{\rho }_{12}$, where ϕ denotes the porosity. The coefficient ${\rho }_{12}$ signifies the mass coupling parameter between the fluid and solid phases and consistently assumes a negative value, ${\rho }_{12}=-{\rho }_f\left(\alpha \left(\omega \right)-1\right)$. Here, α(ω) is a function of frequency called the dynamic tortuosity [10], which characterizes the viscous interactions between the fluid and the solid structure, significantly impacting acoustic wave damping in porous materials. At high frequencies, the expression for dynamic tortuosity α(ω) is given by the following [8,10,11,12,13]:

$$\alpha \left(\omega \right)={\alpha }_{\infty }\left(1+\frac{\delta \left(\omega \right)}{\mathsf{\Lambda }}\sqrt{\frac{2}{j}}\right), \omega ⟶\infty$$

(3)

In this equation, $\alpha \left(\omega \right)$ represents the high-frequency limit of the tortuosity, Λ denotes the viscous characteristic length, and $\delta \left(\omega \right)=\sqrt{2\eta /\omega {\rho }_f}$ (where η is fluid viscosity and ω is angular frequency) corresponds to the viscous skin depth thickness, representing the region where the velocity distribution of the fluid is perturbed by frictional forces at the fluid–frame interface [8,11,12,13].

Parameters P, Q, and R are generalized elastic constants associated with other measurable quantities—namely, $K_f$ (bulk modulus of the pore fluid), $K_s$ (bulk modulus of the elastic solid), and $K_b$ (bulk modulus of the porous skeletal frame)—through the following relationships [8]:

$$P=\frac{\left(1-\phi \right)\left(1-\phi -\frac{K_b}{K_s}\right)K_s+\phi \frac{K_s}{K_f}{K}_b}{\left(1-\frac{K_b}{K_s}\right)-\phi \left(1-\frac{K_s}{K_f}\right)}. Q=\frac{\left(1-\phi -\frac{K_b}{K_s}\right)\phi K_s}{\left(1-\frac{K_b}{K_s}\right)-\phi \left(1-\frac{K_s}{K_f}\right)}. R=\frac{{\phi }^2{K}_s}{\left(1-\frac{K_b}{K_s}\right)-\phi \left(1-\frac{K_s}{K_f}\right)}$$

(4)

The Young modulus and the Poisson ratio of the solid ($E_s$,${\nu }_s$) and the skeletal frame ($E_b$,${\nu }_b$) are dependent on P, Q, and R through the following relations:

$$K_s=\frac{E_s}{3\left(1-2{\nu }_s\right)}, K_b=\frac{E_b}{3\left(1-2{\nu }_b\right)}\mathrm{e}\mathrm{t} N=\frac{E_b}{2\left(1+2{\nu }_b\right)}.$$

(5)

For a cancellous bone occupying the region 0 ≤ x ≤ L (as depicted in Figure 1), the general expression of the transmission coefficient $\mathcal{T}\left(\omega \right)$ is provided as follows [8,12]:

$$\mathcal{T}\left(\omega \right)=\frac{2F_3\left(\omega \right)}{F_3^2\left(\omega \right)-{(1-F_4\left(\omega \right))}^2}$$

(6)

Detailed expressions for $F_3\left(\omega \right)$ and $F_4\left(\omega \right)$ are provided in Refs. [8,12].

The expression of the transmitted field $P^{\mathrm{t}}(x,\omega )$ is identified in terms of the transmitted coefficient $\mathcal{T}\left(\omega \right)$ and the incident field $P^i(x,\omega )$, where they are related in the frequency domain by the following relation:

$$P^{\mathrm{t}}\left(x,\omega \right)=\mathcal{T}\left(\omega \right)P^i(x,\omega )$$

(7)

The time-domain simulated transmitted signal $P_{sim}^{\mathrm{t}}(x,t)$ is obtained numerically by taking the inverse Fourier transform ${\mathrm{Ƒ}}^{-1}$ of Equation (7) as follows:

$$P_{sim}^{\mathrm{t}}\left(x,t\right)={\mathrm{Ƒ}}^{-1}\left(\mathcal{T}\left(\omega \right)P^i\right(x,\omega \left)\right)$$

(8)

3. Numerical Simulations

Numerical simulations of the transmitted waves are conducted by varying the physical parameters of a porous material, corresponding to a spongy bone, and described acoustically according to the modified Biot theory.

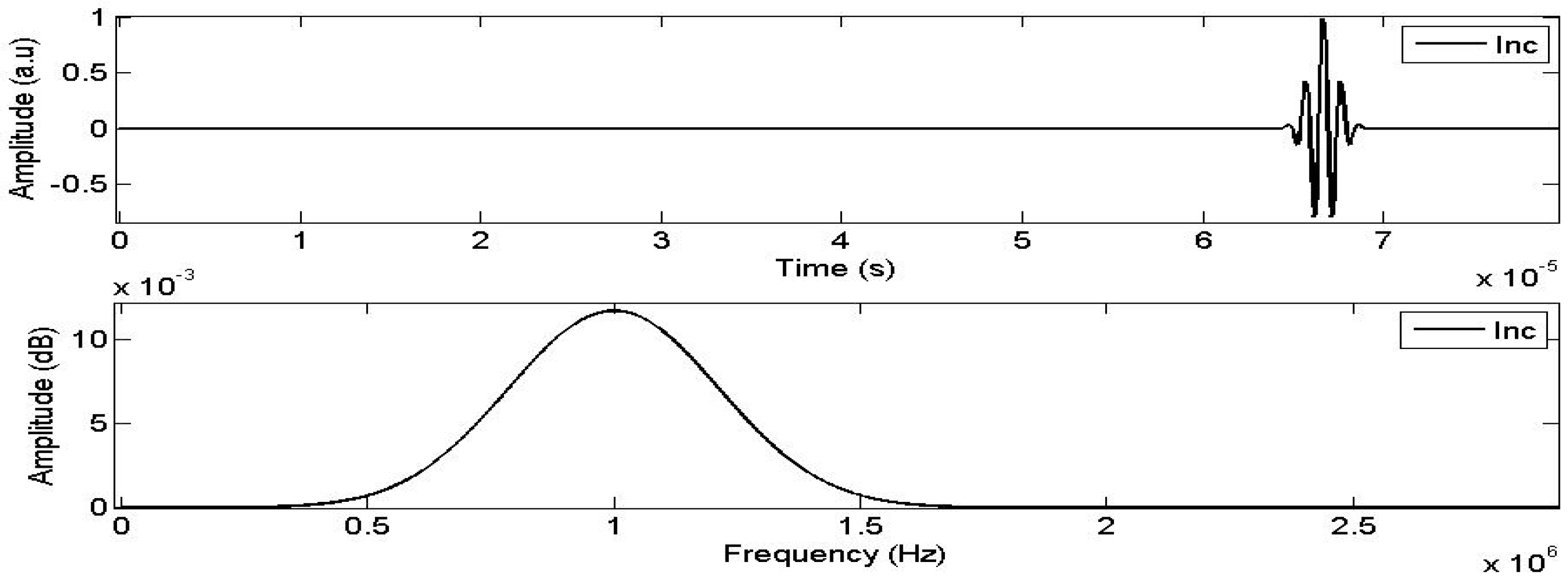
Consider a hypothetical sample (S) of human cancellous bone with a thickness of L = 5.0 cm. The characteristics of this sample are presented in Table 1. The simulated incident signal is generated using the Matlab Gaussian function with unit amplitude, centered at a frequency of 1 MHz (Figure 2).

Table 1. Physical and mechanical parameters representing the hypothetical trabecular human bone sample.

Sample	φ	α∞	Λ (μm)	Es (GPa)	Eb (GPa)	$\left(\mathit{\nu }\mathit{s},\mathit{\nu }\mathit{b}\right)$	ρs (kg±m−3)
S	0.87	1.05	90.0	30.0	2.5	0.40	1990
Fluid	Ρf (kg±m−3)		Kf (GPa)		η (Pas)
	1000		2.3		0.001

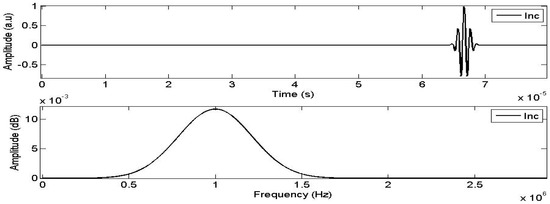
Figure 2. The incident signal (top) and its spectrum (bottom).

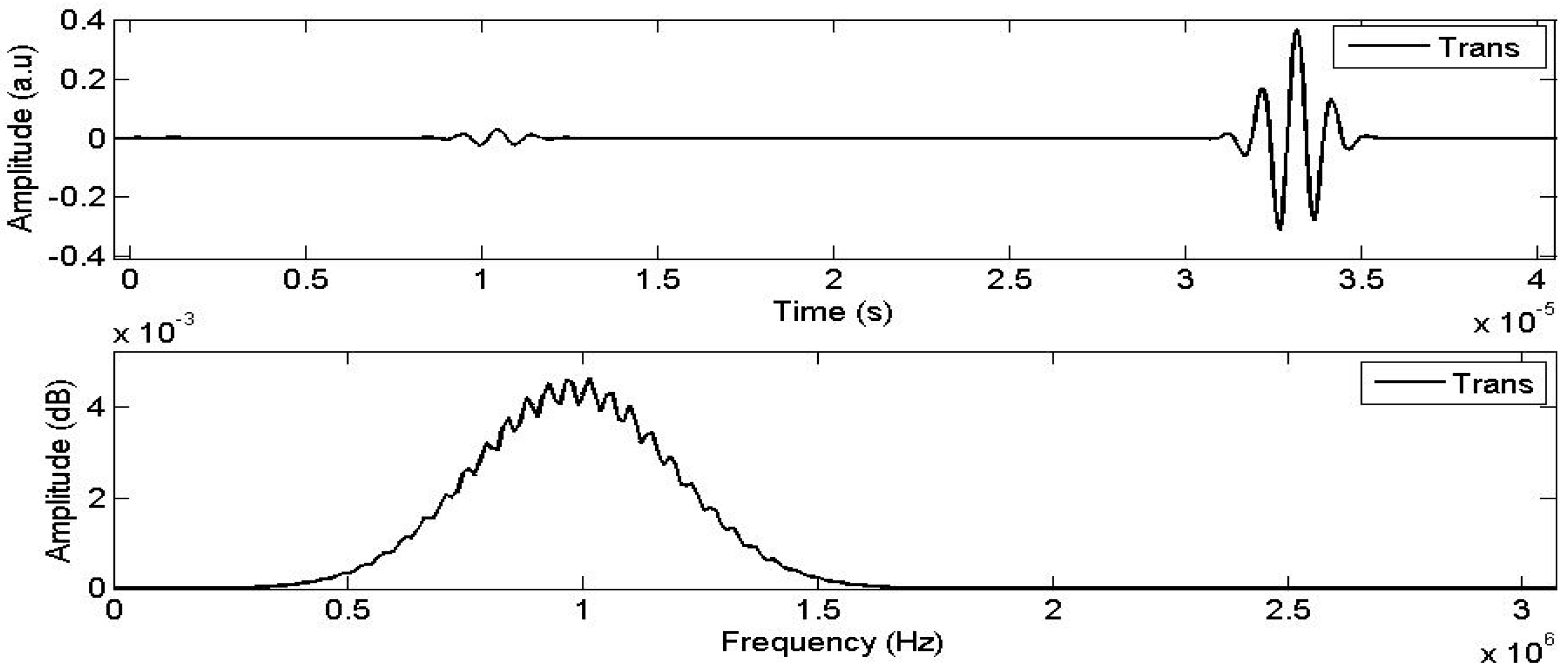
The transmitted signal, corresponding to the parameters given in Table 1, is depicted in Figure 3. This transmitted signal consists of two waves, as predicted by Biot: slow and fast waves. In order to investigate the sensitivity of the physical parameters listed in Table 1, which influence the transmission coefficient, we assess the impact of each parameter on the transmitted waves by applying a variation of ±10% to the physical parameters. This analysis helps illustrate the effect of each parameter on the transmitted signal.

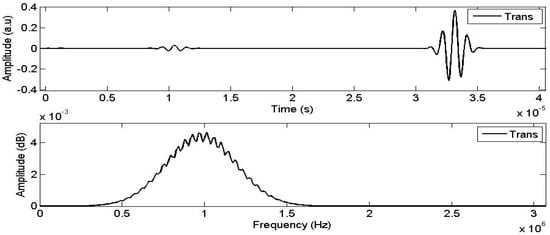
Figure 3. Simulated transmitted signal.

3.1. Influence of Physical Parameters on the Ultrasonic Transmitted Wave

3.1.1. Effect of Porosity (ϕ)

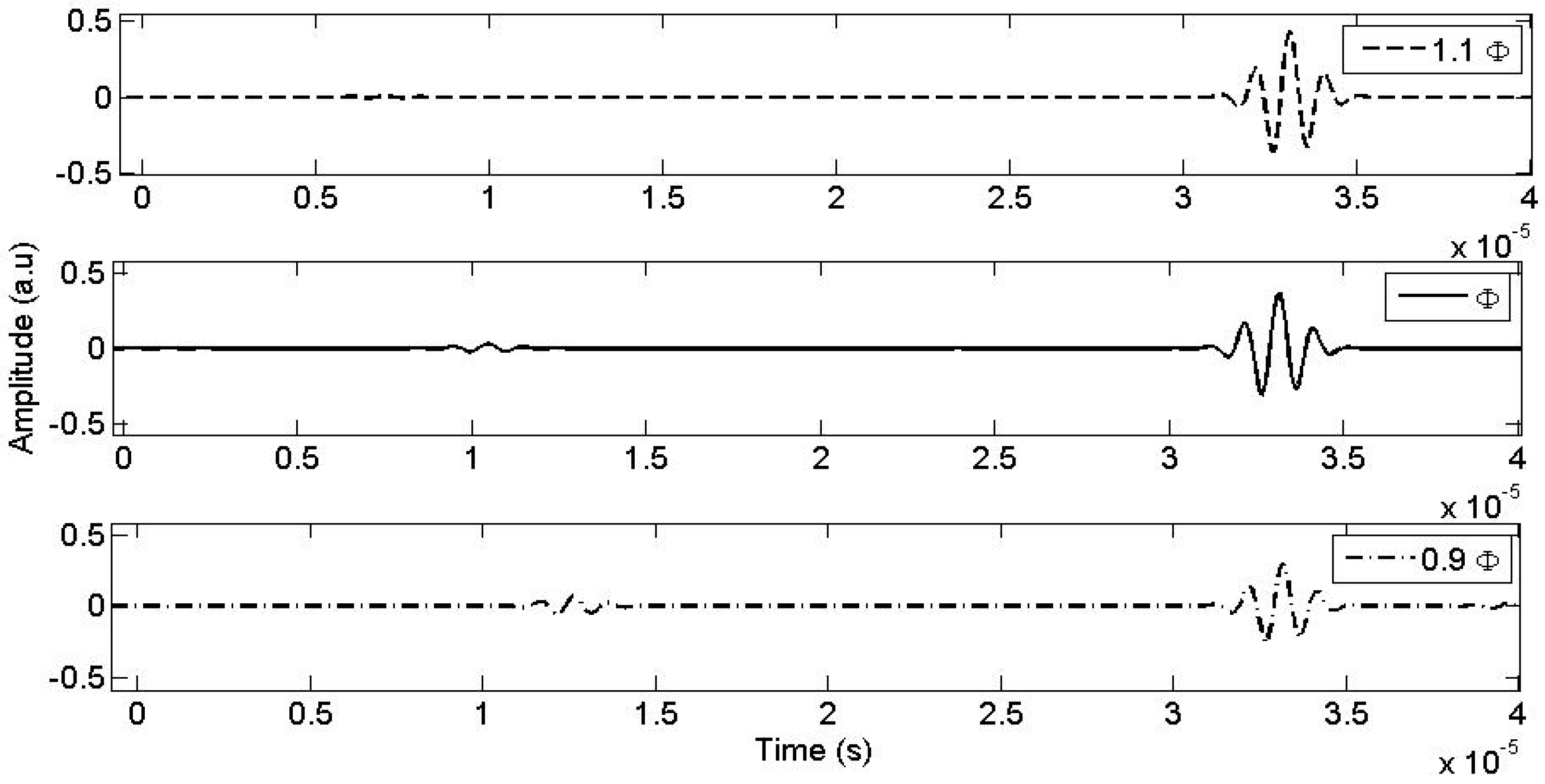
The study of the influence of porosity (ϕ) on the transmitted signal is represented in Figure 4. The continuous signal in this figure represents the simulated transmitted signal obtained using Equation (8) with the physical and mechanical parameters listed in Table 1. The signals represented by the dashed lines are obtained by increasing and decreasing the initial value of ϕ by ±10%, while keeping the values of the other parameters constant. Notably, the influence of porosity (ϕ) on the transmitted signal is relatively small.

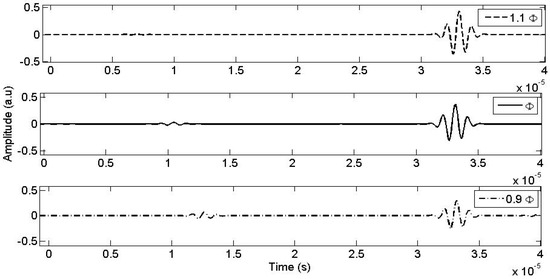
Figure 4. The porosity ϕ influence on the transmitted signal.

A decrease in porosity (ϕ) by −10% results in an approximate 1.62% increase in the amplitude of the transmitted signal (red dashed line), whereas an increase in porosity (ϕ) by +10% leads to an approximate −8.39% decrease in amplitude (blue dashed line). Therefore, the influence of porosity (ϕ) on the transmitted waves is modest.

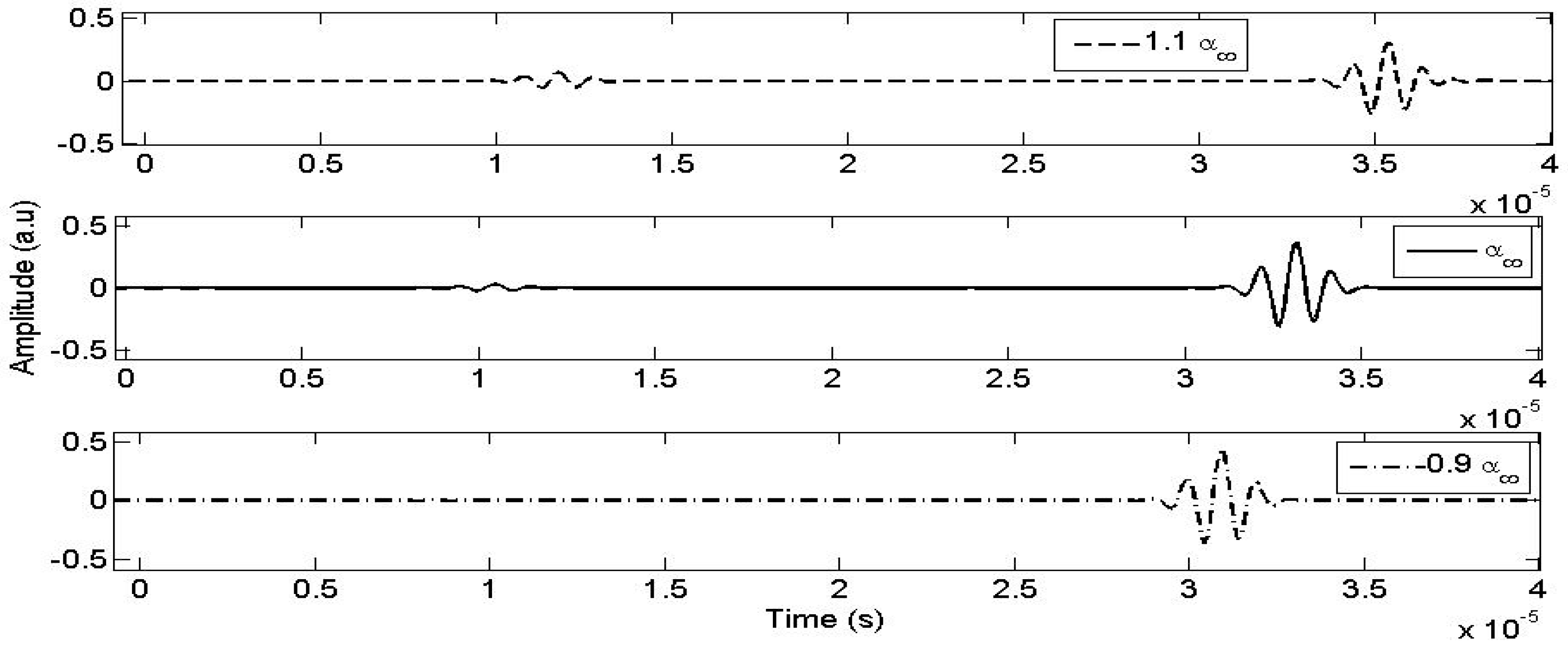
3.1.2. Effect of Tortuosity (${\alpha }_{\mathrm{\infty }}$)

To study the effect of tortuosity (${\alpha }_{\infty }$) on the transmitted wave, the physical and mechanical parameters are held constant while varying tortuosity (${\alpha }_{\infty }$) by ±10%. Figure 5 illustrates that a +10% increase in tortuosity (${\alpha }_{\infty }$) results in a 28.95% increase in the amplitude of the transmitted wave, while a −10% decrease leads to an attenuation of approximately −8.34% in the amplitude of the transmitted wave. It is evident that the tortuosity (${\alpha }_{\infty }$) has a significant impact on the transmitted waves as well as on their propagation speed.

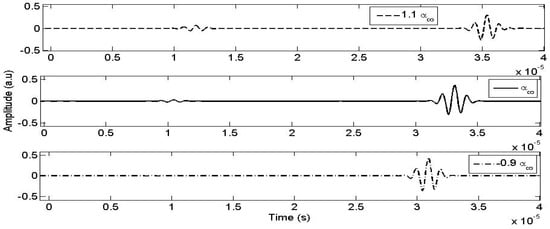
Figure 5. The effect of the tortuosity on transmitted signal.

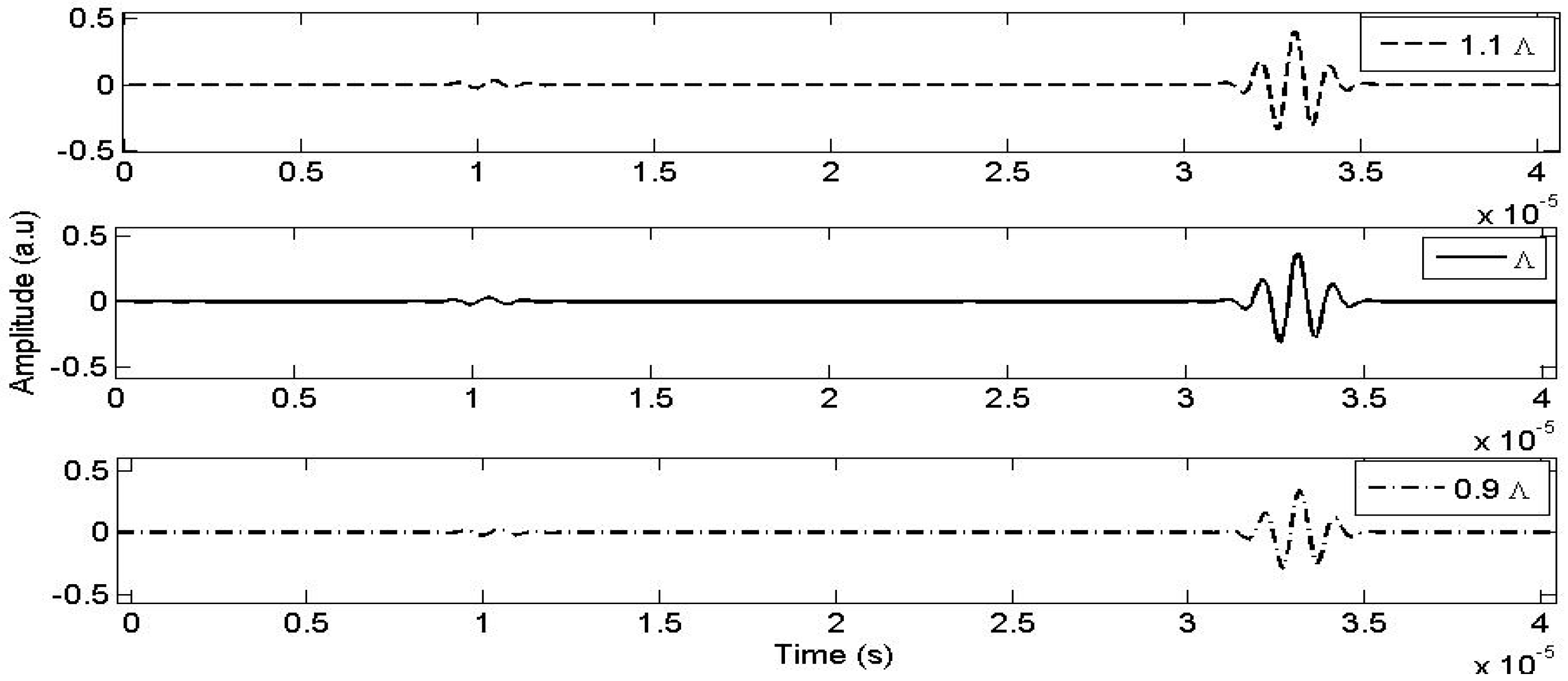
3.1.3. Effect of Viscous Characteristic Length (Λ)

Figure 6 demonstrates the sensitivity of the viscous characteristic length (Λ) on the transmitted signal. It is evident from this figure that this parameter exerts a substantial influence on the transmitted signal. A variation of ±10% in the viscous characteristic length (Λ) results in a decrease of −16.20% and an increase of +22.5% in the amplitude of the transmitted wave. Numerical simulations clearly indicate that the viscous characteristic length (Λ) has a more pronounced influence, similar to tortuosity, on the amplitude of the transmitted signal.

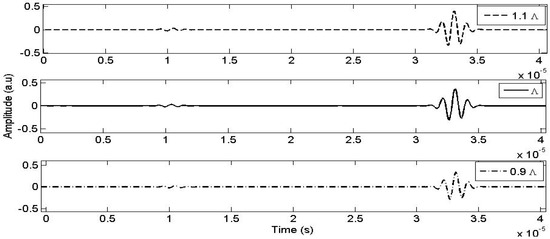
Figure 6. The influence of the viscous characteristic length Λ on the transmitted signal.

4. Conclusions

In this work, the modified Biot model is used to investigate the impact of physical and mechanical parameters on transmitted waves within a 1 MHz frequency band. The findings demonstrate that even slight variations of ±10% in these parameters have a considerable influence on the fast and slow waves in the transmitted signal. Specifically, the viscous characteristic length and tortuosity emerge as key factors shaping wave behavior. The study implies that an inversion process utilizing transmitted waves can effectively determine these parameters, providing valuable insights for diverse applications in fields such as biophysics and material science.