Solving the Optimal Power Flow Problem in Power Systems Using the Mountain Gazelle Algorithm ^†

Abstract

Optimal power flow (OPF) is one of the fundamental mathematical tools currently used to operate power systems within the technical limits of the transmission power system. To determine OPF, a highly non-linear complex problem, it is essential to research power system planning and control. This study presents a practical and trustworthy optimization approach for the OPF problem in electrical transmission power systems. Many intelligence optimization algorithms and methods have recently been developed to solve OPF, particularly the non-linear complex optimization problems. In this paper, a novel meta-heuristic algorithm called the mountain gazelle optimizer (MGO) is suggested for solving the OPF problem. The suggested algorithm applies the improved three single objective functions to the MGO algorithm for the best OPF issue control variable settings. Three objective functions that reflect the minimization of generating fuel cost, the minimizing of active power loss, and the minimizing of voltage deviations have been used to investigate and test the proposed algorithm on the standard IEEE 30-bus test system. The simulation results demonstrate the efficiency of the proposed MGO algorithm; the fuel costs are reduced by 11.407%, power losses are considerably decreased by 51.016%, and the voltage profile is significantly reduced by 91.501%. Furthermore, the outcomes produced by the proposed algorithm have also been contrasted with outcomes produced by applying other comparable optimization algorithms published in recent years. The optimal results are encouraging and demonstrate the resilience and efficacy of the suggested strategy.

1. Introduction

The traditional power flow (PF) analysis will determine an electric power system’s steady-state operation. This entails calculating the magnitude and angle of each voltage at each node in the electrical transmission system [1]. The active and reactive optimum power flow (OPF) in the components of the transmission power systems are calculated. By making the best modifications to the power systems control variables while meeting a variety of equality and inequality requirements, OPF issue may be solved. Generally, OPF solution’s optimization objectives include power loss, fuel cost, and bus voltage profiles [2]. Science and engineering are involved in the investigation of global optimization. Global optimization issues may be used to develop many real-world optimization applications [3].

Effective and reliable optimization techniques are required to tackle global optimization issues effectively. Complicated global optimization issues are challenging to solve using conventional techniques [4]. OPF, particularly the non-linear complicated optimization issues, have recently been solved by many intelligent optimization algorithms and methods including, but not limited to, the moth swarm optimizer (MSO) [5], the manta ray foraging optimizer (MRFO) [6], stud krill herd (SKH) [7], the modified grasshopper optimization algorithm (MGOA) [8], lightning attachment procedure optimization (LAPO) [9], and tunicate swarm optimization (TSO) [10]. We applied the improved artificial bee colony optimization (IABC) [11], the improved gravitational search algorithm (IGSA) [12], the improved electromagnetism-like mechanism (IEM) [13], the coyote optimization algorithm (COA) [14], adaptive teaching learning-based optimization (ATLBO) [15], improved moth-flame optimization (IMFO) [16], and used adaptive constraint differential evolution (ACDE) [17].

The authors used a new salp swarm algorithm (SSA) [18], social spider optimization (SSO) [19], a modified sine–cosine algorithm (MSCA) [20], an enhanced most valuable player algorithm (EMVPA) [21], an improved Archimedes optimization algorithm (IAOA) [22], an adaptive partitioning flower pollination algorithm (APFPA) [23], a moth swarm algorithm (MSA) [24], and an enhanced moth swarm algorithm (EMSA) [25]. Also, researchers applied the tunicate swarm algorithm (TSA) [26], grey wolf optimizer (GWO) [27], the Jaya optimization algorithm (JOA) [28], and improved colliding bodies optimization (ICBO) [29]. These techniques and algorithms are based on the complex behaviors of living things to create diverse local and global search strategies, giving academics a more comprehensive range of algorithms to address optimization issues in various objective functions.

The OPF problem in power systems is formulated and solved in this study using three single-objective functions, known as the mountain gazelle optimizer (MGO) algorithm. This is then evaluated in the standard IEEE 30-bus transmission power system.

2. Problem Formulation

OPF, as previously said, is a power flow problem that determines the best control variable settings for a particular load setting by optimizing an objective function.

2.1. Equality Constraints

The next equations are a representation of the OPF problem equality constraints:

$$P_{G,i}-P_{D,i}-V_i\sum _{j=1}^{NB}{V}_j\left[G_{ij}cos\left({\theta }_{ij}\right)+B_{ij}sin\left({\theta }_{ij}\right)\right]=0$$

(1)

$$Q_{G,i}-Q_{D,i}-V_i\sum _{j=1}^{NB}{V}_j\left[G_{ij}sin\left({\theta }_{ij}\right)+B_{ij}cos\left({\theta }_{ij}\right)\right]=0$$

(2)

2.2. Inequality Constraints

OPF inequality limitations reflect the restrictions placed on physical devices, as well as the restrictions put in place to ensure system security:

(a) 

Power generator constraints

$$V_{G,j}^{min}\le V_{G,i}\le V_{G,i}^{max} i=1, \dots , NG$$

(3)

$$P_{G,i}^{min}\le P_{G,i}\le P_{G,i}^{max} i=1, \dots , NG$$

(4)

$$Q_{G,i}^{min}\le Q_{G,i}\le Q_{G,i}^{max} i=1, \dots , NG$$

(5)

(b) 

Power transformer constraints

$$T_i^{min}\le T_i\le T_i^{max} i=1, \dots , NT$$

(6)

(c) 

Shunt compensator constraints

$$Q_{C,i}^{min}\le Q_{C,i}\le Q_{C,i}^{max} i=1, \dots , NC$$

(7)

(d) 

Security constraints

$$V_{L,i}^{min}\le V_{L,i}\le V_{L,i}^{max} i=1, \dots , NL$$

(8)

$$S_{L,i}\le S_{L,i}^{max} i=1, \dots , Nl$$

(9)

2.3. Objectif Functions

The first objective function examined in this work is to minimize the cost of the generating fuel (Cost), which is given by the following equation:

$${OF}_{Cost}=min\sum _{i=1}^{NG}{a}_i+b_i{P}_{G,i}+c_i{P}_{G, i}^2$$

(10)

The minimization of the total active power losses (APL) in the transmission system is the second objective function, and it may be written as follows:

$${OF}_{APL}=min\sum _{i=1}^{NL}{G}_{ij}\left[V_i^2+V_j^2-2V_i·V_{j}cos\left({\theta }_{ij}\right)\right]=0$$

(11)

The total bus voltage deviation (VD) minimization processes the third objective function. In order to maximize the voltage profile, calculate the load bus voltage variation from 1.0 p.u., which is provided by:

$${OF}_{VD}=min\sum _{i=1}^{NL}\left|V_L-1\right|$$

(12)

3. Application

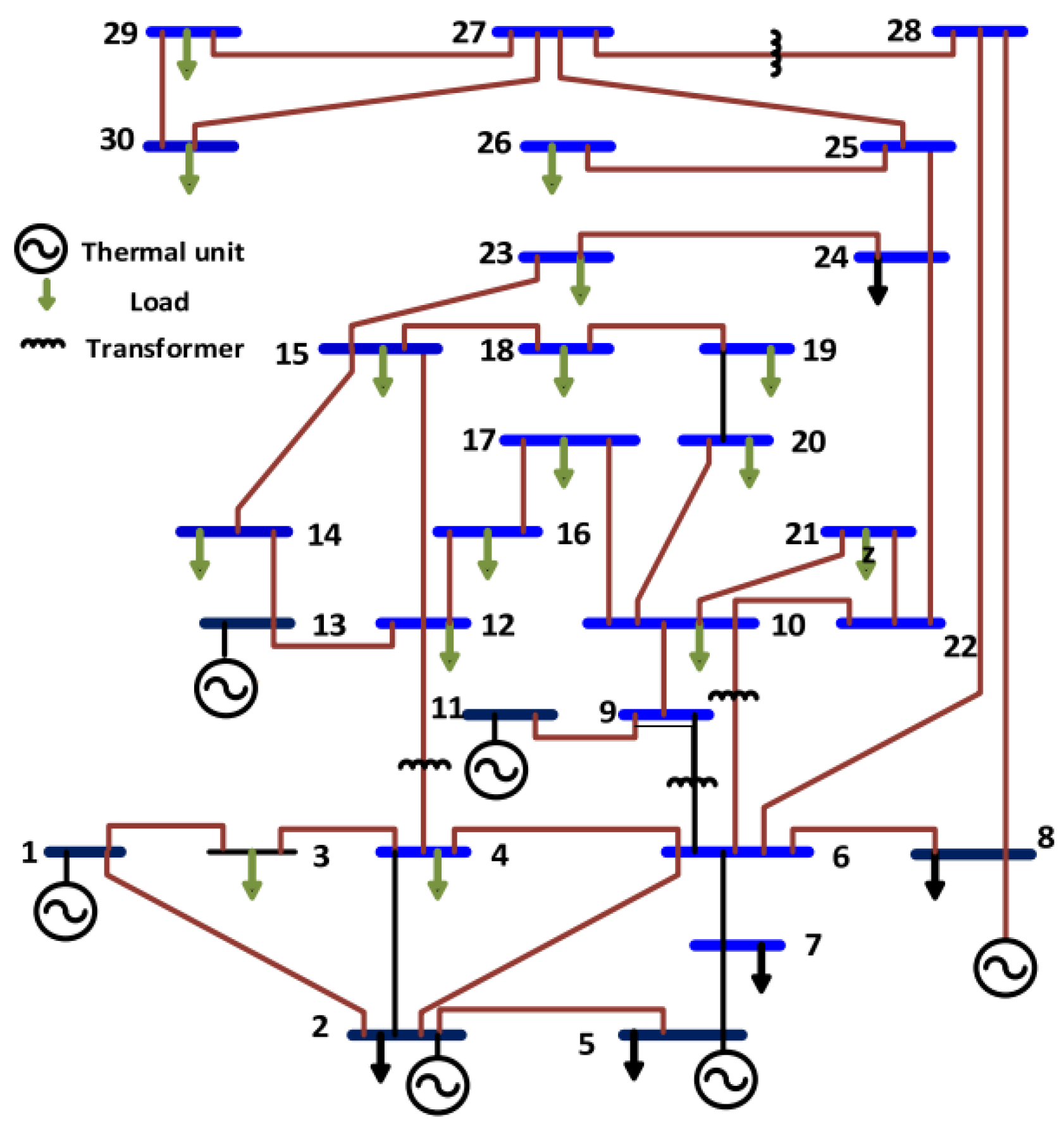
The suggested MGO algorithm has been tested on the typical IEEE 30-bus test transmission system depicted in Figure 1 in order to demonstrate its efficacy. This system is composed of 30 buses and 41 branches. Therefore, this system has 24 design variables. The test transmission system selected for this study includes the following characteristics: six power generators, nine shunt compensations, and four tap-changing power transformers.

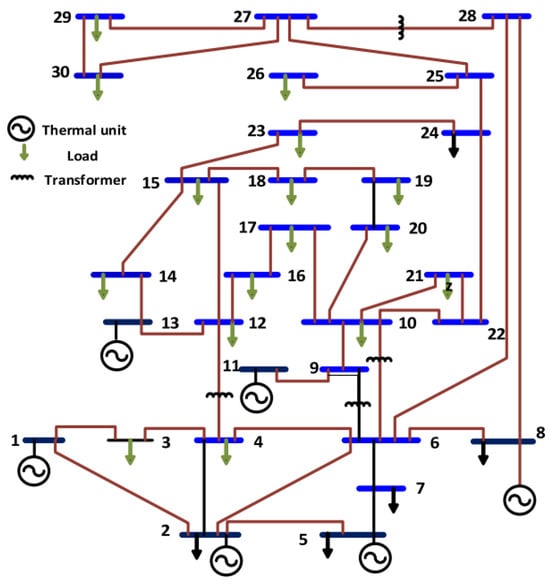
Figure 1. Single line diagram of the IEEE 30-bus test system.

In this test system, three main cases (objective functions) are considered as follows: OPF by considering minimization fuel cost (Case 1), OPF by considering minimization active power loss (Case 2), and OPF by considering minimization voltage deviation (Case 3). Table 1 represents the optimal control settings obtained by the applied GMO algorithm for various case studies in this paper. The simulation results demonstrate the proposed MGO algorithm’s efficiency: fuel costs are reduced by 11.407%, power losses are decreased by 51.016%, and the enhanced voltage profile is significantly reduced by 91.501%.

Table 1. Optimal control settings for the applied OPF cases.

Variables	Initial Case	Case 1	Case 2	Case 3
PG.1 (MW)	99.2220	177.0569	51.2508	175.5896
PG.2 (MW)	80.0000	48.6920	79.9999	48.7895
PG.5 (MW)	50.0000	21.3006	49.9999	21.8117
PG.8 (MW)	20.0000	21.0849	35.0000	22.0798
PG.11 (MW)	20.0000	11.8890	30.000	12.4188
PG.13 (MW)	20.0000	12.0000	39.9999	12.3840
VG.1 (p.u.)	1.0500	1.0999	1.1000	1.0413
VG.2 (p.u.)	1.0400	1.0878	1.0976	1.0239
VG.5 (p.u.)	1.0100	1.0617	1.0800	1.0102
VG.8 (p.u.)	1.0100	1.0694	1.0869	1.0045
VG.11 (p.u.)	1.0500	1.0999	1.1000	1.0612
VG.13 (p.u.)	1.0500	1.0999	1.0999	0.9879
Cost ($/h)	901.9500	799.0679	999.7273	803.3069
PLoss (MW)	5.8225	8.6244	2.8521	9.7722
VD (p.u.)	1.1496	1.8576	2.0572	0.0977

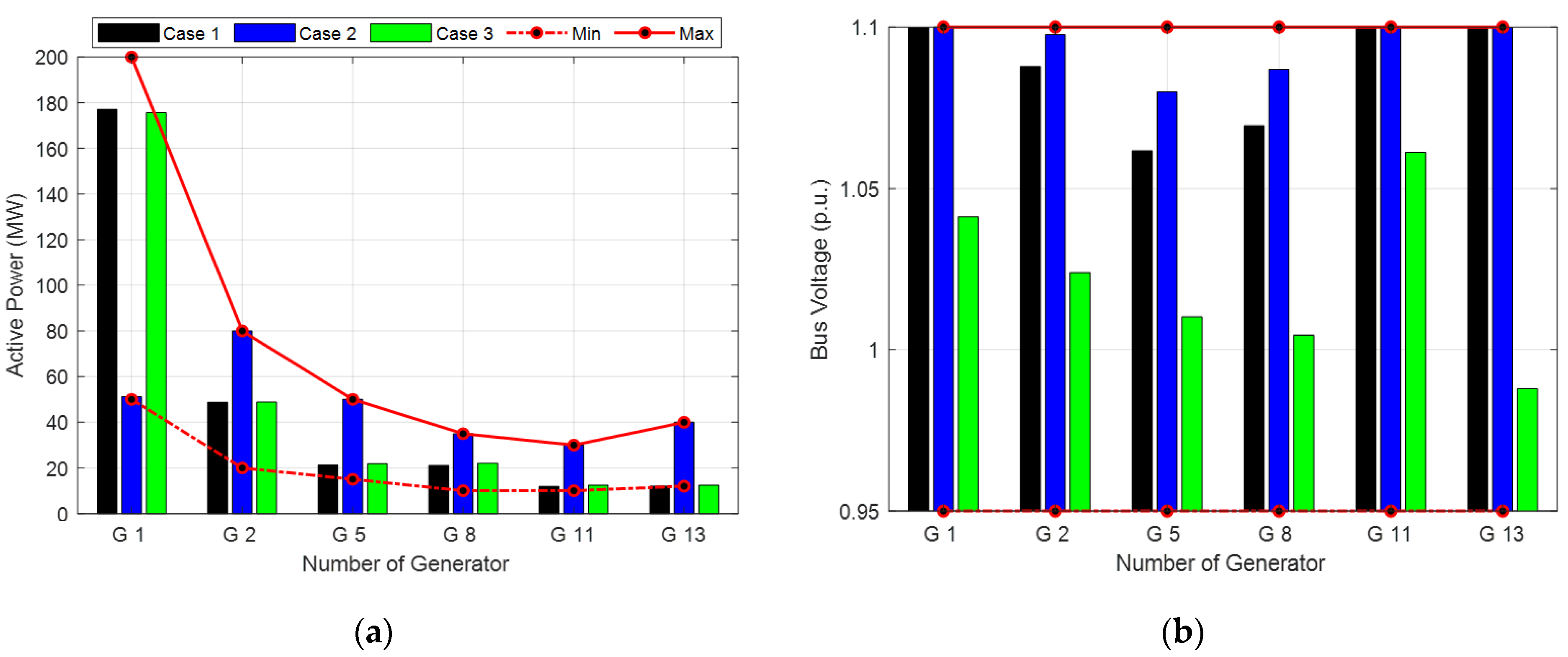
Figure 2 represents the optimal parameters for the active power injected and the bus voltage of the generator. The values of active power injected by the generator and the bus voltage in the test system are acceptable within the lower and upper limits.

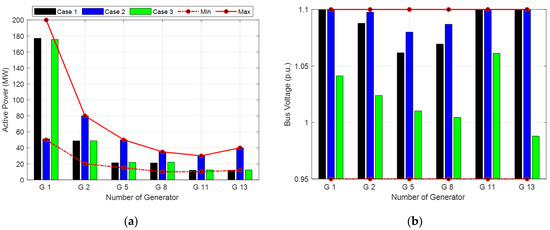
Figure 2. Optimal parameters: (a) power injected by the generator; (b) bus voltage of the generator.

Table 2 compares the simulation results from the applied MGO algorithm to those from other methods and algorithms recently described in the literature for the three case studies. For the case studies in this paper, the proposed MGO algorithm successfully applied various strategies documented in the literature used in this investigation. The computational results of the MGO algorithm are highly comparable with those obtained by applying other comparable optimization methods and techniques.

Table 2. Comparison of optimal results with the existing literature.

Case 1			Case 2			Case 3
Ref.	Optimization Algorithms	Cost ($/h)	Ref.	Optimization Algorithms	PLoss (MW)	Ref.	Optimization Algorithms	VD (p.u.)
[5]	MSO	801.5710	[14]	COA	3.0952	[23]	APFPA	0.1095
[6]	MRFO	801.3908	[15]	ATLBO	3.0906	[24]	MSA	0.1084
[7]	SKH	800.5141	[16]	IMFO	3.0905	[25]	EMSA	0.1073
[8]	MGOA	800.4744	[17]	ACDE	3.0840	[13]	IEM	0.1063
[9]	LAPO	800.0078	[18]	SSA	2.9620	[26]	TSA	0.1060
[10]	TSO	799.6041	[19]	SSO	2.9454	[27]	GWO	0.1037
[11]	IABC	799.3210	[20]	MSCA	2.9334	[28]	JOA	0.1031
[12]	IGSA	799.2817	[21]	EMVPA	2.8659	[20]	MSCA	0.1030
[13]	IEM	799.1116	[22]	IAOA	2.8590	[29]	ICBO	0.1014
Applied MGO		799.0679	Applied MGO		2.8521	Applied MGO		0.0977

It is clear from the optimal results that the MGO gave a better reduction in the fuel cost active loss and voltage deviation for all cases over other algorithms and methods used in the comparison.

4. Conclusions

In this study, an improvement of the mountain gazelle optimizer algorithm, called the MGO, has been applied to solve the problem of OPF. This article uses a suitable constraint handling strategy in various single-objective functions for the optimum power flow issue and its efficacy. The most important thing is to satisfy system restrictions, and effective constraint-handling techniques are helpful in this regard. The transmission power system must be operated within predetermined boundaries for system security and dependability. Compared to existing complicated algorithms and methods for discovering the OPF solution under the same restrictions, the exhibited numerical simulations employing the suggested MGO approach have established its excellent performance, effectiveness, and resilience. The MGO may be used in future research to address various optimization issues in electricity transmission networks, including the best placement for renewable energy sources and the most effective placement of FACTS devices.