Artificial Neural Networks Multicriteria Training Based on Graphics Processors ^†

Abstract

The report considers the task of training a multilayer perceptron, formulated as a problem of multiobjective optimization under uncertainty. To solve this problem, the principle of vector minimax was used. A parallel software implementation of a hierarchical evolutionary algorithm for solving a multicriteria optimization problem under uncertainty based on a GPU is presented.

1. Introduction

Currently, the technology of the neuroevolutionary synthesis of management and decision-making models is being intensively developed, which is considered as a promising means of implementing intelligent algorithms for analyzing information and management under conflict and uncertainty in real time [1,2,3,4,5]. The effectiveness of the neuroevolutionary approach for solving this class of problems is determined by the ability to take into account uncertain factors, such as conflict uncertainty, the multicriteria of management goals, and the uncertainty of environmental conditions. In this context, it is expedient to formalize the task of training an artificial neural network (ANN) in the form of a multicriteria optimization problem under uncertainty (MCOU). In [6,7], a coevolutionary technology for solving the MCOU problem was developed, which, as the results of computational experiments show, has an extremely high computational complexity. In [8,9,10,11,12], it was shown that a promising area of research is the parallel implementation of computing technology based on graphics processors (GPUs). In this article, a parallel GPU implementation of a coevolutionary technology for solving the MCOU problem is proposed.

In Section 2, the formulation of the ANN training problem is formulated in the form of an MCOU problem, where the principle of vector minimax is applied for its solution. Section 3 presents a parallel GPU-based implementation of the MCOU hierarchical evolutionary algorithm software. Section 4 presents the results of a computational experiment on a test problem.

2. Problem Statement

The statement of the training problem for a multilayer perceptron (MP) is formulated as an MCOU problem:

$$⟨\mathbf{W}\mathbf{,}\mathbf{Z}\mathbf{,}\mathbf{F}\mathbf{(}\mathbf{w}\mathbf{,}\mathbf{z}\mathbf{)}⟩,$$

(1)

where $\mathbf{w}\in \mathbf{W}\subset {\mathbf{E}}^{{\mathbf{r}}_{\mathbf{w}}}$ is a vector of weight coefficients of MP synaptic connections; $\mathbf{z}\in \mathbf{Z}\subset {\mathbf{E}}^{{\mathbf{r}}_{\mathbf{z}}}$ is a vector of uncertain factors; $\mathbf{Z}$ is a finite set of possible values of the uncertain factor; and $\mathbf{F}\mathbf{(}\mathbf{w}\mathbf{,}\mathbf{z}\mathbf{)}\mathbf{=}[{\mathit{f}}_1\mathbf{(}\mathbf{w}\mathbf{,}\mathbf{z}\mathbf{)},\cdots {\mathit{f}}_m\mathbf{(}\mathbf{w}\mathbf{,}\mathbf{z}\mathbf{)}{]}^T\in {\mathbf{E}}^m$ is a vector criterion defined on the Cartesian product $\mathbf{W}\times \mathbf{Z}$.

In problem (1), it is required to determine the value of the vector $\mathbf{w}\in \mathbf{W}$, which provides the minimum values for the components of the vector criterion $\mathbf{F}\mathbf{(}\mathbf{w}\mathbf{,}\mathbf{z}\mathbf{)}$ under the influence of an uncertain factor $\mathbf{z}\in \mathbf{Z}$, about which it is known only that it can take values from a finite set $\mathbf{Z}$.

To solve this problem, it is proposed to use the vector minimax principle. In this case, the original statement of problem (1) is reduced to a deterministic multiobjective optimization problem:

$$\mathbf{V}\mathbf{\left(}\mathbf{w}\mathbf{\right)}\to \underset{\mathbf{w}\in \mathbf{W}}{min},$$

(2)

where $\mathbf{V}\mathbf{\left(}\mathbf{w}\mathbf{\right)}$ is a vector indicator, the components of which are the points of extreme pessimism of the vector criterion $\mathbf{F}\mathbf{(}\mathbf{w}\mathbf{,}\mathbf{z}\mathbf{)}$ on the set $\mathbf{Z}$ with fixed $\mathbf{w}$.

To solve problem (1), (2), the hierarchical evolutionary algorithm (HEA) of the MCOU developed in [6,7] is used. As studies [5,6] show, the HEA MCOU, when used in ANN training tasks, shows a high computational complexity. Therefore, it is proposed to implement the HEA software for solving problem (1), (2), based on the GPU architecture and OpenCL technology.

3. GPU-Based Parallel Implementation of the Hierarchical Evolutionary MCOU Algorithm

The architecture of the developed HEA MCOU software reflects the following main stages of the HEA MCOU implementation.

Stage 1. Formation of a set of points of extreme pessimism (Figure 1).

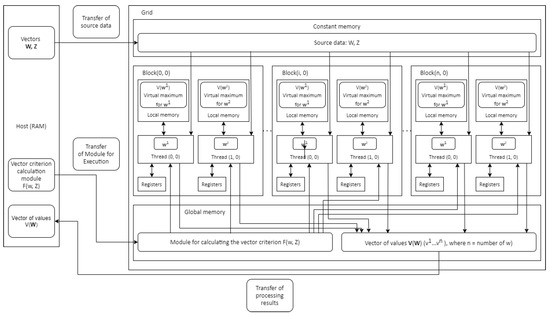
Figure 1. Parallel algorithm for finding a set of points of extreme pessimism on the GPU.

Step 1. The initial population $\mathbf{W},\left|\mathbf{W}\right|=\mathit{n}$ is formed on the host (CPU).

Step 2. Constant memory is allocated on the GPU, into which arrays $\mathbf{Z}$ and $\mathbf{W}$ are entered. A buffer is allocated in the global memory of the GPU for the set of points of extreme pessimism $\mathbf{V}\mathbf{\left(}\mathbf{W}\mathbf{\right)}$.

Step 3. A grid is formed on the GPU that determines the number of working blocks and the threads executed in them.

Step 4. The kernel is called with a subsequent transfer from the CPU to each thread of a set of instructions for execution. Threads start to work in parallel. Within each thread, the corresponding set of values of the vector criterion $\mathbf{F}\mathbf{(}\mathbf{w}\mathbf{,}\mathbf{Z}\mathbf{)}$ is calculated for each $\mathbf{w}\in \mathbf{W}$ and the extreme pessimism point $\mathbf{V}\mathbf{\left(}\mathbf{w}\mathbf{\right)}$ is calculated on the set $\mathbf{F}(\mathbf{w},\mathbf{Z})$, which is stored in the local memory of the thread. Upon completion, each thread transfers its value $\mathbf{V}\mathbf{\left(}\mathbf{w}\mathbf{\right)}$ to the global memory of the GPU. After the GPU has signaled that all threads have terminated, the CPU moves the array $\mathbf{V}\mathbf{\left(}\mathbf{W}\mathbf{\right)}$ from the GPU’s global memory to the CPU’s RAM.

Stage 2. Assessment of the fitness of each point $\mathbf{w}\in \mathbf{W}$ (Figure 2).

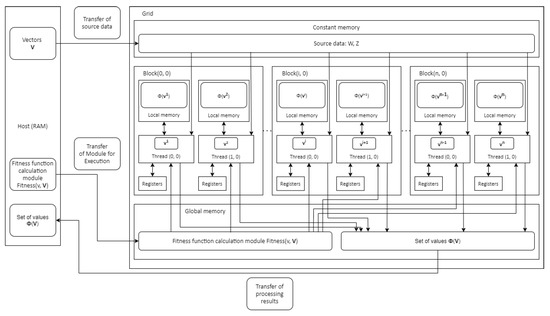
Figure 2. Parallel algorithm for calculating fitness function values on GPU.

Step 5. Constant memory is allocated on the GPU, into which array $\mathbf{V}\mathbf{\left(}\mathbf{W}\mathbf{\right)}$ is entered. In the GPU’s global memory, a buffer is allocated for the set of values of the fitness function $\Phi \left(\mathbf{V}\mathbf{\left(}\mathbf{W}\mathbf{\right)}\right)$.

Step 6. A new grid is formed on the GPU.

Step 7. The kernel is called and threads are started to work in parallel. Within each thread, the corresponding value of the fitness function $\Phi \mathbf{\left(}\mathbf{V}\mathbf{\right)}$ is calculated for each element of $\mathbf{V}\in \mathbf{V}\mathbf{\left(}\mathbf{W}\mathbf{\right)}$, which is stored in the local memory of the thread. Upon completion, each thread transfers its $\Phi \mathbf{\left(}\mathbf{V}\mathbf{\right)}$ value to the GPU’s global memory. After the GPU sends a signal to terminate all threads, the CPU transfers array $\Phi \mathbf{\left(}\mathbf{V}\mathbf{\right(}\mathbf{W}\mathbf{\left)}\mathbf{\right)}$ from the GPU’s global memory to the CPU’s RAM.

Next, a population of descendants is formed on the CPU and the execution of stages 1, 2 is repeated.

The developed algorithm can be easily modified to solve the MCOU problem (1), (2), where there are many uncertain factors.

The developed software is cross-platform, as CUDA and OpenCL technologies are available on various operating systems, both on Windows and Linux.

4. Computational Experiment

The effectiveness of the developed technology was tested on the following test task MCOU:

$$\Gamma =⟨\mathbf{X}\mathbf{,}\mathbf{Z}\mathbf{,}\mathbf{F}\mathbf{(}\mathbf{x}\mathbf{,}\mathbf{z}\mathbf{)}⟩,$$

(3)

where $\mathbf{x}=[{\mathit{x}}_1,{\mathit{x}}_2{]}^T\in \mathbf{X}$ is the vector of control parameters; $\mathbf{z}=[{\mathit{z}}_1,{\mathit{z}}_2{]}^T\in \mathbf{Z}$ is the vector of uncertain factors; and $\mathbf{F}\mathbf{(}\mathbf{x}\mathbf{,}\mathbf{z}\mathbf{)}\mathbf{=}\mathbf{[}{\mathit{f}}_1\mathbf{(}\mathbf{x}\mathbf{,}\mathbf{z}\mathbf{)}\mathbf{,}{\mathit{f}}_2{\mathbf{(}\mathbf{x}\mathbf{,}\mathbf{z}\mathbf{)}\mathbf{]}}^T$ is the vector performance indicator with components:

$${\mathit{f}}_1\mathbf{(}\mathbf{x}\mathbf{,}\mathbf{z}\mathbf{)}=x_1^2+x_2^2-x_1(z_1^2-z_2^2),$$

(4)

$${\mathit{f}}_2\mathbf{(}\mathbf{x}\mathbf{,}\mathbf{z}\mathbf{)}=x_1^2-x_2^2-x_1(z_1^2+z_2^2).$$

(5)

The restrictions were set in the form:

$$\mathbf{X}=\{0\le x_1,x_2\le 2\},$$

(6)

$$\mathbf{Z}=\{{\mathbf{z}}^i,i=\overline{1,\left|\mathbf{Z}\right||}0\le z_1,z_2\le 2\}.$$

(7)

It is required to maximize the components of the vector efficiency indicator on the set $\mathbf{X}\times \mathbf{Z}$ based on the vector maximin principle.

Figure 3, Figure 4 and Figure 5 show the results of searching for a set of vector maximins using the HEA MCOU (elite points in each generation are highlighted in red). Algorithm parameters: population cardinality $|\tilde{\mathbf{X}}|=1000$; $\left|\mathbf{Z}\right|=1000$; real coding and SBX-crossover were used.

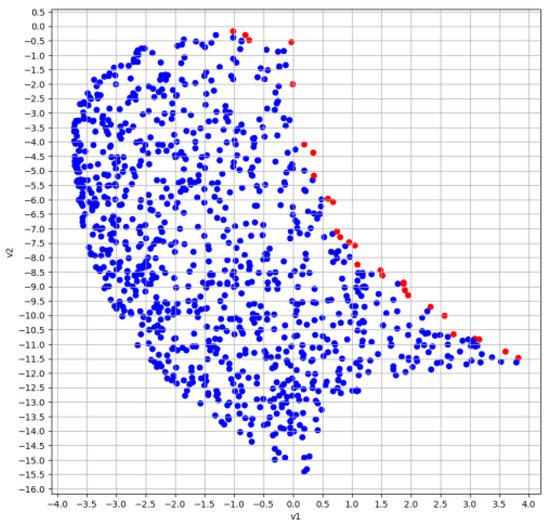
Figure 3. Evolutionary MCOU algorithm, generation No. 1. Elite points in each generation are highlighted in red.

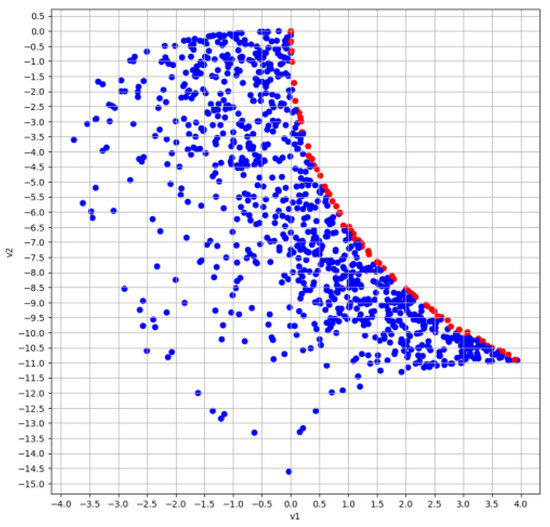
Figure 4. Evolutionary MCOU algorithm: generation No. 5.

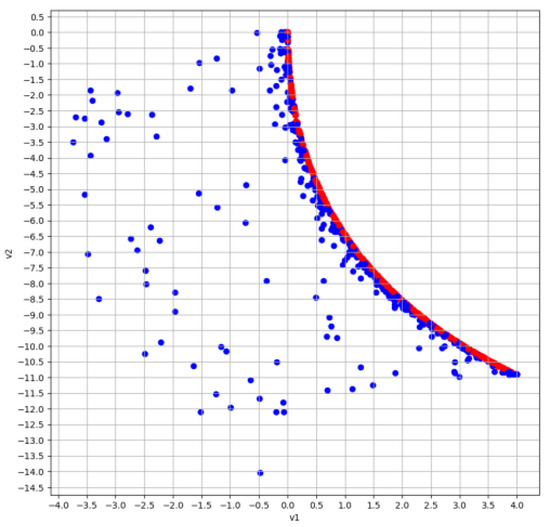
Figure 5. Evolutionary MCOU algorithm: generation No. 10.

Table 1 provides a comparative analysis of the running time of sequential and parallel evolutionary algorithms for solving the considered MCOU test task.

Table 1. Comparative analysis of sequential and parallel MCOU algorithms.

Population Size $|\tilde{\mathit{X}}|$	Running Time of the Parallel Algorithm ${\mathit{t}}_{\mathit{par}},$ s	Running Time of the Sequential Algorithm ${\mathit{t}}_{\mathit{seq}},$ s
10	0.1353302	0.0003806
50	0.1354179	0.0049311
100	0.1397946	0.0129666
500	0.1476841	0.2834744
1000	0.1611041	1.0414738
5000	0.2373939	26.2836442
10,000	0.3495695	104.6257208
50,000	0.3617121	2623.5825713
100,000	0.6700136	10,134.2378412

A comparative analysis shows that, with a small population size $|\tilde{\mathbf{X}}|\le 500$, the running time of the parallel evolutionary algorithm MCOU $t_{par}$ is greater than or comparable to the running time of the sequential algorithm $t_{seq}$. This is due to the fact that the parallel algorithm spends additional time preparing and transferring data to the GPU. However, with a further increase in the size of populations, the advantage of the parallel evolutionary MCOU algorithm in relation to the sequential analog increases. In particular, for $|\tilde{\mathbf{X}}|=100,000$, the running time of the parallel evolutionary MCOU algorithm is $t_{par}\cong {10}^{-4}{t}_{seq}$.

5. Conclusions

The formulation of the MP training problem was formalized as an MCOU problem, where the vector minimax principle was used for its solution.

A parallel implementation of a hierarchical evolutionary algorithm for searching for a set of vector minimaxes in the MCOU problem based on GPU and OpenCL technology is presented. The developed algorithm can be easily modified to solve the MCOU problem (1), (2), where the set of uncertain factors is infinite.

The results of the computational experiment on the test task show a significant advantage of the parallel GPU implementation of the developed co-evolutionary MCOU algorithm in relation to the sequential analog.