Abstract
The development of effective gas-liquid mixing systems in mechanically agitated vessels is typically evaluated in terms of the degree of bubbles dispersion. For instance, adequate gas distribution reduces the formation of oxygen-deficient regions and ensures suitable metabolic pathways in bioreactors. In this regard, the gas holdup is a direct measurement of the process performance because the bubbles’ characteristics determines the gas volume fraction inside the vessel. The accurate estimation of this parameter using empirical correlations provides a better insight and a rapid prediction of the mixing process characteristics, which is crucial for designing stirred tanks. However, a challenge in obtaining empirical correlations is related to the experimental ranges of geometrical and process system conditions. In fact, the existing gas holdup correlations have not considered gas dispersion in yield pseudoplastic fluids using a coaxial mixer that comprises concentric shafts rotating independently. As an opportunity in mixing process system design, this study aims to develop empirical gas holdup correlations for an aerated anchor-PBT coaxial mixing system containing a xanthan gum solution, which behaves as a yield stress fluid. The electrical resistance tomography technique was employed to measure the gas holdup based on the conductivity variation throughout the vessel. A central composite design of experiments was conducted to account for the effect of central impeller speed, anchor speed, and gas flow rate on the mixing performance. The results demonstrated a non-monotonic effect of the central impeller speed on the gas holdup, which indicates a variation in the flow regime. Furthermore, the results showed that the gas holdup was increased by decreasing the anchor speed or increasing the aeration rate applied to the system. The developed correlations were statistically assessed and a good agreement with the experimental data was verified, which enabled us to accurately estimate the gas holdup within the range of operating variables investigated.
1. Introduction
Efficient gas-liquid mixing systems have been continuously investigated for different industrial applications. In fact, there is not a single design that can be employed optimally in all process conditions due to the complex mechanisms of these multiphase mixing systems. Although different applications encompass particular constraints, the process effectiveness of aerated mechanically-agitated vessels is normally evaluated in terms of the bubble dispersion throughout the liquid phase. Therefore, several parameters can be measured or estimated to characterize the gas dispersion in stirred tanks, such as gas holdup, mass transfer coefficient, mixing time, bubble size, cavity size, and power consumption [1,2,3,4,5].
One important application of multiphase mixing systems takes place in bioreactors, where an adequate gas distribution is required to avoid the formation of oxygen-deficient regions [6,7]. Several of these bioreactors comprise non-Newtonian fluids in which the agitation mechanism needs to overcome the mixing challenges arising from the rheological nature of these fluids [8,9,10]. In view of that, this work aims to characterize the gas dispersion in pseudoplastic fluids possessing yield stress in terms of the gas holdup and investigate the effect of different process conditions on the mixing performance.
2. Materials and Methods
A coaxial mixer comprised of an anchor impeller and pitched blade turbine (PBT) was employed in this study as shown in Figure 1. An upward pumping flow in the co-rotation mode was investigated for dispersing gas in a xanthan gum solution (1 wt%). To evaluate the gas holdup under a wide range of operating conditions, the experimental data was obtained using the electrical resistance tomography (ERT) technique and the sampling data was determined by the central composite response surface methodology. The ERT measured the conductivity distribution in each of the four radial planes delimitated by 16 electrodes allocated equally around the bioreactor, as shown in Figure 1. The gas holdup was then calculated using the simplified Maxwell’s equation [11], considering that the conductivity of the liquid phase is much higher than that of the gas conductivity.
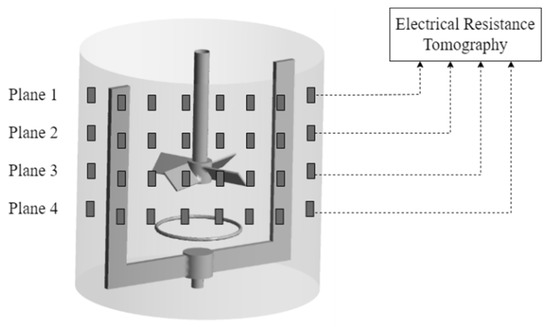
Figure 1.
Experimental setup.
A total of 18 experiments were run by varying the central impeller speed (), anchor speed (), and gas flow rate () according to the coded values defined in Table 1. The independent variables combination for each run was defined from the central composite methodology using the Design-Expert 13 software.

Table 1.
Independent variables analyzed in the central composite design.
3. Results and Discussion
The main effects of the independent variables were evaluated according to Figure 2, which was obtained experimentally from the response surface methodology. The variables’ range defined in Figure 2 results from the coded values between −1 and +1. In fact, the star values (±1.414) represent the additional points in the design of experiments that were used to obtain a quadratic model. The results indicate that gas holdup slightly decreases when increasing the anchor impeller speed, which indicates its minor negative effect (Figure 2a). With respect to the gas flow rate, a more significant effect on the gas holdup was observed by showing a higher increase rate in the gas holdup when increasing the gas flow rate (Figure 2c). The positive effect of the gas flow rate on the gas holdup is expected, however, care should be taken to avoid the development of the flooding regime in the mixing system. In fact, the non-monotonic effect of the central impeller speed (Figure 2b) suggests a variation in the flow regime within the variable’s range evaluated. The initial decrease in the gas holdup indicates that an increase in the shear rate is promoting the bubble breakage mechanism and favoring the gas distribution, which reduces the bubble sizes and further decreases the volume occupied by the gas in the stirred tank. Once it reaches a complete dispersion regime at approximately 430 rpm, the improvement of gas dispersion by increasing the central impeller speed enhances the gas holdup in the mixing system.
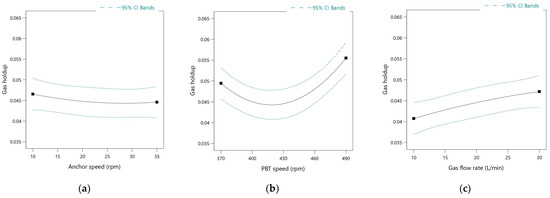
Figure 2.
One-factor effect of the independent parameters on the global gas holdup within 95% confidence interval bands: (a) Anchor speed at and ; (b) Central impeller speed at and ; (c) Gas flow rate at and .
An analysis of variance was performed to fit a quadratic model considering both the main effects and the significant variables’ interaction for predicting the gas holdup using coded values. Equation (1) was obtained with a correlation coefficient of 0.9161, and it was observed that the variables’ interactions have a significant effect on the gas holdup (, especially the interaction between anchor speed and gas flow rate.
Furthermore, a hill climb optimization built-in algorithm in Design Expert 13 was utilized to obtain the process condition that maximizes the gas holdup within the range of variables investigated. It is worth noting that an additional constraint was defined for the system, in which the gas volume fraction should be in the interval between 0 and 1. In that case, different local maximums were identified that corroborate the complex mixing phenomenon. Therefore, optimum solutions should be obtained for specific scenarios and considering multiple optimization criteria. For instance, at 20 L/min, a better configuration was obtained at rpm and rpm. This condition was obtained aiming at minimizing the central impeller speed, which directly affects the energy consumption, and maximizing the gas holdup. In fact, additional investigation on the power consumption of these mixing systems, as well as on the fluid flow and gas distribution will shed light on which criteria should be applied for obtaining the optimized mixing performance.
The polynomial equation obtained in this study can be employed as an additional source of gas holdup prediction for mixing systems within the operational conditions analyzed. Alternatively, the experimental data can be used to obtain a non-linear dimensionless expression, which expresses an actual physical meaning of the mixing characteristics. However, it is worth mentioning that a preliminary analysis that results in the mathematical formulation obtained from the design of experiments is crucial to determine which variables significantly affect the mixing performance in order to be considered in a posterior dimensional analysis.
4. Conclusions
This study investigated the mixing performance of a coaxial mixer for dispersing gas in a xanthan gum solution, which is a yield-pseudoplastic fluid. The effectiveness was characterized in terms of gas holdup obtained from the ERT technique combined with a central composite response surface methodology. Results show the main effect of anchor speed, central impeller speed, and gas flow rate on the gas holdup. The anchor speed has a small negative effect on the gas holdup, whereas the aeration rate positively affects the mixing effectiveness. On the other hand, the central impeller speed has a non-monotonic effect on the gas holdup, in which its minimum value occurs at around 430 rpm. This behavior indicates that a complete dispersed regime is obtained when the central impeller speed is equal to or higher than 430 rpm. Furthermore, a polynomial expression for predicting the gas holdup in any operating condition within the variables’ range was evaluated in this study. Although the model obtained is purely mathematical, it provides an insight and expresses the actual influence of the variables on the gas holdup considering their interaction. Finally, the empirical correlation demonstrates a significant effect of variables’ interaction, especially the interaction between aeration rate and anchor speed, which means that evaluating each factor individually results in overall misleading conclusions about the influence of the design parameters on the development of gas-liquid mixing operations.
Author Contributions
P.L.B.: Conceptualization, Methodology, Software, Validation, Formal analysis, and Writing—original draft; F.E.-M.: Conceptualization, Resources, Methodology, Writing—review & editing, Supervision, Project administration and Funding acquisition. A.L.: Conceptualization, Resources, Methodology, Writing—review & editing, Supervision, Project administration and Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Sciences and Engineering Research Council of Canada grant number RGPIN-2019-04644 and RGPIN-2019-05644.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The financial support of the Natural Sciences and Engineering Research Council of Canada (NSERC) is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Solomon, J.; Elpson, T.P.; Nienow, A.W.; Pace, G.W. Cavern Sizes in Agitated Fluids with a Yield Stress. Chem. Eng. Commun. 1981, 11, 143–164. [Google Scholar] [CrossRef]
- Gabelle, J.-C.; Augier, F.; Carvalho, A.; Rousset, R.; Morchain, J. Effect of Tank Size on kLa and Mixing Time in Aerated Stirred Reactors with Non-Newtonian Fluids. Can. J. Chem. Eng. 2011, 89, 1139–1153. [Google Scholar] [CrossRef]
- Xie, M.; Xia, J.; Zhou, Z.; Zhou, G.; Chu, J.; Zhuang, Y.; Zhang, S.; Noorman, H. Power consumption, local and average volumetric mass transfer coefficient in multiple-impeller stirred bioreactors for xanthan gum solutions. Chem. Eng. Sci. 2014, 106, 144–156. [Google Scholar] [CrossRef]
- Hashemi, N.; Ein-Mozaffari, F.; Upreti, S.R.; Hwang, D.K. Experimental investigation of the bubble behavior in an aerated coaxial mixing vessel through electrical resistance tomography (ERT). Chem. Eng. J. 2016, 289, 402–412. [Google Scholar] [CrossRef]
- Jamshidzadeh, M.; Ein-Mozaffari, F.; Lohi, A. Local and overall gas holdup in an aerated coaxial mixing system containing a non-Newtonian fluid. AIChE J. 2020, 66, e17016. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E. Prediction of Gas-Liquid Mass Transfer Coefficient in Sparged Stirred Tank Bioreactors. Biotechnol. Bioeng. 2005, 92, 761–772. [Google Scholar] [CrossRef] [PubMed]
- Lone, S.R.; Kumar, V.; Seay, J.R.; Englert, D.L.; Hwang, H.T. Mass Transfer and Rheological Characteristics in a Stirred Tank Bioreactor for Cultivation of Escherichia coli BL21. Biotechnol. Bioprocess Eng. 2020, 25, 766–776. [Google Scholar] [CrossRef]
- Wyma, A.; Martin-Alarcon, L.; Walsh, T.; Schmidt, T.A.; Gates, I.D.; Kallos, M.S. significantly impacts bioreactor shear stress quantification. Biotechnol. Bioeng. 2018, 115, 2101–2113. [Google Scholar] [CrossRef]
- Cappello, V.; Plais, C.; Vial, C.; Augier, F. Bubble size and liquid-side mass transfer coefficient measurements in aerated stirred tank reactors with non-Newtonian liquids. Chem. Eng. Sci. 2020, 211, 115280. [Google Scholar] [CrossRef]
- Lins Barros, P.; Ein-Mozaffari, F.; Lohi, A. Gas dispersion in Non-Newtonian Fluids with Mechanically Agitated Systems: A Review. Process 2022, 10, 275. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1881; Volume 1. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).