Comparative Study of Optimization Techniques Based PID Tuning for Automatic Voltage Regulator System ^†

Abstract

A comparative study is performed to design an optimal PID controller for an automatic voltage regulator system using different optimization techniques. The presented approaches are referred to as particle swarm optimization (PSO) algorithm, cuckoo search optimization (CSO) algorithm, moth flame optimization (MFO) algorithm, water cycle optimization (WCO) algorithm, teaching–learning-based optimization (TLBO) algorithm, and hill climbing optimization (HCO) algorithm. Transient response parameters, which are rise time Tr, settling time Ts, and percentage overshoot Mp, are used as comparison criteria. The integral time absolute error ITAE is the used performance index. All the proposed optimization techniques improved the transient response of the AVR system in a different way and gave good preliminary results.

1. Introduction

In an electrical power system, the AVR is used to maintain the terminal voltage magni-tude of a generator [1]. Controlling the generator excitation keeps the magnitude of this voltage at a specific level. In general, traditional tuning methods such as Ziegler–Nichols (ZN) and gain-phase margin make it difficult to find optimal controller parameters [2]. As a result, several optimization techniques for tuning controller parameters have been proposed. Some of these optimization techniques which used as tuning methods to improve the performance of the (PID) controller are particle swarm optimization (PSO) [3,4], cuckoo search optimization (CSO) algorithm [5,6], moth flame optimization (MFO) algorithm [7,8], water cycle optimization (WCO) algorithm [9,10], teaching–learning-based optimization (TLBO) [11,12,13]. Hill climbing optimization (HCO) algorithm [14] is tested for the first time in the AVR system in this work. Fractional order PID (FOPID) [15], PID-acceleration (PIDA) [16], gray PID (GPID) [17], and fuzzy logic PID (FLPID) [18] are some of the other controller types used to improve the dynamic response of AVR systems in the literature.

The rest of this paper is organized as follows. Section 2 describes the AVR system and its block diagram model with the used values. Section 3 describes the implementation of the proposed optimizations techniques and provides comparison of the results of the numerical simulations. Section 4 concludes the paper with a summary of the research’s main findings.

2. AVR System

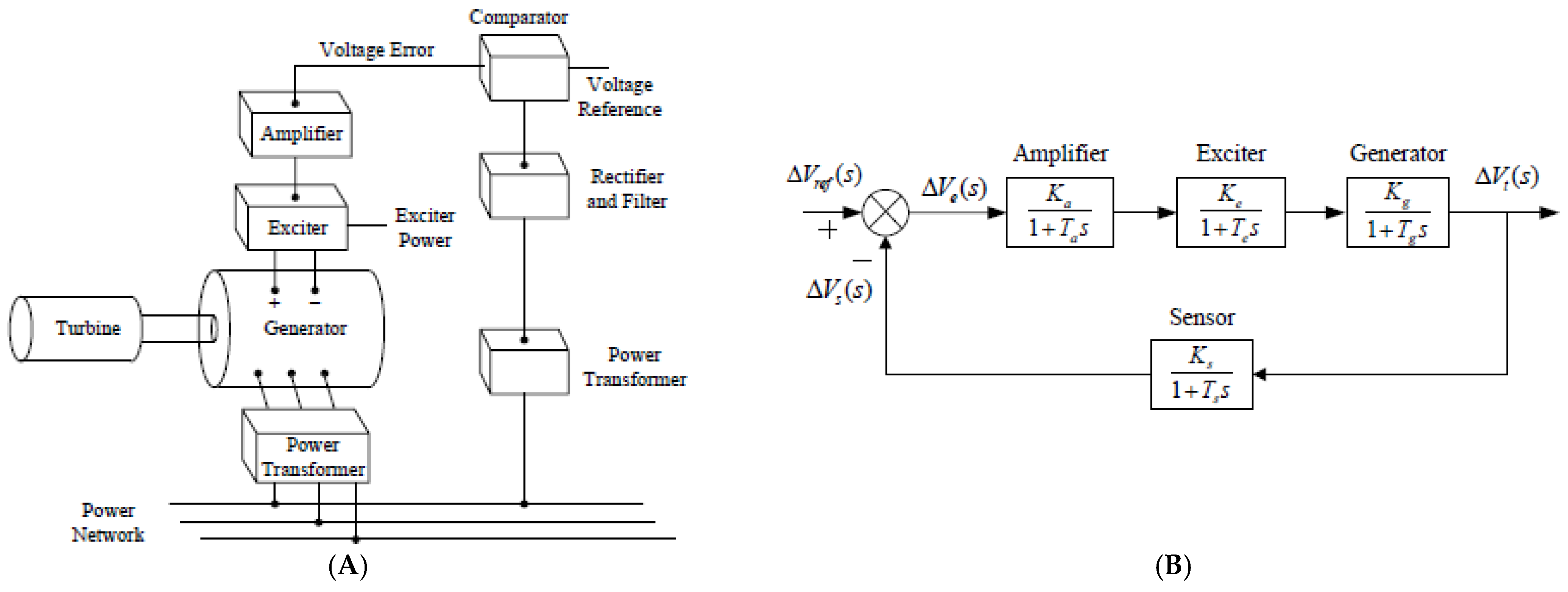
The primary consumer demand in the power system is the quality of electrical energy. In addition, the majority of equipment is designed to operate at predetermined voltage and frequency levels, since the interaction between voltage control and frequency control in a power generation system is usually weak enough that they can be analyzed separately. Moreover, a small variation in voltage can result in a significantly large variation in reactive power flow, which can result in massive power loss and, as a result, economic loss. To avoid this, the automatic voltage regulator (AVR) system is used in power generation sites to ensure voltage stability at the generator terminal via the excitation system. An AVR system and its model are shown in Figure 1.

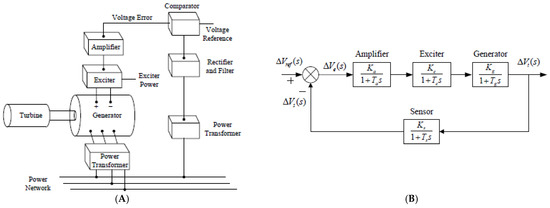
Figure 1. (A) AVR system. (B) Block diagram of the AVR system.

∆Vref(s), ∆Vs(s), ∆Ve(s), and ∆V_t(s) are the reference input voltage, sensor output voltage, error voltage, and generator terminal voltage, respectively. Table 1 shows the boundary values of AVR system components as well as the values used in the AVR system.

Table 1. Boundary values of the AVR system.

Model	Parameter Ranges	Used Values in AVR System
Amplifier	10 ≤ Ka ≤ 40 0.02 ≤ Ta ≤ 0.1	KA = 10 TA = 0:1
Exciter	1 ≤ Ke ≤ 2 0.4 ≤ Te ≤ 1	Ke = 1 Te = 0:4
Generator	1 ≤ Kg ≤ 2 1 ≤ Tg ≤2	Kg = 1 TG = 1
Sensor	Kr = 1 0.001 ≤ Tr ≤ 0.006	KR = 1 TR = 0:01

The uncontrolled system transfer function is:

$$G(s)=\frac{0.1s+10}{0.0004s^4+0.0454s^3+0.555s^2+1.5s+11}$$

(1)

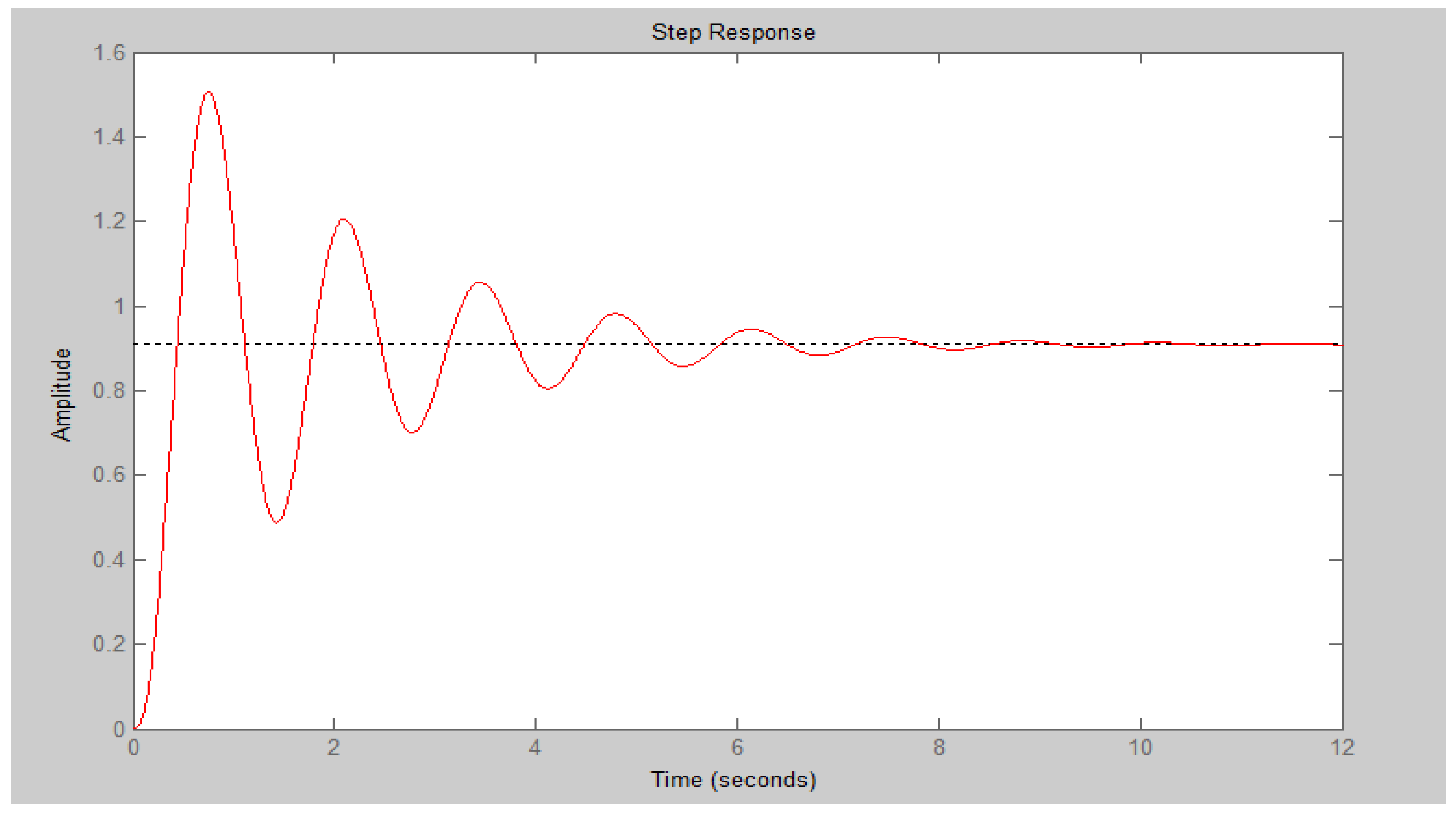
Although stable, the AVR system’s step response is extremely oscillatory without a controller, as illustrated in Figure 2.

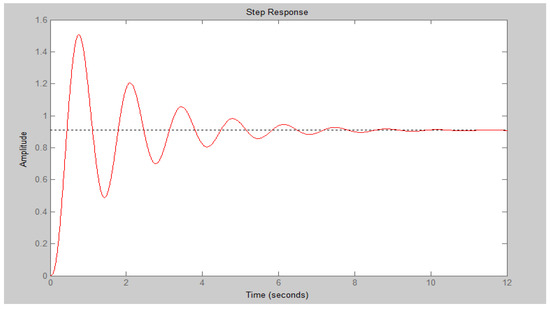
Figure 2. Step response of AVR system in the absence of a controller.

Table 2 summarizes the transient response parameters of the AVR system in the absence of the controller.

Table 2. Transient performance of the AVR system without controller.

Rise Time (s) Tr	Settling Time 2% (s) Ts	Overshoot Mp (%)	Steday State Error Ess
0.261	6.99	65.7	0.091

These results show that by utilizing a PID controller, the transient response of the AVR system can be improved and the steady state error can be removed.

3. Implementation of Proposed Optimization Techniques

The primary goal of this work is to design and construct a high-performance PID controller for AVR systems in synchronous generators. The design challenge is stated as an optimization control problem, and the proposed optimization algorithms are used to find optimal controller parameters. Particle swarm optimization (PSO), cuckoo search optimization (CSO), moth flame optimization (MFO), water cycle optimization (WCO), teaching–learning-based optimization (TLBO), and hill climbing (HCO) have been tested, and a comparison has been carried out. The integral time absolute error (ITAE) is the performance index used in this work to examine and build the suggested OA-PID controller, which is given as

$$\stackrel{T}{\mathrm{Integral}\mathrm{time}\mathrm{absolute}\mathrm{error}ITAE={\displaystyle {\int }_0^{}}t|e(t)|dt}$$

(2)

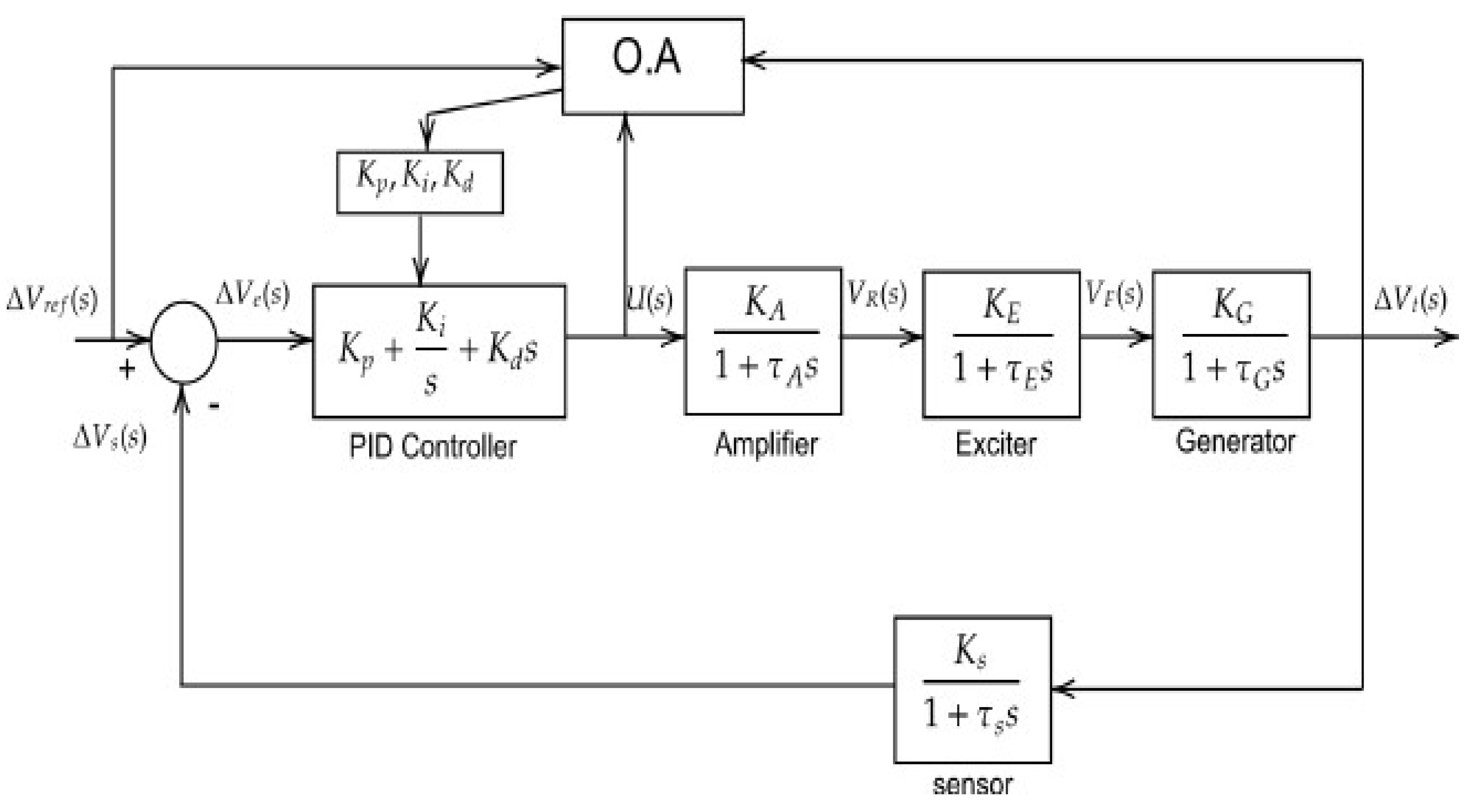
The block diagram of the AVR system with the proposed OA-PID controller is shown in Figure 3.

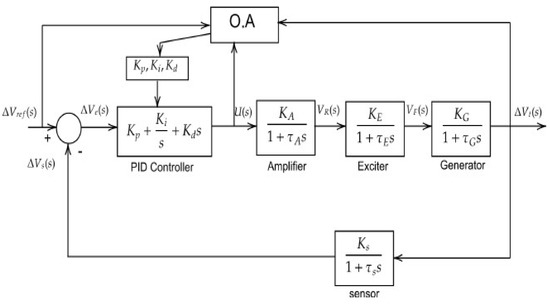
Figure 3. AVR system with proposed OA-PID Controller.

Table 3 shows the adjusted and optimal PID controller settings acquired by proposed optimization techniques and the transient response analysis results after the simulation procedure.

Table 3. Optimized PID parameters and transient response analysis results.

Optimization Technique	Controller Parameters Kp–Ki–Kd	Tr: 0.1→0.9	Ts + 2%	Mp (%)
PSO-ITAE	0.7027–0.5471–0.37852	0.1969	1.3466	1.718
CSO-ITAE	0.6999–0.54672–0.37904	0.1967	1.3498	1.7266
MFO-ITAE	1.5643–1.0713–0.5132	0.1319	0.7518	22.7511
WCO-ITAE	1.4802–1.0153–0.4809	0.1386	0.7769	21.2312
TLBO-ITAE	1.2298–1.8472–0.3944	0.1623	0.8533	16.3603
HCO-ITAE	0.5900–0.4200–0.2000	0.3272	0.5131	0

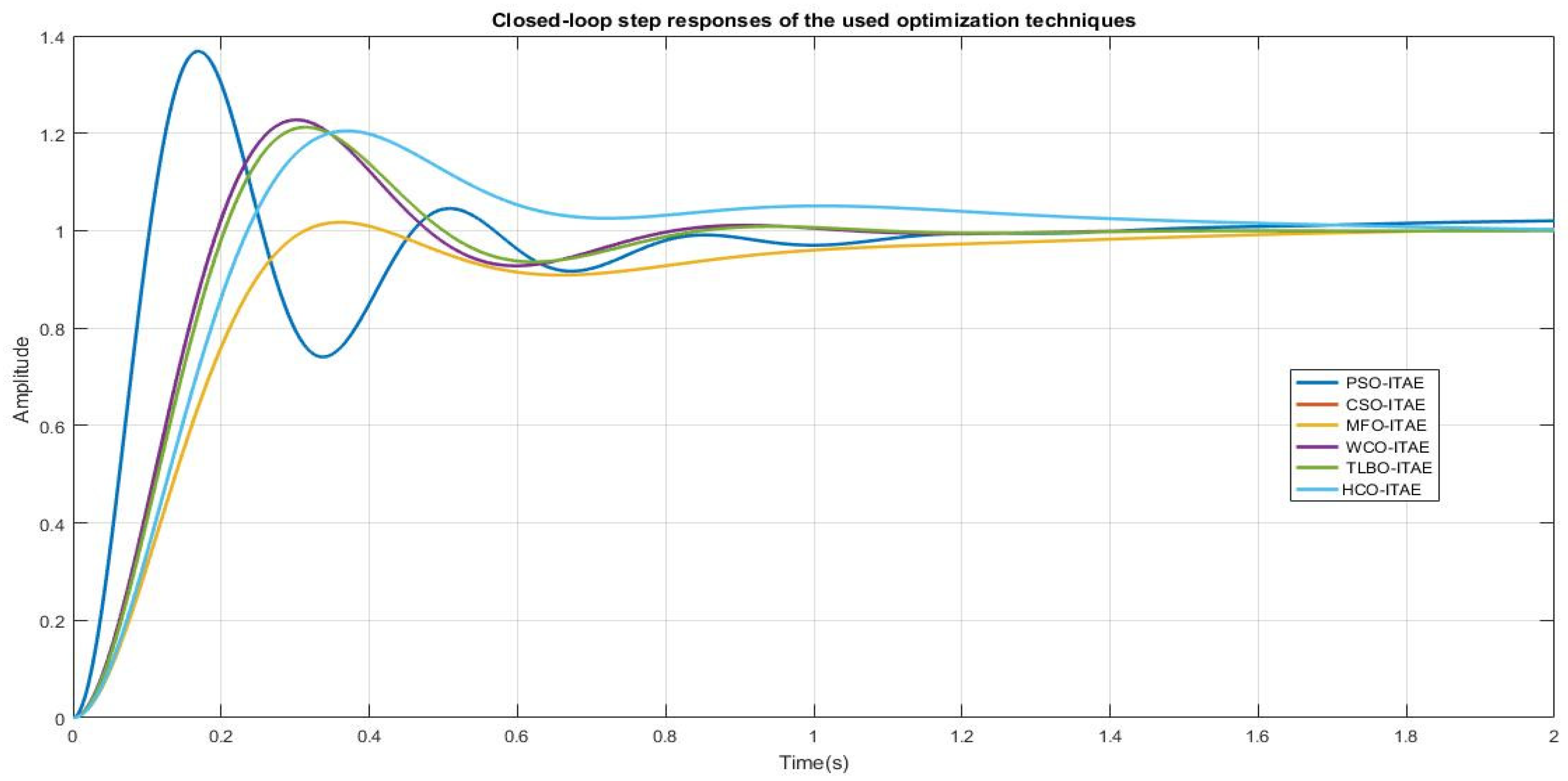
The comparative simulation results obtained for the terminal voltage step response of the AVR system with the different optimization techniques are shown in Figure 4.

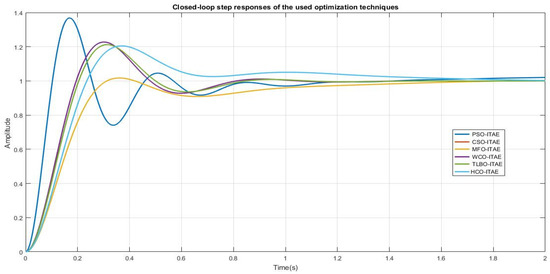
Figure 4. Terminal voltage response curves of the AVR system with various optimization techniques.

It is evident from Figure 4 and Table 3 that the MFO, WCO, and TLBO techniques delivered a response with a high percentage overshoot and quicker rise time than the PSO, HCO, and CSO methods. On the other hand, the HCO technique yielded a system with no oscillation and rapid settling time compared to the other optimization techniques. Furthermore, the PSO and CSO performances are almost the same, producing a response with little overshoot and long settling time. The HCO tuned PID controller with the ITAE fitness function generates a superior control performance in terms of improved overshoot and settling time.

4. Conclusions

The main goal of this study is to design an optimal PID controller parameter for the AVR system using different optimization techniques. A comparison based on integral time absolute error ITAE performance index and transient response parameters was carried out. The most obvious finding to emerge from this study is that all optimization techniques have improved the system performance compared to the uncontrolled case. The second major finding was that each optimization algorithm improves some parameters and, at the same time, deteriorates another one. However, it is worth noting that the hill climbing (HCL) technique yields generally better results in terms of percentage overshoot and settling time. Finally, the current study has only examined one performance index and focused on transient analysis. A natural progression of this work is to analyze the system performance based on other objective functions and other stability criteria and consider a hybridization between best optimization techniques.