The Extended Embedded Self-Shielding Method in SCALE 6.3/Polaris ^†

Abstract

The SCALE transport lattice code, Polaris, has been previously developed to generate few-group homogenized cross sections for whole-core nodal diffusion simulators in which the embedded self-shielding method (ESSM) is used for resonance self-shielding calculations to process cross sections. Although the ESSM capability has been very successful in light-water reactor analysis, it may require enhancements in computational efficiency; treatment of spatially dependent resonance self-shielding effects; and handling of interrelated resonance effects among fuel, cladding, and control rod materials. Therefore, this study focuses on improving computational efficiency by using a Dancoff-based Wigner–Seitz approximation combined with a material-based resonance categorization, through which a spatially dependent ESSM capability is developed to accurately estimate self-shielded cross sections inside the fuel. Benchmark results show that the new capability significantly enhances computational efficiency and accuracy for spatially dependent local zones within the fuel and through depletion.

1. Introduction

SCALE/Polaris [1,2] is a two-dimensional (2D) transport lattice physics code developed to generate few-group homogenized cross sections for whole-core nodal diffusion simulators for light-water reactor (LWR) analysis. Key characteristics of the SCALE/Polaris code include (1) direct use of the SCALE/AMPX [3] multigroup (MG) library, (2) an embedded self-shielding method (ESSM) [4,5] for resonance self-shielding calculation, (3) application of the method of characteristics (MOC) for spatial discretization, and (4) coupling with the SCALE/ORIGEN application programming interface for transmutation calculations.

The Polaris ESSM capability was developed to overcome some drawbacks of the physical subgroup method [6,7], including errors arising from the least-squares fitting used to obtain subgroup data from resonance cross section tables, which are MG self-shielded cross sections expressed as a function of background cross sections. Since the subgroup method may not be applied to very thermal groups owing to poor subgroup data quality, subgroup self-shielding calculations are restricted to specified energy groups [8]. In contrast, the ESSM approach avoids errors in resonance data reconstruction and has no limitations on energy groups or nuclides. The Polaris ESSM is based on the intermediate resonance (IR) approximation [9], and its implementation builds on the subgroup implementation using MOC for fixed-source transport calculations [10]. Although the MOC-based ESSM capability in Polaris is very powerful, there remains a need for improvements in (1) computational efficiency, (2) spatially dependent self-shielding, and (3) treatment of improper resonance interference between fuel and cladding or control rod materials. This study focuses on addressing these three challenges.

Recently, the equivalent Dancoff-factor cell (EDC) model [11,12,13] for ultrafine resonance treatment and the subgroup method in a coarse group structure has gained popularity because of its excellent computational efficiency along with comparable accuracy. A key feature of the EDC method is the conversion of the whole domain into constituent cylindrical cells, with the outermost radii of the cylindrical cells adjusted to reproduce the same Dancoff factors as those obtained from the whole domain. The origin of the EDC method—specifically when and by whom it was first proposed—remains unclear. Since the release of SCALE 6.0 in 2009 [14], the SCALE code package [1] has employed the EDC method, also referred to as the Dancoff-based Wigner–Seitz approximation, by adjusting the outermost radii of single or multiple pin cells using Dancoff factors calculated with the SCALE/MCDancoff module. The conventional ESSM has since been enhanced with the Dancoff-based Wigner–Seitz approximation to improve computational efficiency.

Stoker and Weiss developed a method for spatially dependent resonance cross sections in a fuel rod, ref [15], which was later reformulated by Matsumoto et al. through a generalization of the conventional Dancoff method and the Stoker–Weiss method [16]. These methods proved successful in estimating spatially dependent self-shielded cross sections. However, they cannot be applied to nonuniform temperature distributions within a fuel rod, as noted in the cited literature. Kim et al. [17] improved spatially dependent resonance self-shielding methods to account for nonuniform temperature distributions and attempted to couple them with the ESSM procedure. In this study, Kim’s spatially dependent ESSM is further improved and integrated with the Dancoff-based Wigner–Seitz approximation to more accurately predict local self-shielded cross sections inside the fuel.

Since the original ESSM sequence in Polaris was implemented with an excessive treatment of resonance interference between fuel and cladding or control rods, special resonance cross section tables are required for resonance nuclides such as ⁹¹Zr and ⁹⁶Zr in the cladding and control rods. These special resonance cross section tables for ⁹¹Zr and ⁹⁶Zr should not be applied to materials other than cladding. The ²³⁵U and ²³⁸U resonance cross section tables are similar; however, error cancellations occur between resonance interference and the intrinsic reactivity bias introduced by energy group collapsing. To address this issue, the ESSM implementation was improved to estimate background cross sections on a material-specific basis. For example, separate ESSM fixed-source calculations are performed for fuel and cladding. In the present study, the material categorization capability has been completed by combining spatially dependent ESSM with the Dancoff-based Wigner–Seitz approximation and improvement in resonance data. Test ENDF/B-VII.1 AMPX 56- and 252-group libraries were developed for this material categorization capability, incorporating super-homogenization (SPH) factors to compensate for reaction rate biases introduced by energy group collapsing.

2. Methods

2.1. Embedded Self-Shielding Method

The time-independent Boltzmann neutron transport equation assuming isotropic scattering, no upscattering, and no external source is

$$\widehat{\mathrm{\Omega }}\cdot \nabla {\psi }_k+{\displaystyle \sum _i{\Sigma }_{i,t}^k(u){\psi }_k(u,\hat{\mathrm{\Omega }})}={\displaystyle \sum _i{\displaystyle {\int }_{u-{\Delta }_i}^u{\Sigma }_{i,s}^k(u^{\prime }){\varphi }_k(u^{\prime })\frac{{\mathrm{e}}^{u^{\prime }-u}}{1-{\alpha }_i}d{u}^{\prime }}},$$

(1)

where

$\widehat{\mathrm{\Omega }}$ = neutron direction;

$u$ = lethargy at neutron energy (=ln(E₀/E));

${\psi }_k$ = angular flux at zone k;

${\varphi }_k$ = scalar flux at zone k;

${\Sigma }_{i,t(s,a)}^k$ = macroscopic total (scattering, absorption) cross section for nuclide i.

In Equation (1),

$$\begin{array}{l}{\Sigma }_{i,x} = N_i{\sigma }_{i,x},\\ {\Sigma }_{i,t}^k(u)={\Sigma }_{i,s}^k(u)+{\Sigma }_{i,a}^k(u),\\ {\alpha }_i={(A_i-1)}^2/{(A_i+1)}^2,\\ {\Delta }_i=-\ln ({\alpha }_i),\end{array}$$

(2)

where ${\sigma }_{i,x}$ denotes the microscopic cross section for reaction x, and N and A are the atomic number density and the atomic mass number, respectively.

Equation (1) is further simplified through application of the IR approximation [8] into an MG form and can be rewritten as

$$\widehat{\mathrm{\Omega }}\cdot \nabla {\psi }_{k,g}+{\displaystyle \sum _i({\Sigma }_{i,a,g}^k+{\lambda }_{i,g}{\Sigma }_{i,p}^k){\psi }_{k,g}(\widehat{\mathrm{\Omega }})}={\displaystyle \sum _i{\lambda }_{i,g}{\Sigma }_{i,p}^k},$$

(3)

where ${\lambda }_{i,g}$ is an IR parameter at group g and Σ_i,p denotes the potential cross section. Equation (3) is called the fixed-source ESSM transport equation, and it can be solved with the same transport solver that is used for the eigenvalue calculation.

The background cross section (${\sigma }_b$) is not a fully physical quantity but rather a heuristic parameter used to retrieve the correct self-shielded cross section for a given composition and geometry. The key requirement is consistency among the procedures used for self-shielded cross section generation and application. In a heterogeneous system, the self-shielded scalar flux can be obtained by solving Equation (3) with a self-shielded absorption cross section obtained using either a deterministic or Monte Carlo solution of Equation (1). The corresponding background cross section for the resonance nuclide R can then be determined as follows:

$${\sigma }_{R,b,g}={\displaystyle \frac{{\Sigma }_{b,g}}{N_R}}={\displaystyle \frac{{\sigma }_{a,g}{\varphi }_g}{1-{\varphi }_g}}.$$

(4)

Once the background cross section for each nuclide is determined, then effective self-shielded cross sections can be read from the resonance cross section table. However, in solving Equation (3) to obtain the background cross section within a transport code, the absorption cross sections are initially unknown. Therefore, the background cross sections and self-shielded absorption cross sections must be determined iteratively.

2.2. Limitation of the Embedded Self-Shielding Method

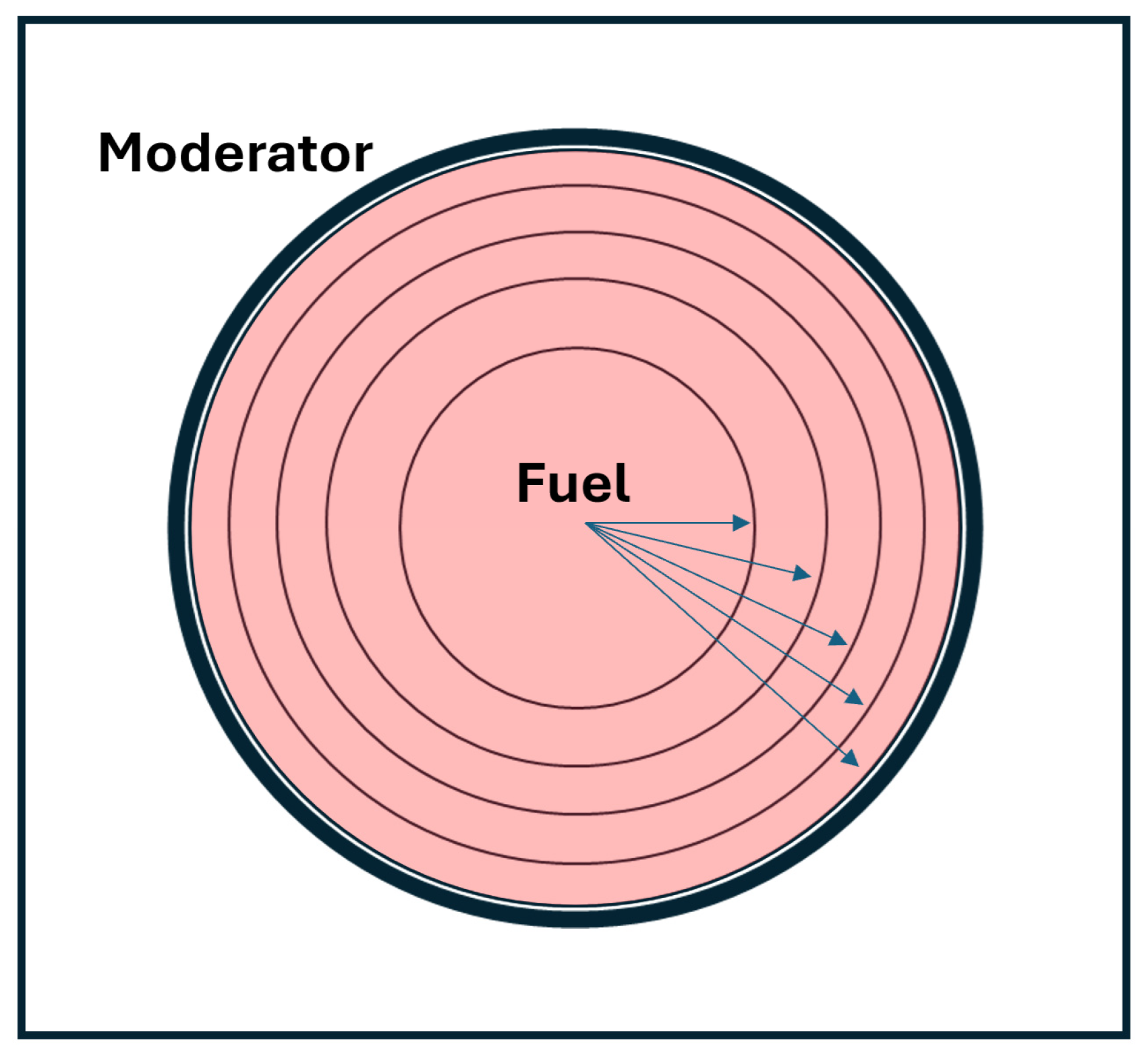
Conventional ESSM [5] has a limitation in predicting spatial variations in resonance self-shielded cross sections within a fuel region: it does not explicitly calculate spatially dependent equivalence cross sections. As a result, conventional ESSM provides accurate pin-averaged quantities of interest, but intra-pin quantities of interest—which are important for fuel performance modeling—may be inaccurate. Figure 1 and Table 1 illustrate a typical pressurized water reactor (PWR) pin configuration with five equivalent-volume radial rings within the fuel.

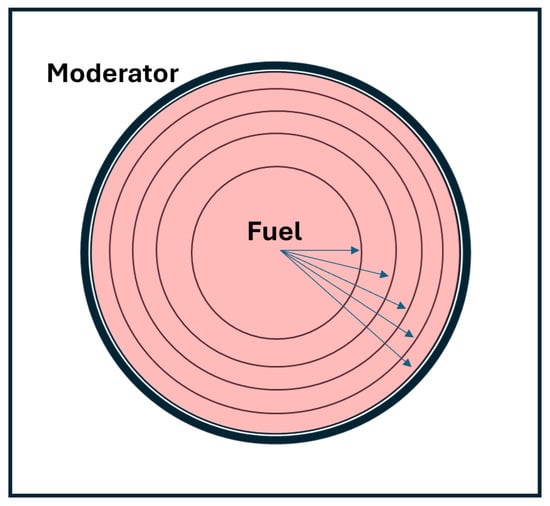
Figure 1. Single-pin configuration with five radial rings.

Table 1. Geometry and composition specifications for single-pin configuration.

Material	Radius (cm)	Temperature (K)	Atomic Number Density (/b-cm)
			Al Clad		Zr Clad
Fuel	0.4025	600	235U	9.39467 × 10−4	235U	9.39467 × 10−4
			238U	2.22624 × 10−2	238U	2.22624 × 10−2
			16O	4.64223 × 10−2	16O	4.64223 × 10−2
Clad	0.4759	600	27Al	6.02611 × 10−2	90Zr	2.17036 × 10−2
					91Zr	4.73302 × 10−3
					92Zr	7.23452 × 10−3
					94Zr	7.33155 × 10−3
					96Zr	1.18115 × 10−3
Moderator	1.2620 (pitch)	600	1H	4.71309 × 10−2	1H	4.71309 × 10−2
			16O	2.35654 × 10−2	16O	2.35654 × 10−2

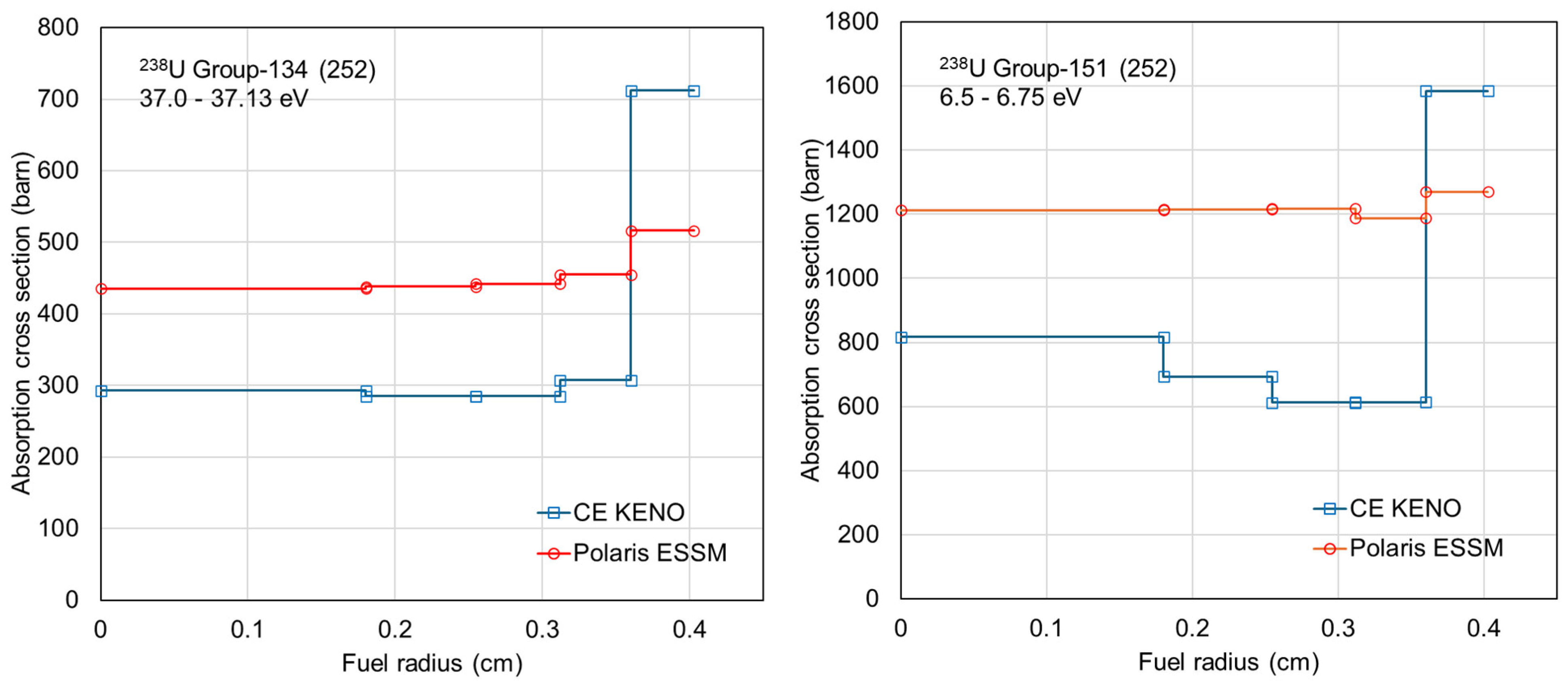
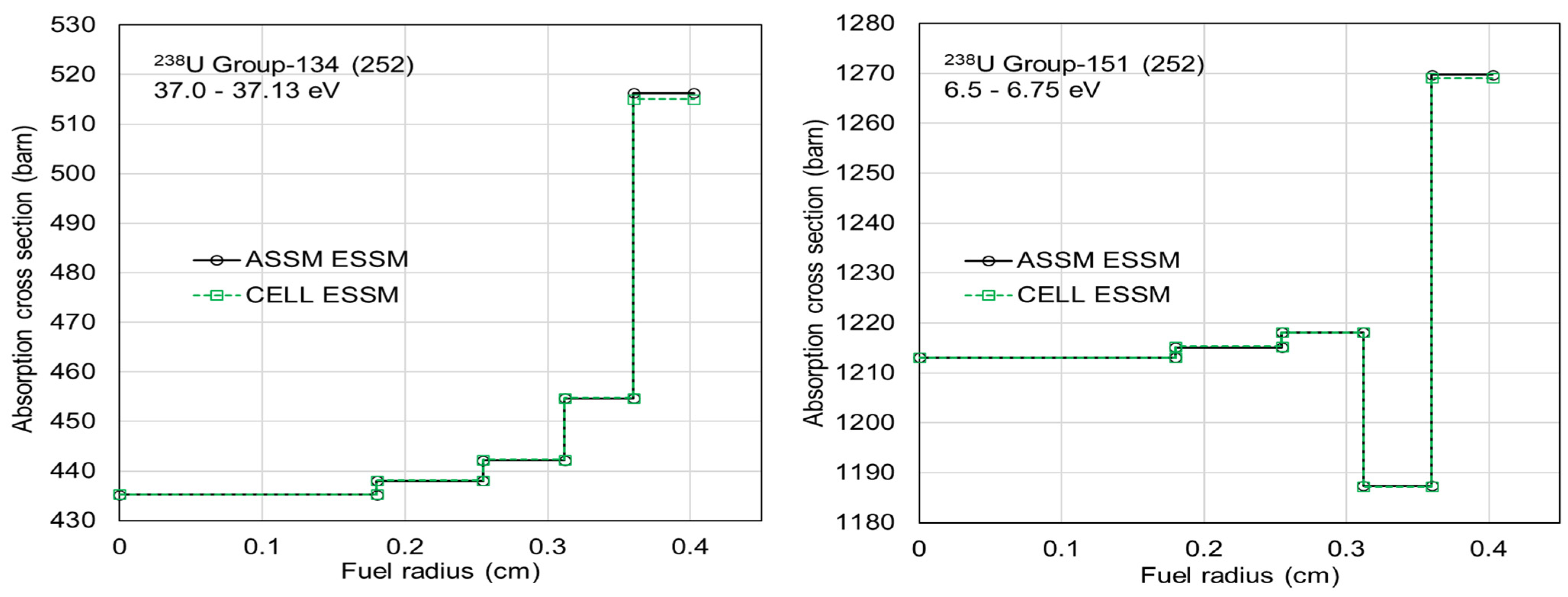
The ESSM calculation was performed for the PWR pin by using SCALE/Polaris, and the reference solution was obtained from the continuous-energy (CE) Monte Carlo calculation using SCALE/KENO. Ring-dependent self-shielded absorption cross sections for group-134 (37.0–37.13 eV) and group-151 (6.5–6.75 eV) within the SCALE 6.3 252-group structure for ²³⁸U are compared in Figure 2. Significant differences are observed in the ring-dependent self-shielded absorption cross sections between the CE Monte Carlo and Polaris ESSM calculations for ²³⁸U.

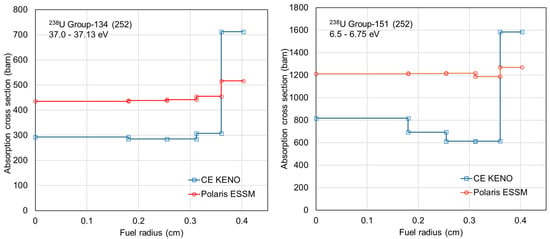
Figure 2. Comparison of ring-dependent self-shielded absorption cross sections for ²³⁸U.

The Polaris calculations were performed for single-pin configurations with Al and Zr cladding using the ENDF/B-VII.1 AMPX 56- and 252-group libraries. Special resonance data for ⁹¹Zr and ⁹⁶Zr were included in the AMPX 56-group library. As shown in the benchmark results in Table 2, the Polaris calculations for Al and Zr clads exhibit significant reactivity swings of approximately 400 pcm due to the clad material. While Al does not include any large resonance, Zr includes large capture resonances. These reactivity swings arise from an intrinsic limitation of the conventional ESSM, caused by strong, unphysical resonance interference between the Zr clad and fuel. Special resonance data for ⁹¹Zr and ⁹⁶Zr improve the Polaris results for the Zr clad case but do not resolve the issue for the Al clad case. Consequently, a material grouping capability is required to avoid the need for special resonance data and to ensure applicability to any clad material.

Table 2. Benchmark result for single-pin configuration.

Clad Material	Al		Zr
CE KENO kinf.	1.38583		1.37884
Polaris ESSM Δkinf. (pcm) *	56-group	252-group	56-group	252-group
	−382	−276	−54	196

* Polaris–KENO.

2.3. Dancoff-Based Wigner–Seitz Approximation

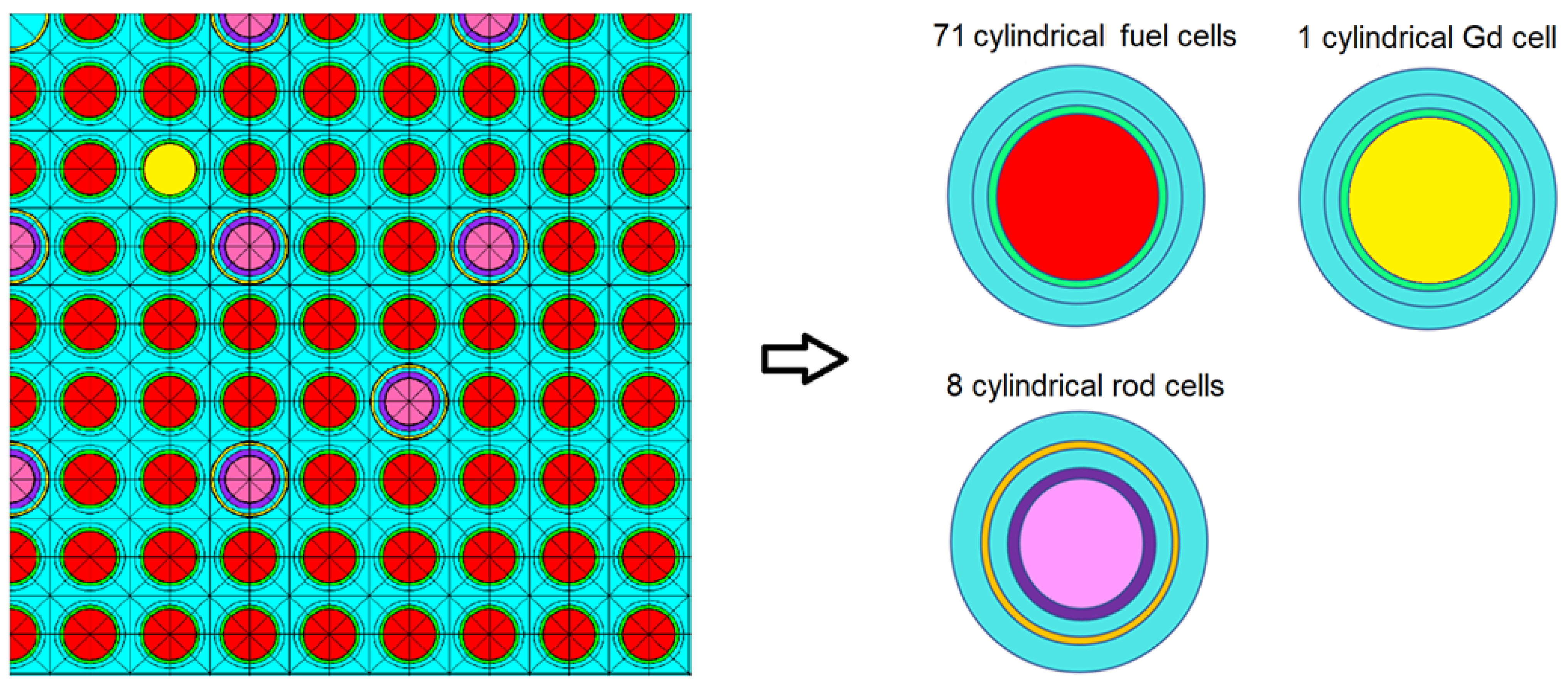
Two-dimensional MOC-based fixed-source transport calculations with black absorber approximation are performed to obtain Dancoff factors for fuels, control rods, and burnable poisons. Equivalent cylindrical pin cells with moderator are constructed with preserving volumes, as shown in Figure 3. The outermost radii of these cells are then adjusted to reproduce the same Dancoff factors as those obtained from the 2D MOC calculations for all constituent cylindrical cells. Fixed-source ESSM calculations are performed using a one-dimensional (1D) cylindrical collision probability method for all constituent cells. In addition, 1-group ESSM calculations are carried out for the entire domain to ensure that no resonance materials, such as structural materials, are omitted.

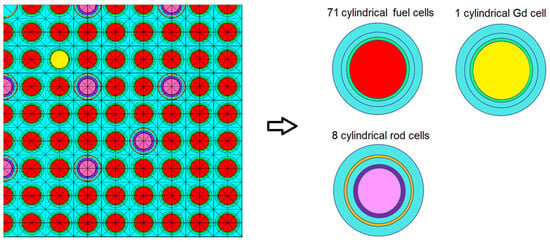
Figure 3. Domain decomposition into 1D cylindrical cells.

Dancoff factors can be obtained by solving the fixed-source transport equation, shown in Equation (5), using 2D MOC in which a black absorber with 10⁵ cm⁻¹ total cross sections (Σ_k,i,t) is assigned to the resonance material zone.

$$\widehat{\mathrm{\Omega }}\cdot \nabla {\psi }_k+{\displaystyle \sum _i{\Sigma }_{k,i,t}{\psi }_k(\widehat{\mathrm{\Omega }})}={\displaystyle \sum _i{\Sigma }_{k,i,p}},$$

(5)

where ψ_k indicates angular flux at the material zone k, i is the nuclide, and Σ_k,p is the potential cross section. The Dancoff factor (D_k) is calculated using Equation (6):

$$D_k=1.0-{\widehat{l}}_k({\Sigma }_{k,t}{\varphi }_k-{\Sigma }_{k,p})/(1.0-{\varphi }_k),$$

(6)

where ${\widehat{l}}_k$ is the mean chord length for the resonance material and ϕ_k is the scalar flux.

2.4. Spatially Dependent Embedded Self-Shielding Method

Stoker and Weiss proposed a simple method to obtain spatially dependent resonance cross sections in a cylindrical fuel rod [15]. Matsumoto et al. [16] developed a spatially dependent Dancoff method (SDDM) based on the conventional Dancoff method and the Stoker–Weiss approach. The present study focuses on developing a novel method of extending the conventional ESSM to accurately provide spatially dependent, effective cross sections at the intra-pin level by integrating the Stoker–Weiss method or SDDM with ESSM.

A detailed derivation of the SDDM equations is introduced in Stoker and Weiss [15] and Matsumoto et al. [16]. The resultant equations are presented here. The neutron spectrum for fuel rods with radial rings can be described as follows:

$${\varphi }_k(E)={\displaystyle \frac{1}{E}}{\displaystyle \sum _{m=1}^4{F}_m{\displaystyle \sum _{n=1}^2\frac{{\alpha }_n{\beta }_n}{l_m{\Sigma }_t+{\alpha }_n}}}.$$

(7)

In Equation (7), Σ_t is the macroscopic total cross section at fuel region k, and l_m is the mean chord length. Table 3 defines a mean chord length and F_m used in Equation (7). In Table 3, R is defined as the fuel pellet outer radius, $s_0=2\pi R$, V_k is an area of radial ring k, and ${\rho }_k=r_k/R$.

Table 3. Definition of functions l_m and F_m.

m	${\mathit{l}}_{\mathit{m}}$	${\mathit{F}}_{\mathit{m}}$
1	$l_1({\rho }_k)={\displaystyle \frac{2R}{\pi }}(\sqrt{1-{\rho }_k^2}+{\displaystyle \frac{1}{{\rho }_k}}{\sin }^{-1}{\rho }_k+{\displaystyle \frac{\pi }{2}}{\rho }_k)$	${\displaystyle \frac{s_0{\rho }_k{l}_1({\rho }_k)}{4V_k}}$
2	$l_2({\rho }_k)={\displaystyle \frac{2R}{\pi }}(\sqrt{1-{\rho }_k^2}+{\displaystyle \frac{1}{{\rho }_k}}{\sin }^{-1}{\rho }_k-{\displaystyle \frac{\pi }{2}}{\rho }_k)$	$-{\displaystyle \frac{s_0{\rho }_k{l}_2({\rho }_k)}{4V_k}}$
3	$l_3({\rho }_{k-1})={\displaystyle \frac{2R}{\pi }}(\sqrt{1-{\rho }_{k-1}^2}+{\displaystyle \frac{1}{{\rho }_{k-1}}}{\sin }^{-1}{\rho }_{k-1}+{\displaystyle \frac{\pi }{2}}{\rho }_{k-1})$	$-{\displaystyle \frac{s_0{\rho }_{k-1}{l}_3({\rho }_{k-1})}{4V_k}}$
4	$l_4({\rho }_{k-1})={\displaystyle \frac{2R}{\pi }}(\sqrt{1-{\rho }_{k-1}^2}+{\displaystyle \frac{1}{{\rho }_{k-1}}}{\sin }^{-1}{\rho }_{k-1}-{\displaystyle \frac{\pi }{2}}{\rho }_{k-1})$	${\displaystyle \frac{s_0{\rho }_{k-1}{l}_4({\rho }_{k-1})}{4V_k}}$

There are two options for ${\alpha }_n$ and ${\beta }_n$ suggested by Stoker and Weiss and Matsumoto et al. Stoker and Weiss introduced ${\alpha }_1=2.0$, ${\alpha }_2=3.0$, ${\beta }_1=2.0$, and ${\beta }_2=-1.0$. Matsumoto et al. introduced Equations (8)–(10) using a Dancoff factor to consider the neighboring effect. C is obtained from the Dancoff factor (D) using D = 1/(1 + C):

$${\alpha }_{1,2}={\displaystyle \frac{(5C+6)\mp \sqrt{C^2+36C+36}}{2(C+1)}},$$

(8)

$${\beta }_1={\displaystyle \frac{(4C+6)/(C+1)-{\alpha }_1}{{\alpha }_2-{\alpha }_1}}, \mathrm{and}$$

(9)

$${\beta }_2=1-{\beta }_1.$$

(10)

A formula for a flux-weighted MG self-shielded cross section can be derived as

$${\sigma }_{i,x,g}^k={\displaystyle \frac{{\displaystyle \int {\sigma }_{i,x}^k(E){\varphi }_k(E)dE}}{{\displaystyle \int {\varphi }_k(E)dE}}}={\displaystyle \frac{{\displaystyle \sum _{m=1}^4{F}_m}{\displaystyle \sum _{n=1}^2{\beta }_n{R}_{i,x,g}^k({\sigma }_{i,b,g}^{n,m,k})}}{1-{\displaystyle \sum _{m=1}^4{F}_m}{\displaystyle \sum _{n=1}^2{\beta }_n\frac{R_{i,a,g}^k({\sigma }_{i,b,g}^{n,m,k})}{{\sigma }_{i,b,g}^{n,m,k}}}}}, \mathrm{and}$$

(11)

$${\sigma }_{i,b,g}^{n,m}={\displaystyle \frac{{\displaystyle \sum _{j=all}{N}_j{\lambda }_{j,g}{\sigma }_{j,p}}+{\alpha }_n/l_m}{N_i}},$$

(12)

where Ν_i is the atomic number density, ${\sigma }_{i,b,g}$ is a microscopic background cross section for nuclide i, and R_i,x,g is a resonance integral for reaction x, defined as

$$R_{i,x,g}({\sigma }_{i,b,g}^{nm})={\displaystyle \frac{{\sigma }_{i,x,g}{\sigma }_{i,b,g}^{nm}}{{\sigma }_{i,a,g}+{\sigma }_{i,b,g}^{nm}}}.$$

(13)

The Stoker–Weiss equation is used solely to adjust the radial shapes of cross sections, whereas the average self-shielded cross section for an entire fuel pellet is determined by the conventional ESSM. Therefore, the first step is to perform the conventional ESSM calculation to obtain (1) average macroscopic background cross sections over fuel and (2) microscopic self-shielded cross sections. The second step is to solve the Stoker–Weiss equation and apply the resulting radial cross section shapes to each radial ring, as follows:

$${\widehat{\sigma }}_{i,x,g}^k={\sigma }_{i,x,g}^k{\displaystyle \frac{{\displaystyle \sum _{k^{\prime }}{\sigma }_{i,x,g}^{k^{\prime }}({\sigma }_{i,b,g}^{k^{\prime },ESSM}){\varphi }_g^{k^{\prime }}}}{{\displaystyle \sum _{k^{\prime }}{\sigma }_{i,x,g}^{k^{\prime }}{\varphi }_g^{k^{\prime }}}}},\hspace{1em}{k}^{\prime }\in K,$$

(14)

where K denotes fuel pin identification, and k is a radial ring inside K.

SCALE/Polaris was improved to include options for self-shielding calculation, as provided in Table 4.

Table 4. SCALE/Polaris input options for ESSM.

Key	Option	Description	Example
Method	ASSM	Conventional ESSM without spatially dependent	Method = “ASSM”
	CELL	Cell Dancoff-based * ESSM without spatially dependent	Method = “CELL”
	IP	Conventional ESSM + spatially dependent	Method = “IP”
	CELL_IP	Cell Dancoff-based ESSM + spatially dependent	Method = “CELL_IP”

* Dancoff-based Wigner–Seitz approximation.

2.5. Material-Based Category and Library Improvement

The original ESSM implementation performs iterative fixed-source calculations, updating background and absorption cross sections for all materials simultaneously. This approach can result in negative equivalence cross sections and unphysical resonance interference between fuel and cladding or control rods. To address this issue, the ESSM implementation was improved to perform separate fixed-source calculations for each material, thereby avoiding negative equivalence cross sections and unphysical resonance interference. The ESSM material grouping capability [18] was developed, as summarized in Table 5.

Table 5. SCALE/Polaris input option for ESSM material grouping.

Parameter	Type	Details	Default
MGi	String	Material group name for ESSM group i. All materials in the model with a material ID that contains the material group name will have their ESSM escape cross section calculations performed together. The method used to perform these calculations will be designated by meti.	ALL
meti	String	The ESSM calculation method to be used by material group MGi. Acceptable values are either “G” for full group-wise treatment, or “I” for the Enhanced Neutron Current-based tabular “Interpolation” approximation method.	G
Ei	Real	Energy values in units of eV that specify the energies to be used for tabular interpolation. These values must be provided in ascending order.	0.1 1 10

2.6. AMPX Multigroup Cross Section Processing

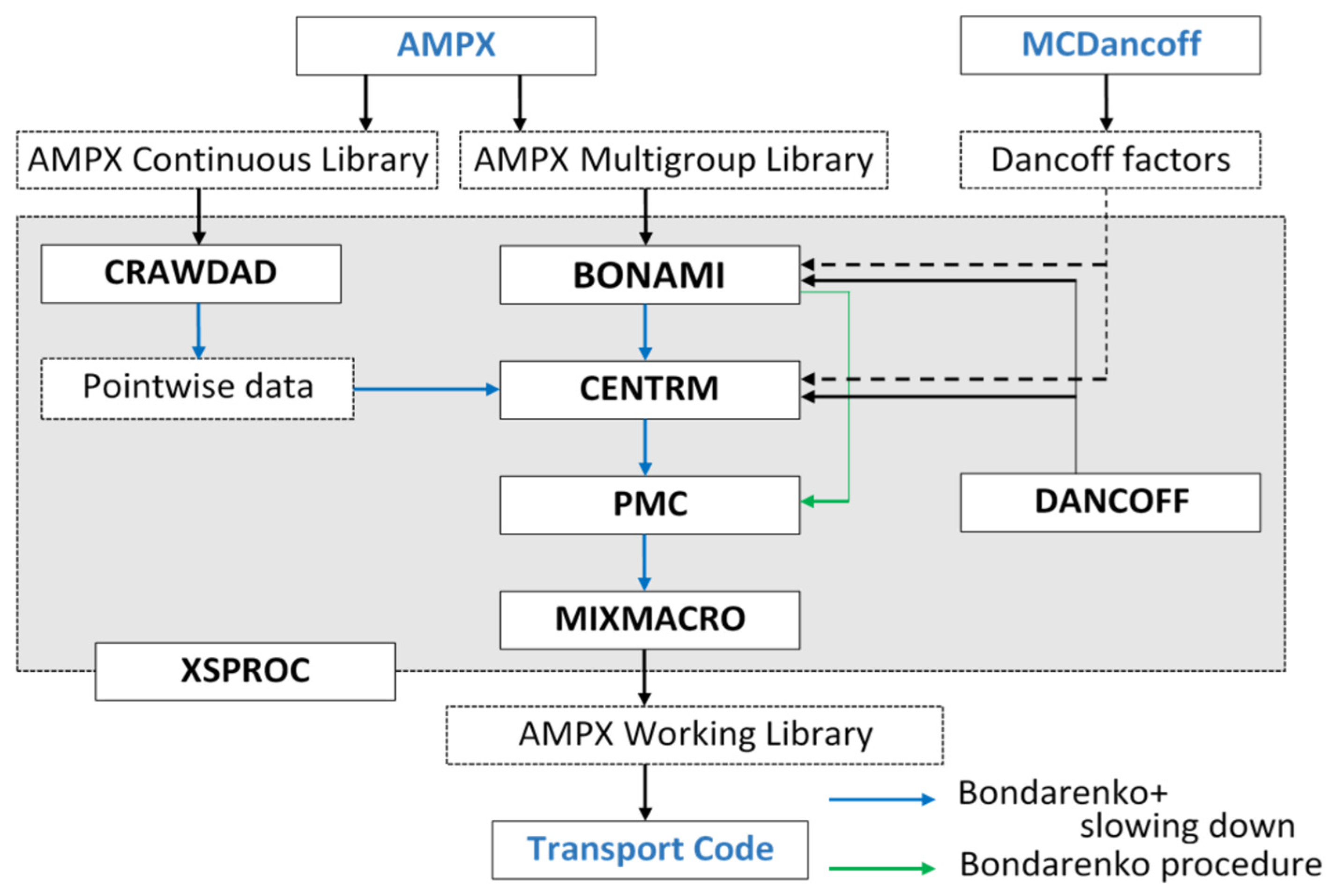
The SCALE neutron transport modules, including Polaris, NEWT, KENO, and Shift, require MG neutron cross sections to solve the Boltzmann transport equation and obtain the neutron flux distribution and eigenvalue. Evaluated nuclear data (e.g., ENDF/B) are processed to generate MG cross sections using AMPX-6 [3] and SCALE code packages. While SCALE transport modules such as NEWT, KENO, and Shift use effective self-shielded MG cross sections processed by SCALE/XSProc (Figure 4), the SCALE/Polaris lattice physics code directly uses the AMPX MG library. This library includes Bondarenko F-factors for various neutron reactions, defined as the ratios of resonance self-shielded cross sections to infinite dilution cross sections as a function of background cross sections for all energy groups, including both resolved and unresolved resonances. Resolved resonance F-factors are generated using the narrow resonance (NR) approximation, while unresolved resonance F-factors are generated by the probability table method based on the NR approximation.

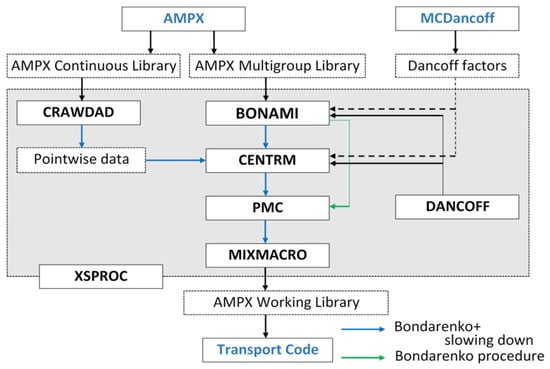
Figure 4. Flowchart of the XSProc procedure.

The AMPX MG library generation procedure includes six steps. (a) The AMPX MG library is generated using temperature-dependent pointwise (PW) weighting functions obtained from CENTRM PW slowing-down transport calculations. The resonance data are generated using the NR approximation. (b) IR parameters are generated, and the resonance data are updated with new data obtained from XSProc-CENTRM homogeneous slowing-down calculations using LAMBDA and IRFFACTOR-hom [19]. (c) Resonance data are updated with new data calculated by XSProc-CENTRM heterogeneous slowing-down calculations for important resonance nuclides using IRFFACTOR-het [19]. (d) Transport correction factors are generated for ¹H by performing a fixed-source transport calculation. (e) Epithermal and non-epithermal upscattering resonance data are generated for ²³⁸U using the CE SCALE Monte Carlo code CE-KENO [19] and the ESSM [5]. SPH factors are obtained and incorporated into the resonance data. (f) The final step is to use AJAX to generate the final AMPX MG library with data prepared in steps (a) through (f).

2.7. SPH Method for ²³⁸U Resonance Data

In performing coarse group transport calculations using the Bondarenko method for resonance self-shielding, three types of approximations are introduced as follows: (1) angle-independent total cross section, (2) P₀ flux moment-weighted scattering matrices, and (3) implicit resonance interference based on the Bondarenko iteration. To address these issues simultaneously, various SPH methods have been developed to conserve reaction rates between high-order solutions and low-order approximations.

Collapsing energy groups from fine to coarse introduces angle-dependent total cross sections and high-order flux moment-weighted scattering matrices. Because angular fluxes and high-order flux moments are problem-dependent, it is not possible to generate coarse group resonance data and scattering matrices that fully account for the angle dependence of nuclear data. In addition, self-shielded cross section tables are generated by considering resonance interference effects between nuclides such as ²³⁸U and ²³⁵U in the CENTRM PW slowing-down calculation. This approach can provide improved agreement for specific cases in MG resonance self-shielded cross sections or reaction rates between reference and Polaris solutions.

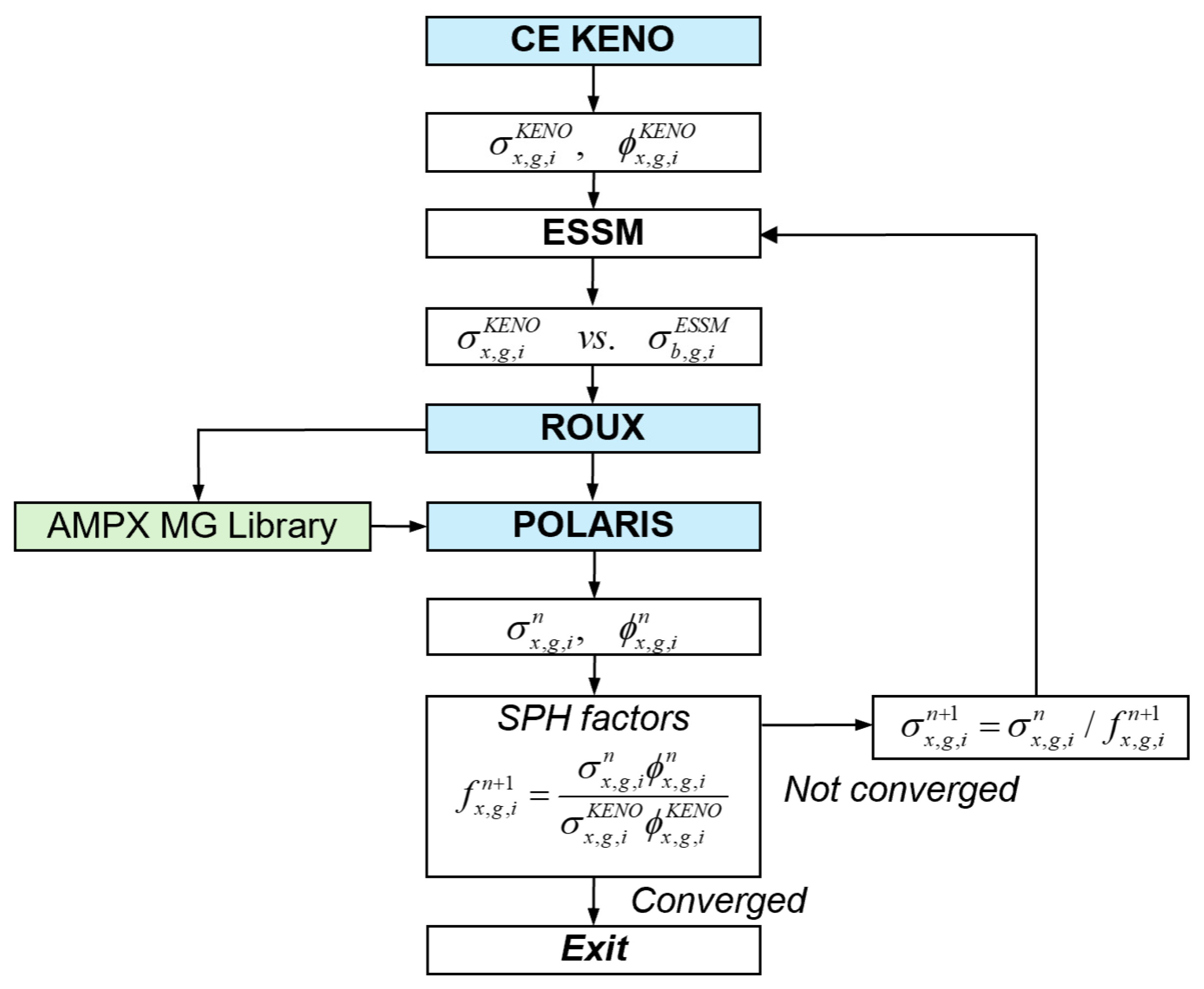
SPH was employed to address the issues described previously by conserving reaction rates between high-order reference solutions and low-order Polaris calculations. The procedure shown in Figure 5 begins with KENO models, including the same variation cases used in heterogeneous IRFFACTOR studies [19,20]. Next, the MG self-shielded cross sections are tallied, and the corresponding background cross sections are estimated using ESSM calculations to complete the self-shielded cross section tables. The updated resonance data are then incorporated into the AMPX MG library using ROUX. Finally, Polaris calculations are performed for the same variation cases to obtain the group-wise SPH factors, defined in Equations (15) and (16).

$$f_{x,g,i}^{n+1}={\displaystyle \frac{{\sigma }_{x,g,i}^n{\varphi }_{x,g,i}^n}{{\sigma }_{x,g,i}^{KENO}{\varphi }_{x,g,i}^{KENO}}},$$

(15)

$${\sigma }_{x,g,i}^{n+1}={\sigma }_{x,g,i}^n/f_{x,g,i}^{n+1},$$

(16)

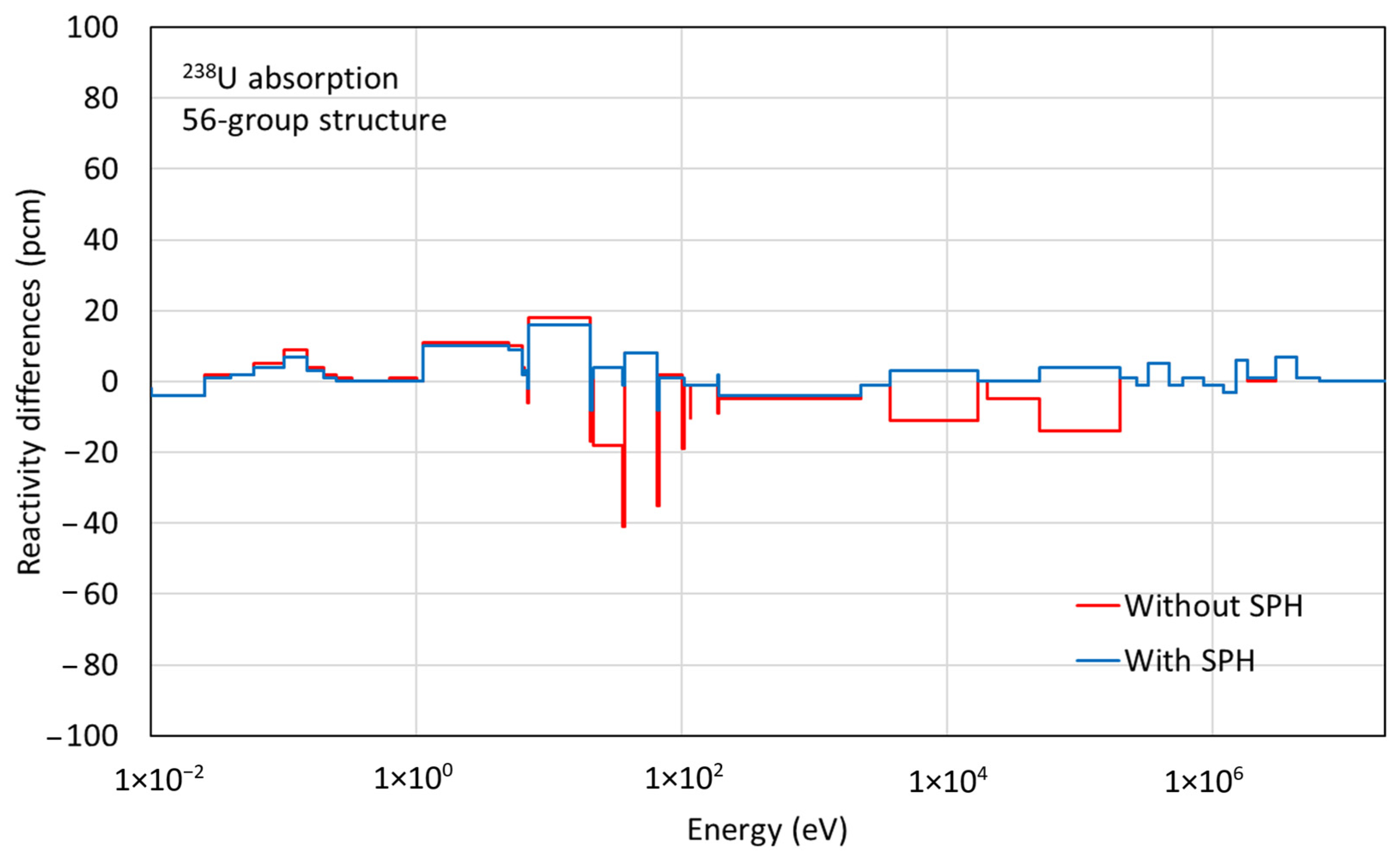
where ${\sigma }_{x,g,i}$ denotes a microscopic cross section of reaction x of nuclide i at group g, and ${\varphi }_{x,g,i}$ is the scalar flux. Figure 6 compares the 56-group absorption reaction rate differences in ²³⁸U compared to the CE Monte Carlo results with and without SPH factors for a single fuel pin, showing significant improvement when SPH factors are applied. New test ENDF/B-VII.1 AMPX 56- and 252-group libraries, incorporating SPH factors for ²³⁸U, were developed for this investigation.

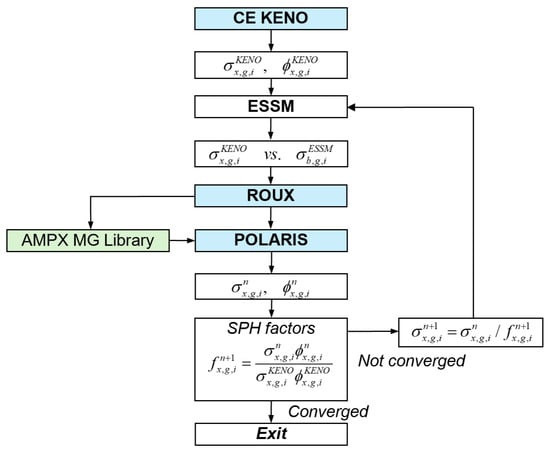
Figure 5. Flowchart of the SPH procedure.

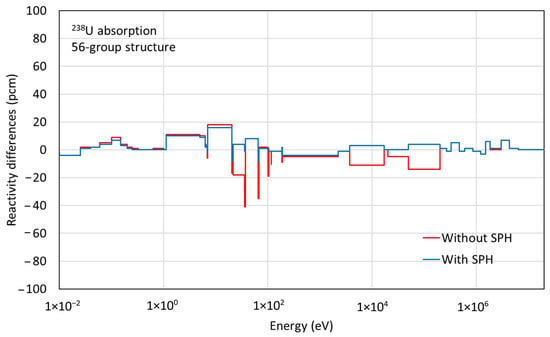
Figure 6. Comparisons of ²³⁸U 56-group reaction rates with and without SPH factors.

3. Benchmark Calculations and Results

3.1. Single-Pin Problem

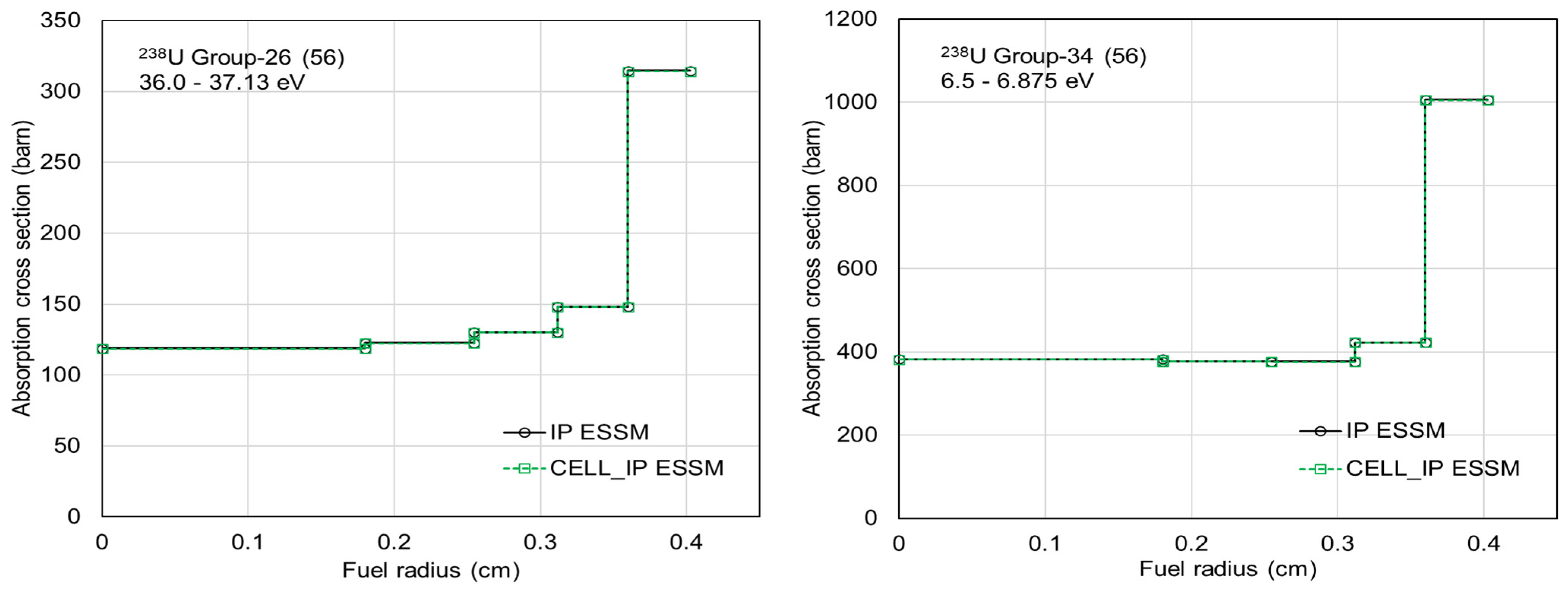
As indicated in Table 4, Polaris supports four ESSM options: ASSM, CELL, IP, and CELL_IP. While the ASSM and CELL options are based on the conventional ESSM, the IP and CELL_IP options support accurate calculation of spatially dependent self-shielded cross sections. The CELL and CELL_IP options provide faster self-shielding calculations compared with the ASSM and IP options, respectively. The same benchmark calculations used for Figure 2 were performed using the various ESSM options with the AMPX 56- and 252-group libraries. Figure 7 compares ring-dependent self-shielded absorption cross sections for group-134 (37.0–37.13 eV) and group-151 (6.5–6.75 eV) within the SCALE 252-group structure for ²³⁸U. The consistent ring-dependent self-shielded cross sections indicate that Polaris results with the CELL ESSM option are in agreement with results obtained using the ASSM ESSM option. Figure 8 compares ring-dependent self-shielded absorption cross sections for group-26 (37.0–37.13 eV) and group-34 (6.0–6.875 eV) within the SCALE 56-group structure for ²³⁸U. Similarly, the consistent ring-dependent self-shielded cross sections indicate that Polaris results with the CELL_IP ESSM option are in agreement with those obtained using the IP ESSM option.

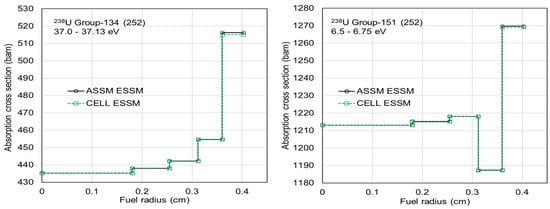
Figure 7. Comparison of ring-dependent self-shielded absorption cross sections between the ASSM and CELL ESSMs at 252-group structure for ²³⁸U.

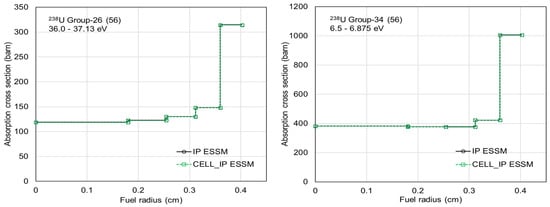
Figure 8. Comparison of ring-dependent self-shielded absorption cross sections between the IP and CELL_IP ESSMs at 56-group structure for ²³⁸U.

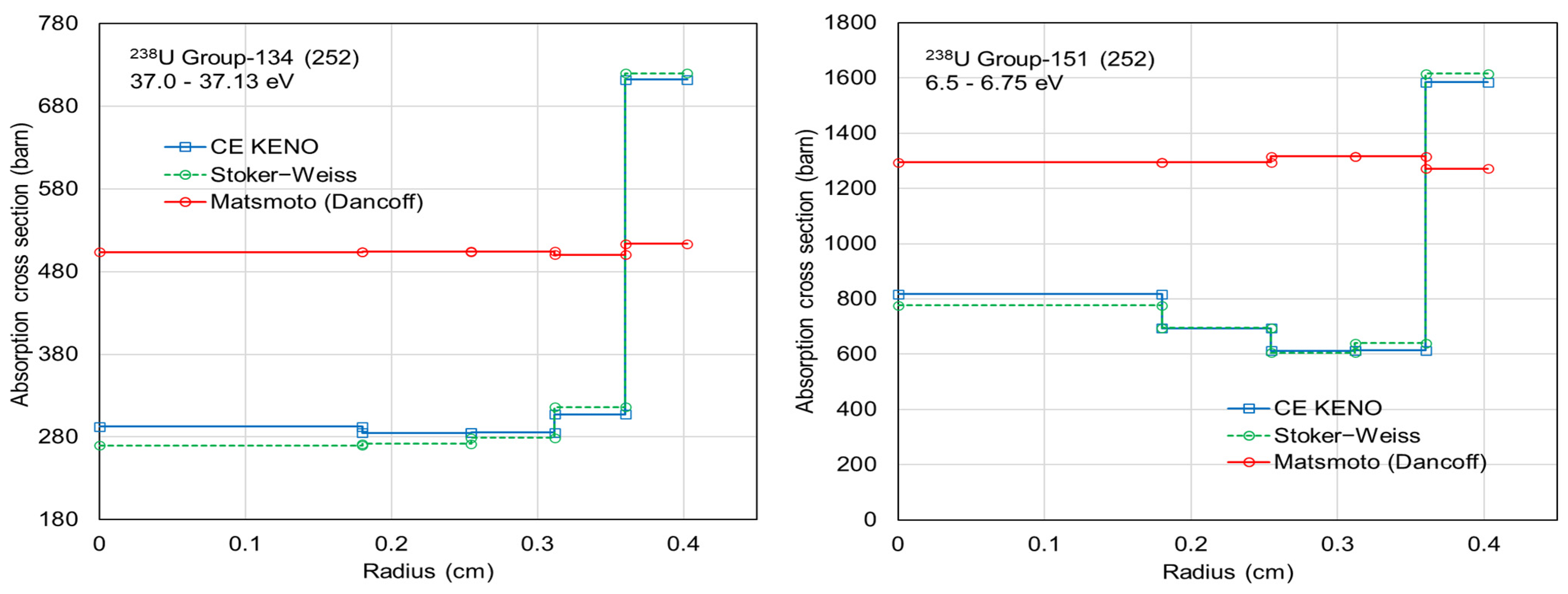
While Stoker and Weiss proposed a simple formula for a_n and b_n, Matsumoto et al. introduced Equations (8)–(10) incorporating the Dancoff factor to account for neighboring effects. Both approaches were implemented into Polaris, and a sensitivity calculation was performed for the two options. Figure 9 compares ring-dependent self-shielded cross sections using CELL_IP for groups 134 and 151 within the 252-group structure between the reference solutions and the Stoker–Weiss and Matsumoto procedures. The Dancoff factor was obtained from Equation (6) by performing a fixed-source calculation with a black absorber. While ring-dependent self-shielded cross sections obtained using the Matsumoto procedure are not consistent with the reference solution, those obtained using the Stoker–Weiss procedure are in very good agreement with the reference. Matsumoto et al. did not provide a clear definition of the Dancoff factors, and the unclear definition may have resulted in unphysical ring-dependent self-shielded cross sections.

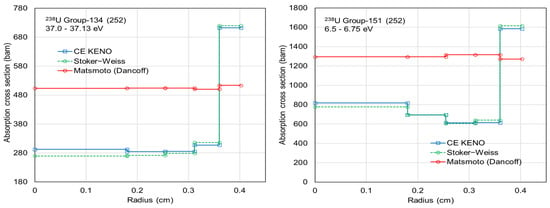
Figure 9. Comparison of ring-dependent self-shielded absorption cross sections between the Stoker–Weiss and Matsumoto procedures at 252-group structure for ²³⁸U.

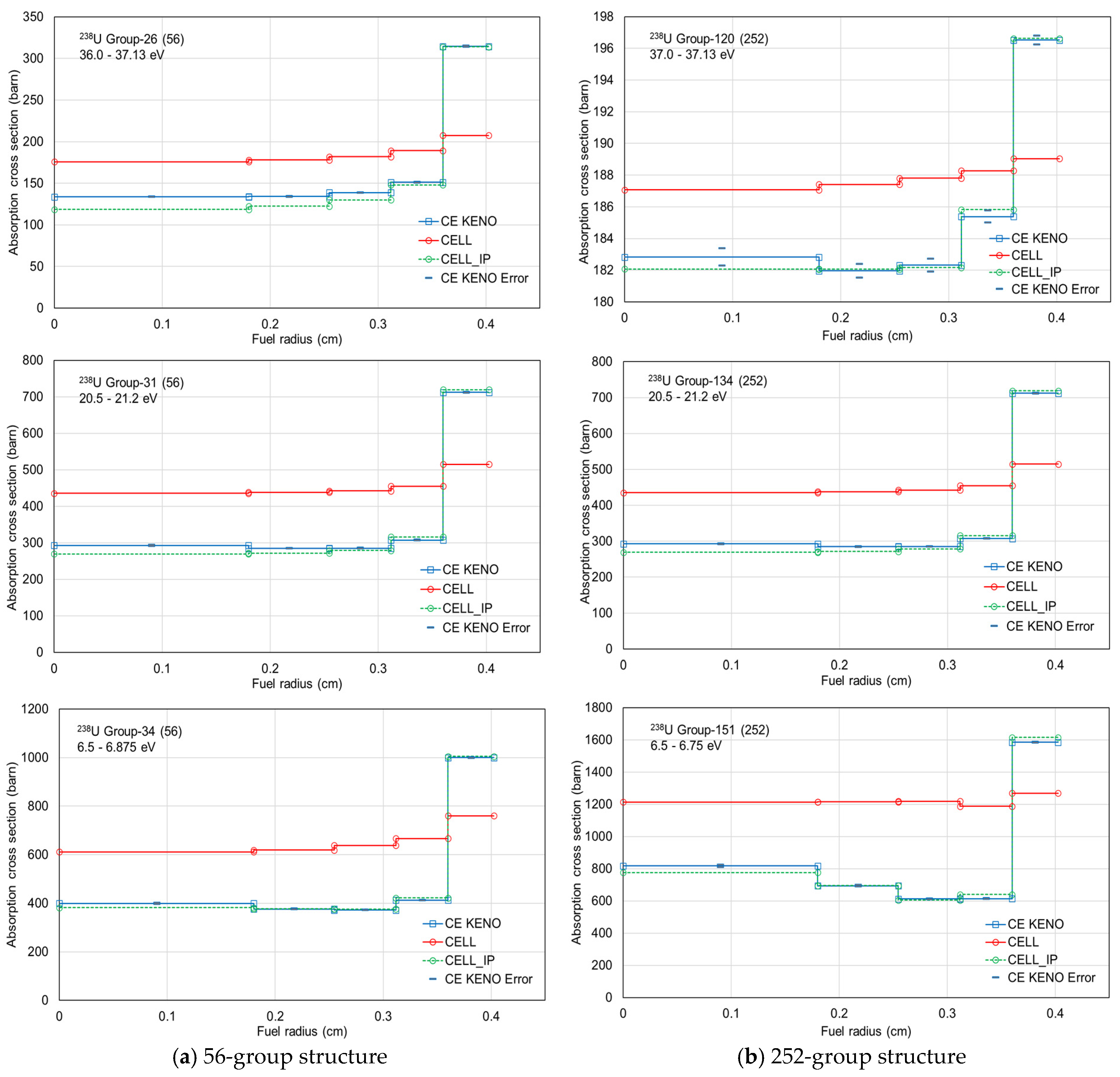
Since Figure 7 and Figure 8 demonstrate that the CELL and CELL_IP ESSM options correspond to the ASSM and IP ESSM options, respectively, the performance of CELL and CELL_IP for ring-dependent self-shielded cross sections was evaluated. Figure 10 compares ring-dependent self-shielded absorption cross sections for group-26 (36.0–37.13 eV), group-31 (20.5–21.2 eV), and group-34 (6.5–6.875 eV) within the SCALE 56-group structure, as well as for group-120 (37.0–37.13 eV), group-134 (20.5–21.2 eV), and group-151 (6.5–6.75 eV) within the SCALE 252-group structure for ²³⁸U. The ring-dependent self-shielded absorption cross sections obtained using the CELL_IP ESSM option are in very good agreement with the reference solutions.

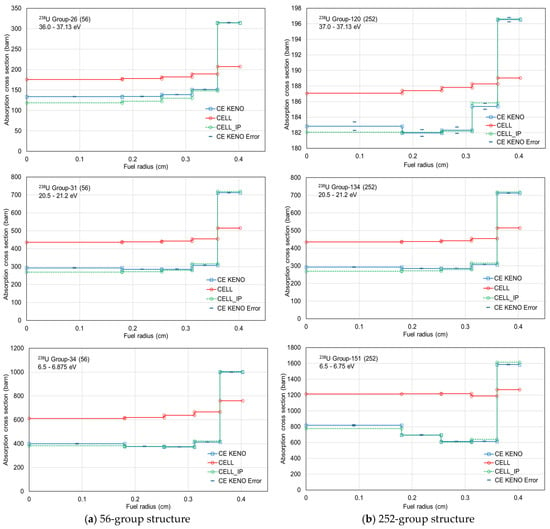
Figure 10. Comparison of ring-dependent self-shielded absorption cross sections between the CELL and CELL_IP ESSM options.

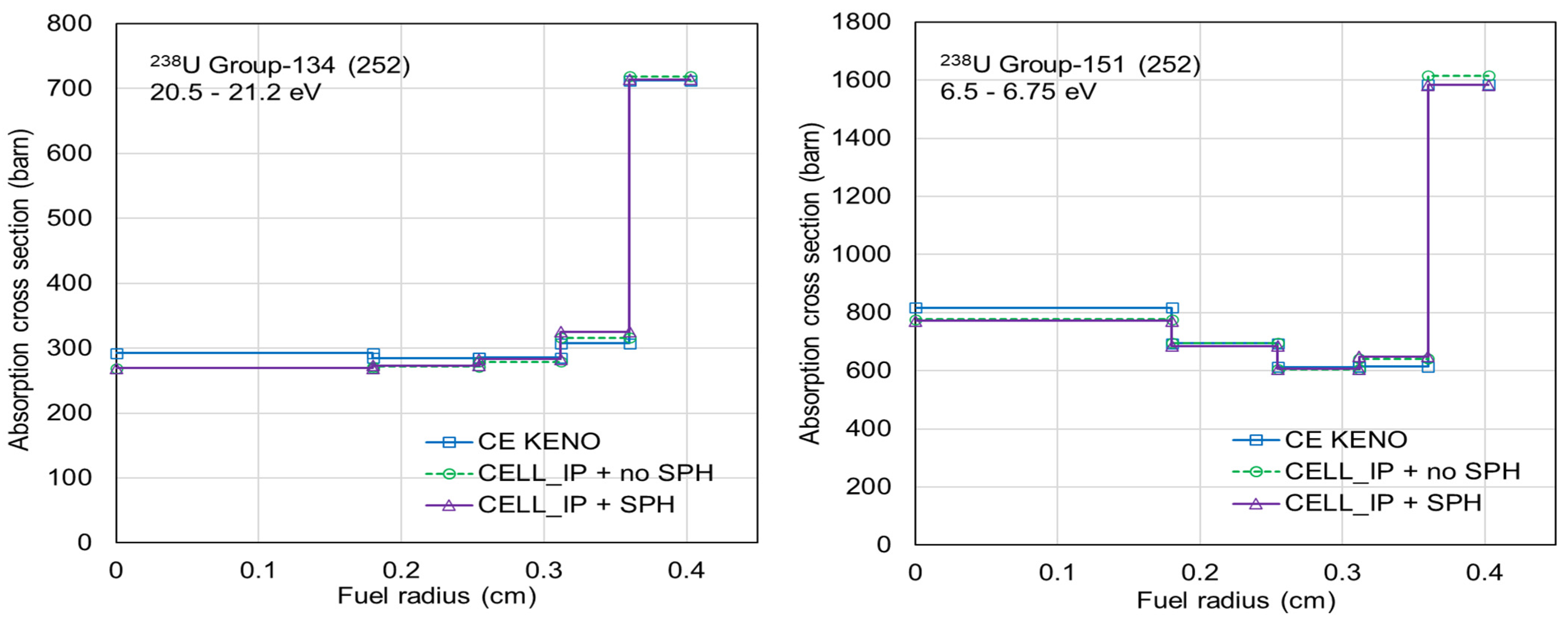
New test ENDF/B-VII.1 AMPX 56- and 252-group libraries were developed by incorporating the ²³⁸U SPH factors into the resonance self-shielded cross sections. Polaris benchmark calculations with the CELL_IP ESSM option were then performed using these ENDF/B-VII.1 AMPX 56- and 252-group libraries, both with and without the SPH factors for ²³⁸U. Figure 11 compares ring-dependent self-shielded cross sections for group-134 (20.5–21.2 eV) and group-151 (6.5–6.75 eV) for ²³⁸U within the SCALE 252-group structure, illustrating the effect of including the SPH factors, with only slight differences observed.

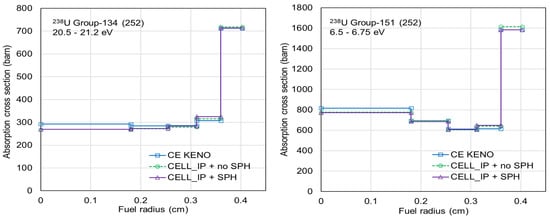
Figure 11. Comparison of ring-dependent self-shielded absorption cross sections between the CELL_IP ESSMs with and without SPH factors.

3.2. VERA Core Physics Benchmark Progression Problems

The VERA core physics benchmark progression problems used in this study were developed to provide a framework for developing and demonstrating advanced capabilities in reactor physics methods and software [21]. Most of the benchmark data are based on the initial core loading of Watts Bar Nuclear Plant, Unit 1, a Westinghouse-designed 17 × 17 PWR that is representative of reactors built in the United States during the 1980s and 1990s.

For this study, the single-physics 2D benchmark problems were selected to evaluate the neutron cross section library for the CASL VERA neutronics simulator MPACT. Table 6 lists the VERA progression problems used for benchmarking. Detailed specifications of geometry and composition are provided by Godfrey [21]. Reference solutions were obtained using CE KENO with ENDF/B-VII.1.

Table 6. Description of the VERA progression problems.

Case	Description	235U wt %	Temperature (K)			Moderator
			Mod.	Clad	Fuel	g/cm3	PPM
1A	PWR pin	3.1	565	565	565	0.743	1300
1B	PWR pin	3.1	600	600	600	0.661	1300
1C	PWR pin	3.1	600	600	900	0.661	1300
1D	PWR pin	3.1	600	600	1200	0.661	1300
1E	PWR pin + IFBA	3.1	600	600	600	0.743	1300
2A	PWR FA, no BP	3.1	565	565	565	0.743	1300
2B	PWR FA, no BP	3.1	600	600	600	0.661	1300
2C	PWR FA, no BP	3.1	600	600	900	0.661	1300
2D	PWR FA, no BP	3.1	600	600	1200	0.661	1300
2E	PWR FA + 12 Pyrex	3.1	600	600	600	0.743	1300
2F	PWR FA + 24 Pyrex	3.1	600	600	600	0.743	1300
2G	PWR FA + 24 AgInCd control rod	3.1	600	600	600	0.743	1300
2H	PWR FA + 24 B4C control rod	3.1	600	600	600	0.743	1300
2I	PWR FA + instrument thimble	3.1	600	600	600	0.743	1300
2J	PWR FA + instrument thimble + 24 Pyrex	3.1	600	600	600	0.743	1300
2K	PWR FA + zoned enrichment + 24 Pyrex	3.1/3.6	600	600	600	0.743	1300
2L	PWR FA + 80 IFBA	3.1	600	600	600	0.743	1300
2M	PWR FA + 128 IFBA	3.1	600	600	600	0.743	1300
2N	PWR FA + 104 IFBA + 20 WABA	3.1	600	600	600	0.743	1300
2O	PWR FA + 12 gadolinia	1.8/3.1	600	600	600	0.743	1300
2P	PWR FA + 24 gadolinia	1.8/3.1	600	600	600	0.743	1300

Benchmark calculations were performed with various ESSM options (ASSM, CELL, IP, and CELL_IP) in Polaris using the ENDF/B-VII.1 AMPX 56- and 252-group libraries, both with and without SPH factors for ²³⁸U. Default ray options were applied for the ESSM and eigenvalue MOC calculations, except for the IFBA (Integral Fuel Burnable Absorber) fuel pin and assembly cases (1E, 2L, 2M, and 2N), where a ray spacing of 0.001 cm was used. In addition, three and five intra-pin radial rings were modeled in Polaris for the UO₂ fuel and gadolinia rods, respectively. All Polaris calculations were performed with P₂ scattering. For the AMPX 56- and 252-group libraries without SPH factors, no material grouping was applied, whereas for the corresponding libraries with SPH factors for ²³⁸U, material grouping for fuels, cladding, and control rods was employed.

Table 7, Table 8, Table 9 and Table 10 present the benchmark calculation results, comparing the eigenvalues and pin power distributions obtained with Polaris against those from CE-KENO. The eigenvalues and pin power distributions show very good consistency across the ASSM, CELL, IP, and CELL_IP ESSM options. Although the Polaris ASSM and CELL ESSMs yield less accurate spatially dependent self-shielded cross sections, they still provide excellent agreement in multiplication factors with CE-KENO.

Table 7. VERA benchmark results with the AMPX 56-group library without SPH.

Case	KENO	Shift	ASSM			CELL			IP			CELL_IP
			Δk a	S.D. b	Max. c	Dk	S.D.	Max.	Δk	S.D.	Max.	Δk	S.D.	Max.
1a	1.18692	1	115			113			86			83
1b	1.18211	−25	132			120			98			85
1c	1.17131	−4	93			80			57			44
1d	1.16245	−7	104			91			64			51
1e	0.77165	7	−111			−112			−129			−130
2a	1.18186	28	67	0.13	−0.31	58	0.13	−0.31	47	0.13	−0.31	38	0.13	−0.31
2b	1.18315	2	90	0.12	0.30	75	0.12	0.29	66	0.12	0.30	51	0.12	0.29
2c	1.17357	9	80	0.09	0.26	65	0.09	0.26	54	0.09	0.26	38	0.09	0.26
2d	1.16529	−22	73	0.12	−0.32	57	0.12	−0.32	43	0.12	−0.32	27	0.12	−0.32
2e	1.06933	−4	31	0.12	−0.42	28	0.13	−0.42	12	0.12	−0.42	8	0.13	−0.42
2f	0.97571	1	−7	0.16	−0.42	−5	0.16	−0.42	−25	0.16	−0.42	−23	0.16	−0.43
2g	0.84798	6	−84	0.14	0.41	151	0.16	0.38	−100	0.14	0.41	136	0.16	0.38
2h	0.78820	17	72	0.22	0.47	39	0.21	0.47	58	0.22	0.47	25	0.21	0.47
2i	1.17964	−6	64	0.10	−0.34	56	0.10	−0.34	44	0.10	−0.34	35	0.10	−0.34
2j	0.97498	−26	−7	0.17	−0.39	−4	0.17	−0.40	−25	0.17	−0.39	−22	0.17	−0.40
2k	1.01985	17	14	0.15	−0.54	22	0.15	−0.54	−2	0.15	−0.54	5	0.15	−0.54
2l	1.01863	7	42	0.13	0.29	35	0.13	0.29	24	0.13	0.29	16	0.13	0.29
2m	0.93877	−1	38	0.14	−0.39	32	0.14	−0.39	21	0.14	−0.39	15	0.14	−0.39
2n	0.86951	−13	27	0.19	−0.40	20	0.19	−0.40	10	0.19	−0.40	4	0.19	−0.40
2o	1.04737	15	92	0.12	0.25	54	0.12	−0.25	78	0.12	0.25	40	0.12	−0.25
2p	0.92678	−11	61	0.17	0.52	3	0.18	0.57	52	0.16	0.51	−6	0.17	0.56

^a Kinf. difference in pcm (Polaris–KENO), ^b standard deviation in percentage for pin power distribution, ^c maximum pin power difference in percentage.

Table 8. VERA benchmark results with the AMPX 56-group library with SPH.

Case	KENO	Shift	ASSM			CELL			IP			CELL_IP
			Δk	S.D.	Max.	Δk	S.D.	Max.	Δk	S.D.	Max.	Δk	S.D.	Max.
1a	1.18692	1	32			28			−3			−7
1b	1.18211	−25	71			59			30			17
1c	1.17131	−4	55			41			17			3
1d	1.16245	−7	66			52			29			15
1e	0.77165	7	−104			−105			−125			−126
2a	1.18186	28	−26	0.13	−0.31	−49	0.13	−0.31	−49	0.13	−0.31	−73	0.13	−0.31
2b	1.18315	2	18	0.12	0.30	−16	0.12	0.29	−11	0.12	0.30	−45	0.12	0.29
2c	1.17357	9	29	0.09	0.26	−6	0.09	0.26	3	0.09	0.26	−32	0.09	0.26
2d	1.16529	−22	19	0.12	−0.31	−15	0.12	−0.31	−5	0.12	−0.31	−40	0.12	−0.31
2e	1.06933	−4	−34	0.12	−0.41	−50	0.12	−0.40	−56	0.12	−0.41	−73	0.12	−0.40
2f	0.97571	1	−50	0.15	−0.41	−60	0.15	−0.42	−71	0.15	−0.41	−81	0.15	−0.42
2g	0.84798	6	−78	0.21	0.50	−123	0.20	0.48	−96	0.21	0.50	−143	0.20	0.48
2h	0.78820	17	50	0.20	−0.46	17	0.18	−0.43	33	0.20	−0.46	0	0.18	−0.43
2i	1.17964	−6	−26	0.10	−0.34	−49	0.10	−0.34	−49	0.10	−0.34	−73	0.10	−0.34
2j	0.97498	−26	−48	0.16	−0.38	−58	0.16	−0.37	−70	0.16	−0.38	−80	0.16	−0.37
2k	1.01985	17	−29	0.15	−0.53	−40	0.14	−0.52	−49	0.15	−0.53	−60	0.14	−0.53
2l	1.01863	7	−23	0.13	0.30	−30	0.13	0.30	−44	0.13	0.30	−51	0.13	0.30
2m	0.93877	−1	−14	0.14	−0.39	−16	0.14	−0.39	−34	0.14	−0.39	−36	0.14	−0.39
2n	0.86951	−13	−16	0.18	−0.37	−14	0.17	−0.36	−35	0.18	−0.37	−33	0.17	−0.36
2o	1.04737	15	18	0.11	0.26	−37	0.12	−0.25	−3	0.11	0.26	−58	0.12	−0.25
2p	0.92678	−11	5	0.16	0.51	−73	0.17	0.55	−14	0.16	0.51	−91	0.17	0.55

Table 9. VERA benchmark results with the AMPX 252-group library without SPH.

Case	KENO	Shift	ASSM			CELL			IP			CELL_IP
			Δk	S.D.	Max.	Δk	S.D.	Max.	Δk	S.D.	Max.	Δk	S.D.	Max.
1a	1.18692	1	13			9			−4			−8
1b	1.18211	−25	17			7			−3			−14
1c	1.17131	−4	−8			−19			−27			−37
1d	1.16245	−7	15			4			−4			−15
1e	0.77165	7	−73			−75			−83			−85
2a	1.18186	28	−15	0.13	−0.32	−31	0.13	−0.32	−24	0.13	−0.32	−40	0.13	−0.32
2b	1.18315	2	−7	0.12	0.30	−28	0.12	0.30	−19	0.12	0.30	−39	0.12	0.30
2c	1.17357	9	−3	0.10	0.26	−23	0.10	0.26	−13	0.10	0.26	−34	0.10	0.26
2d	1.16529	−22	2	0.12	−0.32	−18	0.12	−0.32	−9	0.12	−0.32	−29	0.12	−0.32
2e	1.06933	−4	−13	0.12	−0.40	−25	0.12	−0.40	−21	0.12	−0.40	−33	0.12	−0.40
2f	0.97571	1	−21	0.14	−0.41	−30	0.14	−0.41	−29	0.14	−0.41	−38	0.14	−0.41
2g	0.84798	6	−45	0.13	0.33	67	0.14	−0.33	−52	0.13	0.33	61	0.14	−0.33
2h	0.78820	17	51	0.17	−0.44	27	0.16	−0.45	45	0.17	−0.44	21	0.16	−0.45
2i	1.17964	−6	−14	0.10	−0.34	−29	0.10	−0.34	−22	0.10	−0.34	−38	0.10	−0.34
2j	0.97498	−26	−20	0.15	−0.36	−29	0.15	−0.36	−28	0.15	−0.36	−37	0.15	−0.36
2k	1.01985	17	−13	0.13	−0.50	−19	0.14	−0.51	−21	0.14	−0.50	−27	0.14	−0.51
2l	1.01863	7	13	0.13	0.30	−1	0.13	0.30	4	0.13	0.30	−9	0.13	0.30
2m	0.93877	−1	32	0.14	−0.38	20	0.14	−0.38	24	0.14	−0.38	12	0.14	−0.38
2n	0.86951	−13	24	0.17	−0.35	16	0.17	−0.36	16	0.17	−0.35	8	0.17	−0.36
2o	1.04737	15	53	0.11	−0.25	31	0.12	−0.24	46	0.11	−0.25	24	0.11	−0.24
2p	0.92678	−11	49	0.16	0.52	23	0.16	0.53	44	0.16	0.52	18	0.16	0.53

Table 10. VERA benchmark results with the AMPX 252-group library with SPH.

Case	KENO	Shift	ASSM			CELL			IP			CELL_IP
			Δk	S.D.	Max.	Δk	S.D.	Max.	Δk	S.D.	Max.	Δk	S.D.	Max.
1a	1.18692	1	−16			−20			−37			−41
1b	1.18211	−25	3			−8			−21			−33
1c	1.17131	−4	−21			−32			−42			−54
1d	1.16245	−7	2			−9			−20			−31
1e	0.77165	7	−27			−30			−39			−42
2a	1.18186	28	−54	0.13	−0.32	−71	0.13	−0.32	−67	0.13	−0.32	−85	0.13	−0.32
2b	1.18315	2	−32	0.12	0.3	−56	0.12	0.3	−48	0.12	0.30	−72	0.12	0.30
2c	1.17357	9	−25	0.1	0.26	−49	0.1	0.26	−39	0.10	0.26	−63	0.10	0.26
2d	1.16529	−22	−21	0.12	−0.32	−44	0.12	−0.32	−36	0.12	−0.32	−59	0.12	−0.32
2e	1.06933	−4	−24	0.12	−0.38	−38	0.12	−0.38	−36	0.12	−0.38	−50	0.12	−0.38
2f	0.97571	1	−10	0.14	−0.4	−21	0.14	−0.4	−22	0.14	−0.40	−33	0.14	−0.40
2g	0.84798	6	145	0.14	0.31	106	0.13	0.3	136	0.14	0.31	96	0.13	0.30
2h	0.78820	17	68	0.16	−0.44	38	0.15	−0.45	58	0.16	−0.44	29	0.15	−0.45
2i	1.17964	−6	−52	0.1	−0.33	−69	0.1	−0.34	−65	0.10	−0.33	−82	0.10	−0.34
2j	0.97498	−26	−9	0.14	−0.34	−20	0.14	−0.34	−20	0.14	−0.34	−31	0.14	−0.34
2k	1.01985	17	8	0.13	−0.49	−4	0.13	−0.49	−3	0.13	−0.49	−15	0.13	−0.49
2l	1.01863	7	4	0.13	0.31	−8	0.13	0.31	−8	0.13	0.31	−19	0.13	0.31
2m	0.93877	−1	37	0.14	−0.39	29	0.14	−0.39	26	0.14	−0.39	17	0.14	−0.39
2n	0.86951	−13	48	0.16	−0.34	41	0.16	−0.34	37	0.16	−0.34	31	0.16	−0.34
2o	1.04737	15	38	0.11	−0.26	17	0.12	−0.25	28	0.11	−0.26	7	0.12	−0.25
2p	0.92678	−11	54	0.16	0.52	30	0.16	0.52	46	0.16	0.52	22	0.16	0.52

Table 11 compares the computing times of the ASSM, CELL, IP, and CELL_IP ESSM options using the AMPX 56- and 252-group libraries. The additional computing time required for spatially dependent self-shielding calculations is negligible, as is the associated memory overhead. The cell Dancoff-based Wigner–Seitz approximation for ESSM (CELL and CELL_IP) significantly enhances computational efficiency, achieving speedup factors of approximately 8 for fuel pins and greater than 10 for assemblies, without loss of accuracy.

Table 11. Comparison of computing times.

Case	56-Group				252-Group
	ASSM	CELL	IP	CELL_IP	ASSM	CELL	IP	CELL_IP
1A	0.17	0.02 (8) *	0.17	0.02 (8)	0.73	0.09 (8)	0.82	0.09 (8)
1B	0.17	0.02 (8)	0.17	0.02 (8)	0.74	0.09 (8)	0.83	0.09 (8)
1C	0.18	0.02 (8)	0.17	0.02 (8)	0.72	0.09 (8)	0.83	0.09 (8)
1D	0.17	0.02 (8)	0.17	0.02 (8)	0.73	0.09 (8)	0.82	0.09 (8)
1E	0.18	0.02 (7)	0.18	0.02 (8)	0.79	0.10 (8)	0.91	0.10 (8)
2A	10.86	1.09 (10)	11.45	1.07 (10)	54.98	4.70 (12)	54.03	4.39 (13)
2B	11.26	1.08 (10)	11.01	1.10 (10)	57.22	4.50 (13)	53.28	4.62 (12)
2C	10.71	1.07 (10)	10.68	1.08 (10)	53.39	4.73 (11)	53.01	4.63 (12)
2D	10.59	1.16 (9)	10.46	1.08 (10)	53.99	4.70 (11)	54.02	4.70 (11)
2E	12.26	1.16 (11)	12.03	1.09 (11)	58.22	4.65 (13)	57.32	4.63 (13)
2F	12.74	1.08 (12)	12.24	1.08 (12)	59.93	4.65 (13)	61.13	4.50 (13)
2G	12.65	1.23 (10)	12.43	1.22 (10)	65.44	5.42 (12)	63.14	5.35 (12)
2H	11.98	1.19 (10)	12.02	1.22 (10)	58.98	5.22 (11)	59.26	5.09 (12)
2I	11.79	1.07 (11)	11.51	1.07 (11)	59.77	4.62 (13)	58.63	4.71 (13)
2J	12.54	1.13 (11)	12.46	1.08 (12)	59.54	4.66 (13)	60.89	4.58 (13)
2K	12.55	1.03 (12)	12.58	1.03 (12)	59.86	4.39 (14)	60.39	4.48 (13)
2L	11.24	1.13 (10)	11.93	1.12 (10)	65.47	3.69 (18)	61.83	4.15 (16)
2M	11.91	1.15 (10)	11.35	1.14 (10)	74.43	4.05 (18)	66.35	5.23 (14)
2N	11.97	1.17 (10)	13.07	1.14 (10)	65.06	3.98 (16)	62.55	4.64 (14)
2O	11.41	1.14 (10)	11.25	1.12 (10)	58.68	4.94 (12)	58.27	4.86 (12)
2P	11.38	1.20 (10)	11.42	1.18 (10)	59.66	5.17 (12)	59.27	5.00 (12)

* Value in parenthesis is factor of speedup compared with ASSM.

3.3. Nonuniform and Uniform Fuel Temperature Benchmark Problems

Seoul National University developed a benchmark suite for intra-pellet uniform and nonuniform temperature distribution cases [22]. Table 12 provides the geometrical and compositional specifications, including dimensions, nuclides, and atomic number densities. Table 13 shows the nonuniform temperature profiles as functions of power and average fuel temperature.

Table 12. Geometrical and compositional data.

Material	Outer Radius (cm)	Atomic Number Density (Atoms/Barn-cm)
3.0 wt % UO2	0.4127 (5 equivalent volume zones)	235U	7.13479 × 10−4	16O	4.69825 × 10−2
		238U	2.27778 × 10−2
Gap	0.4203	16O	1.00000 × 10−8
Clad	0.4862	90Zr	2.22157 × 10−2	94Zr	7.18475 × 10−3
		91Zr	4.79136 × 10−3	96Zr	1.13334 × 10−3
		92Zr	7.24405 × 10−3
Coolant	1.2870 Pitch	1H	4.65690 × 10−2	16O	2.32840 × 10−2

Table 13. Nonuniform temperature profiles as a function of power.

		Temperature (K)
Power Level (%)		50	75	100	125	150	175	200
Pellet	1	787.4	897.7	1017.9	1148.2	1288.2	1437.7	1596.3
	2	754.7	843.7	939.3	1041.7	1150.6	1266.0	1387.5
	3	723.1	792.2	865.1	942.0	1022.7	1107.3	1195.6
	4	683.0	728.3	774.9	823.2	873.0	924.3	977.1
	5	669.2	708.3	748.4	789.4	831.4	874.3	918.2
	Average	723.5	794.0	869.1	948.9	1033.2	1121.9	1214.9
Gap		606.1	610.2	614.0	617.7	621.2	624.7	628.1
Clad		606.1	610.2	614.0	617.7	621.2	624.7	628.1
Coolant		586.7	586.7	586.7	586.7	586.7	586.7	586.7

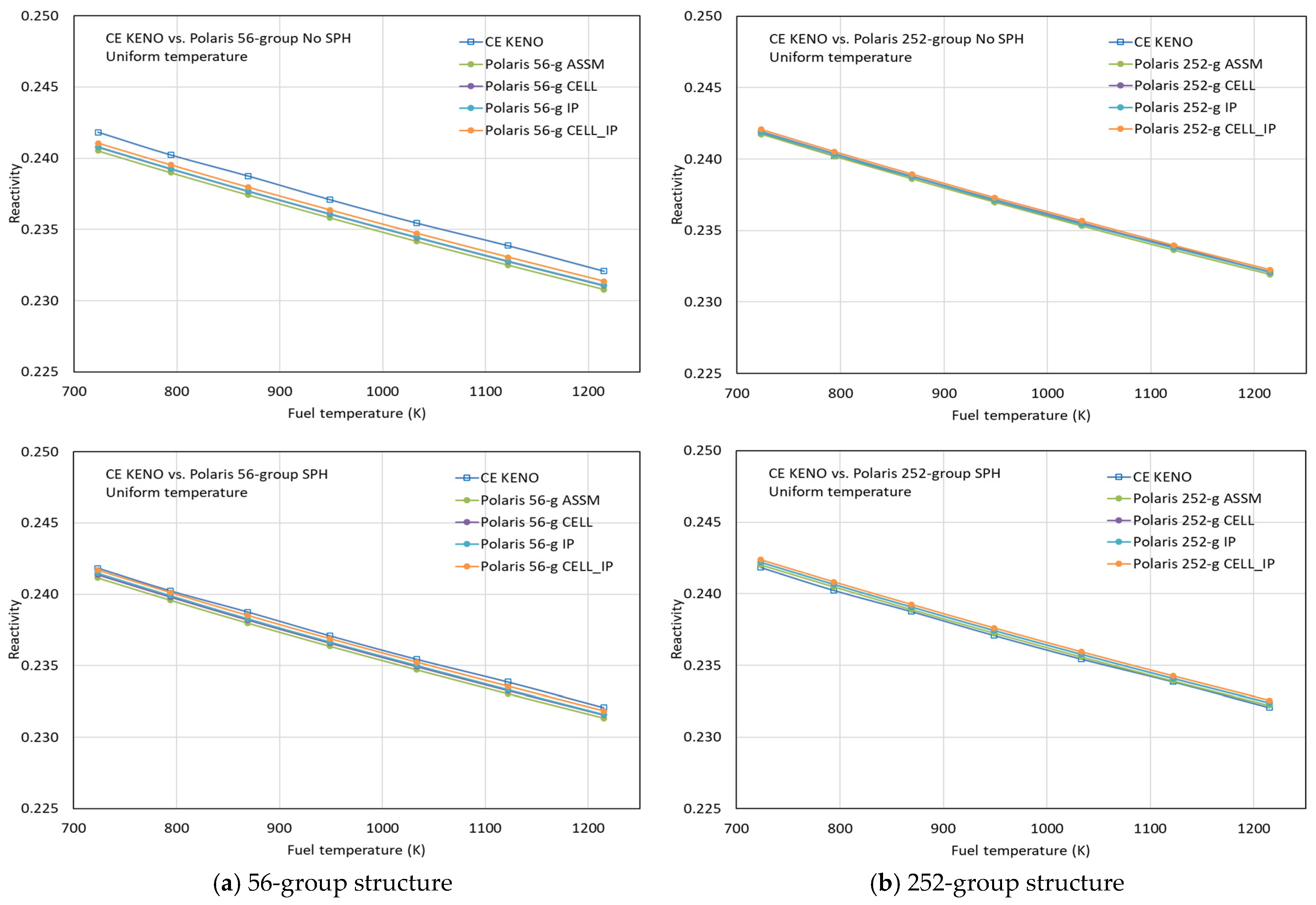
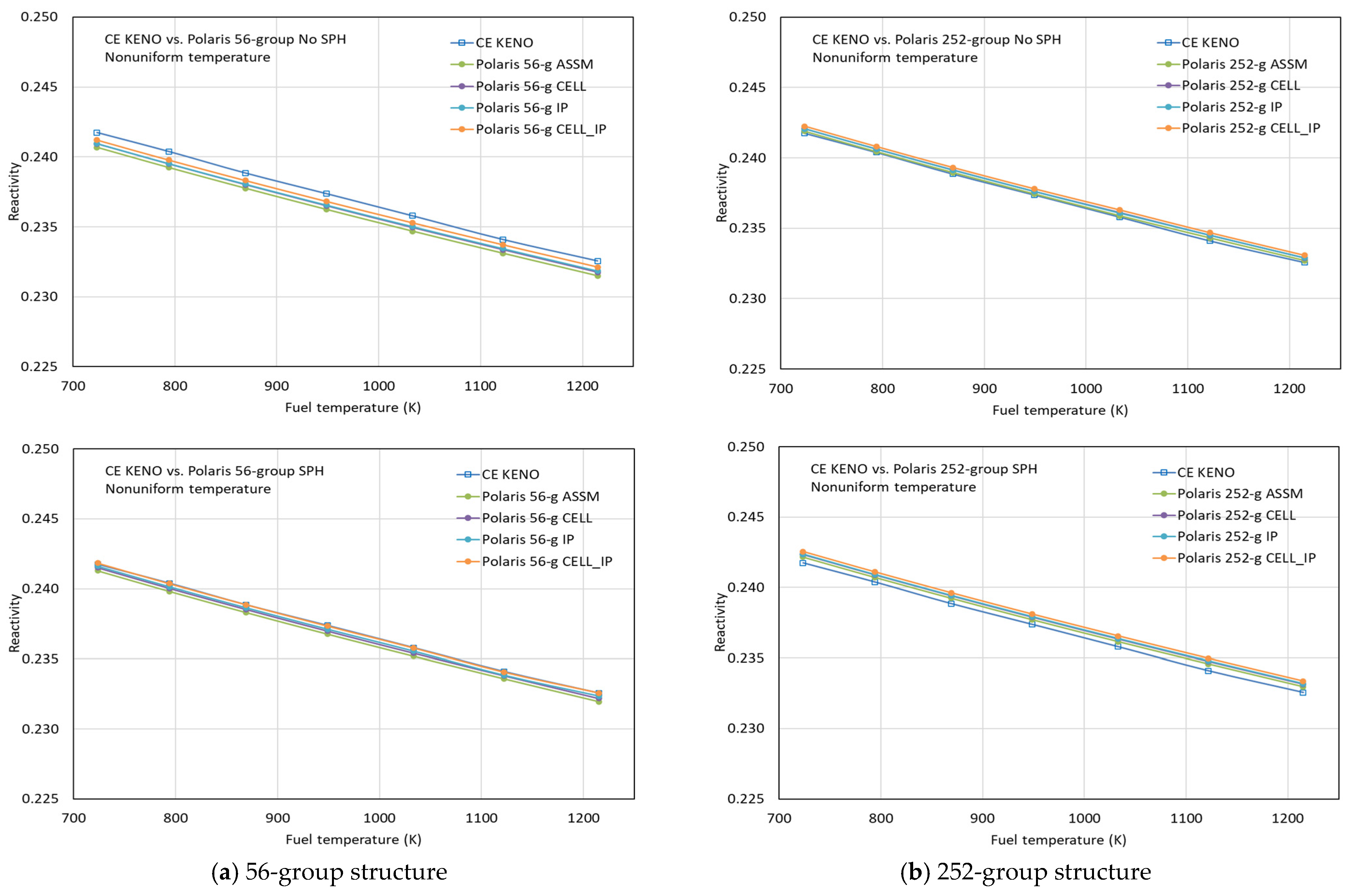
Benchmark calculations were performed for uniform and nonuniform temperature profiles using Polaris with P₂ scattering and various ESSM options, including ASSM, CELL, IP, and CELL_IP. Figure 12 compares the reactivities for the uniform temperature profile obtained by CE KENO and Polaris with the different ESSM options, using the ENDF/B-VII.1 AMPX 56- and 252-group libraries with and without considering SPH factors for ²³⁸U. The Polaris results with the various ESSM options are highly consistent with the CE KENO results, with some improvement observed in the AMPX 56-group results when SPH factors are applied.

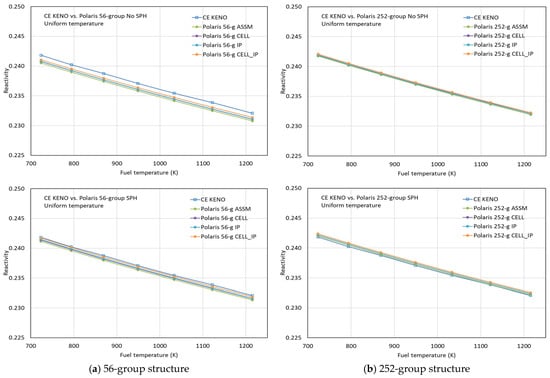
Figure 12. Comparison of reactivities for the uniform temperature distributions.

Figure 13 compares the reactivities for the nonuniform temperature profile obtained by CE KENO and Polaris with the ASSM, CELL, IP, and CELL_IP options, again using the ENDF/B-VII.1 AMPX 56- and 252-group libraries with and without SPH factors for ²³⁸U. The Polaris results show very good consistency with the CE KENO results. A similar improvement is observed for the nonuniform temperature profile in the AMPX 56-group results when SPH factors are applied. Strictly speaking, a fully spatially dependent ESSM capability for nonuniform temperature profiles could not be implemented in Polaris because of limitations in the Polaris metadata structure.

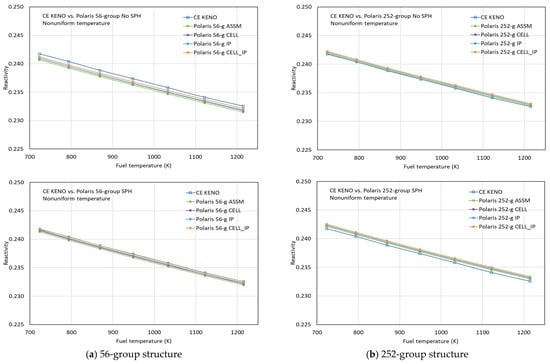
Figure 13. Comparison of reactivities for the nonuniform temperature distributions.

Equations (7) and (11) include approximation for nonuniform temperature distribution. Assuming a single resonant nuclide without resonance interference, Equation (7) can be rewritten in MG form as derived using the subgroup method for nonuniform temperature distribution. This is accomplished by introducing correction factors for absorption cross sections that result from nonuniform temperature distribution [17]:

$${\varphi }_{k,g}={\displaystyle \sum _{m=1}^4{F}_m{\displaystyle \sum _{n=1}^2{\beta }_n\frac{{\alpha }_n/l_m}{{\Sigma }_{a,g}^k\cdot f_{a,g}^{n,m,k}+\lambda {\Sigma }_{p,g}^k+{\alpha }_n/l_m}}},$$

(17)

where

$$f_{i,a,g}^{n,m,k}(T_k)={\displaystyle \frac{{\sigma }_{i,a,g}^k(T_k,{\sigma }_{i,b,g}^{n,m,k})}{{\sigma }_{i,a,g}^k(T_{ave.},{\sigma }_{i,b,g}^{n,m,k})}}={\displaystyle \frac{R_{i,a,g}^k(T_k,{\sigma }_{i,b,g}^{n,m,k})}{R_{i,a,g}^k(T_{ave.},{\sigma }_{i,b,g}^{n,m,k})}}\cdot {\displaystyle \frac{{\sigma }_{i,b,g}^{n,m,k}-R_{i,a,g}^k(T_{ave.},{\sigma }_{i,b,g}^{n,m,k})}{{\sigma }_{i,b,g}^{n,m,k}-R_{i,a,g}^k(T_k,{\sigma }_{i,b,g}^{n,m,k})}}.$$

(18)

The correction factors can simply be applied to adjust background cross sections. Therefore, spatially dependent self-shielded cross sections for uniform and nonuniform temperature distributions can be obtained by

$${\sigma }_{i,x,g}^k={\displaystyle \frac{{\displaystyle \sum _{m=1}^4{F}_m}{\displaystyle \sum _{n=1}^2{\beta }_n{R}_{i,x,g}^k({\widehat{\sigma }}_{i,b,g}^{n,m,k})}}{1-{\displaystyle \sum _{m=1}^4{F}_m}{\displaystyle \sum _{n=1}^2{\beta }_n\frac{R_{i,a,g}^k({\widehat{\sigma }}_{i,b,g}^{n,m,k})}{{\widehat{\sigma }}_{i,b,g}^{n,m,k}}}}},$$

(19)

where

$${\widehat{\sigma }}_{i,b,g}^{n,m,k}={\displaystyle \frac{{\sigma }_{i,b,g}^{n,m,k}}{f_{i,a,g}^{n,m,k}}}.$$

(20)

Even though this capability was not implemented into Polaris, the Polaris results for nonuniform temperature profiles with the IP and CELL + IP ESSM are very consistent with the CE KENO results. However, this capability would be very useful for high-fidelity multi-physics whole-core calculations.

3.4. Mosteller Benchmark Problems

The Mosteller benchmark [23] was developed to verify the Doppler temperature reactivity coefficient. The compositional and geometrical specifications are provided in Table 14 and Table 15.

Table 14. Atomic number densities of UO₂ fuels.

Temp (K)	Nuclide	Atomic Number Density (1024/cm3) vs. 235U Enrichment wt %
		0.711	1.6	2.4	3.1	3.9	4.5	5.0
600	16O	4.61171 × 10−2	4.61218 × 10−2	4.61260 × 10−2	4.61297 × 10−2	4.61339 × 10−2	4.61371 × 10−2	4.61397 × 10−2
	234U	0.00000 × 100	3.00175 × 10−6	4.50257 × 10−6	5.81576 × 10−6	7.31651 × 10−6	8.44205 × 10−6	9.37998 × 10−6
	235U	1.66029 × 10−4	3.73618 × 10−4	5.60420 × 10−4	7.23867 × 10−4	9.10661 × 10−4	1.05075 × 10−3	1.16749 × 10−3
	238U	2.28925 × 10−2	2.26843 × 10−2	2.24981 × 10−2	2.23352 × 10−2	2.21490 × 10−2	2.20093 × 10−2	2.18930 × 10−2
900	16O	4.59967 × 10−2	4.60014 × 10−2	4.60056 × 10−2	4.60093 × 10−2	4.60134 × 10−2	4.60166 × 10−2	4.60192 × 10−2
	234U	0.00000 × 100	2.99391 × 10−6	4.49081 × 10−6	5.80057 × 10−6	7.29740 × 10−6	8.42000 × 10−6	9.35548 × 10−6
	235U	1.65595 × 10−4	3.72642 × 10−4	5.58956 × 10−4	7.21977 × 10−4	9.08283 × 10−4	1.04801 × 10−3	1.16445 × 10−3
	238U	2.28328 × 10−2	2.26251 × 10−2	2.24393 × 10−2	2.22768 × 10−2	2.20911 × 10−2	2.19519 × 10−2	2.18358 × 10−2
1200	16O	4.58763 × 10−2	4.58810 × 10−2	4.58852 × 10−2	4.58889 × 10−2	4.58929 × 10−2	4.58961 × 10−2	4.58987 × 10−2
	234U	0.00000 × 100	2.98607 × 10−6	4.47905 × 10−6	5.78538 × 10−6	7.27829 × 10−6	8.39795 × 10−6	9.33098 × 10−6
	235U	1.65161 × 10−4	3.71666 × 10−4	5.57492 × 10−4	7.20087 × 10−4	9.05905 × 10−4	1.04527 × 10−3	1.16141 × 10−3
	238U	2.27731 × 10−2	2.25659 × 10−2	2.23805 × 10−2	2.22184 × 10−2	2.20332 × 10−2	2.18945 × 10−2	2.17786 × 10−2
1500	16O	4.61171 × 10−2	4.61218 × 10−2	4.61260 × 10−2	4.61297 × 10−2	4.61339 × 10−2	4.61371 × 10−2	4.61397 × 10−2
	234U	0.00000 × 100	3.00175 × 10−6	4.50257 × 10−6	5.81576 × 10−6	7.31651 × 10−6	8.44205 × 10−6	9.37998 × 10−6
	235U	1.66029 × 10−4	3.73618 × 10−4	5.60420 × 10−4	7.23867 × 10−4	9.10661 × 10−4	1.05075 × 10−3	1.16749 × 10−3
	238U	2.28925 × 10−2	2.26843 × 10−2	2.24981 × 10−2	2.23352 × 10−2	2.21490 × 10−2	2.20093 × 10−2	2.18930 × 10−2

Table 15. Atomic number densities of moderator and clad.

Material	Radius (cm)	Temperature (K)	Atomic Number Density (1024/cm3)
UO2 fuel	0.39398	600, 900, 1200	See Table 14
Gap	0.40226	600	16O	2.68714 × 10−5
Clad	0.45972	600	90Zr	2.17036 × 10−2	91Zr	4.73302 × 10−3	92Zr	7.23452 × 10−3
			94Zr	7.33155 × 10−3	96Zr	1.18115 × 10−3
Coolant	1.26678	600	1H	4.42326 × 10−2	16O	2.21163 × 10−2	10B	1.02133 × 10−5
			11B	4.11098 × 10−5

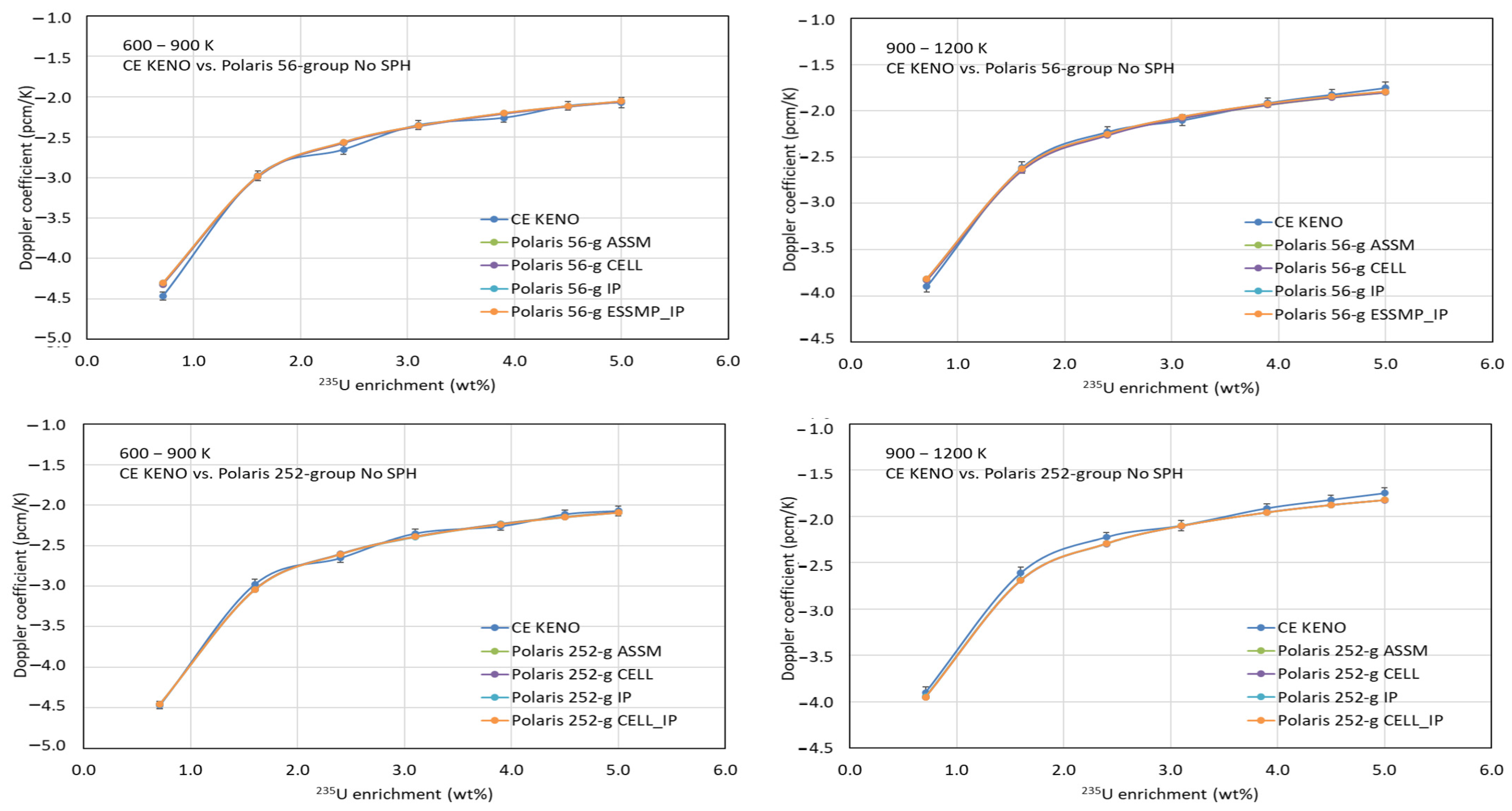
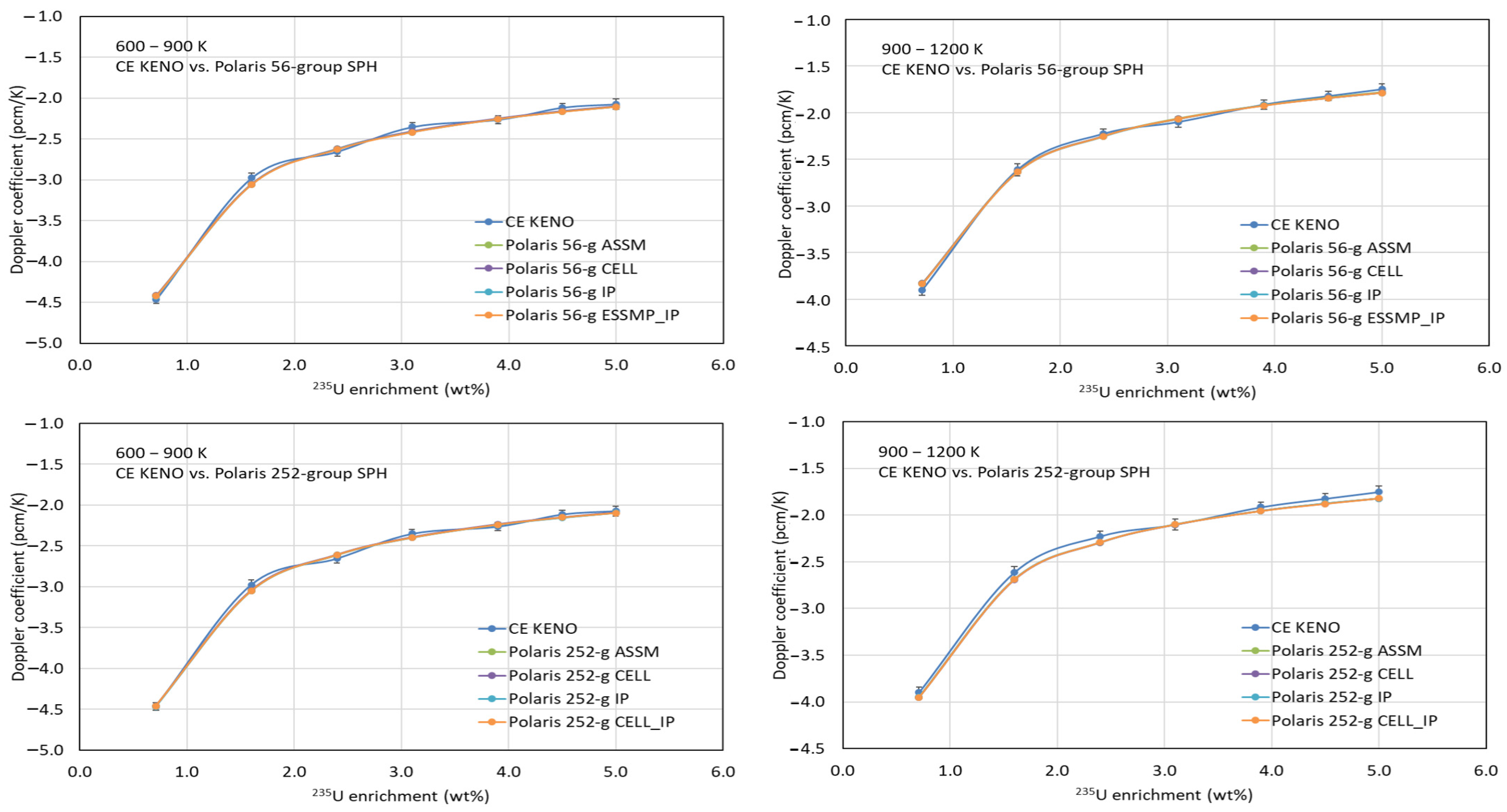
Benchmark calculations were performed using CE KENO and Polaris with the ENDF/B-VII.1 AMPX 56- and 252-group libraries, both with and without considering SPH. Figure 14 and Figure 15 compare Doppler temperature coefficients from KENO and Polaris using various ESSM options (ASSM, CELL, IP, and CELL_IP), both with and without considering SPH, respectively. The comparisons show very good agreement between Polaris and the Monte Carlo results across all temperature ranges.

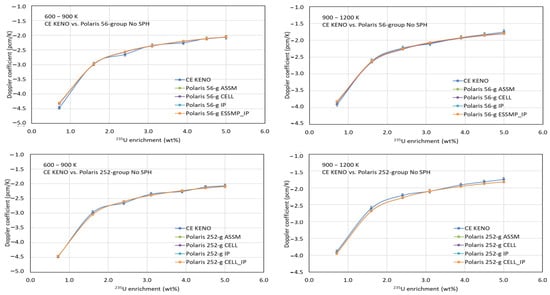
Figure 14. Comparison of Doppler coefficient (without SPH).

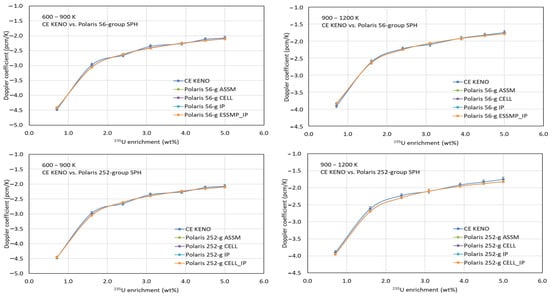
Figure 15. Comparison of Doppler coefficient (with SPH).

3.5. VERA Depletion Benchmark Problems

The VERA PWR depletion benchmark problems [24] were developed based on the VERA progression problems [21]. These benchmark problems provide detailed geometrical and material data derived from VERA progression problems #1 and #2. The depletion benchmark suite includes eight single-pin and 16 fuel assembly problems with various fuel temperatures, ²³⁵U enrichments, control rods, and burnable poisons. Three representative problems were selected for this study, as listed in Table 16.

Table 16. Single-pin and assembly depletion benchmark problems.

Case	Description	Temperature (K)			Moderator Density (g/cc)	235U wt %	Power Density (w/gU)
		Moderator	Clad	Fuel
1C	Pin 3.1w/o TF = 900 K	600	600	900	0.700	3.1	40.0
2A	FA no poisons TF = 565 K	565	565	565	0.743	3.1	40.0
2O	FA 12 gadolinia	600	600	900	0.700	3.1/1.8	40.0

Benchmark calculations were performed for cases 1C, 2A, and 2O of the VERA PWR depletion problems [24] using Polaris with the ENDF/B-VII.1 AMPX 56- and 252-group libraries, both with and without SPH factors for ²³⁸U. Reference solutions were obtained using CE Shift and Serpent calculations, in which the same fission κ (recoverable energy per fission) values were applied, and capture κ (recoverable energy per capture) values were incorporated into the fission κ values, as specified in the VERA PWR depletion benchmark problems.

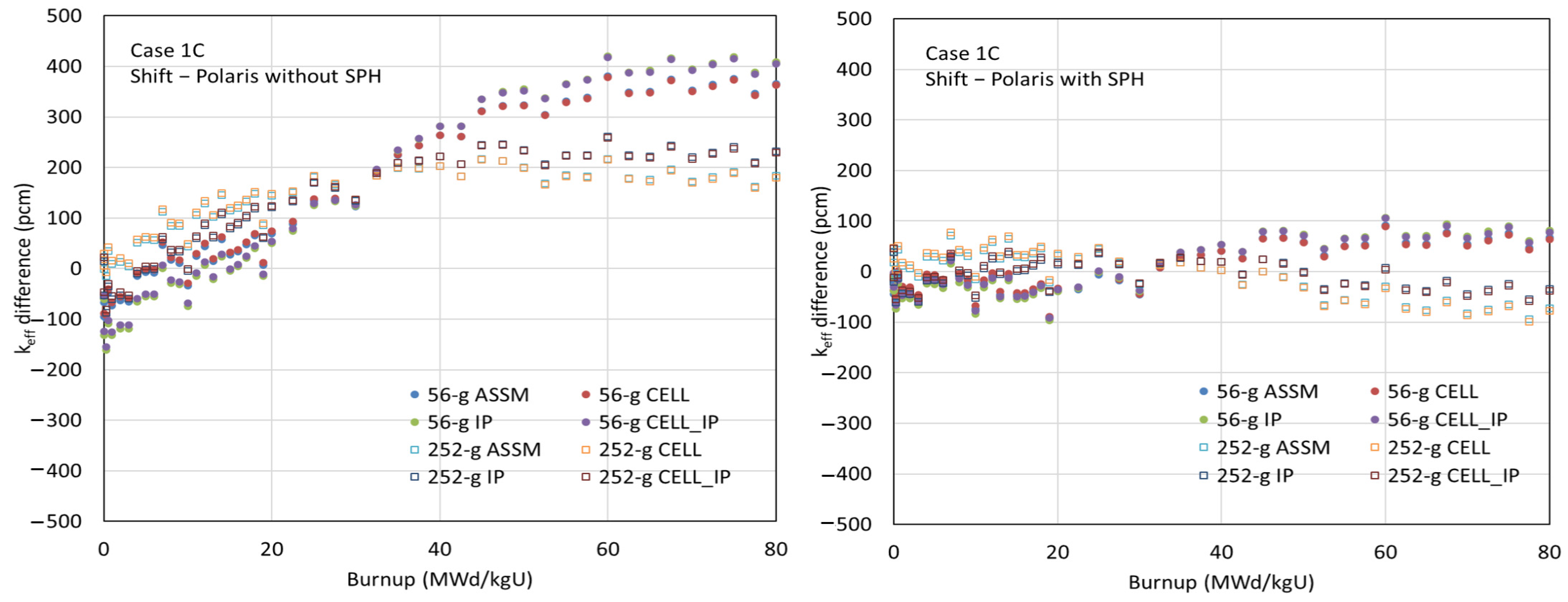
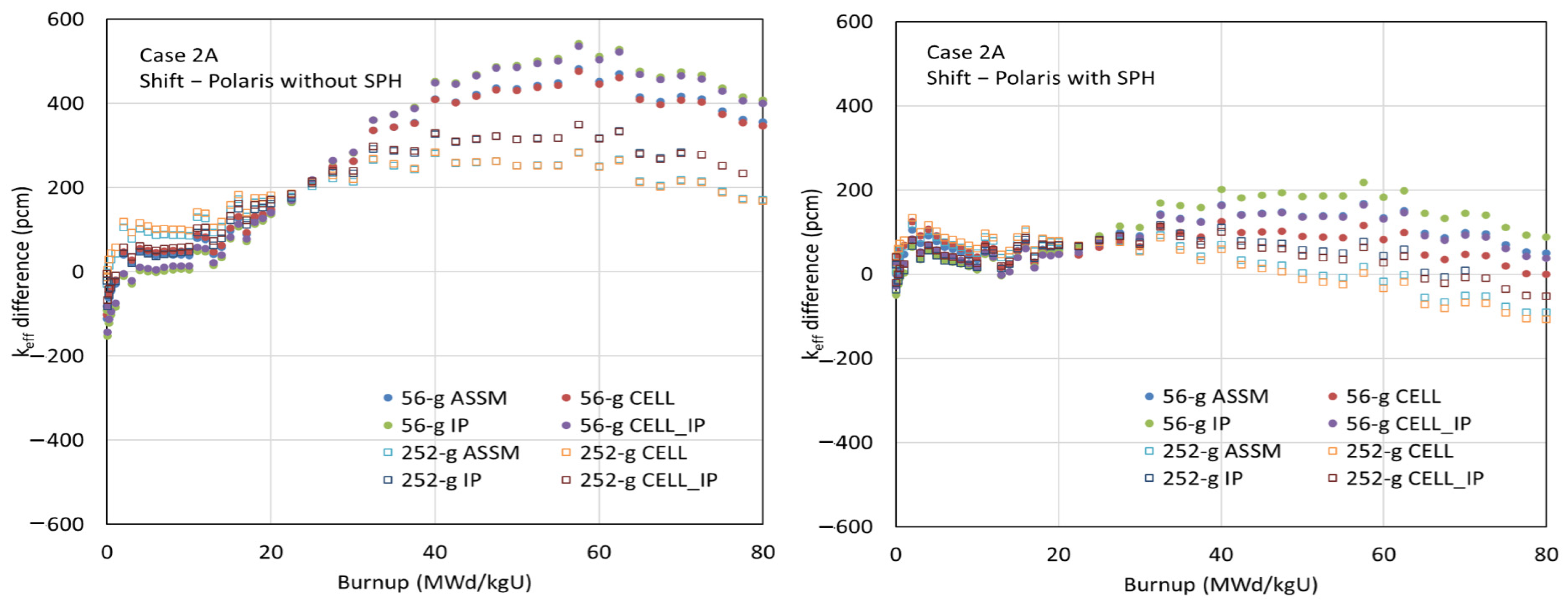
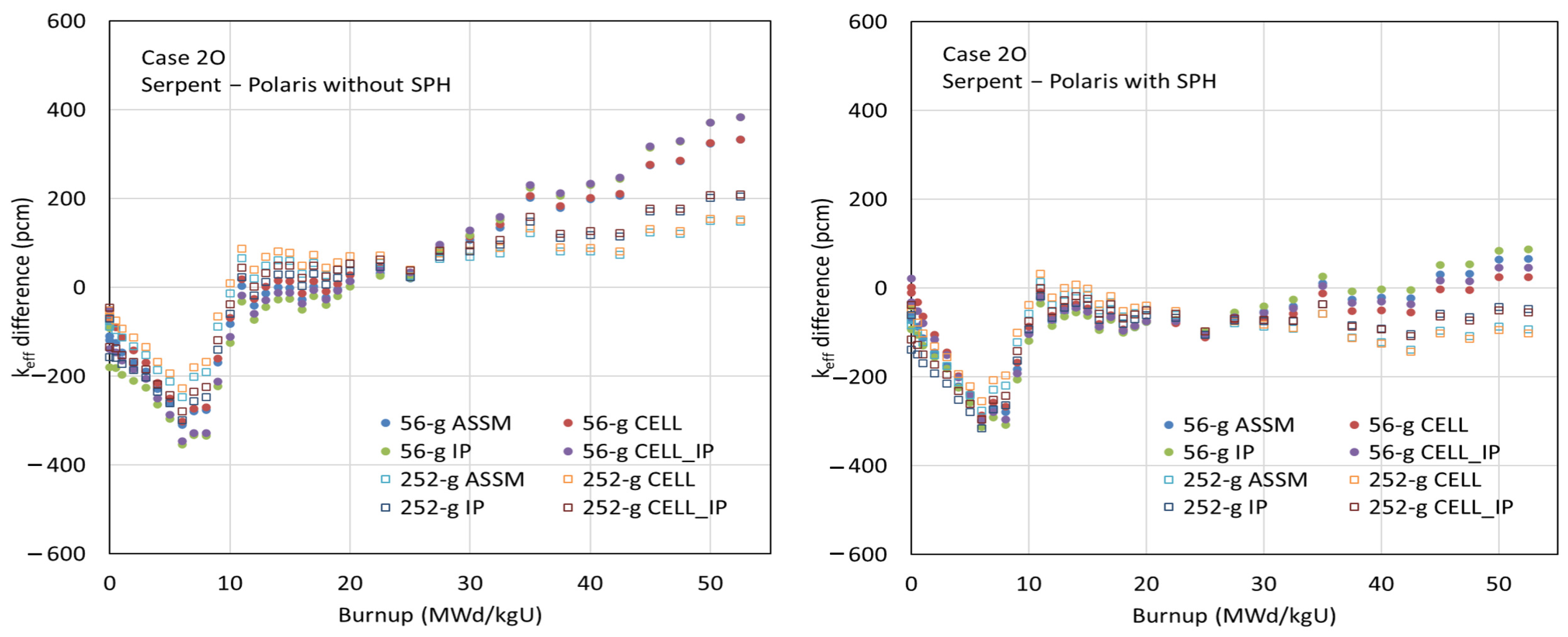
Figure 16, Figure 17 and Figure 18 compare the multiplication factors as a function of burnup for cases 1C, 2A, and 2O between the CE Shift and Polaris results using various ESSM options, with the ENDF/B-VII.1 AMPX 56- and 252-group libraries, both with and without SPH factors for ²³⁸U. The left-hand graphs in the figures show the benchmark results using the AMPX 56- and 252-group libraries without SPH factors. Slight reactivity differences are observed among the ESSM options—ASSM, CELL, IP, and CELL_IP—indicating that the less accurate spatially dependent self-shielded cross sections in ASSM and CELL do not significantly affect the depletion results.

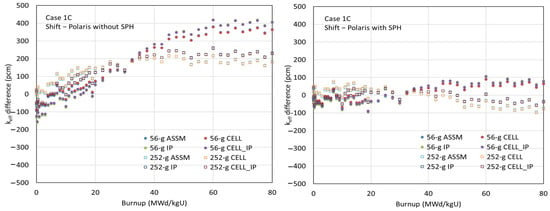
Figure 16. Comparison of the multiplication factors as a function of burnup for case 1C.

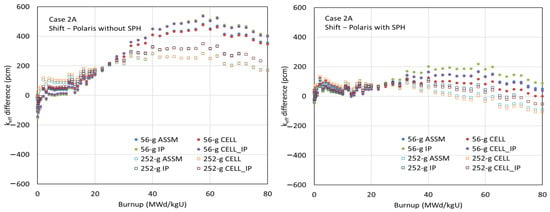
Figure 17. Comparison of the multiplication factors as a function of burnup for case 2A.

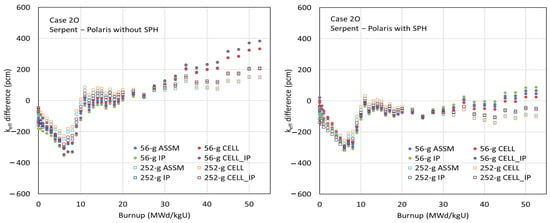
Figure 18. Comparison of the multiplication factors as a function of burnup for case 2O.

Although excellent agreement in multiplication factors is observed at zero burnup between the AMPX MG libraries with and without SPH factors, significant reactivity biases appear at high-burnup points when SPH factors are not considered. In the conventional ESSM, strong unphysical resonance interference occurs between clad and fuel, necessitating special resonance data, particularly for ⁹¹Zr and ⁹⁶Zr in coarse group structures. Even though the interference between clad and fuel is weaker in fine group structures, error cancellation can still impact the depletion results, introducing large reactivity biases at high burnup. It is physically expected that collapsing energy groups from fine to coarse in a problem-independent manner introduces reaction rate differences due to the lack of angle-dependent total cross sections and P₀ flux moment weighting.

As shown in the figures, the depletion benchmark results using the AMPX MG libraries with SPH factors and material grouping are highly consistent with the reference results obtained from CE Monte Carlo calculations.

4. Conclusions

The ESSM is currently the primary resonance self-shielding method used in SCALE’s lattice physics code, Polaris. In this study, the conventional ESSM has been extended to accomplish the following:

• Provide accurate, spatially dependent effective cross sections at the intra-pin level using the Stoker–Weiss method.
• Include a material grouping capability to avoid special resonance data, supported by a new resonance data generation procedure incorporating SPH factors.
• Significantly enhance computational efficiency in ESSM self-shielding calculations.

Although the conventional ESSM remains acceptable, as demonstrated in the benchmark results, the extended ESSM offers improved accuracy and computational efficiency. The conventional ESSM exhibits significant errors in spatially dependent self-shielded cross sections when multiple intra-pin radial rings are included. Additionally, it introduces strong unphysical resonance interference between fuel and cladding, which requires special resonance data—particularly for ⁹¹Zr and ⁹⁶Zr in coarse group structures—and can result in reactivity biases at high burnup. This resonance interference leads to some error cancellation, which is unphysical but may not require adjustments to resonance data inherently introduced during energy group collapsing. Because the ESSM equations are solved numerically using the MOC in Polaris, the computations are expensive, accounting for approximately 30% of the total computing time.