Abstract
Calorimetry is an old experimental technique (first instrument developed in S. XVIII), but it is broadly used and still provides key information for understanding biological processes at the molecular level, particularly, cooperative phenomena in protein interactions. Here, we review and highlight some key aspects of biological calorimetry. Several biological systems will be described in which calorimetry was instrumental for modeling the behavior of the protein and obtaining further biological insight.
1. Biological Calorimetry
Biological calorimetry emerged as an experimental technique very early after the Scientific Revolution. In the eighteenth century, Lavoisier and Laplace built a purely isothermal calorimeter that allowed for monitoring the heat associated with guinea pig respiration and established that this process was a kind of combustion coupled with oxygen consumption [1]. That was quite a complex system and a top-down strategy, compared to the contemporary widely-applied bottom-up approach, where systems are broken down into (simple) elements. As the foundations of thermodynamics were progressively laid, calorimeters were used primarily to study chemical reactions. In order to tackle biological interactions, where non-covalent bonds are broken and formed, high-sensitivity instrumentation is required, and this became possible in the 1960s (for a historical perspective on calorimetry, see [2]).
Heat (Q) is a universal property that accompanies virtually any process. Heat is thermal energy (i.e., other than work) transferred between different elements within a system or between the system and its surroundings throughout the process. Heat can then be used to monitor any process. In particular, when studying a chemical reaction, the associated heat provides fundamental information at the molecular level about the underlying interactions that are broken and formed throughout the process. Although the heat is a process function, it becomes a state function (equal to the enthalpy change, ΔH0) when the process proceeds at constant pressure.
In the laboratory or in living systems, chemical reactions occur under constant pressure (usually, the atmosphere acts as a general barostat) and temperature (using isothermal baths). Thus, under these conditions, the fundamental thermodynamic potential that governs the feasibility of processes is the Gibbs energy (ΔG0). The Gibbs energy is made up of the enthalpy change and the entropic contribution (−TΔS0). Both enthalpic and entropic contributions are the reflection of different interatomic interactions and changes taking place in the system under study, thus providing fundamental information on the process. The Gibbs energy change is usually estimated from equilibrium constants (Keq), which are determined experimentally, either directly (by determining the equilibrium concentrations of reactants) or indirectly (by analyzing a property of the system that is proportional to the advance of the reaction). Equilibrium constants and thermodynamic parameters are defined with respect to a standard concentration (C0 = 1 M), which is used to render the equilibrium constants dimensionless and establish the Gibbs energy and entropy scales.
There are different types of calorimeters available for use, depending on the type of process to be studied or the type of information to be accessed experimentally. Thus, calorimeters may be isothermal or non-isothermal (as in combustion, drop, or scanning calorimeters), where heat or thermal power is measured as a function of time under isothermal or non-isothermal conditions. Calorimeters can be classified according to the experimental procedure when mixing reactants (titration, batch, or flow calorimeters) or according to the measurement principle (heat flux, isoperibol, heat compensation, or adiabatic). For a comprehensive description of all types of calorimeters, see [3].
Currently, there are two main high-sensitivity calorimeters employed in biological calorimetry: the isothermal titration calorimeter (ITC), employed for studying interactions between biomolecules, and the differential scanning calorimeter (DSC), employed for studying the structural stability of biological macromolecules. The former provides information about non-covalent interactions (hydrogen bonds, van der Waals interactions, electrostatic interactions, and hydrophobic interactions, all of them of an electrostatic nature) involved in the formation of molecular complexes, and the latter provides information about the same non-covalent interactions responsible for the adoption of a 3D conformation in biomacromolecules [4,5,6,7]. Comprehensive experimental planning involving variations in the experimental conditions and modifications in the reacting molecules may provide a complete description of the process under study, useful for characterizing physiological interactions and understanding pathological processes. One of the greatest advantages of ITC is the ability to simultaneously provide two layers of thermodynamic information about the interaction under study—binding affinity and binding enthalpy—which represents a major benefit to study binding, compared to other existing techniques, when dealing with macromolecular interactions with several binding sites.
2. Protein Interactions
As explained above, biomolecular interactions can be studied using an ITC instrument. In this type of calorimeter, a solution of titrant molecule is step-wise added from an injecting syringe into a titrand molecule solution located in the calorimetric cell. Titrant and titrand molecules form a complex, and the addition of titrant aliquots is continued until (almost) all titrant binding sites in the titrand molecules are occupied. The progress of the binding reaction is monitored through the heat of the interaction (directly related to the enthalpy of the interaction). Therefore, the calorimetric titration is indeed a standard chemical titration, similar to an acid-base or redox titration, in which the indicator or reporter is the heat.
Proteins are the main acting molecules in living systems, performing a wide variety of functions (signaling, recognition, catalysis, movement, transport, scaffolding, structure, reservoir, etc.). For functioning, all proteins must interact with other biomolecules. These interactions can, in principle, be studied by ITC, allowing for the determination of the different binding parameters (Gibbs energy, enthalpy and entropy changes) which conform the thermodynamic binding signature or profile for a given interaction. Additional parameters, such as the heat capacity change (ΔCP) or the number of protons exchanged upon the formation of the complex (ΔnH), can be determined, complementing the basic thermodynamic signature.
Recombinant technology has allowed for the cloning and efficiently expressing of a large number of proteins with physiological and pathological relevance, as well as the study their interactions with their biological partners. The identification of the functional groups responsible for a given interaction, as well as the conformational or quaternary changes coupled to the interaction, is crucial for the possibility of modulating those interactions through structural/functional modifications of the interacting molecules or through small interfering molecules (relevant in biotechnology and drug discovery).
3. Binding Affinity and Cooperativity
A molecule interacting with a protein is called a ligand, regardless of the size and chemical nature of the molecule. The binding affinity, or strength of the complex, is quantified either by the association equilibrium constant (Ka) or the dissociation equilibrium constant (Kd), which are defined for a given chemical reaction by applying the law of mass action. They are related to the Gibbs energy of interaction through a basic relationship:
This Equation provides a useful, albeit arbitrary, scale for the Gibbs energy of interaction, which depends on the concentration of the standard state (usually 1 M). However, this equation does not provide the actual Gibbs energy of interaction in a real scenario (i.e., protein and ligand mixed together at certain finite concentrations), but rather the Gibbs energy of interaction in an idealized scenario for a molecular complex.
If, under certain conditions, a protein only populates a single conformational state (A), and the ligand binds exclusively to that conformational state, the apparent binding affinity of the ligand coincides with the intrinsic affinity given by Ka (or Kd). However, if the protein can also adopt an alternative conformational state (B) that is unable to bind the ligand, the apparent binding affinity is given by [8]:
where K is the conformational equilibrium constant relating both protein states (K = [B]/[A]). Depending on the population distribution of the conformational states, the apparent binding affinity will be similar to the intrinsic affinity of state A (K ≈ 0), or much lower (K >> 1). This result can be generalized: any conformational state that is not compatible with ligand binding will reduce the apparent binding affinity. Furthermore, if that alternative state B also binds the ligand, but with different affinity with respect to state A, the apparent binding affinity is given by the ensemble-weighted average of both intrinsic affinities [8,9]:
Then, depending on the population distribution of the conformational states (i.e., K) and the relative strength of the interaction for both states (Ka,A and Ka,B), the apparent binding affinity can be similar to the intrinsic affinity of state A (K ≈ 0), similar to the intrinsic affinity of state B (K >> 1), or an intermediate value. This result can also be generalized: when different conformational states exhibit different binding affinities, the apparent binding affinity is a population average of the intrinsic binding affinities.
Ligand binding and conformational stability in a protein are intimately connected. The binding of a ligand to a given protein leads to the formation of a complex establishing new intermolecular interactions between the protein and the ligand (and the protein with itself). The binding contributes additional stability for the protein, which is expressed as an excess average Gibbs energy:
where [L] is the concentration of the free ligand.
In general, a given protein has a conformational landscape consisting of a set of structurally distinguishable (i.e., different conformations) and significantly populated conformational states. Those states bind the ligand with affinity Ka,i (≥0), and the stability Gibbs energy of each state is modulated by ligand binding according to:
where ΔGi is the overall stability energy of the protein conformational state i, ΔGi,int is the intrinsic stability energy (without the contribution of the ligand binding, and equal to the difference in conformational Gibbs energy between state i and state 0: Gi − G0), and <ΔGi,bind> is the additional contribution to stability from ligand binding (see Equation (4)). The population of each protein conformational state, Pi, is given by:
In all these expressions, the native state is taken as the reference state (ΔGi = Gi − G0), which is the fundamental state with the lowest energy under native (e.g., physiological) conditions. Several situations can be distinguished: (1) Ka,i = Ka,0, the state i is stabilized, to an extent, similar to state 0; (2) Ka,i < Ka,0, the state i is stabilized to a lesser extent than state 0; and (3) Ka,i > Ka,0, the state i is stabilized to a greater extent than state 0. All conformational states can be classified in two groups: those states unable to bind the ligand (Ka,i = 0), and those states able to bind the ligand, albeit with different binding affinities (Ka,i > 0). The binding of the ligand will stabilize (i.e., increase the population of) those states with which the ligand interacts preferentially, and destabilize (i.e., decrease the population) those states with which the ligand does not interact. The extent of the stabilization and the increase in population depend on the ligand binding affinity for that state (compared, mainly, with the binding affinity of the reference native state, but also to that of any other state) and the concentration of the free ligand.
The interplay between ligand binding and conformational equilibrium, reflected in the ligand-induced redistribution of populations of states within the protein conformational landscape, represents the molecular basis of the allosteric control in proteins [8,10,11]. Initially, allostery was defined as a property of biological macromolecules featuring cooperative ligand binding and the regulation of ligand affinity by effectors [12], usually associated with the functional regulation in enzymes by effector binding to sites different from that of the substrate. Thus, there was a link between allostery and binding cooperativity, but this link was not very clear. Allosterism, in a broad sense, consists of the conformational equilibrium modulated by ligand binding, i.e., the preferential stabilization of certain conformational states induced by ligand binding [8]. The consideration of just two conformational states, 0 (native) and 1 (non-native), with binding affinities Ka,0 and Ka,1, will reveal key features:
The first equation is trivial, but the second equation indicates that the stabilization energy depends on the difference in intrinsic stabilization energy and the ligand binding affinity between the two states. Therefore, ligand binding may occur preferentially (or exclusively) to the native state (Ka,0 > 0, Ka,i = 0), resulting in a further stabilization of the native state (increase in the population of the native state and decrease in the population of the non-native state). This situation corresponds to the lock-and-key binding model, if the native state is largely predominant compared to the non-native state (large ΔG1,int), or to the conformational selection binding model, if both conformational states exhibit comparable populations (small ΔG1,int), and ligand binding promotes the conformational change from the non-native state to the native state (population equilibrium shift towards the native state). On the other hand, ligand binding may occur preferentially (or exclusively) to the non-native state (Ka,0 = 0, Ka,i > 0), resulting in a further stabilization of the non-native state (increase in the population of the non-native state and decrease in the population of the native state). This situation corresponds to the conformational selection binding model, if both conformational states exhibit comparable populations (small ΔG1,int), or the induced fit binding model, if the native state is largely predominant compared to the non-native state (large ΔG1,int), and ligand binding promotes the conformational change from the native state to the non-native state (population equilibrium shift towards the non-native state). Therefore, the lock-and-key binding model corresponds to a scenario with a highly predominant native state that is further stabilized by ligand binding; the conformational selection model corresponds to a scenario with comparably populated native and non-native states, and one of them is further stabilized by ligand binding; the induced fit model corresponds to a scenario with a highly predominant native state, and the non-native state, with little or negligible population, is further stabilized by ligand binding. Thus, apart from the controversy over whether conformational selection or induced fit models can be discriminated by kinetic experiments [13,14], or whether some structural features of the protein govern and dictate the particular cooperativity process [15], the main difference between both models is the magnitude of ΔG1,int (i.e., the populations of both states in the absence of ligand), and leads to the conclusion that the induced fit is a special case of conformational selection [16]. The conformational change is the macroscopic reflection of the shift in the population of states induced by the ligand binding. This is an important point: the ligand does not cause a conformational change as a result of the collision with the protein, but a population shift between pre-existing protein conformational states.
As mentioned above, ligand binding may be coupled to conformational changes in the protein, which represents the molecular basis for allosteric control and binding cooperativity in macromolecules with several binding sites. Cooperativity and allosterism are two phenomena that depend not only on the intrinsic structural and functional properties of the protein, but also on the ligand: ligands binding to the same binding site on the protein may not only bind with similar or different affinity, but they also may elicit similar or different allosteric or cooperative effects [17,18,19].
Binding cooperativity arises when several ligands bind to the same protein at different sites, and the binding parameters for ligand binding depend on the site occupancy. If the ligands are identical, the cooperativity effect is homotropic, while if the ligands are different, the cooperativity effect is heterotropic [8]. Cooperativity is positive or negative, depending on whether the binding affinity increases or decreases with binding site occupancy. Cooperativity may be due to direct ligand–ligand interaction upon binding, or to long-distance ligand–ligand interaction mediated by conformational changes in the protein. Allosterism and cooperativity are therefore, related phenomena. Equations (5) and (6) can be easily generalized and extended to proteins with more than one binding site for a given ligand [20,21].
Although cooperativity can be shown by monomeric and oligomeric proteins, emphasis has been placed on oligomeric proteins, and cooperativity models have been developed, namely the Monod–Wyman–Changeux model [22] and the Koshland–Némethy–Filmer model [23].
Allosterism and binding cooperativity are linked phenomena. Binding cooperativity is often associated with allosterism because the cooperativity effect is a reflection of population shifts between protein conformational states (alteration of the protein conformational landscape) with different ligand binding affinities. However, allosterism does not require binding cooperativity because the modulation of the conformational landscape may occur with no cooperativity; as shown in Equations (5) and (6), there may be allosteric control in proteins with no binding cooperativity (a single ligand binding site). Allostery and binding cooperativity are linked, and the effector may be the same ligand (homotropic) or a different ligand (heterotropic).
4. Cooperativity Models
The MWC and KNF models are simplifications of the general allosteric model, a model that considers all relevant conformational states and all possible ligation states (Figure 1) [8]. The general allosteric model is often impractical because it considers many conformational and binding affinity constants. Both models have been successful in reproducing the cooperative behavior in proteins. Of course, any model is an idealized simplified representation of the real system. There is no way to demonstrate that a given model is right or correct; we can only discard useless models.
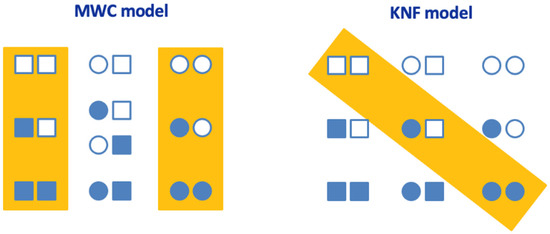
Figure 1.
Cooperativity models in oligomeric proteins. The general allosteric model for a protein with two binding sites is shown. Each subunit can adopt two conformationally and functionally different conformations: T (tense) conformation (square), and R (relaxed) conformation (circle). The orange rectangle encloses the relevant conformational states in each model. Empty and filled subunits represent ligand-free and ligand-bound subunits, respectively.
Both models share some features. For example, the basic versions of both models consider identical subunits (i.e., homo-oligomeric protein), and each subunit can adopt two conformationally and functionally different conformations; intersubunit contacts and interactions provide the energetic coupling for the long-range effects induced by the ligand. Ligand binding drives the conversion between the different states, acting as an inhibitor or an activator of the protein subunits.
However, each model shows key differences. For example, the MWC model considers a concerted conformational change in all subunits, while the KNF model considers a sequential conformational change. Therefore, the MWC model requires only two overall conformational states of the oligomeric protein, while the KNF model requires more than two.
4.1. Monod–Wyman–Changeux (MWC) Model
The MWC (or concerted) model considers that each subunit adopts two functionally different conformations (relaxed, R; and tense, T) in equilibrium in the absence/presence of a ligand. The two conformations show different binding affinities for the ligand (Ka,R > Ka,T), and this is the driving force for the binding and the cooperative effect. In the absence of a ligand, the T conformation predominates, and ligand binding induces a concerted conformational change in which all subunits within an oligomeric protein simultaneously undergo the conformational change towards the R conformation. Therefore, there are no mixed conformational states, with subunits adopting different conformations within a given oligomer. The conformational change is the macroscopic reflection of the population shift between two previously co-existing overall oligomeric conformations.
Subunits undergo the conformational change in a concerted fashion: the conformational change of one subunit makes all other subunits undergo such conformational changes as a kind of nucleation step, with an energetic penalization absent for binding to the remaining sites. The conformational change is accompanied by an altered ligand binding affinity and an altered function. Importantly, the binding of the ligand within a given conformational state (R or T) is not cooperative: all binding sites are identical and behave in an independent fashion, but there is a conformational selection mechanism because the R state has a higher binding affinity for the ligand.
A key feature of the MWC model is the dissimilarity between the fraction of protein subunits bound to the ligand and the fraction of protein subunits with altered activity or which are functionally different (having undergone the conformational change from T to R state). Then, the fraction of activated or inhibited subunits may be considerably different from the fraction of ligand-bound subunits. A key limitation of the basic MWC is the inability to describe negative binding cooperativity.
Caseinolytic Protease (ClpP)
Caseinolytic protease (ClpP) is a tetradecameric protein considered a bacterial target for drug design (Figure 2). At pH 7.6 (phosphate buffer), ClpP shows a moderate stability (unfolding temperature of 62 °C, which was further increased to 83 °C in the presence of 100 μM bortezomib, a boronic proteasome inhibitor) [24]. It has been reported that ClpP can be activated by inhibitors binding in the active site, a finding difficult to explain.
For modeling the binding of the ligand to ClpP, the following MWC binding polynomial was employed:
where Ka,R and Ka,T are the ligand association constants for the R and T states, γ is the conformational equilibrium constant for both states (γ = [T]/[R]), and [L] is the concentration of (free) ligand. The binding polynomial contains all information on the conformational landscape, with the relative statistical weights for each state [8,25,26].
Using an integrated experimental biophysical approach including ITC, it was possible to prove that bortezomib interacts with the serine located within the active site in each subunit, mimicking a peptidic substrate, and inducing a concerted allosteric change in ClpP, resulting in initial activation and subsequent inhibition [27]. At 35 °C, pH 7.6, and low ionic strength, the binding parameters for the R state were: Ka,R = 8.0 × 104 M−1, ΔHR = −0.9 kcal/mol, and those for the T state were: Ka,R = 8.0 × 104 M−1, ΔHR = −0.1 kcal/mol. The conformational parameters were: γ = 3.3, and ΔHγ = −0.3 kcal/mol; this indicated that in the absence of a ligand, 33% of the subunits were located in the R state, and 77% of the subunits were adopting the T state conformation. Thus, the binding of bortezomib seems to be entropically driven, with a very small favorable enthalpy, although this must be taken with caution because the experiments were performed with HEPES, which has a non-zero ionization enthalpy and, although the affinity is not affected, it might make the apparent, observed binding profile different than the intrinsic binding profile (i.e., the partition into enthalpy and entropy).
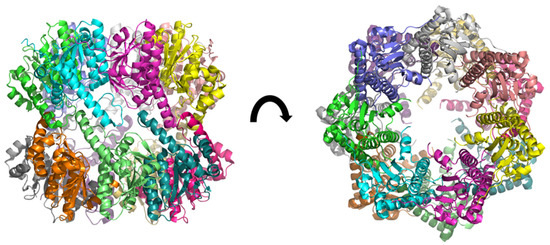
Figure 2.
3D structure of ClpP from Mycobacterium tuberculosis, determined by cryo-electromicroscopy at 3.10 Å of resolution (pdb ID: 6vgk) [28]. The fourteen subunits are shown in different colors. Two heptameric rings form a dimer resulting in a heptadecameric protein.
The ITC experiments performed with ClpP and bortezomib and the analysis performed by applying the MWC model were instrumental for observing the cooperative binding, for determining the binding affinity for bortezomib, for determining the conformational equilibrium constant (γ) between the R state and T state, and for estimating the concentration for the apparent conversion of bortezomib from an activator to an inhibitor of ClpP, which was in complete agreement with direct inhibition studies. Thus, from the inhibition assays, the concentration of bortezomib for maximal ClpP activity was 12.5 μM, and, from the ITC studies, the concentration of bortezomib for maximal fraction of bortezomib-free R-state subunits (i.e., able to catalyze the substrate) was 9 μM. This explains the dual role of bortezomib as an activator-inhibitor, and is rooted in the non-equivalence between the fraction of protein subunits bound to bortezomib and the fraction of protein subunits undergoing the conformational change.
To our knowledge, this work represents one of the very few applications of the MWC model in ITC experiments. The analysis of ITC data is often deemed complex, and the application of a cooperativity model increases this complexity. However, the experimental set-up in ITC is quite simple, which partially reduces the overall complexity of the experimental strategy, and makes ITC a powerful tool to unravel and describe intricate biomolecular interaction mechanisms.
4.2. Koshland–Némethy–Filmer (KNF) Model
The basic KNF (or sequential) model considers that each subunit may adopt two functionally different conformations in equilibrium in the absence/presence of a ligand. Only one of the two conformations is able to bind the ligand, and this is the driving force for the binding and the cooperative effect. The non-binding-competent conformation predominates in the absence of the ligand, and ligand binding to a certain subunit induces a conformational change in the other subunits towards the binding-competent conformation, resulting in increased ligand binding affinity (positive cooperativity), or reduced ligand binding affinity (negative cooperativity). Therefore, there are mixed conformational states, with subunits adopting different conformations in a given oligomer.
Subunits do not undergo the conformational change in an independent fashion: the conformational change of one subunit makes the other neighboring subunits more likely (more thermodynamically favorable) to undergo such conformational change, by reducing the energy required for such a change. The conformational change is accompanied by an altered ligand binding affinity and an altered function.
A key feature of the KNF model is the equivalence between the fraction of protein subunits bound to the ligand and the fraction of protein subunits with altered activity or functional differences. A key point of the KNF is the ability to describe both positive and negative binding cooperativity.
4.2.1. Nucleoplasmin (NP)
Nucleoplasmin (NP) is a pentameric protein with histone chaperone activity: it acts as a reservoir for histones H2A-H2B and can displace sperm nuclear basic proteins and linker histones from the chromatin fiber of sperm and quiescent somatic nuclei (Figure 3). NP mediates histone exchange during gene expression and participates in nucleosome assembly. At pH 7, NP and NP-core (without the tail domains) showed a very high structural stability, with unfolding temperatures of 110 and 118 °C, and unfolding enthalpies of 160 and 245 kcal/mol, respectively, indicating that the disordered tails destabilize the pentameric structure [29]. Phosphorylations associated with the activation of NP caused a reduction in stability. The thermal unfolding of NP was irreversible, but chemical unfolding was reversible; at pH 6.5 and 25 °C, the unfolding Gibbs energy of NP was 48 kcal/mol [30], close to the gross estimation of 35 kcal/mol from thermal unfolding at pH 7.
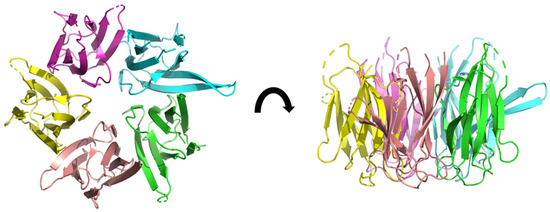
Figure 3.
The 3D structure of NP (core domain) from Xenopus laevis, determined by X-ray diffraction at 2.30 Å of resolution (pdb ID: 1k5j) [31]. The five subunits are shown in different colors. Some loops are disordered and appear incomplete (dashed segments).
For modeling the binding of the ligand to NP, the following KNF binding polynomial was employed:
where Ka is the intrinsic ligand association constant for each protein subunit, and the kis are interaction constants reflecting internal interactions between subunits within the pentamer altered upon ligand binding. This binding polynomial is an extension of a former expression applied to cholera toxin, a pentameric protein interacting with the oligosaccharide portion of ganglioside GM1, the toxin cell surface receptor [32].
ITC experiments revealed that the NP pentamer can accommodate five histones, either H2A-H2B dimers or linker H5 through a binding interaction characterized by negative cooperativity [33]. The NP core and tail domains play a fundamental role in the interaction with histones. The analysis of the biomolecular NP–histones interaction employing the KNF cooperative model revealed a negative cooperativity-based regulatory mechanism for the linker histones and nucleosomal histones exchange. At 25 °C, pH 7.4, and physiological ionic strength, the intrinsic binding parameters for H5 were: Ka = 1.0 × 1010 M−1 (Kd = 0.1 nM), and ΔH = 11.7 kcal/mol; and those for H2A–H2B were: Ka = 1.5 × 107 M−1, (Kd = 67 nM) and ΔH = −3.5 kcal/mol. Then, the binding of H5 is entropically driven, whereas the binding of H2A-H2B is favored by both enthalpy and entropy. Again, this must be taken with caution because the experiments were performed with PIPES, which has a non-zero ionization enthalpy. The binding of additional histone molecules is accompanied by a cumulative reduction in binding affinity, with a larger energetic penalty in the case of H5 compared to the H2A-H2B dimer. Thus, the fifth H5 binds with Kd = 210 nM, and the fifth H2A-H2B dimer binds with Kd = 1 μΜ. In order to provide additional evidence for the suitability of the interaction model, reverse titrations were performed (i.e., titrating NP into histone solutions), which provided similar binding parameters to those from direct titrations.
H2A-H2B dimer and H5 interacted, with very different intrinsic affinities. This different “affinity window” for both histone types might allow NP to fulfill its histone chaperone role, simultaneously acting as a reservoir for the core histones and a chromatin decondensing factor. In addition, both histone types show a considerably different cooperativity mechanism: in the case of H5, there is a marked negative cooperativity effect stemming mainly from a global conformational change in NP coupled to ligand binding, whereas in the case of the H2A-H2B dimer, there is a less dramatic negative cooperativity effect mainly involving direct ligand–ligand interaction between bound ligands.
This work provides a good example of how a given protein scaffold may exhibit significantly different binding features (affinity and cooperativity), depending on the ligand with which it is interacting.
4.2.2. Aspartate Transcarbamoylase (ATCase)
Aspartate transcarbamoylase, or aspartate carbamoyltransferase (ATCase), catalyzes the synthesis of N-carbamoyl-L-aspartate from carbamoyl phosphate (CP) and L-aspartate (Asp), the first step in the pyrimidine biosynthetic pathway. The basic ATCase unit consists of a catalytic homotrimer with three active sites at the interfaces between subunits (Figure 4), and it is a target for drug discovery in cancer.
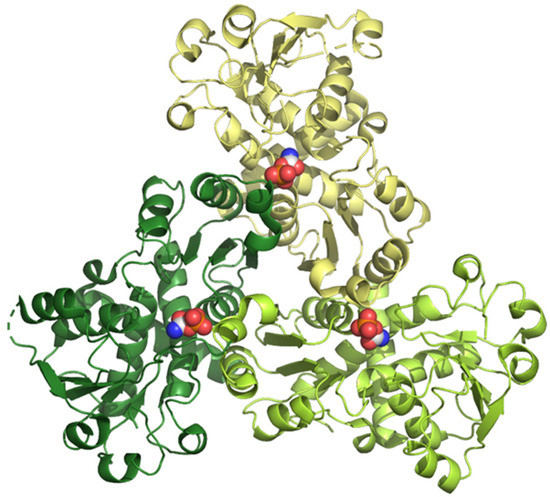
Figure 4.
3D structure of human ATCase determined by X-ray diffraction at 2.10 Å of resolution (pdb ID: 5g1o) [34]. The three subunits are shown in different colors, and the substrate carbamoyl phosphate is shown in CPK mode.
The ATCase from E. coli, which is the most widely studied, is a paradigm of feedback inhibition and a model of cooperativity and allosteric regulation. Asp binds with positive cooperativity. In addition, the ATCase is the target of N-phosphonacetyl-L-aspartate (PALA), a potent inhibitor that resembles the transition state of the reaction.
Human ATCase exhibits structural similarity to that from E. coli, showing positive cooperativity for Asp, according to enzymatic assays. For modeling the binding of the ligand to ATCase, the following KNF binding polynomial was employed:
where Ka is the intrinsic ligand association constant for each protein subunit, and the kis are interaction constants reflecting internal interactions between subunits within the trimer altered upon ligand binding.
According to ITC experiments, at 15 °C and pH 8.3 (buffer Tris with 150 mM NaCl and 2% glycerol) human ATCase interacted with PALA with negative cooperativity (Kd1 = 0.017 μM, Kd2 = 0.027 μM, and Kd3 = 1.4 μM) with an entropically driven binding, but, interestingly, the binding of CP, the other substrate, showed no cooperativity at all (Kd = 6.3 μM for the three sites), along with a mainly entropically driven binding [34].
In plants, ATCase is also an essential enzyme for de novo pyrimidine biosynthesis, but with the particularity of being regulated by feedback inhibition of uridine 5-monophosphate (UMP). Similar to human ATCase, according to ITC experiments, and at 25 °C and pH 7 (buffer Tris with 100 mM NaCl and 2% glycerol), ATCase from Arabidopsis thaliana showed an interaction with CP, with no cooperativity (Kd = 80 μM for the three sites), and with a mixed binding (favored by entropy and enthalpy) [35]. The interaction with UMP was characterized by negative cooperativity (Kd1 = 0.21 μM, Kd2 = 2.3 μM, and Kd3 = 1.6 μM) with a mainly entropically driven binding. Moreover, surprisingly, the binding of PALA was restricted to a single protomer in the trimer (Kd = 0.6 μM), with an entropically driven binding; the binding of the first PALA molecule precluded the binding of additional PALA molecules.
This work provides another example of how the same protein scaffold exhibits different binding features (affinity and cooperativity) depending on the interacting ligand.
4.2.3. NAD(P)H Dehydrogenase [Quinone] 1 (NQO1)
NQO1 is a FAD-dependent homodimeric cytosolic protein catalyzing the two-electron reduction of quinones, thus acting as a detoxifying/antioxidant enzyme and activating cancer prodrugs (Figure 5). NQO1 interacts with transcription factors linked to cancer progression, such as p53, p73α, and HIF-1α, inhibiting their proteasomal degradation. In addition, it is overexpressed in certain cancers.
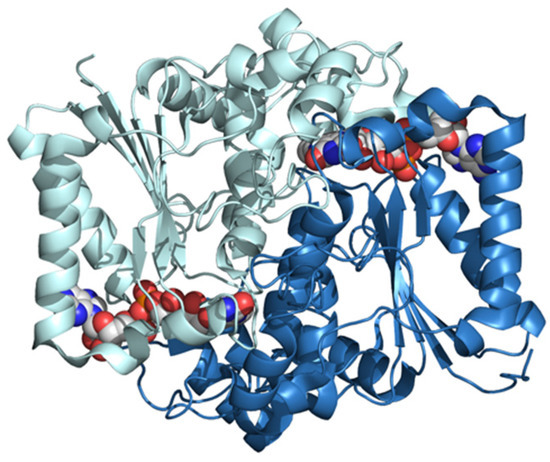
Figure 5.
The 3D structure of human NQO1 determined by X-ray diffraction at 2.01 Å of resolution (pdb ID: 5ea2) [36]. The two subunits are shown in different colors. FAD bound to each subunit is shown in the CPK mode.
At pH 7.4, NQO1 shows a moderate structural stability, with an unfolding temperature of 52 °C and an unfolding enthalpy of 65 kcal/mol [37]. For modeling the binding of the ligand to NQO1, the following KNF binding polynomial was employed:
where Ka is the intrinsic ligand association constant for each protein subunit, and k1 is the interaction constant reflecting the internal interactions between subunits within the dimer altered upon ligand binding.
According to ITC experiments at pH 7.4, NQO1 interacted with FAD with considerable affinity (Ka = 8.8 × 107 M−1), according to an enthalpically driven binding (ΔH = −22.2 kcal/mol). The binding was characterized by a slight negative cooperativity (Kd1 = 11 nM and Kd2 = 21 nM), with a marked temperature dependence [38]. In fact, at 15 °C, the cooperative effect is not apparent. This emphasizes the need to always perform titrations at different temperatures in order to reveal potential subtle cooperative effects. The cooperativity enthalpy is quite large (Δh = −12 kcal/mol) compared to the cooperativity Gibbs energy (Δg = 0.4 kcal/mol). Reverse titrations of NQO1 into FAD were previously described and interpreted as non-cooperative binding [39]. However, proper analysis of the reverse titrations concluded that the direct and reverse titrations were in complete agreement [38].
The cancer-associated mutant NQO1 P187S also showed negative cooperativity, although with lower affinity (Ka = 8.1 × 106 M−1), through a less enthalpically driven binding (ΔH = −17.6 kcal/mol). However, for this mutant, the fold reduction in affinity for the second ligand was similar to that of NQO1 WT (Kd1 = 120 nM and Kd2 = 200 nM), but the cooperativity enthalpy was positive (Δh = 3.1 kcal/mol). This shows that, in biological interactions, intrinsic (e.g., mutations) and extrinsic (e.g., solution conditions) changes often affect the enthalpy/entropy more than the Gibbs energy.
Interestingly, the removal of the C-terminal domain in NQO1 led to a non-cooperative binding of FAD (Ka = 1.1 × 107 M−1), through an enthalpically driven binding (ΔH = −17.6 kcal/mol). This result highlights the important role of the C-terminal domain in the cooperative binding of FAD to NQO1.
5. Conclusions
The main difference between the MWC model and the KNF model lies in the scale of conformational changes. In both models, the binding affinity for a new ligand molecule is altered upon the binding of a previous ligand molecule, but the MWC model considers that this occurs by a quaternary conformational change involving the entire homo-oligomeric protein, from the T state to the R state, in a concerted fashion, according to a conformational selection model, and the overall molecular symmetry is always maintained. On the other hand, the KNF model considers that these conformational changes occur at the level of the tertiary structure within the homo-oligomeric protein, with neighboring subunits changing conformation, with successive ligand binding in a sequential fashion, according to an induced fit model, and the overall molecular symmetry is broken by ligand binding. Unlike the MWC model, the KNF model offers the possibility of describing negative cooperativity. In addition, a main difference between the MWC and KNF models is that ligand binding in the MWC model occurs by conformational selection, whereas in the KNF model, it occurs by induced fit.
ITC is a powerful technique for studying biomolecular interactions. Since ITC allows for the determination of both binding affinity and binding enthalpy, it is a particularly suitable technique to address interactions in proteins with multiple binding sites, exhibiting either independent or cooperative binding. Very often, the cooperativity effects are reflected to a larger extent in enthalpies and entropies compared to their reflection in the Gibbs energies or the equilibrium constants. This is a pervasive phenomenon in biological interactions: enthalpy and entropy are more sensitive than the Gibbs energy to intrinsic or extrinsic changes in the interaction. The simplicity of the experimental set-up contrasts with a rather complex data analysis in the case of several binding sites, but, through careful planning, ITC provides a direct insight into intermolecular interactions and target engagement, an appropriate and precise determination of binding parameters, and the unveiling of the hidden subtleties associated with often complex biomolecular interactions.
The KNF model is more often employed in ITC than is the MWC model because it is easier to implement for data analysis, but even so, applying cooperative models represents a challenging task. The MWC model only requires three equilibrium constants (with their respective enthalpies), regardless of the number of protein subunits within the oligomer, but the KNF model may require more than three equilibrium constants. The fact that negative cooperativity is almost as common as positive cooperativity, and that the MWC model is only applicable to positive cooperativity, may have resulted in less frequent use of the MWC model. In fact, the last applications of the MWC model in ITC experiments, before our work on the interaction of bortezomib and ClpP, date from the 1980s (see [40] as an example).
Biological calorimetry, a centuries-old technique, is indeed a fairly large set of specialized techniques developed for different purposes, but sharing a common theme based on measuring heat or thermal power associated with a certain process of interest. ITC is part of this great family of experimental tools, and it provides very useful and valuable information on biomolecular interactions. ITC is mainly employed to confirm target engagement in drug discovery and to extract thermodynamic information in simple cases with 1:1 binding. The examples of interactions described in this short review illustrate how ITC may reveal key features in complex biological interactions that might remain hidden when employing other binding techniques.
Author Contributions
Conceptualization, A.V.-C.; writing—original draft preparation, O.A. and A.V.-C.; writing—review and editing, O.A., S.V. and A.V.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Spanish Ministry of Economy and Competitiveness [BFU2016-78232-P to A.V.C.] and the Ministry of Science and Innovation MCIN/AEI/ 10.13039/501100011033/; “ERDF A way of Making Europe” [PID2021-127296OB-I00 to A.V.C.]; the Miguel Servet Program from Instituto de Salud Carlos III [CPII13/00017 to OA]; the Fondo de Investigaciones Sanitarias from Instituto de Salud Carlos III and the European Union (ERDF/ESF, “Investing in your future”) [PI18/00349 and PI21/00394 to O.A.]; the Diputación General de Aragón [Protein Targets and Bioactive Compounds Group E45_20R to A.V.C., and Digestive Pathology Group B25_20R to O.A.]; and the Centro de Investigación Biomédica en Red en Enfermedades Hepáticas y Digestivas (CIBERehd).
Data Availability Statement
Not applicable.
Acknowledgments
The authors express their gratitude to the collaborators responsible for the research projects involving the ClpP protease (Paul Schanda and Hugo Fraga, from Institut de Biologie Structurale, Genoble, France), nucleoplasmin (Maria Angeles Urbaneja, from Universidad del Pais Vasco, Bilbao, Spain), ATCase (Santiago Ramon-Maiques, from Instituto de Biomedicina de Valencia, Spain), and NQO1 (Angel Luis Pey, from Universidad de Granada, Spain).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lavoisier, A.L.; de Laplace, P.S. Mémoire sur la chaleur. Mém. Acad. R. Sci. 1784, 1780, 355–408. [Google Scholar] [CrossRef]
- Bastos, M. (Ed.) Biocalorimetry: Foundations and Contemporary Approaches; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Sarge, S.M.; Höhne, G.W.H.; Hemminger, W. Calorimetry: Fundamentals, Instrumentation and Applications; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2014. [Google Scholar]
- Freire, E.; Mayorga, O.L.; Straume, M. Isothermal titration calorimetry. Anal. Chem. 1990, 62, 950A–959A. [Google Scholar] [CrossRef]
- Jelesarov, I.; Bosshard, H.R. Isothermal titration calorimetry and differential scanning calorimetry as complementary tools to investigate the energetics of biomolecular recognition. J. Mol. Recognit. 1999, 12, 3–18. [Google Scholar] [CrossRef]
- Freire, E. Differential scanning calorimetry. Methods Mol. Biol. 1995, 40, 191–218. [Google Scholar] [CrossRef] [PubMed]
- Claveria-Gimeno, R.; Vega, S.; Abian, O.; Velazquez-Campoy, A. A look at ligand binding thermodynamics in drug discovery. Expert Opin. Drug Discov. 2017, 12, 363–377. [Google Scholar] [CrossRef]
- Wyman, J.; Gill, S.J. Binding and Linkage: Functional Chemistry of Biological Macromolecules; University Science Books: Mill Valley, CA, USA, 1990. [Google Scholar]
- Eftink, M.; Biltonen, R.L. Thermodynamics of interacting biological systems. In Biological Microcalorimetry; Beezer, A.E., Ed.; Academic Press: London, UK, 1980. [Google Scholar]
- Kar, G.; Keskin, O.; Gursoy, A.; Nussinov, R. Allostery and population shift in drug discovery. Curr. Opin. Pharmacol. 2010, 10, 715–722. [Google Scholar] [CrossRef]
- Tsai, C.-J.; Nussinov, R. A Unified view of “how allostery works”. PLoS Comput. Biol. 2014, 10, e1003394. [Google Scholar] [CrossRef]
- Monod, J.; Changeux, J.P.; Jacob, F. Allosteric proteins and cellular control systems. J. Mol. Biol. 1963, 6, 306–329. [Google Scholar] [CrossRef]
- Paul, F.; Weikl, T.R. How to distinguish conformational selection and induced fit based on chemical relaxation rates. PLoS Comput. Biol. 2016, 12, e1005067. [Google Scholar] [CrossRef]
- Hammes, G.G.; Chang, Y.C.; Oas, T.G. Conformational selection or induced fit: A flux description of reaction mechanism. Proc. Natl. Acad. Sci. USA 2009, 106, 13737–13741. [Google Scholar] [CrossRef]
- Morea, V.; Angelucci, F.; Tame, J.R.H.; Di Cera, E.; Bellelli, A. Structural basis of sequential and concerted cooperativity. Biomolecules 2022, 12, 1651. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, P.; Di Cera, E. Induced fit is a special case of conformational selection. Biochemistry 2017, 56, 2853–2859. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.; Holyoak, T.; McDonald, G.; Gui, C.; Fenton, A.W. Differentiating a ligand’s chemical requirements for allosteric interactions from those for protein binding. Phenylalanine inhibition of pyruvate kinase. Biochemistry 2006, 45, 5421–5429. [Google Scholar] [CrossRef]
- Liu, Y.; Schön, A.; Freire, E. Optimization of CD4/gp120 inhibitors by thermodynamic-guided alanine-scanning mutagenesis. Chem. Biol. Drug Des. 2013, 81, 72–78. [Google Scholar] [CrossRef]
- Courter, J.R.; Madani, N.; Sodroski, J.; Schön, A.; Freire, E.; Kwong, P.D.; Hendrickson, W.A.; Chaiken, I.M.; LaLonde, J.M.; Smith, A.B. 3rd. Structure-based design, synthesis and validation of CD4-mimetic small molecule inhibitors of HIV-1 entry: Conversion of a viral entry agonist to an antagonist. Acc. Chem. Res. 2014, 47, 1228–1237. [Google Scholar] [CrossRef]
- Vega, S.; Abian, O.; Velazquez-Campoy, A. A unified framework based on the binding polynomial for characterizing biological systems by isothermal titration calorimetry. Methods 2015, 76, 99–115. [Google Scholar] [CrossRef]
- Vega, S.; Abian, O.; Velazquez-Campoy, A. Handling complexity in biological interactions. J. Therm. Anal. Calorim. 2019, 138, 3229–3248. [Google Scholar] [CrossRef]
- Monod, J.; Wyman, J.; Changeux, J.-P. On the nature of allosteric transitions—A plausible model. J. Mol. Biol. 1965, 12, 88–118. [Google Scholar] [CrossRef] [PubMed]
- Koshland, D.E., Jr.; Némethy, G.; Filmer, D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry 1966, 5, 365–385. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, Y.; Yang, T.; Li, T.; Ju, Y.; Song, Y.; He, J.; Liu, H.; Bao, R. Inhibiting Mycobacterium tuberculosis ClpP1P2 by addressing the equatorial handle domain of ClpP1 subunit. BioRxiv 2019. [Google Scholar] [CrossRef]
- Schellman, J.A. Macromolecular binding. Biopolymers 1975, 14, 999–1018. [Google Scholar] [CrossRef]
- Wyman, J. Linked functions and reciprocal effects in hemoglobin: A second look. Adv. Protein Chem. 1964, 19, 223–286. [Google Scholar] [CrossRef] [PubMed]
- Felix, J.; Weinhäupl, K.; Chipot, C.; Dehez, F.; Hessel, A.; Gauto, D.F.; Morlot, C.; Abian, O.; Gutsche, I.; Velazquez-Campoy, A.; et al. Mechanism of the allosteric activation of the ClpP protease machinery by substrates and active-site inhibitors. Sci. Adv. 2019, 5, eaaw3818. [Google Scholar] [CrossRef] [PubMed]
- Vahidi, S.; Ripstein, Z.A.; Juravsky, J.B.; Rennella, E.; Goldberg, A.L.; Mittermaier, A.K.; Rubinstein, J.L.; Kay, L.E. An allosteric switch regulates Mycobacterium tuberculosis ClpP1P2 protease function as established by cryo-EM and methyl-TROSY NMR. Proc. Natl. Acad. Sci. USA 2020, 117, 5895–5906. [Google Scholar] [CrossRef] [PubMed]
- Taneva, S.G.; Muñoz, I.G.; Franco, G.; Falces, J.; Arregi, I.; Muga, A.; Montoya, G.; Urbaneja, M.A.; Bañuelos, S. Activation of nucleoplasmin, an oligomeric histone chaperone, challenges its stability. Biochemistry 2008, 47, 13897–13906. [Google Scholar] [CrossRef]
- Franco, G.; Bañuelos, S.; Falces, J.; Muga, A.; Urbaneja, M.A. Thermodynamic characterization of nucleoplasmin unfolding: Interplay between function and stability. Biochemistry 2008, 47, 7954–7962. [Google Scholar] [CrossRef]
- Dutta, S.; Akey, I.V.; Dingwall, C.; Hartman, K.L.; Laue, T.; Nolte, R.T.; Head, J.F.; Akey, C.W. The crystal structure of nucleoplasmin-core: Implications for histone binding and nucleosome assembly. Mol. Cell. 2001, 8, 841–853. [Google Scholar] [CrossRef]
- Schön, A.; Freire, E. Thermodynamics of intersubunit interactions in cholera toxin upon binding to the oligosaccharide portion of its cell surface receptor, ganglioside GM1. Biochemistry 1989, 28, 5019–5024. [Google Scholar] [CrossRef]
- Taneva, S.G.; Bañuelos, S.; Falces, J.; Arregi, I.; Muga, A.; Konarev, P.V.; Svergun, D.I.; Velazquez-Campoy, A.; Urbaneja, M.A. A mechanism for histone chaperoning activity of nucleoplasmin: Thermodynamic and structural models. J. Mol. Biol. 2009, 393, 448–463. [Google Scholar] [CrossRef]
- Ruiz-Ramos, A.; Velazquez-Campoy, A.; Grande-Garcia, A.; Moreno-Morcillo, M.; Ramon-Maiques, S. Structure and functional characterization of human aspartate transcarbamoylase, the target of the anti-tumoral drug PALA. Structure 2016, 24, 1081–1094. [Google Scholar] [CrossRef]
- Bellin, L.; Del Caño-Ochoa, F.; Velazquez-Campoy, A.; Möhlmann, T.; Ramon-Maiques, S. Mechanisms of feedback inhibition and sequential firing of active sites in plant aspartate transcarbamoylase. Nat. Commun. 2021, 12, 947. [Google Scholar] [CrossRef]
- Pidugu, L.S.; Mbimba, J.C.; Ahmad, M.; Pozharski, E.; Sausville, E.A.; Emadi, A.; Toth, E.A. A direct interaction between NQO1 and a chemotherapeutic dimeric naphthoquinone. BMC Struct. Biol. 2016, 16, 1. [Google Scholar] [CrossRef]
- Pey, A.L.; Megarity, C.F.; Timson, D.J. FAD binding overcomes defects in activity and stability displayed by cancer-associated variants of human NQO1. Biochim. Et Biophys. Acta Mol. Basis Dis. 2014, 1842, 2163–2173. [Google Scholar] [CrossRef]
- Claveria-Gimeno, R.; Velazquez-Campoy, A.; Pey, A.L. Thermodynamics of cooperative binding of FAD to human NQO1: Implications to understanding cofactor-dependent function and stability of the flavoproteome. Arch. Biochem. Biophys. 2017, 636, 17–27. [Google Scholar] [CrossRef]
- Lienhart, W.D.; Strandback, E.; Gudipati, V.; Koch, K.; Binter, A.; Uhl, M.K.; Rantasa, D.M.; Bourgeois, B.; Madl, T.; Zangger, K.; et al. Catalytic competence, structure and stability of the cancer-associated R139W variant of the human NAD(P)H:quinone oxidoreductase 1 (NQO1). FEBS J. 2017, 284, 1233–1245. [Google Scholar] [CrossRef]
- Barisas, B.G.; Gill, S.J. Thermodynamic analysis of carbon monoxide binding by hemoglobin trout I. Biophys. Chem. 1979, 9, 235–244. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).