Pathways to Adjust Partial Safety Factors for the Design of Steel-Reinforced Concrete Structures

Abstract

Annex A of EN 1992-1-1:2023—recently revised and amended in the context of the Second Generation of Eurocodes—introduces a method to adjust partial safety factors for the resistance side alongside a set of factors for different conditions and design situations, both for new and existing structures. The method proposed in Annex A is complemented by a set of stochastic models for relevant basic variables and forms a rather simple and objective format to adjust the partial safety factors from the default values offered in EN 1990:2023. Yet, over the last few years, advanced reliability-based methods aligned with modern computational tools have proved to enable rather robust and efficient structural reliability assessments. A thorough comparative analysis is imperative to understand how distinct reliability-based methods can be applied to adjust partial safety factors in the design of new structural components composed of steel-reinforced concrete. This analysis sheds light on the use of different methods to derive partial safety factors for the resolution of common engineering problems and offers inferences regarding possible implications in terms of safety and economic efficiency of design solutions.

1. Introduction

In structural reliability studies, the presence of aleatory and epistemic uncertainties—primarily resulting from (natural) variability and incomplete knowledge, respectively—is widely acknowledged [1]. By being aware of the presence of these uncertainties, one of the prime requirements of structural engineering is to guarantee that every design calculation results in sufficiently low failure probabilities of a structure [1,2]. To ensure reliable structural designs, the partial safety factor format is one of the most widely adopted approaches in modern structural codes or guidelines (e.g., [3,4]). The partial safety factor format results from the application of a semi-probabilistic approach, in which a safety verification is simplified to assess whether a structural component fulfills a given set of inequalities regarding the resistance and the load sides. Here, the design values of basic variables account for the reliability requirement by means of partial safety factors that are normally calibrated with reliability-based approaches. Modern structural codes and guidelines consider distinct partial safety factors resulting from different choices and assumptions adopted in calibration procedures [3,4]. For example, a set of assumptions are considered in [5] based on the work of [2,6]. These assumptions support the specification of statistical values of the variable effective depth and the calibration of the partial safety factor for reinforcing steel ${\gamma }_S$ as part of the new EN 1992-1-1:2023 [7]—a recently revised code in the context of the Second Generation of Eurocodes. Precisely, in EN 1992-1-1:2023, a set of reference partial safety factors influencing the resistance side are offered (Table 1). Reference values are provided for reinforcing steel ${\gamma }_S$, for concrete ${\gamma }_C$, and for modulus of elasticity ${\gamma }_{CE}$. Additionally, EN 1992-1-1:2023 includes a partial safety factor for shear and punching shear without shear reinforcement ${\gamma }_V$. This factor replaces ${\gamma }_C$ in all the formulae for calculating the shear and punching resistance in components without shear reinforcement [5]. Notwithstanding, these (reference) partial safety factors can be adjusted providing that different conditions and design situations are verified, including that the uncertainties of the basic variables are somehow reduced (e.g., [8,9]).

Table 1. Partial safety factors for the resistance side (Table 4.3 (NDP) of EN 1992-1-1:2023 [7]).

Design Situations	Reinforcing and Prestressing Steel ${\mathit{\gamma }}_{\mathit{S}}$	Concrete ${\mathit{\gamma }}_{\mathit{C}}$ and Modulus of Elasticity ${\mathit{\gamma }}_{\mathit{CE}}$	Shear and Punching Shear Without Shear Reinforcement ${\mathit{\gamma }}_{\mathit{V}}$
Persistent and transient design situation	1.15	1.5 a	1.4
Fatigue design situation	1.15	1.5	1.4
Accidental design situation	1.0	1.15	1.15
Serviceability limit state	1.0	1.0	–

Note: The partial safety factors for materials correspond to geometric deviations of Tolerance Class 1 and Execution Class 2 of EN 13670 [10]. ^a The value for ${\gamma }_{CE}$ applies when the indicative value for the modulus of elasticity according to 5.1.4 (2) of EN 1992-1-1:2023 [7] is utilized. A value ${\gamma }_{CE}$ = 1.30 applies when the modulus of elasticity is determined according to 5.1.4 (1).

In this context, the new Annex A of EN 1992-1-1:2023 offers a method to adjust partial safety factors for the resistance side (hereby denoted as ${\gamma }_M$, a term representing ${\gamma }_S$ for steel reinforcement, ${\gamma }_C$ for concrete, and ${\gamma }_V$ for shear and punching shear without shear reinforcement). Additionally, this annex introduces a set of values for design situations and conditions alongside stochastic models for a group of relevant basic variables influencing the design of structural components—and, ultimately, the partial safety factors on the resistance side. The premise of these provisions is that adjusted (i.e., meaning reduced) partial safety factors can be utilized in design on the basis of enhanced knowledge of material and geometric properties as well as model uncertainties in combination with strict quality control requirements adopted in the production of building materials (e.g., reinforcing steel and concrete). The previous version of Annex A (part of EN 1992-1-1:2004 + AC:2010 [11]) already includes provisions for the adjustment of partial safety factors on the basis of (i) enhanced quality control (paragraph A.2.1) and (ii) experimental test values: measured geometrical data (paragraph A.2.2) and, particularly for existing structures, experimental data of concrete compressive strength ${\mathit{f}}_{ck}$ according to the specifications of EN 13791:2019 [12] (paragraph A.2.3). These provisions implicitly recognize that a reduction in the variation of geometric and material strength properties can be attained through more stringent quality control measures, which are exercised in controlling deviations on the dimensions of critical sections and on the values of concrete compressive strength, respectively. Under similar principles, the premises of the new version of Annex A are enhanced and applied to a wider set of conditions and design situations. Provisions are detailed for in situ concrete members (new and existing) as well as for precast concrete members. To support the interpretation of Annex A, an additional document entitled “Background document to 4.3.3 and Annex A. Partial safety factors for materials“ (hereby denoted as $\mathit{Background} \mathit{document}$) [5] has been produced.

Simultaneously, other initiatives to adjust partial safety factors have been emerging over the years. For the design of new structures, for example, the German Committee for Structural Concrete (DAfStb) has recently introduced a preliminary version of a guideline entitled Procedure for the derivation of safety factors in concrete structures using probabilistic methods [13]. This two-part document covers the basics for time-invariant design considerations and guides the use of methods to derive partial safety factors when decoupling the load and resistance sides. In the context of existing structures, specific standards and guidelines have also been developed at both international and national levels [14]. The international standards include ISO 13822: 2010 [15] and the European Technical Specifications TS CEN/TC 17440:2020 [16], which include provisions to assess existing structures and guidance to adjust partial safety factors based on condition evaluation and material testing. These standards and specifications have been complemented by other related background documents, including the fib Bulletin 80 [17] and the handbook from Diamantidis and Holickỳ [18], providing a practical procedure to update design values for each basic variable using the method of partial factors. More recently, the fib Model Code 2020 [19] was systematically revised to provide state-of-the-art pre-normative guidance and synthesis of international research with concrete industry and engineering expertise [14]. Following the fib proposals, the group of experts under IABSE TG 1.3 investigated the use of probabilistic and semi-probabilistic methods in the reliability assessment of existing (road) bridges [14] and demonstrated applications of the theoretical principles illustrated in [20], where provisions of Annex A in EN 1992-1-1:2023 are considered. In Germany, the research project ZfPStatik [21,22,23,24] aimed at proposing recommendations for actions about inspection-based reliability analysis of existing bridges by seeking to integrate the benefits of semi-probabilistic and probabilistic assessment concepts and enabling the incorporation of measured data into the reliability analysis of existing structures through partial safety factor modification.

With the recent developments in code generation, standardization, and guidance for both new and existing structures, technological advances in computational capabilities have been emerging over recent decades. For example, Level III methods—e.g., Monte Carlo with Importance Sampling or Monte Carlo with Subset Sampling—and other more avant-garde approaches have gradually become more robust and efficient. Multiple investigations have demonstrated that the use of such methods in the resolution of common structural problems results in a great degree of accuracy and precision. In [25], an overview on the development of classical reliability methods is offered, followed by first- and second-order approximations and extensions, numerical integration, and simulation methods, all developed to address difficulties encountered when classical methods are applied to realistic structural systems. Another study [26] demonstrated that variance reduction techniques are capable of generating a wide range of solutions with high precision and satisfactory computational efficiency.

Such computational progress introduces promising possibilities to optimize design solutions and to reduce uncertainty in structural reliability assessments without compromising the target reliability levels recommended in structural codes, as in EN 1990:2002 + A1:2005 + A1:2005/AC:2010 [27] and, more recently, in its revised version EN 1990:2023 [28]. Concurrently, multiple uncertainty quantification platforms specifically developed to tackle structural reliability problems have been made publicly available to support and motivate engineering practitioners and scientific research communities embracing a probabilistic-based rationale in structural design. For example, the TesiproV software package [29]—an open-source package for structural reliability assessments developed by the Hochschule Biberach University of Applied Sciences and RWTH Aachen (both in Germany) in the free software environment R [30]—was released in 2022 [26,31]. Other examples are the Feasible Reliability Engineering Tool (FREeT) [32] and the UQLab [33]. It is expected that new software platforms will emerge over the coming years due to the predominance of data science and scientific computing in all fields of research and engineering applications [25].

Given such developments, it is relevant to investigate to what extent the recently introduced provisions of Annex A are compatible with the use of existing reliability-based approaches and what implications might be inherent in the design of concrete structures. This analysis is vital for practitioners to be aware of the limitations of the new provisions in Annex A as well as their potential in order to consciously comply with the principles of reliability and economy expected in the design of new concrete structures. On these grounds, this investigation follows a preliminary analysis described in [34]. Section 2 and Section 3 of this manuscript focus on the approaches to adjust partial safety factors and their fundamentals. Through a numerical analysis offered in Section 4, different structural reliability levels are compared, namely the results attained with the use of the simplified method included in Annex A of EN 1992-1-1:2023 and those resulting from the use of more advanced reliability-based methods. The manuscript provides a discussion on the possible implications for practical structural problems. Section 5 offers the main conclusions of this investigation, and closes this manuscript with an outlook on future research directions.

2. Methods: Partial Safety Factors Through the Method in Annex A of EN 1992-1-1:2023

2.1. Method in Annex A of EN 1992-1-1:2023

Annex A of EN 1992-1-1:2023 [7] offers a simplified method to adjust partial safety factors for the resistance side ${\gamma }_M$. The ${\gamma }_M$ value is attained from the ratio between the characteristic values ${\mathit{R}}_k$ and the design values ${\mathit{R}}_d$ of the resistance side on the basis of the provisions offered in EN 1990:2002 + A1:2005 + A1:2005/AC:2010 [27] (Equation (1)):

$${\gamma }_M={\displaystyle \frac{R_k}{R_d}}={\displaystyle \frac{\exp ({\alpha }_R·{\beta }_{tgt}·V_{RM})}{{\mu }_{RM}}}$$

(1)

with the index $\mathit{M}$ referring to material properties, thereby concerning steel reinforcement $\mathit{S}$, concrete $\mathit{C}$, and shear and punching shear without shear reinforcement $\mathit{V}$. In Equation (1), the term ${\alpha }_R$ refers to the sensitivity factor for resistance (reference value equal to 0.8 according to Table A.4 (NDP) of Annex A in EN 1992-1-1:2023). The term ${\beta }_{tgt}$ refers to the target value for the reliability index, which, according to Table A.4 (NDP) of Annex A, is equal to 3.8 for persistent or transient design situations over a 50-year design period. The term ${\mathit{V}}_{RM}$ represents the coefficient of variation for concrete $V_{RC}$, for steel reinforcement $V_{RS}$, or for shear and punching shear (without shear reinforcement) $V_{RV}$ (Equations (2), (3), or (4), respectively). According to EN 1990:2023, Equations (2)–(4) can be used for a ${\mathit{V}}_{RM}$ value smaller than 0.20.

$$V_{RS}=\sqrt{V_{fy}^2+V_d^2+V_{{\theta }_S}^2}$$

(2)

$$V_{RC}=\sqrt{V_{fc}^2+V_{{\eta }_{is}}^2+V_{A_c}^2+V_{{\theta }_C}^2}$$

(3)

$$V_{RV}=\sqrt{{\left({\displaystyle \frac{V_{fc}}{3}}\right)}^2+{\left({\displaystyle \frac{V_{{\eta }_{is}}}{3}}\right)}^2+V_d^2+V_{{\theta }_V}^2+V_{res,v}^2}$$

(4)

The term ${\mu }_{RM}$ corresponds to the bias factor for concrete ${\mu }_{RC}$, for steel reinforcement ${\mu }_{RS}$, or for shear and punching shear (without shear reinforcement) ${\mu }_{RV}$ (Equations (5), (6), and (7), respectively).

$${\mu }_{RS}={\displaystyle \frac{f_{ym}}{f_{yk}}}·{\mu }_d·{\mu }_{{\theta }_S}$$

(5)

$${\mu }_{RC}={\displaystyle \frac{f_{cm}}{f_{ck}}}·{\mu }_{{\eta }_{is}}·{\mu }_{A_C}·{\mu }_{{\theta }_C}$$

(6)

$${\mu }_{RV}={\left({\displaystyle \frac{f_{cm}}{f_{ck}}}·{\mu }_{{\eta }_{is}}\right)}^{1/3}·{\mu }_d·{\mu }_{{\theta }_V}$$

(7)

The variables in Equations (2)–(7) are described in Table 2.

Table 2. Description of basic variables used in Equations (2)–(7).

Variable	Description
${\mathit{f}}_y$	Yield strength
${\mathit{f}}_{yk}$	Yield strength (characteristic value)
${\mathit{f}}_{ym}$	Yield strength (mean value)
$\mathit{d}$	Effective depth
${\mathit{f}}_c$	Compressive strength (control specimen)
${\mathit{f}}_{ck}$	Compressive strength (characteristic value)
${\mathit{f}}_{cm}$	Compressive strength (mean value)
${\eta }_{is}$	In situ factor
${\mathit{A}}_C$	Concrete area
$\mathit{res},\mathit{v}$	Residual uncertainties (accounting for the less sensitive variables affecting punching shear)
${\theta }_S$	Model uncertainty (reinforcement steel)
${\theta }_C$	Model uncertainty (concrete)
${\theta }_V$	Model uncertainty (shear and punching shear without shear reinforcement)

As briefly introduced in Section 1, Annex A includes a set of stochastic models for relevant basic variables involved on the resistance side. These models are defined in terms of bias factors ${\mu }_X$ and coefficients of variation ${\mathit{V}}_X$. An extract of this data is offered in Table 3. Note, however, that no distribution type is included in Annex A. The premises adopted for the specification of these stochastic models are mostly described in the $\mathit{Background} \mathit{document}$ [5].

Table 3. Stochastic models assumed for the calibration of ${\gamma }_V$ proposed in EN 1992-1-1:2023 [7] according to Table 4.3 (NDP).

Stochastic Model for the Calibration of ${\mathit{\gamma }}_{\mathit{V}}$	Coefficient of Variation ${\mathit{V}}_{\mathit{X}}$	Bias Factor a ${\mathit{\mu }}_{\mathit{X}}$
Concrete compressive strength ${\mathit{f}}_{c,cyl}$	${\mathit{V}}_{f_c}$ = 0.100	${\mathit{f}}_{cm}/{\mathit{f}}_{ck}$ = exp(1.645 ${\mathit{V}}_{f_c}$) d
In situ factor ${\eta }_{is}$ e	${\mathit{V}}_{{\eta }_{is}}$ = 0.120	${\mu }_{{\eta }_{is}}$ = 0.95
Effective depth $\mathit{d}$	${\mathit{V}}_d$ = 0.050 b	${\mu }_d$ = 0.95 b
Model uncertainty ${\theta }_V$	${\mathit{V}}_{{\theta }_V}$ = 0.107 g	${\mu }_{{\theta }_V}$ = 1.10 g
Residual uncertainties	${\mathit{V}}_{Re{s}_V}$ = 0.046 h	–
Coefficient of variation and bias factor of resistance for shear and punching shear (members without shear reinforcement)	${\mathit{V}}_{RV}$ = 0.137 i	${\mu }_{RV}$ = 1.085 i

^a The values in this column refer to ratio between mean value and values utilized in the design formulae (characteristic or nominal). ^b These values are valid for $\mathit{d}$ = 200 mm. For other effective depths: ${\mathit{V}}_d$ = 0.05 (200/$\mathit{d}$${)}^{2/3}$ and ${\mu }_d$ = 1 − 0.05 (200/$\mathit{d}$${)}^{2/3}$. ^d This formula replaces the relationship given in Table 5.1 for the purpose of Annex A. ^e In situ factor ${\eta }_{is}$ accounts for the difference between actual in situ concrete strength in the structure ${\mathit{f}}_{c,ais}$ and the strength of the control specimen ${\mathit{f}}_c$. ^g The partial safety factor ${\gamma }_V$ is calibrated for the case of punching according to 8.4 of EN 1992-1-1:2023 and applies also for the case of shear without shear reinforcement according to 8.2.2. of EN 1992-1-1:2023. ^h The residual uncertainties refer to aggregate size, reinforcement area, and spacing and column size. ⁱ Based on the statistical values above and calculated using Equations (4) and (7).

From Equation (1), the reliability index $\beta$ is estimated as

$$\beta ={\displaystyle \frac{\ln ({\gamma }_R·{\mu }_R)}{{\alpha }_R·V_R}}$$

(8)

2.2. Considerations on the Fundamentals of the Method in Annex A of EN 1992-1-1:2023

2.2.1. Annex D of EN 1990:2002 + A1:2005 + A1:2005/AC:2010

The method offered in Annex A of EN 1992-1:2023 (Equation (1)) is streamlined from the procedure included in Annex D of EN 1990:2002 + A1:2005 + A1:2005/AC:2010 [27]. The code offers a procedure to determine the partial safety factor for the resistance side, in which experimental data is compared to the empirical values estimated for the resistance model. The overarching procedure entails several steps, as listed in the Appendix A section of this manuscript (Table A1).

In order to use the Annex D procedure, a resistance function ${\mathit{r}}_t$ should be derived, which is denoted as

$${\mathit{r}}_t={\mathit{g}}_{rt}\left(\underline{\mathit{X}}\right)$$

(9)

Here, the vector of the basic variables $\underline{\mathit{X}}$ may refer, for example, to realizations of concrete compressive strength, yield strength, or geometrical properties.

In the procedure, the theoretical estimate ${\mathit{r}}_t$ is compared to the experimental one ${\mathit{r}}_e$, which is, in principle, based on numerical (advanced FEM-analyses) or physical (laboratory) test results [35]. The procedure considers possible deviations due to random and model uncertainties. To account for the relationship between the theoretical and the experimental estimates, the resistance function expressed in Equation (9) may be rewritten with a correction factor $\mathit{b}$:

$$\mathit{r}=\mathit{b}·{\mathit{g}}_{rt}\left(\underline{\mathit{X}}\right)=\mathit{b}·{\mathit{g}}_{rt}\left\{{\mathit{X}}_1,{\mathit{X}}_2,\dots ,{\mathit{X}}_i\right\}$$

(10)

Furthermore, approximations about the moments of distributions of basic variables can be found by expansion in a Taylor series about the mean values [35]. Considering that the Taylor series is truncated after the linear terms, i.e.,

$$\mathit{r}\cong \mathit{b}·{\mathit{g}}_{rt}\left(\underline{{\mathit{X}}_m}\right)+\sum _{i=1}^n\mathit{b}·({\mathit{X}}_i-{\mathit{X}}_{m,i})·{\displaystyle \frac{\partial {\mathit{g}}_{rt}}{\partial {\mathit{X}}_i}}$$

(11)

the first-order mean value $\mathit{E}\left(\mathit{r}\right)$ and the coefficient of variation ${\mathit{V}}_{rt}$ of the resistance are determined through Equations (12) and (13), respectively:

$$\mathit{E}\left(r\right)\cong \mathit{b}·{\mathit{g}}_{rt}\left(\underline{{\mathit{X}}_m}\right)$$

(12)

$${\mathit{V}}_{rt}^2\cong {\displaystyle \frac{1}{{\mathit{g}}_{rt}^2\left(\underline{{\mathit{X}}_m}\right)}}·\sum _{i=1}^n{\left({\displaystyle \frac{\partial {\mathit{g}}_{rt}}{\partial {\mathit{X}}_i}}·{\sigma }_i\right)}^2$$

(13)

Note that Equation (13) is based on the assumption that the basic variables are stochastically independent and are obtained from the truncated series of Equation (11).

Annex D explicitly allows for a simplification of the general procedure, where the resistance function is described by a simple product function:

$$\mathit{r}=\mathit{b}·{\mathit{r}}_t·\delta =\mathit{b}\left\{{\mathit{X}}_1·{\mathit{X}}_2·\dots ·{\mathit{X}}_i\right\}·\delta$$

(14)

with the random variable $\delta$ referring to the error term (i.e., model uncertainties). For Equation (14), the mean value $\mathit{E}\left(\mathit{r}\right)$ and the variance ${\mathit{V}}_r^2$ can be estimated through Equations (15) and (16), respectively.

$$\mathit{E}\left(\mathit{r}\right)\cong \mathit{b}\left\{E\left({\mathit{X}}_1\right)·E\left({\mathit{X}}_2\right)·\dots ·E\left({\mathit{X}}_i\right)\right\}=\mathit{b}·{\mathit{g}}_{rt}\left(\underline{{\mathit{X}}_m}\right)={\mu }_{RM}·{\mathit{R}}_k$$

(15)

$${\mathit{V}}_r^2\cong ({\mathit{V}}_{\delta }^2+1)·\left[\prod _{i=1}^j({\mathit{V}}_{Xi}^2+1)\right]-1={\mathit{V}}_{RM}^2$$

(16)

As is implicit from the general procedure, the term ${\mathit{V}}_{\delta }$ refers to the coefficient of variation of the error term (i.e., model uncertainties) $\delta$. In turn, the term ${\mathit{V}}_{Xi}$ refers to the coefficient of variation of the basic variables ${\mathit{X}}_i$. Equation (17) combines the effect of scatter due to design model and scatter due to the basic variables:

$$({\mathit{V}}_r^2+1)=({\mathit{V}}_{\delta }^2+1)({\mathit{V}}_{rt}^2+1)$$

(17)

with ${\mathit{V}}_{rt}^2$ = ${\sum }_{i=1}^j{\mathit{V}}_{Xi}^2$. The code allows to simplify Equation (17) if the coefficients of variation ${\mathit{V}}_{\delta }$ and ${\mathit{V}}_{rt}$ are small:

$${\mathit{V}}_r^2\cong {\mathit{V}}_{\delta }^2+{\mathit{V}}_{rt}^2={\mathit{V}}_{RM}^2$$

(18)

If a large number of tests are available ($\mathit{n}$ > 100), the design value of the resistance should satisfy the following condition:

$${\mathit{r}}_d=\mathit{b}·{\mathit{g}}_{rt}\left(\underline{{\mathit{X}}_m}\right)·\exp (-{\mathit{k}}_{d,\infty }·\mathit{Q}-0.5·{\mathit{Q}}^2)$$

(19)

with ${\mathit{k}}_{d,\infty }$ being the design fractile factor for $\mathit{n}$ → ∞ (this value is offered in Annex D: ${\mathit{k}}_{d,\infty }$ = 3.04). The term $\mathit{Q}$ is expressed as

$$\mathit{Q}={\sigma }_{\ln \left(r\right)}=\sqrt{ln({\mathit{V}}_{rt}^2+1)}$$

(20)

In this way, the design value of the resistance considers both uncertainties—the one due to the scatter of the basic variables and the one related to simplifications introduced in the design model [35]. It also corresponds to the selected reliability level $\beta$ according to consequence classes and corresponding reliability classes.

By assuming $\mathit{b}$ = 1.0 and ${\mathit{k}}_{d,\infty }$ = ${\alpha }_R$·$\beta$ in Equation (19), the reliability index $\beta$ can be estimated as

$$\beta =-{\displaystyle \frac{1}{{\alpha }_R·\mathit{Q}}}·\left(\ln \left({\displaystyle \frac{{\mathit{r}}_d}{{\mathit{g}}_{rt}\left(\underline{{\mathit{X}}_m}\right)}}\right)+0.5·{\mathit{Q}}^2\right)$$

(21)

By using the assumptions expressed in Equations (22) and (23):

$${\mathit{r}}_d={\displaystyle \frac{1}{{\gamma }_R}}·{\mathit{g}}_{rt}\left(\underline{{\mathit{X}}_{nom}}\right)$$

(22)

$${\mu }_R={\displaystyle \frac{\underline{{\mathit{X}}_m}}{\underline{{\mathit{X}}_{nom}}}}$$

(23)

Equation (21) can be extended to Equation (24)

$$\beta ={\displaystyle \frac{1}{{\alpha }_R·\mathit{Q}}}·\ln ({\gamma }_R·{\mu }_R)-{\displaystyle \frac{1}{{\alpha }_R·\mathit{Q}}}·0.5·{\mathit{Q}}^2$$

(24)

with $\underline{{\mathit{X}}_{nom}}$ referring to the nominal values of the basic input variables. Note that, for coefficients of variation ${\mathit{V}}_R$ smaller than 0.20, the expression Q can be expressed by ${\mathit{V}}_R$ with a deviation of less than 1%. The approximated $\beta$ value is estimated as

$${\beta }_{tgt}\cong {\displaystyle \frac{\ln ({\gamma }_R·{\mu }_R)}{{\alpha }_R·{\mathit{V}}_R}}-{\displaystyle \frac{1}{{\alpha }_R·{\mathit{V}}_R}}·0.5·{\mathit{V}}_R^2$$

(25)

By comparing the estimation of the reliability index $\beta$ through the approach proposed in Annex A (Equation (8)), only the second leg of Equation (25) is different. Note that, for a sensitivity factor ${\alpha }_R$ of 0.8 and for a ${\mathit{V}}_{RM}$ value smaller than 0.2, the second leg results are smaller than 0.125. Yet, Equation (8) is still a simplification of Annex D and leads to higher reliability indices $\beta$.

2.2.2. Mean Value First-Order Second Moment

The basis of the approach offered in Annex D of EN 1990:2002 + A1:2005 + A1:2005/AC:2010 [27] is the Mean Value First-Order Second Moment (MVFOSM) method. The MVFOSM method was proposed by Freudenthal in the 1950s [36] and was utilized to derive early versions of reliability-based design formats (e.g., [37,38,39,40]). In a nutshell, the MVFOSM method is the simplest and least expensive reliability-based technique that belongs to the family of First-Order Reliability Methods (FORMs). The method is based on the first-order Taylor series approximation of the limit state function $\mathit{g}({\mathit{x}}_1,\dots ,{\mathit{x}}_m)$, which is linearized at the mean values $\overrightarrow{m}$ of the basic variables (i.e., the derivatives of the function are at the mean values) (e.g., [39,41,42,43,44,45,46]):

$$\mathit{g}({\mathit{x}}_1,\dots ,{\mathit{x}}_n)\approx \mathit{g}({\mathit{m}}_{x1},\dots ,{\mathit{m}}_{xn})+\sum _{i=1}^m({\mathit{x}}_i-{\mathit{m}}_{xi}){\displaystyle \frac{\partial g}{\partial {\mathit{x}}_i}}{|}_{m_i}$$

(26)

The mean value ${\mathit{m}}_M$ is determined as

$${\mathit{m}}_M\approx \mathit{g}\left(\underline{\mathit{m}}\right)$$

(27)

The coefficient of variation ${\mathit{V}}_M$ is estimated as

$${\mathit{V}}_M^2={\displaystyle \frac{{\sigma }_M^2}{{\mathit{m}}_M^2}}$$

(28)

with the variance ${\sigma }_M^2$ being defined as

$${\sigma }_M^2\approx \sum _{i=1}^n{\left({\displaystyle \frac{\partial g}{\partial {\mathit{x}}_i}}{|}_{m_i}\right)}^2·{\sigma }_{Xi}^2$$

(29)

The reliability index $\beta$ results as

$$\beta ={\displaystyle \frac{{\mathit{m}}_M}{{\sigma }_M}}$$

(30)

Nonetheless, the MVFOSM method is known to have two main limitations (e.g., [39,41,42,43,44,45,46]). First, the results are only exact (i.e., “truly” accurate) for linear functions since the Taylor approximation is conducted at the mean value of the joint density function of the basic variables, In case the function is highly nonlinear, a linear approximation to such nonlinear function introduces an integration error and leads to less accurate estimations of the mean and variance of the limit state function. The accuracy associated with the estimated mean and variance deteriorates rapidly as the degree of nonlinearity of the limit state function increases (e.g., [39,41,42,43,44,45,46]).

Second, the MVFOSM method has an invariance problem (e.g., [39,41,42,43,44,45,46]). The results produced by an MVFOSM fail to remain constant under different but mathematically equivalent formulations of the limit state function. This is a problem not only for nonlinear limit state functions but also for certain linear forms [44]. This problem is illustrated through the basic example offered in Table 4, where it can be observed that, for a mathematically equivalent function, three distinct reliability indices $\beta$ are obtained when they are determined with the MVFOSM method. By calculating the reliability index $\beta$ according to an Advanced First-Order Reliability Method (A-FORM) (in this case, the algorithm of Hasofer and Lind [37] was adopted; see Section 3), the invariant reliability problem appears to be tackled.

Table 4. Illustration of the invariance problem in the MVFOSM.

Limit State Function: $\mathit{g}(\mathit{r},\mathit{e})$ = 0	MVFOSM	A-FORM (According to Hasofer–Lind Algorithm [37])
$\mathit{g}(\mathit{r},\mathit{e})$ = ${\mathit{r}}^3$ − $\mathit{e}$ − 2 = 0	$\beta$ = 5.33	$\beta$ = 10.85
$\mathit{g}(\mathit{r},\mathit{e})$ = ${\mathit{r}}^2$ − ${\displaystyle \frac{e}{r}}$ − ${\displaystyle \frac{2}{r}}$ = 0	$\beta$ = 7.84	$\beta$ = 10.85
$\mathit{g}(\mathit{r},\mathit{e})$ = ${\displaystyle \frac{r^3}{e}}$ − 1 − ${\displaystyle \frac{2}{e}}$ = 0	$\beta$ = 4.31	$\beta$ = 10.85

Assumptions for the basic variables in terms of mean value and standard deviation: $\mathit{r}$ ∼ normally distributed (5; 0.3); $\mathit{e}$ ∼ normally distributed (3; 0.4).

The challenges around the MVFOSM formulation are symbolically illustrated in Figure 1 for the simple case representing the basic variables $\mathit{r}$ and $\mathit{e}$ in which $\mathit{g}(\mathit{r},\mathit{e})$ = ${\mathit{r}}^3$ − $\mathit{e}$ − 2 (see assumptions for the basic variables in Table 4). As explained, the Taylor approximation in the MVFOSM method is at the mean value, which is the origin in the standard normal space. Alternatively, when using an A-FORM (in this case, the algorithm of Hasofer and Lind [37] was also utilized), the Taylor approximation is at the so-called “design-point” (see Section 3). As observed in Figure 1, the approximation at the mean value introduces an integration error, which can be expressive in dependency of the curvature of the function. In this case, the ${\beta }_{Taylor,MV}$ determined with an MVFOSM is smaller than the ${\beta }_{Taylor,DP}$ computed with an A-FORM method, thereby potentially leading to more conservative design solutions. Note, however, that a distinct limit state function with a different curvature may change the trend of the estimated structural reliability level.

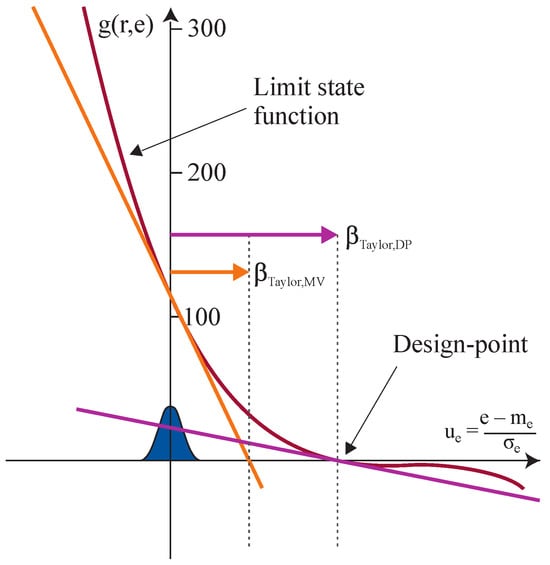
Figure 1. Side view of the limit state function $\mathit{g}(\mathit{r},\mathit{e})$ = ${\mathit{r}}^3$ − $\mathit{e}$ − 2 (see assumptions for the basic variables in Table 4) and Taylor approximations according to MVFOSM at the mean value and A-FORM at the design-point.

3. Methods: Adjusting Partial Safety Factors Through Advanced Reliability-Based Methods

In structural engineering, the use of advanced reliability-based methods—commonly designated as Level II and Level III methods—is not a recent topic and is thoroughly covered in the literature (e.g., [3,25,42]). Yet, for the sake of clarity, a brief overview of the most common methods is offered in this section.

In a nutshell, Level II methods consist of approximating the limit state function to a first- or second-order function using First- or Second-Order Reliability Method (FORM or SORM, respectively). As described in Section 2, the MVFOSM method [36] is the most basic approach belonging to the family of FORM methods. However, to tackle the invariant reliability problem in MVFOSM, Hasofer and Lind [37] proposed an A-FORM, where the reliability index $\beta$ is defined as the shortest distance from the origin of reduced variables to the limit state surface in the standard normal space [39]. This method entails an iterative and linear approximation to the limit state function (i.e., the term first-order), and its linearization occurs around the most probable failure point—so-called design-point u* (Figure 2a,b). The computational procedure of the method can be summarized in the following steps (e.g., [41]):

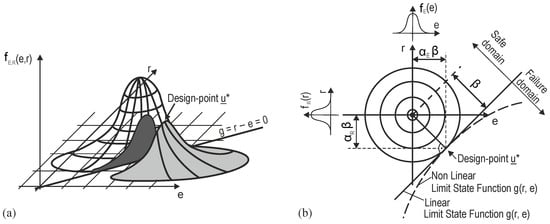
Figure 2. (a) Joint distribution density for two independent variables in the function $\mathit{g}(\mathit{r},\mathit{e})$ = $\mathit{r}$ ${\displaystyle -}$ $\mathit{e}$ and (b) respective projection of joint distribution density (adapted from [3,27,44,47,48,49]).

• The basic input variables are transformed using probabilistic transformation methods to the standard Gaussian image space. For the simplest case, when the two variables r (resistance) and e (load) are involved, the transformation is illustrated in Figure 2b.
• Then, the transformed image failure surface is approximated through a Taylor series expansion by a tangent hyperplane at the projection point by assuming suitable regularity of the failure surface at this point. The nearest point on the failure surface $\mathit{g}\left({\underline{\mathit{u}}}^{*}\right)=0$ is located by iteration. This is the design-point u*. The efficiency of the method depends on the algorithm utilized for the location of the design-point u*, which leads to the following optimization problem:

  $${\underline{\mathit{u}}}^{*}=argmin\parallel \underline{\mathit{u}}\parallel$$

  (31)
  In addition to the Hasofer and Lind [37] algorithm, the Rackwitz–Fiessler algorithm [50] and the NLPQL algorithm of Schittkowski [51], among others, are valid first-order calculation approaches.
• When the design-point u* is located, the probability of failure $p_f$ is assessed through

  $${\mathit{p}}_f=\Phi (-\beta )$$

  (32)

  with $\Phi$ corresponding to the integral of the standard normal distribution. The distance from the origin—labeled as the reliability index $\beta$—is then determined as

  $$\beta =-{\Phi }^{-1}\left({\mathit{p}}_f\right)$$

  (33)

Follow-up techniques based on SORM emerged to improve the accuracy of A-FORM methods. They are particularly relevant for strongly nonlinear limit state functions (e.g., [52]). SORM methods consist of approximating the limit state surface at the design-point u* by a second-order surface, which enables a better estimate of the probability of failure than using a single linear approximation at the global minimum distance point. These were developed by numerous academics, e.g., Breitung [53], Tvedt [54], and Hochenbichler et al. [55].

Level III methods are those that enable an even more accurate estimation of the probability of failure than those determined with Level II methods. Here, the safety verification is carried out with probabilistic methods with full consideration of the distribution functions of the basic variables and the exact limit state functions. To this end, a multi-dimensional integration of the function might be performed by means of direct integration by simplifying the integration through transforming the integral to a multi-normal joint probability density function or by applying numerical integration (e.g., Crude Monte Carlo simulations) [3,26,38]. These techniques are considered simple and robust, enabling handling any limit state function independent of its complexity [56]. The efficiency of Crude Monte Carlo simulation in its standard form does not depend on the dimension of the random variable space [56]. This technique is deemed accurate thanks to the strong law of large numbers and the central limit theorem if infinite computing budget is available. However, for complex structural problems, these simulations can demand considerable computational power and be rather time-consuming (e.g., [3,26,38,45]). To overcome such drawbacks, variance reduction techniques can reduce the variance (i.e., the error) of the estimator to obtain an accurate estimator in comparison to the Crude Monte Carlo estimator at the same computational costs (e.g., [57]). In principle, the computational cost of a sample run is reduced and the accuracy is maintained by using the same number of runs [45]. A wide range of variance reduction techniques are now available, such as Adaptive Sampling (e.g., [58,59,60]), Line Sampling (e.g., [61,62]), and Conditional Expectation techniques, including Directional Simulation [63] and Axis-Orthogonal Simulation [61], just to name a few. Albeit not particularly modern, Monte Carlo Importance Sampling remains one of the most well-established variance reduction techniques utilized to solve structural reliability problems either in its classic form (e.g., [41]) or through further algorithm adjustments, such as Sequential Importance Sampling [64]. Also, the Subset Sampling (SuS) technique has seen growing acceptance for exhibiting high precision and computational efficiency in the calculation of small failure probabilities and for being independent of prior knowledge obtained from simplified reliability techniques (e.g., first-order approximation techniques) (e.g., [65]).

4. Numerical Analysis

4.1. Numerical Example 1

In this numerical example, the following equation of a product form was considered:

$$R\left(\underline{\mathit{X}}\right)={\displaystyle \frac{X_1·X_2·X_3}{{\gamma }_{hyp}}}$$

(34)

The stochastic models for the basic variables $X_i$ are summarized in Table 5. The assessment of this numerical example followed the assumption that the basic variables are characterized by a normal distribution. Additionally, a hypothetical partial safety factor ${\gamma }_{hyp}$ equal to 1.60 was adopted. The probability of failure $p_f$ and the corresponding reliability index $\beta$ were estimated according to distinct methods. Equation (1) was utilized for the method proposed in Annex A of EN 1992-1-1:2023. Note that, according to EN 1990:2002 + A1:2005/AC:2010 [27], Equation (1) can be employed for ${\mathit{V}}_{RM}$ smaller than 0.20, as demonstrated in Table 5. For the application of Equation (1), a sensitivity factor ${\alpha }_R$ of 0.8 was considered, which is a reference value given in Table A.4 (NDP) of Annex A and in EN 1990:2002 + A1:2005/AC:2010. Equation (25) was utilized for the calculation according to Annex D of EN 1990:2002 + A1:2005/AC:2010. The assessment on the basis of A-FORM [37] and MC-IS (e.g., [41]) considered Equations (32) and (33), respectively.

Table 5. Numerical example 1: stochastic models for the basic variables.

Variable	Dist.	Bias Factor	Coefficient of Variation	Sensitivity Factor *
$X_1$	ND	1.05	0.15	0.85
$X_2$	ND	1.07	0.11	0.46
$X_3$	ND	1.10	0.07	0.26

${\mathit{V}}_{RM}$ = $\sqrt{{\mathit{V}}_{X_1}^2+{\mathit{V}}_{X_2}^2+{\mathit{V}}_{X_3}^2}$ = 0.199 < 0.20. ND: normal distribution. * Determined with A-FORM according to the algorithm of [37].

The results listed in Table 6 demonstrate that, under the assumption of a normal distribution, the calculation according to the method proposed in Annex A of EN 1992-1-1:2023 leads to a reliability index $\beta$ of 4.29, the highest value of the entire set of results. The calculation according to Annex D of EN 1990:2002 + A1:2005/AC:2010 yields a slightly smaller $\beta$ value: $\beta$ = 4.18. This variation is explained by the second leg of Equation (25), which is not considered in the method proposed in Annex A (Equation (1)). The calculation according to A-FORM generates a further reduced $\beta$ value ($\beta$ = 3.66), and the evaluation with the MC-IS leads to the smallest $\beta$ value of the entire scope of methods ($\beta$ = 3.57). The difference between the maximum and minimum $\beta$ values is 16.8%.

Table 6. Numerical example 1: comparison of probabilities of failure ${\mathit{p}}_f$ and reliability indices $\beta$.

Approach	Prob. of Failure ${\mathit{p}}_{\mathit{f}}$	Reliability Index $\mathit{\beta }$
Annex A	8.93 · ${10}^{-6}$	4.29
Annex D	1.46 · ${10}^{-5}$	4.18
A-FORM	1.26 · ${10}^{-4}$	3.66
MC-IS	1.79 · ${10}^{-4}$	3.57

4.2. Numerical Example 2

Let us now assume the same Equation (34) but with distinct stochastic models for the basic variables $X_1$, $X_2$, and $X_3$ (Table 7). As indicated in Table 7, the combined coefficient of variation ${\mathit{V}}_{RM}$ is smaller than the limit value established in EN 1990:2002 + A1:2005/AC:2010 [27] equal to 0.20. The same hypothetical partial safety factor ${\gamma }_{hyp}$ equal to 1.60 was considered. The results listed in Table 8 indicate that the method proposed in Annex A yields the highest $\beta$ value generated by the whole set of methods: $\beta$ = 4.98. The results follow the same trend identified in numerical example 1 with a slightly smaller $\beta$ value produced by the provisions of Annex D, with $\beta$ = 4.92. The use of advanced reliability-based approaches led to smaller $\beta$ values ($\beta$ = 4.62), with the results of the Monte Carlo simulation with Importance Sampling being the smallest of the whole set of results: $\beta$ = 4.56. The reliability indices $\beta$ estimated in this example indicate a difference of 8.43% between the maximum and minimum $\beta$ values, which is smaller than the difference calculated in numerical example 1.

Table 7. Numerical example 2: stochastic models for the basic variables.

Variable	Dist.	Bias Factor	Coefficient of Variation	Sensitivity Factor *
$X_1$	ND	1.03	0.07	0.70
$X_2$	ND	0.95	0.06	0.56
$X_3$	ND	0.97	0.05	0.45

${\mathit{V}}_{RM}$ = $\sqrt{{\mathit{V}}_{X_1}^2+{\mathit{V}}_{X_2}^2+{\mathit{V}}_{X_3}^2}$ = 0.10 < 0.20. ND: normal distribution. * Determined with A-FORM according to the algorithm of [37].

Table 8. Numerical example 2: comparison of probabilities of failure ${\mathit{p}}_f$ and reliability indices $\beta$.

Approach	Prob. of Failure ${\mathit{p}}_{\mathit{f}}$	Reliability Index $\mathit{\beta }$
Annex A	3.20 · ${10}^{-7}$	4.98
Annex D	4.30 · ${10}^{-7}$	4.92
A-FORM	1.90 · ${10}^{-6}$	4.62
MC-IS	2.60 · ${10}^{-6}$	4.56

4.3. Sensitivity Analysis of Influence on the Basic Variables

The results of both numerical examples suggest that the stochastic models selected for the basic variables play a critical role in the estimation of the reliability index $\beta$ alongside the methods selected for this estimation (i.e., Annex A, Annex D, A-FORM, and MC-IS). To illustrate such variation, the sensitivity factors of each basic variable were determined for each numerical example, expressing the weight (or importance) of the variable for the estimation of the $\beta$ values (Table 5 and Table 7). In both numerical examples, the basic variable $X_1$ has the highest sensitivity factor: 0.85 in numerical example 1 (Table 5) and 0.70 in numerical example 2 (Table 7). Therefore, the stochastic model of the variable $X_1$ was carefully analyzed.

Figure 3 represents the variation in the bias factor for the variable $X_1$ (i.e., the blue curve corresponds to numerical example 1, and the orange curve corresponds to numerical example 2). In both examples, the bias factors of $X_1$ that were determined with the methods proposed in Annex A of EN 1992-1-1:2023 [7] and Annex D of EN 1990:2002 + A1:2005/AC:2010 [27] led to higher reliability indices $\beta$ than those determined with advanced methods, i.e., A-FORM and MC-IS. In numerical example 1, the difference between these two groups of $\beta$ values (i.e., methods according to Annex A and according to Annex D vs. advanced methods) is approximately constant over the whole range of values considered for the bias factor. For the first group of methods, the $\beta$ values varied approximately between 3.9 and 4.1, while, for the second group of methods, the $\beta$ values varied approximately between 3.3 and 3.7. A similar trend is visible in numerical example 2, where the difference between the $\beta$ values generated by these two groups of methods appears approximately constant over the scope of values allocated to bias factors. Even though this difference is slightly smaller than the one attained in numerical example 1, an increased bias factor for the variable $X_1$ leads to a sharper increase in the $\beta$ values than the trend in numerical example 1. For the first group of methods, the $\beta$ values varied approximately between 4.7 and 5.8, while, for the second group of methods, the $\beta$ values varied approximately between 4.2 and 5.0.

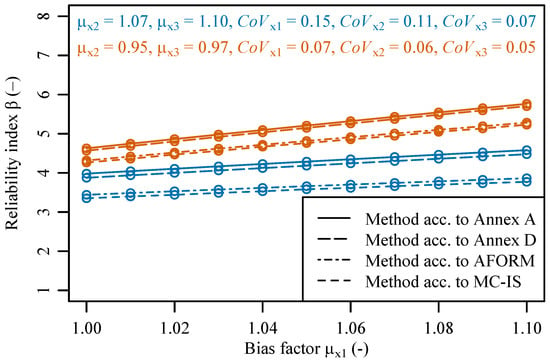
Figure 3. Sensitivity analysis for the bias factors of the basic variable $X_1$ on the reliability indices $\beta$ determined according to different methods (blue curve corresponds to numerical example 1, and the orange curve corresponds to numerical example 2).

Figure 4 represents the behavior of the coefficients of variation for the variable $X_1$ (i.e., the blue curve corresponds to numerical example 1 and the orange curve corresponds to numerical example 2). Similar to the trend in numerical example 1, the reliability indices $\beta$ generated with the methods prescribed in Annex A of EN 1992-1-1:2023 and in Annex D of EN 1990:2002 + A1:2005/AC:2010 led to higher $\beta$ values than those determined with the advanced methods, i.e., A-FORM and MC-IS. In numerical example 1, the differences between the sets of $\beta$ values generated through these two groups tend to decrease over the whole spectrum of coefficients of variation considered in the analysis. The difference is wider for the coefficients of variation between 0.01 and 0.06. For example, for a coefficient of variation of 0.01, the $\beta$ values vary approximately between 5.2 and 6.5. The difference gradually decreases up to a coefficient of variation of 0.06, with the $\beta$ values being in the range of 5.0 to 6.0, respectively, for the simplified methods (i.e., Annex A and Annex D) and for the advanced methods (i.e., A-FORM and MC-IS). The difference becomes approximately constant up to the coefficient of variation of 0.15, where the $\beta$ values vary between 3.8 and 4.8. Likewise, in numerical example 2, the difference between the sets of $\beta$ values generated through these two groups is approximately constant over the whole range of coefficients of variation. The $\beta$ values generated by the two groups differ by around 0.5-0.6. Yet, a sharp decrease in the trend for $\beta$ values is visible for coefficients of variation higher than 0.06. While for a coefficient of variation of 0.01 the $\beta$ values sit between 6.0 and 6.7, for a coefficient of variation of 0.06, the $\beta$ values sit between 4.9 and 5.4, reaching $\beta$ values in the range of 3.2 to 2.8 when the coefficient of variation for the variable $X_1$ is equal to 0.15.

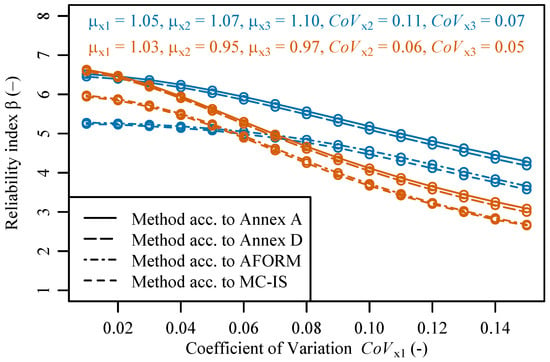
Figure 4. Sensitivity analysis for coefficients of variation of the basic variable $X_1$ on the reliability indices $\beta$ determined according to different methods (blue curve corresponds to numerical example 1, and the orange curve corresponds to numerical example 2).

4.4. Discussion

The results of both numerical examples suggest that the application of the method proposed in Annex A of EN 1992-1-1:2023 [7] needs to be carefully interpreted since, based on the adopted premises for the investigated examples, the method leads to the least conservative solutions. Thus, in practical structural problems, such a tendency may lead to unsafe design solutions. For a more detailed analysis and “exact” solutions, a full-probabilistic approach should be adopted in combination with advanced reliability-based approaches.

Nonetheless, it should be emphasized that the method proposed in Annex A of EN 1992-1-1:2023 is easy to utilize, which is especially advantageous for practitioners. The method enables accounting for the individual uncertainties of the basic variables involved in the adjustment of such partial safety factors. When specific material or geometric information becomes available from laboratory or in situ testing, such information can be incorporated in the stochastic models of the basic variables in a simplistic manner. Moreover, for situations where limited data exists, the use of this method might be beneficial. The method offers potential for preliminary assessments before more detailed reliability-based analyses are conducted.

Another point concerns the role of stochastic models for the basic variables. The sensitivity analysis conducted in Section 4.3 demonstrated that, since the method proposed in Annex A considers the bias factors and the coefficients of variation, even minor input changes can greatly affect the resulting $\beta$ values. This analysis highlights the importance of selecting robust models for the most relevant basic variables.

5. Conclusions

From this investigation, the following conclusions are derived:

• The newly revised Annex A of EN 1992-1-1:2023 introduces a rather simple and objective format to adjust partial safety factors for the resistance side (concrete ${\gamma }_C$, reinforcing steel ${\gamma }_S$, and shear and punching shear without shear reinforcement ${\gamma }_V$). Since it does not require complex probabilistic-based knowledge, its simplicity is an advantage for engineering practitioners.
• Considering the characteristics of the simplified method, it can be argued that it might be an interesting approach to assess the feasibility of adjusting partial safety factors in preliminary analyses.
• Yet, the theoretical foundations of the simplified method in Annex A have some well-known challenges:

  –

  By being a simplified approach of Annex D of EN 1990:2002, the proposed method only applies to design verifications with a specific mathematical formulation (i.e., a function applicable to a product form) and for the cases of small coefficients of variation of basic variables.

  –

  The limitations applied to the MVFOSM method—as one of the most basic reliability-based approaches—are also applicable to the proposed method. Among those limitations are the inaccuracy of the results when applied in nonlinear limit state functions as well as the invariance problems associated with the specific mathematical formulation of limit state functions.

  –

  These limitations may influence the accuracy of the resulting probabilities of failure and reliability indices and have implications on the reliability of the structural component being designed.

• The use of advanced reliability-based methods—such as Level II or Level III methods— has demonstrated efficiency and accurate results in the assessment of structural reliability level and thus for the adjustment of partial safety factors.
• Conditional on the assumptions taken in the numerical examples, the results indicate that the reliability indices obtained from the simplified method can be higher than those attained with advanced reliability-based methods. These results suggest that the use of the simplified method might have to be carefully evaluated when applied to the resolution of real structural problems.
• This investigation demonstrated that the stochastic models for the basic variables should be carefully selected since minor input changes can significantly affect $\beta$ values.

From this investigation, a set of avenues was identified for future work. A thorough verification and validation of the factors offered in Annex A of EN 1992-1-1:2023 is recommended. To this end, individual and combined failure mechanisms and their impact on the proposed values shall be investigated. For those analyses, a wide scope of modern and robust reliability-based techniques and computational platforms are available (e.g., [25,26,29,31,32,33]). Another possibility is to consider more advanced stochastic models for the basic variables through the use of Bayesian updating methods (e.g., [66,67,68,69,70,71,72]). These are particularly useful when experimental data or expert input is available. The inclusion of a methodology that considers the interplay between quality control, stochastic models of the basic variables, reliability levels, and their differentiation and corresponding partial factor reduction can be further investigated (e.g., [68,69,70,71,72]). Further work could be considered concerning existing structures since Annex A of EN 1992-1-1:2023 also includes provisions for existing structures. A specific application could be in the field of structural resilience (e.g., [73,74,75,76,77]). Structural resilience analyses aim at assessing the capacity to withstand and recover efficiently from extreme events [77]. For this reason, the concept of resilience can be applied to preventive assessment. The implications of adjusted partial safety factors on the resilience of a structural component, while maintaining the required safety level, might be investigated.