What Is the Internal Pressure That Initiates Damage in Cementitious Materials during Freezing and Thawing? A Micromechanical Analysis
Abstract
:1. Introduction
2. Fundamentals of Continuum Micromechanics
3. Multiscale Model for Freezing Mortar
3.1. Microcracking of Mortar
3.2. Stiffness of Partially Frozen Mortar
3.3. Pressure Required at Microcrack Initiation
3.4. Air-Pores Reduce the Internal Pressure
4. Results
5. Discussion
6. Conclusions
- Multiscale modeling using a combination of micromechanics, fracture mechanics and poromechanics provides a deeper insight into the mechanism of damage and failure of cementitious materials such as concrete and mortar during freezing and thawing.
- All parameters in the model are physical and can be measured experimentally.
- Microcrack initiation occurs when the internal pressure is above the unsaturated tensile strength of the material.
- The critical pressure for microcrack initiation depends on path history, i.e., for the same state of ice saturation, higher pressures are required for microcrack growth during freezing than during thawing.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| REV | Representative Elementary Volume |
| w/c | Water-to-cement ratio |
References
- UN. World Urbanization Prospects: The 2018 Revision; Technical Report; UN Department of Economic and Social Affairs Population Division: New York, NY, USA, 2018. [Google Scholar]
- Powers, T.C.; Helmuth, R. Theory of volume changes in hardened portland-cement paste during freezing. In Proceedings of the Highway Research Board, Washington, DC, USA, 13–16 January 1953; Volume 32. [Google Scholar]
- Scherer, G.W.; Valenza, J. Mechanisms of frost damage. Mater. Sci. Concr. 2005, 7, 209–246. [Google Scholar]
- Scherer, G.W. Freezing gels. J. Non-Cryst. Solids 1993, 155, 1–25. [Google Scholar] [CrossRef]
- Coussy, O.; Monteiro, P.J. Poroelastic model for concrete exposed to freezing temperatures. Cem. Concr. Res. 2008, 38, 40–48. [Google Scholar] [CrossRef]
- Setzer, M.J. Micro-ice-lens formation in porous solid. J. Colloid Interface Sci. 2001, 243, 193–201. [Google Scholar] [CrossRef]
- Zhou, T.; Mirzadeh, M.; Pellenq, R.J.M.; Bazant, M.Z. Freezing point depression and freeze-thaw damage by nanofluidic salt trapping. Phys. Rev. Fluids 2020, 5, 124201. [Google Scholar] [CrossRef]
- Guo, J.; Sun, W.; Xu, Y.; Lin, W.; Jing, W. Damage Mechanism and Modeling of Concrete in Freeze–Thaw Cycles: A Review. Buildings 2022, 12, 1317. [Google Scholar] [CrossRef]
- Vu, G.; Diewald, F.; Timothy, J.J.; Gehlen, C.; Meschke, G. Reduced order multiscale simulation of diffuse damage in concrete. Materials 2021, 14, 3830. [Google Scholar] [CrossRef] [PubMed]
- Timothy, J.J.; Meschke, G. A cascade continuum micromechanics model for the effective elastic properties of porous materials. Int. J. Solids Struct. 2016, 83, 1–12. [Google Scholar] [CrossRef]
- Li, S.; Wang, G. Introduction to Micromechanics and Nanomechanics; World Scientific Publishing Company: Hackensack, NJ, USA, 2008. [Google Scholar]
- Qu, J.; Cherkaoui, M. Fundamentals of Micromechanics of Solids; Wiley Online Library: Hoboken, NJ, USA, 2006; Volume 735. [Google Scholar]
- Benveniste, Y. A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech. Mater. 1987, 6, 147–157. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Pichler, B.; Hellmich, C.; A. Mang, H. A combined fracture-micromechanics model for tensile strain-softening in brittle materials, based on propagation of interacting microcracks. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 111–132. [Google Scholar] [CrossRef]
- Dormieux, L.; Kondo, D.; Ulm, F.J. Microporomechanics; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Pichler, B.; Hellmich, C. Upscaling quasi-brittle strength of cement paste and mortar: A multi-scale engineering mechanics model. Cem. Concr. Res. 2011, 41, 467–476. [Google Scholar] [CrossRef]
- Iskhakov, T.; Giebson, C.; Timothy, J.J.; Ludwig, H.M.; Meschke, G. Deterioration of concrete due to ASR: Experiments and multiscale modeling. Cem. Concr. Res. 2021, 149, 106575. [Google Scholar] [CrossRef]
- Mura, T. Micromechanics of Defects in Solids; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
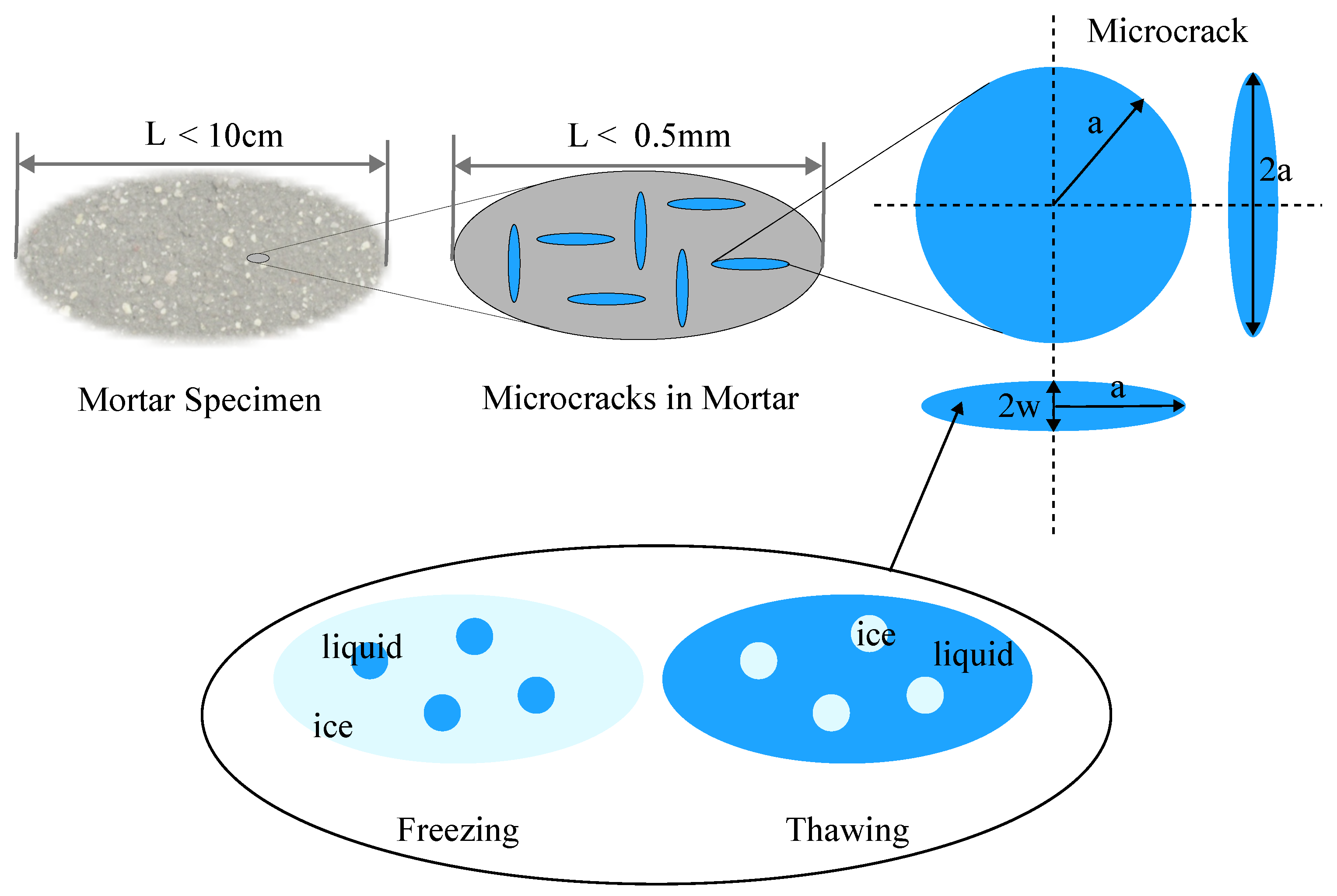
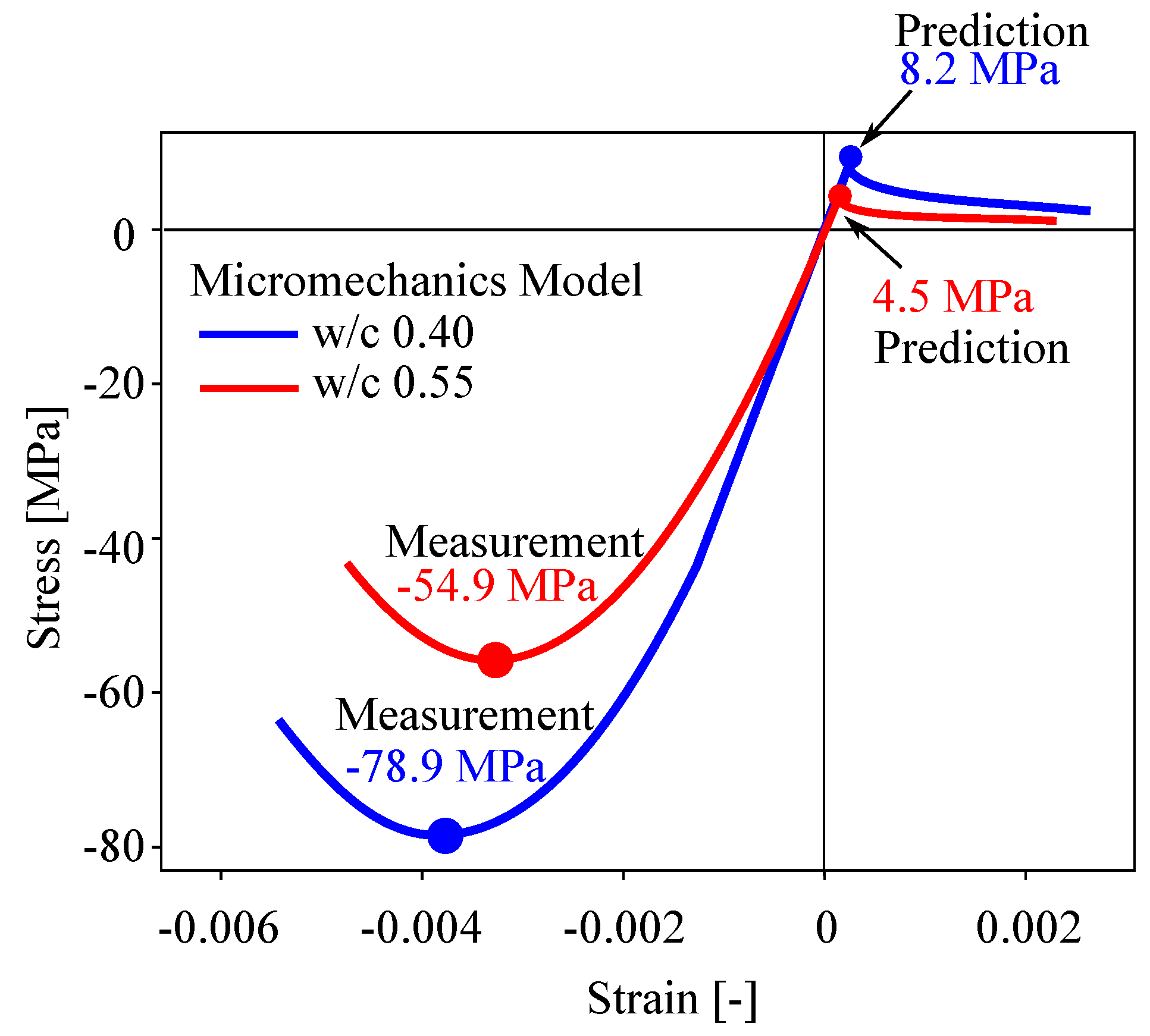
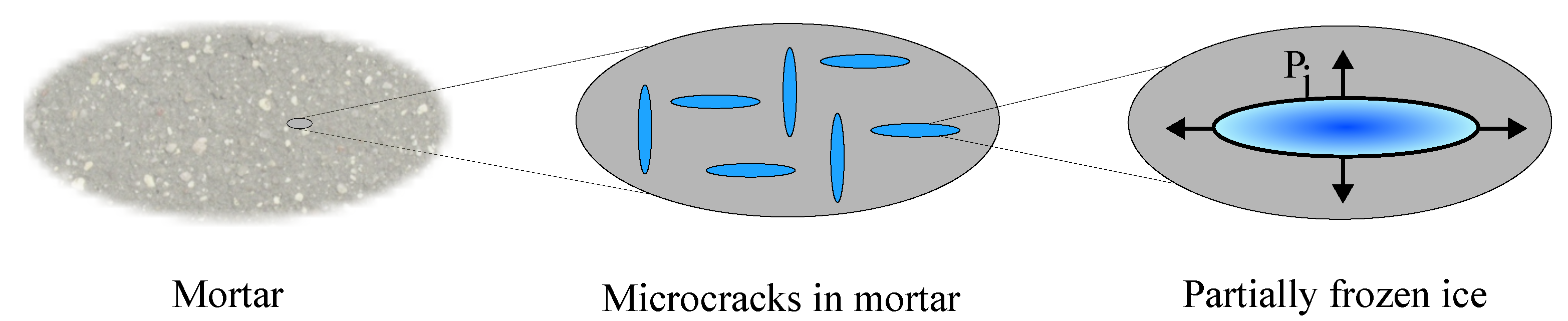

| Property | M-40 | M-55 |
|---|---|---|
| Cement type | CEM I | |
| Water-to-Cement ratio (w/c) | 0.4 | 0.55 |
| Cement content | 680 kg/m | 560 kg/m |
| Water content | 272 kg/m | 308 kg/m |
| Fine aggregate content | 1360 kg/m | 1312 kg/m |
| Young’s Modulus | 34.5 GPa | 30.15 GPa |
| Compressive strength | 78.90 MPa | 54.9 MPa |
| Microcrack size | 100 μm | |
| Microcrack aspect ratio (w/a) | 0.1 | |
| Calibrated Model Parameters | ||
| 0.073 [-] | 0.025 [-] | |
| 0.22 N/m | 0.09 N/m | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Timothy, J.J.; Haynack, A.; Kränkel, T.; Gehlen, C. What Is the Internal Pressure That Initiates Damage in Cementitious Materials during Freezing and Thawing? A Micromechanical Analysis. Appl. Mech. 2022, 3, 1288-1298. https://doi.org/10.3390/applmech3040074
Timothy JJ, Haynack A, Kränkel T, Gehlen C. What Is the Internal Pressure That Initiates Damage in Cementitious Materials during Freezing and Thawing? A Micromechanical Analysis. Applied Mechanics. 2022; 3(4):1288-1298. https://doi.org/10.3390/applmech3040074
Chicago/Turabian StyleTimothy, Jithender J., Alexander Haynack, Thomas Kränkel, and Christoph Gehlen. 2022. "What Is the Internal Pressure That Initiates Damage in Cementitious Materials during Freezing and Thawing? A Micromechanical Analysis" Applied Mechanics 3, no. 4: 1288-1298. https://doi.org/10.3390/applmech3040074
APA StyleTimothy, J. J., Haynack, A., Kränkel, T., & Gehlen, C. (2022). What Is the Internal Pressure That Initiates Damage in Cementitious Materials during Freezing and Thawing? A Micromechanical Analysis. Applied Mechanics, 3(4), 1288-1298. https://doi.org/10.3390/applmech3040074






