Abstract
The use of cross-linking polymers such as liquid silicone rubber (LSR) can replicate serviceable surfaces with nano- and microstructures via the injection molding process. Laser ablation can be used to introduce microstructures into molding tools, while nanostructures are generated via PVD coating processes on the tools. This is why nanostructures are built using self-organized layer growth. The aim of this study was to generate evidence of direction-dependent coefficients of friction of elastomeric surfaces in dry or lubricated contact in boundary friction. Models of the dry friction of elastomeric surfaces, such as Schallamach waves or stick-slip cycles, were used to describe the friction modulation of such surfaces. Assumptions for model contacts against smooth partners, both dry and with lubrication, as well as assumptions for the interaction of structures with smooth surfaces, were investigated. It was found that for elastomer surfaces with Shore hardness 50, nanostructures are suitable for creating a direction-dependent friction increase in static and sliding friction. Friction reductions with defined microstructures are possible if their periodicity seems to interact with the wavelength of possible Schallamach waves. The choice of lubrication determines the forced wetting of the contact, but due to the structuring, there is a continuous transition to mixed friction.
1. Introduction
When soft bodies slide against relatively rigid bodies, phenomena such as the Schallamach wave [1] occur, especially at low pressures and low sliding speeds. In general, stick-slip instabilities of soft surfaces occur, which, in certain constellations, can grow into wave-like, wrinkled movements. These waves can cause vibrations, noise, structural wear and seal leakage in machine elements such as seals, sliding elements, tires and conveyor belts. Intensive efforts are being made to either prevent or predict these negative effects. For the latter, detailed knowledge is constantly being expanded. Structures, coatings or lubricants are used to mitigate these effects.
Polytetrafluoroethylene (PTFE) or Perfluoropolyether (PFPE) grease is a low-cohesive-energy lubricant commonly used for elastomer contacts. It is often used to reduce friction and wear when oil-based lubrication is not applicable. PTFE transfer layers of 15 nm allow a local coefficient of friction as low as 0.03 to 0.04 [2], and if filled with alumina nanoparticles, its wear resistance can be improved by a factor of 1000 [3]. However, its use is increasingly being avoided, so substitutes are being sought. The possibilities of using structuring or coating are increasingly interesting.
Promising approaches have been chosen for the combined use of coatings and structures [4]. For the optimized use of both possibilities, many degrees of freedom can be selected, so efforts ranging from simple geometric approaches to the mapping of bioinspired solutions have been undertaken, and successes have been achieved. A recent review of multi-scale surface texturing in tribology was presented by Grützmacher et al. [5]. The different texturing methods listed included microcutting, microcoining, chemical etching, chemical vapor deposition, physical vapor deposition, focused ion beam texturing, thermal laser interference texturing and electrical beam texturing, but not molding. Various tribological systems were listed, from dry to lubricated cases, but none with a focus on elastomeric surfaces was found. Ripoll et al. [6] investigated the contact behavior of textures in plastic by finite element simulation, and Liu et al. [7] investigated the effect of grooves in coated steel surfaces.
A desired change in the friction behavior via nanostructured surfaces, for example, can be separated according to different possibilities depending on elasticity, interaction energies, interlocking and contact control.
By using a soft, low-modulus contact partner or flexible structural elements, friction can be increased. The controlled loosening of the adhesive bond can be achieved analogously to a gecko foot via a targeted deformation of the structure. In a contact with granular media, the friction can be increased by enhancing the interlocking effect by adapting the shape of the granules and the structure. Bioinspired surfaces inspired by the gecko with the aim of increasing friction were investigated by Tramsen et al. [8,9].
By using a high-modulus contact partner and reducing the contact areas, friction can be reduced. By using a structure adapted to the sliding stick-slip contact, the friction can also be reduced with a low-modulus contact partner in analogy to the skin of a Californian king snake.
M. Scherge and S. Gorb [10] introduced essential tribological descriptions for the micro- and nanotribology of structures, which are still applied today and include the description of the velocity dependence of friction in stick-slip processes, the influence of adhesion, capillary action and viscoelasticity, the description of interactions via energies and the effect of topography on friction features. They already described nanoscale stick-slip processes and defined a critical velocity that is antiproportional to the slip time. Their work focused, among other things, on the adhesive function of insect feet on smooth surfaces. Ch. Greiner recently studied the tribological effect of the skin of the sandfish [11], which is able to swim fish-like through desert sand. The effect tends to be exerted via the change in interlocking. They applied bioinspired structures with a dimple shape in steel via laser texturing and performed dry and lubricated tribological measurements for comparison [12]. In individual cases, a reduction in friction of 80% was obtained for lubricated contacts at higher speeds. A 50% reduction in dry friction of polyetheretherketon (PEEK) against steel could be obtained, but the normal pressure was well below that of a technical application at 0.05 MPa to generate resistant PEEK structures. For dry contact, a structure can dominantly enable a friction coefficient reduction by simply reducing the contact area. Various bioinspired surfaces have been imaged and investigated using high-resolution techniques, but these are not yet applicable on a large technical scale.
Our own work has shown a reduction in friction of >20% for prismatic structures in cyclic olefin copolymer and dimpled structures in polyethylene (PE). For the prismatic structures, the formation of a reduced real contact area was causal and visible. The low wear resistance caused by the high plastic deformability of PE was problematic. These results motivated the following approach.
To avoid the rapid wear of the structure, elastomers are preferable to thermoplastics.
The wear of elastomers in smooth contacts is described by fatigue processes [13]. The deformation of an adhesively sliding contact generates tensile strains, which drive a fatigue crack network.
The formation of friction on elastomers was systematically studied by Wu-Bavouzet et al. [14], among others, in contacts with smooth surfaces. The effect of surface elasticity, interfacial energies and viscosity on the formation of continuous or stick-slip-dominated gliding was described. At least three different velocity regimes were distinguished for dry contacts. At low speeds, thermal fluctuations determine the formation of the adhesive bond and produce continuous gliding. At higher speeds, a minimum of the frictional force versus velocity is generated due to the energetic equivalency of elastic strain and adhesion. High velocities lead to a cyclic tearing off from the adhesively formed contact and a reduction in the pronounced contact surface. As a result, a slip movement occurs in the surface until a bonding or stick phase occurs again. The elastic length that is overcome until a slip phase occurs again is described by the ratio of interfacial energies and shear elasticity. The ratio of this length and the mean slip velocity is a characteristic time that is important for deriving further mechanisms. At higher speeds, continuous sliding is achieved. For contacts with a large elastic length, depending on the pressure and the sliding velocity, the formation of Schallamach waves occurs [15]. The description and modeling of the formation of a Schallamach wave are under continuous development, and its validation depends on experimental and numerical characterization. The basic description is that, prior to contact, the elastomer is lifted by the pressure in the form of a lip, which develops as a wave in or around the contact. Rand and Crosby [16,17] described how these waves develop with their wavelength or speed as a function of the elastic length. Schapery [18] described a model that includes the stable formation of Schallamach wavelengths lschallamach in a certain window of the interfacial shear stress and elastic modulus. This model describes interfacial cracks and the associated energy release rate. To do this, he used analytical assumptions in a Fourier transform of the crack process. The main result is the modeled coupling of the wavelength, crack length and contact length, wave velocity, release frequency and sliding velocity to the energy release rate for a gliding step at the interface. The descriptions were obtained for linear elasticity, but he assigned universal validity to the obtained dependencies.
Several authors described the separation of the interface by spreading and as a function of viscosity. The description of the spreading energy of two lubricated contact partners was given by Israelachvili [19]. Martin et al. [20] described a characteristic speed for the spreading of a film in relation to the spreading energy and viscosity. Wu-Bavouzet [14] described a characteristic speed for forced wetting corresponding to the elastic length of the closed contact and the contact radius of hard partners.
Different calculation methods for obtaining elasticity from Shore hardness measurements were reviewed by Ucar [21] for elastomers, among others. This can be calculated, e.g., via the empirical Battermann–Köhler correlation [22].
Zhibo et al. [23] carried out a sensitive measurement coupled for the characterization of Schallamach waves in a spherical contact. Here, small wrinkles and their spiral-like development in the entrance area of a spherical contact were investigated to explain the initiation of Schallamach waves. The results showed both the decreasing and increasing development of the wave velocity. According to the authors, the finely resolved contacts of a spherical contact show the distribution of the wavelength and speed.
For microscopically rough lubricated contacts, film formation can be assumed to be in the form of mixed friction, with the solid-state interaction decreasing with increasing speed and an increasing hydrodynamic fraction. Here, the effective roughness of both partners is set in a ratio to the characteristic film height h [24]. If this ratio is 1, predominantly hydrodynamic lubrication is achieved.
The motivation for the investigations in this thesis is to test industrial-grade molded elastomer surfaces with nano- and microstructure for their altered frictional behavior. The measured changes are then challenged with the mechanistic hypotheses of soft, adhesive or lubricated liquid silicone rubber surfaces. Central questions with respect to the periodic length of structures lstruc and their shape are:
- (A)
- Is the elastic length l of the interface crack suitable to separate the friction behaviors of nano- and microstructured surfaces?
- (B)
- Can these friction modulations be generated in dry or lubricated conditions?
- (C)
- Can anisotropic friction be generated at 90° or 180°?
- (D)
- What is the effect of structuring the mean distance lstruc with respect to lschallamach on the magnitude of the coefficient of friction?
- (E)
- Can the friction coefficient modulations be brought into interference with the hypothetical tendency to form Schallamach waves, and what is the effect of this as a function of the sliding speed?
In order to clarify this, different structures were produced for molding:
- Isotropic and anisotropic statistical nanostructures via pyramids and rodlike structures;
- Isotropic and anisotropic microstructures produced via polishing with pyramid nanostructures;
- Linear groove structures for defined geometric structures with pyramid nanostructures;
- A molded skin of the California king snake as a biologically motivated structure.
2. Materials and Methods
2.1. Materials
Liquid silicone rubber from DOW (SILASTIC™ RBL-9200-50 LSR, Shore A 50) was chosen as the polymer material.
Except for the forming process of the snakeskin structure (Figure 1b,c), a steel substrate was chosen for the molding forms. All steel forms were mirror-polished with a particle size of 3 µm to Ra ≈ 5 nm, and the created microstructures were roughened by polishing with 15 µm particles to Ra ≈ 500 nm afterwards (Figure 1a). Laser-ablated linear groove microstructures were applied after mirror polishing (Figure 2).
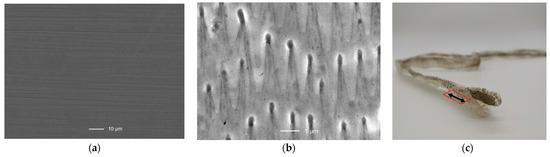
Figure 1.
Reference structure of formed surfaces: (a) linear brushed/polished surface for anisotropic microstructures; (b) in nickel, the cast abdominal skin of the California king snake and the chosen 0° orientation of gliding for investigation (c).

Figure 2.
Laser-ablated steel surfaces: (a) after directional ablation, (b) and (c) bi-scale structure of isotropic pyramids on laser-ablated surfaces.
To produce nanostructured molding forms, PVD layers were deposited on mirror-polished surfaces (Figure 3). The growth of PVD layers depends on the substrate roughness, the binding energy between layer atoms and the substrate and the activation energy of the layer atoms for surface and volume diffusion. A phenomenological understanding of the structure formation as a function of the deposition parameters (e.g., energy, temperature and pressure) is provided by so-called structure zone models [25,26]. The roughness of the substrate surface also influences the coated layer microstructure that forms [27]. If, for example, the coating is applied at oblique incidence, roughness peaks shadow areas of the surface. This knowledge is used to specifically create structured surfaces in the PVD coating process using TiAlN and TaN coatings.

Figure 3.
PVD nanostructure: (a) isotropic pyramid structure (diameter ~100 nm), (b) isotropic rod structure (diameter ~300 nm) and (c) anisotropic pyramid structure.
The viscosity of the plastic is decisive for the molding of nanostructures on plastic surfaces, which is determined by the temperature. In LSR processing by injection molding, a cold molding compound (20 °C) is injected into a hot cavity (130 °C–200 °C). Due to the high temperature in the mold, the plastic begins to cross-link, and the viscosity increases. If the cross-linking is too fast, there is a risk that nanostructures will not be completely molded. In addition to the selection of the optimal processing parameters, an improvement should be achieved through dynamic temperature control; i.e., the mold wall temperature is actively changed during the injection molding cycle. Thus, the cavity is filled at a low temperature, whereby structurally accurate nanostructures are formed. At the end of the filling process, the mold wall temperature is increased so that the plastic cross-links [28]. For the variothermal molding of microstructures, high molding quality can be measured. This was checked with the accuracy of the impressed linear grooves (Figure 4).
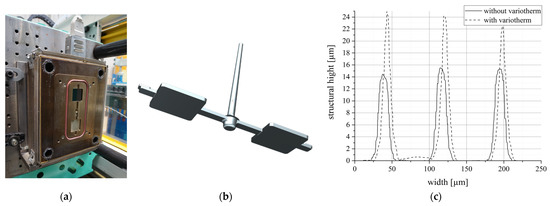
Figure 4.
Molding process. (a) Injection mold with structured inserts and frame heating, (b) demonstrator component with two structured plates (40 × 40 mm) and bar casting and (c) influence of variothermal temperature control on impression quality of grooves with critical process parameters.
The aspect ratio of the molded grooves is higher than that of the nanostructures, but the polymer structures must allow an impression to be taken. Unfortunately, the impression of nanostructures is not equally easy to evaluate via SEM. The vapor depositions or applied energies necessary for high contrast lead to the reshaping of the surface. The resolution achieved indicates good imaging (Figure 5). A check of the impression of different structures is therefore only possible later as an effective check of the friction measurement.
2.2. Tribological Experiments
Ball-on-plate experiments (Figure 6) were used to carry out oscillatory tribological experiments. A rotational rheometer developed by Anton Paar GmbH (Ostfildern, Germany) was used, which was equipped with a tribological measuring unit. In this way, very low but also high velocities and deflections (0.1 µm/s to 1.4 m/s) can be obtained by the rotation of the polished steel ball [29,30]. Conducting the oscillatory experiments in this range of sliding speeds (oscillatory mode) makes it possible to record friction data in the static friction and boundary lubrication regimes. Using a data acquisition rate of 10 data points per decade, the loading torque was increased on a logarithmic scale at an oscillation frequency of 1 Hz.

Figure 6.
Tribological testing set-up: ball-on-plate after cutting out of specimen (exemplary specimen plates).
The tribological experiments were performed in the ball-on-plate geometry (Figure 6).
The polymer specimens were in contact with a steel tribosystem with a 100Cr6 steel ball (diameter ½”, Ra = 0.15 µm: Rz = 1.4 µm, Rku = 3.85, RPc = 37/cm), which was integrated in the tribometer and used as a tribological partner.
The polymer specimens were cut in the shape of rectangular plates (4 mm × 2 mm × 12 mm) for the ball-on-plate contact and glued to steel holding plates.
Demineralized water was produced (viscosity η = 1 mm2/s at 25 °C), and ethylene glycol (EG) (viscosity η = 21 mm2/s at 25 °C) was obtained from Fluka, München, Germany.
The local loading situation is that of a ball gliding on top of three glued LSR plates. This method results in a measured mean value of three contacts if the choice of the cut and the preparation have been made accordingly. For this purpose, the contacts of different molded specimens were compiled. The method itself is hardly susceptible to scattering due to the mild surface roughness of the sphere and the spherical contact. In addition, the stability of the contacts is ensured in advance by a series of 5 oscillation tests and compared with the subsequent sliding test over the height of the adhesion threshold. A precise presentation would distract from the core of the paper. In contrast to a Hertzian contact, the local pressure is limited by hyperelasticity. That means that an elastomer with the hyperelasticity parameter C1 = 1 MPa can barely be loaded with a contact pressure above 0.1 MPa. When normal loads are further increased, the contact area is increased instead (Figure 7). The increased macroscopic or microscopic contact surface is the major reason for the high adhesive friction of elastomers. Consequently, the local slip follows not only the gliding motion but also the hyperelastic forming of the contact. This is why there is a strong slip movement, even orthogonal to the gliding motion of the ball. Hyperelastic deformation also has no relevant effect on surface buckling (height) but leads to a dominant shear deformation in the surface. These calculated findings are different from the results of plastic or elastic textures in the literature [6,7].
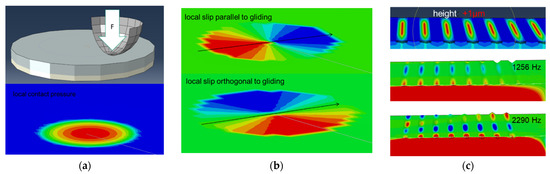
Figure 7.
Loading situation of friction test with a ball on a plate: (a) Each plate is loaded with a normal force that produces broad contact pressure distribution due to the hyperelasticity of LSR. (b) Macroscopic gliding and hyperelastic deformation result in a 2D slip situation. (c) A modal analysis of the groove structure in contact reveals a secondary deformation in height caused by flattening but a frequency-dependent deformation in the gliding direction caused by groove opening–closing cycles.
2.3. Contact Angle Measurements
The sessile drop method was used by placing 2 µL droplets on the samples on a contact angle measurement device produced by Data Physics GmbH (Filderstadt, Germany). Three standard liquids (water, ethylene glycol and diiodomethane) were used to characterize the unknown surface and interfacial energies. The droplet profile is recognized and recorded by the software of the instrument, and the contact angle is calculated automatically. A detailed description of the procedure, calculations and interpolations was given by Wahed et al. [29].
3. Results
3.1. Energies
The work of spreading Wspreading and the work of adhesion W12 can be determined from surface and interfacial energies, which in turn are determined by contact angle measurements. All calculations and interpolations for the interaction energies were carried out according to the procedure described by Wahed et al. [29], and the resulting energies are summarized in Figure 8.
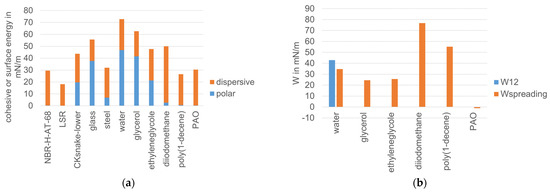
Figure 8.
Energetic situation: (a) Surface energies of LSR compared to other materials and cohesive energies of liquids, (b) adhesive energy W12 of solid partners (dry contact) and Wspreading energy of the lubricated systems for an LSR50–steel contact (lubricated contact).
The surface energy of LSR is low and has no measurable polar part. It is also lower than that of nitrile butadien rubber (NBR-H-AT-68). The surface energy of the skin of a California king snake is much higher and has a strong polar part, which is very close to the cohesive energy of ethylene glycol. Consequently, liquids with a high polar part of cohesive energy, such as water or ethylene glycol, form a non-spreading contact with LSR to any partner. The energetic loss in forced wetting is the same as that of the dry interfacial energy between LSR and steel. This should lead to a large increase in water-lubricated friction. Industrial oils such as PAO have a slight spreading tendency with LSR.
3.2. Friction Measurements
3.2.1. General Friction Data
The sensitivity in determining the changed contact behavior by oscillation measurements, which reveal the transition from adhesion to sliding, is high (Figure 9a). Three different injection molding process parameters lead to distinguishable tribological results when lubricated with ethylene glycol. This means that the molding and the resulting structuring of the LSR are parameter-dependent. The spreading energies (not shown) are reflected as a tendency in the level of the coefficient of friction curves. On the one hand, even the smallest changes in the effective spreading energy can be found due to a changed stiction tendency (at low velocity; red-to-blue curve). On the other hand, the extended shear of a clearly built-up structure in contact could lead to extended elastic paths before the system can slip (higher friction at high velocity; green; see Equation (2)).
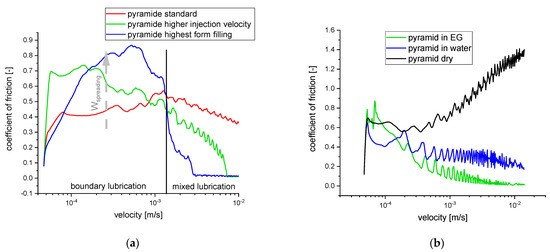
Figure 9.
(a) Measurements of Stribeck-type velocity sweep measurements on early pyramid structures for characterization of friction regimes in ethylene glycol (EG) for different molding parameters: standard (red), higher injection velocity (green) and highest form-filling (blue) parameter. (b) Velocity-dependent behavior of friction for dry (black) low-viscosity lubrication (blue: water) and medium-viscosity lubrication (green: ethylene glycol).
In this way, the standard method of molding was chosen, as it shows the greatest structural effects, which is why the highest mapping quality of the mold structure is assumed.
For this standard molding procedure, a comparison of the Stribeck curves for the dry condition and different viscous lubricants (Figure 9b; water and EG) shows (1) that at low speeds, an increase in friction compared to the dry condition is avoided if, at the lower viscosity of water, an effectively increased structural fraction in the contact reduces the forced wetting of LSR with the lubricant, and (2) that at increased velocity for the greater viscosity of ethylene glycol, friction reduction due to film formation occurs earlier.
3.2.2. Is the Elastic Length l of the Interface Crack Suitable to Separate the Friction Behavior of Nano- and Microstructured Surfaces?
According to Rand [16], who inferred typical and specific length values (Equation (2)), we obtain (for LSR50 against steel, W12: 50 mN/m; Shore50: G = 0.8 MPa (Equation (1))) a value of l = W12/GBatterman-Köhler = 0.06 µm (G: shearing modulus of elasticity; Shore: Shore hardness A; W12: adhesive energy of solid partners).
By applying Rand’s correlations to this value, we extrapolate the following possible values: λschallamach~3 µm, vschallamach~5 nm/s, and ~fschallamach 1 kHz @ ~ v: ~mm/s. By comparing the result for l with the periodic distance of pyramidal and rod structures (Figure 3), we find a similar length scale for pyramids. However, the longer rods of the rodlike structure form longer distances compared to l.
Using the findings of Rand for Schallamach waves at a gliding velocity of mm/s, a value of λschallamach~3 µm would be in the range of micrometer structures. According to Zhibo [23], the broad distribution of Schallamach wavelengths shows a progression from smaller to longer waves λschallamach. The progression of waves starts from small wrinkles of ~80 µm/s at v = 1 mm/s and ends with waves of ~190 µm/s at v = 10 mm/s. The experimental conditions used by Zhibo when loading PDMS (Shore43) against glass (W12 ~ 40 mN/m) were similar to our system.
Since many interactions are assumed in the evaluation of the structures, a comparison of the effect of a specific change is useful. For this purpose, the following were compared:
- Isotropic and anisotropic pyramid nanostructures;
- A pyramid nanostructure on a mirrorlike surface and on a ground surface;
- An isotropic ground surface and a linear and thus anisotropic ground surface.
When looking at the results (Figure 10), the velocity sweep measurement does not reveal a specific minimum at a certain velocity but a broad transition from 0.1 to 0.4 mm/s for the different surfaces. One has to bear in mind that the tribological contact also creates slip movement in the orthogonal direction (Figure 7). In this respect, the changed friction of an anisotropic sample is also understood with parts of the orthogonal movement. Micro- and nanostructures were obtained with anisotropy with reduced friction and with isotropy with increased friction, respectively. The use of a microstructure obtained by polishing further lowers the friction value.
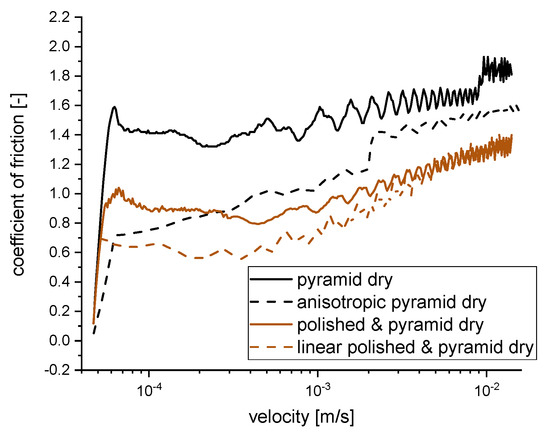
Figure 10.
Dry frictional behavior with anisotropy for pyramid-structured and polished surfaces.
3.2.3. Can These Friction Modulations Be Generated in Dry or Lubricated Conditions?
Since the frictional impact of anisotropy was already found, the behavior of anisotropy itself was investigated by comparing longitudinal and orthogonal and dry and lubricated systems (Figure 11). For dry contact, the reduction in friction by anisotropy is reduced itself when the gliding direction on the structure is orthogonal to the anisotropy direction, since it should be more isotropic-like. The strong anisotropy of pyramidal nanostructures in dry contact is altered by lubrication. An orthogonal gliding direction with respect to anisotropy could form channel-like superstructures of the lubricant in the surface. This facilitated movement of lubricant, even in a boundary contact, would reduce adhesive friction by the partial shearing of the lubricant instead. In contrast, an anisotropic structure suppresses slip by film formation and increases friction in the transition to slip. Consequently, the friction of the isotropic structure is maintained between the extremes of the anisotropic structures for water as well as for ethylene glycol.
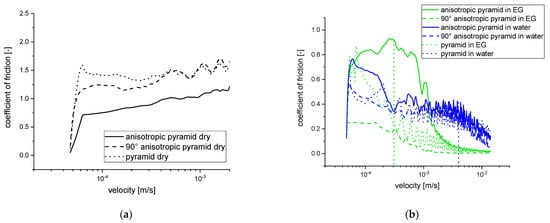
Figure 11.
Ninety-degree anisotropy of friction for anisotropic pyramids in comparison to isotropic pyramids: (a) dry and (b) water and ethylene glycol (EG). Vertical broken lines indicate the transition to mixed lubrication.
It was found that, depending on the lubricant, the transition to mixed friction takes place above a characteristic speed. Reduced friction at increased velocity can be found above roughly 3 mm/s for water and above 0.3 mm/s for ethylene glycol. Additionally, according to Wu-Bavouzet [14], the transition would be found at (Equation (3)) vcharacteristic,water = Wspreading/viscosity(l/6.35 mm)1/3 = 1.20 mm/s and vcharacteristic,ethyleneglycol = Wspreading/viscosity(l/6.35 mm)1/3 = 0.33 mm/s (Wspreading: spreading energy; viscosity: dynamic viscosity; l: elastic length; R: radius of the sphere in contact).
The characteristic velocity can therefore be used to calculate velocity regimes when structures have a profound influence on friction and when they do not.
3.2.4. What Effect on Friction Can Be Expected for Different Structures?
A large number of measured surfaces were analyzed by forming a comparative friction value. To generate such a value, the measured friction was averaged from 0.03 to 0.3 mm/s, which in principle, covers the transition from sticking to sliding. Since the focus of the investigation is to define different usable friction values for similar systems, the relative friction values were compared. The friction of the isotropic pyramid structure was classified as the best understood and chosen as a reference. For this one, the surface was smoothed on the microscale by mirror polishing before coating, and a large increase in the coefficient of friction was obtained. The comparison of the specific friction values can be seen in Figure 12.

Figure 12.
Overview of the friction coefficient reduction for differently structured surfaces under the three test conditions (dry/water/ethylene glycol (EG)): dry and the comparison with lubricated systems for friction coefficient reduction.
In dry contact, lower friction values are achieved for all other structures. Based on this reduction, one can directly determine the usable anisotropy of the nanostructure or the effect of a microstructure by polishing. Only the structure of a molded snakeskin has a similarly high friction to the reference, but due to other reasons, it has a high microscale texture.
As already obtained, the effect of a nanostructure is reversed with lubrication, so there is an increase in the coefficient of friction for ethylene glycol. The variation in lubricated friction using structures based on dimples at 0.05 MPa pressure previously measured by Schneider et al. [12] was used as a benchmark. The linear groove structures can exceed this variation in their effect, where it should be mentioned that in our applied test, much higher contact pressures (in the range of 0.5 to 1 MPa due to hyperelasticity) were realized.
For water, due to the low viscosity and high cohesion energy, the energetic change of the interface and partly the viscous mixed friction have a dominant effect, so the structures sometimes lead to higher or lower friction values. For the molded snakeskin, a clear increase in the friction value is also obtained here. The shape and amplitude of the molded snakeskin texture are suspected to be the reason for this.
3.2.5. Can Anisotropic Friction Be Generated at 90° or 180°?
Again, the friction value covering the transition from sticking to sliding from 0.03 to 0.3 mm/s was chosen (Figure 13). Since the focus of the investigation is on the change with 90°- and 180°-rotated sliding for anisotropic structures, instead of a uniform value, a 0° friction value for each anisotropic structure was chosen as a reference. In each case, an increase in friction was measured. The variation in the friction of a bioinspired asymmetrically structured surface made by Tramsen et al. [8] for dry contact was chosen for comparison. The chosen nanostructure of the rodlike structure is equally able to produce increased friction. For the ethylene glycol-lubricated contact, the friction variation for the snakeskin or nanopyramid structure is impressively high. The effect of the nanopyramid structure is illustrated above in Figure 11b.
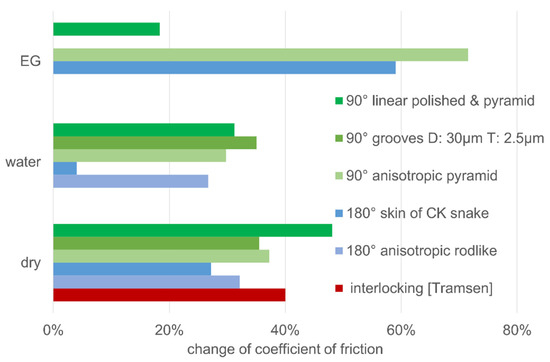
Figure 13.
Overview of the friction coefficient anisotropy of differently structured surfaces under the three test conditions (dry/water/ethylene glycol (EG)) as well as the reference of 40% friction coefficient reduction: dry and the comparison with lubricated systems for friction coefficient reduction.
The effect of the California king snakeskin structure is specific and was further compared (Figure 14). In detail, depending on the direction, Δµ of 27% was obtained for dry contact, and Δµ of 59% was obtained in ethylene glycol. Further analysis of this topic is beyond the scope of this work and was discussed for dry contact in [31].
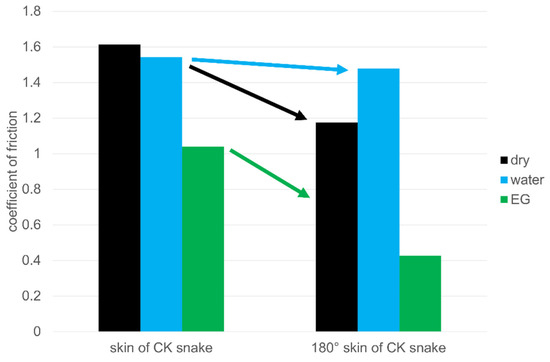
Figure 14.
Anisotropic friction values in the examination of real snakeskin molded in LSR as a bioinspired reference structure.
3.2.6. Friction of Periodic Microstructure Grooves
Since the results for nanostructures have already been tested for a correlation with the elastic length of the incipient crack of an interface, the question remains open as to whether a possible superimposed correlation of the Schallamach wavelength and the periodicity lstruc of the microstructure could be relevant. Due to the described ongoing development of the understanding of Schallamach waves, simple parameters in the form of linear grooves were chosen.
- (A)
- What is the effect of structuring the mean distance lstruc with respect to lschallmach on the magnitude of the coefficient of friction?
- (B)
- Can the friction coefficient modulations be brought into interference with the hypothetical tendency to form Schallamach waves, and what is the effect of this as a function of the sliding velocity?
Periodic microstructure grooves were incorporated by the forming process. A simple geometric system can be set by the distance D of grooves, the length of the contact surface B and the depth of the grooves T (see the cut view in Figure 15).
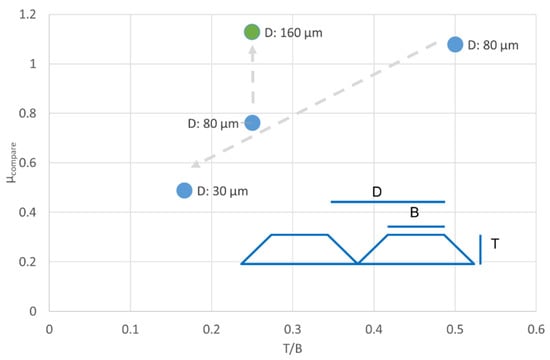
Figure 15.
Linear groove structures were tested, which were created in the LSR surface with different defined parameters (D, B and T) by laser structuring of molds.
The essential assumption of the following estimations is the simplifying assumption of the opening–closing cycles of V-shaped grooves in order to increase the mobility of gliding by shearing the blocks between the grooves.
The presumed effect of Schallamach waves on friction is the reduction in the gliding velocity at a closed interface due to the movement of a Schallamach wave. Thus, it can be assumed that the dynamic friction at a closed interface scales with ln(v) [32]. Schapery [18] described the relative change in velocity as the ratio of the attached surface to the distance between the detached surfaces of a wave. In our case, D/B is a predefinition of this ratio, so the friction µ ~ ln(D/B) should be obtained (see Equations (4) and (5); µ0 and v0: friction and velocity at the minimum of friction versus the velocity of rate and state models).
This dependency was assumed and not followed up. Instead, a ratio of 2 for D/B was always chosen. A hysteretic energy loss (Wloss) of the opening and closing of the grooves should scale with the loss due to shear, in the sense that a fraction µhysteretic is the product of ~shear and the loss fraction of the shear modulus of elasticity (Gloss). The possible shear is estimated with the maximum T/B ratio (Equation (6)).
This ratio was tested with three variants of four cases (2.5 µm/15 µm; 20 µm/80 µm and 10 µm/40 µm; 20 µm/40 µm). As expected, friction increases with the T/B ratio (Figure 15).
The effect of the interference of the natural frequency of the elastic surface with the frequency of the detachment of Schallamach waves was tested via a single test variation for a fixed T/B ratio = ¼. For this purpose, the distance D was doubled. The excitation of a detachment by such a structure would occur at a sliding velocity of v with a frequency of v/D (Equation (7), min (µ): minimum of µ).
An excited oscillation would have a maximum amplitude of vibration and thus less friction if the natural frequency of the surface shear or the frequency of the Schallamach waves matched that of the excitation. The decrease in friction as D varies follows the approach to the optimal excitation frequency, so the optimum ratio of v/D is higher.
4. Discussion
Four different types of structures were molded in LSR, and three were made to test different hypotheses: isotropic and anisotropic statistical nanostructures via pyramid and rodlike structures, isotropic and anisotropic microstructures produced via polishing with pyramid nanostructures, and linear groove structures for defined geometric structures with pyramid nanostructures.
While the structure of the molds could be measured well via SEM and interferometry, this was challenging for the molded LSR surfaces, which reformed under electron irradiation. However, the presence of the tribological effect of the expected nanostructures was tested using different model hypotheses for elastomer surfaces.
Zhibo’s assumptions, which assume a broad distribution of Schallamach waves, were reinforced. No singular transitions or specific regimes were determined despite the wide variation in the sliding velocity, but a possible transition range of 0.1 to 0.3 mm/s was obtained. In contrast to mild anisotropy for a microstructure made by brush polishing, the pyramid nanostructure does show a strong increase in friction, and in the case of anisotropic structures, it occurs in the longitudinal but not in the orthogonal direction.
According to the general calculation of an elastic length l of 60 nm for plane surfaces, it is in the range of the pyramid size of the nanostructure. Therefore, the effective surface elasticity Geff should be reduced in relation to the shear stiffness of a pyramid or rod in accordance with the sliding motion. A decrease in Geff would increase the effective elastic length leff. An increase in leff of about 10% would lead to a 30% higher vschallamach (according to Schapery) and, therefore, a decrease in frequency. This could explain the large increase in dry friction. This increase for pyramid structures is reduced for rodlike structures in the direction of the rod elements. The stiffness of inclined rods does not allow a strong decrease in Geff.
In comparison, the chosen nanostructures have a stronger influence through anisotropy than the microstructures. This influence is presumably great when the periodicity of the structures coincides with the elastic length. For microstructures, on the one hand, the relative area share of the anisotropic structures in the total area is lower. On the other hand, the macroscopic load of a sliding sphere also has a high proportion of shear deformation and sliding orthogonal to the direction of movement. This leads to the partial averaging of the direction-dependent effect in microscopic structures and to a reduction in the anisotropic friction change.
The introduction of a lubricant changes the energetic situation at the gliding surface as well as the mechanical interaction. Depending on the viscosity, reduced friction results in increasing velocity after the wetting transition to a mixed-lubricated state. A characteristic velocity for this wetting transition can be calculated by the spreading energy of the system and the viscosity of the lubricant according to the description by Wu-Bavouzet. Anisotropic friction was obtained not only at 90° but also at 180°. A 180° anisotropy should be a logical consequence of the shear deformation of inclined pyramidal or rodlike structures.
This 180° anisotropy was extraordinarily high for the molded structure taken from the snakeskin. Here, only the tribological effect is of concern. This 3D structure was analyzed in detail by Baum et al.
Linear periodic microstructure grooves were used in contrast to statistical or biological surfaces. The groove size and the periodicity parameter varied slightly. An optimal groove structure could further reduce friction by the forced excitation of periodic elements corresponding to Schallamach waves. The optimal groove spacing seems to be less than 30 µm, and the optimal groove depth could be less than 1/6 of the spacing.
5. Conclusions
The molding of nanostructures is already known from thermoplastic processing. However, these exhibit plastic behavior under load in their application and can therefore not be described as permanently resistant. Elastomers can be used to increase resistance. The material behavior can even be modified to such an extent that the viscoelastic portion predominates. Therefore, an LSR material was chosen for these investigations. Decisive for the molding of nanostructures is the viscosity of the plastic, which is determined by the temperature. In addition to the selection of optimal processing parameters, an improvement was achieved by means of dynamic temperature control. The nanostructures were realized using a deposition process for ternary nitride hard materials on steels. Three methods were used to create anisotropic structures
- “Disturbing” the isotropic growth process by skewing the substrate in the process;
- Choosing a layer material with, e.g., an anisotropic layer structure;
- Pre-structuring the substrate (e.g., by grinding and polishing).
The structures thus created on a hyperelastic surface of LSR were shown to have a tribological effect, although the presumed contact area was hardly changed by elastic movements or local elastic deformations orthogonal to the sliding surface.
Nanostructures:
- Can increase the adhesive friction of surfaces during sliding;
- Increase the wetting tendency of liquids and decrease adhesive friction.
Mesostructures:
- Increase the movement amplitude of stick-slip and decrease dry friction;
- Absorb shear deformation at low velocities;
- Reduce film formation during lubrication and increase friction.
Structures:
- Enable frictional anisotropy.
Author Contributions
Conceptualization, C.K., A.F. and M.H.D.; investigation, C.K. and D.F.W.; writing, C.K.; review and editing, D.F.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Baden-Württemberg Stiftung, Grant/Award Number: Biofunctional materials surfaces.
Data Availability Statement
Not applicable.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Schallamach, A. How does rubber slide? Wear 1971, 17, 301–312. [Google Scholar] [CrossRef]
- Von Goeldel, S.; Reichenbach, T.; König, F.; Mayrhofer, L.; Moras, G.; Jacobs, G.; Moseler, M. A Combined Experimental and Atomistic Investigation of PTFE Double Transfer Film Formation and Lubrication in Rolling Point Contacts. Tribol. Lett. 2021, 69, 1–16. [Google Scholar] [CrossRef]
- Burris, D.L.; Sawyer, W.G. Improved wear resistance in alumina-PTFE nanocomposites with irregular shaped nanoparticles. Wear 2006, 260, 915–918. [Google Scholar] [CrossRef]
- Vogel, S.; Brenner, A.; Schlüter, B.; Blug, B.; Kirsch, F.; van Roo, T. Laser Structuring and DLC Coating of Elastomers for High Performance Applications; Universitätsbibliothek der RWTH Aachen: Aachen, Germany, 2022. [Google Scholar]
- Grützmacher, P.G.; Profito, F.J.; Rosenkranz, A. Multi-Scale Surface Texturing in Tribology—Current Knowledge and Future Perspectives. Lubricants 2019, 7, 95. [Google Scholar] [CrossRef]
- Ripoll, M.R.; Podgornik, B.; Vižintin, J. Finite element analysis of textured surfaces under reciprocating sliding. Wear 2011, 271, 952–959. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Yi, S.; Ge, X.; Chen, X.; Luo, J. Enhancement of friction performance of fluorinated graphene and molybdenum disulfide coating by microdimple arrays. Carbon 2020, 167, 122–131. [Google Scholar] [CrossRef]
- Tramsen, H.T.; Gorb, S.N.; Zhang, H.; Manoonpong, P.; Dai, Z.; Heepe, L. Inversion of friction anisotropy in a bio-inspired asymmetrically structured surface. J. R. Soc. Interface 2018, 15, 20170629. [Google Scholar] [CrossRef]
- Tramsen, H.T.; Heepe, L.; Homchanthanakul, J.; Wörgötter, F.; Gorb, S.N.; Manoonpong, P. Getting grip in changing environments: The effect of friction anisotropy inversion on robot locomotion. Appl. Phys. A 2021, 127, 1–9. [Google Scholar] [CrossRef]
- Scherge, M.; Gorb, S. Biological Micro-and Nanotribology: Nature’s Solutions; Springer: Berlin, Germany; London, UK, 2011. [Google Scholar]
- Wu, W.; Lutz, C.; Mersch, S.; Thelen, R.; Greiner, C.; Gomard, G.; Hölscher, H. Characterization of the microscopic tribological properties of sandfish (Scincus scincus) scales by atomic force microscopy. Beilstein J. Nanotechnol. 2018, 9, 2618–2627. [Google Scholar] [CrossRef]
- Schneider, J.; Djamiykov, V.; Greiner, C. Friction reduction through biologically inspired scale-like laser surface textures. Beilstein J. Nanotechnol. 2018, 9, 2561–2572. [Google Scholar] [CrossRef]
- Fukahori, Y.; Sakulkaew, K.; Busfield, J. Elastic–viscous transition in tear fracture of rubbers. Polymer 2013, 54, 1905–1915. [Google Scholar] [CrossRef]
- Wu-Bavouzet, F.; Clain-Burckbuchler, J.; Buguin, A.; De Gennes, P.-G.; Brochard-Wyart, F. Stick-Slip: Wet Versus Dry. J. Adhes. 2007, 83, 761–784. [Google Scholar] [CrossRef]
- Fukahori, Y.; Gabriel, P.; Busfield, J. How does rubber truly slide between Schallamach waves and stick–slip motion? Wear 2010, 269, 854–866. [Google Scholar] [CrossRef]
- Rand, C.J.; Crosby, A.J. Insight into the periodicity of Schallamach waves in soft material friction. Appl. Phys. Lett. 2006, 89, 261907. [Google Scholar] [CrossRef]
- Rand, C.J.; Crosby, A.J. Friction of soft elastomeric wrinkled surfaces. J. Appl. Phys. 2009, 106, 064913. [Google Scholar] [CrossRef]
- Schapery, R. A model for the prediction of rubber friction with Schallamach waves. Tribol. Int. 2019, 143, 106018. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Martin, P.; Brochard-Wyart, F. Dewetting at Soft Interfaces. Phys. Rev. Lett. 1998, 80, 3296–3299. [Google Scholar] [CrossRef]
- Ucar, H.; Basdogan, I. Dynamic characterization and modeling of rubber shock absorbers: A comprehensive case study. J. Low Freq. Noise, Vib. Act. Control 2017, 37, 509–518. [Google Scholar] [CrossRef]
- Battermann, W.; Köhler, R. Elastomere Federung, Elastische Lagerungen: Grundlagen Ingenieurmässiger Berechnungund Konstruktion; W. Ernst: Berlin, Germany, 1982. [Google Scholar]
- Zhibo, C.; Zhaoqian, S.; Dandan, H.; Genzong, L.; Jian, W.; Benlong, S.; Yuyan, L.; Youshan, W. From small wrinkles to Schallamach waves during rubber friction: In situ experiment and 3D simulation. Polym. Test. 2021, 96, 107084. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part 1—Theoretical Formulation. J. Lubr. Technol. 1976, 98, 223–228. [Google Scholar] [CrossRef]
- Anders, A. A structure zone diagram including plasma-based deposition and ion etching. Thin Solid Film. 2009, 518, 4087–4090. [Google Scholar] [CrossRef]
- Thornton, J.A. The microstructure of sputter-deposited coatings. J. Vac. Sci. Technol. A Vac. Surf. Film. 1986, 4, 3059–3065. [Google Scholar] [CrossRef]
- Burmeister, F.; Hagen, J.; Denter, J.; Wirth, M.; Fromm, A.; Kleer, G. Hybrid Inorganic-Organic Functional Coatings for Injection Molding Applications. Plasma Process. Polym. 2009, 6, S1–S5. [Google Scholar] [CrossRef]
- Weißer, D.F.; Walz, D.; Schmid, J.; Mayer, D.; Deckert, M.H. Calculating the temperature and degree of cross-linking for liquid silicone rubber processing in injection molding. J. Adv. Manuf. Process. 2020, 3, 13. [Google Scholar] [CrossRef]
- Abdel-Wahed, S.A.; Koplin, C.; Jaeger, R.; Scherge, M. On the Transition from Static to Dynamic Boundary Friction of Lubricated PEEK for a Spreading Adhesive Contact by Macroscopic Oscillatory Tribometry. Lubricants 2017, 5, 21. [Google Scholar] [CrossRef]
- Koplin, C.; Abdel-Wahed, S.A.; Jaeger, R.; Scherge, M. The Transition from Static to Dynamic Boundary Friction of a Lubricated Spreading and a Non-Spreading Adhesive Contact by Macroscopic Oscillatory Tribometry. Lubricants 2019, 7, 6. [Google Scholar] [CrossRef]
- Baum, M.J.; Heepe, L.; Fadeeva, E.; Gorb, S.N. Dry Friction of Microstructured Polymer Surfaces Inspired by Snake Skin; Gottfried Wilhelm Leibniz Universität Hannover; Technische Informationsbibliothek (TIB): Hannover, Germany, 2014. [Google Scholar]
- Putelat, T.; Dawes, J.H.; Willis, J.R. On the microphysical foundations of rate-and-state friction. J. Mech. Phys. Solids 2011, 59, 1062–1075. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
