Composite Material Elastic Effective Coefficients Optimization by Means of a Micromechanical Mechanical Model
Abstract
:1. Introduction
2. Methodology
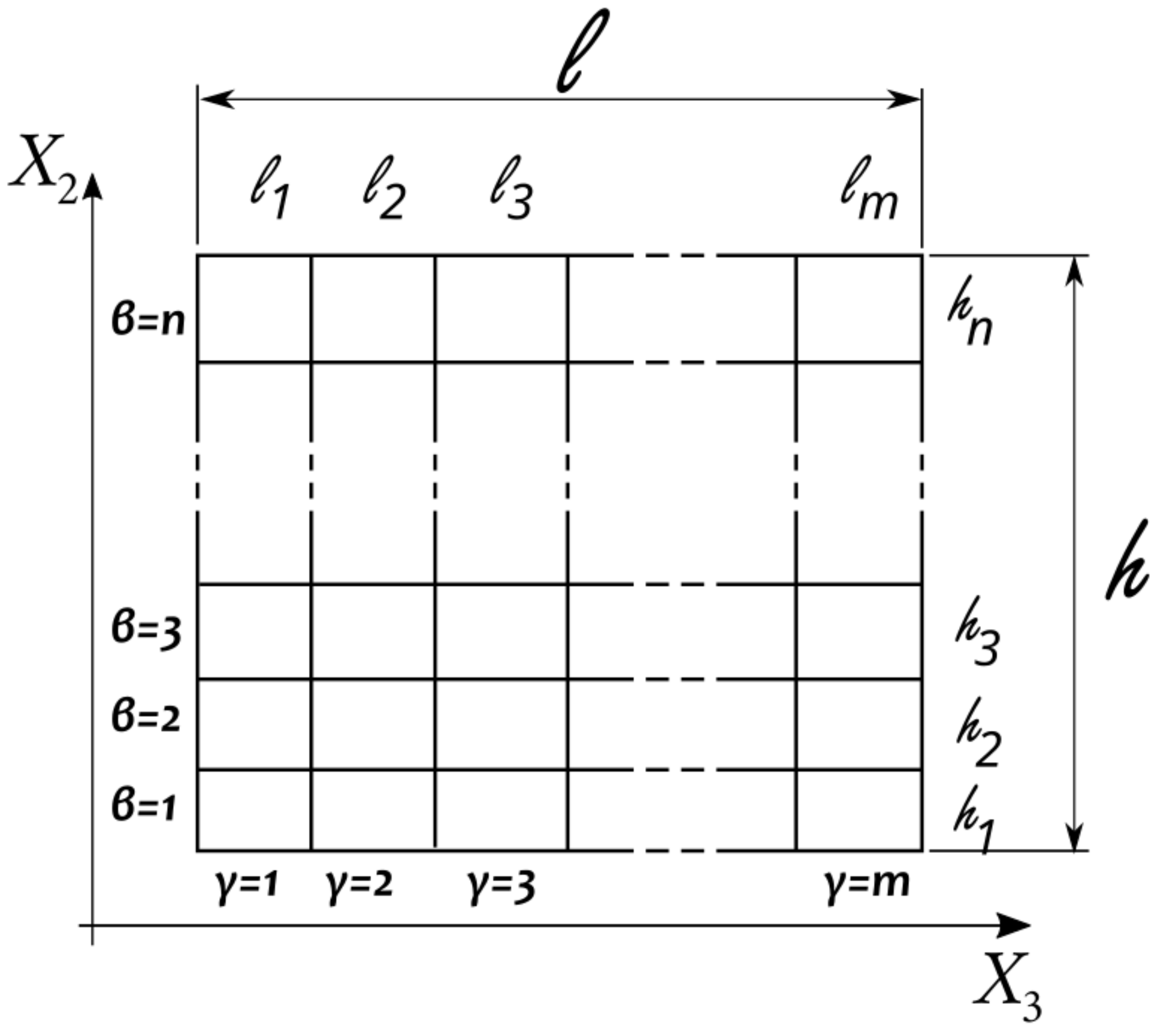
2.1. Micromechanical Modeling
- Periodic fiber packaging RUCs depicted in Table 1, which can model RUCs with one or a maximum of two fibers. The characteristics are also the constraints related to the maximum allowable Vf. A major advantage of this type is the ability to approach the circular geometry of the fiber by discretizing the RUC in a large number of subcells.
- Random fiber packing arrangements, depicted in Table 2. These types can incorporate more than two fibers in one RUC in a random arrangement. Another characteristic of this RUC type is that it also allows for including fibers in close contact with others. Both types also allow for the control of RUC’s aspect ratio R:
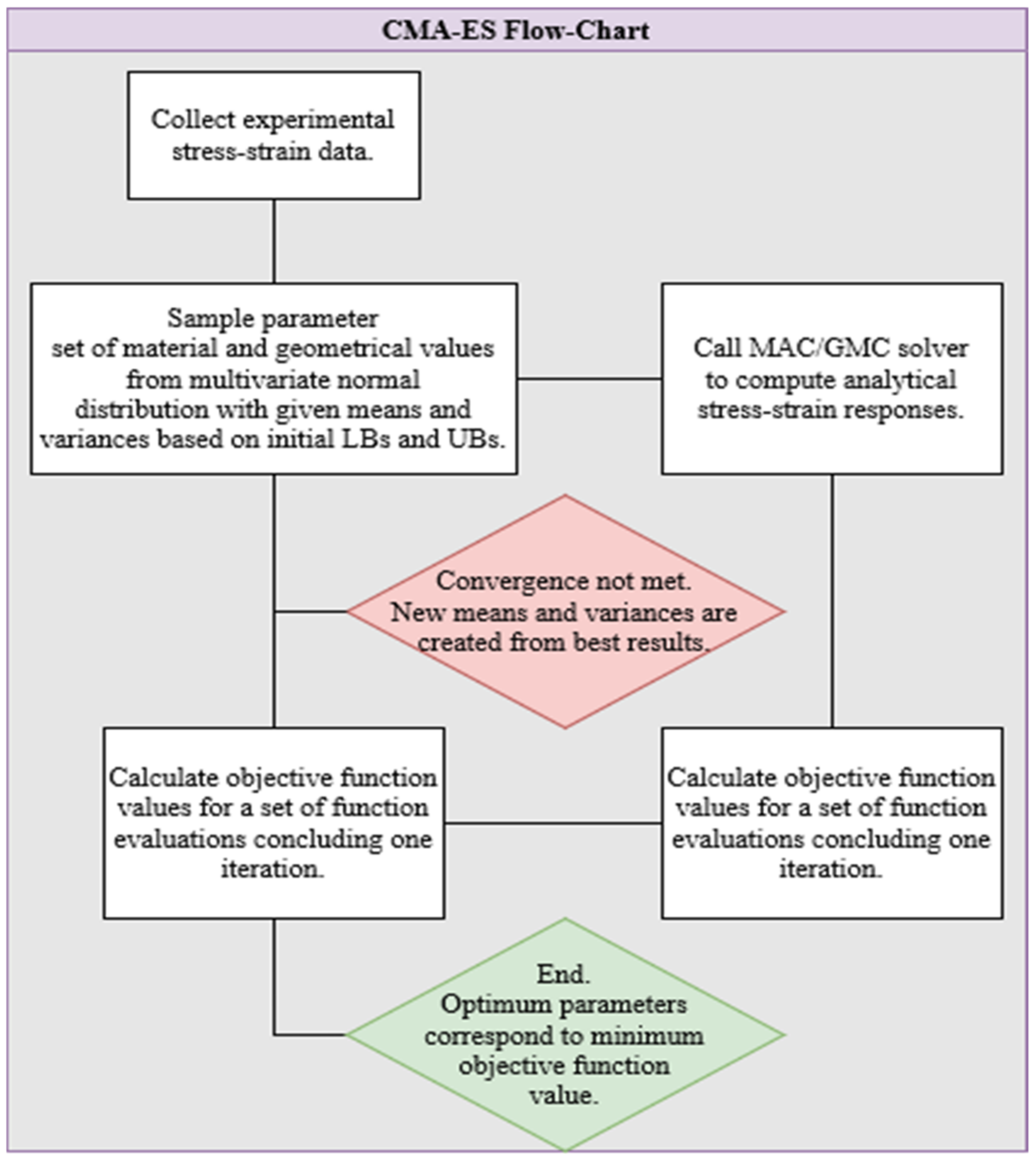
2.2. Coupling GMC to CMA–ES Optimization Strategy
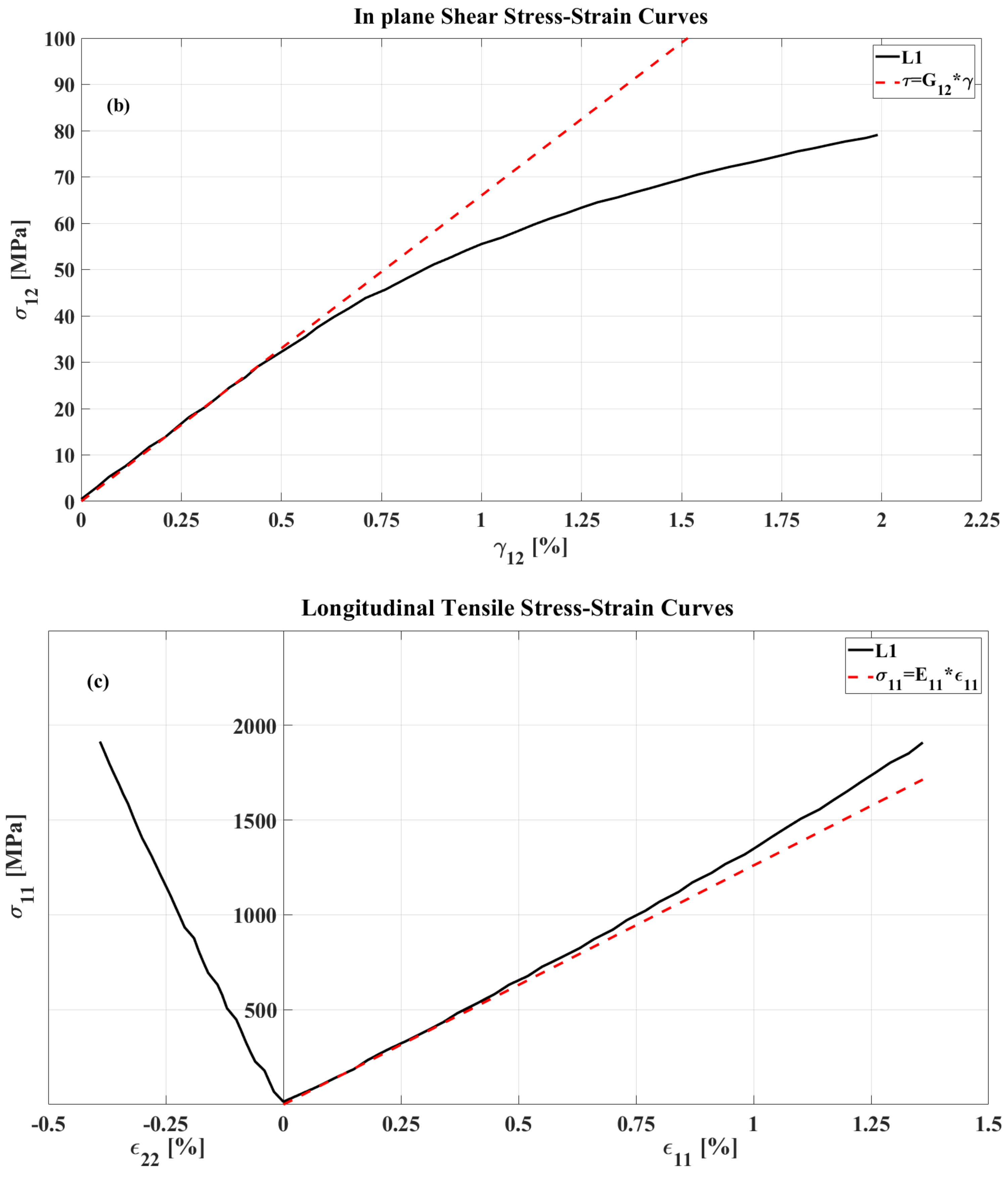
3. Experimental Data
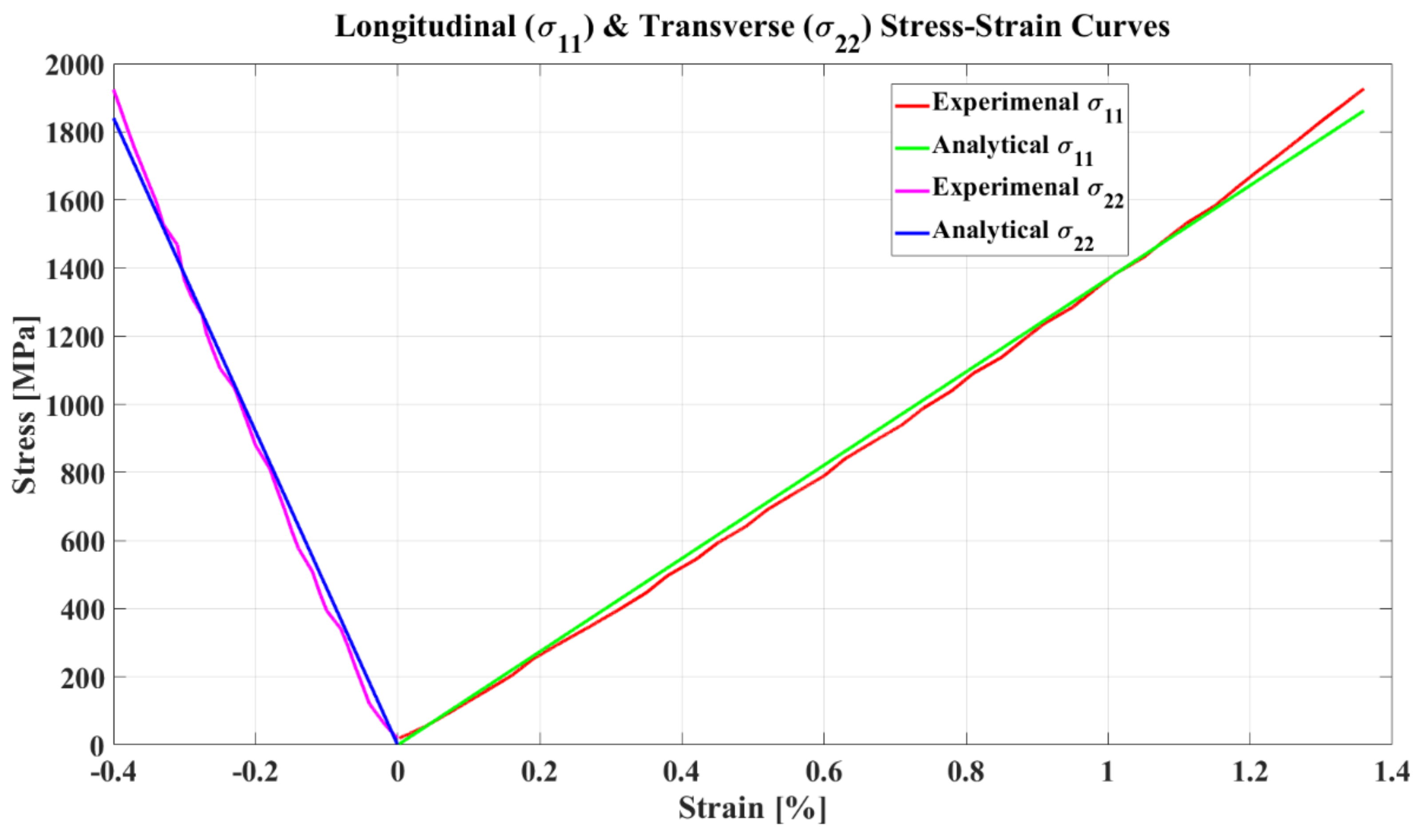
4. Results and Discussion
4.1. Effective Properties: Influence of Fiber Architecture
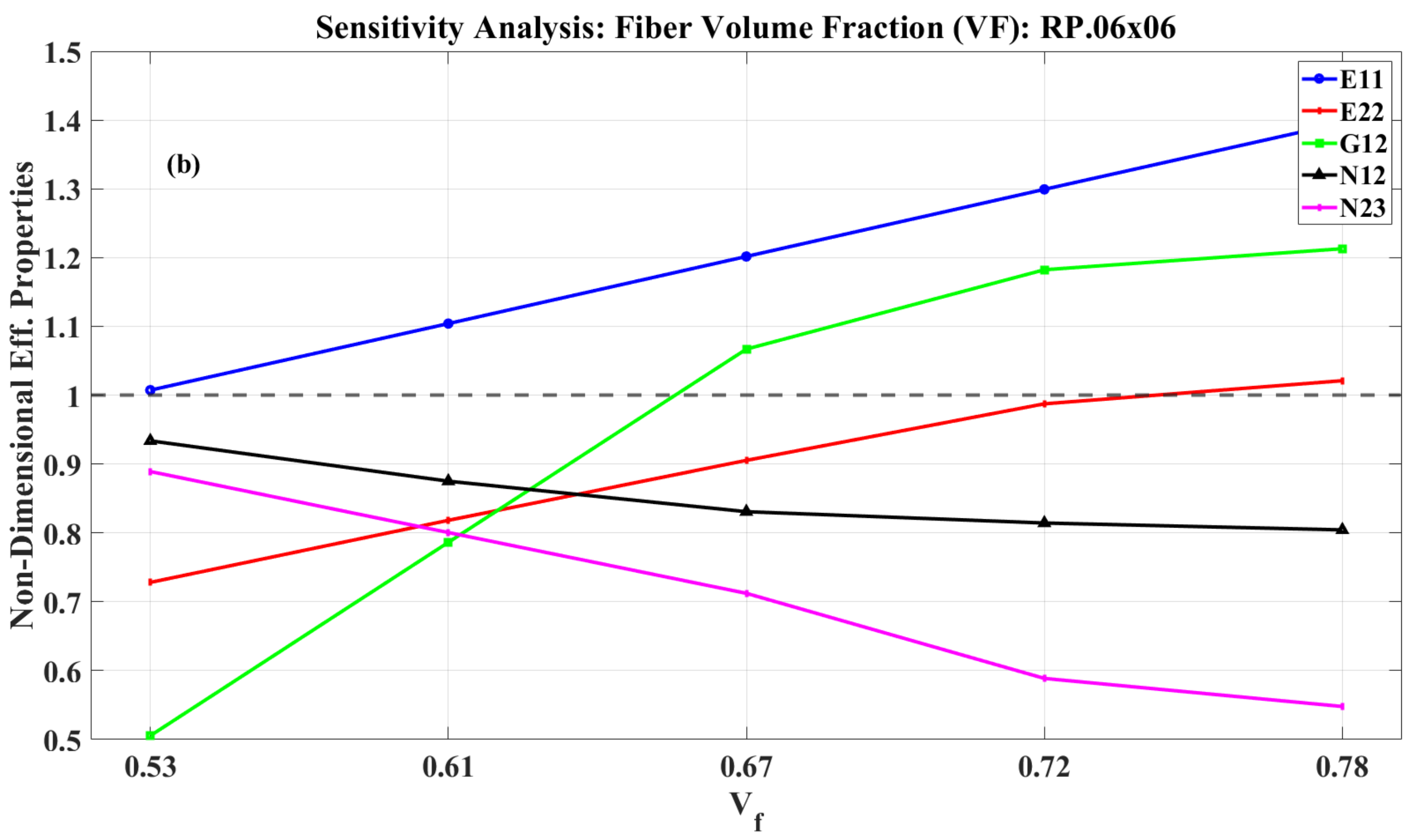
4.2. Effective Properties: Influence of Volume fraction
4.3. Influence of Constituents Mechanical Properties
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Voigt, W. Lehrbuch der Kristallphysik; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1966. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Bohm, H.J. A Short Introduction to Basic Aspects of Continuum Micromechanics; ILSB-Arbeitsbericht 206; Vienna University of Technology: Vienna, Austria, 2010. [Google Scholar]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Met. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Pan, J.; Bian, L. A re-formulation of the Mori–Tanaka method for predicting material properties of fiber-reinforced polymers/composites. Colloid Polym. Sci. 2019, 297, 529–543. [Google Scholar] [CrossRef]
- Barral, M.; Chatzigeorgiou, G.; Meraghni, F.; Léon, R. Homogenization using modified Mori-Tanaka and TFA framework for elastoplastic-viscoelastic-viscoplastic composites: Theory and numerical validation. Int. J. Plast. 2020, 127, 102632. [Google Scholar] [CrossRef] [Green Version]
- Mercier, S.; Molinari, A.; Berbenni, S.; Berveiller, M. Comparison of different homogenization approaches for elastic–viscoplastic materials. Model. Simul. Mater. Sci. Eng. 2012, 20, 024004. [Google Scholar] [CrossRef]
- Desrumaux, F.; Meraghni, F.; Benzeggagh, M.L. Generalised Mori-Tanaka Scheme to Model Anisotropic Damage Using Numerical Eshelby Tensor. J. Compos. Mater. 2001, 35, 603–624. [Google Scholar] [CrossRef]
- Charalambakis, N.; Chatzigeorgiou, G.; Chemisky, Y.; Meraghni, F. Mathematical homogenization of inelastic dissipative materials: A survey and recent progress. Contin. Mech. Thermodyn. 2018, 30, 1–51. [Google Scholar] [CrossRef] [Green Version]
- Benveniste, Y. Revisiting the generalized self-consistent scheme in composites: Clarification of some aspects and a new formulation. J. Mech. Phys. Solids 2008, 56, 2984–3002. [Google Scholar] [CrossRef]
- Hashin, Z. Thermoelastic properties of fiber composites with imperfect interface. Mech. Mater. 1990, 8, 333–348. [Google Scholar] [CrossRef]
- Hervé-Luanco, E.; Joannès, S. Multiscale modelling of transport phenomena for materials with n-layered embedded fibres. Part I: Analytical and numerical-based approaches. Int. J. Solids Struct. 2016, 97–98, 625–636. [Google Scholar] [CrossRef]
- Benveniste, Y.; Milton, G. The effective medium and the average field approximations vis-à-vis the Hashin–Shtrikman bounds. II. The generalized self-consistent scheme in matrix-based composites. J. Mech. Phys. Solids 2010, 58, 1039–1056. [Google Scholar] [CrossRef]
- Christensen, R.; Lo, K. Solutions for effective shear properties in three phase sphere and cylinder models. J. Mech. Phys. Solids 1979, 27, 315–330. [Google Scholar] [CrossRef]
- Sekkate, Z.; Aboutajeddine, A.; Seddouki, A. Elastoplastic mean-field homogenization: Recent advances review. Mech. Adv. Mater. Struct. 2022, 29, 449–474. [Google Scholar] [CrossRef]
- Ortolano, J.M.; Hernandez, J.A.; Oliver, J.A. A Comparative Study on Homogenization Strategies for Multi-Scale Analysis of Materials; Monograph CIMNE: Barcelona, Spain, 2013; Volume 135. [Google Scholar]
- Aboudi, J. Micromechanical Analysis of Composites by the Method of Cells. Appl. Mech. Rev. 1989, 42, 193–221. [Google Scholar] [CrossRef]
- Wang, J.; Andreasen, J.; Karihaloo, B. The solution of an inhomogeneity in a finite plane region and its application to composite materials. Compos. Sci. Technol. 2000, 60, 75–82. [Google Scholar] [CrossRef]
- Sangani, A.S.; Lu, W. Elastic coefficients of composites containing spherical inclusions in a periodic array. J. Mech. Phys. Solids 1987, 35, 1–21. [Google Scholar] [CrossRef]
- Cohen, I. Simple algebraic approximations for the effective elastic moduli of cubic arrays of spheres. J. Mech. Phys. Solids 2004, 52, 2167–2183. [Google Scholar] [CrossRef]
- Paley, M.; Aboudi, J. Micromechanical analysis of composites by the generalized cells model. Mech. Mater. 1992, 14, 127–139. [Google Scholar] [CrossRef]
- Aboudi, J. Micromechanical Analysis of Composites by the Method of Cells—Update. Appl. Mech. Rev. 1996, 49, S83–S91. [Google Scholar] [CrossRef]
- Fish, J. Multiscale Methods; Oxford University Press: Oxford, UK, 2009. [Google Scholar] [CrossRef]
- Kanouté, P.; Boso, D.P.; Chaboche, J.L.; Schrefler, B.A. Multiscale Methods for Composites: A Review. Arch. Comput. Methods Eng. 2009, 16, 31–75. [Google Scholar] [CrossRef]
- Feyel, F.; Chaboche, J.-L. FE2 multiscale approach for modelling the elastoviscoplastic behaviour of long fibre SiC/Ti composite materials. Comput. Methods Appl. Mech. Eng. 2000, 183, 309–330. [Google Scholar] [CrossRef]
- Pan, L.; Adams, D.O.; Rizzo, F.J. Boundary element analysis for composite materials and a library of Green’s functions. Comput. Struct. 1998, 66, 685–693. [Google Scholar] [CrossRef]
- Liu, Y.; Nishimura, N.; Otani, Y.; Takahashi, T.; Chen, X.L.; Munakata, H. A Fast Boundary Element Method for the Analysis of Fiber-Reinforced Composites Based on a Rigid-Inclusion Model. J. Appl. Mech. 2005, 72, 115–128. [Google Scholar] [CrossRef]
- Pindera, M.-J.; Bednarcyk, B.A. An efficient implementation of the generalized method of cells for unidirectional, multi-phased composites with complex microstructures. Compos. Part B Eng. 1999, 30, 87–105. [Google Scholar] [CrossRef]
- Aboudi, J. The Generalized Method of Cells and High-Fidelity Generalized Method of Cells Micromechanical Models—A Review. Mech. Adv. Mater. Struct. 2004, 11, 329–366. [Google Scholar] [CrossRef]
- Hansen, N. The CMA Evolution Strategy: A Comparing Review. In Towards a New Evolutionary Computation; Springer: Berlin/Heidelberg, Germany, 2007; pp. 75–102. [Google Scholar] [CrossRef]
- Hinton, M.J.; Kaddour, A.S.; Soden, P.D. Failure Criteria in Fibre-Reinforced-Polymer Composites; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar] [CrossRef]
- Giagopoulos, D.; Arailopoulos, A. Computational framework for model updating of large scale linear and nonlinear finite element models using state of the art evolution strategy. Comput. Struct. 2017, 192, 210–232. [Google Scholar] [CrossRef]
- Zacharakis, I.; Giagopoulos, D.; Arailopoulos, A.; Markogiannaki, O. Optimal finite element modeling of filament wound CFRP tubes. Eng. Struct. 2022, 253, 113808. [Google Scholar] [CrossRef]
- Colvin, G.E.; Swanson, S.R. In-Situ Compressive Strength of Carbon/Epoxy AS4/3501-6 Laminates. J. Eng. Mater. Technol. 1993, 115, 122–128. [Google Scholar] [CrossRef]
- Ditcher, A.K.; Rhodes, F.E.; Webber, J.P.H. Non-linear stress-strain behaviour of carbon fibre reinforced plastic laminates. J. Strain Anal. Eng. Des. 1981, 16, 43–51. [Google Scholar] [CrossRef]
- Swanson, S.R.; Toombes, G.R. Characterization of Prepreg Tow Carbon/Epoxy Laminates. J. Eng. Mater. Technol. 1989, 111, 150–153. [Google Scholar] [CrossRef]
- Swanson, S.; Messick, M.; Toombes, G. Comparison of torsion tube and Iosipescu in-plane shear test results for a carbon fibre-reinforced epoxy composite. Composites 1985, 16, 220–224. [Google Scholar] [CrossRef]
- Böhm, H.; Rammerstorfer, F.; Weissenbek, E. Some simple models for micromechanical investigations of fiber arrangement effects in MMCs. Comput. Mater. Sci. 1993, 1, 177–194. [Google Scholar] [CrossRef]
- Mueller, A. A finite element method for microstructural analysis. Compos. Eng. 1994, 4, 361–376. [Google Scholar] [CrossRef]
- Nakamura, T.; Suresh, S. Effects of thermal residual stresses and fiber packing on deformation of metal-matrix composites. Acta Met. Mater. 1993, 41, 1665–1681. [Google Scholar] [CrossRef]
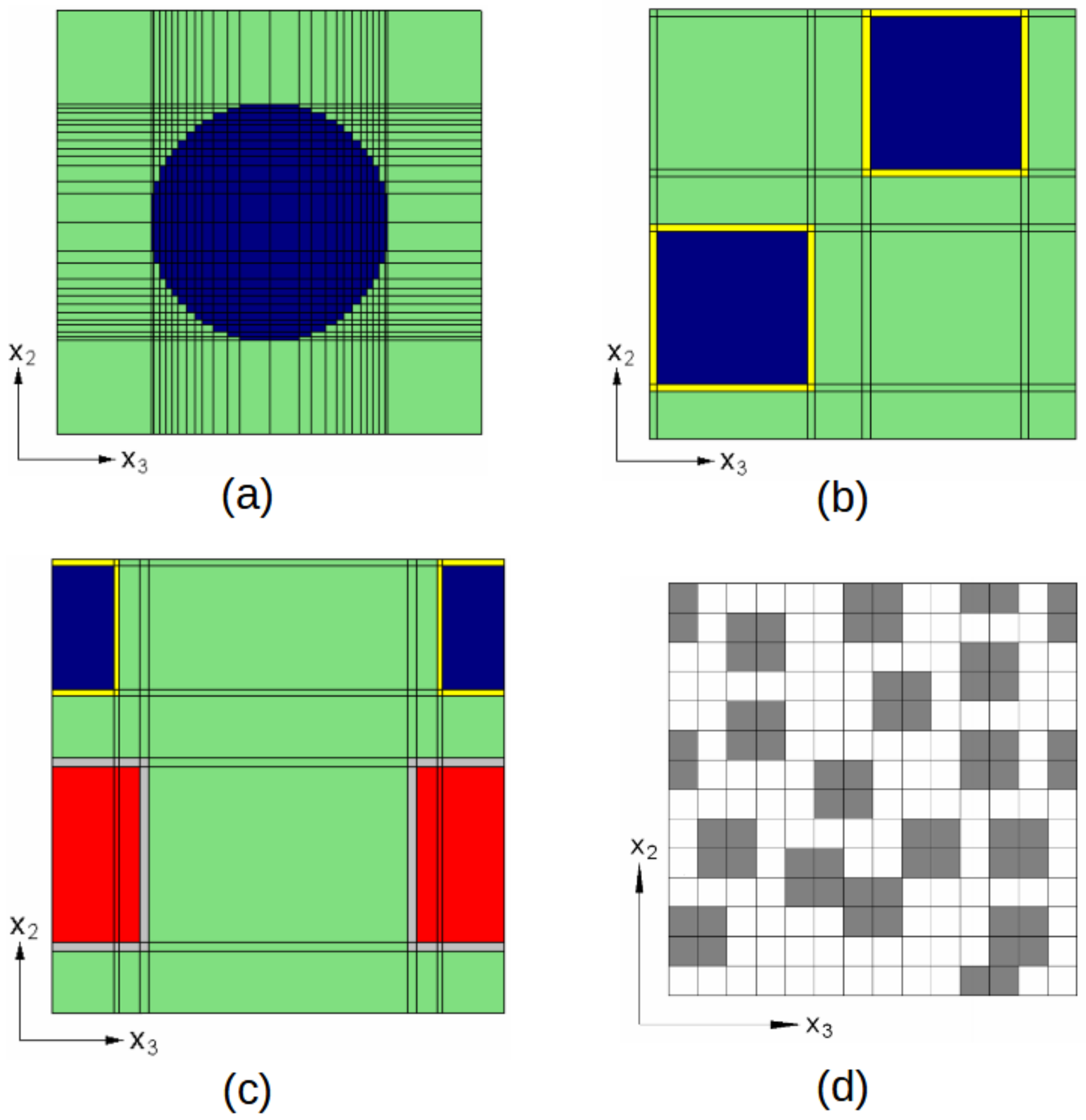




| ID | ||
|---|---|---|
| HEX |  | Hexagonal Pack Constraints on the fiber volume fraction () |
| REC.100 |  | Rectangular Pack: Square R 1 = 1.0 Constraints on the fiber volume fraction () None |
| REC.120 |  | Rectangular Pack: R = 1.20 > 1.0 Constraints on the fiber volume fraction () |
| REC.075 |  | Rectangular Pack: R = 0.75 < 1.0 Constraints on the fiber volume fraction () |
| ID | ||
|---|---|---|
| RP.06 × 06 |  | Square 6 × 6 (R = 1.0) Subcells along horizontal axis: 6 Subcells along vertical axis: 6 Total subcells: 36 Subcells corresponding to fiber: 6/10 × 36~21 |
| RP.14 × 10 |  | Rectangle 14 × 10 (R = 1.4) Subcells along horizontal axis: 14 Subcells along vertical axis: 10 Total subcells: 140 Subcells corresponding to fiber: 6/10 × 140~85 |
| RP.14 × 14 |  | Square 14 × 14 (R = 1.0) Subcells along horizontal axis: 14 Subcells along vertical axis: 14 Total subcells: 196 Subcells corresponding to fiber: 6/10 × 140~118 |
| Subcells along Horizontal Axis: 6 Subcells along Vertical Axis: 6 Total Subcells: 36 | ||||
|---|---|---|---|---|
RP.058 Fiber subcells: 20 = 0.56 | RP.061 Fiber subcells: 22 = 0.61 | RP.067 Fiber subcells: 24 = 0.67 | RP.072 Fiber subcells: 26 = 0.72 | RP.077 Fiber subcells: 28 = 0.77 |
| AS4 | 3501-6 | AS4/3501-6 | |
|---|---|---|---|
| Fiber volume fraction Vf (%) | 60 | ||
| Longitudinal modulus: E11 (GPa) | 225 | 4.2 | 126 |
| Transverse modulus: E22 (GPa) | 15 | 4.2 | 11 |
| In-plane shear modulus G12 (GPa) | 15 | 1.567 | 6.6 |
| Major Poisson’s ratio v12 | 0.2 | 0.34 | 0.28 |
| Through-thickness Poisson’s ratio v23 | - | 0.34 | 0.4 |
| Longitudinal tensile strength XT (MPa) | 3350 | 69 | 1950 |
| Longitudinal compressive strength XC (MPa) | 2500 | 250 | 1480 |
| Transverse tensile strength YT (MPa) | - | 69 | 48 |
| Transverse compressive strength YC (MPa) | - | 50 | 200 |
| In-plane shear strength S12 (MPa) | - | 1. | 79 |
| Longitudinal tensile failure strain ε1T (%) | 1.488 | - | 1.38 |
| Longitudinal compressive failure strain ε1C (%) | 1.111 | - | 1.175 |
| Transverse tensile failure strain ε2T (%) | - | - | 0.436 |
| Transverse compressive failure strain ε2C (%) | - | - | 2.0 |
| In-plane shear failure strain ε12u (%) | - | - | 2.0 |
| Strain energy release rate GIC (J/m2) | - | - | 220 |
| COMPOSITE VF = 60% | EXP | REC100 | HEX | ||
|---|---|---|---|---|---|
| Longitudinal modulus: E11 (GPa) | 126 | 136.7 | 8% (1) | 136.7 | 8% (1) |
| Transverse modulus: E22 (GPa) | 11 | 9.3 | −15% | 8.9 | −19% |
| Transverse modulus: E33 (GPa) | - | 9.3 | - | 8.9 | - |
| In-plane shear modulus G23 (GPa) | - | 2.9 | - | 2.9 | - |
| In-plane shear modulus G13 (GPa) | - | 4.4 | - | 4.1 | - |
| In-plane shear modulus G12 (GPa) | 6.6 | 4.4 | −34% | 3.9 | −40% |
| Major Poisson’s ratio: v12 | 0.28 | 0.25 | −10% | 0.25 | −9% |
| Through-thickness Poisson’s ratio: v23 | 0.4 | 0.27 | −32% | 0.30 | −24% |
| COMPOSITE VF = 60% | EXP | REC075 | REC100 | REC120 | |||
|---|---|---|---|---|---|---|---|
| Longitudinal modulus: E11 (GPa) | 126 | 136.7 | 8% (1) | 136.7 | 8% (1) | 136.7 | 8% (1) |
| Transverse modulus: E22 (GPa) | 11 | 9.1 | −17% | 9.3 | -15% | 9.6 | −11% |
| Transverse modulus: E33 (GPa) | - | 9.9 | - | 9.3 | - | 9.2 | - |
| In-plane shear modulus G23 (GPa) | - | 2.9 | - | 2.9 | - | 2.9 | - |
| In-plane shear modulus G13 (GPa) | - | 6.5 | - | 4.4 | - | 3.9 | - |
| In-plane shear modulus G12 (GPa) | 6.6 | 3.7 | −44% | 4.4 | −34% | 5.4 | −18% |
| Major Poisson’s ratio: v12 | 0.28 | 0.27 | −4% | 0.25 | −10% | 0.24 | −14% |
| Through-thickness Poisson’s ratio: v23 | 0.4 | 0.25 | −37% | 0.27 | −32% | 0.28 | −30% |
| COMPOSITE VF = 60% | EXP | RP.06 × 06 | RP.14 × 10 | RP.14 × 14 | |||
|---|---|---|---|---|---|---|---|
| Longitudinal modulus: E11 (GPa) | 126 | 133.0 | 6% (1) | 138.3 | 10% | 137.1 | 9% |
| Transverse modulus: E22 (GPa) | 11 | 8.1 | −26% | 8.3 | −25% | 8.3 | −25% |
| Transverse modulus: E33 (GPa) | - | 8.1 | - | 8.3 | - | 8.2 | - |
| In-plane shear modulus G23 (GPa) | - | 2.9 | - | 3.0 | - | 2.9 | - |
| In-plane shear modulus G13 (GPa) | - | 3.4 | - | 3.6 | - | 3.5 | - |
| In-plane shear modulus G12 (GPa) | 6.6 | 3.4 | −48.0% | 3.6 | −45% | 3.6 | −45% |
| Major Poisson’s ratio: v12 | 0.28 | 0.26 | −8% | 0.25 | −9% | 0.25 | −9% |
| Through-thickness Poisson’s ratio: v23 | 0.4 | 0.35 | −11% | 0.35 | −12% | 0.35 | −12% |
| COMPOSITE RP.06 × 06 | EXP | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fiber volume fraction Vf (%) | 58 | 61 | 67 | 72 | 77 | ||||||
| Longitudinal modulus: E11 (GPa) | 126 | 126.9 | 1% (1) | 139.1 | 10% | 151.4 | 20% | 163.7 | 30% | 175.9 | 40% |
| Transverse modulus: E22 (GPa) | 11 | 8.0 | −27% | 9.0 | −18% | 9.9 | −9% | 10.9 | −1% | 11.2 | 2% |
| Transverse modulus: E33 (GPa) | - | 8.0 | - | 8.6 | - | 9.3 | - | 10.3 | - | 10.9 | - |
| In-plane shear modulus G23 (GPa) | - | 2.8 | - | 3.0 | - | 3.2 | - | 3.6 | - | 4.0 | - |
| In-plane shear modulus G13 (GPa) | - | 3.3 | - | 3.5 | - | 3.9 | - | 5.7 | - | 6.5 | - |
| In-plane shear modulus G12 (GPa) | 6.6 | 3.3 | −49% | 5.2 | −21% | 7.0 | −7% | 7.8 | −18% | 8.0 | 21% |
| Major Poisson’s ratio: v12 | 0.28 | 0.26 | −7% | 0.25 | −12% | 0.23 | −17% | 0.23 | −19% | 0.23 | −20% |
| Through-thickness Poisson’s ratio: v23 | 0.4 | 0.36 | −11% | 0.32 | −20% | 0.28 | −29% | 0.23 | −41% | 0.22 | −45% |
| COMPOSITE REC.120 | EXP | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fiber volume fraction Vf (%) | 53 | 56 | 59 | 61 | 64 | 67 | |||||||
| Longitudinal modulus: E11 (GPa) | 126 | 121.2 | −4% | 127.9 | 1.5% | 134.5 | 7% | 138.9 | 10% | 145.5 | 16% | 152.2 | 21% |
| Transverse modulus: E22 (GPa) | 11 | 8.8 | −20% | 9.2 | −17% | 9.5 | −13% | 9.8 | −11% | 10.2 | −8% | 10.6 | −4% |
| Transverse modulus: E33 (GPa) | - | 8.5 | - | 8.7 | - | 9.0 | - | 9.3 | - | 9.6 | - | 9.9 | - |
| In-plane shear modulus G23 (GPa) | - | 2.7 | - | 2.8 | - | 2.9 | - | 3.0 | - | 3.1 | - | 3.3 | - |
| In-plane shear modulus G13 (GPa) | - | 3.4 | - | 3.6 | - | 3.8 | - | 3.9 | - | 4.2 | - | 4.5 | - |
| In-plane shear modulus G12 (GPa) | 6.6 | 4.3 | −35% | 4.7 | −29% | 5.2 | −21% | 5.6 | −15 | 6.6 | −5% | 7.2 | 9% |
| Major Poisson’s ratio: v12 | 0.28 | 0.26 | −9% | 0.25 | −11% | 0.25 | −12% | 0.24 | −14% | 0.24 | −15% | 0.23 | −17% |
| Through-thickness Poisson’s ratio: v23 | 0.4 | 0.31 | −23% | 0.29 | −26% | 0.28 | −30% | 0.27 | −32% | 0.26 | −36% | 0.24 | −39% |
| # | Param | LB | MEAN | UB | Result |
|---|---|---|---|---|---|
| 1 | 191.25 | 225.00 | 258.75 | 231.314 | |
| 2 | 12.75 | 15.00 | 17.25 | 13.494 | |
| 3 | 0.17 | 0.20 | 0.23 | 0.227 | |
| 4 | 0.0595 | 0.07 | 0.0805 | 0.075 | |
| 5 | 12.75 | 15.00 | 17.25 | 15.965 | |
| 6 | 3.57 | 4.20 | 4.83 | 4.292 | |
| 7 | 0.289 | 0.34 | 0.391 | 0.383 | |
| 8 | 50.00% | 60.00% | 70.00% | 58.41% | |
| 9 | 0.75 | 1.00 | 1.25 | 0.890 |
| # | Param | Experimental | Result | Discrepancy |
|---|---|---|---|---|
| 1 | 126.00 | 136.90 | 8.65% | |
| 2 | 11.00 | 9.149 | −16.83% | |
| 3 | 0.28 | 0.2977 | 6.32% | |
| 4 | 0.40 | 0.3351 | −16.23% | |
| 5 | 6.60 | 3.914 | −40.70% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zyganitidis, I.; Arailopoulos, A.; Giagopoulos, D. Composite Material Elastic Effective Coefficients Optimization by Means of a Micromechanical Mechanical Model. Appl. Mech. 2022, 3, 779-798. https://doi.org/10.3390/applmech3030046
Zyganitidis I, Arailopoulos A, Giagopoulos D. Composite Material Elastic Effective Coefficients Optimization by Means of a Micromechanical Mechanical Model. Applied Mechanics. 2022; 3(3):779-798. https://doi.org/10.3390/applmech3030046
Chicago/Turabian StyleZyganitidis, Ioannis, Alexandros Arailopoulos, and Dimitrios Giagopoulos. 2022. "Composite Material Elastic Effective Coefficients Optimization by Means of a Micromechanical Mechanical Model" Applied Mechanics 3, no. 3: 779-798. https://doi.org/10.3390/applmech3030046
APA StyleZyganitidis, I., Arailopoulos, A., & Giagopoulos, D. (2022). Composite Material Elastic Effective Coefficients Optimization by Means of a Micromechanical Mechanical Model. Applied Mechanics, 3(3), 779-798. https://doi.org/10.3390/applmech3030046





