Quantum Behavior in a Non-Bonded Interaction of BN ^{(+, −, 0)} B @ (5, 5) BN: Second-Order Jahn–Teller Effect Causes Symmetry Breaking

Abstract

The anion, cation, and radical structural forms of B₂N ^(−,0,+) were studied in the case of symmetry breaking (SB) inside a (5, 5) BN nanotube ring and were also compared in terms of non-covalent interaction between these two parts. The non-bonded system of B₂N ^(−,0,+) and the (5, 5) BN nanotube not only causes SB for BNB but also creates an energy barrier in the range of 10⁻³ Hartree of due to this non-bonded interaction. Moreover, several SBs appear via asymmetry stretching and symmetry bending normal mode interactions according to the multiple second-order Jahn–Teller effect. We also demonstrated that the twin minimum of BNB’s potential curve arises from the lack of a proper wave function with permutation symmetry, as well as abnormal charge distribution. Through this investigation, considerable enhancements in the energy barriers due to the SB effect were also observed during the electrostatic interaction of BNB (both radical and cation) with the BN nanotube ring. Additionally, these values were not observed for the isolated B₂N ^(−,0,+) forms. This non-bonded complex operates as a quantum rotatory model and as a catalyst for producing a range of spectra in the IR region due to the alternative attraction and repulsion forces.

1. Introduction

B₂N ^(−,0,+) structures are susceptible to the symmetry breaking (SB) effect triggered by the pseudo-second-order Jahn–Teller effect. These structures can result in non-bonded attraction or repulsion within (5, 5) BN nanotubes (BNNTs), potentially causing either real or artefactual interactions [1,2,3,4]. Over the past few decades, several experimental and theoretical discussions have been conducted regarding BNB structures [1,2,3,4,5,6,7,8,9,10,11,12]. However, there has been little significant work on the SB of B₂N ^(−,0,+) structures in non-covalent systems within homogenous rings, such as (5, 5) BN nanotubes (BNNTs), aside from our previous work [13,14,15,16] and work by our colleagues at the University of Texas, Austin [17,18]. In 1989 Martin et al. conducted an extensive study on B_nN_3−n (n = 0, 1, 2 and 3) simultaneously. They observed an asymmetric linear structure for neutral B₂N⁽⁰⁾ in its ground state, with low bending vibration ranging from 71 to 73 cm⁻¹ [1]. Generally, researchers agree on a linear combination in ground states for B₂N ⁽⁻⁾ and B₂N ⁽⁰⁾ with terms of (${\tilde{X}}^1{\sum }_g^{+} )$ and (${\widetilde{X }}^2{\sum }_u^{+})$, respectively. Consequently, Paldus [9] minimized the B$N^{\left(0\right)}$B radical through an extensive calculation of multi-reference coupled clusters in both singlet and doublet positions [RMR CCSD (T)] by using basis sets (cc-pVDZ, cc-pVTZ, and cc-pVQZ). Asmis et al. demonstrated and analyzed a mode value of ${\widetilde{A }}^2{\sum }_g^{+}(B_2{N}^{-})$ of 6329 ± 39 cm⁻¹ after ${\widetilde{X }}^2{\sum }_u^{+}$[2]. They interpreted these states through a photoelectron spectrum as two equations, ${\tilde{X}}^1{\sum }_g^{+} \to {\widetilde{ X}}^2{\sum }_u^{+}+ e^{-}$ and ${\tilde{X}}^1{\sum }_g^{+} \to {\tilde{A}}^{ 2}{\sum }_g^{+}+ e^{-}$, with linear symmetry transitions at 355 and 266 nm, respectively. Moreover, through the IR spectrum for ${\widetilde{A }}^2{\sum }_g^{+}-{\widetilde{X }}^2{\sum }_u^{+},$ the electronic band was observed at 6000 cm⁻¹ [7]. According to Walsh’s theorem [19], a linear $\pi$-block of B$N^{(-, 0, +)}$ includes 11 electrons in valence orbitals. By adding an extra electron, the configuration can shift towards the ground state as follows: $({\tilde{X}}^2{\sum }_u^{+})\to ({\tilde{X}}^1{\sum }_g^{+} )$. Moreover, the (5, 5) BN nanotube structure enables us to create multiple reactive sites for the B₂N ^(−,0,+) @ (5, 5) BN system, including functional groups similar to core/shell systems. In this work, a B₂N ^(−,0,+) @ (5, 5) BNNT system was simulated from the viewpoint of quantum non-bonded interactions, considering the attraction or repulsion forces between BN ^(−,0,+) B ions. In this activity, we confirmed the creation of several energy barriers for the BN ^(−,0,+) B system during its interaction and quantum rotation inside (5, 5) BNNTs. We also discussed how the external field of (5, 5) BNNT rings would lead to a stronger pseudo-second-order Jahn–Teller effect [20,21,22] for certain BN ^(−,0,+) B ions in various states.

2. Theoretical Background

2.1. Quantum Theory of the BN ^{(+, −, 0)} B @ (5, 5) BNNT

In quantum mechanics, it has been confirmed that the total wave function of our system, which includes ${\Phi }_n^{BNB}$ and ${\Phi }_m^{(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}$ in the overall structure of the non-bonded combination of ${\Phi }_n^{BNB}$ @${\Phi }_m^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}$, is anti-symmetric under the permutation of electron coordinates. Moreover, it can also be proven that the product states under intermolecular exchange cannot be anti-symmetric. Therefore, an anti-symmetrization operator could be defined for this behavior as “$\tilde{A}$” [23]. This approach is interpreted according to the Eisenschitz statement [24], which indicates that the anti-symmetrized unperturbed states are no longer eigen-functions of H ⁽⁰⁾ with the commutator$[\tilde{A}, H^{\left(0\right)}]\ne 0$. In addition to the projected excited states, ${\tilde{A}}^{BNB-\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}{\varnothing }_n^{BNB}{\varnothing }_m^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}$ can be represented as a linear relationship [23,24,25]. The first-order equation for energy, which includes exchange terms, can be rearranged as follows:

$${ E}_{antisymm}^{\left(1\right)}={\displaystyle \frac{⟨{\Phi }_0^{\mathrm{B}\mathrm{N}\mathrm{B}}{\Phi }_0^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}\left|V^{\mathrm{B}\mathrm{N}\mathrm{B}-\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}{\tilde{A}}^{\mathrm{B}\mathrm{N}\mathrm{B}-\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}\right|{\Phi }_0^{\mathrm{B}\mathrm{N}\mathrm{B}}{\Phi }_0^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}⟩}{⟨{\Phi }_0^{\mathrm{B}\mathrm{N}\mathrm{B}}{\Phi }_0^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}\left|{\tilde{A}}^{\mathrm{B}\mathrm{N}\mathrm{B}-\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}\right|{\Phi }_0^{\mathrm{B}\mathrm{N}\mathrm{B}}{\Phi }_0^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}⟩}}$$

(1)

Although the exchange term is commensurate, it arises from the overlapping between BN ^{(+, −, 0)} B and the (5, 5) BNNT rings, making it difficult to calculate the related energies. Thus, its wave functions decay exponentially due to the exchange interaction, which depends on changes in distance variables [23,24,25]. Consequently, a $(5,5) \mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ ring, especially with a small diameter, could be effectively utilized in this non-bonded model to enhance overlap. (In our model, exchange interactions should be neglected.) We also observed that although this interaction is generally attractive, in certain positions, it shifts towards repulsive forces due to the diameter of the $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ rings and the presence of ionic or radical states. Therefore, RS-PT theory [23,24,25,26,27,28,29] was utilized, taking into account the exchange factor. The unperturbed Hamiltonian was estimated by summing two monomer Hamiltonians. Meanwhile, we assume that the total Hamiltonian is the sum of these two sections, as shown in the following equation:

$$H^{\left(0\right)}\equiv H^{BNB}+H^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}$$

(2)

In this case, the unperturbed states can be written as follows:

$${\varnothing }_n^{BNB}\& H^{BNB}{\varnothing }_n^{BNB}=E_n^{BNB}{\varnothing }_n^{BNB}\& H^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}{\varnothing }_n^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}=E_n^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}{\varnothing }_n^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}$$

(3)

$$E_{electrostatic}^{\left(1\right)}=⟨{\Phi }_0^{BNB}{\Phi }_0^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}\left|V^{BNB-\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}\right|{\Phi }_0^{BNB}{\Phi }_0^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}⟩$$

(4)

Charge densities of BNB parts can be measured using the equation

$${\mathsf{\rho }}_{\mathrm{t}\mathrm{o}\mathrm{t}(\mathrm{r})}^{\mathrm{B}\mathrm{N}\mathrm{B}}={\sum }_{{\mathsf{\alpha }}_{\mathrm{i}}}{\mathrm{z}}_{{\mathsf{\alpha }}_{\mathrm{i}}}\mathsf{\delta }\left(\mathrm{r}-{\mathrm{R}}_{{\mathsf{\alpha }}_{\mathrm{i}}}\right)-{\mathsf{\rho }}_{\mathrm{e}\mathrm{l}}^{\mathrm{B}\mathrm{N}\mathrm{B}}(\mathrm{r})$$

(5)

In this equation, ${\mathsf{\alpha }}_{\mathrm{i}}$ represents the nucleus of boron and nitrogen atoms with position vector R${\mathsf{\alpha }}_{\mathrm{i}}$. The Dirac delta, Z_α δ(r − R${\mathsf{\alpha }}_{\mathrm{i}}$), can be used to express the changes in these nuclei over the n − 1 electron coordinates of B₂N ^(−,0,+) as follows:

$${\mathsf{\rho }}_{\mathrm{e}\mathrm{l}}^{\mathrm{B}\mathrm{N}\mathrm{B}}\left(\mathrm{r}\right)=\mathrm{n}\int |{\mathrm{\varnothing }}_0^{\mathrm{B}\mathrm{N}\mathrm{B}}\left(\mathrm{r},{\mathrm{r}}_2^{\prime },{\mathrm{r}}_3^{\prime },\dots ,{\mathrm{r}}_{\mathrm{n}}^{\prime }\right){|}^2\mathrm{d}{\mathrm{r}}_2^{\prime },{\mathrm{d}\mathrm{r}}_3^{\prime }\dots ,{\mathrm{d}\mathrm{r}}_{\mathrm{n}}^{\prime }$$

(6)

It can be shown that the first-order expression can be rearranged as

$${\mathrm{E}}_{\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c}}^{\left(1\right)}=\iint {\mathsf{\rho }}_{\mathrm{t}\mathrm{o}\mathrm{t}}^{\mathrm{B}\mathrm{N}\mathrm{B}}\left({\mathrm{r}}_1\right){\displaystyle \frac{1}{{\mathrm{r}}_{12}}}{\mathsf{\rho }}_{\mathrm{t}\mathrm{o}\mathrm{t}}^{(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}({\mathrm{r}}_2){\mathrm{d}\mathrm{r}}_1{\mathrm{d}\mathrm{r}}_2$$

(7)

Equations (2)–(8) confirm the RS-PT energy related to the electrostatic interaction of BN ^{(+, −, 0)} B @ (5,5) BNNT. This interaction was simulated in this work by using the following equation:

$$∆\mathrm{E}={\mathrm{E}}_{(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}-\mathrm{B}\mathrm{N}\mathrm{B}}-({\mathrm{E}}_{(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}+{\mathrm{E}}_{\mathrm{B}\mathrm{N}\mathrm{B}})$$

(8)

All relative motions, including vibration and rotation, in the BN ^(−,0,+) B @ (5, 5) BNNT system affect the charge densities in both the ground and excited states. We measured the ion–dipole and dipole–dipole parameters, as well as non-overlapping parts for the B$N^{(-, 0, +)}$B @ $(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ system across various electronic states. For the ionic forms, the ion–dipole interactions of $B{N}^{(-, +)}B$ inside $(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ can also be estimated. These interactions are created as either intermolecular forces or a rather special kind of force, such as multipolar attraction, which is related to the distance (${\displaystyle \frac{1}{R_{AB}^n}}$). This piece of information confirms that attraction can be produced in the ground state between $\left(\mathrm{B}{\mathrm{N}}^{\left(-,0\right)}\mathrm{B}\right)$ and the $(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ ring. In contrast, repulsion appears between $\left(\mathrm{B}{\mathrm{N}}^{\left(+\right)}\mathrm{B}\right)$ and $(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ rings (Figure 1). In the excited state, particles generate an attractive force towards each other. Based on the free rotation of $B{N}^{\left(0\right)}B$, the total electrostatic dipole–dipole interaction is evidently much weaker and lower than the non-averaged one [30]. The total electrostatic interaction energies and charge distributions can be estimated as follows:

$$U_{(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}-BNB}={\sum }_{\mu ϵ\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}{\sum }_{vϵBNB}{\displaystyle \frac{q_{\mu }{q}_v}{r_{\mu v}}}$$

(9)

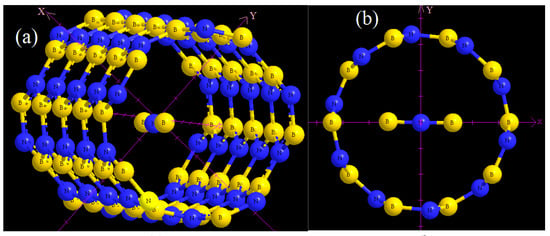
Figure 1. Optimized configuration of BNB inside $(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$: (a) vertical position and (b) horizontal position.

The charge distribution of these molecule and ions inside the $(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ ring is highly polarized. The Hamiltonian should be considered based on the Born–Oppenheimer approximation for all pairs of non-bonded interactions.

$$H^{\left(Nonbonded\right)}=H^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}+H^{\mathrm{B}2\mathrm{N}}$$

(10)

where the unperturbed states can be written as ${\Phi }_k^{\left(\mathrm{5,5}\right)BNNT}{\Phi }_m^{\left\{\mathrm{B}2\mathrm{N}\right\}}$ with

$$H^{\left\{\right(\mathrm{5,5}\left)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}\right\}}{\Phi }_k^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}=E_k^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}{\Phi }_k^{\left(\mathrm{5,5}\right)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}$$

(11)

and

$$H^{\mathrm{B}2\mathrm{N}}{\Phi }_m^{\mathrm{B}2\mathrm{N}}={\Phi }_m^{\mathrm{B}2\mathrm{N}}$$

(12)

Here, we measured the electrostatic energies of the monomer’s wave functions using a multipole expansion [31,32,33,34].

2.2. The Interactions Between BNB and $(5,5)BNNT$

Figure 2 shows the structure of a BNB molecule and a $(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ ring at a distance R (from the BNB molecule to each B-N bond of the $(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ ring). It is worth noting that the wave function may be too small due to overlap and can be omitted. Particles with indices $i$∈$\mathrm{B}\mathrm{N}\mathrm{B}$ and $j\in$ $(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ are considered in this model, with a total Hamiltonian shown as $=H^{\left(0\right)}+H^{\left(1\right)}$. This Hamiltonian combines two parts: (A) a free molecule, $H^{\left(0\right)}=H^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}+H^{\mathrm{B}\mathrm{N}\mathrm{B}}$, and (B) an interaction operator,

$$H^{\left(1\right)}={\sum }_{i\in \mathrm{B}\mathrm{N}\mathrm{B}}{\sum }_{j\in \mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}{\displaystyle \frac{q_i{q}_j}{r_{ij}}}$$

(13)

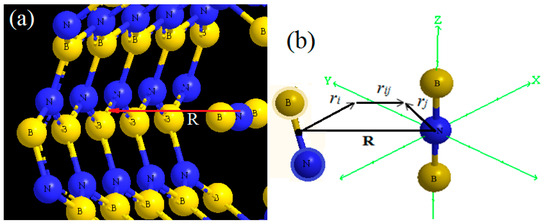
Figure 2. (a) BNB located at distance R from the B-N unit of a BNNT ring; (b) $i\in \mathrm{B}\mathrm{N}\mathrm{B}$ and $\in$ $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$, $r_i=(x_i,y_i,z_i)$ and $r_j=(x_j,y_j,z_j)$, with R= (0, 0, R) and r_ij = r_j − r_i + R. The red arrow demonstrate the distance between atom N from B₂N to atom B from center of BNNT.

One of the B-N bonds in the $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ ring interacts with BNB molecules to create an external potential denoted by $″V_{(r_i)}″$ for BN ^{(−, 0, +)} B. This potential is defined as $V_{(r_i)}=\sum _{j\in \mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}{\displaystyle \frac{q_j}{r_{ij}}}$. Therefore, we can express it as

$$H^{\left(1\right)}={\sum }_{i=1}^n{q}_i{V}_{\left(ri\right)}={\sum }_{i=1}^n{q}_{i}V(x_i,y_{i,}{z}_i)$$

(14)

By making a substitution into Equation (1) and rearranging Equations (9)–(14), Equations (15)–(17) result in the following:

$$\begin{gathered} H^{\left(1\right)}= {\displaystyle \frac{{\sum }_{(i=1)\in BNB}^n{q}_i{\sum }_{(j=1)\in \mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}^n{q}_j}{R}}+{\displaystyle \frac{{\sum }_{(i\in BNB)}^n{q}_i{r}_i{q}^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}}{R^2}}-{\displaystyle \frac{{\sum }_{(j\in BNB)}^n{q}_j{r}_j{q}^{BNB}}{R^2}}+ \\ {\displaystyle \frac{{\mu }_x^{BNB}{\mu }_x^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}+{\mu }_y^{BNB}{\mu }_y^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}-{2\mu }_z^{BNB}{\mu }_z^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}}{R^3}} \end{gathered}$$

(15)

Here the total charges can be measured as

$$\begin{gathered} q^{BNB}={\sum }_{(i=1)\in BNB}^n{q}_i,q^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}2}={\sum }_{(j=1)\in SiO2}^n{q}_j andthedipoleoperatorsare \\ {\mu }^{BNB}={\sum }_{(i=1)\in BNB}^n{q}_i{r}_i, {\mu }^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}={\sum }_{(j=1)\in SiO2}^n{q}_j{r}_j \end{gathered}$$

(16)

The operator H ⁽¹⁾ represents the electrostatic interactions of the dipole moments and charges for the B${\mathrm{N}}^{(-,0,+)}$B @ $(5,5)\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ system. The operator for the dipole–dipole interaction tensor can be presented as follows:

$${\displaystyle \frac{{\mu }_x^{BNB}{\mu }_x^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}+{\mu }_y^{BNB}{\mu }_y^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}-{2\mu }_z^{BNB}{\mu }_z^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}}{R^3}}={\displaystyle \frac{{\mu }^{BNB}{\mu }^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}-3{\mu }_z^{BNB}{\mu }_z^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}}{R^3}}={\displaystyle \frac{{\mu }^{BNB}.\widehat{T}.{\mu }^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}}{R^3}}$$

(17)

The interaction tensor can be arranged as $\widehat{T}$=$\left[\begin{array}{ccc}{T}_{xx}& T_{yy}& T_{zz}\\ T_{yx}& T_{yy}& T_{yz}\\ T_{zx}& T_{zy}& T_{zz}\end{array}\right]$=$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& -2\end{array}\right]$. This can also be expressed in more general terms.

The application of the Schrödinger equations between the isolated BNB and $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ can be written as $H^{BNB}{\Phi }_{K_1}^{BNB}$=$E_{K_1}^{BNB}{\Phi }_{K_1}^{BNB}$ and $H^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}{\Phi }_{K_1}^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}$=$E_{K_1}^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}{\Phi }_{K_1}^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}$. The eigenvalues of unperturbed terms ($H^{\left(0\right)}{\Phi }_K^{\left(0\right)}$=$E_K^{\left(0\right)}{\Phi }_K^{\left(0\right)}$, with ${\Phi }_K^{\left(0\right)}={\Phi }_{K_1}^{BNB}{\Phi }_{K_2}^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}$) are $E_K^{\left(0\right)}=E_{K_1}^A+E_{K_2}^B$.

Therefore, the first-order energy can be measured using the following equation:

$$E_0^{\left(1\right)}= ⟨{\Phi }_0^{\left(0\right)}\left|H^{\left(1\right)}\right|{\Phi }_0^{\left(0\right)}⟩=⟨{\Phi }_0^{ABNB}{\Phi }_0^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}\left|H^{\left(1\right)}\right|{\Phi }_0^{BNB}{\Phi }_0^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}⟩$$

(18)

Moreover, the multipole expansion of this integral can be separated by the Cartesian coordinates ($x_i,y_i,z_i$) and ($x_j,y_j,z_j$) of molecules $i\in$ BNB and$\in$ $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$.

The permanent multipole moments are $<{\mu }^{BNB}>=⟨{\Phi }_0^{BNB}\left|{\mu }^{BNB}\right|{\Phi }_0^{BNB}⟩$ and $<{\mu }^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}>=⟨{\Phi }_0^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}\left|{\mu }^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}\right|{\Phi }_0^{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}⟩$. Similar to the above equation, the second-order energy can be written as follows:

$$E_0^{\left(2\right)}={\sum }_{k\ne 0}{\displaystyle \frac{⟨{\Phi }_0^{\left(0\right)}\left|H^{\left(1\right)}\right|{\Phi }_K^{\left(0\right)}⟩⟨{\Phi }_K^{\left(0\right)}\left|H^{\left(1\right)}\right|{\Phi }_0^{\left(0\right)}⟩}{E_0^{\left(0\right)}-E_k^{\left(0\right)}}}$$

(19)

Here k denotes the excited state, which is divided into two parts as k = (k₁, K₂). In addition, summation over k$\ne$ 0 results into a split into three sums in the excited state. These are k₁ ≠ 0 and K₂ = 0 for BNB, k₂ ≠ 0 and k₁ = 0 for the $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$, and (k_1, k₂) ≠ 0 for the non-bonded combination of the system of BNB inside the $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$. Here, we assume that the $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ has a ground state configuration, while BN ^(−,0,+) B can be excited to different energy levels. The main important issue is to understand the electrostatic interaction between BNB and the $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ environment. The electrostatic interactions of the BNB exhibit multiple turning points with several parts of the $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ loops. Consequently, the first bond of the B-N position in the first segment of the $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ has been estimated, while the other loops have been kept frozen. Meanwhile, this action will continue systematically to consider all positions (Figure 2). We also selected each B-N bond in front of each part in the $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ subunit and then measured the non-bonded interaction between these two parts [14]. According to our previous works [13,14,15], dipole expansions are utilized in electromagnetic field approaches due to the charge distributions [31,32,33,34]. Due to the lack of experimental evidence, the theoretical simulations can be improved by the concepts of dipole moment and angular momentum. These can be defined as a sum of spherical harmonics as follows:

$$f(\theta ,\phi )={\displaystyle \sum _{l=0}^{\infty }{\displaystyle \sum _{m=-l}^l{C}_l^m{Y}_l^m(\theta ,\phi )}}$$

(20)

According to the total electrostatic interaction energy (U_BNNT-BNB) from Equation (9), the charge distribution of the $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ ring can be polarized through BNB due to the electromagnetic field induced by the ring environment. The dipole moment arising from the electric charge distribution usually produces powers according to the distance (r) as well as angular dependence (Ө and Φ). The dipole moment can be analyzed based on two cases: one where the charge distribution is located near the origin, resulting in exterior dipole moments, and another where the charges are far from the origin, resulting in interior dipole moments. Therefore, it can usually be calculated by considering both interior and exterior dipole contributions [14,31,32,33,34].

For BNB, it can be considered that Ө = Φ = 0, meaning that the dipole moment vectors should be located on the BNB axis. Due to the measurement of dipole moments, the r component can be predicted for both cationic and radical forms of BNB. These molecules exhibit a tendency to rotate within three distinct conical surfaces. Therefore, it can be concluded that the dipole moment arises from the linear structure of the BNB molecule. Under extrinsic factors, the physico-chemical properties of the radical, anion, and cation of the BNB-BNNT non-bonded combination forms will be completely altered by the electrical current passing through the ring. Consequently, the three types of ions, i.e., cationic, anionic, and radical, enable the generation of ions from each other frequently. As a result the radial vector of the dipole moment (r) becomes quantized during the formation of three cone levels.

Finally, the BSSE was used to calculate the binding energies of pseudo-systems, including the ghost atom, in its normal position within any real molecule when applying a normal basis function that was fitted. Since they do not have a nuclear charge or any electrons to contribute to the molecule, we need to use an appropriate ghost basis set file for each atom involved in the calculation. After that we can copy the basis set file and remove the frozen core. In quantum chemistry, measurements using different basis sets are susceptible to basis set superposition error (BSSE). When atoms interact, their basic functions overlap, causing each part to "borrow" functions from nearby parts. In order to improve the calculation of derived properties such as energy, we need to consider using BSSE.

3. Results and Computational Details

The system was minimized using the CASSCF (10, 12) level, which included EPR-II, EPR-III, and AUG-cc-pvqz basis sets for ionic forms. Meanwhile, for the radical form, the UHF and ROHF methods were also taken into consideration. Energy minimization of B₂${\mathrm{N}}^{(-,0,+)}$ in ground and excited states within the BNNT ring was measured using the M062x/6-31g*, M062x/EPR-II, B3p86/EPR-ii, B3p86/6-31g*, and B3LYP/6-31g* levels of theory. The BNNT ring was also optimized using the DFT method (Table 1 and Table 2 and Supplementary Tables S1 and S2). All ab initio calculations were performed using Gaussian 09 software, as well as additional correlated software: Games (modified by Head Gordon), Chem3D, and AIM within this version of Gaussian programming software [35].

Table 1. Electric Potential (EP) and Isotropic Fermi Contact Couplings (IFCCs) (MHz) for isolated and non-isolated B₂$N^{(-, 0, +)}$.

State (* Ne)	$E_e+$ $-104\left(Hartree\right)$ Isolated BNB	Configuration (Energy of $\left|\alpha \right.⟩\ast$ $\left(Homo-Lumo\right)$**	$\beta$ electron Configuration Total Energy of $\left|\beta \right.⟩\ast$ Beta virtual **	$r_e\left(B_{1}N\right)$ $r_e\left(N{B}_2\right)$ (*) in BNNT	$A_1$ $(\mathrm{2,1},3,-2,-1)$ $A_2$ $(\mathrm{2,1},3,-1,-2)$	$B^{{EP}_1}-N^{{EP}_2}-B^{{EP}_3}$ * Dipole ** IFCC(N,B1,B2) isolated	$B^{{EP}_1}-N^{{EP}_2}-B^{{EP}_3}$ * Dipole ** IFCC(N,B1,B2)in BNNT(non-isolated
${\widetilde{X }}^2{\Sigma }_u^{+}$ ($D_{\infty h})$ (* 17e)	$-{1.6396769 }^d$	${\left[{\mathit{A}}^{\prime }\right]{\pi }_u^4,4\sigma }_g^2{,3\sigma }_u^1\left|\alpha \right.⟩=-{0.42481}^{ d}$ $\ast (-34.74888{) }^d$ $\ast \ast (-0.49245{) }^d$	$\left[{\mathit{B}}^{\prime }\right],{4\sigma }_g^1\left|\beta \right.⟩$=−0.24839 d $\ast (-34.06919{) }^d$ **${\left(-0.18739\right)}^d$	$1.3179$d ${1.3179 }^d$	$A_1=180.{0 }^d$ $A_2=180.0^{ d}$	${\widetilde{X }}^2{\Sigma }_u^{+}$ ($D_{\infty h})$ (*17e)	$-1.639676{9 }^{d }$
${\widetilde{ B}}^4{\Pi }_g$ (*17e)	$-0.029701{9 }^h$ $-0.0141200^{ a}$	${\left[{\mathit{A}}^{\prime }\right]\pi }_u^4,{\pi }_{g,}^2{\sigma }_g^1\left|\alpha \right.⟩=-0.26901^h$ $\ast (-35.04479{)}^{\mathit{h}}$ $\ast (-0.30130{)}^{ h}$	$\left[{\mathit{A}}^{\prime }\right],{\pi }_u^2\left|\beta \right.⟩=-0.4965^{ h}$ $\ast (-33.74799)$ $\ast \ast (-0.50601)$	$\ast 1.308{1 }^x$ $\ast 1.308{1 }^x$	${\ast A}_1=180.{0 }^x$ ${\ast A}_2=180.{0 }^x$	${EP}_1={EP}_3=-11.4{0 }^x$ ${EP}_2=-18.4{0 }^x$ $\ast 0.00$ $\mathrm{*}\mathrm{*}20.9,399.2,399.2^{ x}$	${EP}_1={EP}_3=-11.2{5 }^x$ ${EP}_2=-18.1{7 }^{x }$ $\ast 0.03$ $\mathrm{*}\mathrm{*}9.4,389.5,401.6^x$
${\widetilde{X }}^1{\Sigma }_g^{+}$ (*18e)	${-0.1965675}^{ a}$ $-0.201911{5 }^{a^{\prime }}$ $-0.195017{0 }^{a^{″}}$	${\left[{\mathit{A}}^{\prime }\right]1{\pi }_u^4,4\sigma }_g^2{,3\sigma }_u^2=-0.13904^{ a}$ $\ast E\left(\left|\alpha \right.⟩\right)=-32.486{47 }^a$ $\ast \ast -0.36286$	-	$\ast 1.335^{ y}$ $\ast 1.33{5 }^y$	$A_1=\ast 180.0^{ y}$ $A_2=\ast 180.{0 }^y$	${EP}_1={EP}_3=-11.6{3 }^y$ ${EP}_2=-18.{6 }^y$ $\ast 0.00$	${EP}_1={EP}_3=-11.14^{ y}$ ${EP}_2=-18.1{6 }^y$ $\ast 0.01$
${\widetilde{ A}}^3{\Pi }_u$ (*18e)	$-0.088468{6 }^a$ $-0.1164695^{ h}$ $-0.0809445^{{ a}^{\prime }}$ $-0.0792590^{{ a}^{\prime \prime }}$	[C]${{\pi }_u^4,3\sigma }_u^1,{1\pi }_g^1\left|\alpha \right.⟩$=${-0.03986}^h$ $\ast E\left(\left|\alpha \right.⟩\right)=-32.7972{1 }^h$ $\ast \ast -0.2594{1 }^h$	${\left[{\mathit{C}}^{\prime }\right]\pi }_{u,}^4{,4\sigma }_g^1\left|\beta \right.⟩$ =${-0.01559 }^h)$ $\ast E\left(\left|\beta \right.⟩\right)=-32.26335^{ h}$ $\ast \ast -0.14777^{ h}$	$\ast 1.342{2 }^w$ $\ast 1.3422$	$A_1=\ast 180.0^{ w }$ $A_2=\ast 180.{0 }^w$	${EP}_1={EP}_3=-11.6{7 }^w$ ${EP}_2=-18.{60 }^w$ $\ast 0.00$0 $\ast \ast -\mathrm{15.7,208.2,208.2}$	${EP}_1={EP}_3=-11.1{9 }^w$ ${EP}_2=-18.1{6 }^w$ $\ast 0.00$6 $\ast \ast -\mathrm{10.9,300.5,218.5}$
${\widetilde{X }}^2{\Sigma }_u^{+}$ ($D_{\infty h})$	${-0.0781959 }^b$	${\left[{\mathit{A}}^{\prime }\right]{\pi }_u^4,4\sigma }_g^2{,3\sigma }_u^1\left|\alpha \right.⟩=-0.4463{9 }^b$ $\ast \ast (-0.48609{) }^b$	$\left[{\mathit{B}}^{\prime }\right],{4\sigma }_g^1\left|\beta \right.⟩=-0.2617{9 }^b$ $\ast (-34.15039{) }^b$ $\ast \ast (-0.17700{)}^{ b}$	$\mathrm{*}1.3200^{ z}$ $\ast 1.320{0 }^z$	${\ast A}_1=180.{0 }^z$ ${\ast A}_2=180.0^{ z}$	${EP}_1={EP}_3=-11.4{1 }^z$ ${EP}_2=-18.2{9 }^z$ $\ast 0.000$ $\mathrm{*}\mathrm{*}-27.9,429.9,429.9^{ z}$	${EP}_1={EP}_3=-11.3{1 }^z$ ${EP}_2=-18.21^{ z}$ $\ast 1.4340$ $\mathrm{*}\mathrm{*}-16.1,\mathrm{519.9,549}.2^z$
$\widetilde{B }$3Σg (*16e)	$-1.760920{0 }^a$ $-1.776714{0 }^h$ $-1.762850{5 }^{a^{\prime }}$ $-1.759055{5 }^{a^{″}}$	${\{\left[{\mathit{A}}^{\prime }\right]4\sigma }_g^1{,3\sigma }_u^1,{\pi }_u^4,{\} }^a$ ${\pi }_u^2\left|\alpha \right.⟩=-0.7432{3 }^a$ $\ast E\left(\left|\alpha \right.⟩\right)(-37.33372{) }^a$ $\ast \ast (-0.53385{) }^a$	$\{\left[{\mathit{A}}^{\prime }\right],{\pi }_u^2\left|\beta \right.⟩{=-0.75222\}}^a$ $\ast E\left(\left|\beta \right.⟩\right)(-35.72475{) }^a$ $\ast \ast (-0.52131^a$	$\ast 1.297{6 }^w$ $\ast 1.297{6 }^w$	$A_1=\ast 180.{0 }^w$ $A_2=\ast 180.0^{ w}$	${EP}_1={EP}_3=-11.{04 }^w$ ${EP}_2=-18.{07 }^w$ $\ast 0.000$ $\ast \ast \mathrm{26.6,592.5,605.1}$	${EP}_1={EP}_3=-11.{1 }^w$ ${EP}_2=-18.{01 }^w$ $\ast 0.2600$ $\ast \ast \mathrm{25.5,600.4,612.5}$

a, QCISD/EPR-III; d, CASSCF(11,12)/UHF; z, b3p86/6-31g*; a′, MP₄D/EPR-III//QCISD/EPR-III; x, b3lyp/6-31g*; a″, MP₄SDQ/EPR-III//QCISD/EPR-III; g, CASSCF(10,12)ROHF AUG-cc-pvqz; y, m062x/epr-ii; b, QCISD/EPR-III(${\theta }_{const}=180.0); \left[ A \right],{1\sigma }^2,2{\sigma }^2,3{\sigma }^2,{4\sigma }^2,{5\sigma }^2$; w, b3lyp/6-31g*; c, QCISD/EPR-II; $\left[A^{\prime }\right],{1\sigma }_g^2,{1\sigma }_u^2{,2\sigma }_g^2,{3\sigma }_g^2{,2\sigma }_u^2$; v, CASSCF(11,12)/ AUG-cc-pvqz; c′, MP₄D/ EPR-II// QCISD/EPR-II; $\left[B \right], {\sigma }^1,{\sigma }^1,{\sigma }^1{,\sigma }^1,{\sigma }^1,{\pi }^2$; n, CBS4O; c″, MP₄SDQ/EPR-II// QCISD/ EPR-II; [$B^{\prime }$],${1\sigma }_g^1,{2\sigma }_g^1{,1\sigma }_u^1,{3\sigma }_g^1{,2\sigma }_u^1,{1\pi }_u^2$; u, TD/EPR-II; f, CBS-lq; h, QCISD(T)/EPR-III; [C],${1\sigma }_g^2,{1\sigma }_u^2{,2\sigma }_g^2,{3\sigma }_g^2{,2\sigma }_u^2,{4\sigma }_g^2 ; \left[C^{\prime }\right],{1\sigma }_g,{1\sigma }_u{,2\sigma }_g{,3\sigma }_g{,2\sigma }_u$; k, TD/EPR-III//QCISD (T)/EPR-III; $K^{\prime }$, TD/EPR-III//QCISD /EPR-III; [D], ${1\sigma }_g^2,{2\sigma }_{g,}^2{1\sigma }_u^2,{3\sigma }_g^2{,2\sigma }_u^2$.

Table 2. Energies of B₂${\mathit{N}}^{(-,0,+)}$ @ BNNT.

State $E_e\left(Hartree\right)$ of BNB inside BNNT (+104)		All electron Configuration $\ast (Homo-Lumo)$	$\beta$ electron $r_e\left(B_{1}N\right),r_e\left(N{B}_2\right)$ $\ast (Homo-Lumo)$ in BNNT
Radical (17e)
${\widetilde{X }}^2{\Sigma }_u^{+}$ ${(D}_{\infty h})$	${-0.3253895 }^a$	${\left[A^{\prime }\right]{\pi }_u^4,4\sigma }_g^2{,3\sigma }_u^1\left|\alpha \right.⟩=-0.3245{2 }^a$ $\ast (-0.11397{) }^a$	$\left[B^{\prime }\right],{4\sigma }_g^1\left|\beta \right.⟩=-0.2618{0 }^a$ $\ast (-0.10659{) }^a$	$1.299{9 }^a$,$-1.298{67}^{ a}$ $∆ =0.03$
${\widetilde{X }}^2{\Sigma }_u^{+}$ ($D_{\infty h})$	$-0.70927{0 }^b$	${\left[A^{\prime }\right]{\pi }_u^4,4\sigma }_g^2{,3\sigma }_u^1\left|\alpha \right.⟩=-0.2913{4 }^b$ $\ast (-0.06778{) }^b$	$\left[B^{\prime }\right],{4\sigma }_g^1\left|\beta \right.⟩$=$=-0.2732{0 }^a$ *${\left(-0.03864\right) }^b$	$1.3198^{ b}$,$-1.319{8 }^b$ $∆ =0.02$
${\widetilde{ B}}^4{\Pi }_g$ ($C_{\infty v})$	${-0.4160880 }^c$	${\left[A^{\prime }\right]\pi }_u^4,{\pi }_{g,}^2{\sigma }_g^1\left|\alpha \right.⟩=-0.2451{7 }^c$ $\ast (-0.05878{)}^{\mathit{c}}$	$\left[A^{\prime }\right],{\pi }_u^2\left|\beta \right.⟩-0.2805{7 }^c$ $\ast (-0.05587{) }^c$	$1.306{5 }^c$,$-1.316{8 }^c$ $∆ =0.04$
Anion (18e)
${\widetilde{X }}^1{\Sigma }_g^{+}$ ($C_{\infty v})$	${-0.4985275 }^c$	${\left[A^{\prime }\right]{\pi }_u^4,\sigma }_g^2{,\sigma }_u^2=-0.1671{2 }^c$ $\ast (-0.08038{)}^{\mathit{c}}$	-	$1.34{51}^{ c}$,$-1.32{6 }^c$ $∆ =0.02$
${\widetilde{ A}}^3{\Pi }_u$ ${(D}_{\infty h})$	$-0.5794230^{ c}$	[C]${{\pi }_u^4,3\sigma }_u^1,{1\pi }_g^1\left|\alpha \right.⟩$=${-0.08563 }^c$ $\ast (-0.06068{)}^{\mathit{c}}$	${\left[C^{\prime }\right]\pi }_{u,}^4{,4\sigma }_g^1\left|\beta \right.⟩={-0.0999 }^c$ $\ast (-0.0591{)}^{\mathit{c}}$	$1.34{11}^{ c}$,$-1.30{15 }^c$ $∆ =0.01$
${\widetilde{ A}}^3{\Pi }_u$ ($C_{\infty v})$	${-0.5777980 }^c$	[C]${{\pi }_u^4,3\sigma }_u^1,{1\pi }_g^1\left|\alpha \right.⟩$=${-0.08579 }^c$ $\ast (-0.06179{)}^{\mathit{c}}$	${\left[C^{\prime }\right]\pi }_{u,}^4{,4\sigma }_g^1\left|\beta \right.⟩={-0.1030}^{ c}$ $\ast (-0.05844{)}^{\mathit{c}}$	$1.37{11 }^c$,$-1.30{11 }^c$ $∆ =0.03$
Cation (16e)
$\widetilde{B }$3Σg ($D_{\infty h})$	${-0.12761975 }^c$	${\{\left[A^{\prime }\right]4\sigma }_g^1{,3\sigma }_u^1,{\pi }_u^4,\}$ ${\pi }_u^2\left|\alpha \right.⟩={-0.44236 }^c$ $\ast (-0.10744{)}^{\mathit{c}}$	$\{\left[A^{\prime }\right],{\pi }_u^2\left|\beta \right.⟩{=-0.43209\} }^c$ $\ast (-0.0471{4)}^c$	$1.286{5 }^c$,$-1.306{5 }^c$ $∆ =0.01$
$\widetilde{B }$3Σg ($C_{\infty v})$	${-0.1125985 }^c$	${\{\left[A^{\prime }\right]4\sigma }_g^1{,3\sigma }_u^1,{\pi }_u^4,\}$ ${\pi }_u^2\left|\alpha \right.⟩={-0.45361 }^c$ $\ast (-0.11862{)}^{\mathit{c}}$	$\{\left[A^{\prime }\right],{\pi }_u^2\left|\beta \right.⟩{=-0.42857\} }^c$ $\ast (-0.0339{9)}^c$	$1.3456^{ c}$,$-1.289{9 }^c$ $∆ =0.03$

a, M062x/6-31g*; b, B3p86/6-31g*; c, B3LYP/6-31g*; $\left[ A \right],{1\sigma }^2,2{\sigma }^2,3{\sigma }^2,{4\sigma }^2,{5\sigma }^2;\left[A^{\prime }\right],{1\sigma }_g^2,{1\sigma }_u^2{,2\sigma }_g^2,{3\sigma }_g^2{,2\sigma }_u^2;\left[B \right],{\sigma }^1,{\sigma }^1,{\sigma }^1{,\sigma }^1,{\sigma }^1,{\pi }^2$; [$B^{\prime }$], ${1\sigma }_g^1,{2\sigma }_g^1{,1\sigma }_u^1,{3\sigma }_g^1{,2\sigma }_u^1,{1\pi }_u^2;$[C], ${1\sigma }_g^2,{1\sigma }_u^2{,2\sigma }_g^2,{3\sigma }_g^2{,2\sigma }_u^2,{4\sigma }_g^2;\left[C^{\prime }\right],{1\sigma }_g,{1\sigma }_u{,2\sigma }_g{,3\sigma }_g{,2\sigma }_u$; [D], ${ 1\sigma }_g^2,{2\sigma }_{g,}^2{1\sigma }_u^2,{3\sigma }_g^2{,2\sigma }_u^2.$

ECPs were measured using QCISD/EPR-III, m062x/6-31g, b3p86/6-31g, HF/EPR-ii, HF/6-31g*, and m062x/EPR-ii for BNB ^{(−, 0, +)} in different scenarios within a (5, 5) BNNT environment. Attraction and repulsion energies between the BNNT ring and BNB ^{(−, 0, +)} components in excited and ground states were calculated and are listed in Table 2 and Table 3 (as well as in Supplementary Tables S2 and S3) at different levels of theory.

Table 3. ECP fitting for BNB@ (5, 5) BNNT (Supplementary Table S3).

State of BNB	$\mathit{\gamma }={\displaystyle \frac{{\mathbf{V}}_{\mathbf{B}}-{\mathbf{V}}_{\mathbf{N}}}{{\mathbf{r}}_{\mathbf{B}\mathbf{N}}}}$	force$=({\Sigma }_x^2$+${\Sigma }_y^2+ {\Sigma }_y^2{)}^{{\displaystyle \frac{1}{2}}}$, $\theta =$ angle of force vector, ${\delta (q}_B-q_N)$ from ECP	$B^{{\delta q}_1}-N^{{\delta q}_2}-B^{{\delta q}_3}$ ${∆=r}_1\left(B_{1}N\right)-r_2\left(B_{2}N\right)$ “Isolated BNB” Charges from ESP fitting
${\widetilde{X }}^2{\Sigma }_u^{+}$ Radical	${\mathit{\gamma }=4.7184 }^a$ ${\mathit{\gamma }=4.7168 }^b$ ${\mathit{\gamma }=4.7191 }^c$ ${\mathit{\gamma }=4.7186 }^d$ - - - -	$0.89,-38.18°$, 0.806 a $0.86, 53.92°$, 0.804 a $0.88, 55.22°$, 0.807 a $0.93, -37.11°,$ 0.806 a - - - -	${{∆}^u =0.0 \& \delta q}_1={\delta q}_3=-0.055,{\delta q}_2=0.11$ ${{∆}^u =0.01 \& \delta q}_1=-0.16,{\delta q}_3=0.07,{\delta q}_2=0.10$ ${{∆}^k =0.01 \& \delta q}_1={\delta q}_3=-0.09,{\delta q}_2=0.19$ ${{∆}^k =0.04 \& \delta q}_1=-0.14,{\delta q}_3=0.04,{\delta q}_2=0.14$ ${{∆}^k =0.04 \& \delta q}_1=-0.12,{\delta q}_3=0.02,{\delta q}_2=0.14$ ${{∆}^y =0.0 \& \delta q}_1={\delta q}_3=-0.045,{\delta q}_2=0.09$ ${{∆}^y =0.02 \& \delta q}_1=0.06,{\delta q}_3=-0.12,{\delta q}_2=0.08$ $\hspace{1em}\hspace{1em}{{∆}^y =0.01 \& \delta q}_1=0.09,{\delta q}_3=-0.13,{\delta q}_2=0.05$
${\widetilde{X }}^1{\Sigma }_g^{+}$ Anion	${\mathit{\gamma }=4.6644 }^a$ ${\mathit{\gamma }=4.6630 }^b$ ${\mathit{\gamma }=4.6651 }^c$ ${\mathit{\gamma }=4.6649 }^d$ - - - -	$1.28, 88.21°,$0.232 $1.35, -3.39°,$0.228 $1.23, 2.79°,$0.232 $1.41, 89.59°,$0.242 - - - -	${{∆}^z=-1 \& \delta q}_1={\delta q}_3=-0.6,{\delta q}_2=0.2$ ${{∆}^z =-0.9 \& \delta q}_1=-0.9,{\delta q}_3=-0.9,{\delta q}_2=0.9$ ${{∆}^z =-1 \& \delta q}_1=-0.99,{\delta q}_3=-0.91,{\delta q}_2=0.90$ ${{∆}^z=-1 \& \delta q}_1=-0.35,{\delta q}_3=-0.37,{\delta q}_2=-0.28$ ${{∆}^x =-1 \& \delta q}_1=-0.86,{\delta q}_3=-0.94,{\delta q}_2=0.80$ ${{∆}^x =-1 \& \delta q}_1=-0.78,{\delta q}_3=-0.94,{\delta q}_2=0.72$ ${{∆}^x =-1 \& \delta q}_1=-0.75,{\delta q}_3=-0.91,{\delta q}_2=0.66$ $\hspace{1em}\hspace{1em}{{∆}^x =-1 \& \delta q}_1=-0.67,{\delta q}_3=-0.90,{\delta q}_2=0.57$
${\widetilde{X }}^1{\Sigma }_g^{+}$ Cation		- - - -	${{∆}^x =+1 \& \delta q}_1=0.78,{\delta q}_3=0.84,{\delta q}_2=-0.62$ ${{∆}^x =+1 \& \delta q}_1=0.73,{\delta q}_3=0.85,{\delta q}_2=-0.58$ ${{∆}^{x }=+1 \& \delta q}_1=0.70,{\delta q}_3=0.80,{\delta q}_2=-0.50$ $\hspace{1em}\hspace{1em}{{∆}^x =+1 \& \delta q}_1=0.75,{\delta q}_3=0.75,{\delta q}_2=-0.50$

a, QCISD/EPR-III; b, m062x/6-31g*; c, b3p86/6-31g*; d, hf/epr-iixhf/6-31g*

The EPR-III and EPR-II basis sets by Barone [36], have been shown to be suitable for ESP distributions. EPR-II is a double-ζ set with a single set of polarization functions, making it suitable for atoms from boron to fluorine [34,36]. In addition, EPR-III is a triple-ζ basis set consisting of diffuse functions with double d-polarization. In EPR-III, the s-part is also modified for accurate optimization in the nuclear region for boron to fluorine atoms [36,37,38,39,40,41,42,43,44] (Table 1 and Table 2 and Supplementary Tables S1 and S2). The active space for CASSCF methods is determined based on the number of valence electrons and orbital configurations. A total of 11 active electrons were considered for insertion into 12 active orbitals specifically for B₂N⁽⁰⁾, with an additional 10 and 12 being added for B₂N(+) and B₂N(−), respectively. Spin–orbital coupling during various spin states has also been estimated during CASSCF calculations [45]. The Quadratic CI calculations with single and double substitutions [43] have also been used for measurement. One-electron items include bonding analysis and atoms in molecules of Bader’s theory (AIM) [44]. In addition, we explored the coupling of vibrations. Additionally, we included the time-dependent DFT and extended multi-configuration with second-order perturbation theory. We found that the coupling of spin–orbitals, along with electron– and hole–vibration couplings, is sufficient to describe the mechanistic link between observed structural distortions and the SOJT framework.

Natural bond orbital and population analyses based on multipole momentum and electrostatic potentials were conducted using the Merz–Kollman–Singh [45], Chelp [46], or Chelp-G [47] approaches. Hyper-polarizabilities and polarizabilities were measured in a simplified manner using the CISD and QCISD methods. Double numerical differentiation for energies was defined using the “pol=En only” keyword in BNB systems. Since the charges from molecular electrostatic potentials (MESPs) may not be well-suited for larger molecules, as the innermost atoms are placed far away from the MESP centers, CHELPG (Charges of Electrostatic Potentials including Grid reticulation) was applied to fit and reproduce the MESPs at various points around the molecule (see Table 3 and Supplementary Table S3). A comprehensive discussion of the detailed result basis set and the Hamiltonian effects on charge distribution was provided by Martin et al. [48]. In this work all calculations were performed using the Gaussian program package [35]. Minimization was achieved through frequency measurements to confirm proper geometries in a true minimum (Table 3).

4. Discussion

The discussion can be separated into three sub-sections, containing (a) structural concepts, (b) energetic concepts, and (c) physical and chemical properties. The related results are shown in Table 1, Table 2 and Table 3, as well as several (Supplementary Materials Tables S1–S3). The results of the energies from attraction and repulsion among various BNB ^{(-, 0, +)} and (5, 5) BNNT rings are listed in Table 4. The data of the physical parameters for both isolated and non-isolated structures of B2$N^{(-,0,+)}$ are listed in Table 5.

Table 4. Attraction & Repulsion energies (eV) of BNB ^{(−, 0, +)} @ (5,5)BNNT.

${+∆ =r}_1\left(B_{1}N\right)-r_2\left(B_{2}N\right)$ ${-∆ =r}_2\left(B_{2}N\right)-r_1\left(B_{1}N\right)$

$∆E_{Repulsion(+)}^{\mathbf{A}ttraction\left(-\right)}\left(eV\right)=E_t-(E_{\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}}$+$E_{BNB})$

Ground State

${\widetilde{X }}^2{\Sigma }_u^{+}$(Radical)

${\widetilde{X }}^1{\Sigma }_g^{+}$(Anion)

${\widetilde{X }}^1{\Sigma }_g^{+}$(Cation)

$\pm {∆}^{ a}$

$\pm {∆}^{ b}$

$\pm {∆ }^c$

$\pm {∆ }^d$

$\pm {∆ }^e$

$\pm {∆ }^f$

$\pm {∆ }^g$

$\pm {∆ }^h$

${∆E }^a$

${∆E }^b$

${∆E }^c$

${∆E}^{ d}$

${∆E }^e$

${∆E }^f$

${∆E }^g$

${∆E }^h$

0.000 0.005 0.01 0.02 0.03 0.035 0.038 0.05 0.06 0.062 0.065 0.067 0.07 0.075 − −

0.000 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.091 0.092 0.095 0.10 0.11 0.13

0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.075 0.077 0.08 − − − − −

0.00 0.01 0.02 0.03 0.04 0.05 − − − − − − − − − −

0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.12 0.14 0.17 0.20 0.25

0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 − − − − − − −

0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 − − − − − − − −

0.00 − − − − − − − − − − − − − − −

−13.342 −14.222 −14.139 −14.1780 −14.215 −14.965 −14.5463 −14.241 −14.431 −14.459 −14.432 −14.980 −3.544 −3.346 − −

−13.654 −14.399 −14.399 −14.356 −14.510 −14.549 −14.456 −14.587 −14.734 −14.555 −14.666666 −13.705 −13.704 −13.7080 −13.702 −13.799

−3.073 −4.099 −3.765 −3.0999 −3.145 −3.126 −3.863 −4.123 −4.152 −3.299 − − − − − −

−1.5871 −1.700 −1.649 −1.599 −1.489 −1.555 − − − − − − − − − −

−5.443 −5.508 −5.499 −5.515 −5.543 −5.608 −5.609 −5.601 −5.587 −5.589 −5.599 −5.6999 −5.7345 −5.808 −5.865 −6.111

−2.531 −2.699 −2.699 −2.709 −2.709 −2.709 −2.691 −2.698 −2.999 − − − − − − −

0.362 0.211 0.249 0.245 0.265 0.275 0.301 0.309 − − − − − − − −

0.809 − − − − − − − − − − − − − − −

$\pm {∆ }^i$

$\pm {∆ }^j$

$\pm {∆ }^k$

Exited State

${\widetilde{ B}}^4{\Pi }_g$(Radical)

${\widetilde{ A}}^3{\Pi }_u$ (Anion)

$\widetilde{B }$3Σg (Cation)

${∆E}^{ i}$

${∆E }^j$

${∆E }^k$

0.00   0.01   0.02   0.03   0.05   0.052   0.055   0.06   0.09

0.00   0.01   0.04   0.06   0.08   0.10   -   -   -

0.00 0.01 0.04 0.05 0.06 0.00 − −

−4.701 −4.691 −4.654 −4.632 −4.555 −4.765 −5.432 −5421 −5.343

−7.763 −7.450 −7.324 −7.55 −7.618 −7.632 − − −

−3.432 −3.654 −3.243 −3.253 −3.643 − − − −

a,$UHF/EPR-II and r_e=1.3105$ f$M062x/epr-II and r_e=1.335$; b, $UHF/6-31$ g*$and r_e=1.3089$; g, $HF/6-31g\ast and r_e=1.302$; c, $B_{3}P86/6-31$ g*$and r_e=1.3198$; d, $M062x/6-31$ g*$and r_e=1.3206$; e, $HF/6-31$ g*$and r_e=1.3371$; h, $B3P86/epr-II//\mathrm{C}\mathrm{A}\mathrm{S}\mathrm{S}\mathrm{C}\mathrm{F}(11, 12)\mathrm{r}\mathrm{o}\mathrm{h}\mathrm{f}\mathrm{A}\mathrm{U}\mathrm{G}-\mathrm{c}\mathrm{c}-\mathrm{p}\mathrm{v}\mathrm{q}\mathrm{z},and r_e=1.294$; i, $B3lyp/6-31g\ast //\mathrm{q}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{d}\left(\mathrm{T}\right)/\mathrm{e}\mathrm{p}\mathrm{r}-\mathrm{i}\mathrm{i}\mathrm{i},and r_e=1.3079$; j, $B3lyp/6-31g\ast //\mathrm{q}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{d}\left(\mathrm{T}\right)/\mathrm{e}\mathrm{p}\mathrm{r}-\mathrm{i}\mathrm{i}\mathrm{i},and r_e=1.3422$; k, $B3lyp /6-31g\ast //\mathrm{q}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{d}\left(\mathrm{T}\right)/\mathrm{e}\mathrm{p}\mathrm{r}-\mathrm{i}\mathrm{i}\mathrm{i},and r_e=1.2976.$

Table 5. Several physical properties, such as anisotropic spin dipole coupling (ASDF), Electric Potential, and Isotropic Fermi Contact Coupling {$\mathrm{I}\mathrm{F}\mathrm{C}\mathrm{C}\left[\mathrm{f}\left(∆\right)\right]$,$\mathrm{I}\mathrm{F}\mathrm{C}\mathrm{C}\left[\mathrm{f}\left(\mathsf{\theta }\right)\right]$}, of isolated and non-isolated forms of B₂${\mathrm{N}}^{(-,0,+)}$.

State (*Ne)	isolated BNB (re = 1.3176) IFCC for nitrogen			ASDF of non-isolated BNB	Hybrids Coefficient&	$E_{{acceptor}_{\left(j\right)}}-E_{{Donor}_{\left(i\right)}}$ $\ast \mathrm{F}\mathrm{o}\mathrm{c}\mathrm{k}\mathrm{M}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x}(F_{i,j},a.u.)$	Atomic occupancies *
	$∆ and \theta$	IFCC f($∆)$	IFCC f($\theta )$	Baa, Bbb, Bcc
${\widetilde{X }}^2{\Sigma }_u^{+}$ (*17e)	0.0, 0.0	−29.8, −29.8		N f: −11.2, −9.4, 20.5	${\left|\psi \right.⟩}_{BD\left(1\right)}=0.91S{P}_{N_1}^{1.01}+0.41 S{P}_{B_2}^{2.4{6 }^a}$ ${\left|\psi \right.⟩}_{BD\left(2\right)}=0.96S{P}_{N_1}^{1.0}+0.29S{P}_{B_2}^{1.{0 }^a}$ ${\left|\psi \right.⟩}_{BD\left(3\right)}=0.96S{P}_{N_1}^{1.0}+0.29S{P}_{B_2}^{1.{0 }^a}$ ${\left|\psi \right.⟩}_{B{D}^{\ast }\left(1\right)}=0.28S{P}_{N_1}^{1.0}-0.95 S{P}_{B_2}^{1.{0 }^a}$ ${\left|\psi \right.⟩}_{B{D}^{\ast }\left(2\right)}=0.42S{P}_{N_1}^{1.01}-0.90 S{P}_{B_3}^{0.{95 }^a}$ ${\left|\psi \right.⟩}_{B{D}^{\ast }\left(3\right)}=0.70S{P}_{B_2}^{0.97}-0.70 S{P}_{B_3}^{0.{97 }^a}$	${\left|\psi \right.⟩}_{B{D}^{\ast }\left(2\right)}-{\left|\psi \right.⟩}_{BD\left(1\right)}\cong 2.01$ * 0.094 ${{\left|\psi \right.⟩}_{B{D}^{\ast }\left(3\right)}-\left|\psi \right.⟩}_{BD\left(1\right)}\cong 1.00$ * 0.089 ${{\left|\psi \right.⟩}_{B{D}^{\ast }\left(1\right)}-\left|\psi \right.⟩}_{BD\left(2\right)}\cong 0.7$ * 0.029	$\left|\alpha \right.⟩N:2s^{0.77}2P_x^{0.84}2P_y^{0.84}2P_z^{0.87}$ $\left|\alpha \right.⟩B:2s^{0.76}2P_x^{0.79}2P_y^{0.79}2P_z^{0.40}$ $\left|\beta \right.⟩N:2s^{0.80}2P_x^{0.86}2P_y^{0.86}2P_z^{0.83}$ $\left|\beta \right.⟩B:2s^{0.50}2P_x^{0.69}2P_y^{0.69}2P_z^{0.16}$
	0.02, 3.0	−29.1, −29.8		B f: −24.0, −21.0, 45.0
	0.04, 10.0	−26.6, −29.8		B f: −22.6, −19.8, 42.4
	0.06, 20.0	−23.5, −29.9		N g: −8.9, −8.9, 17.8
	0.08, 30.0	−20.5, −29.9		B g: −21.6, −21.4, 42.9
	0.085, 40.	−19.7, −29.6		B g: −21.6, −21.4, 42.9
${\widetilde{X }}^1{\Sigma }_g^{+}$ (*18e)	- - - - - -	- - - - - -		- - - - - -	${\left|\psi \right.⟩}_{BD\left(1\right)}=0.90S{P}_{N_1}^{1.01}+0.43 S{P}_{B_2}^{2.2{6 }^a}$ ${\left|\psi \right.⟩}_{BD\left(2\right)}=0.66S{P}_{N_1}^{1.0}+0.75S{P}_{B_2}^{1.{0 }^a}$ ${\left|\psi \right.⟩}_{BD\left(3\right)}=0.95S{P}_{N_1}^{1.0}+0.32S{P}_{B_2}^{1.{0 }^a}$ ${\left|\psi \right.⟩}_{B{D}^{\ast }\left(1\right)}=0.44S{P}_{N_1}^{1.01}-0.90 S{P}_{B_2}^{2.{24 }^a}$ ${\left|\psi \right.⟩}_{B{D}^{\ast }\left(2\right)}=0.75S{P}_{N_1}^{1.0}-0.67 S{P}_{B_3}^{1.0^{ a}}$ ${\left|\psi \right.⟩}_{B{D}^{\ast }\left(3\right)}=0.32S{P}_{N_1}^{1.0}-0.94 S{P}_{B_3}^{1.{0 }^a}$	${\left|\psi \right.⟩}_{B{D}^{\ast }\left(3\right)}-{\left|\psi \right.⟩}_{BD\left(1\right)}\cong 1.94$ * 0.107 ${{\left|\psi \right.⟩}_{B{D}^{\ast }\left(1\right)}-\left|\psi \right.⟩}_{BD\left(1\right)}\cong 0.73$ * 0.021 ${{\left|\psi \right.⟩}_{B{D}^{\ast }\left(3\right)}-\left|\psi \right.⟩}_{BD\left(3\right)}\cong 1.94$ * 0.107	$\left|\alpha ,\beta \right.⟩N:2s^{1.59}2P_x^{1.70}2P_y^{1.70}2P_z^{1.66}$ $\left|\alpha ,\beta \right.⟩B:2s^{0.97}2P_x^{0.14}2P_y^{0.14}2P_z^{0.37}$ - - - -
$\widetilde{B }$3Σ+ (*16e)	- - -	- - -		N f: −10.5, 1.5, 9.0 - -	${\left|\psi \right.⟩}_{BD\left(1\right)}=0.90S{P}_{N_1}^{1.0}+0.42 S{P}_B^{0.7{2 }^h}$ ${\left|\psi \right.⟩}_{BD\left(2\right)}=0.96S{P}_{N_1}^{1.0}+0.26S{P}_B^{1.{0 }^h}$ ${\left|\psi \right.⟩}_{BD\left(3\right)}=0.96S{P}_{N_1}^{1.0}+0.26S{P}_B^{1.{0 }^h}$ ${\left|\psi \right.⟩}_{B{D}^{\ast }\left(1\right)}=0.42S{P}_{N_1}^{1.0}-0.90 S{P}_{B_2}^{1.{0 }^h}$	${\left|\psi \right.⟩}_{B{D}^{\ast }\left(3\right)}-{\left|\psi \right.⟩}_{BD\left(1\right)}=1.98$ * 0.119 ${{\left|\psi \right.⟩}_{B{D}^{\ast }\left(1\right)}-\left|\psi \right.⟩}_{BD\left(2\right)}=0.77$ * 0.028 ${{\left|\psi \right.⟩}_{B{D}^{\ast }\left(1\right)}-\left|\psi \right.⟩}_{BD\left(2\right)}\cong 0.7$ * 0.029	$\left|\alpha \right.⟩N:2s^{0.78}2P_x^{0.81}2P_y^{0.81}2P_z^{0.87}$ $\left|\alpha \right.⟩B:2s^{0.72}2P_x^{0.92}2P_y^{0.92}2P_z^{0.44}$ $\left|\beta \right.⟩N:2s^{0.77}2P_x^{0.87}2P_y^{0.87}2P_z^{0.86}$ $\left|\beta \right.⟩B:2s^{0.10}2P_x^{0.62}2P_y^{0.62}2P_z^{0.08}$ -
	-	-		B f: 26.3, −22.1, 48.5
				B f: −27.4, −22.3, 49.8
${\widetilde{ A}}^3{\Pi }_u$ (*18e)				N f: −10.7, −10.6, 21.3	${\left|\psi \right.⟩}_{BD\left(1\right)}=0.91S{P}_{N_1}^{1.0}+0.40 S{P}_{B_2}^{1.6{2 }^h}$ ${\left|\psi \right.⟩}_{BD\left(2\right)}=0.97S{P}_{N_1}^{1.0}+0.26S{P}_{B_2}^{1.{0 }^h}$ ${\left|\psi \right.⟩}_{BD\left(3\right)}=0.91S{P}_{N_1}^{1.0}+0.40S{P}_{B_3}^{1.{62 }^h}$ ${\left|\psi \right.⟩}_{BD\left(4\right)}=0.70S{P}_{B_2}^{0.51}+0.70S{P}_{B_3}^{0.51}$ ${\left|\psi \right.⟩}_{B{D}^{\ast }\left(1\right)}=0.4S{P}_{N_1}^{1.0}-0.91 S{P}_{B_2}^{1.{62 }^h}$ ${\left|\psi \right.⟩}_{B{D}^{\ast }\left(2\right)}=0.26S{P}_{N_1}^{1.0}-0.97 S{P}_{B_3}^{1.{0 }^h}$ ${\left|\psi \right.⟩}_{B{D}^{\ast }\left(3\right)}=0.40S{P}_{N_1}^{1.0}-0.91 S{P}_{B_3}^{1.{62 }^h}$ ${\left|\psi \right.⟩}_{B{D}^{\ast }\left(4\right)}=0.70S{P}_{B_2}^{0.51}-0.70 S{P}_{B_3}^{0{51 }^h}$	${\left|\psi \right.⟩}_{B{D}^{\ast }\left(3\right)}-{\left|\psi \right.⟩}_{BD\left(1\right)}\cong 1.94$ * 0.107 ${{\left|\psi \right.⟩}_{B{D}^{\ast }\left(4\right)}-\left|\psi \right.⟩}_{BD\left(1\right)}\cong 1.01$ * 0.064 ${{\left|\psi \right.⟩}_{B{D}^{\ast }\left(1\right)}-\left|\psi \right.⟩}_{BD\left(2\right)}\cong 0.73$ * 0.021 - -	$\left|\alpha \right.⟩N:2s^{0.75}2P_x^{0.81}2P_y^{0.60}2P_z^{0.86}$ $\left|\alpha \right.⟩B:2s^{0.74}2P_x^{0.09}2P_y^{0.70}2P_z^{0.43}$ $\left|\beta \right.⟩N:2s^{0.80}2P_x^{0.87}2P_y^{0.90}2P_z^{0.86}$ $\left|\beta \right.⟩B:2s^{0.46}2P_x^{0.06}2P_y^{0.04}2P_z^{0.16}$ - - - -
				B f: −15.5, −15.0, 30.5
				B f: −15.6, −15.1, 30.6

a, QCISD/EPR-III; h, QCISD(T)/EPR-III; f, b3lyp/6-31g*(pop=ChelpG); g, m062x/6-31g* pop=Chelp-G.

4.1. Discussion on Structure

The BNB radical has a linear structure in its ground state (${\tilde{X}}^2{\sum }_u^{+})$ with a molecular orbital sequence of ${1\sigma }_g^2,{1\sigma }_u^2{,2\sigma }_g^2,{3\sigma }_g^2{,2\sigma }_u^2,{1\pi }_u^4,{4\sigma }_g^2,3{\sigma }_u^1$.

Meanwhile, the lowest excited state is guessed to be ${\tilde{A}}^2{\Sigma }_{\left(g\right)}^{+}$, with a molecular orbital sequence of ${1\sigma }_g^2,{1\sigma }_u^2{,2\sigma }_g^2,{3\sigma }_g^2{,2\sigma }_u^2,{1\pi }_u^4,{4\sigma }_g^1,3{\sigma }_u^2$.

In addition, ${\tilde{B}}^2{\Pi }_{\mathit{g}}$, which is an excited state with a molecular orbital sequence of ${{1\sigma }_g^2,{1\sigma }_u^2{,2\sigma }_g^2,{3\sigma }_g^2{,2\sigma }_u^2,{\pi }_u^4,4\sigma }_g^2,{1\pi }_g^1$ (above ${\tilde{A}}^2{\Sigma }_g^{+}$), obeys the Jahn–Teller effect. The further excited state is related to the ${(}^4{\Pi }_{\mathit{g}})$ of the triplet state. As can be seen in Figure 3, according to Knight’s works [4], a cyclic radical or anion B₂$N^{(-, 0)}$ could not appear. In the cation structure, a bulge can be observed at 90° in the calculation of the MP₄DQ and MP₄DSQ levels of theory; therefore, this bulge confirms a cyclic B₂$N^{+}$.

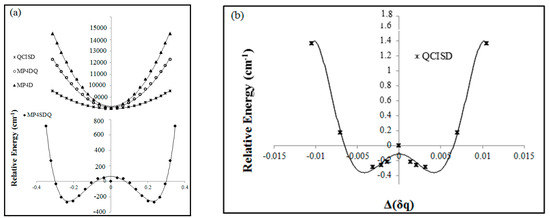
Figure 3. The B₂$N^{(-, 0, +)}$ case from the viewpoint of SM (symmetry breaking) in several calculations versus the B-N-B bond for (a,b) cation, (c) radical, and (d) anion structures.

By considering the wave function, it was found which BNB with $D_{\infty h}$ symmetry containing a real wave function must be converted into the irreducible representation (of the $D_{\infty h}$ point group). In addition, ${“4\sigma }_g^2”$ and $“3{\sigma }_u^1”$ have degeneracy when two B–N bonds are asymmetrically stretched (similarly, the $6\sigma$ and $7\sigma$ MOs have the same symmetry and degeneracy). Therefore, $[the core]6\sigma ,$ which corresponds to an excited state, has a strong interaction containing singlet and triplet states. In this case the non-isolated configuration energy increases significantly (Table 4). This phenomenon may be due to an artefactual symmetry breaking, which can pose a challenge in the concept of a real Jahn–Teller distortion or artificial model. Distortions for non-isolated BNB compared with isolated ones have two specifications: high distortion energy and irregular symmetry breaking (Table 1, Table 2, Table 3, Table 4 and Table 5 and Figure 4).

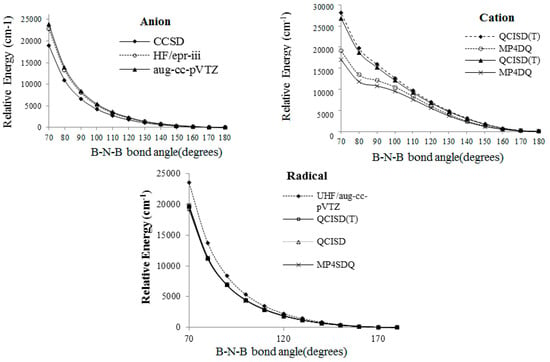
Figure 4. B₂$N^{(-, 0, +)}$ from the viewpoint of symmetry breaking versus B-N-B bond angle according to several methods.

Finally, we are going to understand the differences in the electromagnetic properties of BNB as an isolated structure compared with its localization in the BNNT ring. In the $D_{\infty h}$ symmetry of the isolated form, the unpaired electron is delocalized, while in the asymmetric $C_{\infty v}$ structure, it is localized on one of the B atoms. Investigation of the structures has shown that a system with broken symmetry, $C_{\infty v}$, can stabilize the non-bonded interaction compared with the symmetric $D_{\infty h}$ geometry.

4.2. Discussion on Energy

Various DFT methods, including B3p86, B3lyp, m062x, m06-L, and m06, are discussed in relation to non-bonded interactions between BNB ^{(−, 0, +)} and BNNTs in various scenarios. The novel methods m062x, m06-L, and m06-HF show promising results in non-bonded measurements, making them useful for calculating energies based on distances with medium (∼2–5 Å) and long ($\ge$5 Å) ranges [49]. However, the B3LYP method is unable to predict van der Waals information for medium-range interactions [49,50]. Studies in recent decades have confirmed inaccuracies in medium-range exchange energies leading to large systematic errors in the prediction of molecular properties [51,52,53,54,55]. Although DFT methods are unable to perfectly exhibit second-order Jahn–Teller distortion for isolated BNB, these levels of theory for BN^{(−, 0, +)}B-BNNT systems can estimate the second-order Jahn–Teller effect for BNB approximately, which is useful for further comparison (Table 1, Table 2 and Table 3 and Figure 5) [56,57,58,59].

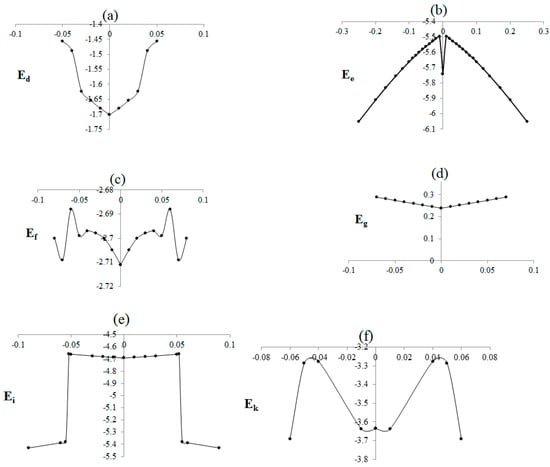
Figure 5. Relative energies of B₂$N^{(-,0,+)}$ versus B-N-B bond of a BNB@95,5) BNNT system, where (a,b) ${\widetilde{X }}^2{\Sigma }_u^{+}$ (radical), (c,d) ${\widetilde{X }}^1{\Sigma }_g^{+}$ (anion), (e) ${\widetilde{X }}^1{\Sigma }_g^{+}$, and (f) ${\widetilde{ B}}^4{\sigma }_g$.

In Table 4, the calculation data for m062x with Epr-ii and 6-31g* can be seen and compared with B3P86 and B3LYP, showing lower values. Interestingly, both the m062x and B3LYP methods show attraction for BN ^{(−, 0)} B and repulsion for BN ⁽⁺⁾ B with the BNNT ring. Table 1 lists the energy differences for the global minima and local minima for both $\left|\alpha \right.⟩$ and $\left|\beta \right.⟩$. It also confirms that the total energies for both methods are the same as the spin–orbitals depending on the bending angles of A₁ and A₂, which have an extremely low frequency of around 70 cm⁻¹ from bending vibration. As it is indicated in Table 1 and Table 2, the energy of ${\widetilde{X }}^2{\Sigma }_u^{+}$ in the state of $\left|\alpha \right.⟩=-0.44641$ for isolated BNB ⁽⁰⁾ is higher than that of $\left|\alpha \right.⟩=-0.32452$ for non-isolated BNB ⁽⁰⁾, and so is the one for $\left|\beta \right.⟩=-0.26341>-0.26180$. The energies of ${\widetilde{ B}}^4{\Pi }_g$, can be shown as

$${\left|\alpha \right.⟩}_{isolated}=-0.26899>{\left|\alpha \right.⟩}_{non-isolated}=-0.24517$$

(21)

and

$${\left|\beta \right.⟩}_{isolated}=-0.4965>{\left|\beta \right.⟩}_{non-isolated}=-0.28057$$

(22)

Consequently, the differences between these cases indicate that $\left|\beta \right.⟩$ is significantly higher in stability than $\left|\alpha \right.⟩$, so the isolated ${\widetilde{ B}}^4{\Pi }_g$ form has more stability compared with the non-isolated form. Moreover, the $\left|\alpha \right.⟩$ orbital has higher stabling compared with the non-isolated form for both the cation and anion structures. The energies of $\left|\alpha \right.⟩$ and $\left|\beta \right.⟩$ valance-occupied MOs for the first triplet excited state$({1\sigma }_g^2,{1\sigma }_u^2{,2\sigma }_g^2,{3\sigma }_g^2{,2\sigma }_u^2,{4\sigma }_g^2{{,1\pi }_u^4,4\sigma }_u^1,{1\pi }_g^1)$ are ${1\pi }_g^1\left|\alpha \right.⟩=-0.03986$, ${4\sigma }_u^1\left|\alpha \right.⟩$= −0.23701 and ${\{1\pi }_u^2\left|\alpha \right.⟩=-0.25466,-0.25136\},$ while those for $\left|\beta \right.⟩$ are ${\{1\pi }_u^2\left|\beta \right.⟩=-0.28802,-0.27730\}$, and ${4\sigma }_g^2\left|\beta \right.⟩=-0.01559$.

Since the energy of $\left|\alpha \right.⟩$ is higher than that of $\left|\beta \right.⟩$, it can be concluded that there is a stronger correlation in the anion form compared with the other forms. In the ${\tilde{A}}^3{\Sigma }_g^{+}$ excited state, an electron moves from the highest occupied molecular orbital (HOMO), $3{\sigma }_u$, to the $4{\sigma }_u$ MO, which is devoted the ${\widetilde{ A}}^3{\Pi }_u$ state, appearing considerably above the previous state.

According to the values in the tables and Supplementary Tables S1 and S2, the energy differences between the two states (${\widetilde{A }}^2{\Sigma }_g^{+}$) and (${\widetilde{X }}^2{\sum }_u^{+})$ {(k – a) and (k – k′)} are 5829.75 cm⁻¹ and 5834.79 cm⁻¹, respectively. These amounts are closer to the photoelectron spectroscopy calculations which were performed by Asmis et al. [2]. Consequently ${\widetilde{ B}}^2{\Pi }_{\mathit{g}}$ (excited state above ${\widetilde{A }}^2{\Sigma }_g^{+}$) is subject to the Renner–Teller effect according to the data in Table 1, Table 2, Table 3 and Table 4, which is confirmed for the BNB radical in the BNNT field in neutral B₂N {(${\tilde{X}}^2{\sum }_u^{+}$) and $({\tilde{A}}^2{\sum }_g^{+})$, though in a high energy level.

4.3. Calculation of Physical Properties

Electrical parameters and electrostatic potential (EP), including the geometry of BNB in the excited and ground states, as well as HOMO/LUMO and Isotropic Fermi Contact Couplings (MHz), under the external field of a (5, 5) BNNT were calculated. The data are shown in Table 1 and Table 2. The ESP fitting, i.e., $\gamma ={(\mathrm{V}}_{\mathrm{B}}-{\mathrm{V}}_{\mathrm{N}})/{\mathrm{r}}_{\mathrm{B}\mathrm{N}}$, and the force energies of both attraction and repulsion for the BNB ^{(−, 0, +)} @ (5, 5) BNNT ring system, including NBO information, are reported (in Table 3, Table 4 and Table 5). Anisotropic spin dipole coupling (MHZ) and the differences ($E_{{acceptor}_{\left(j\right)}}-E_{{Donor}_{\left(i\right)}}$) are also listed in Table 5. The data in Table 5 correspond to the IFCC amounts, including the EP of the BNB ^{(−, 0, +)} @ (5, 5) BNNT ring system. It is notable that the EP is not influenced by the external field caused by the ring, while the IFCC is. In addition, the dipole moment of the ${\widetilde{X }}^2{\Sigma }_u^{+}$($D_{\infty h})$ radical can change from 0.000 (for isolated BNB) to 1.4436 (for non-isolated BNB); therefore, IFCC also varies between these two limits. In addition, multiple initial orientations of B₂N inside the BNNT ring were explored, such as axial/equatorial, vertical, and placements at other degrees (Figure 6). A systematic potential energy surface scan was performed over rotational and translational coordinates to perform quantized rotation. Moreover, vibrionic couplings are important for understanding non-adiabatic processes, especially near points of conical intersections. In this study vibrionic coupling and non-adiabatic coupling or derivative coupling were considered for the interaction between electronic and nuclear vibrational motions of our system. Since direct calculation of vibrionic coupling is challenging due to difficulties associated with its evaluation, in our model, vibrational and electronic interactions were calculated according to the Born–Oppenheimer approximation.

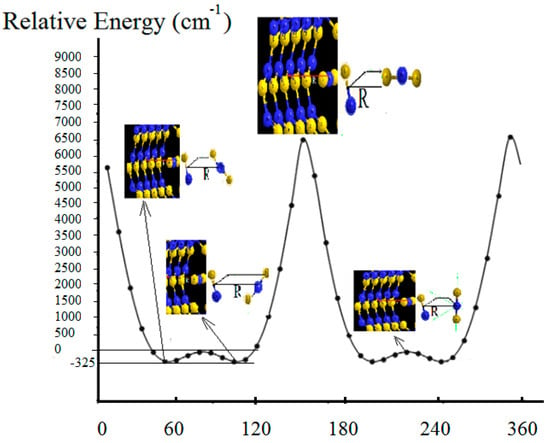
Figure 6. Potential energy surface (PES) scan using CASSCF (10, 12)/AUG-cc-pvqz.

The MESP fitting for charges as well as partial charges for two boron atoms and one nitrogen atom ($B^{{\delta q}_1}-N^{{\delta q}_2}-B^{{\delta q}_3}$) in the range from $∆ =0.01$ to $∆ =0.08$ exhibited a value of zero for the radical system, approximately (Table 3 and Supplementary Table S3). Interestingly, the summation of partial charges in $B^{{\delta q}_1}-N^{{\delta q}_2}-B^{{\delta q}_3}$ for the BNB radical inside the BNNT ring is not zero, with amounts in the ranges of 0.1–0.2 for ${∆}^u ,$0.1 to −0.32 for ${∆}^k$, and 0.13 to 0.22 for ${∆}^y$ (Supplementary Table S3). This is due to the fact that the unpaired electron of nitrogen is localized while BNB is under the influence of the external field of the BNNT ring, causing a charge transfer between BNB and the BNNT. Obviously, the differences among${∆}^u,{ ∆}^k$, and ${∆}^y$ are attributed to the various methods and basis sets used. For the excited state of radical forms, although the change in MESPs for both the excited state(${\widetilde{ B}}^4{\Pi }_g$) and ground state (${\widetilde{X }}^2{\sum }_u^{+})$ is negligible, as opposed to the ground state (S = 1 of the BNB radical), the IFCC is not considerable for S = 3/2 (Table 1 and Table 5). The sum of partial charges ($B^{{\delta q}_1}-N^{{\delta q}_2}-B^{{\delta q}_3}$) for all items is −1, indicating an anion form. However, the total partial charge of $B^{{\delta q}_1}-N^{{\delta q}_2}-B^{{\delta q}_3}$ for the BNB anion inside the BNNT ring is not −1, and it changes from mostly around −0.9, −0.8, and in one case, −0.6 for ${∆}^z=-0.6 to-0.7$ and for ${∆}^x=-0.8 to-0.9$. As a result, the total partial charge for all the items of BN ⁽⁻⁾ B is less than −1 (Supplementary Table S3). This is because the unpaired electron of nitrogen is localized while BNB is under the influence of the external field of the BNNT ring. It seems that the anion isolated in the field of the BNNT ring changes to a combination of radical and anion forms. Finally, the stability sequences are calculated as follows: {BNB ⁽⁻⁾ > BNB ⁽⁰⁾ > BNB ⁽⁺⁾ for non-isolated}$\gg${BNB ⁽⁺⁾ > BNB ⁽⁰⁾ > BNB ⁽⁻⁾ for isolated}.

5. Conclusions

Several states of the linear BNB molecule both in isolated position and inside a BNNT field were calculated using various ab initio methods based on multi-reference wave functions. CASSCF calculations predict a symmetry-broken (SB) structure for BNB with unequal bond lengths, as does perturbation theory with second-order perturbation theory. Therefore, knowing the spin–orbital couplings and electron– and hole–vibration couplings is important to describing the mechanistic link between observed structural distortions and the SOJT framework. We also examined the case of ${\widetilde{ B}}^2{\Pi }_g$ (excited state above ${\widetilde{A }}^2{\Sigma }_g^{+}$) according to the Renner–Teller effect, which is confirmed for the BNB radical in a BNNT field, as well as for neutral B₂N {(${\tilde{X}}^2{\sum }_u^{+}$) and $({\tilde{A}}^2{\sum }_g^{+} )$. We also discussed the differences among the electromagnetic properties of BNB as an isolated structure compared with its localization in a BNNT ring. We found that according to the total electrostatic interaction energy (U_BNNT-BNB) from Equation (9), the charge distribution of the $\mathrm{B}\mathrm{N}\mathrm{N}\mathrm{T}$ ring can be polarized through BNB due to the electromagnetic field induced by the ring environment. We also found that the twin minimum of BNB’s potential curve arises from the lack of a proper wave function of permutation symmetry, as well as abnormal charge distribution. Moreover, we found that in the $D_{\infty h}$ symmetry of the isolated form, the unpaired electron is delocalized, while in the asymmetric $C_{\infty v}$ structure, it is localized on either one of the B atoms. Investigation of the structures proved that a system with broken symmetry, $C_{\mathit{\infty }\mathit{v}}$, could stabilize the non-bonded interaction compared with the symmetric $D_{\infty h}$ geometry. Since the quantum behavior under an external field is completely different in an isolated position, important information can be obtained from any external field that affects the quantum systems of the mentioned molecules. We also recommend that researchers use various external fields that can affect small molecules to obtain valuable information.