Interaction Between Gravitational Waves and Trapped Bose–Einstein Condensates

Abstract

Inspired by recent proposals for detecting gravitational waves by using Bose–Einstein condensates (BECs), we investigated the interplay between these two phenomena. A gravitational wave induces a phase shift in the fidelity amplitude of the many-body quantum state. We investigated the enhancement of the phase shift in the case of Bose condensates confined by an anisotropic harmonic potential, considering both ideal and interacting BECs.

1. Introduction

The connection between general relativity and Bose–Einstein condensates (BECs) is gaining increasing importance, both for the possibility of detecting events such as gravitational waves (GWs) and for investigating still obscure aspects of Einstein’s theory. A recent development in this field is a theory known as emergent gravity, whose prime point is that gravity is not a fundamental interaction and that spacetime is a composite object behaving approximately like a superfluid. It is thus possible to study certain cosmological phenomena in analogy with BECs [1,2], and to perform simulations of the effects of GWs on BECs [3]. A further application of BECs on cosmological research is the possibility to exploit them for GW detection, in order to develop a more compact tool than today’s interferometers (such as LIGO (Laser Interferometer Gravitational Wave Observatory) and Virgo [4,5]) to investigate multimessanger astronomy. As shown in Refs. [6,7,8], the GW constitutes a source term for the phonons of the condensate, and the intrinsic coherence of the latter provides an enhancement mechanism which can, generally, compensate for the exceptionally small magnitude of the GW, which is of the order of ${10}^{-20}$. For a comprehensive review about the interaction between macroscopic quantum systems and gravity see, e.g., Ref. [9].

In this paper, we begin by deriving the GW equation and its solution in vacuum from the Einstein field equations in Section 2. Subsequently, after providing a brief overview of an established description of a BEC in a flat spacetime (Section 3), we extend the analysis to a more general curved spacetime and generalize the Gross–Pitaevskii equation in Section 4. Finally, in Section 5, we explore the interaction between GWs and BECs, assessing its detectability across various interaction strengths between the atoms constituting the condensate. To achieve this, it is necessary to combine two theoretical frameworks: general relativity and quantum mechanics, which are complementary but still have few common points. For this purpose, the GW is considered classically as a geometric background on which all physical phenomena described by quantum field theory (QFT) occur. In general, an approach can involve quantizing the gravitational field and, consequently, treating both the gravitational and matter fields within a quantum-mechanical framework. This approach has been pursued in various, including Ref. [10], which propose using BECs as a medium to detect gravitons originating from a stochastic GW background. While this line of inquiry is indeed intriguing, it lies beyond the scope of the present study.

2. Gravitational Waves

GWs are a perturbation of the metric of the spacetime and the equation that describes them is obtained from the Einstein field equations [11]

$$R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }={\displaystyle \frac{8\pi G}{c^4}}{T}_{\mu \nu }$$

(1)

and imposing the weak field condition $g_{\mu \nu }={\eta }_{\mu \nu }+h_{\mu \nu }$, where ${\eta }_{\mu \nu }=\mathrm{diag}(-1,+1,+1,+1)$ is the Minkowski metric and $|h_{\mu \nu }|\ll 1$. $R_{\mu \nu }$ represents the Ricci curvature tensor, $T\mu \nu$ is the energy-momentum tensor, the Greek letter indices take values 0 (time, t), 1, 2, and 3 (space: x, y, and z, correpondingly), G is the Newtonian constant of gravitation, and c denotes the speed of light in vacuum. Proceeding with the calculations and choosing the Donder gauge ${\partial }^{\mu }{h}_{\mu \nu }-{\displaystyle \frac{1}{2}}{\partial }_{\nu }{h}_{\alpha }^{\alpha }=0$, with denoting coordinate derivatives: ${\partial }_{\nu }\equiv \partial /\partial x_{\nu }$, and the TT-gauge (transverse-traceless gauge), which implies $h_{\alpha }^{\alpha }=0$, one obtains the following result:

$$\left({\displaystyle \frac{1}{c^2}}{\partial }_t^2-{\nabla }^2\right)h_{\mu \nu }={\displaystyle \frac{16\pi G}{c^4}}{T}_{\mu \nu }$$

(2)

which are indeed the equations of the GWs, with ${\nabla }^2={\partial }_x^2+{\partial }_y^2+{\partial }_z^2$.

Equation (2) is not straightforwardly solvable analytically, primarily due to the expression of the tensor $T_{\mu \nu }$. Therefore, let us consider the most simple solution, namely that in vacuum. In this case, the solution is a plane wave $h^{\mu \nu }=\mathrm{Re}\left\{A^{\mu \nu }{e}^{i{k}_{\sigma }{x}^{\sigma }}\right\}$, where $k^{\alpha }{k}_{\alpha }=0$, with $k^{\alpha }$ the wave vector, and

$$A_{\left(\mathrm{TT}\right)}^{\mu \nu }=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& A_{+}& A_{\times }& 0\\ 0& A_{\times }& -A_{+}& 0\\ 0& 0& 0& 0\end{array}\right),$$

(3)

where the subscript symbols denote the two possible polarizations, namely the plus polarization (“+”) and the cross polarization (“×”).

From now onward, we only consider GWs propagating along the z-axis with plus polarization, for which the metric perturbation takes the form $h^{\mu \nu }=\mathrm{diag}(0,h,-h,0)$ resulting in the modification of the infinitesimal line element:

$$d{s}^2=g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }=-c^{2}d{t}^2+(1+h)d{x}^2+(1-h)d{y}^2+d{z}^2,$$

(4)

where $h=h(z,t)$.

3. Bose–Einstein Condensates

The QFT Hamiltonian for identical non-relativistic particles of mass m in a flat spacetime is given by [12]

$${\widehat{H}}_{\mathrm{flat}}=\int d^{3}r{\widehat{\psi }}^{+}(\overrightarrow{r},t)\left[-{\displaystyle \frac{{\hslash }^2}{2m}}{\nabla }^2+U\left(\overrightarrow{r}\right)\right]\widehat{\psi }(\overrightarrow{r},t)$$

$$+{\displaystyle \frac{1}{2}}\int d^{3}r{d}^3{r}^{\prime }{\widehat{\psi }}^{+}(\overrightarrow{r},t){\widehat{\psi }}^{+}({\overrightarrow{r}}^{\prime },t)V(\overrightarrow{r},{\overrightarrow{r}}^{\prime })\widehat{\psi }({\overrightarrow{r}}^{\prime },t)\widehat{\psi }(\overrightarrow{r},t),$$

(5)

where $\widehat{\psi }(\overrightarrow{r},t)$ is the quantum field operator, $U\left(\overrightarrow{r}\right)$ is the trapping potential, $V(\overrightarrow{r},{\overrightarrow{r}}^{\prime })$ the inter-particle potential of the interaction between particles, $\overrightarrow{r}$ is the particle radius-vector, ℏ is the reduced Planck constant, and the superscript “+” denotes the Hermitian conjugate. In order to describe a bosonic field, it is necessary to impose the following equal-time commutation rule:

$$[\widehat{\psi }(\overrightarrow{r},t),{\widehat{\psi }}^{+}({\overrightarrow{r}}^{\prime },t)]=\delta (\overrightarrow{r}-{\overrightarrow{r}}^{\prime }),$$

(6)

where $[\widehat{A},\widehat{B}]=\widehat{A}\widehat{B}-\widehat{B}\widehat{A}$ and $\delta (·)$ is the Dirac delta function. When bosonic particles are cooled below the critical temperature $T_c$ (which depends on the particle density and is on the order of $\mathrm{nK}$), they lose their individuality and form a single entity where all particles occupy the same state. This phenomenon is known as a Bose–Einstein condensate, which is one of the few quantum phenomena observable on a macroscopic scale. In the case where $N\gg 1$, with N number of particles, and $T\ll T_c$, the field $\widehat{\psi }(\overrightarrow{r},t)$ acquires significant ’classical’ relevance, and it is possible to exploit the many-body coherent states (cs) $|{\Psi }_{\mathrm{cs}}⟩$, introduced by Roy Glauber [13] and George Sudarshan [14] in the 1960s, such that

$$\widehat{\psi }(\overrightarrow{r},t)|{\Psi }_{\mathrm{cs}}⟩=\psi (\overrightarrow{r},t)|{\Psi }_{\mathrm{cs}}⟩.$$

(7)

This method allows us to study the condensate through the use of the complex bosonic scalar field $\psi (\overrightarrow{r},t)$. In this way, one can circumvent the formalism of QFT and return to the more familiar quantum-mechanical description by studying the wave function $\psi (\overrightarrow{r},t)$, while keeping in mind that $\psi (\overrightarrow{r},t)$ represents a complex bosonic scalar field. For ultracold and dilute atoms, one can safely impose a binary contact interaction:

$$V(\overrightarrow{r},{\overrightarrow{r}}^{\prime })=\gamma \delta (\overrightarrow{r}-{\overrightarrow{r}}^{\prime }),$$

(8)

where $\gamma =4\pi {\hslash }^2{a}_{\mathrm{s}}/m$ with $a_{\mathrm{s}}$ as the scattering (s) length. In this way, one obtains the following Hamiltonian:

$${\widehat{H}}_{\mathrm{flat}}=\int d^{3}r\left\{{\widehat{\psi }}^{+}(\overrightarrow{r},t)\left[-{\displaystyle \frac{{\hslash }^2}{2m}}{\nabla }^2+U\left(\overrightarrow{r}\right)\right]\widehat{\psi }(\overrightarrow{r},t)+{\displaystyle \frac{\gamma }{2}}{\widehat{\psi }}^{+}{(\overrightarrow{r},t)}^2\widehat{\psi }{(\overrightarrow{r},t)}^2\right\}$$

(9)

from which, exploiting coherent states, the Gross–Pitaevskii equation (GPE) derives

$$i\hslash {\partial }_t\psi (\overrightarrow{r},t)=\left[-{\displaystyle \frac{{\hslash }^2}{2m}}{\nabla }^2+U\left(\overrightarrow{r}\right)+\gamma {\left|\psi (\overrightarrow{r},t)\right|}^2\right]\psi (\overrightarrow{r},t).$$

(10)

Equation (10) obtained independently by Eugene Gross [15,16] and Lev Pitaevskii [17] is a nonlinear Schrödinger equation and it describes exceptionally accurately the BEC dynamics of the experiments with alkali-metal atoms.

4. Bose–Einstein Condensates in Curved Spacetime

In order to describe comprehensively the BECs in a curved spacetime, one has to start from a Lorentz-invariant action, i.e., the Klein–Gordon one, to which the quartic term is added. Since the condensate is obtained at considerably low temperatures, which results in relatively low thermal speeds, it is necessary to perform the non-relativistic limit. That is, one obtains the GPE in curved spacetime (see, e.g., Refs. [6,18]) that corresponds to mboxEquation (10), where the Laplace operator ${\nabla }^2$ is replaced by ${\nabla }_g^2$, the latter being the Laplace operator in the curved spacetime.

Imposing the arrival of a GW propagating in the z-direction with the plus polarization (i.e., $g^{\mu \nu }={\eta }^{\mu \nu }+h^{\mu \nu }$ with $h^{\mu \nu }=\mathrm{diag}(0,h,-h,0)$) through the BEC, one obtains the following equation:

$$i\hslash {\partial }_t\psi (\overrightarrow{r},t)=\left[-{\displaystyle \frac{{\hslash }^2}{2m}}\left({\nabla }^2+h({\partial }_x^2-{\partial }_y^2)\right)+U\left(\overrightarrow{r}\right)+\gamma {\left|\psi (\overrightarrow{r},t)\right|}^2\right]\psi (\overrightarrow{r},t).$$

(11)

Equation (11) represents one of the main equations for the current investigation of the interaction between GWs and BECs. This mean-field equation is reliable provided that the nonlinear term is sufficiently small, namely for $\gamma \ll 1$.

The detection of GWs is a crucial experimental milestone, right due to the magnitude of this phenomenon h of the order $\mathcal{O}\left({10}^{-20}\right)$. Interferometric techniques have made it possible to overcome this hurdle thanks to the use of resonant cavities, managing to gain the necessary orders of magnitude. The use of such large detectors, however, is not straightforward, and in view of a larger-scale implementation of multimessenger astronomy, other possibilities are being considered. Here, therefore, we examine why BECs represent an opportunity in this regard.

5. Quantum Fidelity and Enhanced Phase Shift

Equation (11) suggests that the QFT Hamiltonian of the bosonic scalar field interacting with a GW propagating along the z-axis with the plus polarization can be expressed as

$$\widehat{H}={\widehat{H}}_{\mathrm{flat}}+{\widehat{H}}_{\mathrm{int}},$$

(12)

where ${\widehat{H}}_{\mathrm{flat}}$ is the Hamiltonian (9) of the bosonic field in flat spacetime, while ${\widehat{H}}_{\mathrm{int}}$ is defined as

$${\widehat{H}}_{\mathrm{int}}=\int {\widehat{\psi }}^{+}(\overrightarrow{r},t)\left(-{\displaystyle \frac{{\hslash }^2}{2m}}h(z,t)({\partial }_x^2-{\partial }_y^2)\right)\widehat{\psi }(\overrightarrow{r},t)d^{3}r.$$

(13)

At this point, let us exploit a characteristic property of BECs which are BECs’ coherent states $|{\Psi }_{\mathrm{cs}}⟩$ (of unit norm) satisfying the eigenvalue equation,

$$\widehat{\psi }(\overrightarrow{r},t)|{\Psi }_{\mathrm{cs}}⟩=\psi (\overrightarrow{r},t)|{\Psi }_{\mathrm{cs}}⟩=\sqrt{N}{\varphi }_{\mathrm{gs}}\left(\overrightarrow{r}\right)e^{-{\displaystyle \frac{i}{\hslash }}\mu t}|{\Psi }_{\mathrm{cs}}⟩,$$

(14)

where the wavefunction $\psi (\overrightarrow{r},t)$ is normalized to the enhancement factor N, while the wavefunction ${\varphi }_{\mathrm{gs}}\left(\overrightarrow{r}\right)$, that is instead normalized to one, represents the ground-state (gs) of the BEC in flat spacetime with chemical potential $\mu$. Explicitly, ${\varphi }_{\mathrm{gs}}\left(\overrightarrow{r}\right)$ satisfies the stationary GPE equation

$$\left[-{\displaystyle \frac{{\hslash }^2}{2m}}{\nabla }^2+U\left(\overrightarrow{r}\right)+\gamma N{\left|{\varphi }_{\mathrm{gs}}\left(\overrightarrow{r}\right)\right|}^2\right]{\varphi }_{\mathrm{gs}}\left(\overrightarrow{r}\right)=\mu {\varphi }_{\mathrm{gs}}\left(\overrightarrow{r}\right).$$

(15)

One can now define the time evolution operator ${\widehat{U}}_{\mathrm{int}}\left(t\right)$ associated with the interaction of the GW:

$${\widehat{U}}_{\mathrm{int}}\left(t\right)=exp\left(-{\displaystyle \frac{i}{\hslash }}{\int }_0^t{\widehat{H}}_{\mathrm{int}}\left(t^{\prime }\right)d{t}^{\prime }\right).$$

(16)

Let us also introduce the fidelity amplitude, $\mathcal{F}\left(t\right)$, a complex number which quantifies of how much the many-body quantum state remains unchanged over time:

$$\mathcal{F}\left(t\right)=⟨{\Psi }_{\mathrm{cs}}\left|{\widehat{U}}_{\mathrm{int}}\left(t\right)\right|{\Psi }_{\mathrm{cs}}⟩.$$

(17)

Notice that $F\left(t\right)={\left|\mathcal{F}\left(t\right)\right|}^2$ is instead the familiar fidelity, that is, a non-negative real number. Certainly, $\mathcal{F}\left(t\right)=1$ points to no change while $\mathcal{F}\left(t\right)=0$ signals a complete change, i.e., zero fidelity. From a theoretical point of view, the GW alters the coherent state by shifting the value of $\mathcal{F}$ away from 1 being appropriate since quantum mechanics allows for the definite distinction of only orthogonal states. By expanding the exponential in a Taylor series in $Nh$, one obtains

$$\mathcal{F}\left(t\right)=1-iN\xi \left(t\right)+\mathcal{O}\left(N^2{h}^2\right),$$

(18)

where

$$N\xi \left(t\right)=N{\displaystyle \frac{\hslash }{2m}}{\int }_0^{t}d{t}^{\prime }\int d^{3}rh(z,t^{\prime }){\varphi }_{\mathrm{gs}}^{*}\left(\overrightarrow{r}\right)({\partial }_y^2-{\partial }_x^2){\varphi }_{\mathrm{gs}}\left(\overrightarrow{r}\right).$$

(19)

Notice that the enhancement factor N comes from the substitution reported in Equation (14), since $\xi \left(t\right)$ depends only on the single-particle time-independent wavefunction ${\varphi }_{\mathrm{gs}}\left(\overrightarrow{r}\right)$. Let us stress that $\xi \left(t\right)$, being proportional to h, is of the order $\mathcal{O}\left({10}^{-20}\right)$. However, as shown by Equation (18), the time-dependent relative phase between the two many-body quantum states scales as $N\xi \left(t\right)$. The main reason to favor the detection of GWs through BECs is the possibility to make use of this enhancement mechanism proportional to the number of particles N, which, generally can compensate for the relatively small magnitude of h.

Nonetheless, the experimental feasibility in creating condensates does not allow (to date, where $N\approx {10}^7$) us to compensate over twenty orders of magnitude of the GW (i.e., $hN\approx {10}^{-13})$, but new paths are opening wide towards the use of ultracold Helium, which consists of considerably more particles ($\mathcal{O}\left({10}^{20}\right)$), but on the other hand, just less than $10\%$ of them are under the condensation threshold.

5.1. Anisotropic Harmonic Confinement

In this Section, we calculate $\xi \left(t\right)$, defined in Equation (19), for a Bose–Einstein condensate trapped by an anisotropic harmonic potential:

$$U\left(\overrightarrow{r}\right)={\displaystyle \frac{1}{2}}m({\omega }_x^2{x}^2+{\omega }_y^2{y}^2+{\omega }_z^2{z}^2).$$

(20)

By using the technique of Feshbach resonances [19,20,21], it is now possible [22] to vary the interaction strength between the particles in a condensate, changing the scattering length $a_{\mathrm{s}}$ even considering it as zero.

5.1.1. Non-Interacting Bosons

For non-interacting bosons in the condensate, the ground-state wavefunction is given by

$${\varphi }_{\mathrm{gs}}\left(\overrightarrow{r}\right)={\displaystyle \frac{1}{{\left({\pi }^3{\sigma }_x^2{\sigma }_y^2{\sigma }_z^2\right)}^{\frac{1}{4}}}}exp\left[-\left({\displaystyle \frac{x^2}{2{\sigma }_x^2}}+{\displaystyle \frac{y^2}{2{\sigma }_y^2}}+{\displaystyle \frac{z^2}{2{\sigma }_z^2}}\right)\right],$$

(21)

where

$${\sigma }_i=\sqrt{{\displaystyle \frac{\hslash }{m{\omega }_i}}}\mathrm{with}i=x,y,z.$$

(22)

The choice of a Gaussian shape trial function is justified in the limit of weak interacting bosons, due to the feature that the exact ground-state of the linear Schrödinger equation with harmonic potential has this functional form. Let us now insert Equation (21) in Equation (19), obtaining

$$\begin{array}{cc}\hfill \xi \left(t\right)& ={\displaystyle \frac{\hslash }{2m}}{\displaystyle \frac{{\sigma }_y-{\sigma }_x}{\sqrt{\pi }{\sigma }_x{\sigma }_y{\sigma }_z}}{\int }_0^{t}d{t}^{\prime }{\int }_{-\infty }^{+\infty }dzh(z,t^{\prime })e^{-{(z/{\sigma }_z)}^2}.\hfill \end{array}$$

(23)

Note that even in this case, if the condensate is symmetric in the plane perpendicular to the propagation direction of the GW, i.e., ${\sigma }_x={\sigma }_y$, the GW does not produce observable effects on it. Now, using the simplest possible expression for the GW, which is

$$h(t,z)=h_{0}cos(k_{g}z-{\omega }_{g}t)$$

(24)

with ${\omega }_g=c{k}_g$, with ${\omega }_g$ and $k_g$ denoting the GW angular frequency and wave vector, respectively, and $h_0$ the GW amplitude, one obtains

$$N\xi \left(t\right)=N{\displaystyle \frac{h_0}{2}}\sqrt{{\displaystyle \frac{\hslash }{m}}}\left(\sqrt{{\omega }_x}-\sqrt{{\omega }_y}\right)e^{-{\displaystyle \frac{\hslash }{4m{c}^2}}{\displaystyle \frac{{\omega }_g^2}{{\omega }_z}}}sin\left({\omega }_{g}t\right).$$

(25)

Equation (25) gives the phase shift, due to a GW, on a non-interacting BEC subjected to an anisotropic harmonic trapping potential. Note that the response of the condensate is oscillatory, as one would expect for a wave phenomenon.

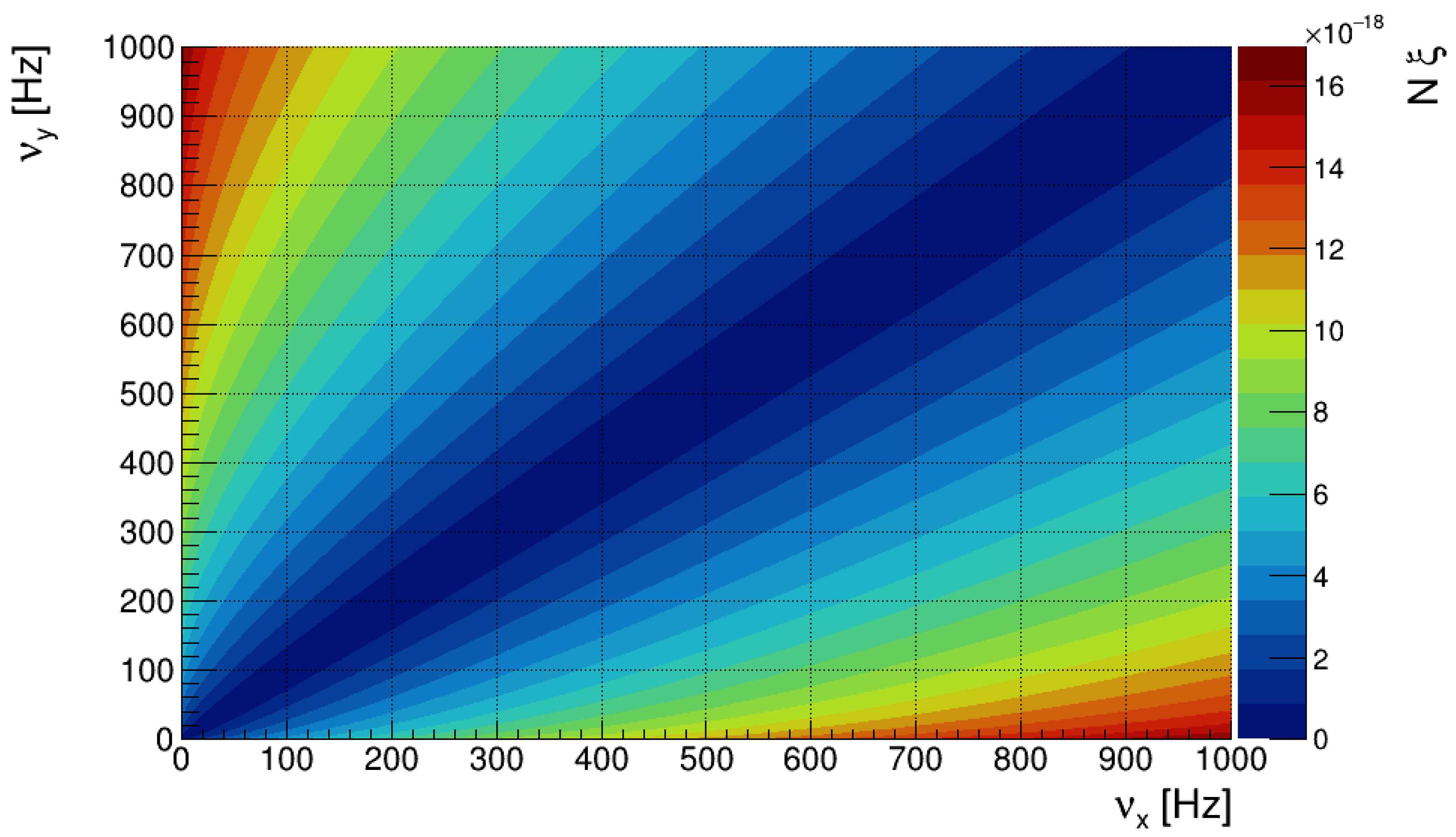
Figure 1 shows a two-dimensional plot depicting the amplitude of $\xi \left(t\right)$, i.e., $N\xi (t=\pi /\left(2{\omega }_g\right))$, as a function of the confinement frequencies ${\nu }_x={\omega }_x/\left(2\pi \right)$ and ${\nu }_y={\omega }_y/\left(2\pi \right)$, with $\omega$s denoting the angular frequencies in the $xy$-plane. Figure 1 is obtained given a condensate consisting of non-interacting ⁸⁷Rb atoms and keeping constant the values of ${\omega }_z=2\pi \times 150\mathrm{Hz}$, $h_0={10}^{-20}$ and $N={10}^7$. Figure 1 shows how the phase amplitude induced by the GW and enhanced by the number of particles can reach the magnitude of $\mathcal{O}\left({10}^{-17}\right)$, if the confinement frequencies perpendicular to the propagation direction of the wave are appropriately chosen. This order of magnitude also confirms the approximation made by expanding the time evolution operator in a series. It is also of importance to stress that the amplitude of $N\xi$ is independent of both the GW frequency and the confinement frequency along the z direction, since the exponential term in Equation (25) is close to 1. Any significant damping effect on the amplitude can only be observable for values of ${\omega }_g^2\gg 4m{c}^2{\omega }_z/\hslash$.

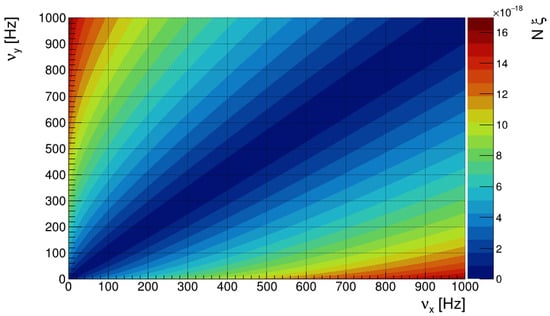
Figure 1. Phase shift $N\xi \left(t\right)$ (25) first in Figs. at $t=\pi /\left(2{\omega }_g\right)$ as a function of the confinement frequencies in the $xy$ plane, for non-interacting ⁸⁷Rb atoms, with fixed values of ${\nu }_z=150\mathrm{Hz}$, $h_0={10}^{-20}$, and $N={10}^7$.

5.1.2. Interacting Bosons

The GPE (10) is not straightforwardly solvable analytically, but nevertheless, it is possible to make use of approximate methods to also evaluate the interacting case with $\gamma \ne 0$. We remind that the GPE is reliable if the nonlinear term is sufficiently small. In the case of harmonic confinement, this condition means that $N{a}_{\mathrm{s}}/{\ell }_H\ll 1$, where ${\ell }_H$ is the geometric mean of the characteristic harmonic lengths in the three directions: ${\ell }_H={\left({\ell }_x{\ell }_y{\ell }_z\right)}^{1/3}$ with ${\ell }_x=\sqrt{\hslash /\left(m{\omega }_X\right)}$, ${\ell }_y=\sqrt{\hslash /\left(m{\omega }_y\right)}$, and ${\ell }_z=\sqrt{m/\left(m{\omega }_z\right)}$. In Ref. [23], a variational approach was used with a Gaussian trial function of the same form of Equation (21), where ${\sigma }_i$ are the variational parameters. In other words, ${\sigma }_x$, ${\sigma }_y$, and ${\sigma }_z$ are not set equal to the three characteristic harmonic lengths ${\ell }_x$, ${\ell }_y$, and ${\ell }_z$. Instead, the three ${\sigma }_i$ are determined by minimizing the GPE energy functional. In Ref. [23], it is shown that, in the strongly repulsive regime, the parameters ${\sigma }_i^{*}$ that minimize the ground-state energy have the following form:

$${\sigma }_x^{*}={\left({\displaystyle \frac{\Gamma {\hslash }^{\frac{3}{5}}{\omega }_y{\omega }_z}{m{\omega }_x^4}}\right)}^{{\displaystyle \frac{1}{5}}},{\sigma }_y^{*}={\left({\displaystyle \frac{\Gamma {\hslash }^{\frac{3}{5}}{\omega }_z{\omega }_x}{m{\omega }_y^4}}\right)}^{{\displaystyle \frac{1}{5}}},{\sigma }_z^{*}={\left({\displaystyle \frac{\Gamma {\hslash }^{\frac{3}{5}}{\omega }_x{\omega }_y}{m{\omega }_z^4}}\right)}^{{\displaystyle \frac{1}{5}}},$$

(26)

where

$$\Gamma =\gamma {\displaystyle \frac{N}{{\left(2\pi \right)}^{\frac{3}{2}}}}.$$

(27)

Given, as in Section 5.1.1, a Gaussian-type wave function, the procedure for calculating $N\xi \left(t\right)$ leads to

$$N\xi \left(t\right)=N{\displaystyle \frac{h_0}{2}}{\left({\displaystyle \frac{{\hslash }^{\frac{11}{5}}}{m^2\sqrt{\Gamma {\omega }_z}}}\right)}^{{\displaystyle \frac{2}{5}}}{e}^{-{\displaystyle \frac{{\omega }_g^2}{4c^2}}{\left({\displaystyle \frac{\Gamma {\hslash }^{\frac{3}{5}}{\omega }_x{\omega }_y}{m{\omega }_z^4}}\right)}^{{\displaystyle \frac{2}{5}}}}\left({\left({\displaystyle \frac{{\omega }_x^4}{{\omega }_y}}\right)}^{{\displaystyle \frac{1}{5}}}-{\left[{\displaystyle \frac{{\omega }_y^4}{{\omega }_x}}\right)}^{{\displaystyle \frac{1}{5}}}\right]sin\left({\omega }_{g}t\right).$$

(28)

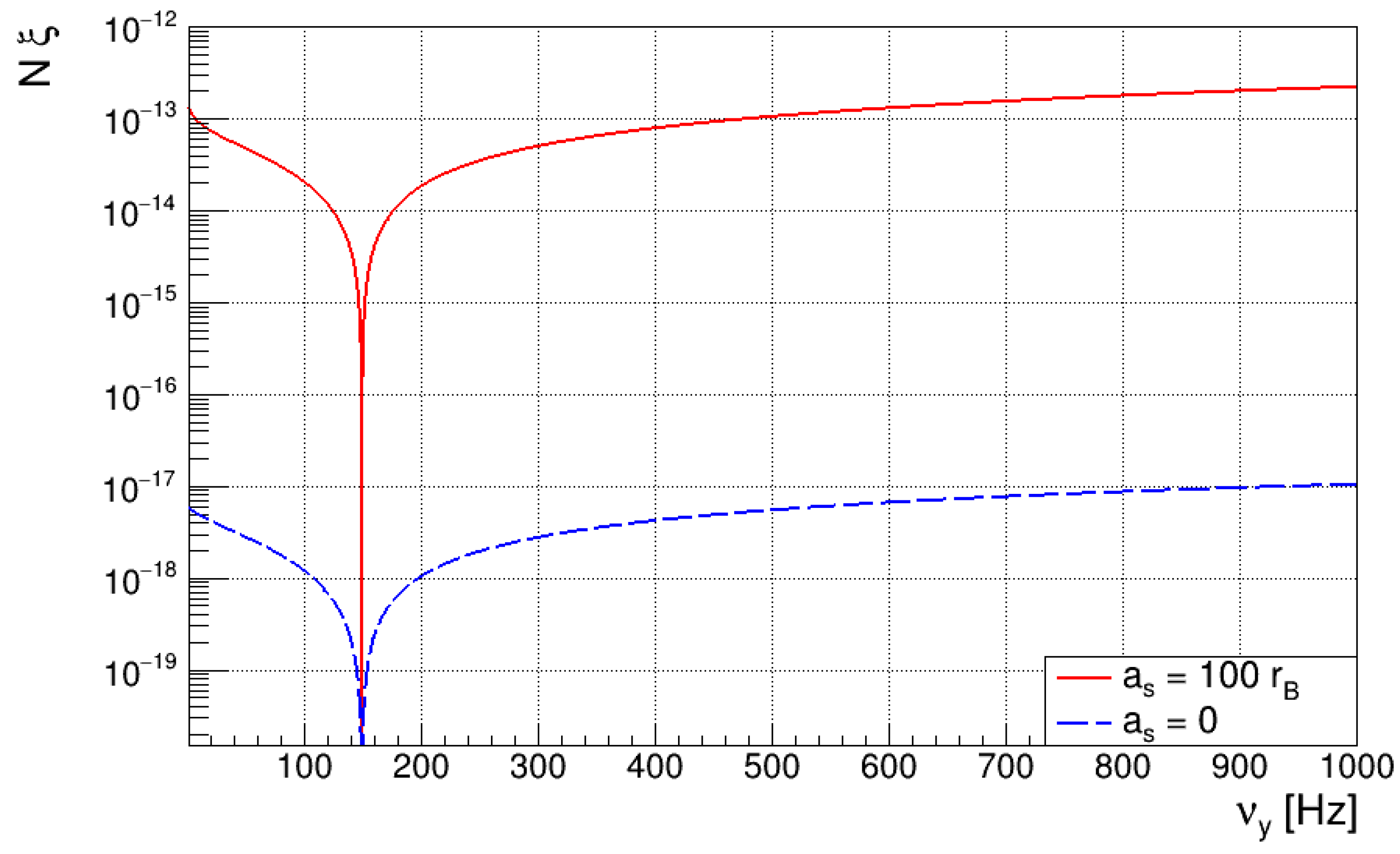
Figure 2 shows the amplitude of $N\xi \left(t\right)$, for a condensate of interacting (red line) and non-interacting (blue line) ⁸⁷Rb atoms, as a function of the confinement frequency along the y axis. Assuming a value of $h_0={10}^{-20}$ for the GW and $N={10}^7$, the amplitude of the interacting BEC is of the order of ${10}^{-13}$, which, in this case, also confirms the approximation made by expanding the time evolution operator in a series. For typical values of the scattering length of ⁸⁷Rb, i.e., around $100r_{\mathrm{B}}$ (with $r_{\mathrm{B}}$ the Bohr radius), the amplitude $N\xi$ is four orders grater than that related to the non-interacting BEC. This suggests that condensates of interacting atoms are preferable over the latter for future GW detection.

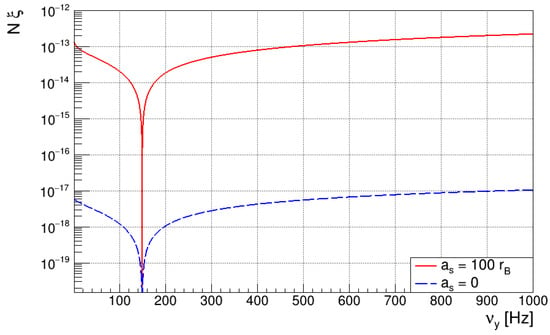
Figure 2. $N\xi \left(t\right)$ at $t=\pi /\left(2{\omega }_g\right)$ (25) for a condensate of interacting ⁸⁷Rb atoms as a function of the confinement frequency along the y-axis, for the two values of the scattering length $a_{\mathrm{s}}$, with $r_{\mathrm{B}}$ the Bohr radius. The parameters ${\nu }_z=150\mathrm{Hz}$, ${\nu }_x=150\mathrm{Hz}$, $h_0={10}^{-20}$, and $N={10}^7$ are used.

Also let us note that, as verified in Section 5.1.1, the amplitude is independent of the GW frequency, since the exponent of Equation (28) is of the order of $\mathcal{O}\left({10}^{-36}{\omega }_g^2\right)$.

6. Conclusions

We have discussed the interaction Hamiltonian between a gravitational wave and Bose–Einstein condensate, as reported in Equation (13). We have then computed the fidelity amplitude at first-order with respect to $hN$, obtaining Equation (18), which shows an enhancement mechanism of the phase that is proportional to the number of particles constituting the condensate N. Therefore, the latter can, generally, serve as a potential mechanism for detecting gravitational waves. Building upon the existing literature, we evaluate the magnitude of the interaction in the case of condensates confined by an anisotropic harmonic potential across three different configurations: non-interacting bosons, leading to Equation (25) and interacting particles, resulting in Equation (28). Additionally, as illustrated in Figure 2, we have demonstrated that the effect of the gravitational wave is better pronounced for condensates of interacting atoms. As suggested by Ralf Schützhold, in the future, one can experimentally produce a NOON-like ($\left(\right|N,0⟩+|0,N⟩)/\sqrt{2}$) state [6]:

$$|\mathrm{NOON}⟩\left(0\right)=|{\Psi }_{\mathrm{cs}}{⟩}_A{|0⟩}_B+{|0⟩}_A{|{\Psi }_{\mathrm{cs}}⟩}_B$$

(29)

at time $t=0^{-}$ (with the minus sign superscript denoting the limit as time approaches zero from the left), that is a macroscopic superposition of the BEC in two different configurations A and B. Then, if the GW interacts only with the BEC that is in the configuration A, at time t, one has

$$|\mathrm{NOON}⟩\left(t\right)=e^{iN\xi \left(t\right)}|{\Psi }_{\mathrm{cs}}{⟩}_A{|0⟩}_B+{|0⟩}_A{|{\Psi }_{\mathrm{cs}}⟩}_B.$$

(30)

Thus, the NOON state acquires a relative phase that is exactly the one of the fidelity amplitude, for a relatively small time interval. NOON states ${|N⟩}_A{|0⟩}_B+{|0⟩}_A{|N⟩}_B$ with up to $N=10$ quanta were already produced with photons and phonons [24,25]; however, their experimental realization with ultracold bosonic atoms is yet to be achieved.

In conclusion, the main message of this paper is that, at a fixed number N of atoms, tuning the s-wave scattering length $a_{\mathrm{s}}$ of the inter-atomic interaction, one can increase by several orders of magnitude the many-body phase $N\xi \left(t\right)$ (25) which signals the arrival of a gravitational wave.