Abstract
The automated identification and evaluation of potential attack paths within infrastructures is a critical aspect of cybersecurity risk assessment. However, existing methods become impractical when applied to complex infrastructures. While machine learning (ML) has proven effective in predicting the exploitation of individual vulnerabilities, its potential for full-path prediction remains largely untapped. This challenge stems from two key obstacles: the lack of adequate datasets for training the models and the dimensionality of the learning problem. To address the first issue, we provide a dataset of 1033 detailed environment graphs and associated attack paths, with the objective of supporting the community in advancing ML-based attack path prediction. To tackle the second, we introduce a novel Physics-Informed Graph Neural Network (PIGNN) architecture for attack path prediction. Our experiments demonstrate its effectiveness, achieving an F1 score of for full-path prediction. We also introduce a self-supervised learning architecture for initial access and impact prediction, achieving F1 scores of and , respectively. Our results indicate that the PIGNN effectively captures adversarial patterns in high-dimensional spaces, demonstrating promising generalization potential towards fully automated assessments.
1. Introduction
Information Systems (ISs) are socio-technical structures integrating organizational and technological components [,] to support business operations, decision-making, and management []. IS security can be compromised by vulnerabilities arising from software flaws and misconfigurations. Consequently, organizations must assess and manage risks associated with IS []. Risk-based IS management has been a key focus since the 1990s [,,,], providing a structured approach to identifying, analyzing, and mitigating potential threats []. A key aspect of IS risk management is risk assessment [,], which consists of three phases: risk identification, risk analysis, and risk evaluation.
Attack Path Analysis (APA) is a method for the risk assessment of attack scenarios applied in complex environments [,,]. A typical APA framework consists of an adversary model, an environment model, and an optimization algorithm [,]. Early APA frameworks used graphical approaches to model adversarial behavior and systems [,], later evolving into probabilistic models [,,,,,,,,,,,,,]. Modern APA frameworks generally fall into adversary-oriented [,,,,,,,,,] or system-oriented methods [,,,,,,,,,,,,,,] and can vary in their level of abstraction. Higher-abstraction models keep scenario exploration tractable [,,], while lower abstraction offers more detailed analysis but is computationally intensive [,,,,,,].
For a given environment, APA frameworks provide risk assessment decision support in three main directions: (1) deductive reasoning, i.e., identifying the impact of an attack path (consequence) given its starting point (cause), (2) inductive reasoning, i.e., determining the initial access point of the attack path given its impact, and (3) a combination of both, i.e., identifying the full path when both the cause and consequence are fixed (see Section 2.3 for formal notation). Yet, as infrastructures grow more complex and adversary techniques evolve, uncertainty makes these settings increasingly challenging and existing model-based methods impractical and prone to imprecisions [,,]. To address this issue, state-of-the-art (SoTA) data-driven methods like Exploit Prediction Scoring System (EPSS) [] leverage machine learning (ML) algorithms to predict exploitation likelihood in a model-agnostic manner, outperforming model-based equivalents [,,,,,,].
This research focuses on a subclass of ML algorithms known as deep learning (DL) [], which uses Deep Neural Networks (DNNs) for function approximation, motivated by the “universal approximation theorem” []. A DNN designed to predict full attack paths in any given environment must learn the joint distribution of adversary behavior and environmental characteristics across various combinations. However, the feasibility of generalizing over such a high-dimensional space remains unclear, as no public dataset currently supports this learning task. Existing APA datasets typically provide either detailed attack sequences or environmental properties but not both [,]. For instance, datasets derived from cyber threat intelligence (CTI) report mining offer rich APA details but lack broader environmental descriptions, focusing only on the affected scope []. Conversely, macro-level datasets [] aggregate public breach reports across diverse environments but do not include attack path details. Reinforcement Learning (RL) environments could be considered an alternative. However, RL-based approaches suffer from a similar trade-off: high-fidelity emulated frameworks demand significant computational resources, while lightweight simulated frameworks can only represent limited environments []. Ultimately, constructing such a dataset from real-world attack paths remains an open challenge, as organizations are generally reluctant to disclose detailed information about their infrastructure and incidents [,,,,,].
Our research aims to bridge this gap by making the following contributions: (1) framing and sharing a deep learning dataset of detailed environments with corresponding attack paths and (2) implementing and training DNN architecture for conducting inductive, deductive, and hybrid setting risk assessments. Through these contributions, this paper seeks to answer the following research questions:
| (RQ) Can adversary behavior be generalized across multiple environments to achieve full path prediction accuracy comparable to SoTA exploit prediction methods ? |
This paper is organized as follows: Section 2 will present the materials and methods, including our dataset and algorithms; Section 3 will present the experimental results on inductive, deductive, and hybrid settings; Section 4 will discuss the limits of this research along with new opportunities; and Section 5 will conclude this paper. To ensure the reproducibility of our findings, all data and algorithms presented in this paper can be found in the replication package (https://github.com/mbdlrocks/PhD_Replication_Package/tree/master/Physics-Informed-GNN%20(PIGNN), accessed on 7 April 2025). Readers are encouraged to explore the repository for further implementation details or to train their own models on the dataset.
2. Materials and Methods
Section 2.1 first presents the motivations for creating a new dataset and discusses the challenges and limitations of this approach. Section 2.2 then provides a brief introduction to physics-informed neural networks (PINNs), along with the motivations for applying them to attack path prediction. Next, Section 2.3 formalities the learning problem we address. Finally, we introduce two prediction architectures (see Section 2.4) and describe our training procedures, covering both physics-informed learning (see Section 2.5) and self-supervised learning (see Section 2.6).
2.1. Dataset
As discussed in Section 1, to the best of our knowledge, no existing dataset satisfies our criteria—namely, capturing a diverse range of detailed environments along with their associated attack paths. Given these constraints, we opted for a synthetic data-generation approach to conduct experimentation. Our goal was to construct a dataset that allowed us to experimentally evaluate the computational feasibility of generalizing across the high-dimensional spaces of environments and attack. Generating such a dataset and making it suitable for statistical learning presents several challenges, notably (1) ensuring technically realistic attack paths and environments while balancing granularity with dimensionality (see Section 2.1.1), (2) identifying and mitigating potential biases in feature distribution (see Section 2.1.2), and (3) structuring data efficiently for learning algorithms (see Section 2.1.3).
2.1.1. Realistic Attacks and Environments
The dataset consists of 1033 samples, each containing an environment and an attack path. As discussed in Section 2.2, this dataset is sufficient for a physics-informed architecture which can generalize with limited training samples. We combined simulation and expert validation methods: environment graphs were simulated using BloodHound [], a tool for auditing Active Directory (AD) environments, and attack paths for each environment were retrieved using Caldera [], an APA framework for automated red teaming. This approach enables the rapid generation of environments and the selection of relevant Techniques, Tactics, and Procedures (TTPs), emulating an adversary (see []). Similar approaches combining automation with expert oversight for path generation have been proposed by other authors [,], in which generated paths are manually reviewed by experts. In our case, the initial dataset was reduced from 1150 graphs to 1033 (≃10.17%) after manual inspection. There are also limits to this approach, which we discuss in Section 4.
The environments represent AD domains as directed graphs , with nodes representing Users, Computers, Domains, Group Policy Objects (GPOs), and Organizational Units (OUs) (see [] for details). The edges encode non-traversable relationships (e.g., inherits properties from []) and traversable ones (e.g., can open a session on ). Node features provide additional information regarding the entities (e.g., vulnerabilities, privileges). Each network consists of 100 users with dedicated computers, connected across four subnets, with an average of 15% vulnerable hosts per environment. For further details, we kindly invite the reader to refer to the dataset documentation.
Each attack path (see Figure 1) represents an “identity snowball” attack scenario [,,], in which an adversary gains initial access to a low-privileged account (e.g., via phishing) and escalates privileges by compromising additional accounts and systems. The goal is ultimately to reach the Domain Administrator (DA) [,]. While this attack model is widely popular among security auditors, it is also leveraged by known threat groups [], who use Bloodhound to find the shortest paths to high-value targets []. Given its relevance in both offensive and defensive security and motivated by existing research, we focused on this scenario for our experiments.
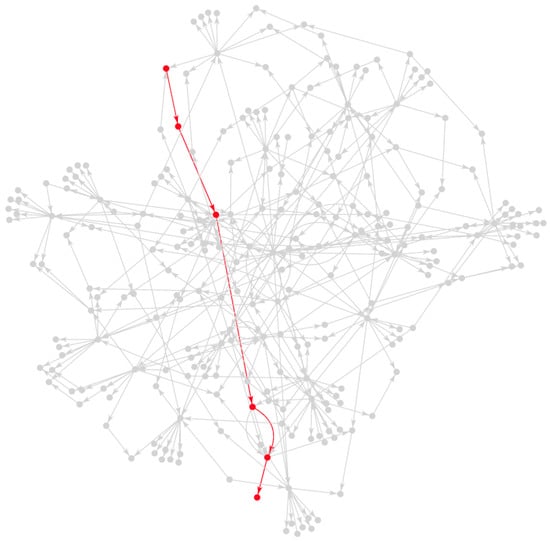
Figure 1.
Sample graph from the dataset (dimensionality has been reduced for better visualization); the path in red is the prediction objective.
2.1.2. Exploratory Data Analysis
A key aspect to examine in our generated samples is the type of edges traversed in attack paths. As shown in Figure 2(bottom left), the most frequently exploited edges are AdminTo edges (representing user accounts with administrative privileges on a system []), MemberOf edges (indicating group membership relationships []), and HasSession edges (corresponding to adversaries accessing stored credentials on a machine []). In Figure 2(top), we observe that these edge types follow an approximately normal distribution across graphs. If they were not normally distributed and exhibited a strong correlation with attack paths, the dataset could be skewed, potentially leading to biased models. Similar patterns are observed for edge counts and connection density (i.e., the number of parallel edges between two nodes), as illustrated in Appendix A Figure A1, Figure A2 and Figure A3.
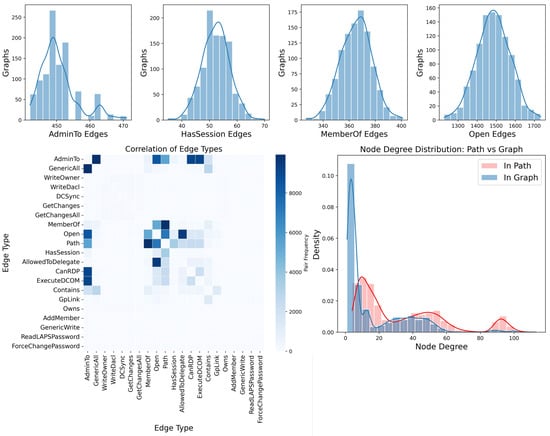
Figure 2.
(top) Distribution of the four edge types most associated with attack paths; (bottom left) correlation matrix of edge types; (bottom right) distribution of node degree in attack paths compared to overall node degree.
Regarding the nodes composing attack paths, Figure 2(bottom right) shows that their degree distribution slightly differs from that of the overall graph. This is expected, as nodes inside the path necessarily have a minimum degree of two. Finally, the analysis of the path length distribution reveals no overrepresented lengths, which is desirable; a bias in path lengths could indicate unintended artifacts in the generation algorithm. For additional metrics, we refer the reader to the replication package (https://github.com/mbdlrocks/PhD_Replication_Package/tree/master/Physics-Informed-GNN%20(PIGNN)/_visualisations_.ipynb, accessed on 7 April 2025) and Appendix A, where Table A1 provides an overview of the dataset.
2.1.3. Data Structure for Learning
Graphs and associated paths are preprocessed for PyTorch [] and provided as .pt files. This preprocessing step is responsible for (1) converting the raw graph into an adequate tensor-based format and (2) ensuring that all graphs have the correct dimensions. The preprocessing script can be found in the replication package (https://github.com/mbdlrocks/PhD_Replication_Package/tree/master/Physics-Informed-GNN%20(PIGNN)/_Preprocessing_, accessed on 7 April 2025). In the dataset, denoted by , each sample is a tuple comprising an adjacency tensor and a graph signal tensor , with d the number of different edge types and p the node features. For a given graph , the label is an adjacency matrix where if an edge between nodes i and j is part of the attack path. The dataset comprises unique samples, each containing node features and unique edge types. The tensor-based format conversion is also illustrated in Figure 3.
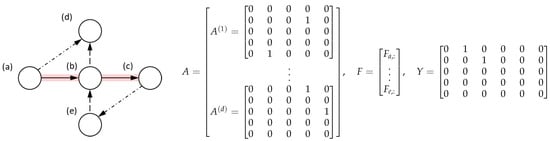
Figure 3.
Illustrative example of graph tensor-based formatting, with . For each unique edge type (as indicated by the line types), an adjacency matrix is generated and combined with other edge types (forming tensor ). The signal tensor is constructed from the node features, while the target is the path adjacency matrix (represented by the red lines).
This dataset is the first of its kind and should be considered as a prototype for future enhancements. We purposefully restricted some of its aspects (e.g., the assumption that attacks originate from user accounts rather than public-facing systems or restriction to identity snowball attacks). These design choices, along with the reliance on automatically generated synthetic data instead of ground-truth samples, should be understood in the context of this paper’s objective—demonstrating the efficiency of learning-based algorithms for APA. At the same time, they enabled the rapid development of a sufficiently robust experimental setting for testing our methods. For future enhancements or for organizations appropriating the dataset, start-node probabilities could be aligned with internal phishing campaign results. Another key aspect of this dataset is its extensibility through graph-based structures. Notably, existing cybersecurity knowledge graphs (CSKGs) [,,,,,] can be used to add new nodes and (non-traversable) edges to environments []. This data augmentation proposal is discussed in Section 4.
2.2. Physics-Informed Learning
In Section 1, we presented the generalization of attack paths across high-dimensional environments as one of the key challenges of this research. To address this challenge, we introduce a Physics-Informed Graph Neural Network (PIGNN).
Physics-informed neural networks (PINNs) [], also known as Theory-Trained Neural Networks (TTNs) []—or, more generally, model-based deep learning []—are designated as an emerging research field of neural network architectures that integrates prior knowledge of physical laws and known interaction logic into the learning process.
| In the context of attack path prediction across high-dimensional environments, using PINNs instead of agnostic Deep Neural Networks presents two key advantages: (1) incorporating known interaction principles and properties into the training restricts the space of feasible learnable solutions and thereby enhances the generalizability of the function approximation, and (2) by embedding this prior knowledge, PINNs also effectively augment the information content of the available data, enabling convergence towards accurate solutions with a limited number of training samples. |
To include known interaction principles into the training, we crafted a custom “physics-informed” loss function. In our case, this loss function exploits known properties of graph theory to penalize the network when predictions are incoherent with domain knowledge, e.g., if predicted adjacency matrix describes a graph containing cycles or branches. The loss function is detailed in Section 2.5.
2.3. Formal Problem Setting
Given the dataset , we define the corresponding learning task for each of the three risk assessment problem objectives discussed in Section 1:
|
Here, learning means minimizing the empirical risk over all predictions given our model (parametrised by ), e.g., in path prediction, over the set of possible parameters , find , which minimizes , where measures the error between our prediction and the ground truth attack path adjacency matrix .
2.4. Architecture
The neural architecture is composed of two main blocks, as illustrated in Figure 4. The first block is a graph convolution block, responsible for generating a tensor , in which each node v is associated with a vector , called the embedding of v. The embedding vector encodes the signal vector (given by ) relative to the graph structure (given by A). The embeddings are then fed forward into the second block.
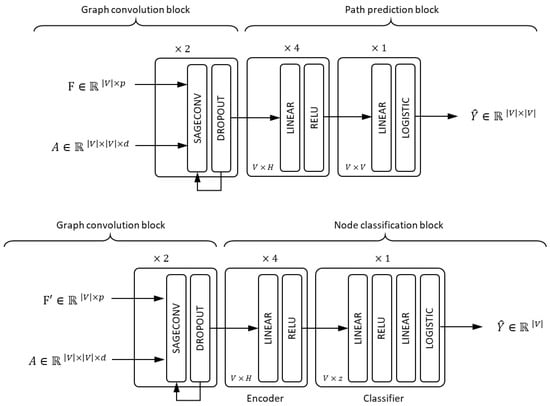
Figure 4.
(top) Full architecture for path prediction: inputs are graph adjacency tensor A and signal tensor F, output is path adjacency matrix ; (bottom) full architecture for start/end node classification: inputs are graph adjacency tensor A and modified signal tensor or , output is start/end node classification vector , which corresponds to or .
The second block depends on problem at hand. For full path prediction, is fed into a multilayer perceptron (MLP) [] which outputs a prediction matrix . For start/end node prediction, is fed into an encoder which outputs a compressed representation of , denoted by . This latent representation is then fed into a classifier which outputs a vector of , where, after applying a threshold, only the start/end node value is set to 1.
2.4.1. Graph Convolution Block
Graph Convolutional Networks (GCNs) [] are neural networks designed for learning embeddings in graphs. Graph convolution was introduced in [] as a way to learn graph structures using neural networks. GraphSAGE [] is a specific GCN architecture which relies on sample-and-aggregate convolution (SAGEConv) layers to efficiently learn the embeddings on directed graphs. During inference, for each node , the SAGEConv first aggregates feature representations from its immediate neighbors via a learnable aggregation function. The aggregate is then concatenated with the node’s own feature vector. The resulting vector is then processed by a learnable fully connected layer and an element-wise non-linear activation function. The output from the final layer serves as the learned embedding of v. In this paper, we use a slightly different version of the SAGEConv original implementation [], which employs batch matrix multiplication (BMM) for fast aggregation, detailed in Algorithm 1 and illustrated in Figure 5.
| Algorithm 1 Inference with BMM SAGEConv layer |
|
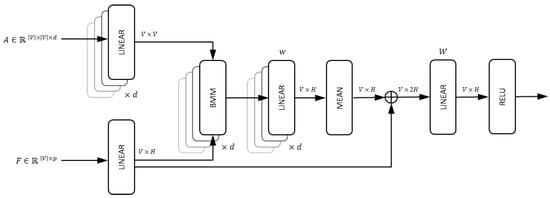
Figure 5.
Schematic representation of the BMM SAGEConv; LINEAR blocks are trainable parameters, BMM designates batch matrix multiplication used for aggregation operation, and ⊕ designates the concatenation operation.
In our path prediction architecture, the first block consists of two BMM SAGEConv layers (see Figure 4). During inference, both F and A are input into the first BMM SAGEConv layer. F is used to retrieve , and A is used to identify the neighbors of v. The trained layer produces the first embedding tensor . This tensor is then passed through an activation function, specifically Rectified Linear Unit (ReLU). The Rectified Linear Unit (ReLU) is a standard non-linear function used in deep learning frameworks []; the function is defined as . After activation, the signal is passed through the second layer along with A. The second BMM SAGEConv generates the final embedding tensor, . During training, each BMM SAGEConv layer is followed by a dropout layer to prevent overfitting. The layer randomly zeroes some of the elements of the input tensor with a probability p. For details on the block implementation and to maintain section conciseness, please refer to the replication package. For algorithmic complexity analysis, see Appendix E.
| The BMM SAGEConv layer k, given , can be written compactly as follows: |
2.4.2. Path Prediction Task
During full path prediction, the graph embeddings are used to generate the attack path matrix . Specifically, these embeddings are processed by a multilayer perceptron (MLP) [] with fully connected hidden layers, each with learnable parameters. Each hidden layer comprises 512 neurons, followed by a ReLU activation function. The final hidden layer is fully connected to an output layer with neurons, followed by a normalization step. Normalization is applied using a logistic function that scales the logits from the preceding layer. The logistic function, denoted is a standard non-linear function which can be used for normalization. The function is defined as . This transformation produces the matrix , where each element is constrained to the range . The matrix serves as the final adjacency matrix encoding the attack paths, where indicates the probability that an edge belongs to the attack path. To convert this probability to categorical (0 or 1) values, we compute the model’s Receiver Operating Characteristic (ROC) curve (see Appendix D) and determine the optimal threshold using Youden’s J index []. The threshold value is provided in Section 3. Figure 4 illustrates the path prediction block.
2.4.3. Node Classification Task
A distinct architecture is employed for the start/end node classification task. During inference, an encoder [] compresses the input embedding tensor into a lower-dimensional representation , where . The encoder consists of fully connected layers with trainable parameters and ReLU activations, progressively reducing the dimensionality () to compress the embeddings. The latent representation is then passed to an MLP [], responsible for classification. The MLP processes through a fully connected layer followed by a ReLU activation, then a second fully connected layer with normalization. It outputs a probability vector . The probabilities are then converted to a prediction vector, where all values are set to 0 except for a single index corresponding to the predicted start or end node, using Youden’s J index, as previously discussed. Two separate classifiers are trained: one for predicting start nodes and the other for end nodes. For algorithmic complexity, refer to Appendix E.
2.5. Path Prediction Training
All blocks are trained end-to-end, meaning that for a given problem set, the graph convolution and path prediction (or node classification) blocks are optimized simultaneously. All models are trained using the Adaptive Moment Estimation (ADAM) optimizer [], a standard approach in deep learning []. The optimizer computes the gradients of the model loss with respect to its parameters. The path prediction architecture is trained by optimizing its parameters using a physics-informed loss function. The node classification architecture, in contrast, is trained with a regular (non physics-informed) loss function.
To train the path-prediction architecture, we define the following loss function:
where is a masked-weighted binary cross-entropy (MWBCE) loss (see Section 2.5.1), and is a physics-informed loss (see Section 2.5.2). The hyperparameters and balance the contribution of each loss term to the total loss.
2.5.1. Data Loss
Since the target prediction matrix is highly sparse, the data loss incorporates a masking strategy to mitigate the class imbalance. Without masking, the network tends to learn parameters that predict , which minimizes the loss but does not predict meaningful path structures.
We define the masking mechanism in such that a subset of negative label entries () is randomly sampled within the target adjacency matrix Y while all positive labels () are retained. Let denote this mask for an entry , defined as follows:
where is the masking coefficient that determines the fraction of values included in the loss computation. We set to a small value to force the network to focus on edges composing the attack path. We also introduce a weighting mechanism. Let be the weighting coefficient for type-II errors, defined as follows:
where and denote the number of positive and negative entries, respectively. Since is typically large, we introduce a scaling factor , set to . We then define as the weighting coefficient for positive labels. With the mask and weight coefficient defined, the weighted binary cross entropy (WBCE) loss is:
Averaging over the unmasked elements for training samples in batch size N, the data loss is thus computed as follows:
This formulation ensures that the loss focuses on the most relevant edges while preventing the model from collapsing to a trivial all-zeros prediction.
2.5.2. Physics-Inspired Loss
The physics-informed loss ensures that the predicted adjacency matrix adheres to domain knowledge. In our case, it implies that the graph described in the predicted matrix (1) contains no branches, (2) consists of a single connected path component, with all other nodes remaining isolated, (3) contains no cycles. If the network’s prediction violates these constraints, and thus increase. Formally, given the physics-inspired loss is written as follows:
2.5.3. Degree Component
The objective of is to enforce structural constraints by penalizing predictions based on node degree values. This component ensures that the predicted graph contains no branches. For , the predicted adjacency matrix, let be the out-degree of every node i and be the in-degree of every node i. We also define , where is the active set of non-isolated nodes. To define , we compute:
The three intermediary components penalize the network when it predicts a graph which contains (a) multiple potential start nodes () or (b) multiple end nodes () or (c) when intermediary nodes do not have exactly one incoming edge and one outgoing edge (). We average over batch size to compute the degree component, written as follows:
| The degree component ensures that the predicted graph follows a structured, single-path format without branches. This is achieved by analyzing the in-degree and out-degree of each node in the active set, which represent the number of incoming and outgoing connections, respectively. If multiple nodes are identified as potential starting points (having no incoming edges) or multiple nodes are seen as ending points (having no outgoing edges), the model is penalized, and parameters are updated accordingly. Additionally, intermediary nodes should have exactly one incoming and one outgoing connection to maintain a proper sequence. The loss function sums up these penalties across all graphs in a batch, ensuring the network consistently learns to predict non-branching paths. |
2.5.4. Cycle Component
The second component of is the cycle loss, which penalizes predicted graphs that contain cycles. This ensures that the predicted graph remains acyclic. Formally, let be the scaled predicted matrix:
and let be the number of cycles of length k in . To retrieve , we compute the weighted sum for cycles of length and average it over the batch size N, written as follows:
| The cycle component prevents the presence of loops in the predicted graph. A cycle means that one can start from a node, follow the connections, and return to the same node. This is undesirable in our context, so the model is penalized if cycles are detected. Mathematically, this is achieved using the adjacency matrix of the graph: by raising this matrix to successive powers, we can count the number of paths of different lengths. If a sum of these paths indicates a cycle, a penalty is applied. This ensures that the predicted structure is strictly forward-moving, preventing redundant or circular paths. |
2.5.5. Connectivity Component
The last component of is the connectivity loss, denoted as . Its purpose is to penalize predictions that contain more than one path. To achieve this, we use the algebraic connectivity [] and the spectral properties of path graphs []. Formally, let be the Laplacian of the graph, and let be the eigenvalues of . We define C as the number of components in the graph, a small value, and an estimate of the maximum path length from the matrix :
If only contains a path and isolated nodes, then we expect components in the graph. Based on this value, we can compute:
We know from spectral graph theory [] that the expected eigenvalues of a path-graph of length should follow . Thus, we define the second penalty component as the mean squared error of the expected and observed spectrum, written as follows:
Averaging over batch size N, we obtain the connectivity component loss, written as follows:
| The connectivity component ensures that the predicted graph consists of a single connected path rather than multiple disconnected segments. This is achieved using the Laplacian matrix, which describes the structure of the graph. The eigenvalues of this matrix provide information about how connected the graph is: in particular, the number of zero eigenvalues indicates how many separate components exist. If the number of components does not match the expected value for a properly connected path, the model is penalized. Additionally, spectral graph theory tells us the expected eigenvalues for an ideal path graph, so a second penalty is added if the observed eigenvalues deviate from this expected pattern. By enforcing these constraints, the model learns to generate graphs that form a single continuous sequence without fragmentation. |
2.6. Start/End Node Training
When training for a start/end node classification task, is not required since the objective is to classify individual nodes rather than predict structured paths.
2.6.1. Encoder Self-Supervised Training
The encoder can either be trained end-to-end along with the graph convolution block or fine-tuned using a pre-trained graph convolution block. This second setting is useful when the graph convolution block has been pre-trained, e.g., for path prediction (see replication package, where flag freeze=False/True can be set to test both modes).
The encoder is trained in a self-supervised way using a decoder, i.e., a neural network with the exact same configuration but inverse. This encoder–decoder architecture is known as an “autoencoder”. Autoencoders [] were introduced with the objective of learning to reconstruct an input signal with minimal error. The core idea behind autoencoders is to train a neural network that can generate low-dimensional representations in its intermediate layers, known as the latent space, denoted z. The encoder is responsible for learning the mapping , which represents the latent space. The decoder is responsible for learning , which reconstructs the input from the latent space. To train the autoencoder, the loss function measures the reconstruction error, i.e., minimizing the difference between and x over all training samples.
The autoencoder loss function can be written as follows:
The input to the encoder is the embedding matrix , and the output is the reconstructed version, denoted . Once the autoencoder is trained, we remove the decoder and serialize the encoder with a classification layer, forming the encoder–classifier block (see Figure 4), which is trained end-to-end while fine-tuning the encoder.
2.6.2. Classifier Supervised Training
With the encoder–classifier block (see Figure 4), our objective is to learn how to predict the end node given the start node, i.e., given , predict where , and given , predict where . During training, we mask the column vector corresponding to “End Node” or “Start Node” feature, thus obtaining . The classifier is then trained to predict a vector , where only the entry corresponding to the start/end node should be set to after thresholding.
The loss function for the classifier is the Binary Cross Entropy (BCE) averaged over batch size N, i.e.,
3. Results
This section presents our results. We discussed the last version of EPSS [] in Section 1, which has a ROC-AUC score of and F1 score of . We evaluated our models against it, as one of our objectives is to extend EPSS’s functionality to full path prediction with at least equal performance.
3.1. Evaluation
We trained the full-path prediction architecture using K-fold cross-validation (see Appendix B) with , meaning that in each epoch, the model was trained on 80% of the dataset, while the remaining 20% was used for testing. Each fold underwent training for 20 epochs. To evaluate performance, we measured the model’s F1 score (see Appendix C) and ROC-AUC score (see Appendix D) for each fold. K-fold cross-validation enhances the robustness of performance evaluation by ensuring that every data point is used for both training and validation. By averaging the results across all folds, this approach mitigates the impact of data variability and reduces the risk of biased performance estimates that could arise from a single train–test split. Additionally, it helps to assess the model’s generalizability, as it is trained and evaluated on multiple subsets of the dataset. The results are illustrated in Figure 6.
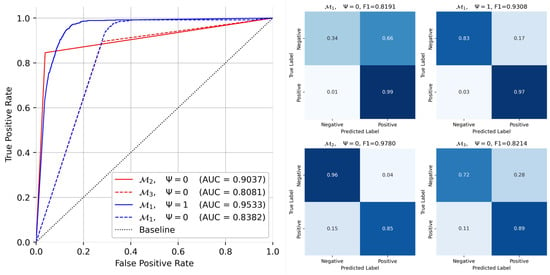
Figure 6.
(left) Plot showing the ROC curves of the four models. is the path prediction architecture with () and without the () component, and and are the node classification models for start and end node classification, respectively; (right) the quadrant shows the confusion matrix for the corresponding models.
The following parameters were set: , , , , batch size , and initial learning rate . As the loss component tends to be larger than the two others, setting to reduce its contribution to the loss helps to stabilize training. We used an exponential decay learning rate scheduler with decay rate . This scheduler was responsible for reducing the learning rate every epoch (see replication package for details). We set the mask coefficient , and the dropout probability in BMM SAGEConv layers was set to , meaning that each neuron had an equivalent probability of being “dropped out” of the loss computation during training, which helped to avoid overfitting. These hyperparameters were found to be optimal using the grid search strategy []. We trained all models on an NVIDIA GeForce GTX 1660 Ti GPU with 6GB of memory.
Having retrieved the ROC curves of the four models, we could compute Youden’s J statistic [], which indicates the optimal threshold with respect to the prediction task. The thresholds obtained are shown in Table 1. Finally, the thresholds were set for each of the models, and we could measure the F1 score (see Appendix C for details).
| For path prediction (), we obtained a final evaluation F1 score of and ROC-AUC , which is superior to the EPSS performance. For start/end node classification (), we obtained an F1 score of and ROC-AUC of for start node prediction and F1 score of and ROC-AUC for end node prediction. |

Table 1.
Performance benchmark of the path prediction architecture with and without physics-informed loss . uses the physics-informed loss, and does not. and are the start-node and end-node predictors, respectively; the thresholds obtained using Youden’s J index of each model were used to compute F1 scores.
3.2. Ablation Study
Table 1 presents the performance of the path prediction architecture with and without across different folds of the dataset. The results show that the model , trained with the physics-informed loss, consistently outperforms the baseline model in every fold. Additionally, the evaluation metrics exhibit relatively low variability across folds, indicating that the model’s performance is stable and reliable.
3.3. Sensitivity Analysis
We conducted a sensitivity analysis with the objective of measuring the importance of each node feature and edge type in the architecture prediction. To estimate this value, we used the SHAP algorithm [] (see Appendix F). Figure 7, Figure 8 and Figure 9 show the results of our analysis for , with the PIGNN and and the start-node and exit-node prediction models, respectively. Features and edge types are ordered on the Y-axis of each plot, in descending order. The dot colors indicate the value of the input (blue for values , red for values ), and the dot location on the X-axis indicates the influence of the value on the prediction.
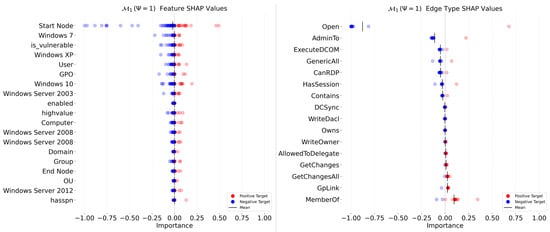
Figure 7.
Sensitivity analysis of node features (left) and edge types (right) using SHAP for .
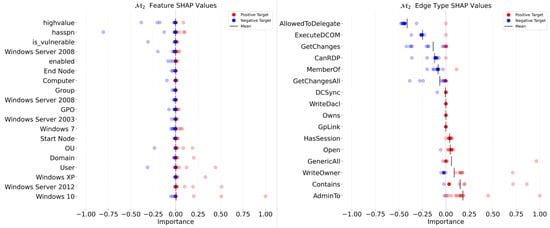
Figure 8.
Sensitivity analysis of node features (left) and edge types (right) using SHAP for .
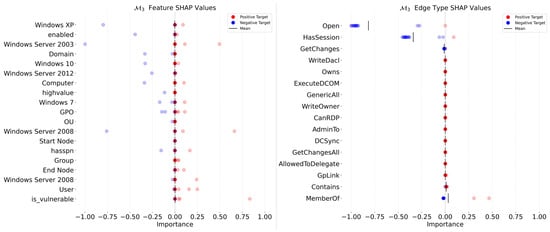
Figure 9.
Sensitivity analysis of node features (left) and edge types (right) using SHAP for .
For (see Figure 7), (1) Open edges with low values—corresponding to edges that do not have a corresponding network route—are very influential in preventing concurrent edges from being included in the predicted attack path. It appears that the PIGNN learned this association, which is coherent with domain knowledge, as non-routed paths cannot be exploited by an attacker. (2) the AdminTo, ExecuteDCOM, GenericAll, CanRDP, and HasSession edges are also positively correlated with the prediction, meaning that such edges are perceived as likely to be part of the attack path by the neural network. This is also expected, as these edges correspond to easily exploitable lateral movement techniques, and as discussed in Section 2.1, the AdminTo and HasSession features are highly correlated with ground-truth attack paths. From the feature SHAP values, we can observe that (3) the Start Node property exhibits a large influence on the neural network depending on its value. This could be an indicator that the feature is used by the network to decide whether to include or exclude the nodes in the path. This makes sense, as any node with this attribute set is necessarily included in the path. (4) Most of the other features are centered around 0 with relatively narrow amplitude. Overall, these results seem to indicate that the network focuses largely on the edge types rather than node attributes, with the exception of the entry node.
For (see Figure 8), the initial access node predictor, we can observe that ExecuteDCOM, AllowedToDelegate, MemberOf, GetChanges, and GetChangesAll are correlated with negative predictions. The last two are commonly associated with the Domain Admin, and as such, it appears that the network might have learned to associate nodes supporting these edges as less likely to be initial access nodes. Conversely, AdminTo edges are strongly correlated with positive predictions. This edge type is associated with a user account, and links to potential HasSession edges from the target system. It would make sense that the network learned to identify nodes followed by an AdminTo edge as likely initial access nodes for identity snowball attacks. Regarding node features, we can observe that operating system characteristics are correlated with positive predictions, while user account attributes, e.g., hasSpn, are negatively correlated with predictions.
For (see Figure 9), the impact node predictor, we can observe the following: (1) Open, HasSession, and GetChanges are highly correlated with the decision—when the input node does not have these types of edges, it is less likely to be predicted as an initial access node. We can make the same observation for MemberOf edge type, but the correlation is weaker. Considering that the attack paths describe identity snowball attacks—meaning that the “optimal” exit node is the Domain Controller node—this node must have existing Open edges with all other nodes in the graph. As such, it makes sense that the network has learned to identify nodes with high counts of Open edges as likely exit nodes. The same observation applies to GetChanges, as these edges generally originate from DA nodes. Regarding features, the correlation with decision is fuzzier. Most features have a more centered impact, which means that their influence on the decision actually depends on the sample and does not exhibit a strong correlation with the decision.
4. Discussion
The results shown in Section 3 provide valuable insights into the research question outlined in Section 1. Our results indicate that generalizing over environments and adversary characteristics across multiple environments is feasible—even with a limited dataset—using physics-informed learning. Our results show that our approach achieves strong performance across all three risk assessment tasks discussed in Section 2.3: (1) deductive reasoning, e.g., identifying the ending of an attack path (consequence) given its starting point (cause), (2) inductive reasoning, e.g., determining the starting point of the attack path given its ending, or (3) a combination of both, e.g., identifying the full path when both the cause and consequence are fixed.
Based on our ablation study (see Section 3.2), it appears that incorporating physics-informed loss components enhances training efficiency with limited samples, aligning with existing research on PINNs, as discussed in Section 2.2. In our case, implementing the physics-informed loss increases the F1 score by more than 10%. When studying which features are impactful for the prediction models (see Section 3.3), we observed that edges were more important than most node attributes. This observation is promising for new research opportunities. As discussed in Section 1 and [], we are currently studying data augmentation strategies based on CSKG. Such data augmentation techniques rely on topological representations of knowledge to represent information, which our network seems to be adapted to. These preliminary results are promising and pave the way for further research. In [], we discussed ongoing experiments exploring the use of the Common Attack Pattern and Enumeration Catalogue (CAPEC) [] as a source for data augmentation in a real environment. A key advantage of leveraging graph structures for augmentation is that the graph convolution block presented in Algorithm 1 can process the enriched data directly, without requiring modifications to the existing convolution block.
Certain design choices and reliance on automated tools currently impose limitations on the full potential of the proposed methods and dataset. Namely, constraints applied during data generation—such as restricting to identity snowball attacks, using fixed-size graphs, and maintaining a limited level of detail—were intentionally set to keep the problem tractable in this first experiment. Having established this proof of concept, we propose expanding the dataset in future research through data augmentation by collecting real-world data and introducing additional nodes and edges to the graph. From a broader perspective, we believe this research contributes insights that extend beyond security risk assessment. Our findings make a compelling case for incorporating more structural reasoning in the design of deep learning models. While the “model-agnostic” nature of neural networks remains a defining characteristic [], our results suggest that crafting loss functions constrained by domain knowledge can enhance generalization.
5. Conclusions
In this paper, we investigated potential applications of Physics-Informed Graph Neural Networks (PIGNNs) for automated attack path prediction. In Section 1, we presented the motivations for this research. We developed three main research objectives: (1) building and releasing a dataset for experiments with Deep Neural Network (DNN)-based Attack Path Analysis (APA), (2) experimenting with the PIGNN for three risk assessment learning problems (inductive, deductive, and hybrid), and (3) reaching SoTA performance, which is evaluated against EPSS, the current SoTA for learning-based attack prediction.
Section 2 presented our methods for crafting our dataset along with an exploratory data analysis of potential biases and limitations. Then, we introduced our methods for building physics-informed neural networks. By leveraging graph-theory-based properties, we defined a physics-informed loss function, denoted by , which penalizes the prediction model when the predicted path contradicts domain knowledge and expected path properties. We used this loss function to train two distinct architectures. The first is based on a Graph Neural Network (GNN) and multilayer perceptron (MLP) and aims at predicting full attack paths for a given environment, start node and end node. The second architecture we proposed also makes use of a GNN, along with an autoencoder (AE) designed to identify the most likely initial access nodes in the environment given an impact node or an impact node given the initial access node. While the full-path prediction architecture is useful for exploring potential risk scenarios with preset boundaries (e.g., as suggested in many risk management frameworks []), the start/end node classification architecture is also useful for incident response and threat analysis (e.g., an adversary has been spotted on a system, and the model can help to determine the initial access of the infection chain).
Section 3 presented our results after training the models using K-fold cross validation. We obtained a final evaluation F1 score of and ROC-AUC , which is superior to the EPSS performance. For start/end node classification, we obtained an F1 score of and ROC-AUC of for start node prediction and F1 score of and ROC-AUC for end node prediction. We also included an ablation study, showing that the physics-informed loss function correlates to a model performance increase, and conducted a sensitivity analysis using SHAP. We observed that the full-path model relies more on the topological properties of the graph than the node properties, which is promising for CSKG-based data augmentation strategies. Finally, Section 4 discussed potential research opportunities emerging from this research, along with the limitations of our procedure.
Author Contributions
Conceptualization, M.F.; methodology, M.F.; software, M.F.; validation, M.F., P.-E.A. and M.M.; formal analysis, M.F.; writing—original draft preparation, M.F.; writing—review and editing, M.F., P.-E.A. and M.M.; visualization, M.F.; supervision, P-E.A. and M.M.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data and algorithms presented in this paper can be found in the replication package (https://github.com/mbdlrocks/PhD_Replication_Package/tree/master/Physics-Informed-GNN%20(PIGNN), accessed on 7 April 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Summary of Statistics
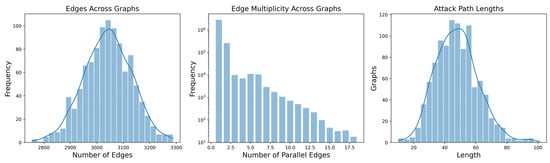
Figure A1.
(left) distribution of edge counts; (center) distribution of n-tuple parallel edges between two nodes; (right) distribution of attack path lengths.
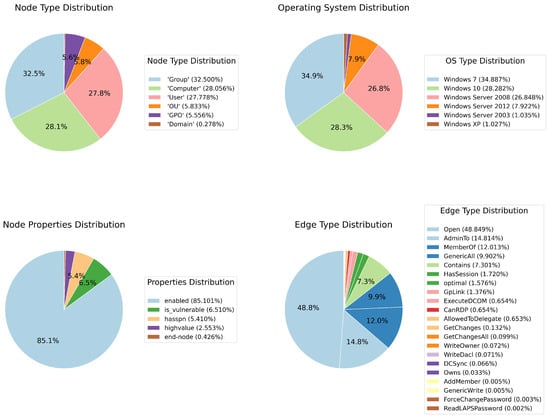
Figure A2.
(top left) Distribution per node type; (top right) distribution per operating system type; (bottom left) distribution of node selected properties; (bottom right) distribution of edge types.
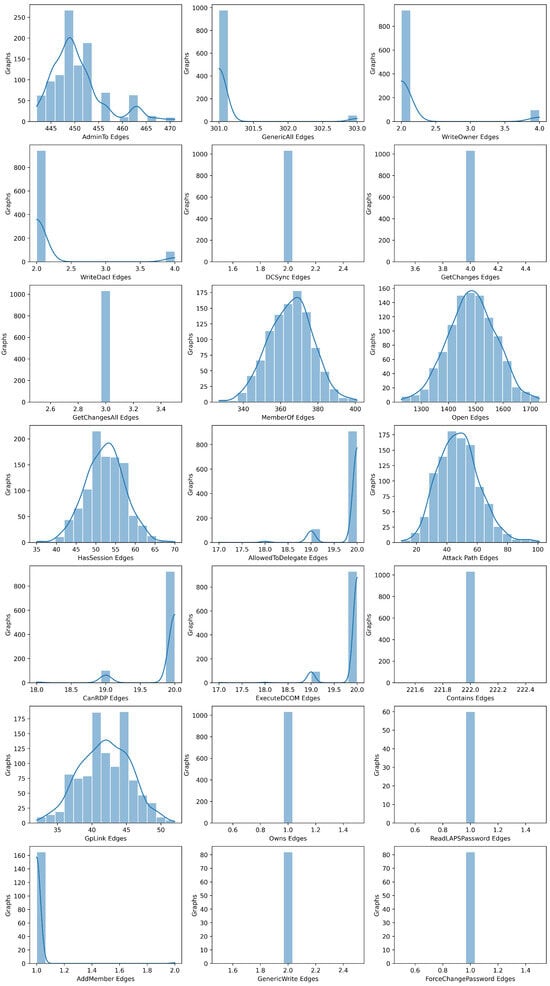
Figure A3.
Distribution of edge types across graphs.

Table A1.
Statistical summary of the dataset.
Table A1.
Statistical summary of the dataset.
| Num_Nodes | Num_Edges | Density | Avg_Degree | Median_Degree | Max_Degree | |
|---|---|---|---|---|---|---|
| count | 1033 | 1033 | 1033 | 1033 | 1033 | 1033 |
| mean | 361.0 | 3040.83 | 0.0234 | 16.85 | 5.88 | 423.89 |
| std | 0.0 | 90.19 | 0.0007 | 0.50 | 0.32 | 3.27 |
| min | 361.0 | 2755 | 0.0212 | 15.26 | 5 | 414 |
| 25% | 361.0 | 2979 | 0.0229 | 16.50 | 6 | 422 |
| 50% | 361.0 | 3043 | 0.0234 | 16.86 | 6 | 424 |
| 75% | 361.0 | 3102 | 0.0239 | 17.19 | 6 | 426 |
| max | 361.0 | 3288 | 0.0253 | 18.22 | 6 | 437 |
Appendix B. K-Fold Cross Validation
K-fold cross-validation is a resampling technique used to evaluate the performance of a model by partitioning the dataset into K equal-sized subset “folds”. The model is trained on folds and tested on the remaining fold, repeating the process K times with a different test fold each time. This method helps to mitigate overfitting and provides a more robust estimate of model performance. The value of K affects the bias–variance trade-off. A small K results in higher bias but lower variance, as the training set is smaller in each fold. A larger K reduces bias by using more data for training but increases variance due to the smaller test sets.
Appendix C. F1 Score
The F1 score is a standard measure of performance for classification model. In multi-class or imbalanced classification settings, different strategies exist for computing the overall F1 score: micro, macro, and weighted F1 scores.
Micro F1 aggregates the contributions of all classes by computing the global sums of True Positives (), False Positives (), and False Negatives () then applying the computation:
Macro F1, on the the other hand, computes the F1 score independently for each class:
where N is the number of classes, and is the F1 score for class i. Macro F1 treats all classes equally, making it sensitive to class imbalance since it does not consider class frequency.
In this research, we used Weighted F1, which accounts for class imbalance by weighting each class’s F1 score by the number of true instances in that class:
where is the proportion of true instances of class i in the dataset:
This approach ensures that the contribution of each class is proportional to its prevalence, making it more suitable when dealing with imbalanced datasets.
Appendix D. ROC-AUC Measure
The Area Under the Curve (AUC) for the Receiver Operating Characteristic (ROC) curve (ROC-AUC) evaluates the ability of a binary classifier to distinguish between positive and negative classes. Given a batch of size N where each sample corresponds to a flattened predicted matrix , denoted by , and a flattened ground truth matrix , denoted by , the ROC curve is constructed by varying a threshold and computing the True Positive Rate (TPR) and False Positive Rate (FPR):
where is the indicator function. The AUC is then computed as the integral:
which can be approximated [] with the number of positive samples and the number of negative samples, as follows:
To evaluate our models, we used the batch-averaged AUC, computed as follows:
Appendix E. Complexity Analysis
This section analyzes the time complexity of the proposed algorithms. We apply the following notation: Let denote the time complexity of model operating on a graph G, determined by the growth rate of . We are interested in analyzing the time complexity of , the path prediction architecture, and , the start/end node prediction architecture.
Appendix E.1. Path Prediction Architecture
and both operate on the same data inputs, i.e., a directed multigraph with self-loops. d is the maximum number of parallel edges between any pair of nodes, p is the maximum number of labels per node, is the set of edges, and is the set of nodes. Since are used to build F, the signal tensor, and A, the adjacency tensor, we can state the following:
Now, we assume the following inequalities: —meaning that the number of edge types does not exceed the total number of edges in the graph. In other words, d does not include edge types that do not have at least one edge in the G. Later in this section, we drop this assumption to observe the effect on time complexity. We also assume that and , which is consistent with the data augmentation strategy we proposed, i.e., the graph structure is tracked by edges rather than nodes. We can state the following:
The first block of is the graph convolution block, denoted by . The computational complexity of Algorithm 1 is primarily determined by the aggregation step within the loop over edge types. Initializing the node feature tensor and the auxiliary matrix requires . The main computational cost arises in the aggregation step, where, for each edge type, the algorithm computes the inverse degree matrix and performs a matrix multiplication . This results in a complexity of per iteration. Since this operation is repeated for each of the d edge types, the total cost of the loop is . The final transformation step, involving a matrix multiplication and activation function, contributes an additional .
In practice, this operation is optimized using the torch.bmm() API. See the implementation in Listing A1, where the message_passing() function is responsible for the aggregation step, while the forward() function is responsible for concatenation and activation. The message-passing algorithm performs batch matrix multiplication to efficiently multiply the signal tensor F with each of the d adjacency matrices composing the adjacency tensor A. Each of the d matrices is then transformed through a linear layer ( in Algorithm 1) and summed. When the forward() function calls the message-passing algorithm, the sum is transformed through a linear layer and then passed through an activation function. The forward function returns the K-th layer embedding. In the overall implementation, this function pair is called K times.
The overall complexity of the algorithm can be approximated as . As K and H are architecture-dependent, we can state the following:
Now, considering the inequalities in Equation (A12), is at most . We can express the worst-case time complexity of the convolution block in terms of only as follows:
Now, we update the inequalities presented in Equation (A12) and no longer assume —meaning that there can be more edge types than actual edges in the graph. Practically speaking, this results in the adjacency tensor A containing null matrices for certain edge types. In that case, the lower bound is no longer valid, and the total time complexity must include d:
| Listing A1. implementation. |
| class BMMSageConvLayer(nn.Module): … def message_passing(self, x: torch.Tensor, adj_tensor: torch.Tensor): batch_size, num_nodes, _ = x.shape aggregated_neigh_embeds = [] for i in range(adj_tensor.shape[3]): adj_matrix = adj_tensor[:, :, :, i] neigh_embeds_i = torch.bmm(adj_matrix, x) neigh_embeds_i = self.lin_neighbors[i](neigh_embeds_i) aggregated_neigh_embeds.append(neigh_embeds_i) neigh_embeds = sum(aggregated_neigh_embeds) return neigh_embeds def forward(self, x: torch.Tensor, adj_tensor: torch.Tensor): neigh_embeds = self.message_passing(x, adj_tensor) x_self = self.lin_self(x) out = neigh_embeds + x_self return self.act(out) class DNN(nn.Module): … def forward(self, x): x = F.relu(self.fc1(x)) … x = torch.sigmoid(self.fc5(x)) return x |
Overall, Equation (A15) is the generalization of the time complexity of the graph convolution block, while Equation (A14) applies to cases where the architecture fits perfectly the dataset dimensions (which is the case in this paper).
To complete the architecture , we have to add the complexity of the prediction block. The block comprises fully connected hidden layers, each containing 512 neurons with ReLU activations. The computational cost of a single fully connected layer mapping m input neurons to n output neurons is , where m and n are architecture-dependent. The last hidden layer maps n to an output of size , contributing an additional . As this term dominates the overall computation, the total complexity of the MLP can be approximated as . The logistic normalization function is applied element-wise and does not significantly impact the asymptotic complexity. Thus, the second block exhibits a quadratic complexity with respect to the number of nodes . As both blocks’ time-complexity is dominated by the quadratic term , overall, this gives us a generalized time-complexity for the architecture as follows:
Appendix E.2. Node Classification Architecture
The second architecture, denoted by , is composed of the same graph convolution block , with a different second block. We previously determined that the time complexity of the convolution block is .
The time complexity of the node classification block, which does not vary depending on whether we are predicting start/end, is determined by the encoder and the classification MLP. This block’s implementation is illustrated in Listing A2. The encoder compresses the input embeddings into a lower-dimensional representation through fully connected layers with ReLU activations, progressively reducing the feature size from . The computational cost of a fully connected layer mapping m input neurons to n output neurons is , where are all architecture-dependent parameters. Summing across all layers, the total complexity of the encoder is approximately , which can be reduced to .
The classifier processes the compressed representation through two fully connected layers, with the first mapping followed by a ReLU activation and the second mapping with a point-wise normalization step. This results in an additional complexity of . As the quadratic term dominates for large graphs, the overall complexity of the start/end node classification block is approximated as . Combined with the convolution block, the overall complexity of the architecture is dominated by the quadratic term:
| Listing A2. implementation. |
| class AE(torch.nn.Module): … def forward(self, x): encoded = self.encoder(x) decoded = self.decoder(encoded) return decoded … class EncoderWithClassifier(nn.Module): … def forward(self, x, adj_tensor): batch_size, num_nodes, _ = x.shape node_embeddings = self.graphsage(x, adj_tensor) … latent_repr = self.encoder(node_embeddings)s classification_output = self.classifier(latent_repr) … return classification_output |
Appendix F. Shapley Additive Explanations (SHAP)
The SHAP algorithm [] is a method from cooperative game theory [], where the feature (or group of features) value for a data point acts as players in a coalition. The j feature’s value in model M is computed as follows:
which breaks down to the following: is the coalition vector of maximum size M; this vector indicates which features are included in the coalition. Each entry can either be 0 (feature j not included) or 1 (feature j included). The coalition represents a specific configuration of features being evaluated for their contributions to the model’s prediction; represents the average model output when no features are present. It serves as a reference point against which the contributions of the features are measured; is the feature attribution, which quantifies the impact of each feature j on the prediction. A positive indicates that the feature contributes positively to the predicted output, while a negative value indicates a negative contribution.
SHAP values offer four key properties []: additivity, which allows for independent computation of each feature’s contribution to the final prediction; local accuracy, such that values equal the difference between the expected and actual model output for a given input, providing accurate local interpretation of the model’s predictions; missingness, attributing zero values for missing or irrelevant features; and consistency, as values remain unchanged unless a feature’s contribution is altered, ensuring consistent interpretation across different architectures and parameters.
References
- Minden, S.L.; Henderson, M. From information to a system. Behav. Healthc. Tomorrow 2000, 9, 31–33. [Google Scholar] [PubMed]
- Servigne, S. Conception, architecture et urbanisation des systèmes d’information. In Encyclopædia Universalis; Encyclopædia Universalis: Boulogne-Billancour, France, 2010; pp. 1–15. [Google Scholar]
- Yu, E.S.K. Information Systems. In The Practical Handbook of Internet Computing; Chapman and Hall/CRC: London, UK, 2004. [Google Scholar]
- Eling, M.; McShane, M.; Nguyen, T. Cyber risk management: History and future research directions. Risk Manag. Insur. Rev. 2021, 24, 93–125. [Google Scholar] [CrossRef]
- Alavi, M.; Weiss, I.R. Managing the risks associated with end-user computing. J. Manag. Inf. Syst. 1985, 2, 5–20. [Google Scholar] [CrossRef]
- Rainer, R.K., Jr.; Snyder, C.A.; Carr, H.H. Risk analysis for information technology. J. Manag. Inf. Syst. 1991, 8, 129–147. [Google Scholar] [CrossRef]
- Eloff, J.H.; Labuschagne, L.; Badenhorst, K.P. A comparative framework for risk analysis methods. Comput. Secur. 1993, 12, 597–603. [Google Scholar] [CrossRef]
- Whitman, M.E.; Mattord, H.J. Principles of Information Security; Thomson Course Technology: Boston, MA, USA, 2009. [Google Scholar]
- Naik, N.; Jenkins, P.; Grace, P.; Song, J. Comparing attack models for IT systems: Lockheed Martin’s Cyber Kill Chain, MITRE ATT&CK Framework and Diamond Model. In Proceedings of the 2022 IEEE International Symposium on Systems Engineering (ISSE), Vienna, Austria, 24–26 October 2022; pp. 1–7. [Google Scholar]
- Elmiger, M.; Lemoudden, M.; Pitropakis, N.; Buchanan, W.J. Start thinking in graphs: Using graphs to address critical attack paths in a Microsoft cloud tenant. Int. J. Inf. Secur. 2024, 23, 467–485. [Google Scholar] [CrossRef]
- Dunagan, J.; Zheng, A.X.; Simon, D.R. Heat-ray: Combating identity snowball attacks using machinelearning, combinatorial optimization and attack graphs. In Proceedings of the ACM SIGOPS 22nd Symposium on Operating Systems Principles, Big Sky, MT, USA, 11–14 October 2009; pp. 305–320. [Google Scholar]
- Irfan, A.N.; Chuprat, S.; Mahrin, M.N.; Ariffin, A. Taxonomy of cyber threat intelligence framework. In Proceedings of the 2022 13th International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 19–21 October 2022; pp. 1295–1300. [Google Scholar]
- Cohen, F. Simulating cyber attacks, defences, and consequences. Comput. Secur. 1999, 18, 479–518. [Google Scholar] [CrossRef]
- Kuhl, M.E.; Sudit, M.; Kistner, J.; Costantini, K. Cyber attack modeling and simulation for network security analysis. In Proceedings of the 2007 Winter Simulation Conference, Washington, DC, USA, 9–12 December 2007; pp. 1180–1188. [Google Scholar]
- Abraham, S.; Nair, S. A Novel Architecture for Predictive CyberSecurity Using Non-Homogenous Markov Models. 2015. Available online: https://ieeexplore.ieee.org/document/7345354 (accessed on 7 April 2025).
- Woodard, M.; Marashi, K.; Sarvestani, S.S.; Hurson, A.R. Survivability evaluation and importance analysis for cyber–physical smart grids. Reliab. Eng. Syst. Saf. 2021, 210, 107479. [Google Scholar] [CrossRef]
- Holm, H.; Shahzad, K.; Buschle, M.; Ekstedt, M. P2CySeMoL: Predictive, Probabilistic Cyber Security Modeling Language. IEEE Trans. Dependable Secur. Comput. 2014, 12, 626–639. [Google Scholar] [CrossRef]
- Holm, H.; Shahzad, K.; Buschle, M. P2 CySeMoL: Predictive, Probabilistic Cyber Security Modeling Language (No Date). Available online: https://ieeexplore.ieee.org/document/6990572 (accessed on 7 April 2025).
- Holm, H.; Shahzad, K.; Buschle, M. Quantifying & Minimizing Attack Surfaces Containing Moving Target Defenses. 2015. Available online: http://ieeexplore.ieee.org/document/7287449 (accessed on 7 April 2025).
- Hong, J.B.; Kim, D.S.; Haqiq, A. What Vulnerability Do We Need to Patch First? Available online: https://ieeexplore.ieee.org/document/6903625 (accessed on 7 April 2025).
- Lippmann, R.P.; Ingols, K.W. An Annotated Review of Past Papers on Attack Graphs; MIT Lincoln Laboratory: Lexington, MA, USA, 2005. [Google Scholar]
- Valja, M.; Korman, M.; Shahzad, K. Integrated Metamodel for Security Analysis, IEEE Xplore Login (No Date A). Available online: http://ieeexplore.ieee.org/docurnent/7070437 (accessed on 7 April 2025).
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Yusuf, S.E.; Mengmeng, G.; Hong, J.B. Security Modelling and Analysis of Dynamic Enterprise Networks. 2016. Available online: http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=7876345 (accessed on 7 April 2025).
- Ekin, T. Augmented Probability Simulation Methods for Non-Cooperative Games. Available online: https://arxiv.org/abs/1910.04574 (accessed on 7 April 2025).
- Miller, S.; Wagner, C.; Aickelin, U.; Garibaldi, J.M. Modelling Cyber-Security Experts’ Decision Making Processes using Aggre-gation Operators. arXiv 2016, arXiv:1608.08497. [Google Scholar] [CrossRef]
- Applebaum, A.; Miller, D.; Strom, B.; Korban, C.; Wolf, R. Intelligent, automated red team emulation. In Proceedings of the Annual Computer Security Applications Conference, ACSAC, Los Angeles, CA, USA, 5–9 December 2016; pp. 363–373. [Google Scholar]
- Miller, H.; Griffy-Brown, C. Developing a Framework and Methodology for Assessing Cyber Risk for Business Leaders. J. Appl. Bus. Econ. 2018, 20, 34–50. [Google Scholar]
- Sarraute, C.; Buffet, O.; Hoffmann, J. POMDPs make better hackers: Accounting for uncertainty in penetration testing. In Proceedings of the AAAI Conference on Artificial Intelligence, AAAI, Toronto, ON, Canada, 22–26 July 2012; Volume 26, pp. 1816–1824. [Google Scholar]
- Molina-Markham, A.; Winder, R.K.; Ridley, A. Network defense is not a game. arXiv 2021, arXiv:2104.10262. [Google Scholar]
- Goel, D.; Ward-Graham, M.H.; Neumann, A.; Neumann, F.; Nguyen, H.; Guo, M. Defending active directory by combining neural network based dynamic program and evolutionary diversity optimisation. In Proceedings of the Genetic and Evolutionary Computation Conference, Boston, MA, USA, 9–13 July 2022; pp. 1191–1199. [Google Scholar]
- Han, Y.; Rubinstein, B.I.; Abraham, T.; Alpcan, T.; De Vel, O.; Erfani, S.; Hubczenko, D.; Leckie, C.; Montague, P. Reinforcement learning for autonomous defence in software-defined networking. In Proceedings of the Decision and Game Theory for Security: 9th International Conference, GameSec 2018, Seattle, WA, USA, 29–31 October 2018; Proceedings 9. Springer: Berlin/Heidelberg, Germany, 2018; pp. 145–165. [Google Scholar]
- Han, Y.; Hubczenko, D.; Montague, P.; De Vel, O.; Abraham, T.; Rubinstein, B.I.; Leckie, C.; Alpcan, T.; Erfani, S. Adversarial reinforcement learning under partial observability in autonomous computer network defence. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Baillie, C.; Standen, M.; Schwartz, J.; Docking, M.; Bowman, D.; Kim, J. Cyborg: An autonomous cyber operations research gym. arXiv 2020, arXiv:2002.10667. [Google Scholar]
- Dhir, N.; Hoeltgebaum, H.; Adams, N.; Briers, M.; Burke, A.; Jones, P. Prospective artificial intelligence approaches for active cyber defence. arXiv 2021, arXiv:2104.09981. [Google Scholar]
- Gangupantulu, R.; Cody, T.; Park, P.; Rahman, A.; Eisenbeiser, L.; Radke, D.; Clark, R.; Redino, C. Using cyber terrain in reinforcement learning for penetration testing. In Proceedings of the 2022 IEEE International Conference on Omni-layer Intelligent Systems (COINS), Barcelona, Spain, 1–3 August 2022; pp. 1–8. [Google Scholar]
- Li, L.; Fayad, R.; Taylor, A. Cygil: A cyber gym for training autonomous agents over emulated network systems. arXiv 2021, arXiv:2109.03331. [Google Scholar]
- Andrew, A.; Spillard, S.; Collyer, J.; Dhir, N. Developing optimal causal cyber-defence agents via cyber security simulation. arXiv 2022, arXiv:2207.12355. [Google Scholar]
- Bradley, J.; Atkins, E. Toward continuous state—Space regulation of coupled cyber—Physical systems. Proc. IEEE 2011, 100, 60–74. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, L.; Ye, J. Cyber-attack detection for photovoltaic farms based on power-electronics-enabled harmonic state space modeling. IEEE Trans. Smart Grid 2021, 13, 3929–3942. [Google Scholar] [CrossRef]
- He, R.; Xie, H.; Deng, J.; Feng, T.; Lai, L.; Shahidehpour, M. Reliability modeling and assessment of cyber space in cyber-physical power systems. IEEE Trans. Smart Grid 2020, 11, 3763–3773. [Google Scholar] [CrossRef]
- Yang, L.; Cao, X.; Li, J. A new cyber security risk evaluation method for oil and gas SCADA based on factor state space. Chaos, Solitons Fractals 2016, 89, 203–209. [Google Scholar] [CrossRef]
- Ajmal, A.B.; Shah, M.A.; Maple, C.; Asghar, M.N.; Islam, S.U. Offensive security: Towards proactive threat hunting via adversary emulation. IEEE Access 2021, 9, 126023–126033. [Google Scholar] [CrossRef]
- Ajmal, A.B.; Khan, S.; Alam, M.; Mehbodniya, A.; Webber, J.; Waheed, A. Toward effective evaluation of cyber defense: Threat based adversary emulation approach. IEEE Access 2023, 11, 70443–70458. [Google Scholar] [CrossRef]
- Yoo, J.D.; Park, E.; Lee, G.; Ahn, M.K.; Kim, D.; Seo, S.; Kim, H.K. Cyber attack and defense emulation agents. Appl. Sci. 2020, 10, 2140. [Google Scholar] [CrossRef]
- Eckhart, M.; Ekelhart, A. Digital twins for cyber-physical systems security: State of the art and outlook. In Security and Quality in Cyber-Physical Systems Engineering: With Forewords by Robert M. Lee and Tom Gilb; Springer: Cham, Switzerland, 2019; pp. 383–412. [Google Scholar]
- Dietz, M.; Vielberth, M.; Pernul, G. Integrating digital twin security simulations in the security operations center. In Proceedings of the 15th International Conference on Availability, Reliability and Security, Dublin, Ireland, 25–28 August 2020; pp. 1–9. [Google Scholar]
- Dietz, M.; Englbrecht, L.; Pernul, G. Enhancing industrial control system forensics using replication-based digital twins. In Proceedings of the Advances in Digital Forensics XVII: 17th IFIP WG 11.9 International Conference, Virtual Event, 1–2 February 2021; Revised Selected Papers 17. Springer: Berlin/Heidelberg, Germany, 2021; pp. 21–38. [Google Scholar]
- Homaei, M.; Gutiérrez, O.M.; Núñez, J.C.S.; Vegas, M.A.; Lindo, A.C. A Review of Digital Twins and their Application in Cybersecurity based on Artificial Intelligence. arXiv 2023, arXiv:2311.01154. [Google Scholar] [CrossRef]
- Suhail, S.; Iqbal, M.; Hussain, R.; Jurdak, R. ENIGMA: An explainable digital twin security solution for cyber–physical systems. Comput. Ind. 2023, 151, 103961. [Google Scholar] [CrossRef]
- Allison, D.; Smith, P.; Mclaughlin, K. Digital Twin-Enhanced Incident Response for Cyber-Physical Systems. In Proceedings of the 18th International Conference on Availability, Reliability and Security, Benevento, Italy, 29 July–1 August 2023; pp. 1–10. [Google Scholar]
- Empl, P.; Schlette, D.; Zupfer, D.; Pernul, G. SOAR4IoT: Securing IoT Assets with Digital Twins. In Proceedings of the 17th International Conference on Availability, Reliability and Security, Vienna, Austria, 23–26 August 2022; pp. 1–10. [Google Scholar]
- Coppolino, L.; Nardone, R.; Petruolo, A.; Romano, L.; Souvent, A. Exploiting digital twin technology for cybersecurity monitoring in smart grids. In Proceedings of the 18th International Conference on Availability, Reliability and Security, Benevento, Italy, 29 July–1 August 2023; pp. 1–10. [Google Scholar]
- François, M. GraphETL: Construction d’une plateforme versatile pour la modélisation du risque cyber. In Proceedings of the INFormatique des ORganisations et Systèmes d’Information et de Décision (INFORSID)—Forum JCJC, 42e édition, Nancy, France, 28–31 May 2024; pp. 105–120. [Google Scholar]
- François, M.; Arduin, P.E.; Merad, M. Artificial Intelligence & Cybersecurity: A Preliminary Study of Automated Pentesting with Offensive Artificial Intelligence. In Proceedings of the International Conference on Information and Knowledge Systems; Springer: Berlin/Heidelberg, Germany, 2021; pp. 131–138. [Google Scholar]
- François, M.; Arduin, P.E.; Merad, M. Classification of Decision Support Systems for Cybersecurity. In Proceedings of the 15th Mediterranean Conference on Information Systems (MCIS) and the 6th Middle East & North Africa Conference on digital Information Systems (MENACIS), Madrid, Spain, 6–9 September 2023. [Google Scholar]
- Jacobs, J.; Romanosky, S.; Suciu, O.; Edwards, B.; Sarabi, A. Enhancing Vulnerability Prioritization: Data-driven Exploit Predictions with Community-driven Insights. In Proceedings of the 2023 IEEE European Symposium on Security and Privacy Workshops (EuroS&PW), Delft, The Netherlands, 3–7 July 2023; pp. 194–206. [Google Scholar]
- FIRST. Common Vulnerability Scoring System. Available online: https://www.first.org/ (accessed on 7 April 2025).
- Jacobs, J.; Romanosky, S.; Edwards, B.; Adjerid, I.; Roytman, M. Exploit prediction scoring system (epss). Digit. Threat. Res. Pract. 2021, 2, 1–17. [Google Scholar] [CrossRef]
- Allodi, L.; Massacci, F. A preliminary analysis of vulnerability scores for attacks in wild: The ekits and sym datasets. In Proceedings of the 2012 ACM Workshop on Building Analysis Datasets and Gathering Experience Returns for Security, Raleigh, NC, USA, 15 October 2012; pp. 17–24. [Google Scholar]
- Allodi, L.; Massacci, F. Comparing vulnerability severity and exploits using case-control studies. ACM Trans. Inf. Syst. Secur. (TISSEC) 2014, 17, 1–20. [Google Scholar] [CrossRef]
- Younis, A.A.; Malaiya, Y.K. Comparing and evaluating CVSS base metrics and microsoft rating system. In Proceedings of the 2015 IEEE International Conference on Software Quality, Reliability and Security, Vancouver, BC, Canada, 3–5 August 2015; pp. 252–261. [Google Scholar]
- Suciu, O.; Nelson, C.; Lyu, Z.; Bao, T.; Dumitraș, T. Expected exploitability: Predicting the development of functional vulnerability exploits. In Proceedings of the 31st USENIX Security Symposium (USENIX Security 22), Boston, MA, USA, 10–12 August 2022; pp. 377–394. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA; Boston, MA, USA, 2016. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- François, M.; Arduin, P.; Merad, M. Latent States: Model Based Machine Learning Perspectives on Cyber Resilience. In Proceedings of the IEEE 4th Intelligent Cybersecurity Conference (ICSC), Valencia, Spain, 17–20 September 2024. [Google Scholar]
- Rahman, M.R.; Mahdavi-Hezaveh, R.; Williams, L. A literature review on mining cyberthreat intelligence from unstructured texts. In Proceedings of the 2020 International Conference on Data Mining Workshops (ICDMW), Virtual, 17–20 November 2020; pp. 516–525. [Google Scholar]
- Takko, T.; Bhattacharya, K.; Lehto, M.; Jalasvirta, P.; Cederberg, A.; Kaski, K. Knowledge mining of unstructured information: Application to cyber domain. Sci. Rep. 2023, 13, 1714. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Reddi, V.J. Deep reinforcement learning for cyber security. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3779–3795. [Google Scholar] [CrossRef] [PubMed]
- Skopik, F.; Settanni, G.; Fiedler, R. A problem shared is a problem halved: A survey on the dimensions of collective cyber defense through security information sharing. Comput. Secur. 2016, 60, 154–176. [Google Scholar] [CrossRef]
- Sedenberg, E.M.; Dempsey, J.X. Cybersecurity information sharing governance structures: An ecosystem of diversity, trust, and tradeoffs. arXiv 2018, arXiv:1805.12266. [Google Scholar]
- Pala, A.; Zhuang, J. Information sharing in cybersecurity: A review. Decis. Anal. 2019, 16, 172–196. [Google Scholar] [CrossRef]
- Nolan, A. Cybersecurity and Information Sharing: Legal Challenges and Solutions; Congressional Research Service: Washington, DC, USA, 2015; Volume 5. [Google Scholar]
- Murdoch, S.; Leaver, N. Anonymity vs. trust in cyber-security collaboration. In Proceedings of the 2nd ACM Workshop on Information Sharing and Collaborative Security, Denver, CO, USA, 12 October 2015; pp. 27–29. [Google Scholar]
- Dandurand, L.; Serrano, O.S. Towards improved cyber security information sharing. In Proceedings of the 2013 5th International Conference on Cyber Conflict (CYCON 2013), Talinn, Estonia, 4–7 June 2013; pp. 1–16. [Google Scholar]
- Specter Ops BloodHound. 2024. Available online: https://bloodhound.readthedocs.io/en/latest/ (accessed on 7 April 2025).
- The MITRE Corporation. CALDERA AEP. 2020. Available online: https://caldera.mitre.org (accessed on 7 April 2025).
- MITRE. Caldera Profile for Identity Snowball Attacks. 2025. Available online: https://github.com/mitre/stockpile/blob/master/data/adversaries/1bac97ca-77fc-4c9a-835e-4de1b1b7f639.yml (accessed on 7 April 2025).
- Goel, D.; Neumann, A.; Neumann, F.; Nguyen, H.; Guo, M. Evolving Reinforcement Learning Environment to Minimize Learner’s Achievable Reward: An Application on Hardening Active Directory Systems. In Proceedings of the Genetic and Evolutionary Computation Conference, Melbourne, Australia, 15–19 July 2023; pp. 1348–1356. [Google Scholar]
- Goel, D.; Moore, K.; Guo, M.; Wang, D.; Kim, M.; Camtepe, S. Optimizing Cyber Defense in Dynamic Active Directories through Reinforcement Learning. In Proceedings of the European Symposium on Research in Computer Security; Springer: Berlin/Heidelberg, Germany, 2024; pp. 332–352. [Google Scholar]
- Microsoft. Microsoft Active Directory—ADDS Glossary. Available online: https://learn.microsoft.com/en-us/windows-server/identity/ad-ds/plan/appendix-a--reviewing-key-ad-ds-terms (accessed on 7 April 2025).
- MITRE. ATT&CK S0521—Bloodhound. Available online: http://attack.mitre.org (accessed on 7 April 2025).
- MITRE. T1021—Remote Services. 2025. Available online: http://attack.mitre.org (accessed on 7 April 2025).
- MITRE. T1210—Exploitation of Remote Services. 2025. Available online: http://attack.mitre.org (accessed on 7 April 2025).
- MITRE. TA006—Credential Access. 2025. Available online: http://attack.mitre.org (accessed on 7 April 2025).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Hogan, A.; Blomqvist, E.; Cochez, M.; d’Amato, C.; Melo, G.D.; Gutierrez, C.; Kirrane, S.; Gayo, J.E.L.; Navigli, R.; Neumaier, S.; et al. Knowledge graphs. ACM Comput. Surv. (Csur) 2021, 54, 1–37. [Google Scholar] [CrossRef]
- Agrawal, G.; Pal, K.; Deng, Y.; Liu, H.; Baral, C. AISecKG: Knowledge Graph Dataset for Cybersecurity Education. In Proceedings of the AAAI-MAKE 2023: Challenges Requiring the Combination of Machine Learning 2023, San Francisco, CA, USA, 27–29 March 2023. [Google Scholar]
- Hong, W.; Yin, J.; You, M.; Wang, H.; Cao, J.; Li, J.; Liu, M.; Man, C. A graph empowered insider threat detection framework based on daily activities. ISA Trans. 2023, 141, 84–92. [Google Scholar] [CrossRef]
- Dasgupta, S.; Piplai, A.; Ranade, P.; Joshi, A. Cybersecurity Knowledge Graph Improvement with Graph Neural Networks. In Proceedings of the 2021 IEEE International Conference on Big Data (Big Data), Virtual, 15–18 December 2021; pp. 3290–3297. [Google Scholar]
- Li, H.; Shi, Z.; Pan, C.; Zhao, D.; Sun, N. Cybersecurity knowledge graphs construction and quality assessment. Complex Intell. Syst. 2023, 10, 1201–1217. [Google Scholar] [CrossRef]
- Salva, S.; Regainia, L. A catalogue associating security patterns and attack steps to design secure applications. J. Comput. Secur. 2019, 27, 49–74. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics informed deep learning (Part I): Data-driven solutions of nonlinear partial differential equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Rad, M.T.; Viardin, A.; Schmitz, G.; Apel, M. Theory-training deep neural networks for an alloy solidification benchmark problem. Comput. Mater. Sci. 2020, 180, 109687. [Google Scholar]
- Shlezinger, N.; Whang, J.; Eldar, Y.; Dimakis, A. Model-based deep learning. Proc. IEEE 2023, 111, 465–499. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Monti, F.; Boscaini, D.; Masci, J.; Rodola, E.; Svoboda, J.; Bronstein, M.M. Geometric deep learning on graphs and manifolds using mixture model cnns. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5115–5124. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive Representation Learning on Large Graphs. arXiv 2017, arXiv:1706.02216. [Google Scholar]
- Youden, W. Statistical Techniques. In NBS Special Publication; NIST: Gaithersburg, MD, USA, 1969; p. 421. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Wu, C.W. Algebraic connectivity of directed graphs. Linear Multilinear Algebra 2005, 53, 203–223. [Google Scholar] [CrossRef]
- Purple, N. Spectral Graph Theory 2019. Available online: http://math.uchicago.edu/~may/REU2019/REUPapers/Purple.pdf (accessed on 7 April 2025).
- McClell, J.L.; Rumelhart, D.E.; PDP Research Group. Parallel Distributed Processing, Volume 2: Explorations in the Microstructure of Cognition: Psychological and Biological Models; MIT Press: Cambridge, MA, USA, 1987; Volume 2. [Google Scholar]
- Liashchynskyi, P.; Liashchynskyi, P. Grid search, random search, genetic algorithm: A big comparison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4768–4777. [Google Scholar]
- MITRE. CAPEC-Common Attack Pattern Enumeration and Classification (CAPEC). Technical Report. 2020. Available online: https://capec.mitre.org (accessed on 5 May 2020).
- Breiman, L. Statistical modeling: The two cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Calders, T.; Jaroszewicz, S. Efficient AUC optimization for classification. In Proceedings of the European Conference on Principles of Data Mining and Knowledge Discovery; Springer: Berlin/Heidelberg, Germany, 2007; pp. 42–53. [Google Scholar]
- Hart, S. Shapley value. In Game Theory; Springer: Berlin/Heidelberg, Germany, 1989; pp. 210–216. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).