Abstract
Proper climatic conditions in greenhouses are one of the major parameters to ensure optimum crop development. The installation of heating and cooling systems are the common solution to form a proper microclimate inside the greenhouse. However, the operation of these systems is accompanied by energy consumption. Therefore, many methods and alternative systems are sought to encounter this issue. A system which has been examined as an alternative solution for full or partial cover of a greenhouse is the Earth to Air Heat Exchanger (EAHE). Up to now, many research works have concentrated on the investigation and operation of such systems. In this study, a method to enhance the efficiency of the EAHE is examined based on the simultaneous flow of water (Water assisted earth to air heat exchanger—WAEAHE) following the concept of a double pipe heat exchanger which has been widely used in other applications. Furthermore, the improvement of the systems’ efficiency is investigated via the application of fins on the internal pipe of the heat exchanger. For the purpose of the study, different case studies have been investigated in order to reach safe results conserving the parameters affecting its efficiency. The results of the theoretical analysis have shown that the application of an internal water pipe can increase the system’s efficiency sufficiently, while it is further increased with the application of fins. In fact, the application of fins can lead to an increase of the overall heat transfer coefficients varying from 36–68%. In the current study, only the energy efficiency of the system was estimated. This system needs to be further investigated to be technically and financially efficient and applicable in actual case studies.
1. Introduction
Greenhouses are meeting an ongoing development in the last 30 years. The main advantage of greenhouses is the fact that the proper conditions for crop development can succeed inside the structure with the application of artificial equipment. One of the most important parameters for retaining the proper conditions inside the greenhouse is temperature. The proper temperature level inside a greenhouse structure is maintained using heating systems during the colder periods and with cooling systems during the warmer periods. One common option is the use of heating and cooling systems that are operating with conventional energy sources. However, the operation of such systems is combined with energy consumption, operational costs, and environmental issues. Therefore, alternative options for supporting these operations are sought and applied to make greenhouse crop development more sustainable.
Greenhouse cooling systems are used mostly in regions where the temperature is relatively high during the day and can create issues for the crop. The systems that are widely used to confront high temperatures are the fan and pad system (FPS) and the fog system (FS) [1]. The FPS is simple to operate and provides a sufficient drop of temperature inside the structure. On the other hand, it has some disadvantages, such as high cost of installation and lack of conditions’ uniformity inside the structure [2]. The FS can also provide sufficient cooling in a greenhouse [1]. In general, this system succeeds in giving better uniformity of temperature and relative humidity inside the greenhouse, compared to the FPS. However, the temperature drop inside the greenhouse is not as high as the one achieved by the FPS and the technical issues that might arise are more frequent [3]. Both systems are accompanied with energy and water consumption. Passive systems are also used to enhance the cooling capacity of the greenhouse. Some of the most important methods are the installation of shading nets, thermal screens, and special plastic materials with UV block, the painting of the covering materials with a white color, etc. [4,5]. All these methods contribute to retaining the temperature in proper levels inside the greenhouse, by blocking the incoming solar radiation. Passive systems operate usually as adjuvant systems to the dynamic cooling systems already described.
A system already studied and applied in greenhouses is the Earth to Air Heat Exchanger System (EAHES). The EAHES utilizes the fact that the ground has constant temperature in depths between 2.0–6.0 m. The temperature level depends on the average temperature of the region and the soil composition. The system consists of a tube or tubes which are buried in the ground [6] to the depth level where the temperature is constant and usually higher compared to the average winter temperature [6] and lower compared to the average summer temperature [7]. Air is forced to move inside the tube with the assistance of a fan. The energy consumption of the system is relatively low, as the only energy consumed is for the operation of the fan. Since the system combines the use of electricity and the energy stored in the ground it can be considered as a hybrid system. The tube has the proper size to extract heat from the ground during the colder periods or to transfer heat to the ground during the warmer months. Many studies have been conducted concerning the cooling capacity and efficiency of EAHES for greenhouse cooling. The annual performance of an EAHES has been experimentally studied in India for covering the cooling needs of a small greenhouse [8]. The EAHES was supporting a 34.32 m2 greenhouse in the region of Delhi India. The EAHES consisted of a PVC pipe (39 m length, 0.06 m diameter), which was placed in a certain pattern for maximum heat interaction with the ground. The air was circulating through the tube network via a blower (335 W/150 kg/h). The results showed that for summer operation, the temperature drop obtained using the system was up to 4 °C, while the cooling potential of the system was about 5 kWh [8]. In an experimental study in Thailand [7], an earth to air heat exchanger was installed in 1 m depth of the ground surface (38.5 m length). The air was distributed inside the greenhouse via a centrifugal blower (216 kg/h). It was observed that during the afternoon hours of the warm period, the system could lead to a temperature drop of between 1–7 °C [7]. In a study conducted in Turkey in 2011 [9], the overall thermal coefficient of the earth tube buried in the ground was experimentally evaluated. The EAHES which was examined was supposed to be used for greenhouse cooling. The tube diameter was about 0.56 m and it had a length of 47 m. The tube was buried at a depth of 3 m. For the air movement, a blower with 736 W power capacity and 5300 m3/h volumetric flow rate was adjusted to the pipeline. According to this work, a temperature difference of 1–5 °C between the inlets, an outlet air of the tube, could be almost achieved, and the mean thermal resistance of the tube in steady state conditions was estimated at around 0.021 K m2 W−1 [9]. In general, it has been found that the energy savings occurring using EAHES for greenhouse climatic conditions formation are around 35–40% [9]. The design of the EAHES has also been extensively studied to reach the optimum results. There are many works concentrating on tubes materials [10] or proper depth of installation and estimated optimum length via experimental systems or modeling [6,10,11,12]. In recent research works, the issue of condensation of humidity content of the air flowing in the EAHE has been investigated. It was found that water condensation inside the tube can lead to a reduction of the EAHE system efficiency [13].
The improvement of the EAHES efficiency can be achieved via variations of the tube geometry and positioning in the ground. All these design parameters have been thoroughly studied in the literature. It has been found that the use of PVC instead of concrete or carbon steel, as the tube material, is more efficient in terms of heat transfer and pressure drop which results in shorter tube length [14]. In other research works, the proper tube diameter has been investigated. Even if it has been proven that the tube diameter is strictly connected with the tube length and pressured drop [11], in most works, the diameter of a single tube EAHES varies between 0.1–0.3 m [14,15]. However, in the literature, many studies with smaller diameters can be found as energy conservation systems, mostly in warm regions where the cooling needs are more intense in all type of buildings [16]. Multiple pipe heat exchangers have also been studied as a method for confronting the issues of long tubes and pressure drop [17]. In any case, the implementation of single or multiple pipe EAHE relays on the design parameters selection, as it has been found that if a single tube EAHE is designed properly, it can present the same pressure losses and energy consumption as with a multiple pipe arrangement [18]. The depth of the EAHES installation also should be chosen considering both technical and economical parameters. The installation in depths more than 5 m can result in high installation costs and result in a less efficient result in general [14]. It occurs that there are some rough design limits that should not be exceeded in order for the EAHES to be efficient in terms of heat transfer capability, operation, and cost. Until now, most of the abovementioned parameters have been thoroughly studied and have reached a certain level of optimization. Some alternative forms of the EAHES are sought, mostly to reduce the necessary length of the tube and depth of installation. A promising idea is to utilize the water found underground towards this direction. Water can act as a mean for enhancing the cooling rate of the air as it is usually available in greenhouses (nearby drills) and has a sufficient thermal capacity [19]. The use of water for EAHE systems has already been studied with very interesting results. The adjustment of the EAHE for greenhouse heating and cooling in the irrigation channel has been proven to enhance the efficiency of the EAHE system in an experimental work where the system was purposed to operate both for heating and cooling [20]. The cooperation of an EAHE system and evaporative cooling has also been investigated via a thermal model [21]. It was found that the cooperation of the evaporative cooling system with the EAHE system can lead to a significant reduction of the EAHE length, in an experimental work [21]
Double pipe heat exchangers are a fully developed method for heat transfer between a warmer and colder fluid. The double-pipe heat exchanger (DPHE) is a very simple to operate and technically fully developed heat transfer device. It is used in many applications concerning the chemical, food, and agriculture industry worldwide [22]. In the DPHE, one fluid flows inside an inner pipe and the other fluid flows in an annular space which is surrounding the inner pipe [23]. On the other hand, the performance of a double pipe heat exchanger can be enhanced due to the application of fins. Finned tubes can increase the thermal performance of a heat exchanger depending on the shape, size, and placement of the fin. Via the presence of fins, convective heat transfer is enhanced from surfaces due to the heat transfer area increase [24]. In this work, it will be theoretically studied whether the implementation of an inner pipe where water is circulating in an EAHE system can improve the system’s efficiency. The cases that will be compared will be the simple double pipe heat exchanger and the double pipe heat exchanger with the application of fins to the inner pipe’s external surface. Drill water will be used as the cold mean circulating in the inner tube. To the authors’ best knowledge, no similar study has been performed in the past concerning the improvement of an EAHES for greenhouse cooling by these two approaches. In this work a comparative analysis including both the cases of a simple double pipe heat exchanger and a finned pipe heat exchanger adjusted in the EAHE system is presented. The proposed system is orientated for greenhouse cooling so the peculiarities of this case should be considered (temperature, air flow, etc.). The double pipe heat exchanger system is a fully developed, relatively simple, and low-cost solution for improving the heat exchange rate of an EAHES. This study can be of great interest both for producers and designers of alternative energy systems.
2. Materials and Methods
2.1. Theoretical Case Study Description
The evaluation of the described system will be performed in a case study where cooling needs are not that high. Thus, the greenhouse is assumed to be in north Greece in the region of Kozani where the greenhouse cooling needs are not sufficient, and greenhouses can operate during the summer months without the use of a very intense cooling system. In this case, systems such as the EAHE can meet a sufficient part of the cooling needs of the greenhouse. The height of the greenhouse indicates that this is not orientated for a high value crop, where usually all the systems used are fully developed conventional systems. The size of the greenhouse was also chosen to be a relatively small structural unit. If the installation of an EAHE system was examined in a large greenhouse, all the values of the parameters examined should be very high (dimensions of the pipes, equipment capacity, etc.) and maybe not in realistic levels. In Table 1, the location, climatic conditions, as well as the dimensions and technical characteristics of the greenhouse are presented. The climatic data have been taken by the European Union (EU) tool Photovoltaic Geographical Information System (PVGIS) [25] for the coordinates given in Table 1.

Table 1.
Case study region and greenhouse description.
During summer months, greenhouses require about 60 exchanges of air per hour [26]. This requirement defines the flow rate that is necessary for the incoming air, and it occurs 103,296 m3/h. However, in a system such as the WAEAHE, the air flow cannot be that much. The cooling that is provided is supplementary so it will be assumed an air flow of about 10,000 (m3/h).
In Scheme 1, the proposed system is illustrated.
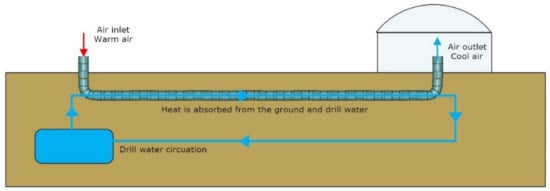
Scheme 1.
Schematic description of WAEAHE operation for greenhouse cooling.
For the needs of the study, it will be evaluated whether the operation of the system as a simple double pipe heat exchanger (C.S.1) or a double pipe heat exchanger with an internal finned pipe (C.S.2) are effective enough to provide the necessary cooling inside the structure. The two different cases are shown in Scheme 2. In Scheme 3, a more detailed schematic description of the double finned pipe heat exchanger is illustrated.
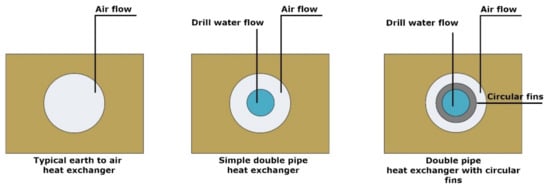
Scheme 2.
Cross sections of the options for the WAEAHE compared to the typical arrangement of an EAHE.
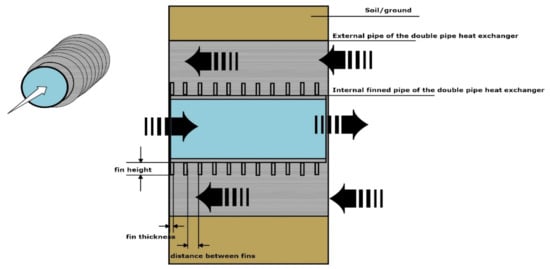
Scheme 3.
Schematic description of the finned double pipe heat exchanger.
2.2. Mathematical Model
The heat loss from the pipe to the ground can be estimated by Equation (1) as described in the literature [27]
kg: Ground thermal conductivity (W m−1K−1)
Τp: Average pipe temperature (°C)
Tg: Average ground temperature (°C)
db: Depth of buried pipe (m)
rp: radius of pipe (m)
To calculate the heat flow rate between the working fluids of the designed WAEAHE, the energy balance Equations (2) and (3) will be used. These Equations concern each fluid separately. On the other hand, the heat flow rate will be also calculated via Equation (4). These two different approaches are useful, to calculate different parameters of the heat exchange.
: Heat flow (W)
: Cold mean (water) flow rate (kg s−1)
: Warm mean (air) flow rate (kg s−1)
: Specific heat for the cold mean at average operation temperature (kJ kg−1 K−1)
: Specific heat for the cold mean at average operation temperature (kJ kg−1 K−1)
: Temperature difference for the cold mean inlet and outlet (°C)
: Temperature difference for the warm mean inlet and outlet (°C)
h: Overall heat transfer coefficient (W m−2 K−1)
A: heat transfer surface area (m2)
ΔΤlog: Logarithmic mean temperature difference (K)
The overall heat transfer coefficient h is calculated using Equation (5). This Equation describes 3 main heat exchange mechanisms. The first is the heat transfer mechanism with convention due to the internal flow. The second heat transfer mechanism is by conduction between through the internal pipe wall. The third heat transfer mechanism is by convection due to the flow through the annular cross section formed by the internal pipe and the external pipe where the air is flowing. In Equation (5), it has been assumed that Fouling factors are negligible and there are no efficiency factors for the fins.
s: Thickness of the internal pipe wall (m)
λ: Thermal conductivity of wall material (W m−1 K−1)
ai: Internal flow convection heat transfer coefficient (W m−2 K−1)
ao: External flow convection heat transfer coefficient (W m−2 K−1)
The convection heat transfer coefficients are calculated by Equation (6).
Nu: Nusselt number
λ: Thermal conductivity of fluid in average temperature (W m−1 K−1)
Lch: Characteristic length of solid element in convective heat transfer
To calculate the Nusselt number, the definition of the flow is required. In order to evaluate whether the flow is laminar or turbulent, the Reynolds number calculation is necessary as described in Equation (7)
Re: Reynolds number
u: Velocity of the fluid (m s−1)
d: Characteristic linear dimension (m)
v: Kinematic viscosity (m2/s−1)
For laminar flow, the Nusselt number is given by Equation (8), while for turbulent flow by Equation (9) in the case of pipe internal flow.
Nud: Nusselt number for pipe with characteristic diameter (d)
Pr: Prandtl number
din: Pipe internal diameter (m)
L: Pipe length (m)
Gzd refers to Graetz number which is calculated by Equation (10), while ξ is the friction coefficient calculated by Equation (11).
Gzd = 1.615 × [(Re × Pr × (di/l)](1/3)
ξ = (1.82 × log(Red) – 1.5)−2
In the case of the flow in an annular cross section, the only variation compared to the Equations (7)–(10) concerning the calculation the Reynolds and Nusselt number is the definition of the diameter. In this geometry, the hydraulic diameter di is chosen and it is given by Equation (12).
dh = do − di
dh: hydraulic diameter (m)
do: External diameter of the annular cross section (m)
di: Internal diameter of the annular cross section (m)
When fins are applied in a pipe, the convection heat transfer coefficient is affected, and the heat transfer phenomena are more intense. In the present study, the fins that will be installed on the pipe will be chosen to be of circular shape (annual fins). This type of fin is applied in many commercial applications concerning heat exchangers and has been used widely in the industry, used for air-conditioning and heat-recovery systems, as an application to enhance the heat transfer from the side of air movement [28]. The material of the fins has been chosen to be the same as the pipe (steel). Since annular fins are a very common application in heat exchanger finned tubes, technical issues such as the welding of the fins on the tube or pipe have been overwhelmed. In this case, the convective heat transfer coefficient by the side where the fins are applied is calculated by Equation (13)
: modified convection heat transfer coefficient after the application of the fins (W m−2 K−1)
δR: fin thickness (m)
δ1: fin allocation (m)
aR: adjusted convection heat transfer coefficient (W m−2 K−1)
a: initial convection heat transfer coefficient for the pipe (W m−2K−1)
The adjusted convection heat transfer coefficient depends on the value m which is defined be Equation (14):
λR: Conductivity of the of the fin (W m−1K−1)
Equations (2)–(14) are based in common methodologies for heat transfer phenomena and heat exchanger sizing and design as described in the literature [29,30,31,32].
Another issue that will be examined is the pressure drop of the air flow. The pressure drop is given by Equation (15) [33].
ΔP: Pressure drop (Pa)
f: friction factor
L: Pipe length (m)
ρ: air density (kg/m3)
u: air velocity (m/sec)
d: diameter
2.3. Assumptions and Initial Design Parameters Selection
In the present study, the length of the heat exchanger will be estimated by assuming the parameters that are presented in Table 2, based on assumptions or the literature.

Table 2.
System design assumptions.
The critical parameter to be defined by the calculation will be the WAEAHE system length. This parameter will show whether the proposed modifications are realistic and cost effective compared to the already successful EAHE system.
3. Results
3.1. Energy Balance Calculations
The first step to estimate the basic parameters of the system is the calculation of the heat that must be transferred by the warm mean (air) to colder mean (water and soil). Based on the assumptions already made, Equation (3) for air results in a necessary heat loss amount by the air to the water and soil that it is equal to 213.64 kW. Equation (1) which is related to the conduction heat transfer by the air to the ground leads to a heat loss of 30.67 W/m. That means that this heat loss amount will be evaluated when the length of the pipe will be estimated. Therefore, it will be not taken into account in the current phase of the calculation. So, it will be evaluated that the larger amount of heat loss must be absorbed by the inner water pipe. There are 2 variables that must be defined in Equation (2), mass transfer of the cold mean and outlet temperature. If counter flow is considered, since it is the most efficient, the water cannot exit the pipe at a temperature higher than 28 °C. Since temperatures of working fluids are not extremely high or low, it will be estimated that the temperature rise of water will not be higher than 6 °C, so the cases that are presented in Table 3 will be evaluated.

Table 3.
Scenarios for water outlet.
3.2. Evaporative Heat Transfer Coefficient Caclulation
The length of the heat exchanger is evaluated by Equation (4). Having already assumed the working fluids inlet and outlet temperatures, the overall heat transfer coefficient h for CS 1 and 2 and scenarios A, B, and C, will be evaluated. Equation (5) must be applied for each of the abovementioned cases. In Table 4, the physical properties of the working fluids that will be used in the methodology described are presented.

Table 4.
Physical properties of working fluids for each scenario.
For the fin pipe there will be assumed two alternative arrangements to evaluate the effect of the different allocation. In Table 5, the different fin arrangements for the inner pipe are presented.

Table 5.
Fin arrangement cases.
The Reynolds number and Nusselt number for inner and annular flow are presented in Table 6 for all case studies described above. The Re number occurred by application of Equation (7) for all the cases applying the inner diameter of the internal pipe of the DPHE. So, in this case, the application of fins is not affecting the Re number. The only parameter that is affecting the calculation of Re is the fluid velocity (water flow provided by the pump) as the viscosity is also chosen to have a specific value. Since all Re numbers that occurred lead to turbulent flow, Equation (9) is used to calculate the Nu number. Respectively, the convective heat transfer coefficient occurs by the use of Equation (6). For the calculation of ai value, the thermal conductivity of water is taken into account in the mean temperature of operation as well as the Lch, which in the case of pipes is the diameter where the flow is realized. When it comes to fins application, the methodology of Equations (13) and (14) is followed, where the fins dimensions and allocation should be taken into account, as well as the fin material. All the fin specifications that are used for this Equations are presented in Table 2 (material) and Table 5 (dimensions). For the flow realized on the annular cross section, there is only one case, as the air flow is chosen to be 10,000 m3/h. The diameter chosen is the hydraulic diameter as described in Equation (12), while the viscosity is chosen according to the mean temperature of the air flowing in the pipe and it is defined by the values given in Table 2.

Table 6.
Convective heat transfer calculations.
Based on Equation (5), the overall heat transfer coefficient can be calculated for each case and therefore, using Equation (4), the heat transfer surface for the required process. For the calculation of the length, the geometrical analysis of the pipe must be performed. The pipe is a cylinder with base diameter equal to the diameter of the inner pipe and height the length of the pipe. The heat exchange surface of the cylinder is the peripherical surface of the cylinder. If this surface is expanded, a rectangle occurs with one side equal with the perimeter of the circle that is defined by the inner pipe cross section, and the other side the length of the pipe. By dividing the known value of the surface occurred by Equation (4) to the dimension of the diameter of the circle, the pipe length occurs for each case study. So, in Table 7, both the overall heat transfer coefficient for each case as well as the required surface of the heat exchanger calculations are presented.

Table 7.
Overall heat transfer coefficient and necessary heat transfer surface.
It is observed that the application of fins has a significant contribution to heat exchange phenomena. The result is that the desirable heat exchange is realized with smaller pipe length. This leads to many advantages, in terms of reduced pressure losses, less installation cost, less available space, etc. In Scheme 4, Scheme 5 and Scheme 6, the variation of the overall heat transfer for same flow characteristics is shown. This percentage increase occurs when comparing the heat transfer coefficients for each case study as shown in Table 7 in the column with the parameter h. So, the comparison is between the values considering scenario A, scenario B, and scenario C and how the application of the fins leads to an increase of the overall heat transfer coefficient between the simple DPHE and the first arrangement of fins, and then, between the 2 different fin arrangements.
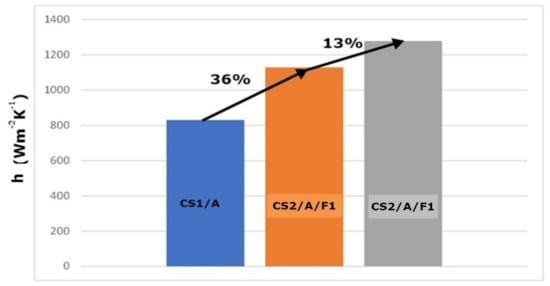
Scheme 4.
Overall heat transfer coefficient behavior after the application of 2 different fin arrangements for the case CS1/A.
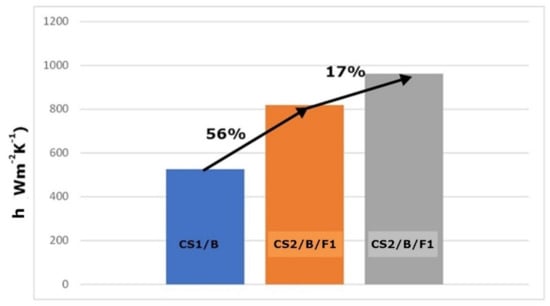
Scheme 5.
Overall heat transfer coefficient behavior after the application of 2 different fin arrangements for the case CS1/B.
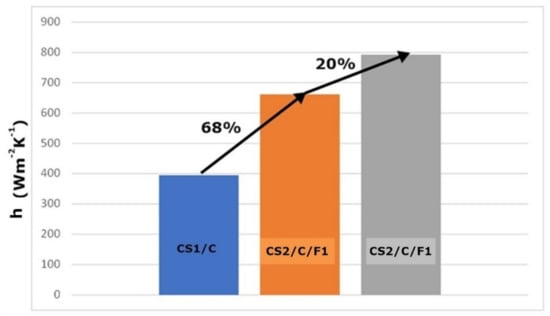
Scheme 6.
Overall heat transfer coefficient behavior after the application of 2 different fin arrangements for the case CS1/C.
As far as concerns the pressure drop observed, based on Equation (15), Table 8 occurs.

Table 8.
Pressure drop per case study and scenario.
4. Discussion
As is observed in the Scheme 4, Scheme 5 and Scheme 6, the effect of the fin’s application has a positive effect on the heat transfer coefficient in all cases examined. In the case study with the lower flow rate, the increase percentage is higher, compared to the rest cases. This can be explained since the flow characteristics have less impact on the convective heat transfer. So, any modifications on the pipes have a greater impact on the convective heat transfer coefficient of the inner flow. In addition, it is observed that the finned pipe presents a significant increase on the overall heat transfer coefficient compared to the simple pipe. The increase of the overall heat transfer coefficient is much less when the application of the fins becomes denser. So, a further denser arrangement of the fins will not lead necessarily to such positive results. In such a case, other factors should be taken into consideration if this approach is chosen (denser fins), such as cost and technical parameters (ease of manufacturing, etc.).
In Table 8, the pressure drop of the air flow is presented based on Equation (15). To define the allowable pressure drop in any heat exchanger application, the pressure of the fluid at the outlet should be defined. In the examined case, there are no special requirements for the air pressure at the outlet of the pipe. The cool air just needs to enter the greenhouse. The greenhouse should be equipped with air recirculation fans that will ensure the uniform distribution of the air inside the structure. However, the higher the pressure drop the higher the capacity of the equipment inside the greenhouse structure. So, in the cases CS1/B, CS1/C, and CS2/C/F1, where the pipe length is relatively high, the pressure drop is significant, and this should be considered when choosing the fan that will support the system. Another parameter that has not been included in the calculation but may affect the heat transfer coefficient, especially after an operation period, is the fouling factors due to the fin application. The fin arrangement creates available space between the fins for dirt deposits, rust, or other factors that may have a negative effect on the overall heat transfer coefficient. Fouling on the air side is mostly due to the dust and it may affect the heat transfer coefficient [35]. A solution toward this direction is the use of filters at the air inlet to retain a large percentage of dust and dirt prevailing in the outdoor air. Another issue that arises by the fouling factors occurring in the annular cross section is the extra pressure drop inside [36]. The issue of fouling factors is very frequent in any type of heat exchanger. In the examined WAEAHE, the critical area is between the fins. To avoid such a case, frequent cleaning of the heat exchanger is necessary. However, it should be noticed that beyond dirt and dust deposits, any other type of fouling (such as biofouling) is difficult to occur as the steel selected is stainless steel and the working mean is air. It is strongly recommended to install filters in the air inlet.
It should be noticed that the modification of materials, fin type, and arrangement can lead to a sufficient change of the heat transfer coefficient. For example, the use of aluminum or copper for fin would provide better thermal properties both to the pipe and the fins. The fins type and arrangement could also change the thermal properties of the inner pipe. In this study, the selection of materials and fin arrangement were performed based on the more realistic approach in terms of cost as the application is addressed in agricultural applications. The examined design approach leads to a significant increase of the overall heat transfer coefficient and as a result, to the reduction of the heat exchanger length. This variation may reduce the length of the pipe in a sufficient way. The reduction of the pipe length is a very important issue in such systems, mostly for technical rather than financial reasons. The first important parameter is that the necessary land for the application of the system is reduced while at the same time, the reduced pipe length leads to less pressure drop for both flows. However, there are some factors that should not be overlooked. At first, the application of this design requires additional equipment (pumps), as well as the presence of a drill, compared to the simple EAHE system. Drills are usually available near greenhouses, but the operation of the equipment is accompanied with energy consumption which in some way encounters the energy conservation by artificial cooling. On the other hand, the installation of such a system is more difficult from a technical point of view compared to a simple EAHE system. So, both cost and energy consumption parameters should be further examined to ensure the efficiency of the system in an actual application.
Comparing the system that was examined in the current theoretical study with other research works leads to some important outcomes. Previous research works are mostly experimental or model development works, which focus on smaller greenhouses to evaluate in which grade the cooling needs of the greenhouse are met with the use of the EAHE system. Other works do not include the installation of high-capacity equipment for water circulation. However, the fan capacity seems to be much higher [7,8]. This means that the gain in cooling operation that is provided by the water is replaced by a larger air flowrate. The results show that in general, the fin application and higher water flowrate can lead to a relatively small pipe length. In the examined system, the parameters that affect the efficiency are relying in a large percentage on the water temperature and flowrate. That means that the parameters discussed in previous works concerning the depth of installation, or pipe diameter, are still important but not dominant.
5. Conclusions
In this theoretical study, the possibility of enhancing the efficiency of the already successful idea of an EAHE system, with the integration of the DPHE system, was examined. The inner pipe application in the EAHE system can positively contribute to the further cooling of the air that is flowing in the EAHE system. The results of the study showed that the application of a finned pipe inside the EAHE can lead to a significant increase of the overall heat transfer coefficient compared to the DPHE. The fins arrangement should be carefully designed to succeed with the best possible result. Three scenarios have been examined, as far as it concerns the water flow in the inner pipe. As shown by the results, the highest the water flow, the more efficient the heat exchange between the annular space and the inner pipe. That leads to a more realistic WAEAHE length but there are some considerations using such a system. The high flow rate, though, is accompanied with higher energy consumption. In addition, the fouling factors that can be potentially formed, as well as the pressure drop, need to be further examined. So, there are still some design parameters that must be considered in order for the system to be applied, such as the installation and operation cost, due to the additional equipment required for its operation. Based on the energy analysis performed in the current work, it seems that the WAEAHE system can have a positive effect on the cooling of greenhouses.
Author Contributions
Conceptualization, V.K.F. and S.D.K.; methodology, V.K.F. and A.G.M.; writing—original draft preparation, V.K.F., V.P.F.; writing—review and editing, A.G.M., T.A.K.; visualization, V.K.F., S.D.K.; supervision, V.K.F., T.A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare conflict of interest.
Nomenclature
| A | heat transfer surface area (m2) |
| a | initial convection heat transfer coefficient for the pipe (W m−2 K−1) |
| ai | internal flow convection heat transfer coefficient (W m−2 K−1) |
| an | convection heat transfer coefficient (W m−2 K−1) |
| ao | external flow convection heat transfer coefficient (W m−2 K−1) |
| aR | adjusted convection heat transfer coefficient (W m−2 K−1) |
| modified convection heat transfer coefficient after the application of the fins (Wm−2 K−1) | |
| specific heat for the cold mean at average operation temperature (kJ kg−1 K−1) | |
| specific heat for the cold mean at average operation temperature (kJ kg−1 K−1) | |
| d | diameter (m) |
| db | depth of buried pipe (m) |
| dch | characteristic linear dimension (m) |
| dh | hydraulic diameter (m) |
| di | internal diameter of the annular cross section (m) |
| din | pipe internal diameter (m) |
| do | external diameter of the annular cross section (m) |
| f | friction factor |
| Gzd | Graetz number |
| h | overall heat transfer coefficient (W m−2 K−1) |
| kg | ground thermal conductivity (W m−1 K−1) |
| L | pipe length (m) |
| Lch | characteristic length of solid element in convective heat transfer |
| cold mean (water) flow rate (kg s−1) | |
| warm mean (air) flow rate (kg s−1) | |
| m | fin adjustment value |
| Nu | Nusselt number |
| Nud | Nusselt number for pipe with characteristic diameter d |
| Pr | Prandtl number |
| heat flow (W) | |
| Qg | heat loss to the ground (W) |
| rp | radius of pipe (m) |
| Re | Reynolds number |
| s | thickness of the internal pipe wall (m) |
| Τp | average pipe temperature (°C) |
| Tg | average ground temperature (°C) |
| u | velocity (m/s) |
| v | kinematic viscosity (m2/s−1) |
| ΔP | pressure drop (Pa) |
| temperature difference for the cold mean inlet and outlet (°C) | |
| temperature difference for the warm mean inlet and outlet (°C) | |
| ΔΤlog | logarithmic mean temperature difference (K) |
| δR | fin thickness (m) |
| δ1 | fin allocation (m) |
| η | dynamic viscosity (kg m−1 s−1) |
| λ | thermal conductivity (W m−1 K−1) |
| ξ | friction coefficient |
| ρ | air density (kg/m3) |
References
- Bucklin, R.A.; Henley, R.W.; McConnell, D.B. Fan and Pad Greenhouse Evaporative Cooling Systems—CIR1135; Department of Agricultural and Biological Engineering, University of Florida/Institute of Food and Agricultural Sciences Extension: Gainesville, FL, USA, 1993. [Google Scholar]
- Sapounas, A.A.; Nikita-Martzopoulou, C.H.; Bartzanas, T.; Kittas, C. Fan and Pad Evaporative Cooling System for Greenhouses: Evaluation of a Numerical and Analytical Model. Acta Hortic. 2008, 797, 131–137. [Google Scholar] [CrossRef] [Green Version]
- Öztürk, H.H. Evaporative Cooling Efficiency of a Fogging System for Greenhouses. Turk. J. Agric. For. 2003, 27, 49–57. [Google Scholar]
- Teitel, M.; Gahali, Y.; Barak, M.; Lemcoff, H.; Antler, A.; Wenger, E.; Amir, R.; Gantz, S.; Harhel, D. The effect of shading nets on greenhouse microclimate. Acta Hortic. 2012, 952, 731–738. [Google Scholar] [CrossRef]
- Abdel-Ghany, A.M.; Al-Helal, I.M.; Alzahrani, S.M.; Alsadon, A.A.; Ali, I.M.; Elleithy, R.M. Covering materials incorporating radiation-preventing techniques to meet greenhouse cooling challenges in arid regions: A review. Sci. World J. 2012, 2012, 906360. [Google Scholar] [CrossRef] [PubMed]
- Bojic, M.; Trifunovic, N.; Papadakis, G.; Kyritsis, S. Numerical simulation, technical and economic evaluation of air-to-earth heat exchanger coupled to a building. Energy 1997, 22, 1151–1158. [Google Scholar] [CrossRef]
- Mongkon, S.; Thepa, S.; Namprakai, P.; Pratinthong, N. Cooling performance and condensation evaluation of horizontal earth tube system for the tropical greenhouse. Energy Build. 2013, 66, 104–111. [Google Scholar] [CrossRef]
- Tiwari, G.N.; Akhtar, M.A.; Shukla, A.; Khan, M.E. Annual thermal performance of greenhouse with an earth–air heat exchanger: An experimental validation. Renew. Energy 2006, 31, 2432–2446. [Google Scholar] [CrossRef]
- Ozgener, O.; Ozgener, L.; Goswami, D.Y. Experimental prediction of total thermal resistance of a closed loop EAHE for greenhouse cooling system. Int. Commun. Heat Mass Transf. 2011, 38, 711–716. [Google Scholar] [CrossRef]
- Sakhri, N.; Menni, Y.; Ameur, H. Effect of the pipe material and burying depth on the thermal efficiency of earth-to-air heat exchangers. Case Stud. Chem. Environ. Eng. 2020, 2, 100013. [Google Scholar] [CrossRef]
- Bisoniya, T.S. Design of earth–air heat exchanger system. Geotherm. Energy 2015, 3, 1–10. [Google Scholar]
- Zhang, C.; Wang, J.; Li, L.; Wang, F.; Gang, W. Utilization of Earth-to-Air Heat Exchanger to Pre-Cool/Heat Ventilation Air and Its Annual Energy Performance Evaluation: A Case Study. Sustainability 2020, 12, 8330. [Google Scholar] [CrossRef]
- Qi, D.; Zhao, C.; Li, S.; Chen, R.; Li, A. Numerical Assessment of Earth to Air Heat Exchanger with Variable Humidity Conditions in Greenhouses. Energies 2021, 14, 1368. [Google Scholar] [CrossRef]
- Muehleisen, R.T. Simple design tools for earth-air heat exchangers. In Proceedings of the Fifth National Conference of IBPSA-USA, SimBuild, Madison, WI, USA, 1–3 August 2012. [Google Scholar]
- Vakakis, F.; Nikita-Martzopoulou, C. Technologies description and evaluation in terms of development. In Techno Economical Estimatition of Available Passive Solar and Hybrid Technologies for Livestock Building Heating and Cooling; Center of Renewable Energy Sources and Saving: Athens, Greece, 1991. [Google Scholar]
- Pakari, A.; Ghani, S. Energy Savings Resulting from Using a Near-Surface Earth-to-Air Heat Exchanger for Precooling in Hot Desert Climates. Energies 2021, 14, 8044. [Google Scholar] [CrossRef]
- Amanowicz, Ł.; Wojtkowiak, J. Thermal performance of multi-pipe earth-to-air heat exchangers considering the non-uniform distribution of air between parallel pipes. Geothermics 2020, 88, 101896. [Google Scholar] [CrossRef]
- Amanowicz, Ł.; Wojtkowiak, J. Comparison of Single and Multipipe Earth-to-Air Heat Exchangers in Terms of Energy Gains and Electricity Consumption: A Case Study for the Temperate Climate of Central Europe. Energies 2021, 14, 8217. [Google Scholar] [CrossRef]
- Jakhar, S.; Soni, M.S.; Gakkhar, N. Performance Analysis of Earth Water Heat Exchanger for Concentrating Photovoltaic Cooling. Energy Procedia 2016, 90, 145–153. [Google Scholar] [CrossRef]
- Yang, L.-H.; Huang, B.-H.; Hsu, C.-Y.; Chen, S.-L. Performance analysis of an earth–air heat exchanger integrated into an agricultural irrigation system for a greenhouse environmental temperature-control system. Energy Build. 2019, 202, 109381. [Google Scholar] [CrossRef]
- Bansal, V.; Mathur, J. Performance enhancement of earth air tunnel heat exchanger using evaporative cooling. Int. J. Low-Carbon Technol. 2009, 4, 150–158. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Lee, K.-S.; Li, B. Optimal design of a double pipe heat exchanger based on the outward helically corrugated tube. Int. J. Heat Mass Transf. 2019, 135, 706–716. [Google Scholar] [CrossRef]
- Mehrabian, M.A.; Mansouri, S.H.; Sheikhzadeh, G.A. The overall heat transfer characteristics of a double pipe heat exchanger: Comparison of experimental data with predictions of standard correlations. Int. J. Eng. Trans. B Appl. 2002, 15, 395–406. [Google Scholar]
- Mokheimer, E.M. Heat transfer from extended surfaces subject to variable heat transfer coefficient. Heat Mass Transf. 2003, 39, 131–138. [Google Scholar] [CrossRef]
- European Commission. Photovoltaic Geographical Information System (PVGIS), EU Science Hub-The European Commission’s Science and Knowledge Service. Available online: https://ec.europa.eu/jrc/en/pvgis (accessed on 10 October 2021).
- Watson, A.; Gómez, C.; Buffington, D.E.; Bucklin, R.A.; Henley, R.W.; McConnell, D.B. Greenhouse Ventilation, AE-10; Department of Agricultural and Biological Engineering, University of Florida/Institute of Food and Agricultural Sciences Extension: Gainesville, FL, USA, 1987. [Google Scholar]
- Kusuda, T. Heat Transfer Analysis of Underground Heat and Chilled-Water Distribution Systems; Department of Commerce/National Bureau of Standards/National Engineering Laboratory/Center for Building Technology: Washington, DC, USA, 1981.
- Nemati, H.; Moghimi, M.A.; Sapin, P.; Markides, C. Shape optimisation of air-cooled finned-tube heat exchangers. Int. J. Therm. Sci. 2020, 150, 106233. [Google Scholar] [CrossRef]
- Paspalas, K.G. Heat Exchanges; Tziolas Publications: Thessaloniki, Greece, 2014. [Google Scholar]
- Shah, R.K.; Sekulic, D.P. Fundamentals of Heat Exchanger Design; John Wiley & Sons, Inc. Publications: Hoboken, NJ, USA, 2003. [Google Scholar]
- Mousiopoulos, N.S. Introduction to Heat Transfer, 2nd ed.; Giahoudi Publications: Thessaloniki, Greece, 2006. [Google Scholar]
- Lienhard, J.H., IV; Lienhard, J.H., V. A Heat Transfer Textbook, 5th ed.; Dover Publications: Mineola, NY, USA, 2019; ISBN 978-0-48683-735-2. [Google Scholar]
- Lee, H.J.; Ryu, J.; Lee, S.H. Influence of Perforated Fin on Flow Characteristics and Thermal Performance in Spiral Finned-Tube Heat Exchanger. Energies 2019, 12, 556. [Google Scholar] [CrossRef] [Green Version]
- Carvill, J. Chapter 3: Thermodynamics and heat transfer. In Mechanical Engineer’s Data Handbook; Elsevier: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Sarfraz, O.; Bach, C. A Literature Review on Heat Exchanger Air Side Fouling in Heating, Ventilation and Air conditioning (HVAC) Applications. In Proceedings of the International Refrigeration and Air Conditioning Conference, Purdue, IN, USA, 11 –14 July 2016; Available online: http://docs.lib.purdue.edu/iracc/1663 (accessed on 10 October 2021).
- Nel, H.J.; Lombaard, I.; Liebenberg, L.; Meyer, J.P. Fouling of an air-cooled heat exchanger, and alternative design approach. In Proceedings of the 14th IAHR Cooling Tower and Air-Cooled Heat Exchanger Conference, Stellenbosch, South Africa, 1–3 December 2009. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).