An Improved Variable Step-Size Normalized Subband Adaptive Filtering Algorithm for Signal Clipping Distortion

Abstract

The safe and stable operation of power systems and other dynamic systems relies on accurate perception of their dynamic processes. Voltage, current, and other measurement signals carry critical information about the system’s state. However, under conditions such as equipment damage, aging, and non-ideal operational conditions of devices under test, over-range phenomena may occur, leading to biased estimation issues in adaptive filters. To address this problem, this paper proposes a variable-parameter subband adaptive filtering algorithm with signal clipping distortion awareness. The algorithm first uses the Expectation-Maximization (EM) process to achieve high-fidelity restoration of damaged signals. Then, by integrating an intelligent steady-state detector and a dual-mode control mechanism, the adaptive filter can adjust key parameters such as step-size, forgetting factor, and regularization parameter based on state perception results. Finally, theoretical analysis proves the unbiased nature of the proposed method. Validation using real-world data from a high-penetration renewable energy power system shows that the algorithm achieves fast tracking during transient events and provides high-precision estimation during steady-state operation, offering an effective solution for real-time, high-accuracy processing of dynamic measurement data in power systems.

1. Introduction

The core goal of adaptive filtering theory is to build an intelligent processor that can automatically adjust parameters to track the dynamics of time-varying systems [1,2]. The theoretical foundation traces back to the least mean square (LMS) algorithm proposed by Widrow and Hoff, which constructs linear weights to track the linear relationship between input and output, offering computational simplicity and ease of implementation [3]. It has become a cornerstone in the field of linear adaptive filtering. The theoretical framework of linear filters, including stability, convergence, and steady-state performance analysis, has been well developed [4,5]. Later, to improve convergence speed, the Recursive Least Squares (RLS) algorithm was introduced [6], which, although increasing computational complexity by introducing the inverse of the data matrix, achieves fast convergence. Compared to nonlinear adaptive filters based on the Volterra series and those incorporating deep learning models, nonlinear filters, while capable of handling a broader range of nonlinear systems, often come with high computational load, local minima risks, and difficulties in theoretical analysis [7,8]. Therefore, in scenarios requiring high real-time performance and limited computational resources, linear filters, with their reliable theoretical foundation and excellent practicality, remain the preferred solution for system identification and other tasks.

Although linear adaptive filtering algorithms perform excellently under ideal conditions, their theoretical superiority heavily depends on a key assumption: the observation data is complete and unaltered [9]. However, this assumption is often violated in large-scale distributed sensing systems such as the Internet of Things (IoT) and wireless sensor networks. Sensor nodes may suffer from clipping, where the observed signal exceeds the measurement range due to limitations in physical range, hardware failures, or communication errors [10]. This nonlinear measurement distortion breaks the inherent linear relationship between the expected signal and the filter output, directly causing the adaptive update rule based on the least mean square error criterion to produce biases [11,12]. This bias, introduced by data loss mechanisms, is fundamentally different from the issues caused by step size or signal correlation [13,14]. Ignoring this bias will cause any advanced step-size optimization strategy to fail, leading to severe performance degradation or even divergence. In response to the challenge of “clipped data,” adaptive filtering research is undergoing a paradigm shift from “ideal data models” to “non-ideal measurement robust models.” Early research attempts to model clipping as a special nonlinear case [15,16]. For instance, based on the Tobit model, the conditional expectation of clipped expected signals was used for unbiased estimation, leading to the clipped regression NSAF (CR-NSAF). This method provides statistical support for clipping compensation. However, existing methods mostly focus on handling one-way clipping, and there is insufficient research on multi-type asymmetric clipping scenarios.

Additionally, classical linear adaptive filtering [17] algorithms face an inherent contradiction due to fixed step sizes: in LMS and its derivatives, the step size is usually fixed, leading to an irreconcilable trade-off between convergence speed and steady-state error [18]. A large step size enables fast convergence but induces large steady-state fluctuations near the optimal solution, while a small step size achieves high steady-state accuracy but results in slow convergence [19]. This contradiction is especially prominent when dealing with non-stationary signals. To overcome the limitations of fixed step sizes, Variable Step Size (VSS) technology emerged as an important optimization direction for adaptive filtering algorithms [20]. The core idea of VSS is to make the step size a function dynamically adjusted according to the algorithm’s operational state. The general principle is to use a large step size during the initial convergence stage or when the system undergoes sudden changes [21,22], and automatically reduce the step size as the algorithm approaches the steady-state to fine-tune the solution, thereby reducing steady-state error [23]. Common VSS strategies generally associate the step size with some statistical measure of the error signal (such as error power or correlation function). VSS concepts can be incorporated into various linear adaptive filter algorithms, resulting in improved algorithms like VSS-LMS and VSS-NLMS, significantly improving the performance of traditional algorithms in non-stationary environments.

After addressing the step-size adaptability issue, another key challenge for linear adaptive filters is that the convergence speed can be significantly reduced due to gradient noise amplification when the input signal is highly correlated colored noise. To overcome this bottleneck, Subband Adaptive Filtering (SAF) was introduced. The innovation of SAF lies in its use of multi-rate signal processing theory, where the filter bank decomposes the input and desired signals into multiple subbands [24]. This effectively reduces the autocorrelation within each subband, while maintaining a low computational complexity through down-sampling [25]. Within the SAF framework, Normalized Subband Adaptive Filtering (NSAF) further optimizes the step-size selection strategy by normalizing the power of each subband. Naturally, this paper combines the VSS concept with NSAF forms the Variable Step Size NSAF (VSS-NSAF) algorithm, which inherits the advantages of NSAF in handling colored signals while further optimizing transient and steady-state performance through the step-size adaptation mechanism, representing an important advancement in handling complex signals.

Given this, this paper aims to develop a more universal robust adaptive filtering framework to address the bidirectional asymmetric signal clipping problem in complex environments. The main contributions of this paper are:

1.

To address the performance degradation of adaptive filters caused by signal clipping in measurement systems, this paper proposes a Variable Step-Size Normalized Subband Adaptive Filter (VSS-NSAF) algorithm tailored for clipping distortion. The algorithm is capable of accurately tracking signals across a broad range of clipping severities. Furthermore, we provide a theoretical proof that the proposed method achieves strictly unbiased recovery of clipped signals.

2.

The algorithm integrates the NSAF framework with a variable step-size adaptation mechanism. By utilizing the subband decomposition structure and enabling dynamic adjustment of the step size, it effectively manages the tracking and optimization of nonlinear signals under severe clipping conditions, resulting in significantly faster convergence under steady-state error constraints.

3.

Through simulations based on actual power system cases, verifying that the proposed algorithm outperforms existing algorithms in convergence speed, steady-state accuracy, and robustness in multi-type heavy clipping scenarios.

Section 2 provides a detailed review of the basic NSAF algorithm and highlights its limitations in clipping distortion scenarios. Section 3 introduces a signal reconstruction method based on the expectation-maximization process. Section 4 proposes a variable step-size strategy for NSAF. Section 5 presents an unbiasedness proof of the proposed method. Section 6 validates the method across multiple scenarios. Section 7 concludes the paper.

2. Background: Normalized Subband Adaptive Filter and Its Limitations in Clipping Distortion

The Normalized Subband Adaptive Filter (NSAF) has emerged as a powerful solution for identifying systems with colored input signals, a common scenario in power systems where voltages and currents are rich in harmonics and inter-harmonics. By decomposing the full-band signal into multiple subbands, the NSAF effectively whitens the input signal within each subband, leading to significantly faster convergence compared to the Normalized Least Mean Square (NLMS) algorithm. The core update equation for the standard NSAF [26] is given by:

$$\mathbf{w}(n+1)=\mathbf{w}\left(n\right)+\mu \sum _{i=1}^N{\displaystyle \frac{{\mathbf{U}}_i\left(n\right)e_i\left(n\right)}{\parallel {\mathbf{U}}_i{\left(n\right)\parallel }^2+\delta }}$$

(1)

where $\mathbf{w}\left(n\right)$ is the adaptive filter weight vector, $\mu$ is a fixed step-size, ${\mathbf{U}}_i\left(n\right)$ is the input vector for the i-th subband, $e_i\left(n\right)=d_i\left(n\right)-{\mathbf{U}}_i^T\left(n\right)\mathbf{w}\left(n\right)$ is the subband error signal, and $\delta$ is a small regularization constant, $\mathbf{d}\left(n\right)$ is desire signal.

However, a critical limitation of the standard NSAF arises in the presence of clipping distortion, which is frequently encountered in power system measurements due to sensor saturation or limiter circuits designed to protect analog-to-digital converters.We model the clipping process as follows. The latent, unclipped desired signal $d\left(n\right)$ is assumed to be related to the filter output by $d\left(n\right)={\mathbf{u}}^T\left(n\right){\mathbf{w}}^{*}+v\left(n\right)$, where ${\mathbf{w}}^{*}$ is the true system and $v\left(n\right)\sim \mathcal{N}(0,{\sigma }_v^2)$ is additive white Gaussian noise. The observed, clipped signal [27]$d_c\left(n\right)$ is given by:

$$d_c\left(n\right)={\mathcal{C}}_{[b,a]}\left(d\left(n\right)\right)=\left\{\begin{array}{cc}{U}_{\max },\hfill & d\left(n\right)\in [U_{\max },+\infty )\hfill \\ d\left(n\right),\hfill & d\left(n\right)\in (U_{\min },U_{\max })\hfill \\ U_{\min },\hfill & d\left(n\right)\in (-\infty ,U_{\min }]\hfill \end{array}\right.$$

(2)

where $U_{\max }$ and $U_{\min }$ are the bilateral clipping thresholds of the signal, respectively. Therefore, it is evident that we can obtain the following equation:

$$E\left[d_c\left(n\right)\right]\ne {\mathbf{U}}^T\left(n\right){\mathbf{w}}^{*}.$$

(3)

So, when the desired signal $d\left(n\right)$ is clipped, the error signal $e_i\left(n\right)$ becomes contaminated with a non-Gaussian, correlated noise component. This distortion severely biases the gradient estimate in (1), leading to:

(1)

Significant misadjustment and reduced convergence accuracy.

(2)

Inability to unbias identify the true system response.

3. Restoration of Clipping Distortion Signals Based on the Maximization of Expectation Process

The nonlinearity introduced by clipping distortion causes direct maximum likelihood estimation of $p\left(d_c\left(n\right)\right|\mathbf{w})$ to yield biased results. To address this, we treat the complete data as $(d\left(n\right),d_c\left(n\right))$ and establish a hierarchical Bayesian model:

$$p(d\left(n\right),d_c\left(n\right)|\mathbf{w})=p\left(d_c\left(n\right)\right|d\left(n\right))·p\left(d\left(n\right)\right|\mathbf{w}),$$

(4)

where $p\left(d_c\left(n\right)\right|d\left(n\right))$ is the censoring likelihood, which is a Dirac delta function at the boundary points in the censored regions and an impulse function in the non-censored interval. We enhance the E-step by incorporating importance sampling to more stably approximate the posterior distribution of the latent variable. Specifically, given the current weight estimate ${\mathbf{w}}^{(k-1)}$ and the observation $d_c\left(n\right)$, we construct an importance sampling distribution $q\left(d\right(n\left)\right)$ that matches the clipped Gaussian distribution $p\left(d\left(n\right)\right|d_c\left(n\right),{\mathbf{w}}^{(k-1)})$. The E-step objective function is adjusted to:

$$Q\left(\mathbf{w}\right|{\mathbf{w}}^{(k-1)})={\mathbb{E}}_q\left[{\displaystyle \frac{p\left(d\left(n\right)\right|d_c\left(n\right),{\mathbf{w}}^{(k-1)})}{q\left(d\right(n\left)\right)}}logp(d\left(n\right),d_c\left(n\right)|\mathbf{w})\right].$$

(5)

After omitting constant terms from the log-likelihood, this expectation simplifies to:

$$Q\left(\mathbf{w}\right|{\mathbf{w}}^{(k-1)})\propto -{\mathbb{E}}_q\left[{\left(d\left(n\right)-{\mathbf{U}}^T\left(n\right)\mathbf{w}\right)}^2\right].$$

(6)

To improve numerical stability and generalization capability, we introduce a Tikhonov regularization term in the M-step, formulating the following optimization problem:

$${\mathbf{w}}^{\left(k\right)}=arg\underset{\mathbf{w}}{min}\left\{{\left(\widehat{d}\left(n\right)-{\mathbf{U}}^T\left(n\right)\mathbf{w}\right)}^2+\lambda {\parallel \mathbf{w}-{\mathbf{w}}^{(k-1)}\parallel }^2\right\},$$

(7)

where $\widehat{d}\left(n\right)=\mathbb{E}\left[d\left(n\right)\right|d_c\left(n\right),{\mathbf{w}}^{(k-1)}]$ is the conditional expectation of the latent variable, and $\lambda$ is the regularization coefficient. This problem has a closed-form solution:

$${\mathbf{w}}^{\left(k\right)}={\mathbf{w}}^{(k-1)}+\mu ·{\displaystyle \frac{\mathbf{U}\left(n\right)(\widehat{d}\left(n\right)-{\mathbf{U}}^T\left(n\right){\mathbf{w}}^{(k-1)})}{{\parallel \mathbf{U}\left(n\right)\parallel }^2+\lambda }},$$

(8)

where $\mu$ is the step-size factor. The conditional expectation $\widehat{d}\left(n\right)$ is computed using the method of moments, considering three censoring scenarios. To this end, we first define two standardized deviation variables:

$$\begin{array}{cc}\hfill z_{\min }\left(n\right)& ={\displaystyle \frac{U_{\min }-{\mathbf{U}}^T\left(n\right){\mathbf{w}}^{(k-1)}}{{\sigma }_v}},\hfill \\ \hfill z_{\max }\left(n\right)& ={\displaystyle \frac{U_{\max }-{\mathbf{U}}^T\left(n\right){\mathbf{w}}^{(k-1)}}{{\sigma }_v}}.\hfill \end{array}$$

(9)

where ${\sigma }_v$ is the standard deviation of the measurement noise $v\left(n\right)$, and $\varphi (·)$ and $\mathrm{\Phi }(·)$ denote the probability density function (PDF) and the cumulative distribution function (CDF) of the standard normal distribution, respectively.

• When $d\left(n\right)\le U_{\min }$ (lower censoring):

  $$\widehat{d}\left(n\right)={\mathbf{U}}^T\left(n\right){\mathbf{w}}^{(k-1)}-{\sigma }_v·{\displaystyle \frac{\varphi \left(z_{\min }\left(n\right)\right)}{\mathrm{\Phi }\left(z_{\min }\left(n\right)\right)}}.$$

  (10)
• When $U_{\min }<d\left(n\right)<U_{\max }$ (no censoring):

  $$\widehat{d}\left(n\right)=d_c\left(n\right).$$

  (11)
• When $d\left(n\right)\ge U_{\max }$ (upper censoring):

  $$\widehat{d}\left(n\right)={\mathbf{U}}^T\left(n\right){\mathbf{w}}^{(k-1)}+{\sigma }_v·{\displaystyle \frac{\varphi \left(z_{\max }\left(n\right)\right)}{1-\mathrm{\Phi }\left(z_{\max }\left(n\right)\right)}}.$$

  (12)

Finally, we unify the update rule for all scenarios into a form with adaptive weights. Defining the weight function $\gamma \left(n\right)=\mathrm{\Phi }\left(z_{\min }\left(n\right)\right)+(1-\mathrm{\Phi }\left(z_{\max }\left(n\right)\right))$, which measures the severity of censoring, the global weight update rule in a multi-subband structure (e.g., within the NSAF framework) becomes:

$${\mathbf{w}}^{(k+1)}={\mathbf{w}}^{\left(k\right)}+\mu \sum _{i=0}^{N-1}{\gamma }_i\left(n\right){\displaystyle \frac{{\mathbf{U}}_i\left(n\right)({\widehat{d}}_i\left(n\right)-{\mathbf{U}}_i^T\left(n\right){\mathbf{w}}^{\left(k\right)})}{\parallel {\mathbf{U}}_i{\left(n\right)\parallel }^2+\lambda }},$$

(13)

where ${\widehat{d}}_i\left(n\right)$ is the conditional expectation estimate for the i-th subband.

4. Theoretical Framework and Derivation of the Improved VSS-NSAF Algorithm

This chapter details the complete theoretical framework of the improved Variable Step-Size Normalized Subband Adaptive Filter (VSS-NSAF) algorithm tailored for power system measurements. The core innovation of this algorithm lies in the introduction of an Intelligent Steady-State Detector and a Dual-Mode Control Mechanism, enabling it to automatically distinguish and optimally handle both the transient and steady-state operational conditions of a power system. Its theoretical framework can be viewed as a complete closed-loop control system following a “sensing-decision-execution” paradigm.

The operation of the improved algorithm is based on a clear state machine model, whose core is the mode-switching function $S\left(n\right)$. This function categorizes the algorithm’s operational state into two distinct modes:

1.

Transient / Convergence Mode ($\mathit{S}\left(\mathit{n}\right)=\mathbf{0}$): Corresponds to the dynamic process following a disturbance, fault, or sudden load change in the power system. The objective of the algorithm in this mode is to rapidly track system changes and converge to a new equilibrium point.

2.

Steady-State Mode ($\mathit{S}\left(\mathit{n}\right)=\mathbf{1})$: Corresponds to the stable operation of the power system. The objective here is to perform fine-tuning, maximizing estimation accuracy and suppressing the effects of measurement noise.

The algorithm dynamically determines its current mode by continuously monitoring the statistical properties of the error and weight sequences. Based on this determination, it adjusts its internal parameters and update strategy, thereby achieving an optimal balance between transient and steady-state performance. The entire theoretical derivation of the algorithm revolves around this core concept.

4.1. Intelligent Steady-State Detection and Mode Switching

The intelligent steady-state detector serves as the “sensing” organ that enables the algorithm’s adaptive capability. Its theoretical basis is as follows: when the power system enters a steady-state operation, the filter weights approach their optimal solution, and the error signal primarily consists of uncorrelated measurement noise. Consequently, the statistical properties of the error sequence and the weight increment sequence will stabilize. Two detection statistics are defined:

1.

Error Power Fluctuation:

$$D_e\left(n\right)=\sqrt{{\displaystyle \frac{1}{L_w}}\sum _{k=0}^{L_w-1}{\left(e^2(n-k)-{\overline{e}}^2\left(n\right)\right)}^2}$$

(14)

where ${\overline{e}}^2\left(n\right)={\displaystyle \frac{1}{L_w}}{\sum }_{k=0}^{L_w-1}{e}^2(n-k)$ is the mean of the error power within the window. This statistic quantifies the fluctuation amplitude of the recent error energy.

2.

Weight Update Fluctuation:

$$D_w\left(n\right)=\sqrt{{\displaystyle \frac{1}{L_w}}\sum _{k=0}^{L_w-1}{\left({\parallel \Delta \mathbf{w}(n-k)\parallel }^2-\overline{\Delta {\mathbf{w}}^2}\left(n\right)\right)}^2}$$

(15)

where $\Delta \mathbf{w}\left(n\right)=\mathbf{w}\left(n\right)-\mathbf{w}(n-1)$. This statistic quantifies the intensity of the changes in the filter weights.

Based on the above statistics, the mode-switching function $S\left(n\right)$ is defined as:

$$S\left(n\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{D}_e\left(n\right)<{\gamma }_e\mathrm{and}{D}_w\left(n\right)<{\gamma }_w\mathrm{for}K\mathrm{consecutive}\mathrm{iterations}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(16)

This definition implies that the algorithm authoritatively switches from the transient mode to the steady-state mode only if both the error and weight increments remain stable simultaneously for a duration of K iterations. This mechanism, based on the joint decision of dual indicators and persistent confirmation, significantly enhances the robustness of state identification, effectively avoiding misjudgments caused by instantaneous noise or disturbances.

The effectiveness of this switching mechanism fundamentally relies on the rational selection of thresholds ${\gamma }_e$ and ${\gamma }_w$. Theoretical analysis reveals distinct sensitivity characteristics for these two parameters based on their physical definitions:

• Asymmetric Sensitivity of ${\gamma }_{\mathbf{e}}$: Since $D_e\left(n\right)$ essentially estimates the residual error power, ${\gamma }_e$ acts as a discriminator against the background noise floor ${\sigma }_v^2$. If ${\gamma }_e$ is set below the noise floor (${\gamma }_e<{\sigma }_v^2$), the condition $D_e\left(n\right)<{\gamma }_e$ becomes physically impossible to satisfy due to the inherent randomness of measurement noise. This leads to a “cliff-like” failure where the algorithm is permanently locked in the transient mode. Conversely, setting ${\gamma }_e>{\sigma }_v^2$ provides a safety margin, resulting in a robust response where performance degrades only gradually with excessive over-estimation.
• Symmetric Sensitivity of ${\gamma }_w$: The parameter ${\gamma }_w$ governs the equilibrium of weight convergence. It exhibits a symmetric “basin-like” sensitivity. A value that is too small (over-strict) prevents the algorithm from locking into the steady state even when convergence is reached, while a value that is too large (over-loose) induces “jitter” by falsely identifying transient spikes as stable states. Therefore, ${\gamma }_w$ requires a selection within a specific order of magnitude to maintain the optimal balance.

This theoretical basis explains the specific sensitivity behaviors—asymmetric for ${\gamma }_e$ and symmetric for ${\gamma }_w$—which will be empirically verified in the simulation results.

4.2. Dual-Mode Parameter Adaptive Control

Once the operational mode is determined, the algorithm enters the “decision” stage, where a dual-mode controller dynamically adjusts key parameters to optimize performance for each mode. The control strategy is as follows:

1.

Variable Step-Size Mechanism: The step size $\mu \left(n\right)$ is the most critical parameter for balancing convergence speed and steady-state accuracy. Its update law depends on the mode:

$$\mu \left(n\right)=\left\{\begin{array}{cc}{\mu }_{\max }-({\mu }_{\max }-{\mu }_{\min })·min\left(1,{\displaystyle \frac{{\widehat{\sigma }}_e^2\left(n\right)-{\sigma }_v^2}{\kappa {\sigma }_v^2}}\right),\hfill & S\left(n\right)=0\hfill \\ max\left({\mu }_{\min },{\mu }_{\max }·{\displaystyle \frac{{\sigma }_v^2}{{\widehat{\sigma }}_e^2\left(n\right)+{\sigma }_v^2}}\right),\hfill & S\left(n\right)=1\hfill \end{array}\right.$$

(17)

where ${\mu }_{\max }$ and ${\mu }_{\min }$ are the upper and lower bounds of the step size, and $\kappa$ is a scaling parameter that controls the sensitivity of the step size to the error power deviation. In the transient mode ($S\left(n\right)=0$), the step size is positively correlated with the instantaneous error power, ensuring strong tracking capability during dynamic processes. In the steady-state mode ($S\left(n\right)=1$), the step size is compressed to near its minimum value ${\mu }_{\min }$, enabling extremely fine adjustments and significantly improving steady-state accuracy. The smoothness of the error power estimate ${\widehat{\sigma }}_e^2\left(n\right)$ is controlled by the variable forgetting factor $\rho \left(n\right)$.

2.

Variable Forgetting Factor: The error power estimate is given by:

$${\widehat{\sigma }}_e^2\left(n\right)=\rho \left(n\right){\widehat{\sigma }}_e^2(n-1)+(1-\rho \left(n\right)){\displaystyle \frac{1}{N}}\sum _{i=1}^N{e}_i^2\left(n\right)$$

(18)

The forgetting factor $\rho \left(n\right)$ adapts with the mode:

$$\rho \left(n\right)=S\left(n\right)·{\rho }_{\mathrm{slow}}+(1-S\left(n\right))·{\rho }_{\mathrm{fast}}$$

(19)

Here, ${\rho }_{\mathrm{fast}}\approx 0.90$ is used in the transient mode, allowing the estimator to respond quickly to system changes. Conversely, ${\rho }_{\mathrm{slow}}\approx 0.995$ is used in the steady-state mode, enabling deep smoothing of the estimate and effectively suppressing the influence of measurement noise.

3.

Adaptive Regularization: The regularization parameter $\delta \left(n\right)$ ensures numerical stability. Its adjustment strategy is:

$$\delta \left(n\right)={\delta }_0·(1+\alpha S\left(n\right))$$

(20)

where ${\delta }_0$ is the baseline regularization parameter, and $\alpha$ is a positive coefficient that determines the magnitude of regularization enhancement in the steady state. Increasing the regularization parameter in the steady-state mode prevents abnormally large updates that could occur if the input energy in certain subbands becomes very low (e.g., when the signal crosses zero), further enhancing the algorithm’s robustness during long-term operation.

The rationale behind the adaptive regularization strategy in (20) stems from the interpretation of NSAF as a regularized Newton-type algorithm. The weight update in each subband can be viewed as the solution to the following regularized least-squares minimization problem at iteration n:

$$\Delta {\mathbf{w}}_i^{*}\left(n\right)=arg\underset{\Delta \mathrm{w}}{min}\left({\left|e_i\left(n\right)-{\mathbf{U}}_i^T\left(n\right)\Delta \mathbf{w}\right|}^2+\delta \left(n\right){\parallel \Delta \mathbf{w}\parallel }^2\right)$$

(21)

where $\Delta \mathbf{w}$ represents the weight update vector, and $\delta \left(n\right)$ acts as the Tikhonov regularization parameter (analogous to the Levenberg-Marquardt damping factor). The theoretical justification for the state-dependent adjustment is as follows:

• Transient Mode ($\mathit{S}\left(\mathit{n}\right)=\mathbf{0}$): During dynamic changes, the system requires rapid tracking of the optimal Wiener solution. A large regularization parameter would introduce a “shrinkage bias” to the weight vector, artificially constraining the update magnitude and significantly slowing down convergence. Therefore, $\delta \left(n\right)$ is maintained at a minimal baseline value ${\delta }_0$, serving primarily to ensure numerical stability (i.e., preventing division by zero) when the input vector norm $\parallel {\mathbf{U}}_i{\left(n\right)\parallel }^2$ is extremely small.
• Steady-State Mode ($\mathit{S}\left(\mathit{n}\right)=\mathbf{1}$): Once the filter converges, the weight vector fluctuates around the optimal solution driven primarily by measurement noise. A critical issue in subband adaptive filtering is gradient noise amplification, which typically occurs in subbands with low excitation energy (i.e., small $\parallel {\mathbf{U}}_i{\left(n\right)\parallel }^2$). In these subbands, the inverse term $1/(\parallel {\mathbf{U}}_i\left(n\right){\parallel }^2+\delta \left(n\right))$ becomes large, significantly amplifying the noise component within the error signal. By switching to a larger regularization parameter $\delta \left(n\right)={\delta }_0(1+\alpha )$, we effectively improve the condition number of the implicit inversion operation. This imposes a stricter penalty on the weight update magnitude, effectively damping the high-variance weight jitter caused by noise in low-energy directions. Although this introduces a negligible bias, it significantly reduces the Excess Mean Square Error (EMSE), thereby enhancing the overall steady-state estimation accuracy.

4.3. Weight Update and Smooth Execution

After the parameters are determined, the algorithm enters the “execution” stage. First, the standard normalized subband update is performed:

$${\mathbf{w}}^{\prime }(n+1)=\mathbf{w}\left(n\right)+\mu \left(n\right)\sum _{i=1}^N{\displaystyle \frac{{\mathbf{U}}_i\left(n\right)e_i\left(n\right)}{\parallel {\mathbf{U}}_i{\left(n\right)\parallel }^2+\delta \left(n\right)}}$$

(22)

To further enhance steady-state performance, a smoothing operation is introduced specifically in the steady-state mode ($S\left(n\right)=1$):

$$\mathbf{w}(n+1)={\mathbf{w}}^{\prime }(n+1)+\eta \left({\displaystyle \frac{1}{M}}\sum _{m=0}^{M-1}\mathbf{w}(n-m)-{\mathbf{w}}^{\prime }(n+1)\right)$$

(23)

The essence of this operation is a slight adjustment of the currently updated weights towards the moving average of the recent weights. Mathematically, this is equivalent to a low-pass filtering process, which effectively attenuates high-frequency jitter in the weights caused by measurement noise. Consequently, the weight estimates in the steady state become smoother and more stable, leading to a significant improvement in steady-state estimation accuracy. This step is a key technique for achieving superior performance in the steady-state mode.

In summary, the improved VSS-NSAF algorithm derived in this chapter, through rigorous formalization, constructs a complete adaptive filtering solution tailored to the characteristics of power system measurements. Its intelligent state sensing and dual-mode control mechanism effectively resolve the conflict between convergence speed and steady-state accuracy inherent in traditional algorithms operating in complex dynamic environments.

5. Unbiasedness Proof of the Proposed Estimator

To analyze the steady-state performance of the improved algorithm, this section provides a rigorous proof that when the filter weights $\mathbf{w}\left(n\right)$ converge to the optimal weights ${\mathbf{w}}_o$ of the unknown system, the conditional expectation estimate of the latent variable $d\left(n\right)$, denoted by $\widehat{d}\left(n\right)=\mathbb{E}\left[d\left(n\right)\right|d_c\left(n\right),\mathbf{w}]$, is an unbiased estimator. That is, $\mathbb{E}\left[\widehat{d}\left(n\right)\right]={\mathbf{U}}^T\left(n\right){\mathbf{w}}_o$. This property serves as the theoretical cornerstone for the algorithm’s ability to achieve precise steady-state estimation. The proof is as below.

First, according to the signal restoration theory based on the Expectation-Maximization (EM) process described in Chapter 2, the conditional expectation of the latent variable $d\left(n\right)$, given the observed value $d_c\left(n\right)$ and the current weight estimate $\mathbf{w}$, depends on its clipping region. We define three mutually exclusive and exhaustive clipping scenarios and their probabilities:

1.

Lower clipping Region ($d\left(n\right)\le U_{\min }$):

$$\begin{array}{cc}\hfill p_1& =Pr\{d\left(n\right)\le U_{\min }\mid \mathbf{U}\left(n\right),\mathbf{w}\}=\mathrm{\Phi }\left({\lambda }_{\min }\right),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill \mathrm{where}{\lambda }_{\min }& ={\displaystyle \frac{U_{\min }-{\mathbf{U}}^T\left(n\right)\mathbf{w}}{{\sigma }_v}}.\hfill \end{array}$$

(25)

In this region, the conditional expectation of the latent variable is:

$$\mathbb{E}\left[d\left(n\right)\right|d_c\left(n\right),\mathbf{w},d\left(n\right)\le U_{\min }]={\mathbf{U}}^T\left(n\right)\mathbf{w}-{\sigma }_v·\mathrm{\Omega }\left({\lambda }_{\min }\right),$$

(26)

where $\mathrm{\Omega }\left({\lambda }_{\min }\right)={\displaystyle \frac{\varphi \left({\lambda }_{\min }\right)}{\mathrm{\Phi }\left({\lambda }_{\min }\right)}}$ is the inverse Mills ratio.

2.

No clipping Region ($U_{\min }<d\left(n\right)<U_{\max }$):

$$\begin{array}{cc}\hfill p_2& =Pr\{U_{\min }<d\left(n\right)<U_{\max }\mid \mathbf{U}\left(n\right),\mathbf{w}\}=\mathrm{\Phi }\left({\lambda }_{\max }\right)-\mathrm{\Phi }\left({\lambda }_{\min }\right),\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill \mathrm{where}{\lambda }_{\max }& ={\displaystyle \frac{U_{\max }-{\mathbf{U}}^T\left(n\right)\mathbf{w}}{{\sigma }_v}}.\hfill \end{array}$$

(28)

In this region, the observed value is the true value, hence the conditional expectation is:

$$\mathbb{E}\left[d\left(n\right)\right|d_c\left(n\right),\mathbf{w},U_{\min }<d\left(n\right)<U_{\max }]=d_c\left(n\right).$$

(29)

Considering that $d\left(n\right)={\mathbf{U}}^T\left(n\right){\mathbf{w}}_o+v\left(n\right)$ and in this region $d_c\left(n\right)=d\left(n\right)$, its expectation is ${\mathbf{U}}^T\left(n\right){\mathbf{w}}_o$.

3.

Upper clipping Region ($d\left(n\right)\ge U_{\max }$):

$$\begin{array}{cc}\hfill p_3& =Pr\{d\left(n\right)\ge U_{\max }\mid \mathbf{U}\left(n\right),\mathbf{w}\}=1-\mathrm{\Phi }\left({\lambda }_{\max }\right).\hfill \end{array}$$

(30)

In this region, the conditional expectation of the latent variable is:

$$\mathbb{E}\left[d\left(n\right)\right|d_c\left(n\right),\mathbf{w},d\left(n\right)\ge U_{\max }]={\mathbf{U}}^T\left(n\right)\mathbf{w}+{\sigma }_v·\mathrm{\Omega }(-{\lambda }_{\max }),$$

(31)

where $\mathrm{\Omega }(-{\lambda }_{\max })={\displaystyle \frac{\varphi \left({\lambda }_{\max }\right)}{1-\mathrm{\Phi }\left({\lambda }_{\max }\right)}}$.

Now, consider the conditional expectation $\widehat{d}\left(n\right)$ of the latent variable $d\left(n\right)$ based on the current model throughout the entire adaptive filtering process. According to the law of total expectation, it can be expressed as a weighted sum of the conditional expectations under the three scenarios mentioned above:

$$\begin{array}{cc}\hfill \widehat{d}\left(n\right)& =\mathbb{E}[d\left(n\right)\mid d_c\left(n\right),\mathbf{U}\left(n\right),\mathbf{w}]\hfill \\ \hfill & =p_1·\mathbb{E}\left[d\left(n\right)\right|d_c\left(n\right),\mathbf{w},d\left(n\right)\le U_{\min }]\hfill \\ \hfill & +p_2·\mathbb{E}\left[d\left(n\right)\right|d_c\left(n\right),\mathbf{w},U_{\min }<d\left(n\right)<U_{\max }]\hfill \\ \hfill & +p_3·\mathbb{E}\left[d\left(n\right)\right|d_c\left(n\right),\mathbf{w},d\left(n\right)\ge U_{\max }]\hfill \\ \hfill & =p_1\left({\mathbf{U}}^T\left(n\right)\mathbf{w}-{\sigma }_v\mathrm{\Omega }\left({\lambda }_{\min }\right)\right)\hfill \\ \hfill & +p_2·d_c\left(n\right)\hfill \\ \hfill & +p_3\left({\mathbf{U}}^T\left(n\right)\mathbf{w}+{\sigma }_v\mathrm{\Omega }(-{\lambda }_{\max })\right).\hfill \end{array}$$

(32)

The steady state of the algorithm corresponds to the situation where the filter weights $\mathbf{w}\left(n\right)$ converge to the true system weights ${\mathbf{w}}_o$. Let $\mathbf{w}={\mathbf{w}}_o$, then $d\left(n\right)={\mathbf{U}}^T\left(n\right){\mathbf{w}}_o+v\left(n\right)$. We compute the expectation of $\widehat{d}\left(n\right)$ in the steady state, $\mathbb{E}[\widehat{d}\left(n\right)\mid \mathbf{w}={\mathbf{w}}_o]$. Note that in the no clipping region, $d_c\left(n\right)=d\left(n\right)={\mathbf{U}}^T\left(n\right){\mathbf{w}}_o+v\left(n\right)$, therefore $\mathbb{E}[d_c\left(n\right)\mid {\mathbf{w}}_o,U_{\min }<d\left(n\right)<U_{\max }]={\mathbf{U}}^T\left(n\right){\mathbf{w}}_o+\mathbb{E}[v\left(n\right)\mid U_{\min }<d\left(n\right)<U_{\max }]$. For a zero-mean Gaussian noise $v\left(n\right)$, under symmetric clipping conditions, its conditional expectation is zero. For generality, we use the moment properties of the clipped Gaussian distribution.

In the steady state ($\mathbf{w}={\mathbf{w}}_o$), define the standardized boundary parameters:

$${\gamma }_{\min }={\displaystyle \frac{U_{\min }-{\mathbf{U}}^T\left(n\right){\mathbf{w}}_o}{{\sigma }_v}},{\gamma }_{\max }={\displaystyle \frac{U_{\max }-{\mathbf{U}}^T\left(n\right){\mathbf{w}}_o}{{\sigma }_v}}.$$

(33)

Substituting the probabilities and conditional expectations into the total expectation Formula (32) and simplifying using the properties of the clipped Gaussian distribution:

$$\begin{array}{cc}\hfill \underset{\mathbf{w}\left(n\right)\to {\mathbf{w}}_o}{lim}\mathbb{E}\left[\widehat{d}\left(n\right)\right]& =\mathrm{\Phi }\left({\gamma }_{\min }\right)\left({\mathbf{U}}^T\left(n\right){\mathbf{w}}_o-{\sigma }_v\mathrm{\Omega }\left({\gamma }_{\min }\right)\right)\hfill \\ \hfill & +\left(\mathrm{\Phi }\left({\gamma }_{\max }\right)-\mathrm{\Phi }\left({\gamma }_{\min }\right)\right)\left({\mathbf{U}}^T\left(n\right){\mathbf{w}}_o+\mathbb{E}[v\left(n\right)\mid {\gamma }_{\min }<v\left(n\right)/{\sigma }_v<{\gamma }_{\max }]\right)\hfill \\ \hfill & +(1-\mathrm{\Phi }\left({\gamma }_{\max }\right))\left({\mathbf{U}}^T\left(n\right){\mathbf{w}}_o+{\sigma }_v\mathrm{\Omega }(-{\gamma }_{\max })\right).\hfill \end{array}$$

(34)

According to the properties of the clipped standard Gaussian distribution, within the interval $({\gamma }_{\min },{\gamma }_{\max })$, the conditional expectation of the random variable $v\left(n\right)/{\sigma }_v$ is $\mathbb{E}[v\left(n\right)/{\sigma }_v\mid {\gamma }_{\min }<v\left(n\right)/{\sigma }_v<{\gamma }_{\max }]={\displaystyle \frac{\varphi \left({\gamma }_{\min }\right)-\varphi \left({\gamma }_{\max }\right)}{\mathrm{\Phi }\left({\gamma }_{\max }\right)-\mathrm{\Phi }\left({\gamma }_{\min }\right)}}$. Therefore, $\mathbb{E}[v\left(n\right)\mid {\gamma }_{\min }<v\left(n\right)/{\sigma }_v<{\gamma }_{\max }]={\sigma }_v{\displaystyle \frac{\varphi \left({\gamma }_{\min }\right)-\varphi \left({\gamma }_{\max }\right)}{\mathrm{\Phi }\left({\gamma }_{\max }\right)-\mathrm{\Phi }\left({\gamma }_{\min }\right)}}$.

Substituting this relation into (34) and simplifying:

$$\begin{array}{cc}\hfill \underset{\mathbf{w}\left(n\right)\to {\mathbf{w}}_o}{lim}\mathbb{E}\left[\widehat{d}\left(n\right)\right]& ={\mathbf{U}}^T\left(n\right){\mathbf{w}}_o\left(\mathrm{\Phi }\left({\gamma }_{\min }\right)+\mathrm{\Phi }\left({\gamma }_{\max }\right)-\mathrm{\Phi }\left({\gamma }_{\min }\right)+1-\mathrm{\Phi }\left({\gamma }_{\max }\right)\right)\hfill \\ \hfill & +{\sigma }_v\left[-\mathrm{\Phi }\left({\gamma }_{\min }\right)\mathrm{\Omega }\left({\gamma }_{\min }\right)+(\mathrm{\Phi }\left({\gamma }_{\max }\right)-\mathrm{\Phi }\left({\gamma }_{\min }\right)){\displaystyle \frac{\varphi \left({\gamma }_{\min }\right)-\varphi \left({\gamma }_{\max }\right)}{\mathrm{\Phi }\left({\gamma }_{\max }\right)-\mathrm{\Phi }\left({\gamma }_{\min }\right)}}\right.\hfill \\ \hfill & \left.+(1-\mathrm{\Phi }\left({\gamma }_{\max }\right))\mathrm{\Omega }(-{\gamma }_{\max })\right]\hfill \\ \hfill & ={\mathbf{U}}^T\left(n\right){\mathbf{w}}_o·1\hfill \\ \hfill & +{\sigma }_v\left[-\varphi \left({\gamma }_{\min }\right)+\varphi \left({\gamma }_{\min }\right)-\varphi \left({\gamma }_{\max }\right)+\varphi \left({\gamma }_{\max }\right)\right]\hfill \\ \hfill & ={\mathbf{U}}^T\left(n\right){\mathbf{w}}_o+{\sigma }_v·0\hfill \\ \hfill & ={\mathbf{U}}^T\left(n\right){\mathbf{w}}_o.\hfill \end{array}$$

(35)

This proof demonstrates that the latent variable estimate $\widehat{d}\left(n\right)$ obtained by the signal restoration method based on the EM process is an unbiased estimator of the true expectation ${\mathbf{U}}^T\left(n\right){\mathbf{w}}_o$ when the algorithm converges. This excellent statistical property ensures that the improved VSS-NSAF algorithm proposed in this chapter can overcome the bias introduced by measurement nonlinearities in the steady state, thereby achieving high-precision system identification results.

6. Case Study

To evaluate the performance of the proposed VSS-NSAF algorithm across diverse scenarios, two system-level testing environments are constructed: a simulated signal system and the CSEE-VC-88 high-penetration renewable energy simulation platform. The simulated signal system employs a 128-tap adaptive filter, where the input is a white noise sequence shaped by an autoregressive (AR) model with the transfer function:

$$T\left(z\right)={\displaystyle \frac{1}{1-0.6z^{-1}}}$$

(36)

The system input is a random vector with zero mean and unit variance. The CSEE-VC-88 system, developed by the China Electric Power Research Institute, serves as a representative simulation platform for high-renewable-penetration power grids. It is designed to emulate small-signal oscillatory instability triggered by increasing wind speed. The output signals exhibit autocorrelation, and Gaussian white noise at 20 dB and 40 dB is superimposed to replicate realistic measurement noise.

All algorithms, including baseline comparisons, are implemented using cosine modulated filter banks with $N=4$ subbands. Performance is assessed using the normalized mean square deviation (NMSD), defined as:

$$\mathrm{NMSD}=10{log}_{10}\left({\displaystyle \frac{E[\parallel \mathbf{w}\left(k\right)-{\mathbf{w}}_0{\parallel }_2^2]}{\parallel {\mathbf{w}}_0{\parallel }_2^2}}\right)$$

(37)

To improve statistical reliability, all results are averaged over approximately 500 Monte Carlo trials.

This study conducts four validation experiments:

1.

Analysis of the convergence and steady-state performance of the VSS-NSAF algorithm under various parameter settings;

2.

Evaluation of tracking performance with non-stationary signals;

3.

Filtering performance assessment under different degrees of signal clipping;

4.

Validation of the adaptability of the VSS-NSAF algorithm to wideband measurement signals in real-world power systems.

6.1. Computational Complexity Comparison

Table 1 presents a comprehensive comparison of the computational load between the proposed VSS-NSAF and the competitive algorithms per iteration. The computational complexity is quantified in terms of the number of multiplications and additions. The symbols used in the table are defined as follows: M denotes the number of adaptive tap weights, N is the number of subbands, and L represents the length of the analysis and synthesis filters. The parameter P indicates the probability of unanticipated signal clipping. Furthermore, specific to the proposed algorithm, $P_{ss}$ ($0\le P_{ss}\le 1$) denotes the probability of the algorithm operating in the steady-state mode (i.e., $S\left(n\right)=1$), and $L_w$ is the length of the sliding window employed for steady-state detection.

Table 1. Computational Complexity Comparison of Various Adaptive Filtering Methods.

Method	Computational Load (Multiplications/Additions)
NSAF	$3M+NL+2(L+1)$
DSU-NSAF [28]	$(1-P)\left[3M+NL+2(L+1)\right]$
CR-NSAF [27]	$8M+NL+2L+7$
UT-NSAF [29]	$(3+P)M+NL+2(L+1+P)$
VSS-NSAF	$(4+P+P_{ss})M+NL+2(L+1+P+L_w)$

As observed in Table 1, the DSU-NSAF achieves the lowest computational burden by skipping updates during truncation events, at the cost of performance. The CR-NSAF incurs the highest fixed complexity ($8M$) due to its complex compensation mechanism. The proposed VSS-NSAF algorithm introduces a moderate increase in computational load compared to the UT-NSAF ($3M+PM$). Specifically, the intelligent steady-state detector requires calculating the norm of the weight increment vector, contributing a fixed overhead of $1M$. Furthermore, the smoothing update strategy, which is exclusively triggered in the steady-state mode, adds a dynamic load of $P_{ss}M$. Consequently, the complexity of VSS-NSAF fluctuates between $(4+P)M$ in the transient phase and $(5+P)M$ in the steady phase. Despite this slight increase, the computational cost of VSS-NSAF remains significantly lower than that of CR-NSAF, while providing a superior trade-off between convergence speed and steady-state accuracy through the variable step-size and dual-mode control mechanisms.

6.2. Convergence and Steady-State Analysis Under Varying Parameter Settings

The convergence behavior of the VSS-NSAF algorithm is primarily influenced by three key parameters: the maximum step size ${\mu }_{\max }$, ${\rho }_f$, and ${\rho }_s$. To investigate this, several parameter configurations are tested in the experiment to analyze the convergence rate and steady-state error of the algorithm under varying conditions. This analysis aims to assess how parameter tuning affects the algorithm’s stability and adaptive performance in the time domain. The normalized mean square deviation (NMSD) curves corresponding to different parameter settings, as well as sensitivity plots illustrating the influence of these parameters on performance metrics and step size among the total process, are presented in Figure 1, Figure 2 and Figure 3.

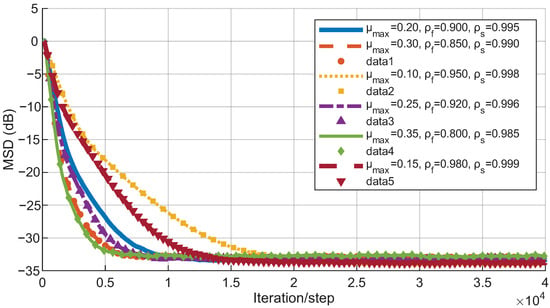
Figure 1. NMSD variations of the VSS-NSAF algorithm under different parameter configurations.

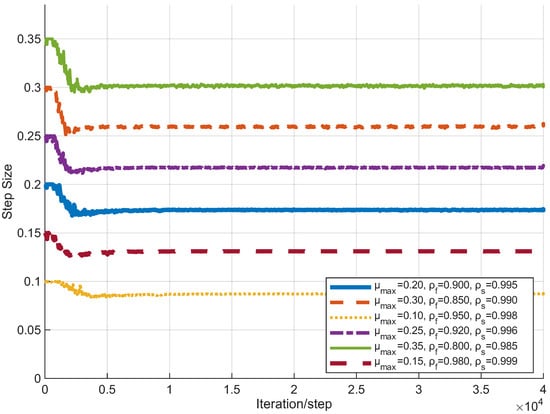
Figure 2. Evolution of the step size over iterations.

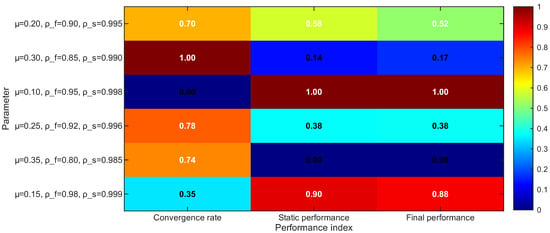
Figure 3. Sensitivity analysis of parameters on performance metrics.

The Figure 1 and Figure 2 illustrate the performance of the Variable Step-Size Nonlinear Smoothing Adaptive Filter (VSS-NSAF) algorithm under different parameter settings. The NMSD, which quantifies the error between the estimated and desired outputs, serves as a performance indicator—the lower the NMSD, the better the performance. As the number of iterations increases, the NMSD consistently decreases, indicating that the algorithm converges and reduces error across all parameter configurations. A larger maximum step size ${\mu }_{\max }$ generally leads to faster initial convergence, characterized by a more rapid drop in NMSD. Conversely, a smaller ${\mu }_{\max }$ results in slower convergence but ensures a steady reduction in NMSD over time.

The VSS-NSAF algorithm dynamically adjusts its step size, which typically stabilizes as the estimation error decreases. Larger values of ${\mu }_{\max }$ (e.g., ${\mu }_{\max }=0.30$ or ${\mu }_{\max }=0.35$) enable faster convergence, while smaller values (e.g., ${\mu }_{\max }=0.15$) yield slower step-size decay, reflecting a more cautious adaptation process. Although step-size variation significantly affects convergence speed—larger step sizes accelerate convergence—it has minimal influence on the steady-state error, as all step sizes eventually stabilize at small values. This behavior highlights a key advantage of the VSS-NSAF algorithm: it achieves faster convergence with minimal compromise in steady-state performance, demonstrating robustness across different parameter configurations.

6.3. Tracking Performance Evaluation with Non-Stationary Signals

In non-stationary signal environments, adaptive filters must exhibit strong adaptability. To evaluate this, we design a continuous non-stationary signal task in which a parameter inversion is introduced at the 1000th iteration. Furthermore, before the system fully recovers from the initial disturbance, a second non-stationary perturbation is applied by halving the parameters. This experimental setup is intended to assess the algorithm’s responsiveness and adaptability to signals with time-varying statistical properties. The experimental results are presented in Figure 4 and Figure 5.

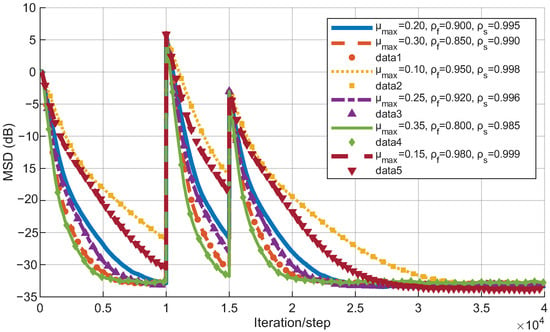
Figure 4. NMSD variations of the VSS-NSAF algorithm under different parameter configurations based on non-stationary signals.

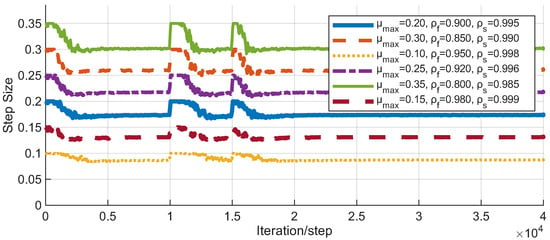
Figure 5. Evolution of the step size over iterations based on non-stationary signals.

As illustrated in Figure 4 and Figure 5, the VSS-NSAF algorithm exhibits a clear convergence trend under all parameter configurations, with the mean square deviation (MSD) consistently decreasing, indicating effective adaptation to the initial stationary signal. During two successive abrupt signal changes, the green solid line ($\mu =0.35$) and the purple dashed line ($\mu =0.25$) exhibit faster descent rates, demonstrating an advantage in convergence speed. This suggests that a broader step-size selection range enables the algorithm to converge more rapidly to new signal states. Ultimately, all configurations stabilize at an NMSD level below $-30\mathrm{dB}$, confirming that the algorithm successfully adapts to varying signal characteristics.

Additionally, examining the evolution of the step size during training reveals that step sizes tend to increase immediately following perturbations. A larger permissible range for the step size results in a shorter duration at high step sizes, thereby accelerating convergence and subsequently enabling fine-grained steady-state adjustment via smaller step sizes. Hence, the VSS-NSAF algorithm can momentarily increase its step size to enhance dynamic tracking of non-stationary signals while still maintaining robust steady-state convergence performance.

6.4. Sensitivity Analysis of Threshold Parameters

To evaluate the robustness of the VSS-NSAF algorithm against parameter variations, we conducted a systematic sensitivity analysis. The experiments were performed under an SNR of 30 dB with symmetric clipping ($U_{\max }=15,U_{\min }=-15$). The steady-state NMSD was recorded while varying ${\gamma }_e$ and ${\gamma }_w$. The results are depicted in Figure 6.

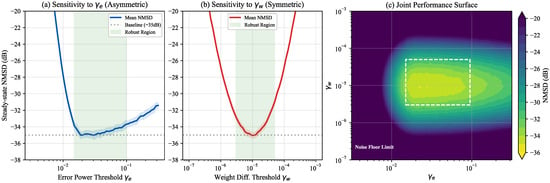
Figure 6. Sensitivity analysis of the algorithm performance with respect to threshold parameters. (a) Impact of varying ${\gamma }_e$ (fixed ${\gamma }_w={10}^{-5}$), showing distinct asymmetric behavior; (b) Impact of varying ${\gamma }_w$ (fixed ${\gamma }_e=0.02$), showing symmetric valley-like behavior; (c) Joint parameter heat map indicating the robust operation zone.

As shown in Figure 6, the experimental results align perfectly with the theoretical analysis in Section 4.1:

1.

Asymmetric Response to ${\gamma }_{\mathbf{e}}$ (Figure 6a): The algorithm exhibits a sharp performance degradation (“cliff effect”) when ${\gamma }_e<0.01$. This confirms that the threshold must effectively bound the noise floor. However, for ${\gamma }_e\in [0.015,0.1]$, the NMSD remains stable around −35 dB with negligible fluctuations (standard deviation $\approx 0.43$ dB), demonstrating high robustness on the upper side.

2.

Symmetric Response to ${\gamma }_{\mathbf{w}}$ (Figure 6b): The sensitivity to ${\gamma }_w$ forms a symmetric “basin.” The algorithm maintains optimal performance within a wide logarithmic range of ${\gamma }_w\in [3\times {10}^{-6},5\times {10}^{-5}]$. Deviations outside this range lead to a gradual increase in steady-state error, yet the algorithm does not diverge.

3.

Joint Robustness (Figure 6c): The joint contour plot identifies a broad “Operating Zone” (marked by the dashed rectangle). Within this region, the proposed VSS-NSAF consistently achieves the target NMSD of approximately −35 dB, proving that precise fine-tuning is not required for practical applications.

Based on these findings, the recommended parameter sets are ${\gamma }_e\in [0.015,0.05]$ and ${\gamma }_w\in [5\times {10}^{-6},5\times {10}^{-5}]$, which were used in the subsequent experiments.

6.5. Filtering Robustness Under Varying Levels of Signal Clipping

In the preceding sections, we conducted a detailed investigation into the detrimental impact of clipping distortion on adaptive filtering. However, in practical systems, clipping distortion may exhibit diverse characteristics. In some cases, the clipping is symmetric, while in others, it is asymmetric. To evaluate the robustness of the proposed algorithm under such conditions, we designed two sets of experiments. The first experiment simulates symmetric clipping, with $U_{\max }=15$ and $U_{\min }=-15$. The second experiment examines performance under asymmetric clipping, where $U_{\max }=12$ and $U_{\min }=-8$. These experiments aim to assess the algorithm’s capability to preserve filtering performance in the presence of varying types of distortion. The corresponding results are presented in Figure 7 and Figure 8.

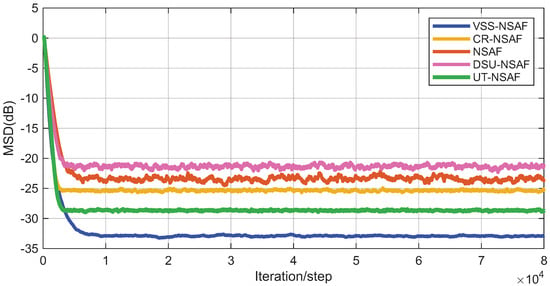
Figure 7. Performance evaluation under symmetric clipping.

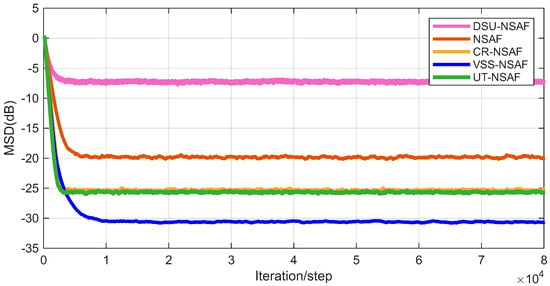
Figure 8. Performance evaluation under asymmetric clipping.

As shown in Figure 7 and Figure 8, we compare several algorithms commonly used for mitigating clipping distortion, including NSAF, CR-NSAF, UT-NSAF, and DSU-NSAF. Among them, the proposed method, CR-NSAF, and UT-NSAF all exhibit active clipping recovery capabilities. The proposed approach consistently outperforms the others under both symmetric and asymmetric clipping conditions. Notably, UT-NSAF achieves nearly identical performance across both scenarios, indicating minimal sensitivity to clipping severity. In contrast, CR-NSAF suffers significantly in asymmetric settings due to its design assumption of one-sided clipping.

The superior performance of our method can be attributed to two main factors: (1) the signal recovery module is capable of extracting richer information from the clipped data, capturing both the original signal and the noise components; and (2) the variable step-size mechanism in the VSS-NSAF framework enhances steady-state accuracy. Moreover, with increasing clipping severity, both DSU-NSAF and CR-NSAF exhibit noticeable performance degradation, primarily due to information loss and limited support for two-sided clipping. In contrast, UT-NSAF and the proposed VSS-NSAF method maintain robust and stable performance, demonstrating strong resilience to varying degrees of clipping distortion.

6.6. Adaptability Assessment Using Real-World Wideband Power System Signals

In the final experiment, we utilized a high-penetration renewable energy power grid simulation case published by the China Electric Power Research Institute. Within this simulation, wind speed was intentionally increased in a wind farm scenario, leading to oscillatory behavior in the wind turbine outputs. These oscillation signals were processed using the proposed method, as well as three benchmark algorithms: NSAF, CR-NSAF, and DSU-NSAF. Since in wideband oscillatory conditions, the time-domain amplitude has a relatively minor impact on system security and stability compared to the oscillation frequency and amplitude in the frequency domain, we applied Fourier decomposition to the filtered signals and evaluated the filtering performance in the frequency domain. To further examine noise robustness, zero-mean Gaussian white noise was added to the simulation data at signal-to-noise ratios (SNRs) of 40 dB and 20 dB, respectively. The resulting spectral decomposition of the filtered signals is presented in Figure 9 and Figure 10.

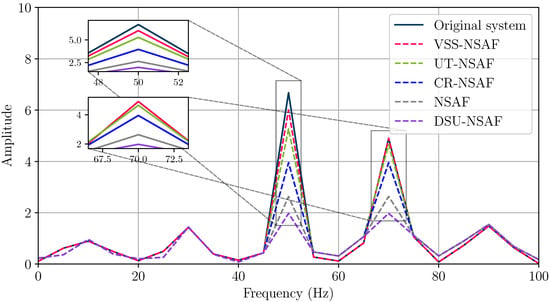
Figure 9. Oscillation spectrum analysis under 40 dB noise.

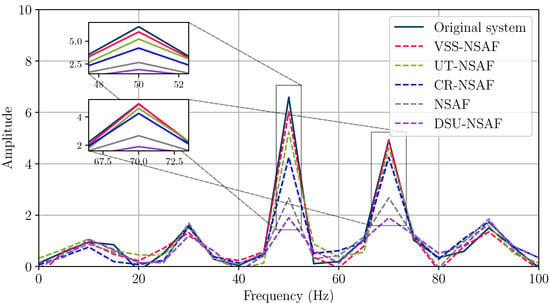
Figure 10. Oscillation spectrum analysis under 20 dB noise.

The spectral analysis results presented in Figure 9 and Figure 10 clearly demonstrate the superior filtering performance of the proposed VSS-NSAF algorithm under both 40 dB and 20 dB noise conditions. Compared to the benchmark algorithms—NSAF, CR-NSAF, and DSU-NSAF—the VSS-NSAF more accurately preserves the dominant oscillation components in the frequency domain, particularly around 50 Hz and 70 Hz, while effectively suppressing noise-induced spectral distortions. Notably, under lower SNR conditions (20 dB), the performance degradation of CR-NSAF and DSU-NSAF becomes more pronounced, highlighting their sensitivity to increased noise. In contrast, VSS-NSAF maintains robust frequency selectivity and amplitude resolution, underscoring its strong adaptability to wideband oscillatory disturbances in realistic power system environments. These results validate the practical applicability of the proposed algorithm for real-world power grid signal processing tasks, especially in scenarios involving high noise levels and dynamic oscillatory behavior.

The spectral analysis results shown in Figure 9 and Figure 10 clearly demonstrate that the proposed VSS-NSAF algorithm delivers outstanding filtering performance under both 40 dB and 20 dB noise conditions. Compared to the baseline algorithms (NSAF, CR-NSAF, UT-NSAF, and DSU-NSAF), VSS-NSAF more accurately preserves the dominant oscillatory components in the frequency domain—especially around 50 Hz and 70 Hz—while effectively suppressing noise-induced spectral distortions.

Although UT-NSAF performs similarly to the proposed method in both scenarios, a performance gap remains. Notably, the CR-NSAF algorithm fails to reveal the primary oscillation frequencies in either case, potentially undermining disturbance tracing and fault diagnosis in the system. Moreover, at the lower signal-to-noise ratio of 20 dB, the spectra produced by NSAF and DSU-NSAF become incapable of accurately tracking the oscillatory components, indicating high sensitivity to noise.

In contrast, the proposed VSS-NSAF algorithm maintains strong frequency selectivity and amplitude resolution, highlighting its robust adaptability to broadband oscillatory interference in practical power system environments. These findings confirm the practical significance of the proposed method for real-world power grid signal processing, especially under conditions of high noise and dynamically varying oscillations.

7. Conclusions

In this paper, we proposed a Variable Step-Size Normalized Subband Adaptive Filter (VSS-NSAF) algorithm specifically designed to address the challenges of clipping distortion in power system signals. The proposed method achieves strictly unbiased recovery of clipped signals, ensuring both theoretical soundness and practical accuracy. Furthermore, we introduced a novel step-size adaptation strategy compatible with the NSAF framework, which significantly enhances convergence speed, particularly under steady-state conditions. Extensive simulations based on realistic power grid scenarios demonstrated that the proposed algorithm consistently outperforms existing methods—such as NSAF, CR-NSAF, UT-NSAF and DSU-NSAF—in terms of convergence rate, steady-state precision, and robustness under severe clipping distortion. However, it is worth noting that the current theoretical framework primarily relies on the assumption of Gaussian background noise, and its performance under highly dynamic clipping thresholds remains to be fully explored. Therefore, our future work will focus on developing unbiased adaptive filters tailored for time-varying clipping levels and non-Gaussian noise environments to further enhance the adaptability of the proposed method.