Voice Transformation Using Two-Level Dynamic Warping and Neural Networks

Abstract

Voice transformation, for example, from a male speaker to a female speaker, is achieved here using a two-level dynamic warping algorithm in conjunction with an artificial neural network. An outer warping process which temporally aligns blocks of speech (dynamic time warp, DTW) invokes an inner warping process, which spectrally aligns based on magnitude spectra (dynamic frequency warp, DFW). The mapping function produced by inner dynamic frequency warp is used to move spectral information from a source speaker to a target speaker. Artifacts arising from this amplitude spectral mapping are reduced by reconstructing phase information. Information obtained by this process is used to train an artificial neural network to produce spectral warping information based on spectral input data. The performance of the speech mapping compared using Mel-Cepstral Distortion (MCD) with previous voice transformation research, and it is shown to perform better than other methods, based on their reported MCD scores.

1. Introduction

Voice transformation (VT) refers to the process of changing speech so that speech uttered by one speaker (the source speaker) sounds as if another speaker (the target speaker) had spoken it, for example, transforming from a male voice to a female voice [1]. VT has applications such as text-to-speech synthesis (TTS), international dubbing, health-care, multi-media, language education, music, security-related usage, vocal restoration, speech-to-speech translation, and preprocessing for speech recognition, etc. [2,3,4].

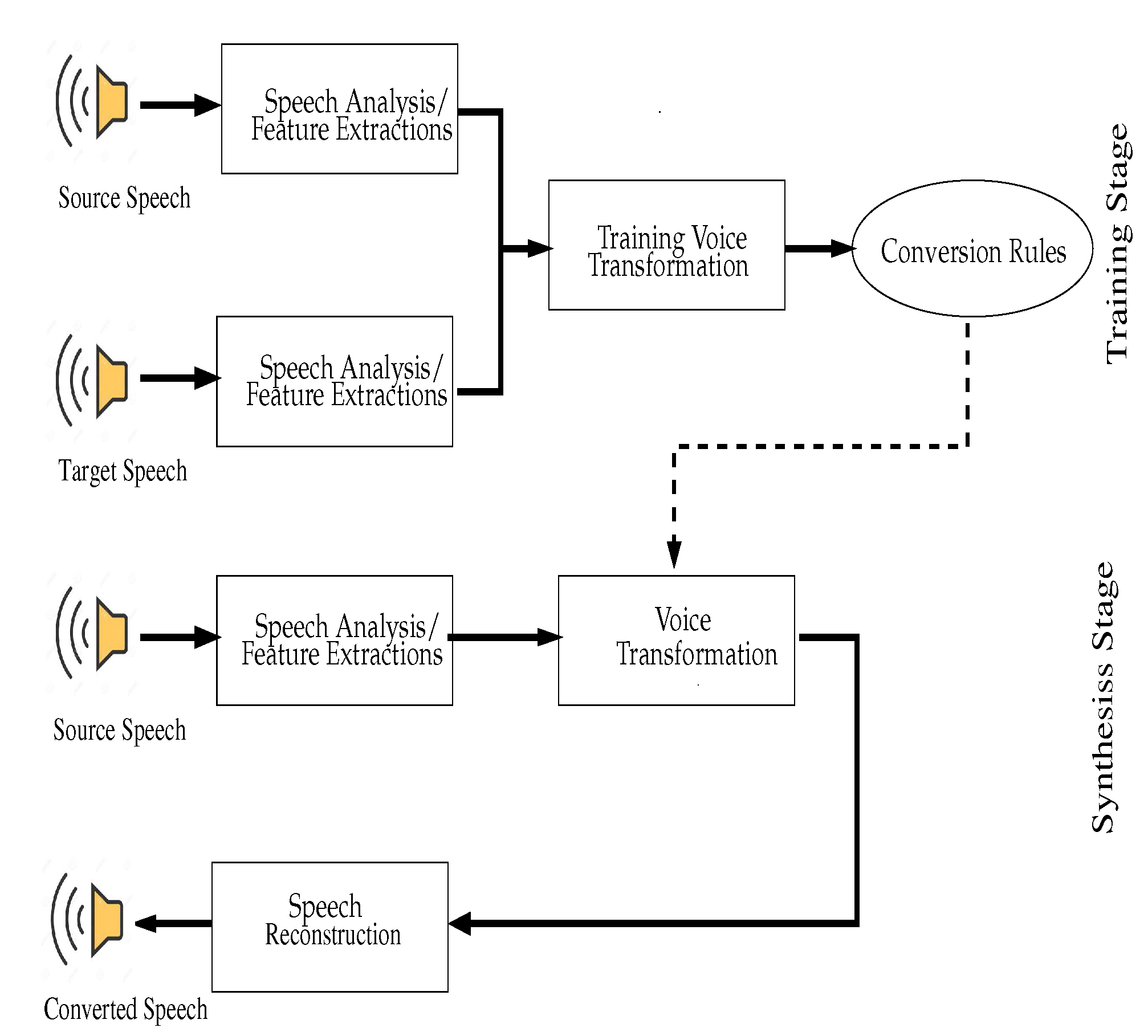
The general framework for VT is shown in Figure 1 [5]. In a training stage, performed offline, features are extracted from both source and target speech sources. VT, which maps information from the source speech to target speech, is trained to form conversion rules. In the actual operation, these conversion rules are used to convert features from a source to a target.

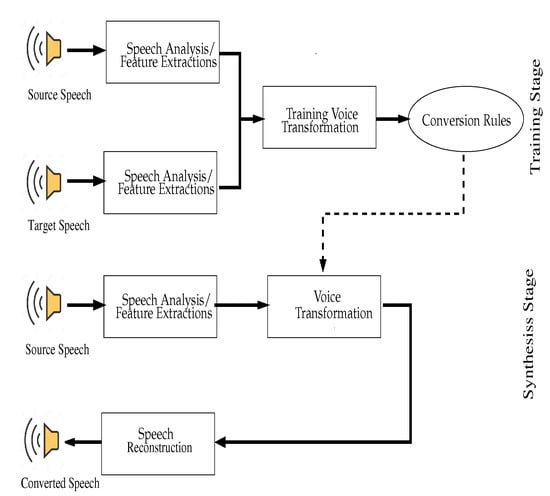
Figure 1. Typical voice transformation system.

In this work, the spectral features computed using the DFT are transformed using a neural network (NN). Speech signals are aligned using dynamic warping (DW) which aligns both temporally and spectrally to produce training data which is used to train a NN. The NN is trained to produce the spectral mapping functions determined by the frequency-domain warping. Several NN structures (differing numbers of layers, and differing numbers of neurons per layer) were examined to determine which had best performance, as measured by mel-cepstral distortion (MCD). On the basis of MCD, this method was compared with previously developed methods, and is shown to perform well. The test set was based on transformation of a male speaker to a female speaker. Future work will test this architecture transformations between different speakers.

2. Previous Voice Transformation Research

Early work on VT dates back to 1990, when the author in [6] proposed using a vector quantization approach, where the vector-quantized speech features are mapped spectrally via codebook mapping. The features transformed include acoustic features such as pitch, formant frequencies and bandwidth, spectral tilt, etc. [7,8]. These features are extracted and represented using vector quantized codebooks. Generally, codebooks are generated for both source speakers and target speaker. DTW is used to find the correspondence between these vectors. These correspondences are then accumulated to find a histogram, which is used as a weighting function to compute the mapping codebook from source speaker to a target speaker. In the synthesis step, the speech iwas quantized using the speaker’s codebook, then all feature parameters are transformed with the mapping codebook from the training step, and finally the speech is synthesized with LPC vocoder.

To improve this general approach, the authors in [9] propose a method of doing VT based on Pitch Synchronous Overlap and Add (PSOLA) to improve the quality of the converted speech signal. In this work, the authors introduced DFW to achieve VT.

Gaussian Mixture Models (GMMs) have been used for VT [10,11,12,13,14,15,16,17]. GMMs model the source and target data with a GMM to produce transformation functions for each Gaussian component [11]. Two approaches have been used for GMM-based VT techniques: first modeling the source and target information separately using a GMM [18], and second modeling the joint density GMM (JDGMM) between source and target speakers [10]. The conversion function is typical assumed to be probabilistic piecewise linear mapping function for each Gaussian. The unknown parameters are calculated by solving the normal linear conversion equations for a least squares solution [18]. The combination of the spectral source aligned vectors and the corresponding target aligned spectral vectors is used to estimate GMM parameters for the joint density model by using expectation maximization algorithm [11]. Although this algorithm works effectively, its conversion performance is still insufficient [19]. The performance of the standard GMM based VT method have been improved by implementing sophisticated techniques, such as Gaussian process regression [20,21], also using WaveNet vocoder in GMM-based voice conversion to improve the naturalness of the synthetic voice [15,16]. An improvement can be achieved by incorporating a trajectory-based conversion algorithm to achieve temporal correlation in the conversion process [18]. Additional features were modeled in order to reduce the over-smoothing effect of the transformed signal parameters, such us transformation based on matrix variate GMMs, in which joint features from the source and target speakers are represented as matrices using multiple frame features [14], global variance [22] and modulation spectrum [23]. Furthermore, a real-time conversion process has also been successfully implemented for state-of-the-art GMM-based VT [24].

As an alternative to the GMM, which relies on probabilistic mappings between the source and target parameters, DFW seeks to warp the source spectral information in frequency, in order to compensate for the differences between the spectral features of the source and the target speakers, to most closely match that of the target speaker [25]. Cepstral information was extracted from both source and target speakers to do DFW [26,27]. In [15] a new framework was proposed by combining frequency warping and exemplar-based method to achieve VT, where the target was represented by applying frequency warping on the high-resolution spectrum. The warping function is generated by a sparse interpolation from a dictionary of exemplar warping functions.

Neural networks have also been used for VT, where the NNs map the source speech feature vectors into the feature vectors of the target speaker [28,29]. The work [2] is an early effort using NN to transform the source speaker formants to target speaker formants using a feedforward NN. In [30], the authors proposed a method for VT using NN with three layers. This method is based on LPC spectral features using radial basis function NN. In [31] the authors compared using a NN and GMM for VT. GMMs capture the joint distribution of the source features and the target feature, while the work in [31] directly maps the spectral source feature information onto the spectral target feature information. Additionally, with GMM they use maximum likelihood parameters generation (MLPG) to obtain a smooth trajectory of spectral features, while the mapping with NN provide best transformation results without using MLPG.

Long short-term memory (LSTM) NNs have been used for VT [32]. The joint use of deep bidirectional (DB) LSTM and identify vectors (i-vectors) [33], Kullback–Leibler divergence and deep NN-based approach [34], and DBLSTM based Recurrent NNs [35,36], have been recently used for VT. More recently, Generative Adversarial Networks (GAN) such as VAW-GAN [37], CycleGAN [38,39], and many-to-many mapping with StarGAN [40] further advance the state-of-the-art.

Previous methods generally work by extracting a parametric acoustic parameter (such as pitch, MFCC, etc.) and transforming this parameter from one speaker to another based on estimated joint densities. This introduces complexities associated with this initial parameter estimation. The approach taken here avoids the need to find parametric acoustic parameters, or to model the joint density, and instead deals directly with spectral information. (That is, this is analogous to spectral estimation, where a parametric model might be used, such as AR or ARMA, or the spectrum may be estimated directly using the DFT.) NNs are used to learn the transformation which maps the spectral information of one speaker to another speaker. We have found that this basic idea yields improvements when the spectral information from the preceding and following speech segments are used to provide context. The transformation is achieved using a two-level DW. Based on the two-level DW it is straightforward to map the source speech to target speech when both are available.

3. Voice Transformation Process

3.1. Two-Level Dynamic Warping

The transformation in our VT is accomplished using a two-level DW transformation which aligns signals both temporally (DTW) and spectrally (DFW).

Let $i=1,2$ denote the index of a speaker, with $i=1$ representing the source speaker and $i=2$ representing the target speaker. Let ℓ be the index of a segment of speech, where successive segments may be overlapping. Let ${\mathbf{r}}_i(\ell ,:)$ denote the time-domain signal associated with the ℓth segment of speech. This is a vector of length $2K=512$. This was transformed using a 512-point FFT. This was normalized as follows. Let $D_i(\ell ,j)$, $i=1,2$, $\ell =1,2,\dots ,L_i$, $j=1,2,\dots ,K$ be the magnitude of the positive frequency coefficients in the DFT of ${\mathbf{r}}_i(\ell ,:)$. The feature vector is produced by

$${\mathbf{s}}_i(\ell ,j)=\frac{D_i(\ell ,j)}{\frac{1}{K{L}_i}\sqrt{{\sum }_{\ell =1}^{L_i}{\sum }_{j=1}^K{D}_i{(\ell ,j)}^2}},\ell =1,2,\dots ,L_i,j=1,2,\dots ,K.$$

A sequence of these feature vectors is denoted as

$$S_i=\{{\mathbf{s}}_i(1,:),{\mathbf{s}}_i(2,:),\dots ,{\mathbf{s}}_i(L_i,:)\},i=1,2.$$

(1)

Here, $L_1$ and $L_2$ denote the number of source and target feature vectors. Let $d_T({\ell }_1,{\ell }_2)$ denote the minimum cost between the sequences $S_1$ (source) and $S_2$ (target), up to segment indices ${\ell }_1$ and ${\ell }_2$, computed using DTW to align the segments in time. (The subscript T refers to time warping.) As usual for DTW [41], $d_T({\ell }_1,{\ell }_2)$ is recursively computed as

$$d_T({\ell }_1,{\ell }_2)=d({\mathbf{s}}_1({\ell }_1,:),{\mathbf{s}}_2({\ell }_2,:))+min\{d_T({\ell }_1-1,{\ell }_2),d_T({\ell }_1,{\ell }_2-1),d_T({\ell }_1-1,{\ell }_2-1)\}.$$

(2)

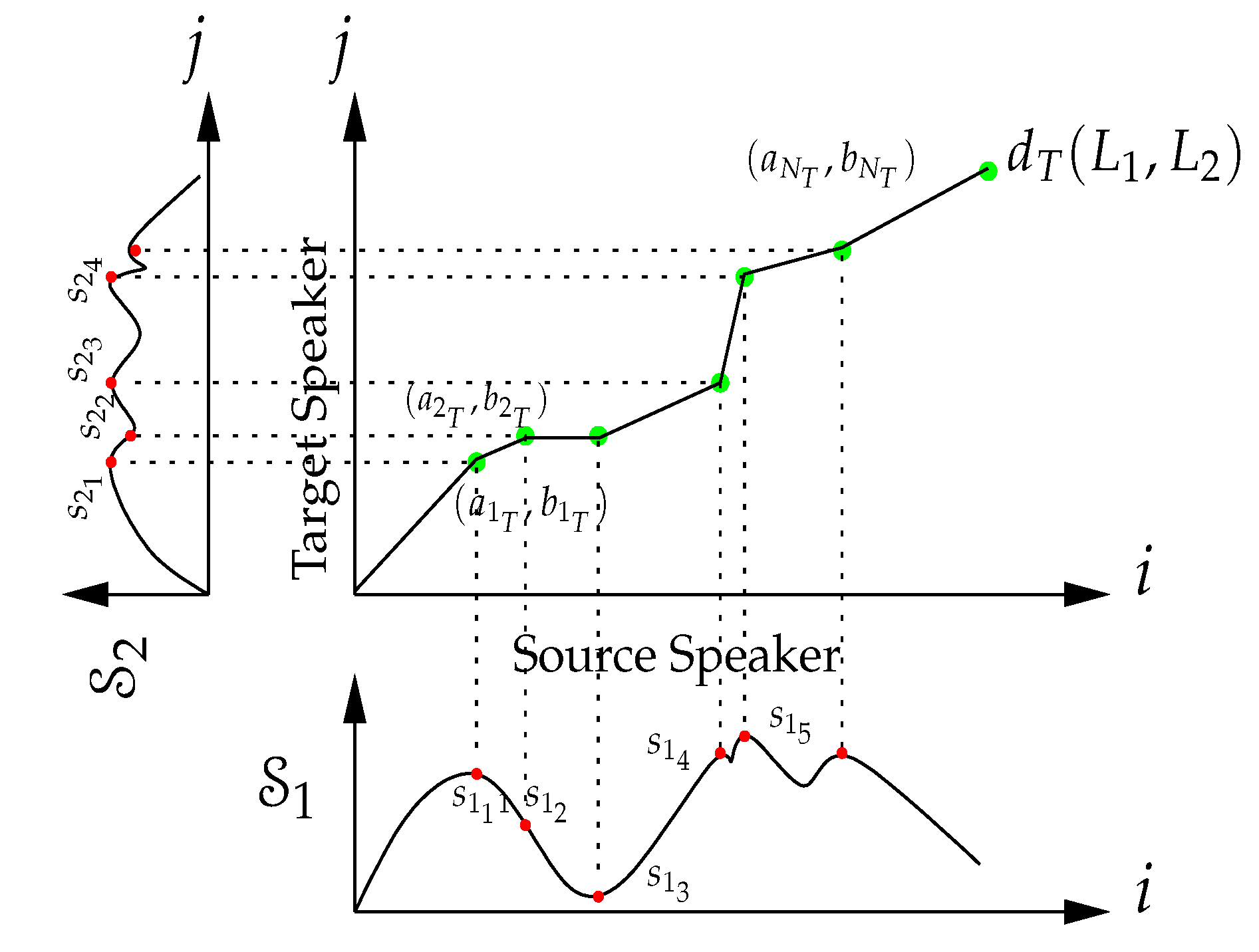
Here, $d({\mathbf{s}}_1({\ell }_1,:),{\mathbf{s}}_2({\ell }_2,:))$ is the distance between individual feature vectors at segments ${\ell }_1$ and ${\ell }_2$. This is computed using DFW, as described below. Conceptually, the dynamic warping aligns the peaks and valleys between the source and target data, as suggested by Figure 2. When ${\ell }_1=L_1$ and ${\ell }_2=L_2$, the temporal warping process determines an overall warped metric distance $d_T(L_1,L_2)$ between the sequences $S_1$ and $S_2$. DTW computes a sequence of indices ${\mathbf{a}}_T=(a_T\left(1\right),a_T\left(2\right),\dots ,a_T\left(N_T\right))$ and ${\mathbf{b}}_T=(b_T\left(1\right),b_T\left(2\right),\dots ,b_T\left(N_T\right))$, which are called the temporal warping function paths. The temporal warping function paths define a time-aligned (TA) function ${\mathbf{s}}_{1,TA}$ such that the sequence

$${\mathbf{s}}_{1,TA}(a_T\left(j\right),:)={\mathbf{s}}_1(b_T\left(j\right),:),j=1,2,\dots ,N_T$$

is as similar to $S_2$ as possible.

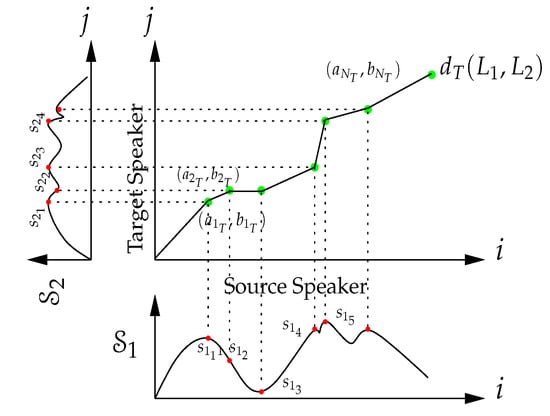
Figure 2. Distance measure for outer dynamic warping for VT.

The distance between two feature vectors in (2), $d({\mathbf{s}}_1({\ell }_1,:),{\mathbf{s}}_2({\ell }_2,:))$, can itself be computed using warping between the components of these individual vectors. Because these vectors represent frequency information, this is DFW. DFW is computed in a way similar to the DTW. Let ${\mathbf{s}}_i={\mathbf{s}}_i({\ell }_i,:)$, $i=1,2$ denote the spectral information vectors at segment ${\ell }_i$ that is passed to the DFW function from the (outer) DTW function. The elements of ${\mathbf{s}}_i$ are denoted by $s_i\left(k\right)$. DFW is applied to calculate the distance between ${\mathbf{s}}_1$ and ${\mathbf{s}}_2$ as

$$d_F(k_1,k_2)=\mathrm{dist}(s_1\left(k_1\right),s_2\left(k_2\right))+min\{d_F(k_1-1,k_2),d_F(k_1,k_2-1),d_F(k_1-1,k_2-1)\},$$

(3)

where the subscript ${}_F$ refers to a frequency (or spectral) warping process, and $\mathrm{dist}(s_1\left(k_1\right),s_2\left(k_2\right))$ represents the metric distance between elements of the feature spectral vectors. The metric distance, $\mathrm{dist}(s_1\left(k_1\right),s_2\left(k_2\right))$, used looks only at the magnitude of the spectral information, so

$$\mathrm{dist}(s_1\left(k_1\right),s_2\left(k_2\right))=\left(\right||s_1\left(k_1\right)|-|s_2\left(k_2\right)\left|\right|).$$

(4)

When there are low energy speech segments (such as from unvoiced speech) which have no particular spectral information to match, the distance $d({\mathbf{s}}_1,{\mathbf{s}}_2)$ is generally noninformative. In order to downplay this effect the small energy segments, the minimimum energy $E_{min}=min(\parallel {\mathbf{s}}_1{\parallel }^2,\parallel {\mathbf{s}}_2{\parallel }^2)$, is used to scale the distance, as follows. At the end of frequency warping process, the metric distance between spectral vectors to be used in (2) is computed as $d({\mathbf{s}}_1,{\mathbf{s}}_2)=E_{min}{d}_F(K,K)$.

The DFW on each feature vector produces a sequence of indices ${\mathbf{a}}_F=(a_F\left(1\right),a_F\left(2\right),\dots ,a_F\left(N_F\right))$ and ${\mathbf{b}}_F=(b_F\left(1\right),b_F\left(2\right),\dots ,b_F\left(N_F\right))$. ${\mathbf{a}}_F$ and ${\mathbf{b}}_F$ are called the spectral warping function paths. Here $N_F$ is the length of the spectral warping paths, which may be different from segment to segment.

The temporally aligned feature vector of speaker ${\mathbf{s}}_{1_{TA}}$ is transformed to spectrally match the target spectrum information of speaker ${\mathbf{s}}_2$ by creating a modified, spectrally-aligned (SA), feature vector according to

$$\begin{array}{c}\hfill {\widehat{s}}_{1,TF}\left(a_F\left(i\right)\right)=s_{1,TA}\left(b_F\left(i\right)\right),i=1,2,\cdots ,N_F.\end{array}$$

(5)

This SA map drags spectral components of source vectors to produce transformed voice spectra. Each time-aligned and spectrally-aligned segment is inverse Fourier transformed to produce the time signal for segment ℓ, ${\widehat{\mathbf{r}}}_2(\ell ,:)$. This time signal is windowed (we used a Hamming window of length 512 with 16-ms overlapping when the sample rate was 16,000 samples/sec) and the overlapping segments are added together.

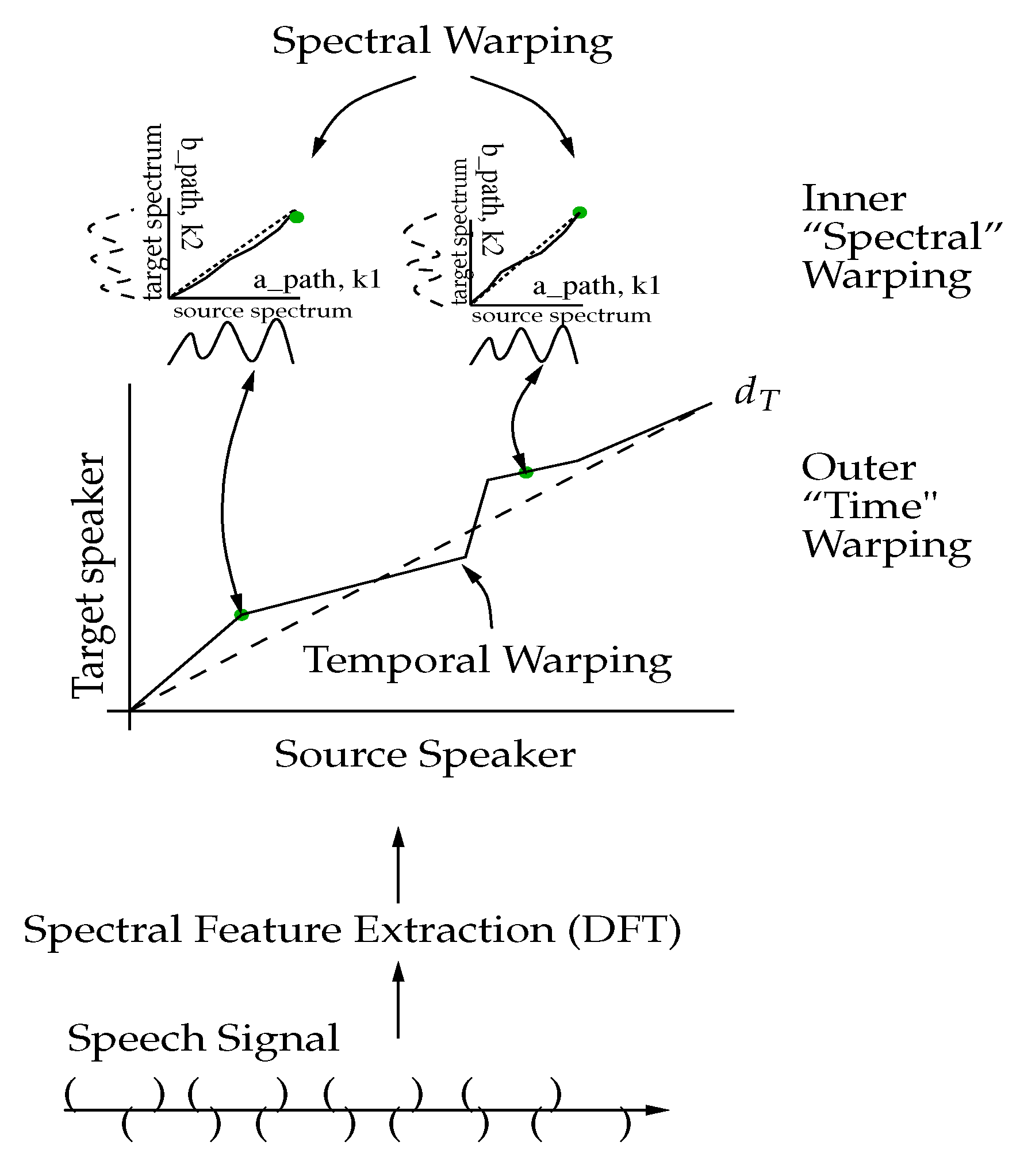
The combination of the inner and outer warping processes applied to speech signal is portrayed in Figure 3. Starting at the bottom of the diagram, a speech signal is split into different overlapping segments. Spectral features are computed for each segment. These spectral feature vectors are passed through DTW for time alignment, and at every stage of DTW, the metric between vectors is computed using DFW. The method for doing two-level DW to achieve VT is given in Algorithm 1.

Algorithm 1: Dynamic Warping ($DW$) for Voice Transformation.

Input: First spectral sequence, $S_1=\{{\mathbf{s}}_1(1,1:n_T),{\mathbf{s}}_1(2,1:n_T),\dots ,{\mathbf{s}}_1(n_F,1:n_T)\}$ Second spectral sequence, $S_2=\{{\mathbf{s}}_2(1,1:m_T),{\mathbf{s}}_1(2,1:m_T),\dots ,{\mathbf{s}}_1(m_F,1:m_T)\}$ window size $w_T$ for DTW process window size $w_F$ for DFW process Output: Distance between $S_1$ and $S_2$ Indices $\mathbf{a}\left(N\right)$ and $\mathbf{b}\left(N\right)$ for temporal alignment Indices $\mathbf{b}\left(M\right)$ and $\mathbf{b}\left(M\right)$ for spectral alignment Begin Initialize DTW array, $DTW=array[0\dots n_T,0\dots m_T]$ Initialize DFW array, $DFW=array[0\dots n_S,0\dots m_F]$ Adapt window size, $w_T=max(w_T,abs(n_T-m_T))$ For$i_T=1to{n}_T$  For $j_T=1to{m}_T$   $DTW[i_T,j_T]=\infty$  End For$j_T$ End For $i_T$ Set $DTW[0,0]=0$ For $i_F=1to{n}_F$  For$j_F=1to{m}_F$   $DTW[i_F,j_F]=\infty$  End For $j_F$ End For $i_F$ Set $DFW[0,0]=0$ For$i_T=1to{n}_T$  For$j_T=max(1,i_T-w_T)tomin(m_T,i_T+w_T)$    Adapt window size, $w_F=max(w_F,abs(n_S-m_F))$    For $i_F=1to{n}_F$     For $j_F=max(1,i_F-w_F)tomin(m_F,i_F+w_F)$     $cost=abs\left(abs\left(S_1(i_T,i_F)\right)\right)-\left(abs\left(S_2(j_T,j_F)\right)\right)$     $DFW[i_F,j_F]:=cost+minimum(DTW[i_F-1,j_F],$                       $DFW[i_F,j_F-1]$,                       $DFW[i_F-1,j_F-1])$   End For $j_F$  End For $i_F$  Searching minimum path through $DFW[i_F,j_F]$, save ${\mathbf{a}}_F,{\mathbf{b}}_F$  $cos{t}_{new}=DFW[n_F,m_F]$  Minimum energy [${\mathbf{s}}_1$ and ${\mathbf{s}}_2$]  $d=E_{min}cos{t}_{new}$  $DTW[i_T,j_T]:=d+minimum(DTW[i_T-1,j_T],$                     $DTW[i_T,j_T-1]$,                     $DTW[i_T-1,j_T-1])$ End For $j_T$ End For $i_T$ Searching minimum path through $DTW[i_T,j_T]$, save ${\mathbf{a}}_T,{\mathbf{b}}_T$

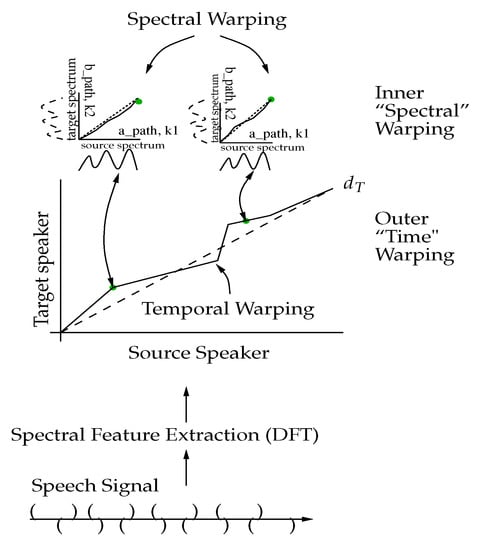
Figure 3. Inner/outer dynamic warping.

3.2. Experiment Description and a Proof of Concept Result

Experiments were carried out on CMU ARCTIC database [42]. The database consisted of seven primary sets of recordings, recorded by two US males, one Canadian male with English accent, one Scottish male with English accent, one Indian male, and two US females. Each speaker recorded a set of 1132 English utterances, most being between one and four seconds long and between 5 to 15 words long. The prompt list was designed to be phonetically balanced American English and have diphone coverage representative of the source material. The sound files were recorded in a soundproof booth at 16,000 samples/sec with simultaneous EGG measurements (the speech needed to be clean, or else background disturbances affected the transformed speech). The lexical and phonetic descriptions derived from the US English front-end module. In experiments presented here, one US male and one US female were chosen to do VT from male to female. While this was a limited experiment, since the transformation process was general (being based on DW of spectral features), this was considered a valid proof of concept for this initial experiment.

After identifying the starting point and ending point of the first 720 sentences of CMU ARCTIC database, each sentence was temporally segmented into 32-ms segments, using a Hamming window with 16-ms overlapping, zero-padded, then transformed using a 512-point FFT then normalized as described above. DW was applied on these features and the features of the first 600 sentences were used to train the NN and a separate set of 120 sentences were used for testing the trained NN.

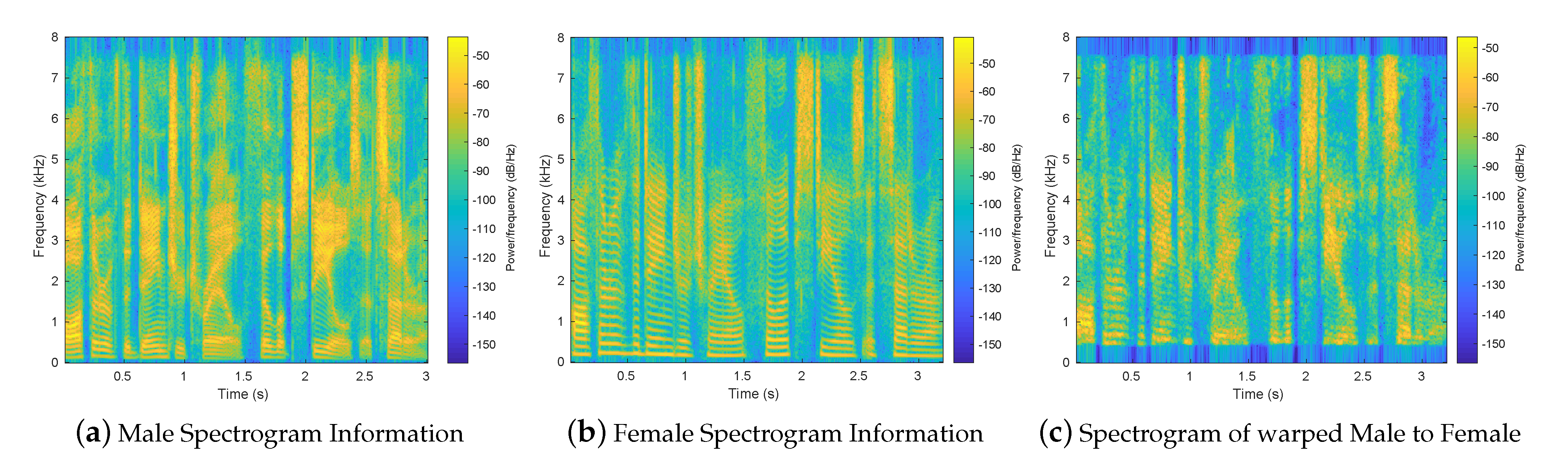
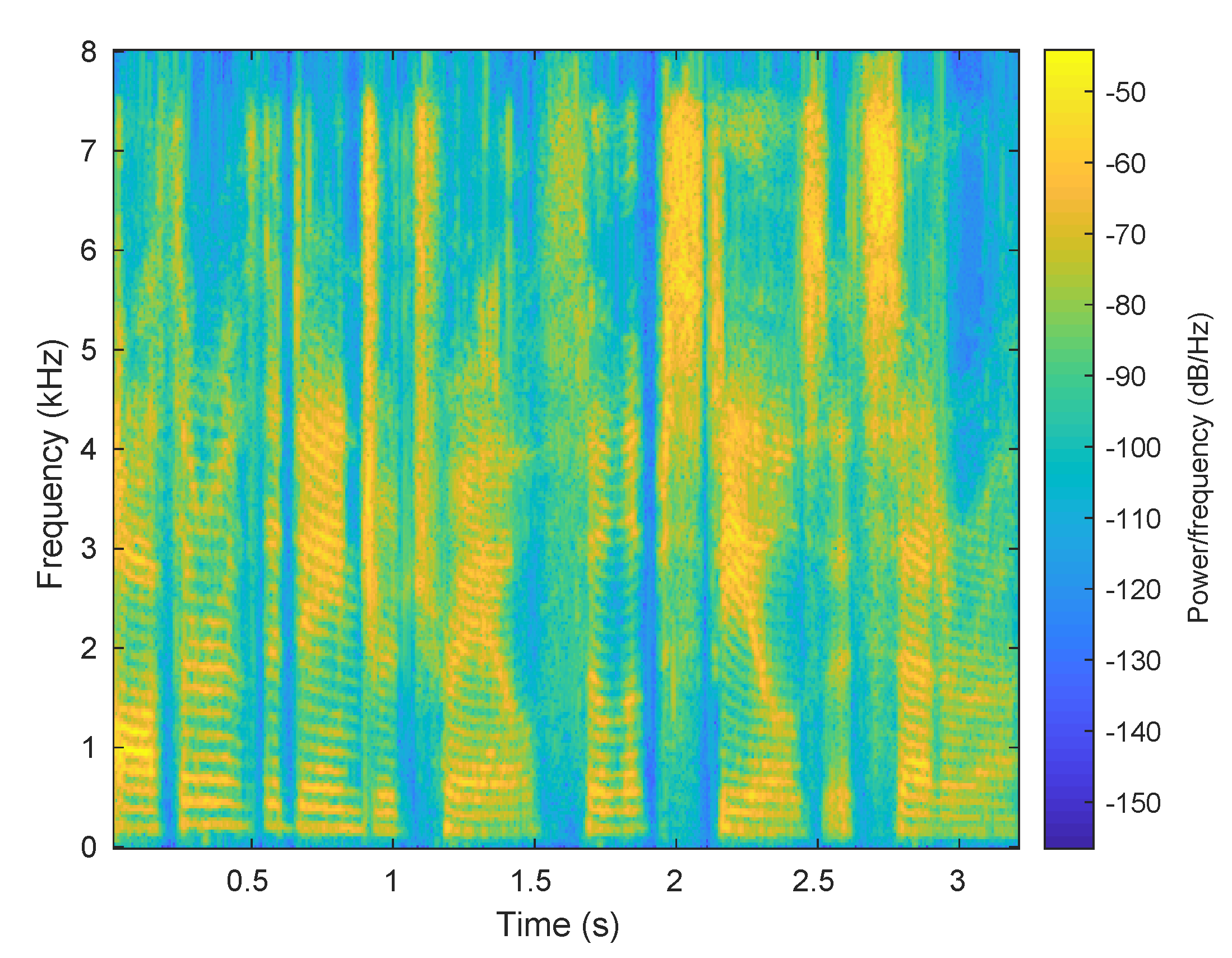
Figure 4a shows a typical spectrogram for a male speaker, using the phrase “Author of the danger trail, Philip Steels, etc.” from the CMU ARCTIC database. Figure 4b shows the spectrogram for a female speaker for the same phrase. Figure 4c shows the VT from male speaker to female speaker. After transformation, the overall energy distribution looked similar to the spectrogram of the female speaker. The fine-scale variations (the ripples in frequency) evident in Figure 4a,b are due to pitch. These lines are also in Figure 4c, but the pitch details are fuzzier. The resulting speech had very severe processing artifacts. (It did not sound very good.) Since the transformation only involved shifting magnitude spectral information, we were led to suspect that the problem might result from a mismatch between the magnitude and phase information of the warped signal.

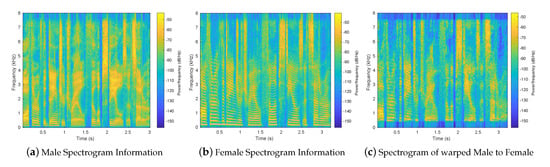
Figure 4. Spectrogram for male, female and warped male to female.

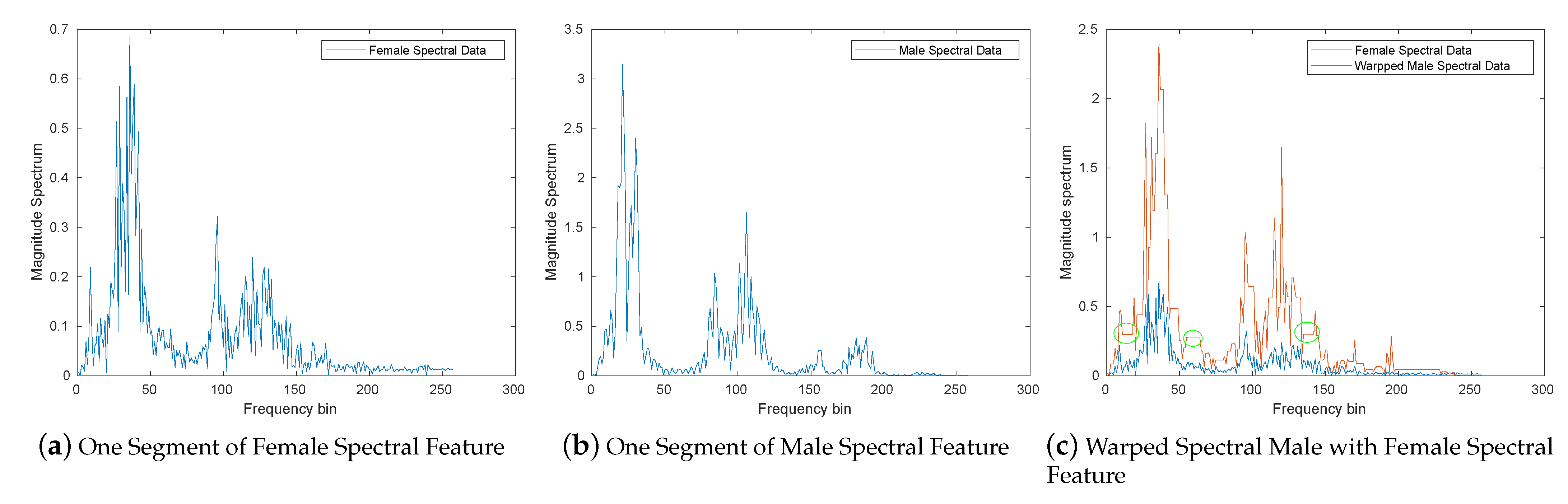
Figure 5a shows the spectral feature information for one segment of speech for the female speaker. Figure 5b shows the spectral feature information for one time-aligned segment of speech for the male speaker. By applying the DFW, the peaks and valleys of the male spectrum were generally aligned to the peaks and valleys of the female spectrum, as portrayed in Figure 5c. In warping the spectral information, artifacts were introduced into the signal which were not typical of speech. For example, Figure 5c shows that the warping smeared some spectral values across several frequency bins (indicated with green circles) in the plot, resulting in regions of the spectrum that had constant spectral magnitude.

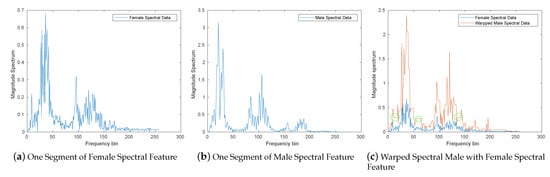
Figure 5. One spectral segment feature for male, female and warped male to female.

We found that the quality of the speech was significantly improved by using a phase reconstruction algorithm on the warped speech. In this work, the Griffin–Lim algorithm [43] was applied to do phase reconstruction after the spectral transformation has been accomplished [44].

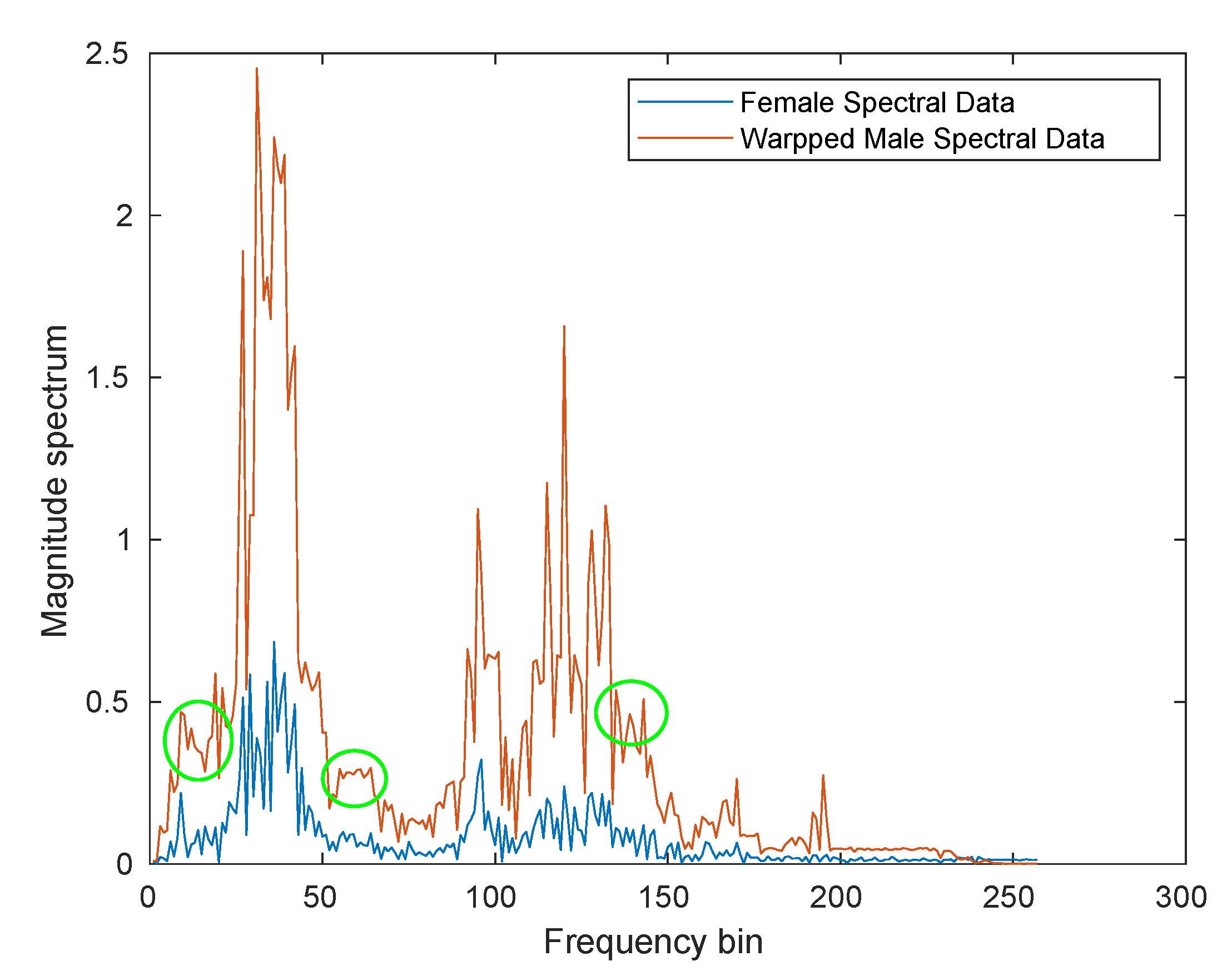
Figure 6 shows the spectrogram for the warped speech after phase reconstruction. The pitch lines were stronger (less fuzzy) after the GLA phase reconstruction. Figure 7 shows the spectral feature information for one segment of speech for the female speaker with the time aligned spectral warped segment for male from the phrase mentioned above. The peaks and valleys were still aligned, but the regions where there were spectral flats in Figure 5c, denoted by the green circles, were replaced with more speech-like spectra.

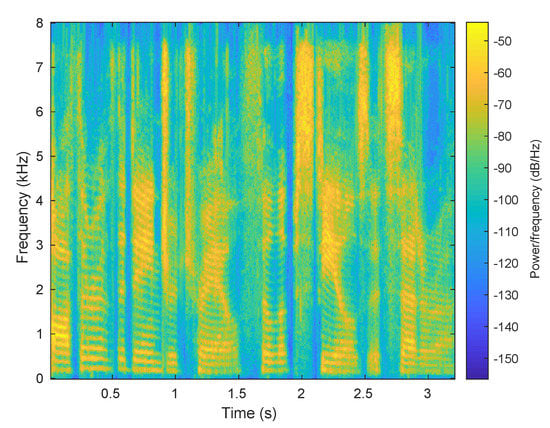
Figure 6. Spectrogram information for warped male to female with using GLA.

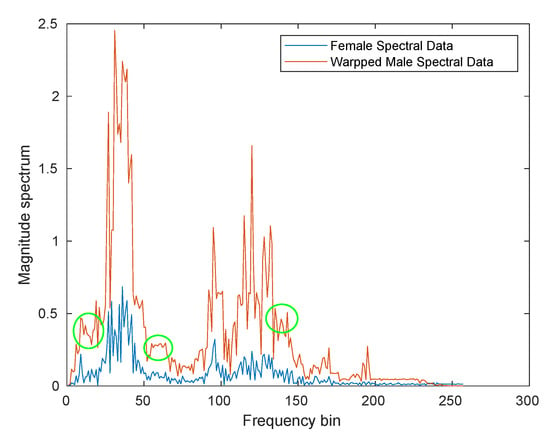
Figure 7. One spectral segment feature for warped male to female with GLA.

Table 1 shows the MCD score obtained using warping with and without the GLA phase reconstruction. The MCD was nearly 3 dB better when GLA phase reconstruction was used. The audio file also sounded significantly better. This verified that the MCD was valid as a measure of audio quality, and that the phase reconstruction was an important part of the VT. Phase reconstruction was used in all transformation experiments described below.

Table 1. MCDs obtained for 2-Level DW with and without GLA.

No.	Two-Level DW Method	MCD [dB]
1	DW, with phase reconstruction	2.4
2	DW, without phase reconstruction	6.3

4. Spectral Warping Using NN

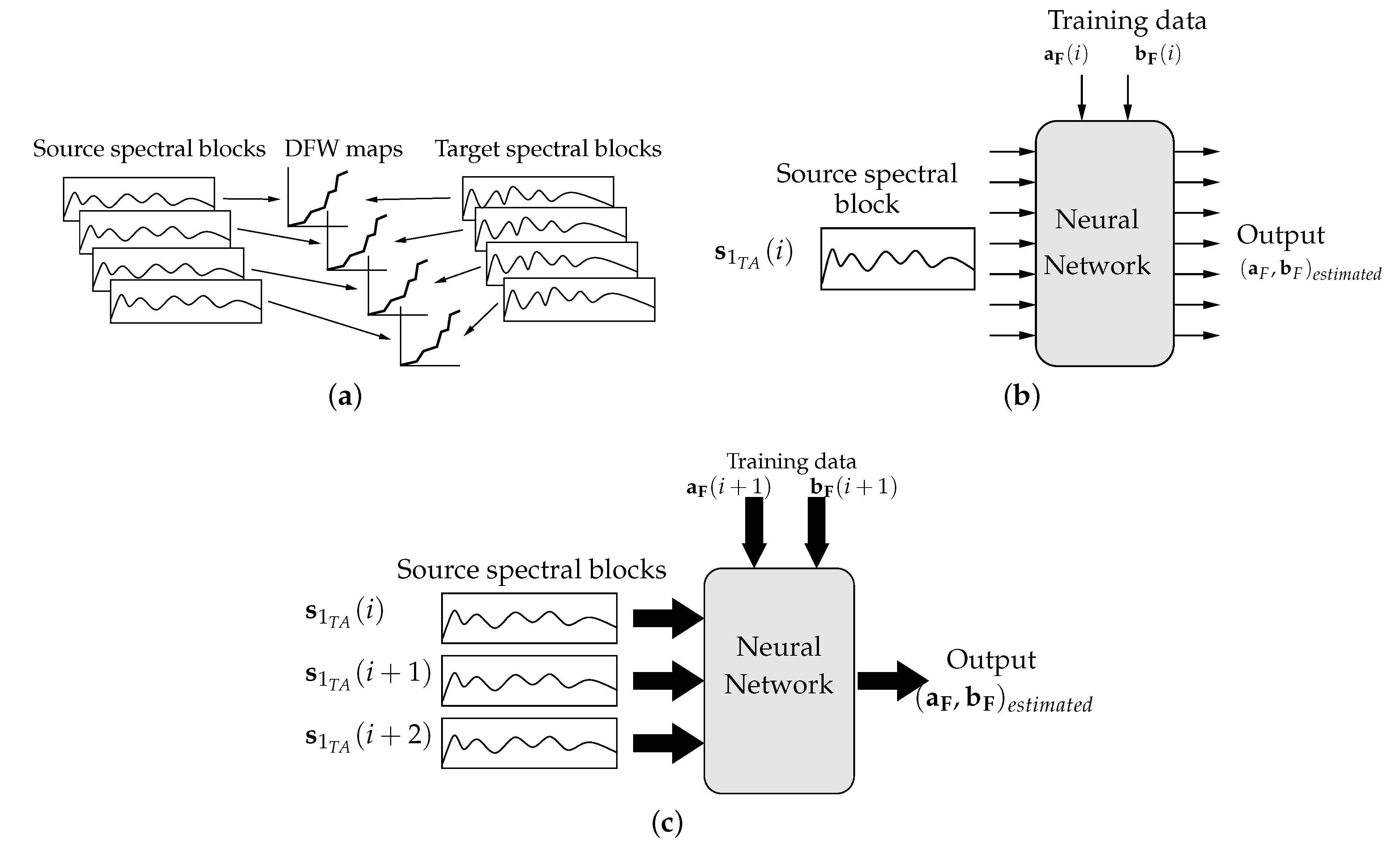
The proof-of-concept experiments above demonstrated that spectral mapping followed by phase reconstruction produces effective VT. For a complete, viable VT system, it is necessary to establish conversion rules for transforming speech when the target speaker saying the desired phrase is not available. These conversion rules are represented using a NN which is trained to accept spectral inputs from the source speech and to produce the spectral warping function paths, ${\mathbf{a}}_F$ and ${\mathbf{b}}_F$. The process is outlined in Figure 8. The input data for training the NN is the magnitude of the spectrum of a segment of speech that has been time-aligned with the target speech. The spectral information for segments of speech from source and target are used in DW to find the $({\mathbf{a}}_F,{\mathbf{b}}_F)$ spectral warping information, as suggested by Figure 8a. The NN is trained to produce this $({\mathbf{a}}_F\left(i\right),{\mathbf{b}}_F\left(i\right))$ information when the magnitude spectrum for the segment ${\mathbf{s}}_{1_{TA}}$ is the input. This is suggested by the NN diagram in Figure 8b.

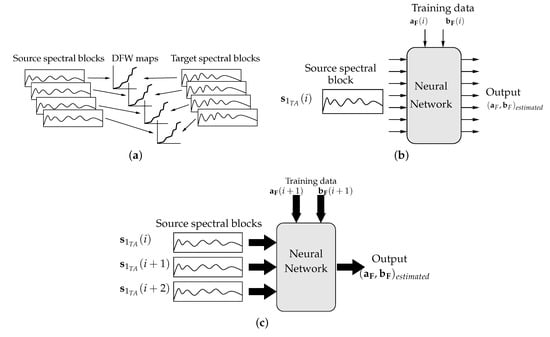
Figure 8. Spectrogram for male, female and warped male to female. (a) Making DFW training data. (b) Training a neural network—one input spectral vector. (c) Training a neural network—three input spectral vectors.

It was found that better VT was produced when the NN uses the spectral magnitude from the preceding segment ${\mathbf{s}}_{1_{TA}}\left(i\right)$ and the following segment ${\mathbf{s}}_{1_{TA}}(i+1)$ as inputs, to provide context for the current segment ${\mathbf{s}}_{1_{TA}}(i+2)$. This configuration is suggested in Figure 8c.

Interpolating the Data to Achieve Constant Length

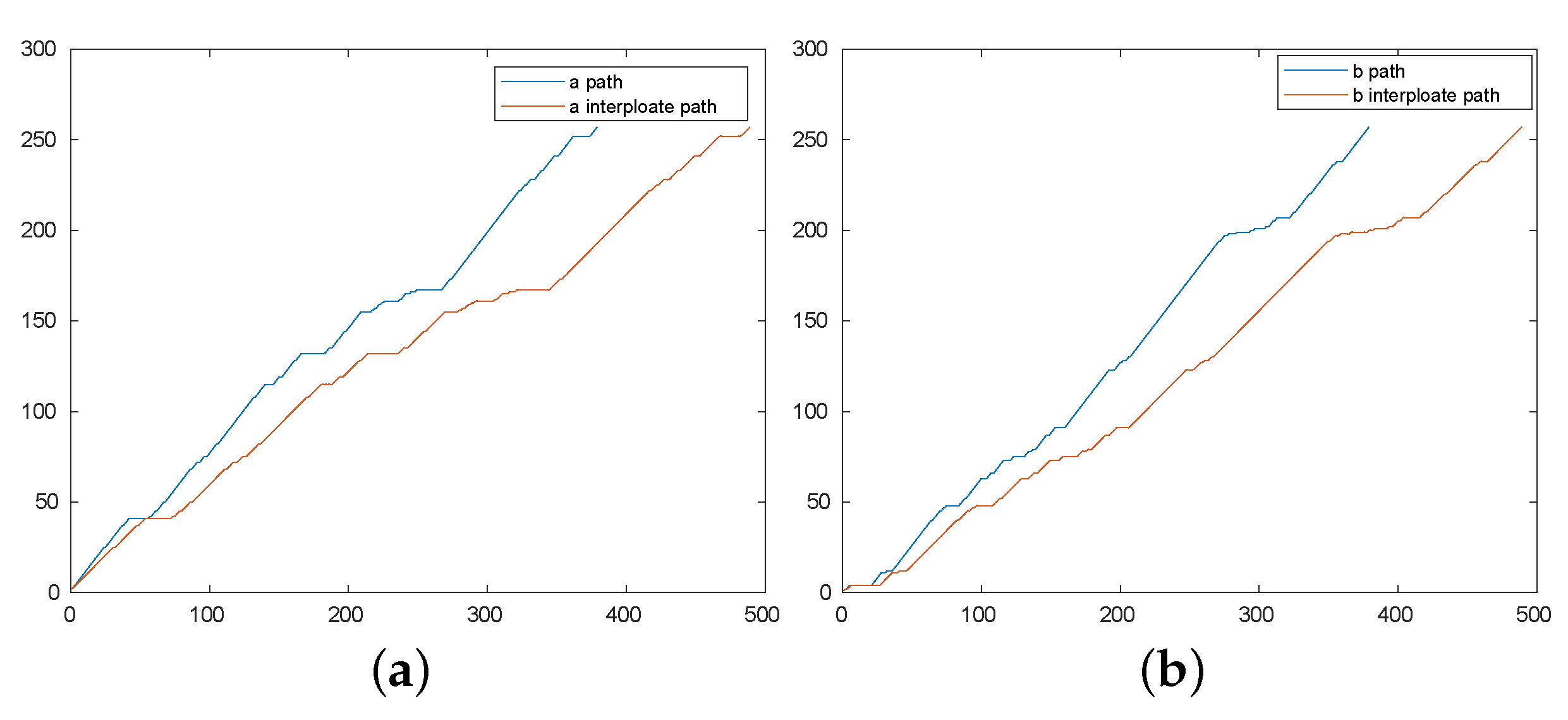
As noted above, the length of the warping path $({\mathbf{a}}_F,{\mathbf{b}}_F)$ may vary among the different segments of speech. This varying length poses a problem for a NN which has a fixed number of outputs. Rather than zero-pad the outputs of the NN to produce a desired length (which would create artifacts) the ${\mathbf{a}}_F$ and ${\mathbf{b}}_F$ are interpolated to produce a modified ${\mathbf{a}}_F$ and ${\mathbf{b}}_F$ which is the same (maximum) length for all segments of the speech vector. In our experiments the maximum length of the warping paths was 482 (as determined from training data). The interpolation is described using Matlab-like notation and functions. Let ${max}_{\mathrm{index}}$ denote the maximum length of the interpolated vectors. The interpolation procedes in two steps. First, interpolated indices are computed according to

$$\tilde{n}=[1:{\max }_{\mathrm{index}}]\times \frac{\mathrm{length}\left(\mathbf{a}\right)}{{max}_{\mathtt{index}}};$$

Then interpolation among the $\mathbf{a}$ values using these interpolated indices is computed by

$$\tilde{\mathbf{a}}=\mathrm{interpolate}(\mathbf{a},[1:\mathrm{length}\left(\mathbf{a}\right)],\tilde{n})$$

The sequence $\mathbf{b}$ is similarly interpolated. Figure 9 illustrates un-interpolated function paths for $\mathbf{a}$ and $\mathbf{b}$ with interpolated paths ($\tilde{\mathbf{a}}$ and $\tilde{\mathbf{b}}$ respectively). The interpolated $\tilde{\mathbf{a}}$ and $\tilde{\mathbf{b}}$ have the same general shape as the original $\mathbf{a}$ and $\mathbf{b}$, but have length 482, as desired. The NN is trained to produce the interpolated warping sequences at its output.

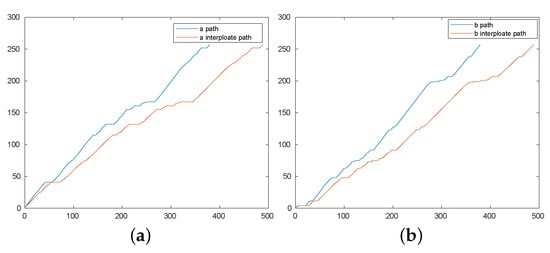
Figure 9. Un-interpolated and interpolated paths. (a) $\mathbf{a}$ and $\tilde{\mathbf{a}}$. (b) $\mathbf{b}$ and $\tilde{\mathbf{b}}$.

5. Mel-Cepstral Distortion as an Objective Measure

We use Mel-Cepstral Distortion (MCD) to evaluate the quality of the transformed speech, and to be able to compare our work to other work in the literature. MCD has been used as an objective error measure for evaluating the quality of synthetic voice [10]. It is a measure of the difference between two sequences of mel-cepstra. It is computed as

$$MCD=(10/ln10)\sqrt{2\sum _{i=1}^{25}{(m{c}_i^{\left(t\right)}-m{c}_i^{\left(w\right)})}^2}$$

(6)

where $m{c}_i^{\left(t\right)}$ and $m{c}_i^{\left(w\right)}$ represent the mel-cepstrum of the target speech and warped speech, respectively.

We used MCD both as a way of evaluating the performance of different NN architectures, as well as a tool for comparing with previous VT research which reports MCD scores.

6. NN Architecture Experiments

A series of experiments was conducted to determine an effective NN structure. Two different input models were considered. In the first model, a single input block of time-aligned spectral magnitude data, ${\mathbf{s}}_{1,TA}(:,i)$, is presented as the input of the NN. There are 256 inputs in the block (corresponding to the positive frequencies of the DFT of a 512-sample segment of speech). The NN has 482 outputs for each element of $\mathbf{a}$ and $\mathbf{b}$ for a total of 964 outputs. (482 is the largest length of the $\mathbf{a},\mathbf{b}$ data that was found among the training data.) This architecture is referred to as the 1-IP/1-OP model.

In the second model, three consecutive time-aligned vectors $({\mathbf{s}}_{1,TA}(:,i),{\mathbf{s}}_{1,TA}(:,i+1),{\mathbf{s}}_{1,TA}(:,i+2))$ were used as the input, for a total of 768 inputs. The three inputs provided temporal/frequency context for the central block. There were still 964 outputs. This architecture is called the 3-IP/1-OP model.

Training was performed by Tensorflow and Keras to estimate the warping paths. The neural architecture was developed in a series of phases, as described below. Initialize weights were selected at random. Each optimizer was trained for different learning rates (1, 0.1, 0.01, 0.001, 0.0001 and 0.00001); we found that a learning rate of 0.001 achieved the best results. Our NN models were trained with different optimizers (Gradient Descent, Adam and RMS Prop). The best optimizer for this work was the Gradient Descent. The NN architecture was developed in a series of phases, as described below.

6.1. Phase One

This phase was designed as a proof of concept: can a NN learn the spectral warping function paths? For this phase, a single phrase was selected to be trained using the two input models mentioned above. This phase also provided a basis for exploring different NN architectures. For all these tests, the phrase, “Author of the danger trail, Philip Steels, etc.” was selected from the CMU-ARCTIC database.

We experimented with both input models on different number of layers in order determine a good architecture. Table 2 shows the number of nodes in each layer and the output function used for that layer for both architecture. The notation 256L 500R 900R 1000R 964L means that this NN had 5-layers with 256 inputs, 964 output nodes with 500, 900, and 1000 neuron nodes in the hidden layers. L and R represent “linear” and “ReLU” activation output functions, respectively. This table also shows results for architectures described in later phases of development.

Table 2. MCDs obtained for different architectures.

Phase No.	Input Model	Architecture Type	NN Architecture	MCD [dB]
		5	256L 600R 1200R 1000R 964L	20.5
	1-IP-1-OP	6	256L 600R 1000R 1500R 1000R 964L	18.01
		7	256L 600R 1000R 1500R 2000R 1500R 964L	18.002
		19	500L 1500R 2500R 3500R 4500R 5040R 6459R 7459R	3.3
			8459R 9459R 10459R 8459R 7939R 6939R 5500R 4500R
			3500R 2500R 964L
Phase One		20	500L 1500R 2500R 3500R 4500R 5040R 6459R 7459R	5.5
			8459R 9459R 10459R 9459R 8459R 7939R 6939R 5500R
			4500R 3500R 2500R 964L
		5	768L 4500R 6500R 6939R 964L	16.85
		6	768L 4500R 6500R 7040R 6939R 964L	15.3
	3-IP-1-OP	7	768L 4500R 6500R 8040R 8939R 6939R 964L	12.92
		9	768L 4500R 6500R 7040R 9459R 8939R 7939R 6939R 964L	7.5
		10	768L 4500R 6500R 7040R 9459R 10459R 8939R 7939R 6939R 964L	4.7
		19	1500L 2500R 3500R 4500R 6500R 7040R 8459R	2.25
			9459R 10459R 10459R 9459R 8459R 7939R 6939R 5500R 4500R
			3500R 2500R 964L
		20	1500L 2500R 3500R 4500R 6500R 7040R 8459R 9459R	3.5
			10459R 11459R 10459R 9459R 8459R 7939R 6939R 5500R 4500R
			3500R 2500R 964L
Phase Two	3-IP-1-OP	19	1500L 2500R 3500R 4500R 6500R 7040R 8459R 9459R	4.8
			10459R 9459R 8459R 7939R 6939R 5500R 4500R 3500R
			2500R 964L
Phase Three	3-IP-1-OP	Six-Clusters.Each Cluster trained for 19 layers	1500L 2500R 3500R 4500R 6500R 7040R 8459R 9459R 10459R	2.8
			10459R 9459R 8459R 7939R 6939R 5500R 4500R 3500R 2500R
			964L
Phase Four	1-IP-1-OP	7	256L 64R (k = 3) 100R (k = 3) 150R (k = 3) 100R (k = 3) FL D100R 964L	13.33
	3-IP-1-OP	5	768L 64R (k = 3) 100R (k = 3) FL D100R 964L	13.5

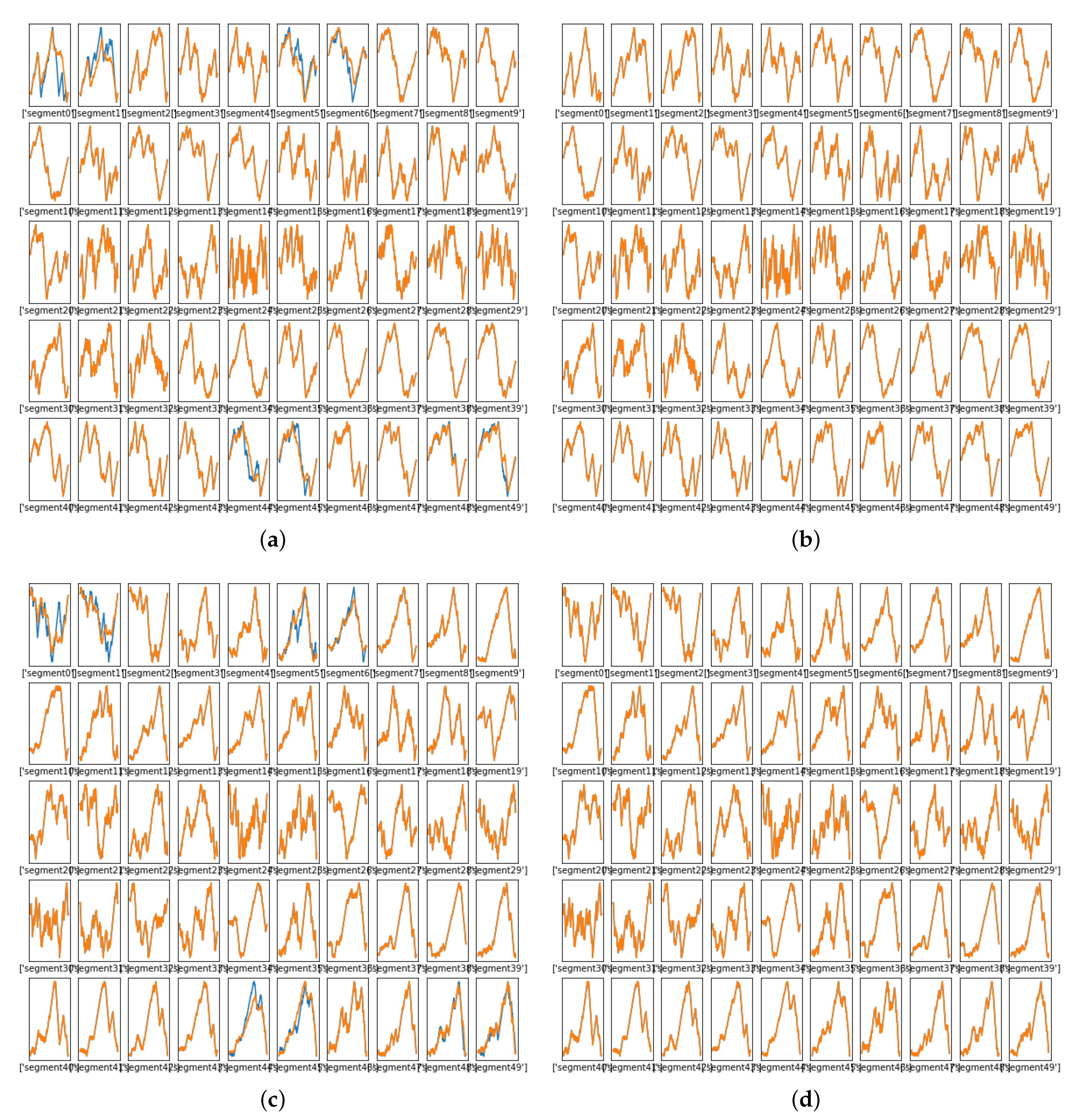
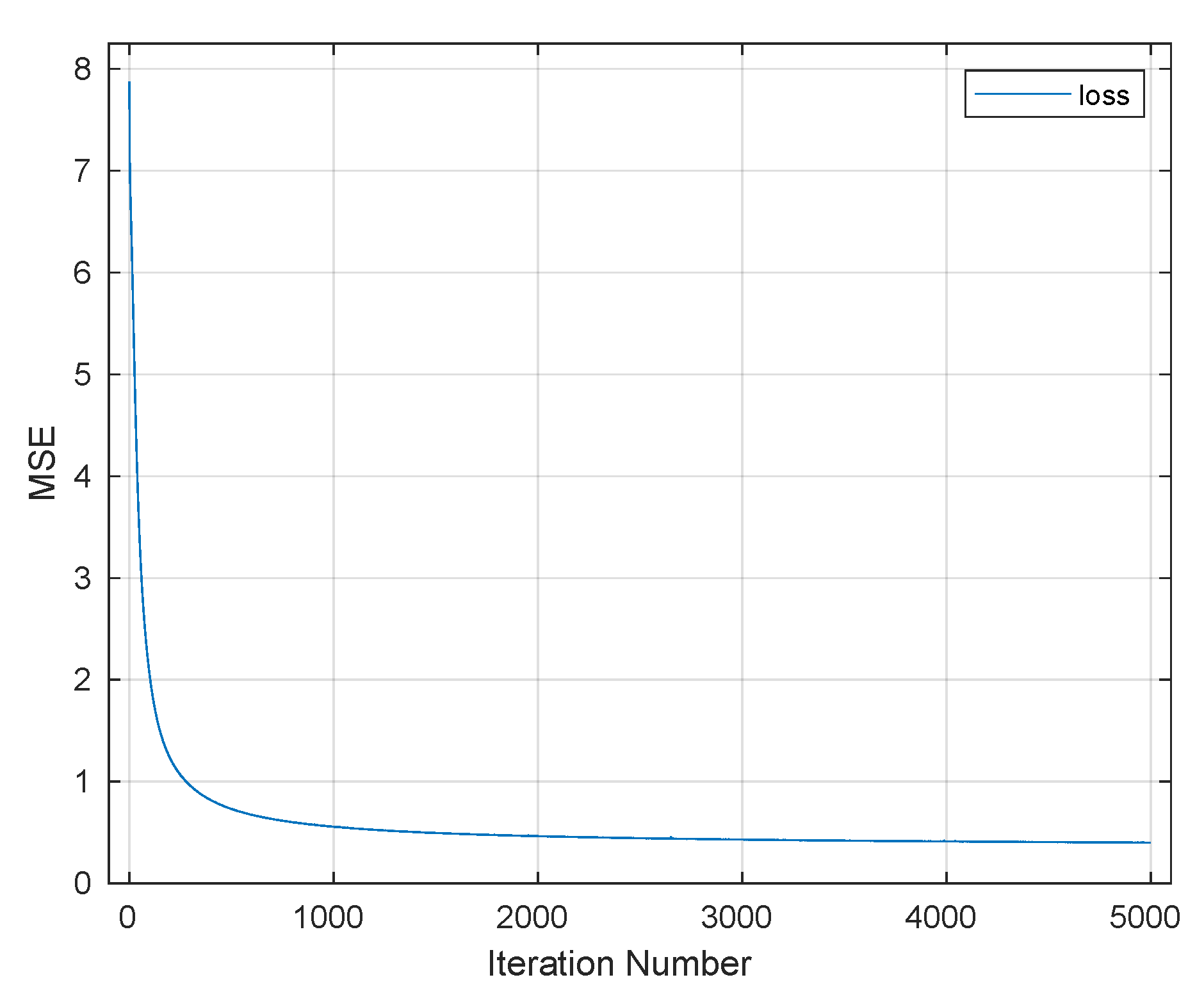
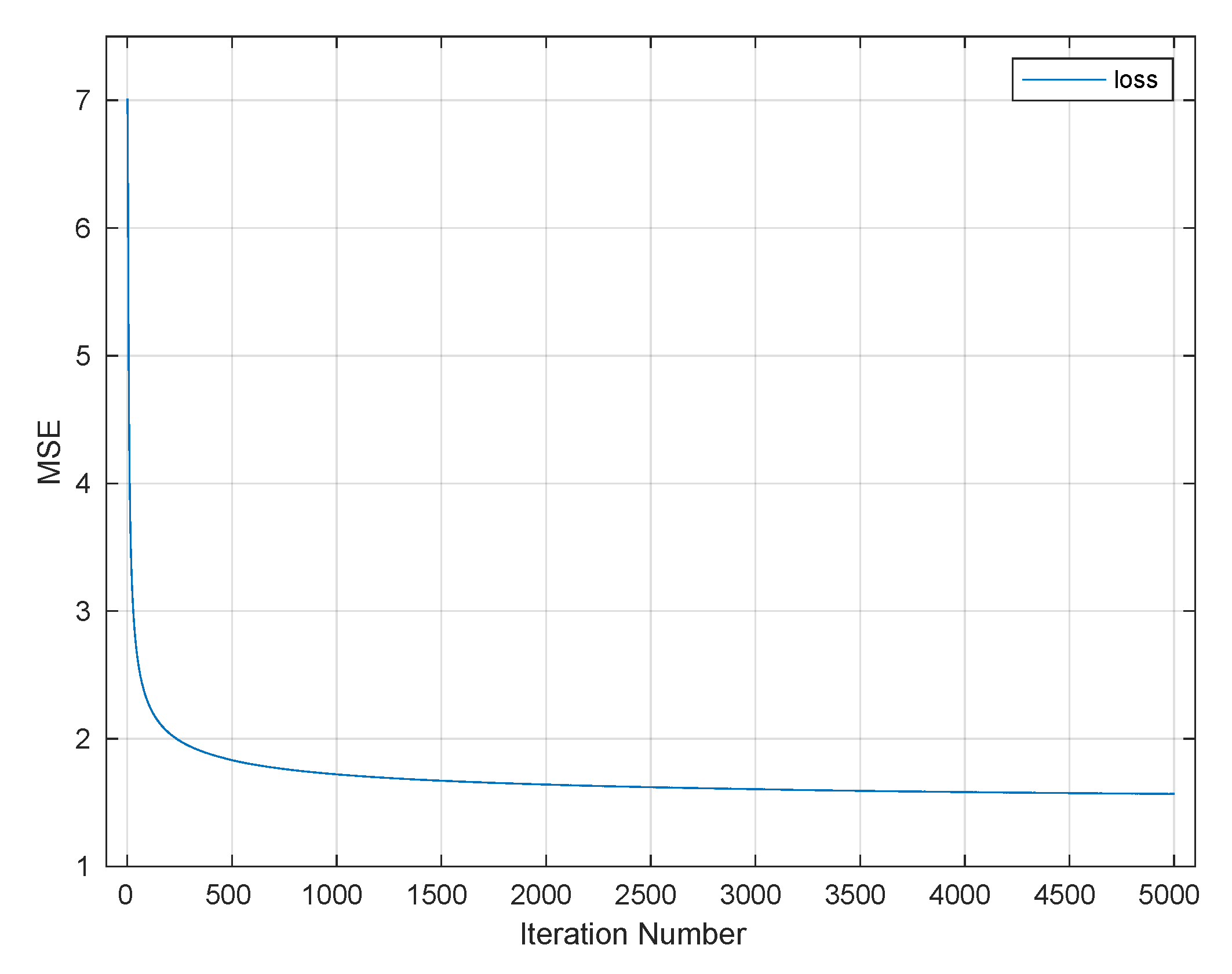
Figure 10 shows how the NN learned warping paths at various segments of the selected speech signal for different training iterations. In this figure, each subplot represents the mapping for one spectral segment of speech. In each of these, the blue plots shows the “truth” from DW the paths; the NN-learned paths are in orange. In this figure, the horizontal axes are the sequence of indices (1–468) and the vertical axes are the values of the ${\mathbf{a}}_F$, truth and learned. Figure 10a uses the 19-layers-1-IP/1-OP architecture. There was fairly good matching between the training data and the NN output, but Figure 10b, produced using the 19-layers-3-IP/1-OP architecture showed better results, with the training data being virtually indistinguishable from the NN outputs. Figure 10c,d shows how the NN learned a $\mathbf{b}$ warping path at various segments of the selected speech signal after 5000 training iterations. Again an excellent match was achieved with 3-IP/1-Op architecture. Not only was the NN better trained as demonstrated by these figures, but the quality of the audible transformed signal was significantly better when the three-input NN was used. Figure 11 shows the MSE between the true and estimated warping paths for the selected architecture (3-IP/1-OP) with 5000 training iterations, demonstrating that the learning essentially converged by that point.

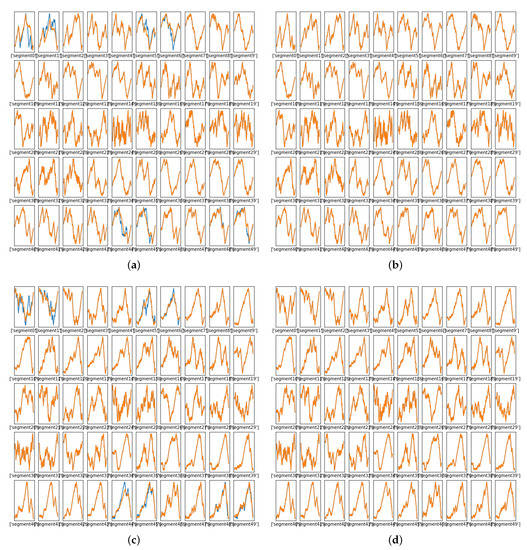
Figure 10. Learned warping paths, phase one, 5000 training iterations. (a) Warping path $\mathbf{a}$ produced using 1-IP/1-OP architecture. (b) Warping path $\mathbf{a}$ produced using 3-IP/1-OP architecture. (c) Warping path $\mathbf{b}$ produced using 1-IP/-1-OP architecture. (d) Warping path $\mathbf{b}$ produced using 3-IP/1-OP architecture.

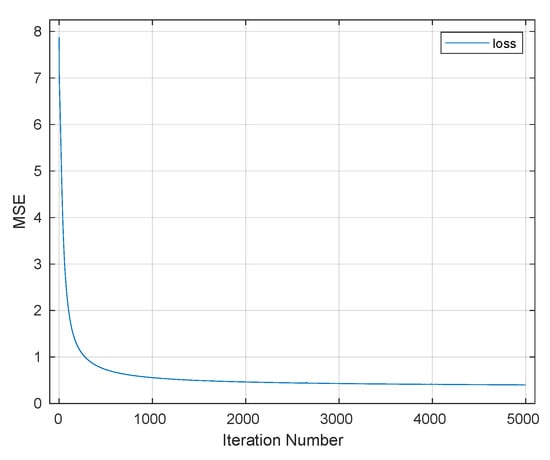
Figure 11. Mean squared error (l curve), phase one.

The use of three input blocks provided results superior to the single input block model. On the basis of the MCD values from Table 2 and Figure 10b,d, we concluded that the NN used in the phases of this experiment should be based on the 19-layers-3-IP/1-OP architecture.

6.2. Phase Two

After validating from Phase One that the NN was able to produce good transformed speech for a single phrase, the NN was trained to deal with multiple phrases. In this phase, training was conducted using 600 phrases from a single speaker for training, and a separate set of 120 phrases from a single speaker was used to test. The selected NN architecture was trained for 10,000 iterations.

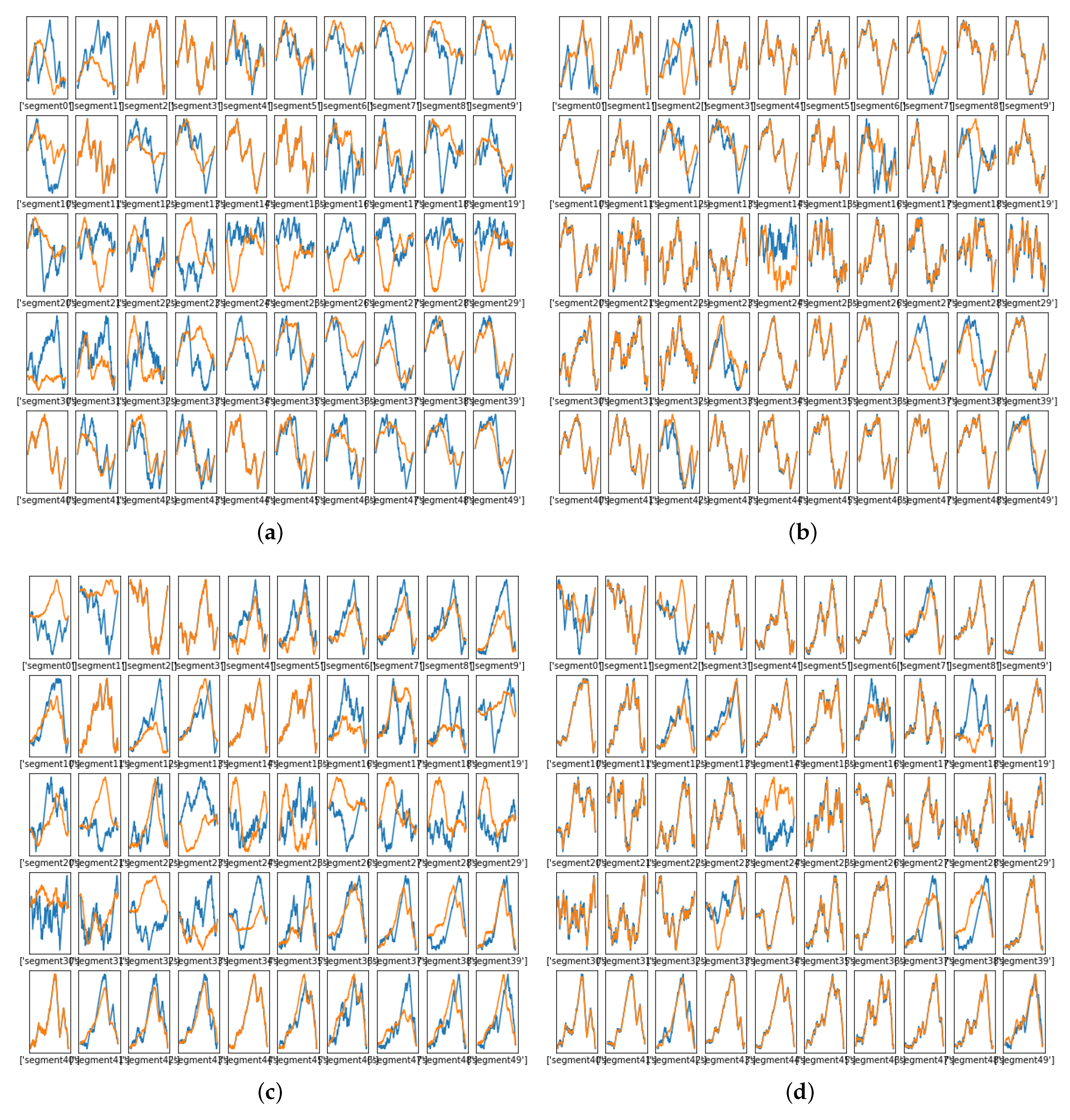
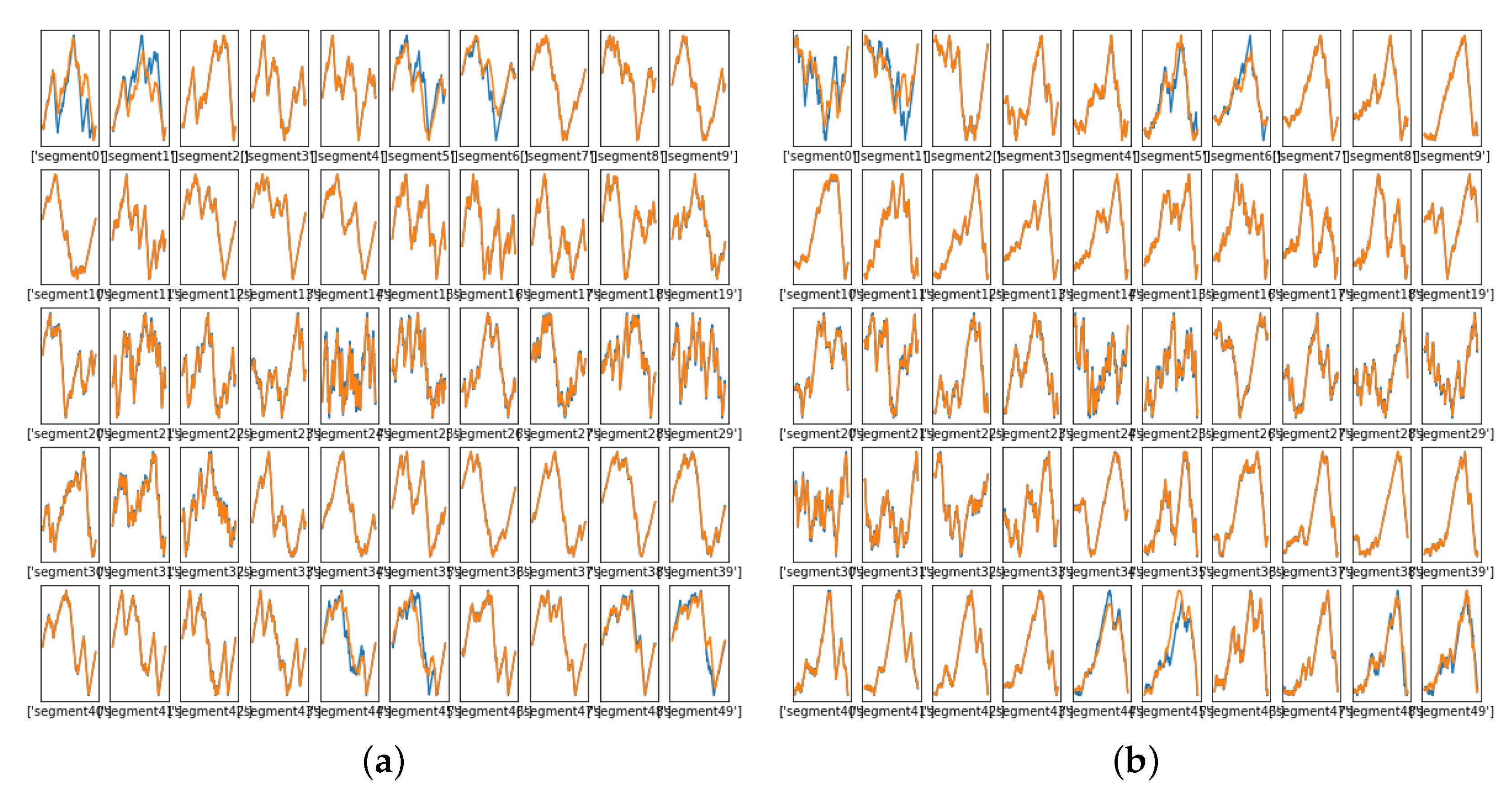
Figure 12 shows the warping paths for some of the segments, where the DW path (truth) is shown in blue and the learned path is in orange. The NN learned some of the warping paths well. Figure 12b, which was produced using the selected architecture after 10,000 training iterations, showed more matching between the ${\mathbf{a}}_F$ warping path and the learned path than Figure 12a, which was produced at 2500 training iterations. Figure 12d, which was produced at 10,000 training iterations, showed more matching between the ${\mathbf{b}}_F$ warping path and the learned path than Figure 12c, which produced at 2500 training iterations. By 10,000 training iterations, many of the warping functions were learned well, but there was still a significant number that were not learned well. Figure 13 shows the MSE between the true values of the warping paths and the estimated one.

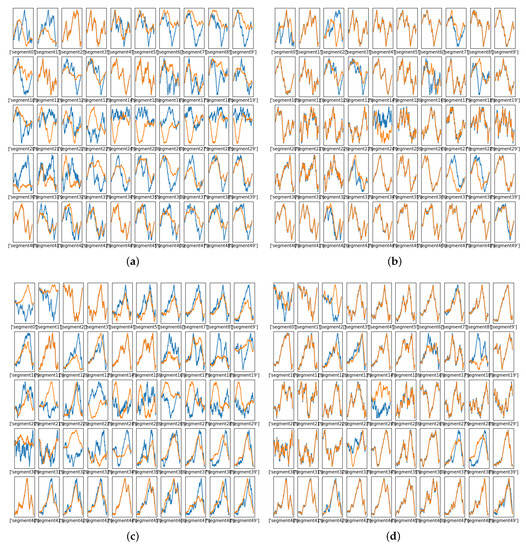
Figure 12. Learned warping path $\mathbf{a}$, Phase Two. (a) Warping path $\mathbf{a}$, 2500 iterations. (b) Warping path $\mathbf{a}$, 10,000 iterations. (c) Warping path $\mathbf{b}$, 2500 iterations (d) Warping path $\mathbf{b}$, 10,000 iterations.

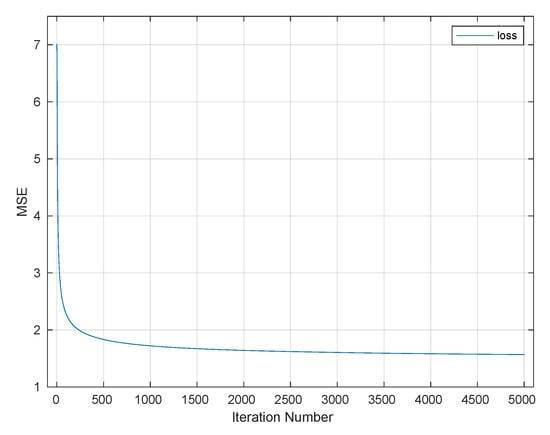
Figure 13. Mean squared error learning curve, Phase Two.

6.3. Phase Three

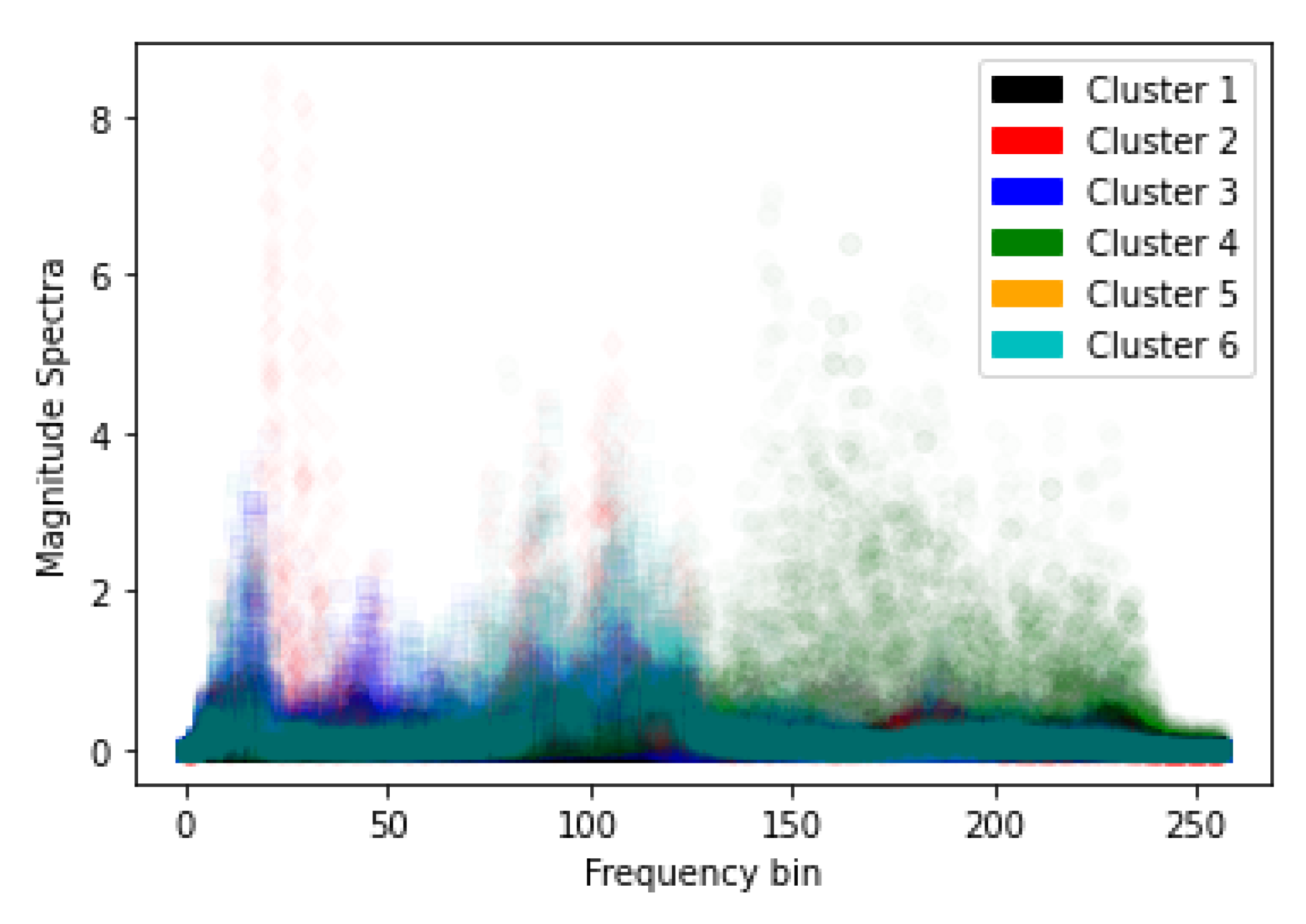
While the results of Phase Two were promising, there was still significant error in the estimates of the warping functions. To further improve the performance, it was determined to assist the NN by decomposing the problem into smaller pieces by clustering. To this end, several NNs were trained, each to be responsive to data pertaining to a particular cluster, where clustering was accomplished using k-means clustering. Different numbers of clusters were tried: $k=4,5,6,10,15,20$. It was found that $k=6$ clusters gave good performance. Figure 14 shows the $k=6$ clusters for the selected spectral data from the 600 training phrases. The six clusters are shown using different colors.

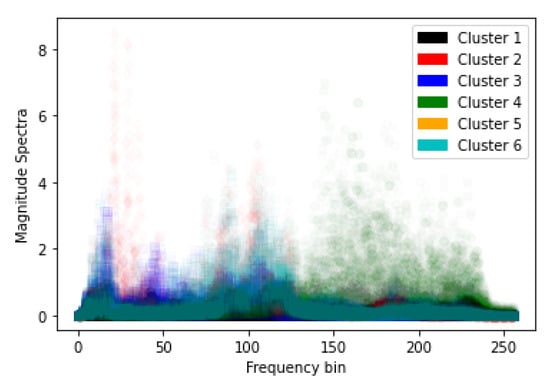
Figure 14. Clustering of spectral information from 600 phrases ($k=6$).

In the training stage, data from each of the k clusters were used to train k NNs. In the synthesis stage, for each segment of speech data it was determined which cluster the associated feature vector best matched, and the $({\mathbf{a}}_F,{\mathbf{b}}_F)$ warping functions were obtained from the corresponding NN. These were used to provide the spectral warping.

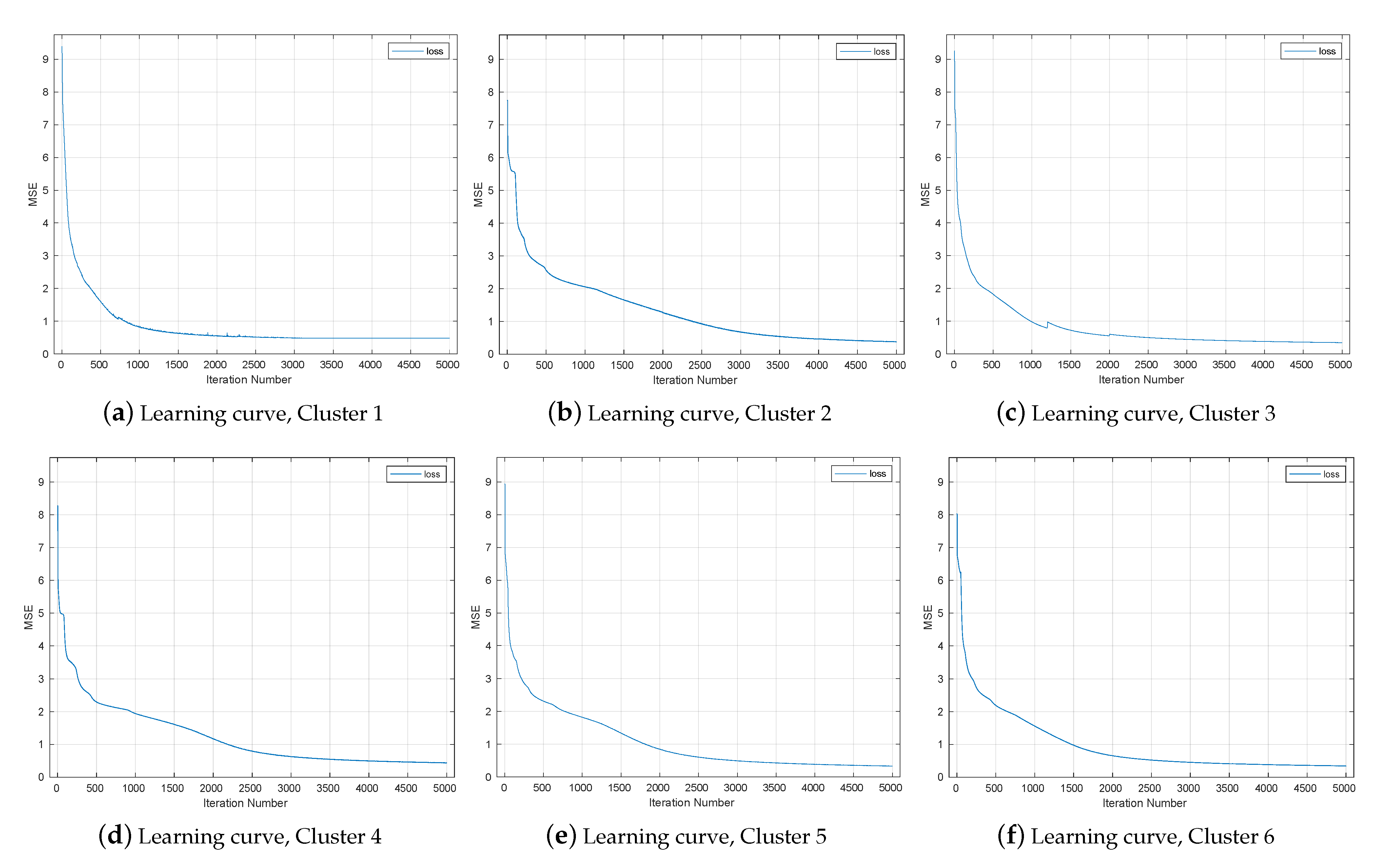
Figure 15a,b show how the clustering NN learned the paths $\mathbf{a}$ and $\mathbf{b}$, respectively, at 5000 training iterations. The DW path (truth) is shown in blue and the NN-learned path is in orange. At this point, the final sound at the 5000 training iterations is much better than the final sound produced from Phase Two, with little signal processing artifacts. Figure 16 shows the MSE between the true values of the warping paths ($\mathbf{a}$ and $\mathbf{b}$) and the estimated paths for each of the six clusters. Interestingly, the learning demonstrated by the MSE varied from cluster to cluster. The MCD value for this phase is reported in Phase Three row of Table 2.

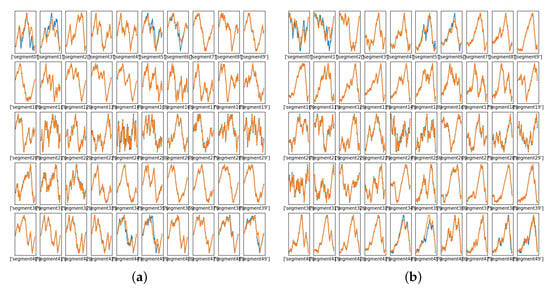
Figure 15. Learned warping paths $\mathbf{a}$ and $\mathbf{b}$, Phase Three. (a) Warping path $\mathbf{a}$, 5000 iterations. (b) Warping path $\mathbf{b}$, 5000 iterations.

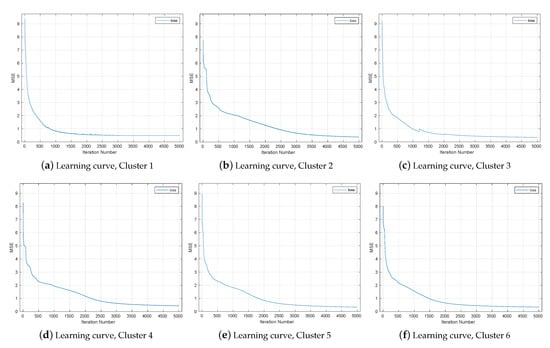
Figure 16. Mean squared error (learning curve) using cluster method.

6.4. Other NN Structures

The fully connected NN structures described above were shown to produce the warping functions with good fidelity. However, they took a lot of training and a lot of memory. In the interest of reducing the NN complexity, we examined convolutional NN structures (CNNs). However, CNNs failed to produce good acoustic results. The MCD scores for CNN architectures are reported in Table 2 as Phase Four. The CNN structures performed significantly worse than the fully connected NN structures.

7. Comparison

From Table 2 the average MCD across the test data was MCD = 2.8 dB. By contrast, in [32], the MCD for male to female conversion was 5.5 dB. The performance of our method was better than reported in [5], which used NN and reported an average MCD of 6.55. The work of VT using NN in [31] reported MCD of 6.1 dB. In all comparisons made, our method was significantly better (as measured by MCD) than previous work. Table 3 shows more comparison between this work and other works, mentioned in the references part, that used MCD scores to evaluate their works. The method presented here worked better than all previous work that reported performance using MCD.

Table 3. Comparative MCDs from previous work.

Reference Number	Reference Year	MCD [dB]
This Works	2020	2.8
[30]	2002	5.6
[32]	2015	5.9
[33]	2016	5.1
[16]	2019	5.09
[29]	2020	4.11

8. Summary and Conclusions

VT has been achieved by employing two-level DW in combination with NN structures. The DW does both temporal and spectral alignment. The path warping functions from DFW are used to train a NN to produce the warping functions. These warping functions were interpolated to provide vectors of constant length. The warped amplitude spectra are shaped by phase reconstruction, which was shown to dramatically improve the speech quality.

To provide sufficient representation capability on larger training data sets, we found it necessary to cluster the training data, training each segment separately then combining the results. This produced low error in the representation of the warping functions.

Based on comparisons with mel-cepstral scores, the VT approach provides performance competitive with previous works.

The primary focus of this work has been on the development of the two-level DW and design of a NN architecture to do VT. Future work will consider transformation among different classes of speakers, including dealing with speakers with different accents.