Abstract
In many complex applications, both data heterogeneity and homogeneity are present simultaneously. Overlooking either aspect can lead to misleading statistical inferences. Moreover, the increasing prevalence of complex, non-Euclidean data calls for more sophisticated modeling techniques. To address these challenges, we propose a density data response additive model, where the response variable is represented by a distributional density function. In this framework, individual effect curves are assumed to be homogeneous within groups but heterogeneous across groups, while covariates that explain variation share common additive bivariate functions. We begin by applying a transformation to map density functions into a linear space. To estimate the unknown subject-specific functions and the additive bivariate components, we adopt a B-spline series approximation method. Latent group structures are uncovered using a hierarchical agglomerative clustering algorithm, which allows our method to recover the true underlying groupings with high probability. To further improve estimation efficiency, we develop refined spline-backfitted local linear estimators for both the grouped structures and the additive bivariate functions in the post-grouping model. We also establish the asymptotic properties of the proposed estimators, including their convergence rates, asymptotic distributions, and post-grouping oracle efficiency. The effectiveness of our method is demonstrated through extensive simulation studies and real-world data analysis, both of which show promising and robust performance.
1. Introduction
With advances in modern technology, data are increasingly collected at discrete time points or over continuous intervals, leading to the growing prominence of functional data in contemporary statistical analysis [1]. Functional data analysis (FDA) offers a range of statistical methods tailored to the unique features of this data type, with functional regression becoming a widely adopted approach for modeling relationships between responses and predictors. Extensive research in this field can be broadly classified into three main categories, depending on whether the responses and predictors are functional or scalar. The first category considers both responses and predictors as functional data, with notable contributions from [2,3]. The second category focuses on functional responses with scalar predictors, as studied by [4]. The third category addresses scalar responses with functional predictors, exemplified by the work of [5,6]. These classifications highlight the diverse applications of functional regression and underscore the continued growth of this research area.
As a specialized type of functional data, distributional or density function data have become increasingly prevalent across a variety of research fields. These data arise in contexts such as cross-sectional or intraday stock returns [7], mortality densities [8], and intra-hub connectivity distributions in neuro-imaging [9]. Unlike conventional functional data, which typically involve time-ordered or sequential measurements, distributional data capture the entire underlying structure without reliance on sample ordering. This characteristic allows them to effectively reveal complex relationships that might be overlooked by standard functional data analysis methods. In recent years, with the growing use of distributional data, there has been a rising interest in developing regression models where random distributions serve as either responses or predictors. These models provide a more nuanced understanding of variable relationships when scalar representations are insufficient. Specifically, this article focuses on a function-on-scalar regression framework, where density functions act as responses and scalar variables as predictors. This flexible and robust approach offers a powerful tool for tackling real-world problems involving complex distributional data and holds promise for uncovering deeper insights into the mechanisms underlying observed phenomena.
Density functions, when viewed as elements of a Hilbert space, do not form a linear subspace due to their inherent constraints of nonnegativity and unit integral. These constraints pose challenges for the direct application of traditional linear methods to density functions. To overcome these difficulties, several approaches have been developed. A notable strategy is to adopt a geometric viewpoint by choosing an appropriate metric. For example, Ref. [10] utilized an infinite-dimensional extension of Aitchison geometry to construct a density-on-scalar linear regression model within Bayes–Hilbert spaces. This framework respects the intrinsic structure of density functions while maintaining their essential properties. Similarly, Ref. [11] proposed a distribution-on-distribution regression approach based on the Wasserstein metric and the tangent bundle of the Wasserstein space. This method offers a powerful framework for modeling relationships between probability distributions and provides a more meaningful measure of distances between distributions from a probabilistic perspective.
An alternative approach to addressing the constraints of density functions is to map them into a Hilbert space via transformation methods. For instance, Ref. [12] proposed a continuous and invertible transformation, such as the log-quantile-density (LQD) transformation, that maps probability densities into an unconstrained space of square-integrable functions. This transformation effectively removes the restrictions imposed by nonnegativity and normalization, allowing density functions to be analyzed as elements of a standard Hilbert space. Building on this idea, Ref. [13] developed an additive regression model with densities as responses, enabling the integration of density functions into regression frameworks, which can be expressed as follows.
Here, denotes the density for the ith unit, and represents the LQD transformation. In this model, the function captures the baseline effect, while represents the additive effect of the l-th covariate . The term is the error function associated with the i-th unit, accounting for random variation in the model. By adopting this framework, the model enables a deeper understanding of the underlying structure and relationships within the data, providing a powerful tool for statistical inference in applications involving density functions.
Model (1) is well-suited for homogeneous data, where observations exhibit uniform characteristics. However, numerous empirical studies have shown that real-world data often display both intra-class homogeneity and inter-class heterogeneity. In such cases, treating the data as entirely homogeneous may overlook important group differences, potentially leading to inaccurate or inefficient statistical inferences. Intra-class homogeneity implies that observations within the same group share similar patterns, while inter-class heterogeneity acknowledges that different groups may behave distinctly. Ignoring either aspect can result in suboptimal modeling. To address this challenge, latent group-structured regression models can be employed. These models explicitly accommodate both intra-class homogeneity and inter-class heterogeneity, enabling more accurate estimation and improved prediction. By incorporating latent group structures, the model differentiates between groups while preserving shared characteristics within each group, thereby enhancing efficiency and the reliability of statistical conclusions. Latent group-structured regression thus offers a powerful framework for analyzing heterogeneous data and provides valuable insights into complex processes across various applications.
This phenomenon is particularly evident when analyzing COVID-19 data alongside various influencing factors. To evaluate the progression of the epidemic in individual countries relative to the global context, we consider the relative daily mortality rate over a 240-day period for each country as the response variable. The daily mortality rate is defined as the number of deaths per day normalized by the country’s total population, and the relative rate is calculated as the ratio of each country’s mortality rate to the global total. This relative daily mortality rate is treated as a density function, representing the distribution of mortality over time. To align the time scale across countries, we set the first day with at least 30 reported deaths as time zero for each country. The density of the relative daily mortality rate following this benchmark reflects how each country’s epidemic trajectory contributes to the global situation. This study includes data from 149 countries, with the corresponding densities of relative daily mortality rates illustrated in Figure 1. A detailed examination reveals both homogeneity and heterogeneity in the shapes of these density functions. While some countries display similar patterns, suggesting homogeneity, others exhibit distinct trends, highlighting the heterogeneous impact of the pandemic across regions. This coexistence of shared and divergent characteristics underscores the complex nature of the COVID-19 crisis, where common responses and varying regional effects both play critical roles in shaping the global health emergency.
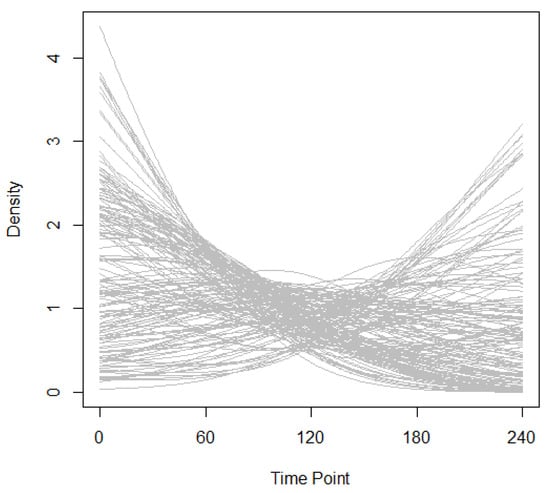
Figure 1.
Density functions of relative daily COVID-19 mortality rates in 149 countries over a 240-day period.
For further analysis, six predictors are considered to explain the variation in relative daily mortality rates: ‘aging’ (the percentage of the population aged 65 and over), ‘beds’ (the number of hospital beds per 1000 people), ‘physicians’ (the number of physicians per 1000 people), ‘nurses’ (the number of nurses per 1000 people), ‘GDP’ (gross domestic product per capita in US dollars), and ‘diabetes’ (the percentage of the population with diabetes). Given the global nature of the epidemic, it is reasonable to assume that the effects of these predictors on relative daily mortality rates are broadly consistent across countries. However, other unobserved factors, such as national epidemic prevention strategies and cultural practices, may contribute to both inter-group heterogeneity and intra-group homogeneity. For example, China’s public health policies and social behaviors differ markedly from those in countries like the United Kingdom and the United States. These differences may manifest as heterogeneity in the intercept functions. As shown in Section 3.2.1, the United Kingdom and the United States are classified into the same group, while China falls into a different group. This observation highlights the necessity of adopting an additive model that incorporates subject-specific intercept functions and latent group structures, thereby capturing intra-group homogeneity and inter-group heterogeneity, i.e.,
Here, denotes the density of the relative daily mortality rate for country i, and represents the vector of covariates. The function denotes the LQD transformation. Specifically, the intercept function is modeled as if country i belongs to group k, where is one of K group-specific functions.
A substantial body of literature has introduced various methods for identifying latent group structures in data situated within Euclidean spaces. For instance, Ref. [14] proposed a distance-based clustering algorithm applied to kernel estimates of nonparametric regression functions. Building on this, Ref. [15] developed an extension using a multiscale statistic, thereby avoiding the need to select a specific bandwidth. Ref. [16] introduced the classifier-Lasso (C-Lasso), a shrinkage method designed for linear panel data models with latent group structures. This approach was further extended by [17], who proposed a penalized sieve estimation-based C-Lasso method tailored for heterogeneous, time-varying panel data. Additionally, Ref. [18] presented a kernel-based hierarchical agglomerative clustering (HAC) algorithm that imposes fewer restrictive assumptions than earlier approaches, making it more flexible for complex data structures. Collectively, these contributions offer significant methodological advances for analyzing functional and panel data, providing robust tools for uncovering latent group structures in heterogeneous datasets.
In this study, we employ the hierarchical agglomerative clustering (HAC) method to identify latent group structures within the data. Specifically, we first apply HAC to the estimated individual intercept functions, enabling the classification of the density functions into four distinct groups, each reflecting a different epidemic pattern. The resulting clusters are presented in Figure 2, providing strong empirical support for the use of a functional additive model with latent group structures in the intercept function, underscoring its necessity for effectively capturing the heterogeneous dynamics of COVID-19 data.
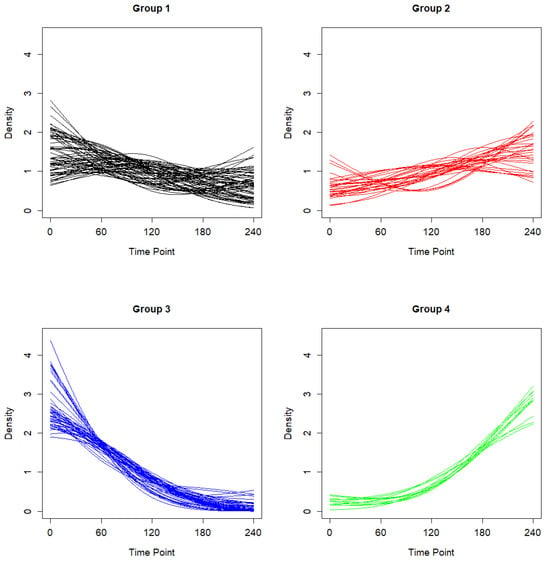
Figure 2.
Density functions of relative daily COVID-19 mortality rates over a 240-day period, displayed by cluster. Results are presented for four distinct groups identified through hierarchical clustering.
To capture both intra-group homogeneity and inter-group heterogeneity that are present in the data, we extend the additive functional regression model for density responses originally proposed by [13], allowing it to accommodate heterogeneity in the density functions:
and
Here, denotes a partition of the index set , such that , and for any . Moreover, we assume that for all , indicating that the group-specific intercept functions are distinct across groups. The number of groups K, as well as the group membership for each individual, are assumed to be unknown and must be inferred from the data.
In the proposed model, represent random density functions, each associated with a p-dimensional covariates vector , all defined on a common support . Without loss of generality, we assume . Let denote the LQD transformation, such that . The function captures the subject-specific intercept, while are the bivariate additive components. For identification purposes, we impose the constraint for all and . The error processes are assumed independent with zero conditional mean and covariance function .
Clearly, the proposed model (2) naturally extends the functional additive model framework. In particular, when the subject-specific functions are homogeneous, that is, when , model (2) simplifies to the additive functional regression model for density responses introduced by [13]:
While the LQD transformation introduced by [12] effectively facilitates the representation of density functions in a linear space, and the subsequent additive model proposed by [13] enables regression modeling with density-valued responses, both approaches assume that the data are homogeneous across observations. This assumption may be overly restrictive in real-world applications where population-level heterogeneity is prevalent. The key innovation of our work lies in the integration of the LQD transformation with latent group structure learning within the additive modeling framework. By simultaneously estimating subject-specific density functions and uncovering latent group memberships, our method captures both within-group similarity and between-group variation. This joint modeling approach not only enhances interpretability and predictive power but also expands the applicability of density regression methods to heterogeneous settings, marking a substantive advancement over the existing literature.
In practical applications, only random samples drawn from the underlying densities are typically observed. To handle this, we begin by estimating each density using the modified kernel density estimation method proposed by [12], combined with the LQD transformation. Next, we employ the hierarchical agglomerative clustering (HAC) method, which requires estimates of the subject-specific functions, to identify and estimate the latent group structure. To accomplish this, we introduce a three-step estimation procedure that leverages the advantages of both spline smoothing and local polynomial smoothing techniques. In the first step, for computational efficiency, we use a B-spline series approximation to estimate the subject-specific functions and the additive components . Based on these initial estimates of , the second step applies the HAC method to determine the group membership for each subject. While spline smoothing is efficient computationally, it poses challenges when establishing asymptotic properties. Therefore, in the third step, we use backfitted local linear regression to improve the estimation efficiency of the group-specific functions and the additive components . We further establish several theoretical results, including the uniform convergence rates of the estimators, consistency of both the estimated number of groups and their memberships, asymptotic normality of the group-specific functions, and properties of the post-clustering additive component estimators. These findings provide a rigorous theoretical basis for the proposed approach.
The remainder of this paper is organized as follows. Section 2 describes the materials and methods, including preliminary work, identification and estimation Method, and theoretical results. Specifically, Section 2.1 introduces the modified kernel estimation method along with the LQD transformation for density functions, which serve as the foundational steps. Section 2.2 outlines the procedure for identifying and estimating the latent group structures and the additive components within the model. The theoretical results are presented in Section 2.3. In Section 3.1, Monte Carlo simulations are conducted to evaluate the performance of the proposed method. Section 3.2 demonstrates the application of our approach to COVID-19 and GDP data analysis. Finally, Section 4 offers a conclusion of the findings and Section 5 discusses potential directions for future research. Detailed proofs of the theoretical results and additional numerical results are provided in the supplementary materials.
2. Materials and Methods
2.1. Preliminaries
This section presents the preliminary concepts and methods necessary for the development of the proposed model.
2.1.1. LQD Transformation
Let denote the class of all univariate continuous probability density functions , each defined on a common support S. Without loss of generality, we assume this support is the unit interval . We further impose a mild moment condition on the elements of , requiring that the second moment is finite: . This condition ensures that the densities possess a reasonable level of regularity, which is necessary for performing statistical inference and functional representations in Hilbert spaces.
For any density , let denote the corresponding cumulative distribution function (CDF). Because z is continuous and supported on , the CDF is strictly increasing and continuous on this interval. We define the quantile function as the inverse of the CDF F, i.e.,
which returns the value of such that the cumulative probability up to is equal to u. The quantile density function, denoted by , is then given by the derivative of the quantile function with respect to u, i.e.,
To enable more effective statistical analysis of probability densities, we adopt a transformation that maps each into a linear space . Specifically, we apply the LQD transformation proposed by [12], which is defined as
The log-quantile-density (LQD) transformation offers a principled approach to representing probability density functions within a linear and unconstrained functional space. By applying a logarithmic transformation to the quantile density function, it maps densities—originally constrained to be nonnegative and integrate to one—into real-valued, square-integrable functions in the Hilbert space. This facilitates the use of standard statistical techniques such as functional principal component analysis, regression, and clustering, while avoiding common difficulties associated with directly modeling densities, including boundary behavior and normalization constraints.
A key strength of the LQD transformation lies in its invertibility, which ensures that the original density function can be uniquely reconstructed from its transformed representation. In addition, the transformation preserves smoothness from the underlying quantile function and benefits from the numerical stability of the logarithmic scale. These properties make the LQD framework both analytically tractable and computationally robust. Further theoretical details, including its continuity, differentiability, and induced geometry, are discussed in [12].
2.1.2. Modified Density Estimation
One of the main challenges in fitting a regression model with a density-valued response lies in the fact that, in practical applications, the true density function , and consequently its transformation , is unobservable. Instead, it must be estimated from the random sample drawn from , denoted by , with the associated covariate vector . Without loss of generality, we assume a common sample size across units, i.e., for all i.
To mitigate the boundary bias commonly encountered in conventional kernel density estimators, Ref. [12] proposed a modified kernel density estimator , defined as follows:
Here, the weight function is defined as for , and for , and equals 1 otherwise. The kernel function is assumed to be of bounded variation and symmetric around 0. For bandwidth , satisfies the regularity conditions: , and the integrals , and are all finite. Unlike standard kernel density estimators, the modified estimator corrects for boundary effects and enjoys a uniform consistency property. Specifically,
2.2. Identification and Estimation Method
In this section, we outline a three-step procedure for identifying latent group structures and estimating the additive components in the proposed model. The complete procedure is summarized in Algorithm 1.
| Algorithm 1 Identifying Heterogeneity in Additive Model with Density-Valued Responses |
| Data: , where , . 1. Density Estimation: Modified kernel density estimator . 2. Transformed Density: 3. Initial Estimation: B-spline approximation . 4. HAC Algorithm: Estimated group sets
|
2.2.1. Initial Estimation
The spline series approximation method is widely used for estimating unknown nonparametric functions. Comprehensive treatments of this approach can be found in [19,20]. Let denote the set of B-spline basis functions of order q with interior knots, where . Similarly, for each covariate (), let represent the set of B-spline basis functions of order q with interior knots, where . We then define the normalized spline basis for () as . Additionally, the scaled version of is denoted by . Throughout, we generally take the spline order to be .
We define the tensor product of B-spline bases as The spline approximations for the subject-specific functions and the bivariate components are then expressed as follows
The corresponding estimations are given by
where is a vector of dimension that satisfies the following conditions:
Remark 1.
Theoretically, any number of grid points can be selected from each density for spline estimation in (6). Without loss of generality, we set the number of observation T equal to the length of grid.
2.2.2. Identifying Latent Group Structures via HAC Algorithm
Building upon the initial estimates of the subject-specific functions given in Equation (5), the classic HAC (hierarchical agglomerative clustering) algorithm can be applied to identify the latent groups assuming the number of groups K.
Previous studies have explored various distance measures for clustering functional data. For example, Ref. [21] used the -distance to capture differences in nonlinear coefficient functions, while Ref. [14] adopted the -distance in combination with the k-means clustering procedure to group functions exhibiting similar overall patterns. In contrast, Ref. [15] proposed a multiscale clustering method based on the -distance to emphasize local deviations. Building on this literature and the general framework of [22], we adopt the -distance as a flexible similarity measure that can capture discrepancies across different scales of the functions. Specifically, the pairwise distance between the two subject-specific functions is defined as
which is approximated in practice by
The clustering procedure using HAC is summarized in Algorithm 1 and detailed as follows. Assume that the number of groups K is given. First, we compute the complete pairwise distance matrix among all subjects based on their estimated subject-specific functions. Each subject initially forms a singleton cluster. At each step of the algorithm, the two clusters with the smallest inter-cluster distance are merged, which balances sensitivity to within-cluster variation and between-cluster separation.
After each merge, the distance matrix is updated to reflect the new clustering configuration, and the process repeats. This agglomeration continues until exactly K clusters remain. The final partition represents the inferred latent group structure among the subject-specific functions. By leveraging the flexibility of the -distance and the hierarchical nature of HAC, this method effectively captures both global and local heterogeneity across individuals, leading to interpretable and data-driven functional groupings.
2.2.3. Estimation of Latent Group Structures
Given the true group membership, model (2) can be expressed in the following group-structured form:
To estimate the group-specific functions and the bivariate additive component functions , we apply the backfitted local linear algorithm proposed by [23]. Define
By plugging in the initial estimate , we compute the estimate of adjusted function as
For each fixed point , the function can be approximated using the first-order Taylor expansion
We define the weighted squared function as
where is a nonnegative kernel function with bandwidth , and represents the estimated membership set for group k. Minimizing yields the estimator for , denoted by , which is given by
where the weights are defined as and the constants are given by for .
Using these estimates, we can estimate as follows:
where denotes the indicator function. For each , we approximate by
Since the point-wise estimates of for each may lack smoothness due to their dependence on the estimated density responses , an additional local smoothing step is implemented along the direction of u. For each , we define the following function:
Here, is a nonnegative kernel function with bandwidth . By minimizing , the refined estimator of , denoted by , can be expressed as
where the weights are defined as and for .
2.2.4. Selection of Number of Groups
The identification of latent group structures, as previously discussed, typically assumes that the number of groups, K, is known. However, in practical applications, this assumption often does not hold. One of the key challenges in clustering is determining the appropriate number of groups when K is unknown. To address this issue, we adopt an information criterion-based approach, as proposed by [18], to select the optimal number of groups. This method provides a systematic framework to balance model fit and complexity, helping to prevent overfitting while still capturing the underlying structure of the data. By applying this approach, we can achieve a more accurate and robust estimation of the latent group structure, even in the absence of prior knowledge of the true number of groups.
Denote
where
and is a tuning parameter whose value may rely on the sample size n.
The number of latent groups can be estimated by minimizing the information criterion , i.e.,
where denotes a pre-specified upper bound on the number of groups.
In the simulation studies, we consider two choices for the tuning parameter :
where , and denotes the cardinality of group . These two choices correspond to different information criteria: the generalized Bayesian information criterion (GBIC) when , and the generalized Akaike information criterion (GAIC) when . Additional information criteria can be found in [18,21].
2.2.5. Selection of Bandwidth
In this study, we utilize the leave-one-out cross-validation (LOO-CV) method to select the optimal bandwidth parameters. Let denote the vector of bandwidths corresponding to different components of the model. Given a specified number of latent groups K, the optimal bandwidth vector is determined by minimizing the mean squared error (MSE) criterion, calculated through the cross-validation procedure as follows:
where denotes the estimated group membership. For each , the terms and are the estimates of and with bandwidth , respectively, obtained using all observations except the t-th one. This criterion evaluates the discrepancy between the predicted and observed values, and minimizing it leads to bandwidth selections that yield the most accurate estimation of the model’s functional components, while accounting for the underlying group structure in the data.
In practical implementation, the leave-one-out cross-validation (LOO-CV) within our multi-step estimation procedure is carefully designed to balance computational feasibility and accuracy. Specifically, during each iteration of bandwidth selection, the model is refitted T times by leaving out one time point at a time, rather than omitting an entire subject, to maintain stable estimation given the functional nature of the responses. After latent group memberships are estimated in the initial clustering step, the group-specific functions and covariate effects are re-estimated at each LOO fold. To mitigate the computational burden, we employ efficient updating strategies that reuse intermediate calculations from the full data fit wherever possible, such as caching kernel weights and smoothing matrices. Additionally, the dimensionality reduction inherent in the latent grouping substantially decreases the effective number of parameters to estimate, thus accelerating the cross-validation procedure. Although this LOO-CV approach increases computational demand compared to simpler bandwidth selection methods, it ensures optimal tuning by directly assessing prediction performance while respecting the heterogeneity and structure present in the data. In our experiments, the computational cost remained manageable and scaled approximately linearly with the number of time points and groups, making the procedure practical for moderate-sized datasets.
2.3. Theoretical Results
Throughout this paper, for any fixed interval , we denote the space of l-th order continuously differentiable functions functions by , and the class of Lipschitz continuous functions with a fixed constant by Let and denote the supports of and , respectively. Clearly, . The following assumptions are imposed to establish the asymptotic properties of the proposed estimators.
- (A1)
- For any , the function z is differentiable, and there exists a constant , such that , , and are all bounded above by M.
- (A2)
- (a) The kernel function is Lipschitz-continuous, bounded, and symmetric about 0. Furthermore, for some constant . (b) The kernel function satisfies the following regularity conditions , , , and . The same conditions are assumed to hold for the kernel density .
- (A3)
- The error terms satisfy the moment conditions: for some , , and for some , . For each , the conditional covariance function has finite, non-decreasing eigenvalues , satisfying .
- (A4)
- The latent group functions , , have continuous second-order derivatives over the support interval, i.e., , and their first derivatives satisfy a Lipschitz condition for some constant . In addition, the additive component functions , are continuous on and twice continuously partially differentiable with respect to both u and , where is a compact subset of .
- (A5)
- (a) The density of covariate , , is continuous and bounded, and its marginal densities have continuous derivatives for all . (b) The joint density functions and , for and , are continuous and partially differentiable with respect to u and , with continuous second-order partial derivatives.
- (A6)
- (a) Let , where denotes the th element of the distance matrix introduced earlier. Then it holds that . (b) There exists a positive constant , such that the size of each group is bounded below by a proportion of the total sample size, i.e., .
- (A7)
- The numbers of grid points and bandwidths satisfy the following growth conditions as :, , , , .
Remark 2.
Assumption (A1) is basic and essential for deriving the consistency of densities after transformation. The conditions in (A2) on the kernel function are mild and can be satisfied by commonly used kernel functions such as uniform and Epanechnikov kernels. Assumption (A3) contains the moment conditions which are crucial for deriving the uniform convergence and other asymptotic properties based on the kernel function. The smoothness conditions for the component functions in (A4) and (A5) are greatly relaxed. Assumption (A6) (a) indicates that δ can converge to zero at an appropriate rate, and (b) is useful in proving the consistency of the estimated group number via the information criterion proposed earlier. The conditions in (A7) are commonly applied in kernel smoothing to ensure the optimal convergence rates.
Assumption (A1) is fundamental and ensures the consistency of the transformed densities. The conditions imposed in (A2) on the kernel function are relatively mild and are satisfied by many commonly used kernels, such as the uniform and Epanechnikov kernels. Assumption (A3) imposes moment conditions that are essential for establishing uniform convergence and other asymptotic properties of the kernel-based estimators. The smoothness requirements specified in (A4) and (A5) for the component functions are relatively weak and allow for a broad class of functions. Assumption (A6)(a) ensures that the separation measure δ diminishes at a suitable rate, while part (b) plays a critical role in establishing the consistency of the estimated number of groups using the proposed information criterion. Finally, the conditions in (A7) reflect standard choices in kernel smoothing and are necessary to achieve optimal convergence rates.
We begin by establishing the uniform consistency of the initial estimators, as presented in Theorem 1.
Theorem 1.
Suppose that Assumptions (A1)–(A4) and (A7) hold. Let and denote the initial estimators of and , respectively, as defined in Equation (5), for , . Then, as and , the following results hold:
- (i)
- (ii)
Theorems 2 and 3 further establish that both the number of groups K and the membership of group structures can be consistently identified with probability approaching one.
Theorem 2.
Suppose that Assumptions (A1)–(A5) hold and the true number of latent groups K is known. Let denote the true group structure for , , and let be its corresponding estimate. Then, as , it holds that:
Theorem 3.
Suppose that Assumptions (A1)–(A7) hold. Let K be the true number of latent groups, and let be its estimate obtained via the proposed information criterion, then as , we have:
Theorem 4.
Suppose that Assumptions (A1)–(A7) hold and that the true number of latent groups K is known. Then, as and , the following results hold:
- (i)
- (ii)
Theorem 4 establishes the uniform convergence for the oracle post-clustering estimators of the group-specific functions and the additive components. To further derive the asymptotical normality of and , we define the following kernel-related moments:
Theorem 5.
Suppose that Assumptions (A1)–(A7) hold, and let denote the estimated number of latent groups. Then, as , the following asymptotic normality results hold for all and :
- (i)
where the asymptotic bias is and the asymptotic variance is ;
- (ii)
where the asymptotic bias is and the asymptotic variance is .
The asymptotic distributions established in Theorem 5 provide the theoretical foundation for conducting statistical inference on the group-specific estimators and the refined estimators .
3. Results
3.1. Numerical Study
In this section, we conduct a simulation study to evaluate the performance of the proposed estimation procedure under the model specified in (2). We consider the setting with latent groups and covariates. The regression model (2) with latent group structure given in (3) is
where the conditional mean function is given by , and the group-specific baseline functions are defined as:
with additive component functions
for . The groups’ memberships are defined by , , , with group sizes set as , , and .
The covariates are generated via the transformation , , where is the cumulative distribution function of the standard normal distribution, and are bivariate normal random vectors with mean zero and covariance matrix . The random error term is defined as , where and , independently.
The conditional mean functions correspond to the LQD transformations of the conditional density . More specifically, the inverse of the log-quantile transformation is given by , where . Consequently, the conditional distribution function and quantile function satisfy
To generate the response observations, for each , let , independently of . The observed responses at time points are then given by , such that , where are the random response densities. Without loss of generality, we assume that . We consider combinations of sample sizes , and numbers of observations . Each scenario is replicated 200 times. For the initial estimation step, the spline basis functions are of order , with interior knots for .
Figure 3 and Figure 4 present the average performance of the pre- and post-clustering estimators for the group-specific baseline functions and the bivariate additive components, respectively, under the setting and . In each figure, the true functions, as well as the pre- and post-clustering estimates, are shown sequentially from left to right, allowing for visual comparison of the estimation accuracy before and after clustering.
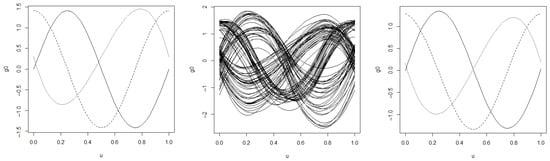
Figure 3.
Average estimates of latent group structure function . The solid, dashed, and dotted lines in the first and last panels correspond to the curves of the function for each of the three respective latent groups. Obtained from 200 Monte Carlo replications with sample size and . Left panel: true group-specific functions, middle panel: pre-clustering estimates, right panel: post-clustering estimates.
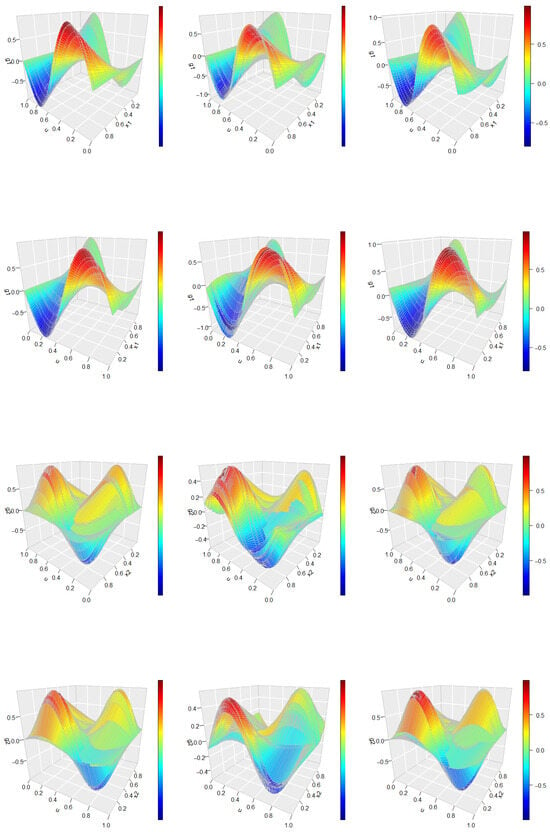
Figure 4.
Average estimates of bivariate additive component functions (top two rows) and (bottom two rows). Obtained from 200 Monte Carlo replications with sample size and . Left panel: true functions, middle panel: pre-clustering estimates, right panel: post-clustering estimates. Each component function is visualized from two different viewing angles.
As shown in Figure 3, although the pre-clustering estimates roughly capture the overall shapes of the true density functions, notable deviations remain. In particular, the estimated curves exhibit discrepancies in capturing extreme values, despite aligning reasonably well with the true locations of minima and maxima. In contrast, the post-clustering estimates offer a more accurate approximation of the true density functions. These estimates not only reflect the general shape of each curve but also closely match the true values at critical points, including extrema and turning points. A similar pattern is observed in Figure 4, which presents the estimation results for the bivariate additive components. These findings collectively highlight the effectiveness of the proposed identification and estimation procedure.
Let denote the set of true groups and denote the estimated clustering. To evaluate the performance of the clustering algorithm, we consider two widely used evaluation metrics. The first is Purity, a standard measure in clustering analysis, defined as The second metric is the normalized mutual information (NMI), which quantifies the similarity between clusters [24]. Here, we define the NMI between the estimated clusters and true clusters C. It is defined as where the mutual information between and C is given by and the entropy of the estimated clustering is , with defined similarly for the true clustering. Both purity and NMI are invariant to permutations of cluster labels, making them suitable for evaluating the quality of clustering results. Values closer to 1 indicate better alignment between the estimated and true clusters, reflecting higher clustering accuracy.
To evaluate the effectiveness of the proposed procedure, we compare the performance of three estimators. The first is the pre-clustering estimator, , which is computed without accounting for any group structure. The second is the oracle estimator, with given K, which assumes knowledge of the true number of true groups. The third is the post-clustering estimator, , constructed based on the estimated group memberships obtained from the data. To assess the performance of these estimators, we use the root MSE (RMSE). Specifically, for the pre-clustering estimator, the RMSEs are defined as and The RMSEs for the oracle and post-clustering estimators are defined in the same way.
Table 1, Table 2 and Table 3 summarize the results obtained under various settings, including the estimated values of K, as well as the averages and standard deviations of NMI, purity, and RMSE for the estimators. First, with respect to the clustering algorithm’s performance, the results using the GAIC and GBIC criteria were largely consistent. Under both criteria, the accuracy of the estimated was consistently high. Moreover, the NMI and purity values improved as the sample size n and the number of observations T increased. In particular, when and , the true number of clusters K was correctly identified in 100% of the runs, with NMI and purity values approaching 1. Second, regarding the performance of the estimators, as shown in Table 2 and Table 3, the RMSEs for all estimators decreased as both the sample size n and the number of observations T increased. Across all scenarios, the oracle and post-clustering estimators consistently outperformed the pre-clustering estimators. The difference in performance between them diminished with increasing n and T. Notably, at and , the performances of the oracle and post-clustering estimators were nearly indistinguishable. Furthermore, the performance of the post-clustering estimators under the GAIC and GBIC criteria was almost identical.

Table 1.
Estimated number of K, and average and standard deviations of NMI and purity.

Table 2.
Average and standard deviation of RMSEs for the latent group structures.

Table 3.
Average and standard deviation of RMSEs for the bivariate additive components’ estimations.
3.2. Real Data Analysis
In this section, we demonstrate the proposed methodology through two case studies in the social sciences.
3.2.1. COVID-19 Data
As outlined in Section 1, our primary goal is to explore the relationships between epidemic trends across different countries and various socioeconomic factors. To this end, we compiled a comprehensive COVID-19 dataset containing the daily number of deaths from 22 January 2020, to 15 December 2020, for 190 countries and regions. This dataset is publicly accessible via the Coronavirus Resource Center at Johns Hopkins University, accessed on 15 January 2021 (https://coronavirus.jhu.edu/). Considering the different starting points of the pandemic across countries, we standardized the observation period to 240 days, beginning from the earliest date on which any country reported at least 30 deaths. The relative daily mortality rate was selected as the response variable for our analysis.
To ensure the validity of our analysis under the assumptions of the proposed methodology, we restricted the sample to countries with covariate values lying within a compact support, defined by the empirical minimum and maximum observed values for each predictor. Countries with socioeconomic covariate values outside these ranges were excluded to avoid extrapolation beyond the data support, which could lead to unreliable model estimates. This step resulted in the exclusion of 41 countries from the original 190, leaving a final sample of 149 countries. The exclusion criteria aimed to mitigate the influence of outliers or extreme covariate values that may distort the model fitting and inference. While this filtering may introduce some bias by omitting countries with unique socioeconomic characteristics, it is necessary to ensure comparability and stable estimation across units.
For the six socioeconomic predictors introduced in Section 1, we obtained the most recent data available from 2019, sourced from the World Bank, accessed on 27 March 2021 (https://data.worldbank.org/indicator). These predictors serve as key explanatory variables, enabling a detailed investigation of factors shaping the progression of the COVID-19 pandemic in different national contexts.
Since the raw data consist of relative mortality rates aggregated over daily intervals, we first applied smoothing techniques to construct the functional density responses , , depicted over time (see Figure 1). The marked differences in the shapes of these density functions motivated the incorporation of a latent group fixed effect in the functional additive model:
We applied the HAC algorithm to classify the spline estimates of , with the number of clusters selected based on an information criterion. Supplementary Figure S1 displays the GAIC and GBIC values for different clusters counts. As shown in the figure, the optimal number of clusters was identified as four. The group memberships are detailed in Supplementary Table S1.
Following the clustering step, we used a backfitted local linear regression method to refine the estimates of the group-specific functions and . The estimated latent group structures are presented in Figure 5, while the corresponding density functions are displayed in Figure 2. Notably, Group 4 exhibited a trend distinct from that of the other groups. In this cluster, the relative daily mortality rate increased over time, resulting in higher mortality rates compared to the global average during the study period. In contrast, Group 3 exhibited a high initial daily mortality rate, which declined sharply over time, suggesting that the epidemic was relatively well controlled in these countries. Group 1 also experienced a decline in mortality rates over time, although less pronounced than that in Group 3. Finally, Group 2 displayed relatively mild fluctuations in the relative daily mortality rate compared to the other groups. These findings highlight the heterogeneous progression of the epidemic across countries, as reflected in the differing trajectories of relative mortality rates within each latent group.
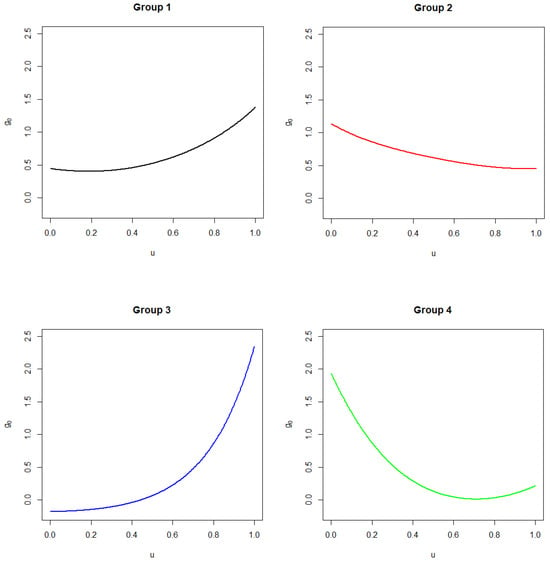
Figure 5.
Estimation of latent group structures .
To quantify the contribution of each of the selected socioeconomic variables and the individual function, we employed an empirical version of the fraction of variance explained (FVE) criterion [13]. Specifically, the empirical FVE of the l-th covariate is defined as the ratio , where , . Here, , and .
The model selection was conducted using a backward elimination procedure, sequentially removing the predictor with the smallest FVE among those included at each step. The process was terminated when the mean squared error (MSE), defined as , increased after removing a predictor. Here, denotes the fitted density for observation i at the d-th step, and the initial fit corresponds to with representing the total number of predictors at the start.
To further validate the variable selection obtained from the backward elimination procedure, we conducted significance testing for the retained predictors by calculating their p-values using a bootstrap approach. The variables ‘aging’, ‘physicians’, and ‘GDP’ demonstrated strong statistical significance, with respective p-values of 0.011, 0.028, and 0.009. These results indicate that these predictors have meaningful effects on the response variable and justify their inclusion in the final model. In contrast, the excluded variables ‘beds’, ‘nurses’, and ‘diabetes’ exhibited p-values greater than 0.1, consistent with their removal due to lack of a significant contribution. Overall, the p-value analysis confirms the robustness of the backward elimination process and highlights the key role of included predictors in explaining the observed variation.
Figure 6 illustrates the effects of the three predictors, ‘aging’, ‘physicians’, and ‘GDP’, through heat maps, with corresponding FVE values of 45.52%, 59.42%, and 73.98%, respectively. The heat map for ‘physicians’ reveals that the influence of this predictor on the relative daily mortality rate varies over time. Specifically, countries with a high number of physicians per 1000 people exhibit an initial peak followed by a decline to a minimum, whereas countries with fewer physicians display the opposite trend. Similar or contrasting patterns can be observed in the heat maps for ‘aging’ and ‘GDP.’ These findings indicate that the effects of these socioeconomic factors on COVID-19 mortality dynamics are not constant, but rather evolve over time, with their impact differing according to the country’s specific characteristics.
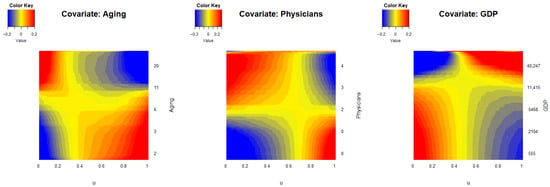
Figure 6.
Heat maps of additive component functions. The predictors include ‘aging’ (the percentage of the population aged 65 and above), ‘physicians’ (the number of physicians per 1000 people), and GDP (gross domestic product per capita in U.S. dollars).
To evaluate the overall performance of the proposed methodology, we computed the RMSEs of pre- and post-clustering estimators for the fitted densities, defined as , where , with and representing the pre- and post-clustering estimators, respectively. For comparison, we also calculated the RMSE for the homogeneous additive model (1) proposed by [13]. The RMSEs for the pre- and post-clustering estimates were 0.6972 and 0.3751, respectively, while the homogeneous additive model yielded an RMSE of 0.8433. These results underscore the importance of accounting for heterogeneity in relative daily mortality rates across countries. The clustering-based approach substantially improves the model’s effectiveness in analyzing COVID-19 data. Additionally, Supplementary Figure S2 displays the observed and fitted density curves for three representative countries from each group. Overall, the estimated density functions closely matched the observed density curves, demonstrating the robustness of the model and its ability to accurately capture the underlying dynamics of the epidemic across diverse national contexts.
Building on the analysis, our study reveals significant heterogeneity in COVID-19 epidemic trajectories across countries, while quantitatively assessing the dynamic influence of key socioeconomic factors. By leveraging the LQD-based functional additive model combined with clustering, we identified four latent groups reflecting distinct patterns of relative daily mortality rates. The fraction of variance explained (FVE) analysis highlighted aging population, number of physicians, and GDP as the most influential predictors, whose effects vary meaningfully over time. This temporal variation underscores that the impact of these factors is not static but closely tied to country-specific healthcare capacity and economic conditions, offering valuable insights for designing timely and targeted public health interventions.
Despite demonstrating robust performance in capturing complex epidemic heterogeneity and time-varying covariate effects, the proposed methodology has some limitations. The approach relies heavily on accurate functional estimation and smoothing, which may be sensitive to data noise and missingness, especially in countries with incomplete reporting. Moreover, the model currently includes a limited set of socioeconomic variables; future work could enhance explanatory power by incorporating additional factors such as policy responses or population mobility. While the clustering procedure improves model fit substantially, the choice of the number of groups depends on information criteria, introducing some subjectivity. Overall, this study provides a novel framework for understanding epidemic dynamics through functional data analysis, but further efforts are needed to improve data quality and extend model complexity for broader applicability.
3.2.2. GDP Data
GDP per capita is widely recognized as a fundamental indicator for evaluating a country’s macroeconomic performance and overall level of economic development. It serves as a proxy for the standard of living, economic productivity, and general well-being of a nation’s population. In this empirical application, we investigate the relationship between per capita GDP and a set of key socioeconomic variables that are believed to influence a country’s economic trajectory. The proposed model is specified as follows:
where denotes the literacy rate (i.e., the percentage of educated individuals aged 15 years and above) of country i; is the total population; refers to the per capita GDP in the base year; and represents the average per capita GDP over the 50-year period. By incorporating these covariates, the model facilitates an in-depth examination of how factors such as educational attainment, demographic scale, and historical economic performance jointly shape a country’s economic development. This framework enables a nuanced understanding of the mechanisms underlying economic growth, capturing both current and long-term socioeconomic influences.
The data utilized in this analysis were sourced from the World Bank database, accessed on 25 March 2021 (https://data.worldbank.org), covering the period from 1970 to 2019. After excluding countries with incomplete records, the final dataset comprised countries, each observed over time points. To examine the relative economic standing of each country within a global context, we adopted the same methodological framework described in Section 3.2.1 to estimate the relative per capita GDP density for each country. The resulting density estimates, presented in Figure 7, reveal substantial heterogeneity in economic trajectories across nations over time.
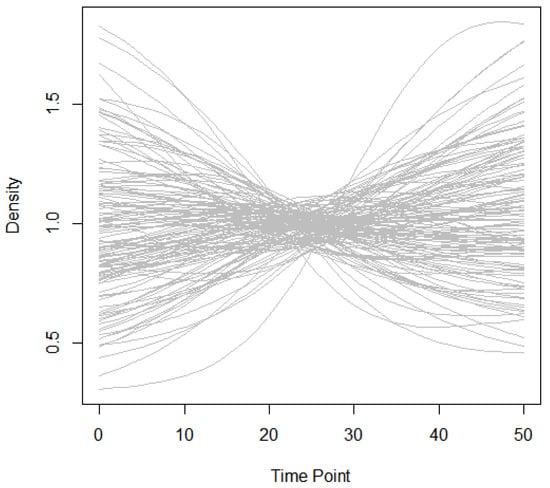
Figure 7.
Densities of relative per capita GDP in 123 countries over a period of 50 years.
To uncover and classify latent group structures based on the estimated density functions, we implemented the proposed procedure and applied the hierarchical agglomerative clustering (HAC) algorithm. The clustering results, displayed in Supplementary Figure S3, were assessed using two model selection criteria, the Generalized Bayesian Information Criterion (GBIC) and Generalized Akaike Information Criterion (GAIC), both of which consistently indicated that the individual-specific functions should be partitioned into three distinct clusters. The corresponding group memberships, capturing countries with similar patterns in the distributions of relative per capita GDP, are summarized in Supplementary Table S2.
Following the identification of latent group structures, post-clustering estimation was performed to refine the group-specific functions, yielding the estimates for each cluster. These refined functions, along with the corresponding density functions of relative per capita GDP for the three identified groups, are illustrated in Figure 8. The clustering results offer valuable insights into the heterogeneity of economic development trajectories across countries, emphasizing distinct patterns in their relative economic positions over time with respect to the global average.
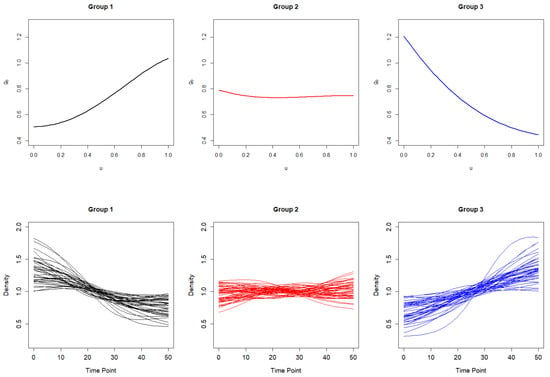
Figure 8.
Estimation of latent group structures (First Row) and corresponding density functions of relative per capita GDP for each group (Second Row).
The relative per capita GDP in Group 3 showed a clear upward trend over time, indicating that these countries have been gaining economic influence in the global landscape. Conversely, Group 1 experienced a downward trend, suggesting a decline in their relative position within the world economy. Group 2, meanwhile, displayed a more stable pattern, with steady growth and less pronounced fluctuations compared to the other groups. These distinct trajectories highlight the diverse paths of economic development among countries, reflecting both emerging economic powers and those facing stagnation or decreasing influence on the global stage.
A backward elimination procedure, guided by the fraction of variance explained (FVE) criterion, was employed to select the most significant predictors for the final model. At each step, the predictor contributing the least to explaining variance was removed, and the model was refitted. To validate the statistical significance of the retained variables, p-values were calculated for each predictor in the final model using a bootstrap procedure to account for the complexity of the functional additive framework. The resulting p-values for the key predictors were 0.021 for ‘education’, 0.015 for ‘population’, and 0.001 for ‘average GDP’, indicating strong evidence that all three variables significantly influence the response. The variable ‘oriGDP’ was excluded due to a comparatively high p-value (0.35) and low contribution to the explained variance, confirming its lack of significance. Incorporating p-values alongside the FVE criterion provides a robust validation of the selected model, ensuring that the retained covariates are not only important in terms of explained variance but also statistically significant, thereby strengthening the interpretability and reliability of the final additive model.
Figure 9 presents heat maps illustrating the effects of these predictors, with corresponding FVE values of 50.75%, 15.41%, and 30.42%, respectively. The heat map for ‘education’ reveals its dynamic influence on relative per capita GDP over time. In particular, countries with higher literacy rates experienced a stronger impact in earlier periods, which gradually diminished, whereas countries with lower literacy rates exhibited the opposite trend. The patterns associated with the remaining predictors display either similar or contrasting dynamics, underscoring the complex and evolving relationship between these socioeconomic factors and economic development across countries.
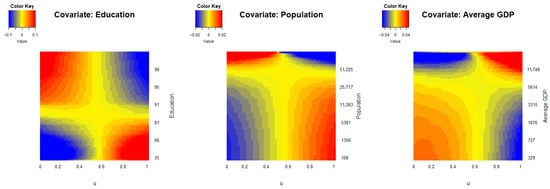
Figure 9.
Heat maps of additive component functions. The predictors include ‘education’ (literacy rate), ‘population’ (total population), and ‘average GDP’ (average per capita GDP over a 50-year period).
The RMSE values for the pre- and post-clustering estimations were 0.6385 and 0.2971, respectively, whereas the RMSE for the homogeneous additive model was 0.7962. These results highlight the necessity of incorporating heterogeneity into the analysis and demonstrate the superior performance of the proposed identification and clustering procedure when applied to the GDP data. Furthermore, three representative countries were selected from each identified group, and the corresponding observed and fitted density curves are illustrated in Supplementary Figure S4. Overall, the fitted densities closely match the observed curves, underscoring the robustness and accuracy of the proposed model in capturing the underlying economic dynamics across different countries.
In summary, this study highlights the critical role of accounting for heterogeneity in modeling the economic development of countries over time. By uncovering latent group structures through advanced clustering techniques, we are able to distinguish distinct trajectories in relative per capita GDP that reflect varying economic realities across nations. The inclusion of key socioeconomic covariates—education, population, and average GDP—provides a nuanced understanding of how these factors interact dynamically with economic outcomes. Our results demonstrate that these influences are neither static nor uniform, but rather evolve in complex ways depending on a country’s specific context and developmental stage. The superior predictive accuracy of the clustering-based approach, as evidenced by significantly reduced RMSE values compared to homogeneous models, underscores the value of embracing heterogeneity in such analyses.
While the methodology proves robust and insightful, it also has limitations that open avenues for future research. For instance, the assumption of fixed group memberships over time may not fully capture the fluidity of economic changes and transitions experienced by countries. Incorporating time-varying clustering or allowing for overlapping group structures could offer a more flexible and realistic modeling framework. Additionally, extending the model to integrate a broader set of covariates—such as technological innovation, institutional quality, or trade openness—would deepen our understanding of the multifaceted drivers behind economic growth. Overall, this work lays a strong foundation for more refined and comprehensive studies, aiming to better inform policymakers and economists about the diverse paths of economic development on the global stage.
4. Conclusions
Acknowledging the simultaneous presence of both heterogeneity and homogeneity in individual effects within the data, as well as the growing need to analyze complex non-Euclidean data, we extend the additive model introduced by [13] to accommodate heterogeneous subpopulations. In this extended framework, the response variable is a density function; individual effect curves are assumed to be homogeneous within groups but vary across groups, while the covariates share common additive bivariate functions. Building on the foundational work of [12], we employ a transformation technique to map density functions into a linear space, facilitating more effective analysis and modeling.
To estimate the unknown subject-specific functions and additive bivariate components, we employed a B-spline series approximation approach. The latent group structures were identified using the well-established hierarchical agglomerative clustering (HAC) algorithm. Our method consistently recovered the true latent groups with probability approaching one. Moreover, to improve the efficiency of the initial estimates, we constructed backfitted local linear estimators for both the grouped individual effect curves and the additive bivariate functions in the post-clustering model. We rigorously established the asymptotic properties of the resulting estimators, including their convergence rates, asymptotic distributions, and post-grouping oracle efficiency. The effectiveness of the identification and clustering procedure was demonstrated through Monte Carlo simulations and two real data applications. These results underscore the efficiency and validity of the proposed model compared to the conventional additive functional regression model that does not account for heterogeneity.
5. Discussion
Many challenging problems remain for future research. The exponential growth of data in recent decades often surpasses available computational resources, rendering traditional functional data analysis methods, which typically rely on limited sample sizes, less effective. A critical question is how to identify latent group structures in large-scale datasets efficiently. Additionally, while this study focused on latent group identification using scalar covariates, numerous practical applications could benefit from incorporating functional covariates to better capture dynamic relationships between predictors and responses. Developing novel methods that integrate both scalar and functional covariates is therefore a promising direction. Moreover, in this work, density functions were transformed into a linear space via a continuous and invertible mapping. Future research may explore approaches that model density function responses directly, without relying on such transformations. These avenues present exciting opportunities for further advancement in the field.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/stats8030071/s1, The supplementary materials include the detailed proof of the theoretical results as well as additional numerical results. Figure S1: The values of GBIC (the solid line) and GAIC (the dotted line) under varying numbers of groups for the COVID-19 data; Figure S2: Examples of fitted density (dotted line) and observed density (solid line) for the COVID-19 data. From top to bottom: Group 1 through 4; Figure S3: The values of GBIC (the solid line) and GAIC (the dotted line) under varying numbers of groups for the GDP data. Figure S4: Examples of fitted density (dotted line) and observed density (solid line) for the GDP data. From top to bottom: Group 1 through 4; Table S1: Group memberships for the COVID-19 data; Table S2: Group memberships for the GDP data. References [12,18,19,25,26,27,28,29,30] are cited in the Supplementary Materials.
Author Contributions
Conceptualization, Z.H., T.L. and J.Y.; data curation, Z.H.; formal analysis, Z.H.; funding acquisition, T.L. and J.Y.; methodology, Z.H., T.L. and J.Y.; project administration, T.L., J.Y. and N.B.; supervision, T.L., J.Y. and N.B.; writing—original draft, Z.H.; writing—review and editing, Z.H., T.L., J.Y. and N.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Li and You. Li’s research is supported by grants from the Humanities and Social Science Fund of the Ministry of Education of China (No. 21YJA910001). You’s research is supported by grants from the National Natural Science Foundation of China (NSFC) (No.11971291).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original datasets employed in this study are publicly accessible from the official website of Johns Hopkins University, accessed on 15 January 2021, at https://www.jhu.edu/ and the World Bank’s online platform, accessed on 27 March 2021, at https://data.worldbank.org/.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ramsay, J. When the data are functions. Psychometrika 1982, 47, 379–396. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, J. Functional single index models for longitudinal data. Ann. Stat. 2011, 39, 362–388. [Google Scholar] [CrossRef]
- Cheng, M.; Honda, T.; Li, J. Efficient estimation in semivarying coefficient models for longitudinal/clustered data. Ann. Stat. 2016, 44, 1988–2017. [Google Scholar] [CrossRef]
- Hilgert, N.; Mas, A.; Verzelen, N. Minimax adaptive tests for the functional linear model. Ann. Stat. 2013, 41, 838–869. [Google Scholar] [CrossRef]
- Luo, X.; Zhu, L.; Zhu, H. Single-index varying coefficient model for functional responses. Biometrics 2016, 72, 1275–1284. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Huang, C.; Zhu, H. A functional varying-coefficient single-index model for functional response data. J. Am. Stat. Assoc. 2017, 112, 1169–1181. [Google Scholar] [CrossRef]
- Kokoszka, P.; Miao, H.; Petersen, A.; Shang, H.L. Forecasting of density functions with an application to cross-sectional and intraday returns. Int. J. Forecast. 2019, 35, 1304–1317. [Google Scholar] [CrossRef]
- Petersen, A.; Müller, H. Fréchet regression for random objects with Euclidean predictors. Ann. Stat. 2019, 47, 691–719. [Google Scholar] [CrossRef]
- Petersen, A.; Chen, C.; Müller, H. Quantifying and visualizing intraregional connectivity in resting-state functional magnetic resonance imaging with correlation densities. Brain Connect. 2019, 9, 37–47. [Google Scholar] [CrossRef]
- Talská, R.; Menafoglio, A.; Machalová, J.; Hron, K.; Fiserová, E. Compositional regression with functional response. Comput. Stat. Data Anal. 2018, 123, 66–85. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Müller, H. Wasserstein Regression. J. Am. Stat. Assoc. 2023, 118, 869–882. [Google Scholar] [CrossRef]
- Petersen, A.; Müller, H. Functional data analysis for density functions by transformation to a Hilbert space. Ann. Stat. 2016, 44, 183–218. [Google Scholar] [CrossRef]
- Han, K.; Müller, H.; Park, B. Additive functional regression for densities as responses. J. Am. Stat. Assoc. 2020, 115, 997–1010. [Google Scholar] [CrossRef]
- Vogt, M.; Linton, O. Classification of nonparametric regression functions in longitudinal data models. J. R. Stat. Soc. Ser. B 2017, 79, 5–27. [Google Scholar] [CrossRef]
- Vogt, M.; Linton, O. Multiscale clustering of nonparametric regression curves. In Cemmap Working Paper CWP08/18; University of Cambridge: Cambridge, UK, 2018. [Google Scholar]
- Su, L.; Shi, Z.; Phillips, P. Identifying latent structures in panel data. Econometrica 2016, 84, 2215–2264. [Google Scholar] [CrossRef]
- Su, L.; Wang, X.; Jin, S. Sieve estimation of time-varying panel data models with latent structures. J. Bus. Econ. Stat. 2019, 37, 334–349. [Google Scholar] [CrossRef]
- Chen, J. Estimating latent group structures in time-varying coefficient panel data models. Econom. J. 2019, 22, 223–240. [Google Scholar] [CrossRef]
- De Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 1978. [Google Scholar]
- Stone, C. The use of polynomial splines and their tensor products in multivariate function estimation. Ann. Stat. 1994, 22, 118–171. [Google Scholar]
- Chen, J.; Li, D.; Wei, L.; Zhang, W. Nonparametric homogeneity pursuit in functional-coefficient models. J. Nonparametric Stat. 2021, 33, 387–416. [Google Scholar] [CrossRef]
- Cardot, H.; Ferraty, F.; Sarda, P. Functional linear model. Stat. Probab. Lett. 1999, 45, 11–22. [Google Scholar] [CrossRef]
- Fan, J. Local linear regression smoothers and their minimax efficiencies. Ann. Stat. 1993, 21, 196–216. [Google Scholar] [CrossRef]
- Ke, Z.; Fan, J.; Wu, Y. Homogeneity pursuit. J. Am. Stat. Assoc. 2015, 110, 175–194. [Google Scholar] [CrossRef]
- Bosq, D. Nonparametric Statistics for Stochastic Processes, 2nd ed.; Lecture Notes in Statist; Springer: New York, NY, USA, 1998; Volume 110. [Google Scholar]
- Wang, L.; Yang, L. Spline-backfitted kernel smoothing of nonlinear additive autoregression model. Ann. Stat. 2007, 35, 2474–2503. [Google Scholar] [CrossRef]
- Pei, Y.; Huang, T.; You, J. Nonparametric fixed effects model for panel data with locally stationary regressors. J. Econom. 2018, 202, 286–305. [Google Scholar] [CrossRef]
- DeVore, R.; Lorentz, G. Constructive Approximation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1993; Volume 303. [Google Scholar]
- Masry, E. Multivariate local polynomial regression for time series: Uniform strong consistency and rates. J. Time Ser. Anal. 1996, 17, 571–599. [Google Scholar] [CrossRef]
- Ruppet, D.; Wand, P. Multivariate locally weighted least squares regression. Ann. Stat. 1994, 22, 1346–1370. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).