Comparing Robust Haberman Linking and Invariance Alignment

Abstract

Linking methods are widely used in the social sciences to compare group differences regarding the mean and the standard deviation of a factor variable. This article examines a comparison between robust Haberman linking (HL) and invariance alignment (IA) for factor models with dichotomous and continuous items, utilizing the $L_{0.5}$ and $L_0$ loss functions. A simulation study demonstrates that HL outperforms IA when item intercepts are used for linking, rather than the original HL approach, which relies on item difficulties. The results regarding the choice of loss function were mixed: $L_0$ showed superior performance in the simulation study with continuous items, while $L_{0.5}$ performed better in the study with dichotomous items.

1. Introduction

When comparing multiple groups in confirmatory factor analysis (CFA; [1]) or item response theory (IRT; [2,3]) models with respect to a factor variable, certain identification assumptions are required. A common approach assumes that item parameters remain consistent across groups, a property referred to as measurement invariance [4,5]. This principle is frequently discussed in the social sciences [5,6]. In the IRT literature, the lack of invariance is called differential item functioning (DIF; [7,8,9,10,11]).

To address violations of measurement invariance, the invariance alignment (IA) method [12,13,14,15], also known as alignment optimization [16,17], has been proposed for comparing groups in unidimensional factor models. The IA method aims to maximize the number of item parameters that are (approximately) invariant while permitting limited deviations. This approach enhances the robustness of group comparisons in the presence of measurement invariance violations. The IA method is frequently applied in social sciences for analyzing questionnaire data [18,19,20,21,22,23,24,25].

The Haberman linking (HL; [26]) method, as a particular linking method [27,28,29], has been developed for group comparisons in IRT models. While it is widely applied in educational testing, it remains largely unfamiliar to practitioners in other fields (but  see [30,31,32,33,34] for exceptions). This trend is also reflected in the citation counts of the original sources of IA and HL. The original IA article of Asparouhov and Muthén (2014, Structural Equation Modeling [12]) has been cited 849 times according to Google Scholar, 440 times according to Web of Science, and 392 times according to CrossRef (as of 22 November 2024). In contrast, the original HL article of Haberman (2009, ETS Research Report [26]) has only 80 citations according to Google Scholar and 32 citations according to CrossRef (as of 22 November 2024).

Notably, HL appears to share significant similarities with the invariance alignment (IA) method. As noted in [35], researcher “Matthias von Davier, in particular, also highlighted how the alignment optimization [i.e., invariance alignment] method is very similar to the simultaneous test-linking approach proposed by Haberman (2009)” [35].

This article examines a comparison between HL and the IA method. Specifically, a robust version of HL, termed robust HL, is contrasted with IA in the presence of fixed differential item functioning (DIF) effects, which follows a sparsity structure; that is, only a subset (i.e., the minority) of item parameters exhibit DIF. This article builds on previous work of the author in a precursor article [36], published in 2020 in the Stats journal. To facilitate the comparison between the HL and IA linking methods, the robust loss functions $L_{0.5}$ and $L_0$ are employed in both HL and IA. A recently proposed differentiable approximation of the $L_0$ loss function is applied for HL and IA for the first time. As in [36], HL was modified to enable linking based on item intercepts instead of item difficulties.

The findings in this article, from two simulation studies, show that the modified HL specification with linking based on item intercepts closely resembles IA and, in several contexts, outperforms it. Moreover, in contrast to previous work in [36], the simulation studies in this article involved only three groups, rather than a larger number of groups, and manipulated the DIF effect size and the number of items to more thoroughly investigate the generalizability of the findings from the comparison of HL and IA. Previous work pointed out that the performance of different loss functions strongly depends on the size of the DIF effect sizes, where more robust (i.e., less biased) results are typically obtained with larger DIF effect sizes. In addition, more robust results can be expected with a larger number   of items.

The structure of the article is as follows. Section 2 reviews unidimensional factor models for dichotomous and continuous items. The robust $L_{0.5}$ and $L_0$ functions are discussed in Section 3. Descriptions of IA and HL with robust loss functions are provided in Section 4 and Section 5, respectively. Section 6 presents results from a simulation study with dichotomous items, while Section 7 discusses findings from a simulation study using continuous items. Finally, Section 8 concludes the article with a discussion.

2. Unidimensional Factor Model

This section discusses unidimensional factor models for dichotomous items in   Section 2.1 and for continuous items in Section 2.2. Let ${\mathit{X}}_g=(X_{1g},\dots ,X_{Ig})$ denote the vector of $I>1$ items in group $g=1,\dots ,G$. The vector of items $\mathit{X}$ is related to a normally distributed factor variable ${\theta }_g$, commonly referred to as the trait or ability variable in IRT. It is assumed that ${\theta }_g$ is normally distributed with mean ${\mu }_g$ and standard deviation (SD) ${\sigma }_g$ in group g. For identification reasons, we assume that ${\mu }_1=0$ and ${\sigma }_1=1$ holds in the first group. In the unidimensional factor models, it is assumed that items $X_{ig}$ are conditionally independent given the latent variable ${\theta }_g$. This implies that

$$\mathsf{P}(X_{1g},\dots ,X_{Ig}|{\theta }_g)=\prod _{i=1}^I\mathsf{P}\left(X_{ig}\right|{\theta }_g).$$

(1)

Equation (1) represents the local independence assumption in IRT for dichotomous items, and it implies uncorrelated residual variables in the factor model for continuous items.

2.1. Dichotomous Items

We now describe the unidimensional factor model for dichotomous items ${\mathit{X}}_g\in {\{0,1\}}^I$. The function $P_{ig}\left(\theta \right)=\mathsf{P}(X_{ig}=1|{\theta }_g)$ for $i=1,\dots ,I$ in group g is referred to as the item response function (IRF). The IRF of the two-parameter logistic (2PL) model [37] is   defined as

$$P_{ig}\left(\theta \right)=\mathrm{\Psi }\left(a_{ig}(\theta -b_{ig})\right)\mathrm{with}{\theta }_g\sim \mathsf{N}({\mu }_g,{\sigma }_g^2),$$

(2)

where $a_{ig}$ and $b_{ig}$ denote the item discrimination and the item difficulty $b_{ig}$, respectively, and $\mathrm{\Psi }\left(x\right)={(1+exp(-x))}^{-1}$ is the logistic distribution function.

The 2PL model in (2) can be equivalently expressed with item intercepts ${\nu }_{ig}$ instead of item difficulties $b_{ig}$. Then, the 2PL model is parametrized as

$$P_{ig}\left(\theta \right)=\mathrm{\Psi }\left(a_{ig}\theta +{\nu }_{ig}\right)\mathrm{with}{\theta }_g\sim \mathsf{N}({\mu }_g,{\sigma }_g^2),$$

(3)

where ${\nu }_{ig}=-a_{ig}{b}_{ig}$, or $b_{ig}=-a_{ig}/{\nu }_{ig}$.

The parameters of the 2PL model can be consistently estimated using marginal maximum likelihood estimation (MML; [38,39,40]). When estimating the 2PL model (2) separately in group g, the identification constraints ${\mu }_g=0$ and ${\sigma }_g=1$ must be applied. The identified item parameters ${\widehat{a}}_{ig}$ and ${\widehat{b}}_{ig}$ in this specification are given as

$${\widehat{a}}_{ig}=a_{ig}{\sigma }_g\mathrm{and}{\widehat{b}}_{ig}={\displaystyle \frac{b_{ig}-{\mu }_g}{{\sigma }_g}}.$$

(4)

2.2. Continuous Items

The unidimensional factor model for continuous items in CFA is defined as

$$X_{ig}={\nu }_{ig}+a_{ig}{\theta }_g+{\xi }_{ig}\mathrm{with}{\theta }_g\sim \mathsf{N}({\mu }_g,{\sigma }_g^2)\mathrm{and}{\xi }_{ig}\sim \mathsf{N}(0,{\omega }_{ig}),$$

(5)

where ${\nu }_{ig}$ is the item intercept and $a_{ig}$ is the item discrimination, respectively. The residual variables ${\xi }_{ig}$ are uncorrelated with the factor variable ${\theta }_g$.

The parameters of the unidimensional factor model (5) can be estimated with maximum likelihood [1,41]. When estimating the unidimensional model (5) separately in group g, the identification constraints ${\mu }_g=0$ and ${\sigma }_g=1$ must again be applied. Under this specification, the identified item parameters ${\widehat{a}}_{ig}$ and ${\widehat{\nu }}_{ig}$ are expressed as

$${\widehat{a}}_{ig}=a_{ig}{\sigma }_g\mathrm{and}{\widehat{\nu }}_{ig}={\nu }_{ig}+a_{ig}{\mu }_g={\nu }_{ig}+{\displaystyle \frac{{\widehat{a}}_{ig}}{{\sigma }_g}}{\mu }_g.$$

(6)

3. $L_{0.5}$ and $L_0$ Loss Functions

In this paper, DIF effects are treated as outliers that should be excluded from group comparisons [42,43,44,45,46,47,48]. Group differences are calculated using robust location measures, which are estimated via robust loss functions [49,50,51].

A flexible class of such a robust loss function is the $L_p$ (with $p>0$) loss function, refs. [36,52,53,54,55] defined as

$$\rho \left(x\right)={\left|x\right|}^p\mathrm{for}p>0.$$

(7)

The case $p=2$ (i.e., the $L_2$ loss function) corresponds to the widely known square loss function, while $p=1$ (i.e., the $L_1$ loss function) corresponds to median regression [56,57]. However, the loss function $\rho$ is not differentiable at $x=0$ for $p\le 1$. To address this, a differentiable approximation of $\rho$ is given by

$$\tilde{\rho }\left(x\right)\simeq {\left({\left|x\right|}^2+\epsilon \right)}^{p/2},$$

(8)

where $\epsilon >0$ is a tuning parameter that controls the approximation error of $\tilde{\rho }$ relative to $\rho$ [12]. In practice, values such as $\epsilon =0.01$ (see [12] for $p=0.5$ and $p=0.25$) or   $\epsilon =0.001$ [36,58] have been effectively applied in various contexts.

The left panel in Figure 1 depicts the exact $L_{0.5}$ loss function as a black solid line and its approximation as a red dashed line. The two functions are nearly identical except near the nondifferentiable point $x=0$.

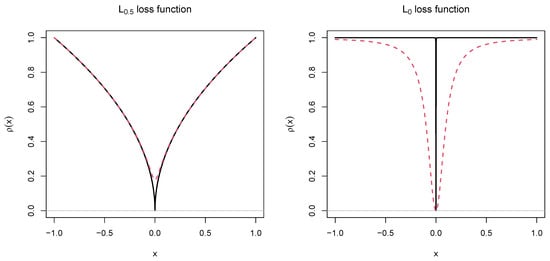
Figure 1. $L_{0.5}$ loss function (left panel) and $L_0$ loss function (right panel). The exact functions are displayed with black solid lines, while their differentiable approximations are displayed in red dashed lines.

As an alternative to the $L_p$ loss function, the $L_0$ loss function [59,60] is defined as

$$\rho \left(x\right)=\mathbf{1}(x\ne 0),$$

(9)

where $\mathbf{1}$ denotes the indicator function. This loss function takes the value 0 for $x=0$ and 1 for $x\ne 0$, effectively counting the number of deviations from 0. The $L_0$ loss function is particularly well suited for scenarios involving partial invariance, where only a small number of DIF effects deviate from zero. An approximation of this loss function is given by (see [61])

$$\tilde{\rho }\left(x\right)\simeq {\displaystyle \frac{x^2}{x^2+\epsilon }},$$

(10)

where $\epsilon >0$ is a tuning parameter. The choice $\epsilon =0.01$ has been shown to perform well across various settings [62,63].

In the previous work of the author [36], the $L_0$ loss function was approximated using the $L_p$ loss function with a very small value of $p=0.02$. However, in our experience based on simulation studies involving structural equation models [62], the $L_0$ approximation (10) outperforms the differentiable approximation of the $L_{0.02}$ loss function in (8) in terms of the precision of parameter estimates. Consequently, this article focuses solely on the $L_0$   loss function.

The right panel in Figure 1 depicts the exact $L_0$ loss function as a black solid line and its approximation as a red dashed line. Note that the $L_0$ function is even discontinuous at the point $x=0$, and there are moderate deviations of the approximation $\tilde{\rho }$ from the exact $L_0$ loss function $\rho$.

The $L_p$ loss function with $p<1$, such as $p=0.5$, is preferred over $p=1$ in situations involving asymmetric error distributions (e.g., outliers). For instance, all outlying DIF effects in one group might be either positive or negative, creating a scenario of unbalanced DIF. In such cases, the $L_1$ loss function has been found to perform inadequately.

4. Invariance Alignment

In this section, we review the estimation of the IA method proposed by Asparouhov and Muthén [12,14]. The IA method has been discussed for continuous items [12], dichotomous items [14], and polytomous items [64].

The originally proposed IA method estimates group means $\mathit{\mu }$ and group SDs $\mathit{\sigma }$ in a single step. However, it has been shown that the optimization can be split into two successive steps: first, estimating $\mathit{\sigma }$, and then estimating $\mathit{\mu }$, as in HL [36]. The IA method relies on estimated item discriminations ${\widehat{a}}_{ig}$ (or the log-transformed item discriminations $log{\widehat{a}}_{ig}$ and item intercepts ${\widehat{\nu }}_{ig}$ ($i=1,\dots ,I$; $g=1,\dots ,G$).

First, group SDs can be obtained by minimizing the optimization function

$$H_1\left(\mathit{\sigma }\right)=\sum _{i=1}^I\sum _{g\ne h}\rho \left({\displaystyle \frac{{\widehat{a}}_{ig}}{{\sigma }_g}}-{\displaystyle \frac{{\widehat{a}}_{ih}}{{\sigma }_h}}\right),$$

(11)

where $\rho$ represents the $L_p$ or $L_0$ loss function. Note that the original IA method also involves weights for pairs of groups g and h, which accounts for different sample sizes in the optimization function. We omit the inclusion of weights here, as these weights become irrelevant when all sample sizes per group are equal.

For identification purposes, one can either set ${\sigma }_1=1$ or apply the constraint ${\prod }_{g=1}^G{\sigma }_g=1$; the latter constraint is implemented in the popular Mplus software [65].

As an alternative to the optimization function $H_1$ in (11), log-transformed group SDs $\mathit{s}=(s_1,\dots ,s_G)$ with $s_g=log\left({\sigma }_g\right)$ could alternatively be estimated based on log-transformed item discriminations $log{\widehat{a}}_{ig}$ by minimizing

$${\tilde{H}}_1\left(\mathit{s}\right)=\sum _{i=1}^I\sum _{g\ne h}\rho \left(log{\widehat{a}}_{ig}-log{\widehat{a}}_{ih}-s_g+s_h\right),$$

(12)

where group SDs can be estimated as ${\widehat{\sigma }}_g=exp\left({\widehat{s}}_g\right)$ based on estimated values ${\widehat{s}}_g$ for $g=1,\dots ,G$.

In the second step, group means $\mathit{\mu }$ are estimated based on previously estimated group SDs $\widehat{\mathit{\sigma }}$ by minimizing

$$H_2\left(\mathit{\mu }\right)=\sum _{i=1}^I\sum _{g\ne h}\rho \left({\widehat{\nu }}_{ig}-{\widehat{\nu }}_{ih}-{\displaystyle \frac{{\widehat{a}}_{ig}}{{\widehat{\sigma }}_g}}{\mu }_g+{\displaystyle \frac{{\widehat{a}}_{ih}}{{\widehat{\sigma }}_h}}{\mu }_h\right).$$

(13)

Again, the originally proposed IA method uses the $L_{0.5}$ loss function, which employs the power $p=0.5$.

In the Mplus implementation of the $L_p$ loss function with $p=0.5$ and $p=0.25$, the default tuning parameter in the differentiable approximation of the loss function is   $\epsilon =0.01$ [36,63,65]. However, selecting $\epsilon =0.001$ may be beneficial in many contexts [63,66]. The choice $\epsilon =0.01$ in the $L_0$ loss function was found to yield the best performance [66].

5. Haberman Linking

The originally proposed HL method [26] estimates group means $\mathit{\mu }$ and group SDs $\mathit{\sigma }$ based on log-transformed item discriminations ${\widehat{a}}_{ig}$ and item difficulties ${\widehat{b}}_{ig}$.

In the first step, the log-transformed group standard deviations $s_g=log{\sigma }_g$ are estimated ($g=1,\dots ,G$). In the second step, group means ${\mu }_g$ are estimated. For identification purposes, the constraints $s_1=0$ (implying ${\sigma }_1=1$) and ${\mu }_1=0$ are imposed.

Log-transformed SDs $\mathit{s}$ and log-transformed joint item discriminations $\mathit{\alpha }=({\alpha }_1,\dots ,{\alpha }_I)$, where $a_i=exp\left({\alpha }_i\right)$ for $i=1,\dots ,I$, are obtained by minimizing the following optimization function:

$$H_1(\mathit{s},\mathit{\alpha })=\sum _{i=1}^I\sum _{g=1}^G\rho \left(log{\widehat{a}}_{ig}-{\alpha }_i-s_g\right),$$

(14)

where $\rho$ is the $L_p$ or $L_0$ loss function. The original HL method uses the $L_2$ loss function [26]. However, because distribution parameters need to be consistently estimated without being influenced by outlying DIF effects, this article employs differentiable approximations of robust loss functions, specifically $L_{0.5}$ and $L_0$.

Subsequently, group means $\mathit{\mu }$ and joint item difficulties $\mathit{b}=(b_1,\dots ,b_I)$ are determined by minimizing

$$H_2(\mathit{\mu },\mathit{b})=\sum _{i=1}^I\sum _{g=1}^G\rho \left({\widehat{\sigma }}_g{\widehat{b}}_{ig}-b_i+{\mu }_g\right),$$

(15)

where the estimated SDs ${\widehat{\sigma }}_g=exp\left({\widehat{s}}_g\right)$ are inserted in the optimization function. Similar to the optimization function (14) for SDs, the original HL method uses the $L_2$ loss function.

As an alternative to the optimization function in (15), a modified optimization function in HL uses item intercepts ${\widehat{\nu }}_{ig}=-{\widehat{a}}_{ig}{\widehat{b}}_{ig}$ instead of item difficulties ${\widehat{b}}_{ig}$ (see also [36]). The use of item intercepts is motivated by their role in IA. In this adaptation to HL, the group means $\mathit{\mu }$ and joint item intercepts $\mathit{\nu }=({\nu }_1,\dots ,{\nu }_I)$ are determined by minimizing

$${\tilde{H}}_2(\mathit{\mu },\mathit{\nu })=\sum _{i=1}^I\sum _{g=1}^G\rho \left({\widehat{\nu }}_{ig}-{\nu }_i-{\displaystyle \frac{{\widehat{a}}_{ig}}{{\widehat{\sigma }}_g}}{\mu }_g\right).$$

(16)

There is a lack of research comparing the performance of the optimization functions $H_2$ and ${\tilde{H}}_2$ in HL, particularly in comparing HL with these optimization functions to IA. As an exception, the author’s precursor article [36] included these two specifications, but they were only analyzed for a moderate or large number of groups, with a fixed DIF effect size and a fixed number of items. This article aims to provide additional insights into the performance of these two specifications for a smaller number of groups and more extended data-generating models.

6. Simulation Study 1: Dichotomous Items

6.1. Method

The 2PL model for $G=3$ groups was used as the IRF in the data-generating model. The latent factor variable $\theta$ was normally distributed within each group, with group means ${\mu }_1=0$, ${\mu }_2=0.3$, and ${\mu }_3=-0.5$. The SDs were ${\sigma }_1=1$, ${\sigma }_2=1.2$, and ${\sigma }_3=0.8$.

The simulation study was conducted for $I=10$ and $I=20$ items. Group-specific parameters $a_{ig}$ and $b_{ig}$ for each item $i=1,\dots ,I$ and for groups $g=1,2,3$ were based on fixed base item parameters, with DIF effects remaining constant across replications within a simulation condition. We now describe the item parameter choice in the $I=10$ item condition. For the $I=20$ condition, the item parameters were duplicated. For 10 items, the base item discriminations $a_i$ were all set to 1.00. The base item difficulties $b_i$ were set as 0.21, −1.47, 0.09, 0.55, −0.67, 0.77, 0.99, −1.75, 0.10, and 1.17, resulting in a mean item difficulty of 0.000 and an SD of 0.999. For the $I=20$ condition, the item parameters were duplicated. The base item parameters are also available at https://osf.io/kcnyu (accessed on 22 November 2024).

Fixed uniform DIF effects were assumed, meaning that DIF could occur in item difficulties, while item discriminations were not prone to DIF. Specifically, group-specific item difficulties $b_{ig}$ were simulated as $b_i+f_{ig}\delta$, where the factor $f_{ig}$ was chosen as either 1 and $-1$, indicating DIF items, or 0 for DIF-free items. In the first group, the factor was 1 for the first item and −1 for the second item, while all other items did not exhibit DIF. In the second group, DIF effects were simulated for the third and fourth items with a factor of 1. In the third group, DIF effects were simulated for the fifth and sixth items with a factor of −1. Note that the DIF effects were canceled out in the first group, but they were all positive in the second group and negative in the third group, resulting in unbalanced DIF. The size $\delta$ of the DIF effect was set to 0, 0.3, and 0.6, representing no DIF, small DIF, and large DIF, respectively.

The sample sizes per group were selected as $N=250$, 500, 1000, and 2000 to represent typical sample sizes in small- to large-scale testing applications of the 2PL model [67,68].

In each of the 4 (sample size N) × 3 (DIF effect $\delta$) × 2 (number of items I) = 24 cells of the simulation, 3000 replications were conducted. The 2PL model was first estimated separately in each of the three groups. Linking was performed in four specifications. First, IA was carried out using two approaches: the original method, based on untransformed item discriminations ([12]; method IA1, using optimization functions (11) and (13)), and an alternative method based on log-transformed item discriminations, similar to the approach used in HL (method IA2, using optimization functions (12) and (13)). In addition, we used the originally proposed HL ([26]; method HL1, using optimization functions (14) and (15)), which relies on item difficulties, and an HL implementation that employed item intercepts (method HL2, using optimization functions (14) and (16)). These four specifications were applied to both the $L_{0.5}$ (i.e., $p=0.5$) and $L_0$ (i.e., $p=0$) loss functions, resulting in a total of 8 different linking methods. The $L_2$ loss function was not considered, as it has been shown in [36] to produce biased parameter estimates in IA and HL when unbalanced DIF is present. Furthermore, the simulated DIF effects were asymmetric, rendering the $L_1$ loss function ineffective in providing nearly unbiased linking estimates. For identification purposes, the distribution parameters in the first group were fixed at ${\mu }_1=0$ and ${\sigma }_1=1$, while ${\mu }_g$ and ${\sigma }_g$ were freely estimated for the second and third groups.

We evaluated the bias and the root mean square error (RMSE) for the ${\widehat{\mu }}_g$ and ${\widehat{\sigma }}_g$ estimates. Additionally, a relative RMSE was calculated, with IA1 using the $L_{0.5}$ loss function (i.e., $p=0.5$) serving as the reference method (set to a relative RMSE of 100). To summarize the results across groups, the average absolute bias and average relative RMSE were computed for both the ${\widehat{\mu }}_g$ and ${\widehat{\sigma }}_g$ estimates across the two groups.

All analyses for this simulation study were carried out with the statistical software R (Version 4.4.1 [69]). The 2PL model was estimated with the function sirt::rasch.mml2() function from the R package sirt (Version 4.2-89 [70]). HL and IA were estimated with the sirt::linking.haberman.lq() and sirt::invariance.alignment() functions from the same R package, respectively. Replication material for this simulation study can be assessed at https://osf.io/kcnyu (accessed on 22 November 2024).

6.2. Results

Table 1 summarizes the average absolute bias and average relative RMSE for the estimated group means, ${\widehat{\mu }}_g$. When $\delta =0$ (no DIF), all methods exhibited minimal bias, with values near 0.00 for larger sample sizes (N). As $\delta$ increased, bias grew across all methods. IA1, IA2, and HL2 performed similarly in terms of bias, while HL1 demonstrated the poorest performance.

Table 1. Simulation Study 1 (dichotomous items): Average absolute bias and average relative root mean square error (RMSE) for estimated group means ${\widehat{\mu }}_g$ as a function of the DIF effect $\delta$, number of items I, and sample size N.

			Average Absolute Bias								Average Relative RMSE
			$\mathit{p}=\mathbf{0.5}$				$\mathit{p}=\mathbf{0}$				$\mathit{p}=\mathbf{0.5}$				$\mathit{p}=\mathbf{0}$
$\mathit{\delta }$	$\mathit{I}$	$\mathit{N}$	IA1	IA2	HL1	HL2	IA1	IA2	HL1	HL2	IA1 ‡	IA2	HL1	HL2	IA1	IA2	HL1	HL2
0	10	250	0.02	0.02	0.00	0.02	0.02	0.02	0.00	0.02	100	101	114	102	122	121	140	123
		500	0.01	0.02	0.00	0.02	0.01	0.01	0.00	0.01	100	101	113	101	118	119	136	118
		1000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	100	111	100	114	115	128	113
		2000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	100	108	99	108	108	118	106
	20	250	0.01	0.02	0.00	0.02	0.01	0.01	0.00	0.01	100	100	110	101	123	123	137	121
		500	0.01	0.01	0.00	0.01	0.01	0.01	0.00	0.01	100	100	109	100	117	117	130	117
		1000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	100	108	100	111	111	122	110
		2000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	100	105	99	104	104	110	102
0.3	10	250	0.07	0.07	0.06	0.07	0.06	0.06	0.07	0.06	100	101	117	102	121	122	146	121
		500	0.06	0.06	0.06	0.06	0.06	0.06	0.06	0.06	100	101	115	101	121	121	144	119
		1000	0.05	0.05	0.06	0.05	0.04	0.05	0.06	0.04	100	101	117	100	120	121	145	118
		2000	0.03	0.03	0.04	0.03	0.02	0.02	0.04	0.02	100	100	128	98	112	112	158	108
	20	250	0.07	0.07	0.06	0.07	0.06	0.06	0.07	0.06	100	101	112	101	121	121	141	121
		500	0.06	0.06	0.06	0.06	0.06	0.06	0.06	0.05	100	100	110	101	122	122	139	121
		1000	0.05	0.05	0.06	0.05	0.04	0.04	0.05	0.03	100	100	114	99	116	116	141	111
		2000	0.03	0.03	0.04	0.03	0.01	0.01	0.03	0.01	100	100	123	97	97	97	140	92
0.6	10	250	0.10	0.10	0.11	0.10	0.08	0.08	0.10	0.08	100	101	120	100	121	122	152	120
		500	0.06	0.06	0.08	0.06	0.03	0.03	0.07	0.03	100	100	129	100	118	119	164	115
		1000	0.03	0.03	0.05	0.03	0.00	0.00	0.03	0.00	100	100	132	96	108	107	163	101
		2000	0.02	0.02	0.02	0.02	0.00	0.00	0.00	0.00	100	100	122	95	101	101	128	95
	20	250	0.09	0.09	0.10	0.09	0.07	0.07	0.10	0.06	100	100	117	101	120	120	150	119
		500	0.06	0.06	0.07	0.05	0.02	0.02	0.05	0.02	100	100	121	98	108	108	147	105
		1000	0.03	0.03	0.04	0.03	0.00	0.00	0.01	0.00	100	100	120	96	101	101	125	97
		2000	0.02	0.02	0.02	0.02	0.00	0.00	0.00	0.00	100	100	111	96	96	97	105	92

Note. p = power used in the $L_p$ loss function; IA1 = invariance alignment (IA) with untransformed item discriminations ${\widehat{a}}_{ig}$ as originally proposed by Asparouhov and Muthén (2014 [12]), using optimization   functions (11) and (13); IA2 = IA based on log-transformed item discriminations ${\widehat{\alpha }}_{ig}$, using (12) and (13); HL1 = Haberman linking (HL) based on item difficulties ${\widehat{b}}_{ig}$, as originally proposed by Haberman (2009 [26]), using (14) and (15); HL2 = HL based on item intercepts ${\widehat{\nu }}_{ig}$, using (14) and (16). ^‡ The linking method IA1 with $p=0.5$ was the reference method for computing the relative RMSE. Absolute bias values larger than 0.025 are printed in bold font. Relative RMSE values larger than 104.5 are printed in bold font, while values smaller than 99.5 are printed in a gray background color.

In terms of RMSE, IA2 closely resembled IA1 for $p=0.5$ and $p=0$. HL1 consistently showed the highest RMSE, although HL2 outperformed IA1 and IA2 in certain conditions with larger sample sizes. Increasing the number of items from 10 to 20 slightly reduced bias; however, bias converged to zero as sample sizes increased.

For the $L_p$ loss function, $p=0$ resulted in less bias than $p=0.5$, but estimates based on $L_0$ were more variable, as reflected in higher RMSE values for most conditions. Overall, the HL2 method, as an alternative to HL1, was competitive with IA1 for estimating group means. HL2 offered particular advantages with large DIF effects (i.e., for $\delta =0.6$).

Table 2 presents the average absolute bias and relative RMSE for the estimated SDs ${\widehat{\sigma }}_g$. Across all conditions, bias was small for all methods, with slightly better performance observed at larger values of I and N. This outcome was expected, as DIF was introduced only in item difficulties, not in item discriminations.

Table 2. Simulation Study 1 (dichotomous items): Average absolute bias and average relative root mean square error (RMSE) for estimated group standard deviations ${\widehat{\sigma }}_g$ as a function of the DIF effect $\delta$, number of items I, and sample size N.

			Average Absolute Bias								Average Relative RMSE
			$\mathit{p}=\mathbf{0.5}$				$\mathit{p}=\mathbf{0}$				$\mathit{p}=\mathbf{0.5}$				$\mathit{p}=\mathbf{0}$
$\mathit{\delta }$	$\mathit{I}$	$\mathit{N}$	IA1	IA2	HL1	HL2	IA1	IA2	HL1	HL2	IA1 ‡	IA2	HL1	HL2	IA1	IA2	HL1	HL2
0	10	250	0.01	0.01	0.01	0.01	0.02	0.02	0.02	0.02	100	103	104	104	131	133	135	135
		500	0.01	0.00	0.00	0.00	0.01	0.01	0.01	0.01	100	102	103	103	129	130	129	129
		1000	0.00	0.00	0.00	0.00	0.01	0.01	0.01	0.01	100	101	101	101	126	126	125	125
		2000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	100	99	99	118	118	116	116
	20	250	0.01	0.00	0.01	0.01	0.01	0.01	0.01	0.01	100	101	104	104	136	137	137	137
		500	0.00	0.00	0.00	0.00	0.01	0.01	0.00	0.00	100	101	102	102	131	131	130	130
		1000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	100	101	101	122	122	121	121
		2000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	100	99	99	111	112	109	109
0.3	10	250	0.02	0.01	0.01	0.01	0.02	0.02	0.02	0.02	100	103	104	104	133	134	137	137
		500	0.01	0.01	0.01	0.01	0.01	0.01	0.01	0.01	100	102	103	103	130	131	130	130
		1000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	101	102	102	125	126	126	126
		2000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	100	99	99	119	119	116	116
	20	250	0.01	0.00	0.00	0.00	0.01	0.01	0.01	0.01	100	102	103	103	134	135	134	134
		500	0.00	0.00	0.00	0.00	0.01	0.01	0.01	0.01	100	101	102	102	130	131	130	130
		1000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	101	101	101	121	122	121	121
		2000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	100	99	99	112	112	109	109
0.6	10	250	0.01	0.01	0.01	0.01	0.02	0.02	0.02	0.02	100	102	104	104	133	133	133	133
		500	0.01	0.01	0.01	0.01	0.01	0.01	0.01	0.01	100	102	102	102	130	131	129	129
		1000	0.01	0.00	0.00	0.00	0.01	0.01	0.01	0.01	100	101	101	101	125	126	124	124
		2000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	100	99	99	119	119	117	117
	20	250	0.01	0.01	0.01	0.01	0.01	0.01	0.01	0.01	100	102	104	104	134	136	137	137
		500	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	101	103	103	131	131	132	132
		1000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	101	101	101	124	124	123	123
		2000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	100	100	99	99	113	114	110	110

Note. p = power used in the $L_p$ loss function; IA1 = invariance alignment (IA) with untransformed item discriminations ${\widehat{a}}_{ig}$ as originally proposed by Asparouhov and Muthén (2014 [12]), using optimization   functions (11) and (13); IA2 = IA based on log-transformed item discriminations ${\widehat{\alpha }}_{ig}$, using (12) and (13); HL1 = Haberman linking (HL) based on item difficulties ${\widehat{b}}_{ig}$, as originally proposed by Haberman (2009 [26]), using (14) and (15); HL2 = HL based on item intercepts ${\widehat{\nu }}_{ig}$, using (14) and (16). ^‡ The linking method IA1 with $p=0.5$ was the reference method for computing the relative RMSE. Absolute bias values larger than 0.025 are printed in bold font. Relative RMSE values larger than 104.5 are printed in bold font, while values smaller than 99.5 are printed in a gray background color.

RMSE values were generally higher for the HL methods compared to the IA methods; however, these differences diminished as sample size N increased. The $L_p$ loss function with $p=0.5$ outperformed $p=0$ in terms of relative RMSE.

Overall, HL2 performed similarly to, if not better than, IA1 for dichotomous items. Only a few conditions favored $p=0$ over $p=0.5$.

7. Simulation Study 2: Continuous Items

7.1. Method

In this second simulation study, HL and IA were compared for continuous items. The data-generating model followed the simulation from Asparouhov and Muthén [12]. Continuous item responses were simulated using a unidimensional factor model with $G=3$ groups. The normally distributed factor variable was measured by either $I=5$ or $I=10$ normally distributed items.

The group means of the factor variable were set to 0, 0.3, and 1.0, while the group SDs were set to 1, 1.5, and 1.2, respectively. Item responses were generated with uniform DIF and nonuniform DIF. The following describes the item parameters in the condition with $I=5$ items. Each group had one noninvariant item intercept, ${\nu }_{ig}$, and one noninvariant item discrimination, $a_{ig}$. For all groups, invariant item discriminations and residual variances of the indicator variables were set to $a_{ig}=1$ ($i=1,\dots ,5$), and invariant item intercepts were set to ${\nu }_{ig}=0$. The noninvariant item parameters in the first group were ${\nu }_{51}=0.5$ and $a_{13}=1.4$. The noninvariant item parameters in the second group were ${\nu }_{12}=-0.5$ and $a_{52}=0.5$. The noninvariant item parameters in the third group were ${\nu }_{23}=0.5$ and $a_{43}=0.3$. In the $I=10$ item condition, the item parameters were doubled.

The sample sizes $N=250$, 500, 1000, and 2000 were selected to reflect typical applications of the IA method [15,16].

In each of the 4 (sample size N) × 2 (number of items I) = 8 cells of the simulation, 3000 replications were performed. The unidimensional factor model was estimated in the first step using the R (Version 4.4.1 [69]) function sirt::invariance_alignment_cfa_config() from the R package sirt (Version 4.2-89 [70]). Subsequently, the linking methods HL1, HL2, IA1, and IA2, as described in Simulation Study 1 (see Section 6.1), were applied for the powers $p=0.5$ and $p=0$ in the $L_p$ loss function. Consistent with the previous simulation study, the average absolute bias and average relative RMSE were used as outcome measures. The method IA1 with $p=0.5$ again served as the reference method for calculating the relative RMSE. As in Simulation Study 1, the HL and IA methods were implemented using the sirt::linking.haberman.lq() and sirt::invariance.alignment() functions from the same sirt package, respectively. Replication material for this simulation study is available at https://osf.io/kcnyu (accessed on 22 November 2024).

7.2. Results

Table 3 presents the average absolute bias and average relative RMSE for the estimated group means (${\widehat{\mu }}_g$) and group standard deviations (${\widehat{\sigma }}_g$). Both estimates improved in terms of bias as the sample size N increased. For sample sizes of at least 1000, the bias across all methods became negligible (i.e., 0.01 or lower), particularly under $p=0$. The HL2 method consistently outperformed HL1, especially at smaller N and I, demonstrating the advantage of using item intercepts over item difficulties in HL. Additionally, HL2 outperformed both IA1 and IA2 across all conditions of this simulation study for $p=0.5$ and $p=0$. Lower RMSE values were observed for $p=0$ compared to $p=0.5$ across the four linking methods in many scenarios. The $L_0$ loss function performed less favorably than the $L_{0.5}$ loss function only at small sample sizes.

Table 3. Simulation Study 2 (continuous items): Average absolute bias and average relative root mean square error (RMSE) for estimated group means ${\widehat{\sigma }}_g$ and estimated group standard deviations ${\widehat{\sigma }}_g$ as a function of the number of items I, and sample size N.

			Average Absolute Bias								Average Relative RMSE
			$\mathit{p}=\mathbf{0.5}$				$\mathit{p}=\mathbf{0}$				$\mathit{p}=\mathbf{0.5}$				$\mathit{p}=\mathbf{0}$
Par	$\mathit{I}$	$\mathit{N}$	IA1	IA2	HL1	HL2	IA1	IA2	HL1	HL2	IA1 ‡	IA2	HL1	HL2	IA1	IA2	HL1	HL2
${\widehat{\mu }}_g$	5	250	0.03	0.03	0.04	0.03	0.01	0.01	0.04	0.01	100	100	114	97	107	106	126	100
		500	0.02	0.02	0.02	0.02	0.00	0.00	0.02	0.00	100	100	116	96	102	102	124	95
		1000	0.01	0.01	0.01	0.01	0.00	0.00	0.01	0.00	100	100	109	95	97	97	114	91
		2000	0.01	0.01	0.01	0.01	0.00	0.00	0.00	0.00	100	100	100	96	97	97	97	93
	10	250	0.03	0.03	0.03	0.03	0.01	0.01	0.02	0.01	100	100	104	98	104	103	113	97
		500	0.02	0.02	0.02	0.02	0.00	0.00	0.01	0.00	100	100	102	97	99	98	104	94
		1000	0.01	0.01	0.01	0.01	0.00	0.00	0.00	0.00	100	100	99	97	98	98	97	95
		2000	0.01	0.01	0.01	0.01	0.00	0.00	0.00	0.00	100	100	99	97	97	97	95	94
${\widehat{\sigma }}_g$	5	250	0.06	0.05	0.04	0.04	0.02	0.01	0.01	0.01	100	100	94	94	98	96	93	93
		500	0.03	0.03	0.03	0.03	0.00	0.00	0.00	0.00	100	99	93	93	95	92	89	89
		1000	0.02	0.02	0.02	0.02	0.00	0.00	0.00	0.00	100	100	95	95	95	93	91	91
		2000	0.01	0.01	0.01	0.01	0.00	0.00	0.00	0.00	100	100	97	97	93	93	91	91
	10	250	0.05	0.05	0.04	0.04	0.01	0.01	0.00	0.00	100	100	96	96	97	95	92	92
		500	0.03	0.03	0.02	0.02	0.00	0.00	0.00	0.00	100	100	96	96	95	94	92	92
		1000	0.02	0.02	0.02	0.02	0.00	0.00	0.00	0.00	100	100	97	97	95	94	92	92
		2000	0.01	0.01	0.01	0.01	0.00	0.00	0.00	0.00	100	101	99	99	93	92	92	92

Note. Par = parameter group; IA1 = invariance alignment (IA) with untransformed item discriminations ${\widehat{a}}_{ig}$ as originally proposed by Asparouhov and Muthén (2014 [12]), using optimization   functions (11) and (13); IA2 = IA based on log-transformed item discriminations ${\widehat{\alpha }}_{ig}$, using (12) and (13); HL1 = Haberman linking (HL) based on item difficulties ${\widehat{b}}_{ig}$, as originally proposed by Haberman (2009 [26]), using (14) and (15); HL2 = HL based on item intercepts ${\widehat{\nu }}_{ig}$, using (14) and (16). ^‡ The linking method IA1 with $p=0.5$ was the reference method for computing the relative RMSE. Absolute bias values larger than 0.025 are printed in bold font. Relative RMSE values larger than 104.5 are printed in bold font, while values smaller than 99.5 are printed in a gray background color.

8. Discussion

In this paper, we compared the linking methods robust HL and IA for the $L_{0.5}$ (i.e., $p=0.5$) and $L_0$ (i.e., $p=0$) loss functions. It turned out that robust HL performed similarly, if not better than IA, if it was applied in a variant relying on item intercepts instead of item difficulties. Importantly, the originally proposed HL, which relies on item difficulties instead of item intercepts, was clearly inferior to IA. The findings for the loss function choice $L_{0.5}$ vs. $L_0$ were mixed. In our first simulation study, involving dichotomous items, RMSE values were larger for the $L_0$ loss function. In contrast, RMSE values were smaller for $L_0$ in the second simulation study, involving continuous items. However, in the two studies, the bias in estimated group means and SDs was smaller for $L_0$ than for $L_{0.5}$, indicating that $L_0$ always comes with higher variable parameter estimates.

As with any simulation study, our study also has several limitations. First, future studies might focus on comparing HL and IA for polytomous item responses. Second, we applied HL and IA to two-parameter models. The linking methods could also be applied in estimation settings for one-parameter models, namely, the Rasch model in IRT for dichotomous items [71] or the tau-equivalent measurement model for continuous items [72]. Alternatively, the item discriminations could be assumed as invariant across groups, while item intercepts are freely estimated in the first step. In the second step, only item intercepts are linked, reducing the uncertainty in estimated item discriminations during linking. Third, linking errors and total error estimation [73] could be developed and evaluated for IA.

In contrast to IA, both simulation studies revealed that additionally estimated item parameters in HL did not provide efficiency losses in the parameter estimates. Hence, HL might be preferred over IA for statistical reasons, and it has the advantage compared to IA that joint item parameters (i.e., that can be interpreted as item parameters in the partial invariance situation) are simultaneously estimated. In contrast, a subsequent estimation step is required in IA to determine joint item parameter estimates and DIF effects for items.

Finally, if robust HL or IA methods are utilized in the linking procedure, items with large DIF effects are essentially excluded from group comparisons. In this way, it is presupposed that the construct being measured will not be changed by eliminating these items from comparisons involving the factor variable. This view implies that these DIF items are deemed as construct-irrelevant. However, it might be dangerous to treat these DIF items with robust linking functions in group comparisons if they are essentially part of the construct (i.e., they are construct-relevant; see [74,75,76,77,78] but see [79,80] for alternative views).