Several Topics on Transverse Momentum-Dependent Fragmentation Functions
Abstract
1. Introduction
2. Factorization and Evolution
2.1. Evolution Equations for TMD FFs
2.2. TMD Factorization at the Higher Twist
3. Spin-Dependent TMD FFs
3.1. The Intuitive Definition of TMD FFs
3.2. The Definition of TMD FFs from the Parton Correlators
3.3. The Spin Dependence
3.4. Decomposition Result for Spin-Dependent TMD FFs
3.5. TMD FFs of Antiquarks and Gluons
4. Experiment and Phenomenology
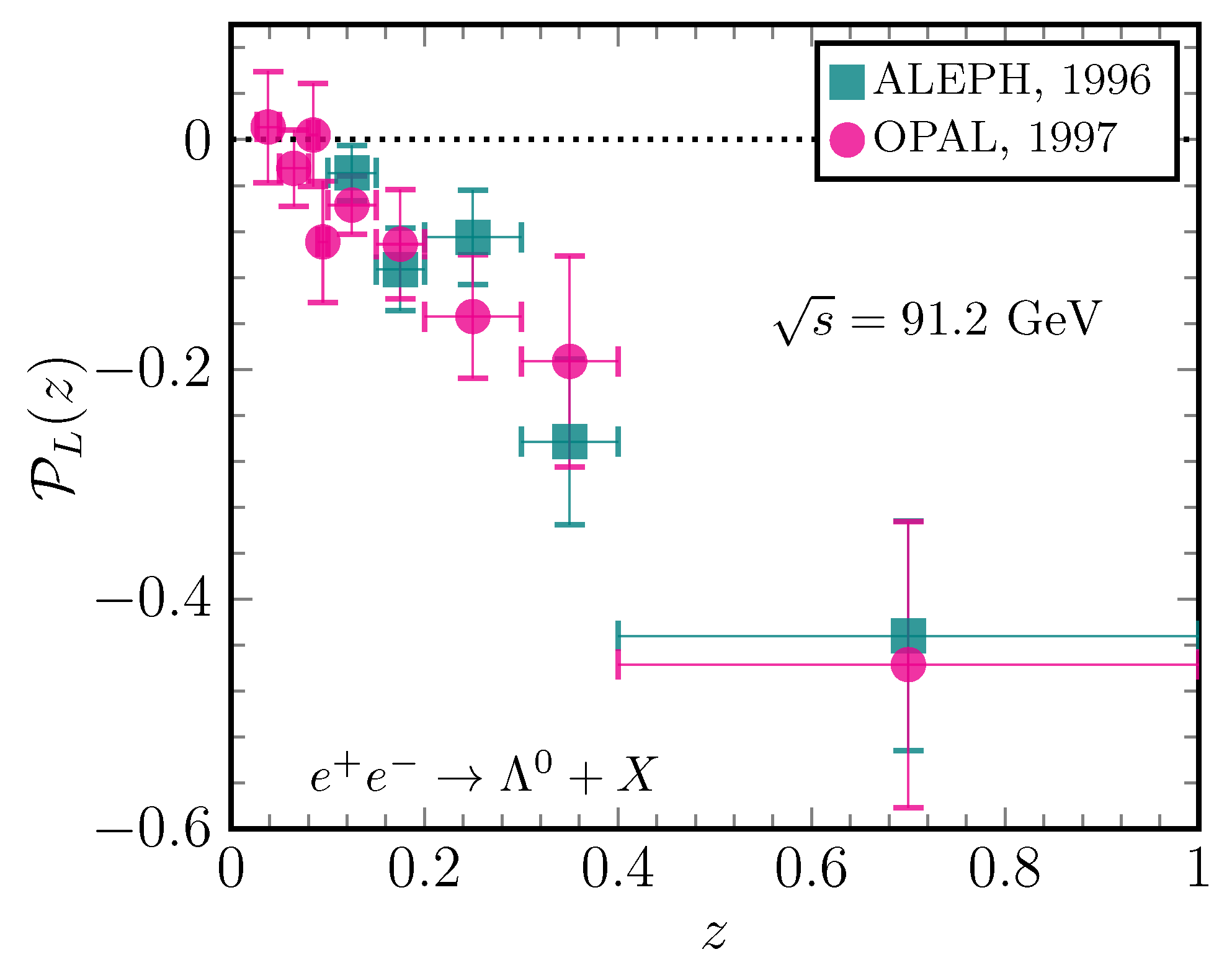
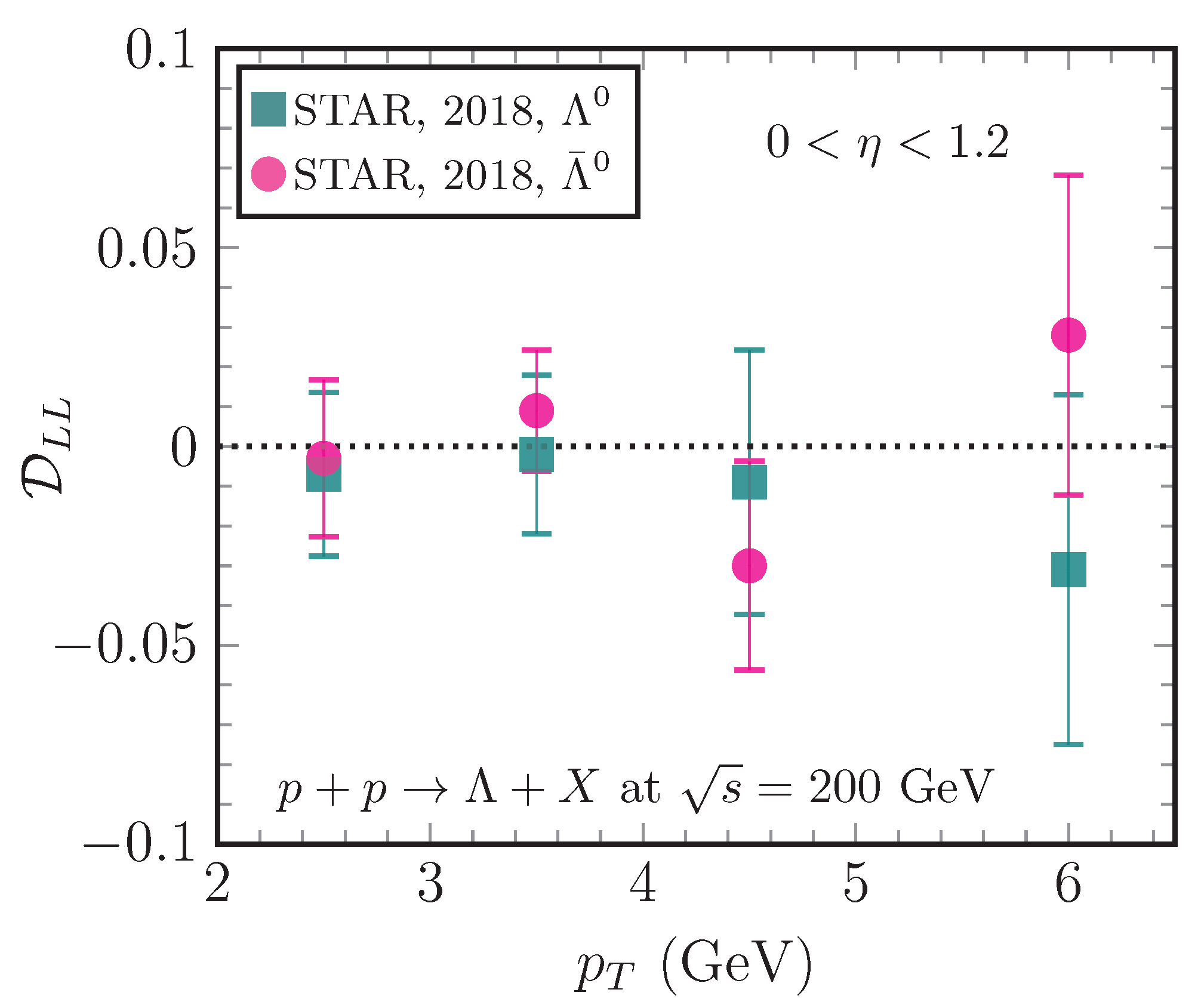
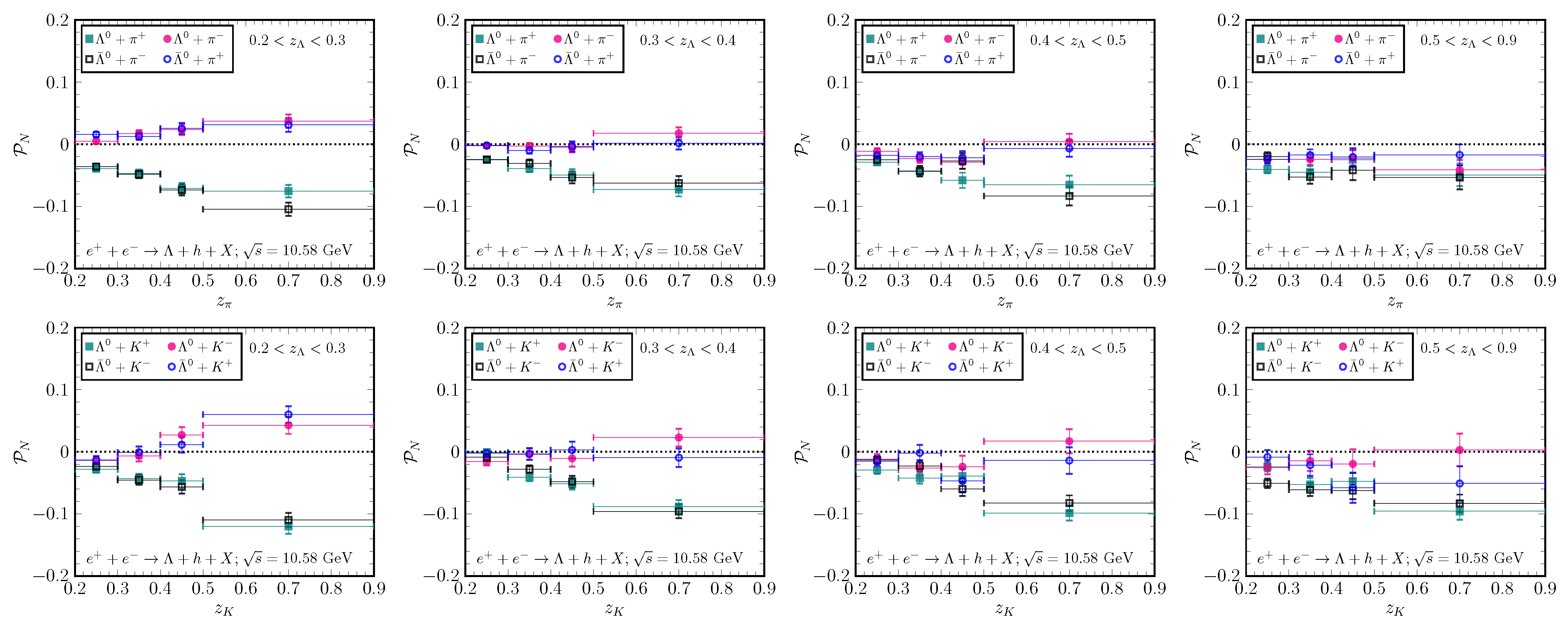
4.1. Hyperons
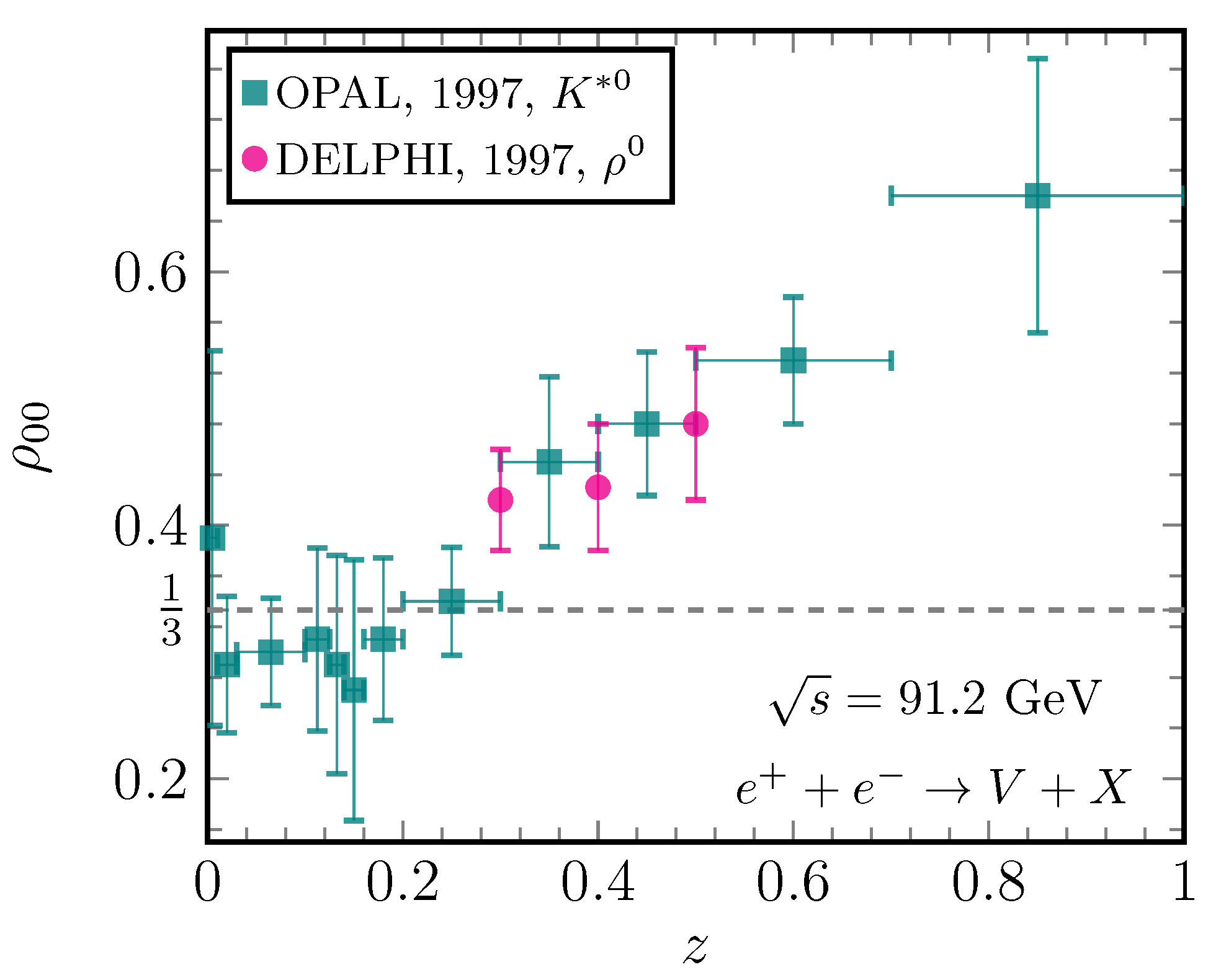
4.2. Vector Mesons
5. Model Calculation
6. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fritzsch, H.; Gell-Mann, M.; Leutwyler, H. Advantages of the Color Octet Gluon Picture. Phys. Lett. B 1973, 47, 365–368. [Google Scholar] [CrossRef]
- Yang, C.N.; Mills, R.L. Conservation of Isotopic Spin and Isotopic Gauge Invariance. Phys. Rev. 1954, 96, 191–195. [Google Scholar] [CrossRef]
- Metz, A.; Vossen, A. Parton Fragmentation Functions. Prog. Part. Nucl. Phys. 2016, 91, 136–202. [Google Scholar] [CrossRef]
- Bjorken, J.D.; Paschos, E.A. Inelastic Electron Proton and gamma Proton Scattering, and the Structure of the Nucleon. Phys. Rev. 1969, 185, 1975–1982. [Google Scholar] [CrossRef]
- Feynman, R.P. Photon-Hadron Interactions. Basic Books. 1973. [Google Scholar]
- Berman, S.M.; Bjorken, J.D.; Kogut, J.B. Inclusive Processes at High Transverse Momentum. Phys. Rev. D 1971, 4, 3388. [Google Scholar] [CrossRef]
- Mueller, A.H. Cut Vertices and their Renormalization: A Generalization of the Wilson Expansion. Phys. Rev. D 1978, 18, 3705. [Google Scholar] [CrossRef]
- Collins, J.C.; Soper, D.E. Parton Distribution and Decay Functions. Nucl. Phys. B 1982, 194, 445–492. [Google Scholar] [CrossRef]
- Collins, J.C.; Soper, D.E.; Sterman, G.F. Factorization of Hard Processes in QCD. Adv. Ser. Direct. High Energy Phys. 1989, 5, 1–91. [Google Scholar] [CrossRef]
- Collins, J. Foundations of Perturbative QCD; Cambridge University Press: Cambridge, UK, 2013; Volume 32. [Google Scholar]
- Collins, J.C.; Soper, D.E. Back-To-Back Jets in QCD. Nucl. Phys. B 1983, 193, 381, Erratum in Nucl. Phys. B 1983, 213, 545. [Google Scholar] [CrossRef]
- Aybat, S.M.; Rogers, T.C. TMD Parton Distribution and Fragmentation Functions with QCD Evolution. Phys. Rev. D 2011, 83, 114042. [Google Scholar] [CrossRef]
- Kang, Z.B.; Shao, D.Y.; Zhao, F. QCD resummation on single hadron transverse momentum distribution with the thrust axis. JHEP 2020, 12, 127. [Google Scholar] [CrossRef]
- Boglione, M.; Simonelli, A. Factorization of e+e−→HX cross section, differential in zh, PT and thrust, in the 2-jet limit. JHEP 2021, 02, 076. [Google Scholar] [CrossRef]
- Boglione, M.; Simonelli, A. Universality-breaking effects in e+e− hadronic production processes. Eur. Phys. J. C 2021, 81, 96. [Google Scholar] [CrossRef]
- Makris, Y.; Ringer, F.; Waalewijn, W.J. Joint thrust and TMD resummation in electron-positron and electron-proton collisions. JHEP 2021, 02, 070. [Google Scholar] [CrossRef]
- Collins, J.C. Fragmentation of transversely polarized quarks probed in transverse momentum distributions. Nucl. Phys. B 1993, 396, 161–182. [Google Scholar] [CrossRef]
- Boer, D.; Mulders, P.J.; Pijlman, F. Universality of T odd effects in single spin and azimuthal asymmetries. Nucl. Phys. B 2003, 667, 201–241. [Google Scholar] [CrossRef]
- Guan, Y.; Vossen, A.; Adachi, I.; Adamczyk, K.; Ahn, J.K.; Aihara, H.; Sanuki, T.; Chilikin, K.; Cho, K.; Choi, S.-K.; et al. Observation of Transverse Λ/Λ¯ Hyperon Polarization in e+e− Annihilation at Belle. Phys. Rev. Lett. 2019, 122, 042001. [Google Scholar] [CrossRef]
- Matevosyan, H.H.; Kotzinian, A.; Thomas, A.W. Semi-inclusive back-to-back production of a hadron pair and a single hadron in e+e− annihilation. JHEP 2018, 10, 008. [Google Scholar] [CrossRef]
- Gamberg, L.; Kang, Z.B.; Pitonyak, D.; Schlegel, M.; Yoshida, S. Polarized hyperon production in single-inclusive electron-positron annihilation at next-to-leading order. JHEP 2019, 01, 111. [Google Scholar] [CrossRef]
- Anselmino, M.; Kishore, R.; Mukherjee, A. Polarizing fragmentation function and the Λ polarization in e+e− processes. Phys. Rev. D 2019, 100, 014029. [Google Scholar] [CrossRef]
- Anselmino, M.; Mukherjee, A.; Vossen, A. Transverse spin effects in hard semi-inclusive collisions. Prog. Part. Nucl. Phys. 2020, 114, 103806. [Google Scholar] [CrossRef]
- D’Alesio, U.; Murgia, F.; Zaccheddu, M. First extraction of the Λ polarizing fragmentation function from Belle e+e− data. Phys. Rev. D 2020, 102, 054001. [Google Scholar] [CrossRef]
- Callos, D.; Kang, Z.B.; Terry, J. Extracting the transverse momentum dependent polarizing fragmentation functions. Phys. Rev. D 2020, 102, 096007. [Google Scholar] [CrossRef]
- Kang, Z.B.; Lee, K.; Zhao, F. Polarized jet fragmentation functions. Phys. Lett. B 2020, 809, 135756. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Yang, Y.; Lu, Z. The transverse polarization of Λ hyperons in e+e−→Λ↑hX processes within TMD factorization. Eur. Phys. J. C 2021, 81, 289. [Google Scholar] [CrossRef]
- Chen, K.B.; Liang, Z.T.; Pan, Y.L.; Song, Y.K.; Wei, S.Y. Isospin Symmetry of Fragmentation Functions. Phys. Lett. B 2021, 816, 136217. [Google Scholar] [CrossRef]
- Gamberg, L.; Kang, Z.B.; Shao, D.Y.; Terry, J.; Zhao, F. Transverse Λ polarization in e+e− collisions. Phys. Lett. B 2021, 818, 136371. [Google Scholar] [CrossRef]
- D’Alesio, U.; Murgia, F.; Zaccheddu, M. General helicity formalism for two-hadron production in e+e− annihilation within a TMD approach. JHEP 2021, 10, 078. [Google Scholar] [CrossRef]
- D’Alesio, U.; Gamberg, L.; Murgia, F.; Zaccheddu, M. Transverse Λ polarization in e+e− processes within a TMD factorization approach and the polarizing fragmentation function. JHEP 2022, 12, 074. [Google Scholar] [CrossRef]
- Boglione, M.; Gonzalez-Hernandez, J.O.; Simonelli, A. Transverse momentum dependent fragmentation functions from recent BELLE data. Phys. Rev. D 2022, 106, 074024. [Google Scholar] [CrossRef]
- Ellis, R.K.; Furmanski, W.; Petronzio, R. Power Corrections to the Parton Model in QCD. Nucl. Phys. B 1982, 207, 1–14. [Google Scholar] [CrossRef]
- Ellis, R.K.; Furmanski, W.; Petronzio, R. Unraveling Higher Twists. Nucl. Phys. B 1983, 212, 29. [Google Scholar] [CrossRef]
- Qiu, J.W. Twist Four Contributions to the Parton Structure Functions. Phys. Rev. D 1990, 42, 30–44. [Google Scholar] [CrossRef]
- Qiu, J.W.; Sterman, G.F. Power corrections in hadronic scattering. 1. Leading 1/Q2 corrections to the Drell-Yan cross-section. Nucl. Phys. B 1991, 353, 105–136. [Google Scholar] [CrossRef]
- Qiu, J.W.; Sterman, G.F. Power corrections to hadronic scattering. 2. Factorization. Nucl. Phys. B 1991, 353, 137–164. [Google Scholar] [CrossRef]
- Balitsky, I.I.; Braun, V.M. The Nonlocal operator expansion for inclusive particle production in e+e− annihilation. Nucl. Phys. B 1991, 361, 93–140. [Google Scholar] [CrossRef]
- Levelt, J.; Mulders, P.J. Time reversal odd fragmentation functions in semiinclusive scattering of polarized leptons from unpolarized hadrons. Phys. Lett. B 1994, 338, 357–362. [Google Scholar] [CrossRef]
- Levelt, J.; Mulders, P.J. Quark correlation functions in deep inelastic semiinclusive processes. Phys. Rev. D 1994, 49, 96–113. [Google Scholar] [CrossRef]
- Kotzinian, A. New quark distributions and semiinclusive electroproduction on the polarized nucleons. Nucl. Phys. B 1995, 441, 234–248. [Google Scholar] [CrossRef]
- Mulders, P.J.; Tangerman, R.D. The Complete tree level result up to order 1/Q for polarized deep inelastic leptoproduction. Nucl. Phys. B 1997, 461, 197–237, Erratum in Nucl. Phys. B 1997, 484, 538–540. [Google Scholar] [CrossRef]
- Boer, D.; Jakob, R.; Mulders, P.J. Asymmetries in polarized hadron production in e+e− annihilation up to order 1/Q. Nucl. Phys. B 1997, 504, 345–380. [Google Scholar] [CrossRef]
- Kotzinian, A.M.; Mulders, P.J. Probing transverse quark polarization via azimuthal asymmetries in leptoproduction. Phys. Lett. B 1997, 406, 373–380. [Google Scholar] [CrossRef]
- Boer, D.; Mulders, P.J. Time reversal odd distribution functions in leptoproduction. Phys. Rev. D 1998, 57, 5780–5786. [Google Scholar] [CrossRef]
- Boer, D.; Jakob, R.; Mulders, P.J. Leading asymmetries in two hadron production in e+e− annihilation at the Z pole. Phys. Lett. B 1998, 424, 143–151. [Google Scholar] [CrossRef]
- Bacchetta, A.; Mulders, P.J. Deep inelastic leptoproduction of spin-one hadrons. Phys. Rev. D 2000, 62, 114004. [Google Scholar] [CrossRef]
- Boer, D.; Jakob, R.; Mulders, P.J. Angular dependences in electroweak semiinclusive leptoproduction. Nucl. Phys. B 2000, 564, 471–485. [Google Scholar] [CrossRef]
- Bacchetta, A.; Mulders, P.J.; Pijlman, F. New observables in longitudinal single-spin asymmetries in semi-inclusive DIS. Phys. Lett. B 2004, 595, 309–317. [Google Scholar] [CrossRef][Green Version]
- Bacchetta, A.; Diehl, M.; Goeke, K.; Metz, A.; Mulders, P.J.; Schlegel, M. Semi-inclusive deep inelastic scattering at small transverse momentum. JHEP 2007, 02, 093. [Google Scholar] [CrossRef]
- Boer, D. Angular dependences in inclusive two-hadron production at BELLE. Nucl. Phys. B 2009, 806, 23–67. [Google Scholar] [CrossRef][Green Version]
- Eguchi, H.; Koike, Y.; Tanaka, K. Single Transverse Spin Asymmetry for Large-p(T) Pion Production in Semi-Inclusive Deep Inelastic Scattering. Nucl. Phys. B 2006, 752, 1–17. [Google Scholar] [CrossRef]
- Eguchi, H.; Koike, Y.; Tanaka, K. Twist-3 Formalism for Single Transverse Spin Asymmetry Reexamined: Semi-Inclusive Deep Inelastic Scattering. Nucl. Phys. B 2007, 763, 198–227. [Google Scholar] [CrossRef]
- Koike, Y.; Tanaka, K. Master Formula for Twist-3 Soft-Gluon-Pole Mechanism to Single Transverse-Spin Asymmetry. Phys. Lett. B 2008, 646, 232–241, Erratum in Phys. Lett. B 2008, 668, 458–459. [Google Scholar] [CrossRef][Green Version]
- Kanazawa, K.; Koike, Y. Contribution of twist-3 fragmentation function to single transverse-spin asymmetry in semi-inclusive deep inelastic scattering. Phys. Rev. D 2013, 88, 074022. [Google Scholar] [CrossRef]
- Pitonyak, D.; Schlegel, M.; Metz, A. Polarized hadron pair production from electron-positron annihilation. Phys. Rev. D 2014, 89, 054032. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, Z. Polarized Λ hyperon production in semi-inclusive deep inelastic scattering off an unpolarized nucleon target. Phys. Rev. D 2017, 95, 074026. [Google Scholar] [CrossRef]
- Liang, Z.T.; Wang, X.N. Azimuthal and single spin asymmetry in deep-inelastic lepton-nucleon scattering. Phys. Rev. D 2007, 75, 094002. [Google Scholar] [CrossRef]
- Liang, Z.T.; Wang, X.N.; Zhou, J. The Transverse-momentum-dependent Parton Distribution Function and Jet Transport in Medium. Phys. Rev. D 2008, 77, 125010. [Google Scholar] [CrossRef]
- Gao, J.H.; Liang, Z.T.; Wang, X.N. Nuclear dependence of azimuthal asymmetry in semi-inclusive deep inelastic scattering. Phys. Rev. C 2010, 81, 065211. [Google Scholar] [CrossRef]
- Song, Y.k.; Gao, J.h.; Liang, Z.t.; Wang, X.N. Twist-4 contributions to the azimuthal asymmetry in SIDIS. Phys. Rev. D 2011, 83, 054010. [Google Scholar] [CrossRef]
- Song, Y.k.; Gao, J.h.; Liang, Z.t.; Wang, X.N. Azimuthal asymmetries in semi-inclusive DIS with polarized beam and/or target and their nuclear dependences. Phys. Rev. D 2014, 89, 014005. [Google Scholar] [CrossRef]
- Wei, S.y.; Song, Y.k.; Liang, Z.t. Higher twist contribution to fragmentation function in inclusive hadron production in e+e− annihilation. Phys. Rev. D 2014, 89, 014024. [Google Scholar] [CrossRef]
- Wei, S.Y.; Chen, K.b.; Song, Y.k.; Liang, Z.t. Leading and higher twist contributions in semi-inclusive e+e− annihilation at high energies. Phys. Rev. D 2015, 91, 034015. [Google Scholar] [CrossRef]
- Chen, K.b.; Yang, W.h.; Wei, S.y.; Liang, Z.t. Tensor polarization dependent fragmentation functions and e+e−→VπX at high energies. Phys. Rev. D 2016, 94, 034003. [Google Scholar] [CrossRef]
- Wei, S.y.; Song, Y.k.; Chen, K.b.; Liang, Z.t. Twist-4 contributions to semi-inclusive deeply inelastic scatterings with polarized beam and target. Phys. Rev. D 2017, 95, 074017. [Google Scholar] [CrossRef]
- Vladimirov, A.; Moos, V.; Scimemi, I. Transverse momentum dependent operator expansion at next-to-leading power. JHEP 2022, 1, 110. [Google Scholar] [CrossRef]
- Rodini, S.; Vladimirov, A. Definition and evolution of transverse momentum dependent distribution of twist-three. JHEP 2022, 8, 31, Erratum in JHEP 2022, 12, 48. [Google Scholar] [CrossRef]
- Rodini, S.; Vladimirov, A. Factorization for Quasi-TMD Distributions of Sub-Leading Power. arXiv 2022, arXiv:2211.04494. [Google Scholar]
- Ebert, M.A.; Gao, A.; Stewart, I.W. Factorization for azimuthal asymmetries in SIDIS at next-to-leading power. JHEP 2022, 6, 7. [Google Scholar] [CrossRef]
- Balitsky, I.; Tarasov, A. Higher-twist corrections to gluon TMD factorization. JHEP 2017, 7, 95. [Google Scholar] [CrossRef]
- Balitsky, I.; Tarasov, A. Power corrections to TMD factorization for Z-boson production. JHEP 2018, 5, 150. [Google Scholar] [CrossRef]
- Balitsky, I. Gauge-invariant TMD factorization for Drell-Yan hadronic tensor at small x. JHEP 2021, 5, 46. [Google Scholar] [CrossRef]
- Balitsky, I. Drell-Yan angular lepton distributions at small x from TMD factorization. JHEP 2021, 9, 22. [Google Scholar] [CrossRef]
- Gamberg, L.; Kang, Z.B.; Shao, D.Y.; Terry, J.; Zhao, F. Transverse-momentum-dependent factorization at next-to-leading power. arXiv 2022, arXiv:2211.13209. [Google Scholar]
- Collins, J.C.; Soper, D.E. Back-To-Back Jets: Fourier Transform from B to K-Transverse. Nucl. Phys. B 1982, 197, 446–476. [Google Scholar] [CrossRef]
- Collins, J.C.; Soper, D.E.; Sterman, G.F. Transverse Momentum Distribution in Drell-Yan Pair and W and Z Boson Production. Nucl. Phys. B 1985, 250, 199–224. [Google Scholar] [CrossRef]
- Ji, X.D.; Ma, J.P.; Yuan, F. QCD factorization for semi-inclusive deep-inelastic scattering at low transverse momentum. Phys. Rev. D 2005, 71, 034005. [Google Scholar] [CrossRef]
- Ji, X.D.; Ma, J.P.; Yuan, F. QCD factorization for spin-dependent cross sections in DIS and Drell-Yan processes at low transverse momentum. Phys. Lett. B 2004, 597, 299–308. [Google Scholar] [CrossRef]
- Sun, P.; Yuan, C.P.; Yuan, F. Soft Gluon Resummations in Dijet Azimuthal Angular Correlations in Hadronic Collisions. Phys. Rev. Lett. 2014, 113, 232001. [Google Scholar] [CrossRef]
- Sun, P.; Yuan, C.P.; Yuan, F. Transverse Momentum Resummation for Dijet Correlation in Hadronic Collisions. Phys. Rev. D 2015, 92, 094007. [Google Scholar] [CrossRef]
- Becher, T.; Neubert, M. Drell-Yan Production at Small qT, Transverse Parton Distributions and the Collinear Anomaly. Eur. Phys. J. C 2011, 71, 1665. [Google Scholar] [CrossRef]
- Echevarria, M.G.; Idilbi, A.; Scimemi, I. Factorization Theorem For Drell-Yan At Low qT And Transverse Momentum Distributions On-The-Light-Cone. JHEP 2012, 7, 002. [Google Scholar] [CrossRef]
- Chiu, J.Y.; Jain, A.; Neill, D.; Rothstein, I.Z. A Formalism for the Systematic Treatment of Rapidity Logarithms in Quantum Field Theory. JHEP 2012, 05, 084. [Google Scholar] [CrossRef]
- Li, Y.; Neill, D.; Zhu, H.X. An exponential regulator for rapidity divergences. Nucl. Phys. B 2020, 960, 115193. [Google Scholar] [CrossRef]
- Kang, Z.B.; Liu, X.; Ringer, F.; Xing, H. The transverse momentum distribution of hadrons within jets. JHEP 2017, 11, 068. [Google Scholar] [CrossRef]
- Sterman, G.F. Mass Divergences in Annihilation Processes. 1. Origin and Nature of Divergences in Cut Vacuum Polarization Diagrams. Phys. Rev. D 1978, 17, 2773. [Google Scholar] [CrossRef]
- Libby, S.B.; Sterman, G.F. Mass Divergences in Two Particle Inelastic Scattering. Phys. Rev. D 1978, 18, 4737. [Google Scholar] [CrossRef]
- Davies, C.T.H.; Webber, B.R.; Stirling, W.J. Drell-Yan Cross-Sections at Small Transverse Momentum. Nucl. Phys. B 1985, 256, 413–433. [Google Scholar] [CrossRef]
- Landry, F.; Brock, R.; Nadolsky, P.M.; Yuan, C.P. Tevatron Run-1 Z boson data and Collins-Soper-Sterman resummation formalism. Phys. Rev. D 2003, 67, 073016. [Google Scholar] [CrossRef]
- Guzzi, M.; Nadolsky, P.M.; Wang, B. Nonperturbative contributions to a resummed leptonic angular distribution in inclusive neutral vector boson production. Phys. Rev. D 2014, 90, 014030. [Google Scholar] [CrossRef]
- Sun, P.; Isaacson, J.; Yuan, C.P.; Yuan, F. Nonperturbative functions for SIDIS and Drell–Yan processes. Int. J. Mod. Phys. A 2018, 33, 1841006. [Google Scholar] [CrossRef]
- Ladinsky, G.A.; Yuan, C.P. The Nonperturbative regime in QCD resummation for gauge boson production at hadron colliders. Phys. Rev. D 1994, 50, R4239. [Google Scholar] [CrossRef] [PubMed]
- Sun, P.; Yuan, F. Transverse momentum dependent evolution: Matching semi-inclusive deep inelastic scattering processes to Drell-Yan and W/Z boson production. Phys. Rev. D 2013, 88, 114012. [Google Scholar] [CrossRef]
- Aidala, C.A.; Field, B.; Gamberg, L.P.; Rogers, T.C. Limits on transverse momentum dependent evolution from semi-inclusive deep inelastic scattering at moderate Q. Phys. Rev. D 2014, 89, 094002. [Google Scholar] [CrossRef]
- Echevarria, M.G.; Idilbi, A.; Kang, Z.B.; Vitev, I. QCD Evolution of the Sivers Asymmetry. Phys. Rev. D 2014, 89, 074013. [Google Scholar] [CrossRef]
- Kang, Z.B.; Xiao, B.W.; Yuan, F. QCD Resummation for Single Spin Asymmetries. Phys. Rev. Lett. 2011, 107, 152002. [Google Scholar] [CrossRef] [PubMed]
- Collins, J.; Rogers, T. Understanding the large-distance behavior of transverse-momentum-dependent parton densities and the Collins-Soper evolution kernel. Phys. Rev. D 2015, 91, 074020. [Google Scholar] [CrossRef]
- Qiu, J.W.; Zhang, X.F. Role of the nonperturbative input in QCD resummed Drell-Yan QT distributions. Phys. Rev. D 2001, 63, 114011. [Google Scholar] [CrossRef]
- Kang, Z.B.; Prokudin, A.; Sun, P.; Yuan, F. Extraction of Quark Transversity Distribution and Collins Fragmentation Functions with QCD Evolution. Phys. Rev. D 2016, 93, 014009. [Google Scholar] [CrossRef]
- Sivers, D.W. Single Spin Production Asymmetries from the Hard Scattering of Point-Like Constituents. Phys. Rev. D 1990, 41, 83. [Google Scholar] [CrossRef]
- Sivers, D.W. Hard scattering scaling laws for single spin production asymmetries. Phys. Rev. D 1991, 43, 261–263. [Google Scholar] [CrossRef]
- Song, H. Spin-3/2 Polarization in Production of N* by Neutrinos. Phys. Rev. 1967, 162, 1615. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Z.; Liang, Z.T.; Liu, T.; Zhou, Y.J. Inclusive and semi-inclusive production of spin-3/2 hadrons in e+e− annihilation. Phys. Rev. D 2022, 106, 094006. [Google Scholar] [CrossRef]
- Collins, J.C. Leading twist single transverse-spin asymmetries: Drell-Yan and deep inelastic scattering. Phys. Lett. B 2002, 536, 43–48. [Google Scholar] [CrossRef]
- Ji, X.d.; Yuan, F. Parton distributions in light cone gauge: Where are the final state interactions? Phys. Lett. B 2002, 543, 66–72. [Google Scholar] [CrossRef]
- Belitsky, A.V.; Ji, X.; Yuan, F. Final state interactions and gauge invariant parton distributions. Nucl. Phys. B 2003, 656, 165–198. [Google Scholar] [CrossRef]
- Chen, K.b.; Yang, W.h.; Zhou, Y.j.; Liang, Z.t. Energy dependence of hadron polarization in e+e−→hX at high energies. Phys. Rev. D 2017, 95, 034009. [Google Scholar] [CrossRef]
- Chen, K.b.; Liang, Z.t.; Song, Y.k.; Wei, S.y. Spin alignment of vector mesons in high energy pp collisions. Phys. Rev. D 2020, 102, 034001. [Google Scholar] [CrossRef]
- Abdallah, M.S.; Aboona, B.E.; Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, I.; Aggarwal, M.M.; Ahammed, Z.; et al. Pattern of global spin alignment of ϕ and K*0 mesons in heavy-ion collisions. Nature 2023, 614, 244–248. [Google Scholar] [CrossRef]
- Mulders, P.J.; Rodrigues, J. Transverse momentum dependence in gluon distribution and fragmentation functions. Phys. Rev. D 2001, 63, 094021. [Google Scholar] [CrossRef]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of Particle Physics. PTEP 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Augustin, J.E.; Renard, F.M. How to Measure Quark Helicities in e+e−→ Hadrons. Nucl. Phys. B 1980, 162, 341. [Google Scholar] [CrossRef]
- Gustafson, G.; Hakkinen, J. Lambda polarization in e+e− annihilation at the Z0 pole. Phys. Lett. B 1993, 303, 350–354. [Google Scholar] [CrossRef]
- Buskulic, D.; De Bonis, I.; Decamp, D.; Ghez, P.; Goy, C.; Lees, J.P.; Lucotte, A.; Minard, M.N.; Odier, P.; Pietrzyk, B.; et al. Measurement of Lambda polarization from Z decays. Phys. Lett. B 1996, 374, 319–330. [Google Scholar] [CrossRef]
- Ackersta, K.; Alexander, G.; Allison, J.; Altekamp, N.; Anderson, K.J.; Anderson, S.; Arcelli, S.; Asai, S.; Axen, D.; Azuelos, G.; et al. Polarization and forward—Backward asymmetry of Lambda baryons in hadronic Z0 decays. Eur. Phys. J. C 1998, 2, 49–59. [Google Scholar] [CrossRef]
- Kotzinian, A.; Bravar, A.; von Harrach, D. Lambda and anti-Lambda polarization in lepton induced processes. Eur. Phys. J. C 1998, 2, 329–337. [Google Scholar] [CrossRef][Green Version]
- de Florian, D.; Stratmann, M.; Vogelsang, W. QCD analysis of unpolarized and polarized Lambda baryon production in leading and next-to-leading order. Phys. Rev. D 1998, 57, 5811–5824. [Google Scholar] [CrossRef]
- Liang, Z.T.; Boros, C. Hyperon polarization and single spin left-right asymmetry in inclusive production processes at high-energies. Phys. Rev. Lett. 1997, 79, 3608–3611. [Google Scholar] [CrossRef]
- Boros, C.; Liang, Z.t. Spin content of Lambda and its longitudinal polarization in e+e− annihilation at high-energies. Phys. Rev. D 1998, 57, 4491–4494. [Google Scholar] [CrossRef]
- Ma, B.Q.; Soffer, J. Quark flavor separation in Lambda Baryon fragmentation. Phys. Rev. Lett. 1999, 82, 2250–2253. [Google Scholar] [CrossRef]
- Ma, B.Q.; Schmidt, I.; Yang, J.J. Flavor and spin structure of lambda baryon at large x. Phys. Lett. B 2000, 477, 107–113. [Google Scholar] [CrossRef]
- Ma, B.Q.; Schmidt, I.; Yang, J.J. Quark structure of Lambda from Lambda polarization in Z decays. Phys. Rev. D 2000, 61, 034017. [Google Scholar] [CrossRef]
- Liu, C.x.; Liang, Z.t. Spin structure and longitudinal polarization of hyperon in e+e− annihilation at high-energies. Phys. Rev. D 2000, 62, 094001. [Google Scholar] [CrossRef]
- Jaffe, R.L. Polarized Λ’s in the current fragmentation region. Phys. Rev. D 1996, 54, R6581–R6585. [Google Scholar] [CrossRef]
- de Florian, D.; Stratmann, M.; Vogelsang, W. Polarized Lambda production at HERA. In Proceedings of the Workshop on Physics with Polarized Protons at Hera: 1st Meeting; 1997. Available online: https://inspirehep.net/literature/449966 (accessed on 5 March 2023).
- Ashery, D.; Lipkin, H.J. Expected polarization of Lambda particles produced in deep inelastic polarized lepton scattering. Phys. Lett. B 1999, 469, 263–269. [Google Scholar] [CrossRef]
- de Florian, D.; Stratmann, M.; Vogelsang, W. Polarized Lambda baryon production in p p collisions. Phys. Rev. Lett. 1998, 81, 530–533. [Google Scholar] [CrossRef]
- Jager, B.; Schafer, A.; Stratmann, M.; Vogelsang, W. Next-to-leading order QCD corrections to high p(T) pion production in longitudinally polarized pp collisions. Phys. Rev. D 2003, 67, 054005. [Google Scholar] [CrossRef]
- Xu, Q.h.; Liu, C.x.; Liang, Z.t. Longitudinal polarization of hyperons in high p(T) jets in singly polarized pp collisions at high-energies. Phys. Rev. D 2002, 65, 114008. [Google Scholar] [CrossRef]
- Xu, Q.h.; Liang, Z.t.; Sichtermann, E. Anti-lambda polarization in high energy pp collisions with polarized beam. Phys. Rev. D 2006, 73, 077503. [Google Scholar] [CrossRef]
- Adeva, B.; Akdogan, T.; Arik, E.; Arvidson, A.; Badelek, B.; Bardin, G.; Baum, G.; Berglund, P.; Betev, L.; Bird, I.G.; et al. Spin asymmetries A(1) and structure functions g1 of the proton and the deuteron from polarized high-energy muon scattering. Phys. Rev. D 1998, 58, 112001. [Google Scholar] [CrossRef]
- Abe, K.; Akagi, T.; Anthony, P.L.; Antonov, R.; Arnold, R.G.; Averett, T.; Band, H.R.; Bauer, J.M.; Borel, H.; Bosted, P.E.; et al. Measurements of the proton and deuteron spin structure functions g(1) and g(2). Phys. Rev. D 1998, 58, 112003. [Google Scholar] [CrossRef]
- Airapetian, A.; Akopov, N.; Akushevich, I.; Amarian, M.; Aschenauer, E.C.; Avakian, H.; Avakian, R.; Avetisian, A.; Bains, B.; Baumgarten, C.; et al. Measurement of the proton spin structure function g1(p) with a pure hydrogen target. Phys. Lett. B 1998, 442, 484–492. [Google Scholar] [CrossRef]
- Adams, M.R.; Aderholz, M.; Aid, S.; Anthony, P.L.; Ashery, D.; Averill, D.A.; Baker, M.D.; Baller, B.R.; Banerjee, A.; Bhatti, A.A.; et al. Lambda and anti-lambda polarization from deep inelastic muon scattering. Eur. Phys. J. C 2000, 17, 263–267. [Google Scholar] [CrossRef]
- Airapetian, A.; Akopov, N.; Amarian, M.; Aschenauer, E.C.; Avakian, H.; Avakian, R.; Avetissian, A.; Bains, B.; Baumgarten, C.; Beckmann, M.; et al. Measurement of longitudinal spin transfer to Lambda hyperons in deep inelastic lepton scattering. Phys. Rev. D 2001, 64, 112005. [Google Scholar] [CrossRef]
- Airapetian, A.; Akopov, N.; Akopov, Z.; Amarian, M.; Andrus, A.; Aschenauer, E.C.; Augustyniak, W.; Avakian, R.; Avetissian, A.; Avetissian, E.; et al. Longitudinal Spin Transfer to the Lambda Hyperon in Semi-Inclusive Deep-Inelastic Scattering. Phys. Rev. D 2006, 74, 072004. [Google Scholar] [CrossRef]
- Alekseev, M.; Alexakhin, V.Y.; Alexandrov, Y.; Alexeev, G.D.; Amoroso, A.; Austregesilo, A.; Badełek, B.; Balestra, F.; Ball, J.; Barth, J.; et al. Measurement of the Longitudinal Spin Transfer to Lambda and Anti-Lambda Hyperons in Polarised Muon DIS. Eur. Phys. J. C 2009, 64, 171–179. [Google Scholar] [CrossRef]
- Ma, B.Q.; Schmidt, I.; Soffer, J.; Yang, J.J. Lambda, anti-Lambda polarization and spin transfer in lepton deep inelastic scattering. Eur. Phys. J. C 2000, 16, 657–664. [Google Scholar] [CrossRef]
- Zhou, S.s.; Chen, Y.; Liang, Z.t.; Xu, Q.h. Longitudinal polarization of hyperon and anti-hyperon in semi-inclusive deep-inelastic scattering. Phys. Rev. D 2009, 79, 094018. [Google Scholar] [CrossRef]
- Chi, Y.; Du, X.; Ma, B.Q. Nucleon strange s asymmetry to the Λ/ fragmentation. Phys. Rev. D 2014, 90, 074003. [Google Scholar] [CrossRef]
- Gluck, M.; Reya, E.; Stratmann, M.; Vogelsang, W. Models for the polarized parton distributions of the nucleon. Phys. Rev. D 2001, 63, 094005. [Google Scholar] [CrossRef]
- Ma, B.Q.; Schmidt, I.; Yang, J.J. Nucleon transversity distribution from azimuthal spin asymmetry in pion electroproduction. Phys. Rev. D 2001, 63, 037501. [Google Scholar] [CrossRef]
- Ma, B.Q.; Schmidt, I.; Soffer, J.; Yang, J.J. The Flavor and spin structure of hyperons from quark fragmentation. Phys. Rev. D 2000, 62, 114009. [Google Scholar] [CrossRef]
- Yang, J.J. Quark fragmentation functions in a diquark model for Lambda production. Phys. Rev. D 2001, 64, 074010. [Google Scholar] [CrossRef]
- Leader, E.; Sidorov, A.V.; Stamenov, D.B. A New evaluation of polarized parton densities in the nucleon. Eur. Phys. J. C 2002, 23, 479–485. [Google Scholar] [CrossRef][Green Version]
- Blumlein, J.; Bottcher, H. QCD analysis of polarized deep inelastic data and parton distributions. Nucl. Phys. B 2002, 636, 225–263. [Google Scholar] [CrossRef]
- Leader, E.; Stamenov, D.B. Can the polarization of the strange quarks in the proton be positive? Phys. Rev. D 2003, 67, 037503. [Google Scholar] [CrossRef]
- Leader, E.; Sidorov, A.V.; Stamenov, D.B. Longitudinal polarized parton densities updated. Phys. Rev. D 2006, 73, 034023. [Google Scholar] [CrossRef]
- Astier, P.; Autiero, D.; Baldisseri, A.; Baldo-Ceolin, M.; Banner, M.; Bassompierre, G.; Benslama, K.; Besson, N.; Bird, I.; Blumenfeld, B.; et al. Measurement of the Lambda polarization in nu/mu charged current interactions in the NOMAD experiment. Nucl. Phys. B 2000, 588, 3–36. [Google Scholar] [CrossRef]
- Astier, P.; Autiero, D.; Baldisseri, A.; Baldo-Ceolin, M.; Banner, M.; Bassompierre, G.; Besson, N.; Bird, I.; Blumenfeld, B.; Bobisut, F.; et al. Measurement of the anti-Lambda polarization in muon-neutrino charged current interactions in the NOMAD experiment. Nucl. Phys. B 2001, 605, 3–14. [Google Scholar] [CrossRef]
- Ellis, J.R.; Kotzinian, A.; Naumov, D.V. Intrinsic polarized strangeness and Lambda0 polarization in deep inelastic production. Eur. Phys. J. C 2002, 25, 603–613. [Google Scholar] [CrossRef][Green Version]
- Abelev, B.I.; Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.V.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Balewski, J.; Barannikova, O.; Barnby, L.S.; et al. Longitudinal Spin Transfer to Lambda and anti-Lambda Hyperons in Polarized Proton-Proton Collisions at = 200 GeV. Phys. Rev. D 2009, 80, 111102. [Google Scholar] [CrossRef]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; et al. Improved measurement of the longitudinal spin transfer to Λ and hyperons in polarized proton-proton collisions at = 200 GeV. Phys. Rev. D 2018, 98, 112009. [Google Scholar] [CrossRef]
- De Florian, D.; Soffer, J.; Stratmann, M.; Vogelsang, W. Bounds on transverse spin asymmetries for Lambda baryon production in pp collisions at BNL RHIC. Phys. Lett. B 1998, 439, 176–182. [Google Scholar] [CrossRef]
- Gastmans, R.; Wu, T.T. The Ubiquitous Photon: Helicity Method for QED and QCD; 1990; Volume 80. Available online: https://inspirehep.net/literature/302550 (accessed on 5 March 2023).
- Chen, K.; Goldstein, G.R.; Jaffe, R.L.; Ji, X.D. Probing quark fragmentation functions for spin 1/2 baryon production in unpolarized e+e− annihilation. Nucl. Phys. B 1995, 445, 380–398. [Google Scholar] [CrossRef]
- Zhang, H.C.; Wei, S.Y. Probing the longitudinal spin transfer via dihadron polarization correlations in unpolarized e+e− and pp collisions. 2023. Available online: https://inspirehep.net/literature/2621901 (accessed on 5 March 2023).
- Bacchetta, A.; D’Alesio, U.; Diehl, M.; Miller, C.A. Single-spin asymmetries: The Trento conventions. Phys. Rev. D 2004, 70, 117504. [Google Scholar] [CrossRef]
- Chen, K.b.; Liang, Z.t.; Song, Y.k.; Wei, S.y. Longitudinal and transverse polarizations of Λ hyperon in unpolarized SIDIS and e+e− annihilation. Phys. Rev. D 2022, 105, 034027. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, X.; Lu, Z. Predicting the sinϕS Single-Spin-Asymmetry of Λ Production off transversely polarized nucleon in SIDIS. Phys. Rev. D 2021, 103, 114011. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Lu, Z. sin(ϕΛ-ϕS azimuthal asymmetry in transversely polarized Λ production in SIDIS within TMD factorization at the EIC. Phys. Rev. D 2021, 104, 034020. [Google Scholar] [CrossRef]
- Kang, Z.B.; Lee, K.; Shao, D.Y.; Zhao, F. Spin asymmetries in electron-jet production at the future electron ion collider. JHEP 2021, 11, 005. [Google Scholar] [CrossRef]
- Kang, Z.B.; Terry, J.; Vossen, A.; Xu, Q.; Zhang, J. Transverse Lambda production at the future Electron-Ion Collider. Phys. Rev. D 2022, 105, 094033. [Google Scholar] [CrossRef]
- Ellis, J.; Hwang, D.S. Spin Correlations of Lambda anti-Lambda Pairs as a Probe of Quark-Antiquark Pair Production. Eur. Phys. J. C 2012, 72, 1877. [Google Scholar] [CrossRef]
- Ackerstaff, K.; Alexander, G.; Allison, J.; Altekamp, N.; Anderson, K.J.; Anderson, S.; Arcelli, S.; Asai, S.; Axen, D.; Azuelos, G.; et al. Spin alignment of leading K*(892)0 mesons in hadronic Z0 decays. Phys. Lett. B 1997, 412, 210–224. [Google Scholar] [CrossRef]
- Abreu, P.; Adam, W.; Adye, T.; Alekseev, G.D.; Alemany, R.; Allport, P.P.; Almehed, S.; Amaldi, U.; Amato, S.; Andersson, P.; et al. Measurement of the spin density matrix for the rho0, K*0 (892) and phi produced in Z0 decays. Phys. Lett. B 1997, 406, 271–286. [Google Scholar] [CrossRef]
- Ackersta, K.; Alexander, G.; Allison, J.; Altekamp, N.; Ametewee, K.; Anderson, K.J.; Anderson, S.; Arcelli, S.; Asai, S.; Axen, D.; et al. Study of phi (1020), D*+- and B* spin alignment in hadronic Z0 decays. Z. Phys. C 1997, 74, 437–449. [Google Scholar] [CrossRef]
- Abbiendi, G.; Ackerstaff, K.; Alexander, G.; Allison, J.; Altekamp, N.; Anderson, K.J.; Anderson, S.; Arcelli, S.; Asai, S.; Ashby, S.F.; et al. A Study of spin alignment of rho(770)+- and omega(782) mesons in hadronic Z0 decays. Eur. Phys. J. C 2000, 16, 61–70. [Google Scholar] [CrossRef]
- Chukanov, A.; Naumov, D.; Popov, B.A.; Astier, P.; Autiero, D.; Baldisseri, A.; Baldisseri, A.; Baldo-Ceolin, M.; Banner, M.; Bassompierre, G.; et al. Production properties of K*(892)+- vector mesons and their spin alignment as measured in the NOMAD experiment. Eur. Phys. J. C 2006, 46, 69–79. [Google Scholar] [CrossRef]
- Anselmino, M.; Bertini, M.; Murgia, F.; Pire, B. Off diagonal helicity density matrix elements for heavy vector mesons inclusively produced in N N, gamma N and lepton N interactions. Phys. Lett. B 1998, 438, 347–352. [Google Scholar] [CrossRef]
- Anselmino, M.; Bertini, M.; Caruso, F.; Murgia, F.; Quintairos, P. Off diagonal helicity density matrix elements for vector mesons produced in polarized e+e− processes. Eur. Phys. J. C 1999, 11, 529–537. [Google Scholar] [CrossRef]
- Schafer, A.; Szymanowski, L.; Teryaev, O.V. Tensor polarization of vector mesons from quark and gluon fragmentation. Phys. Lett. B 1999, 464, 94–100. [Google Scholar] [CrossRef][Green Version]
- Xu, Q.h.; Liu, C.x.; Liang, Z.t. Spin alignment of vector meson in e+e− annihilation at Z0 pole. Phys. Rev. D 2001, 63, 111301. [Google Scholar] [CrossRef]
- Bacchetta, A.; Mulders, P.J. Positivity bounds on spin one distribution and fragmentation functions. Phys. Lett. B 2001, 518, 85–93. [Google Scholar] [CrossRef]
- Shlyapnikov, P.V. Comparing fragmentation of strange quark in Z0 decays and K+ p reactions. Phys. Lett. B 2001, 512, 18–24. [Google Scholar] [CrossRef]
- Xu, Q.h.; Liang, Z.t. Spin alignments of vector mesons in deeply inelastic lepton nucleon scattering. Phys. Rev. D 2002, 66, 017301. [Google Scholar] [CrossRef]
- Xu, Q.H.; Liang, Z.T. Spin alignment of the high p(T) vector mesons in polarized pp collisions at high-energies. Phys. Rev. D 2003, 67, 114013. [Google Scholar] [CrossRef]
- Xu, Q.H.; Liang, Z.T. Spin alignment of vector mesons in unpolarized hadron hadron collisions at high-energies. Phys. Rev. D 2003, 68, 034023. [Google Scholar] [CrossRef]
- Abelev, B.I.; Aggarwal, M.M.; Ahammed, Z.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Bai, Y.; Balewski, J.; Barannikova, O.; Barnby, L.S.; et al. Spin alignment measurements of the K*0(892) and phi (1020) vector mesons in heavy ion collisions at = 200 GeV. Phys. Rev. C 2008, 77, 061902. [Google Scholar] [CrossRef]
- Kundu, S. Spin alignment measurements of vector mesons with ALICE at the LHC. Nucl. Phys. A 2021, 1005, 121912. [Google Scholar] [CrossRef]
- Ji, X. Parton Physics on a Euclidean Lattice. Phys. Rev. Lett. 2013, 110, 262002. [Google Scholar] [CrossRef]
- Ji, X.; Zhang, J.H.; Zhao, Y. Renormalization in Large Momentum Effective Theory of Parton Physics. Phys. Rev. Lett. 2018, 120, 112001. [Google Scholar] [CrossRef]
- Radyushkin, A.V. Quasi-parton distribution functions, momentum distributions, and pseudo-parton distribution functions. Phys. Rev. D 2017, 96, 034025. [Google Scholar] [CrossRef]
- Orginos, K.; Radyushkin, A.; Karpie, J.; Zafeiropoulos, S. Lattice QCD exploration of parton pseudo-distribution functions. Phys. Rev. D 2017, 96, 094503. [Google Scholar] [CrossRef]
- Khan, T.; Sufian, R.S.; Karpie, J.; Monahan, C.J.; Egerer, C.; Joó, B.; Morris, W.; Orginos, K.; Radyushkin, A.; Richards, D.G.; et al. Unpolarized gluon distribution in the nucleon from lattice quantum chromodynamics. Phys. Rev. D 2021, 104, 094516. [Google Scholar] [CrossRef]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B.; Weisskopf, V.F. A New Extended Model of Hadrons. Phys. Rev. D 1974, 9, 3471–3495. [Google Scholar] [CrossRef]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B. Baryon Structure in the Bag Theory. Phys. Rev. D 1974, 10, 2599. [Google Scholar] [CrossRef]
- Jakob, R.; Mulders, P.J.; Rodrigues, J. Modeling quark distribution and fragmentation functions. Nucl. Phys. A 1997, 626, 937–965. [Google Scholar] [CrossRef]
- Petrov, V.Y.; Pobylitsa, P.V.; Polyakov, M.V.; Bornig, I.; Goeke, K.; Weiss, C. Off—forward quark distributions of the nucleon in the large N(c) limit. Phys. Rev. D 1998, 57, 4325–4333. [Google Scholar] [CrossRef]
- Bentz, W.; Hama, T.; Matsuki, T.; Yazaki, K. NJL model on the light cone and pion structure function. Nucl. Phys. A 1999, 651, 143–173. [Google Scholar] [CrossRef]
- Penttinen, M.; Polyakov, M.V.; Goeke, K. Helicity skewed quark distributions of the nucleon and chiral symmetry. Phys. Rev. D 2000, 62, 014024. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Hwang, D.S.; Schmidt, I. Final state interactions and single spin asymmetries in semiinclusive deep inelastic scattering. Phys. Lett. B 2002, 530, 99–107. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Hwang, D.S.; Schmidt, I. Initial state interactions and single spin asymmetries in Drell-Yan processes. Nucl. Phys. B 2002, 642, 344–356. [Google Scholar] [CrossRef]
- Boer, D.; Brodsky, S.J.; Hwang, D.S. Initial state interactions in the unpolarized Drell-Yan process. Phys. Rev. D 2003, 67, 054003. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Hwang, D.S.; Schmidt, I. Single hadronic spin asymmetries in weak interaction processes. Phys. Lett. B 2003, 553, 223–228. [Google Scholar] [CrossRef]
- Gamberg, L.P.; Goldstein, G.R.; Oganessyan, K.A. Novel transversity properties in semiinclusive deep inelastic scattering. Phys. Rev. D 2003, 67, 071504. [Google Scholar] [CrossRef]
- Bacchetta, A.; Schaefer, A.; Yang, J.J. Sivers function in a spectator model with axial vector diquarks. Phys. Lett. B 2004, 578, 109–118. [Google Scholar] [CrossRef]
- Belitsky, A.V.; Ji, X.d.; Yuan, F. Quark imaging in the proton via quantum phase space distributions. Phys. Rev. D 2004, 69, 074014. [Google Scholar] [CrossRef]
- Yuan, F. Sivers function in the MIT bag model. Phys. Lett. B 2003, 575, 45–54. [Google Scholar] [CrossRef]
- Lu, Z.; Ma, B.Q. Non-zero transversity distribution of the pion in a quark-spectator-antiquark model. Phys. Rev. D 2004, 70, 094044. [Google Scholar] [CrossRef]
- Goeke, K.; Meissner, S.; Metz, A.; Schlegel, M. Checking the Burkardt sum rule for the Sivers function by model calculations. Phys. Lett. B 2006, 637, 241–244. [Google Scholar] [CrossRef]
- Cloet, I.C.; Bentz, W.; Thomas, A.W. Transversity quark distributions in a covariant quark-diquark model. Phys. Lett. B 2008, 659, 214–220. [Google Scholar] [CrossRef]
- Meissner, S.; Metz, A.; Goeke, K. Relations between generalized and transverse momentum dependent parton distributions. Phys. Rev. D 2007, 76, 034002. [Google Scholar] [CrossRef]
- Bacchetta, A.; Conti, F.; Radici, M. Transverse-momentum distributions in a diquark spectator model. Phys. Rev. D 2008, 78, 074010. [Google Scholar] [CrossRef]
- Pasquini, B.; Cazzaniga, S.; Boffi, S. Transverse momentum dependent parton distributions in a light-cone quark model. Phys. Rev. D 2008, 78, 034025. [Google Scholar] [CrossRef]
- Avakian, H.; Efremov, A.V.; Schweitzer, P.; Yuan, F. Transverse momentum dependent distribution function and the single spin asymmetry . Phys. Rev. D 2008, 78, 114024. [Google Scholar] [CrossRef]
- Avakian, H.; Efremov, A.V.; Schweitzer, P.; Yuan, F. Pretzelosity distribution function . In Proceedings of the 2nd International Workshop on Transverse Polarization Phenomena in Hard Processes, Ferrara, Italy, 28–31 May 2008. [Google Scholar] [CrossRef]
- Boffi, S.; Efremov, A.V.; Pasquini, B.; Schweitzer, P. Azimuthal spin asymmetries in light-cone constituent quark models. Phys. Rev. D 2009, 79, 094012. [Google Scholar] [CrossRef]
- Efremov, A.V.; Schweitzer, P.; Teryaev, O.V.; Zavada, P. Transverse momentum dependent distribution functions in a covariant parton model approach with quark orbital motion. Phys. Rev. D 2009, 80, 014021. [Google Scholar] [CrossRef]
- She, J.; Zhu, J.; Ma, B.Q. Pretzelosity and quark orbital angular momentum. Phys. Rev. D 2009, 79, 054008. [Google Scholar] [CrossRef]
- Avakian, H.; Efremov, A.V.; Schweitzer, P.; Yuan, F. The transverse momentum dependent distribution functions in the bag model. Phys. Rev. D 2010, 81, 074035. [Google Scholar] [CrossRef]
- Pasquini, B.; Yuan, F. Sivers and Boer-Mulders functions in Light-Cone Quark Models. Phys. Rev. D 2010, 81, 114013. [Google Scholar] [CrossRef]
- Lu, Z.; Ma, B.Q. Gluon Sivers function in a light-cone spectator model. Phys. Rev. D 2016, 94, 094022. [Google Scholar] [CrossRef]
- Ma, Z.L.; Zhu, J.Q.; Lu, Z. Quasiparton distribution function and quasigeneralized parton distribution of the pion in a spectator model. Phys. Rev. D 2020, 101, 114005. [Google Scholar] [CrossRef]
- Bacchetta, A.; Celiberto, F.G.; Radici, M.; Taels, P. Transverse-momentum-dependent gluon distribution functions in a spectator model. Eur. Phys. J. C 2020, 80, 733. [Google Scholar] [CrossRef]
- Luan, X.; Lu, Z. Sivers function of sea quarks in the light-cone model. Phys. Lett. B 2022, 833, 137299. [Google Scholar] [CrossRef]
- Tan, C.; Lu, Z. Gluon generalized parton distributions and angular momentum in a light-cone spectator model. arXiv 2023, arXiv:2301.09081. [Google Scholar]
- Sharma, S.; Dahiya, H. Twist-4 T-even proton TMDs in the light-front quark-diquark model. arXiv 2023, arXiv:2301.09536. [Google Scholar] [CrossRef]
- Metz, A. Gluon-exchange in spin-dependent fragmentation. Phys. Lett. B 2002, 549, 139–145. [Google Scholar] [CrossRef]
- Gamberg, L.P.; Mukherjee, A.; Mulders, P.J. Spectral analysis of gluonic pole matrix elements for fragmentation. Phys. Rev. D 2008, 77, 114026. [Google Scholar] [CrossRef]
- Nzar, M.; Hoodbhoy, P. Quark fragmentation functions in a diquark model for proton and Lambda hyperon production. Phys. Rev. D 1995, 51, 32–36. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, Z.; Schmidt, I. Transverse polarization of the Λ hyperon from unpolarized quark fragmentation in the diquark model. Phys. Rev. D 2017, 96, 034010. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Y.; Lu, Z. Double Collins effect in e+e−→ΛX process in a diquark spectator model. Phys. Rev. D 2018, 97, 114015. [Google Scholar] [CrossRef]
- Lu, Z.; Schmidt, I. Twist-3 fragmentation functions in a spectator model with gluon rescattering. Phys. Lett. B 2015, 747, 357–364. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, Z.; Schmidt, I. Twist-3 T-odd fragmentation functions G⊥ and in a spectator model. Phys. Lett. B 2016, 761, 333–339. [Google Scholar] [CrossRef]
- Bacchetta, A.; Gamberg, L.P.; Goldstein, G.R.; Mukherjee, A. Collins fragmentation function for pions and kaons in a spectator model. Phys. Lett. B 2008, 659, 234–243. [Google Scholar] [CrossRef]
- Xie, X.; Lu, Z. T-Even Transverse Momentum Dependent Gluon Fragmentation Functions in A Spectator Model. arXiv 2022, arXiv:2210.16532. [Google Scholar]
- Manohar, A.; Georgi, H. Chiral Quarks and the Nonrelativistic Quark Model. Nucl. Phys. B 1984, 234, 189–212. [Google Scholar] [CrossRef]
- Ji, X.D.; Zhu, Z.K. Quark Fragmentation Functions in Low-Energy Chiral Theory. 1993. Available online: https://inspirehep.net/literature/363352 (accessed on 5 March 2023).
- Londergan, J.T.; Pang, A.; Thomas, A.W. Probing charge symmetry violating quark distributions in semiinclusive leptoproduction of hadrons. Phys. Rev. D 1996, 54, 3154–3161. [Google Scholar] [CrossRef] [PubMed]
- Bacchetta, A.; Kundu, R.; Metz, A.; Mulders, P.J. Estimate of the Collins fragmentation function in a chiral invariant approach. Phys. Rev. D 2002, 65, 094021. [Google Scholar] [CrossRef]
- Nam, S.i.; Kao, C.W. Fragmentation functions and parton distribution functions for the pion with the nonlocal interactions. Phys. Rev. D 2012, 85, 034023. [Google Scholar] [CrossRef]
- Nam, S.i.; Kao, C.W. Fragmentation and quark distribution functions for the pion and kaon with explicit flavor-SU(3)-symmetry breaking. Phys. Rev. D 2012, 85, 094023. [Google Scholar] [CrossRef]
- Yang, D.J.; Jiang, F.J.; Kao, C.W.; Nam, S.i. Quark-jet contribution to the fragmentation functions for the pion and kaon with the nonlocal interactions. Phys. Rev. D 2013, 87, 094007. [Google Scholar] [CrossRef]
- Andrianov, A.A.; Espriu, D. Vector mesons in the extended chiral quark model. JHEP 1999, 10, 022. [Google Scholar] [CrossRef][Green Version]
- Bacchetta, A.; Kundu, R.; Metz, A.; Mulders, P.J. The Collins fragmentation function: A Simple model calculation. Phys. Lett. B 2001, 506, 155–160. [Google Scholar] [CrossRef][Green Version]
- Bacchetta, A.; Metz, A.; Yang, J.J. Collins fragmentation function from gluon rescattering. Phys. Lett. B 2003, 574, 225–231. [Google Scholar] [CrossRef]
- Gamberg, L.P.; Goldstein, G.R.; Oganessyan, K.A. A Mechanism for the T odd pion fragmentation function. Phys. Rev. D 2003, 68, 051501. [Google Scholar] [CrossRef]
- Amrath, D.; Bacchetta, A.; Metz, A. Reviewing model calculations of the Collins fragmentation function. Phys. Rev. D 2005, 71, 114018. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity 1. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy With Superconductivity II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Korpa, C.L.; Meissner, U.G. Flavor Mixing Structure Functions in the Nambu-Jona-Lasinio Model. Phys. Rev. D 1990, 41, 1679. [Google Scholar] [CrossRef]
- Shigetani, T.; Suzuki, K.; Toki, H. Pion structure function in the Nambu and Jona-Lasinio model. Phys. Lett. B 1993, 308, 383–388. [Google Scholar] [CrossRef][Green Version]
- Davidson, R.M.; Ruiz Arriola, E. Structure functions of pseudoscalar mesons in the SU(3) NJL model. Phys. Lett. B 1995, 348, 163–169. [Google Scholar] [CrossRef]
- Davidson, R.M.; Ruiz Arriola, E. Parton distributions functions of pion, kaon and eta pseudoscalar mesons in the NJL model. Acta Phys. Polon. B 2002, 33, 1791–1808. [Google Scholar]
- Nguyen, T.; Bashir, A.; Roberts, C.D.; Tandy, P.C. Pion and kaon valence-quark parton distribution functions. Phys. Rev. C 2011, 83, 062201. [Google Scholar] [CrossRef]
- Hutauruk, P.T.P.; Cloet, I.C.; Thomas, A.W. Flavor dependence of the pion and kaon form factors and parton distribution functions. Phys. Rev. C 2016, 94, 035201. [Google Scholar] [CrossRef]
- Field, R.D.; Feynman, R.P. A Parametrization of the Properties of Quark Jets. Nucl. Phys. B 1978, 136, 1. [Google Scholar] [CrossRef]
- Field, R.D.; Wolfram, S. A QCD Model for e+e− Annihilation. Nucl. Phys. B 1983, 213, 65–84. [Google Scholar] [CrossRef]
- Ito, T.; Bentz, W.; Cloet, I.C.; Thomas, A.W.; Yazaki, K. The NJL-jet model for quark fragmentation functions. Phys. Rev. D 2009, 80, 074008. [Google Scholar] [CrossRef]
- Matevosyan, H.H.; Thomas, A.W.; Bentz, W. Calculating Kaon Fragmentation Functions from NJL-Jet Model. Phys. Rev. D 2011, 83, 074003. [Google Scholar] [CrossRef]
- Matevosyan, H.H.; Thomas, A.W.; Bentz, W. Monte Carlo Simulations of Hadronic Fragmentation Functions using NJL-Jet Model. Phys. Rev. D 2012, 83, 114010, Erratum in Phys. Rev. D 2012, 86, 059904. [Google Scholar] [CrossRef]
- Matevosyan, H.H.; Bentz, W.; Cloet, I.C.; Thomas, A.W. Transverse Momentum Dependent Fragmentation and Quark Distribution Functions from the NJL-jet Model. Phys. Rev. D 2012, 85, 014021. [Google Scholar] [CrossRef]
- Matevosyan, H.H.; Thomas, A.W.; Bentz, W. Collins Fragmentation Function within NJL-jet Model. Phys. Rev. D 2012, 86, 034025. [Google Scholar] [CrossRef]
- Casey, A.; Matevosyan, H.H.; Thomas, A.W. Calculating Dihadron Fragmentation Functions in the NJL-jet model. Phys. Rev. D 2012, 85, 114049. [Google Scholar] [CrossRef]
- Bentz, W.; Kotzinian, A.; Matevosyan, H.H.; Ninomiya, Y.; Thomas, A.W.; Yazaki, K. Quark-Jet model for transverse momentum dependent fragmentation functions. Phys. Rev. D 2016, 94, 034004. [Google Scholar] [CrossRef]
- Yang, D.J.; Li, H.N. Gluon fragmentation functions in the Nambu–Jona-Lasinio model. Phys. Rev. D 2016, 94, 054041. [Google Scholar] [CrossRef]
- Yang, D.J.; Li, H.N. Charm fragmentation functions in the Nambu–Jona-Lasinio model. Phys. Rev. D 2020, 102, 036023. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.-B.; Liu, T.; Song, Y.-K.; Wei, S.-Y. Several Topics on Transverse Momentum-Dependent Fragmentation Functions. Particles 2023, 6, 515-545. https://doi.org/10.3390/particles6020029
Chen K-B, Liu T, Song Y-K, Wei S-Y. Several Topics on Transverse Momentum-Dependent Fragmentation Functions. Particles. 2023; 6(2):515-545. https://doi.org/10.3390/particles6020029
Chicago/Turabian StyleChen, Kai-Bao, Tianbo Liu, Yu-Kun Song, and Shu-Yi Wei. 2023. "Several Topics on Transverse Momentum-Dependent Fragmentation Functions" Particles 6, no. 2: 515-545. https://doi.org/10.3390/particles6020029
APA StyleChen, K.-B., Liu, T., Song, Y.-K., & Wei, S.-Y. (2023). Several Topics on Transverse Momentum-Dependent Fragmentation Functions. Particles, 6(2), 515-545. https://doi.org/10.3390/particles6020029