Nonlinear Output Feedback Control for Parrot Mambo UAV: Robust Complex Structure Design and Experimental Validation

Abstract

This paper addresses the problem of controlling quadcopters operating in an environment characterized by unpredictable disturbances such as wind gusts. From a control point of view, this is a nonstandard, highly challenging problem. Fundamentally, these quadcopters are high-order dynamical systems characterized by an under-actuated and highly nonlinear model with coupling between several state variables. The main objective of this work is to achieve a trajectory by tracking desired altitude and attitude. The problem was tackled using a robust control approach with a multi-loop nonlinear controller combined with extended Kalman filtering (EKF). Specifically, the flight control system consists of two regulation loops. The first one is an outer loop based on the backstepping approach and allows for control of the elevation as well as the yaw of the quadcopter, while the second one is the inner loop, which allows the maintenance of the desired attitude by adjusting the roll and pitch, whose references are generated by the outer loop through a standard PID, to limit the 2D trajectory to a desired set path. The investigation integrates EKF technique for sensor signal processing to increase measurements accuracy, hence improving robustness of the flight. The proposed control system was formally developed and experimentally validated through indoor tests using the well-known Parrot Mambo unmanned aerial vehicle (UAV). The obtained results show that the proposed flight control system is efficient and robust, making it suitable for advanced UAV navigation in dynamic scenarios with disturbances.

1. Introduction

The landscape of unmanned aerial vehicles (UAVs) is undergoing a transformational shift driven by advancements in sensor technologies. Miniature drones equipped with cutting-edge technology have emerged as valuable tools for disaster management and strategic operations worldwide. However, fixed-wing quadcopters are complex system that are coupled and underactuated with inherent nonlinearities, hence increasing the complexity of their control strategies and requiring a deep understanding of vehicle dynamics and aerodynamic effects in dynamic and unpredictable environments marked by air turbulence, friction, and magnetic field disturbances.

In the pursuit of precise set point tracking, traditional sliding mode and backstepping controllers have been used, such as in [1,2] where the control strategy was redefined due to their limited consideration of disturbances and uncertainties. The study presented in [3] proposes an approach aimed at enhancing the robustness of trajectory tracking control in systems facing uncertainties by employing discrete switching. However, this approach can induce instability problems. To tackle this issue, the authors introduced an adaptive law to estimate the switching gain, but that comes with challenges, such as overestimating the gain and potentially causing instability as the estimation increases.

To improve flight performance and reject disturbances, several other control methods have been proposed in the literature, such as the disturbance observer-based control (DOBC) and active disturbance rejection control (ADRC) methods, which have attracted the interest of researchers because of their promising results when dealing with intense perturbation rejection. The study by [4] introduced ADRC, a multi-loop methodology incorporating an extended state observer (ESO), nonlinear state error feedback, and a tracking differentiator (TD) to deal with the classical derivative block. While simulations conducted in Matlab/Simulink yielded promising results, experimental validation has not been provided. In the context of the DOBC method with model predictive controllers, Ref. [5] addresses motion control for a four-degrees-of-freedom unmanned underwater vehicle where disturbances affecting the marine vehicle are precisely estimated and rejected. Similarly, in [6] a nonlinear disturbance observer based on predictive control of planar motors was proposed. The effectiveness of the ADRC approach was validated experimentally on a planar motor system.

To develop trajectory tracking, Ref. [7] highlighted the importance of incorporating signal processing, focusing on the combined use of unscented Kalman and cubature Kalman filters. Integrating Kalman filtering and sensor fusion has been addressed in various studies, including those by [8,9] presenting solutions for managing sensor data. This filtering and estimation strategy is especially useful for handling disturbances in dynamic environments. In this work, it is used to improve measurement accuracy and address the challenges of quadcopter control.

Adapting standard Kalman filtering within a control structure aims to push strategic boundaries by enabling accurate measurements, even in noisy conditions. Our goal goes beyond addressing challenges like drag coefficients and aerodynamic friction; we also aim to extend these principles to the dynamics by adding wind to the proposed Parrot Mambo, chosen for its compatibility with Matlab/Simulink. Using Parrot Mambo ensures a smooth transition from simulation to real-world scenarios, thus strengthening the practical relevance of the results. Drawing on recent advancements in the field, our work integrates insights from the backstepping control strategy, building on the analysis of Kalman filtering presented by [10].

The proposed control framework combines advanced filtering methods with a robust backstepping approach and PID regulation to achieve reliable trajectory tracking in dynamic indoor environments. The focus is on the development of a robust strategy of control for both attitude and altitude motion, which would be particularly resilient to external disturbances. The contributions of this work, in comparison to prominent existing works, are succinctly outlined below:

Robust complex nonlinear structure with cascaded backstepping nonlinear controller: A closed-loop system is designed to deal with both altitude and attitude control.

Taking into account external disturbances, sensor failure, and uncertainties, the Extended Kalman filtering (EKF) technique is integrated with the sensors to complete the control structure. The aim is to improve the accuracy of the sensed signals, which is crucial for better control system performance.

Experimental Validation: A significant aspect of this research involves its practical application for validation. The proposed controllers, coupled with the extended Kalman estimation strategy, were tested using indoor experiments taking into account the existence of the magnetic field. The wind disturbance from a fan was also taken into consideration to test the efficacy and robustness of the system in real-life dynamic scenarios.

The rest of the paper is structured as follows: Section 2 introduces the Parrot Mambo unmanned aerial vehicle (UAV)’s hardware and software, along with a dynamic model of the quadcopter. Section 3 details the controller design, emphasizing signal processing within the nonlinear control framework. Section 4 describes the implementation of the control structure for practical testing and analyzes the results obtained from the proposed approach. Section 5 discusses the proposed approach in comparison with previously reported methods. Finally, Section 6 concludes the study and suggests directions for future research.

2. System Description and Mathematical Modeling

This section begins with a detailed description of the sensors, actuators, and real-time data acquisition processes of the Parrot Mambo drone. By elucidating these technical features, we aim to construct an accurate model and provide readers with a clear understanding of the operational dynamics that underpin this study.

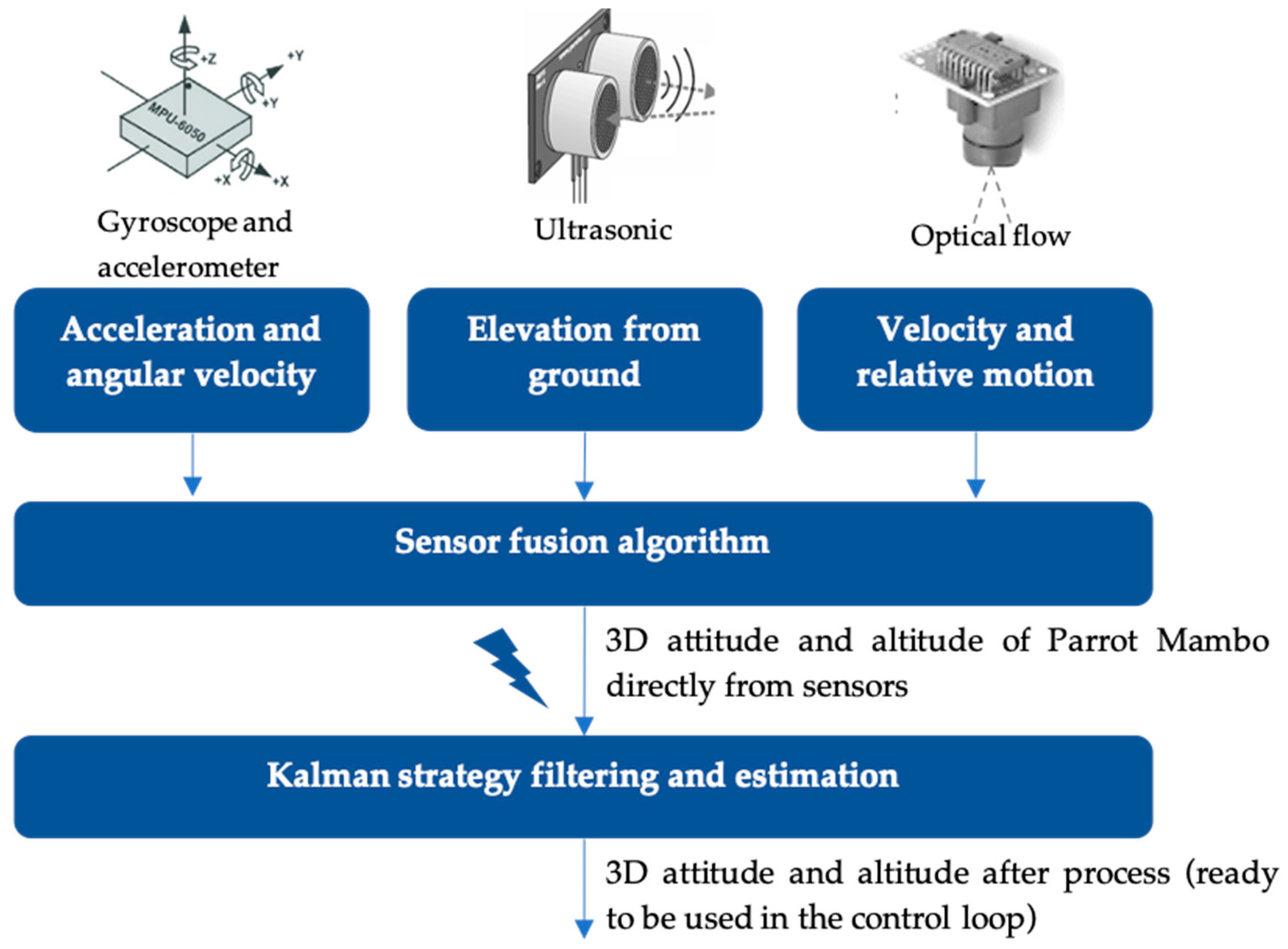
2.1. Parrot Mambo Sensors and Actuators

The Parrot Mambo drone is a versatile quadcopter equipped with a comprehensive set of sensors and actuators that enhance its dynamic capabilities. The propulsion system consists of four propellers, with two of them rotating clockwise (CW) and the other two rotating counterclockwise (CCW). Each propeller is directly connected to a motor, enabling precise control over thrust and orientation during flight. The Parrot Mambo’s material constituents are introduced in [11]; these are shown in Figure 1.

The onboard inertial measurement unit (IMU) of the Parrot Mambo drone includes the MPU6050, manufactured by InvenSense Inc., San Jose, CA, USA integrates a three-axis gyroscope and a three-axis accelerometer, providing essential data for attitude estimation and regulation. This sensor suite ensures that the drone maintains the desired orientation and responds promptly to movement changes. Additionally, ultrasonic sensors contribute to altitude control by measuring the distance between the drone and the ground, facilitating stable vertical positioning. The inclusion of an optical flow sensor enhances the Parrot Mambo’s ability to detect ground movement, enabling precise horizontal positioning. Connectivity options include Bluetooth and a USB connector, allowing wireless communication and data transfer. A lithium polymer battery powers the drone, offering an optimal power-to-weight ratio (PWR).

The Parrot Mambo drone’s sensors, including the MPU6050, ultrasonic sensors, and optical flow sensors, combined with its quadcopter configuration and connectivity options, collectively form a robust platform for experimentation and application in various drone scenarios.

An additional feature that enhances the Parrot Mambo’s capabilities is the inclusion of a camera extension. This component serves as a central unit, establishing a WiFi connection with Matlab to facilitate real-time data generation during flight. While Bluetooth connectivity alone cannot retrieve flight data, the camera extension significantly improves the drone’s communication capabilities. By integrating this extension, the drone ensures seamless wireless communication with Matlab, providing continuous and immediate data generation throughout the flight. This feature not only broadens the scope of the Parrot Mambo’s applications but also increases its value in research and experimentation, offering users a comprehensive and dynamic platform for data-driven analysis.

The physical parameters of the Parrot Mambo model are summarized in

Table 1. Parrot Mambo model physical parameters.

Parameter	Value
$m$	$0.0630 \mathrm{k}\mathrm{g}$
$l$	$0.0624 \mathrm{m}$
$C_{d(x,y,z)}$	${10}^{-1} \mathrm{diag} \left[6.2 4.5 6.9\right] \mathrm{N}\cdot \mathrm{s}/\mathrm{m}$
$C_{a(x,y,z)}$	${10}^{-1} \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g} \left[1 1 1.1\right] \mathrm{N}\cdot \mathrm{s}/\mathrm{m}$
$K_b$	$0.0107 \mathrm{N}\cdot {\mathrm{s}}^2$
$K_d$	$0.7826400 \times {10}^{-3} \mathrm{N}\cdot \mathrm{m}\cdot {\mathrm{s}}^2$
$I_x$	$0.0582857 \times {10}^{-3} \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^2$
$I_y$	$0.0716914 \times {10}^{-3} \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^2$
$I_z$	$0.1 \times {10}^{-3} \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^2$
$J_r$	$0 1021 \times {10}^{-6} \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^2$

below.

2.2. System Mathematical Modeling

In formulating a precise physical model for the Parrot Mambo UAV, it is imperative to meticulously account for various aerodynamic influences, including gravity, propeller thrust, air resistance, aerodynamic torque, and the torque generated by gyroscopic motion. In the pursuit of enhancing the model’s fidelity to real-world dynamics, it becomes paramount to incorporate random uncertainties applied to the sensors, as discussed in [12]. This imperative consideration contributes to a more accurate representation of the quadcopter’s behavior in diverse and unpredictable scenarios. To ensure a comprehensive and nuanced representation, certain assumptions underpin model construction:

• The quadcopter is treated as a rigid body with a symmetrical structure, facilitating a simplified yet robust characterization.
• The alignment of the center of gravity with the quadcopter’s geometrical center is assumed.
• Euler angles governing the orientation of the UAV ($\phi , \theta , \psi$) are constrained within specific bounds: $-\pi <\phi <\pi$, $-\pi <\theta <\pi$, and $-\pi <\psi <\pi .$ This constraint ensures realistic and physically meaningful variations in orientation.
• Both the position and velocity of the UAV are deemed measurable, providing essential parameters for accurate depiction of its motion.
• The thrust and drag forces are considered to be proportionally related to the squared velocity of the propellers, aligning with the principles of aerodynamics and motor dynamics.

By adhering to these assumptions and considerations, the ensuing physical model not only captures the fundamental dynamics of the Parrot Mambo but also integrates the essential elements necessary for precise analyses, as in [11]. Before constructing a mathematical model for the quadcopter, it is crucial to establish two reference notations: $R_g(O, \overrightarrow{I}, \overrightarrow{J}, \overrightarrow{K})$ and $R_b$(o, $\overrightarrow{i}$, $\overrightarrow{j}$, $\overrightarrow{k}$), where $R_g$ is tied to the ground, providing a fixed frame, while $R_b$ is connected to the body of the UAV. The center ‘o’ of $R_b$ aligns with the quadcopter’s mass center, and $(x_{Rb}, y_{Rb}, z_{Rb})$ represents its position relative to the Earth. Euler angles, or $(\phi , \theta , \psi )$, describe how the quadcopter is tilted or turned. To create a realistic quadcopter model, we must consider all aerodynamic effects, especially those influenced by the mechanical movements of the propellers. These factors play a crucial role in shaping the quadcopter’s motion and behavior. Understanding spatial references, positions, orientation dynamics, and aerodynamic effects is essential for building an accurate mathematical model that reflects the real-world behavior of the quadcopter. The modeling approach is based on Newton’s laws and Euler’s theorem. The physical model of the quadcopter can be described by the following equations:

$$\left\{\begin{array}{c}\dot{\eta }=f(\mathrm{\eta },u){+w}_k\\ \zeta =h\left(\mathrm{\eta }\right)+v_k\end{array}\right.$$

(1)

$$\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2={\displaystyle \frac{u_1}{m}}\cos \left({\psi }_1\right)\sin \left({\theta }_1\right)\cos \left({\phi }_1\right)+\sin \left({\psi }_1\right)\sin \left({\phi }_1\right)-{\displaystyle \frac{C_{dx}}{m}}{x}_2+w_k\end{array}$$

(2)

$$\begin{array}{l}{\dot{y}}_1=y_2\\ {\dot{y}}_2={\displaystyle \frac{u_1}{m}}\mathit{cos}\left({\phi }_1\right)\mathit{sin}\left({\psi }_1\right)\mathit{sin}\left({\theta }_1\right)-\mathit{cos}\left({\psi }_1\right)\mathit{sin}\left({\phi }_1\right)-{\displaystyle \frac{C_{dy}}{m}}{y}_2+w_k\end{array}$$

(3)

$$\begin{array}{l}{\dot{z}}_1=z_2\\ {\dot{z}}_2={\displaystyle \frac{u_1}{m}}\mathit{cos}\left({\theta }_1\right)\mathit{cos}\left({\phi }_1\right)-{\displaystyle \frac{C_{dz}}{m}}{z}_2-g+w_k\end{array}$$

(4)

$$\begin{array}{l}{\dot{\phi }}_1={\phi }_2\\ {\dot{\phi }}_2={\displaystyle \frac{l{u}_2}{I_x}}-{\displaystyle \frac{C_{ax}}{I_x}} {{\phi }_2}^2-{\displaystyle \frac{J_r{\Omega }_r}{I_x}}{\theta }_2-{\displaystyle \frac{\left(I_z-I_y\right)}{I_x}}{\theta }_2{\psi }_2+w_k\end{array}$$

(5)

$$\begin{array}{l}{\dot{\theta }}_1={\theta }_2\\ {\dot{\theta }}_2={\displaystyle \frac{{lu}_3}{I_y}}-{\displaystyle \frac{C_{ay}}{I_y}} {{\theta }_2}^2+{\displaystyle \frac{J_r{\Omega }_r}{I_y}}{\phi }_2-{\displaystyle \frac{\left(I_x-I_z\right)}{I_y}}{\phi }_2{\psi }_2+w_k\end{array}$$

(6)

$$\begin{array}{l}{\dot{\psi }}_1={\psi }_2\\ {\dot{\psi }}_2={\displaystyle \frac{u_4}{I_z}} - {\displaystyle \frac{C_{az}}{I_z}} {{\psi }_2}^2 - {\displaystyle \frac{\left(I_y-I_x\right)}{I_z}}{\phi }_2{\theta }_2+w_k\end{array}$$

(7)

where:

-

$w_k$ and $v_k$ are, respectively, the model uncertainties and sensor measurement noise. They correspond to unmeasurable white noise that affects the model dynamics;

-

$u_1$ represents the total thrust force, while $u_2,u_3$ and $u_4$ are the total torque for roll, pitch, and yaw, respectively.

-

${\left(x_1, y_1, z_1\right)}^T$ and ${\left({\phi }_1, {\theta }_1, {\psi }_1\right)}^T$ are, respectively, linear and angular positions.

-

${\left(x_2, y_2, z_2\right)}^T$ and ${\left({\phi }_2, {\theta }_2, {\psi }_2\right)}^T$ are, respectively, linear and angular velocities.

-

To simplify the notation, we define ${\Omega }_r$= ${\omega }_1^2 - {\omega }_2^2 + {\omega }_3^2 - {\omega }_4^2$.

The quadrotor trajectory can be created by combining the speeds of the four rotors. Then, the control inputs can be defined as:

$$\left(\begin{array}{c}{u}_1\\ u_2\\ u_3\\ u_4\end{array}\right)=\left(\begin{array}{cccc}{K}_b& K_b& K_b& K_b\\ K_b& 0& -K_b& 0\\ 0& K_b& 0& -K_b\\ -K_d& K_d& -K_d& K_d\end{array}\right)\left(\begin{array}{c}{\omega }_1^2\\ {\omega }_2^2\\ {\omega }_3^2\\ {\omega }_4^2\end{array}\right)$$

(8)

3. Controller Synthesis

3.1. Control Objectives

The main goal of the study is to ensure accurate control of the reference trajectories $(x^{*}, y^{*}, z^{*})$ in both tracking and regulation modes. To prevent potential instability or erratic movements, the angle ψ is fixed. This guarantees a stable and controlled trajectory while respecting the manufacturer’s motor limitations, ensuring that mechanical and performance constraints are not exceeded. Additionally, the control system should be robust against external disturbances and uncertainties, ensuring safe and reliable operation even in dynamic environments or varying conditions.

3.2. Sensor Fusion Algorithm

To enhance the quadcopter’s accuracy and robustness, various sensors, including ultrasonic, IMU, and optical flow, are integrated as shown in Figure 2. This sensor fusion addresses uncertainties in the physical model and perturbations in sensor measurements. Conventional sensor fusion techniques, including Dempster–Shafer theory, particle filtering (e.g., the Sequential Monte Carlo method discussed by [13]), and the federated filtering approach introduced by [14], which integrate data from multiple sensors within either centralized fusion (CF) or decentralized fusion (DF) frameworks, remain susceptible to the adverse effects of sensor noise contamination. To mitigate this, the EKF approach is employed. Unlike traditional filters that remove radio interference, the EKF is a numerical estimator that reduces noise and improves system reliability by addressing uncertainty through a mathematical approach.

3.3. Overview and Synthesis of Kalman Filtering

3.3.1. Kalman Filtering in Drone Piloting

Noise and uncertainty make controlling the quadcopter a hard task to accomplish; one tool that is known to be powerful enough to overcome these obstacles is Kalman filtering. Ref. [15] highlights the importance of integrating KF, where the experimental results demonstrated that the Kalman-based UAV tracking model significantly outperformed existing particle filters. It iteratively combined dynamic model prediction with noisy sensor data to refine and correct the quadcopter’s state vector, as described in Figure 3. This resulted in robust as well as accurate estimation despite disturbances during the flight. Kalman filtering’s strength lies in finding a good equilibrium between the prediction of the system’s future state, on one hand, and corrections to it based on sensor measurement input, on the other. Thus, guaranteeing unmatchable efficiency when estimating the position and velocity of the UAV. This is why the Kalman algorithm dominates modern-day technology, ranging from GPS receivers to spacecraft and unmanned aerial vehicles.

The Kalman gain is used to adaptively weight the two sources of information model dynamics and sensor data from onboard sensors. These sensors provide essential data about the UAV’s velocity, orientation, and surrounding environment. Achieving stable flight depends on using well-chosen covariance matrices and optimal Kalman gain, enabling robust and adaptive state estimation.

3.3.2. Extended Kalman Filter Synthesis

In the following sections, we delve into the implementation details of the extended Kalman filter for a nonlinear model of the UAV based on [16]’s theory. Initially, the Kalman filter predicts the forthcoming system state based on the current estimated state ${\widehat{\eta }}_{k-1/k-1}$, established upon setting up all initial conditions:

$${\widehat{\eta }}_{0/0}=E\left({\eta }_0\right)$$

(9)

$${\widehat{P}}_{0/0}=E(({\mathsf{\eta }}_0-{\widehat{\eta }}_{0/0}){({\mathsf{\eta }}_0-{\widehat{\eta }}_{0/0})}^T)$$

(10)

As in (1), the model noise $w_k$ can be expressed as a zero-mean white Gaussian noise that captures system model discrepancies or uncertainties. The mathematical format for $w_k ~ \left(0, Q_k\right),$ where $Q_k$ is the covariance matrix of the model noise. The same case applies to observation noise $v_k$, which is a zero-mean white Gaussian noise that represents inaccuracies in sensor measurements and has covariance $R_k$. The mathematical representation for this is $v_k ~ (0, R_k)$.

We denote the state vector ${\eta }_k$ at time step $k$ as follows:

$${\mathsf{\eta }}_k={\left(\begin{array}{cccccc}{x}_k& y_k& z_k& {\phi }_k& {\theta }_k& {\psi }_k\end{array}\right)}^T$$

(11)

The physical model representation in (1) can be assimilated to:

$$\begin{array}{c}\left\{\begin{array}{c}{\mathsf{\eta }}_{\mathrm{k}+1}=f({\mathsf{\eta }}_{\mathrm{k}},u_k){+w}_k\\ {\zeta }_{k+1}=h\left({\mathsf{\eta }}_{\mathrm{k}}\right)+v_k\end{array}\right.\end{array}$$

(12)

Here, $f$ represents the nonlinear system dynamics function, $u_k$ is the control input, and $h$ is the measurement function. $w_k$ and $v_k$ are mutually uncorrelated with zero means $\mathrm{E}\left[w_k v_k^T\right]=0$ for all values of k, where $\mathrm{E}[·]$ stands for the expectation operator. Figure 4 summarizes the EKF approach in the Parrot Mambo’s flight control system (FCS). We then introduce the predicted state ${\tilde{\eta }}_{k/k-1}$.

$${\tilde{\eta }}_{k/k-1}=F({\widehat{\eta }}_{k-1/k-1},u_k)$$

(13)

Furthermore, the level of uncertainty associated with the prediction is as follows:

$${\tilde{P}}_{k/k-1}=E\left(\right({\mathsf{\eta }}_{k/k-1}-{\tilde{\eta }}_{k/k-1}\left){({\mathsf{\eta }}_{k/k-1}-{\tilde{\eta }}_{k/k-1})}^T\right)$$

$${\tilde{P}}_{k/k-1}=F_{k-1} {\widehat{P}}_{k-1/k-1} F_{k-1}^T + Q_{k-1}$$

(14)

Here, $Q_{k-1}$ represents the process noise covariance matrix at k−1, and $F_{k-1}$ is the Jacobian matrix that is given by:

$$F_k={\displaystyle \frac{\mathit{\partial }F({\mathsf{\eta }}_k,u_k)}{\mathit{\partial }{\eta }_k^T}}{|}_{{\eta }_k=\widehat{\eta }(k/(k-1\left)\right)}$$

(15)

where $F_k$ is the Jacobian matrix of partial derivatives of F with respect to ${\eta }_k$.

In the correction step, we incorporate sensor measurements to update the state estimate based on the prediction. First, the optimization of the Kalman filter gain is determined by:

$${\displaystyle \frac{d\left(Tr\right({\tilde{P}}_{k/k-1}\left)\right)}{d{K}_k}}=0$$

(16)

$K_k$ is the Kalman gain matrix, which can be expressed as follows:

$$K_k={\tilde{P}}_{k/k-1} H_k^T {(H_k {\tilde{P}}_{k/k-1} H_k + R_k)}^{-1}$$

(17)

where $H_k$ is the Jacobian matrix of the measurement function evaluated at $k$ given by:

$$H_k={\displaystyle \frac{\partial h\left({\mathsf{\eta }}_k\right)}{\partial {\mathsf{\eta }}_k^T}}{|}_{{\mathsf{\eta }}_k=\tilde{\mathrm{\eta }}(k/k)}$$

(18)

Subsequently, the Kalman filter refines the prediction to ${\tilde{\eta }}_{k/k-1}$ and adjusts the level of uncertainty, ${\tilde{P}}_{k/k-1}$, based on the current state (step k) after receiving measurements ${\zeta }_k$, yielding:

$${\widehat{\mathrm{\eta }}}_{k/k}={\tilde{\mathrm{\eta }}}_{k/k-1}+K_k({\zeta }_k-h({\tilde{\mathrm{\eta }}}_{k/k-1}\left)\right)$$

(19)

We may then update the covariance matrix to reflect the incorporation of sensor measurements. The covariance update equation is given by:

$${\widehat{P}}_{k/k}=(I-K_k{H}_k){\tilde{P}}_{k/k-1}$$

(20)

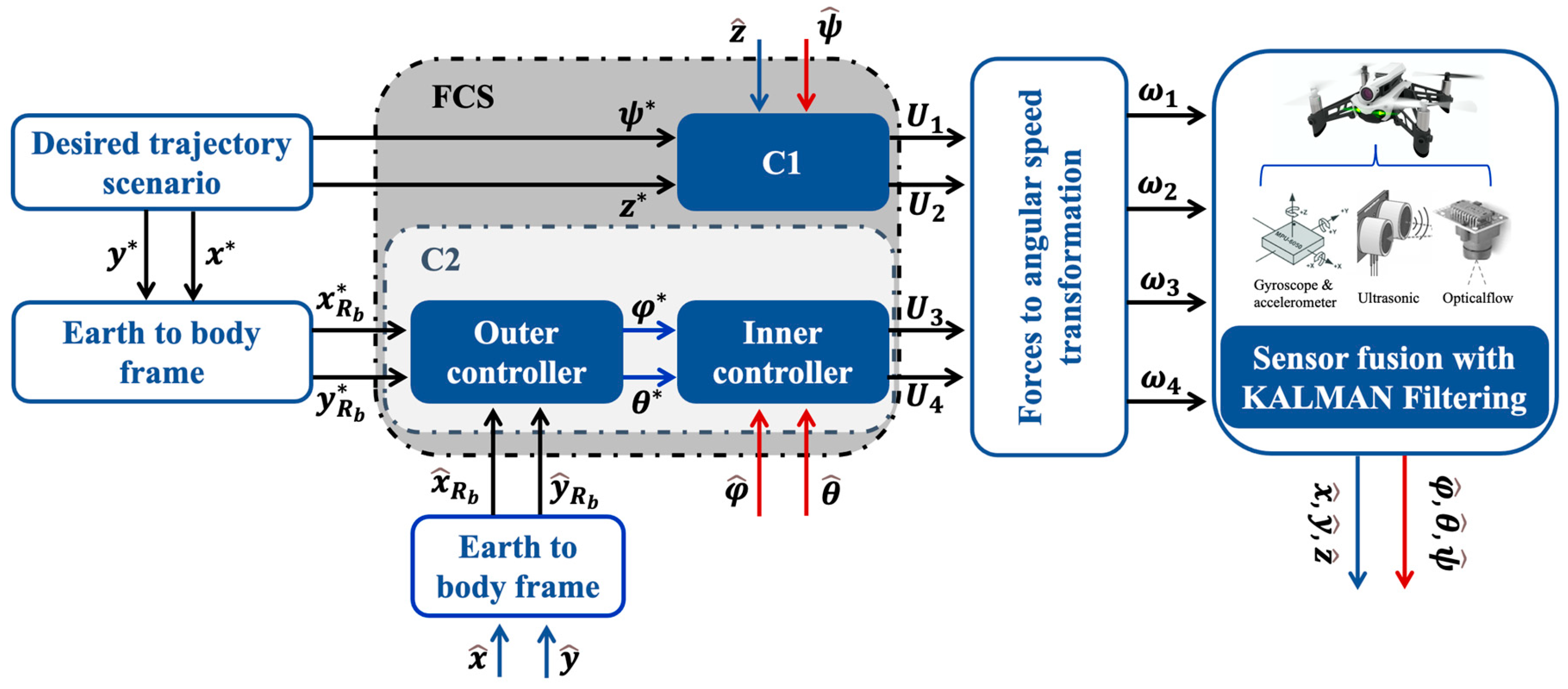
3.4. Control Strategy

The core of the control strategy is the flight control system, but it also relies on the Kalman filter estimator discussed above, along with transfer blocks for Earth-to-body frame transformation and force-to-angular speed transformation, as illustrated in the figure below.

The FCS structure in Figure 5 is based on regulator C1, managing altitude and yaw ($z$ and $\psi$), and regulator C2, controlling roll and pitch ($\phi$ and $\theta$) intrinsically $(x_{Rb}, y_{Rb}).$ Block C1 is a nonlinear backstepping approach, while C2 consists of two nested loops: an inner loop that uses backstepping and an outer loop with a PID controller. This modular control strategy allows flexibility towards different desired scenarios, ensuring optimal performance under varying flight conditions. The output signals from the sensor fusion stage are filtered with EKF. The Earth-to-body frame blocks facilitate coordinate transformations for calculation purposes. The forces-to-angular speed block transfers inputs $u_1, u_2, u_3,$ and $u_4$ to outputs ${\omega }_1, {\omega }_2, {\omega }_3$, and ${\omega }_4,$ which serve as command inputs for the different rotors.

Flight Control System:

C1 block

According to (4) and (7), the instantaneous mathematical model describing the system altitude and yaw angle can be expressed by the following nonlinear differential equations.

$$\left\{\begin{array}{c}\begin{array}{l}{\dot{z}}_1=z_2\\ {\dot{z}}_2={\displaystyle \frac{u_1}{m}}\cos \left({\theta }_1\right)\cos \left({\phi }_1\right)-{\displaystyle \frac{C_{dz}}{m}}{z}_2-g+w_k\end{array}\end{array}\right.$$

(21)

$$\left\{\begin{array}{c}\begin{array}{l}{\dot{\psi }}_1={\psi }_2\\ {\dot{\psi }}_2={\displaystyle \frac{u_4}{I_z}}-{\displaystyle \frac{C_{az}}{I_z}}{{\psi }_2}^2-{\displaystyle \frac{\left(I_y-I_x\right)}{I_z}}{\phi }_2{\theta }_2+w_k\end{array}\end{array}\right.$$

(22)

Let the tracking errors defined as:

$$\begin{array}{c}{e}_{z1}=z_1-{z_1}^{\mathrm{*}}; \\ e_{\psi 1}={\psi }_1-{{\psi }_1}^{\mathrm{*}} \end{array}$$

(23)

where

$e_{z1}$ describes altitude tracking error;

${z_1}^{\mathrm{*}}$ is the desired trajectory altitude specified by a reference model;

$e_{\psi 1}$ is the yaw tracking error;

${{\mathsf{\psi }}_1}^{\mathrm{*}}$ is the desired orientation specified by a reference model.

Step 1: Based on the Equation above, the derivative of the tracking errors therefore is

$$\begin{array}{l}{\dot{e}}_{z1}=z_2-{{\dot{z}}_1}^{\mathrm{*}}\\ {\dot{e}}_{\psi 1}={\psi }_2-{{\dot{\psi }}_1}^{\mathrm{*}}\end{array}$$

(24)

To ensure stability, the first Lyapunov candidate functions are given by:

$$\begin{array}{l}{V}_{1z}={\displaystyle \frac{1}{2}}{e_{z1}}^2\\ V_{1\psi }={\displaystyle \frac{1}{2}}{e_{\psi 1}}^2\end{array}$$

(25)

Its time derivative is given by:

$$\begin{array}{l}{\dot{V}}_{1\mathrm{z}} = {\mathrm{e}}_{\mathrm{z}1}{\dot{e}}_{z1} = {\mathrm{e}}_{\mathrm{z}1} \left(z_2 - {{\dot{z}}_1}^{\mathrm{*}}\right)\\ {\dot{V}}_{1\psi } = {\mathrm{e}}_{\psi 1}{\dot{e}}_{\psi 1} = {\mathrm{e}}_{\psi 1} \left({\psi }_2 - {{\dot{\psi }}_1}^{\mathrm{*}}\right)\end{array}$$

(26)

To ensure stability, the derivative of the Lyapunov functions must be negative. For that, the following new virtual control laws to stabilize the system and zero the tracking errors are suggested:

$$\begin{array}{l}{z_2}^{\mathrm{*}} = -C_{z1} e_{z1} + {{\dot{z}}_1}^{\mathrm{*}}\\ {{\psi }_2}^{\mathrm{*}} = -C_{\psi 1} e_{\psi 1} + {{\dot{\psi }}_1}^{\mathrm{*}}\end{array}$$

(27)

where $C_{z1}$ and $C_{\psi 1}$ are non-zero positive constants.

Now, considering Lyapunov derivative functions, we have:

$$\begin{array}{l}{\dot{V}}_{1\mathrm{z}} = -C_{z1} {e_{z1}}^2\\ {\dot{V}}_{1\psi } = -C_{\psi 1} {e_{\psi 1}}^2\end{array}$$

(28)

Step 2: The augmented second Lyapunov candidate functions are introduced as:

$$\begin{array}{l}{e}_{z2} = z_2 - {z_2}^{\mathrm{*}}\\ e_{\psi 2} = {\psi }_2 - {{\psi }_2}^{\mathrm{*}}\end{array}$$

(29)

Let us consider the following choice for the augmented Lyapunov function:

$$\begin{array}{l}{V}_{2z} = V_{1z} + {\displaystyle \frac{1}{2}}{e_{z1}}^2\\ V_{2\psi } = V_{1\psi } + {\displaystyle \frac{1}{2}}{e_{\psi 1}}^2\end{array}$$

(30)

Using the previous Equations, we obtain:

$$\begin{array}{l}{\dot{V}}_{2\mathrm{z}} = -C_{z1} {e_{z1}}^2 + e_{z2} \left({\dot{z}}_2 - {{\dot{z}}_2}^{\mathrm{*}}\right)\\ {\dot{V}}_{2\psi } = -C_{\psi 1} {e_{\psi 1}}^2 + e_{\psi 2} \left({\dot{\psi }}_2 - {{\dot{\psi }}_2}^{\mathrm{*}}\right)\end{array}$$

(31)

Combining (4), (7), and (31), we have:

$$\begin{array}{l}{\dot{V}}_{2z}=-C_{z1}{e_{z1}}^2+e_{z2}\left({\displaystyle \frac{u_1}{m}}\mathit{cos}\left({\theta }_1\right)\mathit{cos}\left({\phi }_1\right)-{\displaystyle \frac{C_{dz}}{m}}{z}_2-g+C_{z1}{\dot{e}}_{z1}-{{\ddot{z}}_1}^{*}\right)\\ {\dot{V}}_{2\psi }=-C_{\psi 1}{e_{\psi 1}}^2+e_{\psi 2}\left({\displaystyle \frac{u_4}{I_z}}-{\displaystyle \frac{C_{az}}{I_z}} {{\psi }_2}^2-{\displaystyle \frac{\left(I_y-I_x\right)}{I_z}}{\phi }_2{\theta }_2+C_{\psi 1}{\dot{e}}_{\psi 1}-{{\ddot{\psi }}_1}^{*}\right)\end{array}$$

(32)

Our objective is to make ${\dot{V}}_{2i}$ negative by the next choice with $i=\{z;\psi \}$:

$$\begin{array}{l}{\displaystyle \frac{{\mathrm{u}}_1}{\mathrm{m}}}\cos \left({\mathsf{\theta }}_1\right)\cos \left({\mathsf{\phi }}_1\right)-{\displaystyle \frac{{\mathrm{C}}_{\mathrm{d}\mathrm{z}}}{\mathrm{m}}}{\mathrm{z}}_2-\mathrm{g}+C_{z1}{\dot{e}}_{z1}-{{\ddot{z}}_1}^{\mathrm{*}}=-C_{z2}{e}_{z2}\\ {\displaystyle \frac{{\mathrm{u}}_4}{{\mathrm{I}}_{\mathrm{z}}}}-{\displaystyle \frac{{\mathrm{C}}_{\mathrm{a}\mathrm{z}}}{{\mathrm{I}}_{\mathrm{z}}}}{{\mathsf{\psi }}_2}^2-{\displaystyle \frac{\left({\mathrm{I}}_{\mathrm{y}}-{\mathrm{I}}_{\mathrm{x}}\right)}{{\mathrm{I}}_{\mathrm{z}}}}{\mathsf{\phi }}_2{\mathsf{\theta }}_2+C_{\psi 1}{\dot{e}}_{\psi 1}-{{\ddot{\psi }}_1}^{\mathrm{*}}=-C_{\psi 2}{e}_{\psi 2}\end{array}$$

(33)

where ${\mathrm{C}}_{\mathrm{i}2}$ is a positive regulator parameter. The combination of Equation (33) leads to the control laws, given by:

$$\begin{array}{l}{u}_1={\displaystyle \frac{m}{\cos \left({\mathsf{\theta }}_1\right)\cos \left({\mathsf{\phi }}_1\right)}}\left(-C_{z2}{e}_{z2}-{\displaystyle \frac{{\mathrm{C}}_{\mathrm{d}\mathrm{z}}}{\mathrm{m}}}{\mathrm{z}}_2+\mathrm{g}-C_{z1}{\dot{e}}_{z1}+{{\ddot{z}}_1}^{\mathrm{*}}\right)\\ u_4=I_z\left(-C_{\psi 2}{e}_{\psi 2}+{\displaystyle \frac{{\mathrm{C}}_{\mathrm{a}\mathrm{z}}}{{\mathrm{I}}_{\mathrm{z}}}}{{\mathsf{\psi }}_2}^2+{\displaystyle \frac{\left({\mathrm{I}}_{\mathrm{y}}-{\mathrm{I}}_{\mathrm{x}}\right)}{{\mathrm{I}}_{\mathrm{z}}}}{\mathsf{\phi }}_2{\mathsf{\theta }}_2-C_{\psi 1}{\dot{e}}_{\psi 1}+{{\ddot{\psi }}_1}^{\mathrm{*}}\right)\end{array}$$

(34)

C2 block

a.

Inner Loop: Nonlinear Backstepping Control

According to the instantaneous mathematical model describing the Parrot Mambo (1) and similarly to C1, let the tracking errors defined as:

$$\left\{\begin{array}{c} e_{\phi 1}={\phi }_1-{{\phi }_1}^{\mathrm{*}}; e_{\phi 2}={\phi }_2-{{\dot{\phi }}_1}^{\mathrm{*}}-C_{\phi 1} e_{\phi 1}\\ e_{\theta 1}={\theta }_1-{{\theta }_1}^{\mathrm{*}}; e_{\theta 2}={\theta }_2-{{\dot{\theta }}_1}^{\mathrm{*}}-C_{\theta 1} e_{\theta 1}\end{array}\right.$$

(35)

where:

$e_{\phi 1},e_{\theta 1},$ are, respectively, roll, and pitch tracking errors.

$e_{\phi 2}$, $e_{\theta 2}$, are the derivatives of the tacking errors introduced before.

${{\phi }_1}^{*},{{\theta }_1}^{*}$ are the desired orientation specified by a reference model.

Control inputs $u_2$ and $u_3,$ which are responsible for generating the roll and pitch controls, can be calculated as:

$$\begin{array}{c}{u}_2=I_x\left(-C_{\phi 2}{e}_{\phi 2}+{\displaystyle \frac{C_{ax}}{I_x}}{{\phi }_2}^2+{\displaystyle \frac{J_r{\Omega }_r}{I_x}}{\theta }_2+{\displaystyle \frac{\left(I_z-I_y\right)}{I_x}}{\theta }_2{\psi }_2-C_{\phi 1}{\dot{e}}_{\phi 1}+{{\ddot{\phi }}_1}^{\mathrm{*}}\right)\\ u_3=I_y\left(-C_{\theta 2}{e}_{\theta 2}+{\displaystyle \frac{C_{ay}}{I_y}}{{\theta }_2}^2-{\displaystyle \frac{J_r{\Omega }_r}{I_y}}{\phi }_2+{\displaystyle \frac{\left(I_x-I_z\right)}{I_y}}{\phi }_2{\psi }_2-C_{\theta 1}{\dot{e}}_{\theta 1}+{{\ddot{\theta }}_1}^{\mathrm{*}}\right)\end{array}$$

(36)

where $C_{\phi 1}$, $C_{\phi 2}$, $C_{\theta 1}$, and $C_{\theta 2}$ are positive regulator parameters.

b.

Outer loop: PID

A quadcopter can only achieve a translational movement in the $x$–$y$ axes through roll and pitch angle movement, which technically represents the coupling dynamics in the quadcopter. For position control, since the UAV is operating around hovering, the small-angle assumption ($\psi =0;\theta =0;\phi =0$) is applied:

$${\dot{x}}_2={\displaystyle \frac{u_1}{m}}[\cos \left(\psi \right){\theta }_d+\sin \left(\psi \right){\phi }_d]-{\displaystyle \frac{C_{dx}}{m}}{x}_2+w_k$$

(37)

$${\dot{y}}_2={\displaystyle \frac{u_1}{m}}[\sin \left(\psi \right){\theta }_d-\cos \left(\psi \right){\phi }_d]-{\displaystyle \frac{C_{dy}}{m}}{y}_2+w_k$$

(38)

Let the tracking errors of $x$ and $y$ be defined as:

$$e_x=x_1-{x_1}^{\mathrm{*}}; e_y=y_1-{y_1}^{\mathrm{*}}$$

(39)

Therefore, a virtual control signal is proposed to control the x and y positions using the nonlinear decoupling equations:

$${\phi }_d=u_x\mathit{sin}\left(\psi \right)-u_y\mathit{cos}\left(\psi \right)$$

(40)

$${\theta }_d=u_y\mathit{sin}\left(\psi \right)+u_x\mathit{cos}\left(\psi \right)$$

(41)

and can be implemented with:

$$u_x=K_{px}{e}_x+K_{ix}\int e_x+K_{dx}{\dot{e}}_x$$

(42)

$$u_y=K_{py}{e}_y+K_{iy}\int e_y+K_{dy}{\dot{e}}_y$$

(43)

The PID coefficients are determined empirically by tuning the proportional, integral and derivative gains $K_p,{ K}_i$ and $K_d$ based on the observed system responses. This process involved a trial-and-error approach, where the parameters were adjusted one at a time while monitoring the quadcopter’s behavior to achieve balance between performances.

4. Results

This section illustrates the experimental results of the regulator implemented using Matlab/Simulink for a Parrot Mambo UAV to execute the flight controller loops. Experimental validation in the case of indoor navigation, as shown in Figure 6, was performed, providing insights into the real-world performance. To evaluate the performance and accuracy of the Kalman filters employed in the control strategy, as well as the robustness of attitude and altitude control, various scenarios involving the operation of a fan were analyzed. This section presents three types of desired trajectories: step, orbit, and waypoint following. The step and waypoint responses highlight how the FCS addresses the nonlinearity of the control input in the presence of external bounded and unknown disturbance, while orbit demonstrates how the multi-loop controller manages repeated interactions in front of the fan.

4.1. Step Response

Figure 7 and Figure 8 depict the tracking performance under the first scenario of step trajectory. At $t=60 \mathrm{s}$ the fan was activated to inject wind toward the quadcopter. As illustrated in Figure 7, the x and y states converged to their setpoint references within approximately 10 s with no overshoot. The z-axis motion demonstrates that the designed technique could track the desired altitude, achieving a time response of 5 s. The wind applied at $t=60 \mathrm{s}$ was rejected by the FCS within 7 s with few oscillations of the drone, especially on the x and y axes. Euler angles in Figure 8 were maintained around the desired motion, and no oscillation phenomenon was detected. 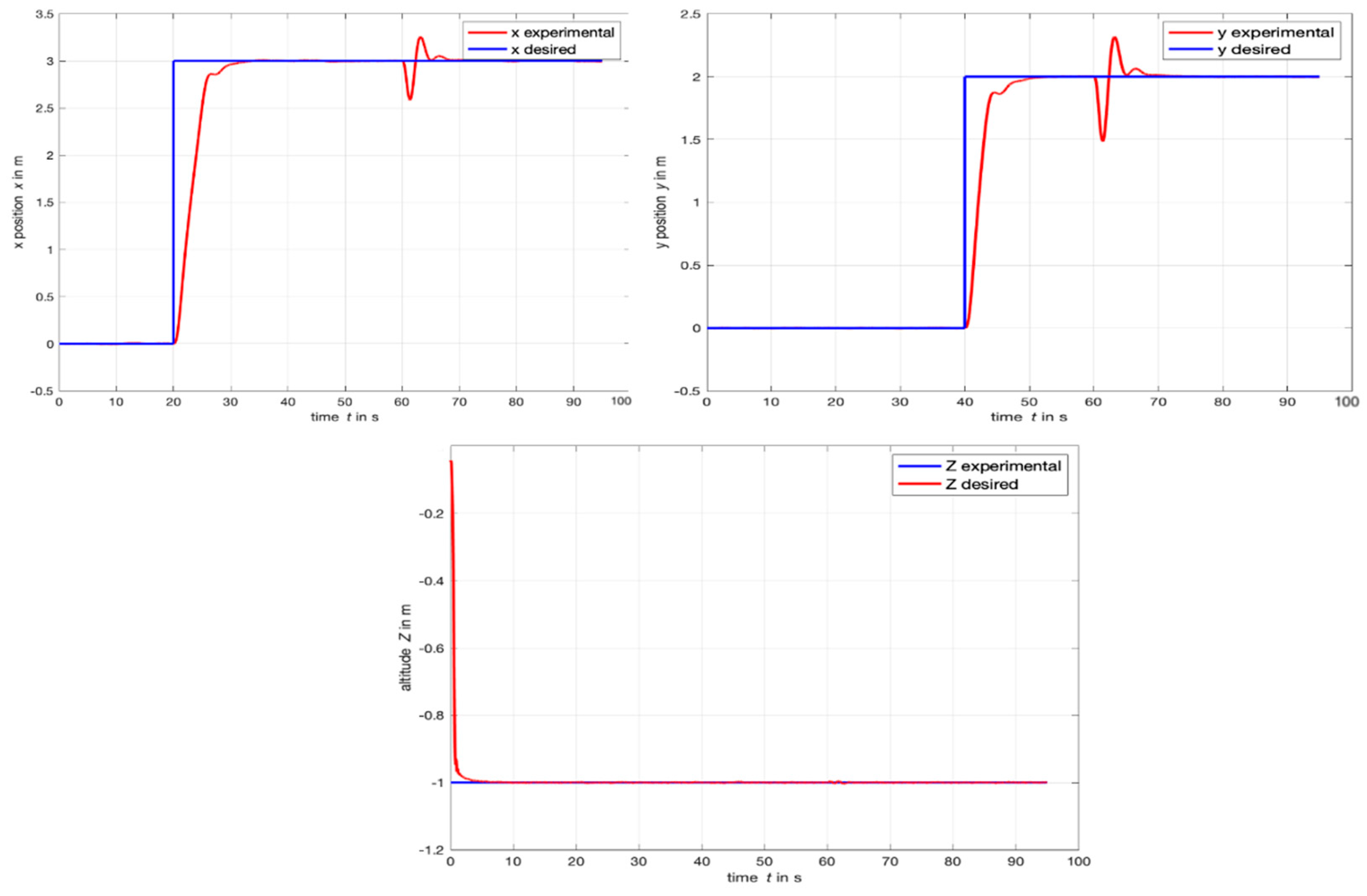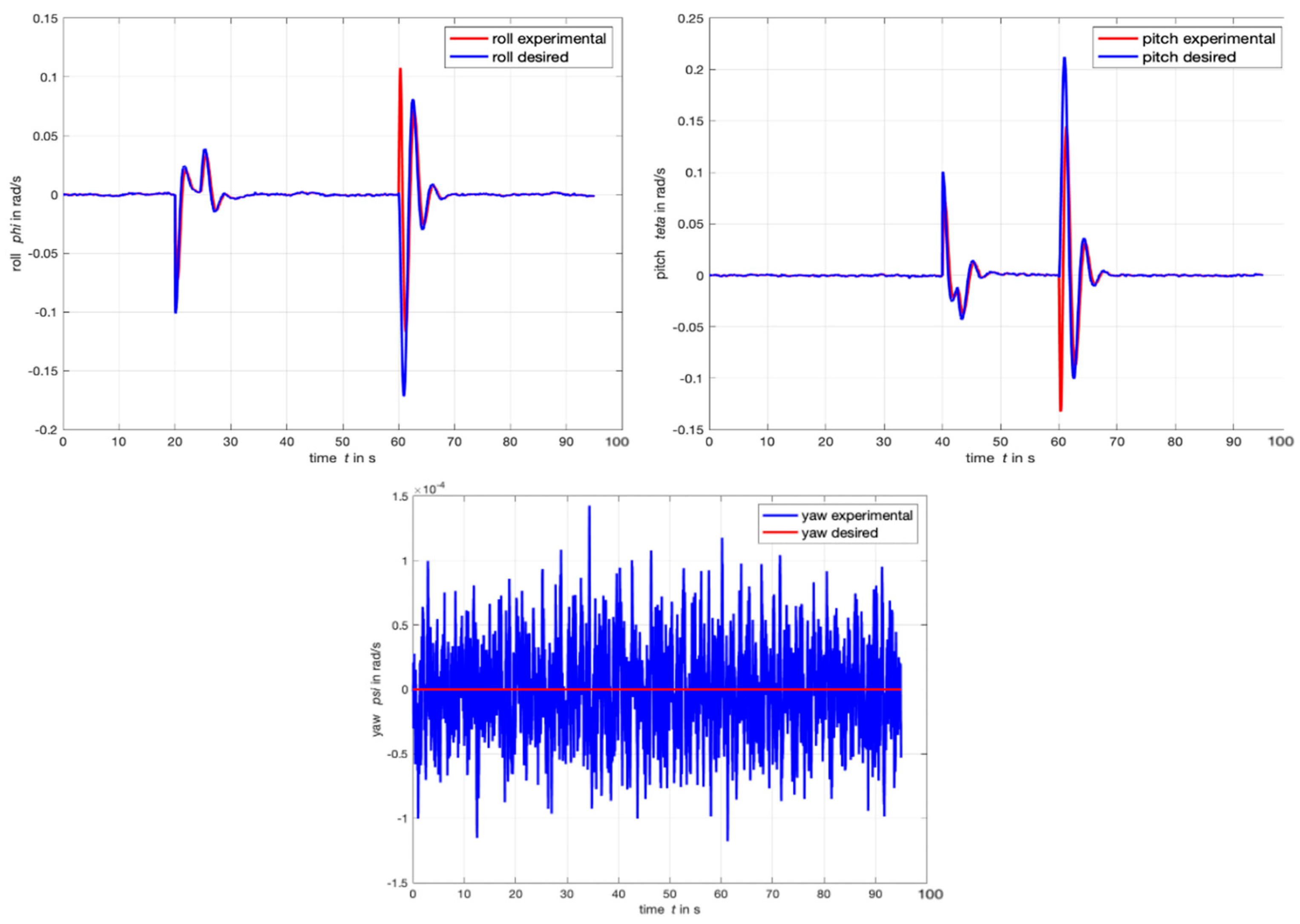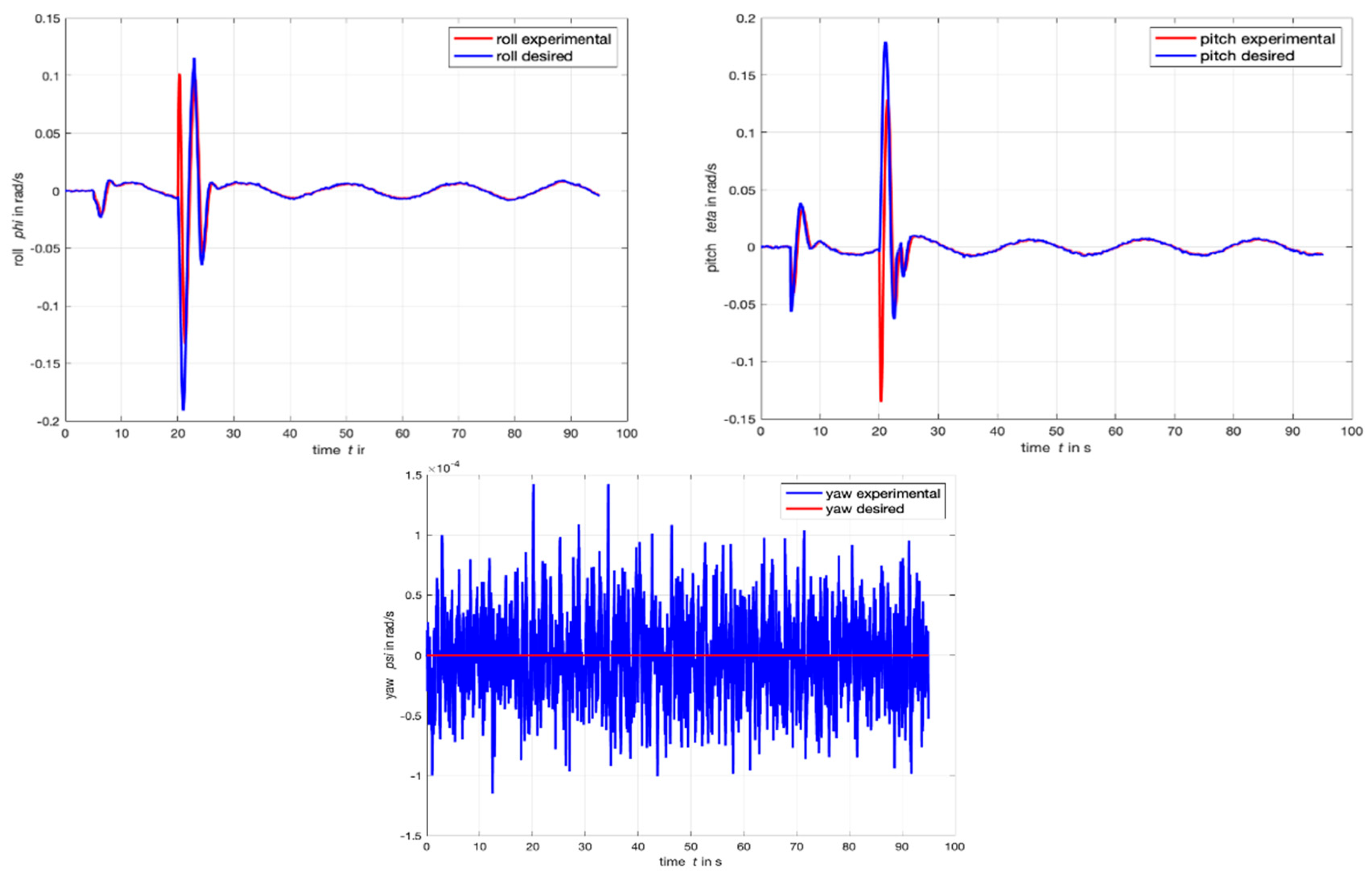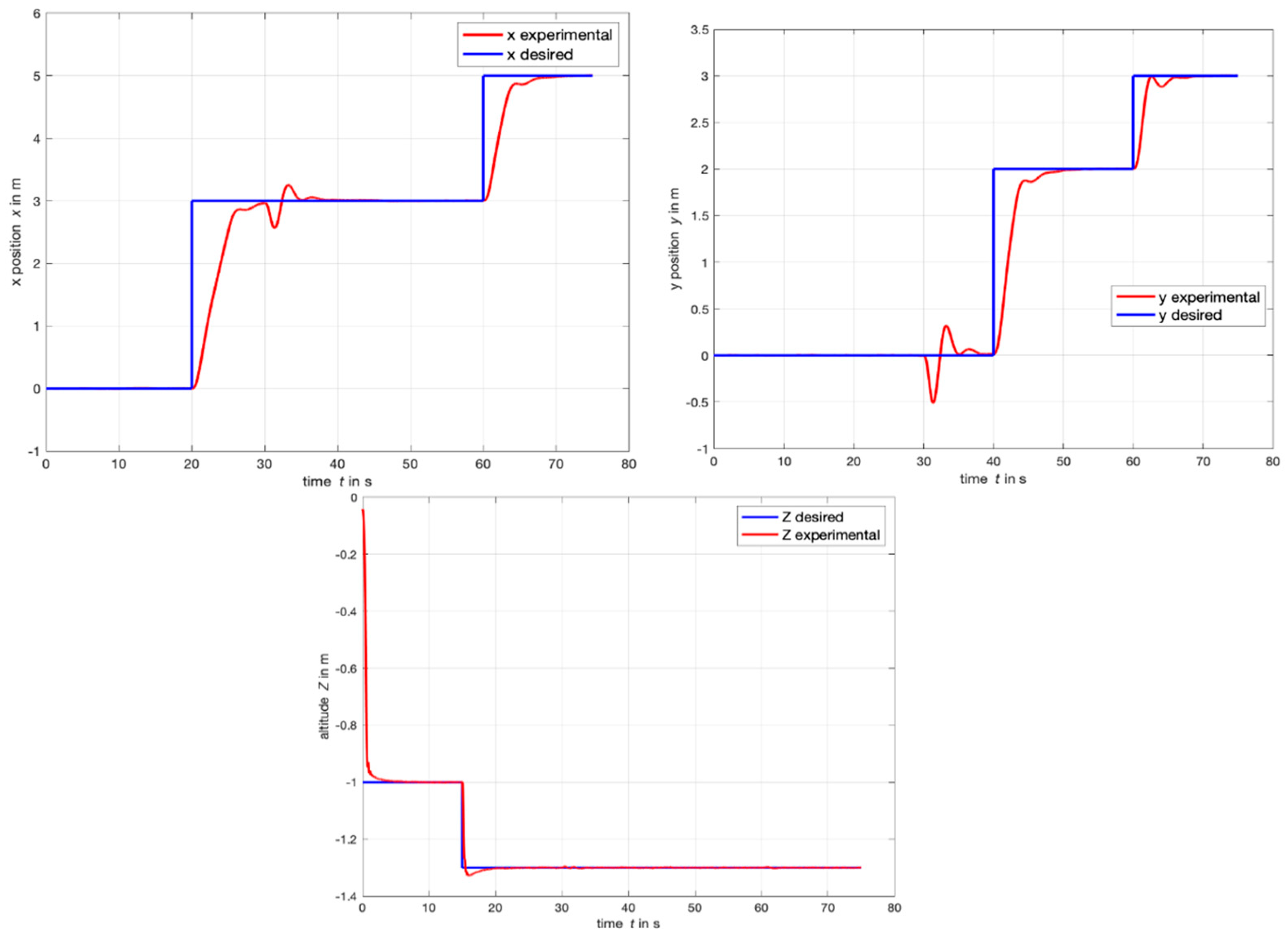Figure 9 illustrates the real-time 3D trajectory for a step response.

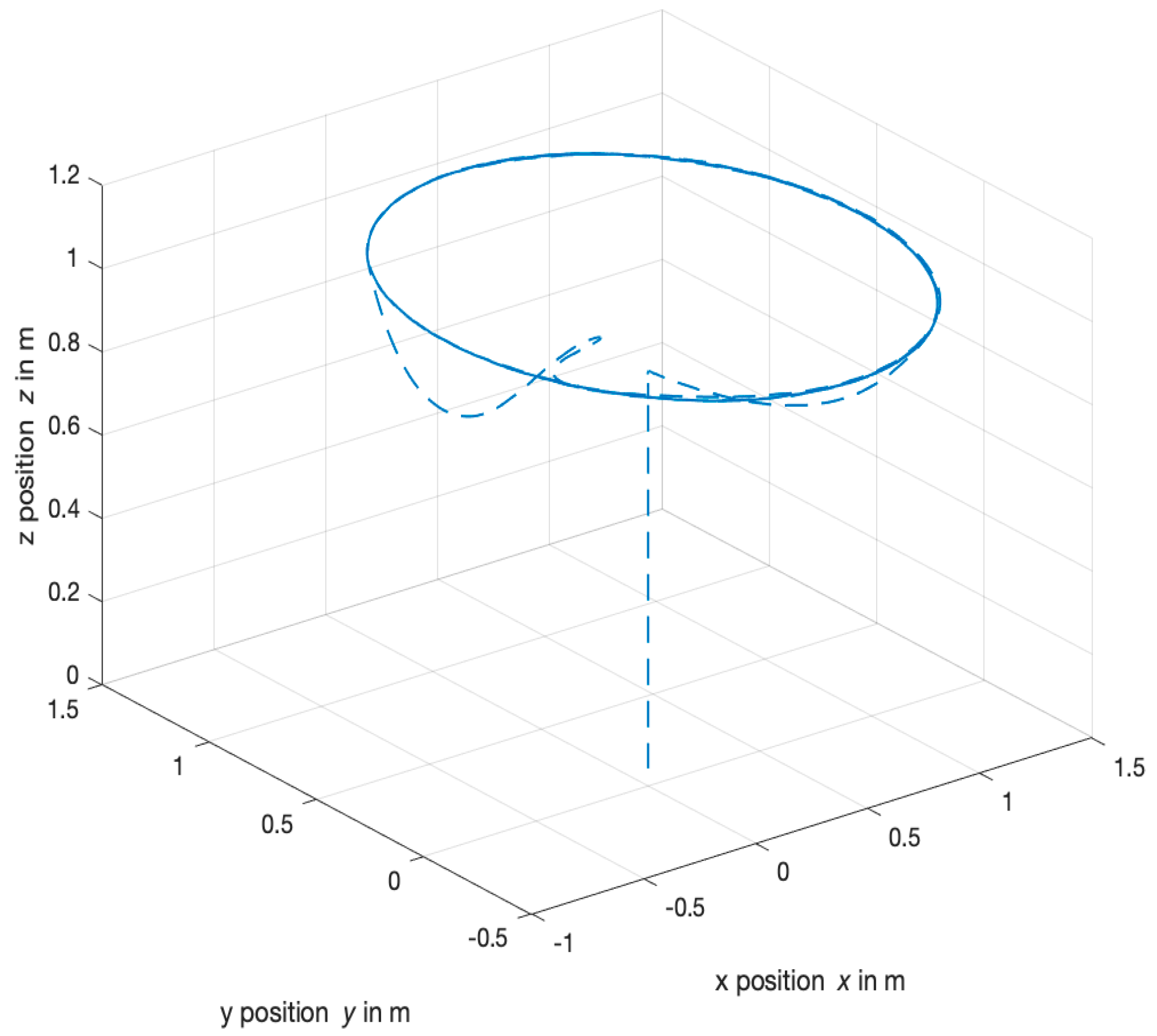
4.2. Orbit Response

Figure 10 and Figure 11 illustrate tracking performance under the second scenario, featuring an orbit motion. At $t=20 \mathrm{s}$, a disturbance was introduced. In Figure 10, the x and y states converged to their setpoints with minimal steady-state error. The FCS effectively rejected the wind disturbance introduced at $t=20 \mathrm{s}$, though significant fan airflow could cause divergence. The Euler angles in Figure 11 were kept near the desired trajectory. Figure 12 shows oscillations whenever the UAV was near the fan, yet the control structure managed the disturbance and tracked the reference. Figure 13 depicts the time response of control inputs $u_1$, $u_2$, $u_3$, and $u_4$, highlighting increased input demand to counteract wind effects when the fan is activated.

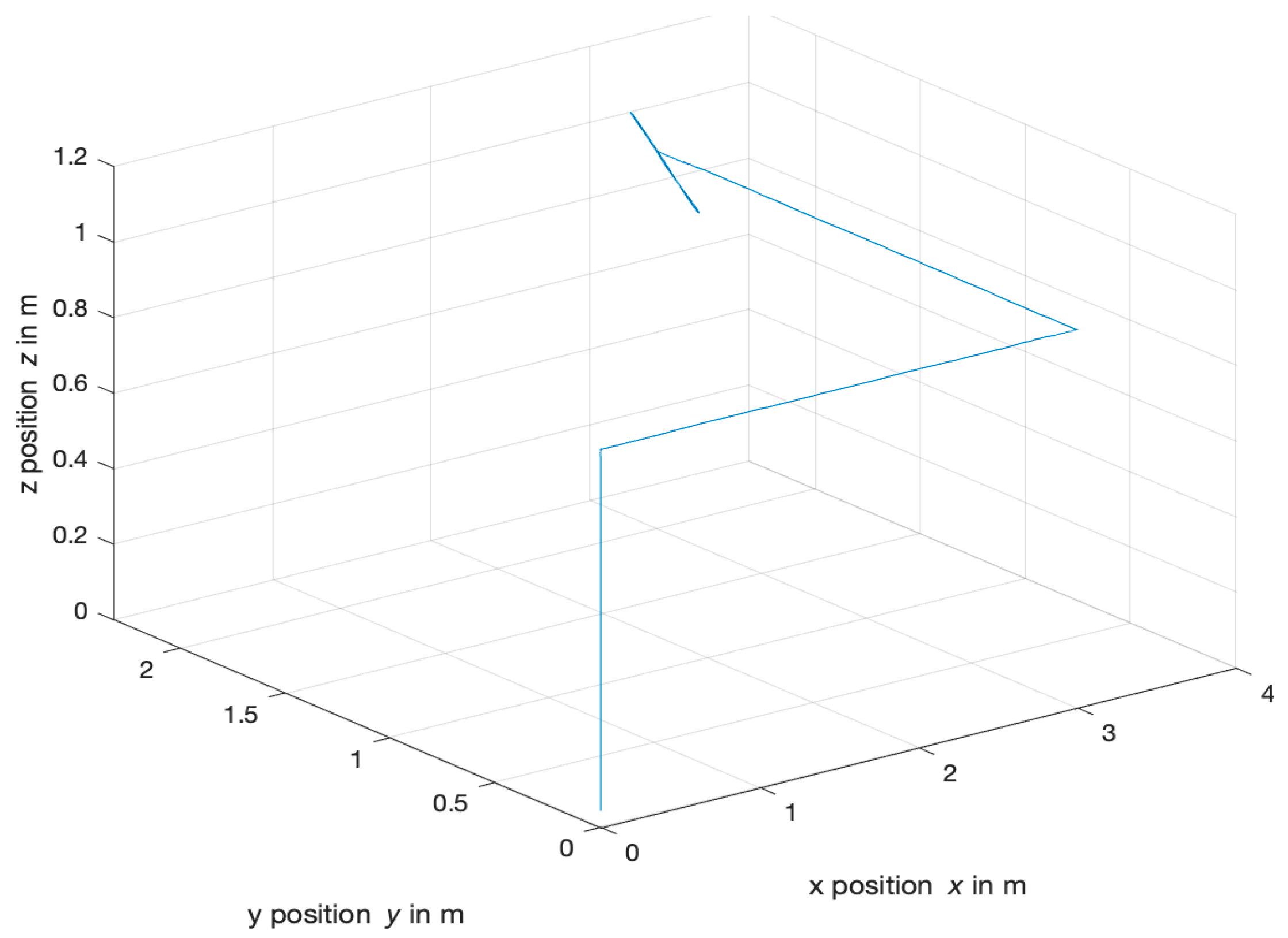
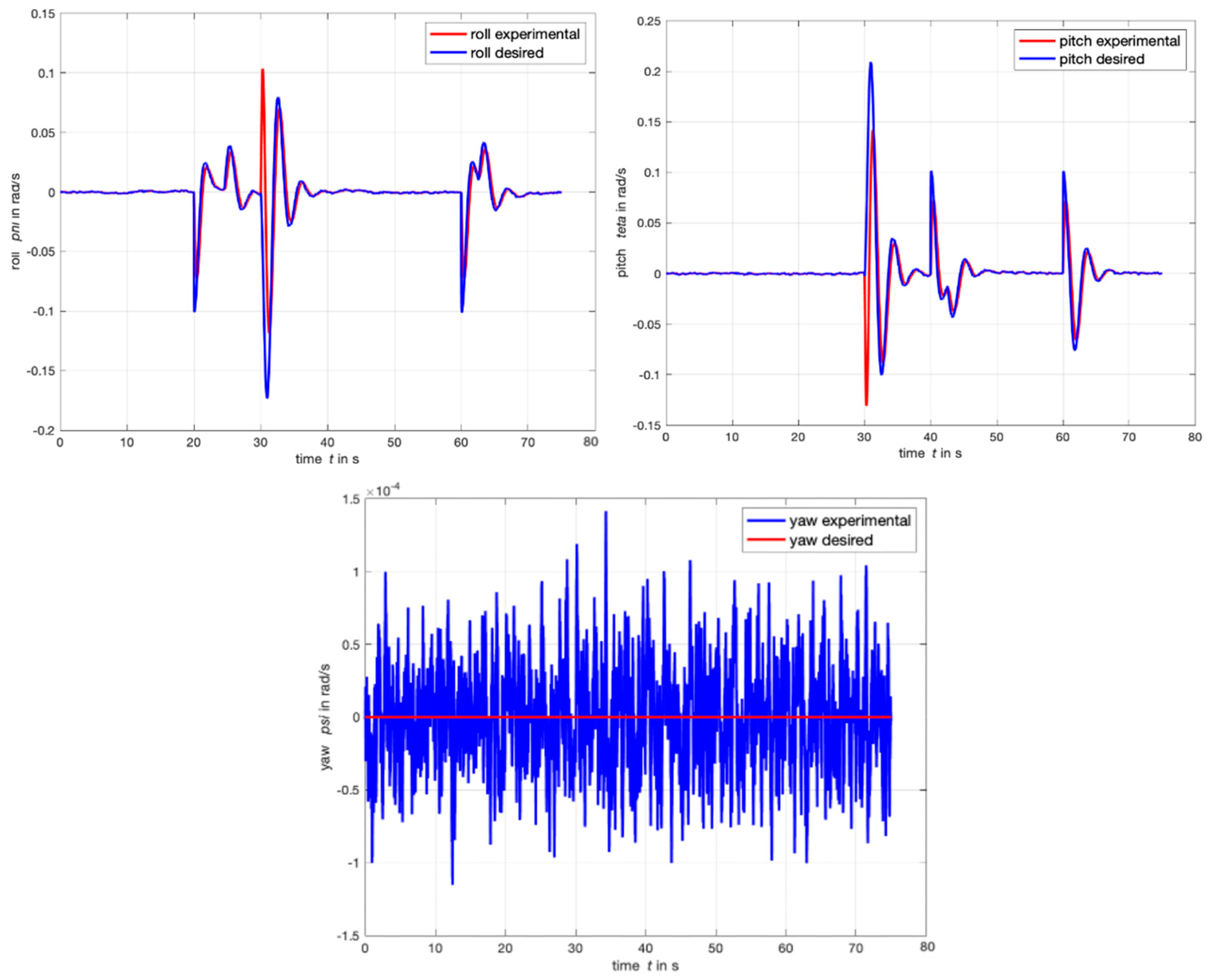
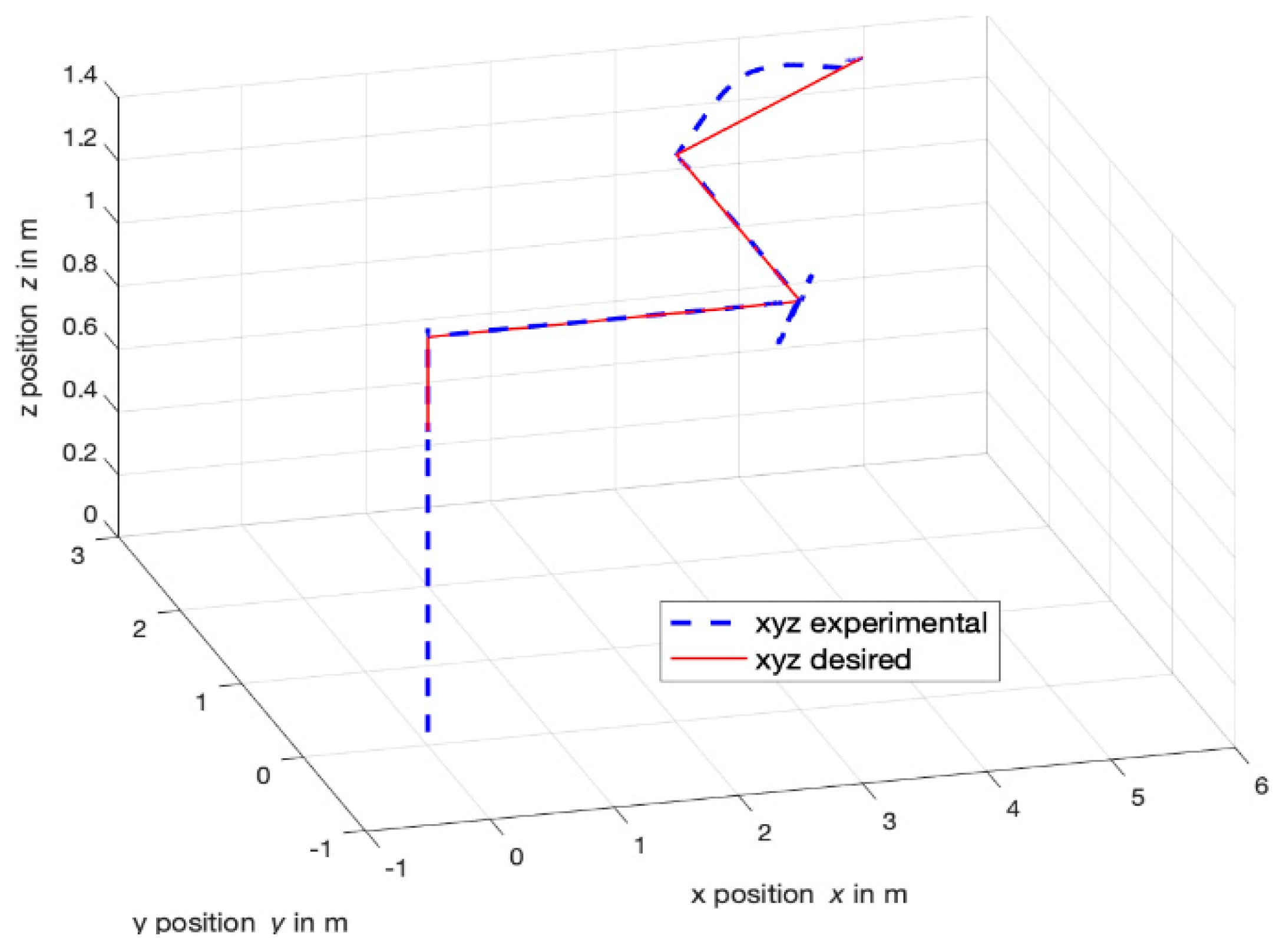
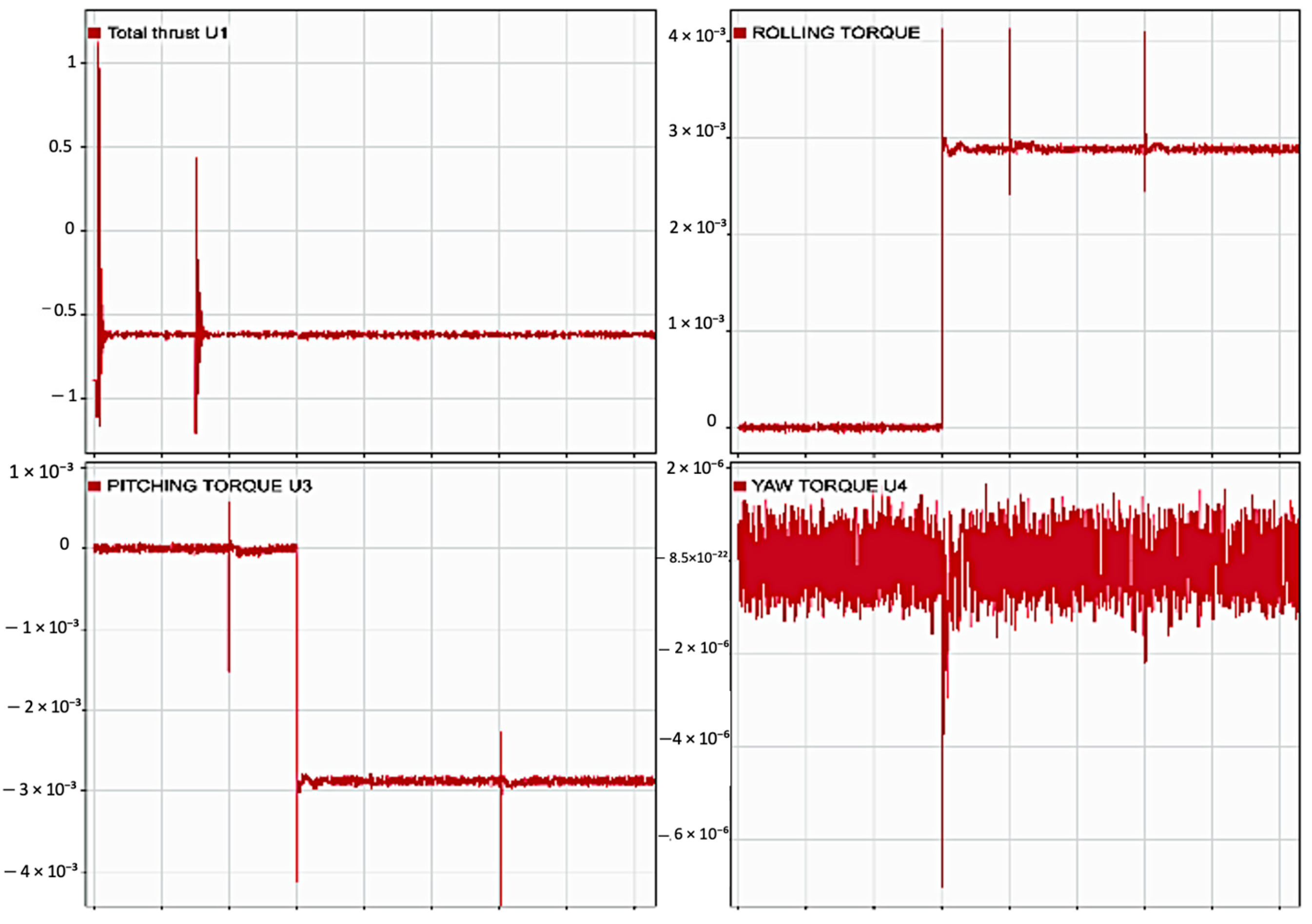
4.3. Waypoint Follower Response

Wind was added at $t=30 \mathrm{s}$ to a waypoint scenario quadrotor to further illustrate the resilience of the FCS. The responses are shown in Figure 14 and Figure 15. The state variables tracked their reference values. The strategy also attenuated the tracking errors with greater commanded inputs to the drone. Figure 16 illustrates the real-time 3D trajectory along with the desired trajectory for a step scenario. Figure 17 shows that the control inputs $u_1$, $u_2$, $u_3$, and $u_4$ converged without saturation.

5. Discussion

The proposed control strategy ensures stable trajectory tracking under indoor disturbances, as demonstrated by the experimental results. In fact, the findings overcome several limitations found in conventional control methods. Studies [17,18] highlight that, while classical PID controllers are simple and widely used, they are unable to handle the nonlinear dynamics of the quadrotor due to their sensitivity to parameter tuning. As a result, they suffer from significant overshoot and long settling times during takeoff and aggressive maneuvers.

The study in [19] took a different approach but reported a similar limitation. It identified the problem of chattering caused by the discontinuous switching function, which results in degraded performance. To address this, the authors in [20] proposed using a continuous saturation function; however, this introduced filtering delays and increased implementation complexity.

In contrast, the backstepping cascade structure with EKF delivers smooth control action, effectively handles system nonlinearities, and maintains tracking accuracy without inducing overshoot or requiring excessive tuning effort. These advantages are clearly confirmed by the experimental results presented above.

6. Conclusions

This paper proposes a robust complex structure with a cascaded backstepping nonlinear controller combined with EKF signal processing for a Parrot Mambo quadcopter. This structure ensures trajectory tracking control of an underactuated UAV, accounting for dynamic and external disturbances. Practical experiments demonstrate that the Parrot Mambo quadcopter operates effectively, handling horizontal wind disruptions while following a desired trajectory. Using the Lyapunov stability criterion, it is shown that the designed control system is successful, with low tracking errors, and capable of withstanding perturbations like air friction, aerodynamic effects, and unknown indoor wind sources. The FCS, EKF, and sensor fusion algorithm enhances quadcopter accuracy, autonomy, and robustness. The findings lay a foundation for optimizing quadcopter control systems. Future research will focus on expanding outdoor testing and exploring advanced control techniques, potentially integrating actuator failure, asymmetrical quadcopter structures and machine learning for increased autonomy and performance.