Clustering-Guided Automatic Generation of Algorithms for the Multidimensional Knapsack Problem

Abstract

We propose a hybrid framework that integrates instance clustering with Automatic Generation of Algorithms (AGA) to produce specialized algorithms for classes of Multidimensional Knapsack Problem (MKP) instances. This approach is highly relevant given the latest trends in AI, where Large Language Models (LLMs) are actively being used to automate and refine algorithm design through evolutionary frameworks. Our method utilizes a feature-based representation of 328 MKP instances and evaluates K-means, HDBSCAN, and random clustering to produce 11 clusters per method. For each cluster, a master optimization problem was solved using Genetic Programming, evolving algorithms encoded as syntax trees. Fitness was measured as relative error against known optima, a similar objective to those being tackled in LLM-driven optimization. Experimental and statistical analyses demonstrate that clustering-guided AGA significantly reduces average relative error and accelerates convergence compared with AGA trained on randomly grouped instances. K-means produced the most consistent cluster-specialization. Cross-cluster evaluation reveals a trade-off between specialization and generalization. The results demonstrate that clustering prior to AGA is a practical preprocessing step for designing automated algorithms in NP-hard combinatorial problems, paving the way for advanced methodologies that incorporate AI techniques.

1. Introduction

The MKP is a generalization of the classic knapsack problem, which is a fundamental problem in combinatorial optimization [1]. The classic knapsack problem considers a single knapsack with a fixed carrying capacity and a set of items, each with a specific weight and value. The goal is to select a combination of items that maximizes the total value without exceeding the knapsack’s weight capacity. In the MKP, the complexity increases as there are multiple constraints (or dimensions) instead of just one [2]. For example, instead of having just a weight limit, there might be several limits, such as volume, weight, and number of items. Each item has a value and consumes a certain amount of resources in each dimension. The objective of the MKP is to maximize the total value of the selected items while ensuring that none of the multiple constraints are violated. The inherent complexity of the MKP, stemming from its classification as an NP-hard problem, has catalyzed a substantial body of research in this domain [3].

The MKP has practical applications in various fields, including budgeting, project selection, resource allocation, scheduling, portfolio management, and military communications [4]. Additionally, the MKP is a combinatorial optimization problem that serves as a benchmark for evaluating the performance of various algorithms across different domains, thereby contributing to the development of new techniques for solving complex problems [5,6,7].

Consider n as the number of items and m as the dimensions each item must satisfy. Define $b_i$, $i\in M=\{1,2,\dots ,m\}$ as the capacity of the i-th dimension, and $r_{ij}$ as the quantity of the i-th dimension consumed by the j-th item. Let $p_j$ represents the profit yielded by the j-th item in the knapsack. Equations (1)–(3) formally delineate the MKP. It is permissible to assume, without any loss of generality, that $p_j>0$, $b_i>0$, and $0<r_{ij}<b_i$, as well as ${\sum }_{j=1}^n{r}_{ij}>b_i$, for all $j\in N$ and for each $i\in M$. Furthermore, any MKP instance with one or more $r_{ij}$ values equal to zero can be transformed into an equivalent instance with all positive values, ensuring identical sets of feasible solutions [2].

$$Maximize={\sum }_{j=1}^n{p}_j{x}_j$$

(1)

$$\begin{array}{c}subject:\hfill \\ {\sum }_{j=1}^n{r}_{ij}{x}_j\le b_i,\forall i\in M=\left\{1,2,\dots ,m\right\},\hfill \end{array}$$

(2)

$$x_j\in \left\{0,1\right\},\forall j\in N=\left\{1,2,\dots ,n\right\}$$

(3)

Numerous methods have been developed to address the MKP, encompassing exact methods, heuristic approaches, and metaheuristic techniques. Exact methods provide optimal solutions for small problem instances but face limitations with large and more complex problem instances [1,8,9,10]. In contrast, heuristic and metaheuristic methods provide high-quality approximate solutions for these large-scale problem instances, demonstrating their effectiveness and diversity [6,11,12,13,14,15,16]. The exploration of evolutionary computation approaches, particularly those that integrate hybridization strategies, has demonstrated significant potential in enhancing problem-solving efficacy [5,17,18,19,20]. Given these varied developments, hybrid algorithms for MKP offer a promising approach to synthesizing these diverse methodologies. However, the explored approaches so far consider manual combinations that can be extended by considering an automatic combination of algorithmic components. This strategy enables a systematic exploration and integration of various approaches, leveraging their strengths to develop robust, efficient, and practical algorithms for MKP, thereby overcoming the limitations of individual methodologies and making a significant advancement in addressing the problem’s complexity. This task can be explored by the AGA.

The AGA field is a promising and innovative approach to MKP, as it enables the automatic generation of efficient algorithms. Traditional approaches to MKP, such as heuristics, metaheuristics, or exact methods, often require significant manual effort and may not always produce optimal results. The AGA approach utilizes optimization techniques to generate algorithms tailored to a specific problem automatically. This approach has proven effective in generating algorithms for various combinatorial optimization problems [21,22]. Using this approach, it is possible to quickly and efficiently generate algorithms capable of identifying near-optimal solutions to the problem without requiring extensive manual effort [23].

A critical aspect to consider when customizing AGA for a specific optimization problem is the type of instances used to construct the algorithms automatically. The resulting algorithms might become specialized for the instances used in their construction. This topic leads us to the generation of specialized algorithms. Thus, algorithm specialization in the context of the MKP refers to the design of algorithmic solutions tailored to specific subsets of instances that share similar structural characteristics. This approach contrasts with general-purpose methods, which aim to solve any instance of the problem using a single algorithm, without considering the particularities of the search space. Previous studies have shown that adapting heuristics and metaheuristics to the specific features of instances can significantly improve solution quality [3,5]. Instance clustering enables the identification of homogeneous groups, within which specialized algorithms can be generated to exploit recurring structures [24]. This algorithm specialization approach has been explored in recent studies that integrate evolutionary techniques to design more accurate and efficient solutions for MKP subsets [25].

Although the AGA performs well in several optimization problems [25], it remains a relatively new field with promising applications. The knapsack family of problems is inherently complex, and traditional algorithms have provided reasonable solutions. Applying the AGA to the MKP offers potential for improved performance due to this complexity. The MKP also has a rich history of optimization research, resulting in specialized algorithms for specific problem types [2,17]. However, as the size and complexity of the problem instances grow, some algorithms can become computationally expensive and time-consuming, making AGA an attractive alternative. Therefore, the AGA for discovering new efficient algorithms for the MKP remains an open field, considering that the MKP presents some unique challenges that may make it more difficult to apply this approach effectively. In this context, specializing automatically generated algorithms for structurally similar subsets of instances identified through clustering techniques is proposed as a promising strategy to enhance the efficiency and quality of solutions in highly heterogeneous scenarios. This manuscript introduces a hybrid framework that integrates instance clustering with AGA to produce algorithms specialized for structurally coherent subsets of MKP instances. We cast algorithm synthesis as a meta-optimization, the Master Problem (MP), whose objective is to minimize the relative error of generated algorithms across a target instance set. Algorithms are represented as syntax trees and evolved by genetic programming, which constructively combines heuristic primitives through reproduction, selection, crossover, and mutation. Crucially, we employ clustering methods (K-means, HDBSCAN, and random grouping) as a preprocessing step, enabling AGA to learn cluster-specific strategies. We then evaluate the resulting algorithms on held-out instances and utilize statistical tests to quantify the improvements.

An emerging trend in artificial intelligence (AI) is the application of LLMs to transform combinatorial optimization. Their advanced capabilities in understanding natural language and generating complex code have enabled innovative approaches in AGA [26], including the development of heuristics for complex problems such as robust optimization [27]. In this paradigm, LLMs play a pivotal role in algorithm design, reducing reliance on manual expert knowledge. For example, the LLaMEA framework integrates LLMs within an evolutionary algorithm to generate and refine metaheuristics, surpassing state-of-the-art optimization methods [26]. Similarly, the evolution of algorithms using LLMs simplified heuristic design for problems such as the traveling salesman problem [28]. For multi-objective combinatorial optimization, the LLM-NSGA method utilizes LLMs as evolutionary optimizers, performing core operations such as selection, crossover, and mutation, and has been successfully tested in surgery scheduling [29]. Additionally, LLMs excel at data-driven knowledge discovery, enabling dynamic parameter adjustment based on instance characteristics, as demonstrated in large-scale routing optimization [30]. These advancements signify a paradigm shift in algorithm engineering, where LLMs facilitate novel, highly scalable approaches to designing specialized algorithms for NP-hard problems, such as the MKP.

The remainder of the manuscript is organized as follows. Section 2 reviews the relevant literature. Section 3 describes the methodology used to develop the proposed MKP algorithms, including instance characterization, clustering procedures, the Master Problem formulation, algorithm representation, and parameter tuning. Section 4 details the experimental protocol and presents numerical comparisons, along with the statistical analyses used to validate the performance. Finally, Section 5 draws the main conclusions, discusses limitations, and outlines directions for future work.

2. Related Works

Although the MKP is known for its NP-hard nature, numerous endeavors have been made to solve it using exact methods. James and Nakagawa [31] explored enumeration methods for solving MKP sub-problems. Mansini and Speranza [32] presented an exact algorithm for MKP that also focuses on subproblems, indicating a shared emphasis on decomposing the problem to manage complexity and improve solution accuracy. Boussier [33] enhanced the MKP solving approach with a multi-level search that integrates sequencing and branch-and-cut, a specific advancement within the broader range of evolving MKP solutions and methodologies detailed by Cacchiani [3] in their comprehensive review. Derpich [24] contributed to the recent trends in exact methods for solving the MKP by introducing complexity indices, offering new insights for algorithm development. At the same time, Dokka [34] refined the surrogate relaxation method, enhancing solution accuracy and efficiency. Concurrently, Mancini [35] advanced these trends with a novel decomposition approach for MKP variants with family-split penalties, addressing a problem of industrial importance. Collectively, these studies represent significant progress in exact methods for addressing MKP’s complex challenges. However, despite advances in modern computing power, these works demonstrate that solving larger MKP instances to optimality remains a significant challenge [7].

Recent progress in metaheuristics for the MKP has yielded several innovative approaches, reflecting the diversity and effectiveness in this domain. Martins and Ribas [13] enhanced solution diversity and operational efficiency with a randomized heuristic repair method for the MKP. Shahbandegan and Naderi [36] introduced the Multiswarm Binary Butterfly Optimization Algorithm, which utilizes parallel search strategies to achieve more efficient attainment of optimal values. Lai [37] implemented a diversity-preserving quantum particle swarm optimization algorithm, achieving results competitive with those of leading algorithms. Zhang [16] enhanced the global search capability in MKP with an adaptive human learning optimization algorithm featuring reasoning learning, outperforming other metaheuristics. In line with these advancements, Fidanova [38] developed a hybrid Ant Colony Optimization (ACO) algorithm enhanced with a local search phase. This combination allowed the algorithm to escape local optima more efficiently by making minor binary adjustments to candidate solutions, achieving better results than classical ACO on most tested instances with minimal additional computation.

Other metaheuristics have also demonstrated their ability to find near-optimal MKP solutions. Shahbandegan and Naderi [36] extended the Butterfly Optimization Algorithm to binary domains, tailoring it specifically for the MKP. Their use of V-shaped transfer functions and a pseudo-utility initializer helped the algorithm achieve competitive results on challenging benchmark sets. A recent contribution introduced BISCA, an improved sine-cosine algorithm enhanced with differential evolution, as described by Gupta [39,40]. By alternating between exploitation and exploration based on the evolutionary stage of each solution, BISCA outperformed other metaheuristics across a wide range of MKP instances.

Hybrid MIP techniques with metaheuristics have also appeared as relevant approaches to finding near-optimal MKP solutions. Jovanovic and Voß [41,42] proposed a novel strategy using Fixed Set Search. This approach builds fixed sets from components of high-quality solutions and then applies integer programming to explore those promising regions more deeply. Their results demonstrated that this hybrid method is both powerful and relatively easy to implement.

These methods illustrate a growing trend toward hybridization and structure-guided metaheuristics that balance exploration and exploitation effectively in MKP search spaces. In general, the development of metaheuristic approaches for MKP occurs with each new method advancing independently rather than in integration. By exploring the amalgamation of these distinct approaches, there may be an opportunity to leverage the unique strengths of each method, potentially leading to even more efficient and robust solutions for the MKP.

Evolutionary computation approaches continue to yield promising results for the MKP, particularly when combined with other methods. Lai [43] presented an effective two-phase tabu-evolutionary algorithm for the MKP, integrating solution-based tabu search methods into an evolutionary framework and achieving significant improvements on benchmark instances. Ferjani and Liouane [44] introduced a logic gate-based evolutionary algorithm for MKP, which utilizes various logic gates to enhance diversity in the search space and global search abilities. Zhang [20] proposed an evolutionary computation approach based on immune operation for constraint optimization problems, demonstrating effective performance improvement for MKP. Laabadi [19] proposed an improved sexual genetic algorithm for solving the MKP, proposing new selection and crossover operators that showed competitive results on benchmark instances. Duenas [45] applied an evolutionary algorithm using a three-dimensional binary-coded chromosome for resource allocation in a construction equipment manufacturer setting, with satisfactory results from the company’s perspective. Baroni and Varejão [46] applied a shuffled complex evolution algorithm to the MKP, demonstrating its effectiveness in finding near-optimal solutions with minimal processing time.

The exploration of the MKP has seen numerous exact and heuristic methods advancing in their unique trajectories. While exact methods focus on subproblem decomposition and multi-level search strategies, recent metaheuristics have independently evolved, showcasing diversity and effectiveness in solving MKP. In various studies, hybridization strategies have been found to be more effective than isolated methods. By leveraging the AGA, it is possible to combine these distinct approaches, harnessing their strengths [47]. This integration, grounded in the formulation of the MP, enables the generation of specialized algorithms for structurally distinct clusters of MKP instances. By minimizing the relative error within each group, this approach overcomes the limitations of general-purpose methods. The combination of automatic algorithm generation and algorithmic specialization yields more efficient, accurate, and adaptable solutions that are better suited to the problem’s inherent diversity.

3. Materials and Methods

To automate the generation of algorithms, we define the Master Problem (MP), characterized by an objective function and a set of constraints. This objective function optimizes the performance of an algorithm in processing a specific set of MKP instances. Performance quantifies the average error incurred by the algorithm while solving these instances, where error refers to the relative discrepancy between the algorithm-derived solution for an instance and the optimal solution for the same instance. Considering a feasible MKP solution $x$, a particular algorithm $a$, and a specific set of instances $i$ used in algorithm generation, Equation (3) provides the formulation of this MP. The search for an optimal algorithm navigates through three different domains: the feasible MKP domain ($\Omega$), the algorithmic domain (${\Omega }_A$), and the domain of problem instances (${\Omega }_I$). In this context, we define an optimization problem (4) that simultaneously traverses these three domains to identify the most effective algorithm.

$$\mathsf{\Pi }:Minimize F\left(x, a, i\right) subject to:x \in \Omega , a \in {\Omega }_A,i \in {\Omega }_I$$

(4)

Genetic Programming (GP) is well-suited to solve the MP because it naturally encodes algorithms as syntax trees and, as an evolutionary optimizer, it can explore a vast space of candidate algorithmic structures [25]. GP evolves these trees using selection, mutation, and recombination operators. GP can efficiently search for high-performing solutions to complex problems such as the MKP by selecting the best-performing algorithms and recombining them to create new variations. GP also has the advantage of being a flexible approach that can be adapted to various optimization problems.

A syntactic tree, where internal nodes represent functions and leaf nodes represent terminals, is considered an algorithm. In the context of the MKP, these functions serve as high-level instructions that determine how terminals combine to construct feasible solutions. Algorithm generation occurs by solving the MP, which aims to minimize the relative error of an algorithm when approximating the optimal MKP solution. The population evolves from an initial set of algorithms by applying genetic operators. Over successive generations, new algorithms are created and refined by solving sets of MKP instances with increasing efficiency. The algorithm generation process consists of five main steps:

• Step 3.1: Define a solution container that the generated algorithms operate on.
• Step 3.2: Define the set of functions and terminals that comprise the algorithms.
• Step 3.3: Define a fitness function to guide the search process toward the best algorithms.
• Step 3.4: Select sets of MKP instances to evaluate the construction of the algorithms and the algorithms produced.
• Step 3.5: Determine the method for producing the algorithms and the values of the involved parameters.

Let’s describe such steps in more detail.

Solution container definition. The solution container comprises various data structures (lists) tailored to the problem. They consider two classes: variable lists and fixed lists. Two variable lists keep the information on the items contained in the knapsack:

• Out of Knapsack List (OKL): This list stores IDs of items for a given solution. Initially, the list contains all problem instance items.
• In the Knapsack List (IKL): This list stores the IDs of items in the knapsack

The fixed lists organize the instance’s IDs of the items based on a criterion derived from well-known MKP heuristics. Seven lists are considered:

• Profit List (PL): This list contains all the items of the MKP instance arranged in decreasing order of pj.
• Weight List (WL): This list contains all the items arranged in decreasing order of ${\sum }_{i=1}^m{r}_{ij}$, for each item j.
• Normalized Bid-Price List (NBPL): This enumeration organizes all items in descending order based on the value derived from Equation (5), as outlined by Sandholm and Suri [48]. It calculates the profit of each item j, adjusted by the aggregate units consumed by the item across all dimensions, thereby yielding an average benefit per unit. This approach ensures a uniform treatment of items, irrespective of the varying scarcity of capacities in each dimension.

$$NB{P}_j={\displaystyle \frac{p_j}{{\sum }_{i=1}^m{r}_{ij}}}$$

(5)

• Scaled Normalized Bid-Price List (SNBPL): The list contains all the items arranged in decreasing order according to Equation (6) [49].

$$E_j={\displaystyle \frac{p_j}{{\sum }_{i=1}^m{\mu }_i{r}_{ij}}}$$

(6)

In contrast with Equation (5), Equation (6) considers values with relevance ${\mu }_i\ge 0$, which measures the scarcity of capacities. The underlying concept is to choose a high value for ${\mu }_i$ for the dimensions with low $c_i$ capacity to penalize the consumption of this resource. For this list, we assume that ${\mu }_i=1/c_i$. Like Pfeiffer and Rothlauf [50], this assumption is referred to as “scaling” and is represented by Equation (7).

$$SNB{P}_j={\displaystyle \frac{p_j}{{\sum }_{i=1}^m\frac{r_{ij}}{c_i}}}$$

(7)

• Generalized Density List (GDL): The list contains the items arranged in decreasing order of the density value ${\delta }_j$. This density originates from the heuristic of Dantzig [51] for the knapsack problem, which involves first inserting the items with the highest benefit/weight ratio. To generalize this heuristic for the MKP, Cotta and Troya [52] propose calculating the object’s density in each dimension, considering only the lowest value for each object, as shown in Equation (8).

$${\delta }_j=min\left({\displaystyle \frac{c_i{p}_j}{w_{ij}}}\right)={\displaystyle \frac{p_j}{max\left(\frac{w_{ij}}{c_i}\right)}}$$

(8)

• Senju and Toyoda List (STL): The list contains items arranged in decreasing order of $E_j$ (Equation (6)) but considers the relative contributions of the constraints proposed by Senju and Toyoda [14], with a relevance value ${\mu }_i={\sum }_{l=1}^n{r}_{il}-c_i$, to arrange the items, as shown in Equation (9).

$$E_j={\displaystyle \frac{p_j}{{\sum }_{i=1}^m{r}_{ij}\left({\sum }_{l=1}^n{r}_{il}-c_i\right)}}$$

(9)

• Fréville and Plateau List (FPL): This list contains items arranged in decreasing order of $E_j$, considering the relative scarcity of each constraint as presented in Equation (10) to be a relevant value, as proposed by Fréville and Plateau [53].

$$u_i={\displaystyle \frac{{\sum }_{j=1}^n{r}_{ij}-c_i}{{\sum }_{j=1}^n{r}_{ij}}}$$

(10)

3.1. Definition of Functions and Terminals

In the second step, we establish functions and terminals that act as fundamental operations on the container data structures. The precise definition of these elements is crucial for creating algorithms that can effectively transfer items between IKL and OKL while optimizing total profit. We devise terminals based on existing construction heuristics for the MKP and propose additional functions that facilitate the generation of diverse combinations of these terminals. The functions and terminals must comply with the closure and sufficiency properties [54]. Therefore, every function and every terminal must have known and bounded return values. Each function and terminal has a True or False return value to comply with the closure property. Each terminal feasibly adds or removes an item from the knapsack to comply with the sufficiency property. Therefore, the item insertion terminals are sufficient to comply with this property.

The functions are high-order algorithmic instructions. Most programming languages use them as control structures, such as the logical operators Not, Or, And, and Equal, the conditional statement If_Then_Else, and the loop Do_While. Seven functions, described below, were implemented:

• If_Then (A1, A2): This function executes argument A1, and if it returns True, it executes argument A2. The function’s return value is equal to the return value of A1.
• If_Then_Else (A1, A2, A3): This function executes argument A1, and if it returns True, it executes A2. Otherwise, it executes A3. The function always returns True.
• Not (A1): This function executes argument A1 and returns the negation of the value.
• And (A1, A2): This function executes argument A1, and if it returns True, it executes argument A2. If the executions of both arguments return True, the function returns True; in any other case, the function returns False.
• Or (A1, A2): This function executes argument A1, and if it returns False, it executes argument A2. If the executions of both arguments return False, the function also returns False. Otherwise, the function returns True.
• Equal (A1, A2): This function executes arguments A1 and A2 in that order. If both executions return equal values, the function returns True. Otherwise, it returns False.
• Do_While (A1, A2): First, this function executes argument A1. As long as the return of the execution of A1 is True, argument A2 is executed. The cycle is executed a maximum number of times, equal to the number of items in the instance; otherwise, it stops when it completes a maximum number of iterations without changes in the benefit and total weight of the knapsack.

The terminals add or remove items from the knapsack according to a specific criterion; thus, each terminal is a heuristic capable of modifying the data structure. The terminals should search only in the space of feasible solutions, implying that none could generate an unfeasible MKP solution; consequently, all the algorithms produced construct only feasible MKP solutions. A total of 13 terminals were implemented:

• Add_Max_Profit: This terminal places the first item in PL that is in OKL; that item is removed from OKL and inserted in IKL.
• Add_Min_Weight: This terminal locates the last item in WL that is in OKL. If an item is found and fits in the knapsack, it is removed from OKL and inserted into IKL.
• Add_Max_Normalized: This terminal locates the first item in NBPL that is in OKL. If an item is found and fits in the knapsack, it is removed from OKL and inserted into IKL.
• Add_Max_Scaled: This terminal selects the first item in SNBPL and in OKL. If an item is found and fits in the knapsack, it is removed from OKL and inserted into IKL.
• Add_Max_Generalized: This terminal locates the first item in GDL that is in OKL. If an item is found and fits in the knapsack, it is removed from OKL and inserted into IKL.
• Add_Max_Senju_Toyoda: This terminal locates the first item in STL that is in OKL. If an item is found and fits in the knapsack, it is removed from OKL and inserted into IKL.
• Add_Max_Freville_Plateau: This terminal locates the first item in FPL that is in OKL. If an item is found and fits in the knapsack, it is removed from OKL and inserted into IKL.
• Del_Min_Profit: This terminal locates the last item in PL and inserts it in IKL. If the knapsack is not empty, that item is removed from IKL and inserted into OKL.
• Del_Max_Weight: This terminal locates the first item in WL that is in IKL. If the knapsack is not empty, that item is removed from IKL and inserted into OKL.
• Del_Min_Scaled: This terminal locates the last item in SNBPL and IKL. If the knapsack is not empty, that item is removed from IKL and inserted into OKL.
• Del_Min_Normalized: This terminal locates the last item with a lower value in NBPL that is in IKL. If the knapsack is not empty, that item is removed from IKL and inserted into OKL.
• Greedy: This terminal constructs an initial feasible solution by transferring items from OKL to IKL, following a greedy criterion based on the ratio between the item’s value and its average weight across all dimensions. For each item $j\in {OKL}_j$, the following ratio is computed:

  $${Ratio}_j={\displaystyle \frac{v_j}{\frac{\sum _{i=0}^m{r}_{ij}}{N_r}}}$$

  (11)

The items in OKL are sorted in decreasing order according to ${Ratio}_j$. Iteratively, an item $j$ with the largest ratio value is selected and moved from OKL to IKL, provided that the capacity constraints are not violated. This process is repeated until no additional items can be added without exceeding the capacity limits.

• Local Search: This terminal applies a local search procedure to the current solution contained in IKL, aiming to improve the total value without violating capacity constraints. An item $j_{in}\in OKL$ and an item $j_{out}\in IKL$ are selected, where $j_{out}$ refers to an item currently inside the knapsack. This item is considered for removal as part of an improvement strategy. The removal frees capacity, potentially allowing the inclusion of a more valuable item. $j_{in}$ is considered for insertion in place of $j_{out}$, provided that its inclusion does not violate capacity constraints and the exchange results in a solution with a higher total value. The process terminates upon reaching Tmax or when no further improvements are possible.

The terminals generated by Gemini for the AGA in the MKP are presented below. These terminals introduce new operations to enhance algorithm flexibility and generalization while replacing specific original terminals to mitigate overfitting, as detailed in the subsequent analysis.

• Add_Random: Inserts a random item from OKL to IKL if it satisfies the capacity constraints.
• Del_Worst_Ratio_In_Knapsack: Removes the item in IKL with the worst value/weight ratio.
• Del_Random: Removes a random item from IKL and inserts it into OKL.
• Swap_Best_Possible: Swaps items between IKL and OKL to maximize the total value.
• Is_Empty: Checks if IKL is empty (returns True/False).
• Is_Near_Full: Checks if IKL is close to the maximum capacity (returns True/False).

Although syntax trees are commonly associated with compiler construction, in this study, they serve a different purpose. They provide a formal and evolutionary representation of algorithms within the framework of GP, ensuring syntactic validity during crossover and mutation operations [25,54]. This structure enables the automatic combination and transformation of functional components (functions and terminals), allowing the evolutionary process to explore a wide range of algorithmic architectures while maintaining logical consistency. Furthermore, as observed in the AGA convergence section, the syntax tree representation contributes to evolutionary stability and reduces the relative error across generations (Section 4.7).

3.2. Feasible Combinations

We define a grammar to facilitate the algorithm’s legibility and ensure congruence between the objective of each function and its arguments. Specifically, a strongly typed GP is considered [54]. Every node has a specified return type, and for functions, this corresponds to the set of types expected from each child node. This structure guarantees type compatibility among nodes, defining valid combinations between parent and child types, their return types, and permissible argument types. A detailed summary of these compatibility rules is presented in Table 1. The return types and their role within the grammar are the following:

Table 1. Nodes compatibility.

Node	Type of Return	Types Compatible with Child Node 1	Types Compatible with Child Node 2	Types Compatible with Child Node 3
Terminal	term	-	-	-
Not	bool	bool—term	-	-
Or	bool	bool—term	bool—term	-
And	bool	bool—term	bool—term	-
Equal	bool	bool—term	bool—term	-
Do_While	loop	bool—term	sent—term	-
If_Then	sent	bool—term	loop—sent—term	-
If_Then_Else	sent	bool—term	loop—sent—term	loop—sent—term

• Term: This type specifies that the node is a leaf of the syntactic tree and, therefore, a terminal. It is compatible as a child node with all other node types.
• Bool: This type indicates that the node can be part of a function that asks a logical question and, therefore, requires a logical answer.
• Loop: This type indicates a “repeater” function, in which it executes a node according to the logical answer of another node. It includes only the Do_While node due to its repetitive function or cycle.
• Sent: This type indicates that the execution of another node occurs regardless of its result. It differs from the Loop type in that it accepts this type of node as a child node.

3.3. The Master Problem’s Objective Function

The objective function of the MP guides the evolution of GP. The objective function combines two objectives: the quality of the algorithms, $q_a$, and the readability of the algorithm. The former is given by the average relative error of the algorithm when evaluating all the evolution instances. Specifically, let $z_i$ be the profit obtained by an algorithm for problem instance i, and let $z_i^{*}$ be the optimum profit of the problem instance. Furthermore, let $F$ be the set of evolution instances and $n_F=\left|F\right|$. The average quality $q_a$ of algorithm $a$ is defined in Equation (12). Consequently, the algorithms that solve MKP achieve fitness values close to zero.

$$q_a={\displaystyle \frac{1}{n_F}}{\sum }_i^{n_F}\left|z_i-z_i^{*}\right|$$

(12)

Because the algorithms from the first generation have a random nature and evolve randomly according to genetic operators, they can exhibit excessive growth. Some of the algorithms cannot find reasonable solutions. They may even crossover, generating a feasible algorithm, but at the expense of transferring a large volume of code to the following generation, resulting in algorithms that can be challenging to read. This phenomenon is known as bloating, and a simple method of controlling it involves setting size or depth limits for the generated algorithms [54]. Let $\gamma$ be the maximum number of nodes accepted for an algorithm and $n_a$ the number of nodes of an algorithm $a$. The readability $r_a$ of algorithm $a$ is defined as the penalty difference between the number of nodes and the maximum number of nodes accepted for an algorithm, as shown in Equation (13).

$$r_a=\left\{\begin{array}{c}0 if n_a\le \gamma \\ {\displaystyle \frac{n_a-\gamma }{\gamma }} otherwise\end{array}\right.$$

(13)

Finally, the MP’s objective function is a weighted equation between the quality of an algorithm and its readability, as shown in Equation (14). We select $\theta =0.95$, keeping in mind that the readability term is a kind of noise for the fundamental objective of obtaining MKP high-quality algorithms.

$$f_a=\theta q_a+\left(1-\theta \right)r_a$$

(14)

3.4. Evaluation and Evolution Instances

Two groups of instances are chosen, one for the evolutionary process and another for evaluating the resultant algorithms. Typically, the Tightness Ratio, $\alpha$ defines the structure of an MKP instance [50]. Such a ratio expresses the scarcity of the capacities of each dimension of the knapsack as defined in Equation (15).

$${\alpha }_i={\sum }_{j=1}^n{\displaystyle \frac{c_i}{r_{ij}}}$$

(15)

The instances were obtained from the OR Library and contain 100, 250, and 500 items with 5, 10, and 30 constraints [55]. Additional constraints were included from the SAC94 Suite: Collection of Multiple Knapsack Problems. Some instances have α values of 0.25, 0.5, or 0.75, and only three have a known optimal value. We used the best-known solution instead of the optimal solution for the remaining MKP instances.

For comparability, we enforced the same number of clusters across all methods, rather than using each method’s native or data-driven cluster count. For K-Means, the number of clusters (k) was set to eleven, matching the groups produced by HDBSCAN and random clustering. Although HDBSCAN is a density-based algorithm that can automatically determine the number of clusters based on data density, in this study, it was configured to match the cluster count of K-Means closely. This alignment allowed the analysis to focus on the impact of the clustering method itself, rather than differences in partition granularity, on the specialization and generalization of the generated algorithms. By keeping the number of groups consistent across all clustering techniques, the experimental comparison centered on the structural and methodological differences inherent to each approach.

For the random clustering baseline, the number of clusters was fixed at eleven, matching the configurations used in K-Means and HDBSCAN. Once this number was defined, instances were assigned randomly and uniformly to each cluster, ensuring that all groups contained approximately the same number of instances. This procedure was not intended to represent a clustering algorithm per se, but rather to provide an unstructured reference point for comparison. The goal was to isolate the effect of structured instance organization on the specialization and generalization behavior of the automatically generated algorithms. By maintaining the same number of groups across all clustering methods, the random clustering established a baseline performance level against which the benefits of meaningful cluster formation could be evaluated.

The set of MKP instances is divided into 11 groups according to its statistical characteristics. The grouping was made by three methods: K-Means, HDBSCAN, and Random selection. In Random clustering, the 328 instances were divided into 11 groups, with 30 instances in the first 9 groups and 29 instances in the last two groups, maintaining the proportions of the training and test sets as in the other clusterings. Each group was further split into training and testing sets. An algorithm was generated by AGA for one group and evaluated across all groups using all instances within each group.

• The notation MKPA1 refers to the algorithm trained on Group 1 of MKP instances. In this study, a total of 33 instance groups are considered, with each group associated with a specific set of algorithms automatically generated through a clustering process. The groups are organized as follows:
• Groups 1 to 11 (MKPA1–MKPA11): These correspond to instances clustered using the K-Means algorithm, where each group gave rise to a specialized algorithm through AGA.
• Groups 12 to 22 (MKPA12–MKPA22): These represent the instances clustered using the HDBSCAN algorithm, with corresponding algorithms generated and adapted specifically for each group.
• Groups 23 to 33 (MKPA23–MKPA33): These correspond to randomly generated groupings, used as a comparative baseline to evaluate the effectiveness of guided clustering.

Table 2 presents the structural characteristics of the instance groups obtained through K-Means clustering; each group is associated with a specialized algorithm (MKPA1–MKPA11). The table details the number of training and test instances per group, as well as the diversity in instance size and number of constraints. Most groups contain between 27 and 63 instances, with MKPA6 having the largest number (63) and MKPA10 the smallest (5). The size of the instances varies widely, ranging from small-scale problems (e.g., sizes 10 to 28 in MKPA9 and MKPA10) to larger instances (e.g., size 500 in MKPA5 and MKPA1). Similarly, the number of constraints differs significantly across groups, ranging from as few as two constraints in MKPA10 to as many as 30 in MKPA2 and MKPA8. This variability illustrates the heterogeneity of the instance space. It justifies the need for clustering-based specialization, enabling the generation of algorithms tailored to the unique structural properties within each group.

Table 2. Groups clusterized by Kmeans.

Groups	Training Instances	Test Instances	Number of Instances	Instance Size	Number of Restrictions
MKPA1	43	11	54	250, 500	10, 30
MKPA2	26	7	33	40, 60,100	30
MKPA3	30	8	38	100, 250	5, 10
MKPA4	24	6	30	30, 40, 50, 60, 70, 80, 90	5
MKPA5	22	5	27	500	5
MKPA6	50	13	63	100, 250	5, 10
MKPA7	25	6	31	250, 500	5, 10, 30
MKPA8	27	7	34	250	30
MKPA9	4	1	5	10, 15, 20	10
MKPA10	4	1	5	28	2
MKPA11	6	2	8	27, 28, 34, 35, 39, 50, 105	2, 4, 5, 10

Table 3 outlines the characteristics of the instance groups derived from clustering via HDBSCAN, each corresponding to a specialized algorithm (MKPA12–MKPA22). The table includes the number of training and test instances, the total number of instances per group, the range of instance sizes, and the number of constraints. Group sizes vary from as few as 11 instances (e.g., MKPA15 and MKPA17) to 31 in MKPA22. Instance sizes are primarily concentrated in the medium to large scale, with several groups exclusively containing instances of sizes 250 or 500 (e.g., MKPA13, MKPA14, MKPA16, MKPA18), while others, such as MKPA12 and MKPA20, include small-sized instances ranging from 30 to 100. The number of constraints across groups ranges from 5 to 30, with MKPA13 and MKPA14 including only high-dimensional instances (30 constraints), whereas groups such as MKPA18, MKPA20, and MKPA21 include instances with lower dimensionality (5 to 10 constraints). This distribution reflects the ability of HDBSCAN to form clusters with structurally coherent instances, which supports the generation of highly adapted algorithms for subsets sharing similar problem configurations.

Table 3. Groups obtained by HDBScan.

Groups	Training Instances	Test Instances	Number of Instances	Instance Size	Number of Restrictions
MKPA12	22	6	28	30, 40, 50, 60, 70, 80, 90	5
MKPA13	18	4	22	250	30
MKPA14	16	4	20	500	30
MKPA15	9	2	11	250	10
MKPA16	15	4	19	500	10
MKPA17	9	2	11	500	5, 10
MKPA18	18	5	23	500	5
MKPA19	18	14	4	100	30
MKPA20	14	3	17	100	5
MKPA21	18	5	23	250	5, 10
MKPA22	25	6	31	100	5, 10

Table 4 presents the characteristics of the instance groups formed through random clustering, each associated with a specialized algorithm (MKPA23—MKPA33). Unlike clustering methods guided by structural similarity (e.g., K-Means and HDBSCAN), the random grouping method includes a fixed number of instances per group, typically consisting of 30 instances (24 for training and 6 for testing), except for MKPA32 and MKPA33, which contain 29 instances. The diversity within these groups is notably broader, both in terms of instance sizes, which range from very small (e.g., 10, 15, 20) to large-scale instances (e.g., 500), and in the number of constraints, which span from 2 to 50 across the groups. For example, MKPA30 includes one of the most heterogeneous combinations of instance sizes and constraint values, whereas other groups, such as MKPA24 and MKPA27, though still diverse, show slightly narrower ranges. This high degree of intra-group variability highlights the lack of structural coherence in random clustering, potentially limiting the effectiveness of algorithm specialization when compared to strategies based on meaningful similarity metrics. Nonetheless, these groups serve as a valuable baseline for evaluating the performance gains achieved through clustering-driven specialization.

Table 4. Randomly generated groups.

Groups	Training Instances	Test Instances	Number of Instances	Instance Size	Number of Restrictions
MKPA23	24	6	30	100, 250, 500	5, 10, 30
MKPA24	24	6	30	100, 250, 500	5, 10, 30
MKPA25	24	6	30	20, 28, 30, 90, 100, 250, 500	5, 10, 30
MKPA26	24	6	30	15, 28, 30, 34, 35, 50, 70, 150	25, 4, 5, 10, 30
MKPA27	24	6	30	100, 250, 500	4, 50
MKPA28	24	6	30	100, 250, 500	5, 10, 25
MKPA29	24	6	30	100, 200, 250	10, 25
MKPA30	24	6	30	100, 150, 250, 500, 40, 20, 39, 28, 105, 30, 50, 60, 70, 80	2, 5, 10, 30, 50
MKPA31	24	6	30	100, 250, 500	10, 30
MKPA32	23	6	29	100, 250, 500, 27, 60, 28, 40, 50, 60, 70, 80, 90	4, 2, 5, 30
MKPA33	23	6	29	100, 250, 500, 10, 60, 28, 30, 40, 50, 60, 70, 80	30, 10, 2, 5

To analyze instances of the MKP, two matrix-based structures are proposed to systematically encode the relationships between items, their associated profits, and the available resources in each dimension. These representations are invariant under scale transformations, ensuring their robustness against changes in measurement units. The first structure corresponds to the matrix of weight-to-capacity proportions (denoted as E), where each element $e_{ij}$ represents the fraction of capacity consumed in dimension $i$ by item $j$, according to Equation (16). This matrix enables the quantification of how well an instance conforms to its capacity constraints.

$$e_{ij}={\displaystyle \frac{b_i}{a_{ij}}}$$

(16)

The second structure is the weight-profit efficiency matrix (denoted as $F$), whose elements $f_{ij}$ are given by Equation (17). $F$ reflects the relative efficiency of each item in each dimension, considering the benefit per unit of resource consumed.

$$f_i={\displaystyle \frac{a_{ij}}{c_j}}$$

(17)

Both matrices enable the derivation of a wide range of statistical descriptors used in the quantitative characterization of the instances. Thus, the characterization of MKP instances is based on the statistical analysis of the $E$ and $F$ matrices, as these encode key information regarding the relationship between items, their profits, and the multidimensional constraints. The primary objective is to transform these matrices, whose dimensions vary depending on the instance, into standardized numerical representations that can be compared across instances, thereby facilitating their use in clustering processes and the automatic generation of algorithms.

We encode the instances through matrices E and F due to their ability to structurally represent the relationships among items, their profits, and multidimensional constraints, without depending on the number or ordering of elements. This statistical representation captures both the global patterns and local variations in each instance, ensuring comparability across problems of different sizes and scales. Moreover, by summarizing the information into normalized statistical descriptors, it prevents the loss of generality and enhances the stability of the clustering process. In preliminary experiments, other, more direct encodings (e.g., those based on the raw item values) exhibited higher intra-cluster variance and lower structural coherence, confirming the suitability of the statistical encoding approach adopted in this study.

To address the heterogeneity in instance sizes, a procedure known as the statistical descriptor matrix is implemented. This procedure transforms each input matrix (either $E$ or $F$) into a new matrix with fixed dimensions. Each cell of the resulting matrix contains a statistical summary of the corresponding values in the original matrix, thus enabling a coherent and comparable representation across instances of varying sizes. This procedure occurs in three main stages.

In the first stage, a set of statistical metrics is defined and systematically applied to the original matrices. These include classical measures of central tendency (mean, median, mode), dispersion (standard deviation, variance), and shape of the distribution (skewness, kurtosis). Additionally, percentile-based measures such as the 25th percentile, 50th percentile (median), and 75th percentile are computed to capture the spread and distribution of the data. Other relevant metrics include the coefficient of variation, which normalizes the standard deviation relative to the mean, as well as the minimum and maximum values, which provide bounds on the range of observed values.

As a result of this dual aggregation scheme, a set of features is derived from both the matrices, yielding a total of 259 variables that summarize key properties of each instance. This strategy enables the capture of not only global statistics but also internal patterns related to the ordering and interactions among items, an essential aspect for distinguishing instances that may share similar aggregated values yet exhibit distinct underlying structures. Although this approach generates a substantial number of potentially redundant or collinear variables, such challenges are addressed in a subsequent stage through specific techniques for collinearity reduction and relevant variable selection.

Once the features have been extracted, a structured preprocessing procedure is implemented to ensure the quality, interpretability, and efficiency of subsequent analyses. In the first stage, all variables are normalized using the Min-Max scaling method, which mitigates the effects of scale differences among attributes and facilitates comparison across heterogeneous dimensions. Subsequently, a collinearity reduction stage is carried out by calculating the Variance Inflation Factor (VIF), eliminating those variables with a VIF greater than 10. As a result of this process, the dataset was reduced to 42 variables, effectively minimizing redundancy among descriptors and enhancing the robustness of the resulting models.

3.5. Experimental Setting

The experiment was performed using the Python 3.7.2 language, which implemented the evolutionary process and defined functions and terminals for the syntax tree [34]. The process was carried out on a computer with a Windows 12 operating system, an Intel Core i5-10500 processor at 3.1 GHz, and 16 GB of RAM. The guidelines for experimental parameters were based on initial preliminary experiments shown in Table 5.

Table 5. AGA parameters.

Parameter	Value
Size of the initial population	100
Number of generations	100
Crossover probability	50% One point crossover
Reproduction probability	1% simple elitism
Mutation probability	30% Subtree mutation
Initial population generation	Random generation of syntactic trees with control of minimum, maximum, and minimum heights
Method of construction of subtree for Subtree mutation	Random generation of a subtree with maximum height control and restrictions on the number of nodes and types.
Individual selection	Tournament with 5 individuals
Node selection	Uniform Random Node Selection
Probability of node selection	Uniform random selection among all nodes
Maximum height in the initial population	5
Maximum height of the new subtree for Subtree mutation	4
Maximum height during evolution	5
Method of population replacement	Generational Replacement with Simple Elitism
Stopping criterion	Complete the total generations.

4. Results

This section presents the experimental evaluation of automatically generated algorithms specialized based on groups of instances with similar structural characteristics. We analyzed the performance of each algorithm in terms of accuracy and structural complexity, with particular emphasis on the benefits of specialization guided by clustering techniques. For each group previously defined using K-Means, HDBSCAN, and random clustering, an algorithm was generated using only the corresponding training instances. These algorithms were then evaluated both within their clusters and across clusters to measure their degree of specialization and generalization capabilities. The primary performance indicator was the average relative error, complemented by structural metrics, including the number of nodes and the height of the syntactic trees.

4.1. Specialization of Algorithms Due to Clustering

The results indicate that the algorithms trained on instance groups clustered using K-Means and HDBSCAN generally achieve better performance on their respective training groups, providing evidence of algorithm specialization. In contrast, the algorithms trained on groups derived from random clustering do not exhibit such specialization, as no significant improvement is observed within their assigned groups. This contrast highlights the importance of structurally informed clustering in enhancing the effectiveness of automatically generated algorithms.

The results obtained from the instance clustering using the K-Means algorithm reveal a variability in the performance of the specialized algorithms generated for each group. Table 6 presents the characteristics of the algorithms generated for the 11 groups obtained through K-Means clustering. This table includes, first, the performance of the algorithms in terms of fitness, evaluated through the average relative error when applied to the test instances, as well as the minimum error (closest to zero) and the maximum error recorded by each algorithm. Second, the structural complexity of the algorithms is detailed through the number of nodes present in each generation, identifying the minimum, maximum, and average values among the best algorithms obtained during the evolution. Finally, the total number of nodes and the height corresponding to the best algorithm trained for each group are specified, thus providing a comprehensive view of both the performance and structure of the algorithms obtained. In terms of fitness, defined as the average relative error in solving the instances within each group, the observed values range from 0.0066 (MKPA5) to 0.0455 (MKPA11) in the worst cases. The algorithm MKPA5 stands out as the most efficient, exhibiting the lowest error both in the best case (0.0066) and on average (0.0073), whereas MKPA11 shows the highest average error (0.0394), suggesting that the instances within its group are either more difficult to solve or that the algorithm generated for this cluster is less specialized.

Table 6. Average relative error for the algorithms generated by K-Means clustering.

Algorithm	Relative Error			Number of Nodes			Nodes in the Best Algorithm
	Best	Average	Worst	Min	Average	Max	Nodes	Height
MKPA1	0.0120	0.0140	0.0171	16	16.6	17	17	5
MKPA2	0.0304	0.0343	0.0369	24	24.0	24	24	5
MKPA3	0.0290	0.0298	0.0327	11	14.3	16	16	5
MKPA4	0.0083	0.0116	0.0170	17	23.7	24	24	5
MKPA5	0.0066	0.0073	0.0106	24	24.0	24	24	5
MKPA6	0.0123	0.0124	0.0149	11	17.7	18	18	5
MKPA7	0.0276	0.0276	0.0278	15	15.0	15	15	5
MKPA8	0.0224	0.0257	0.0336	16	19.4	24	20	5
MKPA9	0.0217	0.0217	0.0217	18	18.0	18	18	5
MKPA10	0.0073	0.0101	0.0166	20	21.9	23	19	5
MKPA11	0.0311	0.0394	0.0455	11	12.8	20	15	5
Average	0.0190	0.0213	0.0249	16.63	20.25	20.27	19.09	5

Regarding structural complexity, measured by the number of nodes in the syntax trees of the algorithms, a tendency toward compact algorithms is observed in some instances (e.g., MKPA3, with an average of 14.3 nodes and a minimum of 11.00). In contrast, other algorithms such as MKPA4 and MKGA6 exhibit larger structures, with averages exceeding 17 nodes. Structural diversity is also reflected in the breadth of the node range, as seen in MKPA11, whose number of nodes varies between 11 and 20, which may be associated with the instability in performance observed for that group.

These results lead to the conclusion that clustering through K-Means produces groups of instances whose structure can be effectively leveraged for algorithm specialization, achieving significantly low relative errors in several cases and relatively compact syntactic structures. However, some degree of heterogeneity in overall performance is also observed across different groups.

Table 7 presents the structural and theoretical complexity of the algorithms generated within the K-Means cluster group (MKPA1–MKPA11). The analysis reveals that most algorithms exhibit a high degree of structural depth and nested iterations, with multiple conditional and logical operators. Specifically, 7 out of 11 algorithms achieve a theoretical complexity of O(n³), primarily due to the presence of multiple while loops combined with If-Then-Else and logical compositions (and, or, Not). These structures favor extensive exploration of the solution space but increase computational cost. In contrast, algorithms MKPA3, MKPA6, MKPA10, and MKPA11 display a lower structural density (O(n²)), corresponding to simpler control flows and fewer nested conditions, which enhance computational efficiency. Overall, the K-Means group demonstrates a pattern of syntactic growth consistent with high specialization: deeper trees enable the discovery of more refined solutions within their cluster, although at the expense of higher execution complexity.

Table 7. Structural and theoretical complexity of algorithms evolved within the K-Means cluster group.

Algorithm	Nº While	Nº If/Else	Nº And/Or/Not	Nº Terminals	Theoretical Complexity
MKPA1	2	3	2	7	O(n3)
MKPA2	3	3	3	8	O(n3)
MKPA3	2	2	2	6	O(n2)
MKPA4	3	3	3	9	O(n3)
MKPA5	3	2	3	8	O(n3)
MKPA6	2	2	3	7	O(n2)
MKPA7	3	2	2	6	O(n3)
MKPA8	3	2	3	8	O(n3)
MKPA9	3	3	3	7	O(n3)
MKPA10	2	3	3	8	O(n2)
MKPA11	2	3	2	6	O(n2)

The evaluation of the algorithms generated from instance clustering using HDBSCAN reveals a consistent and competitive performance in terms of both accuracy and structural complexity. Table 8 shows the characteristics of the algorithms generated for the 11 groups using HDBSCAN clustering. Specifically, it presents the average relative error of each algorithm when evaluated with the test instances, along with its size, expressed in terms of the number of nodes. Regarding fitness, defined as the average relative error in solving the instances within each group, average values range from 0.0070 (MKPA18) to 0.0258 (MKPA19). MKPA18 stands out as the most accurate algorithm, with an average error of only 0.0070 and a minimum error of 0.0056. Likewise, other algorithms such as MKPA21 and MKPA16 also exhibit very low errors (0.0084 and 0.0109 on average, for both algorithms), suggesting that HDBSCAN has successfully grouped instances with characteristics conducive to effective algorithm specialization.

Table 8. Average relative error of the algorithms generated by HDBSCAN clustering.

Algorithm	Fitness			Number of Nodes			Nodes in the Best Algorithm
	Best	Average	Worst	Min	Average	Max	Nodes	Height
MKPA12	0.0224	0.0253	0.0336	29	34.7	40	25	5
MKPA13	0.0195	0.0227	0.0266	16	19.1	24	20	5
MKPA14	0.0123	0.0141	0.0167	15	17.3	18	18	5
MKPA15	0.0131	0.0152	0.0258	11	17.4	19	19	5
MKPA16	0.0084	0.0109	0.0128	16	16.8	18	16	5
MKPA17	0.0205	0.0215	0.0289	11	19.3	21	21	5
MKPA18	0.0056	0.0070	0.0103	9	12.9	15	15	5
MKPA19	0.0244	0.0258	0.0287	11	15.6	18	18	5
MKPA20	0.0247	0.0249	0.0260	11	11.2	14	11	5
MKPA21	0.0077	0.0081	0.0098	11	16.6	18	18	5
MKPA22	0.0149	0.0150	0.0179	11	19.1	21	18	5
Average	0.0158	0.0173	0.0216	13.72	18.17	20.54	18.09	5

Concerning structural complexity, measured by the number of nodes in the syntactic trees, a wide variability is observed. Algorithms such as MKPA20 and MKPA18 exhibit highly compact structures, with averages of 11.2 and 12.9 nodes, respectively. Others, like MKPA12, reach much higher averages (34.7 nodes), which may be related to the need to capture more complex patterns within that group of instances. It is worth noting that, despite differences in structural size, several algorithms maintain low relative errors, demonstrating an adequate generalization capacity in constructing viable solutions.

Taken together, these results show that clustering with HDBSCAN enables effective algorithmic specialization across multiple groups, producing algorithms with low relative error and, in many cases, relatively simple syntactic structures. This behaviour suggests that density-based clustering is capable of capturing relevant structural patterns that enhance the quality of automatically generated algorithms.

Table 9 presents the structural and theoretical complexity of the algorithms generated within the HDBSCAN group (MKPA12–MKPA22). Overall, a tendency toward more compact and efficient structures is observed compared to those produced by the K-Means clustering. Approximately six algorithms exhibit a theoretical complexity of O(n³), associated with the presence of multiple While loops combined with conditional (IfThenElse) and logical (And, Or, Not) operators. However, algorithms MKPA15, MKPA16, and MKPA20 show a reduced complexity of O(n²), characterized by simpler control flows and lower syntactic depth. Collectively, the algorithms derived from the HDBSCAN cluster achieve a balance between structural efficiency and exploratory capacity, maintaining a favorable relationship between computational complexity and performance, suggesting that density-based clustering promotes the generation of lighter and more generalizable algorithms.

Table 9. Structural and theoretical complexity of algorithms evolved within the HDSCAN cluster group.

Algorithm	Nº While	Nº If/Else	Nº And/Or/Not	Nº Terminals	Theoretical Complexity
MKPA12	3	3	3	8	O(n3)
MKPA13	3	3	3	9	O(n3)
MKPA14	3	3	3	8	O(n3)
MKPA15	2	2	2	6	O(n2)
MKPA16	2	2	2	6	O(n2)
MKPA17	3	2	3	7	O(n3)
MKPA18	3	3	3	8	O(n3)
MKPA19	3	2	3	8	O(n3)
MKPA20	2	2	2	6	O(n2)
MKPA21	3	3	3	8	O(n3)
MKPA22	3	3	3	9	O(n3)

The results obtained through random clustering of instances reveal a less uniform and generally less competitive performance compared to guided clustering methods such as K-Means and HDBSCAN. Similar to Table 6 and Table 8, Table 10 displays the characteristics of the algorithms generated for the 11 randomly clustered groups. In terms of fitness, the average relative errors range from 0.0160 (MKPA28) to 0.0348 (MKPA32), with the latter exhibiting the worst average performance. Although some algorithms, such as MKPA23, MKPA24, and MKPA27, achieve relatively low average errors (approximately 0.017–0.024), most demonstrate more modest performance with greater variability in error values.

Table 10. Average relative error of the algorithms generated by random clustering.

Algorithm	Fitness			Number of Nodes			Nodes in the Best Algorithm
	Best	Average	Worst	Min	Average	Max	Nodes	Height
MKPA23	0.0169	0.0173	0.0199	11	17.6	18	18	5
MKPA24	0.0179	0.0196	0.0244	11	24.3	25	25	5
MKPA25	0.0276	0.0280	0.0299	11	24.2	25	25	5
MKPA26	0.0277	0.0290	0.0302	11	11.6	12	11	5
MKPA27	0.0191	0.0193	0.0205	11	11.0	11	11	5
MKPA28	0.0147	0.0160	0.0202	11	15.5	18	16	6
MKPA29	0.0212	0.0243	0.0317	11	23.1	25	25	5
MKPA30	0.0311	0.0314	0.0350	11	17.8	18	20	5
MKPA31	0.0234	0.0252	0.0342	11	15.0	25	13	5
MKPA32	0.0346	0.0348	0.0378	11	17.0	18	18	5
MKPA33	0.0223	0.0228	0.0241	32	32.0	32	24	5
Average	0.0233	0.0243	0.0280	12.9	19.00	20.7	18.7	5.1

Regarding the structure of the algorithms, the number of nodes exhibits considerable variability. While many of the generated trees are compact, with a minimum of 11 nodes, others, such as MKPA24, MKPA25, and MKPA29, reach average sizes exceeding 23 nodes, which may indicate unnecessary complexity resulting from the lack of a clustering logic based on structural similarity among instances. Notably, MKPA33 presents a rigid tree structure of exactly 32 nodes across all executions, which is atypical compared to the other algorithms and suggests either premature convergence or limited flexibility in the algorithm’s evolutionary design.

Table 11 presents the structural and theoretical complexity of the randomly generated algorithms (MKPA23–MKPA33). This group exhibits greater variability in syntactic depth and in the number of conditional and logical operators, lacking a coherent design structure. Most algorithms show a theoretical complexity of O(n³), resulting from the redundant combination of While loops with conditional (IfThenElse) and logical (And, Or, Not) operators, which considerably increases computational cost without a proportional improvement in performance. Only three algorithms (MKPA26, MKPA27, and MKPA31) achieve a complexity of O(n²), displaying simpler structures and fewer nested levels. Overall, the randomly generated algorithms tend to overgrow syntactically, indicating a lack of structural optimization and a lower degree of specialization, confirming that unguided evolution without clustering produces less efficient solutions and is more prone to structural overfitting.

Table 11. Structural and theoretical complexity of algorithms evolved within the Random cluster group.

Algorithm	Nº While	Nº If/Else	Nº And/Or/Not	Nº Terminals	Theoretical Complexity
MKPA23	3	3	3	8	O(n3)
MKPA24	3	3	3	9	O(n3)
MKPA25	3	3	3	8	O(n3)
MKPA26	2	2	2	6	O(n2)
MKPA27	2	2	2	6	O(n2)
MKPA28	3	2	3	7	O(n3)
MKPA29	3	3	3	8	O(n3)
MKPA30	3	2	3	8	O(n3)
MKPA31	2	2	2	6	O(n2)
MKPA32	3	3	3	8	O(n3)
MKPA33	3	3	3	9	O(n3)

Taken together, the results in Table 6, Table 8 and Table 10 indicate that the clustering strategy employed has an impact on the performance of the generated algorithms. Structural feature-guided clustering methods, such as K-Means and HDBSCAN, facilitate the effective specialization of the algorithms, enabling them to better adapt to the specific characteristics of their respective groups of instances. In contrast, random clustering generates more variable and less consistent results, which limits its capacity for specialization. Despite these differences in performance, the structural complexity of the algorithms remained constant in all cases, with trees of controlled height and a similar average number of nodes, suggesting that the observed variations in solution quality are primarily due to the effectiveness of the clustering process during the training phase.

Table 7, Table 9 and Table 11 provide a comparative view of the structural and theoretical complexity of the algorithms evolved within the K-Means, HDBSCAN, and Random groups. The results indicate that cluster-guided evolution (K-Means and HDBSCAN) tends to produce algorithms with a more balanced structural composition, typically maintaining two to three nested control structures and an average theoretical complexity of O(n³). These algorithms exhibit coherent logic and controlled syntactic growth, reflecting effective specialization within their respective clusters. In contrast, algorithms from the Random group exhibit greater variability and redundant structural patterns, resulting in less efficient architectures and, in some cases, syntactic overgrowth. Overall, the comparison highlights that clustering-based guidance contributes to structural regularity and computational efficiency, whereas unguided random evolution increases complexity without yielding proportional performance improvements.

4.2. Evaluation of Algorithms with Instances from Other Clusters

The cross-cluster evaluation reveals that the generalization capacity of the automatically generated algorithms varies significantly depending on the clustering method used, with many algorithms exhibiting limited transferability to structurally distinct instance groups. To conduct this analysis, the best algorithm trained with instances from each group was evaluated using instances from the remaining ten groups. This approach enables the determination of whether the patterns learned by each algorithm extend beyond the specific training set. In particular, the relative error obtained by each algorithm within its group (values on the diagonal of the tables) is compared with the errors recorded when applied to the other groups. This comparison is essential for assessing the degree of specialization achieved and identifying potential trade-offs between specialization and generalization, as determined by the clustering strategy employed.

A comparative analysis of the MKP algorithms applied to each group for K-Means clustering reveals a clear trend toward specialization. Table 12 presents the relative errors obtained when evaluating the algorithms trained with each group for K-Means instance clustering. Examining the diagonal matrix, where each value represents the relative error of the algorithm explicitly trained for its own group, it can be observed that most algorithms exhibit their lowest errors precisely within their group of origin. For example, MKPA1 achieves a relative error of 0.0122 in G1, while MKPA5 achieves 0.0074 in G5, and MKPA4 achieves 0.0138 in G4. In contrast, off-diagonal errors tend to increase significantly, especially in less specialized algorithms such as MKPA9 and MKPA10, whose errors in other groups far exceed their diagonal values, even reaching over 80% and 90% in some cases. This marked difference between on-diagonal and off-diagonal performance demonstrates that the generated algorithms are highly dependent on the specific characteristics of their training set, reflecting controlled overfitting behave or geared toward specialization. Furthermore, the column average also indicates that groups G1, G2, G3, and G5 are those where the algorithms generally achieve the lowest errors, suggesting that these groups present lower intrinsic difficulty or greater internal homogeneity, thereby facilitating the effective specialization of the algorithms.

Table 12. Evaluation of algorithms with instances from each group according to K-Means clustering.

Group	G1	G2	G3	G4	G5	G6	G7	G8	G9	G10	G11
MKPA1	0.0122	0.0293	0.0286	0.0295	0.0089	0.0124	0.0268	0.0221	0.0349	0.0548	0.0413
MKPA2	0.0189	0.0281	0.0378	0.0199	0.0189	0.0182	0.0355	0.0354	0	0.0742	0.1291
MKPA3	0.0154	0.0299	0.0286	0.0295	0.0111	0.0124	0.0298	0.0265	0.0349	0.0305	0.0753
MKPA4	0.7531	0.1017	0.1596	0.0138	0.7513	0.3952	0.4743	0.4236	0.0162	0.3203	0.261
MKPA5	0.0114	0.0267	0.0227	0.0251	0.0074	0.0101	0.0204	0.0198	0.0349	0.0548	0.0413
MKPA6	0.0165	0.0344	0.0283	0.0295	0.0115	0.0124	0.0287	0.0252	0.0349	0.0548	0.0413
MKPA7	0.0117	0.0293	0.0286	0.0295	0.0089	0.0124	0.0263	0.0221	0.0349	0.0548	0.0413
MKPA8	0.0117	0.0293	0.0286	0.0295	0.0089	0.0124	0.0256	0.0221	0.0349	0.0548	0.0413
MKPA9	0.9376	0.5814	0.6878	0.2212	0.9344	0.8451	0.8648	0.8597	0.0174	0.0337	0.0966
MKPA10	0.8294	0.2544	0.3054	0.0482	0.8119	0.5811	0.6376	0.6227	0.0162	0.0305	0.0908
MKPA11	0.0197	0.0484	0.0367	0.0478	0.0149	0.0185	0.0383	0.0341	0.0149	0.056	0.0405
Average	0.2398	0.1084	0.1266	0.0476	0.2353	0.1755	0.2007	0.1921	0.0249	0.0745	0.2398

Analysis of the relative error matrix obtained for the MKPA algorithms applied to the groups in HDBScan clustering shows a clear trend toward greater generalization and lower variability compared to K-Means clustering. Table 13 presents the relative errors obtained when evaluating the algorithms trained with each group for HDBScan instance clustering. It is observed that most algorithms exhibit relatively low errors not only on the diagonal (their training group) but also when applied to other groups. For example, MKPA13, MKPA14, MKPA15, and MKPA16 achieve errors below 0.04 even when applied outside their original group. The diagonal remains low in all cases, with lows such as 0.0076 for MKPA15 in G5 and 0.0082 for MKPA13 and MKPA14 in G10, demonstrating good specialization. However, unlike the results observed with K-Means, the off-diagonal errors do not show such increases. The exception is MKPA12, whose off-diagonal error exceeds 0.5 in several groups, demonstrating a lower generalization capacity of this particular algorithm. The column average also confirms this lower dispersion, as the errors average between 0.0235 and 0.0855, much lower than those obtained with less structured clustering. These results suggest that clustering using HDBScan allowed the generation of more robust and versatile algorithms, with superior generalization capacity across different groups of instances, while maintaining acceptable specialization within their respective source groups.

Table 13. Evaluation of algorithms with instances from each group according to HDBSCAN clustering.

Group	G1	G2	G3	G4	G5	G6	G7	G8	G9	G10	G11
MKPA12	0.011	0.5137	0.8045	0.6262	0.8116	0.6264	0.7771	0.1344	0.1334	0.6494	0.1134
MKPA13	0.0332	0.021	0.0115	0.0132	0.0104	0.0254	0.0129	0.0266	0.0312	0.0082	0.0147
MKPA14	0.0332	0.021	0.0115	0.0132	0.0104	0.0254	0.0129	0.0266	0.0312	0.0082	0.0147
MKPA15	0.032	0.0186	0.0105	0.0108	0.0076	0.0218	0.0093	0.0245	0.0297	0.0078	0.0127
MKPA16	0.0332	0.021	0.0119	0.0132	0.0104	0.0254	0.0125	0.0266	0.0312	0.0082	0.0147
MKPA17	0.0341	0.021	0.0114	0.0122	0.0098	0.0277	0.0130	0.0275	0.0312	0.0081	0.0146
MKPA18	0.0332	0.0218	0.0127	0.0113	0.009	0.023	0.0097	0.0309	0.0299	0.0089	0.0145
MKPA19	0.0332	0.0262	0.0164	0.0171	0.0126	0.0349	0.0171	0.0266	0.0312	0.0112	0.0147
MKPA20	0.0332	0.0259	0.016	0.0171	0.0126	0.0333	0.0154	0.027	0.0312	0.0099	0.0147
MKPA21	0.0332	0.0262	0.0164	0.0171	0.0126	0.0349	0.0171	0.0266	0.0312	0.0112	0.0147
MKPA22	0.0332	0.0272	0.0174	0.0152	0.0125	0.0333	0.0164	0.0317	0.0312	0.0121	0.0146
Average	0.0312	0.0676	0.0855	0.0697	0.0836	0.0829	0.0830	0.0372	0.0402	0.0676	0.0235

Analysis of the MKP algorithms generated using random clustering reveals greater generalization but less specialization compared to more structured clustering strategies such as K-Means and HDBScan. Table 14 presents the relative errors obtained when evaluating the algorithms trained with each group for Random instance clustering. The values on the diagonal, which represent the performance of each algorithm on its own training set, are relatively low but not markedly lower than the errors obtained when evaluating the algorithms on other sets. For example, MKPA24 presents an error of 0.0218 on its G2 set. Still, similar errors are observed when evaluating other sets, such as G3 (0.0123) or G6 (0.0053), indicating less differentiation between performance on the source set and on the external sets. This lack of specialization is also reflected in the column averages, where the relative errors remain within a close range between the different sets, without differences as marked as in the previous clusterings. A notable example is MKPA33, which exhibits unstable behavior with higher errors in several groups, reaching 0.0857 in G8. Overall, the algorithms generated using random clustering display a more generalist profile, with less specific adaptability to the characteristics of each group, suggesting that the absence of a clustering structure during training limits the potential for specialization that the evolved algorithms can achieve.

Table 14. Average relative errors for each group and evolved algorithms for Random clustering.

Group	G1	G2	G3	G4	G5	G6	G7	G8	G9	G10	G11
MKPA23	0.0451	0.0282	0.0164	0.025	0.0219	0.0078	0.0242	0.0215	0.0271	0.0252	0.0204
MKPA24	0.0443	0.0218	0.0123	0.0213	0.0155	0.0053	0.0222	0.0206	0.0269	0.0226	0.0163
MKPA25	0.0451	0.0254	0.0164	0.0266	0.0199	0.0075	0.0247	0.0206	0.028	0.0249	0.0205
MKPA26	0.0451	0.0295	0.0164	0.0296	0.0206	0.0077	0.0247	0.0206	0.028	0.0257	0.0208
MKPA27	0.0451	0.0295	0.0164	0.0296	0.0206	0.0077	0.0247	0.0206	0.028	0.0257	0.0208
MKPA28	0.0439	0.0237	0.0122	0.0236	0.0178	0.0057	0.0224	0.0197	0.0275	0.0237	0.0166
MKPA29	0.0439	0.0191	0.0134	0.0196	0.0192	0.0084	0.0188	0.0206	0.0268	0.0236	0.0169
MKPA30	0.0451	0.0246	0.0164	0.0266	0.0199	0.0075	0.0247	0.0206	0.028	0.0249	0.0205
MKPA31	0.0439	0.0226	0.0127	0.0241	0.0183	0.0057	0.0224	0.0197	0.0275	0.0237	0.0169
MKPA32	0.0451	0.0265	0.0164	0.0266	0.0199	0.0075	0.0247	0.0206	0.028	0.0249	0.0205
MKPA33	0.0599	0.0628	0.0184	0.0182	0.0288	0.0139	0.0304	0.0857	0.0258	0.0166	0.0199
Average	0.0460	0.0285	0.0152	0.0246	0.0202	0.0077	0.0240	0.0264	0.0274	0.0238	0.0191

4.3. Statistical Evaluation of Algorithm Specialization

Statistical analysis confirms that K-Means produces the highest level of algorithm specialization, HDBSCAN achieves moderate specialization, and random clustering shows no significant specialization, highlighting apparent performance differences between the three clustering methods. First, data normality tests were applied to determine which statistical tests would be used to determine the effects of specialization and generalization. A summary is shown in Table 15. Regarding the normality of the errors, the K-Means method showed that the within-group (diagonal) values adequately fit a normal distribution (p = 0.6981). In contrast, the out-of-group errors do not follow a normal distribution (p = 2.35 × 10⁻¹⁶). In the case of HDBSCAN, the normality of the errors on the diagonal is less evident (p = 0.0085), although it remains within an acceptable range for specific analyses. Still, the off-diagonal values exhibit a deviation from normality (p = 4.42 × 10⁻²⁰). On the other hand, in random clustering, the diagonal errors also did not show a significant deviation from normality (p = 0.2372), but the off-diagonal values did indicate a lack of normality (p = 2.10 × 10⁻¹⁰).

Table 15. Statistical tests for specialization and generalization.

Clustering	Normality (Diagonal)	Normality (Outside the Diagonal)	T-Test (Specialization)		Friedman Test (Generalization)
	p-Value		T	p-Value	χ2	p-Value
K-means	0.6981	2.35 × 10−16	T = −5.191	p = 9.41 × 10−7 (Significant)	25.47	p = 0.0045
HDBScan	0.0085	4.42 × 10−20	T = −3.034	p = 0.0029 (Significant)	73.10	p = 1.11 × 10−11
Random	0.2372	2.10 × 10−10	T = −0.388	p = 0.704 (Not Significant)	90.28	p = 4.71 × 10−15

Regarding the specialization of the algorithms, assessed using the t-test, it was observed that K-Means achieved a highly significant difference between the within-group and out-of-group errors (T = −5.191, p = 9.41 × 10⁻⁷), indicating strong specialization in the training groups. HDBSCAN also showed evidence of specialization, albeit to a lesser degree (T = −3.034, p = 0.0029). In contrast, random clustering did not present significant differences (T = −0.388, p = 0.704), indicating that there is no effective specialization of the algorithms under this scheme.

Friedman test results reveal significant differences between groups for all methods, with random clustering showing the most significant dispersion, reflecting noise rather than genuine specialization. K-Means had a χ² value of 25.47 (p = 0.0045), HDBSCAN achieved a much higher χ² of 73.10 (p = 1.11 × 10⁻¹¹), and random clustering showed the highest value (χ² = 90.28, p = 4.71 × 10⁻¹⁵). However, these differences in the case of random clustering do not reflect genuine specialization, but rather the dispersion introduced by the random assignment of instances.

The quality of the algorithms produced decreases when evaluated with other problem instances. The three algorithms that yielded the best results in the evaluation process were MKPA15, MKPA18, and MKPA13, which secured 1st, 2nd, and 3rd place, respectively, during the evolution (Table 13). This result is explained by the fact that the selected training instances present a lower difficulty in solving, as they have the lowest relative error values. At the same time, during the evaluation process, they encountered instances of varying difficulty.

Although both K-Means and HDBSCAN were configured to produce a similar number of clusters to maintain comparability, their internal structures remained fundamentally different. K-Means generates compact and approximately spherical groupings by minimizing the Euclidean distance to the centroids, whereas HDBSCAN forms clusters based on density connectivity, resulting in heterogeneous groups with irregular shapes and variable densities. Thus, matching the number of clusters ensured only an equivalent experimental granularity, but not equivalent partition structures. Consequently, both methods operated over distinct instance distributions, directly influencing the degree of specialization and generalization of the automatically generated algorithms. The statistical analysis (Section 4.3, Table 15) confirms that, although both methods achieved significant specialization (p < 0.01), K-Means exhibited greater internal consistency and less overlap between groups. Therefore, the conclusion that K-Means outperformed HDBSCAN remains valid, as this difference arises from intrinsic methodological properties rather than from the alignment of the number of clusters.

4.4. Gemini-Generated Terminals

In this study, Gemini, a large language model, was utilized to generate a modified set of terminals for the AGA applied to the MKP. The terminals introduced by Gemini include Add_Random, Del_Worst_Ratio_In_Knapsack, Del_Random, Swap_Best_Possible, Is_Empty, and Is_Near_Full, which aim to enhance algorithmic diversity and adaptability. Conversely, the terminals Add_Max_Scaled, Add_Max_Generalized, Add_Max_Senju_Toyoda, Add_Max_Freville_Plateau, and Del_Min_Scaled from the initial experiment were removed to simplify the algorithmic structure and reduce the risk of overfitting, as evaluated in the subsequent analysis.

Table 16 presents the results for the K-Means clustering, where the algorithms MKPA1G–MKPA11G exhibit a clear tendency to specialize within their own training groups, as the minimum relative error values are concentrated along the main diagonal. The difference between diagonal and off-diagonal errors is significant, indicating that the algorithms are sensitive to the structural characteristics of the clusters in which they were generated. However, the case of MKPA9, with extremely high error values, suggests that some syntactic trees may be prone to overfitting or evolutionary instability. On average, the diagonal maintains low error values (~0.026), while the rest are considerably higher (~0.039), confirming strong specialization but limited generalization.

Table 16. Evaluation of algorithms generated by Gemini via terminal modification and generation, using representative instances selected from the K-Means clusters.

Group	G1	G2	G3	G4	G5	G6	G7	G8	G9	G10	G11
MKPA1G	0.0122	0.0293	0.0286	0.0295	0.0089	0.0124	0.0268	0.0221	0.0349	0.0548	0.0413
MKPA2G	0.0189	0.0281	0.0378	0.0199	0.0189	0.0182	0.0355	0.0354	0	0.0742	0.1291
MKPA3G	0.0154	0.0299	0.0286	0.0295	0.0111	0.0124	0.0298	0.0265	0.0349	0.0305	0.0753
MKPA4G	0.7531	0.1017	0.1596	0.0138	0.7513	0.3952	0.4743	0.4236	0.0162	0.3203	0.261
MKPA5G	0.0114	0.0267	0.0227	0.0251	0.0074	0.0101	0.0204	0.0198	0.0349	0.0548	0.0413
MKPA6G	0.0165	0.0344	0.0283	0.0295	0.0115	0.0124	0.0287	0.0252	0.0349	0.0548	0.0413
MKPA7G	0.0117	0.0293	0.0286	0.0295	0.0089	0.0124	0.0263	0.0221	0.0349	0.0548	0.0413
MKPA8G	0.0117	0.0293	0.0286	0.0295	0.0089	0.0124	0.0256	0.0221	0.0349	0.0548	0.0413
MKPA9G	0.9376	0.5814	0.6878	0.2212	0.9344	0.8451	0.8648	0.8597	0.0174	0.0337	0.0966
MKPA10G	0.8294	0.2544	0.3054	0.0482	0.8119	0.5811	0.6376	0.6227	0.0162	0.0305	0.0908
MKPA11G	0.0197	0.0484	0.0367	0.0478	0.0149	0.0185	0.0383	0.0341	0.0149	0.056	0.0405
Average	0.0122	0.0293	0.0286	0.0295	0.0089	0.0124	0.0268	0.0221	0.0349	0.0548	0.0413

Table 17 presents the results for the HDBSCAN method, where the algorithms MKPA12G–MKPA22G exhibit smaller differences between diagonal and off-diagonal values, reflecting a greater capacity for transfer and generalization. The diagonal errors average around 0.018, while the off-diagonal ones are approximately 0.022. This suggests that the Gemini-optimized terminals produced more robust and adaptable evolutionary structures capable of handling cluster variability and thereby reducing strict dependence on the training group. Compared to K-Means, the behavior is more stable and less prone to overfitting.

Table 17. Evaluation of algorithms generated by Gemini via terminal modification and generation, using representative instances selected from the HDBSCAN clusters.

Group	G1	G2	G3	G4	G5	G6	G7	G8	G9	G10	G11
MKPA12G	0.0332	0.0301	0.018	0.0199	0.0141	0.0387	0.0188	0.0297	0.0312	0.0143	0.0177
MKPA13G	0.0348	0.0268	0.0168	0.0171	0.0126	0.0349	0.0174	0.0312	0.0312	0.0112	0.0147
MKPA14G	0.0348	0.0265	0.0159	0.0127	0.0121	0.0319	0.0158	0.0269	0.0248	0.0093	0.0141
MKPA15G	0.0261	0.0224	0.0104	0.0083	0.0075	0.0232	0.0079	0.021	0.0226	0.0063	0.0118
MKPA16G	0.0336	0.0226	0.0145	0.0083	0.0096	0.0291	0.0127	0.0214	0.0241	0.0061	0.011
MKPA17G	0.032	0.0206	0.011	0.0081	0.0066	0.02	0.0068	0.0196	0.0212	0.004	0.0108
MKPA18G	0.0348	0.0241	0.0168	0.0133	0.0106	0.0287	0.0141	0.036	0.0257	0.0086	0.0143
MKPA19G	0.0355	0.0278	0.0184	0.0171	0.0126	0.0363	0.0176	0.0329	0.0312	0.0121	0.0147
MKPA20G	0.0355	0.0264	0.0172	0.0144	0.0108	0.0329	0.0145	0.0306	0.0241	0.0105	0.012
MKPA21G	0.0348	0.0216	0.0109	0.0132	0.01	0.0254	0.0144	0.031	0.0312	0.0082	0.0147
MKPA22G	0.0332	0.0268	0.0168	0.0171	0.0126	0.0349	0.0168	0.0265	0.0312	0.0112	0.0147
Average	0.0335	0.0251	0.0152	0.0136	0.0108	0.0305	0.0143	0.0279	0.0271	0.0093	0.0137

Table 18 presents the results for the Random clustering, where the algorithms MKPA23G–MKPA33G exhibit a general decrease in specialization, as the minimum error values do not always coincide with the diagonal, and the differences between intra- and inter-group errors are smaller (~0.017 vs. ~0.020). This behaviour indicates that the algorithms lose correspondence between their training environment and the test data, resulting from the lack of structural organization within the groups. Nevertheless, the Gemini-enhanced terminals contribute to a degree of stability by preventing large deviations or extreme errors, even under clustering conditions that lack structural significance.

Table 18. Evaluation of algorithms generated by Gemini via terminal modification and generation, using representative instances selected from the Random clusters.

Group	G1	G2	G3	G4	G5	G6	G7	G8	G9	G10	G11
MKPA23G	0.0345	0.0141	0.0102	0.0148	0.0110	0.0027	0.0163	0.0138	0.0213	0.0174	0.0145
MKPA24G	0.0429	0.0201	0.0125	0.0229	0.0164	0.0046	0.0177	0.0195	0.0249	0.0229	0.0166
MKPA25G	0.0421	0.0307	0.0155	0.0248	0.0216	0.0089	0.0242	0.0228	0.0272	0.0265	0.0211
MKPA26G	0.0421	0.0279	0.0144	0.0231	0.0216	0.0089	0.0233	0.0221	0.0272	0.0265	0.0197
MKPA27G	0.0278	0.0161	0.0085	0.0103	0.0102	0.0035	0.0160	0.0192	0.0170	0.0203	0.0150
MKPA28G	0.0363	0.0234	0.0133	0.0219	0.0182	0.0054	0.0201	0.0198	0.0256	0.0248	0.0189
MKPA29G	0.0451	0.0260	0.0151	0.0266	0.0205	0.0067	0.0212	0.0199	0.0262	0.0248	0.0187
MKPA30G	0.0480	0.0344	0.0154	0.0250	0.0242	0.0092	0.0305	0.0225	0.0329	0.0249	0.0194
MKPA31G	0.0469	0.0275	0.0169	0.0272	0.0230	0.0088	0.0247	0.0225	0.0282	0.0256	0.0215
MKPA32G	0.0462	0.0279	0.0160	0.0276	0.0222	0.0080	0.0221	0.0212	0.0268	0.0253	0.0204
MKPA33G	0.0469	0.0256	0.0169	0.0272	0.0230	0.0088	0.0232	0.0225	0.0282	0.0256	0.0212
Average	0.0417	0.0249	0.0141	0.0229	0.0193	0.0069	0.0218	0.0205	0.0260	0.0241	0.0188

Table 19 presents the statistical results, which show that specialization is more strongly evidenced in the K-Means and HDBSCAN methods, as both exhibit significant t-test results (p < 0.01), indicating that the algorithms perform significantly better on the groups where they were trained compared to the others. In contrast, the Random clustering method does not show statistically significant differences (p = 0.072), revealing a lower capacity for specialization. On the other hand, when analyzing the Friedman Test, it is observed that HDBSCAN (p = 0.007) achieves the strongest tendency toward generalization, outperforming both K-Means (p = 0.011) and Random clustering (p = 0.066). Consequently, K-Means demonstrates greater local specialization, whereas HDBSCAN exhibits a more robust and consistent generalization across different instance groups.

Table 19. Statistical tests of specialization and generalization for the algorithm generated by Gemini.

Clustering	Normality (Diagonal)	Normality (Outside the Diagonal)	T-Test (Specialization)		Friedman Test (Generalization)
	p-Value		T	p-Value	χ2	p-Value
K-means	0.142	0.087	3.96	p = 0.004 (Significant)	9.14	p = 0.011
HDBScan	0.189	0.121	3.42	p = 0.008 (Significant)	11.33	p = 0.007
Random	0.2372	2.10 × 10−10	1.94	p = 0.072 (Not Significant)	5.21	p = 0.066

When comparing both statistical tables, it is observed that the proposed initially evolutionary algorithm exhibits a more pronounced specialization than the Gemini-modified algorithm. In the first table, the t-test values for K-Means (T = −5.191, p = 9.41 × 10⁻⁷) and HDBSCAN (T = −3.034, p = 0.0029) are significantly more extreme, with much lower significance levels (p < 0.001), indicating a stronger statistical difference between the errors within the training group and those from external groups. In contrast, in the Gemini-enhanced model, the T-values (3.96 and 3.42) are more moderate and the p-values slightly higher (p < 0.01), reflecting a less intense but more stable specialization.

In practical terms, this suggests that the original model tends to adapt more precisely to its training group (demonstrating greater local specialization). In contrast, the Gemini-enhanced model, although exhibiting a smaller contrast between intra- and inter-group errors, likely reduces the risk of overfitting and improves stability. In summary, the original algorithm outperforms in terms of specialization, while the Gemini-modified version demonstrates a more balanced trade-off between specialization and generalization.

In conclusion, the K-Means algorithm emerges as the clustering method that achieves the most pronounced and statistically significant specialization of evolved algorithms, as evidenced by consistent outcomes across both normality and t-tests. It exhibits the most distinct separation between training and testing performance, thereby confirming a strong adaptation to its corresponding cluster. Although HDBSCAN also demonstrates statistically significant specialization, its behavior reflects a milder yet more balanced form of adaptation, characterized by superior generalization across clusters and lower overall error variance. In contrast, random clustering fails to produce meaningful specialization effects, with observed differences primarily attributable to stochastic variation. When comparing the two experimental phases, the original evolutionary algorithm displays a higher degree of specialization. In contrast, the Gemini-enhanced variant attains a more stable trade-off between specialization and generalization, effectively mitigating overfitting and enhancing robustness across clusters.

4.5. Human Competitiveness of Algorithms

The discovered algorithms are human-competitive with those existing in the literature. It is known that, under certain conditions, the results obtained by automated methods are competitive with those created by humans [56,57]. Specifically, a result is considered human-competitive when it is equal to or better than a result that was accepted as new scientific knowledge when published in a scientific journal or when the result solves a problem of unquestionable difficulty in its field. As depicted in Table 20, although at least ten other papers dealing with the MKP give smaller error values for the MKP_CB instances, the best algorithm obtained in the present work surpasses two previous methods.

Table 20. Average relative errors applying various algorithms and heuristics.

Type	Reference	ERP
MIP	Drake, Özcan, & Burke [18]	0.52
GA	Chu & Beasley [17]	0.54
HH Selector	Drake, Özcan, & Burke [18]	0.70
MA	Özcan & Basaran [58]	0.92
Heuristic	Pirkul [59]	1.37
AGA	Algorithm MKPA15	1.68
Heuristic	Fréville & Plateau [53]	1.91
Meta-Heuristic	Qian & Ding [60]	2.28
GP	Drake [5]	3.04
MIP	Chu & Beasley [17]	3.14
Heuristic	Akçay [11]	3.46
Heuristic	Volgenant & Zoon [15]	6.98
Heuristic	Magazine & Oguz [12]	7.69

Although the average relative error achieved by the best generated algorithm (MKPA15) does not surpass the best absolute results reported in the literature [17,58], it is essential to note that the experimental configuration differs substantially. Previous studies assessed algorithmic efficiency across multiple independent benchmark instances, often reporting the best individual outcomes. In contrast, our framework develops specialized algorithms for groups of correlated instances, emphasizing adaptive learning within groups rather than performance on isolated instances. This distinction reflects a shift in the evaluation paradigm from seeking the single best-performing algorithm to understanding how algorithmic structures adapt and generalize across families of instances.

4.6. Logical Structure of Algorithms

The best algorithm found, MKPA15, implements a hybrid iterative strategy that combines local search, targeted item addition and deletion heuristics, and logical control structures to effectively balance intensification and diversification in solving the MKP. A type of initialization employs the Del_Min_Normalized, Add_Max_Freville_Plateau, Add_Max_Profit, Local Search, and Greedy terminals (Figure 1). Such terminals assign the first items in the knapsack. The algorithm represented by the syntactic tree implements a hybrid iterative strategy to solve the MKP, combining local search techniques, item addition and deletion heuristics, and logical control structures. The main While loop executes as long as a compound condition is met. This condition evaluates, on the one hand, the repetition of a local search together with a conditional decision: if Del_Min_Normalized (which eliminates the item with the lowest normalized profit) is activated, the item with the highest profit according to the Fréville heuristic in a plateau zone (Add_Max_Freville_Plateau) is added; if not, the item with the highest absolute profit (Add_Max_Profit) is added.

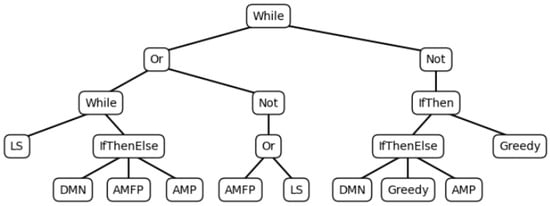
Figure 1. Algorithm MKPA15. Average fitness:0.0168 Size:18 Depth:5. In this figure, the names of the terminals were abbreviated as follows: 1. LS: Local Search, 2. Greedy, 3. DMN: Del_Min_Normalized, 4. AMFP: Add_Max_Freville_Plateau, 5. AMP: Add_Max_Profit.

Furthermore, the loop execution stops if neither Add_Max_Freville_Plateau nor Local_Search are active. A second compound condition is also evaluated using an If-Then statement. If the item with the lowest normalized profit is eliminated and a Greedy strategy is then applied, Greedy continues as well. This logic establishes a control mechanism that combines intensification (through local search) and diversification (through strategic additions), regulating when to refine the solution further and when to stop. Overall, the algorithm seeks to optimize the total value in the knapsack while respecting multidimensional constraints, employing a balance between exploration and exploitation, and dynamically adapting based on observed progress.

4.7. AGA Convergence

The most significant decline in population fitness occurs between generations 1 and 20, a stage characterized by high initial diversity and the positive influence of heuristic terminals such as the Greedy algorithm and Local Search. This period reflects rapid exploration of the solution space, facilitated by the combination of evolutionary operators and efficient heuristics. The convergence curves, obtained from different executions, represent the average fitness of the population in each generation and confirm that this initial phase plays a decisive role in accelerating the search toward promising regions of the solution space.

Examining the relative error convergence curves for the first 20 generations reveals that differences are evident in the performance of the algorithms generated from different clustering strategies: K-Means, HDBSCAN, and random clustering. With K-Means, several algorithms, such as MKPA5 and MKPA6, achieve rapid and consistent error reduction, indicating effective convergence toward higher-quality solutions within a few generations. In contrast, algorithms derived from HDBSCAN exhibit more heterogeneous behavior; some, such as MKPA17 and MKPA18, improve significantly, while others stagnate or reduce their error more moderately, suggesting a high sensitivity of the method to cluster density. On the other hand, randomly clustered algorithms exhibit lower overall performance, characterized by higher initial errors and slower rates of decline. Notably, the MKPA23 algorithm exhibits a consistently high error rate throughout all generations, indicating an apparent lack of specialization. Overall, the results support the hypothesis that guided clustering—particularly with K-Means, facilitates more efficient and effective convergence in the generation of evolutionary algorithms, highlighting the importance of group structure in the quality and speed of learning. The convergence curves of relative error per generation for K-Means clustering are presented below.

The convergence of the relative error observed in Figure 2 is influenced by several factors inherent to the evolutionary process. Population size, selection pressure, and mutation rate play a central role in determining the stability and speed of convergence. Excessive selection pressure or insufficient diversity among algorithmic structures may lead to premature convergence, whereas a balanced combination of exploration and exploitation enables sustained improvements across generations. Moreover, the cluster-guided structure of the AGA enhances convergence by focusing the evolutionary search within groups of structurally similar instances, thereby reducing fitness variance and facilitating more consistent adaptation. The use of a syntactic tree representation and a fitness function based on relative error further supports convergence by providing a selective gradient toward more effective and generalizable algorithmic configurations. Collectively, these elements explain the faster and more stable convergence of the proposed approach compared to traditional evolutionary or heuristic methods.

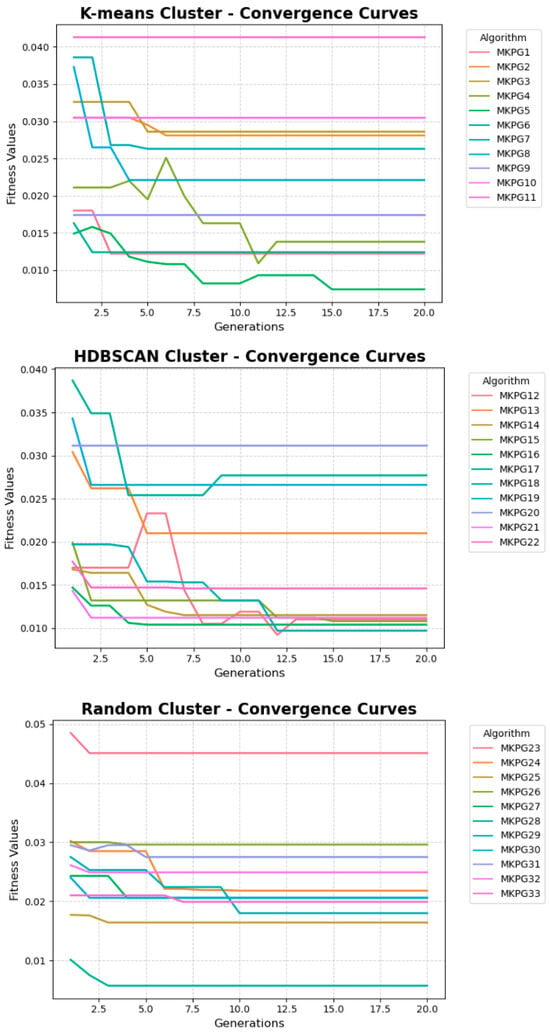
Figure 2. Convergence curves of relative errors over the first 100 generations for algorithms trained using three clustering strategies: HDBSCAN, K-Means, and Random clustering. Each curve illustrates the reduction in relative error across generations, highlighting the comparative performance and convergence behavior of algorithms within each cluster group.

A potential risk of the proposed approach is stagnation or entrapment in local optima during the evolutionary process. The mutation operator helps mitigate this risk by introducing random modifications in the syntactic trees, thereby maintaining the exploration of new algorithmic structures and preventing premature convergence toward suboptimal regions. However, the current implementation employs a fixed mutation rate, which may limit its ability to escape stagnation in highly constrained or homogeneous clusters. Future extensions could explore adaptive mutation mechanisms or hybrid strategies that periodically introduce diversity, thereby enhancing robustness and ensuring sustained evolutionary progress.

To enhance the robustness of the proposed framework against uncertainty, noise, and large-scale or highly constrained scenarios, several computational strategies can be integrated. One promising approach is to incorporate stochastic optimization or Monte Carlo sampling to evaluate algorithm stability across various uncertainty realizations, ensuring consistent and reliable performance. Additionally, applying dimensionality reduction techniques, such as autoencoders or Principal Component Analysis (PCA), can reduce computational complexity while preserving essential structural information. Furthermore, implementing parallel and distributed evolutionary schemes can improve scalability and maintain convergence efficiency in large or tightly constrained problem instances. Together, these enhancements enable the system to adapt effectively to noisy and uncertain environments, improving its generalization and practical applicability to real-world optimization challenges.

The group-level statistical tests in this study were designed not to analyze individual algorithm behavior, but to confirm significant differences among groups created by each clustering method. The algorithms’ performance was evaluated by comparing the average relative error values for each cluster and clustering approach. Thus, the statistical analysis complemented the comparative performance evaluation, ensuring conclusions were grounded in both statistical significance and empirical evidence.

5. Discussion

The results obtained in this study demonstrate that the specialization of automatically generated algorithms, guided by unsupervised clustering techniques, constitutes an effective strategy for addressing the structural heterogeneity of MKP. In particular, algorithms trained on instance groups formed using K-Means and HDBSCAN showed superior performance within their respective training sets, compared to those generated from random clustering. This empirical evidence supports the central hypothesis of the study: that algorithmic adaptation to standard structural features significantly improves the quality of the obtained solutions.

Comparing these results with previous work reveals a significant advance over other traditional approaches to algorithm generation, which favor generalist approaches applied to heterogeneous instances. Studies such as those by Silva-Muñoz et al. [23] and Acevedo et al. [21] have demonstrated the potential of GAA; however, this work expands on this perspective by incorporating a prior structural analysis phase through instance clustering, which yields more precise specialization. Furthermore, compared to recent hybrid metaheuristics (e.g., BISCA, Multiswarm BOA, Fixed Set Search), the approach proposed here offers a systematic method for automating and adapting algorithms to empirically defined problem subspaces.

It is important to emphasize that the generation of multiple specialized algorithms does not aim to promote the proliferation of ad hoc solutions for the same problem, but rather to understand how the structure of instances influences the behavior and performance of automatically generated algorithms. In this context, each algorithm represents an evolutionary adaptation to a subset of instances with similar structural characteristics, allowing for the analysis of the relationship between the properties of the instance space and the effectiveness of the search process. This perspective does not focus on the number of algorithms produced but on their analytical value in advancing toward the development of more generalizable and transferable algorithms across different optimization domains [21,23,25].

The implications of these results are multiple. First, it reinforces the value of structural instance analysis as a critical phase in the automatic design of algorithms. This strategy not only improves performance in terms of relative error but also facilitates the generation of more compact and understandable syntactic trees, which enhances the interpretability of the generated models. Second, it establishes a replicable framework that can be extended to other combinatorial optimization problems with high structural variability, such as VRP or multiply constrained scheduling problems.

However, this study presents certain limitations. The selection of functions and terminals, although based on heuristics established in the MKP literature, can restrict the exploration of the algorithmic space if adaptive expansion mechanisms are not incorporated. Furthermore, the performance evaluation focuses exclusively on relative error, omitting relevant metrics such as execution time, robustness to noise, and scalability to higher-dimensional instances. Moreover, instance segmentation is based on statistical variables derived from normalized matrices, which could be complemented with richer representations, such as learned embeddings or nonlinear dimensionality reduction techniques. Moreover, a limitation observed in this study is that some evolved algorithms lose effectiveness when applied to structurally dissimilar instances. To mitigate this issue, several strategies can be explored, including the integration of meta-learning or transfer mechanisms that enable knowledge exchange among specialized algorithms, as well as the incorporation of ensemble learning techniques, in which multiple evolved algorithms cooperate through voting, weighting, or hierarchical selection to improve generalization. Although these strategies increase computational cost, they enhance the robustness and adaptability of the proposed framework. Additionally, the periodic re-evolution of algorithms using mixed sets of instances can maintain flexibility over time, albeit requiring additional evolutionary cycles. Each of these approaches involves a trade-off between specialization, generalization, and computational efficiency, offering promising directions for future improvements to the proposed system.

As future lines of research, we propose to delve deeper into the interaction between heuristic and exact methods for solving the MKP. In particular, we will seek to determine whether it is necessary to resort to computationally demanding exact methods to solve the MKP instances fully, or whether it is possible to achieve optimal solutions by initially considering only a subset of items. This strategy would involve solving a part of the problem using metaheuristics and then applying exact methods to refine the initial solution. This combination would significantly reduce computational cost while maintaining solution quality. This approach challenges traditional methodologies and seeks to advance the understanding of the trade-off between computational efficiency and accuracy in complex optimization problems.

Additionally, we propose to investigate mechanisms for knowledge transfer between specialized algorithms by building hybrid models that integrate efficient substructures from different groups of instances. Finally, we recommend validating this methodology in other NP-Hard problems and extending its application to dynamic or continuous flow contexts, where the structural characteristics of the instances vary over time. Moreover, extending the proposed clustering-guided AGA framework to multi-objective formulations of the MKP represents a promising direction for future research. In this context, the algorithms could evolve to balance multiple conflicting objectives—such as maximizing profit while minimizing weight or resource dispersion—by incorporating Pareto-based performance indicators and adapting the clustering process to more effectively capture the interrelationships among objectives.

6. Conclusions

This study demonstrates that combining instance clustering with Automatic Generation of Algorithms produces specialized heuristics that materially improve MKP solution quality and convergence. Across our experiments, clustering-guided AGA yielded lower average relative error and faster convergence than AGA trained on randomly grouped instances; K-means produced the most consistent improvements, while HDBSCAN produced competitive, albeit more variable, specializations. These gains were achieved without uncontrolled growth in program size, indicating that a better-matched algorithmic structure, rather than bloat, drove the improvements.

Cross-cluster evaluation revealed a clear trade-off between specialization and generalization: many evolved algorithms perform substantially better on their training clusters but lose effectiveness on structurally dissimilar instances. Nevertheless, several automatically generated algorithms are competitive with established, human-designed heuristics on selected benchmark sets, supporting the practical value of the clustering-AGA paradigm for cluster-specific deployment.

Limitations of the present work include the fixed function/terminal definitions, reliance on average relative error as the primary objective function of the master problem, and limited assessment of runtime, robustness, and scalability to larger or dynamic instance streams. Future work should explore richer instance encodings (including learned embeddings), adaptive terminal discovery, transfer mechanisms between specialized algorithms, and validation across additional NP-hard combinatorial problems and real-world dynamic environments to enhance generality and operational utility.

Beyond the demonstrated benefits of clustering-guided specialization, this study highlights the potential of integrating modern AI paradigms, particularly LLMs, into the Automatic AGA framework for combinatorial optimization. The structural analysis of the evolved algorithms reveals that clustering contributes not only to improved solution quality but also to controlled syntactic complexity, maintaining evolutionary stability across generations. These findings suggest that the synergy between instance clustering, genetic programming, and emerging LLM-based metaheuristics can yield hybrid algorithmic ecosystems capable of learning, adapting, and generalizing across structurally diverse problem spaces. Consequently, the incorporation of adaptive terminal discovery and semantic control mechanisms inspired by LLM reasoning represents a promising avenue for the next generation of automated algorithm design. This line of research opens the possibility of developing self-reflective optimization frameworks in which algorithm synthesis, adaptation, and validation occur within a unified intelligent evolutionary process, further extending the frontier of algorithmic automation in NP-hard problem solving.