A Unified Size-Dependent Theory for Analyzing the Free Vibration Behavior of an FG Microplate Under Fully Simply Supported Conditions and Magneto-Electro-Thermo-Mechanical Loads Considering Couple Stress and Thickness Stretching Effects

Abstract

This work develops a unified size-dependent shear deformation theory (SDSDT) to analyze the free vibration behavior of a functionally graded (FG) magneto-electro-elastic (MEE) microplate under fully simply supported conditions, open- or closed-circuit surface conditions, biaxial compression, magnetic and electric potentials, and uniform temperature changes based on consistent couple stress theory (CCST). The FG-MEE microplate is composed of BaTiO₃ (a piezoelectric material) and CoFe₂O₄ (a magnetostrictive material). Various CCST-based SDSDTs, considering couple stress and thickness stretching effects, can be reproduced by employing a generalized shape function that characterizes shear deformation distributions along the thickness direction within the unified SDSDT. These CCST-based SDSDTs encompass the size-dependent classical plate theory (CPT), first-order shear deformation theory (SDT), Reddy’s refined SDT, exponential SDT, sinusoidal SDT, and hyperbolic SDT. The unified SDSDT is validated by comparing its solutions with relevant three-dimensional solutions available in the literature. After validation and comparison studies, we conduct a parametric study, whose results indicate that the effects of thickness stretching, material length-scale parameter, inhomogeneity index, and length-to-thickness ratio, as well as the magnitude of biaxial compressive forces, electric potential, magnetic potential, and uniform temperature changes significantly impact the microplate’s natural frequency.

1. Introduction

Functionally graded (FG) materials are emerging advanced materials, typically composed of two-phase isotropic elastic, piezoelectric, or magnetic materials mixed in varying volume fractions, thereby combining the advantages of both individual materials [1,2]. This composite material structure can avoid delamination and stress concentration shortcomings caused by sudden changes in material properties between adjacent layers in laminated composite structures. The FG structure’s material properties change smoothly and continuously along its thickness direction or the whole domain. On the other hand, because the constituents’ volume fractions can be designed in advance according to the FG structure’s task requirements, it also provides engineers with flexibility in practical applications [3,4]. Hence, microscale and macroscale FG structures have been commonly employed in advanced industries, including electronics [2], microelectromechanical systems [5], biomedical sectors [2], atomic force microscopes [6], broadband ultrasonic transducers [7], and turbine engines [8].

Many reports indicate that when the scale of an FG structure is reduced from the macroscale to the microscale, its structural behavior differs from that of an FG macroscale structure due to the size-dependent effect. This results in various shear deformation theories derived within the classical continuum mechanics (CCM) framework becoming infeasible for analyzing an FG microscale structure. To address the above issue, several size-dependent theories based on higher-order continuum mechanics (HOCM) have been proposed and presented [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Among these HOCM-based theories, the MCST and the CCST are more commonly employed for analyzing the mechanical behavior of an FG microscale structure than others.

Within the MCST framework, several unified theories based on CCM for analyzing an FG macroscale plate have been reformulated to account for size-dependent effects, thereby developing corresponding unified size-dependent shear deformation theories (SDSDTs) for analyzing an FG microplate. In the unified SDSDTs based on the MCST, a generalized shape function is designed to characterize the through-thickness distribution of shear deformation in the formulation, allowing various two-dimensional (2D) MCST-based SDSDTs to be reproduced by employing specific shear deformation functions within the unified formulation. These SDSDTs include the MCST-based classical plate theory (CPT), first-order shear deformation theory (SDT), Reddy’s refined SDT, sinusoidal SDT, exponential SDT, and hyperbolic SDT. The aforementioned SDSDTs based on the MCST have also been employed to analyze the mechanical behavior of an FG microplate.

Based on the MCST, Trinh et al. [29] developed a unified SDSDT to conduct static buckling, static bending, and free vibration analyses of FG microbeams. Liu and Zhang [30] presented a unified SDSDT to examine the nonlinear dynamic characteristics of a bidirectional FG microbeam. Simsek and Reddy [31] investigated the static buckling behavior of an FG microbeam embedded in a Pasternak elastic medium using various SDSDTs. Li et al. [32] investigated the coupled electro-elastic static bending and free vibration behaviors of an FG piezoelectric microbeam using a size-dependent higher-order SDT. Lou et al. [33] incorporated a higher-order displacement model into the MCST to capture the size-dependent effects influencing an FG microplate’s static buckling, static bending, and free vibration behaviors. Tran et al. [34] proposed a unified SDSDT for analyzing the static buckling and stochastic vibration behaviors of an FG microplate.

Distinct from the unified SDSDTs based on the previously mentioned MCST, within the CCST framework, Wu and Huang [35] and Wu and Lin [19] proposed a unified SDSDT to investigate the static buckling, static bending, and free vibration behaviors of an FG elastic microbeam, as well as the free vibration behavior of a porous FG piezoelectric microplate, respectively. The differences between the critical loads, lowest natural frequencies, and maximum deflections obtained using the MCST and the CCST were examined and discussed. Within the framework of strain gradient elasticity theory, Serpilli et al. [36] developed a size-dependent model to analyze the mechanical behavior of a laminated microbeam with a soft adhesive. Jedreysiak [37] proposed two models for analyzing the mechanical behavior of transversely graded laminates: the tolerance model and the asymptotic model. The tolerance model, which accounts for the microstructure size effect, is applicable for investigating the mechanical behavior of microscale structures. In contrast, the asymptotic model, which ignores the microstructure size effect, is suitable only for examining the mechanical behavior of macroscale structures. Consequently, the tolerance model was employed by Jedrysiak and Kazmierczak-Sobinska [38], Kazmierczak and Jedrysiak [39], and Jedrysiak [40,41] to analyze the dynamic responses of a one-directional thin or moderately thick FG plate. Using both the tolerance and asymptotic models, Tomczyk and Szczerba [42] studied the dynamic problems for thin transversally graded microscale and macroscale shells, respectively. Tomczyk and Szczerba [43] and Kazmierczak and Jedrysiak [44] proposed a new combined asymptotic-tolerance model to investigate the vibration problems of a thin transversally graded plate and the dynamic and stability challenges of a longitudinally graded cylindrical shell.

In recent decades, the development of magneto-electro-elastic (MEE) materials and structures, along with their applications, has received considerable attention due to their outstanding performance and highly coupled, multifield physical behavior when subjected to generalized magneto-electro-mechanical loads in a thermal environment [45]. Among these analyses, the FG-MEE microplate was composed of BaTiO₃ (a piezoelectric material) and CoFe₂O₄ (a magnetostrictive material), whose material properties obey a power-law distribution of the constituents’ volume fraction along the thickness direction. Based on the first-order SDT, Zhang et al. [46] developed an eight-node quadrilateral element to investigate the free vibration characteristics and the static bending behavior of an FG-MEE macroscale plate or shell. Employing the Reissner mixed variational principle, Garcia Lage et al. [47] derived a mixed finite element formulation and subsequently applied it to develop a partial mixed layerwise finite element method for analyzing the static bending behavior of an FG-MEE macroscale plate. Several three-dimensional (3D) solutions of the mechanical behaviors of an FG-MEE macroscale plate or shell have also been presented [48]. Ghadiri and Safarpour [49] incorporated the first-order SDT’s kinematics model into the MCST to analyze the free vibration characteristics of an FG-MEE cylindrical nanoshell embedded in a Winkler elastic medium and placed in a thermal environment. Qu et al. [50] extensively applied the MCST-based first-order SDT to investigate the static bending behavior and free vibration characteristics of an anisotropic FG-MEE plate. Finally, Guo et al. [51] presented 3D solutions for the static bending behavior of an anisotropic multilayered MEE microplate using the state space method.

After a rigorous literature review, we found that there were many more articles related to analyzing MEE macroscale plates than those associated with analyzing MEE microplates. In addition, most relevant analyses were based on the 2D SDSDTs, rather than the quasi-3D MCST/CCST, where the thickness stretching effect is neglected. Thus, their results should be unreliable when the plate of interest becomes thicker. As a result, to capture the thickness stretching effect and account for it in the analysis within the CCST framework, we aim to develop a unified SDSDT capable of analyzing the free vibration characteristics of an FG-MEE microplate. The accuracy of the unified SDSDT will be validated by comparing its solutions with relevant 3D solutions reported in the literature. Furthermore, a parametric study will be conducted to investigate the influence of certain primary effects on the lowest frequency of an FG-MEE microplate. The primary factors encompass thickness stretching, material length-scale parameter, inhomogeneity index, and thickness-to-length ratio effects, as well as the magnitude of biaxial compressive forces, electric potential, magnetic potential, and uniform temperature changes.

2. Formulations

Based on the CCST framework, we develop a unified SDSDT suitable for analyzing the free vibration characteristics of an FG-MEE microplate under fully simply supported conditions and subjected to magneto-electro-thermo-mechanical loads, as shown in Figure 1. The microplate of interest is subjected to biaxial compressive forces at its edges, electric and magnetic potentials on its top and bottom surfaces, and a uniform temperature change. In the following sections, we derive a strong form of the unified SDPT using Hamilton’s principle. The material properties are assumed to follow either a power-law distribution of the constituent materials’ volume fractions along the thickness direction or an exponential function along the thickness direction.

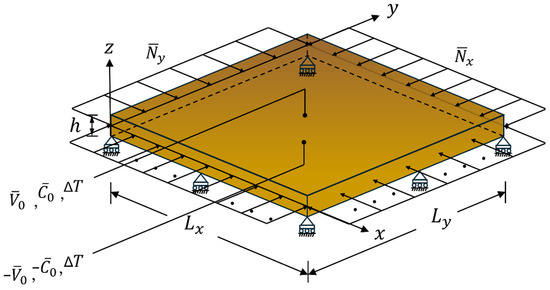
Figure 1. A schematic diagram of an FG-MEE microplate under fully simply supported conditions and magneto-electro-thermo-mechanical loads. FG: functionally graded; MEE: magneto-electro-elastic.

2.1. The Unified Kinematics Model and Relevant Equations

In the unified SDSDT, the generalized displacement components are expressed as follows [18]:

$$u_x\left(x, y, z, t\right)=u\left(x, y, t\right)-z {\displaystyle \frac{\partial w\left(x, y, t\right)}{\partial x}}+f\left(z\right) {\gamma }_x\left(x, y, t\right),$$

(1)

$$u_y\left(x, y, z, t\right)=v\left(x, y, t\right)-z {\displaystyle \frac{\partial w\left(x, y, t\right)}{\partial y}}+f\left(z\right) {\gamma }_y\left(x, y, t\right),$$

(2)

$$u_z\left(x, y, z, t\right)=w\left(x, y, t\right)+\left(Df\right) {\gamma }_z\left(x, y, t\right),$$

(3)

$$\Phi \left(x, y, z, t\right)=-g\left(z\right)\varphi \left(x, y ,t\right)+\left(2z{\overline{V}}_0/h\right),$$

(4)

$$\Psi \left(x, y, z, t\right)=-g\left(z\right)\psi \left(x, y, t\right)+\left(2 z {\overline{C}}_0/h\right),$$

(5)

where $u, v, \mathrm{and} w$ represent the microplate’s mid-plane displacements in the x, y, and z directions, respectively; $\varphi$ and $\psi$ are defined as the microplate’s mid-plane electric and magnetic potentials, respectively; and ${\gamma }_x, {\gamma }_y, \mathrm{and} {\gamma }_z$ denote the microplate’s mid-plane shear rotations in the xz-, yz-, and xy-planes, respectively. ${\overline{V}}_0$ and $-{\overline{V}}_0$ are the constant electric potentials acting at the microplate’s top and bottom surfaces, respectively, and ${\overline{C}}_0$ and $-{\overline{C}}_0$ are the constant magnetic potentials applied to the microplate’s top and bottom surfaces, respectively. $g\left(z\right)$ is given as $g\left(z\right)=\cos \left(\pi z/h\right)$. The generalized displacement fields of the CCST-based CPT and various first- and higher-order SDTs can be obtained by defining $f\left(z\right)$ in the following form:

$$\mathrm{CPT}: f\left(z\right)=0,$$

(6)

$$\mathrm{FOSDT}: f\left(z\right)=z,$$

(7)

$$\mathrm{RRSDT}: f\left(z\right)=z-\left[\left(4z^3\right)/\left(3h^2\right)\right],$$

(8)

$$\mathrm{SSDT}: f\left(z\right)=\left(h/\pi \right)\sin \left(\pi z/h\right),$$

(9)

$$\mathrm{ESDT}: f\left(z\right)=z e^{-\left(2z^2/h^2\right)},$$

(10)

$$\mathrm{HSDT}: f\left(z\right)=z \cosh \left(1/2\right)-h \sinh \left(z/h\right).$$

(11)

The microplate’s strain-displacement relations, following Hadjesfandiari [17], are given as $\epsilon =\left(1/2\right)\left[\nabla u+{\left(\nabla u\right)}^T\right]$, such that

$${\epsilon }_{xx}=u_x{,}_x=u{,}_x-z w{,}_{xx}+f {\gamma }_x{,}_x,$$

(12)

$${\epsilon }_{yy}=u_y{,}_y=v{,}_y-z w{,}_{yy}+f {\gamma }_y{,}_y,$$

(13)

$${\epsilon }_{zz}=u_z{,}_z=\left(D^{2}f\right) {\gamma }_z,$$

(14)

$${\gamma }_{xz}=u_x{,}_z+u_z{,}_x=\left(Df\right)\left({\gamma }_x+{\gamma }_z{,}_x\right),$$

(15)

$${\gamma }_{yz}=u_y{,}_z+u_z{,}_y=\left(Df\right)\left({\gamma }_y+{\gamma }_z{,}_y\right),$$

(16)

$${\gamma }_{xy}=u_x{,}_y+u_y{,}_x=u{,}_y+ v{,}_x-2 z w{,}_{xy}+f\left({\gamma }_x{,}_y+{\gamma }_y{,}_x\right),$$

(17)

where the commas represent the suffix variable’s derivative; $Df=d f/dz$ and $D^{2}f=d^{2}f/d{z}^2;$ the symbol $\nabla$ represents the gradient operator; and the superscript T represents a matrix’s or a vector’s transpose.

The microplate’s electric field-electric potential relationship is given as $E=E_x i+E_y j+E_z k=-\nabla \Phi$, such that [17]

$$E_x=-\Phi {,}_x=g \varphi {,}_x$$

(18)

$$E_y=-\Phi {,}_y=g \varphi {,}_y$$

(19)

$$E_z=-\Phi {,}_z=\left(D g\right)\varphi -\left(2{\overline{V}}_0/h\right),$$

(20)

where $D g=d g\left(z\right)/dz$.

The relationship between the microplate’s magnetic field and magnetic potential is expressed as follows [48]:

$$H_x=-\Psi {,}_x=g \psi {,}_x$$

(21)

$$H_y=-\Psi {,}_y=g \psi {,}_y$$

(22)

$$H_z=-\Psi {,}_z=\left(D g\right)\psi -\left(2{\overline{C}}_0/h\right).$$

(23)

The microplate’s rotation-displacement relationship is expressed as follows [17]:

$$\mathsf{\theta }={\theta }_x i+{\theta }_y j+{\theta }_z k=\left(1/2\right)\mathrm{curl}\left(u\right),$$

(24)

where u denotes the displacement tensor and is expressed as $u=u_x i+u_y j+u_z k$, such that

$${\theta }_x={\theta }_{zy}=\left(1/2\right)\left[2 w{,}_y- \left(Df\right)\left({\gamma }_y-{\gamma }_z{,}_y\right)\right],$$

(25)

$${\theta }_y={\theta }_{xz}=\left(1/2\right)\left[-2 w{,}_x+\left(Df\right)\left({\gamma }_x-{\gamma }_z{,}_x\right)\right],$$

(26)

$${\theta }_z={\theta }_{yx}=\left(1/2\right)\left[ \left(v{,}_x-u{,}_y\right)+f\left({\gamma }_y{,}_x- {\gamma }_x{,}_y\right)\right].$$

(27)

The microplate’s symmetric part of the curvature tensor $\chi$ is expressed as $\chi =\left(1/2\right)\left[\nabla \theta +{\left(\nabla \theta \right)}^T\right]$, such that [17]

$${\chi }_{xx}={\theta }_x{,}_x=w{,}_{xy}+\left(1/2\right)\left(Df\right)\left[-{\gamma }_y{,}_x+{\gamma }_z{,}_{xy}\right],$$

(28)

$${\chi }_{yy}={\theta }_y{,}_y=-w{,}_{xy}+\left(1/2\right)\left(Df\right)\left[{\gamma }_x{,}_y-{\gamma }_z{,}_{xy}\right],$$

(29)

$${\chi }_{zz}={\theta }_z{,}_z=\left(1/2\right)\left(Df\right)\left({\gamma }_y{,}_x-{\gamma }_x{,}_y\right),$$

(30)

$${\chi }_{xz}=\left(1/2\right)\left({\theta }_x{,}_z+{\theta }_z{,}_x\right)=\left(1/4\right)\left[\left(v{,}_{xx}-u{,}_{xy}\right)+f\left({\gamma }_y{,}_{xx}-{\gamma }_x{,}_{xy}\right)+\left(D^{2}f\right)\left(-{\gamma }_y+{\gamma }_z{,}_y\right)\right],$$

(31)

$${\chi }_{yz}=\left(1/2\right)\left({\theta }_y{,}_z+{\theta }_z{,}_y\right)=\left(1/4\right)\left[\left(v{,}_{xy}-u{,}_{yy}\right)+f\left({\gamma }_y{,}_{xy}-{\gamma }_x{,}_{yy}\right)+\left(D^{2}f\right)\left({\gamma }_x-{\gamma }_z{,}_x\right)\right],$$

(32)

$${\chi }_{xy}=\left(1/2\right)\left({\theta }_x{,}_y+{\theta }_y{,}_x\right)=\left(1/2\right)\left(-w{,}_{xx}+w{,}_{yy}\right)+\left(1/4\right)\left(Df\right)\left({\gamma }_x{,}_x-{\gamma }_y{,}_y-{\gamma }_z{,}_{xx}+{\gamma }_z{,}_{yy}\right).$$

(33)

The microplate’s skew-symmetric part of the curvature tensor $\mathit{\kappa }$ is expressed as $\mathit{\kappa }={\kappa }_x i+{\kappa }_y j+{\kappa }_z k=\left(1/2\right)\mathrm{curl}\left(\mathit{\theta }\right)$ [17], such that

$${\kappa }_x={\kappa }_{zy}=\left(1/2\right)\left(-{\theta }_y{,}_z+{\theta }_z{,}_y\right)=\left(1/4\right)\left[\left(-u{,}_{yy}+v{,}_{xy}\right)+f\left(-{\gamma }_x{,}_{yy}+{\gamma }_y{,}_{xy}\right)+\left(D^{2}f\right)\left(-{\gamma }_x+{\gamma }_z{,}_x\right)\right],$$

(34)

$${\kappa }_y={\kappa }_{xz}=\left(1/2\right)\left({\theta }_x{,}_z-{\theta }_z{,}_x\right)=\left(1/4\right)\left[\left(u{,}_{xy}-v{,}_{xx}\right)+f\left({\gamma }_x{,}_{xy}-{\gamma }_y{,}_{xx}\right)+\left(D^{2}f\right)\left(-{\gamma }_y+{\gamma }_z{,}_y\right)\right],$$

(35)

$${\kappa }_z={\kappa }_{yx}=\left(1/2\right)\left(-{\theta }_x{,}_y+{\theta }_y{,}_x\right)=-\left(1/2\right)\left(w{,}_{xx}+w{,}_{yy}\right)+\left(1/4\right)\left(Df\right)\left({\gamma }_x{,}_x+{\gamma }_y{,}_y-{\gamma }_z{,}_{xx}-{\gamma }_z{,}_{yy}\right).$$

(36)

2.2. Generalized Constitutive Equations

The generalized constitutive equations valid for an orthotropic material can be expressed, following Hadjesfandiari and Dargush [16] and Hadjesfandiari [17], as follows:

$$\left\{\begin{array}{c}{\sigma }_{\left(xx\right)}\\ {\sigma }_{\left(yy\right)}\\ {\sigma }_{\left(zz\right)}\\ {\sigma }_{\left(yz\right)}\\ {\sigma }_{\left(xz\right)}\\ {\sigma }_{\left(xy\right)}\end{array}\right\}=\left[\begin{array}{cccccc}{c}_{11}& c_{12}& c_{13}& 0& 0& 0\\ c_{12}& c_{22}& c_{23}& 0& 0& 0\\ c_{13}& c_{23}& c_{33}& 0& 0& 0\\ 0& 0& 0& c_{44}& 0& 0\\ 0& 0& 0& 0& c_{55}& 0\\ 0& 0& 0& 0& 0& c_{66}\end{array}\right] \left\{\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\epsilon }_{zz}\\ {\gamma }_{yz}\\ {\gamma }_{xz}\\ {\gamma }_{xy}\end{array}\right\}-\left[\begin{array}{ccc}0& 0& e_{31}\\ 0& 0& e_{32}\\ 0& 0& e_{33}\\ 0& e_{24}& 0\\ e_{15}& 0& 0\\ 0& 0& 0\end{array}\right] \left\{\begin{array}{c}{E}_x\\ E_y\\ E_z\end{array}\right\}-\left[\begin{array}{ccc}0& 0& q_{31}\\ 0& 0& q_{32}\\ 0& 0& q_{33}\\ 0& q_{24}& 0\\ q_{15}& 0& 0\\ 0& 0& 0\end{array}\right] \left\{\begin{array}{c}{H}_x\\ H_y\\ H_z\end{array}\right\}-\left\{\begin{array}{c}{c}_{\alpha 1}\\ c_{\alpha 2}\\ c_{\alpha 3}\\ 0\\ 0\\ 0\end{array}\right\}\left(\mathsf{\Delta }T\right),$$

(37)

$$\left\{\begin{array}{c}{D}_x\\ D_y\\ D_z\end{array}\right\}=\left[\begin{array}{cccccc}0& 0& 0& 0& e_{15}& 0\\ 0& 0& 0& e_{24}& 0& 0\\ e_{31}& e_{32}& e_{33}& 0& 0& 0\end{array}\right] \left\{\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\epsilon }_{zz}\\ {\gamma }_{yz}\\ {\gamma }_{xz}\\ {\gamma }_{xy}\end{array}\right\}+\left[\begin{array}{ccc}{\eta }_{11}& 0& 0\\ 0& {\eta }_{22}& 0\\ 0& 0& {\eta }_{33}\end{array}\right] \left\{\begin{array}{c}{E}_x\\ E_y\\ E_z\end{array}\right\}+\left[\begin{array}{ccc}{d}_{11}& 0& 0\\ 0& d_{22}& 0\\ 0& 0& d_{33}\end{array}\right] \left\{\begin{array}{c}{H}_x\\ H_y\\ H_z\end{array}\right\}-\left\{\begin{array}{c}0\\ 0\\ e_{\alpha 3}\end{array}\right\}\left(\mathsf{\Delta }T\right),$$

(38)

$$\left\{\begin{array}{c}{B}_x\\ B_y\\ B_z\end{array}\right\}=\left[\begin{array}{cccccc}0& 0& 0& 0& q_{15}& 0\\ 0& 0& 0& q_{24}& 0& 0\\ q_{31}& q_{32}& q_{33}& 0& 0& 0\end{array}\right] \left\{\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\epsilon }_{zz}\\ {\gamma }_{yz}\\ {\gamma }_{xz}\\ {\gamma }_{xy}\end{array}\right\}+\left[\begin{array}{ccc}{d}_{11}& 0& 0\\ 0& d_{22}& 0\\ 0& 0& d_{33}\end{array}\right] \left\{\begin{array}{c}{E}_x\\ E_y\\ E_z\end{array}\right\}+\left[\begin{array}{ccc}{\beta }_{11}& 0& 0\\ 0& {\beta }_{22}& 0\\ 0& 0& {\beta }_{33}\end{array}\right] \left\{\begin{array}{c}{H}_x\\ H_y\\ H_z\end{array}\right\}-\left\{\begin{array}{c}0\\ 0\\ q_{\alpha 3}\end{array}\right\}\left(\mathsf{\Delta }T\right),$$

(39)

$$\left\{\begin{array}{c}{\mu }_x\\ {\mu }_y\\ {\mu }_z\end{array}\right\}=-\left(1/2\right)\left[\begin{array}{ccc}{b}_{11}& 0& 0\\ 0& b_{22}& 0\\ 0& 0& b_{33}\end{array}\right] \left\{\begin{array}{c}{\kappa }_x\\ {\kappa }_y\\ {\kappa }_z\end{array}\right\},$$

(40)

where $c_{ij}$, ${\eta }_{kk}$, and ${\beta }_{kk}$ are the elastic, dielectric permeability, and magnetic permeability coefficients, respectively. $e_{ki}$, $q_{ki}$, and $d_{kk}$ are the piezoelectric, magnetoelastic, and piezomagnetic coefficients, respectively. $c_{\alpha i} (i=1, 2, \mathrm{and} 3)$ are the coupling stress and temperature change coefficients and are expressed as $c_{\alpha i}=c_{1i} {\alpha }_1+c_{2i} {\alpha }_2+c_{3i} {\alpha }_3 (i=1, 2, \mathrm{and} 3)$, for which ${\alpha }_k \left(k=1, 2, \mathrm{and} 3\right)$ are the thermal expansion coefficients. $e_{\alpha 3}$ is the coupling electric flux and temperature change coefficient and is expressed as $e_{\alpha 3}=e_{31} {\alpha }_1+e_{32} {\alpha }_2+e_{33} {\alpha }_3.$ $q_{\alpha 3}$ is the coupling magnetic flux and temperature change coefficient and is expressed as $q_{\alpha 3}=q_{31} {\alpha }_1+q_{32} {\alpha }_2+q_{33} {\alpha }_3.$ $b_{kk} \left(k=1, 2, \mathrm{and} 3\right)$ are the coupling coefficients between the couple-stress and skew-symmetric part of the curvature tensors. For an isotropic material, they are expressed as $b_{11}=b_{22}=b_{33}=16 G l^2$, where l represents the material length-scale parameter, which reflects the couple stress tensor effect and is significant when the structure’s dimensions are reduced to or even lower than the microscale range.

2.3. Strong Form

Based on Hamilton’s principle, we derive the unified SDSDT’s strong form by requiring the relevant energy function’s first-order variation to be zero as follows [17]:

$$\delta {\displaystyle {\int }_{t_1}^{t_2}\left(T-U_s-U_i\right)} dt=0,$$

(41)

where U_s denotes the strain energy function, T denotes the kinetic energy function, and U_i denotes the potential energy function contributed by the magneto-electro-thermo-mechanical loads.

The kinetic energy function’s first-order variation is expressed in the following form:

$$\begin{array}{l}\delta {\displaystyle {\int }_{t_1}^{t_2}T dt}={\displaystyle {\int }_{t_1}^{t_2}\left\{{\displaystyle {\iint }_{\mathsf{\Omega }}\left[-I_0 \right.}\right.}u{,}_{tt}\delta u-I_1 u{,}_{xtt}\delta w-I_3 u{,}_{tt}\delta {\gamma }_x+I_1 w{,}_{xtt}\delta u+I_{2}w{,}_{xxtt}\delta w+I_4 w{,}_{xtt}\delta {\gamma }_x \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-I_3 {\gamma }_x{,}_{tt} \delta u -I_4 {\gamma }_x{,}_{xtt}\delta w-I_5 {\gamma }_x{,}_{tt}\delta {\gamma }_x-I_0 v{,}_{tt}\delta v-I_1 v{,}_{ytt}\delta w-I_{3}v{,}_{tt}\delta {\gamma }_y\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+I_1 w{,}_{ytt}\delta v+I_2 w{,}_{yytt}\delta w+I_4 w{,}_{ytt}\delta {\gamma }_y -I_3 {\gamma }_y{,}_{tt} \delta v-I_4 {\gamma }_y{,}_{ytt}\delta w\\ \left.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-I_5 {\gamma }_y{,}_{tt}\delta {\gamma }_y-I_0 w{,}_{tt}\delta w-I_6 {\gamma }_z{,}_{tt} \delta w-I_6 w{,}_{tt} \delta {\gamma }_z-I_7 {\gamma }_z{,}_{tt} \delta {\gamma }_z\right\} d\mathsf{\Omega } dt\\ \hspace{1em}\hspace{1em}+{\displaystyle {\int }_{t_1}^{t_2}{\displaystyle {\oint }_{\mathsf{\Gamma }}\left\{I_1 \left(u{,}_{tt} n_x+ v{,}_{tt} n_y\right)\delta w-I_2 \left(w{,}_{xtt} n_x+w{,}_{ytt} n_y\right) \delta w\right.}}+\left.I_4 \left({\gamma }_x{,}_{tt}{n}_x+{\gamma }_y{,}_{tt}{n}_y\right) \delta w\right\}d\mathsf{\Gamma } dt,\end{array}$$

(42)

where $\mathsf{\Omega }$ represents the microplate’s mid-surface, and $\mathsf{\Gamma }$ is its boundary edges; $\left(\begin{array}{ccccc}{I}_0& I_1& I_2& I_3& I_4\hspace{1em}{I}_5\end{array}\right)={\displaystyle {\int }_{-h/2}^{h/2} \rho } \left(\begin{array}{ccccc}1& z& z^2\hspace{1em}f& zf& f^2\end{array}\right)dz$; and $\rho$ is defined as the microplate’s mass density.

The strain energy function’s first-order variation in the time interval [t₁, t₂] can be written in the following form:

$$\begin{array}{l}\delta {\displaystyle {\int }_{t_1}^{t_2}{U}_s} dt={\displaystyle {\int }_{t_1}^{t_2}{\displaystyle {\iint }_{\mathsf{\Omega }}{\displaystyle {\int }_{-h/2}^{h/2}\left\{{\sigma }_{\left(xx\right)} \delta {\epsilon }_{xx}+ {\sigma }_{\left(yy\right)}\delta {\epsilon }_{yy}+ {\sigma }_{\left(zz\right)}\delta {\epsilon }_{zz}+{\sigma }_{\left(xz\right)} \delta {\gamma }_{ xz}+{\sigma }_{\left(yz\right)}\delta {\gamma }_{yz}\right.}}} +{\sigma }_{\left(xy\right)} \delta {\gamma }_{xy}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-2{\mu }_{ x} \delta {\kappa }_{ x}-2 {\mu }_y \delta {\kappa }_y-2 {\mu }_z \delta {\kappa }_z-D_x\delta E_x-D_y\delta E_y-D_z\delta E_z\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left.-B_x\delta H_x-B_y\delta H_y-B_z\delta H_z\right\}d\mathsf{\Omega } dz dt\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle {\int }_{t_1}^{t_2}{\displaystyle {\iint }_{\mathsf{\Omega }}\left\{N_{\left(xx\right)}^{ \sigma } \delta u{,}_x-M_{\left(xx\right)}^{ \sigma } \delta w{,}_{xx}+\right.}}{P}_{\left(xx\right)}^{ \sigma } \delta {\gamma }_x{,}_x+N_{\left(yy\right)}^{ \sigma } \delta v{,}_y-M_{\left(yy\right)}^{ \sigma }\delta w{,}_{yy}+P_{\left(yy\right)}^{ \sigma }\delta {\gamma }_y{,}_y\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{1em}+N_{\left(xy\right)}^{ \sigma } \left(\delta u{,}_y+\delta v{,}_x\right)-2M_{\left(xy\right)}^{ \sigma } \delta w{,}_{xy}+P_{\left(xy\right)}^{ \sigma }\left(\delta {\gamma }_x{,}_y+\delta {\gamma }_y{,}_x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+S_{ \left(zz\right)}^{ \sigma } \delta {\gamma }_z+R_{ \left(xz\right)}^{ \sigma } \left(\delta {\gamma }_x+\delta {\gamma }_z{,}_x\right)+R_{\left(yz\right)}^{ \sigma } \left(\delta {\gamma }_y+\delta {\gamma }_z{,}_y\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}-M_{\left[xy\right]}^{ \mu }\left(\delta w{,}_{xx}+\delta w{,}_{yy}\right)+\left(1/2\right)S_{\left[xy\right]}^{ \mu }\left(\delta {\gamma }_x{,}_x+\delta {\gamma }_y{,}_y\right)-\left(1/2\right)S_{\left[xy\right]}^{ \mu }\left(\delta {\gamma }_z{,}_{xx}+\delta {\gamma }_z{,}_{yy}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}-\left(1/2\right)M_{\left[yz\right]}^{ \mu }\left(\delta u{,}_{yy}-\delta v{,}_{xy}\right)-\left(1/2\right)R_{\left[yz\right]}^{ \mu }\left(\delta {\gamma }_x{,}_{yy}-\delta {\gamma }_y{,}_{xy}\right)-\left(1/2\right)T_{\left[yz\right]}^{ \mu } \left(\delta {\gamma }_x-\delta {\gamma }_z{,}_x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}-\left(1/2\right)M_{\left[xz\right]}^{ \mu }\left(\delta u{,}_{xy}-\delta v{,}_{xx}\right)-\left(1/2\right)R_{\left[xz\right]}^{ \mu }\left(\delta {\gamma }_x{,}_{xy}-\delta {\gamma }_y{,}_{xx}\right)+\left(1/2\right) T_{\left[xz\right]}^{ \mu }\left(\delta {\gamma }_y-\delta {\gamma }_z{,}_y\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left.\hspace{1em}\hspace{0.33em}-R_{ x}^D\delta \varphi {,}_x-R_{ y}^D\delta \varphi {,}_y-T_{ z}^D\delta \varphi -R_{ x}^B\delta \psi {,}_x-R_{ y}^B\delta \psi {,}_y-T_{ z}^B\delta \psi \right\}d\mathsf{\Omega }dt,\end{array}$$

(43)

where the generalized force and moment resultants can be expressed in terms of the generalized displacements, which are given in Appendix A.

Performing the integration by parts, we can rewrite Equation (43) in the following form:

$$\begin{array}{l}\delta {\displaystyle {\int }_{t_1}^{t_2}{U}_s} dt={\displaystyle {\int }_{t_1}^{t_2}{\displaystyle {\iint }_{\mathsf{\Omega }}\left\{\left[-N_{\left(xx\right)}^{ \sigma }{,}_x-N_{\left(xy\right)}^{ \sigma }{,}_y-\left(1/2\right)M_{\left[xz\right]}^{ \mu }{,}_{xy}-\left(1/2\right)M_{\left[yz\right]}^{ \mu }{,}_{yy}\right] \delta u\right.}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}+\left[-N_{\left(xy\right)}^{ \sigma }{,}_x-N_{\left(yy\right)}^{ \sigma }{,}_y+\left(1/2\right)M_{\left[xz\right]}^{ \mu }{,}_{xx}+\left(1/2\right)M_{\left[yz\right]}^{ \mu }{,}_{xy}\right]\delta v\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}+\left[-M_{\left(xx\right)}^{ \sigma }{,}_{xx}-2M_{\left(xy\right)}^{ \sigma }{,}_{xy}-M_{\left(yy\right)}^{ \sigma }{,}_{yy}-M_{\left[xy\right]}^{ \mu }{,}_{xx}-M_{\left[xy\right]}^{ \mu }{,}_{yy}\right]\delta w\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +\left[-P_{\left(xx\right)}^{ \sigma }{,}_x-P_{\left(xy\right)}^{ \sigma }{,}_y+R_{\left(xz\right)}^{ \sigma }-\left(1/2\right)R_{\left[xz\right]}^{ \mu }{,}_{xy}-\left(1/2\right)R_{\left[yz\right]}^{ \mu }{,}_{yy}-\left(1/2\right)S_{\left[xy\right]}^{ \mu }{,}_x-\left(1/2\right)T_{\left[yz\right]}^{ \mu }\right] \delta {\gamma }_x\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{1em}\hspace{1em}+\left[-P_{\left(yy\right)}^{ \sigma }{,}_y-P_{\left(xy\right)}^{ \sigma }{,}_x+R_{\left(yz\right)}^{ \sigma }+\left(1/2\right)R_{\left[xz\right]}^{ \mu }{,}_{xx}+\left(1/2\right)R_{\left[yz\right]}^{ \mu }{,}_{xy}-\left(1/2\right)S_{\left[xy\right]}^{ \mu }{,}_y+\left(1/2\right) T_{\left[xz\right]}^{ \mu }\right]\delta {\gamma }_y\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{1em}\hspace{1em}+\left[S_{\left(zz\right)}^{ \sigma }-R_{\left(xz\right)}^{ \sigma }{,}_x-R_{\left(yz\right)}^{ \sigma }{,}_y-\left(1/2\right)S_{\left[xy\right]}^{ \mu }{,}_{xx}-\left(1/2\right)S_{\left[xy\right]}^{ \mu }{,}_{yy}+\left(1/2\right)T_{\left[xz\right]}^{ \mu }{,}_y-\left(1/2\right)T_{\left[yz\right]}^{ \mu }{,}_x\right]\delta {\gamma }_z\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left.\hspace{1em}\hspace{0.33em}\hspace{1em}\hspace{1em}+\left[R_{ x}^D{,}_x+R_{ y}^D{,}_y-T_{ z}^D\right]\delta \varphi +\left[R_{ x}^B{,}_x+R_{ y}^B{,}_y-T_{ z}^B\right]\delta \psi \right\}d\mathsf{\Omega }dt\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{1em}\hspace{1em}+\hspace{0.33em}\mathrm{boundary} \mathrm{condition} \mathrm{terms}.\end{array}$$

(44)

The first-order variation of the potential energy function contributed by the initial stresses is given as

$$\begin{array}{l}\delta {\displaystyle {\int }_{t_1}^{t_2}{U}_i} dt={\displaystyle {\int }_{t_1}^{t_2}{\displaystyle {\iint }_{\mathsf{\Omega }} }\left({\overline{N}}_x \delta {\epsilon }_{xx}^{nl}+{\overline{N}}_y \delta {\epsilon }_{yy}^{nl}\right) d\mathsf{\Omega } dt}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}=-{\displaystyle {\int }_{t_1}^{t_2} }{\displaystyle {\iint }_{\mathsf{\Omega }} \left\{\left({\overline{N}}_x w{,}_{xx}+{\overline{N}}_y w{,}_{yy}+{\overline{R}}_{ x} {\gamma }_z{,}_{xx}+{\overline{R}}_{ y} {\gamma }_z{,}_{yy}\right) \delta w\right.} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left.\left({\overline{R}}_{ x} w{,}_{xx}+{\overline{R}}_{ y} w{,}_{yy}+{\overline{T}}_{ x} {\gamma }_z{,}_{xx}+{\overline{T}}_{ y} {\gamma }_z{,}_{yy}\right) \delta {\gamma }_z\right\}d\mathsf{\Omega } dt\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle {\int }_{t_1}^{t_2} }{\displaystyle {\oint }_{\mathsf{\Gamma }}\left\{\left[{\overline{N}}_x w{,}_x n_x+{\overline{N}}_y w{,}_y n_y+{\overline{R}}_x {\gamma }_z{,}_x n_x+{\overline{R}}_{ y} {\gamma }_z{,}_y n_y\right]\right. }\delta w\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left.\left[{\overline{R}}_x w{,}_x n_x+{\overline{R}}_{ y} w{,}_y n_y+{\overline{T}}_{ x} {\gamma }_z{,}_x n_x+{\overline{T}}_{ y} {\gamma }_z{,}_y n_y\right] \delta {\gamma }_z\right\}d\mathsf{\Gamma }dt,\end{array}$$

(45)

where ${\epsilon }_{xx}^{nl}$ and ${\epsilon }_{yy}^{nl}$ are the von Kármán nonlinear strains expressed as ${\epsilon }_{xx}^{nl}= \left(1/2\right){\left(w{,}_x\right)}^2$ and ${\epsilon }_{yy}^{nl}= \left(1/2\right){\left(w{,}_y\right)}^2.$ ${\overline{N}}_x$, ${\overline{N}}_y$, ${\overline{R}}_x$, ${\overline{R}}_y$, ${\overline{T}}_x$, and ${\overline{T}}_y$ denote the generalized initial in-plane force resultants induced by the external magneto-electro-thermo-mechanical loads, such that ${\overline{N}}_x={\overline{N}}_{ x}^{ 0}+{\overline{N}}_{ x}^{ t}+{\overline{N}}_{ x}^{ e}+{\overline{N}}_{ x}^{ q},$ ${\overline{N}}_y={\overline{N}}_{ y}^{ 0}+{\overline{N}}_{ y}^{ t}+{\overline{N}}_{ y}^{ e}+{\overline{N}}_{ y}^{ q},$ ${\overline{R}}_x={\overline{R}}_{ x}^{ 0}+{\overline{R}}_{ x}^{ t}+{\overline{R}}_{ x}^{ e}+{\overline{R}}_{ x}^{ q},$ ${\overline{R}}_y={\overline{R}}_{ y}^{ 0}+{\overline{R}}_{ y}^{ t}+{\overline{R}}_{ y}^{ e}+{\overline{R}}_{ y}^{ q},$ ${\overline{T}}_x={\overline{T}}_{ x}^{ 0}+{\overline{T}}_{ x}^{ t}+{\overline{T}}_{ x}^{ e}+{\overline{T}}_{ x}^{ q},$ and ${\overline{T}}_y={\overline{T}}_{ y}^{ 0}+{\overline{T}}_{ y}^{ t}+{\overline{T}}_{ y}^{ e}+{\overline{T}}_{ y}^{ q},$ the detailed expressions of which are given in Appendix B.

Substituting Equations (42), (44), and (45) into Equation (43) and setting the coefficients of $\delta u, \hspace{0.33em}\delta v,$ $\delta w, \delta {\gamma }_x,$ $\delta {\gamma }_y, \mathrm{and} \delta \varphi$ to zero, we obtain the unified SDSDT’s strong form expressed as follows:

Euler–Lagrange equations,

$$\delta u:\hspace{1em}-\left(N_{\left(xx\right)}^{ \sigma }\right){,}_x-\left(N_{\left(xy\right)}^{ \sigma }\right){,}_y-\left(1/2\right)\left(M_{\left[yz\right]}^{ \mu }\right){,}_{yy}-\left(1/2\right)\left(M_{\left[xz\right]}^{ \mu }\right){,}_{xy}=-I_0 u{,}_{tt}+I_1 w{,}_{xtt}-I_3 {\gamma }_x{,}_{tt},$$

(46)

$$\delta v:\hspace{1em}-\left(N_{\left(xy\right)}^{ \sigma }\right){,}_x-\left(N_{\left(yy\right)}^{ \sigma }\right){,}_y+\left(1/2\right)\left(M_{\left[yz\right]}^{ \mu }\right){,}_{xy}+\left(1/2\right)\left(M_{\left[xz\right]}^{ \mu }\right){,}_{xx}=-I_0 v{,}_{tt}+I_1 w{,}_{ytt}-I_3 {\gamma }_y{,}_{tt},$$

(47)

$$\begin{array}{l}\delta w:-\left(M_{\left(xx\right)}^{ \sigma }\right){,}_{xx}-2\left(M_{\left(xy\right)}^{ \sigma }\right){,}_{xy}-\left(M_{\left(yy\right)}^{ \sigma }\right){,}_{yy}-\left(M_{\left[xy\right]}^{ \mu }\right){,}_{xx}-\left(M_{\left[xy\right]}^{ \mu }\right){,}_{yy}-{\overline{N}}_{x}w{,}_{xx}-{\overline{N}}_{y}w{,}_{yy}-{\overline{R}}_x {\gamma }_z{,}_{xx}\\ \hspace{1em}\hspace{1em}-{\overline{R}}_y {\gamma }_z{,}_{yy}=-I_1 u{,}_{xtt}-I_1 v{,}_{ytt}-I_0 w{,}_{tt}+I_2 w{,}_{xxtt}+I_2 w{,}_{yytt}-I_4 {\gamma }_x{,}_{xtt}-I_4 {\gamma }_y{,}_{ytt}-I_6 {\gamma }_z{,}_{tt},\end{array}$$

(48)

$$\begin{array}{l}\delta {\gamma }_x:\hspace{1em}-\left(P_{\left(xx\right)}^{ \sigma }\right){,}_x-\left(P_{\left(xy\right)}^{ \sigma }\right){,}_y+\left(R_{\left(xz\right)}^{ \sigma }\right)-\left(1/2\right)\left(S_{\left[xy\right]}^{ \mu }\right){,}_x-\left(1/2\right)\left(R_{\left[xz\right]}^{ \mu }\right){,}_{xy}-\left(1/2\right)\left(R_{\left[yz\right]}^{ \mu }\right){,}_{yy}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\left(1/2\right)\left(T_{\left[yz\right]}^{ \mu }\right)=-I_3 u{,}_{tt}+I_{4}w{,}_{xtt}-I_5 {\gamma }_x{,}_{tt},\end{array}$$

(49)

$$\begin{array}{l}\delta {\gamma }_y:\hspace{1em}-\left(P_{\left(xy\right)}^{ \sigma }\right){,}_x-\left(P_{\left(yy\right)}^{ \sigma }\right){,}_y+\left(R_{\left(yz\right)}^{ \sigma }\right)-\left(1/2\right)\left(S_{\left[xy\right]}^{ \mu }\right){,}_y+\left(1/2\right)\left(R_{\left[xz\right]}^{ \mu }\right){,}_{xx}+\left(1/2\right)\left(R_{\left[yz\right]}^{ \mu }\right){,}_{xy}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left(1/2\right)\left(T_{\left[xz\right]}^{ \mu }\right)=-I_3 v{,}_{tt}+I_4 w{,}_{ytt}-I_5 {\gamma }_y{,}_{tt},\end{array}$$

(50)

$$\begin{array}{l}\delta {\gamma }_z:\hspace{1em}{S}_{\left(zz\right)}^{ \sigma }-\left(R_{\left(xz\right)}^{ \sigma }\right){,}_x-\left(R_{\left(yz\right)}^{ \sigma }\right){,}_y-\left(1/2\right)\left(S_{\left[xy\right]}^{ \mu }\right){,}_{xx}-\left(1/2\right)\left(S_{\left[xy\right]}^{ \mu }\right){,}_{yy}+\left(1/2\right)\left(T_{\left[xz\right]}^{ \mu }\right){,}_y\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\left(1/2\right)\left(T_{\left[yz\right]}^{ \mu }\right){,}_x-{\overline{R}}_{x}w{,}_{xx}-{\overline{R}}_{y}w{,}_{yy}-{\overline{T}}_x {\gamma }_z{,}_{xx}-{\overline{T}}_y {\gamma }_z{,}_{yy}=-I_6 w{,}_{tt}-I_7 {\gamma }_z{,}_{tt},\end{array}$$

(51)

$$\delta \varphi :\hspace{1em}\left(R_{ x}^D\right){,}_x+\left(R_{ y}^D\right){,}_y-T_{ z}^D=0$$

(52)

$$\delta \psi :\hspace{1em}\left(R_{ x}^B\right){,}_x+\left(R_{ y}^B\right){,}_y-T_{ z}^B=0.$$

(53)

Possible boundary conditions at the edges,

$$\mathrm{either} \left(N_{\left(xx\right)}^{ \sigma }\right)n_x+\left(N_{\left(xy\right)}^{ \sigma }\right)n_y+\left(1/2\right)\left(M_{\left[xz\right]}^{ \mu }\right){,}_y{n}_x+\left(1/2\right)\left(M_{\left[yz\right]}^{ \mu }\right){,}_y{n}_y=0 \mathrm{or} u=\widehat{u},$$

(54a)

$$\mathrm{either} -\left(1/2\right)\left(M_{\left[xz\right]}^{ \mu }\right)n_y=0 \mathrm{or} u{,}_x=\widehat{u}{,}_x,$$

(54b)

$$\mathrm{either} -\left(1/2\right)\left(M_{\left[yz\right]}^{ \mu }\right)n_y=0 \mathrm{or} u{,}_y=\widehat{u}{,}_y;$$

(54c)

$$\mathrm{either} \left(N_{\left(xy\right)}^{ \sigma }\right)n_x+\left(N_{\left(yy\right)}^{ \sigma }\right)n_y-\left(1/2\right)\left(M_{\left[xz\right]}^{ \mu }\right){,}_x{n}_x-\left(1/2\right)\left(M_{\left[yz\right]}^{ \mu }\right){,}_x{n}_y=0 \mathrm{or} v=\widehat{v},$$

(55a)

$$\mathrm{either} \left(1/2\right)\left(M_{\left[xz\right]}^{ \mu }\right)n_x=0 \mathrm{or} v{,}_x=\widehat{v}{,}_x,$$

(55b)

$$\mathrm{either} \left(1/2\right)\left(M_{\left[yz\right]}^{ \mu }\right)n_x=0 \mathrm{or} v{,}_y=\widehat{v}{,}_y;$$

(55c)

$$\mathrm{either} \begin{array}{l}\left(M_{\left(xx\right)}^{ \sigma }\right){,}_x{n}_x+\left(M_{\left(yy\right)}^{ \sigma }\right){,}_y{n}_y+\left(M_{\left(xy\right)}^{ \sigma }\right){,}_x{n}_y+\left(M_{\left(xy\right)}^{ \sigma }\right){,}_y{n}_x+\left(M_{\left[xy\right]}^{ \mu }\right){,}_x{n}_x\\ \hspace{1em}+\left(M_{\left[xy\right]}^{ \mu }\right){,}_y{n}_y+{\overline{N}}_{x}w{,}_x{n}_x+{\overline{N}}_{y}w{,}_y{n}_y+{\overline{R}}_x {\gamma }_z{,}_x{n}_x+{\overline{R}}_y {\gamma }_z{,}_y{n}_y\\ \hspace{1em}-I_1\left(u{,}_{tt}{n}_x+v{,}_{tt}{n}_y\right)+I_2\left(w{,}_{xtt}{n}_x+w{,}_{ytt}{n}_y\right)-I_4\left({\gamma }_x{,}_{tt}{n}_x+{\gamma }_y{,}_{tt}{n}_y\right)=0\end{array} \mathrm{or} w=\widehat{w},$$

(56a)

$$\mathrm{either} -\left(M_{\left(xx\right)}^{ \sigma }\right) n_x-\left(M_{\left(xy\right)}^{ \sigma }\right) n_y-\left(M_{\left[xy\right]}^{ \mu }\right) n_x=0 \mathrm{or} w{,}_x=\widehat{w}{,}_x;$$

(56b)

$$\mathrm{either} -\left(M_{\left(xy\right)}^{ \sigma }\right) n_x-\left(M_{\left(yy\right)}^{ \sigma }\right) n_y-\left(M_{\left[xy\right]}^{ \mu }\right) n_y=0 \mathrm{or} w{,}_y=\widehat{w}{,}_y;$$

(56c)

$$\begin{gathered} \mathrm{either} \left(P_{\left(xx\right)}^{ \sigma }\right)n_x+\left(P_{\left(xy\right)}^{ \sigma }\right)n_y+\left(1/2\right)\left(S_{\left[xy\right]}^{ \mu }\right)n_x+\left(1/2\right)\left(R_{\left[xz\right]}^{ \mu }\right){,}_y{n}_x+\left(1/2\right)\left(R_{\left[yz\right]}^{ \mu }\right){,}_y{n}_y=0 \\ \mathrm{or} {\gamma }_x={\widehat{\gamma }}_x, \end{gathered}$$

(57a)

$$\mathrm{either} -\left(1/2\right)\left(R_{\left[xz\right]}^{ \mu }\right)n_y=0 \mathrm{or} {\gamma }_x{,}_x={\widehat{\gamma }}_x{,}_x,$$

(57b)

$$\mathrm{either} -\left(1/2\right)\left(R_{\left[yz\right]}^{ \mu }\right)n_y=0 \mathrm{or} {\gamma }_x{,}_y={\widehat{\gamma }}_x{,}_y;$$

(57c)

$$\begin{gathered} \mathrm{either} \left(P_{\left(xy\right)}^{ \sigma }\right)n_x+\left(P_{\left(yy\right)}^{ \sigma }\right)n_y+\left(1/2\right)\left(S_{\left[xy\right]}^{ \mu }\right)n_y-\left(1/2\right)\left(R_{\left[xz\right]}^{ \mu }\right){,}_x{n}_x-\left(1/2\right)\left(R_{\left[yz\right]}^{ \mu }\right){,}_x{n}_y=0 \\ \mathrm{or} {\gamma }_y={\widehat{\gamma }}_y, \end{gathered}$$

(58a)

$$\mathrm{either} \left(1/2\right)\left(R_{\left[xz\right]}^{ \mu }\right)n_x=0 \mathrm{or} {\gamma }_y{,}_x={\widehat{\gamma }}_y{,}_x,$$

(58b)

$$\mathrm{either} \left(1/2\right)\left(R_{\left[yz\right]}^{ \mu }\right)n_x=0 \mathrm{or} {\gamma }_y{,}_y={\widehat{\gamma }}_y{,}_y;$$

(58c)

$$\begin{gathered} \mathrm{either} \begin{array}{l}{R}_{\left(xz\right)}^{ \sigma }{n}_x+R_{\left(yz\right)}^{ \sigma }{n}_y+\left(1/2\right) S_{\left[xy\right]}^{ \mu }{,}_x{n}_x+\left(1/2\right) S_{\left[xy\right]}^{ \mu }{,}_y{n}_y-\left(1/2\right) T_{\left[xz\right]}^{ \mu } n_y+\left(1/2\right) T_{\left[yz\right]}^{ \mu } n_x\\ \hspace{1em}+{\overline{R}}_{x}w{,}_x{n}_x+{\overline{R}}_{y}w{,}_y{n}_y+{\overline{T}}_x {\gamma }_z{,}_x{n}_x+{\overline{T}}_y {\gamma }_z{,}_y{n}_y=0\end{array} \\ \mathrm{or} {\gamma }_z={\widehat{\gamma }}_z, \end{gathered}$$

(59a)

$$\mathrm{either} -\left(1/2\right) S_{\left[xy\right]}^{ \mu }{n}_x=0 \mathrm{or} {\gamma }_z{,}_x={\widehat{\gamma }}_z{,}_x,$$

(59b)

$$\mathrm{either} -\left(1/2\right) S_{\left[xy\right]}^{ \mu }{n}_y=0 \mathrm{or} {\gamma }_z{,}_y={\widehat{\gamma }}_z{,}_y;$$

(59c)

$$\mathrm{either} -R_{ x}^{ D}{n}_x-R_{ y}^{ D}{n}_y=0 \mathrm{or} \varphi =\widehat{\varphi },$$

(60)

$$\mathrm{either} -R_{ x}^{ B}{n}_x-R_{ y}^{ B}{n}_y=0 \mathrm{or} \psi =\widehat{\psi };$$

(61)

where $\widehat{u}, \widehat{v}, \widehat{w}, {\widehat{\gamma }}_x, {\widehat{\gamma }}_y,\hspace{0.33em}\hspace{0.33em}{\widehat{\gamma }}_z, \widehat{\varphi }, \mathrm{and} \widehat{\psi }$ are the prescribed generalized displacements along the FG-MEE microplate’s edges.

We express the Euler–Lagrange equations in terms of generalized displacements by substituting Equations (A1)–(A21) into Equations (46) through (53) as follows:

$$\delta u:\hspace{1em}{K}_{11}u+K_{12}v+K_{13}w+K_{14} {\gamma }_x+K_{15} {\gamma }_y+K_{16} {\gamma }_z+K_{17} \varphi +K_{18} \psi =-I_0 u{,}_{tt}+I_1 w{,}_{xtt}-I_3 {\gamma }_x{,}_{tt},$$

(62)

$$\delta v:\hspace{1em}{K}_{21}u+K_{22}v+K_{23}w+K_{24} {\gamma }_x+K_{25} {\gamma }_y+K_{26} {\gamma }_z+K_{27} \varphi +K_{28} \psi =-I_0 v{,}_{tt}+I_1 w{,}_{ytt}-I_3 {\gamma }_y{,}_{tt},$$

(63)

$$\begin{array}{l}\delta w:\hspace{1em}{K}_{31} u+K_{32} v+K_{33}w+K_{34} {\gamma }_x+K_{35} {\gamma }_y+K_{36} {\gamma }_z+K_{37} \varphi +K_{38} \psi \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=-I_1 u{,}_{xtt}-I_1 v{,}_{ytt}-I_{0}w{,}_{tt}+I_2\left(w{,}_{xxtt}+w{,}_{yytt}\right)-I_4\left({\gamma }_x{,}_{xtt}+{\gamma }_y{,}_{ytt}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-I_6 {\gamma }_z{,}_t -{\overline{N}}_x w{,}_{xx}-{\overline{N}}_y w{,}_{yy}-{\overline{R}}_x {\gamma }_z{,}_{xx}-{\overline{R}}_y {\gamma }_z{,}_{yy},\end{array}$$

(64)

$$\delta {\gamma }_x:\hspace{1em}{K}_{41}u+K_{42}v+K_{43}w+K_{44} {\gamma }_x+K_{45} {\gamma }_y+K_{46} {\gamma }_z+K_{47} \varphi +K_{48} \psi =-I_3 u{,}_{tt}+I_4 w{,}_{xtt}-I_5 {\gamma }_x{,}_{tt},$$

(65)

$$\delta {\gamma }_y:\hspace{1em}{K}_{51} u+K_{52} v+K_{53}w+K_{54} {\gamma }_x+K_{55} {\gamma }_y+K_{56} {\gamma }_z+K_{57} \varphi +K_{58} \psi =-I_3 v{,}_{tt}+I_4 w{,}_{ytt}-I_5 {\gamma }_y{,}_{tt},$$

(66)

$$\begin{array}{l}\delta {\gamma }_z:\hspace{1em}{K}_{61} u+K_{62} v+K_{63}w+K_{64} {\gamma }_x+K_{65} {\gamma }_y+K_{66} {\gamma }_z+K_{67} \varphi +K_{68} \psi \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\overline{R}}_x w_{xx}+{\overline{R}}_y w_{yy}+{\overline{T}}_x {\gamma }_z{,}_{xx}+{\overline{T}}_y {\gamma }_z{,}_{yy}-I_6 w{,}_{tt}-I_7 {\gamma }_z{,}_{tt},\end{array}$$

(67)

$$\delta \varphi :\hspace{1em}{K}_{71} u+K_{72} v+K_{73}w+K_{74} {\gamma }_x+K_{75} {\gamma }_y+K_{76} {\gamma }_z+K_{77} \varphi +K_{78} \psi =0,$$

(68)

$$\delta \psi :\hspace{1em}{K}_{81} u+K_{82} v+K_{83}w+K_{84} {\gamma }_x+K_{85} {\gamma }_y+K_{86} {\gamma }_z+K_{87} \varphi +K_{88} \psi =0,$$

(69)

where the detailed expressions of K_ij are given in Appendix C for brevity.

3. Applications

Governing Equations (62)–(69) associated with a set of boundary conditions expressed in Equations (54)–(61) constituted a well-posed eigenvalue problem. Navier’s solutions of the FG-MEE microplate’s natural frequency can be obtained.

The fully simply supported boundary conditions of the FG-MEE microplate are expressed in the following form:

At x = 0 and x = L_x,

$$N_{\left(xx\right)}^{ \sigma }+\left(1/2\right)M_{\left[xz\right]}^{ \mu }{,}_y=0,$$

(70a)

v = 0,

(70b)

$$M_{[xz]}^{ \mu }=0,$$

(70c)

$$v{,}_y=0,$$

(70d)

w = 0,

(70e)

$$M_{(xx)}^{ \sigma }+M_{[xy]}^{ \mu }=0,$$

(70f)

$$w{,}_y=0,$$

(70g)

$$P_{(xx)}^{ \sigma }+\left(1/2\right)\left(S_{[xy]}^{ \mu }\right)+\left(1/2\right)\left(R_{[xz]}^{ \mu }\right){,}_y=0,$$

(70h)

$${\gamma }_y=0,$$

(70i)

$$R_{[xz]}^{ \mu }=0,$$

(70j)

$${\gamma }_y{,}_y=0,$$

(70k)

$${\gamma }_z=0,$$

(70l)

$$S_{\left[xy\right]}^{ \mu }=0,$$

(70m)

$$\varphi =0,$$

(70n)

$$\psi =0.$$

(70o)

At y = 0 and y = L_y,

$$u=0,$$

(71a)

$$u{,}_x=0,$$

(71b)

$$M_{[yz]}^{ \mu }=0,$$

(71c)

$$N_{\left(yy\right)}^{ \sigma }-\left(1/2\right)M_{\left[yz\right]}^{ \mu }{,}_x=0,$$

(71d)

w = 0,

(71e)

$$w{,}_x=0,$$

(71f)

$$M_{(yy)}^{ \sigma }+M_{[xy]}^{ \mu }=0,$$

(71g)

$${\gamma }_x=0,$$

(71h)

$${\gamma }_x{,}_x=0,$$

(71i)

$$R_{[yz]}^{ \mu }=0,$$

(71j)

$$P_{(yy)}^{ \sigma }+\left(1/2\right)\left(S_{[xy]}^{ \mu }\right)-\left(1/2\right)\left(R_{[yz]}^{ \mu }\right){,}_x=0,$$

(71k)

$${\gamma }_z=0,$$

(71l)

$$S_{\left[xy\right]}^{ \mu }=0,$$

(71m)

$$\varphi =0,$$

(71n)

$$\psi =0.$$

(71o)

By satisfying the boundary conditions given in Equations (70) and (71), we expand the microplate’s various field variables as a double Fourier series as follows:

$$\left(u, {\gamma }_x\right)={\displaystyle \sum _{\widehat{m}=1}^{\infty } {\displaystyle \sum _{\widehat{n}=1}^{\infty } }\left(u_{ \widehat{m}\widehat{n}}, {\gamma }_{x\widehat{m}\widehat{n}}\right)} \cos \left(\tilde{m}x\right) \sin \left(\tilde{n}y\right) e^{i \omega t},$$

(72)

$$\left(v, {\gamma }_y\right)={\displaystyle \sum _{\widehat{m}=1}^{\infty } {\displaystyle \sum _{\widehat{n}=1}^{\infty } }\left(v_{ \widehat{m}\widehat{n}}, {\gamma }_{y\widehat{m}\widehat{n}}\right)} \sin \left(\tilde{m}x\right) \cos \left(\tilde{n}y\right) e^{i \omega t},$$

(73)

$$\left(w, {\gamma }_z, \varphi , \psi \right)={\displaystyle \sum _{\widehat{m}=1}^{\infty }{\displaystyle \sum _{\widehat{n}=1}^{\infty } } \left(w_{ \widehat{m}\widehat{n}}, {\gamma }_{z\widehat{m}\widehat{n}}, {\varphi }_{\widehat{m}}, {\psi }_{\widehat{m}\widehat{n}}\right)} \sin \left(\tilde{m}x\right) \sin \left(\tilde{n}y\right) e^{i \omega t},$$

(74)

where $\tilde{m}=\widehat{m}\pi /L_x$, and $\tilde{n}=\widehat{n} \pi /L_y$, with $\widehat{m}$ and $\widehat{n}$ representing the half-wave numbers. The symbol $\omega$ represents the microplate’s natural frequency.

Substituting Equations (72)–(74) into Euler–Lagrange Equations (62)–(69) leads to the system of equations as follows:

$$\begin{gathered} \left\{\left[\begin{array}{cccccccc}{k}_{11}& k_{12}& k_{13}& k_{14}& k_{15}& k_{16}& k_{17}& k_{18}\\ k_{21}& k_{22}& k_{23}& k_{24}& k_{25}& k_{26}& k_{27}& k_{28}\\ k_{31}& k_{32}& k_{33}& k_{34}& k_{35}& k_{36}& k_{37}& k_{38}\\ k_{41}& k_{42}& k_{43}& k_{44}& k_{45}& k_{46}& k_{47}& k_{48}\\ k_{51}& k_{52}& k_{53}& k_{54}& k_{55}& k_{56}& k_{57}& k_{58}\\ k_{61}& k_{62}& k_{63}& k_{64}& k_{65}& k_{66}& k_{67}& k_{68}\\ k_{71}& k_{72}& k_{73}& k_{74}& k_{75}& k_{76}& k_{77}& k_{78}\\ k_{81}& k_{82}& k_{83}& k_{84}& k_{85}& k_{86}& k_{87}& k_{88}\end{array}\right]-{\omega }^2\left[\begin{array}{cccccccc}{m}_{11}& 0& m_{13}& m_{14}& 0& 0& 0& 0\\ 0& m_{22}& m_{23}& 0& m_{25}& 0& 0& 0\\ m_{31}& m_{32}& m_{33}& m_{34}& m_{35}& m_{36}& 0& 0\\ m_{41}& 0& m_{43}& m_{44}& 0& 0& 0& 0\\ 0& m_{52}& m_{53}& 0& m_{55}& 0& 0& 0\\ 0& 0& m_{63}& 0& 0& m_{66}& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\right. \\ \hspace{1em}\hspace{1em}\hspace{1em}-\left({\overline{N}}_{ x}^{ 0}\right)\left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& g_{33}^{ c}& 0& 0& g_{36}^{ c}& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& g_{63}^{ c}& 0& 0& g_{66}^{ c}& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]+\left({\overline{V}}_0\right)\left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& g_{33}^e& 0& 0& g_{36}^e& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& g_{63}^e& 0& 0& g_{66}^e& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right] \\ \hspace{1em}\hspace{1em}\hspace{1em}+\left({\overline{C}}_0\right) \left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& g_{33}^q& 0& 0& g_{36}^q& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& g_{63}^q& 0& 0& g_{66}^q& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\left.-\left(\mathsf{\Delta }T\right) \left[\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& g_{33}^{ t}& 0& 0& g_{36}^t& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& g_{63}^t& 0& 0& g_{66}^t& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\right\}\left\{\begin{array}{c}{u}_{\widehat{m}\widehat{n}}\\ v_{\widehat{m}\widehat{n}}\\ w_{\widehat{m}\widehat{n}}\\ {\gamma }_{x\widehat{m}\widehat{n}}\\ {\gamma }_{y\widehat{m}\widehat{n}}\\ {\gamma }_{z\widehat{m}\widehat{n}}\\ {\varphi }_{\widehat{m}\widehat{n}}\\ {\psi }_{\widehat{m}\widehat{n}}\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right\}, \end{gathered}$$

(75)

where the detailed expressions of k_ij, m_ij, and $g_{ij}^k=0$ (k = c, e, q, and t) are given in Appendix D for brevity.

Equation (75) represents various CCST-based SDSDTs’ resulting system equations, which we can employ to evaluate an FG-MEE microplate’s natural frequency when it is subjected to magneto-electro-thermo-mechanical loads, for which its static buckling state has not occurred.

Equation (75) can also be reduced to investigate the microplate’s pure free vibration characteristics, which is expressed in the following matrix form:

$$\left\{\left[\begin{array}{cc}{K}_{11}& K_{12}\\ K_{21}& K_{22}\end{array}\right]-{\omega }^2\left[\begin{array}{cc}{M}_{11}& 0\\ 0& 0\end{array}\right]\right\} \left\{\begin{array}{c}{X}_1\\ X_2\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\end{array}\right\},$$

(76)

$$\mathrm{where} K_{11}=\left[\begin{array}{cccccc}{k}_{11}& k_{12}& k_{13}& k_{14}& k_{15}& k_{16}\\ k_{21}& k_{22}& k_{23}& k_{24}& k_{25}& k_{26}\\ k_{31}& k_{32}& k_{33}& k_{34}& k_{35}& k_{36}\\ k_{41}& k_{42}& k_{43}& k_{44}& k_{45}& k_{46}\\ k_{51}& k_{52}& k_{53}& k_{54}& k_{55}& k_{56}\\ k_{61}& k_{62}& k_{63}& k_{64}& k_{65}& k_{66}\end{array}\right], K_{12}=\left[\begin{array}{cc}{k}_{17}& k_{18}\\ k_{27}& k_{28}\\ k_{37}& k_{38}\\ k_{47}& k_{48}\\ k_{57}& k_{58}\\ k_{67}& k_{68}\end{array}\right],$$

$$K_{21}=\left[\begin{array}{cccccc}{k}_{71}& k_{72}& k_{73}& k_{74}& k_{75}& k_{76}\\ k_{81}& k_{82}& k_{83}& k_{84}& k_{85}& k_{86}\end{array}\right], K_{22}=\left[\begin{array}{cc}{k}_{77}& k_{78}\\ k_{87}& k_{88}\end{array}\right],$$

$$M_{11}=\left[\begin{array}{cccccc}{m}_{11}& 0& m_{13}& m_{14}& 0& 0\\ 0& m_{22}& m_{23}& 0& m_{25}& 0\\ m_{31}& m_{32}& m_{33}& m_{34}& m_{35}& m_{36}\\ m_{41}& 0& m_{43}& m_{44}& 0& 0\\ 0& m_{52}& m_{53}& 0& m_{55}& 0\\ 0& 0& m_{63}& 0& 0& m_{66}\end{array}\right], X_1={\left\{\begin{array}{cccccc}{u}_{\widehat{m}\widehat{n}}& v_{\widehat{m}\widehat{n}}& w_{\widehat{m}\widehat{n}}& {\gamma }_{x\widehat{m}\widehat{n}}& {\gamma }_{y\widehat{m}\widehat{n}}& {\gamma }_{z\widehat{m}\widehat{n}}\end{array}\right\}}^T,$$

$$X_2={\left\{\begin{array}{cc}{\varphi }_{\widehat{m}\widehat{n}}& {\psi }_{\widehat{m}\widehat{n}}\end{array}\right\}}^T.$$

Using a matrix partition technique, we separate Equation (76) into the following form:

$$\left[\left(K_{11}-K_{12} K_{22}^{-1} K_{21} \right)-{\omega }^2 M_{11}\right] X_1=0,$$

(77)

$$X_2=-K_{22}^{-1} K_{21} X_1.$$

(78)

By setting the determinant of the coefficient matrix represented by Equation (77) to zero, we obtain the natural frequency of the FG-MEE microplate as follows:

$$\left|\left(K_{11}-K_{12} K_{22}^{-1} K_{21} \right)-{\omega }^2 M_{11}\right|=0.$$

(79)

Consequently, six natural frequencies are obtained by fixing the wave number pairs. Among these frequencies, the lowest natural frequency of the microplate of interest can be determined.

4. Numerical Examples

4.1. Validation and Comparison

In this section, we utilize various CCST-based SDSDTs to determine the Navier-type analytical solutions for the natural frequency of an FG-MEE or FG piezoelectric microplate under fully simple supports. The accuracy of these CCST-based SDSDTs is validated by comparing their solutions with the relevant 3D solutions reported in the literature. Comparisons among the solutions obtained using different CCST-based SDSDTs are also conducted. The relevant material properties are provided in Table 1.

Table 1. The elastic, piezoelectric, piezomagnetic, dielectric, and magnetic coefficients; mass density, thermal expansion coefficients, and material length-scale parameters of PZT-4, BaTiO₃, and CoFe₂O₄ materials.

Material Properties	PZT-4 [52]	BaTiO3 [53]	CoFe2O4 [53]
$c_{11}=c_{22} \left(\mathrm{GPa}\right)$	139	166.0	286.0
$c_{12} \left(\mathrm{GPa}\right)$	77.8	77.0	173.0
$c_{13}=c_{23} \left(\mathrm{GPa}\right)$	74.3	78.0	170.5
$c_{33} \left(\mathrm{GPa}\right)$	115	162.0	269.5
$c_{44}=c_{55} \left(\mathrm{GPa}\right)$	25.6	43.0	45.3
$c_{66} \left(\mathrm{GPa}\right)$	30.6	44.5	56.5
$e_{31}=e_{32} \left(\mathrm{C} {\mathrm{m}}^{-2}\right)$	−5.2	−4.4	0.0
$e_{33} \left(\mathrm{C} {\mathrm{m}}^{-2}\right)$	15.1	18.6	0.0
$e_{24}=e_{15} \left(\mathrm{C} {\mathrm{m}}^{-2}\right)$	12.7	11.6	0.0
$q_{31}=q_{32} \left({\mathrm{NA}}^{-1}{\mathrm{m}}^{-1}\right)$	0.0	0.0	580.3
$q_{33} \left({\mathrm{NA}}^{-1}{\mathrm{m}}^{-1}\right)$	0.0	0.0	699.7
$q_{24}=q_{15} \left({\mathrm{NA}}^{-1}{\mathrm{m}}^{-1}\right)$	0.0	0.0	550.0
${\eta }_{11}={\eta }_{22} \left({\mathrm{C}}^2 {\mathrm{m}}^{-2} {\mathrm{N}}^{-1}\right)$	6.46 × 10−9	11.2 × 10−9	0.08 × 10−9
${\eta }_{33} \left({\mathrm{C}}^2 {\mathrm{m}}^{-2} {\mathrm{N}}^{-1}\right)$	5.62 × 10−9	12.6 × 10−9	0.093 × 10−9
${\beta }_{11}={\beta }_{22} \left(\mathrm{N} {\mathrm{s}}^2 {\mathrm{C}}^{-2}\right)$	0.0	5.0 × 10−6	−590.0 × 10−6
${\beta }_{33} \left(\mathrm{N} {\mathrm{s}}^2 {\mathrm{C}}^{-2}\right)$	0.0	10.0 × 10−6	157.0 × 10−6
${\alpha }_1={\alpha }_2 \left(1/\mathrm{K}\right)$	NA	15.7 × 10−6	10 × 10−6
${\alpha }_3 \left(1/\mathrm{K}\right)$	NA	6.4 × 10−6	10 × 10−6
$d_{11}=d_{22}=d_{33} \left(\mathrm{N} \mathrm{s} {\mathrm{C}}^{-1}{\mathrm{V}}^{-1}\right)$	0.0	0.0	0.0
$\rho \left(\mathrm{kg} {\mathrm{m}}^{-3}\right)$	7500	5800.0	5300.0
l for the CCST (m)	8.8 × 10−6	8.8 × 10−6	8.8 × 10−6
$\widehat{l}$ for the MCST (m)	17.6 × 10−6	17.6 × 10−6	17.6 × 10−6

The symbols $\widehat{l}$ and l represent the material length-scale parameters in MCST and CCST, respectively. NA: not available.

Two surface conditions (i.e., open- and closed-circuit surface conditions) are considered, and their corresponding surface conditions are expressed in the following form:

(a)

Open-circuit surface conditions

$${\sigma }_{zx}={\sigma }_{zy}={\sigma }_{zz}={\mu }_{zx}={\mu }_{zy}=0, D_z={\widehat{D}}_z^{\pm }, \mathrm{and} B_z={\widehat{B}}_z^{\pm }\mathrm{at} z=\pm h/2,$$

(80)

where $D_z^{\pm }$ and $B_z^{\pm }$ are the applied electric and magnetic fluxes on the top and bottom surfaces. In this analysis, the values of $D_z^{\pm }$ and $B_z^{\pm }$ are set to zero.

(b)

Closed-circuit surface conditions

$${\sigma }_{zx}={\sigma }_{zy}={\sigma }_{zz}={\mu }_{zx}={\mu }_{zy}=0, \varphi =\pm {\overline{V}}_0, \mathrm{and} \psi =\pm {\overline{C}}_0\mathrm{at} z=\pm h/2,$$

(81)

where $\pm {\overline{V}}_0$ and $\pm {\overline{C}}_0$ are the magnitude of the electric and magnetic potentials acting on the top and bottom surfaces.

4.1.1. FG Piezoelectric Microplates

This section considers the pure free vibration problem of an FG piezoelectric microplate under fully simple supports. The microplate’s material properties are assumed to be an exponential function varying along the thickness direction and are expressed in the following form:

$$P_{eff}\left(z\right)=P_b e^{{\kappa }_e\left[\left(1/2\right)+\left(z/h\right)\right]},$$

(82)

where P denotes the material properties, the subscript eff denotes the effective material properties, and ${\kappa }_e$ denotes the inhomogeneity index. When z = h/2, following Equation (82), we obtain $P_t=P_b\hspace{0.33em}{e}^{{\kappa }_e}$ such that ${\widehat{\kappa }}_e=P_t/P_b=e^{{\kappa }_e},$ where the subscripts t and b represent the microplate’s top and bottom surfaces, and the symbol ${\widehat{\kappa }}_e$ represents the material property ratio between the microplate’s top and bottom surfaces. Additionally, we assign the piezoceramic material PZT-4 to the bottom surface, whose material properties are listed in Table 1. For comparison purposes, a dimensionless frequency parameter is defined in the following form: $\overline{\omega }=\omega h \sqrt{{\rho }_b/{\left(c_{11}\right)}_b}$ for Table 2, Table 3 and Table 4.

Table 2. Comparison of the results for the lowest-frequency solutions of a simply supported FG piezoelectric microplate, associated with the flexural vibration mode, under open-circuit surface conditions.

Surface Conditions	$\widehat{\mathit{l}}/\mathit{h}$	${\mathit{L}}_{\mathit{x}}/\mathit{h}$	${\widehat{\mathit{\kappa }}}_{\mathit{e}}$	2D and 3D Size-Dependent Theories Based on the CCST	$\left(\widehat{\mathit{m}}, \widehat{\mathit{n}}\right)$
					(1, 1)	(1, 2)	(1, 3)	(2, 2)
Open-circuit	0.5	5	1	CPT	0.28716	0.68609	1.02396	0.90005
				First-order SDT	0.24919	0.53777	0.93294	0.78305
				Reddy’s refined SDT	0.25378	0.57257	1.02396	0.85218
				Sinusoidal SDT	0.25428	0.57416	1.02396	0.85510
				Exponential SDT	0.25515	0.57665	1.02396	0.85940
				Hyperbolic SDT	0.25375	0.57248	1.02396	0.85199
				3D CCST [54]	0.25922	0.58043	1.02476	0.85664
Open-circuit	0.5	5	10	CPT	0.26847	0.64749	1.02396	0.90005
				First-order SDT	0.23724	0.51880	0.90777	0.75996
				Reddy’s refined SDT	0.24438	0.55881	1.01260	0.83852
				Sinusoidal SDT	0.24467	0.55973	1.01381	0.84039
				Exponential SDT	0.24525	0.56146	1.01411	0.84359
				Hyperbolic SDT	0.24437	0.55876	1.01244	0.83842
				3D CCST [54]	0.24681	0.55954	0.99989	0.83247
Open-circuit	0.5	10	10	CPT	0.06840	0.16938	0.33352	0.26847
				First-order SDT	0.06580	0.15542	0.28852	0.23724
				Reddy’s refined SDT	0.06499	0.15721	0.30019	0.24438
				Sinusoidal SDT	0.06506	0.15739	0.30057	0.24467
				Exponential SDT	0.06520	0.15774	0.30132	0.24525
				Hyperbolic SDT	0.06498	0.15720	0.30018	0.24437
				3D CCST [54]	0.06588	0.15909	0.30276	0.24681
Open-circuit	1	10	10	CPT	0.10503	0.26009	0.51198	0.41227
				First-order SDT	0.09903	0.22931	0.41720	0.34536
				Reddy’s refined SDT	0.10219	0.24859	0.47793	0.38813
				Sinusoidal SDT	0.10224	0.24873	0.47833	0.38841
				Exponential SDT	0.10234	0.24907	0.47926	0.38908
				Hyperbolic SDT	0.10218	0.24858	0.47792	0.38812
				3D CCST [54]	0.10423	0.24862	0.46589	0.38193

Table 3. Comparison of the results for the lowest-frequency solutions of a simply supported FG piezoelectric microplate, associated with the flexural vibration mode, under closed-circuit surface conditions.

Surface Conditions	$\widehat{\mathit{l}}/\mathit{h}$	${\mathit{L}}_{\mathit{x}}/\mathit{h}$	${\widehat{\mathit{\kappa }}}_{\mathit{e}}$	2D and 3D Size-Dependent Theories Based on the CCST	$\left(\widehat{\mathit{m}}, \widehat{\mathit{n}}\right)$
					(1, 1)	(1, 2)	(1, 3)	(2, 2)
Closed-circuit	0.5	5	1	CPT	0.28449	0.68043	1.02396	0.90005
				First-order SDT	0.24181	0.50913	0.85945	0.72805
				Reddy’s refined SDT	0.23337	0.52092	0.92233	0.76963
				Sinusoidal SDT	0.23405	0.52302	0.92721	0.77338
				Exponential SDT	0.23560	0.52702	0.93528	0.77983
				Hyperbolic SDT	0.23335	0.52082	0.92205	0.76943
				3D CCST [54]	0.24803	0.54884	0.96382	0.80666
Closed-circuit	0.5	5	10	CPT	0.26695	0.64416	1.02396	0.90005
				First-order SDT	0.23260	0.49907	0.85288	0.71996
				Reddy’s refined SDT	0.23018	0.52034	0.93044	0.77407
				Sinusoidal SDT	0.23070	0.52197	0.93454	0.77712
				Exponential SDT	0.23191	0.52527	0.94176	0.78274
				Hyperbolic SDT	0.23016	0.52028	0.93022	0.77393
				3D CCST [54]	0.22395	0.50170	0.89103	0.74291
Closed-circuit	0.5	10	10	CPT	0.06800	0.16840	0.33167	0.26695
				First-order SDT	0.06518	0.15318	0.28192	0.23260
				Reddy’s refined SDT	0.06165	0.14859	0.28214	0.23018
				Sinusoidal SDT	0.06177	0.14890	0.28282	0.23070
				Exponential SDT	0.06206	0.14964	0.28436	0.23191
				Hyperbolic SDT	0.06165	0.14858	0.28212	0.23016
				3D CCST [54]	0.06054	0.14514	0.27393	0.22395
Closed-circuit	1	10	10	CPT	0.10476	0.25945	0.51099	0.41129
				First-order SDT	0.09850	0.22703	0.40979	0.34030
				Reddy’s refined SDT	0.09987	0.24188	0.46179	0.37605
				Sinusoidal SDT	0.09995	0.24210	0.46236	0.37646
				Exponential SDT	0.10016	0.24273	0.46394	0.37763
				Hyperbolic SDT	0.09987	0.24188	0.46179	0.37605
				3D CCST [54]	0.09646	0.22651	0.41729	0.34410

Table 4. Comparison of the results for the lowest- and second-lowest-frequency solutions of a simply supported FG-MEE macroscale plate under open- and closed-circuit surface conditions, where $\left(\widehat{m}, \widehat{n}\right)=(1, 1)$.

Surface Conditions	${\mathit{L}}_{\mathit{x}}/\mathit{h}$	${\mathit{\kappa }}_{\mathit{p}}$	Theories	Lowest	Second Lowest
Open-circuit	10	1	CPT	12.1415	28.8462
			First-order SDT	10.9389	28.8444
			Reddy’s refined SDT	9.5951	28.8444
			Sinusoidal SDT	9.6308	28.8444
			Exponential SDT	9.7097	28.8444
			Hyperbolic SDT	9.5941	28.8444
			State space sols [55]	9.5543	28.8389
			Asymptotic sols [56]	9.5545	28.8389
			Discrete sols [57]	9.525	28.762
Open-circuit	10	3	CPT	13.3624	30.4768
			First-order SDT	11.8391	30.4757
			Reddy’s refined SDT	9.9926	30.4757
			Sinusoidal SDT	10.0351	30.4757
			Exponential SDT	10.1411	30.4757
			Hyperbolic SDT	9.9920	30.4757
			State space sols [55]	9.7730	30.0246
			Asymptotic sols [56]	9.7730	30.0246
			Discrete sols [57]	9.747	29.975
Closed-circuit	10	1	CPT	12.0904	28.8462
			First-order SDT	10.8868	28.8444
			Reddy’s refined SDT	9.3344	28.8444
			Sinusoidal SDT	9.3720	28.8444
			Exponential SDT	9.4627	28.8444
			Hyperbolic SDT	9.3338	28.8444
			State space sols [55]	9.5289	28.8390
Closed-circuit	10	3	CPT	13.3030	30.4768
			First-order SDT	11.8082	30.4757
			Reddy’s refined SDT	9.8945	30.4757
			Sinusoidal SDT	9.9400	30.4757
			Exponential SDT	10.0527	30.4757
			Hyperbolic SDT	9.8939	30.4757
			State space sols [55]	9.7667	30.0246

Table 2 and Table 3 present a comparison of the results for the lowest frequency associated with the flexural vibration mode of an FG piezoelectric microplate under fully simple supports and open- and closed-circuit surface conditions, for the cases of $\left(\widehat{m}, \widehat{n}\right)$ = (1, 1), (1, 2), (1, 3), and (2, 2); $L_x/h=$ 5 and 10; ${\widehat{\kappa }}_e=$ 1 and 10; and $\widehat{l}/h=$ 0.5 and 1. As shown in Table 2 and Table 3, the accuracy of various CCST-based SDSDTs compared with the 3D CCST solutions reported in the literature [54] is arranged in descending order as follows: (CCST-based Reddy’s refined SDT, sinusoidal SDT, exponential SDT, and hyperbolic SDT) > CCST-based first-order SDT > CCST-based CPT. The results obtained using the CCST-based Reddy’s refined SDT, sinusoidal SDT, exponential SDT, and hyperbolic SDT are in close agreement with one another.

Their solutions are shown to be in excellent agreement with the 3D solutions [54] obtained using the Hermitian C¹ finite layer method. The frequency solutions for the open-circuit surface conditions are always higher than those for the closed-circuit surface conditions. This is because the electric flux is prescribed at the top and bottom surfaces for the cases of open-circuit surface conditions, leading to the electric potential changing more significantly in the in-plane domain than in the out-of-plane domain for the instances of closed-circuit surface conditions. Thus, the piezoelectric effect on the microplate under open-circuit surface conditions is more significant than that under closed-circuit surface conditions, which results in the lowest frequency of the microplate under open-circuit surface conditions being higher than that under closed-circuit surface conditions.

4.1.2. FG-MEE Macroscale Plates

In Table 4, we consider the pure free vibration problems of an FG-MEE macroscale plate under fully simple supports. The macroscale plate of interest is made of BaTiO₃ (a piezoelectric material) and CoFe₂O₄ (a magnetostrictive material), whose material properties are given in Table 1.

The macroscale plate’s effective material properties are expressed as follows [39]:

$$P_{eff}\left(z\right)=P_F+\left(P_B-P_F\right) {\left[\left(1/2\right)+\left(z/h\right)\right]}^{ {\kappa }_p},$$

(83)

where the subscripts B and F represent the materials BaTiO₃, enriched at the top surface, and CoFe₂O₄, enriched at the bottom surface, respectively. A dimensionless frequency parameter is defined as follows: $\overline{\omega }=\left(\omega L_x^2 /h\right)\sqrt{{\rho }_F/{\left(c_{11}\right)}_F}$.

Table 4 compares the results for the FG-MEE macroscale plate’s lowest and second-lowest frequencies with $\left(\widehat{m}, \widehat{n}\right)=(1, 1)$. Again, the results in Table 4 illustrate that the accuracy of various CCST-based SDSDTs compared to the 3D solutions reported in the literature [55,56,57] is arranged in descending order as follows: (Reddy’s refined SDT, sinusoidal SDT, exponential SDT, and hyperbolic SDT) > first-order SDT > CPT. The results obtained using Reddy’s refined SDT, sinusoidal SDT, exponential SDT, and hyperbolic SDT are closely aligned with one another. Their solutions are in excellent agreement with those obtained by Wu and Lu [55] using the state space method, Tsai and Wu [56] using the perturbation method, and Ramirez et al. [57] using a discrete layer method.

4.2. Parametric Studies

This section examines the free vibration characteristics of an FG-MEE microplate under fully simple supports and magneto-electro-thermo-mechanical loads, where the microplate has not yet undergone static buckling. We conducted a parametric study to investigate the influence of several primary factors affecting the microplate’s natural frequency, including the effects of the material length-scale parameter, length-to-thickness ratio, inhomogeneity index, and the magnitude of magneto-electro-thermo-mechanical loads. The FG-MEE microplate of interest is composed of BaTiO₃, a piezoelectric material, and CoFe₂O₄, a magnetostrictive material, which are the same materials used in Section 4.1.2. The microplate’s effective material properties are estimated using the rule of mixtures and are expressed in Equation (83). The dimensionless frequency parameter is defined in the same form as that used in Section 4.1.2.

4.2.1. Unloaded FG-MEE Microplates Under Open-Circuit Surface Conditions

Figure 2a,b shows the variations in the microplate’s lowest frequency with different values of $\widehat{m}$ and $\widehat{n}$ for the cases of l/h = 0 and l/h = 0.5, respectively.

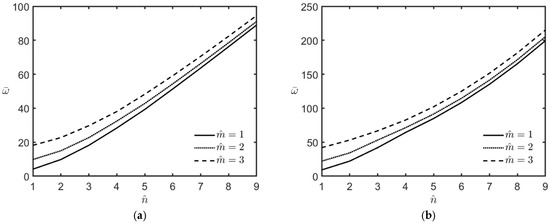
Figure 2. Variations in the lowest frequency of the FG-MEE microplate under open-circuit surface conditions with different sets of wave number pairs for the cases of (a) l/h = 0 and (b) l/h = 0.5.

The relevant geometric parameters are as follows: $L_x=L_y,$ $L_x/h=10,$ and $h=17.8\times {10}^{-6} \mathrm{m}.$ The inhomogeneity index is ${\kappa }_p=3.$ It is shown that the lowest frequency always occurs at $\left(\widehat{m}, \widehat{n}\right)=(1, 1)$, and the lowest frequency appears to increase monotonically when the values of $\widehat{m}$ and $\widehat{n}$ increase. The material length-scale parameter l makes the microplate stiffer, resulting in an increase in its lowest natural frequency.

Figure 3 shows the variations in the microplate’s lowest frequency with the inhomogeneity index for the wave number pairs $\left(\widehat{m}, \widehat{n}\right)=(1, 1)$, (1, 2), and (2, 2). The relevant geometric parameters are as follows: $L_x=L_y,$ $L_x/h=10,$ and $h=17.8\times {10}^{-6}\hspace{0.33em}\mathrm{m}.$ In addition, l/h = 0.5.

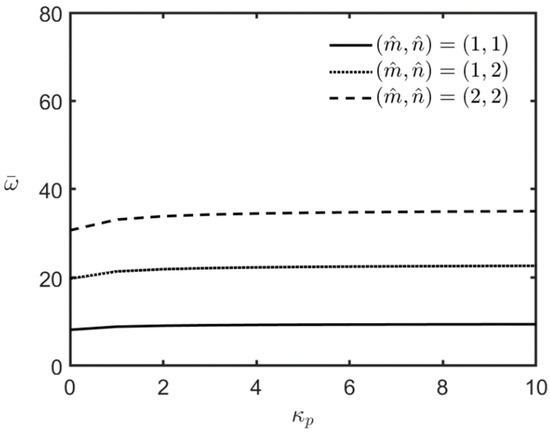
Figure 3. Variations in the lowest frequency of the FG-MEE microplate under open-circuit surface conditions with different values of the inhomogeneity index.

The results in Figure 3 reveal that the microplate’s lowest frequency exhibits only minor changes as the value of the inhomogeneity index increases. This is because the differences between the stiffness coefficients of the phase materials BaTiO₃ and CoFe₂O₄ are minor. An increase in the inhomogeneity index leads to an increase in the volume fraction of the stiffer material CoFe₂O₄, resulting in a minor increase in the microplate’s overall stiffness, which in turn leads to a slight increase in its lowest frequency.

Figure 4 shows the variations in the square microplate’s lowest frequency with the L_x/h ratio. The relevant material parameters are as follows: ${\kappa }_p=3,$ $l/h=0.2, 0.4, \mathrm{and} 0.8,$ and $l=8.8\times {10}^{-6} \mathrm{m}.$ The dimensionless frequency is replaced with the following form: $\widehat{\omega }=\left(10\hspace{0.33em}\omega h\right) \sqrt{{\rho }_F/{\left(c_{11}\right)}_F}$. The microplate’s lowest frequency is shown to decrease when the value of the L_x/h ratio increases. This is because an increase in the L_x/h ratio represents the microplate of interest becoming thinner, resulting in a decrease in the microplate’s overall stiffness and, subsequently, a decrease in its lowest frequency.

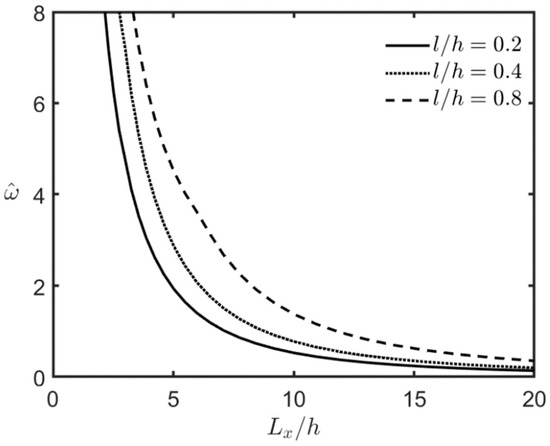
Figure 4. Variations in the lowest frequency of the FG-MEE square microplate under open-circuit surface conditions with different Lx/h ratios.

4.2.2. Loaded FG-MEE Microplates Under Closed-Circuit Surface Conditions

This section examines the free vibration characteristics of an FG-MEE microplate under fully simply supported conditions, closed-circuit surface conditions, and magneto-electro-thermal mechanical loads. Figure 5, Figure 6, Figure 7 and Figure 8 illustrate the variations in the FG-MEE microplate’s lowest frequency with respect to the magnitude of the applied uniform temperature changes, electric potential, magnetic potential, and biaxial compressive loads, respectively. The results in Figure 5, Figure 6 and Figure 8 show that the microplate’s lowest frequency decreases when the magnitude of the uniform temperature changes, electric potential, and biaxial compressive loads increase. This indicates that an increase in the magnitude of uniform temperature changes, electric potential, and biaxial compressive loads results in a set of initial compressive forces induced in the microplate, leading to a decrease in the microplate’s overall stiffness, and consequently, and in turn a decrease in the microplate’s lowest frequency. On the contrary, the results in Figure 7 show that the microplate’s lowest frequency increases when the magnitude of the applied magnetic potential increases due to a set of initial in-plane tension forces induced in the microplate.

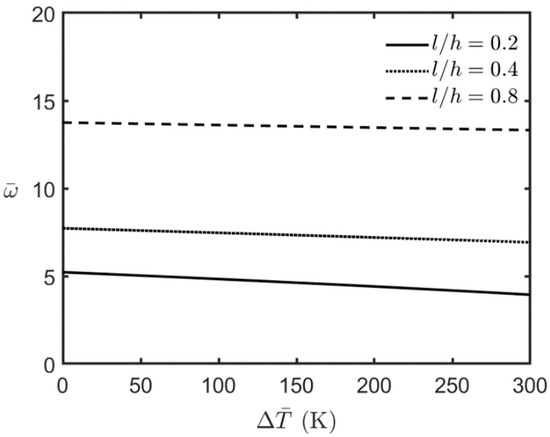
Figure 5. Variations in the lowest frequency of the FG-MEE microplate under closed-circuit surface conditions with different values of the applied uniform temperature changes.

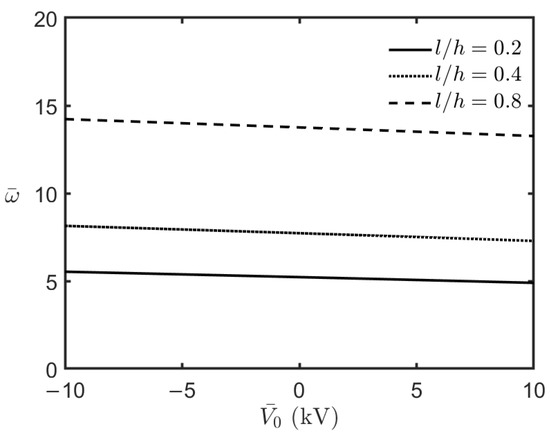
Figure 6. Variations in the lowest frequency of the FG-MEE microplate under closed-circuit surface conditions with different values of the applied electric potential.

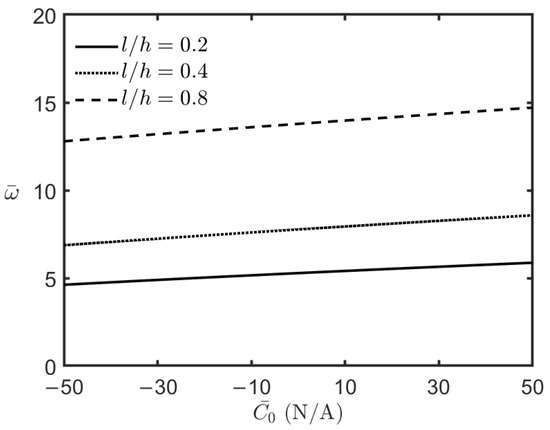
Figure 7. Variations in the lowest frequency of the FG-MEE microplate under closed-circuit surface conditions with different values of the applied magnetic potential.

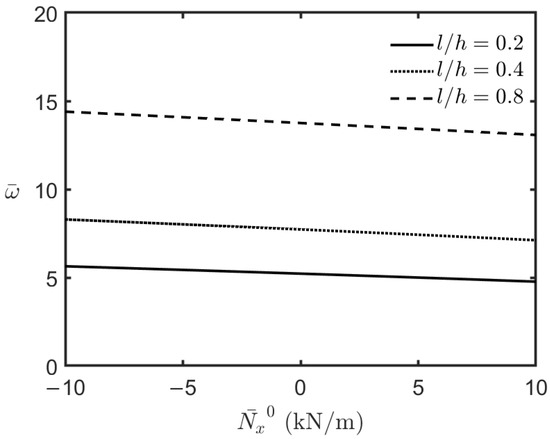
Figure 8. Variations in the lowest frequency of the FG-MEE microplate under closed-circuit surface conditions with different values of the applied biaxial loads.

5. Conclusions

In this work, we developed a unified SDSDT based on the CCST capable of investigating the free vibration characteristics of an FG-MEE microplate under fully simply supported conditions, open- or closed-circuit surface conditions, and magneto-electro-thermo-mechanical loads, where the couple stress and thickness stretching effects are considered. By employing Hamilton’s principle, we obtained the unified SDSDT’s strong form. By utilizing a specific shape function that characterizes the shear deformation distribution along the thickness in this formulation, various CCST-based SDSDTs could be reproduced, including the CCST-based CPT, first-order SDT, Reddy’s refined SDT, sinusoidal SDT, exponential SDT, and hyperbolic SDT. By employing the double Fourier series expansion method, we obtained the Navier-type analytical solutions for the natural frequency of an FG-MEE microplate. The formulation for analyzing an FG-MEE microplate could be simplified to that of an FG-MEE macroscale plate and an FG piezoelectric microplate by setting the material length-scale parameter to zero and the relevant magnetic coefficients to zero, respectively.

In the validation and comparison studies, the solutions of the CCST-based Reddy’s refined SDT, sinusoidal SDT, exponential SDT, and hyperbolic SDT were found to agree closely with one another. Their solutions were shown to be in excellent agreement with relevant 3D solutions reported in the literature. It was noted that the shear deformation effect and the thickness stretching effect made the microplate softer, leading to a decrease in its lowest frequency. The material length-scale parameter effect made the microplate stiffer, resulting in an increase in its lowest resonant frequency.

The parametric studies revealed that increasing the magnitude of the applied uniform temperature changes, electric potential, and biaxial compressive forces decreased the FG-MEE microplate’s lowest frequency. On the contrary, an increase in the magnitude of the applied magnetic potential increased the FG-MEE microplate’s lowest frequency.

The advantage of the consistent couple stress theory (CCST) over the traditional couple stress theory is that the number of material length-scale parameters required for analyzing an elastic body is reduced from two to one. Additionally, the strong and weak forms of the CCST have been demonstrated to be feasible for developing analytical and numerical methods, respectively. In contrast, the traditional couple stress theory has been shown to pose an indeterminate problem, hindering its application. Furthermore, the couple stress effect is significant when the structure’s dimensions are stretched approaching the microscale, i.e., $1\times {10}^{-6}\mathrm{m}$. Other higher-order strain gradient effects become significant when the structure’s dimensions are stretched approaching the nanoscale, i.e., $1\times {10}^{-9}\mathrm{m}$. Therefore, the application of CCST is appropriate for the structure’s dimensions between the micrometer and nanometer ranges.

Because the results of the free vibration characteristic of an FG-MEE microplate subjected to magneto-electro-thermo-mechanical loads are rare, the solutions presented in this study can provide a reference for their validation and comparison when a new relevant theory is proposed. In addition, the unified SDSDT could be extended to analyze the static bending, static buckling, and dynamic buckling behaviors of an FG-MEE microplate. Its weak formulation could also be employed to develop relevant numerical methods such as the finite element method and the meshless method.