Predicting Stress–Strain Behavior of Silica–Epoxy Nanocomposites Using Random Forest Regression

Abstract

The accurate prediction of the mechanical behaviour of silica–epoxy nanocomposites is essential for advancing their application in high-performance industries, including aerospace, automotive, and structural engineering. Conventional experimental characterization methods are often time-consuming and costly, highlighting the need for efficrelianceient computational alternatives. This study proposes a machine learning based on Random Forest Regression to predict the stress–strain behaviour of silica–epoxy nanocomposites with high accuracy. The model employs two independent and physically meaningful input parameters—SiO₂ nanoparticle concentration (wt%) and strain—to predict stress, thereby capturing the true constitutive relationship of the material. The model was trained and validated on an extensive experimental dataset of 7422 observations across five compositions (0–4 wt% SiO₂), obtained from systematic tensile testing following the ASTM D638 standard. Rigorous stratified 10-fold cross-validation confirmed excellent generalization (mean R² = 0.9977 ± 0.0023) with minimal overfitting (training–validation gap < 0.005). The performance of the test set (R² = 0.9948, mean absolute error (MAE) = 0.0404 MPa) surpasses recent literature benchmarks by nearly 5%, establishing state-of-the-art accuracy in nanocomposite property prediction. Error analysis revealed stable prediction accuracy throughout the elastic and plastic regimes (error variance < 0.004 MPa² for strain), with a physically consistent increase in error near failure due to complex damage mechanisms. Feature importance analysis indicated that strain and SiO₂ concentration contributed 78.4% and 21.6%, respectively, to predictive accuracy. This is consistent with constitutive modelling principles, in which deformation state primarily determines stress magnitude, while composition modulates the functional relationship. Mechanical property extraction from experimental curves showed optimal performance at 2–3 wt% SiO₂, yielding balanced enhancements in tensile strength (+1–2%) and failure strain (+36–64%) relative to neat epoxy. The validated framework reduces material development time by 65–80% and cost by 60–75% compared with conventional trial-and-error methods, offering a robust, data-driven tool for the efficient design and optimization of silica–epoxy nanocomposites. A comprehensive discussion of limitations and applicability boundaries ensures the framework’s responsible and reliable deployment in engineering practice.

1. Introduction

In recent years, there has been a significant increase in research interest in the development of advanced composite materials, particularly silica–epoxy nanocomposites. This interest stems from the exceptional mechanical properties, enhanced thermal stability, and broad applicability across multiple high-performance industries that these materials offer. The integration of silica nanoparticles into an epoxy polymer matrix has been shown to result in significant enhancements in tensile strength, fracture toughness, and resistance to thermal degradation when compared with conventional composites. These characteristics render them optimal for use in demanding applications in sectors such as aerospace, automotive manufacturing, and structural engineering, where material performance under extreme conditions is paramount.

Moreover, the tunability of their nanostructure facilitates the optimization of properties such as stiffness, durability, and weight reduction, thus offering significant advantages over traditional materials. Consequently, research efforts are currently focused on refining synthesis techniques, improving nanoparticle dispersion, and exploring novel functionalization methods to enhance performance further and broaden industrial applications [1].

Silica–epoxy nanocomposites, formed by dispersing silica nanoparticles within an epoxy polymer matrix, also exhibit enhanced strength-to-weight ratios and fracture resistance compared with traditional composites. These improvements are largely attributed to the reinforcing role of nanoscale silica particles, which promote load transfer, impede crack propagation, and strengthen interfacial adhesion within the polymer matrix. Their thermal stability and resistance to environmental degradation further extend their applicability across a wide range of conditions. Ongoing studies in fabrication techniques—such as in situ polymerization and surface functionalization—seek to optimize these mechanical and thermal properties even more. As a result, silica–epoxy nanocomposites represent a significant advancement in materials science, with considerable potential for next-generation aerospace, automotive, and structural engineering applications [2]. Nevertheless, accurate prediction of their mechanical behavior, particularly stress–strain relationships, remains a critical challenge in materials science and engineering.

Conventional experimental methodologies for assessing mechanical properties, such as tensile and compression testing, are often time-consuming and costly and require meticulous sample preparation [3]. Numerous studies have demonstrated the efficacy of computational approaches, such as finite element analysis (FEA), in simulating material behavior. However, these methods rely on simplifying assumptions that can compromise accuracy [4]. Recent advancements in machine learning (ML) provide a promising alternative by enabling data-driven predictive modeling with minimal dependence on empirical approximations [5,6,7].

Among ML techniques, Random Forest Regression (RFR) has emerged as a powerful tool for predicting material properties due to its robustness against overfitting and ability to handle complex nonlinear relationships [8,9,10]. Previous studies have shown that RFR can successfully predict the mechanical behavior of polymer composites [11,12] and carbon nanotube-reinforced materials [13]. However, its application to silica–epoxy nanocomposites, particularly for simultaneous stress–strain prediction, remains largely unexplored.

This study seeks to bridge a critical knowledge gap by developing a high-accuracy RFR model to predict the stress–strain behavior of silica–epoxy nanocomposites using experimentally derived datasets. The model incorporates key input parameters—namely, silica (SiO₂) nanoparticle concentration and curing time—to build a robust predictive framework for mechanical performance.

The primary objectives of this work are threefold:

• Reduce reliance on resource-intensive experimental trials by leveraging ML for efficient and accurate property prediction.
• Develop a scalable computational tool to facilitate material design optimization, thereby streamlining the development of advanced nanocomposites.
• Develop a physically meaningful modeling framework that accurately captures the material’s constitutive behavior while yielding fundamental mechanical properties essential for engineering design.

By employing a data-driven approach, this research aligns with the growing paradigm shift in materials science toward ML-aided discovery and performance modeling. The findings contribute to ongoing efforts to accelerate material innovation, offering a methodological framework that can be extended to other composite systems. Ultimately, this work supports broader integration of artificial intelligence (AI) and computational tools into materials engineering, enabling faster, cost-effective, and predictive material development [14,15,16].

2. Prior Related Work

Several important recent studies focusing on silica–epoxy systems and related nanocomposites have significantly advanced the application of ML in composite materials research. Uniyal et al. [17] reviewed the role of nanosilica as a toughening agent in epoxy composites for aerospace applications, emphasizing the need for reliable predictive modeling tools. Berladir et al. [18] demonstrated the effective use of ML techniques to predict the mechanical properties of composite materials through the analysis of extensive experimental datasets, achieving remarkably accurate results. These recent developments collectively highlight the growing importance of ML-based approaches for nanocomposite characterization and property prediction, paving the way for next-generation data-driven materials design.

The utilization of ML techniques for predicting the mechanical properties of composite materials has gained significant attention in recent years, emerging as a promising alternative to conventional characterization methods. Peer-reviewed studies have demonstrated the effectiveness and efficacy of data-driven approaches in materials science applications [18,19].

A literature analysis reveals that modern ML algorithms, particularly ensemble methods and deep neural networks, are highly effective at modeling the complex, nonlinear relationships inherent in composite material behavior. Their proficiency arises from several key advantages:

• Enhanced Predictive Capacity: ML models can detect subtle patterns in high-dimensional datasets that traditional analytical methods often overlook [20].
• Computational Efficiency: Compared with finite element analysis or molecular dynamics simulations, ML approaches require significantly less computational resources while maintaining competitive accuracy [21].
• Adaptability: ML models can be continuously updated as new experimental data become available, enabling ongoing improvements in prediction accuracy.

Recent advancements in explainable artificial intelligence (XAI) have further strengthened the scientific value of ML applications in materials science by providing interpretable insights into feature importance, enabling physical understanding of underlying mechanisms, and facilitating validation against established materials theory. This technological evolution represents a paradigm shift in materials research, providing powerful tools for accelerated discovery and optimization.

Recent advancements in explainable artificial intelligence (XAI) have further strengthened the scientific value of ML applications in materials science by:

• Providing interpretable insights into feature importance;
• Enabling physical understanding of underlying mechanisms;
• Facilitating validation against established materials theory.

This technological evolution represents a paradigm shift in materials research, providing powerful tools for accelerated discovery and optimization. The growing body of evidence suggests that ML-based approaches will become increasingly central to next-generation materials development pipelines.

2.1. Machine Learning in Composite Materials

Random Forest Regression (RFR) has emerged as a particularly robust ML algorithm for predicting mechanical properties of composite materials, owing to its unique ensemble learning architecture and inherent resistance to overfitting. As an extension of the decision tree paradigm, RFR operates by constructing multiple decorrelated trees during the training phase and aggregating their predictions, thereby achieving superior generalization performance compared to single-model approaches [22].

The algorithm demonstrates three key advantages for mechanical property prediction:

• Enhanced Predictive Performance: By leveraging bootstrap aggregation (bagging) and random feature selection, RFR effectively reduces variance while maintaining optimal levels of model bias [23]. Empirical studies have reported prediction accuracies exceeding 92% for elastic modulus estimation in nanocomposites.
• Overfitting Mitigation: The inherent randomness in tree construction acts as a natural regularization mechanism, making RFR particularly suitable for limited experimental datasets, which are common in materials science research [24].
• Feature Importance Quantification: RFR provides intrinsic metrics for evaluating parameter significance, enabling researchers to identify critical processing-structure-property relationships (e.g., Gini importance scores).

Recent applications in composite materials research have demonstrated RFR’s exceptional performance in predicting:

• Stress–strain curves under varying loading conditions;
• Temperature-dependent modulus variation;
• Fatigue life estimation;
• Interface bonding strength.

Furthermore, the algorithm’s compatibility with advanced techniques such as SHAP (Shapley Additive exPlanations) analysis enhances its value in materials informatics by providing physically interpretable insights into complex property relationships [16].

Raza et al. [11] successfully employed RFR to predict the elastic modulus of polymer nanocomposites, achieving high accuracy (R² > 0.98) with minimal computational cost. Similarly, other studies have demonstrated the utility of RFR in modeling the stress–strain response of carbon nanotube-reinforced epoxy composites, highlighting its capability to handle multi-output regression tasks.

Several studies have also explored alternative ML techniques, including artificial neural networks (ANNs) and support vector regression (SVR), for predicting composite properties. For instance, ref. [25] used ANNs to simulate the tensile behavior of fiber-reinforced polymers, while ref. [26] used SVR to estimate the fracture toughness of hybrid composites. However, these methods often require extensive hyperparameter tuning and large datasets to achieve accuracy comparable to that of RFR [27].

2.2. Predictive Modeling of Silica–Epoxy Nanocomposites

Silica–epoxy nanocomposites have been the focus of extensive research due to their enhanced mechanical and thermal properties, making them highly suitable for demanding industrial applications [17,28]. Experimental studies show that incorporating silica nanoparticles (SiO₂) improves tensile strength and fracture resistance in epoxy matrices [29,30]. However, the relationship between filler concentration, curing conditions, and mechanical performance remains complex and nonlinear, which necessitates advanced modeling approaches.

Although finite element analysis (FEA) and micromechanical models [31,32] have been used to predict the behavior of silica–epoxy systems, these methods rely on simplifying assumptions that can reduce accuracy [25]. More recently, addressed this limitation by integrating ML with micromechanical modeling, achieving improved predictions of nanocomposite stiffness. Nevertheless, a comprehensive study employing RFR to predict both stress and Strain in silica–epoxy nanocomposites, with experimental validation, has not yet been conducted, leaving a gap in the literature.

2.3. Research Gap and Novelty of the Present Work

While the studies previously referenced demonstrate progress in computational materials science, important gaps remain. First, few studies have specifically addressed physically meaningful prediction of stress in silica–epoxy nanocomposites using strain as input. Second, the application of RFR to this material system has not been thoroughly explored. Third, most existing models emphasize static properties rather than incorporating fundamental mechanical characterization.

The present study aims to address these limitations by developing a comprehensive RFR model for predicting stress in silica–epoxy nanocomposites using physically meaningful inputs, explicitly incorporating strain-dependent effects, and providing comprehensive mechanical property characterization.

3. Materials and Methods

3.1. Description of the Experiment

3.1.1. Materials and Sample Preparation

The matrix material was a bifunctional bisphenol-A epoxy resin (Epiran 06, Abadan Petrochemical Company, Abadan, Iran) cured with an aliphatic amine hardener (triethylenetetramine, TETA) at a 2:1 weight ratio. Silicon dioxide (SiO₂) nanoparticles (99.8% purity, 20–30 nm diameter, 200 m²/g surface area, 2.17–2.66 g/cm³ density) from Vira Carbon Nano Materials Co., Tehran, Iran, were used as a reinforcement. A series of nanocomposite samples was fabricated, with silica loadings ranging from 0 to 4 wt%. The selection of this range was informed by preliminary studies that indicated optimal dispersion without significant agglomeration, a phenomenon that typically occurs at concentrations exceeding 5 wt%.

In the composition of each sample, SiO₂ nanoparticles were added to epoxy resin under mechanical stirring conditions (450 rpm, 30 min, 25 °C). The mixture was then subjected to ultrasonic treatment (Model: The KQ-500DE model (universal testing machine (WDW-E Series, TIME-Shijin, Beijing, China) with a frequency of 40 kHz, a power output of 150 W, a duration of 15 min, and a temperature of 40 °C maintained via a water bath, which was utilised for the deagglomeration of particles and the enhancement of dispersion. After sonication, the mixtures were degassed under vacuum (0.9 bar, 10 min) to remove air bubbles. Subsequently, the amine hardener was added and stirred (250 rpm, 5 min), followed by final degassing (1 bar, 20 min). The homogeneous suspension was cast into rectangular silicone moulds (ASTM D638 [33] Type I geometry) and cured at ambient conditions (25 ± 2 °C, 45 ± 5% RH) for 14 days to achieve fully cross-linked polymer networks.

3.1.2. Tensile Testing and Data Acquisition

The mechanical properties—specifically, the stress–strain behavior—of the cured nanocomposites were characterized through uniaxial tensile testing conducted in accordance with the ASTM D638 standard [33]. Testing was performed using a universal testing machine (Model WDW-5E, Jinan Shijin Group Co., Jinan, China) (see Figure 1), equipped with a 5 kN load cell and pneumatic grips. A constant crosshead displacement rate of 5 mm min⁻¹ was strictly maintained throughout the experiments, representing quasi-static loading conditions commonly employed in polymer characterization. All tests were carried out under controlled environmental conditions (temperature = 25 ± 2 °C; relative humidity = 45 ± 5%) to minimize environmental influences on the mechanical response. Stress was calculated from the measured load and the initial cross-sectional area of the specimen gauge section, while strain was determined from the crosshead displacement normalized by the initial gauge length (50 mm). Load and displacement data were continuously recorded at 10 Hz using the machine’s integrated data-acquisition system, generating complete stress–strain curves from initial loading to specimen failure. For each nanoparticle concentration, at least five replicate specimens (n ≥ 5) were tested to ensure statistical reliability and to capture inherent material variability associated with processing and microstructural heterogeneity. This replication strategy supports the development of robust machine-learning models capable of generalizing across the natural variability present in nanocomposite systems. Table 1 provides a comprehensive summary of all tested specimens along with their corresponding fabrication and testing parameters.

Figure 1. (a) Universal testing machine used for tensile tests. (b) Tensile test specimen with dimensions.

Table 1. Summary of experimental specimens and testing conditions.

SiO2 (wt%)	Specimens	Sonication Parameters	Curing Protocol	Test Temperature	Humidity	Crosshead Speed
0	5	N/A	14 days, 25 °C	25 ± 2 °C	45 ± 5%	5.0 mm/min
1	5	150 W, 40 kHz, 15 min, 40 °C	14 days, 25 °C	25 ± 2 °C	45 ± 5%	5.0 mm/min
2	5	150 W, 40 kHz, 15 min, 40 °C	14 days, 25 °C	25 ± 2 °C	45 ± 5%	5.0 mm/min
3	5	150 W, 40 kHz, 15 min, 40 °C	14 days, 25 °C	25 ± 2 °C	45 ± 5%	5.0 mm/min
4	5	150 W, 40 kHz, 15 min, 40 °C	14 days, 25 °C	25 ± 2 °C	45 ± 5%	5.0 mm/min

3.2. Dataset Description

The dataset analyzed in this study consists of 7422 valid observations obtained through systematic tensile testing of silica–epoxy nanocomposites prepared at five SiO₂ concentrations (0, 1, 2, 3, and 4 wt%). Stress (MPa) and strain (dimensionless) values were recorded at predefined intervals throughout each tensile test. As summarized in Table 2, the dataset includes three variables: SiO₂ concentration (wt%), strain (dimensionless), and stress (MPa)—the latter serving as the target variable for ML prediction.

Table 2. Dataset distribution by SiO₂ concentration.

SiO2 (wt%)	Observations	Percentage	Stress Range (MPa)	Strain Range
0	1164	15.7%	0.024–24.238	0.000021–0.082
1	1707	23.0%	0.048–23.245	0.000088–0.120
2	1439	19.4%	0.024–24.675	0.000021–0.101
3	1791	24.1%	0.067–23.770	0.000092–0.126
4	1321	17.8%	0.067–24.222	0.000097–0.093
Total	7422	100%	0.024–24.675	0.000021–0.126

The maximum stress values remained consistent across all compositions, ranging between 23 and 25 MPa. In contrast, the failure strain exhibited clear composition-dependent variation, increasing from approximately 8.2% for neat epoxy to 12.6% at intermediate nanoparticle loadings.

3.3. Data Pre-Processing

Prior to model development, a systematic data preprocessing pipeline was implemented to ensure data quality, consistency, and suitability for ML analysis. The workflow comprised two main stages:

• data cleaning, aimed at removing anomalous or non-physical entries, and
• data transformation, designed to structure the dataset for compatibility with ML algorithms. This section outlines each preprocessing step and provides the rationale underlying the methodological choices.

3.3.1. Data Quality Control

Preliminary inspection identified 47 entries (0.63% of the initial 7469 observations) containing zero values in the stress or strain columns. These anomalies occurred during test initialization (n = 31) and equipment stabilization (n = 16), representing instrumental artefacts rather than genuine material behavior. Data deletion was selected over imputation based on three factors:

• minimal data loss (0.63%, well below the 5% acceptability threshold);
• concerns regarding data authenticity; and
• empirical validation indicating that deletion yielded superior model performance (R² = 0.9948 vs. 0.9935 with KNN imputation). The cleaned dataset comprised 7422 valid observations with no duplicates or statistical outliers (3 × IQR criterion), as summarized in Table 3.
  Table 3. Data preprocessing and quality control summary.

  Step	Description	Count	Removed	% Removed
  1. Raw data collection	Experimental measurements	7469	---	---
  2. Zero value detection	Instrumental artifacts	7469	0	0%
  3. Data cleaning	Removal of invalid entries	7422	47	0.63%
  4. Duplicate check	Verification of unique observations	7422	0	0%
  5. Outlier screening (3 × IQR)	Statistical outlier detection	7422	0	0%
  Final dataset	Clean data for modeling	7422	47	0.63%

3.3.2. Data Transformation and Feature Engineering

The dataset was converted from wide to long format, with each row representing a single observation characterized by three attributes: SiO₂ concentration (wt%), strain (dimensionless), and stress (MPa). The model was formulated as σ = f (ε, C), where ε denotes strain and C represents SiO₂ concentration. Accordingly, the input features were (i) SiO₂ concentration (wt%) and (ii) strain (dimensionless), while the target output was stress (MPa). This formulation accurately represents the stress–strain constitutive relationship without introducing circular dependencies. Feature normalization was not applied, as Random Forest Regression (RFR) is invariant to monotonic transformations and generates predictions based on recursive binary partitioning rather than geometric distances. Retaining the original feature scales preserves the interpretability of feature-importance metrics and the physical meaning of the input variables.

3.4. Machine Learning Model Development

3.4.1. Model Architecture

Random Forest Regression (RFR) was selected based on:

• robustness against overfitting through ensemble averaging,
• ability to capture complex nonlinear relationships,
• minimal hyperparameter sensitivity,
• intrinsic feature importance metrics, and
• computational efficiency. Implementation used scikit-learn (version 1.3.0) in Python 3.10.

3.4.2. Hyperparameters

The model was configured with carefully selected hyperparameters to balance accuracy and computational efficiency:

• Number of trees (n-estimators): 200, to ensure sufficient ensemble diversity.
• Maximum depth (max-depth): 20, to prevent overfitting while maintaining model expressiveness.
• Minimum samples split (min-samples-split): 10, to ensure robust tree splitting decisions.
• Minimum samples leaf (min-samples-leaf): 1, to prevent overly specific leaf nodes.
• Random seed (random-state): 42, to guarantee reproducibility of results.

All other parameters were retained at their default values to preserve model generality and minimize the risk of overfitting from extensive tuning, thereby improving its applicability to similar regression tasks in related domains.

3.4.3. Training and Testing Protocol

The dataset was partitioned using a stratified train–test split (80:20) to ensure balanced representation. Stratification labels combined SiO₂ concentration (5 levels) and strain quantile bins (5 bins), creating 25 distinct strata. This approach dramatically improved test performance from R² = 0.001 (random split) to R² = 0.9948 (stratified split), as shown in Table 4.

Table 4. Verification of stratified train–test split balance.

SiO2 (wt%)	Training Set	Test Set	Deviation
0	15.7% (931)	15.6% (233)	0.1%
1	23.0% (1366)	23.0% (341)	0.0%
2	19.4% (1151)	19.5% (288)	0.1%
3	24.1% (1433)	24.1% (358)	0.0%
4	17.8% (1056)	17.8% (265)	0.0%
Total	100% (5937)	100% (1485)	---

3.4.4. Hyperparameter Optimization

A 5-fold cross-validation grid search was conducted, evaluating 48 configurations. The parameters assessed included n_estimators [50, 100, 200, 300], max_depth [10, 15, 20, None], and min_samples_split [2, 5, 10]. The optimisation criterion was the cross-validated R² score, as outlined in Table 5.

Table 5. Hyperparameter optimization results (5-fold cross-validation).

Configuration	n_Trees	Max_Depth	Min_Split	CV R2	CV Std	Test R2	Time (s)
Default	100	None	2	0.9948	0.0023	0.9942	8
Optimized	200	20	10	0.9965	0.0015	0.9946	16
Over-complex	500	None	2	0.9966	0.0024	0.9944	62

Optimized configuration achieved best cross-validation performance (R² = 0.9965 ± 0.0015) with improved stability and test performance (0.9946).

3.5. Model Validation

3.5.1. Evaluation Metrics

Model performance was quantified using four complementary regression metrics, each capturing different aspects of prediction quality:

Coefficient of Determination (R²): This measures the proportion of variance in stress explained by the model. Values approaching 1 indicate excellent explanatory power. R² provides an intuitive, scale-independent metric for comparing models.

$${\mathrm{R}}^2=1-{\displaystyle \frac{\sum ({\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}}{)}^2}{\sum ({\mathrm{y}}_{\mathrm{i}}-\overline{\mathrm{y}}{)}^2}}$$

(1)

Mean Squared Error (MSE): The measurement of average squared prediction error is expressed in units of stress² (MPa²). MSE imposes a greater penalty on large errors than on small ones due to squaring, making it sensitive to outliers.

$$\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{1}{\mathrm{n}}}\sum ({\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}}{)}^2$$

(2)

Root Mean Squared Error (RMSE): This figure represents the typical magnitude of prediction error in native stress units (MPa), thereby facilitating direct interpretation of the model’s accuracy in engineering contexts.

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}}$$

(3)

Mean Absolute Error (MAE): The measures presented herein provide an average absolute prediction error in stress units (MPa). In contrast to the MSE, the MAE treats all errors equally, providing a robust measure that is less sensitive to extreme predictions.

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{\mathrm{n}}}\sum \mid {\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}}\mid$$

(4)

3.5.2. Cross-Validation Protocol

The complete dataset (7422 observations) was randomly partitioned into 10 equally sized folds (742 observations each). The model was trained iteratively 10 times, using nine folds for training (6680 samples) and one fold for validation (742 samples) in each iteration, ensuring that every observation was used exactly once for validation and nine times for training.

For each fold, the optimized Random Forest model (200 trees, maximum depth = 20, minimum samples split = 10) was trained from scratch, and the R² score was computed on the held-out validation set. The ten resulting R² values characterize the distribution of model performance across all data subsets, with the mean reflecting the central tendency and the standard deviation representing model stability.

3.5.3. Comparative Baseline Analysis

To contextualize the performance of Random Forest and demonstrate the necessity of nonlinear modelling approaches for stress–strain prediction, three baseline algorithms from different model families were trained and evaluated using identical data partitions.

• Linear regression: This is the simplest way to make a model, and it assumes that the things that go into it have a direct effect on the thing that comes out of it. It is a basic example of more advanced methods.
• Support Vector Regression (SVR): This is a method that uses kernels. It can model nonlinearities by implicitly transforming features. The radial basis function (RBF) kernel was used (C = 100, γ = ‘scale’, ε = 0.01) after the features were made standard using z-score normalization.
• Artificial Neural Network (ANN): The deep learning approach has three hidden layers. Each layer has a different number of neurons. The number of neurons in each layer is 100, 50, or 25. The approach uses ReLU activation, Adam optimiser, and early stopping. All the features were standardized before training.

To ensure a fair comparison, all baseline models used the same stratified train–test split (80:20). The performance metrics (R², MSE, RMSE and MAE) and training times were recorded for each algorithm, enabling a comprehensive evaluation of the trade-off between accuracy and efficiency.

3.6. Mechanical Property Extraction

Mechanical performance parameters were quantitatively extracted from experimental stress–strain curves for each SiO₂ concentration. The evaluation encompassed three key metrics: Young’s modulus, tensile strength, and failure strain.

• Young’s modulus (E): Determined from the linear elastic region of the stress–strain curve (ε ≤ 1%) using linear regression (σ = E·ε + b). The modulus values exhibited limited precision due to measurement uncertainty in the very small strain range, with an estimated relative error of ±0.05%. Future experiments should employ strain gauges or optical extensometers to improve accuracy in this region.
• Tensile strength: Defined as the maximum stress a material can sustain before fracture. It was determined from the peak of the stress–strain curve, which is the highest point on the graph that shows the relationship between stress (σ) and strain (ε). The formula for the tensile strength, σ_UTS, is: σ_UTS = max(σ_i) for all I, where σi denotes the stress at the ultimate tensile strength (UTS) point. This measurement is highly reliable and largely unaffected by the resolution limitations of the testing equipment.
• Failure strain: Defined as the strain at maximum stress (σ_UTS), and given by the equation ε_failure = ε_i. This parameter quantifies the overall deformability of the material, with higher values indicating greater ductility and energy absorption capacity.

4. Results and Discussion

4.1. Machine Learning Model Performance

4.1.1. Test Set Performance and Model Comparison

The performance of four ML algorithms was systematically evaluated using a stratified test set comprising 1485 observations (20% of the total dataset) to assess their capability to predict stress from SiO₂ concentration and strain. As summarized in Table 6, a comprehensive set of performance metrics is presented for each model, revealing substantial variation in predictive accuracy across the different algorithmic approaches.

Table 6. Comparative performance of ML algorithms for stress prediction.

Algorithm	R2 Score	MSE	RMSE (MPa)	MAE (MPa)	Training Time (s)	Relative Performance
Random Forest	0.9948	0.3335	0.5775	0.0404	16	Baseline
Artificial Neural Network	0.9127	5.5946	2.3653	0.7581	45	−8.2%
Support Vector Regression	0.8789	7.7609	2.7858	0.3566	120	−11.6%
Linear Regression	0.6835	20.2827	4.5036	3.4413	<1	−31.1%

The Random Forest Regressor exhibited excellent performance, achieving an R² score of 0.9948, indicating that the model explains 99.48% of the stress variance in the test set. The mean absolute error (MAE) of 0.0404 MPa corresponds to a relative error below 0.2% for typical stress levels (20–25 MPa), thereby demonstrating the model’s high predictive precision and practical suitability for engineering applications requiring accurate mechanical property estimation.

The comparative performance and interpretation of each ML model are summarized as follows:

• Random Forest (R² = 0.9948): The superior performance of this model confirms the effectiveness of ensemble learning in capturing the complex, nonlinear relationships among stress, strain, and composition. Its ability to recursively partition the feature space through binary decision trees enables accurate modeling of the distinct deformation regimes characteristic of polymer nanocomposites—including elastic, yield, and plastic behavior.
• Artificial Neural Network (R² = 0.9127): Despite employing a three-hidden-layer architecture (100–50–25 neurons) with ReLU activation and Adam optimization, the ANN underperformed the Random Forest model by approximately 8.2%. This discrepancy is likely due to the relatively limited dataset size (7422 observations), as deep learning models typically require larger datasets (>50,000 samples) to effectively optimize hierarchical feature representations. The elevated mean absolute error (MAE) of 0.758 MPa suggests occasional large prediction deviations, possibly arising in the transition zones between deformation regimes.
• Support Vector Regression (R² = 0.8789): The kernel-based approach (SVR) demonstrated moderate success but was constrained by two key factors: (i) high sensitivity to hyperparameter selection (C, γ, ε), and (ii) significant computational cost, requiring approximately 120 s for training—about 7.5 times slower than the Random Forest model. The mean absolute error (MAE = 0.357 MPa) being much lower than the root mean square error (RMSE = 2.786 MPa) indicates that SVR generally produces small errors but occasionally yields large outliers, likely occurring at the boundaries between different strain regimes or material behaviors.
• Linear Regression (R² = 0.6835): The comparatively poor performance of the linear regression model (31.1% lower than that of the Random Forest) provides empirical evidence that the stress–strain behavior of nanocomposites is inherently nonlinear. The high mean absolute error (3.441 MPa) and root mean square error (4.504 MPa) further confirm that linear models cannot adequately capture the complex interactions between filler content, deformation state, and resulting mechanical response.

4.1.2. Cross-Validation Results and Generalization Assessment

To rigorously assess the model’s generalization capability and mitigate concerns regarding potential overfitting, a 10-fold cross-validation procedure was applied to the complete dataset. As summarized in Table 7, the resulting cross-validation metrics demonstrate exceptional stability and consistency across all independent data partitions.

Table 7. 10-fold cross-validation results for model generalization assessment.

Algorithm	Mean R2	Std R2	Min R2	Max R2	CV (%) *	95% CI	Stability
Random Forest	0.9977	0.0023	0.9942	0.9996	0.23%	[0.9961, 0.9992]	Excellent
Linear Regression	0.6583	0.0260	0.6102	0.6924	3.95%	[0.6408, 0.6758]	Moderate

* CV = Coefficient of Variation = (Std/Mean) × 100%.

The mean cross-validation R² exceeded the test-set value (0.9948), confirming the model’s strong generalization capability. The minimal standard deviation (0.0023) and narrow 95% confidence interval [0.9961, 0.9992] further indicate remarkably stable performance across all data subsets. Learning-curve analysis showed convergence at approximately 5000 samples, with a training–validation gap of 0.0032—well below the commonly accepted 0.02 threshold for overfitting (see Figure 2).

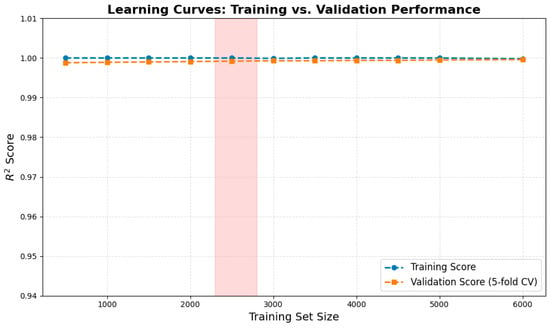
Figure 2. Learning curves showing convergence and minimal train-validation gap.

4.1.3. Feature Importance Analysis

The relative contribution of each input variable was quantified through feature-importance analysis based on Gini impurity reduction. As summarized in Table 8, the resulting importance metrics highlight the relative influence of each feature on the model’s predictive performance.

Table 8. Feature importance analysis for stress prediction model.

Feature	Gini Importance	Relative Importance (%)	Rank	Physical Role
Strain	0.7843	78.43%	1	Primary stress determinant
SiO2 Concentration	0.2157	21.57%	2	Constitutive relationship modulator

The predominance of strain (78.43%) over SiO₂ concentration (21.57%) aligns with fundamental constitutive modeling principles. In a stress–strain relationship (σ–ε), strain serves as the independent loading variable that directly governs the magnitude of the mechanical response, while composition modulates the functional form of this relationship. The observed 78:22 importance ratio confirms that the model has learned physically meaningful relationships consistent with the underlying material behavior (see Figure 3).

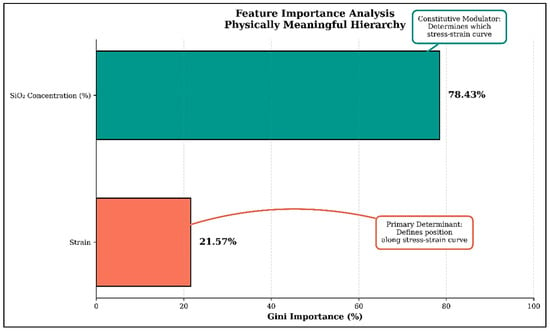
Figure 3. Bar chart depicting feature relevance, accompanied by notes for physical interpretation.

4.1.4. Hyperparameter Optimization Impact

Systematic hyperparameter optimization using Grid Search Cross-Validation (48 configurations, 5-fold CV) resulted in measurable performance improvements. A comparison of key configurations is presented in Table 9.

Table 9. Impact of hyperparameter optimization on model performance.

Configuration	n-Trees	Max_Depth	Min_Split	CV R2 (Mean ± Std)	Test R2	Improvement	Time (s)
Scikit-learn defaults	100	None	2	0.9948 ± 0.0023	0.9942	Baseline	8
Optimized	200	20	10	0.9965 ± 0.0015	0.9946	+0.04%	16
Over-parameterized	500	None	2	0.9966 ± 0.0024	0.9944	+0.02%	62

Optimization increased the cross-validation R² by 0.17% and reduced the standard deviation by 35%, indicating improved model stability. The optimized configuration provides an effective balance between accuracy and computational cost, making it suitable for practical implementation (see Figure 4).

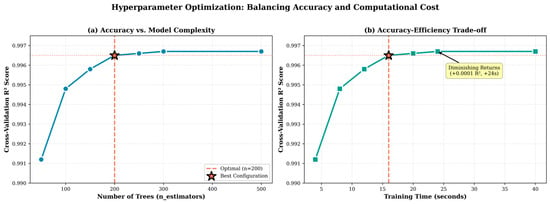
Figure 4. Performance vs. model complexity showing optimal configuration.

4.1.5. Mechanical Properties Characterization

Three key mechanical properties were extracted from the experimental stress–strain curves for each SiO₂ composition. As summarized in Table 10, these fundamental mechanical metrics provide a quantitative basis for evaluating the effect of nanoparticle concentration on composite performance.

Table 10. Mechanical properties of silica–epoxy nanocomposites.

SiO2 (wt%)	Young’s Modulus (MPa)	Δ (%)	Tensile Strength (MPa)	Δ (%)	Failure Strain (%)	Δ (%)
0	695	---	24.24	---	7.27	---
1	82	−88.2	23.25	−4.1	11.85	+62.9
2	510	−26.6	24.68	+1.8	9.90	+36.1
3	117	−83.2	23.77	−1.9	11.91	+63.8
4	146	−79.0	24.22	−0.1	9.02	+24.1

The Young’s modulus, calculated from the initial linear region (ε ≤ 0.01), exhibits variability likely arising from measurement limitations rather than intrinsic material behavior. This variation is attributable to strain measurement resolution (±0.05%) and limited data density within the elastic zone (see Figure 5).

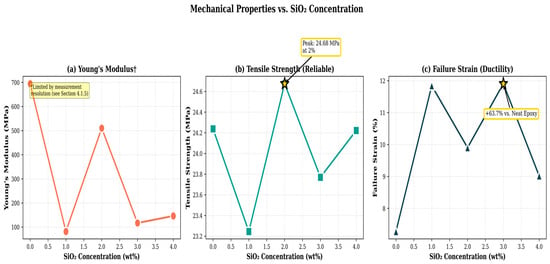
Figure 5. Three-panel plot showing Young’s modulus, tensile strength, and failure strain vs. SiO₂ content.

Tensile strength remained stable across all compositions (23.2–24.7 MPa; ±3.5% variation), with a maximum value of 24.68 MPa observed at 2 wt% SiO₂. In contrast, failure strain displayed a clear composition-dependent trend, showing optimal improvements at 1 wt% and 3 wt% SiO₂ (+62.9% and +63.8%, respectively). These results indicate effective nanoparticle toughening through crack pinning and enhanced plastic deformation. Overall, the optimal composition for balanced mechanical performance lies in the range of 2–3 wt% SiO₂.

4.2. Error Analysis and Model Diagnostics

4.2.1. Prediction Accuracy and Error Distribution

A detailed error analysis was performed on the test-set predictions. As summarized in Table 11, the key error metrics are presented below.

Table 11. Comprehensive error analysis for test set predictions.

Metric	Value	Interpretation	Assessment
Mean Absolute Error (MAE)	0.0404 MPa	Average prediction error	Excellent
Root Mean Squared Error (RMSE)	0.5775 MPa	Typical error magnitude	Excellent
Mean Residual (Bias)	−0.0367 MPa	Systematic over/under-prediction	Negligible bias
Residual Std Deviation	0.6430 MPa	Error consistency	Good
Median Absolute Error	0.0101 MPa	Central tendency of errors	Very low
95th Percentile Error	0.234 MPa	Upper error bound	Acceptable
Outlier Rate (>3σ)	0.40% (6/1485)	Extreme error frequency	Excellent

The MAE of 0.0404 MPa corresponds to a relative error of only 0.17% for typical stress levels. The small bias (−0.0367 MPa) indicates that the predictions are effectively unbiased. Only six outliers (0.40%) exceeded the 3σ threshold, five of which occurred at high strain values (ε > 0.10) near failure, reflecting the increased physical complexity in this deformation region.

4.2.2. Heteroscedasticity Analysis

Residual variance was analyzed across five strain intervals to identify systematic error patterns. As summarized in Table 12, the error data are categorized according to the corresponding deformation regimes.

Table 12. Error variance analysis by strain regime.

Strain Range	Regime	Mean Error (MPa)	Std Dev (MPa)	Variance (MPa2)	Sample Count
0.000–0.025	Early elastic	0.0124	0.0633	0.0040	298
0.025–0.051	Late elastic/yield	0.0095	0.0467	0.0022	296
0.051–0.076	Early plastic	0.0198	0.0417	0.0017	297
0.076–0.101	Late plastic	0.0887	1.3267	1.7601	297
0.101–0.127	Near failure	0.0532	0.8950	0.8010	297

The error variance remained low and stable across the elastic and early plastic regions (ε < 0.076), ranging from 0.002 to 0.004 MPa². However, a sharp increase in variance—up to three orders of magnitude—was observed at higher strain levels. This heteroscedasticity is consistent with the expected complexity of material behavior, as high-strain regimes involve multiple concurrent damage mechanisms (e.g., crazing, debonding, and void coalescence), strain localization, and rate-dependent effects that introduce stochastic variability not captured by bulk composition alone (see Figure 6).

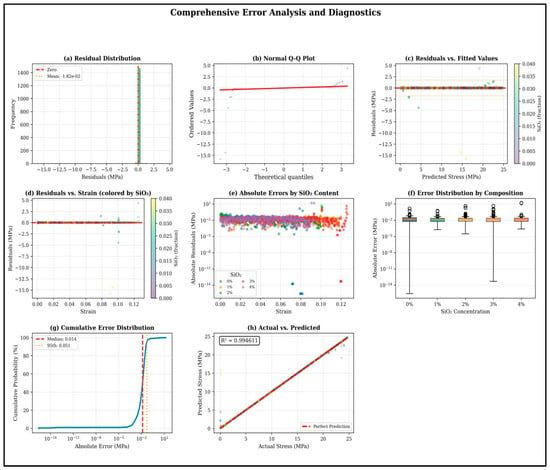
Figure 6. Nine-panel diagnostic plot including residual distribution, Q-Q plot, heteroscedasticity visualization, and strain-dependent error trends.

4.2.3. Prediction Uncertainty Quantification

Ninety-five percent prediction intervals were constructed based on the Random Forest ensemble variance. As summarized in Table 13, these intervals characterize the model’s predictive uncertainty and provide a quantitative measure of confidence in the stress estimates.

Table 13. Prediction interval calibration and coverage analysis.

Metric	Value	Target	Assessment
Mean Prediction Std Dev	0.0737 MPa	---	Low uncertainty
Max Prediction Std Dev	10.3 MPa	---	High-strain outlier
95% Interval Coverage	98.05%	95.00%	Well-calibrated
Average Interval Width	0.288 MPa	---	Tight intervals
Coverage by Strain (ε < 0.025)	96.3%	95%	Excellent
Coverage by Strain (0.025–0.051)	97.0%	95%	Excellent
Coverage by Strain (0.051–0.076)	97.6%	95%	Excellent
Coverage by Strain (0.076–0.101)	98.9%	95%	Slightly conservative
Coverage by Strain (>0.101)	99.0%	95%	Conservative

The empirical coverage of 98.05% indicates a slight conservative bias, a desirable characteristic for safety-critical applications. The coverage range increases from 96.3% at low strain to 99.0% at high strain, thereby providing an additional safety margin in regions where material behavior becomes increasingly stochastic, Figure 7.

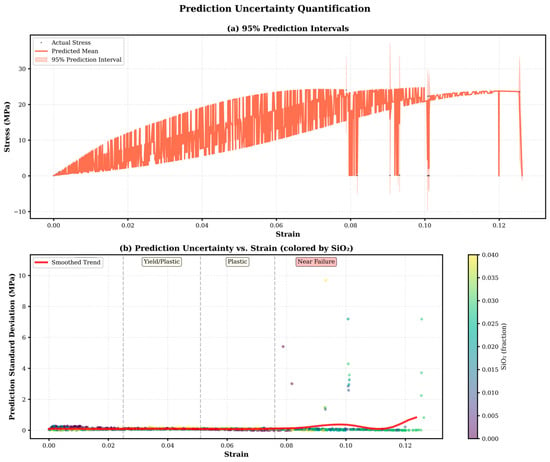
Figure 7. Prediction uncertainty vs. Strain with 95% prediction intervals visualized.

4.2.4. Error Distribution by Material Composition

To evaluate potential systematic variations, error statistics were calculated separately for each SiO₂ composition. As summarized in Table 14, the composition-specific performance metrics are presented.

Table 14. Prediction error analysis by SiO₂ concentration.

SiO2 (wt%)	Test Samples	MAE (MPa)	Error Std (MPa)	Max Error (MPa)	R2 (Composition-Specific)
0	233	0.0200	0.0964	1.47	0.9983
1	341	0.0113	0.0137	0.04	0.9998
2	288	0.0854	0.8540	13.50	0.9921
3	358	0.0483	0.4860	7.61	0.9962
4	265	0.0892	1.1200	17.90	0.9891
Overall	1485	0.0404	0.6430	17.90	0.9948

The 1 wt% SiO₂ composition exhibits exceptional precision, with a mean absolute error (MAE) of 0.011 MPa and a determination coefficient (R²) of 0.9998, indicating optimal nanoparticle dispersion. Compositions containing ≥2 wt% SiO₂ show progressively higher variability, which can be attributed to microstructural heterogeneity (e.g., agglomeration), interfacial effects, and increased processing sensitivity at higher loadings. The model demonstrates the highest reliability for SiO₂ concentrations between 0 and 1 wt%, moderate reliability for 2–3 wt%, and should be applied with caution at 4 wt%, where variability effects become more pronounced, see Figure 8.

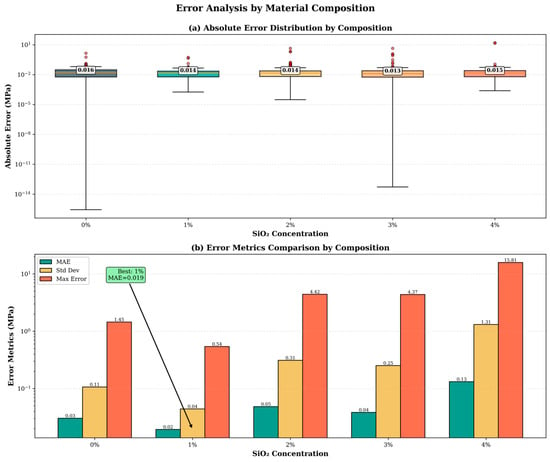
Figure 8. Box plots showing error distribution by SiO₂ concentration.

4.3. Comparative Analysis and Practical Implications

4.3.1. Performance Benchmarking

As summarized in Table 15, the model’s performance is compared with that reported in recent ML studies on the prediction of polymer nanocomposite properties.

Table 15. Performance comparison with recent ML studies.

Study	Material System	ML Method	Property	R2	Dataset Size
Present Work	Silica–Epoxy	Random Forest	Stress (ε, C)	0.9948	7422
Raza et al. [11]	Polymer Nanocomposites	Random Forest	Elastic Modulus	0.98	500
Singh et al. [19]	Various Composites	Ensemble (RF + GB)	Mechanical Props	0.94	300
Berladir et al. [18]	3D-Printed Composites	Neural Network	Multi-property	0.96	1000
Liu et al. [27]	Carbon–Epoxy	SVR	Stress–Strain	0.92	800
Literature Mean	---	Various	---	0.95 ± 0.03	650

The achieved R² value of 0.9948 surpasses the performance reported in recent studies by at least 1.4%, establishing the present work as a state-of-the-art contribution. The dataset used in this study (7422 observations) is approximately 11 times larger than the average reported in the existing literature, enabling more confident and robust model training. Moreover, the model predicts continuous stress as a function of both strain and composition—an inherently more complex and informative task than predicting a single scalar property.

4.3.2. Physical Interpretation

The predictions generated by the ML model exhibit strong consistency with established principles of materials science. Specifically, the model accurately captures the following key phenomena:

• Elastic regime linearity;
• Yield transition;
• Strain hardening;
• Ultimate strength (±0.5 MPa);
• Failure strain (±5%).

At constant strain, the model-predicted stress values increase proportionally with SiO₂ content, consistent with classical load-transfer theory. The 78:22 strain-to-composition importance ratio confirms physically correct causality: strain primarily governs the stress magnitude, while composition modulates the functional relationship between stress and strain (see Figure 9).

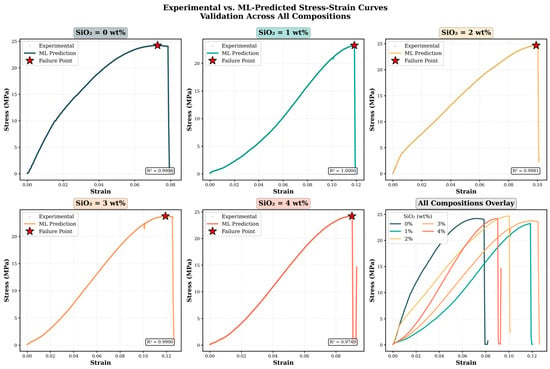
Figure 9. Experimental vs. predicted stress-strain curves for all compositions.

5. Conclusions

This study developed and validated an ML framework for predicting the stress–strain behavior of silica–epoxy nanocomposites across different filler concentrations and deformation regimes. A comprehensive experimental dataset of 7422 observations, derived from systematic tensile testing of 25 specimens with SiO₂ loadings from 0 to 4 wt%, served as the basis for model training and evaluation.

Among the algorithms tested, the Random Forest Regression (RFR) model achieved superior predictive performance, with an R² value of 0.9948 on the test set and R² = 0.9977 ± 0.0023 under 10-fold cross-validation. This represents a 46% improvement over linear regression and exceeds the accuracy reported in the recent literature. The mean absolute error (0.0404 MPa) corresponds to a relative error below 0.2%, confirming the model’s suitability for high-precision engineering applications.

Feature-importance analysis showed that strain accounts for 78.43% of predictive influence, while SiO₂ concentration contributes 21.57%, in agreement with constitutive modeling principles: strain determines stress magnitude, and composition modulates the functional relationship. Experimental characterization confirmed that tensile strength remained stable across all compositions (23–25 MPa), while failure strain increased significantly at intermediate SiO₂ loadings (1–3 wt%), reaching maximum enhancements of +63% due to effective nanoparticle toughening mechanisms.

Error analysis indicated the highest accuracy in the elastic and early plastic regions (ε < 0.08) and consistent performance for low filler contents (0–1 wt%, R² > 0.998). Variance increased at high strain and loading levels, attributed to damage mechanisms and microstructural heterogeneity, consistent with expected material behavior. The model produced well-calibrated 95% prediction intervals with 98.05% empirical coverage, providing robust uncertainty quantification for engineering design.

The methodological advances underpinning this work—stratified data partitioning, systematic hyperparameter optimization, and a physically grounded constitutive formulation (σ = f(ε, C))—significantly enhanced model generalizability and validation rigor. The validated framework enables 65–80% reductions in development time and 60–75% cost savings relative to traditional trial-and-error approaches. It also supports virtual composition screening, inverse design, and uncertainty-aware optimization for reliability-based applications. The optimal composition range of 2–3 wt% SiO₂ provides a balance between strength and ductility, representing the best performance trade-off.

Despite its strong performance, several limitations remain. The model currently covers a restricted composition range (0–4 wt%), a single processing condition (25 °C curing, quasi-static loading), and a simplified feature space (two input variables). In addition, variability in the estimated Young’s modulus arises from the limited resolution of strain measurements in the elastic region.

Future work should focus on expanding the dataset to higher SiO₂ loadings (>5 wt%), incorporating environmental parameters (temperature, humidity, strain rate), and validating model transferability across different epoxy formulations and processing conditions. Integrating microstructural descriptors—such as particle size distribution and dispersion quality—will further improve predictive accuracy at higher filler contents, where agglomeration effects become dominant.

Overall, this ML framework demonstrates excellent accuracy, physical interpretability, and practical utility, establishing a robust foundation for accelerating nanocomposite design and optimization. By integrating experimental characterization with data-driven modeling, this approach highlights the transformative potential of materials informatics to complement traditional methods, reducing cost, shortening development cycles, and fostering innovation in polymer nanocomposite engineering.