Three-Dimensional Deployment Optimization of UAVs Using Symbolic Control for Coverage Enhancement via UAV-Mounted 6G Mobile Base Stations

Abstract

We propose a novel systematic approach for the deployment optimization of unmanned aerial vehicles (UAVs). In this context, this study focuses on enhancing the coverage of UAV-mounted 6G mobile base stations. The number and placement optimization of UAV-mounted 6G mobile base stations, deployed to support terrestrial base stations during periods of increased population density in a given area, are addressed using a symbolic limited optimal discrete controller synthesis technique. Within the scope of this study, the UAVs’ altitude and attitude behaviors are optimized to ensure the most efficient trajectory toward the designated base station coordinates. Additionally, at their new locations, these behaviors are adjusted to facilitate accurate coverage estimation from the base stations they serve. In the deployment optimization of UAVs, the placement of base stations is determined using received signal strength data obtained through the ray-tracing-based channel modeling technique. The channel model considered critical parameters such as path loss, received power, weather loss, and foliage loss. Final average path loss values of 102.3 dB, 111.7 dB, and 127.4 dB were obtained at the carrier frequencies of 7 GHz, 26 GHz, and 140 GHz, respectively. These findings were confirmed with MATLAB-based ray tracing simulations. Our proposed approach is validated through experimental evaluations, demonstrating superior performance compared to existing methods reported in the literature.

1. Introduction

In recent years, mobile communication systems have entered a major transformation process with the increase in user demands, the increase in data traffic, and the need for uninterrupted connection in various scenarios. The sixth-generation (6G) communication technologies, which are developed after the fifth-generation (5G) mobile communication networks, aim to offer not only higher data speeds and lower latency but also much more flexible and comprehensive communication infrastructures. However, achieving the ultra-reliable and low-latency communication capacity promised by 6G is not possible with fixed base stations alone. In particular, environments such as densely populated areas, disaster areas, rural areas, and hard-to-reach areas are among the scenarios where fixed infrastructures are inadequate.

In busy event areas, fixed base stations are often insufficient to meet the sudden increase in data demand. This problem has become even more pronounced in 6G networks, where high-capacity, low-latency, and dynamic service needs are at the forefront. In the literature, various solutions are proposed to improve network performance in such cases. Prominent solutions include unmanned aerial vehicles capable of providing base station services, reconfigurable intelligent surface technologies, portable small cell systems, mobile base stations, and device-to-device communication systems.

Recent studies have shown that drone (ie., UAV)-based base stations significantly increase network capacity in densely populated activity areas where user density suddenly increases [1,2,3]. In response to suddenly increasing user density, these systems dynamically reschedule network resources according to the current situation, and the coverage area is flexibly shaped according to need. Artificial intelligence and machine learning technologies are integrated into these systems. This allows UAVs to autonomously adjust their positions based on user density data, significantly increasing network efficiency [4]. On the other hand, reconfigurable intelligent surfaces (RISs), which can direct electromagnetic signals to areas with poor coverage, stand out as an effective support technology when fixed base stations are insufficient [5]. All these studies emphasize the essential need for flexible and adaptable systems in 6G networks. They draw attention to the importance of mobile and repositionable infrastructures, especially in meeting short-term but high-density demands.

Drone base stations can increase the coverage area, improve the connection quality, and balance the network load due to their high mobility advantage. This approach plays a key role in achieving the goal of “anytime, anywhere connection”, which is among the basic visions of 6G.

Our comprehensive literature review is based on the fact that coverage in certain areas and time periods has been insufficient. Our research idea also involves the deployment optimization of UAV-mounted 6G mobile base stations to address this issue.

A review of the literature reveals that UAV deployments generally involve classical control algorithms or metaheuristic approaches. However, classical control methods suffer from high computational complexity, while metaheuristic approaches are prone to errors. Alternatively, we have observed that the symbolic discrete controller synthesis method enables deployment optimization with both formal correctness and high performance. In this context, our approach employs symbolic limited optimal control algorithms for UAV-mounted 6G mobile base stations.

The main limitation of our approach is related to computational complexity. If the number of states becomes very large, the computation time may increase. However, this issue can be addressed by dividing the system into smaller sub-problems and solving them separately, then combining the results. In most practical cases, a serious delay would only occur in extremely large systems, which can also be simplified through abstraction during the modeling phase. The SDCS method uses a model checking tool, so it has formal verification. Its algorithms check all possible future situations within a time window and always choose the best one. On the other hand, machine learning methods do not give formal guarantees and cannot always find the best result. Because of this, our method shows better and more reliable performance than machine learning approaches.

The control theory of discrete-event systems was first developed as a language theory by ref. [6]. Subsequently, it has been addressed as various modeling formalisms, such as Petri nets, automata, and finite-state machines [7,8]. Early approaches, as presented in refs. [9,10], focus on synthesizing a controller within a feedback system, considering control objectives and system behaviors that have not yet been controlled. However, these approaches only involve Boolean variables. Ref. [11] extended them to encompass reactive models in infinite domains. In the most recent work, ref. [12] has enabled the modeling of previous approaches, which only included input variables, to be formulated as input–output models. On the other hand, optimization studies performed on a cost function have been presented in works such as refs. [10,13,14].

The control theory of discrete-event systems has been widely applied across various domains. Ref. [12] has implemented optimization methods to prevent overloading of the network during the distribution of power grids. Ref. [15] proposed in their study that the symbolic limited optimal control algorithm could replace the Viterbi algorithm for computing the best path in various applications of hidden Markov models. Ref. [16] utilized symbolic control for optimization in task scheduling operations to enhance energy efficiency in hardware circuits.

Moreover, discrete controller synthesis has been applied to solve numerous problems for robotics and UAVs. The authors of ref. [17] conducted trajectory optimization for multi-pocket milling using computer numerical control in their study. Ref. [18] has demonstrated superior results in comparison to literature studies by utilizing the symbolic control approach for altitude control behavior in drones. Ref. [19] systematically incorporated the symbolic discrete controller technique into virtual robotic environment platforms and, by applying it to drones, demonstrated its superior effectiveness in altitude and attitude control behavior compared to methods in the literature.

Upon reviewing the literature, we observed that UAV deployment optimization is typically addressed using either error-prone metaheuristic approaches or classical control methods with high computational complexity. However, the lack of formal correctness or the inability to provide dynamic responses quickly in such safety-critical systems is identified as a gap in the literature. To fill this gap, we employ a symbolic discrete controller synthesis method for UAV deployment optimization, which provides both scalable computational complexity and formal correctness.

Studies in the literature generally focus on the coverage extension potential of drone base stations [20,21,22]. However, comparative performance analysis of fixed and mobile base stations in terms of received signal strength, coverage analysis, and delay spread in dense activity areas using realistic channel models is not sufficiently addressed. In order to fill this gap in the literature, this study analyzes the use of drone base stations in dense activity areas in 6G mobile networks using ray tracing-based simulations when fixed base stations are insufficient. It makes an original contribution by presenting a detailed received signal strength model, coverage analysis, and delay spread comparisons for both fixed and drone base stations.

Using the ray-tracing method, channel propagation characteristics in dense activity areas for three frequency bands that are likely to be used in 6G mobile communication are investigated. Received signal strength, path loss, delay spread, and phase shift parameters of the channel are analyzed. Signal loss due to concrete structures, ambient weather conditions, and foliage was also included in the analysis. The effects of signal fading and reflection were investigated using drones positioned at different heights in the densely populated activity area. The key channel parameters were carefully derived based on the received signal strength (RSS) model for each frequency band. Data from ray-tracing-based measurements were used to evaluate regional variations in signal strength, and the optimal drone height for optimal user coverage was determined. The properties of 6G mobile communication channels in dense activity areas were investigated using a 3D ray-tracing technique.

Contributions: We propose a novel systematic modeling framework for the deployment optimization of UAVs aimed at enhancing the coverage of UAV-mounted 6G mobile base stations. Our approach is fundamentally structured around the following steps:

• Modeling Process: Our approach is modeled as synchronous parallel dataflow equations using the ReaX DCS tool (version 0.17.3) and is decomposed into the following sub-modeling groups:

  −

  Number optimization;

  −

  Placement optimization;

  −

  Altitude and attitude behaviors.

• Network Performance Evaluation: The impact of drone base stations on network performance was evaluated by considering the dense user distribution and different drone base station locations. The potential of drone base stations to increase the service quality in 6G networks was revealed;
• Implementation: It goes beyond the fixed-infrastructure-based solutions that are common in the literature. The practical applicability of drone base stations, which stand out with their mobile and adaptive structures, has been examined. The effectiveness of the proposed solution has been demonstrated especially in cases of short-term high user density. The implementation of the proposed modeling framework in a case study validates the effectiveness of our approach.

The remainder of the article is structured as follows: The next subsection provides a comprehensive literature review. Section 2 provides the technical background related to UAVs, deployment optimization, and base station communication. Section 3 elaborates on the systematic modeling of UAV deployment optimization aimed at enhancing coverage through UAV-mounted 6G mobile base stations, as well as ray-tracing-based channel modeling in the case of a fixed base station in 6G mobile networks. Section 4 reports the findings derived from experimental evaluation. Finally, Section 5 concludes this study by highlighting the key outcomes and providing insights into potential future research avenues.

1.1. Related Work

In recent years, researchers have shown increasing interest in incorporating UAVs into emerging 5G and 6G mobile networks. These studies aim to enhance communication infrastructures and support dynamic user association, often leveraging blockchain-based mechanisms, hybrid network topologies, and adaptive architectures to ensure secure and reliable service provisioning [23,24,25,26,27]. At the same time, several control-oriented approaches have been explored to improve system robustness under challenging conditions such as limited resources, environmental disturbances, or actuator faults. Techniques like symbolic abstraction, predefined-time control, predictive strategies, and safety-critical frameworks have gained particular attention in this regard [28,29,30,31,32]. Building on these efforts, other studies have focused on more collaborative and adaptive control frameworks, including constraint-following schemes, formation-switching techniques, and resilient coordination mechanisms for UAV and robotic systems operating in uncertain environments [33,34,35,36]. Parallel to these developments, optimization-driven approaches have also gained traction. Here, reinforcement learning, metaheuristic algorithms, fuzzy multi-objective methods, and Bayesian optimization strategies have been applied to tackle issues such as path planning, mission efficiency, and energy-aware deployment [37,38,39,40,41]. In addition, recent work has looked at how intelligent sensing, mobility modeling, and real-time task or computation offloading can be enhanced using AI-based estimators and hybrid physical models, especially in situations where data is scarce or uncertainty is high [42,43,44,45,46]. Together, these diverse contributions reflect a growing momentum toward building UAV systems that are not only autonomous and efficient but also adaptive to real-world complexity in next-generation wireless environments.

The use of UAVs as dynamic base stations in 6G-based mobile communication infrastructures has been the subject of increasing research interest in recent years. In this context, computational models developed to optimize both the mission load and the three-dimensional routes of UAVs offer solutions integrated with mobile edge computing. Ref. [47] aimed to reduce mission delay by jointly optimizing the mission offloading rate and UAV route with the KNN-DDPG algorithm. Similarly, ref. [48] proposed a robust mission planning structure that improves both energy efficiency and mission completion time by taking into account time-varying channel conditions in mobile edge computing-assisted systems. On the other hand, ref. [49] considered the temporary deployment of UAV base stations to reduce congestion due to user density in 5G networks and optimized the positioning decisions using machine learning. These studies provide a solid research foundation for the symbolic control-based coverage augmentation approach proposed in this paper by demonstrating the versatile potential of UAVs in areas such as 3D deployment, mission offloading, energy management, and network coverage.

1.1.1. Metaheuristic Approaches for UAV Deployment Optimization

Recent studies have advanced metaheuristics for UAV deployment optimization. Ref. [50] proposed a chaotic Harris Hawks optimization method for 3D UAV placements, demonstrating 12% better coverage than PSO in urban environments. Ref. [51] developed a multi-objective GWO method that improved energy efficiency by 18% in 5G-connected UAV networks. For disaster response scenarios, Ref. [52] introduced an ABC algorithm enhanced with reinforcement learning, reducing deployment time by 27%. Ref. [53] combined simulated annealing with tabu search for jamming-resistant UAV swarms, while ref. [54] achieved dynamic wind adaptation using quantum-inspired genetic algorithms. These approaches collectively address the trade-off between computational complexity and solution quality in large-scale UAV deployments.

1.1.2. Control-Theoretic Techniques for Deployment Optimization

Control strategies have evolved to address real-world UAV deployment challenges. Ref. [55] implemented a control system that could keep the drone’s position accurate to within less than 1 m, even without GPS. Ref. [56] designed a robust sliding-mode controller validated under wind disturbances of up to 15 m/s. For swarm coordination, Ref. [57] proved Nash equilibrium stability in game-theoretic control protocols, and ref. [58] reduced communication overhead by 40% via event-triggered control. Notably, Ref. [59] achieved adaptive control of heterogeneous UAV fleets using neural networks. These techniques highlight the shift from centralized to distributed control paradigms.

1.1.3. Discrete Controller Synthesis in UAV Applications

Formal methods like DCS ensure safety in UAV operations. Ref. [60] synthesized collision-free controllers for high-density UAV traffic management. Ref. [61] handled sensor failures in search-and-rescue missions through probabilistic DCS, while ref. [62] guaranteed complete wildfire coverage using temporal logic integration. Ref. [63] demonstrated cyberattack-resistant routing in military swarms, and ref. [64] optimized charging station throughput by 35%. These works bridge formal verification with real-time UAV control, though computational complexity remains a challenge for ultra-large fleets.

1.1.4. Overview of UAV Base Station Deployment for 6G Coverage Enhancement

In recent years, research on drone base stations has gained significant momentum in order to increase the potential of 6G mobile communication networks. Drone base stations attract attention due to their potential to provide solutions to the capacity and coverage problems of fixed base stations, especially in dense activity areas. In the literature, studies in this area generally focus on creating dynamic network topologies, increasing spectrum efficiency, optimizing energy consumption, and improving user experience. An artificial-intelligence-based method for optimally positioning drone base stations in scenarios with high data traffic density has been proposed by ref. [65]. On the other hand, the use of drone base stations to temporarily extend the coverage area of cellular networks has been discussed in ref. [66]. The resource allocation strategies that can be implemented in this process have been examined in detail. Furthermore, a systems approach to the potential of drone base stations to provide low-latency and reliable communication has been presented by ref. [67]. Thanks to their easy portability and rapid deployment, such base stations appear to offer an effective solution for meeting critical communication needs in areas experiencing high traffic density.

Various technical approaches are being considered to enable drone base stations to operate both more efficiently and sustainably in the long term. For instance, integrating renewable energy sources to increase the energy efficiency of these systems has been addressed [68]. However, studies have been conducted on coordinating multiple drone base stations to both expand coverage and increase network capacity [69]. Moreover, the security and privacy threats that drone base stations may face have been evaluated within the framework of ref. [70], and solutions to these risks have been proposed. Finally, comprehensive analyses have been conducted on the technical challenges and potential advantages of integrating drone base stations into existing 5G infrastructures and future 6G networks [71,72]. All these studies indicate that drone base station technology will play a significant role in the future of mobile communication networks. Therefore, research activities in this area continue to increase.

2. Technical Background of UAV Deployment Optimization and Base Station Communication

2.1. General Structure of UAVs

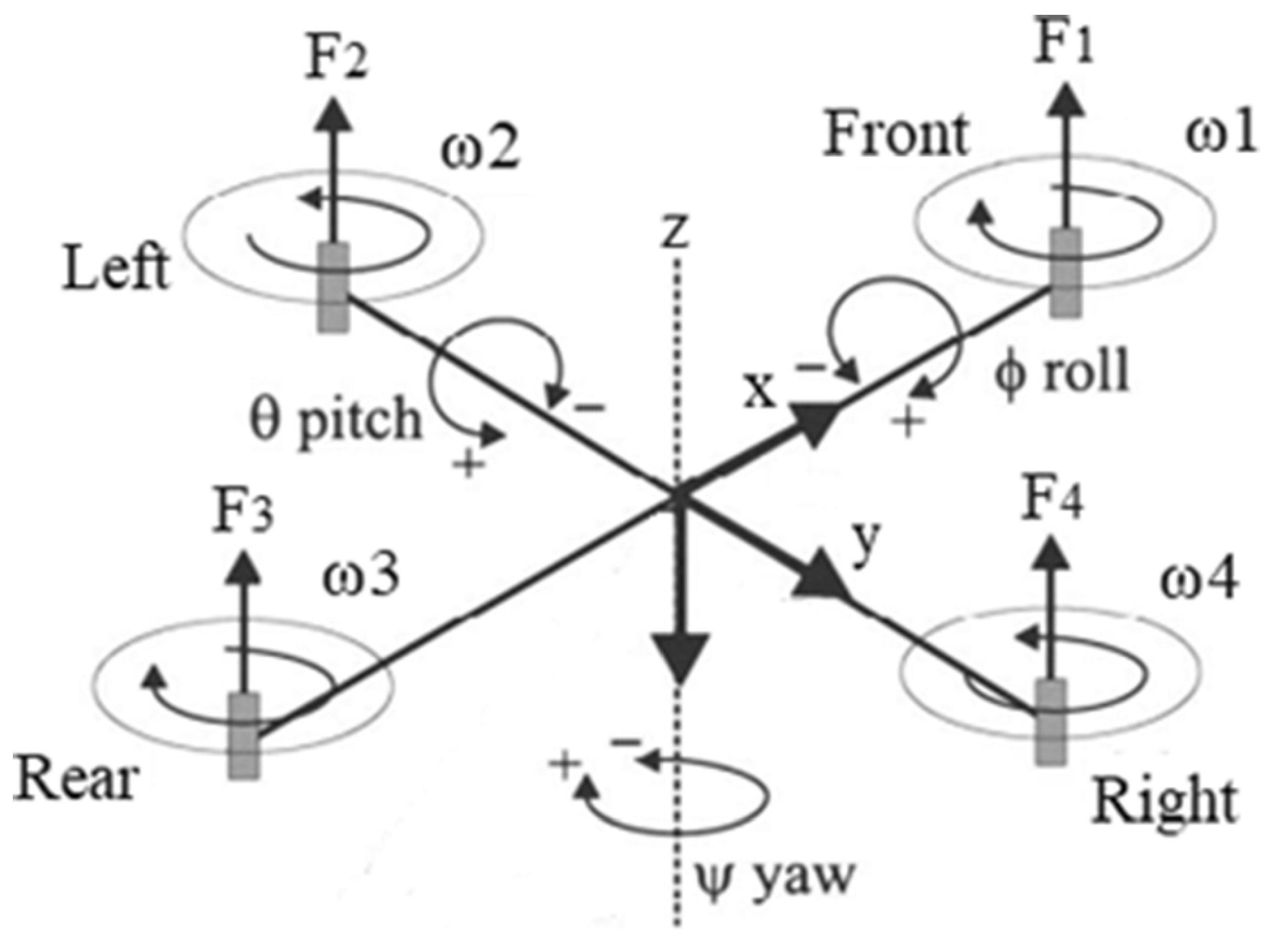
Kinematic and dynamic equations can be used to model UAVs, which are dynamic systems. The purpose of this modeling approach is to record behavior and movements in three dimensions. UAVs typically have six DOFs, which show translational motion in the x, y, and z dimensions and rotational motion in terms of the roll, pitch, and yaw angles. Newton’s and Euler’s laws govern these motions, which are influenced by push, drag, and gravity. The simulation and control models used to evaluate the stability and manoeuvrability of UAVs and develop flight control systems are based on these resulting nonlinear differential equations. These UAV control and simulation equations can be summarized in four parts.

2.1.1. Translational Dynamics (Newton’s Second Law):

$$m·\dot{v}=F_{thrust}+F_{gravity}+F_{drag}$$

(1)

The following equations should be used to express translation dynamics:

$$\begin{array}{cc}\hfill \dot{u}& =rv-qw+{\displaystyle \frac{1}{m}}X\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \dot{v}& =pw-ru+{\displaystyle \frac{1}{m}}Y\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \dot{w}& =qu-pv+{\displaystyle \frac{1}{m}}Z\hfill \end{array}$$

(4)

where $u,v,$ and w are the linear velocities; $p,q,$ and r are the angular velocities, and $X,Y,$ and Z are the forces in the body axes.

2.1.2. Rotational Dynamics (Euler’s Equations):

$$\begin{array}{cc}\hfill \dot{p}& ={\displaystyle \frac{(I_y-I_z)}{I_x}}qr+{\displaystyle \frac{1}{I_x}}L\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \dot{q}& ={\displaystyle \frac{(I_z-I_x)}{I_y}}pr+{\displaystyle \frac{1}{I_y}}M\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \dot{r}& ={\displaystyle \frac{(I_x-I_y)}{I_z}}pq+{\displaystyle \frac{1}{I_z}}N\hfill \end{array}$$

(7)

where $I_x,I_y,$ and $I_z$ are the moments of inertia and $L,M,$ and N are the torques about the respective axes.

2.1.3. Kinematic Equations (Euler Angles):

$$\begin{array}{cc}\hfill \dot{\varphi }& =p+tan\theta (qsin\varphi +rcos\varphi )\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \dot{\theta }& =qcos\varphi -rsin\varphi \hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \dot{\psi }& ={\displaystyle \frac{qsin\varphi +rcos\varphi }{cos\theta }}\hfill \end{array}$$

(10)

where $\varphi$, $\theta$, and $\psi$ represent the roll, pitch, and yaw angles, respectively.

2.1.4. Position in the Inertial Frame:

The transformation from body-frame velocities to inertial-frame positions is given by

$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\end{array}\right]=R(\varphi ,\theta ,\psi )\left[\begin{array}{c}u\\ v\\ w\end{array}\right]$$

(11)

where $R(\varphi ,\theta ,\psi )$ is the rotation matrix from the body frame to the inertial frame.

These nonlinear equations define the interaction between translational and rotational dynamics. They usually get solved by controllers like PID (proportional integral derivative) or through simulation programs like MATLAB (version 2021a)/Simulink (version 2021a).

2.2. UAV Control Systems

The various forms of the setup of UAV platforms depend on the mission requirements, but most prevalent are quadcopters, which are essentially rotary-wing UAVs with four rotors, fixed-wing aircraft, and VTOL (vertical take-off and landing) systems. Every configuration holds varying trade-offs in flight endurance, payload, maneuverability, and control complexity. These UAV frames can be modeled and simulated with software such as MATLAB’s Aerospace Toolbox and Simulink 3D Animation that both enable model-based design and real-time animation of UAV dynamics and interactions with the surrounding world.

Two of the most elementary parameters while flying the UAV on a mission are attitude and altitude, both being necessary for seamless navigation and successful accomplishment of the mission. Altitude may be defined as the height of the UAV from the ground level and is usually monitored by barometric sensors, LiDAR, or GPS. Attitude refers to the UAV’s orientation in space and is characterized by the roll, pitch, and yaw angles, which are usually calculated using onboard IMUs (inertial measurement units). These are the inputs to the control algorithms and play a critical role in the generation of a stable and responsive flight, especially when combined with feedback-controlled systems such as PID controllers. A quadcopter is composed of four rotors and six DOFs consisting of three translations and three rotations. All maneuvers of the quadcopter are performed by varying the propeller angular velocities and direction of rotation. The structural format of a typical quadcopter is illustrated in Figure 1.

MATLAB is a general-purpose modeling, simulation, and realization platform for UAV control systems. It provides rich tool sets, including Simulink and specialized toolboxes such as the UAV Toolbox and the Navigation Toolbox to model systems, the mission plan, and algorithm development. Simulink allows engineers to simulate and model complex dynamic systems using block diagrams, and state estimators and PID controllers can be set and tuned there to offer satisfactory performance. Moreover, MATLAB can be used to simulate flight tests, obtain real-time feedback of sensors, and graph UAV trajectories, and hence it offers an ideal platform for both academic research and industrial development. Figure 2 shows a mobile base station drawn in the MATLAB environment.

UAV deployment optimization involves determining the best number of UAVs and their best locations to achieve objectives such as complete area coverage, effective communication, and optimal use of power. It is a constrained optimization problem with the goal of minimizing the cost or maximizing performance under coverage, communication, and resource constraints. Effective placement plays an important role in mission achievement and depends on the spatial distribution of targets, terrain properties, and the communication range of each UAV.

Path optimization is also an important factor in the deployment of UAVs, with the aim to identify the most efficient paths that UAVs need to follow between mission-critical points. The objective is to minimize flying time, energy expended, or communication delay while avoiding obstacles and remaining in contact with ground stations. Path planning problems, especially those that have multiple waypoints (e.g., flying between three or more locations), are usually formulated with graph-based algorithms such as Dijkstra and A*, or as instances of the traveling salesman problem (TSP). In the case of dynamic environments, adaptive planning methods are used to update paths in real time based on sensor feedback and environmental changes.

PID controllers are usually implemented on UAV systems to regulate flight dynamics, particularly in altitude, attitude, and speed regulation. The PID algorithm relies on responding to the difference between a setpoint and the system state now. The proportional term responds to the current error. The integral term accounts for past errors, and the derivative term accounts for future error trends based on the rate of change. This combination ensures smooth, stable control and quick correction of deviations, making PID a foundational component in both manual and autonomous UAV control systems.

Metaheuristic algorithms provide robust approaches for addressing intractable UAV deployment and routing issues computationally through traditional optimization techniques. These algorithms do not provide any global optimum but are highly efficient in determining the solution close to the optimum within the possible computation time. Typical metaheuristic algorithms include genetic algorithms (GAs), particle swarm optimization (PSO), ant colony optimization (ACO), and simulated annealing (SA), which all have been proven to be efficient in applications using UAVs. These techniques are useful in scenarios involving high-dimensional, multi-objective, and nonlinear search spaces. MATLAB supports many of these algorithms natively or via custom implementations, enabling researchers to apply them to both static placement and dynamic path planning challenges.

2.3. Base Station Communication

Sixth-generation mobile communication networks are new generation communication systems that target very high data rates. The low latency, high capacity, high user density, and wide coverage area targeted by these systems push the limits of traditional fixed base stations. This infrastructure is insufficient, especially in busy event areas such as concert venues, stadiums, disaster areas, and temporary crowded gathering places. In such scenarios, drone base stations stand out as a flexible and time-sensitive solution that increases service quality.

Base stations are low-power radio stations that allow user equipment to receive audio and video waves. Each area (called a cell) contains one or more base stations. The term cellular comes from the division of installed base stations into areas called cells. When user equipment moves from one cell to another, cellular calls are also transferred from one base station to another. Depending on the power level of the antenna, base stations are divided into three categories: macrocells, microcells, and picocells. Macrocells form the main structure in the base station network. They can usually establish connections up to 35 km. Microcells are used to increase the efficiency of the main network. Their limits are usually a few hundred meters. Picocells are base stations with a power of a few watts, and they are usually placed inside a building.

The device scans the radio frequencies around it and detects signals from the available cells. During this scanning process, the mobile device checks both licensed and unlicensed frequency bands. The device measures the signal strength and quality of the cells it finds. It usually evaluates the signal strength and RSSI (received signal strength indicator) parameters. The device selects the most suitable cell according to the strength and quality of the signal it receives. This cell is the base station where the device will register and communicate. If more than one cell seems suitable, the device selects the cell with the strongest signal. Cells broadcast network information such as the PLMN (public land mobile network) ID. The device selects the correct cell according to the ID of the network to which it is registered. After connecting to the selected cell, it communicates with the network and performs the login process. At this stage, the device’s authentication information is shared with the network, and the device is registered to the network.

Ray tracing is a technique used to calculate how electromagnetic waves propagate in an environment. In this technique, the wave is modeled as linear rays coming out of the transmitter. These rays are subject to physical phenomena such as reflection, refraction, diffraction, and absorption by objects in the environment. Information such as amplitude, phase, delay time, and Doppler shift, if any, are calculated for each path. In high-frequency systems such as 6G, electromagnetic waves can be easily blocked by obstacles such as buildings or people, can only travel in certain directions, and can reach the receiver through reflections or scattering. Therefore, classical statistical models (e.g., Rayleigh or Rician models) are not sufficient. Realistic environment geometry and physical effects should be taken into account. This is where ray tracing comes into play. Ray-tracing-based channel modeling with MATLAB is one of the most accurate channel analysis methods for 6G mobile communication systems. This approach is very useful for understanding how fixed and drone base stations will perform in different scenarios.

3. UAV Deployment Optimization: Symbolic Control Model and Ray Tracing Propagation Channel Model for Coverage Enhancement

In this study, we address the issue of coverage enhancement in urban environments during temporary gatherings where a large number of individuals assemble in a designated area for a short period of time, potentially overwhelming the capacity of the central base station. To mitigate this problem, we propose the deployment of UAV-mounted 6G mobile base stations to provide supplementary coverage. In line with this objective, this study focuses on UAV deployment optimization by employing a symbolic discrete controller synthesis approach. The drones first traverse the area using our search algorithm, collecting sample data on signal strength (in dBm) at specific distances. This data is then fed as input into our DCS model, which is used to construct a cost function. Through optimization algorithms, the controller is synthesized to ensure the maximization of the coverage area. Therefore, the signal strength measurement based on ray tracing directly influences the UAV placement decisions. The end-to-end workflow of the proposed framework is illustrated in Figure 3.

Figure 3 comprises two distinct spatial regions. The first region represents the central hub where UAV-mounted 6G mobile base stations are initially deployed. This top-center area contains a finite number of UAV-mounted base stations that are ready for dispatch based on network demands. The second region corresponds to a public event area where a large number of individuals may temporarily gather for an organized activity. Within this area, a single central base station is deployed, and a finite number of user devices, representing people connected to the network, are distributed throughout the space.

The deployment optimization addressed in this study consists of three distinct sub-problems: number optimization of UAV-mounted 6G mobile base stations, path optimization, and placement optimization. The methodology adopted for each of these optimization components is systematically presented in the following sections.

3.1. Overview

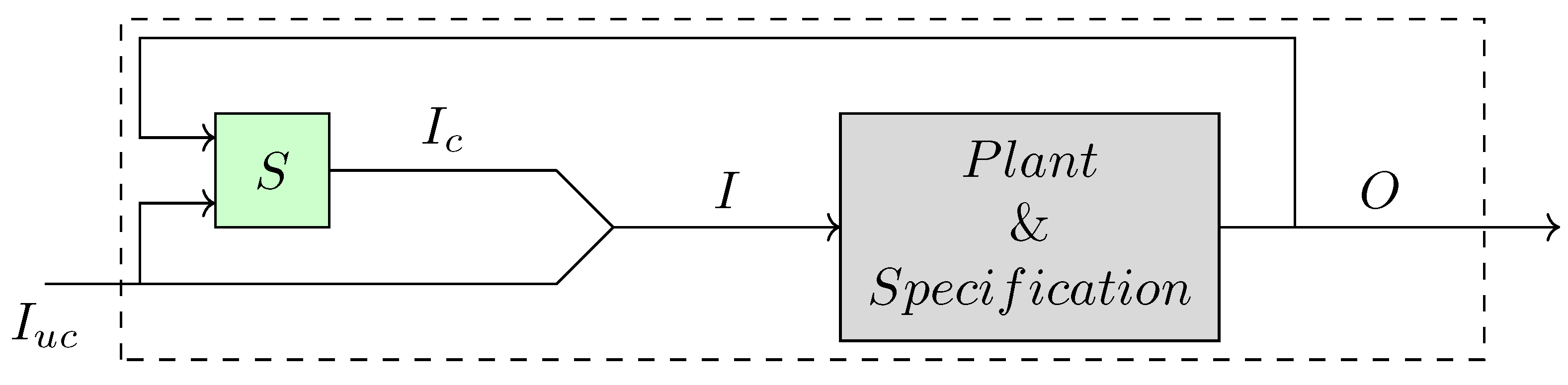
In this study, the deployment optimization problem is addressed through symbolic discrete controller synthesis in scenarios where the central base station located at the hub proves inadequate, leveraging UAV-mounted 6G mobile base stations to ensure coverage extension. The system architecture of the symbolic discrete controller synthesis employed in this study is illustrated in Figure 4. In this study, deployment is modeled as three separate discrete-event optimization problems: number, path, and placement optimizations. Initially, uncontrolled system behaviors are modeled in the DCS tool and the ReaX environment. Subsequently, for each of the number, path, and placement optimizations, specifications representing the desired system behaviors are formally defined and linked to the corresponding models. The underlying model consists of parallel synchronous dataflow equations, and a symbolic discrete controller synthesis process is carried out by applying both safety and optimization algorithms to this specification-augmented model. The resulting controller functions as a manager for the UAVs, operating within the defined scenario to ensure coverage extension through coordinated deployment.

ReaX is a discrete controller synthesis tool that enables the synthesis of controllers through its parallel synchronous dataflow modeling language. It encodes both the uncontrolled system behaviors and the desired specifications and utilizes synthesis algorithms to automatically generate controllers that enforce the specified behaviors. In the body section of a ReaX module, the transitions between system states are defined using equality expressions that reference the current and next values of memory variables. These variables store system state information and enable the encoding of dynamic behavior over time. Additionally, local variables can be introduced as placeholders using simple assignment statements to support intermediate computations or simplify expressions. ReaX also allows the specification of safety objectives by defining invariants that must always hold true throughout system execution. These invariants serve as formal guarantees to ensure that the synthesized controller avoids unsafe or undesired behaviors. For optimization purposes, cost functions can be introduced to guide the synthesis toward more efficient control strategies, such as minimizing resource usage or maximizing performance within the defined constraints.

As shown in Figure 3, the process begins with data obtained from the central base station. Based on this data, a number optimization method is performed to determine the required quantity of UAV-mounted base stations. Subsequently, the calculated number of UAV base stations is dispatched to the designated meeting area. For the UAVs dispatched to the coordinates of the central base station, path optimization is performed by ensuring altitude and attitude control within the shortest possible time. Subsequently, the UAVs are deployed from this location to their new positions within the meeting area. This deployment is guided by a placement optimization process aimed at maximizing the coverage area. Additionally, in order to perform placement optimization, received signal strength data is obtained through the ray-tracing-based channel modeling technique.

3.2. Number Optimization

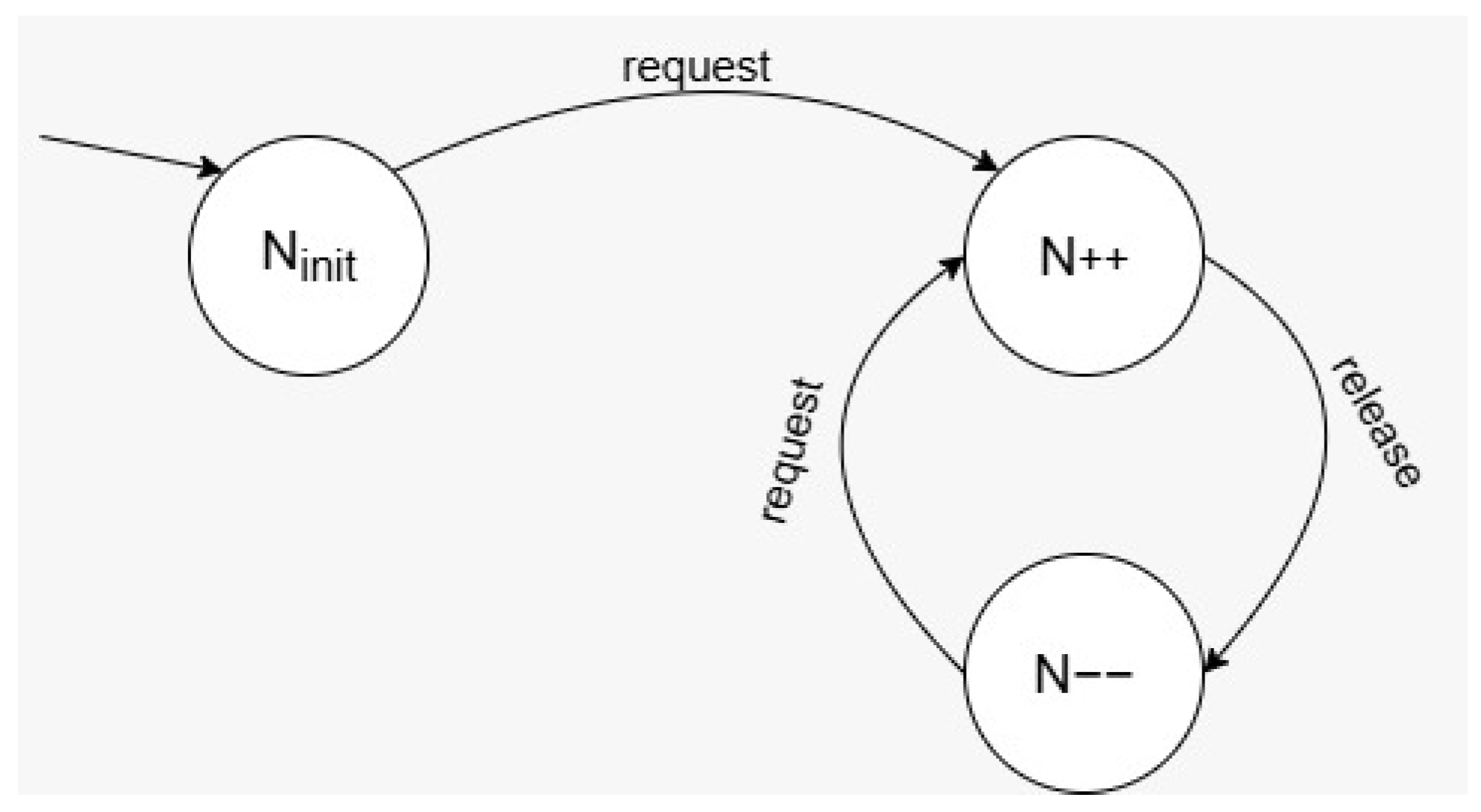
In the initial stage of deployment optimization, it is necessary to determine the number of quadcopters that must be dispatched from the drone base station to the meeting area. The state machine representation of this optimization process is illustrated in Figure 5. This process consists of three phases. In the first phase, the goal is to compute, in a straightforward manner, the minimum number of quadcopters technically required to meet the demand, based on the capacity of the base station. This is formally expressed as follows:

$$n_{\min }=⌈{\displaystyle \frac{D}{C}}⌉$$

(12)

where D denotes the total demand to be satisfied, C is the capacity of a single quadcopter, and $\lceil ·\rceil$ represents the ceiling function.

The second phase takes into account the simultaneous drone demands of different gathering areas. However, in cases where the total number of requests from different regions exceeds the number of available drones, the number of drones to be assigned to each gathering area is updated proportionally based on the relative share of each request. This is formally expressed as follows:

$$n_i=⌊{\displaystyle \frac{d_i}{{\sum }_j{d}_j}}·N_{available}⌋$$

(13)

where $d_i$ denotes the demand for gathering area i and $N_{available}$ is the total number of drones currently available for distribution. The function $\lfloor ·\rfloor$ represents the floor operation to ensure integer allocation.

After performing placement optimization, it becomes clear that the number of drones required for each gathering area may exceed the initial estimate based solely on the base station’s capacity. Therefore, the earlier allocation must be updated accordingly. The revised calculation is given formally as follows:

$$n_i^{final}=Optim.\left(n_i^{updated},⌊{\displaystyle \frac{d_i}{{\sum }_j{d}_j}}·N_{available}⌋\right)$$

(14)

where $n_i^{final}$ denotes the final number of drones assigned to gathering area i, $n_i^{updated}$ is the updated minimum number of drones required after placement optimization, $d_i$ is the demand for gathering area i, ${\sum }_j{d}_j$ is the total demand from all gathering areas, and $N_{available}$ is the total number of drones currently available. The floor function $\lfloor ·\rfloor$ ensures integer allocation, while the operator $Optim.$ guarantees that both capacity and proportional demand considerations are respected.

3.3. Path Optimization

Based on the data obtained from the base station, a path optimization procedure is implemented for each quadcopter designated to be dispatched to a designated gathering area. The dynamics and governing equations relevant to the quadcopter under consideration are presented in Table 1.

Table 1. Dynamics equations of a quadcopter model and their corresponding physical interpretations along each axis of motion, where the descriptions of the symbols are shown in Table 2.

Equation	Description	Equation	Description
$\ddot{x}=g·\theta$	x-axis acceleration (pitch)	$\ddot{\phi }={\displaystyle \frac{u_2}{I_x}}$	Roll acceleration
$\ddot{y}=-g·\phi$	y-axis acceleration (roll)	$\ddot{\theta }={\displaystyle \frac{u_3}{I_y}}$	Pitch acceleration
$\ddot{z}=-g+{\displaystyle \frac{u_1}{m}}$	z-axis acceleration (thrust)	$\ddot{\psi }={\displaystyle \frac{u_4}{I_z}}$	Yaw acceleration

Table 1. Dynamics equations of a quadcopter model and their corresponding physical interpretations along each axis of motion, where the descriptions of the symbols are shown in Table 2.

Equation	Description	Equation	Description
$\ddot{x}=g·\theta$	x-axis acceleration (pitch)	$\ddot{\phi }={\displaystyle \frac{u_2}{I_x}}$	Roll acceleration
$\ddot{y}=-g·\phi$	y-axis acceleration (roll)	$\ddot{\theta }={\displaystyle \frac{u_3}{I_y}}$	Pitch acceleration
$\ddot{z}=-g+{\displaystyle \frac{u_1}{m}}$	z-axis acceleration (thrust)	$\ddot{\psi }={\displaystyle \frac{u_4}{I_z}}$	Yaw acceleration

Table 2. Definitions and descriptions of the symbols employed in the quadcopter dynamics equations shown in Table 1.

Symbol	Description	Symbol	Description
g	Acceleration due to gravity	$I_x$	Moment of inertia around the x-axis
m	Mass of the quadcopter	$I_y$	Moment of inertia around the y-axis
$u_1$	Thrust force	$I_z$	Moment of inertia around the z-axis
$u_2$	Control input for roll	$\phi$	Roll angle
$u_3$	Control input for pitch	$\theta$	Pitch angle
$u_4$	Control input for yaw	$\psi$	Yaw angle

Table 2. Definitions and descriptions of the symbols employed in the quadcopter dynamics equations shown in Table 1.

Symbol	Description	Symbol	Description
g	Acceleration due to gravity	$I_x$	Moment of inertia around the x-axis
m	Mass of the quadcopter	$I_y$	Moment of inertia around the y-axis
$u_1$	Thrust force	$I_z$	Moment of inertia around the z-axis
$u_2$	Control input for roll	$\phi$	Roll angle
$u_3$	Control input for pitch	$\theta$	Pitch angle
$u_4$	Control input for yaw	$\psi$	Yaw angle

Figure 6 presents the details of our strategy. Starting from the equations given in Table 1, the displacement over a time interval t can be computed by integrating the sum of the velocity at each atomic time step and the current velocity. This cumulative distance is then added to the current position, which can be formalized using the following dataflow equations:

$$\begin{array}{cc}\hfill L_x& \stackrel{\Delta }{:=}{L}_x+S_{x}t+{\displaystyle \frac{U_{3}g}{4I_y}}{t}^3,\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill L_y& \stackrel{\Delta }{:=}{L}_y+S_{y}t-{\displaystyle \frac{U_{2}g}{4I_x}}{t}^3,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill L_z& \stackrel{\Delta }{:=}{L}_z+S_{z}t+{\displaystyle \frac{(U_1-gm)}{2m}}{t}^2,\hfill \end{array}$$

(17)

where L represents locations, i.e., points within the coordinate system, and S denotes the velocity of the quadcopter. As a note, the equality symbol ($\stackrel{\Delta }{:=}$) used here does not represent a conventional equality relation. Instead, it indicates that the symbol on the left-hand side takes the value of the expression on the right-hand side at the next instance.

After constructing our model as described above, we execute our safety controller synthesis algorithm to assign values to the controllable variables. The safety objective is represented by the following dataflow equations:

$$f_{\mathcal{S}}\stackrel{\Delta }{:=}{\mathcal{V}}_x\le {\mathcal{C}}_x\wedge {\mathcal{V}}_y\le {\mathcal{C}}_y\wedge {\mathcal{V}}_z\le {\mathcal{C}}_z,$$

(18)

where $f_{\mathcal{S}}$ represents our control objective related to safety properties, while the variables $\mathcal{V}$ encompass all expressions concerning the velocity, position, thrust force limits, and other parameters for the $x,y,z$ coordinates; meanwhile, $\mathcal{C}$ denotes the corresponding threshold values associated with each element of $\mathcal{V}$. In the equation, $f_{\mathcal{S}}$ is treated as an invariant, aimed to be constantly maintained at the value of 1. The valuations assigned to the controllable input variables are chosen to ensure the desired system behavior.

In order to ensure altitude and attitude control behaviors while minimizing travel time, the following cost function was formulated as a dataflow equation:

$$\begin{array}{cc}\hfill f_{\mathcal{O}}\stackrel{\Delta }{:=}& \sum _{i\in N}\mathrm{if}i\mathrm{then}{\kappa }_i,\hfill \end{array}$$

(19)

where $f_{\mathcal{S}}$ represents our control objective related to optimization properties; the objective function, consisting of cascading decision branches, represents the cumulative sum of the positional differences $\kappa$ from the locations of the desired points to that of the drone.

3.4. Placement Optimization

Placement optimization, the final phase of deployment optimization, involves modeling and analyzing electromagnetic wave propagation in the target environment. Placement optimization is represented as a state machine in Figure 7. To achieve this, measurements such as path loss, received signal strength, angular dispersion, and other radio propagation characteristics are collected and modeled using ray-tracing techniques. These models generate data corresponding to different levels or zones within the environment. Based on this information, UAVs are dynamically deployed, with the placement strategy driven by the objective of minimizing path loss; i.e., each UAV is directed toward the region offering the most favorable signal conditions. While the subsequent section details the computation of path loss, the current section outlines the approach to placement optimization based on the path loss values.

The first step in placement optimization involves conducting a systematic area scan to collect path loss data throughout the environment. UAVs perform the scanning process by sampling within the defined boundaries of a 3D coordinate system $(x,y,z)$ corresponding to the designated area ($\mathcal{A}$). Formally, the set of sampling points $\mathcal{S}$ can be defined as

$$\mathcal{S}=\left\{(x_i,y_j,z_k)|x_i=x_0+i\Delta x,y_j=y_0+j\Delta y,z_k=z_0+k\Delta z;i,j,k\in \mathbb{Z},(x_i,y_j,z_k)\in \mathcal{A}\right\}$$

(20)

where $(x_0,y_0,z_0)$ represents the initial position of the UAVs; $\Delta$ denotes the sampling interval; and path loss data is stored at each sampling point $(x_i,y_j,z_k)$.

Secondly, a UAV placement optimization process is carried out to extend the coverage area. For this optimization process, a cost function is constructed using the path loss data. To maximize the coverage area, the optimal coordinates for UAV placement are determined using our optimization algorithm. Let $\mathcal{S}$ denote the set of all sampling points and $\mathcal{U}$ the set of available UAVs. For each UAV $u\in \mathcal{U}$, the placement objective is to minimize the cost function defined as

$$\mathcal{C}(x,y,z)=\alpha ·\mathrm{PL}(x,y,z)+\beta ·d_u(x,y,z)-\gamma ·w(x,y,z)$$

(21)

In this equation, $\mathrm{PL}(x,y,z)$ represents the path loss at the point $(x,y,z)$; $d_u(x,y,z)$ denotes the Euclidean distance between UAV u’s deployment origin and the target point; and $w(x,y,z)$ is a priority weight that reflects the importance of covering the given location. The coefficients $\alpha$, $\beta$, and $\gamma$ are scalar parameters that balance the relative importance of path loss minimization, distance efficiency, and priority coverage within the overall cost function. These coefficients were empirically selected through sensitivity analysis and Pareto front exploration to ensure an effective trade-off between coverage quality, deployment efficiency, and spatial priority.

However, in many cases, when the insufficiency of UAV numbers in the area is taken into account, as described in the number optimization method, the UAV count is updated accordingly. If the number of UAVs $\left|\mathcal{U}\right|$ is insufficient to provide adequate coverage across all priority zones, the algorithm evaluates the need for additional UAVs in a recursive manner, as discussed in the number optimization procedure.

Finally, the UAVs are deployed to the newly determined optimal coordinates. Naturally, this placement process is followed by the path optimization phase, which is modeled to ensure efficient navigation and minimize travel costs.

3.5. Architecture of the Ray-Tracing-Based Channel Modeling System

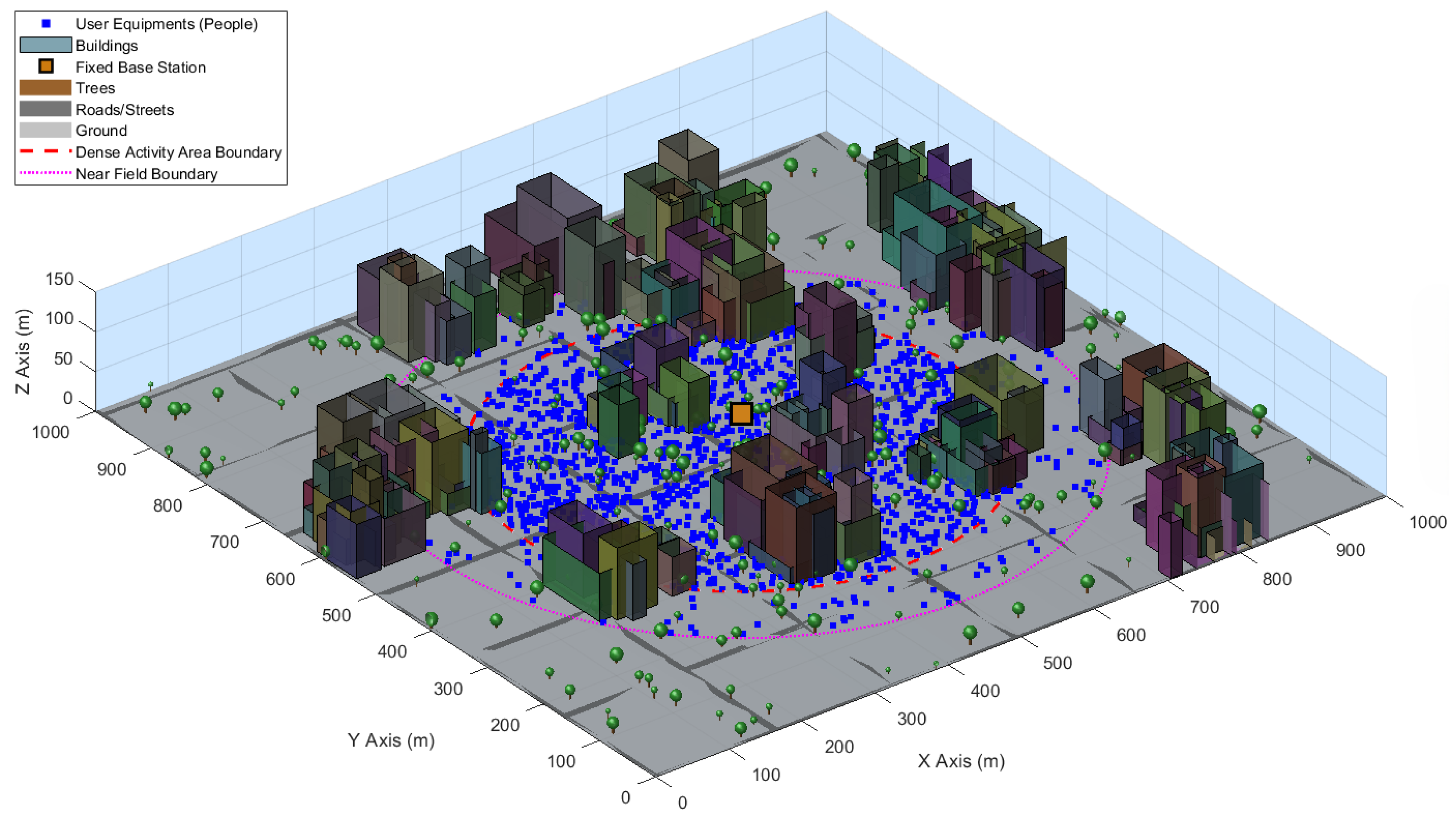
In this study, a virtual settlement area with a density of activity of 1000 m wide, 1000 m long, and 150 m high was constructed in the MATLAB simulation environment. The virtual settlement includes high-rise office buildings, low-rise buildings, and different materials such as glass, concrete, metal, trees, green areas, a base station, and 2000 user equipment, and all of these are presented in Figure 8. This settlement has a flat topography without mountainous terrain or rugged features. This scenario has enabled the easy implementation of drone base stations. The performance of drone base stations in increasing the coverage area in 6G mobile communication networks was investigated.

The proposed system consists of four main components: an environmental modeling module, a ray-tracing algorithm, a channel parameter analysis block, and an evaluation interface where the results are presented with visual–analytical outputs. In the environmental modeling phase, data such as building structures, road geometries, and pedestrian density of the settlement were transferred to the digital environment in detail. A 3D environment simulation was created in the MATLAB simulation environment. The ray-tracing algorithm analyzes multiple path components for a fixed base station and 2000 users. It extracts channel characteristics according to the power model of the received signal. In this way, the channel behavior of 6G networks in dense activity areas where a fixed base station is located is modeled with high spatial and temporal resolution.

Figure 8 presents the ground distribution of 2000 user equipment in the virtual settlement. The locations of all user equipment on the ground were randomly determined in MATLAB according to the normal distribution. The user equipment is shown as blue boxes, and the base station is shown as an orange box. The ground is marked with light gray, and the roads and streets are marked with dark gray. The buildings are displayed in various colors; the trunks of the trees are brown; and the branches are green. The border of the dense activity area within the virtual settlement is indicated with red dashed lines. In addition, the border outside the activity area but close to this area is indicated with pink dots. The location of the drone base station is determined according to the received signal power model.

In the modeling process, user equipment is positioned at a height of 1.5 m according to the requirements of 6G mobile communication systems. This height represents the hand-held scenario of a typical mobile terminal. The carrier frequencies predicted for 6G mobile networks are used in the simulations. Center frequencies of 7 GHz in the FR3 band, 26 GHz in the millimeter wave (mmWave) band, and 140 GHz in the terahertz (THz) band are used. Since signals in the millimeter wave and terahertz wave bands have very short wavelengths and require precise channel modeling, omnidirectional antennas are preferred. On the receiver side, only physically perceptible signals are evaluated by considering the −100 dBm sensitivity threshold [73]. Thus, the channel is modeled according to realistic boundary conditions. In order to represent low-power base station scenarios, the output power of the transmitter is determined as 5 Watts. This value allows for the path losses and multiple reflection effects encountered in the high-frequency bands to be taken into account. It also contributes to the optimization of the ray-tracing algorithm in terms of accuracy and coverage. These technical parameters made it possible to model the system architecture in accordance with both 6G mobile networks’ performance requirements and urban density environmental scenarios.

In this work, a ray-tracing-based approach is used to model the channel characteristics of 6G mobile communication networks in a densely populated residential area. In this regard, the shooting and bouncing rays (SBR) method is applied. In the SBR method, the interaction of electromagnetic signals with environmental surfaces is calculated within the framework of geometric optics principles. Signals are modeled as rays that emergerge from the transmitter. It is assumed that the rays emerging from the transmitter hit and reflect from surrounding objects. All possibilities that the signal can reach the target receiver with different reflections are calculated. In the model, the maximum reflection coefficient is determined as three. This value plays a critical role in evaluating the sustainability of communication under non-line-of-sight (NLoS) conditions. Because in NLoS conditions, the signal reaches the receiver through one or more reflections. The maximum reflection limit of three reflections provides physical realism by taking into account the multipath components on the one hand, while keeping the processing load under control on the other. Thus, effects such as attenuation, scattering, and direction dependency specific to 6G signal propagation are simulated in detail. The analyses were carried out on a virtual settlement area of $1\times 1{\mathrm{km}}^2$, which was created in the MATLAB environment and contains an intensive activity area. In order to evaluate the effect of different carrier frequencies on signal propagation, a foliage depth of 2.5 m was included in the system.

The deterministic ray-tracing method takes into account the effects of environmental structures on the direction and power of the signal. Thus, the coverage area estimation is much more accurate compared to traditional stochastic models. One of the most important advantages of the deterministic ray-tracing technique is that it can make location-based channel estimation based on the real environment’s geometry. This is a key requirement for short-range, high-frequency, and directional communication applications of 6G mobile communication networks. Both realistic channel characterization and reliable coverage analysis for urban areas significantly increase the accuracy and applicability of this study. The parameters used in the beam-monitoring-based channel modeling simulations performed in the MATLAB environment are summarized in

Table 3. Simulation parameters.

Parameter	Value
Carrier Frequency	7, 26, and 140 GHz
UE Antenna Type	Omnidirectional
Tx Antenna Type	Omnidirectional
Transmitter Power	5 W
Maximum Range of the Transmitter	500 m
UEs Height	1.5 m above ground level
Receiver Sensitivity	−100 dBm
Coverage Area	$1\times 1$ km2
Foliage Depth	2.5 m
Material	Building = concrete
Weather	Rain and gas
Scenario	Virtual settlement

. Similarly, the dielectric constants and conductivity values of the materials in the virtual settlement created in the MATLAB environment are presented in

Table 4. Dielectric constant and conductivity values for various materials in the virtual settlement.

Material	Dielectric Constant (${\mathit{\epsilon }}_{\mathit{r}}$)	Conductivity ($\mathit{\sigma }$) [S/m]	References
Concrete	4.0–7.0	0.010–0.5	ITU-R P.2040-3, ITU-R P.1238-12, 3GPP TR 38.901
Glass	5.0–7.5	0.005–0.3	ITU-R P.2040-3, 3GPP TR 38.901
Wood (moist)	7.0–15.0	0.010–0.5	ITU-R P.2040-3, ITU-R P.1238-12
Asphalt	3.0–5.0	0.010–0.3	ITU-R P.2040-3, IEEE 802.11a
Soil (moist)	3.0–6.0	0.005–0.3	ITU-R P.2040-3, 3GPP TR 38.901, IEEE 802.11a

based on the technical reports ITU-R P.2040-3, ITU-R P.1238-12, and 3GPP TR 38.901, as well as the IEEE 802.11ay channel model.

In this study, the 7 GHz, 26 GHz, and 140 GHz frequency bands were chosen because they are expected to be used in 6G mobile communication networks. Although the 26 GHz band is remarkable according to the European 5G/6G road maps, the 7 GHz band offers a more suitable ground for rural/suburban coverage analyzes. Moreover, the 140 GHz band stands out as a critical candidate for near-future ultra-high fast short-distance connections. In these scenarios, the use of omnidirectional antennas was preferred for a neutral evaluation that focuses only on frequency, environment, and channel conditions by purifying the effect of directing system behavior and channel properties.

The −100 dBm level is widely used in the literature as the receiver sensitivity value. This value has been accepted especially for sub-6 GHz systems, but for the 26 GHz and 140 GHz bands, a reference was taken to ideally evaluate the connection limits. However, it requires additional parameters such as metrics at the system level such as the link budget, maximum connection loss, or maximum path loss, in system losses and noise levels. Since these parameters are not among the basic inputs of the ray-tracing algorithm, it is not directly calculated within the scope of this analysis. At the mmWave frequencies, a direct line-of-sight blockage may cause significant loss of the signal and may cause the channel to be on/off. However, especially in urban and indoor environments, the signal continues to reach the recipient and through the scattering of buildings and other surfaces. These indirect paths are critical to provide a limited area of coverage even under NLoS conditions.

Limiting the number of reflections to three in the ray-tracing simulation is primarily based on a trade-off between computational complexity and the practical importance of higher-order multipath components. Delay spread information is used as a critical performance metric to evaluate the temporal distribution characteristics of multipath components at different distribution points in the deployment scenario. In our study, the user capacity of the base station integrated into the drone is determined based on the RRC connected user count limits in 5G and 6G mobile communication systems. Therefore, considering the high-activity scenarios where multiple carrier frequencies are used, a system capacity of 2000 users is modeled as a reasonable upper-bound estimate. All scenarios compared in this work are built for the 140 GHz band. Furthermore, the impact of network performance on the deployment parameters is discussed in detail during the experimental phase.

3.6. Received Signal Power Modeling

In this study, several key parameters influencing the received signal strength were thoroughly examined. These parameters include path loss, multipath propagation effects, and frequency-dependent characteristics of the communication channel. By analyzing these factors, a more accurate and realistic model of signal reception was developed.

3.6.1. Path Loss

Path loss refers to the attenuation experienced by electromagnetic waves propagating from a fixed-position base station to 2000 user equipment. Although mmWave and THz bands, which are planned to be used in 6G mobile communication networks, allow for high data rates, they are quite sensitive to environmental effects. This makes path loss a more important parameter. In this virtual settlement with a dense activity area, signals interact with buildings, vehicles, human presence, and other structures, undergoing numerous reflections, refractions, and scattering. This case causes path loss to vary under both LoS and NLoS conditions. The ray-tracing algorithm used in this study takes into account the path length that the signal travels for each user, the material properties of the surfaces it encounters, and environmental conditions such as rain and vegetation, producing a deterministic path loss model. According to the 3GPP TR 38.901 technical report, the close-in (CI) model path loss used in this study was calculated with the following equation:

$$P{L}_{\mathrm{CI}}\left(d\right)=P{L}_{\mathrm{FS}}\left(d_0\right)+10n{log}_{10}\left({\displaystyle \frac{d}{d_0}}\right)+X_{\sigma }$$

(22)

where $P{L}_{\mathrm{CI}}\left(d\right)$ is the total path loss (in dB) at the distance d between the transmitter and the receiver in meters, while $P{L}_{\mathrm{FS}}\left(d_0\right)$ is the free space path loss for the reference distance $d_0$ (usually 1 m) and is calculated as follows based on the ITU-R P.525 technical report:

$$P{L}_{\mathrm{FS}}\left(d_0\right)=20{log}_{10}\left(f\right)+20{log}_{10}\left(d_0\right)-147.55$$

(23)

where f represents the frequency in Hz. The constant term $147.55$ is obtained from the speed of light and unit conversions. n is the path loss exponent that varies depending on the physical properties of the medium. While it is typically around 2 in open areas, it varies between 2.7 and 4 in urban areas. $X_{\sigma }$ is a zero-mean Gaussian-distributed random variable representing the shadowing effects that occur randomly in the environment. Typically, its standard deviation is chosen between $\sigma =4\sim 10$ dB.

It has been observed that the received signal strength varies not only with the distance but also with the geometric and physical structure of the environment. This approach provides much higher accuracy compared to classical log-distance modeling.

3.6.2. Received Signal Strength

The received signal strength ($P_r$) is calculated using parameters such as transmitter output power, antenna gains, path loss, environmental interactions (reflection, refraction, and scattering), attenuations due to reflection numbers, and the location of the receiver. In this context, the total received power is expressed as the vector sum of multipath components as follows:

$$P_r={\left|\sum _{i=1}^N\sqrt{P_{t_i}}·G_{t_i}·G_{r_i}·e^{-j{\varphi }_i}·{\displaystyle \frac{\lambda }{4\pi d_i}}·L_i\right|}^2$$

(24)

where $P_r$ is the total signal power obtained at the receiver terminal; $P_{t_i}$ is the power transmitted from the transmitter for the ith path; $G_{t_i}$ and $G_{r_i}$ are the antenna gains of the transmitter and the receiver in the ith path direction, respectively; ${\varphi }_i$ is the phase shift of the ith path; $\lambda$ is the carrier wavelength; $d_i$ is the total distance of the ith path; $L_i$ is the total attenuation coefficient including reflection, scattering, and transition losses of the medium; N is the total number of rays obtained by the ray-tracing method; and j is the complex number unit. In the MATLAB environment, the coverage quality across the network was analyzed by calculating the power values received in this model for each of the 2000 user equipment.

3.6.3. Frequency-Dependent Observations

In the 7 GHz band, signals can more easily overcome environmental obstacles and provide wider coverage. Path loss increases significantly in the 26 and 140 GHz bands. The signals in these bands become more sensitive to both distance and environmental effects such as building obstructions, foliage depth, and atmospheric attenuation. This causes significant drops in received signal power, especially under NLoS conditions. These frequency-specific observations in ray-tracing-based simulations emphasize the need for frequency-based optimization of cell placement, carrier selection, and user access strategies in 6G mobile communication networks.

3.6.4. Delay Spread Analysis

In ray-tracing-based simulations, the geometric path length of each ray reaching 2000 user equipment from the fixed-position base station was calculated. Delay times were obtained by considering the propagation speed of the signal in the medium. The propagation delay for each ith path is calculated with the following equation:

$${\tau }_i={\displaystyle \frac{d_i}{c}}$$

(25)

where ${\tau }_i$ represents the total propagation delay of the ith signal path (in seconds); $d_i$ represents the physical length of the path (in meters); and c represents the propagation speed of electromagnetic waves in free space $3\times {10}^8\mathrm{m}/\mathrm{s}$.

In the analysis, it was observed that LoS components have minimum delays. On the other hand, NLoS components with one or more reflections have been observed to have higher delays because the length of the reflected paths is greater than the length of the direct paths. The flowchart summarizing the methodology used in the analysis of 6G mobile communication channels is given in Figure 9.

4. Experimental Evaluation

The experimental evaluation of this study consists of the following sub-steps: First, the plant (i.e., the uncontrolled system behaviors) was modeled in the ReaX (version 0.17.3) environment using parallel synchronous dataflow equations. Then, based on the control objectives described in the methodology section, the model was integrated with discrete controller synthesis algorithms to obtain a controller. This controller was transferred to the simulation environment and implemented in MATLAB (version 2021a). In addition, a linear model was created in the Simulink (version 2021a) environment for the dynamic modeling of drones. The drones and the base stations they carry were designed in SolidWorks (version 2020), and their total mass and moments of inertia were obtained in accordance with the literature. The DCS controller was employed alongside PID controllers optimized using the ACO, ABC, and GWO algorithms, as well as hybridized versions of these metaheuristic techniques.

During the experimental evaluation phase, three optimization problems were addressed: number, path, and placement optimizations. The comparative results for these problems were analyzed and reported in MATLAB using various optimization algorithms. Additionally, for placement optimization, the received signal strength data used was obtained through the proposed ray-tracing-based channel modeling technique, and the corresponding results are also reported.

The details of the success of the developed controllers are presented in

Table 5. Performances of the controllers for movements on the x-, y-, z-axes and the corresponding pitch, roll, yaw angles side by side.

Algorithm	Tr(s)	Tp(s)	Mp(%)	Ts(s)	Ess(%)	Tr(s)	Tp(s)	Mp(%)	Ts(s)	Ess(%)
	X-axis					Pitch
DCS	10.231	14.008	0	14.008	0	0.455	1.376	0	1.376	0
ACO	10.934	14.721	0	14.721	0	0.988	2.634	0	2.634	0
ABC	10.895	14.510	0	14.510	0	0.976	2.638	0.009	2.667	0
GWO	11.023	14.908	0	14.908	0	0.953	2.532	0.008	2.589	0
ACO-ABC	10.980	14.823	0	14.823	0	0.974	2.580	0	2.580	0
ACO-GWO	11.011	14.910	0	14.910	0	0.990	2.635	0	2.635	0
ABC-GWO	10.918	14.704	0	14.704	0	0.974	2.637	0.009	2.660	0
	Y-axis					Roll
DCS	10.231	14.008	0	14.008	0	0.455	1.376	0	1.376	0
ACO	11.102	13.322	0.610	14.923	0	0.844	2.724	0	2.724	0
ABC	10.929	13.320	0.605	14.913	0	0.852	2.730	0	2.730	0
GWO	10.933	13.412	0.701	14.914	0	0.831	2.709	0	2.709	0
ACO-ABC	11.008	13.414	0.620	14.922	0	0.845	2.725	0	2.725	0
ACO-GWO	10.943	13.424	0.711	14.929	0	0.862	2.741	0	2.741	0
ABC-GWO	11.020	13.421	0.623	14.928	0	0.866	2.748	0	2.748	0
	Z-axis					Yaw
DCS	9.010	10.807	0	10.807	0	0.310	1.352	0	1.352	0
ACO	9.010	10.128	0.430	10.835	0	0.384	1.409	0	0	0
ABC	9.010	10.118	0.426	10.820	0	0.382	1.408	0	0	0
GWO	9.010	10.121	0.426	10.823	0	0.361	1.396	0	1.396	0
ACO-ABC	9.010	10.124	0.428	10.831	0	0.379	1.410	0	0	0
ACO-GWO	9.015	10.128	0.429	10.834	0	0.383	1.414	0	0	0
ABC-GWO	9.010	10.125	0.428	10.832	0	0.381	1.409	0	0	0

, which displays the performance of each controller in managing the six degrees of freedom (six DOFs) of the quadcopter. The key evaluation metrics used in the table include the rise time ($T_r$), peak time ($T_p$), maximum overshoot at the peak time ($M_p$), steady-state time ($T_s$), and steady-state error ($E_{ss}$). Results related to the metaheuristic (MH) algorithms were obtained by setting the number of iterations to 100. In addition, Figure 10 illustrates the controller responses along the x-, y-, and z-axes as well as the roll, pitch, and yaw angles.

Considering the results in Table 5, the DCS algorithm provided the best performance in controlling both the vertical and horizontal movements of the quadcopter. The second-best performance was achieved by the PID controller optimized using the ABC algorithm. Furthermore, the DCS algorithm also demonstrated superior performance in regulating the angular movements of the quadcopter along the $\theta$ (theta), $\varphi$ (phi), and $\psi$ (psi) angles. The next-best performance in angular control was obtained using the PID controller optimized with the GWO algorithm.

As shown in Figure 10, the DCS algorithm consistently outperformed all optimized PID controllers across all movement types. A comprehensive evaluation of Table 5 and Figure 10 indicates that the DCS algorithm offered the most effective control performance across all six degrees of freedom for the quadcopter tasked with carrying the base station. The hybridization of MH algorithms did not yield improvements over their standalone implementations. Although the DCS algorithm exhibited the best overall performance, the similarities in outcomes suggest that optimized PID controllers may still serve as viable alternatives, particularly for managing angular motions of the quadcopter.

The results presented in

Table 6. Drone coverage performance for different algorithms and designs.

Algorithm	Design 1			Design 2			Design 3
	U, N = 10	U, N = 14	N	U, N = 50	U, N = 53	N	U, N = 100	U, N = 101	N
DCS	9878	10,000	14	47,898	50,000	53	99,712	100,000	101
ACO	9783	9789	16	45,966	49,893	59	97,639	99,965	105
ABC	9789	9878	22	47,893	49,655	61	97,667	99,932	105
GWO	9804	9909	20	46,772	49,678	60	96,656	99,978	104
ACO-ABC	9815	9932	20	46,978	49,780	59	97,665	99,930	108
ACO-GWO	9798	9945	19	47,809	49,892	60	98,043	99,969	105
ABC-GWO	9812	9956	21	47,985	49,784	62	96,784	99,979	106

were obtained for populations of 10,000, 50,000, and 100,000 individuals, respectively. The capacity of a single drone-mounted base station was set to serve 2000 users, and the experimental area was defined as 100,000 square meters. The performance of the DCS algorithm was evaluated and compared against that of the ACO, ABC, and GWO algorithms, as well as hybridized versions of these MH algorithms. In this context, N denotes the number of drones required to provide coverage for each user, while U represents the total number of users.

MH algorithms can produce varying results that are not necessarily consistent with one another. To statistically evaluate these differences, the Wilcoxon rank-sum test, a nonparametric statistical method, was employed in this study. As shown in

Table 7. p-values obtained by the Wilcoxon rank-sum test.

Algorithm	N = 10	N = 50	N = 100
ACO & ABC	$1.565\times {10}^{-7}$	$3.235\times {10}^{-6}$	$5.236\times {10}^{-6}$
ACO & GWO	$2.395\times {10}^{-6}$	$4.114\times {10}^{-7}$	$2.307\times {10}^{-7}$
ACO & ACO-ABC	$2.525\times {10}^{-6}$	$3.583\times {10}^{-6}$	$2.598\times {10}^{-6}$
ACO & ACO-GWO	$3.193\times {10}^{-6}$	$3.347\times {10}^{-7}$	$1.197\times {10}^{-6}$
ACO & ABC-GWO	$2.128\times {10}^{-6}$	$2.359\times {10}^{-6}$	$2.455\times {10}^{-7}$
ABC & GWO	$2.365\times {10}^{-7}$	$4.167\times {10}^{-6}$	$1.367\times {10}^{-7}$
ABC & ACO-ABC	$3.116\times {10}^{-7}$	$3.445\times {10}^{-7}$	$2.139\times {10}^{-6}$
ABC & ACO-GWO	$1.156\times {10}^{-6}$	$2.151\times {10}^{-7}$	$3.159\times {10}^{-6}$
ABC & ABC-GWO	$2.154\times {10}^{-6}$	$2.189\times {10}^{-6}$	$2.668\times {10}^{-7}$
GWO & ACO-ABC	$2.369\times {10}^{-7}$	$3.460\times {10}^{-7}$	$2.398\times {10}^{-6}$
GWO & ACO-GWO	$1.138\times {10}^{-7}$	$2.187\times {10}^{-6}$	$5.102\times {10}^{-7}$
GWO & ABC-GWO	$2.122\times {10}^{-6}$	$4.129\times {10}^{-6}$	$2.389\times {10}^{-7}$
ACO-ABC & ACO-GWO	$2.142\times {10}^{-6}$	$2.108\times {10}^{-6}$	$1.145\times {10}^{-7}$
ACO-ABC & ABC-GWO	$2.328\times {10}^{-7}$	$3.321\times {10}^{-7}$	$5.426\times {10}^{-7}$
ACO-GWO & ABC-GWO	$3.113\times {10}^{-6}$	$3.348\times {10}^{-7}$	$4.115\times {10}^{-6}$

, all p-values were found to be less than 0.05, indicating statistically significant differences among the results generated by the MH algorithms. Therefore, the null hypothesis ($H_0$), which posits that the models produce equivalent results, is rejected. Consequently, the alternative hypothesis ($H_1$), stating that there are significant differences between the results, is accepted. This confirms that the MH algorithms yielded statistically distinct outcomes across all cases. In simulations, the number of simulations for each cases is 10, while drones starting positions and the distribution of the users were defined randomly for each case.

The performance of the proposed SDCS approach is compared with existing metaheuristic and classical methods, as summarized in

Table 8. Performance comparison of the SDCS approach with existing metaheuristic and classical methods.

Algorithm	Time (s)	Accuracy (%)	Previous Work
SDCS	406	100	-
ACO	521	97.1	[74]
ABC	512	98.3	[75]
GWO	503	95.5	[76]
ACO-ABC	532	97.4	[77]
ACO-GWO	520	96.2	[78]
ABC-GWO	534	97.0	[79]
DDPG	550	97.5	[80]

. Classical control methods often suffer from high modeling complexity and substantial computational demands. On the other hand, metaheuristic approaches lack formal correctness and cannot guarantee optimality in all cases. In contrast, the proposed SDCS approach, being based on a model-checking tool, inherently supports formal verification. Furthermore, the symbolic abstraction employed in SDCS helps overcome the state explosion problem. Since it systematically evaluates all possible paths within a given time window, it yields highly accurate and reliable results.

The proposed SDCS approach begins with modeling the desired system behaviors within the ReaX environment. Following this, the model is compiled to synthesize a controller that guarantees the specified behaviors. Although the synthesis phase may require a short computation time, it is performed only once. Once the controller is generated, it operates in real time, providing instantaneous responses to the system without any delay. In the presence of communication-related issues such as sensor failures or similar disruptions, the proposed path optimization approach continues to operate flawlessly. However, number and placement optimization performances may slightly degrade under such conditions, as reflected in the first column of Table 6. Nevertheless, even in these scenarios, the SDCS method still outperforms the best-performing metaheuristic algorithms.

Each graph presented in Figure 11 shows the log10 (distance) value in meters on the horizontal axis, the RSS value in dBm on the left vertical axis, and the residual error value in dB on the right vertical axis. The logarithmic distance axis allows a clearer observation of signal attenuation over a wide range of distances. This structure increases the modeling accuracy in cases where electromagnetic waves propagating in free space are attenuated compared to the close-in model. The residual error displayed on the right axis represents the difference between the RSS predicted by the model and the simulation results. RSS values are calculated considering the transmitter’s output power (5 W = 37 dBm), the carrier frequency, the close-in path loss model, atmospheric attenuation, vegetation loss, and random noise effects. The model estimation is obtained by linear regression between the log10 distance and RSS. The average RSS value is determined by taking the arithmetic mean of all measurements. The residual error expresses the difference between each simulation value and the model estimation. Outliers are defined as values outside $\pm 2$ standard deviations and are indicated by red circles. This structure is used to evaluate the accuracy and reliability of the proposed channel model. It is seen that RSS values are higher, and signal attenuation occurs more slowly at the 7 GHz frequency. This provides a wider coverage. Attenuation is more pronounced at the 26 GHz frequency. RSS values decrease to lower levels. At the 140 GHz frequency, the signal strength decreases much faster. Atmospheric losses and vegetation-related attenuations become more dominant. Thus, it is concluded that high frequencies have shorter ranges and are more affected by environmental factors. In addition, the number of residual error values and outliers also increases as the frequency increases, which reveals that more user equipment remains outside the coverage area at high frequencies.

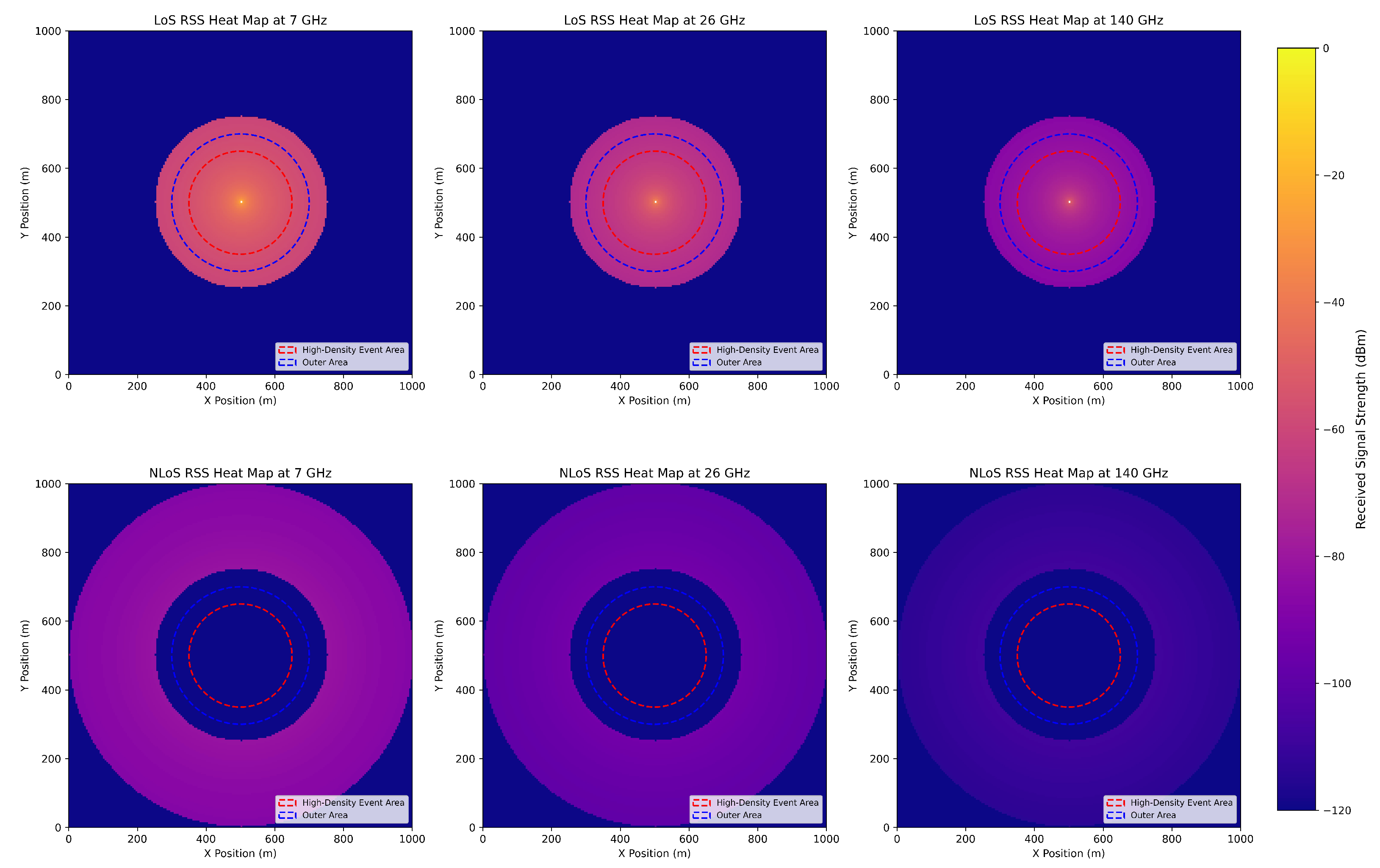
RSS heat maps obtained in a ray-tracing-based simulation environment for a fixed base station in a densely populated activity area in a virtual settlement area are presented in Figure 12. The figure consists of two rows and three columns. The first row indicates the LoS condition, and the second row indicates the NLoS condition. The columns, from left to right, show the RSS distribution for the 7 GHz, 26 GHz, and 140 GHz carrier frequencies, respectively. The urban area was modeled in Matlab, taking into account frequency-dependent properties such as the dielectric constant and the conductivity of buildings, streets, roads, trees, and parks. The color scale represents RSS values between −40 dBm and −110 dBm in each image. The densely populated activity area is shown with a red dashed circle, and the outer area, outside but close to the densely activity area, is shown with a blue dashed circle. Under LoS conditions, signals in the 7 GHz band provided broad coverage, while significant attenuation was observed in the 140 GHz band, with coverage limited to the immediate vicinity of the base station. Under NLoS conditions, signal attenuation became more pronounced, particularly at 26 GHz and 140 GHz, directly impacting both the number of user equipment within the coverage area and the system design.

Table 9. Comparative analysis of frequency and environmental factors in a virtual settlement with buildings, streets, roads, parks, and trees, as well as a foliage depth of 2.5 m.

Params.	RSS with Concrete	Plus Weather	Plus Foliage	Final Path Loss	UEs with Outage	Phase Shift
Freq. (GHz)	Avg. (dBm)				Nb.	Max.	Min.	Avg.
7	−65.2	−67.1	−69.6	102.3	0	178.2	2.3	89.6
26	−74.8	−77.3	−80.9	111.7	0	191.4	4.1	97.2
140	−89.5	−93.2	−97.8	127.4	567	204.7	7.9	106.5

presents the channel parameters obtained for a base station located at a fixed altitude of 50 m for the 7 GHz, 26 GHz, and 140 GHz carrier frequencies. These parameters include key metrics such as RSS, environmental effects (atmospheric losses and foliage attenuation), total path loss, the number of users out of coverage, and phase shifts. Each row quantifies the channel’s response to physical and environmental conditions for a given frequency. The RSS in the concrete column represents the average received signal strength measured under the influence of attenuations caused solely by reinforced concrete buildings. The plus weather and plus foliage columns represent the additional attenuating effects of environmental factors such as atmospheric attenuations (e.g., rain, humidity, and fog) and foliage attenuations (e.g., trees and shrubs), respectively. The proposed three-stage modeling approach allows the channel to be modeled more closely to real-world conditions. The final path loss column reflects the sum of all these effects and presents the total signal loss between the transmitter and the receiver in dB. The user equipments (UEs) in the outage column shows the number of UEs below the receiver sensitivity threshold. This value increases significantly at the 140 GHz carrier frequency. This means that higher frequencies have shorter ranges and are more sensitive to environmental factors. The maximum, minimum, and average values presented under the final phase shift heading indicate the statistical distribution of changes in the signal phase. Phase shift is a parameter that directly affects signal integrity and modulation performance in environments where multipath effects are dominant. Therefore, these values are critical for the design of the system.

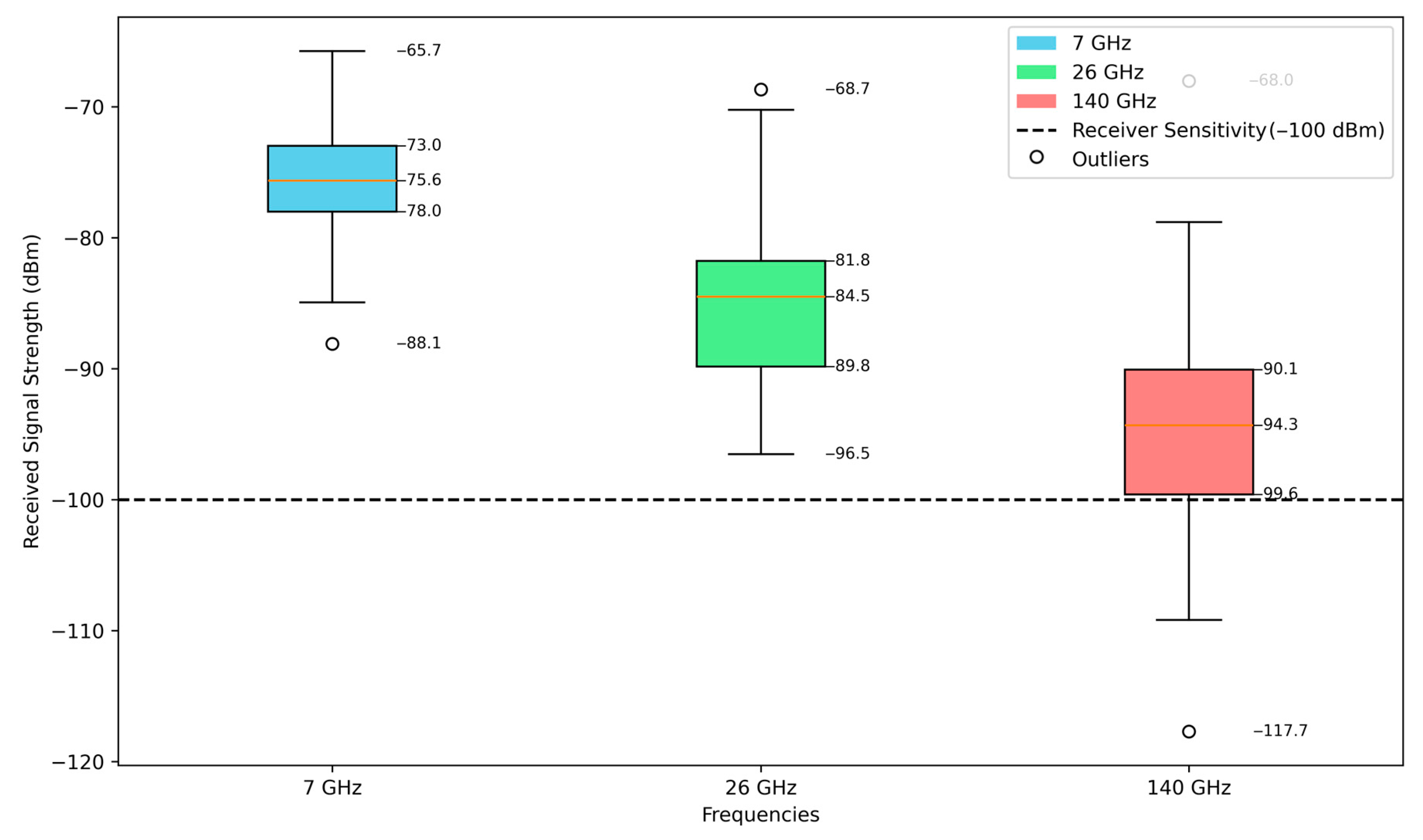
The box plot presented in Figure 13 displays the statistical distribution of received signal strength for three different carrier frequencies (7 GHz, 26 GHz, and 140 GHz). The horizontal axis of the plot consists of categorical values representing each carrier frequency. The vertical axis expresses the received signal strength in decibels-milliwatts (dBm) and includes values in the range of −120 dBm to −60 dBm. Each box represents the distribution of received signal strength values calculated for user equipment and base station distances between 1 and 500 m for the corresponding frequency. The red lines inside the boxes represent the median values. The median values were determined by selecting the middle value when the received signal strength values in the boxes were sorted from smallest to largest. The lower and upper limits of the boxes represent the first (Q1) and third (Q3) quadrants, respectively. The interquartile range (IQR) method was used to calculate the whiskers. The whiskers extend outward by 1.5 times the IQR. Values outside these limits are indicated by red dots as outliers. The received signal strength values are calculated by considering the close-in path loss model, vegetation attenuation, and atmospheric attenuation. Vegetation loss is approximated by an empirical model based on the ITU-R P.833-9 model. Atmospheric attenuation is calculated as a frequency- and distance-dependent model based on the ITU-R P.676-12 model and shows a significant effect at 26 GHz and 140 GHz. In this study, atmospheric attenuation is approximately negligible at 7 GHz. It is modeled as 0.1 dB/m at 26 GHz and 0.4 dB/m at 140 GHz. The total attenuation is evaluated as the sum of these three components. As the carrier frequency increases, the received signal strength decreases significantly. The 7 GHz frequency offers advantages in terms of both path loss and atmospheric and vegetation attenuation. Therefore, it is the frequency with the highest average received signal strength. The 26 GHz frequency is in the mmWave band and exhibits moderate attenuation. At 140 GHz, signal attenuation increased significantly, with the median RSS value dropping to −94.3 dBm. A very low outlier of −117.7 dBm was also observed in this band. It is clear that signal levels in the 140 GHz band are very close to or below the receiver sensitivity limit. Thus, it suggests that this band should be evaluated with caution in outdoor conditions. It also demonstrates that they impose coverage limitations. This negatively impacts connection reliability and increases the number of user equipment outside the coverage area.

Figure 14 shows the change in received signal strength under LoS and NLoS conditions for the 7 GHz, 26 GHz, and 140 GHz carrier frequencies, depending on the delay spread. As delay spread increases, the received signal strength decreases significantly. This decrease is related to the increase in path loss due to the increase in communication distance. It is clearly evident from the graph that signal levels under LoS conditions are higher than those under NLoS conditions. This suggests that the presence of a direct path is a critical factor for transmission quality in 6G systems. Particularly under the 140 GHz frequency, received signal strength levels under NLoS conditions drop to values very close to −100 dBm. This pushes the limits of receiver sensitivity. The analysis results clearly demonstrate the decisive impact of carrier frequency selection and channel conditions (LoS/NLoS) on the performance of 6G mobile communication networks. The 7 GHz frequency offers more stable and robust signal levels across different latencies. The 26 GHz and 140 GHz frequencies exhibit higher attenuation tendencies. This is one of the main challenges facing wireless communication in higher-frequency bands. It highlights the importance of ray-tracing-based channel modeling in densely populated urban areas, crowded event areas, and environments where NLoS conditions prevail. It also highlights the need for complementary solutions, such as drone-based stations, to ensure communication sustainability in such environments. Modeling channel characterization sensitive not only to distance but also to frequency and channel types is a crucial requirement.

The results of the delay spread analysis with respect to the distance between the transmitter and the receiver in both LoS and NLoS scenarios for 7 GHz, 26 GHz, and 140 GHz are presented in

Table 10. Delay spread analysis based on carrier frequencies in LoS and NLoS scenarios.

Scenario	Freq. (GHz)	Max. Delay (ns)	Min. Delay (ns)	Avg. Delay (ns)
LoS	7	15	5.10	10.00
	26	20	5.15	12.58
	140	25	5.20	15.10
NLoS	7	150	51.00	100.00
	26	200	51.50	125.75
	140	250	52.00	151.00

. The maximum delay, minimum delay, and average delay values are given in nanoseconds (ns). When examining LoS conditions, a slight increase in all delay values was observed as the frequency increased. While the average delay for the 7 GHz LoS scenario was 10 ns, this value increased to 15.10 ns in the 140 GHz LoS scenario. This is associated with the shortening of the signal wavelength at high frequencies and the increased prominence of multipath fading even at short distances. In NLoS conditions, a significant increase in delay values was observed for all frequency bands compared to LoS conditions. In the 26 GHz NLoS scenario, the average delay increased from 12.58 ns to 125.75 ns, while the maximum delay increased from 20 ns to 200 ns. This dramatic change is due to the effects of multipath propagation in NLoS environments. In multipath propagation, signals do not reflect from buildings and other obstacles but rather undergo scattering and diffraction. This results in a wider delay spread. Furthermore, a gradual increase in delay values continues as the frequency increases under NLoS conditions. Multipath fading effects become more pronounced in complex environments, especially in the millimeter wave and terahertz bands. Therefore, the problem of intersymbol interference (ISI) must be taken into account in the design of 6G mobile communication systems.

5. Conclusions and Future Work

In this study, UAV deployment optimization has been systematically carried out using the symbolic discrete controller synthesis method with successful results. UAV number and placement optimizations, along with altitude and attitude control behaviors, have been modeled using parallel synchronous dataflow languages. The controller, derived from the application of safety and optimization discrete controller synthesis algorithms, has been used to position the mobile base stations in such a way as to maximize coverage in scenarios where existing central base stations are insufficient. To enhance the placement optimization process, detailed channel characteristics were incorporated into the control design through ray-tracing-based channel modeling with the 3-reflection SBR method. Key channel parameters such as received signal strength, path loss, phase shift, and delay spread were comprehensively analyzed using a ray-tracing-based channel modeling technique. The findings demonstrate that traditional fixed base station infrastructure offers limited performance in densely populated urban environments. Additionally, drone base stations, with their dynamic positioning capabilities, increase capacity by covering user equipment not served by fixed base stations. The proposed SDCS method demonstrates approximately a 17% improvement in the number of drones required compared to the closest approach, ACO, indicating more efficient resource utilization. Additionally, it achieves around a 4% increase in coverage area, reflecting enhanced user coverage capacity. Our approach has been validated through experimental evaluations, yielding significantly successful results compared to existing methods in the literature.

The limitation of our approach is primarily related to its complexity. As the number of states increases significantly, computation times can become lengthy. However, this issue can be addressed by decomposing the problem into smaller DCS sub-problems, which can then be solved as a combination. Moreover, in most cases, substantial computation time only becomes a significant concern when designing extremely large systems, where the system behaviors can often be abstracted during the modeling phase. Since the SDCS approach functions as a model-checking tool, it inherently supports formal verification. Additionally, because the synthesis algorithms account for all possible future states over a given time window, it guarantees the optimal outcome at all times. On the other hand, ML algorithms lack formal correctness and cannot consistently guarantee the best results. Therefore, our approach demonstrates superior performance when compared to ML algorithms.

In future work, similar scenarios will be experimentally tested in real-world environments with frequency-based measurement systems using vector network analyzers, and the resulting data will be compared with the simulation results. This will strengthen the practical validity of the model and provide more concrete contributions to system designs. The approach we propose can be easily applied to similar systems in future work. In such reactive systems, successful outcomes can be attained in accordance with both safety objectives and different optimization targets. While the proposed approach does not explicitly model the UAV’s electrical characteristics, it inherently promotes energy awareness through trajectory optimization, which can contribute to reduced energy consumption. Nevertheless, incorporating detailed models of battery dynamics and electrical characteristics remains an important direction for future work and could further enhance the effectiveness of the proposed framework. Furthermore, the development of various control algorithms can address multicriteria objectives. In future studies, directional antennas with beam-forming capabilities should be included in the ray-tracing-based modeling of air-to-ground communication channels, especially where mmWave and sub-THz frequency bands are used. Further research is needed to investigate energy-efficient network structures and route planning while considering the limited battery capacities of drones. Furthermore, coordination algorithms for overlap-free coverage and resource sharing in scenarios where multiple drone base stations operate simultaneously need to be developed. Finally, within the scope of this study, the work has been addressed experimentally in an artificial setting. The results obtained from real-world applications will serve as an inspiring and pioneering reference for future research, particularly in enhancing the governability of the approach we propose.