Dynamic Recovery and a Resilience Metric for UAV Swarms Under Attack
Abstract
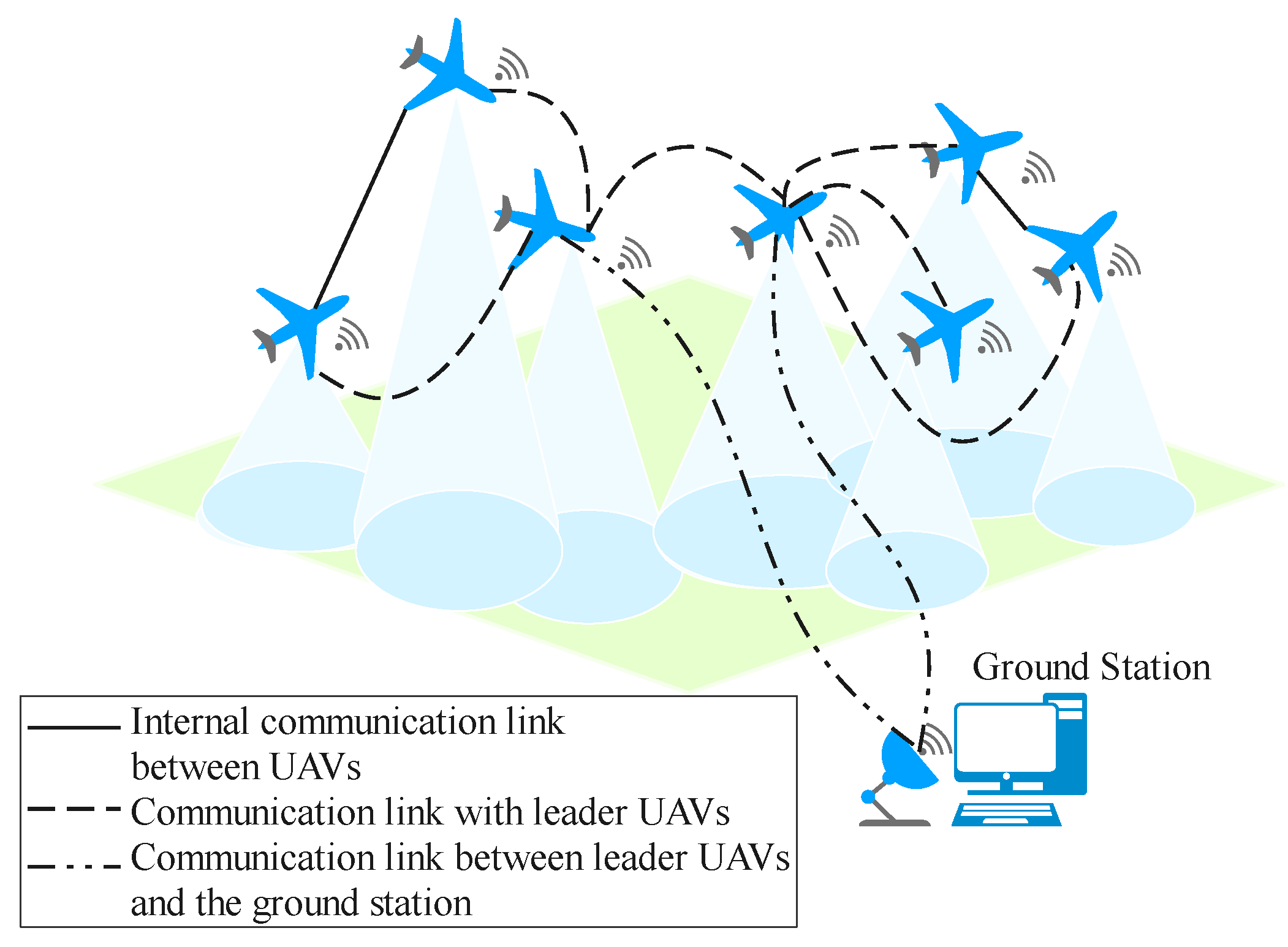
1. Introduction
1.1. Related Work
1.2. Contribution and Paper Organization
- A novel dynamic recovery method is proposed that considers maximizing the speed of consensus after an attack. The method involves a disconnected UAV swarm after an attack, dynamic behaviour, and consensus control of the UAV swarm.
- The performance of the UAV swarm is evaluated from the combined perspectives of consensus, communication, mission, and resources. A comprehensive description of the UAV swarm is provided.
- A resilience metric is further proposed, focusing on the time from stopping recovery to a new consensus state. The metric is sensitive to the change in the time from recovery to the new consensus state.
2. Problem Formulation
3. Proposed Recovery Method
3.1. Swarm Dynamics and Consensus Control
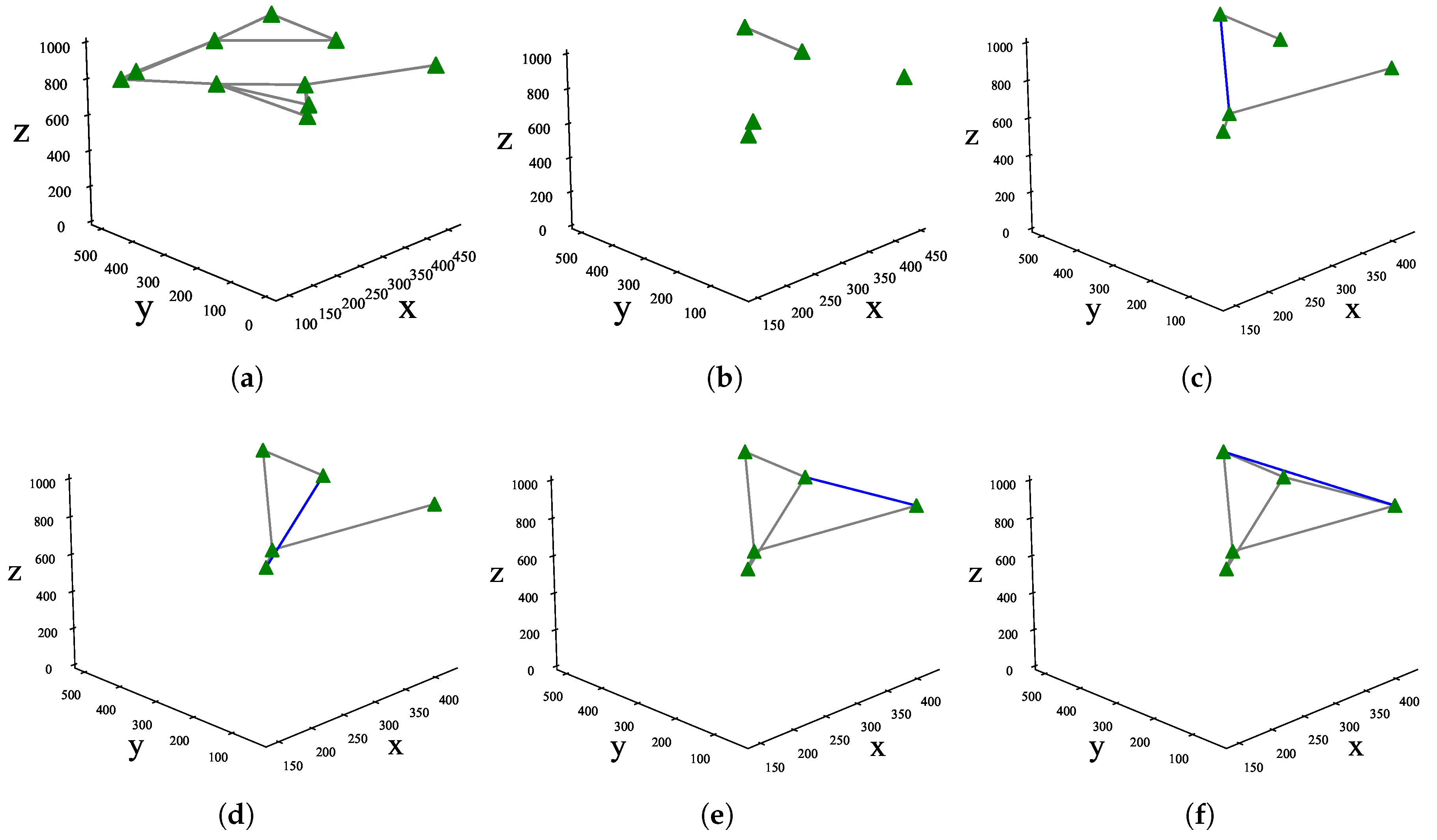
3.2. Swarm Recovery Strategy
| Algorithm 1 Swarm recovery strategy. |
|
1: Input: Disconnected swarm , Adjacency matrix of , threshold 2: Output: Recovered UAV swarm , Adjacency matrix of 3: for each isolated UAV do 4: Find the largest connected connected clustered UAVs within communication range 5: if is not found then 6: Increase communication range until is found 7: end if 8: Add a communication link between and 9: Update the adjacency matrix 10: end for 11: while the swarm is not connected do 12: Identify the largest and smallest UAV cluster 13: Add a link between UAVs with the highest degree in and UAV 14: Update the adjacency matrix 15: end while 16: while Algebraic connectivity improvement do 17: Add communication links according to Equation (10) 18: Update the adjacency matrix 19: end while |
4. Proposed Swarm Performance Indexes and Resilience Metric
4.1. Proposed Swarm Performance Indexes
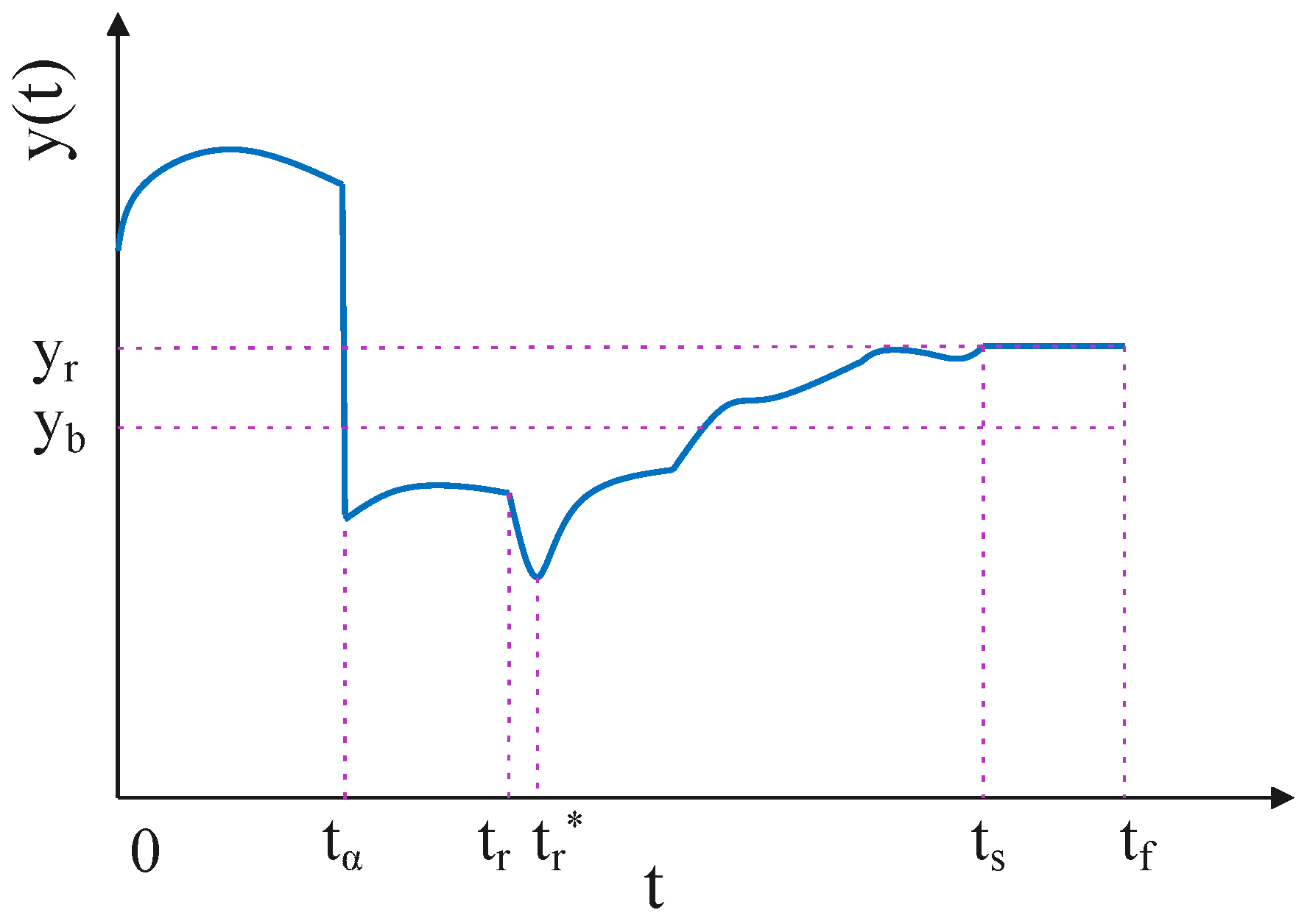
4.2. Proposed Resilience Metric
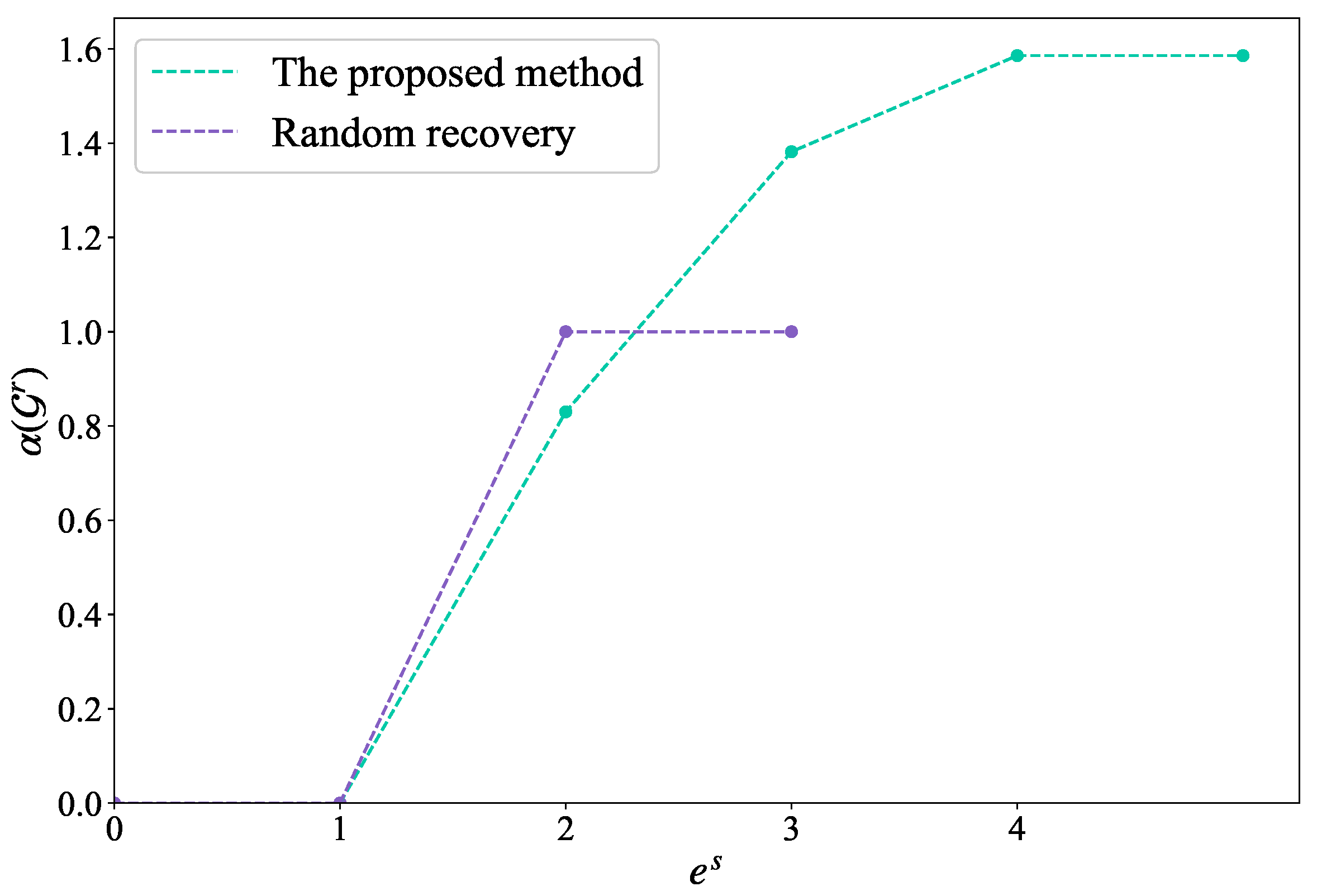
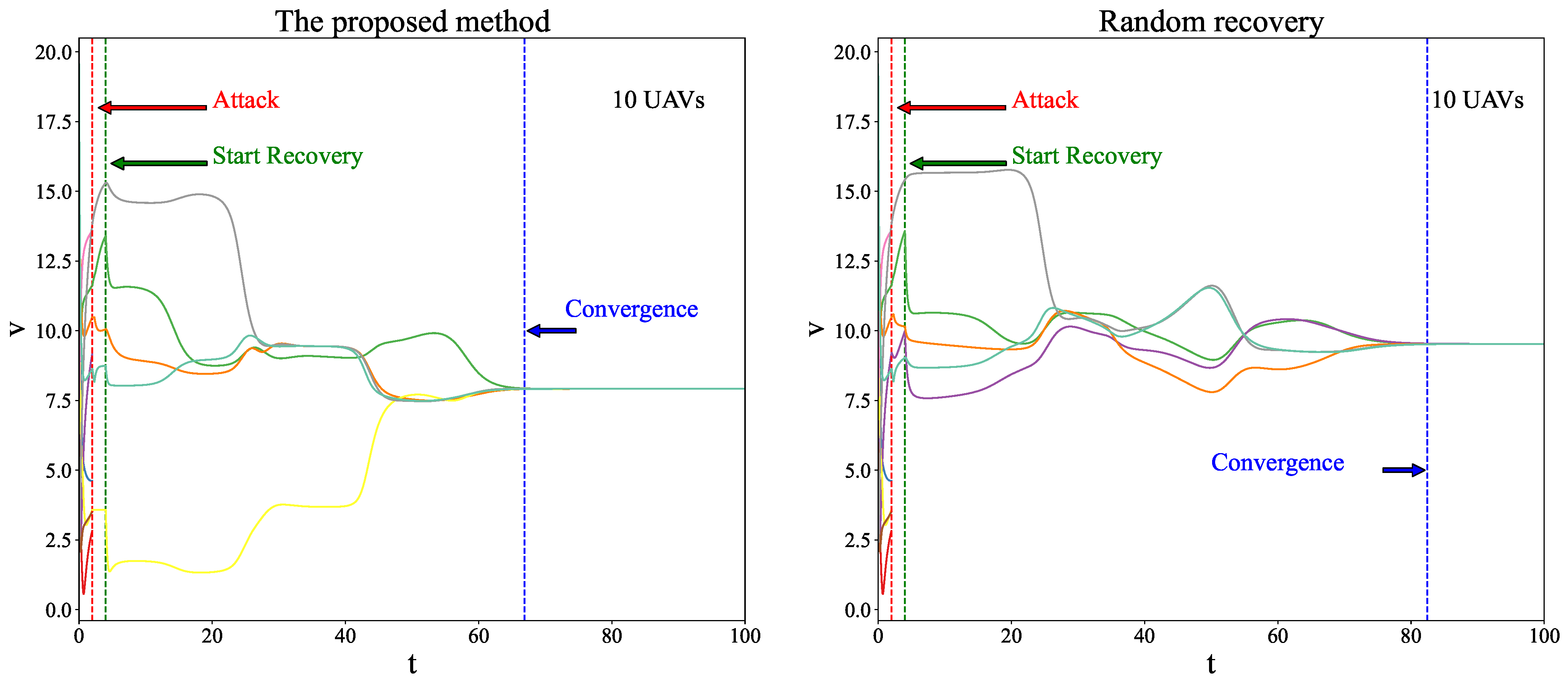
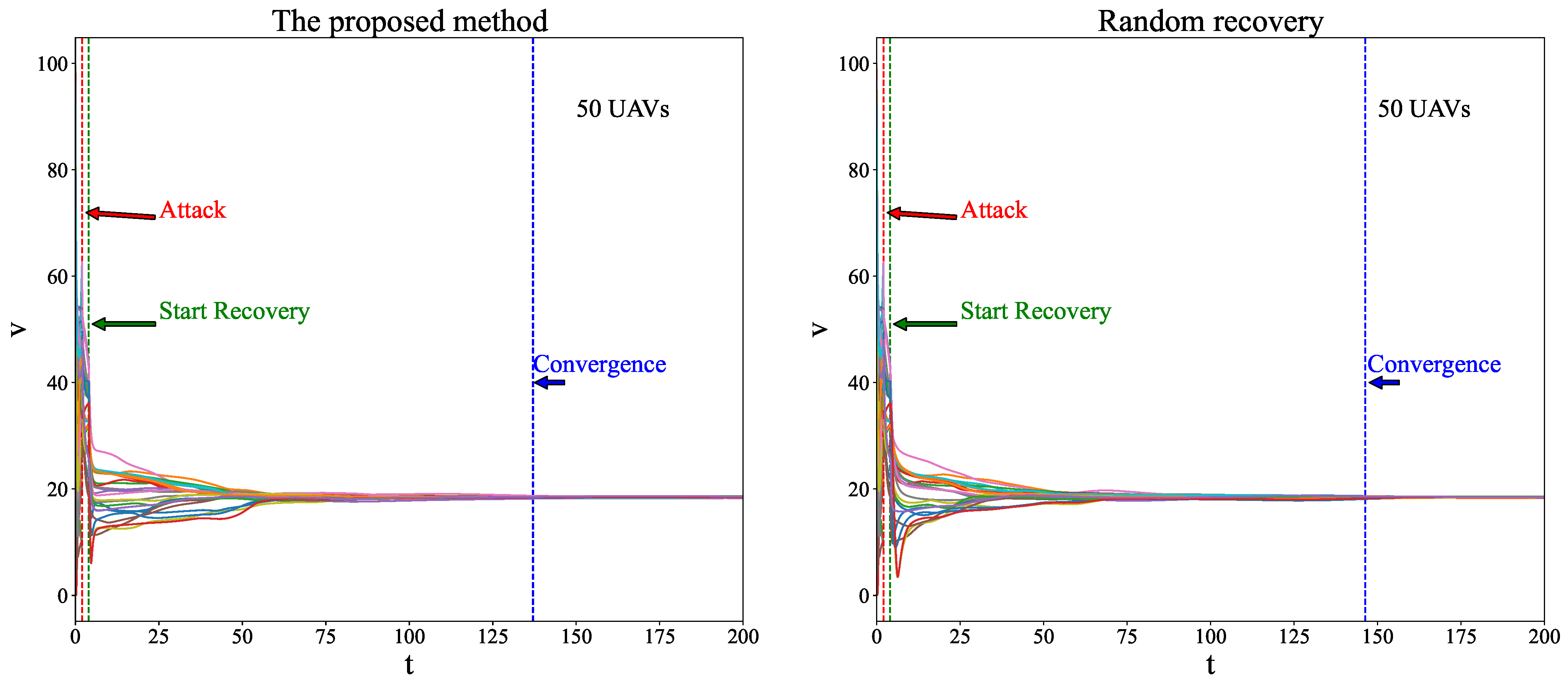
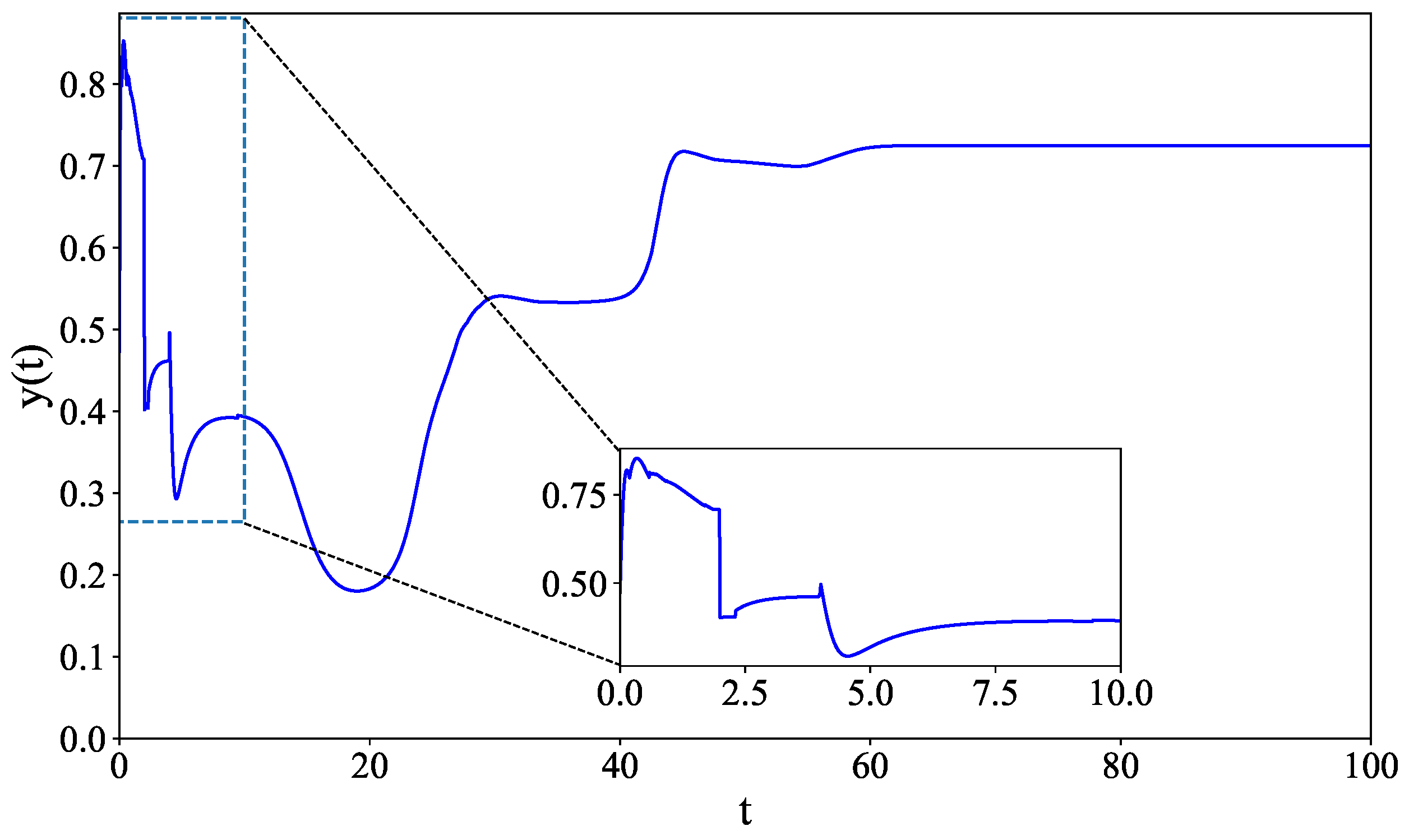
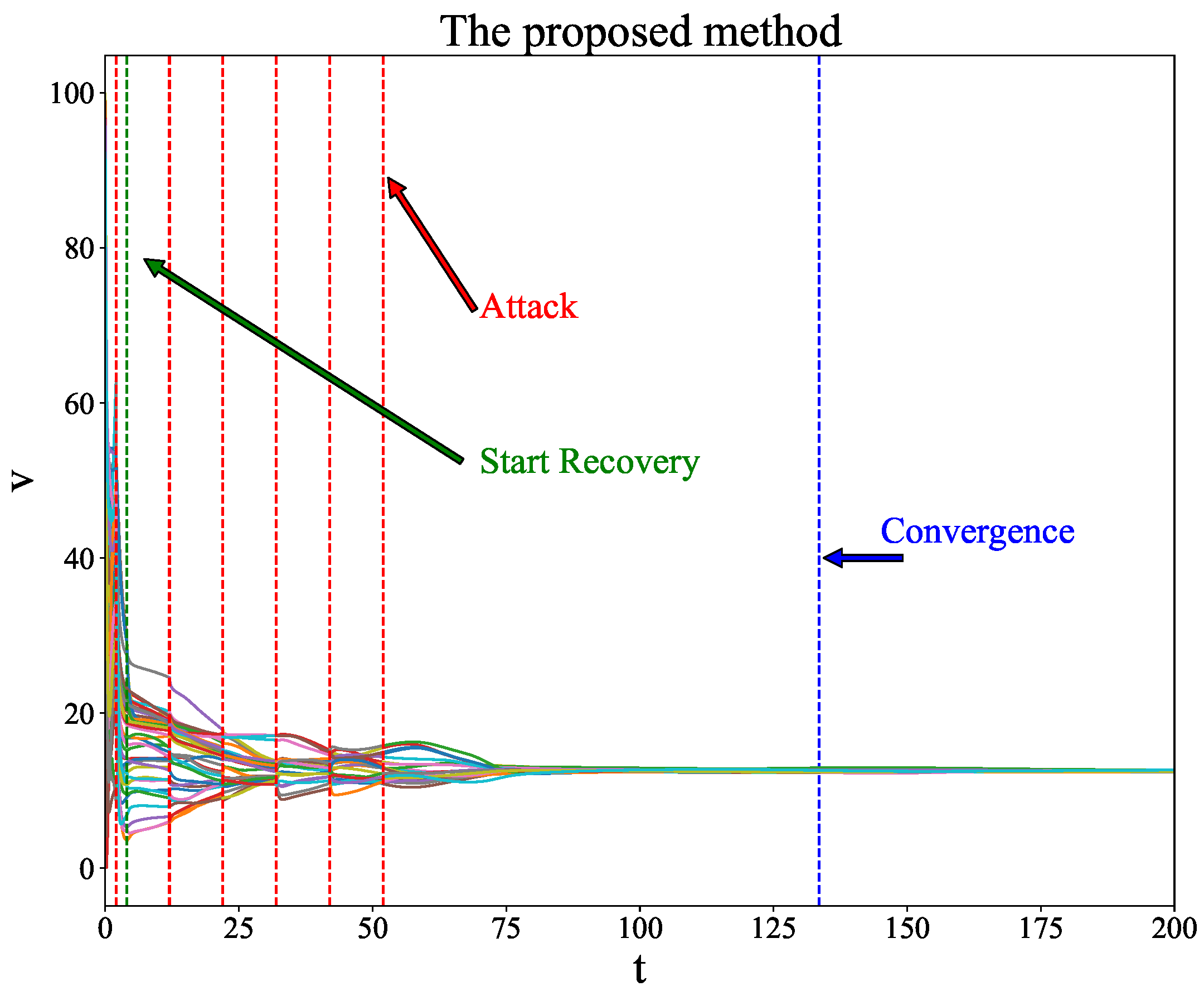
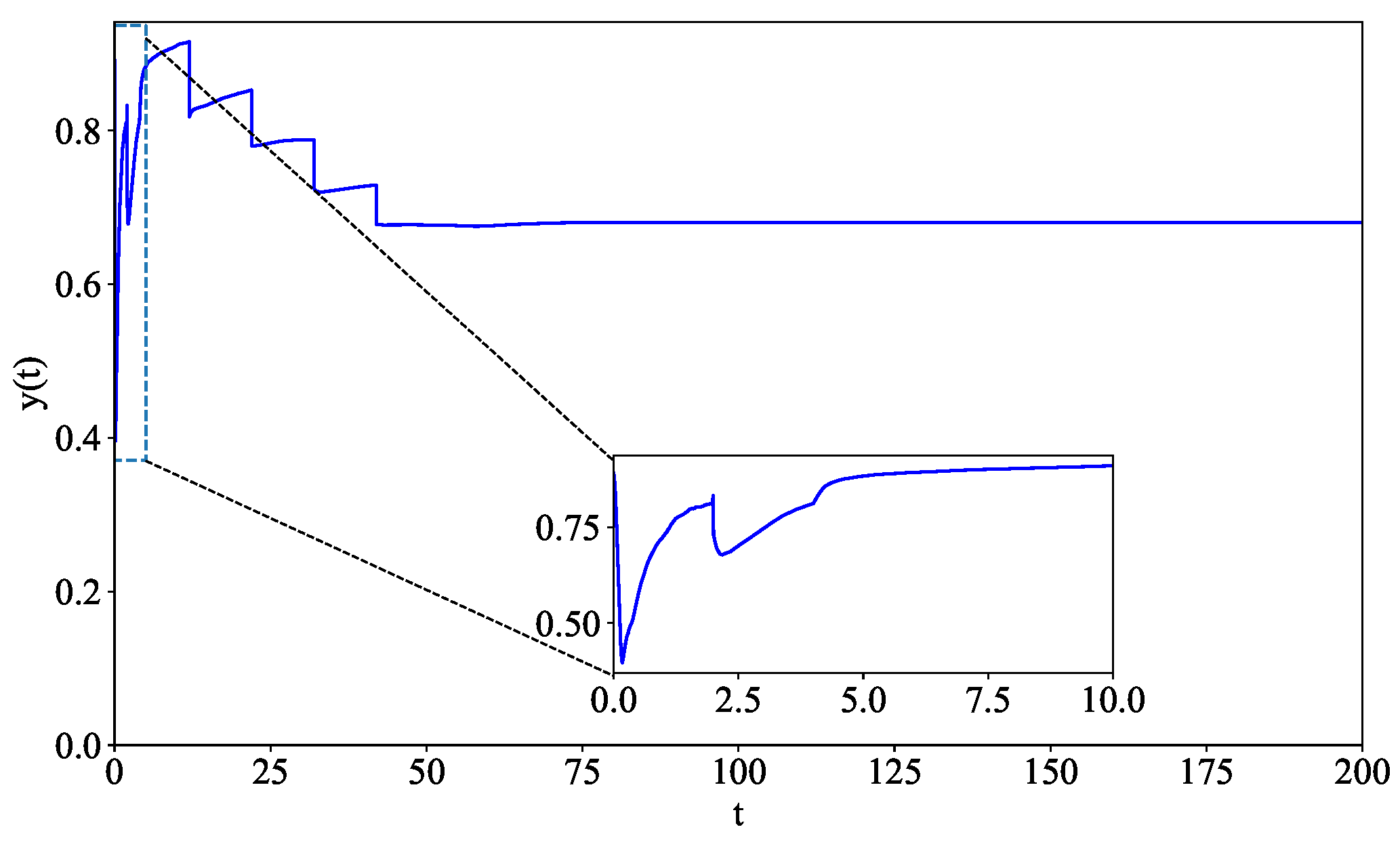
5. Simulation
5.1. Configuration
5.2. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
DURC Statement
Conflicts of Interest
References
- Telikani, A.; Sarkar, A.; Du, B.; Santoso, F.; Shen, J.; Yan, J.; Yong, J.; Yap, E. Unmanned aerial vehicle-aided intelligent transportation systems: Vision, challenges, and opportunities. IEEE Commun. Surv. Tutor. 2025. accepted. [Google Scholar] [CrossRef]
- Joice, A.; Tufaique, T.; Tazeen, H.; Igathinathane, C.; Zhang, Z.; Whippo, C.; Hendrickson, J.; Archer, D. Applications of raspberry pi for precision agriculture—A systematic review. Agriculture 2025, 15, 227. [Google Scholar] [CrossRef]
- Alqefari, S.; Menai, M.E.B. Multi-UAV task assignment in dynamic environments: Current trends and future directions. Drones 2025, 9, 75. [Google Scholar] [CrossRef]
- Rezaee, M.R.; Hamid, N.A.W.A.; Hussin, M.; Zukarnain, Z.A. Comprehensive review of drones collision avoidance schemes: Challenges and open issues. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6397–6426. [Google Scholar] [CrossRef]
- Javed, S.; Hassan, A.; Ahmad, R.; Ahmed, W.; Ahmed, R.; Saadat, A.; Guizani, M. State-of-the-art and future research challenges in UAV swarms. IEEE Internet Things J. 2024, 11, 19023–19045. [Google Scholar] [CrossRef]
- Cao, P.; Lei, L.; Cai, S.S.; Shen, G.; Liu, X.; Wang, X.; Zhang, L.; Zhou, L.; Guizani, M. Computational intelligence algorithms for UAV swarm networking and collaboration: A comprehensive survey and future directions. IEEE Commun. Surv. Tutor. 2024, 26, 2684–2728. [Google Scholar] [CrossRef]
- Wang, X.J.; Zhao, Z.H.; Yi, L.; Ning, Z.; Guo, L.; Yu, F.R.; Guo, S. A Survey on Security of UAV Swarm Networks: Attacks and Countermeasures. ACM Comput. Surv. 2024, 57, 1–37. [Google Scholar] [CrossRef]
- Ye, Z.Y.; Jiang, B.; Yu, Z.Q.; Cheng, Y.H. Adaptive descriptor sliding-mode observer-based dynamic event-triggered consensus of multiagent systems against actuator and sensor faults. IEEE Trans. Cybern. 2025, 55, 672–683. [Google Scholar] [CrossRef]
- Gong, J.Y.; Jiang, B.; Ma, Y.J.; Mao, Z. Distributed adaptive fault-tolerant formation control for heterogeneous multiagent systems with communication link faults. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 784–795. [Google Scholar] [CrossRef]
- Abdelkader, M.; Güler, S.; Jaleel, H. Aerial swarms: Recent applications and challenges. Curr. Robot. Rep. 2021, 2, 309–320. [Google Scholar] [CrossRef]
- Qian, M.S.; Jiang, B.; Liu, H.H.T. Dynamic surface active fault tolerant control design for the attitude control systems of UAV with actuator fault. Int. J. Control Autom. Syst. 2016, 14, 723–732. [Google Scholar] [CrossRef]
- Adam, M.S.; Abdullah, N.F.; Abu-Samah, A.; Amodu, O.A.; Nordin, R. Advanced path planning for UAV swarms in smart city disaster scenarios using hybrid metaheuristic algorithms. Drones 2025, 9, 64. [Google Scholar] [CrossRef]
- Gaydamaka, A.; Samuylov, A.; Moltchanov, D.; Ashraf, M.; Tan, B.; Koucheryavy, Y. Dynamic topology organization and maintenance algorithms for autonomous UAV swarms. IEEE Trans. Mob. Comput. 2024, 23, 4423–4439. [Google Scholar] [CrossRef]
- Manikandan, K.; Sriramulu, R. Optimized path planning strategy to enhance security under swarm of unmanned aerial vehicles. Drones 2022, 6, 336. [Google Scholar] [CrossRef]
- Liang, X.; Liu, L.; He, L.; Shi, Z.; Ren, B. UAV swarm formation reconfiguration based on fixed-time consensus. Syst. Eng. Electron. 2018, 40, 1506–1512. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.W.; Dai, L.; Teo, K.L.; Wang, S. A hybrid offline optimization method for reconfiguration of multi-UAV formations. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 506–520. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Oğuz, S.; Wang, S.P.; Garone, E.; Wang, X.; Dorigo, M.; Heinrich, M.K. Self-reconfigurable hierarchical frameworks for formation control of robot swarms. IEEE Trans. Cybern. 2024, 54, 87–100. [Google Scholar] [CrossRef]
- Shang, B.D.; Shafin, R.; Liu, L. UAV swarm-enabled aerial reconfigurable intelligent surface (SARIS). IEEE Wirel. Commun. 2021, 28, 156–163. [Google Scholar] [CrossRef]
- Tian, J.Y.; Wei, R.X.; Jiang, L.T. Formation construction and reconfiguration control of UAV swarms: A perspective from distributed assignment and optimization. Nonlin. Dynam. 2024, 112, 21171–21191. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, G.; Yang, R.; Feng, Z.; He, W. Resilient Formation Reconfiguration for Leader-Follower Multi-UAVs. Appl. Sci. 2023, 13, 7385. [Google Scholar] [CrossRef]
- Li, H.X.; Sun, Q.; Wang, M.H.; Liu, C.; Xie, Y.; Zhang, Y. A baseline-resilience assessment method for UAV swarms under heterogeneous communication networks. IEEE Syst. J. 2022, 16, 6107–6118. [Google Scholar] [CrossRef]
- Duan, H.; Luo, Q.; Shi, Y.; Ma, G. Hybrid particle swarm optimization and genetic algorithm for multi-UAV formation reconfiguration. IEEE Comput. Intell. Mag. 2013, 8, 16–27. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, F.; Mao, T.; Xiao, Z.; Han, Z.; Xia, X. Reconfiguration for UAV Formation: A Novel Method Based on Modified Artificial Bee Colony Algorithm. Drones 2023, 7, 595. [Google Scholar] [CrossRef]
- Feng, Q.; Hai, X.S.; Sun, B.; Ren, Y.; Wang, Z.; Yang, D.; Feng, Y.H.R. Resilience optimization for multi-UAV formation reconfiguration via enhanced pigeon-inspired optimization. Chin. J. Aeronaut. 2022, 35, 110–123. [Google Scholar] [CrossRef]
- Liu, D.X.; Du, Z.Y.; Liu, X.D.; Luan, H.; Xu, Y.; Xu, Y. Task-based network reconfiguration in distributed UAV swarms: A bilateral matching approach. IEEE/ACM Trans. Netw. 2022, 30, 2688–2700. [Google Scholar] [CrossRef]
- Chen, W.K.; Hai, X.S.; Fan, D.M.; Tan, L.; Zhang, W.; Feng, Q. Resilience-oriented real-time decision-making for autonomous recovery in multi-UAV systems. In Proceedings of the 2024 IEEE 19th Conference on Industrial Electronics and Applications, Kristiansand, Norway, 5–8 August 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Wei, K.; Zhang, T.; Zhang, C. A co-adaptation method for resilience rebound in unmanned aerial vehicle swarms in surveillance missions. Drones 2024, 8, 4. [Google Scholar] [CrossRef]
- Bai, G.H.; Li, Y.J.; Fang, Y.N.; Zhang, Y.A.; Tao, J. Network approach for resilience evaluation of a UAV swarm by considering communication limits. Reliab. Eng. Syst. Safe 2020, 193, 106602. [Google Scholar] [CrossRef]
- Hu, T.Z.; Zong, Y.; Lu, N.Y.; Jiang, B. Toward the resilience of UAV swarms with percolation theory under attacks. Reliab. Eng. Syst. Safe 2025, 254, 110608. [Google Scholar] [CrossRef]
- Markina-Khusid, A.; B Jacobs, R.; Antul, L.; Cho, L.; T Tran, H. A complex network framework for validated assessments of systems of systems robustness. IEEE Syst. J. 2022, 16, 1092–1102. [Google Scholar] [CrossRef]
- Phadke, A.; Antonio Medrano, F.; Chu, T. Engineering resiliency in UAV swarms-A bibliographic analysis. J. Phys. Conf. Ser. 2022, 2330, 012007. [Google Scholar] [CrossRef]
- Li, H.X.; Sun, Q.; Ren, K.Z.; Xie, Y.; Liu, C.; Zhang, Y. Dynamic resilience assessment of UAV swarm for battlefield surveillance mission. In Proceedings of the 2021 IEEE International Conference on Unmanned Systems, Beijing, China, 15–17 October 2021; IEEE: New York, NY, USA, 2021; pp. 472–477. [Google Scholar] [CrossRef]
- Cheng, C.; Bai, G.; Zhang, Y.A.; Tao, J. Resilience evaluation for UAV swarm performing joint reconnaissance mission. Chaos 2019, 29, 053132. [Google Scholar] [CrossRef] [PubMed]
- Phadke, A.; Medrano, F.A.; Starek, M. U-SMART: Unified swarm management and resource tracking framework for unoccupied aerial vehicles. Drone Syst. Appl. 2024, 12, 1–26. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, M.; Sun, B.; Dui, H.; Hai, X.; Ren, Y.; Lu, C.; Wang, Z. Resilience measure and formation reconfiguration optimization for multi-UAV systems. IEEE Internet Things J. 2024, 11, 10616–10626. [Google Scholar] [CrossRef]
- Fiedler, M. Algebraic connectivity of graphs. Czech Math. J. 1973, 23, 298–305. [Google Scholar] [CrossRef]
- Noth, A.; Bouabdallah, S.; Siegwart, R. Dynamic Modeling of Fixed-Wing UAVs; Laboratoty Report; Swiss Federal Institute of Technology: Zurich, Switzerland, 2006. [Google Scholar]
- Sun, D.W.; Kwon, C.; Hwang, I. Hybrid flocking control algorithm for fixed-wing aircraft. J. Guid. Control Dynam. 2019, 42, 2443–2455. [Google Scholar] [CrossRef]
- Jiang, B.; Shen, Q.K.; Shi, P. Neural-networked adaptive tracking control for switched nonlinear pure-feedback systems under arbitrary switching. Automatica 2015, 61, 119–125. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Automat. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Ghosh, A.; Boyd, S. Growing well-connected graphs. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; IEEE: New York, NY, USA, 2006; pp. 6605–6611. [Google Scholar] [CrossRef]
- Vaidya, O.S.; Kumar, S. Analytic hierarchy process: An overview of applications. Eur. J. Oper. Res. 2006, 169, 1–29. [Google Scholar] [CrossRef]
- Anjum, M.N.; Wang, H.; Fang, H. Coverage analysis of random UAV networks using percolation theory. In Proceedings of the 2020 International Conference on Computing, Networking and Communications, Big Island, HI, USA, 17–20 February 2020; pp. 667–673. [Google Scholar] [CrossRef]
- Zhang, P.T.; Wu, T.; Cao, R.H.; Li, Z.; Xu, J. UAV swarm resilience assessment considering load balancing. Front. Phys. 2022, 10, 821321. [Google Scholar] [CrossRef]
- Francis, R.; Bekera, B. A metric and frameworks for resilience analysis of engineered and infrastructure systems. Reliab. Eng. Syst. Safe 2014, 121, 90–103. [Google Scholar] [CrossRef]
| Symbol | Description |
|---|---|
| , , | Swarm before attack, after attack, and at recovery start with added links |
| , , , | Communication links in , links added to at recovery start, links in , and all possible links in a complete graph of excluding existing links |
| N, | Number of UAVs in the swarm before and after attack |
| Algebraic connectivity of swarm | |
| A, | Adjacency matrix of swarm with element indicating edge between i and j |
| B, | Incidence matrix of UAV swarm with l-th edge vector column |
| k | UAV degree |
| UAV cluster | |
| Set of isolated UAVs, special case of UAV cluster | |
| Position of UAV i in 3D space | |
| Velocity of UAV i | |
| Pitch, yaw and roll angles of UAV i | |
| , , | The thrust, drag force and lift of UAV i |
| , , | Virtual input of UAV i: current, before recovery, and when recovery start |
| A binary value represents the signal of recovery | |
| t | Time variable |
| The number of neighbours of UAV i | |
| A smooth pairwise potential function | |
| The vector along the communication link | |
| A bump function. | |
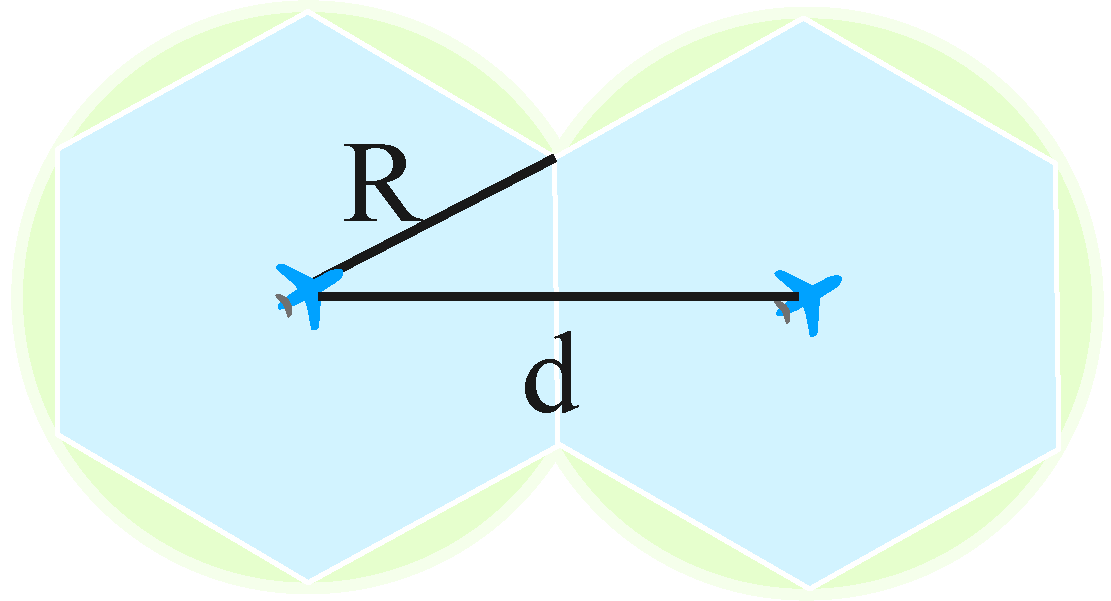
| R | Communication range of the UAVs |
| F, | Normalized Fiedler eigenvector according to , is the ith element of F |
| The number of UAVs in the UAV cluster |
| Symbol | Description |
|---|---|
| , , , | Variant of acceleration, interaction between UAVs, completion of missions, energy management |
| The performance of UAV swarms | |
| The new stable performance after recovery | |
| The percentage of its initial performance before attack. It emphasizes mission success by ensuring the swarm maintains a sufficient level of required functionality | |
| Attack time | |
| The time complete recovery | |
| The time to the new consensus state | |
| The time to the end of the simulation | |
| The proposed resilience metric | |
| E | The ratio of buffer time and time to consensus after recovery |
| A decreasing function that measures the increase in the time it takes to reach the new consensus state | |
| The ratio of the performance of the UAV swarm after reaching the new consensus to | |
| Buffer time: the time after attack time but before recovery time . It allows the UAV swarm to absorb the impact of the attack and prepare for recovery. | |
| The transition time measured as the time interval from the end of the recovery action to the point where the states of all remaining UAVs converge within a predifined threshold |
| Indexes | ||||
|---|---|---|---|---|
| 1 | 3 | 4 | 7 | |
| 0.333 | 1 | 2 | 6 | |
| 0.25 | 0.5 | 1 | 4 | |
| 0.143 | 0.167 | 0.25 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, T.; Zong, Y.; Lu, N.; Jiang, B. Dynamic Recovery and a Resilience Metric for UAV Swarms Under Attack. Drones 2025, 9, 589. https://doi.org/10.3390/drones9080589
Hu T, Zong Y, Lu N, Jiang B. Dynamic Recovery and a Resilience Metric for UAV Swarms Under Attack. Drones. 2025; 9(8):589. https://doi.org/10.3390/drones9080589
Chicago/Turabian StyleHu, Tianzhen, Yan Zong, Ningyun Lu, and Bin Jiang. 2025. "Dynamic Recovery and a Resilience Metric for UAV Swarms Under Attack" Drones 9, no. 8: 589. https://doi.org/10.3390/drones9080589
APA StyleHu, T., Zong, Y., Lu, N., & Jiang, B. (2025). Dynamic Recovery and a Resilience Metric for UAV Swarms Under Attack. Drones, 9(8), 589. https://doi.org/10.3390/drones9080589









