Layout and Rotation Effect on Aerodynamic Performance of Multi-Rotor Ducted Propellers
Abstract
Highlights
- Rotational consistency (co-rotation vs. counter-rotation) is the dominant factor affecting aerodynamic performance, with co-rotation significantly enhancing thrust and efficiency.
- The duct mitigates inter-propeller aerodynamic interference, altering the amplitude and phase of the sinusoidal performance shifts caused by the rotational phase gap.
- Optimizing rotational consistency, particularly using co-rotation, is a critical strategy that plays a crucial role in maximizing the performance of multi-rotor ducted propeller systems.
- This research offers a validated analytical method (ART-ANOVA) and reveals core flow mechanisms, providing a framework to guide the design and optimization of advanced low-altitude aircraft propulsion systems.
Abstract
1. Introduction
2. Research Model and Numerical Methods
2.1. Model Setup
2.2. Numerical Methods
2.3. Mesh Setup
2.4. Aerodynamic Characteristics
3. Results and Discussion
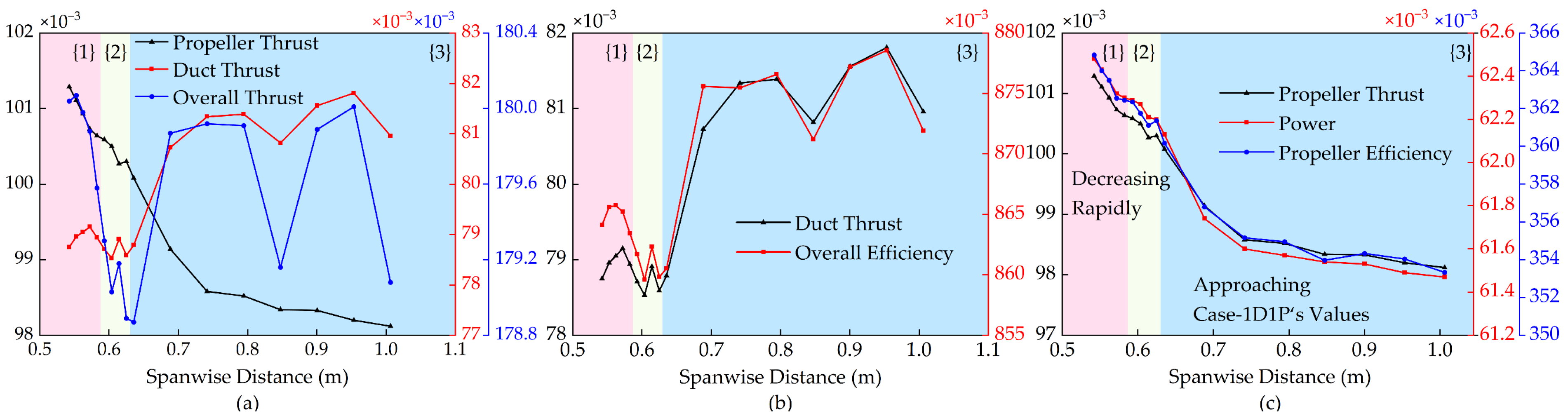
3.1. Influence of Spanwise Layout Parameter on Hovering Aerodynamic Performance
3.2. Influence of Streamwise Layout Parameter on Hovering Aerodynamic Performance
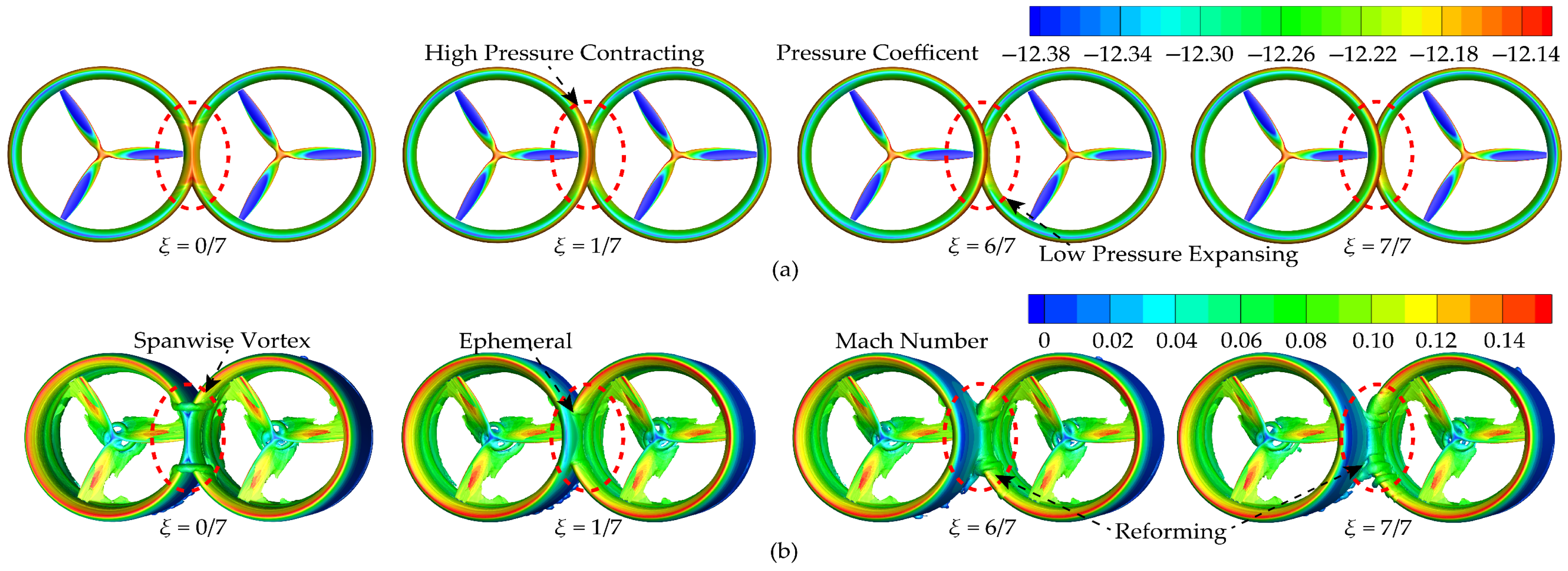
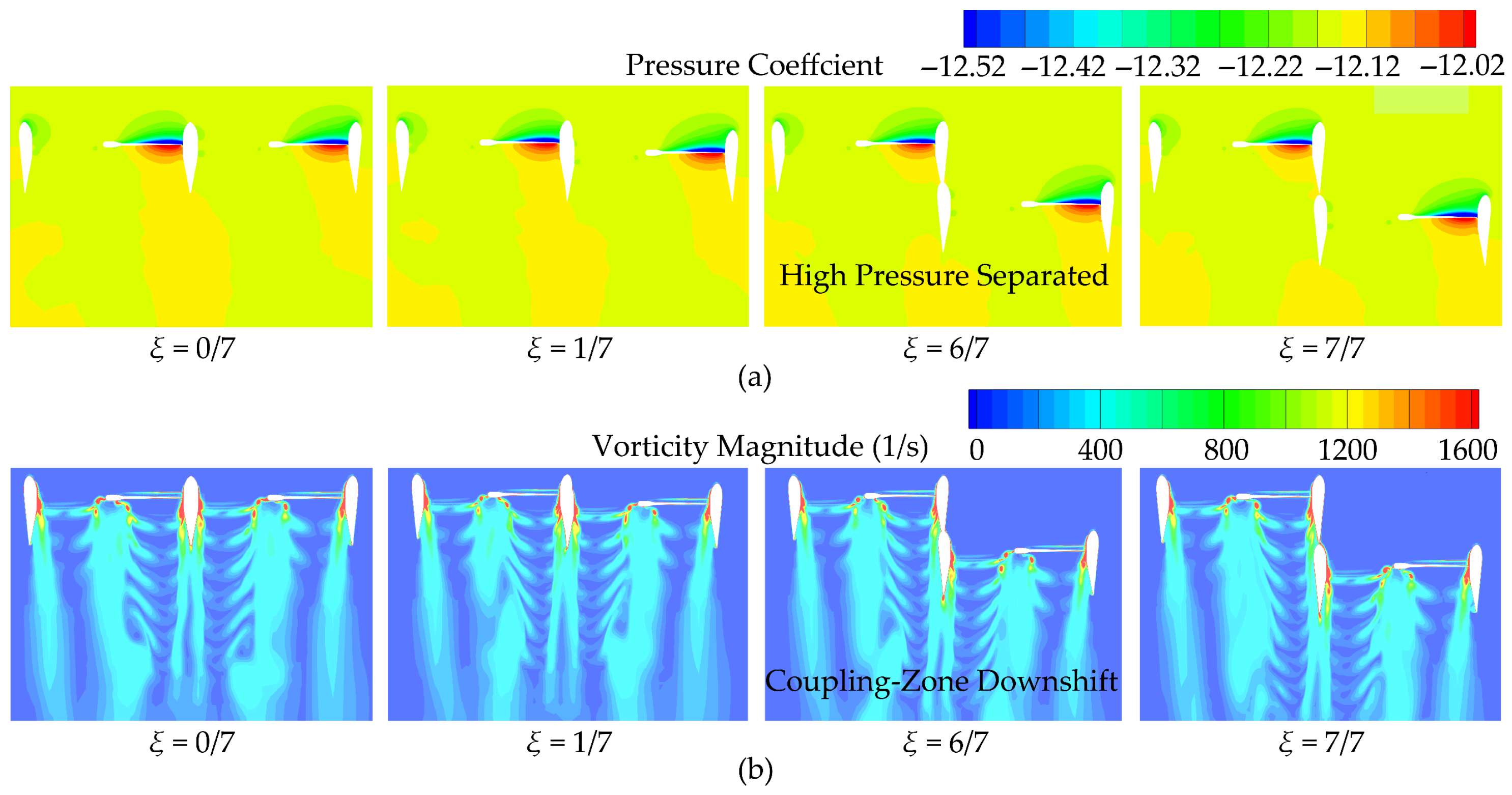
3.3. Influence Patterns and Flow Mechanisms of Rotational Characteristics on Hovering Aerodynamic Performance
3.4. Main and Interaction Effects of Rotational Characteristics on Component Performance
- Quantification of effect dominance, which precisely determines the relative influence of rotational consistency and phase gap on various aerodynamic metrics;
- Exposure of interaction effects, which reveals the significant synergistic or antagonistic relationship between phase gap and rotational consistency that is difficult to isolate through direct flow field inspection.
- Data alignment to eliminate interference from main effects and retain interaction information;
- Rank transformation converting original data to ranks to suit non-parametric testing;
- Variance decomposition solving for partial and pseudo to assess the main effect of the rotational phase gap, the main effect of rotational consistency, and the interaction effect of the rotational phase gap × rotational consistency;
- Significance tests to evaluate the strength of effects through F-values and p-values.
4. Conclusions
- As the layout spacing increases, the aerodynamic interference between the two ducted propellers weakens. The various aerodynamic coefficients of the propellers monotonically decrease. The decreasing trend of propeller aerodynamic performance with increasing spanwise spacing conforms to a Boltzmann distribution, while the decrease with increasing streamwise distance exhibits significant non-linear characteristics. The thrust coefficient of the duct generally shows a plateau characteristic, rapidly increasing within specific intervals and fluctuating within a small range in other intervals;
- The core mechanism by which aerodynamic interference affects the performance of multi-rotor ducted propellers is that the lateral momentum transport generated by aerodynamic interference reduces the streamwise velocity. This alters the pressure through Bernoulli’s principle, affecting the distribution range of high-pressure regions. With changes in spanwise and streamwise layout parameters, aerodynamic interference produces varying trends of enhancement or reduction at the duct leading edge, the intersecting side trailing edge, and below the propellers, leading to corresponding changes in aerodynamic performance;
- The duct weakens the mutual interference between propeller blades on the intersecting side and alters the amplitude and phase of the propeller aerodynamic performance variation with the rotational phase gap. The aerodynamic performance of the propellers exhibits significant sinusoidal periodic fluctuation characteristics, which are particularly evident in co-rotating configurations. Rotational characteristics do not influence the leading-edge flow field but substantially impact the trailing-edge flow field. During co-rotation, the tip vortices on the intersecting side trailing edge couple asymmetrically, forming periodic oscillation characteristics, whereas during counter-rotation, the vortices couple symmetrically, forming a stable flow field;
- ART-ANOVA analysis shows that rotational consistency (co-rotation vs. counter-rotation) has a decisive main effect on all aerodynamic performances; co-rotating conditions can significantly improve thrust and efficiency. In contrast, the main effect of the rotational phase gap and the interaction effect of phase gap × consistency only significantly impact propeller aerodynamic performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ART-ANOVA | Aligned rank transform analysis of variance |
| DNS | Direct numerical simulation |
| eVTOL | Electric vertical take-off and landing |
| FoM | The figure of merit |
| FVM | Finite volume method |
| LES | Large eddy simulation |
| MRF | Multiple reference frame |
| SMM | Sliding mesh model |
| SST | Shear-stress transport |
| URANS | Unsteady reynolds-averaged Navier–Stokes |
References
- Zhang, T.; Barakos, G.N. Review on Ducted Fans for Compound Rotorcraft. Aeronaut. J. 2020, 124, 941–974. [Google Scholar] [CrossRef]
- Wang, R.; Ma, Z.; Huang, X. Experimental Investigation of Ducted Fan Noise Control by Turbulence Grids Insertion between Propellers and Struts. Phys. Fluids 2024, 36, 085109. [Google Scholar] [CrossRef]
- Qian, Y.; Luo, Y.; Hu, X.; Zeng, Z.; Zhang, Y. Improving the Performance of Ducted Fans for VTOL Applications: A Review. Sci. China Technol. Sci. 2022, 65, 2521–2541. [Google Scholar] [CrossRef]
- Luo, Y.; He, Y.; Xu, B.; Ai, T.; Qian, Y.; Zhang, Y. Numerical Simulation and Analysis of a Ducted-Fan Drone Hovering in Confined Environments. Adv. Aerodyn. 2024, 6, 18. [Google Scholar] [CrossRef]
- Chang, S.; Cho, A.; Choi, S.; Kang, Y.; Kim, Y.; Kim, M. Flight Testing Full Conversion of a 40-Kg-Class Tilt-Duct Unmanned Aerial Vehicle. Aerosp. Sci. Technol. 2021, 112, 106611. [Google Scholar] [CrossRef]
- Berra, A.; Trujillo Soto, M.Á.; Heredia, G. Aerodynamic Interaction Minimization in Coaxial Multirotors via Optimized Control Allocation. Drones 2024, 8, 446. [Google Scholar] [CrossRef]
- Li, Y.; Yonezawa, K.; Liu, H. Effect of Ducted Multi-Propeller Configuration on Aerodynamic Performance in Quadrotor Drone. Drones 2021, 5, 101. [Google Scholar] [CrossRef]
- Gohardani, A.S. A Synergistic Glance at the Prospects of Distributed Propulsion Technology and the Electric Aircraft Concept for Future Unmanned Air Vehicles and Commercial/Military Aviation. Prog. Aerosp. Sci. 2013, 57, 25–70. [Google Scholar] [CrossRef]
- Gohardani, A.S.; Doulgeris, G.; Singh, R. Challenges of Future Aircraft Propulsion: A Review of Distributed Propulsion Technology and Its Potential Application for the All Electric Commercial Aircraft. Prog. Aerosp. Sci. 2011, 47, 369–391. [Google Scholar] [CrossRef]
- Leifsson, L.; Ko, A.; Mason, W.H.; Schetz, J.A.; Grossman, B.; Haftka, R.T. Multidisciplinary Design Optimization of Blended-Wing-Body Transport Aircraft with Distributed Propulsion. Aerosp. Sci. Technol. 2013, 25, 16–28. [Google Scholar] [CrossRef]
- Qiao, G.; Zhang, T.; Barakos, G.N. Numerical Simulation of Distributed Propulsion Systems Using CFD. Aerosp. Sci. Technol. 2024, 147, 109011. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, Z.; Zhu, X.; Xu, X. Aerodynamic Design of Multi-Propeller/Wing Integration at Low Reynolds Numbers. Aerosp. Sci. Technol. 2019, 84, 1–17. [Google Scholar] [CrossRef]
- Xue, C.; Zhou, Z. Propeller-Wing Coupled Aerodynamic Design Based on Desired Propeller Slipstream. Aerosp. Sci. Technol. 2020, 97, 105556. [Google Scholar] [CrossRef]
- Lee, H.J.; Lee, D.J. Rotor Interactional Effects on Aerodynamic and Noise Characteristics of a Small Multirotor Unmanned Aerial Vehicle. Phys. Fluids 2020, 32, 047107. [Google Scholar] [CrossRef]
- Schiltgen, B.T.; Freeman, J. Aeropropulsive Interaction and Thermal System Integration within the ECO-150: A Turboelectric Distributed Propulsion Airliner with Conventional Electric Machines. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016; American Institute of Aeronautics and Astronautics: Las Vegas, NV, USA, 2016. [Google Scholar]
- Kim, H.D.; Perry, A.T.; Ansell, P.J. A Review of Distributed Electric Propulsion Concepts for Air Vehicle Technology. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium, Cincinnati, OH, USA, 9 July 2018; American Institute of Aeronautics and Astronautics: Las Vegas, NV, USA, 2018. [Google Scholar]
- Bernardini, G.; Centracchio, F.; Gennaretti, M.; Iemma, U.; Pasquali, C.; Poggi, C.; Rossetti, M.; Serafini, J. Numerical Characterisation of the Aeroacoustic Signature of Propeller Arrays for Distributed Electric Propulsion. Appl. Sci. 2020, 10, 2643. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, W.; Zhang, Y.; Li, K.; Wang, Y. Effects of Distributed Propulsion Crucial Variables on Aerodynamic and Propulsive Performance of Small UAV. In Proceedings of the 2018 Asia-Pacific International Symposium on Aerospace Technology (APISAT 2018), Chengdu, China, 16–18 October 2018; pp. 1535–1550. [Google Scholar]
- Kim, H.D. Distributed Propulsion Vehicles. In Proceedings of the 27th International Congress of the Aeronautical Sciences, Nice, France, 19–24 September 2010. [Google Scholar]
- Zhou, F.; Wang, Y.; Wang, S.; Qin, Y.; Zhang, B. Aero-Propulsion Coupling Effects and Installation Characteristics of a Distributed Propulsion System. Aerosp. Sci. Technol. 2024, 153, 109450. [Google Scholar] [CrossRef]
- Ma, T.L.; Wang, X.S.; Qiao, N.X.; Zhang, Z.L.; Fu, J.C.; Bao, M.M. A Conceptual Design and Optimization Approach for Distributed Electric Propulsion eVTOL Aircraft Based on Ducted-Fan Wing Unit. Aerospace 2022, 9, 690. [Google Scholar] [CrossRef]
- Guo, J.H.; Zhou, Z. Multi-Objective Design of a Distributed Ducted Fan System. Aerospace 2022, 9, 165. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Zhang, W.; Li, W.; Zhang, X.; Lei, T. Experimental Research on Aero-Propulsion Coupling Characteristics of a Distributed Electric Propulsion Aircraft. Chin. J. Aeronaut. 2023, 36, 201–212. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Reynolds, K.; Ting, E.; Nguyen, N. Distributed Propulsion Aircraft with Aeroelastic Wing Shaping Control for Improved Aerodynamic Efficiency. J. Aircr. 2018, 55, 1122–1140. [Google Scholar] [CrossRef]
- Perry, A.T.; Ansell, P.J.; Kerho, M.F. Aero-Propulsive and Propulsor Cross-Coupling Effects on a Distributed Propulsion System. J. Aircr. 2018, 55, 2414–2426. [Google Scholar] [CrossRef]
- De Vries, R.; Van Arnhem, N.; Sinnige, T.; Vos, R.; Veldhuis, L.L.M. Aerodynamic Interaction between Propellers of a Distributed-Propulsion System in Forward Flight. Aerosp. Sci. Technol. 2021, 118, 107009. [Google Scholar] [CrossRef]
- Stokkermans, T.C.A.; Usai, D.; Sinnige, T.; Veldhuis, L.L.M. Aerodynamic Interaction Effects between Propellers in Typical eVTOL Vehicle Configurations. J. Aircr. 2021, 58, 815–833. [Google Scholar] [CrossRef]
- Alvarez, E.J.; Ning, A. High-Fidelity Modeling of Multirotor Aerodynamic Interactions for Aircraft Design. AIAA J. 2020, 58, 4385–4400. [Google Scholar] [CrossRef]
- Li, Z.Y.; Wu, J.H.; Pei, B.R.; Chen, L.; Zou, Z.P.; Lin, H.Y. Numerical Investigation on Aerodynamic Characteristics of Equivalent Distributed Ducted Propellers. Chin. J. Aeronaut. 2025, 38, 103487. [Google Scholar] [CrossRef]
- O’Neill, S. Electric Air Taxis Create Megadeal Buzz. Engineering 2022, 13, 5–8. [Google Scholar] [CrossRef]
- Yilmaz, S.; Erdem, D.; Kavsaoglu, M.S. Performance of a Ducted Propeller Designed for UAV Applications at Zero Angle of Attack Flight: An Experimental Study. Aerosp. Sci. Technol. 2015, 45, 376–386. [Google Scholar] [CrossRef]
- Luo, Y.; Qian, Y.; Zeng, Z.; Zhang, Y. Simulation and Analysis of Operating Characteristics of Power Battery for Flying Car Utilization. eTransportation 2021, 8, 100111. [Google Scholar] [CrossRef]
- Higgins, J.J.; Blair, R.C.; Tashtoush, S. The Aligned Rank Transform Procedure. In Proceedings of the 1990-2nd Annual Conference Proceedings, Manhattan, KS, USA, 26 April 1990. [Google Scholar] [CrossRef]
- Salter, K.C.; Fawcett, R.F. The Art Test of Interaction: A Robust and Powerful Rank Test of Interaction in Factorial Models. Commun. Stat.-Simul. Comput. 1993, 22, 137–153. [Google Scholar] [CrossRef]
- Mansouri, H. Multifactor Analysis of Variance Based on the Aligned Rank Transform Technique. Comput. Stat. Data Anal. 1998, 29, 177–189. [Google Scholar] [CrossRef]
- Wobbrock, J.O.; Findlater, L.; Gergle, D.; Higgins, J.J. The Aligned Rank Transform for Nonparametric Factorial Analyses Using Only Anova Procedures. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Vancouver, BC, Canada, 7 May 2011; Association for Computing Machinery: New York, NY, USA, 2011; pp. 143–146. [Google Scholar]
- Sawilowsky, S.S. Nonparametric Tests of Interaction in Experimental Design. Rev. Educ. Res. 1990, 60, 91–126. [Google Scholar] [CrossRef]
- Conover, W.J.; Iman, R.L. Rank Transformations as a Bridge between Parametric and Nonparametric Statistics. Am. Stat. 1981, 35, 124–129. [Google Scholar] [CrossRef]

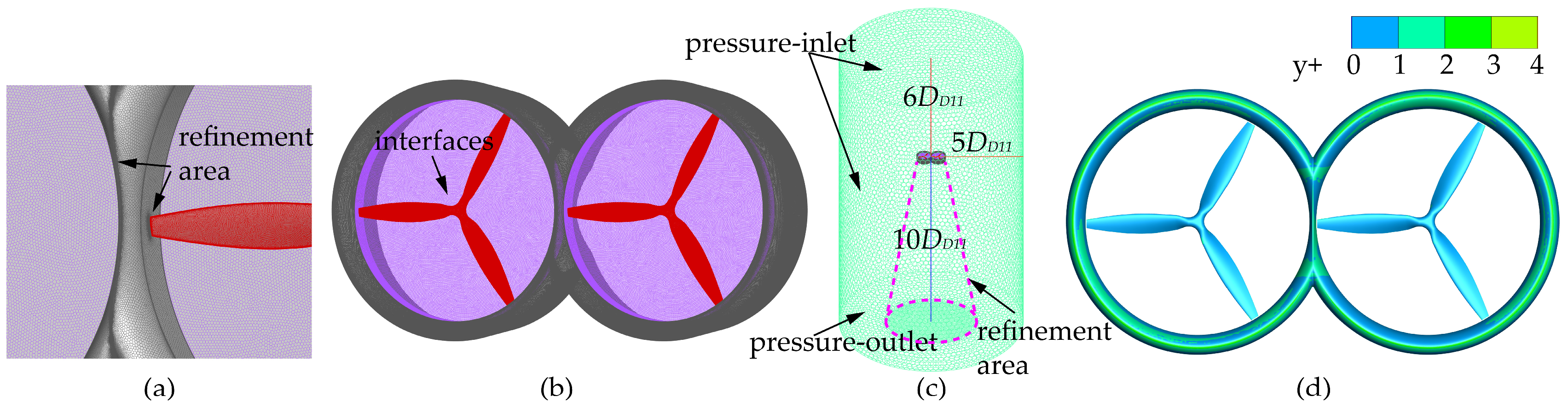







| Parameter | Range | Step |
|---|---|---|
| γ(Case-1D2P) | 1.02~1.2 | 0.02 |
| γ(Case-2D2P) | 1.2~2 | 0.1 |
| ξ | 0~1 | 1/7 |
| Consistency | CW-CCW and CW-CW | / |
| Phase Gap | 0°~120° | 15° |
| Configuration | Number of Cells | Min. Cell Size (Propeller) | Min. Cell Size (Duct) | Wake Refinement Size |
|---|---|---|---|---|
| Case-1D2P | 25.3 million | 0.00015 m | 0.0014 m | 0.012 m~0.048 m |
| Case-2D2P | 19.3 million | 0.00015 m | 0.0014 m | 0.012 m~0.048 m |
| γ | D/m | n/rpm | Tip Ma |
|---|---|---|---|
| 1.02 | 0.5318 | 5588.79 | 0.4573 |
| 1.04 | 0.5313 | 5594.04 | 0.4573 |
| 1.06 | 0.5304 | 5603.04 | 0.4573 |
| 1.08 | 0.5298 | 5609.55 | 0.4573 |
| ≥1.10 | 0.5296 | 5611.54 | 0.4573 |
| Parameters | Effect Term | df | F-Value | Significance | Partial | Pseudo |
|---|---|---|---|---|---|---|
| Total Thrust Coefficient | Phase Gap | 3 | 234.46 | <0.001 | 0.26 | 0.873 |
| Consistency | 1 | 2960.53 | <0.001 | 0.60 | ||
| Phase Gap. × Consist. | 3 | 94.89 | <0.001 | 0.13 | ||
| Propeller Thrust Coefficient | Phase Gap | 3 | 1217.9 | <0.001 | 0.65 | 0.672 |
| Consistency | 1 | 5687.6 | <0.001 | 0.74 | ||
| Phase Gap. × Consist. | 3 | 1408.0 | <0.001 | 0.68 | ||
| Duct Thrust Coefficient | Phase Gap | 3 | 512.15 | <0.001 | 0.44 | 0.694 |
| Consistency | 1 | 5814.59 | <0.001 | 0.74 | ||
| Phase Gap. × Consist. | 3 | 862.76 | <0.001 | 0.57 | ||
| Total Power Coefficient | Phase Gap | 3 | 1082.9 | <0.001 | 0.62 | 0.695 |
| Consistency | 1 | 5991.6 | <0.001 | 0.75 | ||
| Phase Gap. × Consist. | 3 | 1001.0 | <0.001 | 0.58 | ||
| Propeller Efficiency | Phase Gap | 3 | 936.3 | <0.001 | 0.59 | 0.650 |
| Consistency | 1 | 5988.2 | <0.001 | 0.75 | ||
| Phase Gap. × Consist. | 3 | 1690.6 | <0.001 | 0.72 | ||
| Total Efficiency | Phase Gap | 3 | 327.13 | <0.001 | 0.33 | 0.759 |
| Consistency | 1 | 6008.58 | <0.001 | 0.75 | ||
| Phase Gap. × Consist. | 3 | 347.41 | <0.001 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wu, J.; Zhang, P.; Wang, L.; Chen, L.; Zou, Z.; Lin, H. Layout and Rotation Effect on Aerodynamic Performance of Multi-Rotor Ducted Propellers. Drones 2025, 9, 561. https://doi.org/10.3390/drones9080561
Li Z, Wu J, Zhang P, Wang L, Chen L, Zou Z, Lin H. Layout and Rotation Effect on Aerodynamic Performance of Multi-Rotor Ducted Propellers. Drones. 2025; 9(8):561. https://doi.org/10.3390/drones9080561
Chicago/Turabian StyleLi, Zeyu, Jianghao Wu, Pengyu Zhang, Lin Wang, Long Chen, Zhengping Zou, and Haiying Lin. 2025. "Layout and Rotation Effect on Aerodynamic Performance of Multi-Rotor Ducted Propellers" Drones 9, no. 8: 561. https://doi.org/10.3390/drones9080561
APA StyleLi, Z., Wu, J., Zhang, P., Wang, L., Chen, L., Zou, Z., & Lin, H. (2025). Layout and Rotation Effect on Aerodynamic Performance of Multi-Rotor Ducted Propellers. Drones, 9(8), 561. https://doi.org/10.3390/drones9080561








