Finite-Time Adaptive Reinforcement Learning Control for a Class of Morphing Unmanned Aircraft with Mismatched Disturbances and Coupled Uncertainties
Abstract
Highlights
- A novel RL-based adaptive finite-time control scheme for morphing unmanned aircraft is synthesized. It can address mismatched disturbances, coupled uncertainties, and non-affine characteristics, enabling the aircraft’s attitude to converge to the desired value within a finite time.
- The attitude dynamics of the morphing unmanned aircraft are described as a class of mismatched non-affine systems, which are more suitable for practical scenarios and simplify the analysis process compared to previous models.
- Applying reinforcement learning to morphing unmanned aircraft enhances its ability to handle uncertainties, and finite-time reinforcement learning helps limit the control convergence time, thus improving the trajectory-tracking control performance.
- The proposed scheme for RL-based robust adaptive flight control offers a method that can be extended to various aircraft control research fields.
Abstract
1. Introduction
- The attitude dynamics of the morphing unmanned aircraft are described as a class of mismatched non-affine systems, including matched and mismatched disturbances, non-affine input, and internal uncertainties. Compared to previous models [14,48,49], the proposed model is more applicable to practical scenarios and simplifies the analysis process.
- Compared with the literature [13], our work focuses on finite-time control, mismatched disturbances, and coupled uncertainties, while the literature [13] addresses non-affine control systems and control input frequency constraints. Different from the literature [27] on highly flexible aircraft, our method targets morphing unmanned aircraft, devises adaptive finite-time controllers, and ensures finite-time attitude convergence with better performance.
- This paper proposes a design framework for RL-based adaptive anti-disturbance flight control, offering a paradigm that can be extended to various aircraft.
2. Problem Formulation and Preliminaries
2.1. Dynamic Model Description
2.2. Designs of Actor–Critic Neural Networks
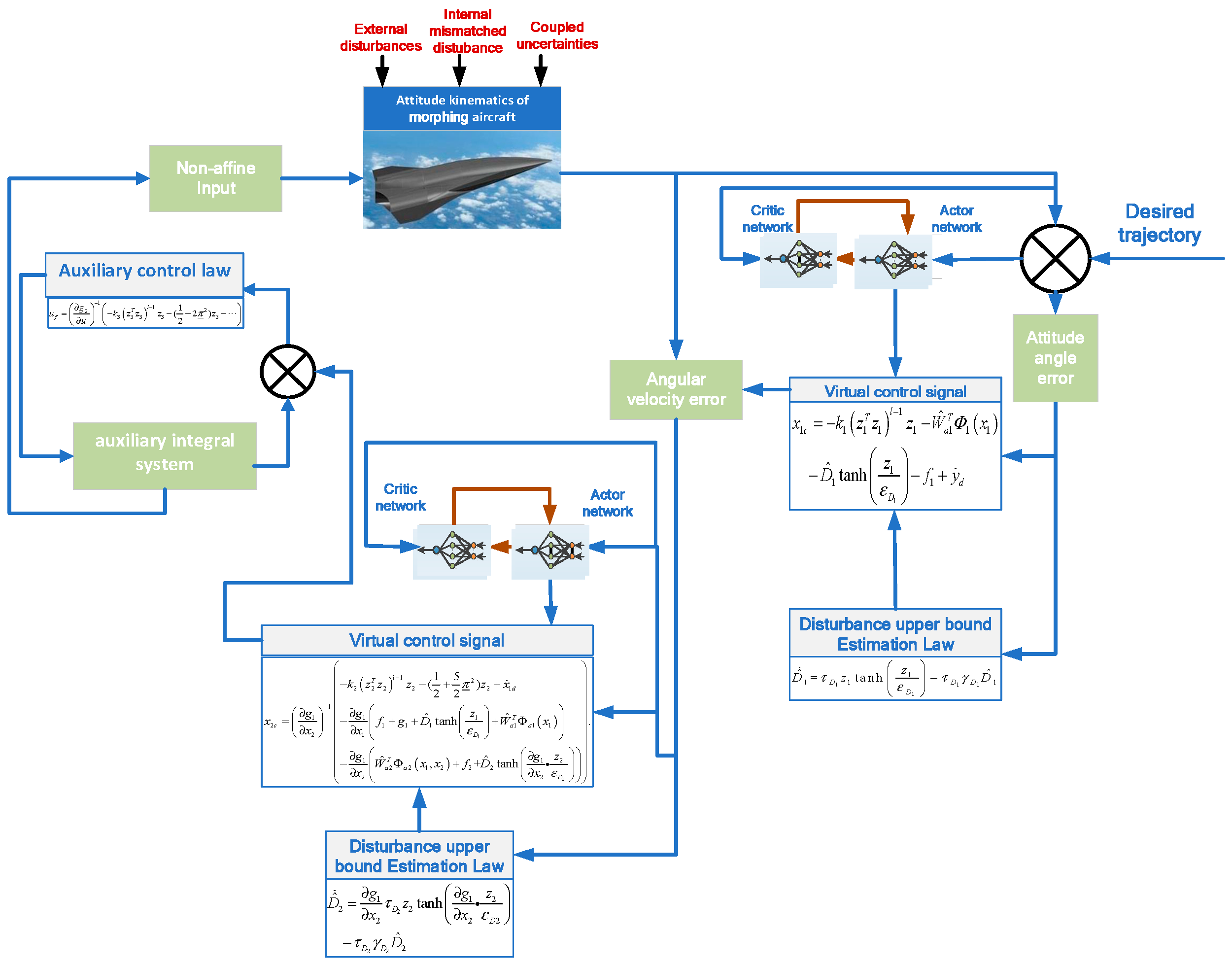
3. Main Results
3.1. The Design of the Augmented System
3.2. Controller Design
3.3. Proof of Stability
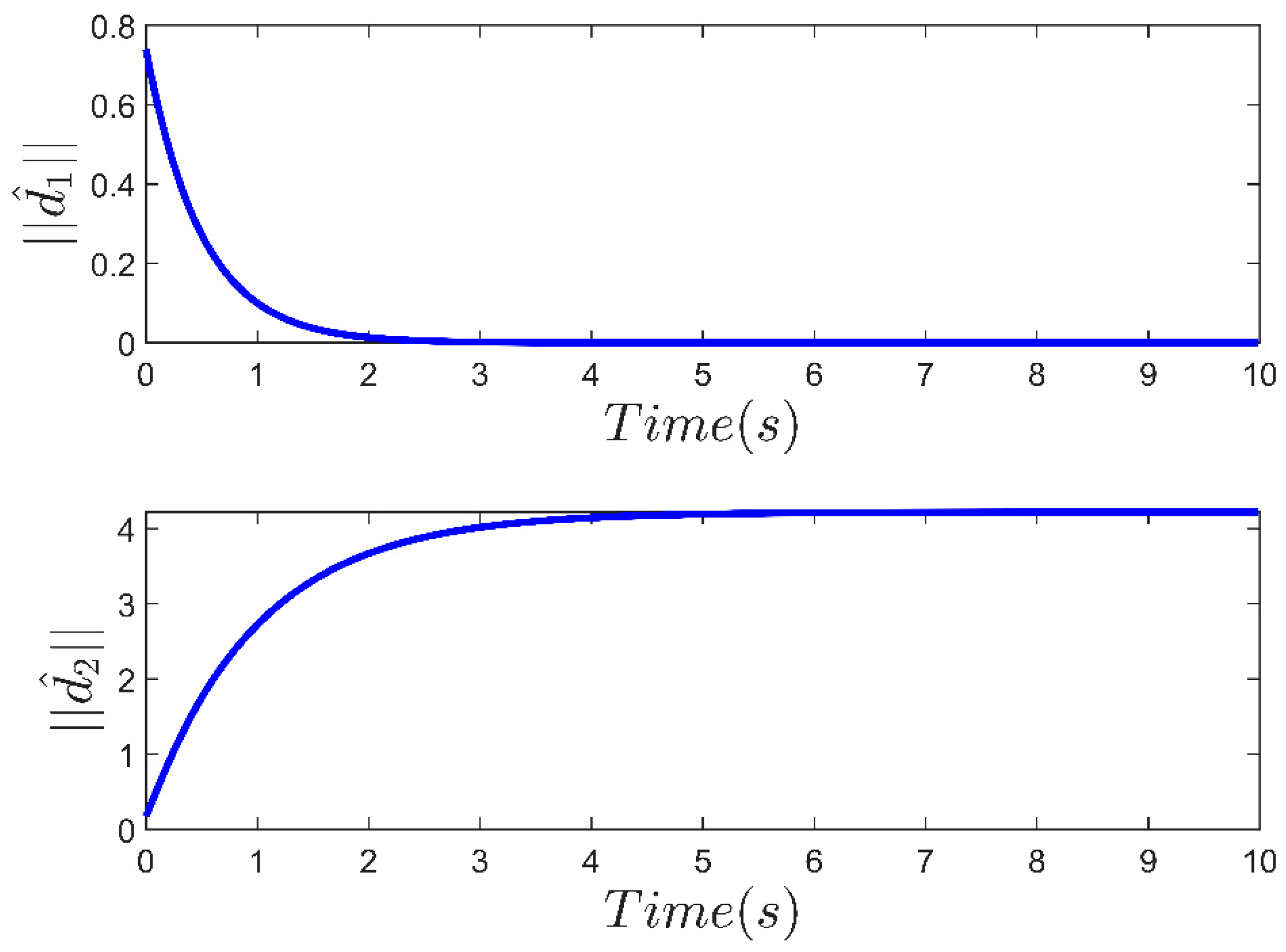
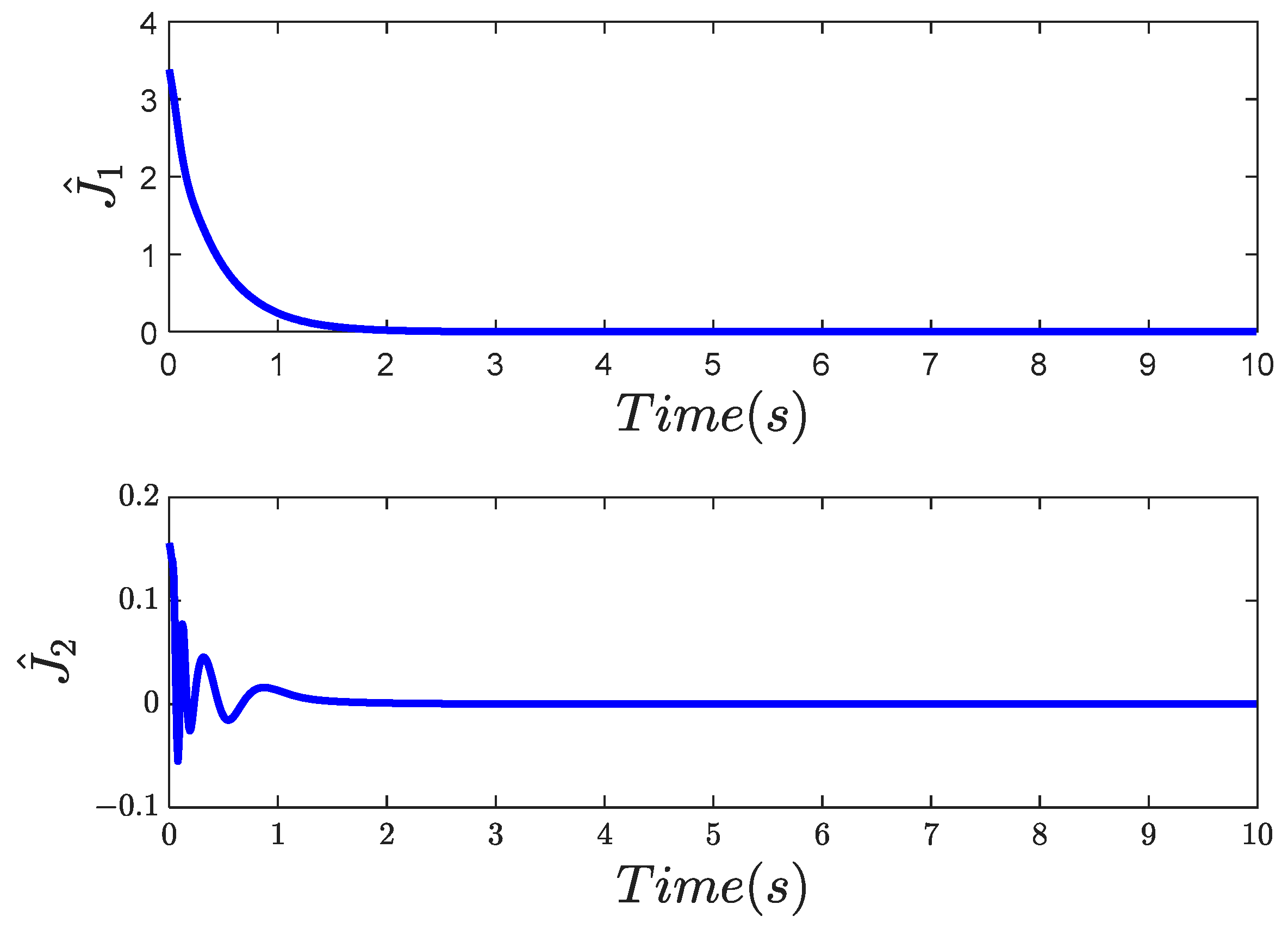
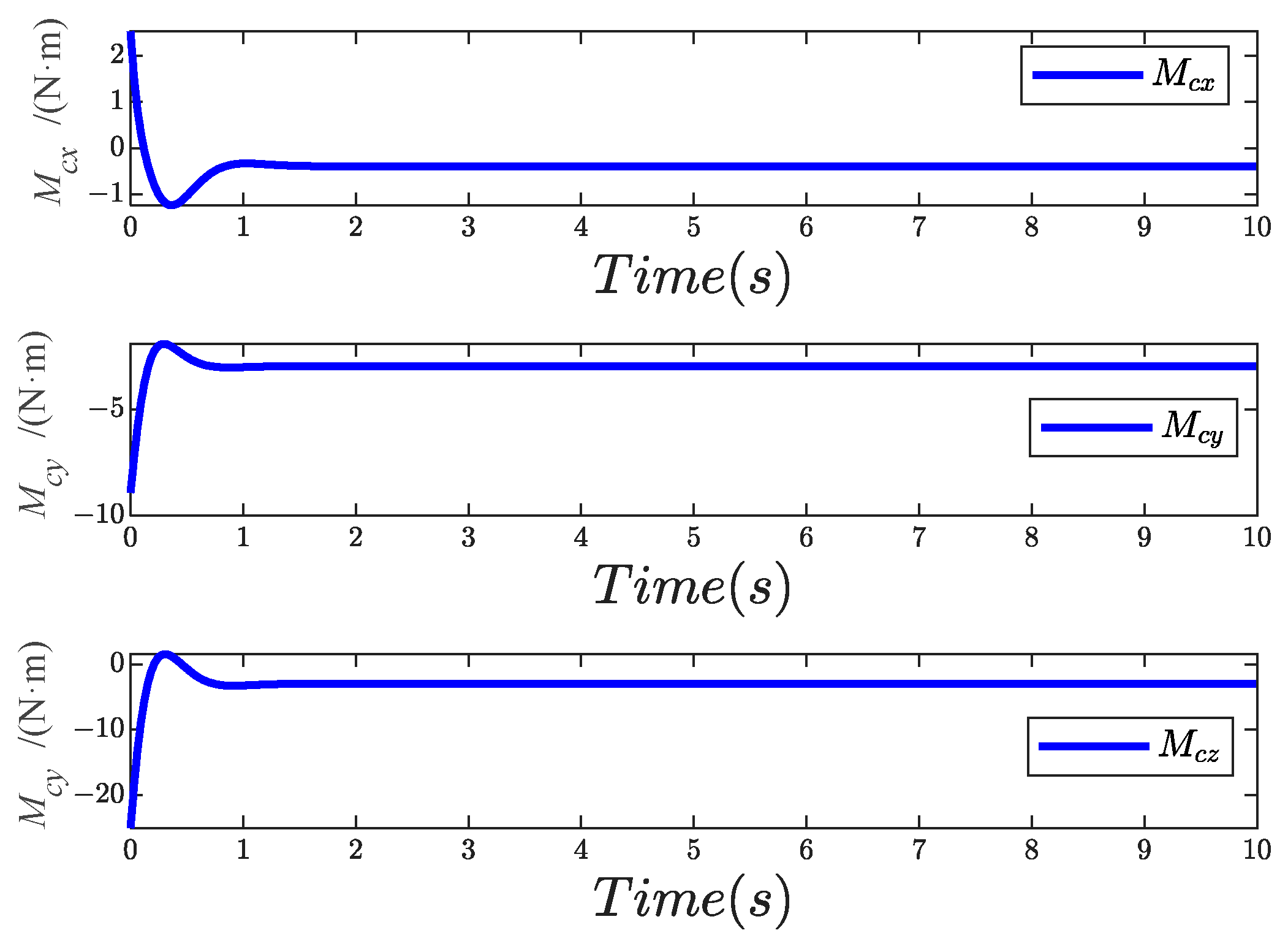
4. Simulation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jha, A.K.; Kudva, J.N. Morphing Unmanned aircraft Concepts, Classifications, and Challenges. In Smart Structures and Materials 2004: Industrial and Commercial Applications of Smart Structures Technologies; Society of Photo Optical: Bellingham, WA, USA, 2004; Volume 5388, pp. 213–224. [Google Scholar]
- Chu, L.; Li, Q.; Gu, F.; Du, X.; He, Y.; Deng, Y. Design, Modeling, and Control of Morphing Aircraft: A Review. Chin. J. Aeronaut. 2022, 35, 220–246. [Google Scholar] [CrossRef]
- Yu, Z.; Zang, Y.; Jiang, B. PID-type fault-tolerant prescribed performance control of fixed-wing UAV. J. Syst. Eng. Electron. 2021, 32, 1053–1061. [Google Scholar]
- Noordin, A.; Mohd Basri, M.A.; Mohamed, Z.; Mat Lazim, I. Adaptive PID controller using sliding mode control approaches for quadrotor UAV attitude and position stabilization. Arab. J. Sci. Eng. 2021, 46, 963–981. [Google Scholar] [CrossRef]
- Wang, P.; Chen, H.; Bao, C.; Tang, G. Review on Modeling and Control Methods of Morphing Vehicle. J. Astronaut. 2022, 43, 853–865. [Google Scholar]
- Ameduri, S.; Concilio, A. Morphing Wings Review: Aims, Challenges, and Current Open Issues of a Technology. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 4112–4130. [Google Scholar] [CrossRef]
- Shardul, G. Study of Various Trends for Morphing Wing Technology. J. Comput. Methods Sci. Eng. 2021, 21, 613–621. [Google Scholar] [CrossRef]
- He, H.; Wang, P. Integrated Guidance and Control Method for High-Speed Morphing Wing Aircraft. Acta Aeronaut. Astronaut. Sin. 2024, 45, 299–312. [Google Scholar]
- Zhang, H.; Wang, P.; Tang, G.; Bao, W. Fixed-Time Sliding Mode Control for Hypersonic Morphing Vehicles via Event-Triggering Mechanism. Aerosp. Sci. Technol. 2023, 140, 108458. [Google Scholar] [CrossRef]
- Abouheaf, M.; Mailhot, N.Q.; Gueaieb, W.; Spinello, D. Guidance Mechanism for Flexible-Wing Aircraft Using Measurement-Interfaced Machine-Learning Platform. IEEE Trans. Instrum. Meas. 2020, 69, 4637–4648. [Google Scholar] [CrossRef]
- Lee, J.; Kim, Y. Neural Network-Based Nonlinear Dynamic Inversion Control of Variable-Span Morphing Aircraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 1624–1637. [Google Scholar] [CrossRef]
- Irfan, S.; Zhao, L.; Ullah, S.; Javaid, U.; Iqbal, S. Differentiator- and Observer-Based Feedback Linearized Advanced Nonlinear Control Strategies for an Unmanned Aerial Vehicle System. Drones 2024, 8, 527. [Google Scholar] [CrossRef]
- Lee, H.; Kim, S.; Kim, Y. Actor-Critic-Based Optimal Adaptive Control Design for Morphing Aircraft. IFAC Pap. 2020, 53, 14863–14868. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, P.; Tang, G.; Chen, H. Disturbance Observer-Based Prescribed Performance Control for Morphing Aircraft. Tactical Missile Technol. 2024, 4, 72–82. [Google Scholar]
- Hu, H.; Li, Y.; Yi, W.; Wang, Y.; Qu, F.; Wang, X. Event-Triggered Neural Network-Based Adaptive Control for a Class of Uncertain Nonlinear Systems. J. Circuits Syst. Comput. 2021, 30, 15. [Google Scholar] [CrossRef]
- Yuan, F.; Liu, Y.-J.; Liu, L.; Lan, J. Adaptive Neural Network Control of Non-Affine Multi-Agent Systems with Actuator Fault and Input Saturation. Int. J. Robust. Nonlinear Control 2024, 34, 3761–3780. [Google Scholar] [CrossRef]
- Anderson, R.B.; Marshall, J.A.; L’Afflitto, A.; Dotterweich, J.M. Model Reference Adaptive Control of Switched Dynamical Systems with Applications to Aerial Robotics. J. Intell. Robot. Syst. 2020, 100, 1265–1281. [Google Scholar] [CrossRef]
- Qi, W.; Teng, J.; Cao, J.; Yan, H.; Cheng, J. Improved Model Reference-Based Adaptive Nonlinear Dynamic Inversion for Fault-Tolerant Flight Control. Int. J. Robust. Nonlinear Control 2023, 33, 10328–10359. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.; Ming, R.; Li, K.; Zhang, W. Dynamic Protocol-Based Control for Hidden Stochastic Jump Multiarea Power Systems in Finite-Time Interval. IEEE Trans. Cybern. 2025, 55, 1486–1496. [Google Scholar]
- Li, G.; Peng, C.; Cao, Z. Finite-time bounded asynchronous sliding-mode control for T-S fuzzy time-delay systems via event-triggered scheme. Fuzzy Sets Syst. 2025, 514, 109400. [Google Scholar] [CrossRef]
- Yu, C.; Jiang, J.; Wang, S.; Han, B. Fixed-Time Adaptive General Type-2 Fuzzy Logic Control for Air-Breathing Hypersonic Vehicle. Trans. Inst. Meas. Control 2021, 43, 2143–2158. [Google Scholar] [CrossRef]
- Hernández-González, O.; Targui, B.; Valencia-Palomo, G.; Guerrero-Sánchez, M.E. Robust cascade observer for a disturbance unmanned aerial vehicle carrying a load under multiple time-varying delays and uncertainties. Int. J. Syst. Sci. 2024, 55, 1056–1072. [Google Scholar] [CrossRef]
- Hernández-González, O.; Ramírez-Rasgado, F.; Farza, M.; Guerrero-Sánchez, M.-E.; Astorga-Zaragoza, C.-M.; M’Saad, M.; Valencia-Palomo, G. Observer for Nonlinear Systems with Time-Varying Delays: Application to a Two-Degrees-of-Freedom Helicopter. Aerospace 2024, 11, 206. [Google Scholar] [CrossRef]
- Qu, C.; Cheng, L.; Gong, S.; Huang, X. Dynamic-Matching Adaptive Sliding Mode Control for Hypersonic Vehicles. Aerosp. Sci. Technol. 2024, 149, 109159. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, Y. Adaptive Event-Triggered Finite-Time Sliding Mode Control for Singular T–S Fuzzy Markov Jump Systems with Asynchronous Modes. Commun. Nonlinear Sci. Numer. Simul. 2023, 126, 107465. [Google Scholar] [CrossRef]
- Shi, X.; Li, Y.; Liu, Q.; Lin, K.; Chen, S. A Fully Distributed Adaptive Event-Triggered Control for Output Regulation of Multi-Agent Systems with Directed Network. Inf. Sci. 2023, 626, 60–74. [Google Scholar] [CrossRef]
- Abbas, M.; Sadati, S.H.; Khazaee, M. Fault-Tolerant Control Design Based on Observer-Switching and Adaptive Neural Networks for Maneuvering Aircraft. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 14689–14698. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, L.; Cao, Y.; Yang, Y.; Wen, S. Learning-Based Fault-Tolerant Control With High-Order Control Barrier Functions. IEEE Trans. Autom. Sci. Eng. 2025, 22, 694. [Google Scholar] [CrossRef]
- Ma, J.; Peng, C. Adaptive Model-Free Fault-Tolerant Control Based on Integral Reinforcement Learning for a Highly Flexible Aircraft with Actuator Faults. Aerosp. Sci. Technol. 2021, 119, 107204. [Google Scholar] [CrossRef]
- Liu, Y.; Jing, Y.; Liu, X.; Li, X. Survey on Finite-Time Control for Nonlinear Systems. Control Theory Appl. 2020, 37, 1–12. [Google Scholar]
- Guo, F.; Zhang, W.; Lv, M.; Zhang, R. Fault-Tolerant Tracking Control of Hypersonic Vehicle Based on a Universal Prescribe Time Architecture. Drones 2024, 8, 295. [Google Scholar] [CrossRef]
- Bingö, Z.; Güzey, H. Finite-Time Neuro-Sliding-Mode Controller Design for Quadrotor UAVs Carrying Suspended Payload. Drones 2022, 6, 311. [Google Scholar] [CrossRef]
- Rang, E.R. Isochrone Families for Second-Order Systems. IEEE Trans. Automat. Contr. 1963, 8, 64–65. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X. Output-Feedback Control Strategies of Lower-Triangular Nonlinear Nonholonomic Systems in Any Prescribed Finite Time. Int. J. Robust Nonlinear Control 2019, 29, 904–918. [Google Scholar] [CrossRef]
- Zhou, T.; Liu, S.; Liu, C. Finite-Time Prescribed Performance Adaptive Fuzzy Control for Nonlinear Systems with Unknown Virtual Control Coefficients. In Proceedings of the 2021 International Conference on Security, Pattern Analysis, and Cybernetics (SPAC), Chengdu, China, 18–20 June 2021; pp. 7–12. [Google Scholar]
- Kang, B.; Li, Y. Adaptive Finite-Time Stabilization of High-Order Stochastic Nonlinear Systems with Unknown Control Direction. In Proceedings of the Conference Digest—2021 International Conference on Security, Pattern Analysis, and Cybernetics (SPAC), Chengdu, China, 18–20 June 2021; pp. 150–155. [Google Scholar]
- Zhu, W.; Zong, Q.; Zhang, X.; Liu, W. Disturbance Observer-Based Multivariable Finite-Time Attitude Tracking for Flexible Spacecraft. In Proceedings of the Chinese Control Conference (CCC), Chongqing, China, 28–30 July 2020; Volume 2020, pp. 1772–1777. [Google Scholar]
- Wang, H.; Kang, S.; Feng, Z. Finite-Time Adaptive Fuzzy Command Filtered Backstepping Control for a Class of Nonlinear Systems. Int. J. Fuzzy Syst. 2019, 21, 2575–2587. [Google Scholar] [CrossRef]
- Zhao, Q.; Duan, G. Concurrent Learning Adaptive Finite-Time Control for Spacecraft with Inertia Parameter Identification under External Disturbance. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3691–3704. [Google Scholar] [CrossRef]
- Bu, X.; Luo, R.; Lei, H. Chattering-avoidance discrete-time fuzzy control with finite-time preselected qualities. IEEE Trans. Fuzzy Syst. 2024, 33, 997–1008. [Google Scholar] [CrossRef]
- Bu, X.; Luo, R.; Lei, H. Fuzzy-neural intelligent control with fixed-time pre-configured qualities for electromechanical dynamics of electric vehicles motors. IEEE Trans. Intell. Transp. Syst. 2024, 26, 1193–1202. [Google Scholar] [CrossRef]
- Luo, R.; He, G.; Li, Y.; Bu, X.; Li, Q. Appointed-time Fuzzy Fault-tolerant Control of Hypersonic Flight Vehicles with Flexible Predefined Behaviors. IEEE Trans. Autom. Sci. Eng. 2025, 22, 13995–14007. [Google Scholar] [CrossRef]
- Lin, X.; Shi, X.; Li, S. Adaptive Tracking Control for Spacecraft Formation Flying System via Modified Fast Integral Terminal Sliding Mode Surface. IEEE Access 2020, 8, 198357–198367. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, T.; Dong, C.; Jiang, W. Chained Smooth Switching Control for Morphing Aircraft. Control Theory Appl. 2015, 32, 949–954. [Google Scholar]
- Cheng, H.; Fu, W.; Dong, C.; Wang, Q.; Hou, Y. Asynchronously Finite-Time H∞ Control for Morphing Aircraft. Trans. Inst. Meas. Control 2018, 40, 4330–4344. [Google Scholar] [CrossRef]
- Chen, H.; Wang, P.; Tang, G. Attitude Control Scheme for Morphing Vehicles with Output Error Constraints and Input Saturation. Acta Aeronaut. Astronaut. Sin. 2023, 44, 408–419. [Google Scholar]
- Sheng, H. Research on Strong Robust Control for Flexible Hypersonic Morphing Vehicle. Master’s Thesis, National University of Defense Technology, Changsha, China, 2021. [Google Scholar]
- Liang, X.; Wang, Q.; Xu, B.; Dong, C. Back-stepping fault-tolerant control for Morphing Unmanned aircraft based on fixed-time observer. Int. J. Control Autom. Syst. 2021, 19, 3924–3936. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, J.; Zhou, Q.; Shi, J. Modified adaptive neural dynamic surface control for Morphing Unmanned aircraft with input and output constraints. Nonlinear Dyn. 2017, 87, 2367–2383. [Google Scholar] [CrossRef]
- Emmanuel, S.A.; Sun, R. Approximation-free prescribed performance control for Nonlinear morphing missile System. Int. J. Eng. Appl. Sci. 2016, 3, 257584. [Google Scholar]
- Wang, Z.; Chang, Y.; Qiu, Y.; Xing, X. RL-based adaptive control for a class of non-affine uncertain stochastic systems with mismatched disturbances. Commun. Nonlinear Sci. Numer. Simul. 2024, 138, 108191. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, S.; Zhou, P.; Zhao, L.; Li, S. Novel Prescribed Performance-Tangent Barrier Lyapunov Function for Neural Adaptive Control of the Chaotic PMSM System by Backstepping. Int. J. Electr. Power Energy Syst. 2020, 121, 105991. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Liu, X.; Lin, C. Finite-time adaptive fuzzy tracking control design for nonlinear systems. IEEE Trans. Fuzzy Syst. 2017, 26, 1207–1216. [Google Scholar] [CrossRef]
- Qian, C.; Lin, W. Non-Lipschitz Continuous Stabilizers for Nonlinear Systems with Uncontrollable Unstable Linearization. Syst. Control Lett. 2001, 42, 185–200. [Google Scholar] [CrossRef]
- Li, M.; Zhang, J.; Li, S.; Wu, F. Adaptive Finite-Time Fault-Tolerant Control for the Full-State-Constrained Robotic Manipulator with Novel Given Performance. Eng. Appl. Artif. Intell. 2023, 125, 106650. [Google Scholar] [CrossRef]
- Wei, Y.; Zhou, P.; Liang, Y.; Wang, Y.; Duan, D. Adaptive finite-time neural backstepping control for multi-input and multi-output state-constrained nonlinear systems using tangent-type nonlinear mapping. Int. J. Robust Nonlinear Control 2020, 30, 5559–5578. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Lin, C.; Zhang, J.; Meng, X. Adaptive Neural Network Finite-Time Output Feedback Control of Quantized Nonlinear Systems. IEEE Trans. Cybern. 2018, 48, 1839–1848. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, S.; Li, S.; Zhou, P. Adaptive Neural Dynamic Surface Control for the Chaotic PMSM System with External Disturbances and Constrained Output. Recent Adv. Electr. Electron. Eng. 2020, 13, 894–905. [Google Scholar]
- Wu, J.; Sun, Y.; Zhao, Q.; Wu, Z.-G. Adaptive neural asymptotic tracking control for a class of stochastic non-strict-feedback switched systems. J. Frankl. Inst. 2018, 359, 1274–1297. [Google Scholar] [CrossRef]
- Chen, K.; Zhu, S.; Wei, C.; Xu, T.; Zhang, X. Output constrained adaptive neural control for generic hypersonic vehi-cles suffering from non-affine aerodynamic characteristics and stochastic disturbances. Aerosp. Sci. Technol. 2021, 111, 106469. [Google Scholar] [CrossRef]
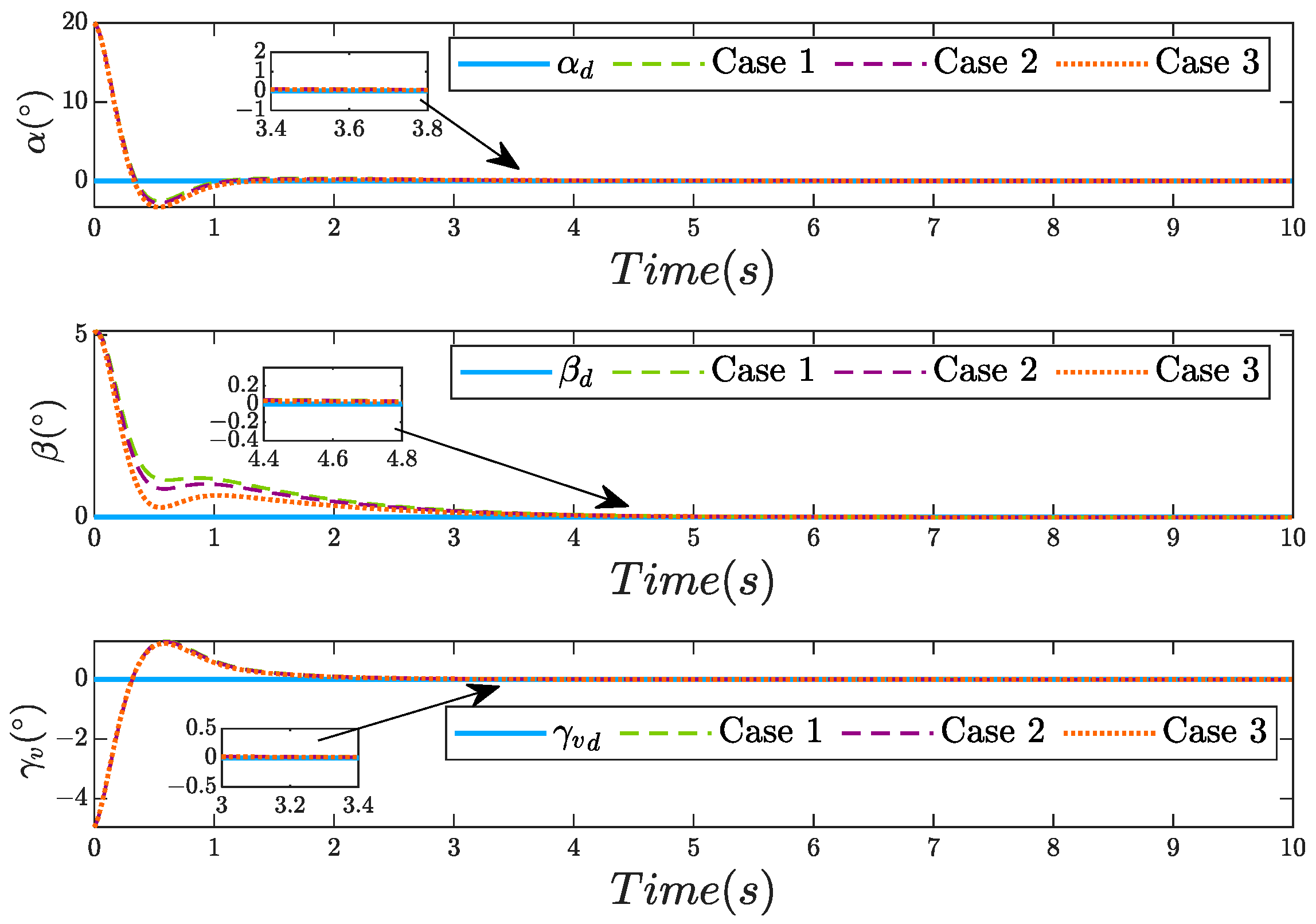



| Cases | ||||
|---|---|---|---|---|
| Case 1 | ||||
| Case 2 | ||||
| Case 3 |
| Method | Steady-State Error (Rad) | Convergence Time (s) |
|---|---|---|
| RLAC | 0.0038, 0.0024, 0.00087 | 0.79, 0.66, 0.82 |
| NNAC | 0.007, 0.0023, 0.001 | 1.43, 4.19, 1.19 |
| AFTC | >0.026, >0.025, >0.0026 | 5.81, >10, 1.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, W.; Wei, Y.; Wang, C.; Wang, Z. Finite-Time Adaptive Reinforcement Learning Control for a Class of Morphing Unmanned Aircraft with Mismatched Disturbances and Coupled Uncertainties. Drones 2025, 9, 562. https://doi.org/10.3390/drones9080562
Ren W, Wei Y, Wang C, Wang Z. Finite-Time Adaptive Reinforcement Learning Control for a Class of Morphing Unmanned Aircraft with Mismatched Disturbances and Coupled Uncertainties. Drones. 2025; 9(8):562. https://doi.org/10.3390/drones9080562
Chicago/Turabian StyleRen, Wei, Yingjie Wei, Cong Wang, and Zheng Wang. 2025. "Finite-Time Adaptive Reinforcement Learning Control for a Class of Morphing Unmanned Aircraft with Mismatched Disturbances and Coupled Uncertainties" Drones 9, no. 8: 562. https://doi.org/10.3390/drones9080562
APA StyleRen, W., Wei, Y., Wang, C., & Wang, Z. (2025). Finite-Time Adaptive Reinforcement Learning Control for a Class of Morphing Unmanned Aircraft with Mismatched Disturbances and Coupled Uncertainties. Drones, 9(8), 562. https://doi.org/10.3390/drones9080562






