Cross-Scene Multi-Object Tracking for Drones: Leveraging Meta-Learning and Onboard Parameters with the New MIDDTD

Abstract

Multi-object tracking (MOT) is a key intermediate task in many practical applications and theoretical fields, facing significant challenges due to complex scenarios, particularly in the context of drone-based air-to-ground military operations. During drone flight, factors such as high-altitude environments, small target proportions, irregular target movement, and frequent occlusions complicate the multi-object tracking task. This paper proposes a cross-scene multi-object tracking (CST) method to address these challenges. Firstly, a lightweight object detection framework is proposed to optimize key sub-tasks by integrating multi-dimensional temporal and spatial information. Secondly, trajectory prediction is achieved through the implementation of Model-Agnostic Meta-Learning, enhancing adaptability to dynamic environments. Thirdly, re-identification is facilitated using Dempster–Shafer Theory, which effectively manages uncertainties in target recognition by incorporating aircraft state information. Finally, a novel dataset, termed the Multi-Information Drone Detection and Tracking Dataset (MIDDTD), is introduced, containing rich drone-related information and diverse scenes, thereby providing a solid foundation for the validation of cross-scene multi-object tracking algorithms. Experimental results demonstrate that the proposed method improves the IDF1 tracking metric by 1.92% compared to existing state-of-the-art methods, showcasing strong cross-scene adaptability and offering an effective solution for multi-object tracking from a drone’s perspective, thereby advancing theoretical and technical support for related fields.

1. Introduction

With the rapid development of drone technology and its wide application in transportation, security, environmental protection and other fields, such as traffic tracking, inspection, wildlife tracking and other tasks, the demand for efficient and accurate air-to-ground multi-object tracking technology (MOT) is growing. These application scenarios require the support of image target tracking as an intermediate technology to achieve effective recognition and tracking of ground targets. Multi-target tracking technology plays a key role in achieving target positioning and tracking. Therefore, air-to-ground multi-target tracking and re-identification technology that assists drones in their role has become a key research direction.

However, from the perspective of drones, it is necessary to deal with problems such as small target size and weak imaging features due to high-altitude flight, irregular target movement, easy occlusion of the target, and frequent entry and exit of the target in the field of view due to drone shaking. The existence of these problems significantly increases the complexity and difficulty of the MOT task and limits its effectiveness in practical applications [1].

Traditional multi-target tracking methods mainly focus on relatively stable environments such as urban or road scenes, and adopt detection-based multi-target tracking methods. These methods first use target detection algorithms to detect all potential targets in each frame of the image, and then use tracking algorithms such as DeepSORT to associate and track these detection results to complete the tracking task. However, in the context of UAVs, the weak imaging features, nonlinear motion patterns, and discontinuous trajectories of the target make it difficult for traditional methods to adapt effectively, especially when processing large-size images, which further affects tracking accuracy and robustness. Moreover, traditional methods merely approach multi-target tracking from the perspective of image features, without leveraging the state information of the aircraft and payload to quantify the dynamic changes in the images.

In order to solve these problems, this paper studies the target detection, trajectory prediction and re-identification methods for multi-target tracking. A lightweight target detection method based on layer decoupling fusion of convolutional attention and global context enhancement, a nonlinear trajectory prediction method based on an adaptive bidirectional long short-term memory network, and a re-identification method based on world coordinate data and knowledge fusion are proposed. In addition, the existing UAV-based tracking datasets are mostly concentrated on pedestrians or vehicle targets in limited environments such as cities or roads, lacking consideration of the relevant parameter information of the drone’s perspective and optoelectronic pod, making it difficult to meet the verification requirements of air-to-ground multi-target tracking algorithms. In response to the above problems, this paper also constructs a drone detection and tracking dataset (MIDDTD) containing drone and optoelectronic pod parameter information, which provides a solid foundation for the effective verification of the algorithm. A typical example of each environment background of the dataset is shown in Figure 1, below.

Figure 1. MIDDTD example display.

The technical route and main innovations of this article are as follows:

• The Model-Agnostic Meta-Learning (MAML) method is employed to enhance trajectory prediction capabilities. By leveraging the adaptability of MAML in quickly adjusting learned parameters to new tasks, more robust and generalized predictions for dynamic object movements are achieved, significantly improving performance in multi-target tracking scenarios.
• A novel approach for trajectory re-identification is introduced, utilizing Dempster-Shafer (DS) theory to effectively manage and combine uncertain information from multiple sources. This method enhances the accuracy of identifying reappearing targets in complex environments, thereby increasing the reliability of the tracking system.
• The MIDDTD is constructed as a comprehensive dataset specifically designed for air-to-ground multi-target tracking. This dataset integrates diverse scenes and detailed drone-specific parameters, including GPS and IMU data, which support the validation of advanced tracking algorithms and address the limitations of existing datasets focused primarily on pedestrian or vehicle targets.

The structure of this paper is as follows: In Section 2, a comprehensive review of related works is presented, highlighting advancements in multi-object tracking and trajectory prediction methodologies. Section 3 details the proposed methodology, including the implementation of the MAML method for trajectory prediction and the application of Dempster-Shafer theory for trajectory re-identification. Section 4 discusses the construction of the MIDDTD as well as the experimental results, showcasing the performance of the proposed approaches. Finally, Section 5 concludes the paper with a discussion of the findings and potential future research directions.

2. Related Work

With the development of deep learning-based object detection tasks, many detection-based MOT methods have been proposed in recent years. The simple online real-time tracking algorithm SORT, proposed by Bewley et al. [2], is one of the earliest MOT algorithms to utilize convolutional neural networks for object detection. This algorithm focuses on inter-frame prediction and association, using a linear velocity model Kalman filter to predict object motion, then measuring the Intersection over Union (IoU) between the detection boxes and tracking boxes, and finally associating the detection results using the Hungarian algorithm. However, the SORT algorithm does not address the problem of frequent target ID changes due to occlusions during long-term tracking. Later, Wojke et al. [3] proposed the DeepSORT algorithm, which improves upon SORT by introducing re-identification features for extracting deep appearance features in the data association part. This allows partially occluded objects to be re-identified. They also introduced a cascade matching strategy to improve the accuracy of target matching. Chen et al. [4] proposed the MOTDT algorithm, which designed a new multi-object tracking framework that integrates deep appearance information with spatial information. They also proposed a hierarchical data association strategy, associating predicted targets with multiple detected targets hierarchically. A soft assignment strategy with a trajectory scoring mechanism was used to associate targets, making full use of re-identification features and spatial information to improve tracking performance. Zhang et al. [5] proposed the ByteTrack method, which associates almost all detection boxes, not just the high-scoring ones. For low-scoring detection boxes, the method utilizes their similarity with tracking fragments to recover true targets and filters out background detections, improving tracking accuracy to some extent. Aharon et al. [6] proposed the BoTSORT method, which introduces global motion compensation technology to estimate background motion and generate more accurate object motion predictions. They also proposed a simple and effective fusion method combining IoU and re-identification cosine distance, establishing a stronger association between detections and trajectories. Du et al. [7] proposed the StrongSORT method, which constructs a connection model without appearance information, achieving a good balance between speed and accuracy through global association that does not rely on appearance information. The Gaussian smoothing interpolation method using Gaussian process regression was employed to mitigate the issue of missed detections. Cao et al. [8] proposed the OcSORT method, which uses target detection observations to correct error accumulation during occlusion. By using an observation center method, they replaced the traditional linear state estimation method, enabling error correction during occlusions and complex motion processes. Maggiolino et al. [9] proposed the DeepOcSORT method, which builds upon OcSORT by adding appearance feature information, improving the performance of the tracking system in dynamic environments.

With the development of the MOT field, many joint detection-based MOT methods have been proposed. Wang et al. [10] proposed the JDE algorithm, which integrates a one-stage object detection network and a pedestrian re-identification (ReID) network, considering the model inference speed. This allows the network to output both detection and re-identification information simultaneously, accelerating the inference speed. Zhang et al. [11] proposed the FairMOT algorithm, where the detection branch uses the anchor-free object detection algorithm CenterNet. At the same time, a parallel branch directly outputs ReID features to distinguish different targets, effectively unifying object detection and re-identification networks. Zhou et al. [12] proposed the CenterTrack algorithm, which enables the simultaneous extraction of detection and target deep features. By performing parallel inference for all targets, the algorithm quickly recovers targets that are missed due to occlusion, enhancing the robustness of the method to overlapping occlusion issues. Yan et al. [13] proposed the Co-MOT algorithm, which addresses the imbalance caused by the label assignment strategy used during training. They introduced a new cooperative–competitive label assignment strategy and the shadow concept. During training, tracked targets are added to the detection query’s matched targets, making the label assignment process more balanced. For query initialization, each query is expanded by a set of shadow copies. This helps maintain the accuracy and stability of the tracking.

Li et al. [14] proposed a residual-aware correlation filter method to address the problem of tracking accuracy degradation due to target scale variation, which affects the quality of appearance models. The method models the residuals between two adjacent frames based on spatial and temporal regularization, and introduces a scale refinement strategy. This algorithm enhances the accuracy of scale estimation and improves tracking precision, but it still suffers from sensitivity to occlusion. Zhang et al. [15] designed a dual-regression correlation filter method to address the issue of tracking drift or failure caused by target appearance changes, background clutter, and similar targets in complex scenes. The method uses a target filter and a global filter, adopting a dual-regression strategy, which enhances the feature-learning ability of the target. However, this increases computational cost, reducing the system’s real-time performance. He et al. [16] aimed to improve the discriminative ability of the tracker by integrating context attention, dimension attention, and spatiotemporal attention into the training and detection stages based on correlation filters. The algorithm uses context attention to consider the relationship between the target and surrounding targets, dimension attention to select feature dimensions relevant to target tracking, and spatiotemporal attention to capture the target’s motion trajectory, enhancing the robustness of the tracking system. However, it still faces the problem of not being able to handle significant target scale variations. Benaly et al. [17] proposed a multi-object tracking algorithm based on a hash set matching approach to improve real-time tracking performance. This algorithm combines HOG and optical flow features for target tracking, further improving real-time processing speed, but still faces the issue of low tracking accuracy. Lusardi et al. [18] designed a re-identification network based on a graph neural network to improve feature extraction capabilities. This network uses center point appearance features to strengthen overall feature extraction ability and incorporates a class-based triplet loss during training to improve the discriminative ability of center point appearance features. The algorithm enhances target re-identification performance but still suffers from poor tracking performance at the edges of the field of view. Batorli et al. [19] designed a novel similarity metric that combines position, appearance, and size information, proposing the PAS-Tracker algorithm, which uses a camera motion compensation model to align tracking positions across frames. While both of the above algorithms exhibit strong robustness in complex environments, they still face challenges with complex dynamic weight strategy designs and the lack of generality in weight designs.

Despite some significant progress in air-to-ground visual target tracking, many challenges remain. For example, the SORT algorithm, which uses convolutional neural networks for object detection and Kalman filters to predict object motion, frequently encounters target ID changes during long-term tracking, particularly performing poorly in occlusion scenarios [20]. DeepSORT improves on this issue by introducing re-identification features and cascade matching strategies, but it still cannot completely avoid ID switching problems. Other methods such as MOTDT, ByteTrack, and BoTSORT show improvements in specific scenarios, but they still fall short in handling weak small-target detection, non-linear trajectory prediction, and trajectory continuity. Additionally, many joint detection MOT methods like JDE, FairMOT, and CenterTrack improve inference speed, but they still face challenges in accuracy and robustness when dealing with target scale variations, occlusions, and complex background interference. In summary, current methods have significant room for improvement in weak small-target detection, non-linear trajectory prediction, and trajectory continuity. The proposed method in this paper effectively addresses these issues by combining convolutional attention modules, global context enhancement, and adaptive, bidirectional, long short-term memory networks, significantly improving the precision and robustness of multi-target tracking; the algorithm structure is shown in Figure 2. Compared to the aforementioned classical methods, the proposed approach achieves an improvement of over 3% in the MOTA metric, particularly demonstrating a 20% reduction in ID switches under scenarios involving occlusion and small/weak targets.

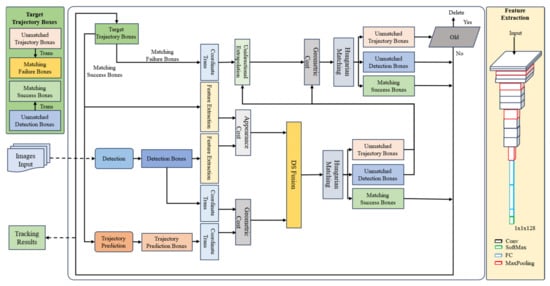
Figure 2. Framework of CST.

3. Method

3.1. Detection

The detection method used in this paper is based on the YOLO network architecture, with ResNet34 [21] as the backbone. Additionally, a Convolutional Block Attention Module (CBAM) [22] is introduced into the backbone network to enhance the model’s focus on the target and improve feature extraction accuracy. The Neck section follows the original structure of YOLOv8 [23], with modules sourced from YOLOv8, offering efficient feature fusion and multi-scale feature expression capabilities. The detection head uses a novel global context-enhanced adaptive sparse convolutional network (CEASC) [24] detection head to improve the model’s ability to detect weak targets. The overall structure is shown in Figure 3.

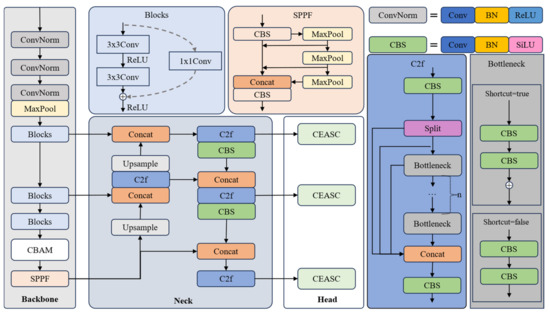
Figure 3. Framework of detection.

In the figure, Conv represents the convolution operation, SPPF is the fast Spatial Pyramid Pooling module used for multi-scale feature fusion, BN is Batch Normalization, and ReLU and SiLU are activation functions. SiLU is smoother compared to ReLU. ConvNorm is a module composed of Conv, BN, and ReLU, while CBS is a module composed of Conv, BN, and SiLU. Upsample is the upsampling operation used to increase the size of the feature map, and MaxPool is the max pooling operation, which reduces computational load while preserving prominent features. The Split operation divides a tensor along a certain dimension into multiple sub-tensors. CBAM is the Convolutional Block Attention Module, and CEASE is the Context Enhancement and Detection Head. The detailed structures of CBAM and CEASE are described below.

3.1.1. CBAM

The Convolutional Block Attention Module (CBAM) can dynamically adjust the important regions within feature maps, allowing the network to focus more on the key target areas and reduce attention to irrelevant background or interfering objects, thereby significantly improving the detection accuracy of small targets from an air-to-ground perspective.

In previous studies, CBAM is typically added to the Neck module to generate feature pyramids. However, when applying CBAM in the Neck module, the attention mechanism weights and filters the features based on already down-sampled feature maps, which may result in CBAM failing to fully utilize the original high-resolution features, leading to the loss of some fine-grained target information, especially for small targets or weak features. This method integrates CBAM directly into the Backbone network, allowing it to enhance attention to key features during the feature extraction process, rather than relying on the Neck to generate feature pyramids [25]. This strategy has two main advantages: first, it reduces the complexity of the Neck module; second, it enables adaptive optimization of features at an early stage of feature extraction. By enhancing the lower-level features, this method effectively improves the detection capability of small targets while reducing false positives and missed detections due to feature detail loss, providing stronger support for overall detection performance.

CBAM is an effective model based on the attention mechanism, consisting of two modules: the channel attention module and the spatial attention module, as shown in Figure 4. These two modules generate a channel attention map and a spatial attention map, respectively, which are then multiplied with the input feature map to refine the features adaptively. In this way, meaningful features along the channel and spatial axes are emphasized, while redundant features are suppressed, as shown in the following formula.

$${\mathrm{F}}^{\prime }={\mathrm{M}}_{\mathrm{c}}(\mathrm{F})\otimes \mathrm{F}$$

(1)

$${\mathrm{F}}^{″}={\mathrm{M}}_{\mathrm{s}}\left({\mathrm{F}}^{\prime }\right)\otimes {\mathrm{F}}^{\prime }$$

(2)

Here, $\otimes$ represents element-wise multiplication, $\mathrm{F}$ is the input feature map, ${\mathrm{M}}_{\mathrm{c}}\left(\mathrm{F}\right)$ is one-dimensional channel attention diagram, and ${\mathrm{M}}_{\mathrm{s}}\left({\mathrm{F}}^{\prime }\right)$ is the two-dimensional space attention diagram.

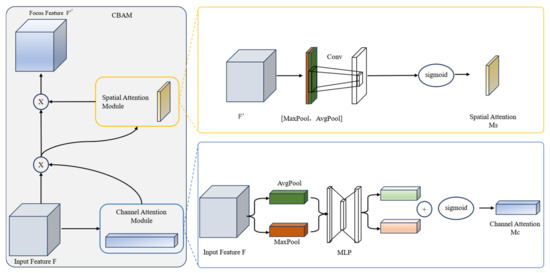
Figure 4. Framework of CBAM.

The channel attention module [26] first performs global max pooling and average pooling operations on the feature maps of different channels, followed by element-wise summation and Sigmoid activation. The formula is as follows:

$$\begin{array}{cc}{\mathrm{M}}_{\mathrm{c}}\left(F\right)& =\sigma \left(MLP\right(\mathrm{AvgPool}\left(F\right))+MLP(\mathrm{MaxPool}\left(F\right)\left)\right)\\ & =\sigma \left({\mathrm{W}}_1\left({\mathrm{W}}_0\left({\mathrm{F}}_{\mathrm{a}\mathrm{v}\mathrm{g}}^{\mathrm{c}}\right)\right)+{\mathrm{W}}_1\left({\mathrm{W}}_0\left({\mathrm{F}}_{max}^{\mathrm{c}}\right)\right)\right)\end{array}$$

(3)

where $\sigma$ is the Sigmoid activation function, ${\mathrm{M}}_{\mathrm{c}}$ denotes the output of the channel attention mechanism, and $\mathrm{F}$ represents the input feature map. $\mathrm{A}\mathrm{v}\mathrm{g}\mathrm{P}\mathrm{o}\mathrm{o}\mathrm{l}$ is the average pooling operation, and $\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{P}\mathrm{o}\mathrm{o}\mathrm{l}$ is the max pooling operation. ${\mathrm{F}}_{\mathrm{a}\mathrm{v}\mathrm{g}}^{\mathrm{c}}$ is the output after the average pooling operation on $\mathrm{F}$, ${\mathrm{F}}_{max}^{\mathrm{c}}$ is the output after the max pooling operation on $\mathrm{F}$, the weights ${\mathrm{W}}_0$ and ${\mathrm{W}}_1$ of the multilayer perceptron (MLP) are shared between the two inputs, and ReLU activation is applied after ${\mathrm{W}}_0$.

The spatial attention module first performs global max pooling and average pooling operations on the pixel values at the same positions across different feature maps [27]. The two pooling results are then concatenated, followed by a 2D convolution operation and Sigmoid activation. The formula is as follows:

$${\mathrm{M}}_{\mathrm{s}}\left(\mathrm{F}\right)=\sigma \left(conv\left(\right[\mathrm{A}\mathrm{v}\mathrm{g}\mathrm{P}\mathrm{o}\mathrm{o}\mathrm{l}\left(\mathrm{F}\right);\mathrm{M}\mathrm{a}\mathrm{x}\mathrm{P}\mathrm{o}\mathrm{o}\mathrm{l}\left(\mathrm{F}\right)\left]\right)\right)$$

(4)

where conv represents the convolution operation.

In this way, CBAM can effectively and automatically adjust the key regions in the feature map, allowing even smaller target areas to be given more attention by the network. This enables the network to focus more on meaningful information during feature extraction, thereby significantly improving the detection accuracy of small targets.

3.1.2. CEASC

The algorithm structure of CEASC is shown in Figure 5, below. In each FPN layer, context enhancement is performed by generating mask features Hi and global features Gi. The detection head is replaced with Context-Enhanced Sparse Convolution (CESC), where SC represents the sparse convolution operation. The ratio of the mask Hi is automatically optimized through the Adaptive Multi-Layer Mask (AMM) scheme. The AMM module enables the model to adaptively generate masks with an appropriate masking ratio, achieving a better balance between accuracy and efficiency.

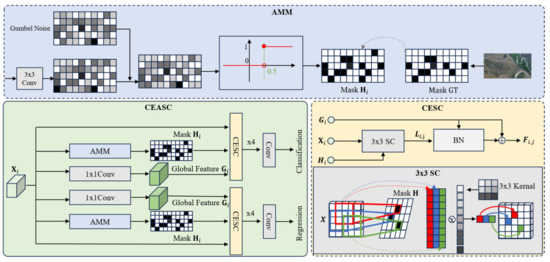
Figure 5. Framework of CEASC.

Sparse convolution dynamically generates sparse masks and performs convolution operations only on the regions of the feature map related to foreground targets, significantly reducing the computation on background regions and focusing on target areas [28]. In blurry images, sparse convolution limits computations to the target region, effectively reducing background interference and improving detection efficiency and accuracy.

Specifically, given the feature map $X_i\in {\mathbb{R}}^{B\times C\times H\times W}$ from the $i$-th layer of the Neck, SC uses a mask network composed of the shared kernel $W_{\mathrm{mask} }\in {\mathbb{R}}^{C\times 1\times 3\times 3}$, where $B,C,H$, and $W$ represent batch size, channel size, height, and width, respectively. The convolution of $X_i$ with $W_{\mathrm{mask} }$ generates a soft feature map $S_i\in {\mathbb{R}}^{B\times 1\times H\times W}$, which is then converted into a mask matrix $H_i\in \{\mathrm{0,1}{\}}^{B\times 1\times H\times W}$ through the Gumbel–Softmax technique [29]. The formula is as follows:

$$H_i=\left\{\begin{array}{ll}\sigma \left({\displaystyle \frac{S_i+g_1-g_2}{\tau }}\right)>0.5& \mathrm{for} \mathrm{training} \\ S_i>0& \mathrm{for} \mathrm{inference} \end{array}\right.$$

(5)

where $g_1,g_2\in {\mathbb{R}}^{B\times 1\times H\times W}$ represent two random Gumbel noises, $\sigma$ is the Sigmoid function, and $\tau$ is the temperature parameter in the Gumbel–Softmax, set to 1 in the experiments.

According to the formula, during inference, only the regions where the mask value is 1 are involved in convolution, thereby reducing the overall computational cost. The sparsity of $H_i$ is controlled by the mask ratio $r\in \left[\mathrm{0,1}\right]$. In existing studies, the manually set mask ratio is typically greater than 0.9. Since the detection framework of the base detector includes a classification head and a regression head, which typically focus on different areas, we introduce a separate mask network for each detection head. Each detection head uses four context-enhanced layers and one convolute layer for prediction.

As mentioned in [30], background information, such as the surrounding background of an object, is helpful for object detection. However, sparse convolution, by focusing convolution on the foreground, may sometimes neglect background areas that contain useful information, potentially reducing overall accuracy, especially when small objects dominate. To address this, the authors of [31] attempted to recover surrounding context information through interpolation, but due to the significant difference between the focal region and the background, this method is not reliable. In this section, we construct a global context enhancement module that jointly utilizes focal information and global context to enhance the missing edge information and fine-grained features in blurry images, while simultaneously improving the stability of subsequent computations.

As shown in Figure 5, we apply point convolution to the feature map $X_i$ to generate the global context feature $G_i$. Since only a small number of elements are processed in sparse convolution, after several rounds of $\mathrm{S}\mathrm{C},G_i$ stabilizes and does not incur significant additional computational overhead.

As an important part of sparse convolution, global context information $G_i$ is embedded into the context-enhanced layer. This layer takes $X_{(i,j)},H_i$, and $G_i$ as input, where $j$ represents the context-enhanced layer at the $j$-th level. Unlike traditional SC, which uses activation elements to compute the statistics for group normalization (GN), we use the mean and standard deviation of $G_i$ for normalization, aiming to compensate for the missing context information. Let $L_{(i,j)}$ be the output feature map after applying SC to $X_{(i,j)}$, then the enhanced feature $F_{(i,j)}$ is obtained by context-enhanced normalization (CE-GN), as shown in the following equation:

$$F_{(i,j)}=w\times {\displaystyle \frac{L_{(i,j)}-\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left[G_i\right]}{\mathrm{s}\mathrm{t}\mathrm{d}\left[G_i\right]}}+b$$

(6)

where mean[.] and std[.] represent the mean and standard deviation, respectively, and w and b are learnable parameters. To further alleviate information loss in sparse convolution and stabilize the training process, we maintain standard dense convolution during training to generate a feature map $C_{(i,j)}$ obtained by convolution over the complete input feature map. Then, by optimizing the mean squared error loss, $C_{(i,j)}$ is used to enhance the sparse feature map $F_{(i,j)}$, with the optimization objective as follows:

$$L_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}}={\displaystyle \frac{1}{4L}}\sum _{i=1}^L\sum _{j=1}^4{∥C_{(i,j)}\times H_i-F_{(i,j)}∥}^2$$

(7)

where $L$ is the number of layers in the Neck.

Finally, a residual structure is applied before the activation layer, adding $G_i$ to $F_{(i,j)}$, i.e., $F_{(i,j)}:=F_{(i,j)}+G_i$, to enhance the retention of context information. The full architecture of the context-enhanced sparse convolution module and context-enhanced normalization layer is shown in Figure 5.

Without additional constraints, sparse detectors tend to generate masks with large activation ratios or small mask ratios to improve accuracy, thereby increasing overall computational cost. To solve this issue, most existing approaches use a fixed activation ratio. However, due to the significant fluctuations of foreground regions in air-to-ground images, a fixed ratio often leads to a significant increase in computation or reduces accuracy due to insufficient foreground coverage. To balance accuracy and efficiency, we use an adaptive multi-layer mask scheme (AMM) that can adaptively control the activation ratio.

Specifically, AMM first estimates an optimal mask ratio based on the ground truth labels. By utilizing label assignment techniques, for the $i$-th Neck layer, we obtain the ground truth classification result $C_i\in {\mathbb{R}}^{h_i\times w_i\times c}$, where $C$ represents the number of classes (including background), and $h_i$ and $w_i$ represent the height and width of the feature map. The estimation formula for the optimal activation ratio $P_i$ in the $i$-th Neck layer is as follows:

$$P_i={\displaystyle \frac{\mathrm{P}\mathrm{o}\mathrm{s}\left(C_i\right)}{\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{l}\left(C_i\right)}}$$

(8)

where $\mathrm{P}\mathrm{o}\mathrm{s}\left(C_i\right)$ and $\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{l}\left(C_i\right)$ represent the number of positive sample pixels and the total number of pixels, respectively.

To guide the network to generate masks with appropriate mask ratios adaptively, the following loss function is used:

$$L_{\mathrm{a}\mathrm{m}\mathrm{m}}={\displaystyle \frac{1}{L}}\sum _i{\left({\displaystyle \frac{\mathrm{P}\mathrm{o}\mathrm{s}\left(H_i\right)}{\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{l}\left(H_i\right)}}-P_i\right)}^2$$

(9)

where ${\displaystyle \frac{\mathrm{P}\mathrm{o}\mathrm{s}\left(H_i\right)}{\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{l}\left(H_i\right)}}$ represents the activation ratio of the mask $H_i$. By minimizing $L_{\mathrm{amm}, }{H}_i$ is forced to follow the same activation ratio as the ground truth foreground ratio $P_i$, thus promoting the generation of an appropriate mask ratio.

By adding the traditional detection loss $L_{\det }$, the overall training loss is formulated as follows:

$$L=L_{\mathrm{d}\mathrm{e}\mathrm{t}}+\alpha \times L_{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}}+\beta \times L_{\mathrm{a}\mathrm{m}\mathrm{m}}$$

(10)

where $\alpha$ and $\beta$ are hyperparameters used to balance the importance of $L_{\mathrm{norm} }$ and $L_{\mathrm{amm}, }$ set to 1 and 10 in the experiments.

3.2. Trajectory Prediction

The adaptive bidirectional long short-term memory (LSTM) network combined with meta-learning built in this paper can effectively improve the model’s performance. Meta-learning learns a universal model initialization across multiple tasks, enabling the model to quickly adapt when facing new tasks. This is particularly significant for trajectory prediction in multi-object tracking tasks, especially in cross-scene or dynamically changing scenes. This method can quickly optimize model parameters using a small amount of historical target trajectory data, reducing adaptation time across scenes and tasks. By teaching the model how to quickly extract useful information from a small amount of data, it enhances the model’s adaptability; the structure is shown in Figure 6.

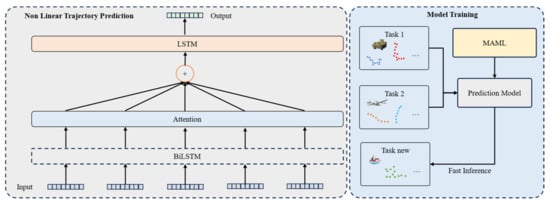
Figure 6. Framework of trajectory prediction.

In meta-learning, the basic unit of training is a task, and the objectives of each task are different. For example, in a trajectory prediction meta-learning task, Task 1 may involve car trajectory prediction, while Task 2 involves aircraft and tank trajectory prediction. The learning data consist of a training task set and a test task set, and each task as a basic unit includes its own training and testing data. To facilitate understanding and distinction, the training set within a task is referred to as the support dataset, and the test set is referred to as the query dataset.

This section is based on MAML (Model-Agnostic Meta-Learning), where the MAML algorithm first randomly initializes the model weights during the model training process. Then, a loop is used to enter each training round. In each training round, a batch of tasks is sampled from the task distribution. Next, for each task, the trajectories and labels are obtained from the support set, and for each trajectory, forward propagation is performed, followed by gradient calculation. The task-specific model weights $\widehat{\theta }$ are updated using the learning rate $\alpha$ through backpropagation. Then, the corresponding task is taken from the query set, and forward propagation is performed without updating the model parameters. Finally, the losses calculated from $\widehat{\theta }$ are summed, and the gradient is computed to update the global model weights $\varnothing$ using the meta-learning rate $\beta$. The specific process flow is shown in Figure 7. The mathematical expression for updating model parameters during the training process is as follows:

$$\widehat{\theta }=\varnothing -\alpha {\nabla }_{\varnothing }l(\varnothing )$$

(11)

where $\varnothing$ represents the initial weights learned from meta-learning, which are the initialization parameters for all training tasks. $l(\varnothing )$ is the loss for the support set task, and ${\nabla }_{\varnothing }l(\varnothing )$ is the gradient of the loss. $\alpha$ represents the learning rate for the task and is independent of the meta-learning rate $\beta$. The gradient parameter update for meta-learning is expressed as follows:

$$\varnothing \leftarrow \varnothing -\beta {\nabla }_{\varnothing }L(\varnothing )$$

(12)

where $\beta$ is the meta-learning rate, determining the step size for each gradient update.

$$L(\varnothing )=\sum _{n=1}^N{l}^n\left({\widehat{\theta }}^n\right)$$

(13)

where ${\widehat{\theta }}^n$ represents the model parameters learned from the $n$-th task, depending on the initial weights $\varnothing ,N$ is the number of tasks, and $l^n\left({\widehat{\theta }}^n\right)$ is the loss function value for the $n$-th task. The gradient computation is as follows:

$${\nabla }_{\varnothing }L(\varnothing )={\nabla }_{\varnothing }\sum _{n=1}^N{l}^n\left({\widehat{\theta }}^n\right)=\sum _{n=1}^N{\nabla }_{\varnothing }{l}^n\left({\widehat{\theta }}^n\right)$$

(14)

$$\nabla l(\widehat{\theta })=\left[{\displaystyle \frac{\partial l\left(\widehat{\theta }\right)}{\partial {\varnothing }_1}},{\displaystyle \frac{\partial l\left(\widehat{\theta }\right)}{\partial {\varnothing }_2}},\dots ,{\displaystyle \frac{\partial l\left(\widehat{\theta }\right)}{\partial {\varnothing }_i}},\dots \right]$$

(15)

$${\displaystyle \frac{\partial l\left(\widehat{\theta }\right)}{\partial {\varnothing }_i}}=\sum _j\left({\displaystyle \frac{\partial l\left(\widehat{\theta }\right)}{\partial {\widehat{\theta }}_j}}{\displaystyle \frac{\partial {\widehat{\theta }}_j}{\partial {\varnothing }_i}}\right)$$

(16)

$${\widehat{\theta }}_j={\varnothing }_j-\alpha {\displaystyle \frac{\partial l(\varnothing )}{\partial {\varnothing }_j}}$$

(17)

The above formula shows the calculation process of $\nabla l\left(\widehat{\theta }\right)$. The MAML method does not make assumptions about the form of the model, such as Bidirectional Long Short-Term Memory (BiLSTM) networks, which are commonly used for sequence prediction tasks. This flexibility is why it is referred to as the model-agnostic meta-learning method. Additionally, the MAML method does not introduce extra parameters for meta-learning, and the training method is based on traditional gradient descent, making it simple and efficient. However, since the goal of this method is to train a set of generalized initial weights, it cannot alter the structural parameters of the model. Therefore, the MAML method can only be applied when the model structure is already determined. The operational steps for the MAML-based trajectory prediction model are shown in Algorithms 1 and Figure 8.

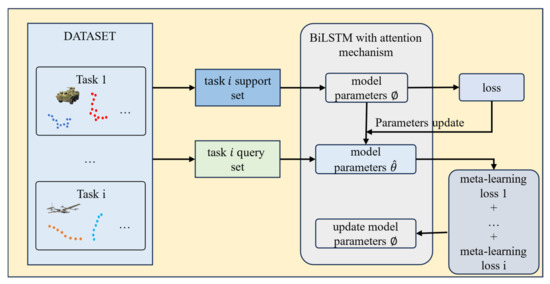
Figure 7. Adaptive trajectory prediction flow chart combined with MAML.

Algorithms 1. The operational steps for the MAML-based trajectory prediction model.
Initialize the weights of the Bidirectional Long Short-Term Memory (BiLSTM) network as ${\theta }_{\mathrm{BiLSTM} }$, the attention mechanism parameters as ${\theta }_{\mathrm{attention} }$, and the meta-learning optimization parameters (learning rates $\alpha$ and $\beta$).
1.	Select a task $D_i=\left\{D_i^{\mathrm{support} },D_i^{\mathrm{query} }\right\}$ from the task set $D$.
2.	Update the task-specific parameters ${\theta }_i^{\prime }$ from the support set $D_i^{\mathrm{support} }$:${ \theta }_i^{\prime }=\theta -\alpha {\nabla }_{\theta }{L}_i^{\mathrm{support} }\left(\theta \right)$
3.	Update the general parameters $\theta$ based on the query set $D_i^{\mathrm{query} }$: $\theta \leftarrow \theta -\beta {\nabla }_{\theta }\sum _{i=1}^N{L}_i^{\mathrm{query} }\left({\theta }_i^{\prime }\right)$
4.	On new task data $D_{\mathrm{new} }^{\mathrm{train} }$, use the meta-learned parameters ${\theta }^{\mathrm{*}}$ to quickly adjust with a small amount of data: ${\theta }_{\mathrm{new} }^{\prime }={\theta }^{\mathrm{*}}-\alpha {\nabla }_{\theta }{L}_{\mathrm{new} }^{\mathrm{support} }\left({\theta }^{\mathrm{*}}\right)$
5.	Input historical trajectory data: $\left\{x_t,y_t,v_t,a_t\right\}$
6.	Extract time-series features:$h_t=\left[{\overrightarrow{h}}_t;\widehat{h_t}\right]$
7.	Calculate the time-step weights: ${\alpha }_t={\displaystyle \frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(e_t\right)}{\sum _{k=1}^T\mathrm{e}\mathrm{x}\mathrm{p}\left(e_k\right)}},e_t=v^{\mathrm{\top }}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(W_h{h}_t+b_h\right)$
8.	Sum the weighted hidden states: $h_{\mathrm{a}\mathrm{t}\mathrm{t}}=\sum _{t=1}^T{\alpha }_t{h}_t$
9.	Use a fully connected layer to generate future trajectory points: $\left\{{\widehat{x}}_{t+1},{\widehat{y}}_{t+1}\right\}$

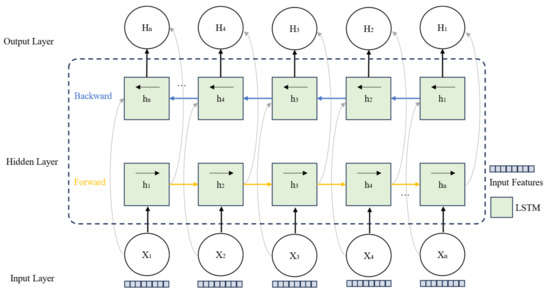
Figure 8. BiLSTM structure diagram.

3.3. Re-Identification

The method developed in this section integrates the geometric position and appearance information of the targets, combined with the parameter information provided by the drone, to convert the target position from image coordinates to world coordinates, thereby enabling accurate cross-frame association of targets. By utilizing the target trajectory memory map in the world coordinate system and integrating multi-source information with Dempster–Shafer (DS) theory, the method is designed to enhance the accuracy of target re-identification and the stability of multi-object tracking in complex scenarios such as occlusion or targets leaving and re-entering the field of view.

3.3.1. Unidirectional Extrapolation and World Coordinate Transformation

By utilizing the rich metadata provided by the drone, including longitude, latitude, altitude, pitch angle, and yaw angle, we can construct a camera model and build the world coordinates based on 3D geometry, as shown in Figure 9.

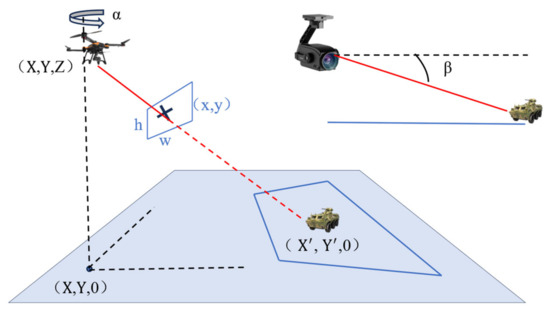
Figure 9. Framework of coordinate transformation.

The intrinsic parameters of the camera can be obtained from the field of view, and the process for calculating coordinate transformation is as follows [32]:

$$K=\left[\begin{array}{ccc}{\displaystyle \frac{w}{2\mathrm{t}\mathrm{a}\mathrm{n}\left(\frac{fov}{2}\right)}}& 0& {\displaystyle \frac{w}{2}}\\ 0& {\displaystyle \frac{w}{2\mathrm{t}\mathrm{a}\mathrm{n}\left(\frac{fov}{2}\right)}}& {\displaystyle \frac{h}{2}}\\ 0& 0& 0\end{array}\right]$$

(18)

where $w$ and $h$ are the image width and height, and $fov$ is the diagonal field of view angle of the camera.

$$fov=2\cdot \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left({\displaystyle \frac{d}{2f}}\right)$$

(19)

where $d$ is the sensor diagonal size and $f$ is the focal length of the lens. Using the data provided by the drone, a rotation matrix between the camera coordinates and the world coordinates can be established for each frame:

$$R(\alpha ,\beta ,0)=\left[\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\beta \right)& -\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha \right)& \mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha \right)\mathrm{s}\mathrm{i}\mathrm{n}\left(\beta \right)\\ \mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\beta \right)& \mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha \right)& \mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha \right)\mathrm{s}\mathrm{i}\mathrm{n}\left(\beta \right)\\ -\mathrm{s}\mathrm{i}\mathrm{n}\left(\beta \right)& 0& \mathrm{c}\mathrm{o}\mathrm{s}\left(\beta \right)\end{array}\right]$$

(20)

where $\alpha$ and $\beta$ are the yaw and pitch angles of the drone’s payload. Specifically, $\alpha ={90}^{\circ }-$ the yaw angle of the payload, and $\beta$ is the pitch angle, with both angles given by the world information data. Combining $K$ and $R$, any detected object $X_i^{2D}$ and its corresponding image coordinates $x_i$ can be projected onto the world coordinates using the 3D direction vector:

$$ra{y}_i=R\cdot K^{-1}\cdot x_i/∥x_i∥\in {\mathbb{R}}^3$$

(21)

Finally, using the altitude information $h$, we compute the intersection of the ray with the ground, assuming the ground is the plane $z=0$:

$$X_i^{3D}={\mathrm{L}\mathrm{o}\mathrm{c}}_{\mathrm{object} }={\mathrm{L}\mathrm{o}\mathrm{c}}_{\mathrm{drone} }+{\displaystyle \frac{Z_{\mathrm{drone} }}{Z_{\mathrm{ray} }}}\cdot ra{y}_i$$

(22)

${\mathrm{L}\mathrm{o}\mathrm{c}}_{\mathrm{object} }$ represents the 3D coordinates of the object in the world coordinate system, ${\mathrm{L}\mathrm{o}\mathrm{c}}_{\mathrm{drone} }$ represents the 3D coordinates of the drone in the world coordinate system, $Z_{\mathrm{drone} }$ represents the height of the drone above the horizontal plane, and $ra{y}_i$ is the direction vector of the target ray, indicating the spatial direction of the target relative to the camera. $Z_{\mathrm{ray} }$ is the value in $ra{y}_i$ that represents the vertical direction. ${\displaystyle \frac{Z_{\mathrm{drone} }}{Z_{\mathrm{ray} }}}$ is the proportion of the vertical distance between the camera and the target, used to calculate the specific 3D intersection point along the ray $ra{y}_i$. The basis of this formula lies in the pinhole camera model and the calculation process of the intersection between a ray and a plane.

For cases where the drone or payload experiences vibration but the target has not left the window, the key is to effectively associate the target that has not left the image, preventing track fragmentation. This typically occurs within a short time window. Given the limited time, we use a direct calculation method based on world coordinates. This approach allows for more efficient tracking and enhances the ability to maintain continuous target tracking under dynamic and challenging conditions.

For each detection at frame $t$, the world coordinates $X_t^{3D}$ are computed using the drone data $m_t$ (GPS, altitude, payload orientation) and the projection $H(\cdot )$, as follows:

$$X_t^{3D}=H\left(m_t\right)\left({\widehat{X}}_t^{2D}\right)$$

(23)

where ${\widehat{X}}^{2D}$ represents the center of the bounding box $X^{2D}$. The bounding box represents the target frame of the object outlined in the image.

For targets that are occluded or leave and re-enter the field of view, we need to closely monitor their potential movement outside the image view. This section introduces the key part of the unidirectional motion extrapolation method. The bidirectional motion extrapolation method is a simple technique that can extrapolate the world coordinates of trajectories leaving the image. Given some trajectories $T_i=\left\{X_{\left(t_n^{\mathrm{enter} }\right)},\dots ,X_{\left(t_t^{\mathrm{exit} }\right)}\right\}$, which enter and leave the image between frames $t^{\mathrm{enter} }$ and $t^{\mathrm{exit} }$, the world coordinates of $T_i$ at time $t^{\prime }$ can be forward-extrapolated as follows:

$$T_i^{3D}=X_{\left(t_i^{\mathrm{xit} }\right)}^{3D}+\mathsf{\Delta }t\cdot V_{\left(T_i\right)}^{\mathrm{exit} }, \mathrm{if} \mathsf{\Delta }t<{\tau }_{\mathrm{memory} }$$

(24)

where $\mathsf{\Delta }t=t^{\prime }-t^{\mathrm{exit} }$, and the velocity of the trajectory as it leaves the field of view is estimated as the following:

$$V_{\left(T_i\right)}^{\mathrm{exit} }={\displaystyle \frac{X_{\left(t_i^{\mathrm{exit} }\right)}^{3D}-X_{\left(t_i^{\mathrm{exit} }-w\right)}^{3D}}{w}}$$

(25)

where $w$ is the window size, a constant. It is assumed that no further inference will be made after a certain time ${\tau }_{\mathrm{memory} }$ because the world coordinates after this time tend to become unreliable and may be confused with new trajectories.

3.3.2. Information Fusion Association Based on DS Theory

Through the constructions in previous chapters, the information available during the information fusion association phase includes three sets of boxes: the trajectory boxes of the tracked targets from previous sequences, the detection boxes from the current frame, and the predicted boxes for the current frame based on previous trajectory boxes.

The detection boxes and predicted boxes are converted to world coordinates using the world coordinate mapping relationship mentioned earlier. Then, the geometric distance cost between the detection and predicted boxes is calculated as follows:

$$C_{\mathrm{geo} }\left(T_i,D_j\right)={∥T_i^{\mathrm{pred} }-X_j^{3D}∥}^2$$

(26)

where $T_i^{\mathrm{pred} }$ is the world coordinate of the trajectory box, and $X_j^{3D}$ is the world coordinate of the detection box. If the error in world coordinates is small, it indicates that the detection box and trajectory box are likely to belong to the same target.

The detection box and trajectory box utilize a convolutional neural network to extract features from the target regions of the boxes, and then the appearance cost between the detection box and trajectory box is computed using the cosine distance, as follows:

$$C_{\mathrm{app} }\left(T_i,D_j\right)=1-\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{F}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\left(T_i\right), \mathrm{Feature} \left(D_j\right)\right)$$

(27)

where $T_i$ is the trajectory box, $D_j$ is the detection box, and if the feature similarity is high, it suggests that they may belong to the same target. The function “Feature” represents the feature extraction function of the CNN, and VGG16 is used as the feature extraction network, with an output of 128 dimensional features.

After obtaining this information, how to use it for association matching is the key. During association matching, the reliability of different information sources needs to be considered. First, due to factors such as occlusion and target scale variation, relying solely on one information source may not be reliable. Additionally, different information sources may lead to contradictory association conclusions, for example, a small geometric distance but mismatched appearance features. Moreover, the weight of different information sources may vary depending on the scene. For instance, in occlusion scenarios, appearance features are more reliable, while in fast-moving scenarios, geometric information becomes more important.

DS theory, through belief assignment and evidence fusion, effectively handles the uncertainty and conflicts of information and provides a flexible mathematical framework for multi-source information fusion. First, by separating confidence and plausibility, DS theory can explicitly express the range of uncertainty of information. Second, the evidence fusion rule in DS theory can reasonably combine information from different sources to generate a global fusion result. Furthermore, DS theory increases the robustness of the fusion result by appropriately allocating the influence of conflicting evidence.

DS theory is a mathematical framework based on set theory, primarily used for uncertainty reasoning and decision-making. Its core includes the following:

(1)

Hypothesis Space: Define a hypothesis space $\Theta$ that contains all possible target matching results.

$$\Theta =\{\mathrm{“}\mathrm{Same}\mathrm{”},\mathrm{“}\mathrm{Different}\mathrm{”}\}$$

(28)

This represents whether two boxes belong to the same target.

(2)

Basic Belief Assignment (BBA): The belief assignment $m\left(A\right)$ represents the degree of support for hypothesis $A\subseteq \Theta$, satisfying the following:

$$m:2^{\Theta }\to [\mathrm{0,1}],\sum _{A\subseteq \Theta }m(A)=1,m(\mathrm{\varnothing })=0$$

(29)

(3)

Belief (Bel): The belief $\mathrm{B}\mathrm{e}\mathrm{l}\left(A\right)$ represents the minimum degree of support for hypothesis $A$, i.e., the total belief in $A$ and all of its subsets:

$$\mathrm{B}\mathrm{e}\mathrm{l}(A)=\sum _{B\subseteq A}m(B)$$

(30)

(4)

Plausibility (PI): The plausibility $\mathrm{P}\mathrm{l}\left(A\right)$ represents the possibility that $A$ is true, including all sets that support $A$ and those that overlap with other hypotheses:

$$\mathrm{P}\mathrm{l}(A)=\sum _{B\cap A\ne \mathrm{\varnothing }}m(B)$$

(31)

(5)

Uncertainty: The difference between belief and plausibility reflects the uncertainty of the evidence:

$$\mathrm{P}\mathrm{l}\left(A\right)-\mathrm{B}\mathrm{e}\mathrm{l}\left(A\right)$$

(32)

For two independent information sources $m_1$ and $m_2$, the DS theory evidence fusion rule is as follows:

$$m(C)={\displaystyle \frac{\sum _{A\cap B=C}{m}_1\left(A\right)\cdot m_2\left(B\right)}{1-\sum _{A\cap B=\mathrm{\varnothing }}{m}_1\left(A\right)\cdot m_2\left(B\right)}}$$

(33)

where $A,B,C$ are subsets of the hypothesis space. The numerator calculates the joint evidence supporting $C$, and the denominator excludes the influence of conflicting evidence.

In multi-object tracking, the two information sources are the appearance cost $C_{\mathrm{app} }$ and the geometric distance cost $C_{\mathrm{geo} }$. For each information source, the basic belief assignment (BBA) is constructed:

For appearance cost:

$$m_{\mathrm{app} }(\mathrm{“}\mathrm{Same}”)=1-C_{\mathrm{app} },m_{\mathrm{app} }(\mathrm{“}\mathrm{Different}”)=C_{\mathrm{app} }$$

(34)

For geometric cost:

$$m_{\mathrm{geo} }(\mathrm{“}\mathrm{Same}”)=1-C_{\mathrm{geo} },m_{\mathrm{geo} }\left(\mathrm{“}Different\mathrm{”}\right)=C_{\mathrm{geo} }$$

(35)

Using the DS theory evidence fusion rule, the appearance and geometric information are fused as follows:

$$m_{\mathrm{fused} }(H)={\displaystyle \frac{\sum _{A\cap B=H}{m}_{\mathrm{app} }\left(A\right)\cdot m_{\mathrm{geo} }\left(B\right)}{1-\sum _{A\cap B=\mathrm{\varnothing }}{m}_{\mathrm{app} }\left(A\right)\cdot m_{\mathrm{geo} }\left(B\right)}}$$

(36)

where $H\in \{$“Same”,”Different”$\}$.

Finally, the fused matching cost is calculated through confidence:

$$C_{\mathrm{fused} }=1-m_{\mathrm{fused} }\left(\mathrm{“}Same\mathrm{”}\right)$$

(37)

The fused matching cost matrix is constructed, where the elements $C_{(i,j)}$ represent the matching cost $C_{\mathrm{fused} }$ between trajectory box $i$ and detection box $j$:

$$C_{(i,j)}=\left\{\begin{array}{ll}{C}_{\mathrm{fused} }& \mathrm{if} C_{\mathrm{fused} }\le {\tau }_{\mathrm{match} }\\ \mathrm{\infty }& \mathrm{if} C_{\mathrm{fused} }>{\tau }_{\mathrm{match} }\end{array}\right.$$

(38)

This cost matrix is used for the Hungarian algorithm to perform matching and find the optimal match, thereby updating the tracking trajectory.

4. Experiments

We evaluate the effectiveness of the proposed method by comparing it with existing multi-object tracking approaches and conducting comprehensive ablation studies.

4.1. Datasets

Most existing datasets mainly focus on pedestrian or vehicle targets in limited environments, such as urban areas or roads, with little consideration of drone perspectives and electro-optical payload parameters. Therefore, constructing a dedicated dataset with diverse scenes and integrating drone flight parameters has become key to improving the performance of air-to-ground multi-target tracking systems. To meet the algorithm validation needs of this paper, we have constructed a large-scale and challenging drone detection and tracking dataset, the MIDDTD. The MIDDTD dataset covers multiple representative scenes, including mountains, urban areas, deserts, villages, and fields, each with distinct geographical environments and background characteristics. This allows for effective testing of multi-target tracking algorithms in complex environments. The dataset design includes three essential tasks: object detection, single-target tracking (SOT), and multi-target tracking, with rich drone-related information annotated in each frame, including GPS data, flight altitude, and electro-optical payload information. Through the design of the dataset, scene division, and the integration of multi-source information, the dataset not only enhances its comprehensiveness and complexity but also provides strong support for the validation of drone-based multi-target tracking and detection algorithms.

Detailed Data Acquisition Process

During data collection, a DJI M210 drone was used for flight acquisition, equipped with a Syuwei ZT6 electro-optical payload. The drone’s corresponding height and GPS information were obtained in real time through the DJI SDK via a Jetson Xavier NX. Additionally, the Jetson Xavier NX communicated with the electro-optical payload via serial port, and real-time attitude data of the payload were retrieved using SDK commands. The camera’s focal length was 20 mm, and its diagonal field of view ($fov$) was 93°. The filming process focused on areas such as the urban district of Xi’an, surrounding mountainous fields, and desert regions near Wuhai. The data acquisition process is shown in Figure 10, below. Over the course of one week, 114 raw video segments were captured, each ranging from 30 s to 5 min in length, with a frame rate of 30 frames per second and a resolution of 1920 × 1080 pixels. After post-processing, including video screening and trimming, 110 video sequences were retained, totaling approximately 99,000 frames. Each video sequence contains between 294 and 2684 frames.

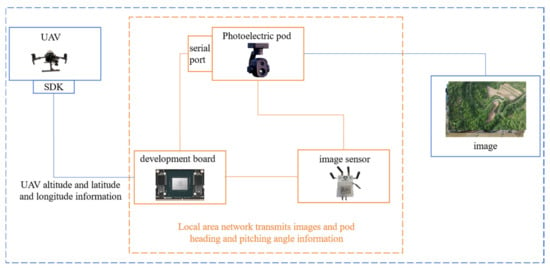
Figure 10. Data acquisition flow chart.

For data annotation, the DarkLabel open-source labeling tool was used. After labeling, the data underwent five rounds of re-checking to ensure accuracy. The final annotations are summarized as follows: the dataset contains 110 video sequences with 99,000 frames, marking approximately 2100 pedestrian and vehicle targets, with around 750,000 bounding boxes. Additionally, each frame includes annotated information on the drone’s altitude, latitude and longitude, as well as the electro-optical payload’s heading and pitch angles.

The dataset defines several different scenes, including mountain, field, desert, urban, and village environments. The filming altitude ranged from 50 m to 600 m, with video durations ranging from 10 to 90 s. The primary target category is vehicles, with a small number of personnel targets. Based on different filming altitudes, the dataset is categorized into low altitude (50–200 m), mid altitude (200–400 m), and high altitude (>400 m). Based on video duration, the dataset is classified into short-duration (10–60 s) and long-duration (60–90 s). Additionally, based on the Sobel gradient mean size of the images, the dataset is divided into clear (gradient mean >= 15) and blurred (gradient mean < 15). For each video, 10 random frames are sampled, and if more than four of them are blurred, the video is classified as blurred; the specific distribution is shown in Figure 11, below.

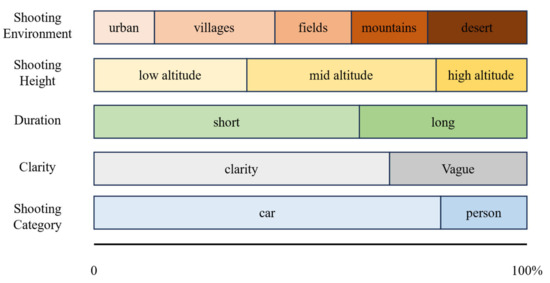
Figure 11. MIDDTD attribute distribution map.

Compared to existing datasets, the dataset constructed in this section may not have the largest number of frames or detection target boxes, but it includes valuable drone and electro-optical payload parameter information for complex ground scenes, which are not found in other datasets.

4.2. Implementation Details

4.2.1. Detection Experiment

We built the code framework in PyTorch 1.10, and the entire training process was conducted on a computer equipped with a single NVIDIA GeForce RTX 4090 GPU. Testing was performed on an Nvidia Jetson Xavier NX edge device.

To ensure the relative feature integrity of small targets, the image size was kept at the original resolution of 1920 × 1080. During network training, the Adam optimizer was used with an initial learning rate of 0.0001, and the learning rate was adjusted using a cosine annealing strategy.

4.2.2. Trajectory Prediction Experiment

To conduct a comprehensive evaluation of the method, the model parameters were first initialized in the experimental implementation. The hidden layer dimension of the bidirectional long short-term memory (BiLSTM) network was set to 128, and the parameters of the temporal attention mechanism were also initialized simultaneously. The learning rates were set as $\alpha =0.001$ for inner optimization and $\beta =0.0001$ for outer optimization.

In the data processing phase, the input trajectory data were normalized, and the trajectories were divided into historical and future trajectories. The length of the historical trajectory was set to 5, while the length of the predicted trajectory was set to 1. If there was no historical trajectory or the historical trajectory length was small at the initial frame, the previous frame was repeated for prediction. Subsequently, a sliding window approach was used to utilize historical trajectory information. Additionally, a batch size of 32 was set to improve training efficiency.

During the meta-training phase, the model was optimized using data from multiple tasks. For each task, the task-specific parameters were adjusted through inner optimization, and then the model’s general parameters were updated via outer optimization, enabling it to quickly adapt to new tasks.

In the new task adaptation phase, a small amount of historical trajectory data were used to update the model parameters through fast gradient descent, achieving rapid adaptation to new scenes.

In the trajectory prediction phase, based on the adapted model, the temporal attention mechanism was used to weight the trajectory features, and future target trajectories were output through a fully connected layer.

The performance of different algorithms on test data is evaluated in detail. The contrast effect is shown in Figure 12, below. The figure below shows the experimental performance of our proposed trajectory prediction method on different trajectory datasets, along with a performance comparison with other methods. Here, X and Y represent the coordinate positions of the target on the image plane, and T represents the frame number of the image sequence where the target is located. The points in the figure indicate trajectory points.

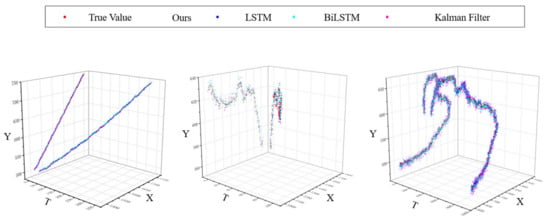
Figure 12. Demonstration of prediction effect of different trajectory prediction algorithms.

4.2.3. Re-Identification Experiment

The re-identification module maps the 2D image coordinates of the detection boxes to 3D world coordinates using the camera’s intrinsic and extrinsic parameter matrices. The intrinsic matrix is calculated using a field of view angle of ${93}^{°}$ and an image size of $1920\times 1080$. The window size $w$ used in the unidirectional extrapolation process is set to 5. The target’s lifespan ${\tau }_{\mathrm{memory} }$ is set to 30. Based on experimental comparison, the matching threshold parameter ${\tau }_{\mathrm{match} }$ is set to 0.7. Due to computational constraints and deployment considerations on UAV edge-devices, we did not directly include computationally intensive Transformer-based methods such as MOTR in our current experimental comparisons [33]. Future work will involve extending our evaluations to include such advanced approaches. Table 1 below shows the performance comparison of MIDDTD dataset on our algorithm and several mainstream tracking algorithms.

Table 1. Results on MIDDTD.

Method	MOTA↑	HOTA↑	IDF1↑	MOTP↑	IDs↓	FPS↑
DeepSORT	0.6498	0.5411	0.6541	0.8444	1304	7
DeepOcSORT	0.6509	0.6230	0.6691	0.8339	1207	6
StrongSORT	0.6497	0.6454	0.6492	0.8425	1258	7
OcSORT	0.6572	0.6182	0.6518	0.8344	1295	9
BoTSORT	0.6811	0.6344	0.6574	0.8429	1219	6
ByteTrack	0.6931	0.6554	0.6581	0.8391	1198	9
Ours	0.7246	0.6827	0.6883	0.8542	907	8

MOTP is a metric designed to assess the precision of object tracking algorithms, primarily measuring a tracker’s accuracy in localizing target positions while disregarding its identification capability and trajectory consistency. As MOTP solely provides information about localization accuracy, it is typically used in conjunction with MOTA, which focuses on evaluating trajectory consistency and matching performance of targets.

MOTA serves as a core evaluation metric in multi-object tracking tasks, specifically measuring a tracker’s capability in target detection and trajectory prediction without considering positional accuracy.

IDF1 is a crucial metric for evaluating multi-object tracking system performance, emphasizing whether a tracker can maintain identity consistency of targets throughout the tracking process. IDF1 comprehensively integrates identity precision (IDP) and identity recall (IDR), providing a unified score that reflects the tracker’s holistic performance in target identity association.

HOTA offers a singular composite score encompassing all elements of multi-object tracking evaluation, while maintaining the capability to be decomposed into sub-metrics for detailed analysis of specific aspects in tracking system performance.

Experimental results show that DeepSORT improves IDF1 through appearance features but underutilizes geometric information in dynamic scenes, resulting in lower MOTA and HOTA [34]. DeepOCSORT, combining motion consistency optimization, shows some improvement in IDF1 and HOTA, but its adaptability to dense scenes remains limited. StrongSORT enhances appearance feature extraction and performs excellently in HOTA, but the lack of geometric information limits overall performance. OcSORT focuses on motion consistency and is suitable for short-term matching, but it lacks appearance feature assistance, resulting in suboptimal IDF1. BoTSORT balances appearance and motion information, reducing ID switches, but its association strategy is somewhat lacking in complex dynamic scenes. ByteTrack significantly improves MOTA by optimizing the use of detections with different confidences. Its efficient cost-matching strategy allows faster operation, but the lack of appearance information for matching detections with different confidences leads to poorer performance in some dynamic scenes. Examples of the model tracking effect and bytetrack tracking effect in this paper are shown in the following Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17.

Figure 13. Graphical representation of multi-target tracking effect in an urban scene.

Figure 14. Graphical representation of multi-target tracking effect in a village scene.

Figure 15. Graphical representation of multi-target tracking effect in a desert scene.

Figure 16. Graphical representation of multi-target tracking effect in a mountain scene.

Figure 17. Graphical representation of multi-target tracking effect in a fields scene.

The proposed method shows relatively balanced performance in multi-object tracking tasks. Compared to existing mainstream methods, it outperforms in several key metrics, especially achieving optimal levels in the core metrics MOTA and HOTA, demonstrating a high balance between detection quality and trajectory association performance. By introducing a geometric and appearance information fusion strategy based on DS theory, the method significantly improves the accuracy of target association, with MOTP increased to 0.8542, further enhancing precise target location prediction. Combining the trajectory prediction model with the unidirectional extrapolation strategy effectively addresses the uncertainty of target motion in complex dynamic scenes. Using a world coordinate-based target location memory map reduces the number of ID switches caused by occlusion or target re-entry, with only 907 ID switches, significantly outperforming other methods. Although the fusion strategy’s computational complexity results in a slightly lower FPS than ByteTrack, it still remains at a high level. Overall, the proposed method significantly surpasses existing mainstream methods in terms of accuracy, stability, and robustness, providing a more efficient and reliable solution for multi-object tracking tasks.

4.3. Ablation Study

In this section, an ablation experiment is designed to validate the impact of introducing world coordinate transformation on the tracking performance of different algorithms. Specifically, after converting the position information in the original method to world coordinates, the cost calculation and matching decision are performed for different algorithms in the world coordinate system. The experimental results are shown in Table 2.

Table 2. Ablation study results on MIDDTD.

Method	MOTA↑	HOTA↑	IDF1↑	MOTP↑	IDs↓
DeepSORT	0.6498	0.5411	0.6541	0.8444	1304
DeepSORT+World Coordinates	0.6655	0.5827	0.6703	0.8534	1205
DeepOcSORT	0.6509	0.6230	0.6691	0.8339	1207
DeepOcSORT+World Coordinates	0.6746	0.6403	0.6783	0.8342	1127
StrongSORT	0.6497	0.6454	0.6492	0.8425	1258
StrongSORT+World Coordinates	0.6541	0.6502	0.6654	0.8455	1068
OcSORT	0.6572	0.6182	0.6518	0.8344	1295
OcSORT+World Coordinates	0.6602	0.6355	0.6503	0.8410	1172
BoTSORT	0.6811	0.6344	0.6574	0.8429	1219
BoTSORT +World Coordinates	0.6791	0.6418	0.6681	0.8532	1003
ByteTrack	0.6931	0.6554	0.6581	0.8391	1198
ByteTrack+World Coordinates	0.7152	0.6760	0.6753	0.8487	1095

The above experimental results show that the introduction of world coordinates significantly improves the performance of multi-object tracking algorithms, particularly in terms of MOTA and ID switches. By converting position information into world coordinates, the geometric association performance of each algorithm is notably enhanced, effectively reducing mismatches and ID switches caused by target occlusion, leaving the field of view, or changes in perspective. For example, DeepSORT’s ID switches decreased from 1304 to 1205, and BoTSORT’s from 1219 to 1003. ByteTrack and BoTSORT showed the most balanced performance after incorporating world coordinates, with MOTA increasing to 0.7152 and 0.6791, respectively, demonstrating a good combination of geometric information and their own high-confidence association strategies. At the same time, improvements in HOTA and MOTP reflect synchronized optimization of object detection and association accuracy. However, for algorithms like StrongSORT that heavily rely on appearance features, the enhancement effect of world coordinates is relatively limited. In terms of efficiency, the introduction of world coordinate information did not significantly increase the computational overhead. Overall, the experimental results fully validate the key role of world coordinates in improving the accuracy and robustness of multi-object tracking tasks.

In this section, the construction method is used to carry out experimental analysis for different scenarios, and the analysis results are shown in Figure 18, below.

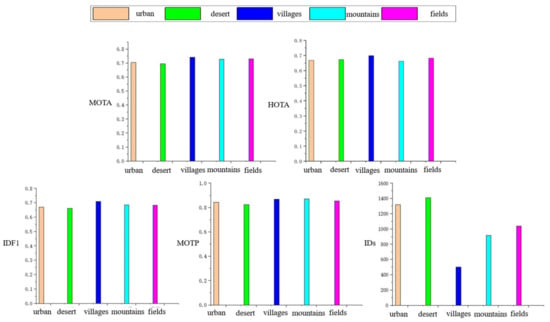
Figure 18. Analysis of multi-target tracking indicators in different scenes.

5. Conclusions

Overall, this paper focuses on multi-object tracking from an air-to-ground perspective.

• A multi-object tracking dataset from the air-to-ground perspective was constructed, containing multiple scenes and annotated with drone GPS coordinates, altitude, and payload attitude parameters. This provides an important foundation for the experiments in subsequent sections and sets evaluation benchmarks for experimental validation.
• A lightweight object detection method based on global context enhancement and layer-decoupling fusion was developed. As the core component of the multi-object tracking method in this paper, this approach improves the performance ceiling for subsequent multi-object tracking.
• A nonlinear trajectory prediction method based on an adaptive BiLSTM network was constructed, further optimizing multi-object tracking performance from the motion feature perspective.
• A target re-identification method based on coordinate data and knowledge fusion was developed. From the perspective of optimization problem solving, it converted and fused the target’s position and feature information, further enhancing the overall performance of multi-object tracking. These four approaches progressively build upon and complement each other, collectively improving the stability of the multi-object tracking system.

Although the target re-identification method based on coordinate data and knowledge fusion proposed in this paper partially addresses the issue of discontinuous target trajectories, it remains somewhat limited in scenarios that require maintaining the continuity of multiple target tracks. Multi-camera, multi-object tracking, which involves multiple drones collaboratively tracking the same scene, is a more complex task. It requires accurate alignment of the world coordinate system and maintaining information sharing and collaboration between multiple drones. On this basis, more spatial information must be obtained to improve the accuracy and stability of target tracking. In future research, we will explore this collaborative scenario in greater depth.