Rapid Optimal Matching Design of Heterogeneous Propeller Propulsion Systems for High-Altitude Unmanned Airships
Abstract
1. Introduction
2. Propulsion System Surrogate Model
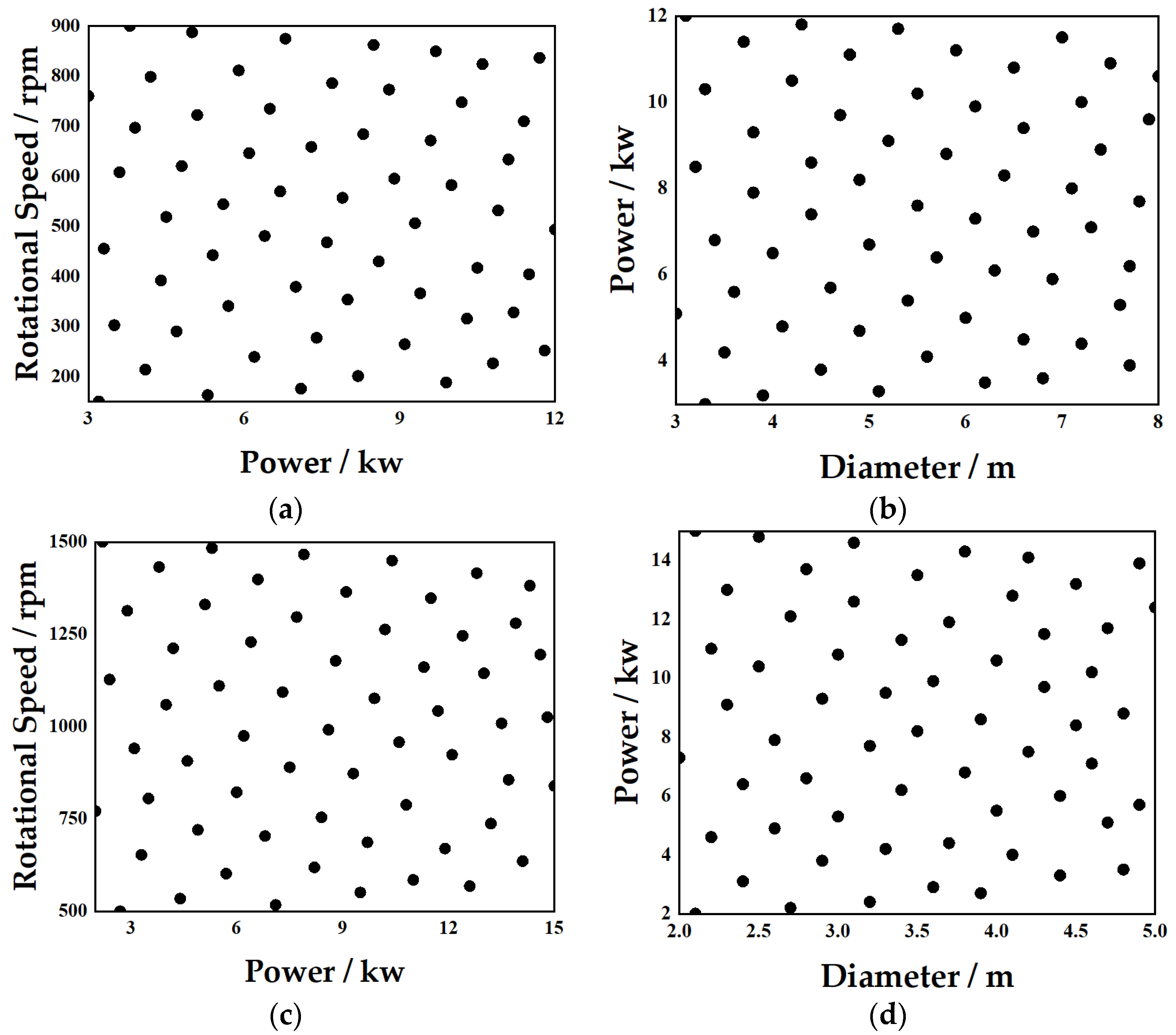
2.1. DOE
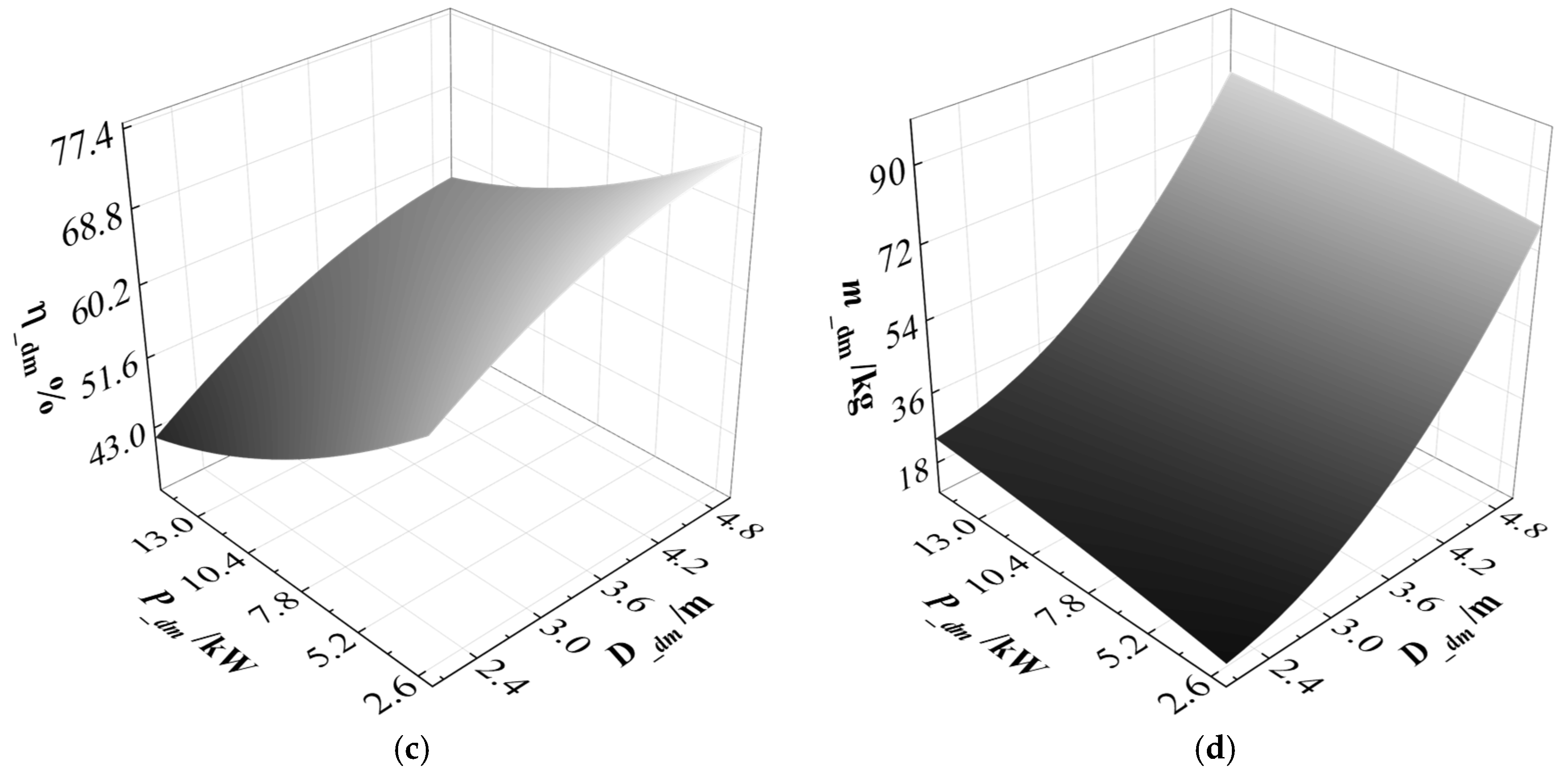
2.2. Surrogate Modeling of the Heterogeneous Propeller Propulsion System
3. Optimization Design Model of the Heterogeneous Propeller Propulsion System
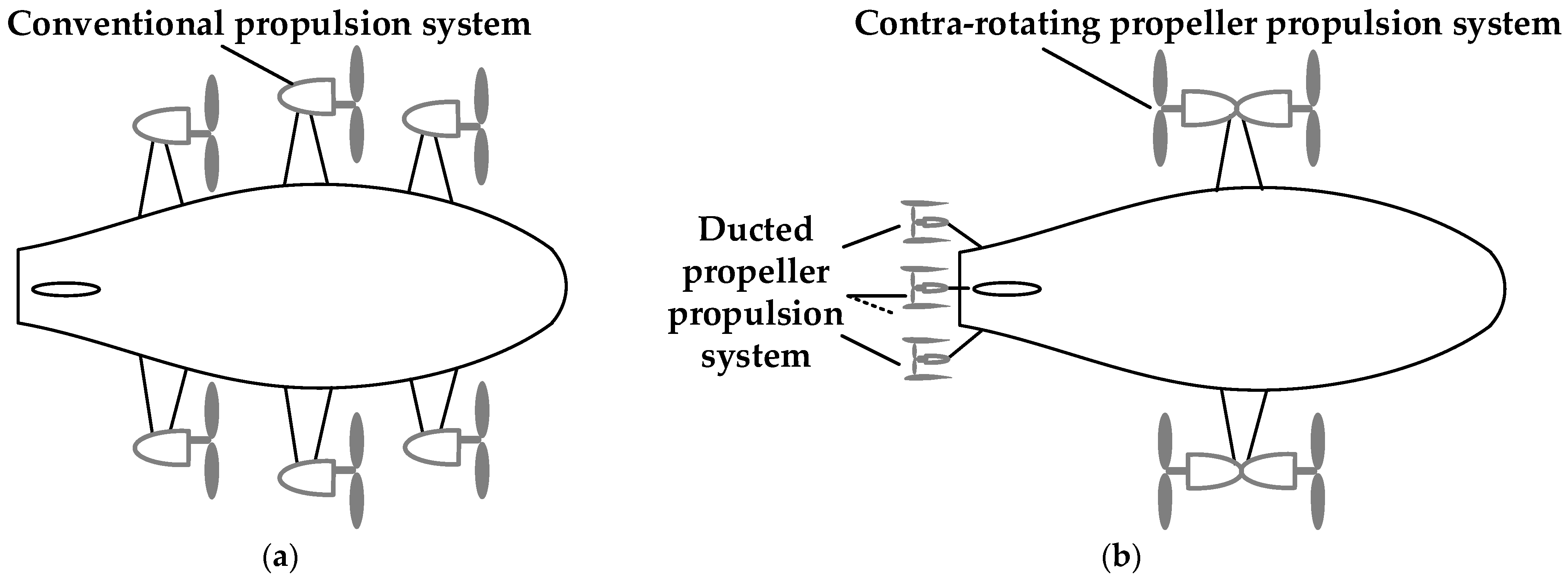
3.1. Rapid Optimization Design Process for Heterogeneous Propeller Electric Propulsion System
3.2. Objective Function
3.3. Design Variables
3.4. Constraints
3.4.1. Motor-Propeller Matching Constraint
3.4.2. Wind-Resistance Thrust-Drag Balance Constraint for High-Altitude Unmanned Airships
3.4.3. Buoyancy-Weight Balance Constraint of the Airships
3.4.4. Day-Night Energy Balance Constraint for High-Altitude Unmanned Airships
4. Results and Discussion
4.1. Optimization Results of a Heterogeneous Propeller Propulsion System
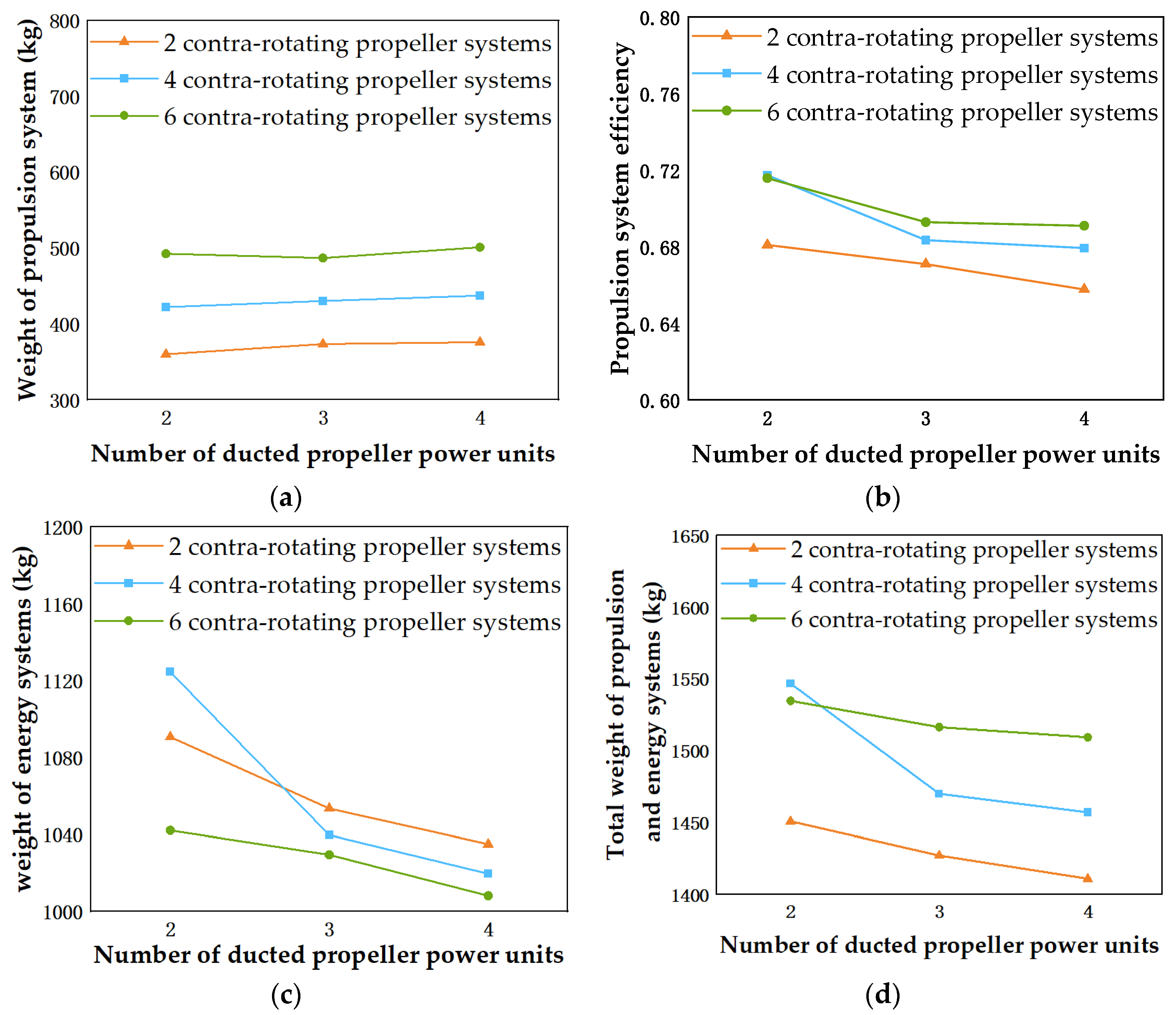
4.2. Analysis of Power Unit Configuration Ratios
5. Conclusions
- A fast optimum power unit design method was established, which combines contra-rotating and ducted propellers to minimize the total weight of the propulsion and energy systems under energy balance constraints.
- The results demonstrate that heterogeneous propulsion configurations can simultaneously reduce energy system weight and improve propulsion efficiency, thereby enhancing the overall endurance capability of high-altitude unmanned airships.
- Parametric analysis indicates that the optimal allocation of contra-rotating and ducted propeller units plays a decisive role in achieving system-level weight reduction, and the optimization framework enables efficient identification of such configurations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- D’Oliveira, F.A.; Melo, F.C.L.D.; Devezas, T.C. High-altitude platforms—Present situation and technology trends. J. Aerosp. Technol. Manag. 2016, 8, 249–262. [Google Scholar] [CrossRef]
- Huang, J. Survey on design technology of distributed electric propulsion aircraft. Acta Aeronaut. Astronaut. Sin. 2021, 42, 624037. [Google Scholar]
- Riccio, E.; Alifano, F.; Baraniello, V.R.; Coiro, D. A Comprehensive Review of Propeller Design and Propulsion Systems for High-Altitude Pseudo-Satellites. Appl. Sci. 2025, 15, 8013. [Google Scholar] [CrossRef]
- Lesieutre, D.J.; Sullivan, J.P. The analysis of counter-rotating propeller systems. SAE Trans. 1985, 94, 564–575. [Google Scholar]
- Hager, R.D. Advanced Turboprop Project; Scientific and Technical Information Division, National Aeronautics and Space Administration: Hampton, VA, USA, 1988; Volume 495. [Google Scholar]
- Hartman, E.P.; Biermann, D. The Aerodynamic Characteristics of Full-Scale Propellers Having 2, 3, and 4 Blades of Clark Y and RAF 6 Airfoil Sections; Scientific and Technical Information Division, National Aeronautics and Space Administration: Hampton, VA, USA, 1938. [Google Scholar]
- Mieloszyk, J.; Galiński, C.; Piechna, J. Contra-rotating propeller for fixed wing MAV: Part 1. Aircr. Eng. Aerosp. Technol. 2013, 85, 304–315. [Google Scholar] [CrossRef]
- Qiao, N.; Ma, T.; Fu, J.; Zhang, L.; Wang, X.; Xue, P. Rapid blade shape optimization for contra-rotating propellers for eVTOL aircraft considering the aerodynamic interference. Aerospace 2023, 10, 54. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Y.; Li, P.; Liu, Y.; Li, Q.; Noack, B. Optimal rotation speed combination of contra-rotating rotors for multicopters. In Proceedings of the AIAA AVIATION 2023 Forum, San Diego, CA, USA, 12–16 June 2023; p. 3239. [Google Scholar]
- Grunwald, K.J.; Goodson, K.W. Aerodynamic Loads on an Isolated Shrouded-Propeller Configuration of Angles of Attack from −10 Degrees to 110 Degrees; National Aeronautics and Space Administration: Washington, DC, USA, 1962. [Google Scholar]
- Yilmaz, S.; Erdem, D.; Kavsaoglu, M.S. Performance of a ducted propeller designed for UAV applications at zero angle of attack flight: An experimental study. Aerosp. Sci. Technol. 2015, 45, 376–386. [Google Scholar] [CrossRef]
- Hu, Y.; Qing, J.; Liu, Z.H.; Conrad, Z.J.; Cao, J.N.; Zhang, X.P. Hovering efficiency optimization of the ducted propeller with weight penalty taken into account. Aerosp. Sci. Technol. 2021, 117, 106937. [Google Scholar] [CrossRef]
- Akturk, A.; Shavalikul, A.; Camci, C. PIV measurements and computational study of a 5-inch ducted fan for V/STOL UAV applications. In Proceedings of the 47th AIAA aerospace sciences meeting including the new horizons forum and aerospace exposition, Orlando, FL, USA, 5–8 January 2009; p. 332. [Google Scholar]
- Akturk, A.; Camci, C. Tip clearance investigation of a ducted fan used in vtol uavs: Part 1—Baseline experiments and computational validation. In Proceedings of the ASME 2011 Turbo Expo: Power for Land, Sea, and Air, Vancouver, BC, Canada, 6–10 June 2011; pp. 331–344. [Google Scholar]
- Chen, S.; Song, B.; Wang, H. Exploring optimum power unit of propulsion system for high altitude airship. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 301–311. [Google Scholar] [CrossRef]
- Dongchen, W.; Bifeng, S.; Jun, J.; Haifeng, W. High-altitude airship propulsion system optimal design and experiment based on energy balance. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 3–16. [Google Scholar] [CrossRef]
- Riboldi, C.E.; Rolando, A.; Regazzoni, G. On the feasibility of a launcher-deployable high-altitude airship: Effects of design constraints in an optimal sizing framework. Aerospace 2022, 9, 210. [Google Scholar] [CrossRef]
- Kahol, O.; Belan, M.; Pacchiani, M.; Montenero, D. Scaling relations for the geometry of wire-to-airfoil atmospheric ionic thrusters. J. Electrost. 2023, 123, 103815. [Google Scholar] [CrossRef]
- Belan, M.; Arosti, L.; Polatti, R.; Maggi, F.; Fiorini, S.; Sottovia, F. A parametric study of electrodes geometries for atmospheric electrohydrodynamic propulsion. J. Electrost. 2021, 113, 103616. [Google Scholar] [CrossRef]
- Belan, M.; Terenzi, R.; Trovato, S.; Usuelli, D. Effects of the emitters density on the performance of an atmospheric ionic thruster. J. Electrost. 2022, 120, 103767. [Google Scholar] [CrossRef]
- Brown, A.; Xu, H.; Gilmore, C.K.; Barrett, S.R. Solid-state electroaerodynamic aircraft design using signomial programming. J. Aircr. 2024, 61, 280–290. [Google Scholar] [CrossRef]
- Lin, D.K.; Simpson, T.W.; Chen, W. Sampling strategies for computer experiments: Design and analysis. Int. J. Reliab. Appl. 2001, 2, 209–240. [Google Scholar]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef]
- Fang, K.T.; Lin, D.K.J.; Winker, P.; Zhang, Y. Uniform Design: Theory and Application. Technometrics 2000, 42, 237–248. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output From a Computer Code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Joseph, R.V.; Hung, Y. Orthogonal-Maximin Latin Hypercube Designs. Stat. Sin. 2012, 18, 171–186. [Google Scholar]
- Yi, J.; Li, X.; Xiao, M.; Xu, J.; Zhang, L. Construction of nested maximin designs based on successive local enumeration and modified novel global harmony search algorithm. Eng. Optim. 2017, 49, 161–180. [Google Scholar] [CrossRef]
- Zhang, M.; Jiao, J.; Zhang, J.; Zhang, Z. High-Efficiency Data Fusion Aerodynamic Performance Modeling Method for High-Altitude Propellers. Drones 2024, 8, 229. [Google Scholar] [CrossRef]
- Jiao, J.; Song, B.-F.; Zhang, Y.-G.; Li, Y.-B. Optimal design and experiment of propellers for high altitude airship. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 1887–1902. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1143. [Google Scholar]
- Valkov, T.V. Aerodynamic loads computation on coaxial hingeless helicopter rotors. In Proceedings of the 28th Aerospace Sciences Meeting, Reno, NV, USA, 8–11 January 1990. [Google Scholar]
- Sargent, P.B.; Anemaat, W.A. Benchmarking a robust panel code for ducted fan VTOL aircraft design. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 4212. [Google Scholar]
- Khoury, G.A. Airship Technology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Kanikdale, T.; Marathe, A.; Pant, R. Multi-Disciplinary Optimization of Airship Envelope Shape. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, NY, USA, 30 August–1 September 2004. [Google Scholar]
- Wang, H.; Song, B.; Zuo, L. Effect of High-Altitude Airship’s Attitude on Performance of its Energy System. J. Aircr. 2007, 44, 2077–2080. [Google Scholar] [CrossRef]




| Surrogate Model Method | Contra-Rotating Motor Efficiency Error | Contra-Rotating Motor Weight Error | Ducted Motor Efficiency Error | Ducted Motor Weight Error |
|---|---|---|---|---|
| RSM | 0.001% | 0.054% | 0.002% | 0.133% |
| Kriging | 0.008% | 0.322% | 0.003% | 0.302% |
| RBF | 0.072% | 2.122% | 0.047% | 1.827% |
| Surrogate Model Method | Contra-Rotating Propeller Efficiency Error | Contra-Rotating Propeller Weight Error | Ducted Propeller Efficiency Error | Ducted Propeller Weight Error |
|---|---|---|---|---|
| RSM | 0.636% | 1.914% | 1.964% | 4.268% |
| Kriging | 1.377% | 4.275% | 2.626% | 7.167% |
| RBF | 0.690% | 1.999% | 2.239% | 7.268% |
| Design Variable | Description | Unit |
|---|---|---|
| Ncp | Number of contra-rotating propeller units | / |
| Pcp | Input power of contra-rotating propellers | kW |
| Dcp | Diameter of contra-rotating propellers | m |
| Ndp | Number of ducted propeller units | / |
| Pdp | Input power of ducted propellers | kW |
| Ddp | Diameter of ducted propellers | M |
| Parameters | Description | Value |
|---|---|---|
| H | Altitude/km | 20 |
| V | Freestream wind speed/m·s−1 | 30 |
| la | Airship length/m | 120 |
| λ | Fineness ratio of the airship | 4 |
| ζhe | Ratio of helium volume to total envelope volume at operating altitude | 0.96 |
| δhe | Pressure difference coefficient of the helium envelope | 1.05 |
| Rair | Specific gas constant of air/J·kg−1·K−1 | 287.05 |
| RHe | Specific gas constant of helium/J·kg−1·K−1 | 2077 |
| Esun | Solar radiation intensity/W·m−2 | 1300 |
| ηso_in | Photovoltaic efficiency of solar cells | 0.28 |
| ηso_out | Output efficiency of solar cells | 0.95 |
| ρsc | Areal density of solar cells/kg·m−2 | 0.25 |
| ηli | Charge–discharge efficiency of energy storage battery | 0.9 |
| Eli | Energy density of energy storage battery/Wh·kg−1 | 280 |
| Parameter | Unit | Baseline Configuration | Optimal Configuration |
|---|---|---|---|
| Number of conventional propulsion units, N | / | 6 | / |
| Number of contra/rotating propeller units, Nc | / | / | 2 |
| Number of ducted propeller units, Nd | / | / | 4 |
| Diameter of conventional propeller, D | m | 5.0 | / |
| Diameter of contra/rotating propeller, Dc | m | / | 7.1 |
| Diameter of ducted propeller, Dd | m | / | 3.8 |
| Power of conventional propeller, P | kW | 14.0 | / |
| Power of contra/rotating propeller, Pc | kW | / | 14.27 |
| Power of ducted propeller, Pd | kW | / | 6.67 |
| Total weight of propulsion system, mpr | kg | 250.38 | 195.19 |
| Weight of energy system, men | kg | 1629.27 | 1034.98 |
| Total weight of propulsion and energy systems, mtotal | kg | 1879.65 | 1410.93 |
| Reduction in total weight compared with baseline | % | / | 24.94 |
| Contra-Rotating Propeller Units | Ducted Propeller Units | Total Propulsion System Weight (kg) | Propulsion System Efficiency (%) | Total Energy System Weight (kg) | Total Weight of Propulsion and Energy Systems (kg) |
|---|---|---|---|---|---|
| 2 | 2 | 360.09 | 68.09 | 1090.68 | 1450.77 |
| 2 | 3 | 373.62 | 67.10 | 1053.48 | 1427.10 |
| 2 | 4 | 375.95 | 65.77 | 1034.98 | 1410.93 |
| 4 | 2 | 422.21 | 71.73 | 1124.53 | 1546.74 |
| 4 | 3 | 430.28 | 68.35 | 1039.69 | 1469.97 |
| 4 | 4 | 437.37 | 67.93 | 1019.64 | 1457.01 |
| 6 | 2 | 492.59 | 71.59 | 1042.10 | 1534.69 |
| 6 | 3 | 486.89 | 69.29 | 1029.51 | 1516.40 |
| 6 | 4 | 501.05 | 69.89 | 1008.21 | 1509.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Wang, X.; Zhang, Z.; Wang, B.; Cheng, J.; Zhang, J. Rapid Optimal Matching Design of Heterogeneous Propeller Propulsion Systems for High-Altitude Unmanned Airships. Drones 2025, 9, 718. https://doi.org/10.3390/drones9100718
Zhang M, Wang X, Zhang Z, Wang B, Cheng J, Zhang J. Rapid Optimal Matching Design of Heterogeneous Propeller Propulsion Systems for High-Altitude Unmanned Airships. Drones. 2025; 9(10):718. https://doi.org/10.3390/drones9100718
Chicago/Turabian StyleZhang, Miao, Xiangyu Wang, Zhiwei Zhang, Bo Wang, Junjie Cheng, and Jian Zhang. 2025. "Rapid Optimal Matching Design of Heterogeneous Propeller Propulsion Systems for High-Altitude Unmanned Airships" Drones 9, no. 10: 718. https://doi.org/10.3390/drones9100718
APA StyleZhang, M., Wang, X., Zhang, Z., Wang, B., Cheng, J., & Zhang, J. (2025). Rapid Optimal Matching Design of Heterogeneous Propeller Propulsion Systems for High-Altitude Unmanned Airships. Drones, 9(10), 718. https://doi.org/10.3390/drones9100718






