Multi-Node Joint Jamming Scheme for Secure UAV-Aided NOMA-CDRT Systems: Performance Analysis and Optimization

Abstract

Unmanned aerial vehicle (UAV) communication using non-orthogonal multiple access-based coordinated direct and relay transmission (NOMA-CDRT) supports both massive connectivity and wide-area coverage, becoming a key technology for future emergency rescue communications. However, relay forwarding and high-quality line-of-sight links may subject UAV-aided NOMA-CDRT to multiple eavesdropping attempts by saboteurs. Therefore, we propose a multi-node joint jamming scheme using artificial noise (AN) for the UAV-assisted NOMA-CDRT to improve the system’s physical layer security. In the proposed scheme, the base station directly serves a nearby user while using a UAV relay to serve a disaster-affected user, and both the users and the UAV relay utilize AN to jointly interfere with eavesdroppers around the users. To accurately characterize and maximize the ergodic secrecy sum rate (ESSR) of the proposed scheme, we derive the corresponding closed-form expressions and design a joint power allocation and interference control (JPAIC) algorithm using particle swarm optimization. Simulations verify the correctness of the theoretical analysis, the ESSR advantage of the proposed scheme compared with the conventional NOMA-CDRT, and the effectiveness of the proposed JPAIC.

1. Introduction

Due to the advantages of wide-area coverage, cost-effectiveness, and deployment flexibility, unmanned aerial vehicle (UAV) communication has been regarded as a crucial enabling technology for future wireless communication networks [1,2,3,4]. UAVs can serve as aerial base stations (BSs) or relays to enhance communication service quality, offering substantial benefits in scenarios such as emergency rescue, post-disaster recovery, and remote area communication [5,6,7]. To further improve spectral efficiency and support massive connections, UAV communication has also been integrated with non-orthogonal multiple access (NOMA) in recent years. Compared with the conventional orthogonal multiple access (OMA), the performance superiority of NOMA is achieved by using power-domain superposition coding and successive interference cancellation (SIC), which allow for the transmission of multi-user signals on the same physical layer resources [8,9]. However, the inherent high-quality line-of-sight (LoS) links and the multi-user information contained in NOMA signals make legitimate nodes of UAV-based NOMA (UAV-NOMA) systems vulnerable to eavesdropping by saboteurs [10,11,12].

To ensure communication security of UAV-NOMA systems, researchers have made significant efforts in direct transmission scenarios. In [12], Zhao et al. proposed a secure transmission scheme for a UAV-NOMA system using multi-antenna beamforming and jointly optimizing power allocation and UAV hovering position. Qian et al. deployed a UAV to collect data from ground sensors and maximized the total secrecy throughput of the UAV-NOMA network by jointly optimizing the scheduling decisions of auxiliary devices and the transmission power of the sensors [13]. Wang et al. proposed a downlink multi-user secure transmission scheme for UAV-NOMA networks based on heterogeneous user needs, achieving the maximization of the minimum secrecy rate through the joint optimization of user scheduling, power allocation, and trajectory design [14]. In [15], Yu et al. derived approximate expressions for the secrecy and reliability outage probabilities of UAV-NOMA-based ultra-reliable and low latency communication networks. The authors in [16] proposed a protection zone scheme for mmWave UAV-NOMA systems to enhance physical layer security by excluding eavesdroppers. Lu et al. designed a secure communication scheme for UAV-NOMA-based mobile edge computing systems, and the authors maximized the security computation capacity by optimizing multiple parameters such as local computing and UAV trajectory [17]. Guo et al. combined UAV-NOMA with simultaneously transmitting and reflecting reconfigurable intelligent surfaces (STAR-RIS), and jointly optimized power control, transmission/reflection coefficients, and the deployment positions of UAV/STAR-RIS to maximize the uplink secure energy efficiency [18]. Diao et al. derived closed-form expressions for connection outage probability, secrecy outage probability, and effective secrecy throughput to characterize the security performance of UAV-NOMA systems with friendly UAV jammers [19]. Sun et al. investigated downlink mmWave simultaneous wireless information and power transfer (SWIPT)-enabled UAV-NOMA systems and derived the corresponding connection outage probability and secrecy outage probability [20]. In [21], Deng et al. optimized the trajectory of a UAV and the transmit power of ground users to ensure the secure and covert communication of the UAV-NOMA system under the threat of eavesdropping UAVs.

Moreover, existing research has investigated secure UAV-NOMA transmission in relay scenarios to promote the diversification of its applications and further improve the communication coverage. In [22], Diao et al. proposed a joint energy transfer and artificial noise (AN) scheme for UAV-NOMA systems in the presence of eavesdropping UAVs. Simulations demonstrated that the proposed scheme promotes green and secure communication in multi-UAV cases. Zhang et al. characterized the performance of a satellite–terrestrial communication system based on NOMA, SWIPT, and UAV relaying by deriving analytical expressions for the secrecy outage probability [23]. To study the security of UAV-NOMA-based cognitive relay systems, the authors in [24] designed an iterative algorithm to maximize the minimum average secrecy rate for secondary users. Zheng et al. derived a closed-form expression for the secrecy outage probability of an underlay cognitive radio-enabled downlink UAV-NOMA network, where the UAV acts as a relay to assist communication between the source and two destination users [25]. The authors in [26] investigated a cognitive multiple input multiple output UAV-NOMA system and minimized the outage probability of the secondary network by optimizing the transmission power and coordinates of the UAV as well as the NOMA power allocation coefficients.

In addition to the pure relay system mentioned above, coordinated direct and relay transmission (CDRT), which evolved from the two-way relay system with analog network coding, is also an important type of relay system [27,28]. Currently, the transmission scheme design for NOMA-based CDRT (NOMA-CDRT) systems has been widely studied, but only a few works focus on secure communication in NOMA-CDRT systems, and these are limited to ground cellular scenarios. For instance, Lv et al. in [29] considered a ground NOMA-CDRT system with one untrusted amplify-and-forward (AF) relay, and designed adaptive cooperative jamming schemes for both downlink and uplink to realize secure transmission. To evaluate the system security performance and provide more insights, Lv et al. further derived a closed-form lower bound of the ergodic secrecy sum rate (ESSR) for the ground NOMA-CDRT system in [30]. Moreover, Lei et al. in [31] introduced physical layer network coding into the untrusted AF relay-based NOMA-CDRT system and utilized inter-user interference and friendly interference signals to enhance system security.

The aforementioned research provides meaningful insights into improving the security of NOMA-CDRT systems, but challenges remain in secure UAV-aided NOMA-CDRT systems: (1) Existing research on secure NOMA-CDRT primarily focused on AF relay configurations and ground communication scenarios. Given the noise amplification characteristics of AF relays and the advantages of flexible UAV deployment, it is crucial to study the secure UAV-aided NOMA-CDRT systems using the decode-and-forward (DF) strategy [32]. However, to the best of our knowledge, no secure UAV-assisted NOMA-CDRT schemes employing DF relays have yet been identified. (2) Existing related work mainly addressed scenarios with untrusted relays and has not sufficiently explored secure NOMA-CDRT in the presence of multiple ground eavesdroppers. (3) The DF characteristics create multiple opportunities for eavesdroppers to intercept legitimate information, and the UAV LoS link further exacerbates this vulnerability.

Motivated by the above observations, this paper studies the secure transmission design and performance optimization of the UAV-aided NOMA-CDRT system with a DF relay. The contributions of this paper are as follows.

• This paper proposes a multi-node joint jamming (MNJJ) scheme using AN to achieve secure UAV-assisted NOMA-CDRT. In the proposed scheme, the BS uses NOMA to provide services to the nearby user while communicating with the disaster-affected user via a UAV relay. Both the users and the UAV collaboratively send AN to interfere with the surrounding eavesdroppers.
• To accurately characterize the security performance of the proposed scheme, we use double factorization and Gaussian–Chebyshev quadrature to derive the closed-form expressions of the ESSR under two conditions: when the legitimate nodes are aware of each other’s AN and when they are not.
• We design a joint power allocation and interference control (JPAIC) algorithm using particle swarm optimization (PSO) for the proposed MNJJ scheme. The proposed JPAIC determines the optimal scheme selection under different conditions and maximizes the ESSR. Simulations demonstrate the ESSR advantages of the proposed MNJJ over the conventional NOMA-CDRT (CNC) and the effectiveness of the proposed JPAIC.

To clearly present the research approach, Figure 1 provides a concise framework of our work. The remainder of this paper is organized as follows. Section 2 introduces the system model, and Section 3 presents the proposed MNJJ scheme. Section 4 provides the ESSR performance analysis and the proposed JPAIC. Section 5 gives the simulation results and Section 6 concludes the paper.

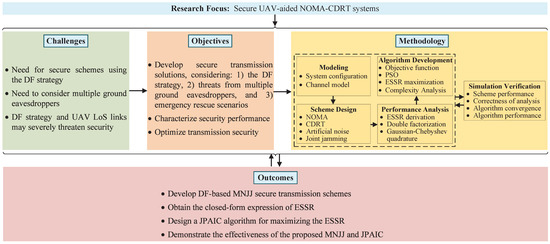
Figure 1. A concise research framework of this paper.

Notation: $f_Z\left(z\right)$ and $F_Z\left(z\right)$ represent the probability density function (PDF) and cumulative distribution function (CDF) of the variable Z, respectively. $\mathcal{CN}(0,1)$ represents a complex Gaussian distribution with mean zero and variance one. $\mathbb{E}[·]$ denotes the expectation operator, $\mathrm{Ei}(·)$ and $\Gamma (·)$ represent the exponential integral function and the Gamma function, respectively. Denote ${\left[z\right]}^{+}=max(z,0)$. $\overline{\Psi }=\Psi ⟨\Theta \to {\Theta }_1⟩$ means replacing all instances of $\Theta$ in $\Psi$ with ${\Theta }_1$ to obtain $\overline{\Psi }$.

2. System Model

2.1. System Configuration

As shown in Figure 2, this paper investigates the physical layer security of a downlink UAV-aided NOMA-CDRT system, which consists of one BS, one DF-based UAV relay, two legitimate users (i.e., $U_1$ and $U_2$), and two eavesdroppers (i.e., $E_1$ and $E_2$). A typical application scenario for the considered system is emergency rescue. Specifically, when the BS in cell 2 is damaged or non-functional due to a sudden disaster or fault, the BS in cell 1 can use the UAV relay to serve $U_2$ while also communicating with its own cell user $U_1$. There are potential eavesdroppers $E_1$ and $E_2$ near users $U_1$ and $U_2$, respectively. These two eavesdroppers with strong computing power attempt to intercept any legitimate information. Assume that all devices are equipped with a single antenna and legitimate nodes can switch between half-duplex and full-duplex modes as needed. A transmission cycle consists of two time slots $t_1$ and $t_2$. Both legitimate signals and AN have zero mean and unit variance.

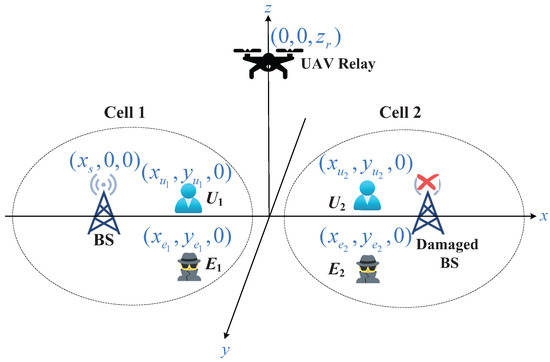
Figure 2. Three-dimensional coordinate framework of a UAV-aided NOMA-CDRT system, including one BS, one UAV relay, two users, and two eavesdroppers.

Hereafter, the subscripts s, r, $u_1$, $u_2$, $e_1$, $e_2$, 1, and 2 represent the BS, UAV, $U_1$, $U_2$, $E_1$, $E_2$, $t_1$, and $t_2$, respectively. Figure 2 establishes a three-dimensional Cartesian coordinate framework, where the coordinate of the node i, $i\in \{s,r,u_1,u_2,e_1,e_2\}$, is expressed as $(x_i,y_i,z_i)$. Without loss of generality, we assume that the BS and the UAV are in the $x-z$ plane, with the ground projection of the UAV at the origin of the $x-y$ plane. The UAV hovers at a fixed height $z_r$ during transmission. The distance between nodes i and $j\in \{s,r,u_1,u_2,e_1,e_2\}$, $j\ne i$, is $d_{ij}=\sqrt{{(x_i-x_j)}^2+{(y_i-y_j)}^2+{(z_i-z_j)}^2}$.

2.2. Channel Model

We assume that all channel links follow quasi-static block fading and include additive white Gaussian noise (AWGN) with zero mean and variance $N_0$. Let $n_i^k$ represent the AWGN at node i during the k-th, $k\in \{1,2\}$, time slot. Define the channel coefficient, channel power, and path loss between ground nodes $\overline{i}\in \{s,u_1,u_2\}$ and $\overline{j}\in \{u_1,e_1,e_2\}$, $\overline{j}\ne \overline{i}$, during the k-th time slot as $h_{\overline{i}\overline{j}}^{k,G}$, $H_{\overline{i}\overline{j}}^{k,G}=|h_{\overline{i}\overline{j}}^{k,G}{|}^2$, and $L_{\overline{i}\overline{j}}^G$, respectively. The small-scale fading of a ground-to-ground (G2G) link is modeled as a Rayleigh distribution, i.e., $h_{\overline{i}\overline{j}}^{k,G}\sim \mathcal{CN}(0,1)$, while the corresponding path loss can be modeled as $L_{\overline{i}\overline{j}}^G={\beta }^G{(d_{\overline{i}\overline{j}})}^{{\alpha }^G}$, where ${\beta }^G={(\frac{4\pi f_c}{c})}^2$ is the path loss coefficient at the unit reference distance, and ${\alpha }^G=3$ is the path loss exponent, usually greater than two for G2G links. The parameter $c=3\times {10}^8$ m/s is the speed of light and $f_c$ is the carrier frequency.

Similarly, we denote the channel coefficient, channel power, and path loss for the air-to-ground (A2G) link from the UAV to ground node $\tilde{j}\in \{u_1,u_2,e_1,e_2\}$ as $h_{r\tilde{j}}^{k,A}$, $H_{r\tilde{j}}^{k,A}=|h_{r\tilde{j}}^{k,A}{|}^2$, and $L_{r\tilde{j}}^A={\beta }_{r\tilde{j}}^A{(d_{r\tilde{j}})}^{{\alpha }^A}$, where ${\beta }_{r\tilde{j}}^A$ and ${\alpha }^A$ are the reference path loss coefficient and path loss exponent for A2G links, respectively. Specifically, we set ${\alpha }^A=2$ and ${\beta }_{r\tilde{j}}^A={10}^{{\beta }_1^A/10+{\beta }_2^A/(10+10C{e}^{-D({\theta }_{r\tilde{j}}-C)})}$ according to the Type B channel model described in [33], where ${\beta }_1^A=10{log}_{10}{(\frac{4\pi f_c}{c})}^2+{\eta }_{NLOS}$, ${\beta }_2^A={\eta }_{LOS}-{\eta }_{NLOS}$, ${\theta }_{r\tilde{j}}=\frac{180}{\pi }arcsin(\frac{z_r}{d_{r\tilde{j}}})$ is the angle of elevation. For suburban areas, we set $C=5.0188$, $D=0.3511$, ${\eta }_{LOS}=0.1$ dB, and ${\eta }_{NLOS}=21$ dB. The small-scale fading of the A2G link is modeled as Nakagami-m fading with shape parameter m, which we consider as an integer for simplicity. The PDF and CDF of $H_{r\tilde{j}}^{A,k}$ can be written as $f_{H_{r\tilde{j}}^{k,A}}(z)={m_{r\tilde{j}}}^{m_{r\tilde{j}}}{z}^{m_{r\tilde{j}}-1}/\Gamma (m_{r\tilde{j}})exp(-m_{r\tilde{j}}z)$, and $F_{H_{r\tilde{j}}^{k,A}}(z)=1-exp(-m_{r\tilde{j}}z){\sum }_{l=0}^{m_{r\tilde{j}}-1}{(m_{r\tilde{j}}z)}^l/l!$. Note that the channel modeling for ground-to-air (G2A) links is the same as for A2G links. Assume $L_{s{u}_1}^H<L_{sr}^A$ due to the typically greater distance between the BS and the UAV compared to the BS and $U_1$.

3. Secure MNJJ Scheme Design

To enhance the system’s physical layer security, this section proposes an MNJJ scheme for the UAV-aided NOMA-CDRT system, as illustrated in Figure 3. The proposed MNJJ includes two time slots, detailed as follows.

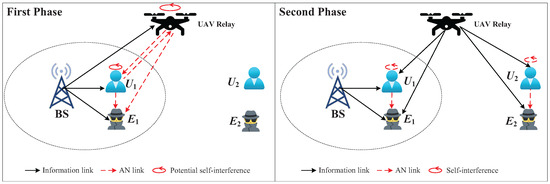
Figure 3. Illustration of the proposed MNJJ scheme for a UAV-aided NOMA-CDRT system.

3.1. First Phase

In $t_1$, the BS broadcasts a superposition coded signal $S_s=\sqrt{a_1{P}_s}{s}_1+\sqrt{a_2{P}_s}{s}_2$, where $P_s$ is the transmission power of the BS, and $s_1$ and $s_2$ are the signals intended for $U_1$ and $U_2$, respectively. Since $U_2$ requires UAV assistance, the power allocation coefficients are set as $a_2>a_1$ and $a_1+a_2=1$. The UAV and $U_1$ switch to full-duplex mode and receive the signal from the BS while simultaneously sending AN $J_r^1$ and $J_{u_1}^1$ to interfere with $E_1$. Here, we consider two cases: (1) Case I, where the legitimate nodes are unaware of each other’s AN, and (2) Case II, where legitimate nodes can know each other’s AN. When considering Case I, simultaneous sending of AN by the UAV and $U_1$ may interfere with each other. In Case II, legitimate nodes can use the known AN to eliminate the corresponding interference from other legitimate nodes by estimating channel and power parameters. To determine the optimal secure transmission method under different cases, we consider three types of the proposed MNJJ: both $U_1$ and the UAV turn on the jamming (i.e., NN), only $U_1$ turns on the jamming (i.e., NF), and only the UAV turns on the jamming (i.e., FN). The received signals at $U_1$, the UAV, and $E_1$ in $t_1$ can be written as

$$y_{u_1}^1=h_{s{u}_1}^{1,G}\sqrt{{\left(L_{s{u}_1}^G\right)}^{-1}{P}_s}{S}_s+h_{r{u}_1}^{1,A}\sqrt{{\left(L_{r{u}_1}^A\right)}^{-1}{\kappa }_r^1{b}_r^1{P}_m}{J}_r^1+h_{u_1{u}_1}^{1,G}\sqrt{{\chi }_{u_1}^1{P}_{RSI}}{J}_{u_1}^1+n_{u_1}^1,$$

(1)

$$y_r^1=h_{sr}^{1,A}\sqrt{{\left(L_{sr}^A\right)}^{-1}{P}_s}{S}_s+h_{u_{1}r}^{1,A}\sqrt{{\left(L_{u_{1}r}^A\right)}^{-1}{\kappa }_{u_1}^1{b}_{u_1}^1{P}_m}{J}_{u_1}^1+h_{rr}^{1,A}\sqrt{{\chi }_r^1{P}_{RSI}}{J}_r^1+n_r^1,$$

(2)

and

$$y_{e_1}^1=h_{s{e}_1}^{1,G}\sqrt{{\left(L_{s{e}_1}^G\right)}^{-1}{P}_s}{S}_s+h_{r{e}_1}^{1,A}\sqrt{{\left(L_{r{e}_1}^A\right)}^{-1}{\chi }_r^1{b}_r^1{P}_m}{J}_r^1+h_{u_1{e}_1}^{1,G}\sqrt{{\left(L_{u_1{e}_1}^G\right)}^{-1}{\chi }_{u_1}^1{b}_{u_1}^1{P}_m}{J}_{u_1}^1+n_{e_1}^1,$$

(3)

where $h_{u_1{u}_1}^{1,G}$ and $h_{rr}^{1,A}$ are the self-interference channel coefficients at $U_1$ and the UAV in $t_1$, respectively, and $P_m$ is the maximum interference power of each node. ${\chi }_{i^{\prime }}^1=0$ and ${\chi }_{i^{\prime }}^1=1$ indicate that the node $i^{\prime }\in \{r,u_1\}$ turns off and turns on jamming in $t_1$, respectively. When ${\chi }_{i^{\prime }}^1=1$, the conditions ${\kappa }_{i^{\prime }}^1=1$ and ${\kappa }_{i^{\prime }}^1=0$ represent Case I and Case II. The interference power coefficient $b_{i^{\prime }}^1$ satisfies $0\le b_{i^{\prime }}^1\le 1$. Note that $b_{i^{\prime }}^1=0$ holds when ${\chi }_{i^{\prime }}^1=0$, and $0<b_{i^{\prime }}^1\le 1$ holds when ${\chi }_{i^{\prime }}^1=1$. The ratio of residual interference power $P_{RSI}$ resulting from self-interference cancellation to noise power $N_0$, denoted as ${\rho }_{RSI}\triangleq \frac{P_{RSI}}{N_0}$, is typically set in the range of 3 dB to 15 dB [34].

The user $U_1$ employs SIC to sequentially decode $s_2$ and $s_1$. Therefore, the signal-to-interference-plus-noise ratios (SINRs) for decoding $s_2$ and $s_1$ at $U_1$ are written as

$${\gamma }_{u_1,s_2}^1={\displaystyle \frac{H_{s{u}_1}^{1,G}{\left(L_{s{u}_1}^G\right)}^{-1}{\rho }_s{a}_2}{H_{s{u}_1}^{1,G}{\left(L_{s{u}_1}^G\right)}^{-1}{\rho }_s{a}_1+H_{r{u}_1}^{1,A}{\left(L_{r{u}_1}^A\right)}^{-1}{\kappa }_r^1{b}_r^1{\rho }_m+H_{u_1{u}_1}^{1,G}{\chi }_{u_1}^1{\rho }_{RSI}+1}},$$

(4)

and

$${\gamma }_{u_1,s_1}^1={\displaystyle \frac{H_{s{u}_1}^{1,G}{\left(L_{s{u}_1}^G\right)}^{-1}{\rho }_s{a}_1}{H_{r{u}_1}^{1,A}{\left(L_{r{u}_1}^A\right)}^{-1}{\kappa }_r^1{b}_r^1{\rho }_m+H_{u_1{u}_1}^{1,G}{\chi }_{u_1}^1{\rho }_{RSI}+1}},$$

(5)

where $H_{u_1{u}_1}^{1,G}=|h_{u_1{u}_1}^{1,G}{|}^2$, ${\rho }_s\triangleq \frac{P_s}{N_0}$, and ${\rho }_m\triangleq \frac{P_m}{N_0}$. Similarly, the UAV directly decodes $s_2$ treating $s_1$ as interference. The corresponding SINR can be written as

$${\gamma }_{r,s_2}^1={\displaystyle \frac{H_{sr}^{1,A}{\left(L_{sr}^A\right)}^{-1}{\rho }_s{a}_2}{H_{sr}^{1,A}{\left(L_{sr}^A\right)}^{-1}{\rho }_s{a}_1+H_{u_{1}r}^{1,A}{\left(L_{u_{1}r}^A\right)}^{-1}{\kappa }_{u_1}^1{b}_{u_1}^1{\rho }_m+H_{rr}^{1,A}{\chi }_r^1{\rho }_{RSI}+1}},$$

(6)

where $H_{rr}^{1,A}=|h_{rr}^{1,A}{|}^2$. Based on (3), the eavesdropper $E_1$ may eavesdrop on both $s_1$ and $s_2$ in $t_1$. Considering the worst case, we assume that $E_1$ has powerful computational capabilities and can directly distinguish signals $s_1$ and $s_2$ from the received signal [35]. The SINRs for $E_1$ to decode $s_2$ and $s_1$ can be written as

$${\gamma }_{e_1,s_2}^1={\displaystyle \frac{H_{s{e}_1}^{1,G}{\left(L_{s{e}_1}^G\right)}^{-1}{\rho }_s{a}_2}{H_{r{e}_1}^{1,A}{\left(L_{r{e}_1}^A\right)}^{-1}{\chi }_r^1{b}_r^1{\rho }_m+H_{u_1{e}_1}^{1,G}{\left(L_{u_1{e}_1}^G\right)}^{-1}{\chi }_{u_1}^1{b}_{u_1}^1{\rho }_m+1}},$$

(7)

and

$${\gamma }_{e_1,s_1}^1={\displaystyle \frac{H_{s{e}_1}^{1,G}{\left(L_{s{e}_1}^G\right)}^{-1}{\rho }_s{a}_1}{H_{r{e}_1}^{1,A}{\left(L_{r{e}_1}^A\right)}^{-1}{\chi }_r^1{b}_r^1{\rho }_m+H_{u_1{e}_1}^{1,G}{\left(L_{u_1{e}_1}^G\right)}^{-1}{\chi }_{u_1}^1{b}_{u_1}^1{\rho }_m+1}}.$$

(8)

3.2. Second Phase

In $t_2$, the UAV forwards the decoded $s_2$ with power $P_r$ to $U_2$, and the BS sends a new signal $s_1^{\prime }$ to $U_1$. At this time, $E_1$ attempts to intercept both $s_1^{\prime }$ and $s_2$, while $E_2$ tries to intercept $s_2$. By using the full-duplex mode, $U_1$ and $U_2$ simultaneously receive signals and transmit AN $J_{u_1}^2$ and $J_{u_2}^2$ with powers $b_{u_1}^2{P}_m$ and $b_{u_2}^2{P}_m$ to interfere with the corresponding eavesdroppers. Here, $0<b_{u_1}^2\le 1$ and $0<b_{u_2}^2\le 1$ denote the self-interference power coefficients at $U_1$ and $U_2$ in $t_2$. Consequently, after self-interference cancellation, the received signal at $U_1$ can be expressed as $y_{u_1}^2=h_{s{u}_1}^{2,G}\sqrt{P_s{\left(L_{s{u}_1}^G\right)}^{-1}}{s}_1^{\prime }+h_{r{u}_1}^{2,A}\sqrt{P_r{\left(L_{r{u}_1}^A\right)}^{-1}}{s}_2+h_{u_1{u}_1}^{2,G}\sqrt{P_{RSI}}{J}_{u_1}^2+n_{u_1}^2$. Since $U_1$ has prior information about $s_2$, it can estimate $h_{r{u}_1}^{2,A}\sqrt{P_r{\left(L_{r{u}_1}^A\right)}^{-1}}$ and then cancel the interference term $h_{r{u}_1}^{2,A}\sqrt{P_r{\left(L_{r{u}_1}^A\right)}^{-1}}{s}_2$ from $y_{u_1}^2$. Based on this, the SINR for $U_1$ to decode $s_1^{\prime }$ in $t_2$ can be written as

$${\gamma }_{u_1,s_1^{\prime }}^2={\displaystyle \frac{H_{s{u}_1}^{2,G}{\left(L_{s{u}_1}^G\right)}^{-1}{\rho }_s}{H_{u_1{u}_1}^{2,G}{\rho }_{RSI}+1}},$$

(9)

where $H_{u_1{u}_1}^{2,G}=|h_{u_1{u}_1}^{2,G}{|}^2$.

Similarly, the received signal at $E_1$ can be written as $y_{e_1}^2=h_{s{e}_1}^{2,G}\sqrt{P_s{\left(L_{s{e}_1}^G\right)}^{-1}}{s}_1^{\prime }+h_{r{e}_1}^{2,A}\sqrt{P_r{\left(L_{r{e}_1}^A\right)}^{-1}}{s}_2+h_{u_1{e}_1}^{2,G}\sqrt{{\left(L_{u_1{e}_1}^G\right)}^{-1}{b}_{u_1}^2{P}_m}{J}_{u_1}^2+n_{e_1}^2$. Considering the worst case, $E_1$ can distinguish signals $s_1^{\prime }$ and $s_2$. In this case, the SINRs for $E_1$ attempting to eavesdrop on $s_1^{\prime }$ and $s_2$ are written as

$${\gamma }_{e_1,s_1^{\prime }}^2={\displaystyle \frac{H_{s{e}_1}^{2,G}{\left(L_{s{e}_1}^G\right)}^{-1}{\rho }_s}{H_{u_1{e}_1}^{2,G}{\left(L_{u_1{e}_1}^G\right)}^{-1}{b}_{u_1}^2{\rho }_m+1}},$$

(10)

and

$${\gamma }_{e_1,s_2}^2={\displaystyle \frac{H_{r{e}_1}^{2,A}{\left(L_{r{e}_1}^A\right)}^{-1}{\rho }_r}{H_{u_1{e}_1}^{2,G}{\left(L_{u_1{e}_1}^G\right)}^{-1}{b}_{u_1}^2{\rho }_m+1}}.$$

(11)

The user $U_2$ receives the relaying signal and its own AN. After self-interference cancellation, the received signal at $U_2$ can be written as $y_{u_2}^2=h_{r{u}_2}^{2,A}\sqrt{P_r{\left(L_{r{u}_2}^A\right)}^{-1}}{s}_2+h_{u_2{u}_2}^{2,G}\sqrt{P_{RSI}}{J}_{u_2}^2+n_{u_2}^2$. Therefore, the SINR for $U_2$ to decode $s_2$ is

$${\gamma }_{u_2,s_2}^2={\displaystyle \frac{H_{r{u}_2}^{2,A}{\left(L_{r{u}_2}^A\right)}^{-1}{\rho }_r}{H_{u_2{u}_2}^{2,G}{\rho }_{RSI}+1}}.$$

(12)

Similarly, the received signal at $E_2$ can be expressed as $y_{e_2}^2=h_{r{e}_2}^{2,A}\sqrt{P_r{\left(L_{r{e}_2}^A\right)}^{-1}}{s}_2+h_{u_2{e}_2}^{2,G}\sqrt{{\left(L_{u_2{e}_2}^G\right)}^{-1}{b}_{u_2}^2{P}_m}{J}_{u_2}^2+n_{e_2}^2$. The SINR for $E_2$ to decode $s_2$ is given by

$${\gamma }_{e_2,s_2}^2={\displaystyle \frac{H_{r{e}_2}^{2,A}{\left(L_{r{e}_2}^A\right)}^{-1}{\rho }_r}{H_{u_2{e}_2}^{2,G}{b}_{u_2}^2{\left(L_{u_2{e}_2}^G\right)}^{-1}{\rho }_m+1}}.$$

(13)

Note that the proposed scheme can be readily extended to a multi-antenna scenario using the existing transmit antenna selection technique [36]. The proposed scheme can be expanded to accommodate more users by utilizing existing user pairing methods, which helps manage system complexity within practical limits [37,38].

4. Performance Analysis and Optimization

This section derives the closed-form expressions for the ESSRs of the NN, NF, and FN for the proposed MNJJ under Case I and Case II to precisely characterize system security performance. Based on ${\gamma }_{u_1,s_1}^1$ and ${\gamma }_{e_1,s_1}^1$, the achievable ergodic secrecy rate (ESR) for $s_1$ is $S{R}_{s_1}={\left[\mathbb{E}\left\{\frac{1}{2}{log}_2(1+{\gamma }_{u_1,s_1}^1)\right\}-\mathbb{E}\left\{\frac{1}{2}{log}_2(1+{\gamma }_{e_1,s_1}^1)\right\}\right]}^{+}$ [39,40,41,42]. Using ${\gamma }_{u_1,s_1^{\prime }}^2$ and ${\gamma }_{e_1,s_1^{\prime }}^2$, the achievable ESR for $s_1^{\prime }$ is $S{R}_{s_1^{\prime }}={\left[\mathbb{E}\left\{\frac{1}{2}{log}_2(1+{\gamma }_{u_1,s_1^{\prime }}^2)\right\}-\mathbb{E}\left\{\frac{1}{2}{log}_2(1+{\gamma }_{e_1,s_1^{\prime }}^2)\right\}\right]}^{+}$. The achievable ergodic rate of $s_2$ over the DF dual-hop link is limited by the weaker link. Additionally, $U_1$ needs to decode $s_2$ first and then decode $s_1$ in $t_1$. Therefore, the achievable ergodic rate for $s_2$ at $U_2$ can be expressed as $L{R}_{s_2}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+min({\gamma }_{u_1,s_2}^1,{\gamma }_{r,s_2}^1,{\gamma }_{u_2,s_2}^2))\right\}$. The reception of $s_2$ at $E_2$ requires the assistance of the UAV relay, and thus, the achievable ergodic rate for $s_2$ at $E_2$ is also constrained by the poorer channel quality in the DF dual-hop link and can be expressed as $\frac{1}{2}{log}_2(1+min({\gamma }_{r,s_2}^1,{\gamma }_{e_2,s_2}^2))$. Due to the DF process of the UAV relay, $E_1$ has the opportunity to eavesdrop on $s_2$ during both $t_1$ and $t_2$. Overall, if either $E_1$ or $E_2$ intercepts $s_2$ during the entire transmission period, it compromises communication security. Therefore, the achievable ergodic rate for $s_2$ at the eavesdroppers is given by $E{R}_{s_2}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+max({\gamma }_{e_1,s_2}^2,min({\gamma }_{r,s_2}^1,{\gamma }_{e_2,s_2}^2),{\gamma }_{e_1,s_2}^1))\right\}$. Based on this, the ESR for $s_2$ is $S{R}_{s_2}={\left[L{R}_{s_2}-E{R}_{s_2}\right]}^{+}$.

For derivation, we present the following valid equations

$${\int }_0^{\infty }{log}_2(1+z)f_Z\left(z\right)dz={\displaystyle \frac{1}{ln2}}{\int }_0^{\infty }{\displaystyle \frac{1-F_Z\left(z\right)}{1+z}}dz,$$

(14)

and

$${\displaystyle \frac{1}{{(z+W)}^b(z+T)}}={\sum }_{b_1=1}^b{-\left({\displaystyle \frac{1}{W-T}}\right)}^{b_1}{\displaystyle \frac{1}{{(z+W)}^{\overline{b}}}}+{\left({\displaystyle \frac{1}{W-T}}\right)}^b{\displaystyle \frac{1}{z+T}},$$

(15)

where $\overline{b}=b-b_1+1$.

4.1. ESR for the Proposed MNJJ in Case I

4.1.1. NN in Case I

The following theorem provides the ESR of $s_1$ for the NN in Case I.

Theorem 1.

When legitimate nodes cannot know each other’s AN (i.e., Case I), the closed-form expression of the ESR for $s_1$ in the NN can be written as $S{R}_{s_1}^{\mathrm{NN}-\mathrm{I}}={\left[L{R}_{s_1}^{\mathrm{NN}-\mathrm{I}}-E{R}_{s_1}^{\mathrm{NN}-\mathrm{I}}\right]}^{+}$, where

$$\begin{array}{cc}\hfill L{R}_{s_1}^{\mathrm{NN}-\mathrm{I}}=& {\displaystyle \frac{{m_{r{u}_1}}^{m_{r{u}_1}}}{2ln2({\Omega }_2-1){{\Omega }_1}^{m_{r{u}_1}}}}\{{\sum }_{i_1=1}^{m_{r{u}_1}}\left\{{\left({\displaystyle \frac{{\Omega }_1}{m_{r{u}_1}-{\Omega }_1}}\right)}^{i_1}-{\left({\displaystyle \frac{{\Omega }_1{\Omega }_2}{m_{r{u}_1}{\Omega }_2-{\Omega }_1}}\right)}^{i_1}\right\}{\Phi }_1\hfill \\ \hfill & +{\left({\displaystyle \frac{{\Omega }_1{\Omega }_2}{m_{r{u}_1}{\Omega }_2-{\Omega }_1}}\right)}^{m_{r{u}_1}}{\Phi }_2-{\left({\displaystyle \frac{{\Omega }_1}{m_{r{u}_1}-{\Omega }_1}}\right)}^{m_{r{u}_1}}{\Phi }_3\},\hfill \end{array}$$

(16)

and

$$E{R}_{s_1}^{\mathrm{NN}-\mathrm{I}}=L{R}_{s_1}^{\mathrm{NN}-\mathrm{I}}⟨m_{r{u}_1}\to m_{r{e}_1},{\Omega }_1\to {\Omega }_4,{\Omega }_2\to {\Omega }_5,{\Omega }_3\to {\Omega }_6⟩,$$

(17)

where

$$\begin{array}{cc}\hfill {\Phi }_1=& exp\left({\displaystyle \frac{m_{r{u}_1}{\Omega }_3}{{\Omega }_1}}\right)\{{(-1)}^{{\overline{i}}_1}{\displaystyle \frac{{{\Omega }_3}^{{\overline{i}}_1-1}\mathrm{Ei}(-{\Omega }_3{m}_{r{u}_1}/{\Omega }_1)}{({\overline{i}}_1-1)!}}\hfill \\ \hfill & +{\displaystyle \frac{exp(-{\Omega }_3{m}_{r{u}_1}/{\Omega }_1)}{{(m_{r{u}_1}/{\Omega }_1)}^{{\overline{i}}_1-1}}}{\sum }_{i_2=0}^{{\overline{i}}_1-2}{\displaystyle \frac{{(-{\Omega }_3{m}_{r{u}_1}/{\Omega }_1)}^{i_2}({\overline{i}}_1-i_2-2)!}{({\overline{i}}_1-1)!}}\},\hfill \end{array}$$

(18)

${\Phi }_2=-exp(\frac{{\Omega }_3}{{\Omega }_2})\mathrm{Ei}(-\frac{{\Omega }_3}{{\Omega }_2})$, ${\Phi }_3=-exp({\Omega }_3)\mathrm{Ei}(-{\Omega }_3)$, ${\Omega }_1=\frac{{(L_{r{u}_1}^A)}^{-1}{b}_r^1{\rho }_m}{{(L_{s{u}_1}^G)}^{-1}{a}_1{\rho }_s}$, ${\Omega }_2=\frac{{\rho }_{RSI}}{{(L_{s{u}_1}^G)}^{-1}{a}_1{\rho }_s}$, ${\Omega }_3=\frac{1}{{(L_{s{u}_1}^G)}^{-1}{a}_1{\rho }_s}$, ${\Omega }_4=\frac{{(L_{r{e}_1}^A)}^{-1}{b}_r^1{\rho }_m}{{(L_{s{e}_1}^G)}^{-1}{a}_1{\rho }_s}$, ${\Omega }_5=\frac{{(L_{u_1{e}_1}^G)}^{-1}{b}_{u_1}^1{\rho }_m}{{(L_{s{e}_1}^G)}^{-1}{a}_1{\rho }_s}$, ${\Omega }_6=\frac{1}{{(L_{s{e}_1}^G)}^{-1}{a}_1{\rho }_s}$, and ${\overline{i}}_1=m_{r{u}_1}-i_1+1$.

Proof. 

See Appendix A.    □

Based on (9) and (10), we let $U_{s_1^{\prime }}^{\mathrm{I}1}\triangleq \frac{H_{s{u}_1}^{2,G}{(L_{s{u}_1}^G)}^{-1}{\rho }_s}{H_{u_1{u}_1}^{2,G}{\rho }_{RSI}+1}$ and $V_{s_1^{\prime }}^{\mathrm{I}1}\triangleq \frac{H_{s{e}_1}^{2,G}{(L_{s{e}_1}^G)}^{-1}{\rho }_s}{H_{u_1{e}_1}^{2,G}{(L_{u_1{e}_1}^G)}^{-1}{b}_{u_1}^2{\rho }_m+1}$. The CDFs of $U_{s_1^{\prime }}^{\mathrm{I}1}$ and $V_{s_1^{\prime }}^{\mathrm{I}1}$ can be easily obtained as $F_{U_{s_1^{\prime }}^{\mathrm{I}1}}(u)=1-exp(-{\Omega }_{8}u)/(1+{\Omega }_{7}u)$ and $F_{V_{s_1^{\prime }}^{\mathrm{I}1}}(v)=1-exp(-{\Omega }_{10}v)/(1+{\Omega }_{9}v)$, where ${\Omega }_7={\rho }_{RSI}/({(L_{s{u}_1}^G)}^{-1}{\rho }_s)$, ${\Omega }_8=1/({(L_{s{u}_1}^G)}^{-1}{\rho }_s)$, ${\Omega }_9={(L_{u_1{e}_1}^G)}^{-1}{b}_{u_1}^2{\rho }_m/({(L_{s{e}_1}^G)}^{-1}{\rho }_s)$, and ${\Omega }_{10}=1/({(L_{s{e}_1}^G)}^{-1}{\rho }_s)$.

Using (14) and  [43] (Equation (3.352.4)), the ESR for $s_1^{\prime }$ can be calculated as

$$\begin{array}{cc}\hfill S{R}_{s_1^{\prime }}^{\mathrm{NN}-\mathrm{I}}=& {\displaystyle \frac{1}{2ln2}}{\left[{\int }_0^{\infty }{\displaystyle \frac{1-F_{U_{s_1^{\prime }}^{\mathrm{I}1}}\left(u\right)}{1+u}}du-{\int }_0^{\infty }{\displaystyle \frac{1-F_{V_{s_1^{\prime }}^{\mathrm{I}1}}\left(v\right)}{1+v}}dv\right]}^{+}\hfill \\ \hfill =& {\displaystyle \frac{1}{2ln2}}[{\displaystyle \frac{1}{({\Omega }_7-1)}}\left(-exp\left({\displaystyle \frac{{\Omega }_8}{{\Omega }_7}}\right)\mathrm{Ei}\left(-{\displaystyle \frac{{\Omega }_8}{{\Omega }_7}}\right)+exp\left({\Omega }_8\right)\mathrm{Ei}\left(-{\Omega }_8\right)\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{({\Omega }_9-1)}}\left(-exp\left({\displaystyle \frac{{\Omega }_{10}}{{\Omega }_9}}\right)\mathrm{Ei}\left(-{\displaystyle \frac{{\Omega }_{10}}{{\Omega }_9}}\right)+exp\left({\Omega }_{10}\right)\mathrm{Ei}(-{\Omega }_{10})\right){]}^{+}.\hfill \end{array}$$

(19)

According to $L{R}_{s_2}$, the ergodic rate of $s_2$ at $U_2$ in the NN is $L{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+U_{s_2}^{\mathrm{I}1})\right\}$, where $U_{s_2}^{\mathrm{I}1}\triangleq min(U_{s_2}^{\mathrm{I}1-1},U_{s_2}^{\mathrm{I}1-2},U_{s_2}^{\mathrm{I}1-3})$, $U_{s_2}^{\mathrm{I}1-1}\triangleq \frac{H_{s{u}_1}^{1,G}{(L_{s{u}_1}^G)}^{-1}{\rho }_s{a}_2}{H_{s{u}_1}^{1,G}{(L_{s{u}_1}^G)}^{-1}{\rho }_s{a}_1+H_{r{u}_1}^{1,A}{(L_{r{u}_1}^A)}^{-1}{b}_r^1{\rho }_m+H_{u_1{u}_1}^{1,G}{\rho }_{RSI}+1}$, $U_{s_2}^{\mathrm{I}1-2}\triangleq \frac{H_{sr}^{1,A}{(L_{sr}^A)}^{-1}{\rho }_s{a}_2}{H_{sr}^{1,A}{(L_{sr}^A)}^{-1}{\rho }_s{a}_1+H_{u_{1}r}^{1,A}{(L_{u_{1}r}^A)}^{-1}{b}_{u_1}^1{\rho }_m+H_{rr}^{1,A}{\rho }_{RSI}+1}$, and $U_{s_2}^{\mathrm{I}1-3}\triangleq {\gamma }_{u_2,s_2}^2$. By using (6), (7), (11), (13), and $E{R}_{s_2}$, the ergodic rate of $s_2$ at the eavesdroppers in the NN can be rewritten as $E{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+V_{s_2}^{\mathrm{I}1})\right\}$, where $V_{s_2}^{\mathrm{I}1}\triangleq max(V_{s_2}^{\mathrm{I}1-1},min(U_{s_2}^{\mathrm{I}1-2},V_{s_2}^{\mathrm{I}1-2}),V_{s_2}^{\mathrm{I}1-3})$, $V_{s_2}^{\mathrm{I}1-1}={\gamma }_{e_1,s_2}^2$, $V_{s_2}^{\mathrm{I}1-2}={\gamma }_{e_2,s_2}^2$, and $V_{s_2}^{\mathrm{I}1-3}=\frac{H_{s{e}_1}^{1,G}{(L_{s{e}_1}^G)}^{-1}{\rho }_s{a}_2}{H_{r{e}_1}^{1,A}{(L_{r{e}_1}^A)}^{-1}{b}_r^1{\rho }_m+H_{u_1{e}_1}^{1,G}{(L_{u_1{e}_1}^G)}^{-1}{b}_{u_1}^1{\rho }_m+1}$. Based on this, the ESR of $s_2$ for the NN in Case I is given in the following theorem.

Theorem 2.

In Case I, the closed-form expression of the ESR for $s_2$ in the NN can be written as $S{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}={\left[L{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}-E{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}\right]}^{+}$, where

$$\begin{array}{c}\hfill L{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}={\displaystyle \frac{a_2\pi }{4ln2a_1{N}_1}}{\sum }_{n_1=1}^{N_1}\sqrt{1-{\left({\phi }_{n_1}\right)}^2}{\displaystyle \frac{1-{\tilde{F}}_{U_{s_2}^{\mathrm{I}1}}\left(u_{n_1}\right)}{1+u_{n_1}}},\end{array}$$

(20)

and

$$\begin{array}{cc}\hfill E{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}=& {\displaystyle \frac{\pi }{4ln2}}\{{\displaystyle \frac{a_2}{a_1{N}_2}}{\sum }_{n_2=1}^{N_2}\sqrt{1-{\left({\phi }_{n_2}\right)}^2}{\displaystyle \frac{1-{\dot{F}}_{V_{s_2}^{\mathrm{I}1}}\left(v_{n_2}\right)}{1+v_{n_2}}}\hfill \\ \hfill & +{\displaystyle \frac{1}{N_3}}\left({\displaystyle \frac{\pi }{2}}-arctan{\displaystyle \frac{a_2}{a_1}}\right){\sum }_{n_3=1}^{N_3}\sqrt{1-{\left({\phi }_{n_3}\right)}^2}{(sec{v}_{n_3})}^2{\displaystyle \frac{1-{\ddot{F}}_{V_{s_2}^{\mathrm{I}1}}(tan{v}_{n_3})}{1+tan{v}_{n_3}}}\},\hfill \end{array}$$

(21)

where ${\tilde{F}}_{U_{s_2}^{\mathrm{I}1}}(u)=1-(1-{\tilde{F}}_{U_{s_2}^{\mathrm{I}1-1}}(u))(1-{\tilde{F}}_{U_{s_2}^{\mathrm{I}1-2}}(u))(1-F_{U_{s_2}^{\mathrm{I}1-3}}(u))$, ${\dot{F}}_{V_{s_2}^{\mathrm{I}1}}(v)=(1-(1-{\tilde{F}}_{U_{s_2}^{\mathrm{I}1-2}}(v))(1-F_{V_{s_2}^{\mathrm{I}1-2}}(v)))F_{V_{s_2}^{\mathrm{I}1-1}}(v)F_{V_{s_2}^{\mathrm{I}1-3}}(v)$, ${\ddot{F}}_{V_{s_2}^{\mathrm{I}1}}(v)=F_{V_{s_2}^{\mathrm{I}1-1}}(v)F_{V_{s_2}^{\mathrm{I}1-3}}(v)$. Additionally, we have

$$\begin{array}{cc}\hfill {\tilde{F}}_{U_{s_2}^{\mathrm{I}1-1}}\left(u\right)=& 1-{\displaystyle \frac{{m_{r{u}_1}}^{m_{r{u}_1}}{(a_2-a_{1}u)}^{m_{r{u}_1}+1}}{\left(({\Omega }_{12}{a}_2-a_1)u+a_2\right){\left(({\Omega }_{11}{a}_2-m_{r{u}_1}{a}_1)u+m_{r{u}_1}{a}_2\right)}^{m_{r{u}_1}}}}exp\left(-{\displaystyle \frac{{\Omega }_{13}{a}_{2}u}{a_2-a_{1}u}}\right),\hfill \\ \hfill {\tilde{F}}_{U_{s_2}^{\mathrm{I}1-2}}\left(u\right)=& 1-exp(-m_{sr}{\Xi }_3\left(u\right)){\sum }_{i_3=0}^{m_{sr}-1}{\sum }_{i_4=0}^{i_3}{\sum }_{i_5=0}^{i_4}\left({\displaystyle \genfrac{}{}{0pt}{}{i_3}{i_4}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{i_4}{i_5}}\right){\displaystyle \frac{{\left(m_{sr}{\Xi }_3\left(u\right)\right)}^{i_3}}{i_3!}}\hfill \end{array}$$

(22a)

$$\begin{array}{cc}\hfill & \times {\displaystyle \frac{{\left({\Omega }_{14}\right)}^{i_3-i_4}{\left({\rho }_{RSI}\right)}^{i_4-i_5}{m_{u_{1}r}}^{m_{u_{1}r}}{m_{rr}}^{m_{rr}}\Gamma (i_3-i_4+m_{u_{1}r})\Gamma (i_4-i_5+m_{rr})}{\Gamma \left(m_{u_{1}r}\right)\Gamma \left(m_{rr}\right){(m_{sr}{\Xi }_1\left(u\right)+m_{u_{1}r})}^{i_3-i_4+m_{u_{1}r}}{(m_{sr}{\Xi }_2\left(u\right)+m_{rr})}^{i_4-i_5+m_{rr}}}},\hfill \end{array}$$

(22b)

$$\begin{array}{cc}\hfill F_{U_{s_2}^{\mathrm{I}1-3}}\left(u\right)=& 1-exp(-m_{r{u}_2}{\Omega }_{16}u){\sum }_{i_6=0}^{m_{r{u}_2}-1}{\sum }_{i_7=0}^{i_6}\left({\displaystyle \genfrac{}{}{0pt}{}{i_6}{i_7}}\right){\displaystyle \frac{\Gamma (i_7+1){\left({\Omega }_{15}\right)}^{i_7}{\left(m_{r{u}_2}{\Omega }_{16}v\right)}^{i_6}}{i_6!{\left({\Omega }_{16}\right)}^{i_7}{(m_{r{u}_2}{\Omega }_{15}v+1)}^{i_7+1}}},\hfill \end{array}$$

(22c)

$$\begin{array}{cc}\hfill F_{V_{s_2}^{\mathrm{I}1-1}}\left(v\right)=& 1-exp(-m_{r{e}_1}{\Omega }_{18}v){\sum }_{i_8=0}^{m_{r{e}_1}-1}{\sum }_{i_9=0}^{i_8}\left({\displaystyle \genfrac{}{}{0pt}{}{i_8}{i_9}}\right){\displaystyle \frac{\Gamma (i_9+1){\left({\Omega }_{17}\right)}^{i_9}{\left(m_{r{e}_1}{\Omega }_{18}v\right)}^{i_8}}{i_8!{\left({\Omega }_{18}\right)}^{i_9}{(m_{r{e}_1}{\Omega }_{17}v+1)}^{i_9+1}}},\hfill \end{array}$$

(22d)

$$\begin{array}{cc}\hfill F_{V_{s_2}^{\mathrm{I}1-2}}\left(v\right)=& 1-exp(-m_{r{e}_2}{\Omega }_{20}v){\sum }_{i_{10}=0}^{m_{r{e}_2}-1}{\sum }_{i_{11}=0}^{i_{10}}\left({\displaystyle \genfrac{}{}{0pt}{}{i_{10}}{i_{11}}}\right){\displaystyle \frac{\Gamma (i_{11}+1){\left({\Omega }_{19}\right)}^{i_{11}}{\left(m_{r{e}_2}{\Omega }_{20}v\right)}^{i_{10}}}{i_{10}!{\left({\Omega }_{20}\right)}^{i_{11}}{(m_{r{e}_2}{\Omega }_{19}v+1)}^{i_{11}+1}}},\hfill \end{array}$$

(22e)

$$\begin{array}{cc}\hfill F_{V_{s_2}^{\mathrm{I}1-3}}\left(v\right)=& 1-{m_{r{e}_1}}^{m_{r{e}_1}}{\displaystyle \frac{exp(-{\Omega }_{23}v)}{({\Omega }_{22}v+1){({\Omega }_{21}v+m_{r{e}_1})}^{m_{r{e}_1}}}},\hfill \end{array}$$

(22f)

where ${\Omega }_{11}=\frac{{(L_{r{u}_1}^A)}^{-1}{b}_r^1{\rho }_m}{{(L_{s{u}_1}^G)}^{-1}{\rho }_s{a}_2}$, ${\Omega }_{12}=\frac{{\rho }_{RSI}}{{(L_{s{u}_1}^G)}^{-1}{\rho }_s{a}_2}$, ${\Omega }_{13}=\frac{1}{{(L_{s{u}_1}^G)}^{-1}{\rho }_s{a}_2}$, ${\Omega }_{14}={(L_{u_{1}r}^A)}^{-1}{b}_{u_1}^1{\rho }_m$, ${\Omega }_{15}=\frac{{\rho }_{RSI}}{{(L_{r{u}_2}^A)}^{-1}{\rho }_r}$, ${\Omega }_{16}=\frac{1}{{(L_{r{u}_2}^A)}^{-1}{\rho }_r}$, ${\Omega }_{17}=\frac{{(L_{u_1{e}_1}^G)}^{-1}{b}_{u_1}^2{\rho }_m}{{(L_{r{e}_1}^A)}^{-1}{\rho }_r}$, ${\Omega }_{18}=\frac{1}{{(L_{r{e}_1}^A)}^{-1}{\rho }_r}$, ${\Omega }_{19}=\frac{b_{u_2}^2{(L_{u_2{e}_2}^G)}^{-1}{\rho }_m}{{(L_{r{e}_2}^A)}^{-1}{\rho }_r}$, ${\Omega }_{20}=\frac{1}{{(L_{r{e}_2}^A)}^{-1}{\rho }_r}$, ${\Omega }_{21}=\frac{{(L_{r{e}_1}^A)}^{-1}{b}_r^1{\rho }_m}{{(L_{s{e}_1}^G)}^{-1}{\rho }_s{a}_2}$, ${\Omega }_{22}=\frac{{(L_{u_1{e}_1}^G)}^{-1}{b}_{u_1}^1{\rho }_m}{{(L_{s{e}_1}^G)}^{-1}{\rho }_s{a}_2}$, ${\Omega }_{23}=\frac{1}{{(L_{s{e}_1}^G)}^{-1}{\rho }_s{a}_2}$, ${\Xi }_1(u)=\frac{{(L_{u_{1}r}^A)}^{-1}{b}_{u_1}^1{\rho }_{m}u}{{(L_{sr}^A)}^{-1}{\rho }_s(a_2-a_{1}u)}$, ${\Xi }_2(u)=\frac{{\rho }_{RSI}u}{{(L_{sr}^A)}^{-1}{\rho }_s(a_2-a_{1}u)}$, ${\Xi }_3(u)=\frac{u}{{(L_{sr}^A)}^{-1}{\rho }_s(a_2-a_{1}u)}$, ${\phi }_{n_1}=cos(\frac{2n_1-1}{2N_1}\pi )$, ${\phi }_{n_2}=cos(\frac{2n_2-1}{2N_2}\pi )$, ${\phi }_{n_3}=cos(\frac{2n_3-1}{2N_3}\pi )$, $u_{n_1}=\frac{a_2(1+{\phi }_{n_1})}{2a_1}$, $v_{n_2}=\frac{a_2(1+{\phi }_{n_2})}{2a_1}$, $v_{n_3}=\frac{\pi (1+{\phi }_{n_3})}{4}+\frac{(1-{\phi }_{n_3})arctan(a_2/a_1)}{2}$, and $N_1$, $N_2$, and $N_3$ are the complexity–accuracy trade-off parameters.

Proof. 

See Appendix B.    □

4.1.2. NF in Case I

When considering the NF in Case I, the conditions ${\kappa }_{i^{\prime }}^1=1$, ${\chi }_{u_1}^1=1$, and ${\chi }_r^1=0$ hold. Based on $S{R}_{s_1}$, (5), and (8), the ESR of $s_1$ for the NF in Case I can be written as $S{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}={\left[L{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}-E{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}\right]}^{+}$, where $L{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+U_{s_1}^{\mathrm{I}2})\right\}$, $E{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+V_{s_1}^{\mathrm{I}2})\right\}$, $U_{s_1}^{\mathrm{I}2}\triangleq \frac{H_{s{u}_1}^{1,G}{(L_{s{u}_1}^G)}^{-1}{\rho }_s{a}_1}{H_{u_1{u}_1}^{1,G}{\rho }_{RSI}+1}$, and $V_{s_1}^{\mathrm{I}2}\triangleq \frac{H_{s{e}_1}^{1,G}{(L_{s{e}_1}^G)}^{-1}{\rho }_s{a}_1}{H_{u_1{e}_1}^{1,G}{(L_{u_1{e}_1}^G)}^{-1}{b}_{u_1}^1{\rho }_m+1}$. When $b_r^1=0$, $U_{s_1}^{\mathrm{I}1}$ degenerates into $U_{s_1}^{\mathrm{I}2}$. Therefore, based on (A1), we can easily obtain $F_{U_{s_1}^{\mathrm{I}2}}(u)=1-\frac{exp(-{\Omega }_{3}u)}{{\Omega }_{2}u+1}$. Using (14), (15), and [43] (Equation (3.352.4)), we can calculate $L{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}$ as

$$\begin{array}{cc}\hfill L{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}& ={\displaystyle \frac{1}{2ln2}}{\int }_0^{\infty }{\displaystyle \frac{exp(-{\Omega }_{3}u)}{(1+u)(1+{\Omega }_{2}u)}}du\hfill \\ \hfill & ={\displaystyle \frac{{\Phi }_2-{\Phi }_3}{2ln2({\Omega }_2-1)}}.\hfill \end{array}$$

(23)

By comparing $V_{s_1}^{\mathrm{I}2}$ and $U_{s_1}^{\mathrm{I}2}$, we can use (23) to obtain

$$\begin{array}{c}\hfill E{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}=L{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}⟨{\Omega }_2\to {\Omega }_5,{\Omega }_3\to {\Omega }_6⟩.\end{array}$$

(24)

Combining (23) and (24), we obtain $S{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}$.

By observing (9) and (10), changes in the values of ${\kappa }_{i^{\prime }}^1$, ${\chi }_{u_1}^1$, and ${\chi }_r^1$ have no effect on the SINRs for $U_1$ and $E_1$ to decode $s_1^{\prime }$ in $t_2$. Hence, we have $S{R}_{s_1^{\prime }}^{\mathrm{NF}-\mathrm{I}}=S{R}_{s_1^{\prime }}^{\mathrm{NN}-\mathrm{I}}$.

Let $U_{s_2}^{\mathrm{I}2-1}\triangleq \frac{H_{s{u}_1}^{1,G}{(L_{s{u}_1}^G)}^{-1}{\rho }_s{a}_2}{H_{s{u}_1}^{1,G}{(L_{s{u}_1}^G)}^{-1}{\rho }_s{a}_1+H_{u_1{u}_1}^{1,G}{\rho }_{RSI}+1}$, $U_{s_2}^{\mathrm{I}2-2}\triangleq \frac{H_{sr}^{1,A}{(L_{sr}^A)}^{-1}{\rho }_s{a}_2}{H_{sr}^{1,A}{(L_{sr}^A)}^{-1}{\rho }_s{a}_1+H_{u_{1}r}^{1,A}{(L_{u_{1}r}^A)}^{-1}{b}_{u_1}^1{\rho }_m+1}$, and $U_{s_2}^{\mathrm{I}2-3}\triangleq {\gamma }_{u_2,s_2}^2$. Based on $L{R}_{s_2}$, the ergodic rate of $s_2$ at $U_2$ for the NF in $t_2$ can be written as $L{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+min(U_{s_2}^{\mathrm{I}2-1},U_{s_2}^{\mathrm{I}2-2},U_{s_2}^{\mathrm{I}2-3}))\right\}$. Since $U_{s_2}^{\mathrm{I}2-1}=U_{s_2}^{\mathrm{I}1-1}⟨b_r^1\to 0⟩$, the CDF of $U_{s_2}^{\mathrm{I}2-1}$ can be directly obtained with the help of (A4), as shown by

$$\begin{array}{c}\hfill F_{U_{s_2}^{\mathrm{I}2-1}}(u)=\left\{\begin{array}{cc}{\tilde{F}}_{U_{s_2}^{\mathrm{I}2-1}}(u)={\tilde{F}}_{U_{s_2}^{\mathrm{I}1-1}}⟨{\Omega }_{11}\to 0⟩,\hfill & u<\frac{a_2}{a_1},\\ 1,\hfill & u\ge \frac{a_2}{a_1}.\end{array}\right.\end{array}$$

(25)

Following the similar steps in (A5) and (A6), the CDF of $U_{s_2}^{\mathrm{I}2-2}$ can be written as

$$\begin{array}{c}\hfill F_{U_{s_2}^{\mathrm{I}2-2}}\left(u\right)=\left\{\begin{array}{cc}{\tilde{F}}_{U_{s_2}^{\mathrm{I}2-2}}\left(u\right),\hfill & u<{\displaystyle \frac{a_2}{a_1}},\\ 1,\hfill & u\ge {\displaystyle \frac{a_2}{a_1}},\end{array}\right.\end{array}$$

(26)

where

$$\begin{array}{cc}\hfill {\tilde{F}}_{U_{s_2}^{\mathrm{I}2-2}}\left(u\right)=& 1-exp(-m_{sr}{\Xi }_3\left(u\right))\hfill \\ \hfill & \hspace{0.17em}\times {\sum }_{i_3=0}^{m_{sr}-1}{\sum }_{i_4=0}^{i_3}\left({\displaystyle \genfrac{}{}{0pt}{}{i_3}{i_4}}\right){\displaystyle \frac{{\left(m_{sr}{\Xi }_3\left(u\right)\right)}^{i_3}{\left({\Omega }_{14}\right)}^{i_3-i_4}{m_{u_{1}r}}^{m_{u_{1}r}}\Gamma (i_3-i_4+m_{u_{1}r})}{i_3!\Gamma \left(m_{u_{1}r}\right){(m_{sr}{\Xi }_1\left(u\right)+m_{u_{1}r})}^{i_3-i_4+m_{u_{1}r}}}}.\hfill \end{array}$$

(27)

Since ${\gamma }_{u_2,s_2}^2$ is the same in both the NN and NF, we have $F_{U_{s_2}^{\mathrm{I}2-3}}\left(u\right)=F_{U_{s_2}^{\mathrm{I}1-3}}\left(u\right)$. Using the order statistics and (20), the closed-form expression for $L{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}$ is

$$\begin{array}{c}\hfill L{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}=L{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}⟨{\tilde{F}}_{U_{s_2}^{\mathrm{I}1}}\left(u_{n_1}\right)\to {\tilde{F}}_{U_{s_2}^{\mathrm{I}2}}\left(u_{n_1}\right)⟩,\end{array}$$

(28)

where ${\tilde{F}}_{U_{s_2}^{\mathrm{I}2}}(u)=1-(1-{\tilde{F}}_{U_{s_2}^{\mathrm{I}2-1}}(u))(1-{\tilde{F}}_{U_{s_2}^{\mathrm{I}2-2}}(u))(1-F_{U_{s_2}^{\mathrm{I}2-3}}(u))$.

Moreover, based on $E{R}_{s_2}$, the ergodic rate of $s_2$ achieved by the eavesdroppers in this case can be rewritten as $E{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+max(V_{s_2}^{\mathrm{I}2-1},min(U_{s_2}^{\mathrm{I}2-2},V_{s_2}^{\mathrm{I}2-2}),V_{s_2}^{\mathrm{I}2-3}))\right\}$, where $V_{s_2}^{\mathrm{I}2-1}=V_{s_2}^{\mathrm{I}1-1}$, $V_{s_2}^{\mathrm{I}2-2}=V_{s_2}^{\mathrm{I}1-2}$, and $V_{s_2}^{\mathrm{I}2-3}=V_{s_2}^{\mathrm{I}1-3}⟨b_r^1\to 0⟩$. Recalling (22d), (22e), and (22f), we have $F_{V_{s_2}^{\mathrm{I}2-1}}(v)=F_{V_{s_2}^{\mathrm{I}1-1}}(v)$, $F_{V_{s_2}^{\mathrm{I}2-2}}(v)=F_{V_{s_2}^{\mathrm{I}1-2}}(v)$, and $F_{V_{s_2}^{\mathrm{I}2-3}}(v)=1-exp(-{\Omega }_{23}v)/({\Omega }_{22}v+1)$. Furthermore, utilizing (21), $E{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}$ can be written as $E{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}=E{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}⟨{\dot{F}}_{V_{s_2}^{\mathrm{I}1}}(v_{n_2})\to {\dot{F}}_{V_{s_2}^{\mathrm{I}2}}(v_{n_2}),{\ddot{F}}_{V_{s_2}^{\mathrm{I}1}}(tan{v}_{n_3})\to {\ddot{F}}_{V_{s_2}^{\mathrm{I}2}}(tan{v}_{n_3})⟩$, where ${\dot{F}}_{V_{s_2}^{\mathrm{I}2}}(v)=(1-(1-{\tilde{F}}_{U_{s_2}^{\mathrm{I}2-2}}(v))(1-F_{V_{s_2}^{\mathrm{I}2-2}}(v)))F_{V_{s_2}^{\mathrm{I}2-1}}(v)F_{V_{s_2}^{\mathrm{I}2-3}}(v)$ and ${\ddot{F}}_{V_{s_2}^{\mathrm{I}2}}(v)=F_{V_{s_2}^{\mathrm{I}2-1}}(v)F_{V_{s_2}^{\mathrm{I}2-3}}(v)$.

Based on this, the ESR of $s_2$ for the NF in Case I is written as $S{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}={\left[L{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}-E{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}\right]}^{+}$.

4.1.3. FN in Case I

Since ${\kappa }_{i^{\prime }}^1=1$, ${\chi }_{u_1}^1=0$, and ${\chi }_r^1=1$, the ESR of $s_1$ for the FN in Case I can be rewritten as $S{R}_{s_1}^{\mathrm{FN}-\mathrm{I}}={\left[L{R}_{s_1}^{\mathrm{FN}-\mathrm{I}}-E{R}_{s_1}^{\mathrm{FN}-\mathrm{I}}\right]}^{+}$, where $L{R}_{s_1}^{\mathrm{FN}-\mathrm{I}}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+U_{x_1}^{\mathrm{I}3})\right\}$, $E{R}_{x_1}^{\mathrm{FN}-\mathrm{I}}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+V_{x_1}^{\mathrm{I}3})\right\}$, $U_{s_1}^{\mathrm{I}3}=U_{s_1}^{\mathrm{I}1}⟨{\rho }_{RSI}\to 0⟩$, and $V_{s_1}^{\mathrm{I}3}=V_{s_1}^{\mathrm{I}1}⟨b_{u_1}^1\to 0⟩$. Following the similar steps in (A2), we have

$$\begin{array}{c}\hfill L{R}_{s_1}^{\mathrm{FN}-\mathrm{I}}=-{\displaystyle \frac{{m_{r{u}_1}}^{m_{r{u}_1}}}{2ln2{{\Omega }_1}^{m_{r{u}_1}}}}\left\{{\sum }_{i_1=1}^{m_{r{u}_1}}{\left({\displaystyle \frac{{\Omega }_1}{m_{r{u}_1}-{\Omega }_1}}\right)}^{i_1}{\Phi }_1-{\left({\displaystyle \frac{{\Omega }_1}{m_{r{u}_1}-{\Omega }_1}}\right)}^{m_{r{u}_1}}{\Phi }_3\right\},\end{array}$$

(29)

and

$$\begin{array}{c}\hfill E{R}_{s_1}^{\mathrm{FN}-\mathrm{I}}=L{R}_{s_1}^{\mathrm{FN}-\mathrm{I}}(m_{r{u}_1}\to m_{r{e}_1},{\Omega }_1\to {\Omega }_4,{\Omega }_3\to {\Omega }_6).\end{array}$$

(30)

By combining (29) and (30), the closed-form expression for $S{R}_{s_1}^{\mathrm{FN}-\mathrm{I}}$ is obtained.

Moreover, the ESR of $s_1^{\prime }$ for the FN in Case I is $S{R}_{s_1^{\prime }}^{\mathrm{FN}-\mathrm{I}}=S{R}_{s_1^{\prime }}^{\mathrm{NN}-\mathrm{I}}$ because ${\gamma }_{u_1,s_1^{\prime }}^2$ and ${\gamma }_{e_1,s_1^{\prime }}^2$ remain unchanged.

Based on $L{R}_{s_2}$ and $E{R}_{s_2}$, the ergodic rates of $s_2$ achieved by $U_2$ and the eavesdroppers in this case can be rewritten as $L{R}_{s_2}^{\mathrm{FN}-\mathrm{I}}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+min(U_{s_2}^{\mathrm{I}3-1},U_{s_2}^{\mathrm{I}3-2},U_{s_2}^{\mathrm{I}3-3}))\right\}$ and $E{R}_{s_2}^{\mathrm{FN}-\mathrm{I}}=\mathbb{E}\left\{\frac{1}{2}{log}_2(1+max(V_{s_2}^{\mathrm{I}3-1},min(U_{s_2}^{\mathrm{I}3-2},V_{s_2}^{\mathrm{I}3-2}),V_{s_2}^{\mathrm{I}3-3}))\right\}$, respectively, where $U_{s_2}^{\mathrm{I}3-1}=U_{s_2}^{\mathrm{I}1-1}⟨{\rho }_{RSI}\to 0⟩$, $U_{s_2}^{\mathrm{I}3-2}=U_{s_2}^{\mathrm{I}1-2}⟨b_{u_1}^1\to 0⟩$, $U_{s_2}^{\mathrm{I}3-3}=U_{s_2}^{\mathrm{I}1-3}$, $V_{s_2}^{\mathrm{I}3-1}=V_{s_2}^{\mathrm{I}1-1}$, $V_{s_2}^{\mathrm{I}3-2}=V_{s_2}^{\mathrm{I}1-2}$, and $V_{s_2}^{\mathrm{I}3-3}=V_{s_2}^{\mathrm{I}1-3}⟨b_{u_1}^1\to 0⟩$. Therefore, we can obtain the CDFs of $U_{s_2}^{\mathrm{I}3-1}$, $U_{s_2}^{\mathrm{I}3-2}$, and $U_{s_2}^{\mathrm{I}3-3}$ by following similar derivation steps as in (22a), (22b), and (22c), which are given as

$$\begin{array}{c}\hfill F_{U_{s_2}^{\mathrm{I}3-1}}\left(u\right)=\left\{\begin{array}{cc}{\tilde{F}}_{U_{s_2}^{\mathrm{I}3-1}}\left(u\right)={\tilde{F}}_{U_{s_2}^{\mathrm{I}1-1}}⟨{\Omega }_{12}\to 0⟩,\hfill & u<{\displaystyle \frac{a_2}{a_1}},\\ 1,\hfill & u\ge {\displaystyle \frac{a_2}{a_1}},\end{array}\right.\end{array}$$

(31)

$$\begin{array}{c}\hfill F_{U_{s_2}^{\mathrm{I}3-2}}\left(u\right)=\left\{\begin{array}{cc}{\tilde{F}}_{U_{s_2}^{\mathrm{I}3-2}}\left(u\right),\hfill & u<{\displaystyle \frac{a_2}{a_1}},\\ 1,\hfill & u\ge {\displaystyle \frac{a_2}{a_1}},\end{array}\right.\end{array}$$

(32)

and

$$\begin{array}{c}\hfill F_{U_{s_2}^{\mathrm{I}3-3}}\left(u\right)=F_{U_{s_2}^{\mathrm{I}1-3}}\left(u\right),\end{array}$$

(33)

where ${\tilde{F}}_{U_{s_2}^{\mathrm{I}3-2}}(u)=1-exp(-m_{sr}{\Xi }_3(u)){\sum }_{i_3=0}^{m_{sr}-1}{\sum }_{i_4=0}^{i_3}\left({\displaystyle \genfrac{}{}{0pt}{}{i_3}{i_4}}\right)\frac{{m_{rr}}^{m_{rr}}{(m_{sr}{\Xi }_3(u))}^{i_3}{({\rho }_{RSI})}^{i_3-i_4}\Gamma (i_3-i_4+m_{rr})}{i_3!\Gamma (m_{rr}){(m_{sr}{\Xi }_2(u)+m_{rr})}^{i_3-i_4+m_{rr}}}$.

Using the order statistics and (20), we have

$$\begin{array}{c}\hfill L{R}_{s_2}^{\mathrm{FN}-\mathrm{I}}=L{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}⟨{\tilde{F}}_{U_{s_2}^{\mathrm{I}1}}\left(u_{n_1}\right)\to {\tilde{F}}_{U_{s_2}^{\mathrm{I}3}}\left(u_{n_1}\right)⟩,\end{array}$$

(34)

where ${\tilde{F}}_{U_{s_2}^{\mathrm{I}3}}\left(u\right)=1-(1-{\tilde{F}}_{U_{s_2}^{\mathrm{I}3-1}}\left(u\right))(1-{\tilde{F}}_{U_{s_2}^{\mathrm{I}3-2}}\left(u\right))(1-F_{U_{s_2}^{\mathrm{I}3-3}}\left(u\right))$.

Similar to (22f), the CDF of $V_{s_2}^{\mathrm{I}3-3}$ can be given by $F_{V_{s_2}^{\mathrm{I}3-3}}(v)=1-{m_{r{e}_1}}^{m_{r{e}_1}}\frac{exp(-{\Omega }_{23}v)}{{({\Omega }_{21}v+m_{r{e}_1})}^{m_{r{e}_1}}}$.

Since $V_{s_2}^{\mathrm{I}3-1}=V_{s_2}^{\mathrm{I}1-1}$ and $V_{s_2}^{\mathrm{I}3-2}=V_{s_2}^{\mathrm{I}1-2}$, the equations $F_{V_{s_2}^{\mathrm{I}3-1}}\left(v\right)=F_{V_{s_2}^{\mathrm{I}1-1}}\left(v\right)$ and $F_{V_{s_2}^{\mathrm{I}3-2}}\left(v\right)=F_{V_{s_2}^{\mathrm{I}1-2}}\left(v\right)$ hold. Referring to (21), the ergodic rate $E{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}$ can be obtained as

$$\begin{array}{c}\hfill E{R}_{s_2}^{\mathrm{FN}-\mathrm{I}}=E{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}⟨{\dot{F}}_{V_{s_2}^{\mathrm{I}1}}\left(v_{n_2}\right)\to {\dot{F}}_{V_{s_2}^{\mathrm{I}3}}\left(v_{n_2}\right),{\ddot{F}}_{V_{s_2}^{\mathrm{I}1}}(tan{v}_{n_3})\to {\ddot{F}}_{V_{s_2}^{\mathrm{I}3}}(tan{v}_{n_3})⟩,\end{array}$$

(35)

where ${\ddot{F}}_{V_{s_2}^{\mathrm{I}3}}(v)=F_{V_{s_2}^{\mathrm{I}3-1}}(v)F_{V_{s_2}^{\mathrm{I}3-3}}(v)$ and ${\dot{F}}_{V_{s_2}^{\mathrm{I}3}}\left(v\right)=(1-(1-{\tilde{F}}_{U_{s_2}^{\mathrm{I}3-2}}\left(v\right))(1-F_{V_{s_2}^{\mathrm{I}3-2}}\left(v\right)))\times F_{V_{s_2}^{\mathrm{I}3-1}}\left(v\right)F_{V_{s_2}^{\mathrm{I}3-3}}\left(v\right)$. Using (34) and (35), the ESR of $s_2$ for the FN in Case I can be written as $S{R}_{s_2}^{\mathrm{FN}-\mathrm{I}}={\left[L{R}_{s_2}^{\mathrm{FN}-\mathrm{I}}-E{R}_{s_2}^{\mathrm{FN}-\mathrm{I}}\right]}^{+}$.

4.2. ESR for the Proposed MNJJ in Case II

4.2.1. NN in Case II

The conditions ${\kappa }_{i^{\prime }}^1=0$, ${\chi }_{u_1}^1=1$, and ${\chi }_r^1=1$ hold when considering for the NN in Case II. The SINRs ${\gamma }_{u_1,s_1}^1$ and ${\gamma }_{e_1,s_1}^1$ under these conditions are equivalent to $U_{s_1}^{\mathrm{I}2}$ and $V_{s_1}^{\mathrm{I}1}$, respectively. Therefore, with the help of (17) and (23), the ESR for $s_1$ in this case can be directly written as $S{R}_{s_1}^{\mathrm{NN}-\mathrm{II}}={\left[L{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}-E{R}_{s_1}^{\mathrm{NN}-\mathrm{I}}\right]}^{+}$.

The parameters ${\kappa }_{i^{\prime }}^1$, ${\chi }_{u_1}^1$, and ${\chi }_r^1$ have no effect on ${\gamma }_{u_1,s_1^{\prime }}^2$ and ${\gamma }_{e_1,s_1^{\prime }}^2$, and thus, the ESR for $s_1^{\prime }$ in this case is $S{R}_{{s_1}^{\prime }}^{\mathrm{NN}-\mathrm{II}}=S{R}_{{s_1}^{\prime }}^{\mathrm{NN}-\mathrm{I}}$.

In this case, the SINRs ${\gamma }_{u_1,s_2}^1$ and ${\gamma }_{r,s_2}^1$ become $U_{s_2}^{\mathrm{I}2-1}$ and $U_{s_2}^{\mathrm{I}3-2}$, respectively, while the remaining SINRs related to $s_2$ are unchanged compared to the proposed NN in Case I. Therefore, using (20), (21), (22a), (22b), (25) and (32), we can directly obtain the ESR of $s_2$ for the NN in Case II as

$$\begin{array}{cc}\hfill S{R}_{s_2}^{\mathrm{NN}-\mathrm{II}}=& [L{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}⟨{\tilde{F}}_{U_{s_2}^{\mathrm{I}1-1}}\left(u_{n_1}\right)\to {\tilde{F}}_{U_{s_2}^{\mathrm{I}2-1}}\left(u_{n_1}\right),{\tilde{F}}_{U_{s_2}^{\mathrm{I}1-2}}\left(u_{n_1}\right)\to {\tilde{F}}_{U_{s_2}^{\mathrm{I}3-2}}\left(u_{n_1}\right)⟩\hfill \\ \hfill & -E{R}_{s_2}^{\mathrm{NN}-\mathrm{I}}⟨{\tilde{F}}_{U_{s_2}^{\mathrm{I}1-2}}\left(v_{n_2}\right)\to {\tilde{F}}_{U_{s_2}^{\mathrm{I}3-2}}\left(v_{n_2}\right)⟩{]}^{+}.\hfill \end{array}$$

(36)

4.2.2. NF in Case II

For the NF in Case II, the conditions ${\kappa }_{i^{\prime }}^1=0$, ${\chi }_{u_1}^1=1$, and ${\chi }_r^1=0$ hold. Under these conditions, the SINRs ${\gamma }_{u_1,s_1}^1$ and ${\gamma }_{e_1,s_1}^1$ become $U_{s_1}^{\mathrm{I}2}$ and $V_{s_1}^{\mathrm{I}2}$, respectively. Based on (23) and (24), the ESR of $s_1$ in this case can be written as $S{R}_{s_1}^{\mathrm{NF}-\mathrm{II}}={\left[L{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}-E{R}_{s_1}^{\mathrm{NF}-\mathrm{I}}\right]}^{+}$.

Similarly, the ESR for $s_1^{\prime }$ in this case can be directly given by $S{R}_{{s_1}^{\prime }}^{\mathrm{NF}-\mathrm{II}}=S{R}_{{s_1}^{\prime }}^{\mathrm{NN}-\mathrm{I}}$.

Compared to the NF in Case I, only ${\gamma }_{r,s_2}^1$ changes among the SINRs related to $s_2$ in the NF for Case II. Specifically, ${\gamma }_{r,s_2}^1=\frac{H_{sr}^{1,A}{(L_{sr}^A)}^{-1}{\rho }_s{a}_2}{H_{sr}^{1,A}{(L_{sr}^A)}^{-1}{\rho }_s{a}_1+1}$. Let $U_{s_2}^{\mathrm{II}2-2}\triangleq {\gamma }_{r,s_2}^1$. The CDF of $U_{s_2}^{\mathrm{II}2-2}$ can be written as

$$\begin{array}{c}\hfill F_{U_{s_2}^{\mathrm{II}2-2}}\left(u\right)=\left\{\begin{array}{cc}{\tilde{F}}_{U_{s_2}^{\mathrm{II}2-2}}\left(u\right)=F_{H_{sr}^{1,A}}\left({\displaystyle \frac{u}{{\left(L_{sr}^A\right)}^{-1}{\rho }_s(a_2-a_{1}u)}}\right),\hfill & u<{\displaystyle \frac{a_2}{a_1}},\\ 1,\hfill & u\ge {\displaystyle \frac{a_2}{a_1}}.\end{array}\right.\end{array}$$

(37)

Based on $L{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}$, $E{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}$, and (37), the ESR of $s_2$ for the NF in Case II can be written as

$$\begin{array}{cc}\hfill S{R}_{s_2}^{\mathrm{NF}-\mathrm{II}}=& [L{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}⟨{\tilde{F}}_{U_{s_2}^{\mathrm{I}2-2}}\left(u_{n_1}\right)\to {\tilde{F}}_{U_{s_2}^{\mathrm{II}2-2}}\left(u_{n_1}\right)⟩\hfill \\ \hfill & -E{R}_{s_2}^{\mathrm{NF}-\mathrm{I}}⟨{\tilde{F}}_{U_{s_2}^{\mathrm{I}2-2}}\left(v_{n_2}\right)\to {\tilde{F}}_{U_{s_2}^{\mathrm{II}2-2}}\left(v_{n_2}\right)⟩{]}^{+}.\hfill \end{array}$$

(38)

4.2.3. FN in Case II

If $U_1$ turns off jamming and the UAV turns on jamming in $t_1$, and the legitimate nodes are aware of each other’s AN, the SINRs ${\gamma }_{u_1,s_1}^1$ and ${\gamma }_{e_1,s_1}^1$ become ${\gamma }_{u_1,s_1}^1=H_{s{u}_1}^{1,G}{\left(L_{s{u}_1}^G\right)}^{-1}{\rho }_s{a}_1$ and ${\gamma }_{e_1,s_1}^1=V_{s_1}^{\mathrm{I}3}$, respectively. The CDF of ${\gamma }_{u_1,s_1}^1$ can be easily obtained as $F_{{\gamma }_{u_1,s_1}^1}\left(u\right)={\Omega }_{13}exp(-{\Omega }_{13}u)$. Therefore, using (14) and [43] (Equation (3.352.4)), the ergodic rate of $s_1$ at $U_1$ in this case can be given by

$$\begin{array}{c}\hfill L{R}_{s_1}^{\mathrm{FN}-\mathrm{II}}=-{\displaystyle \frac{1}{2ln2}}exp\left({\Omega }_{13}\right)\mathrm{Ei}(-{\Omega }_{13}).\end{array}$$

(39)

Consequently, the ESR of $s_1$ in this case can be written as $S{R}_{s_1}^{\mathrm{FN}-\mathrm{II}}={\left[L{R}_{s_1}^{\mathrm{FN}-\mathrm{II}}-E{R}_{s_1}^{\mathrm{FN}-\mathrm{I}}\right]}^{+}$. Similar to $S{R}_{{s_1}^{\prime }}^{\mathrm{NF}-\mathrm{I}}$, the ESR of ${s_1}^{\prime }$ for the FN in Case II can still be written as $S{R}_{{s_1}^{\prime }}^{\mathrm{NF}-\mathrm{II}}=S{R}_{{s_1}^{\prime }}^{\mathrm{NN}-\mathrm{I}}$. In the FN, the SINRs related to $s_2$ are the same in Case I and Case II except for ${\gamma }_{u_1,s_2}^1$. The SINR ${\gamma }_{u_1,s_2}^1$ in Case II is ${\gamma }_{u_1,s_2}^1=\frac{H_{s{u}_1}^{1,G}{\left(L_{s{u}_1}^G\right)}^{-1}{\rho }_s{a}_2}{H_{s{u}_1}^{1,G}{\left(L_{s{u}_1}^G\right)}^{-1}{\rho }_s{a}_1+1}$. Denote $U_{s_2}^{\mathrm{II}3-1}\triangleq {\gamma }_{u_1,s_2}^1$. The CDF of $U_{s_2}^{\mathrm{II}3-1}$ can be written as

$$\begin{array}{c}\hfill F_{U_{s_2}^{\mathrm{II}3-1}}\left(u\right)=\left\{\begin{array}{cc}{\tilde{F}}_{U_{s_2}^{\mathrm{II}3-1}}\left(u\right)=1-exp\left(-{\displaystyle \frac{u}{{\left(L_{s{u}_1}^G\right)}^{-1}{\rho }_s(a_2-a_{1}u)}}\right),\hfill & u<{\displaystyle \frac{a_2}{a_1}},\\ 1,\hfill & u\ge {\displaystyle \frac{a_2}{a_1}}.\end{array}\right.\end{array}$$

(40)

Hence, using (34), (35), and (40), the ESR of $s_2$ for the FN in Case II can be written as

$$\begin{array}{c}\hfill S{R}_{s_2}^{\mathrm{FN}-\mathrm{II}}={\left[L{R}_{s_2}^{\mathrm{FN}-\mathrm{I}}⟨{\tilde{F}}_{U_{s_2}^{\mathrm{I}3-1}}\left(u_{n_1}\right)\to {\tilde{F}}_{U_{s_2}^{\mathrm{II}3-1}}\left(u_{n_1}\right)⟩-E{R}_{s_2}^{\mathrm{FN}-\mathrm{I}}\right]}^{+}.\end{array}$$

(41)

4.3. ESSR for the Proposed MNJJ

Based on the derivation results in Section 4.1 and Section 4.2, the closed-form expression for the ESSR of the proposed MNJJ scheme under various cases can be uniformly expressed as

$$\begin{array}{c}\hfill {ESSR}^{\mathbb{M}}=S{R}_{s_1}^{\mathbb{M}}+S{R}_{s_1^{\prime }}^{\mathbb{M}}+S{R}_{s_2}^{\mathbb{M}},\end{array}$$

(42)

where $\mathbb{M}\in \left\{\mathrm{NN}-\mathrm{I},\mathrm{NF}-\mathrm{I},\mathrm{FN}-\mathrm{I},\mathrm{NN}-\mathrm{II},\mathrm{NF}-\mathrm{II},\mathrm{FN}-\mathrm{II}\right\}$.

4.4. The Proposed JPAIC Algorithm

This section focuses on maximizing the ESSR of the proposed MNJJ scheme by jointly optimizing the power allocation coefficients and interference power coefficients while ensuring the security of each signal transmission. Using the obtained ${ESSR}^{\mathbb{M}}$ as the objective function, we can formulate the corresponding mathematical optimization problem as

$$\begin{array}{cc}\hfill \mathcal{P}:& \underset{a_2,b_{r,}^1,b_{u_1}^1,b_{u_1}^2,b_{u_2}^2}{max}ESS{R}^{\mathbb{M}}\hfill \end{array}$$

(43a)

$$\begin{array}{cc}\hfill & \mathrm{s}.\mathrm{t}.0.5+\epsilon \le a_2\le 1-\epsilon ,\hfill \end{array}$$

(43b)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}{b}_r^1=0,\hfill & if\mathbb{M}\in \left\{\mathrm{NF}-\mathrm{I},\mathrm{NF}-\mathrm{II}\right\},\hfill \\ \epsilon \le b_r^1\le 1,\hfill & if\mathbb{M}\in \left\{\mathrm{NN}-\mathrm{I},\mathrm{FN}-\mathrm{I},\mathrm{NN}-\mathrm{II},\mathrm{FN}-\mathrm{II}\right\},\hfill \end{array}\right.\hfill \end{array}$$

(43c)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cc}{b}_{u_1}^1=0,\hfill & if\mathbb{M}\in \left\{\mathrm{FN}-\mathrm{I},\mathrm{FN}-\mathrm{II}\right\},\hfill \\ \epsilon \le b_{u_1}^1\le 1,\hfill & if\mathbb{M}\in \left\{\mathrm{NN}-\mathrm{I},\mathrm{NF}-\mathrm{I},\mathrm{NN}-\mathrm{II},\mathrm{NF}-\mathrm{II}\right\},\hfill \end{array}\right.\hfill \end{array}$$

(43d)

$$\begin{array}{cc}\hfill & \epsilon \le b_{\overline{u}}^2\le 1,\forall \overline{u}\in \{u_1,u_2\},\hfill \end{array}$$

(43e)

$$\begin{array}{cc}\hfill & S{R}_{\overline{s}}^{\mathbb{M}}>0,\forall \overline{s}\in \{s_1,s_1^{\prime },s_2\},\hfill \end{array}$$

(43f)

where $\epsilon$ represents the optimization accuracy of the variables to be optimized, (43a) restricts the range of power allocation coefficients to satisfy the downlink NOMA criteria, (43c) and (43d) specify the range of interference power coefficients $b_r^1$ and $b_{u_1}^1$ to comply with the state of interference activation or deactivation for the UAV and $U_1$ under different cases, (43e) ensures that $U_1$ and $U_2$ always have interference activated in $t_2$ and that the interference power does not exceed the preset maximum value, and (43f) guarantees that the ESRs of all signals are greater than zero.

The closed-form expression for the optimal solution of the power allocation coefficients and interference coefficients cannot be directly obtained for the above problem. Therefore, we design a JPAIC algorithm using PSO. As shown in Algorithm 1, the five variables to be optimized are treated as particles in a five-dimensional space. By iteratively searching the positions of multiple particles, the optimal fitness value (i.e., the maximum of ${ESSR}^{\mathbb{M}}$) can be obtained. Moreover, the computational complexity of the proposed JPAIC algorithm mainly depends on lines 4–17 in Algorithm 1. Therefore, the computational complexity of the proposed JPAIC algorithm can be easily obtained as $\mathcal{O}(N_P{C}^{\mathbb{M}}+3N_I{N}_P{C}^{\mathbb{M}})$, where $C^{\mathbb{M}}$ represents the computational complexity primarily caused by addition and multiplication in (42).

Algorithm 1 JPAIC Algorithm Using PSO

1: Input the type of the proposed MNJJ scheme $\mathbb{M}$, number of particles $N_P$, number of iterations $N_I$, precision $\epsilon$, and system model parameters include: path loss $L_{\overline{i}\overline{j}}^G$ and $L_{r\tilde{j}}^A$, shape parameter $m_{r\tilde{j}}$, transmission powers $P_s$ and $P_r$, maximum interference power $P_m$, residual self-interference power $P_{RSI}$, and noise power $N_0$.   2: Initialize each particle’s location ${\mathbf{L}}_n=[l_n^1,l_n^2,l_n^3,l_n^4,l_n^5]$, velocity ${\mathbf{v}}_n=[v_n^1,v_n^2,v_n^3,v_n^4,v_n^5]$, and personal best location ${\mathbf{L}}_{n,best}={\mathbf{L}}_n$, where ${\mathbf{v}}_n=\mathbf{0}$, $l_n^q=(l_n^{q,max}-l_n^{q,min}){\delta }_{l_n^q}+l_n^{q,min}$, $q\in \{1,2,\dots ,5\}$. The variables $l_n^1$, $l_n^2$, $l_n^3$, $l_n^4$, and $l_n^5$ correspond to $a_2$, $b_r^1$, $b_{u_1}^1$, $b_{u_1}^2$, and $b_{u_2}^2$, respectively. Here, ${\delta }_{l_n^q}$ is a random number in [0, 1], and $l_n^{q,max}$ and $l_n^{q,min}$ are the maximum and minimum of $l_n^q$ determined by (43b) to (43e).   3: Set the inertia coefficient $\omega =0.7234$ and the learning factors ${\lambda }_1=2.5$ and ${\lambda }_2=3$.   4: Calculate the global best location ${\mathbf{L}}_{gbest}=\underset{{\mathbf{L}}_n\left(0\right),\forall n\in \{1,2,\dots ,N_p\}}{argmax}\left(ESS{R}^{\mathbb{M}}\left({\mathbf{L}}_n\right)\right)$, where the constraint (43f) should be met.   5: while $1\le m\le N_I$ do   6:     for $1\le n\le N_P$ do   7:        Update the velocity ${\mathbf{v}}_n=\omega {\mathbf{v}}_n+{\lambda }_1{\delta }_{n,1}({\mathbf{L}}_{gbest}-{\mathbf{L}}_n)+{\lambda }_2{\delta }_{n,2}({\mathbf{L}}_{n,best}-{\mathbf{L}}_n)$ and individual location ${\mathbf{L}}_n={\mathbf{L}}_n+{\mathbf{v}}_n$, where ${\delta }_{n,1}$ and ${\delta }_{n,2}$ are random numbers in the interval [0, 1].   8:        Check if each element of ${\mathbf{L}}_n$ is within the range specified by (43b) to (43e). If an element exceeds its maximum, set it to the maximum; if it falls below its minimum, set it to the minimum.   9:        Calculate $ESS{R}^{\mathbb{M}}\left({\mathbf{L}}_n\right)$, $ESS{R}^{\mathbb{M}}\left({\mathbf{L}}_{n,best}\right)$, and $ESS{R}^{\mathbb{M}}\left({\mathbf{L}}_{gbest}\right)$ by using (42). When the constraint (43f) does not hold, set the corresponding ESSR to zero. 10:        if $ESS{R}^{\mathbb{M}}\left({\mathbf{L}}_n\right)>ESS{R}^{\mathbb{M}}\left({\mathbf{L}}_{n,best}\right)$ then 11:            ${\mathbf{L}}_{n,best}={\mathbf{L}}_n$. 12:        end if 13:        if $ESS{R}^{\mathbb{M}}\left({\mathbf{L}}_n\right)>ESS{R}^{\mathbb{M}}\left({\mathbf{L}}_{gbest}\right)$ then 14:            ${\mathbf{L}}_{gbest}={\mathbf{L}}_n$. 15:        end if 16:     end for 17: end while 18: Output the optimal coefficient combination ${\mathbf{L}}_{gbest}$ and the maximum ESSR $ESS{R}^{\mathbb{M}}\left({\mathbf{L}}_{gbest}\right)$.

5. Simulation Results

This section employs Monte Carlo simulations to verify the performance merits of the proposed MNJJ scheme and the proposed JPAIC algorithm, as well as the validity of the theoretical analysis. In the simulations, we consider two node location configurations: Location 1 and Location 2. In Location 1, the coordinates of the BS, UAV, $U_1$, $E_1$, $U_2$, and $E_2$ are $(-50,0,0)$, $(0,0,50)$, $(-40,2,0)$, $(-40,0,0)$, $(40,2,0)$, and $(40,0,0)$, respectively. In Location 2, these coordinates change to $(-50,0,0)$, $(0,0,50)$, $(-45,0,0)$, $(-45,2,0)$, $(40,0,0)$, and $(40,5,0)$. We set the carrier frequency to $f_c=2$ GHz, $P_r=P_s$, the maximum interference power to $P_m=40$ dBm, and the noise power to $N_0=-110$ dBm. Additionally, we investigate the performance of the proposed MNJJ scheme under both fixed and optimal power allocation and interference control settings. For the fixed power setting (FPS), the fixed power allocation coefficients are $a_1=0.1$ and $a_2=0.9$, and the fixed interference power coefficients are $b_{u_1}^2=1$ and $b_{u_2}^2=1$. Specifically, we examine: (1) the NN with $b_{u_1}^1=b_r^1=1$; (2) the NF with $b_{u_1}^1=1$ and $b_r^1=0$; and (3) the NF with $b_{u_1}^1=0$ and $b_r^1=1$. Unless otherwise specified, we set the shape parameter of the Nakagami-m channel to 2, the ratio of residual interference to noise power to ${\rho }_{RSI}=3$ dB [34], the optimization precision to $\epsilon =0.01$, the particle swarm size to $N_P=4$, and the number of iterations to $N_I=15$. The markers “NN-I”, “NF-I”, “FN-I”, “NN-II”, “NF-II”, and “FN-II” in the following figures represent NN, NF, and FN in Case I and Case II, respectively. The marker “CNC-I” refers to the CNC scheme in Case I, with the CNC referenced in [27].

5.1. Case I

Figure 4 compares the ESSR of the proposed MNJJ scheme with three types (i.e., the NN, NF, and FN) with that of the CNC scheme in Case I. In this figure, the theoretical curves of the ESSR for the proposed MNJJ perfectly coincide with the corresponding simulation values, which validates the correctness of the theoretical analysis. Under different node location settings, the ranking of the ESSR from highest to lowest is consistently the NF, NN, FN, and CNC. The superiority in ESSR for the proposed MNJJ is attributed to multi-node joint jamming. Since legitimate nodes are unaware of each other’s AN in Case I, the simultaneous interference from the UAV and $U_1$ (i.e., the NN) excessively reduces the SINRs of $s_1$ and $s_2$ at the legitimate nodes. Based on this, the NN has a lower ESSR than the NF in Case I. Compared with the NF, only the UAV in the FN is enabled for interference, and the distance from the UAV to $E_1$ is much greater than the distance from $U_1$ to $E_1$. Therefore, the UAV has the similar interference intensity on $U_1$ and $E_1$ in the FN, making it impossible to guarantee the secrecy rates of $s_1$ and $s_2$. This fact, in turn, causes the ESSR of the FN to be slightly lower than that of the NN. Additionally, in the Location 2 configuration, the legitimate nodes $U_1$ and $U_2$ are closer to the corresponding information sources than the eavesdroppers, leading to a higher ESSR in Location 2 compared to Location 1. From the perspective of ESSR performance, the NF scheme is more suitable for Case I.

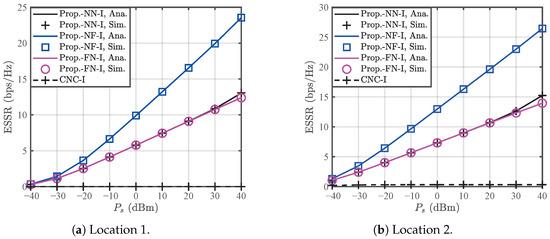
Figure 4. Comparison of the ESSRs of the CNC scheme and the proposed MNJJ scheme with the NN, NF, and FN in Case I.

Figure 5 illustrates the impact of the shape parameter m of the A2G/G2A channel on the ESSRs for the proposed MNJJ and the CNC under $P_s=20$ dBm in Case I. From Figure 5, the proposed NF consistently achieves a higher ESSR than both the NN and FN for different values of m, and the ESSRs of the NN and FN are almost identical. These observations are consistent with the findings in Figure 4. The increase in m has a relatively small impact on the ESSR of each scheme. Typically, a larger m indicates better A2G/G2A channel quality. Since only the link related to $s_2$ in the legitimate links is affected by the A2G/G2A channel, and the ergodic rate of $s_2$ contributes relatively less to the ergodic sum rate, the effect of a larger m on the ergodic sum rate of the legitimate nodes is minimal. Additionally, the eavesdroppers are located near the legitimate users and the ergodic rate of $s_2$ being intercepted is also constrained by the weaker link in the DF two-hop link. Hence, the variation in m has no significant effect on the ergodic sum rate at the eavesdroppers. Based on this, all schemes exhibit good robustness to changes in m.

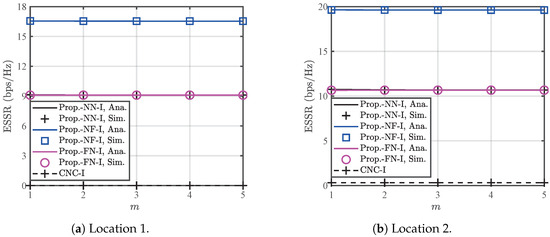
Figure 5. Impact of the A2G/G2A channel shape parameter m on the ESSRs of the CNC scheme and the proposed MNJJ scheme with the NN, NF, and FN in Case I when $P_s=20$ dBm.

Figure 6 shows the variation in ESSR for each scheme under different strengths of the residual interference caused by full-duplex operation. The proposed NF consistently achieves the best ESSR across different values of ${\rho }_{RSI}$. As ${\rho }_{RSI}$ increases, the ESSRs of the proposed NN, NF, and FN gradually decrease, while the ESSR of the CNC remains unchanged. This is because the proposed MNJJ is affected by residual self-interference, and an increase in residual interference strength reduces the ergodic rate of legitimate information without impacting the eavesdropper. In contrast, the CNC scheme is not influenced by these factors.

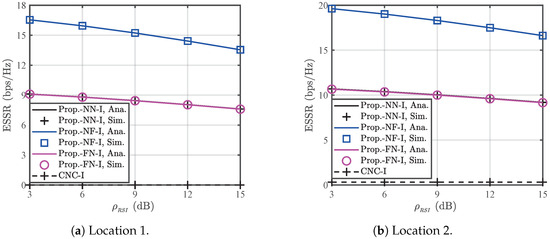
Figure 6. Impact of ${\rho }_{RSI}$ on the ESSRs of the CNC scheme and the proposed MNJJ scheme with the NN, NF, and FN in Case I when $P_s=20$ dBm.

Figure 7 illustrates the variation in ESSR for the proposed MNJJ scheme with the number of iterations of the JPAIC algorithm, with the NN and NF in Case I as examples. The figure shows that the ESSR achieved by the proposed JPAIC algorithm quickly stabilizes after a relatively small number of iterations, indicating its good convergence performance. Note that this convergence analysis also applies to Case II.

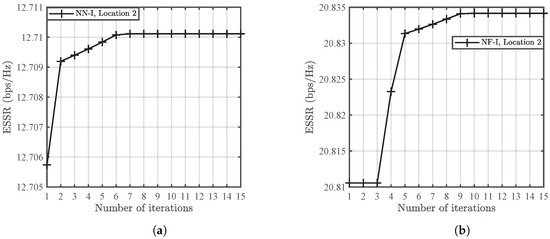
Figure 7. Examples of the convergence analysis of the proposed JPAIC algorithm with $P_s=20$ dBm. (a) Example 1: NN in Case I with Location 2. (b) Example 2: NF in Case I with Location 2.

Figure 8 compares the ESSR of the proposed JPAIC algorithm with that of the FPS, where the proposed JPAIC maximizes the ESSR under the constraint of the ESR for each data stream. The coincidence of the ESSR curve with the corresponding theoretical optimal value (TOV) demonstrates the effectiveness of JPAIC, where the TOV is obtained via an exhaustive search under precision constraints. For the NN and NF, using the proposed JPAIC achieves a better ESSR compared to using FPS because it determines the optimal power allocation and interference power coefficients. An interesting observation is that in Location 1, the ESSR for the FN using both JPAIC and FPS is zero, as the FN struggles to meet the ESR constraints for all data streams. In Location 2, the FN only fails to ensure the security of all data streams at high transmission power. This is because, in Location 2, the legitimate nodes have better channel quality than the eavesdroppers for acquiring information, but high transmission power also allows the eavesdroppers to obtain more legitimate information.

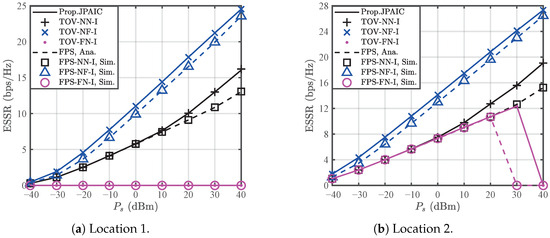
Figure 8. Comparison of the ESSR performance of the proposed JPAIC algorithm and FPS in Case I.

5.2. Case II

Figure 9 shows the ESSRs for the CNC and the proposed MNJJ with the NN, NF, and FN under the condition that legitimate users are aware of each other’s AN. In Case II, the ESSR of the proposed MNJJ is superior to that of the CNC. Additionally, the proposed FN performs slightly better than the NN and NF at low to moderate transmission power, but the reverse is true at high transmission power. This is because interference initiated by $U_1$ and the UAV in $t_1$ weakens the achievable ergodic rates of $s_1$ and $s_2$ at the legitimate nodes due to self-interference, and the ergodic rate of $s_2$ contributes relatively less to the overall achievable ergodic rate. Therefore, the FN can more effectively achieve better ESSR at low to moderate transmission power. However, at high transmission power, the FN cannot prevent eavesdroppers from obtaining more legitimate information due to insufficient interference, resulting in a lower ESSR compared to the NN and NF. Overall, the FN is suitable for small $P_s$ in Case II, while the NF is a more robust choice under all conditions. Figure 10 shows the impact of the shape parameter m on the ESSR of each scheme in Case II. For reasons similar to those in Figure 5, the ESSR remains essentially unchanged with the increase in m. Figure 11 demonstrates that in Case II, the residual self-interference strength remains an important factor affecting the ESSR of the proposed MNJJ.

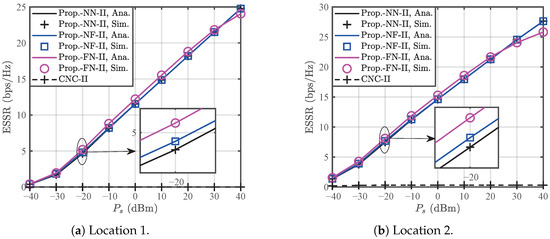
Figure 9. Comparison of the ESSRs of the CNC scheme and the proposed MNJJ scheme with the NN, NF, and FN in Case II.

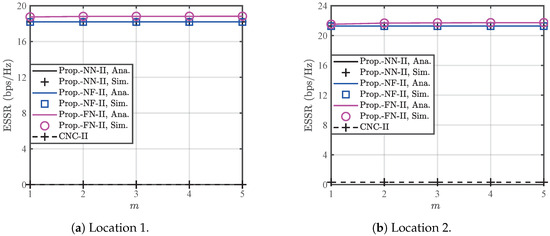
Figure 10. Impact of the A2G/G2A channel shape parameter m on the ESSRs of the CNC scheme and the proposed MNJJ scheme with the NN, NF, and FN in Case II when $P_s=20$ dBm.

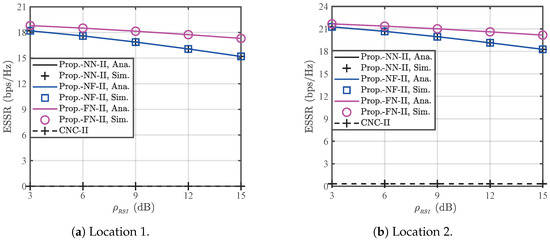
Figure 11. Impact of ${\rho }_{RSI}$ on the ESSRs of the CNC scheme and the proposed MNJJ scheme with the NN, NF, and FN in Case II when $P_s=20$ dBm.

Figure 12 compares the ESSR of the proposed JPAIC with that of the FPS in Case II. From this figure, the effectiveness of the proposed JPAIC in optimizing the ESSR of the proposed MNJJ is validated. Notably, when legitimate users are closer to the corresponding information sources than the eavesdroppers, the FN scheme using the FPS fails to ensure secure transmission of all data streams at high transmission power. However, the proposed JPAIC can address this issue. Therefore, it is evident that the proposed JPAIC not only maximizes the ESSR of the proposed MNJJ but also enhances the robustness of the ESSR performance of the proposed MNJJ. Note that when global channel state information is available at the BS, the BS can use a mini phase before information transmission to send appropriate signaling to $U_1$ and the UAV to control whether $U_1$ and the UAV should turn on jamming. Based on the above simulation validation and discussion, we know that even if global channel state information is not available at the BS, the system can preset $U_1$ and the UAV to be in the turn-on jamming and turn-off jamming state (i.e., NF) during the first phase to achieve robust and good ESSR performance.

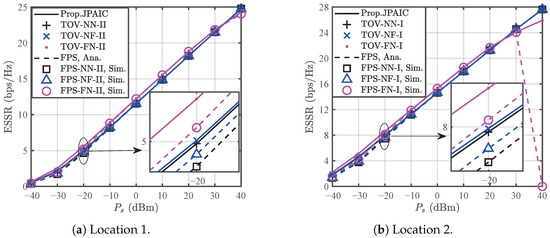
Figure 12. Comparison of the ESSR performance of the proposed JPAIC algorithm and FPS in Case II.

6. Conclusions

This work investigated the physical layer secure transmission in a UAV-assisted NOMA-CDRT system for emergency rescue scenarios. In this system, the BS serves a user in its cell while also using a UAV relay to serve a user in a cell with damaged communication facilities, with eavesdroppers near all users threatening communication security. To ensure secure transmission, we proposed three types of AN-based MNJJ schemes for the considered system, namely NN, NF, and FN. Additionally, the closed-form expressions of the ESSR for the proposed MNJJ schemes were derived under the conditions where legitimate nodes are unaware of AN (i.e., Case I) and aware of AN (i.e., Case II). A JPAIC algorithm using PSO was also designed to further maximize the ESSR while ensuring the secure transmission of each data stream. The simulation results showed that the ESSR of the proposed MNJJ was superior to that of the CNC, and the proposed JPAIC maximized the ESSR of the proposed MNJJ and outperformed the FPS. Furthermore, in Case I, the NF was a preferable secure transmission scheme, while in Case II, the FN provided the best ESSR at low to moderate transmission power, but the NF remained a more robust choice across the entire transmission power range. In future work, we will extend the proposed scheme to multi-antenna scenarios and further enhance its security performance through beamforming design.