The Distributed Adaptive Bipartite Consensus Tracking Control of Networked Euler–Lagrange Systems with an Application to Quadrotor Drone Groups
Abstract
1. Introduction
- (1)
- This paper examines networked ELSs subject to lumped uncertainties, which encompass unknown system matrices, external disturbances, and actuator faults. A neural-network-based adaptive estimator is proposed to offer feedforward compensation for these uncertainties. Furthermore, adaptive updating laws are formulated to guarantee that the estimation errors associated with the lumped uncertainties and actuator faults are bounded, thereby tackling the robust tracking control challenge. In contrast to existing control strategies tailored for ideal systems [11,12,13,15,24], the most significant novelty of this work is the enhanced robustness of unknown systems, enabling the control scheme to be applicable across a range of tasks, including the cooperative control of ELSs in dynamic and complex environments.
- (2)
- This paper addresses the issue of uncertainties in leader agents, where their higher-order dynamic information is globally unknown. To tackle this challenge, an adaptive distributed observer is utilized to estimate the states, state matrix unknown parameters, and output matrix of the leader agent. The convergence of the observer’s estimates is rigorously proven through Lyapunov function analysis. This approach diverges from related works that presuppose the availability of the leader’s complete dynamic information to the follower agents, such as the state matrix or output matrix [7,11,23,28]. The proposed control scheme’s adaptability enhances its applicability to a wider array of consensus-tracking control tasks, including trajectory tracking in intricate marine environments.
- (3)
- This paper introduces a novel positive definite diagonal matrix to facilitate the construction of a distributed observer. This innovative design effectively addresses the challenge of asymmetric Laplacian matrices inherent in directed graphs, thereby offering a viable solution for bipartite consensus tracking control of ELSs under general directed graph conditions. In contrast to existing control schemes confined to undirected graph scenarios [4,9,14,15,21], the controller proposed herein demonstrates a capacity to conserve communication resources.
2. Preliminaries and Problem Formulation
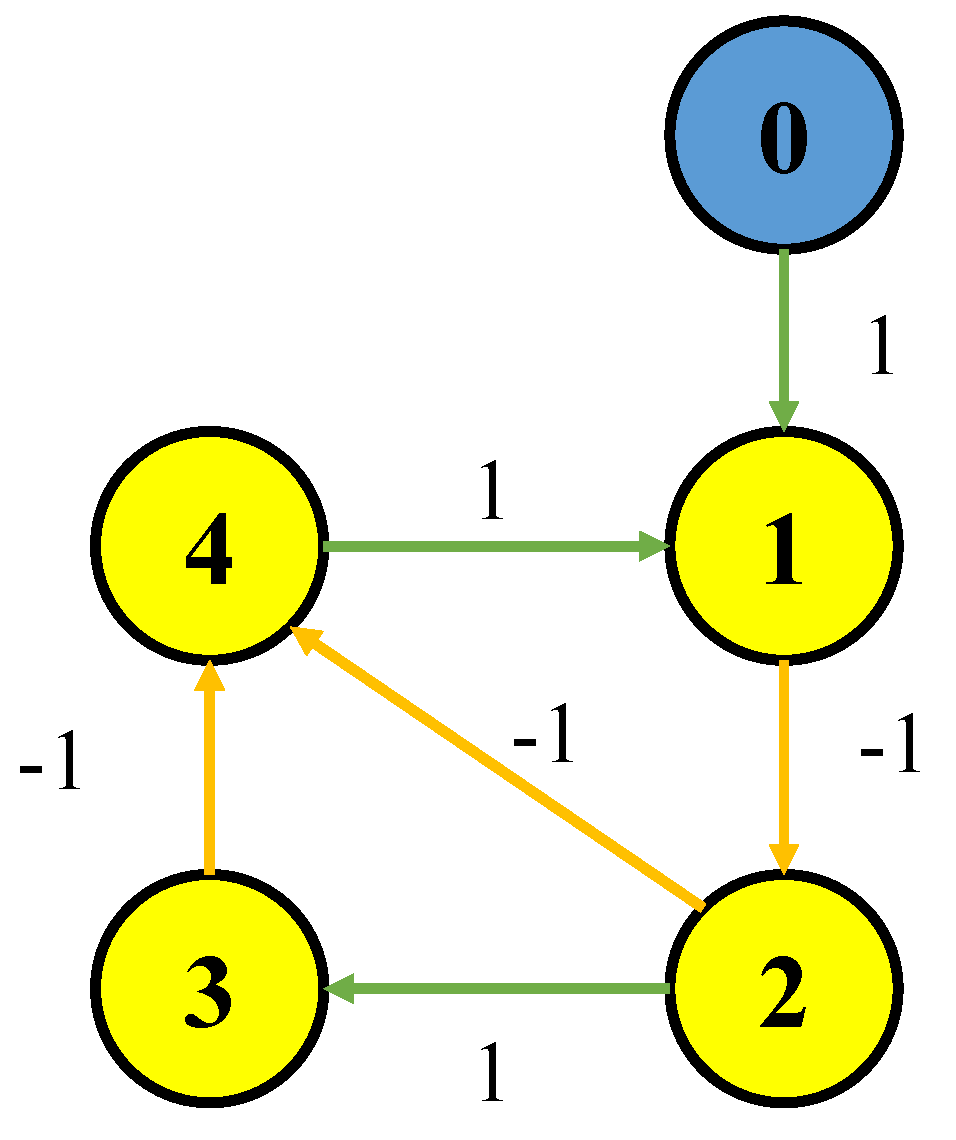
2.1. Graph Theory
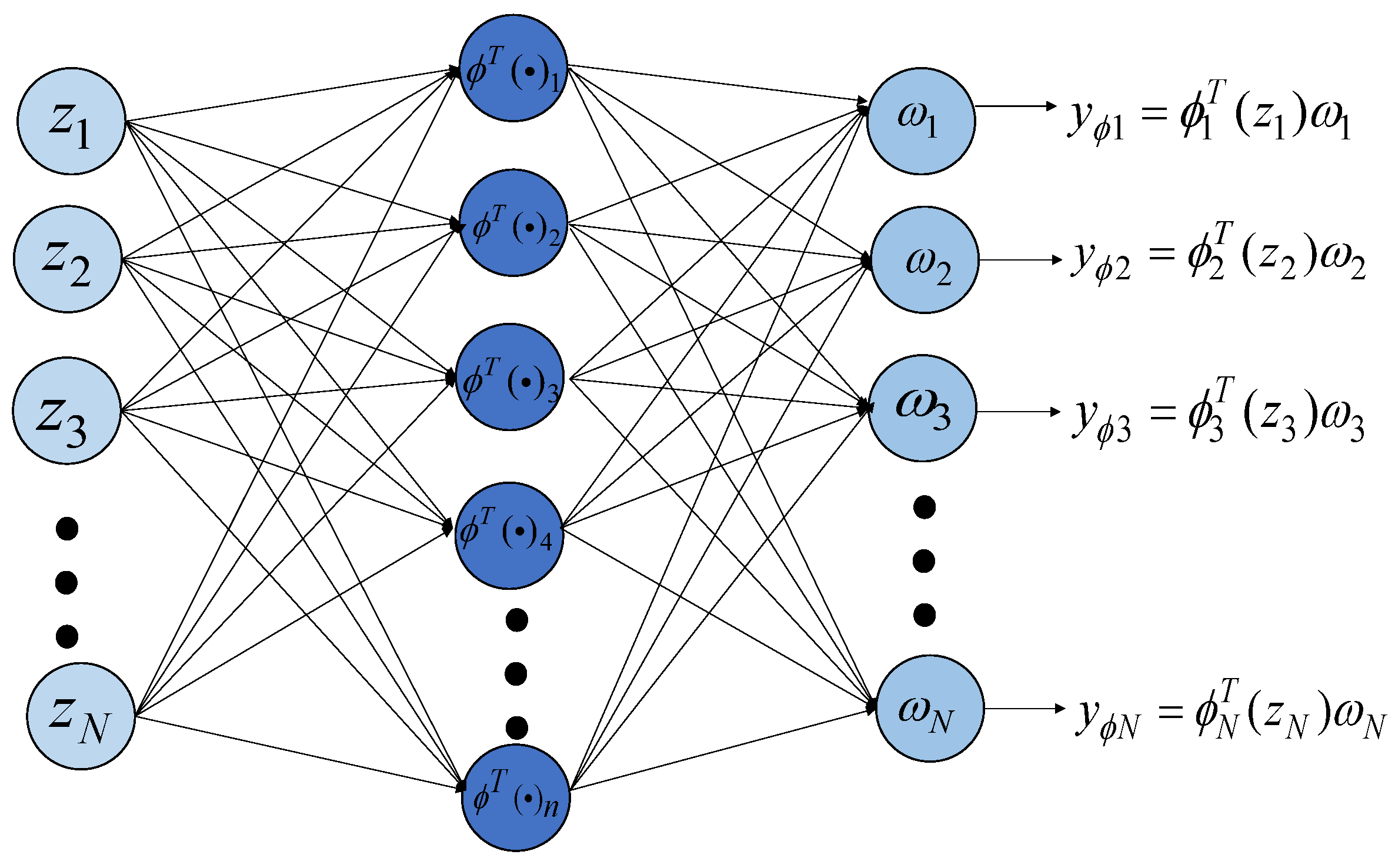
2.2. RBF Neural Network
2.3. Problem Description
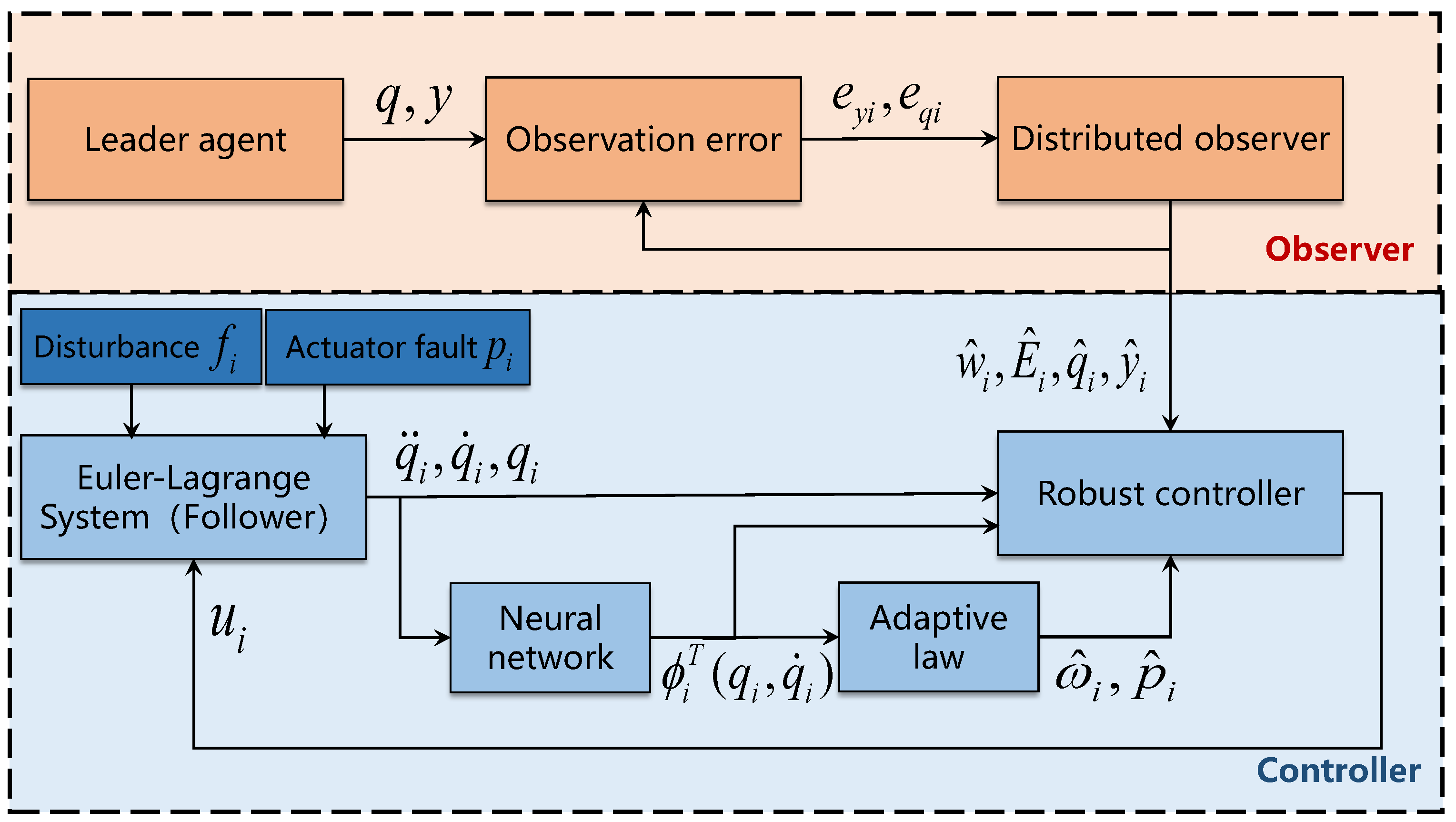
3. Neural-Network-Based Control Scheme Design and Analysis
3.1. Distributed Observer Design and Stability Analysis
3.2. Robust Tracking Controller Design and Stability Analysis
4. Simulation Results
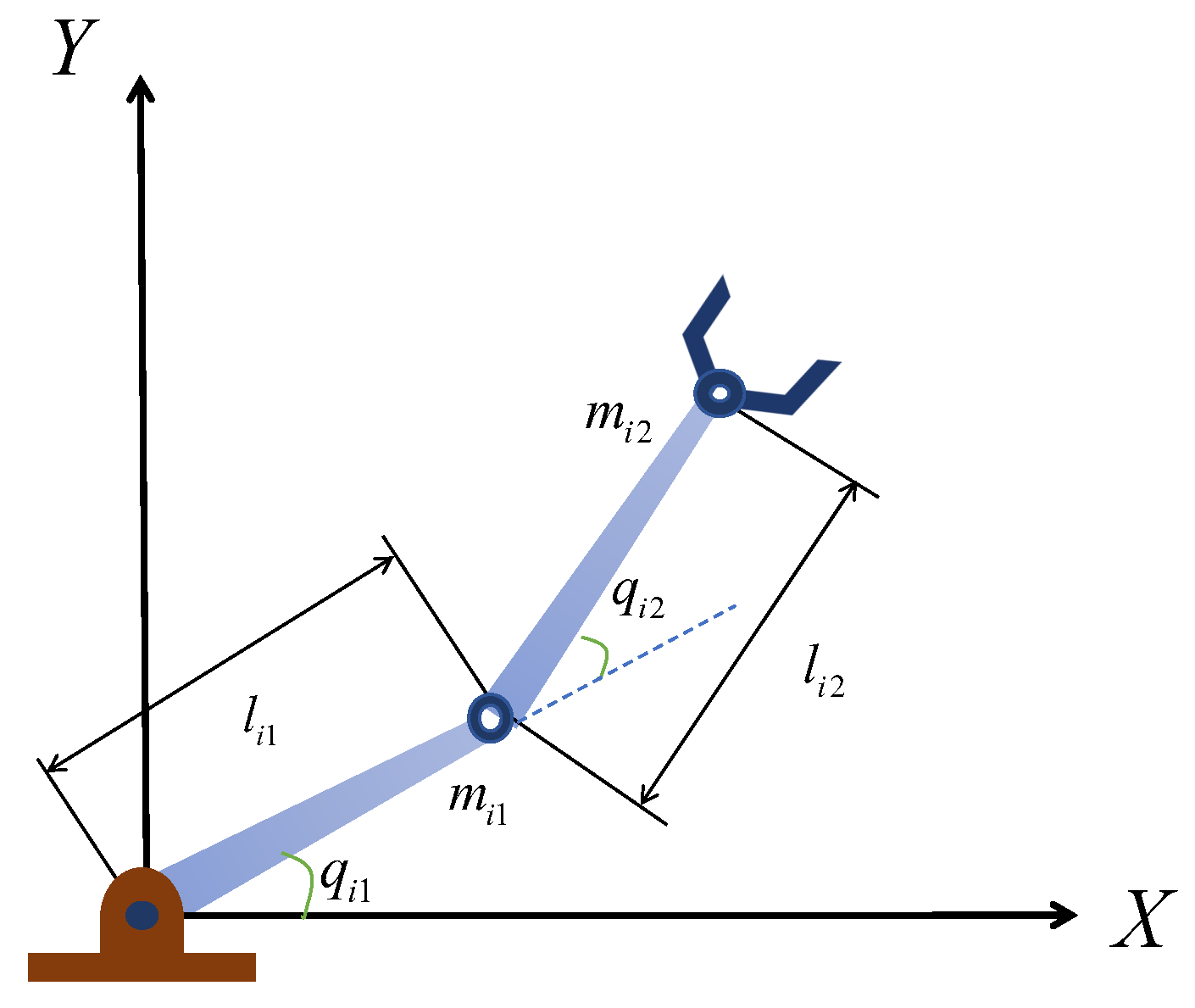
4.1. Example 1: Two-Link Robot Manipulator
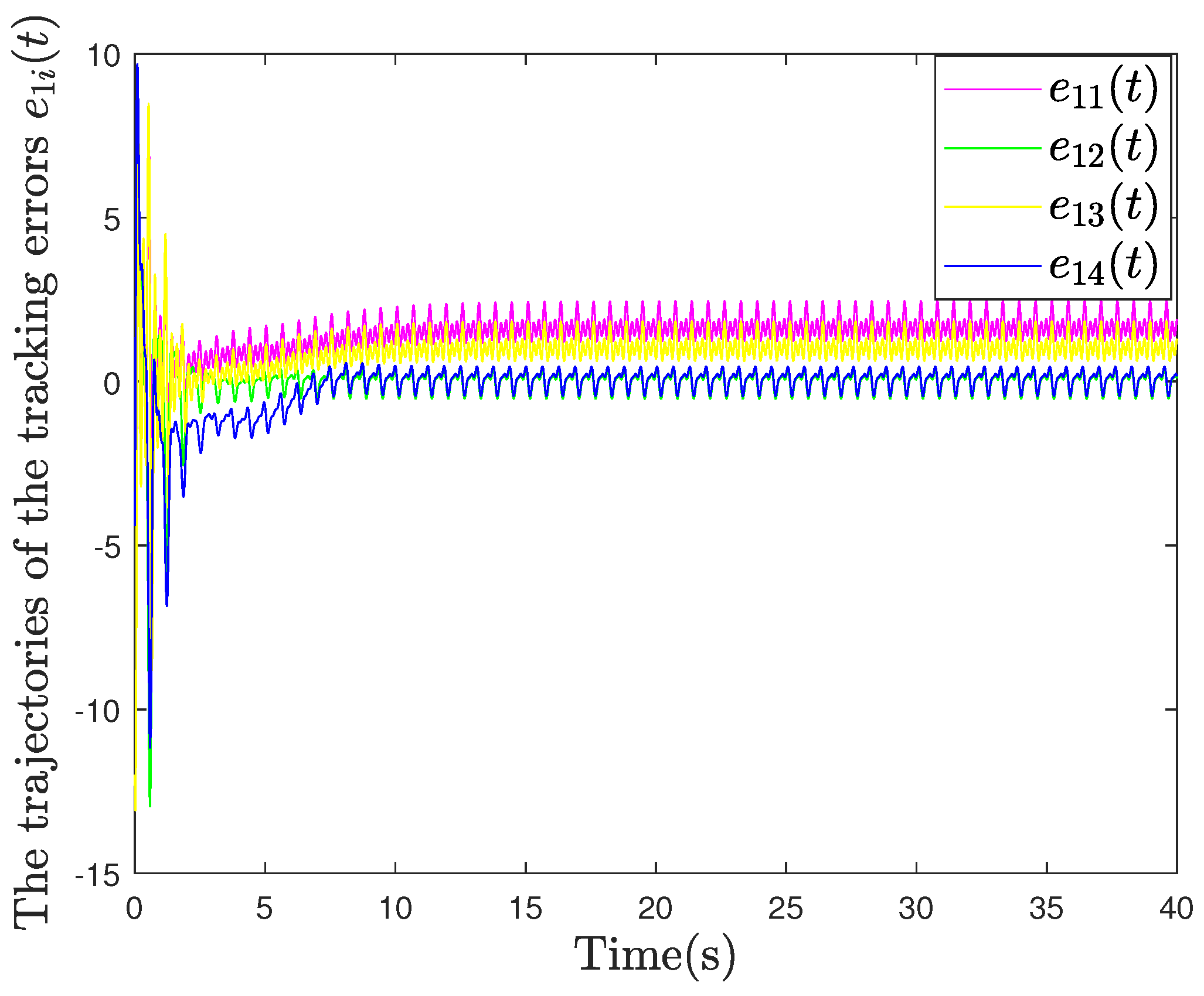
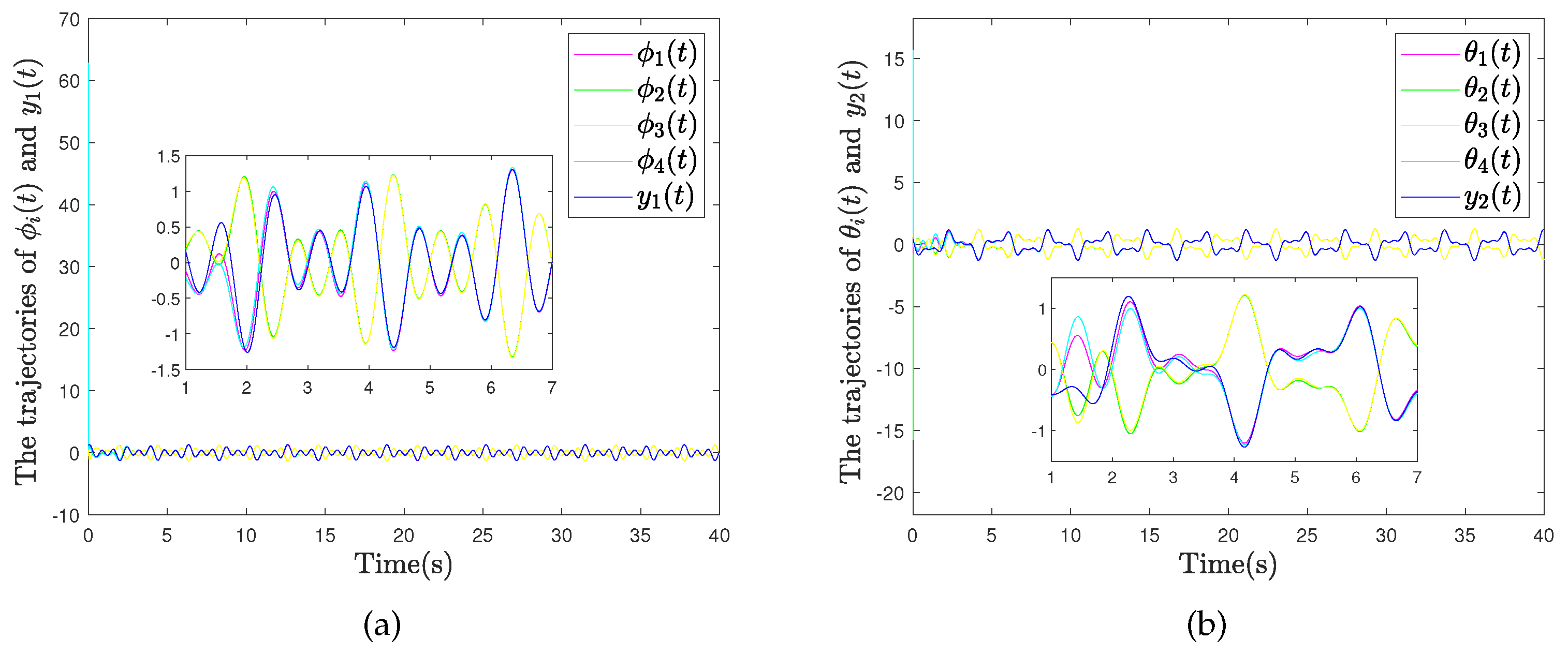
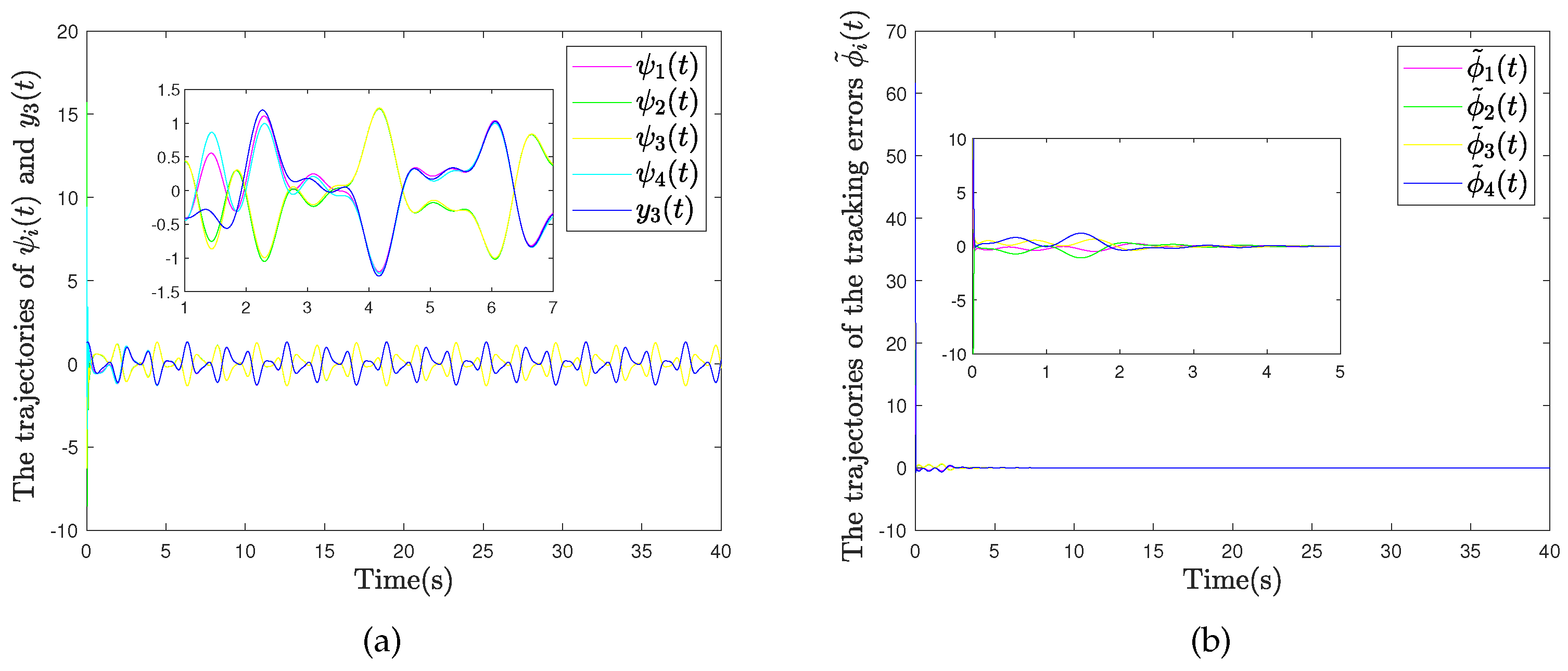
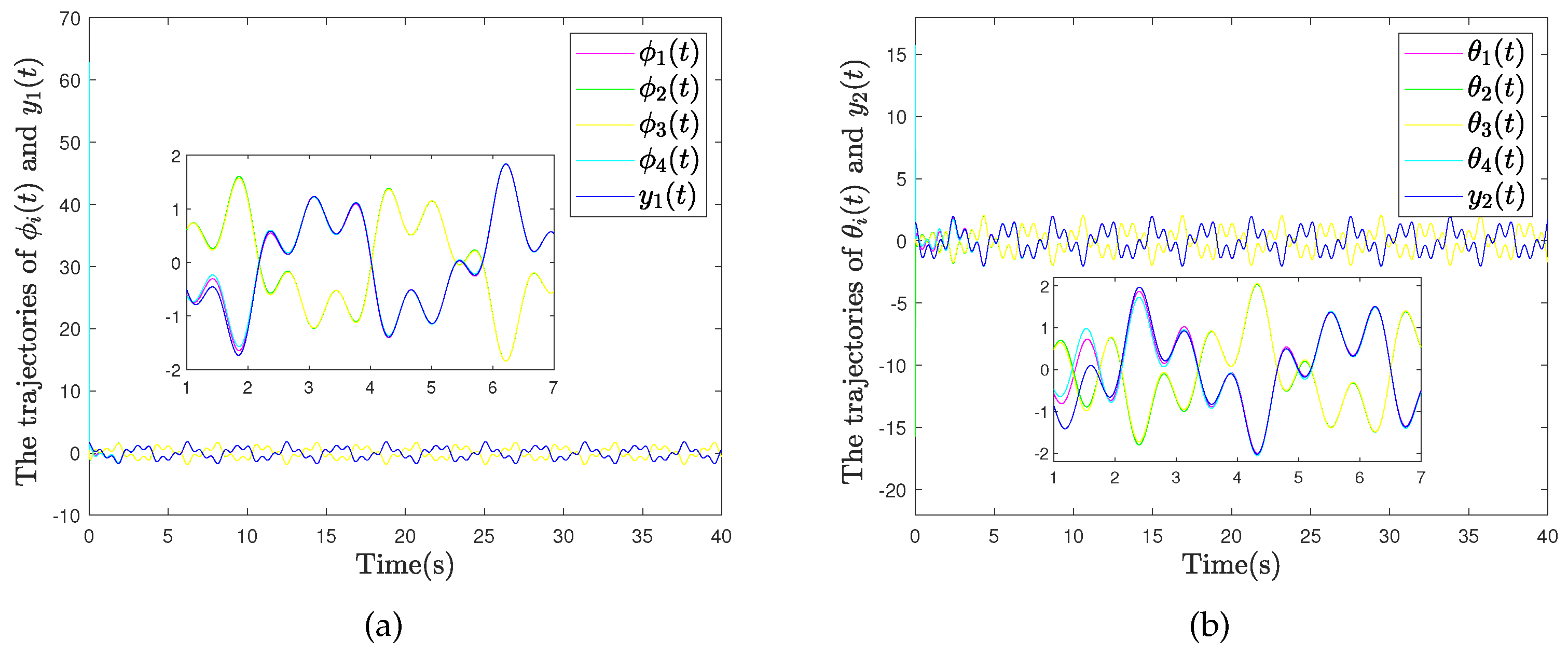
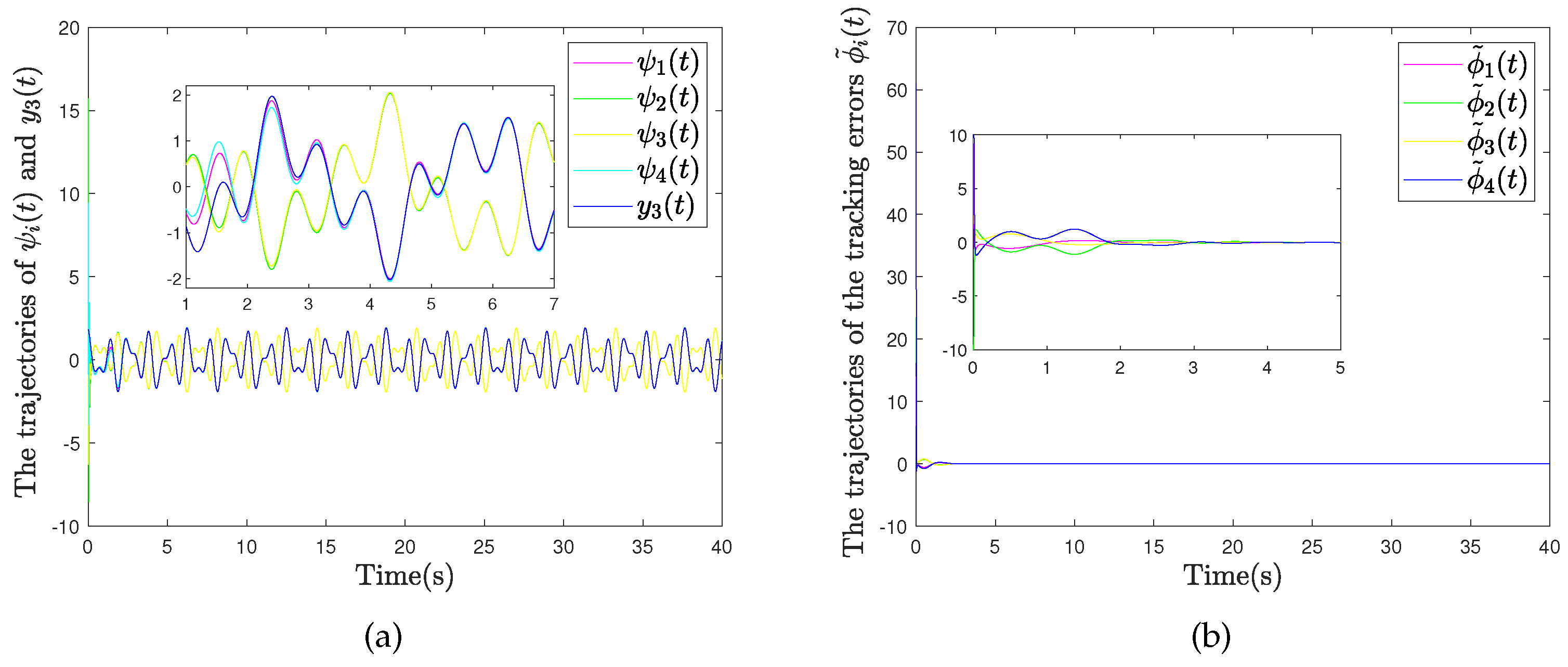
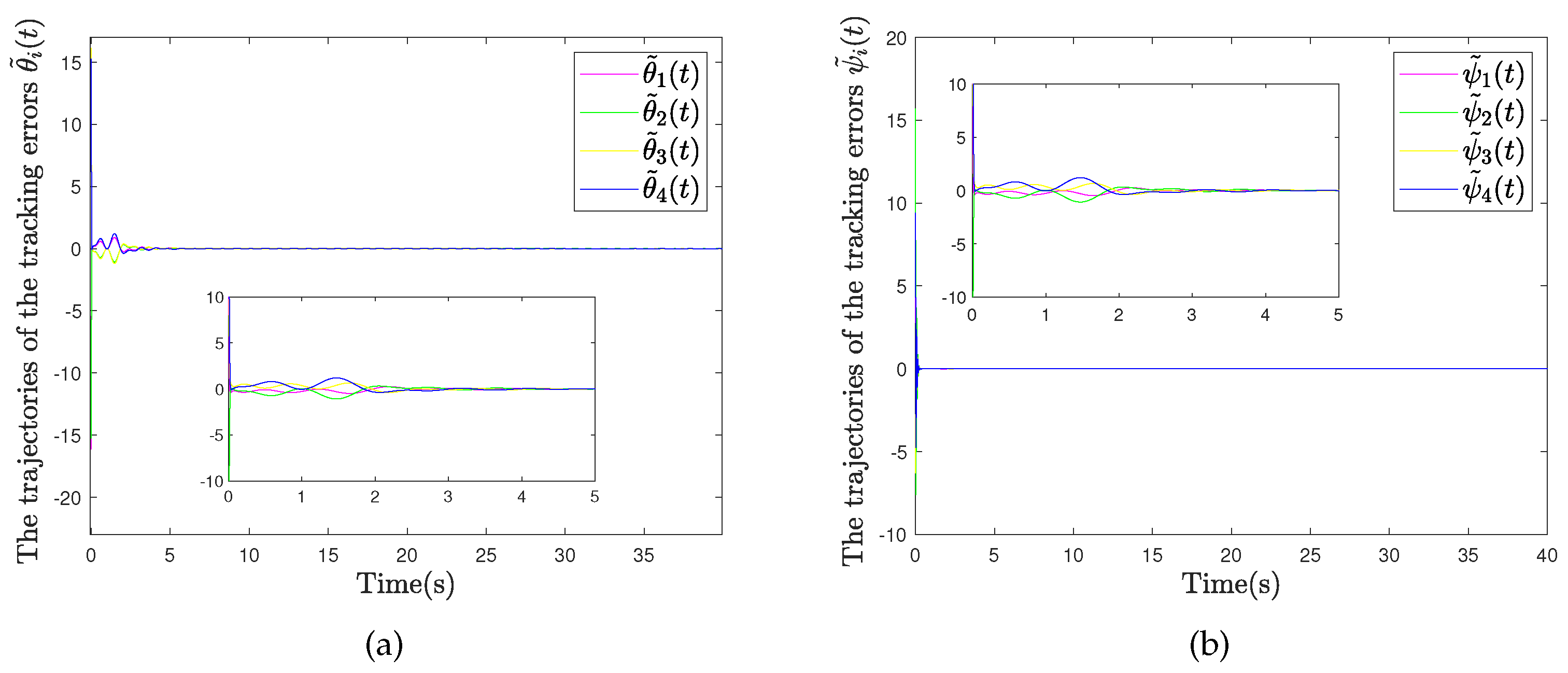
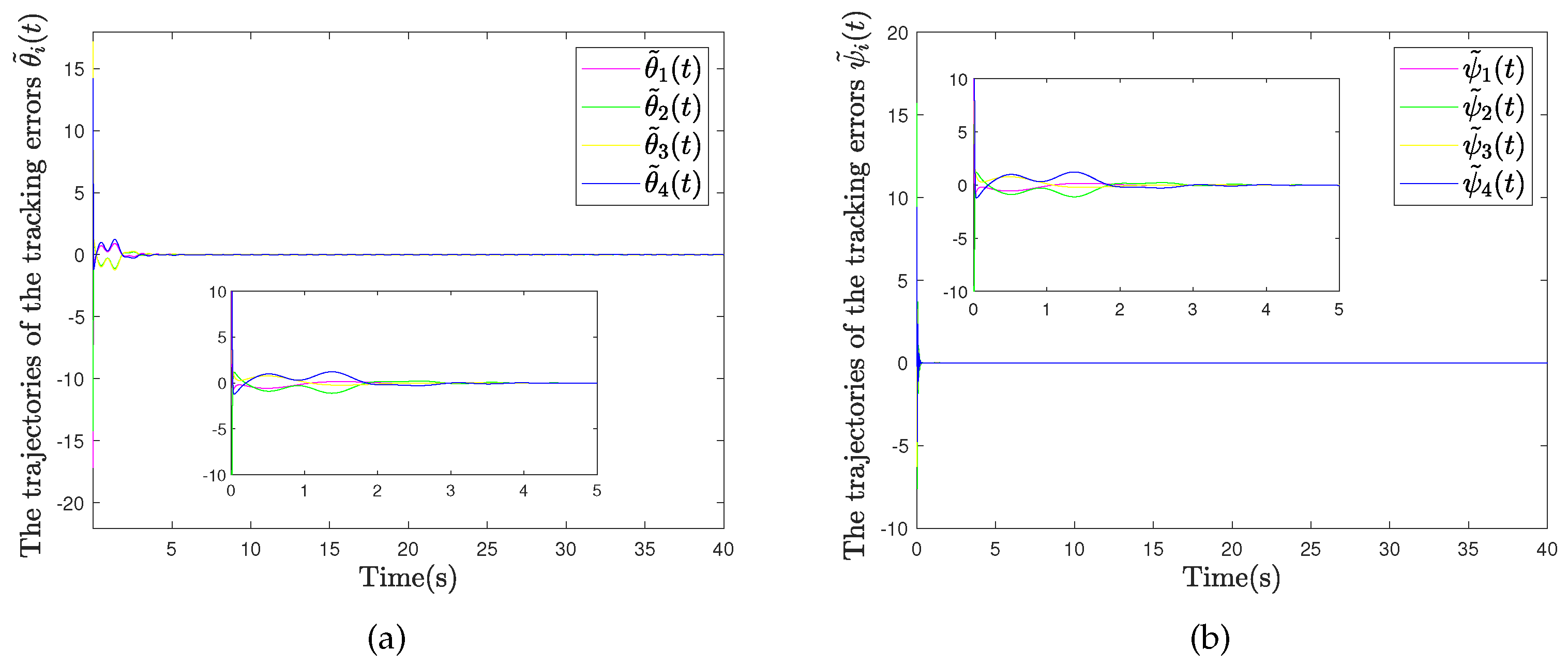
4.2. Example 2: Quadrotor Drone
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, J.; Yassine, A.; Armitage, A.; Hossain, M.S. Multi-Agent Reinforcement Learning for Intelligent V2G Integration in Future Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2023, 1, 15974–15983. [Google Scholar] [CrossRef]
- Xu, D.; Chen, G. The research on intelligent cooperative combat of UAV cluster with multi-agent reinforcement learning. Aerosp. Syst. 2022, 5, 107–121. [Google Scholar] [CrossRef]
- Wang, H.; Tao, J.; Peng, T.; Brintrup, A.; Kosasih, E.E.; Lu, Y.; Tang, R.; Hu, L. Dynamic inventory replenishment strategy for aerospace manufacturing supply chain: Combining reinforcement learning and multi-agent simulation. Int. J. Prod. Res. 2022, 60, 4117–4136. [Google Scholar] [CrossRef]
- Peng, X.J.; He, Y.; Chen, W.H.; Liu, Q. Bipartite consensus tracking control for periodically-varying-delayed multi-agent systems with uncertain switching topologies. Commun. Nonlinear Sci. Numer. Simul. 2023, 121, 107226. [Google Scholar] [CrossRef]
- Wang, H.; Han, Q.L. Distribution of Roots of Quasi-Polynomials of Neutral Type and Its Application-Part II: Consensus Protocol Design of Multi-Agent Systems Using Delayed State Information. IEEE Trans. Autom. Control 2023, 69, 4058–4065. [Google Scholar] [CrossRef]
- Zhao, M.; Peng, C.; Tian, E. Finite-time and fixed-time bipartite consensus tracking of multi-agent systems with weighted antagonistic interactions. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 68, 426–433. [Google Scholar] [CrossRef]
- Wang, B.; Chen, W.; Zhang, B. Semi-global robust tracking consensus for multi-agent uncertain systems with input saturation via metamorphic low-gain feedback. Automatica 2019, 103, 363–373. [Google Scholar] [CrossRef]
- Wang, W.; Wen, C.; Huang, J. Distributed adaptive asymptotically consensus tracking control of nonlinear multi-agent systems with unknown parameters and uncertain disturbances. Automatica 2017, 77, 133–142. [Google Scholar] [CrossRef]
- Wang, X.; Niu, B.; Zhang, J.; Wang, H.; Jiang, Y.; Wang, D. Adaptive Event-Triggered Consensus Tracking Control Schemes for Uncertain Constrained Nonlinear Multi-Agent Systems. IEEE Trans. Autom. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Ren, Z.; Lin, B.; Shi, M.; Li, Z.; Qin, K. UDE-based Consensus Tracking Control of Multi-Agent Systems with Actuator Faults and External Disturbances. In Proceedings of the 2023 6th International Conference on Electronics Technology (ICET), Chengdu, China, 12–15 May 2023; pp. 1282–1288. [Google Scholar]
- Qin, J.; Zhang, G.; Zheng, W.X.; Kang, Y. neural-network-based adaptive consensus control for a class of nonaffine nonlinear multiagent systems with actuator faults. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3633–3644. [Google Scholar]
- Bo, Z.; Wei, W.; Hao, Y. Distributed consensus tracking control of linear multi-agent systems with actuator faults. In Proceedings of the 2014 IEEE Conference on Control Applications (CCA), Juan Les Antibes, France, 8–10 October 2014; pp. 2141–2146. [Google Scholar]
- Lu, X.; Wang, Y.; Yu, X.; Lai, J. Finite-time control for robust tracking consensus in MASs with an uncertain leader. IEEE Trans. Cybern. 2016, 47, 1210–1223. [Google Scholar] [CrossRef] [PubMed]
- Lui, D.G.; Petrillo, A.; Santini, S. Bipartite tracking consensus for high-order heterogeneous uncertain nonlinear multi-agent systems with unknown leader dynamics via adaptive fully-distributed PID control. IEEE Trans. Netw. Sci. Eng. 2022, 10, 1131–1142. [Google Scholar] [CrossRef]
- Tahoun, A.; Arafa, M. Adaptive leader–follower control for nonlinear uncertain multi-agent systems with an uncertain leader and unknown tracking paths. ISA Trans. 2022, 131, 61–72. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Cheng, D. Adaptive fault-tolerant guaranteed performance control for Euler–Lagrange systems with its application to a 2-link robotic manipulator. IEEE Access 2020, 8, 184160–184171. [Google Scholar] [CrossRef]
- Liang, Z.; Wen, H.; Yao, B.; Mao, Z.; Lian, L. Adaptive actuator fault and the abnormal value reconstruction for marine vehicles with a class of Euler–Lagrange system. Ocean Eng. 2024, 297, 117095. [Google Scholar] [CrossRef]
- Wei, C.; Luo, J.; Dai, H.; Yuan, J. Adaptive model-free constrained control of postcapture flexible spacecraft: A Euler–Lagrange approach. J. Vib. Control 2018, 24, 4885–4903. [Google Scholar] [CrossRef]
- Lu, M.; Liu, L. Leader–following consensus of multiple uncertain Euler–Lagrange systems with unknown dynamic leader. IEEE Trans. Autom. Control 2019, 64, 4167–4173. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, Z. Fixed-time synchronization of networked uncertain Euler–Lagrange systems. Automatica 2022, 146, 110571. [Google Scholar] [CrossRef]
- Mei, J.; Ren, W.; Ma, G. Distributed coordinated tracking with a dynamic leader for multiple Euler–Lagrange systems. IEEE Trans. Autom. Control 2011, 56, 1415–1421. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, H.; Chen, Z. Adaptive cooperative tracking and parameter estimation of an uncertain leader over general directed graphs. IEEE Trans. Autom. Control 2022, 68, 3888–3901. [Google Scholar] [CrossRef]
- Cheng, B.; Li, Z. Coordinated tracking of Euler–Lagrange systems over directed graphs via distributed continuous controllers. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 8144–8149. [Google Scholar]
- Miyasato, Y. Adaptive H-inf consensus control of Euler–Lagrange systems on directed network graph. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–6. [Google Scholar]
- Deng, Q.; Peng, Y.; Han, T.; Qu, D. Event-triggered bipartite consensus in networked Euler–Lagrange systems with external disturbance. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2870–2874. [Google Scholar] [CrossRef]
- Li, B.; Han, T.; Xiao, B.; Zhan, X.S.; Yan, H. Leader-following bipartite consensus of multiple uncertain Euler–Lagrange systems under deception attacks. Appl. Math. Comput. 2022, 428, 127227. [Google Scholar] [CrossRef]
- Liu, J.; Li, H.; Luo, J. Bipartite consensus in networked Euler–Lagrange systems with uncertain parameters under a cooperation-competition network topology. IEEE Control Syst. Lett. 2019, 3, 494–498. [Google Scholar] [CrossRef]
- Huang, J.; Xiang, Z. Leader-following bipartite consensus with disturbance rejection for uncertain multiple Euler–Lagrange systems over signed networks. J. Frankl. Inst. 2021, 358, 7786–7803. [Google Scholar] [CrossRef]
- Nardi, F. Neural Network Based Adaptive Algorithms for Nonlinear Control; Georgia Institute of Technology: Atlanta, GA, USA, 2000. [Google Scholar]
- Lewis, F.L.; Dawson, D.M.; Abdallah, C.T. Robot Manipulator Control: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Cai, H.; Huang, J. The leader-following consensus for multiple uncertain Euler–Lagrange systems with an adaptive distributed observer. IEEE Trans. Autom. Control 2015, 61, 3152–3157. [Google Scholar] [CrossRef]
- Wang, S.; Huang, J. Adaptive leader-following consensus for multiple Euler–Lagrange systems with an uncertain leader system. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 2188–2196. [Google Scholar] [CrossRef] [PubMed]
- Hsu, L.; Ortega, R.; Damm, G. A globally convergent frequency estimator. IEEE Trans. Autom. Control 1999, 44, 698–713. [Google Scholar] [CrossRef]
- Fuller, C.R.; von Flotow, A.H. Active control of sound and vibration. IEEE Control Syst. Mag. 1995, 15, 9–19. [Google Scholar] [CrossRef]
- Wang, S.; Huang, J. Cooperative output regulation of linear multi-agent systems subject to an uncertain leader system. Int. J. Control 2021, 94, 952–960. [Google Scholar] [CrossRef]
- Zhao, G.; Hua, C. Leader-following consensus of multiagent systems via asynchronous sampled-data control: A hybrid system approach. IEEE Trans. Autom. Control 2021, 67, 2568–2575. [Google Scholar] [CrossRef]
- Xu, C.; Xu, H.; Su, H.; Liu, C. Adaptive bipartite consensus of competitive linear multi-agent systems with asynchronous intermittent communication. Int. J. Robust Nonlinear Control 2022, 32, 5120–5140. [Google Scholar] [CrossRef]
- Yuan, S.; Yu, C.; Sun, J. Adaptive event-triggered consensus control of linear multi-agent systems with cyber attacks. Neurocomputing 2021, 442, 1–9. [Google Scholar] [CrossRef]
- He, C.; Huang, J. Leader-following consensus for multiple Euler–Lagrange systems by distributed position feedback control. IEEE Trans. Autom. Control 2021, 66, 5561–5568. [Google Scholar] [CrossRef]
- Li, H.; Liu, C.L.; Zhang, Y.; Chen, Y.Y. Practical fixed-time consensus tracking for multiple Euler–Lagrange systems with stochastic packet losses and input/output constraints. IEEE Syst. J. 2021, 16, 6185–6196. [Google Scholar] [CrossRef]
- Cao, W.; Zhang, J.; Ren, W. Leader–follower consensus of linear multi-agent systems with unknown external disturbances. Syst. Control Lett. 2015, 82, 64–70. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Y.; Liu, J. Finite-time leader-following output consensus for multi-agent systems via extended state observer. Automatica 2021, 124, 109133. [Google Scholar] [CrossRef]
- Lu, M.; Han, T.; Wu, J.; Zhan, X.S.; Yan, H. Adaptive bipartite output consensus for heterogeneous multi-agent systems via state/output feedback control. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3455–3459. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, X.; Zhong, X.; Wu, N. Consensus control of leader-following multi-agent systems in directed topology with heterogeneous disturbances. IEEE/CAA J. Autom. Sin. 2021, 8, 423–431. [Google Scholar] [CrossRef]
- Bernstein, D.S. Matrix Mathematics: Theory, Facts, and Formulas; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Zhang, Q.; Delyon, B. A new approach to adaptive observer design for MIMO systems. In Proceedings of the 2001 American Control Conference (Cat. No. 01CH37148), Arlington, VA, USA, 25–27 June 2001; Volume 2, pp. 1545–1550. [Google Scholar]
- Anderson, B. Exponential stability of linear equations arising in adaptive identification. IEEE Trans. Autom. Control 1977, 22, 83–88. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S. A new disturbance attenuation control scheme for quadrotor unmanned aerial vehicles. IEEE Trans. Ind. Inform. 2017, 13, 2922–2932. [Google Scholar] [CrossRef]
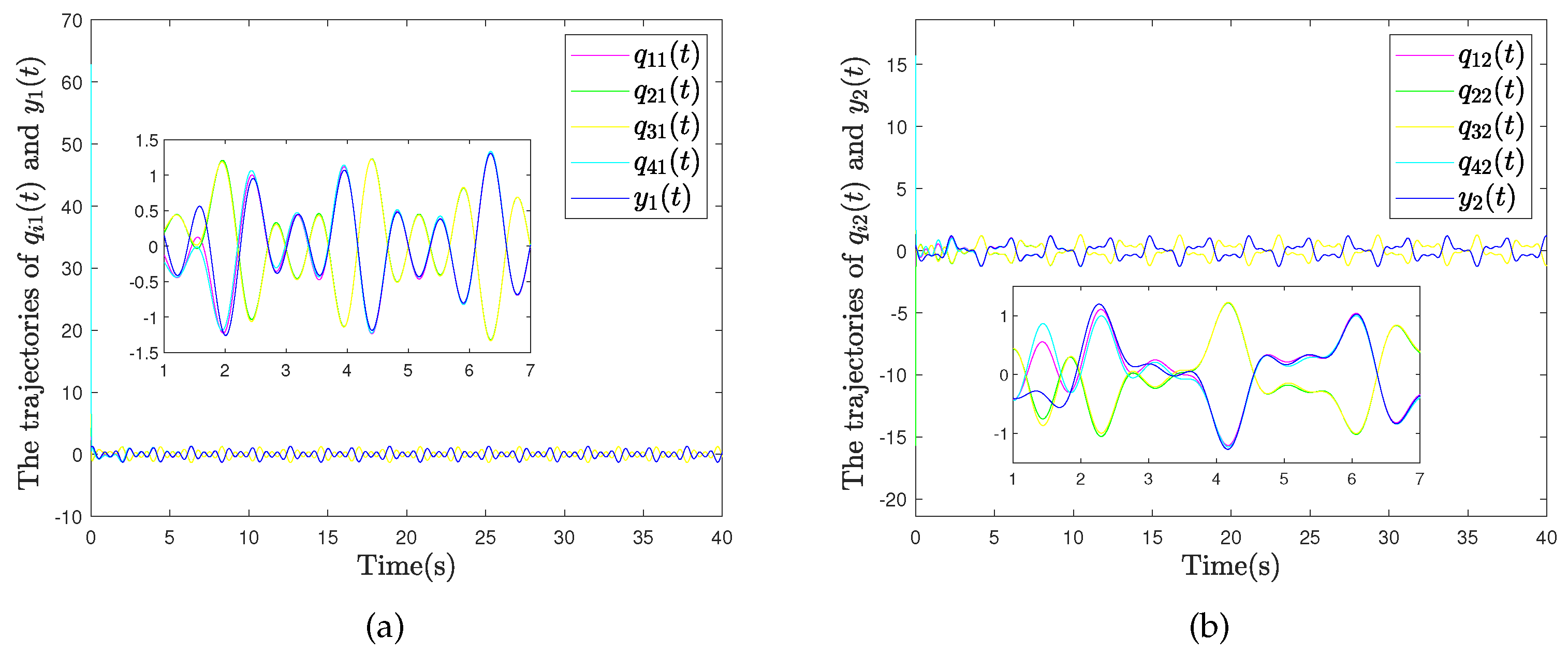
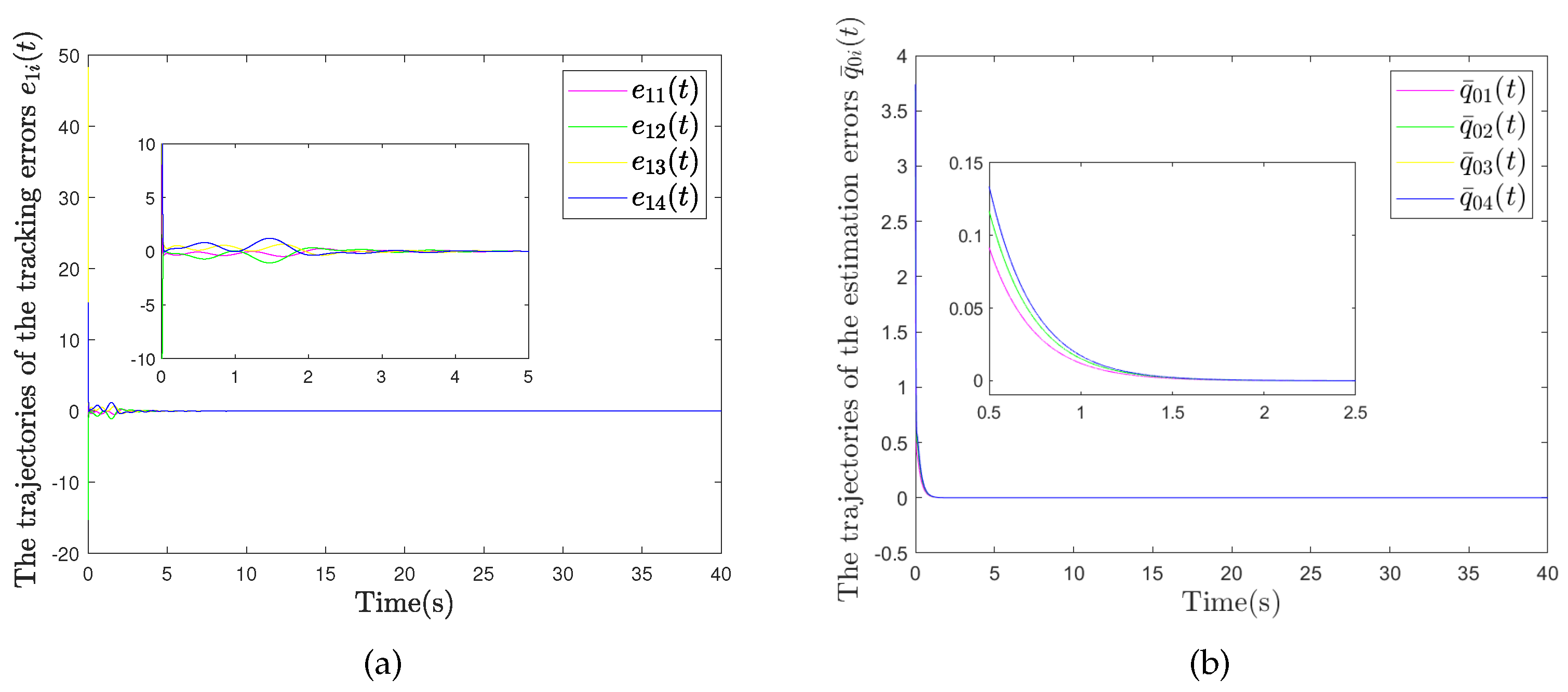
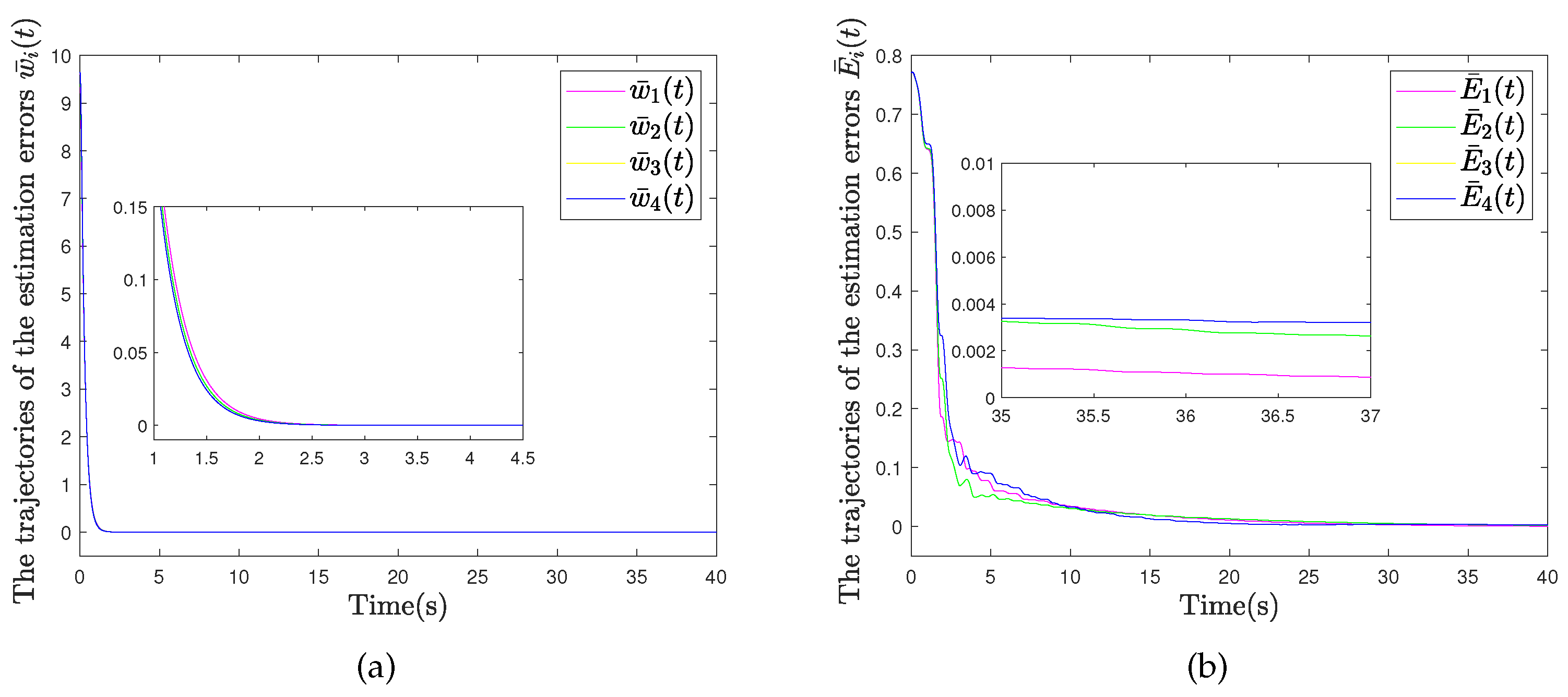
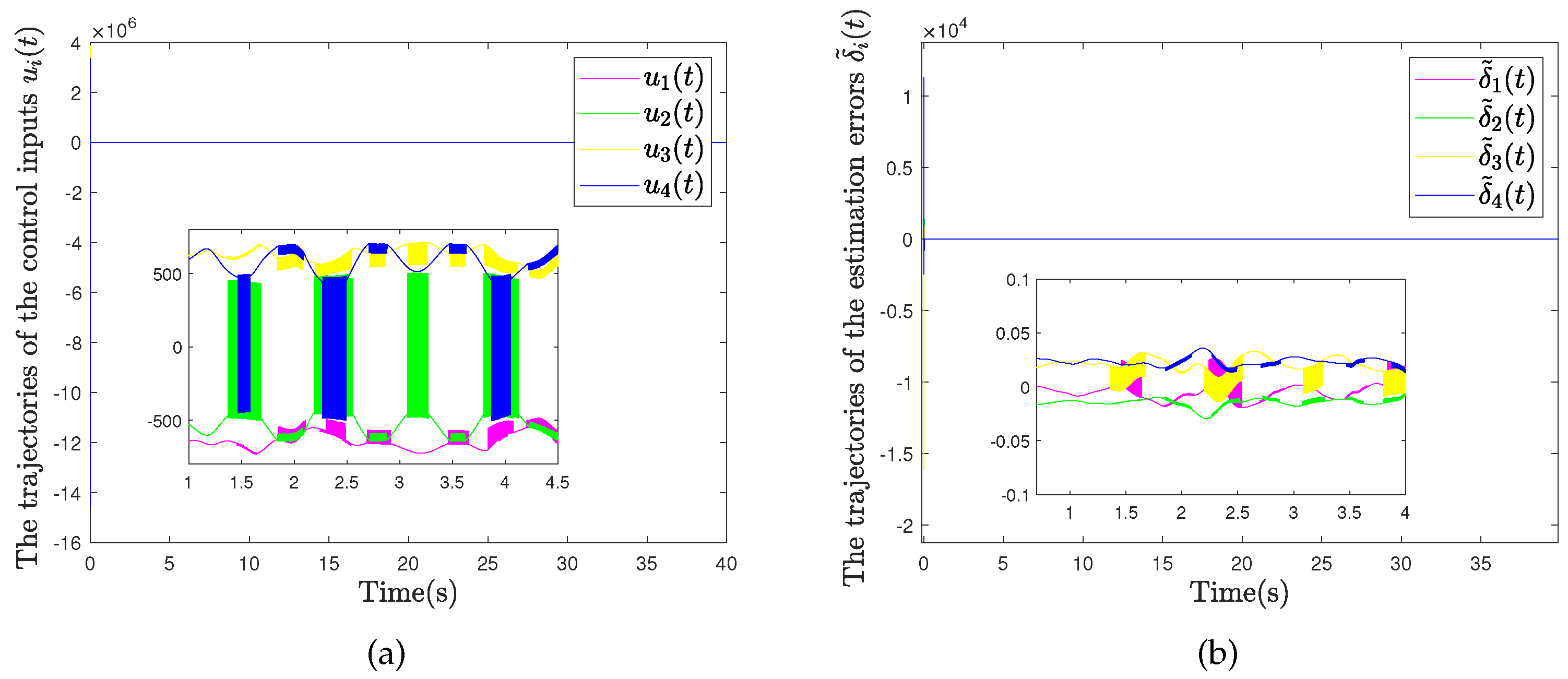
| Symbol | Meaning |
|---|---|
| q | leader’s state |
| y | leader’s output |
| the leader’s state matrix | |
| w | an unknown parameter vector |
| E | the leader’s output matrix |
| the generalized coordinate, velocity, and acceleration | |
| the inertia matrix | |
| the Coriolis and centrifugal terms | |
| the vector of gravitational force | |
| the control input | |
| the unknown external disturbance | |
| the actuator fault | |
| the estimations of q | |
| the estimations of y | |
| the estimations of w | |
| the estimations of E | |
| the column vector of output matrix observation errors | |
| the estimation of | |
| the tracking error vectors | |
| the attitude vector of the quadrotor rigid body | |
| the estimation errors of q | |
| the estimation errors of w |
| Parameter | Manipulator 1 | Manipulator 2 | Manipulator 3 | Manipulator 4 |
|---|---|---|---|---|
| (m) | 0.98 | 1 | 0.96 | 1 |
| (m) | 1 | 0.95 | 1 | 1.02 |
| (kg) | 1.02 | 0.96 | 1.01 | 1.04 |
| (kg) | 1.12 | 1.15 | 1.07 | 1.09 |
| (kg · m2) | 0.23 | 0.21 | 0.19 | 0.21 |
| (kg · m2) | 0.41 | 0.4 | 0.42 | 0.41 |
| The Tracking Errors | Overall Performance and | Overall Performance in [22] and | Steady-State Performance and | Steady-State Performance in [22] and |
|---|---|---|---|---|
| −0.039, 0.280 | 0.979, 1.475 | −0.006, 0.008 | 1.623, 0.325 | |
| 0.065, 0.652 | 0.571, 1.760 | −0.003, 0.009 | 1.360, 0.324 | |
| 0.072, 0.972 | 0.473, 1.708 | −0.006, 0.014 | 1.062, 0.322 | |
| −0.011, 1.192 | 0.091, 1.595 | 0.006, 0.014 | 1.322, 0.366 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; He, H.; Han, C.; Lin, B.; Shi, M.; Qin, K. The Distributed Adaptive Bipartite Consensus Tracking Control of Networked Euler–Lagrange Systems with an Application to Quadrotor Drone Groups. Drones 2024, 8, 450. https://doi.org/10.3390/drones8090450
Li Z, He H, Han C, Lin B, Shi M, Qin K. The Distributed Adaptive Bipartite Consensus Tracking Control of Networked Euler–Lagrange Systems with an Application to Quadrotor Drone Groups. Drones. 2024; 8(9):450. https://doi.org/10.3390/drones8090450
Chicago/Turabian StyleLi, Zhiqiang, Huiru He, Chenglin Han, Boxian Lin, Mengji Shi, and Kaiyu Qin. 2024. "The Distributed Adaptive Bipartite Consensus Tracking Control of Networked Euler–Lagrange Systems with an Application to Quadrotor Drone Groups" Drones 8, no. 9: 450. https://doi.org/10.3390/drones8090450
APA StyleLi, Z., He, H., Han, C., Lin, B., Shi, M., & Qin, K. (2024). The Distributed Adaptive Bipartite Consensus Tracking Control of Networked Euler–Lagrange Systems with an Application to Quadrotor Drone Groups. Drones, 8(9), 450. https://doi.org/10.3390/drones8090450






