Abstract
Unmanned aerial vehicles (UAVs) are extensively employed in pursuit, rescue missions, and agricultural applications. These operations require substantial data and video transmission, demanding significant spectral resources. The ultra-broad bandwidth of 0.1–10 THz in the Terahertz (THz) frequency range is essential for future UAV-based wireless communications. However, the available bandwidth in the THz frequency spectrum varies with transmission distance. To enhance spectral efficiency over this variable bandwidth, we propose using hierarchical modulation (HM) in the overlapped spectrum and traditional quadrature amplitude modulation (QAM) in the non-overlapped spectrum for closer users. Furthermore, we analyze the single-user case and utilize the block-coordinated descent (BCD) method to jointly optimize the modulation order, subcarrier bandwidth, and sub-band power to improve the system sum rate. Finally, considering the mobility and randomness of UAV users, we design a modulation switching rule to dynamically adjust to changes in distance as users move, thereby enhancing data rates. Simulation results demonstrate superior performance in data rate and design complexity compared to existing methods such as hierarchical bandwidth modulation (HBM) and HM schemes.
1. Introduction
UAVs are widely employed in various fields, such as emergency search and rescue operations [1], agricultural irrigation [2], and urban infrastructure development [3], due to their easy deployment and flexible scheduling. As the potential of UAVs is explored, their tasks become more complex, resulting in progressively increasing data transmission rates. The exponential surge in data rates has led to increasing congestion in the wireless spectrum below 10 GHz. As of the end of 2023, there were 13.1 billion mobile devices in use [4]. The THz band, from 0.1 to 10 THz, has significant potential for providing the desired spectrum in wireless communications [5]. The large available bandwidth also provides the faster single-user or aggregate data rates expected to be Terabit-per-second (Tbps) wireless links [4]. Incorporating THz communication into UAVs is a significant future trend. Researchers are increasingly focusing on developing THz communication. Notably, the IEEE 802.15 wireless personal area networks (WPAN) study group, formed around a decade ago and including a THz interest group (IGthz), has released a full-scale IEEE-endorsed wireless standard (IEEE 802.15.3d-2017) trough IEEE 802.15.3d WG. This standard was revised for the second time at the end of 2023 and is expected to include more functionality in future versions [6].
The research and development of THz communications systems, particularly in the lower end of the THz spectrum, up to approximately 300 GHz boosts a plethora of applications, including ultra-high-speed kiosk downloading, real-time wireless high-definition videos, ultrafast massive data transfers among nearby devices, ultrabroadband small cell systems, the novel nano-networks for biomedical and military industries and so on [7,8,9,10,11,12,13]. THz communication could also be used as an alternative to wired backbone connectivity in data centers [14] or as part of large intelligent surface deployments [15] and facilitate mobile wireless mid-range communications such as device-to-device, drone-to-drone, vehicular, or personal communications [16]. Although THz communications present exciting opportunities, they have their own set of challenges that must be addressed before they can reach their full potential. The key technologies in 6G THz wireless communication systems mainly include THz channel modeling, multibeam antenna design, front-end chip design, baseband signal processing algorithms, waveform and modulation design, and resource management schemes. These technologies can provide a strong guarantee for the implementation of THz communication systems. Future research directions on these key components in 6G THz wireless communication systems have also been highlighted [17,18].
UAVs configured with the THz frequency band can provide users with Tbps-level data transmission rates. However, configuring THz frequency band networks poses many new challenges for UAVs due to the inherent characteristics of THz, such as sensitivity to distance variations in terms of path loss [19]. Currently, there are several studies related to THz communication and drone communication. For example, Xu et al. [20] proposed optimizing the total delay of the system in a single drone network by considering drone positioning, bandwidth allocation, and mobile device transmission power. Wang et al. [21] designed a single drone network that optimizes system capacity by adjusting drone location, resource allocation, and mobile device computing offload. Pan et al. [22] aimed to maximize the transmission rate of users in a single UAV network equipped with an IRS through THz sub-band allocation and power control, trajectory optimization of the UAV, and phase shift of the IRS. Jia et al. [23] investigated the use of low orbit satellites to assist UAVs in providing data transmission services for the terrestrial Internet of Things. Reference [24] analyzed the SNR metrics and channel performance under varying conditions of geometric loss and fading channels for UAV-aided THz communications. Reference [25] highlighted the integration of THz-enabled UAVs in future 6G networks to enhance data rate, reliability, and resiliency, addressing challenges like trajectory design and channel allocation through a novel distributed safe multi-agent deep reinforcement learning approach. Reference [26] combined the RIS with UAV-based THz mobile networks and optimizes the IRSs’ phase shifts, UAVs’ trajectories, and system resources to minimize the UAV energy consumption. Reference [27] optimized the multi-layer UAV networks using the THz frequency band to meet the high network demands of delay-sensitive applications in remote areas. Reference [21] discussed the UAV-assisted computation offloading in the THz band to enhance the capabilities of multi-access edge computing for latency-sensitive applications. Reference [28] explored the integration of mmWave, FSO, and THz technologies to enhance data collection capabilities from remote locations through a wireless backhaul link. Reference [29] detailed the application of THz communication in UAV systems, supported by an active reconfigurable intelligent surface (RIS) for enhancing connectivity and reducing interference. Reference [30] utilized advanced distribution models to enhance secure multi-user connectivity for RIS-assisted mixed RF and FSO communications. Reference [31] highlighted the advancement of THz-enabled UAV communications for next-generation networks, focusing on a novel approach that maximizes throughput for ground users through joint optimization of bandwidth, power allocation, and UAV deployment using a non-orthogonal multiple access scheme.
To better support computation-intensive applications, it is necessary to reduce the transmission delay from BS to THz-based UAV servers. Advanced modulation schemes and signal processing techniques can improve transmission rates and thus reduce the transmission delay [32]. There have been several studies exploring THz modulation strategies, but each of them has its own limitations. The references [33,34] proposed a time-spread on–off keying (TSOOK) modulation scheme motivated by the constraint that designing a continuous-wave THz hardware is simply challenging. However, THz-OOK works well only for shorter distances primarily due to the limited Tx power and antenna gains. Moreover, the considered pulse occupies 10 GHz of BW, resulting in huge thermal noise at the receiver. Also, the pulse-based modulation scheme proposed in [35,36] does not do that well in long-range in the presence of multipath due to the inter-symbol interference (ISI). In order to address this limitation, in [37], the novel distance-aware modulation scheme (DAMC) was presented, which enables the utilization of longer-range links. It permits adaptive transmissions of different symbols on non-overlapping and equally spaced sub-windows in parallel. However, the spectral efficiency of this scheme is low due to the non-overlapped and fixed sub-windows. To improve the spectrum efficiency, the conventional modulation schemes such as orthogonal frequency division multiplexing (OFDM) and discrete Fourier transform (DFT) spread OFDM (DFT-s-OFDM), were proposed in the THz regime [38,39]. However, they are not robust to fast time-varying channels with high Doppler spread, resulting in inter-carrier interference (ICI) and degrading the link performance severely, including data rate and bit error rate (BER) [39]. In [40], the authors proposed the distance-adaptive absorption peak modulation (DA-APM), but it is only valid for covert communications due to adopting the frequencies at the peak path loss. Spatial modulation has also been proposed for THz communications [41,42], but this modulation strategy results in a high error rate in THz communications. Recently, a new modulation technique named orthogonal time frequency space (OTFS) was proposed to address high Doppler spread in doubly selective channels [43,44]. Nevertheless, while OTFS has a lower peak-to-average power ratio (PAPR) than a multi-carrier system [45] and shows significant advantages in performance over OFDM [43], the PAPR of OTFS, which grows linearly with the number of symbols, is still problematic for THz transmitters. Therefore, the reference [38] proposed a discrete Fourier transform spread OTFS (DFT-s-OTFS) modulation scheme. However, these modulation schemes still do not solve the high path losses and distance-dependent bandwidth experienced by THz signals in modulation schemes due to the small wavelength and molecular absorption. References [46,47] presented hierarchical bandwidth modulation (HBM) to address these challenges, which is an extension of traditional hierarchical modulation (HM) that introduces a hierarchy in bandwidth by simultaneously servicing users at different symbol rates. We have found that there are few studies on optimizing the modulation strategy for the UAV-based THz communication. From a forward-looking perspective, it is necessary to make efforts to develop and refine modulation strategies that can better exploit the THz spectrum’s properties to achieve the higher data rate for UAV communications.
Motivated by these investigations, we present a new distance- and frequency-dependent adaptive modulation scheme, where the distance and frequency play the important role in the design of the modulation strategy. This work differs from previous studies in the following aspects. First, the subcarrier bandwidth, modulation order, and the transmit power are jointly utilized, which results in the non-convex optimization problem different from the convex problem in [37] fixing the subcarrier bandwidth. We propose a block-coordinated decent (BCD) algorithm to solve this problem. Second, the available bandwidth of the user is closely related to the distance. Therefore, when the user moves, the modulation scheme should be adjusted. However, the adjustment frequency of the adaptive modulation strategy can not be large due to the high overhead and complexity. Thus, it is necessary to design adjustment rules for modulation schemes and derive the adjustment probability as the user moves, which is meaningful but has not been studied in existing works. Finally, in the multi-user case, we propose a new hybrid HM-MQAM (Quadrature Amplitude Modulation with a modulation order of M) modulation by adopting HM on the overlapped frequencies between the farther and closer users because the available bandwidth of the closer user is larger and includes the available bandwidth of the farther user. The MQAM scheme is applied on the remaining frequencies of the closer user. The performance of the proposed modulation scheme is compared with existing modulation schemes, and the simulation results demonstrate the superiority of the proposed modulation scheme. The contributions of this work are summarized as follows.
- In the multi-user case, we propose a new hybrid HM-MQAM scheme by adopting hierarchical modulation on the overlapped frequencies between the farther and closer users and MQAM modulation scheme on the remaining frequencies of the closer user. Our results indicate that the modulation order on the resultant frequencies of the closer user is different from that on the overlapped frequencies. The data rate of the proposed modulation scheme is higher than that of the existing HBM and HM schemes.
- We jointly optimize the subcarrier bandwidth, modulation order, and transmit power and propose the BCD method to solve the non-convex optimization problem.
- We also design the adjustment rules of the adaptive modulation strategy when the user is moving. The adjustment probability of the adaptive modulation scheme is derived according to these adjustment rules.
The remainder of this paper is organized as follows. Section 2 introduces the THz system and channel models. Section 3 proposes a new hybrid HM-MQAM scheme for the multi-user case and compares the performance of the proposed modulation scheme with that of the existing HBM and HM schemes. Section 4 optimizes the distance-adaptive multi-carrier modulation scheme by jointly optimizing the modulation order, subcarrier bandwidth, and transmit power and proposes the BCD method to solve the non-convex optimization problem. In Section 5, the adjustment rules of the modulation scheme are designed when the user moves and the adjustment probability is also derived. In Section 6, numerical results are presented to evaluate the performance of the proposed algorithm and modulation schemes. The paper is concluded in Section 7.
Notations involved in this paper are included in Table 1.

Table 1.
Summary of the Involved Notations.
2. The System and Channel Models for THz Band
We consider a system model where the ground base station communicates with UAVs in the THz spectrum. According to the characteristics of the THz spectrum, UAVs closer to the base station can utilize a wider bandwidth, while those farther away have access to a narrower spectrum. In the single-user case, the quadrature amplitude modulation (QAM) strategy is applied to modulate the information for higher data rates. To characterize the UAV THz channel between the transmitter and receiver, we consider factors such as UAV mobility, altitude, and environmental interactions that are specific to UAV applications. UAVs are mobile and can operate at varying altitudes, which affects the channel characteristics, including path loss and Doppler shifts. Therefore, we include the path gain coefficient in the UAV THz channel model. Beam misalignment, here noted by , is a critical issue in high-frequency communication, such as THz, due to the narrow beamwidths involved. Additionally, multipath fading is a significant factor in UAV communication environments where reflections from buildings, the ground, and other obstacles can impact signal quality. By including these elements, we aim to present a more realistic and practical model of the UAV communication channel. Therefore, the total channel coefficient h [24,30], is expressed as
where , , and are the path gain coefficient, beam misalignment fading coefficient, and the multi-path fading coefficient, respectively. Specifically, the path loss gain is calculated as [39]
where refers to the free space spread gain coefficient caused by the attenuation experienced by the THz wave atmospheric propagation with the isotropic antenna. denotes the absorption gain on the THz band, which is mainly caused by the water vapor molecules in the atmosphere. The parameter d is the distance between a single user and the base station. The transmit and receive antenna gains are represented by and , respectively. The factor is an equalization factor. , are the molecular absorption model at the two major absorption lines, one at about 325 GHz and second at 380 GHz. The parameters , , and g are calculated, respectively, as , and . In , , and g, , , , with the volume of the mixing ratio of water vapor, , where , , , , [39]. The parameters , p, and T denote the relative humidity, the pressure given in hectopascals, and the temperature given in degrees Celsius, respectively.
The beam misalignment fading coefficient , which represents the fractional power collected across Rx with area, A at distance d is expressed as [48,49]
where r is the pointing error expressed as the radial distance of the transmission and reception beams. The parameters with the error function , , . The parameters a and are the radius of the receiver effective area and the transmit beam footprint at distance d.
The multi-path fading coefficient is modeled as - distributed [50],
where is a fading parameter, whereas and denote the fading channel envelope’s normalized variance and -root mean value, respectively. It is to be noted here that the - distribution is a generalized form of many well-known fading distributions, e.g., Rayleigh ( = 2, = 1), Nakagami-m ( = 2, and is the fading parameter), and so on.
According to [48], the joint distribution of is
where the parameter . is the variance of the pointing error displacement at the receiver.
An efficient distance-based available bandwidth is obtained by setting the path loss below the threshold . The path loss threshold is obtained [12]
where highly directional antennas or antenna arrays are advocated to overcome the the significant path loss in THz band communication, we consider , , and [12]. The resulting path loss value is computed as dB, which will be used throughout our analysis. When the available bandwidth windows are established, each frequency window is further divided into multiple non-overlapped sub-windows for multi-carrier modulation. Each sub-window’s modulation order, bandwidth, and transmission power are jointly optimized to maximize the data rate.
3. The Hybrid HM-QAM Scheme for Multi-User Scenario
In the multi-user case, we initially assume two users for analytical simplicity, which can be expanded to scenarios with more than two users. The system model is shown in Figure 1. User 1 is located closer to the base station at distance , and User 2 is farther away at distance (). Based on distance dependence, the available bandwidths for User 1 and User 2 are and , respectively, with the condition for simplicity. It is important to note that the fixed relationship is for analytical simplicity. In practical scenarios, dynamic bandwidth allocation based on real-time conditions such as user mobility, traffic demand, and channel conditions might be more effective. The available bandwidth for the closer user includes the available bandwidth for the farther user, and thus, the overlapped bandwidth for the two users is , with the remaining available bandwidth for the closer user being B.
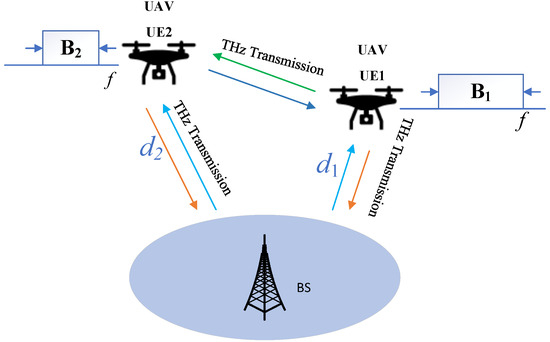
Figure 1.
The UAV-based THz system model.
We apply HM modulation schemes on the overlapped frequencies for both closer and farther users, and a QAM modulation scheme on the non-overlapped frequencies for the closer user. In the HM modulation scheme, the closer user () experiences less path loss compared to the farther user (). Consequently, the modulation order for the closer user is higher than that for the farther user on the overlapped frequencies due to better channel quality allowing for higher data rates. Because of the mobility of the UAVs, the available frequencies for the closer and farther users vary, necessitating adjustments in the modulation order to match environmental conditions. In scenarios with more than two users, coordination among multiple UAVs can help optimize overall system performance, ensuring fair bandwidth distribution and minimizing interference. In the UAV THz communication system, energy efficiency is also a concern since UAVs have limited energy resources. Efficient power management and routing algorithms are essential to prolong the operational time of the UAVs while ensuring reliable THz transmissions. Although this work focuses on modulation schemes, energy efficiency will be addressed in future research.
In the traditional hierarchical modulator (HM), the closer user applies the higher modulation order than the farther user. However, the farther user and closer user have the same available bandwidth and they have the same symbol rate with , where is the symbol duration of the closer user.
The hierarchical bandwidth modulation (HBM) exploits the distance-dependence available bandwidth of the THz frequency [46]. The available bandwidth of the closer user is larger than the farther user. The symbol duration is adjusted according to the available bandwidth with for the closer user and for the farther user. Hence, the symbol rate of the closer user is and the symbol rate of the farther user is . In HBM, although the modulation order of closer user and farther user is different, the modulation order of the closer user is the same on all the available frequencies, which is not reasonable and adaptive.
Motivated by these observations, we propose the hybrid HM-QAM strategy. Besides exploiting the distance-dependence of the available bandwidth of the THz frequency, we also combine the advantages of HM and QAM. In this modulation scheme, the base station adopts the HM scheme on the overlapped frequencies between the closer and farther users and the QAM scheme on the remaining frequencies of closer users. The HM-QAM scheme is formulated as
In the above optimization problem, constraints , , and denote the bit error requirements , , and . According to [51], the BER of -QAM with can be obtained as , where for and for . Therefore, the modulation order can be derived as the maximum power of 2 that has the form of , , and constraints.
The parameters , , and are the modulation order of the farther user, at the overlapped frequencies of the closer user and at the remaining frequencies of the closer user. By analyzing the above optimization problem, we can see that when the inequality constraints , , and are met with equality, the objective function is maximized, and the maximal data rate is
When , the above optimization problem is transformed into optimizing and to maximize the data rate. Due to , by setting , we can deduce the optimal to maximize the data rate. Then, by adopting the one-dimension search, we can obtain the optimal . The detailed algorithm is shown in Algorithm 1.
Before analyzing the computing complexity of Algorithm 1, we discuss the complexity of the proposed hybrid HM-QAM modulation schemes compared to HM and HBM schemes. The proposed hybrid HM-QAM scheme demonstrates better performance than both HM and HBM, as shown in Section 6. However, the computational complexity of hybrid HM-QAM is higher than that of HM and HBM. Specifically, in the hybrid HM-QAM scheme, the base station applies HM to overlapped frequencies and QAM to the remaining frequencies for closer users. In contrast, HM and HBM simply assign a higher modulation order to the closer user than to the farther user. Both hybrid HM-QAM and HBM involve dynamic bandwidth adjustment based on distance, which introduces additional computations compared to HM. Additionally, in HM, both users have the same symbol rate, which does not significantly increase complexity. Conversely, HBM and hybrid HM-QAM adjust the symbol duration, increasing the complexity in symbol rate calculations and synchronization. Finally, implementing the HM scheme is relatively straightforward with existing communication hardware and software. However, implementing HBM and hybrid HM-QAM requires more advanced hardware capable of dynamic symbol rate adjustments and sophisticated software for real-time bandwidth management. Despite the higher complexity, the proposed hybrid HM-QAM offers greater flexibility, potentially better performance, and high adaptability and efficiency. With the rapid advancement of hardware and software technologies, the proposed strategy is achievable.
| Algorithm 1 1-D Search Extreme Point Algorithm |
|
Algorithm 1 includes one outer loop, and in each iteration, there are 6 mathematical operation. Therefore, the total computation complexity is , where t is the search step size. Due to the convexity of the optimization problem in each iteration, Algorithm 1 can finally attain an optimal value. Therefore, we can see that the computational cost is determined by the step size. When the step is smaller, the computation cost is larger and vice versa. However, when the step size t is smaller, the optimal solution is more accurate. For large-scale or high-dimensional problems, due to low efficiency and scalability, exhaustive search algorithms can lead to extremely high computational and time costs. In practice, if the search process or stopping conditions are improperly set, it might only find local optimal solutions. Therefore, it is necessary to consider various optimization strategies, such as using heuristic methods to reduce the search space, or utilizing high-performance computing resources to enhance the processing speed, thereby improving the usability and efficiency of exhaustive search algorithms in real-world problems.
For HM, the modulation scheme is formulated as
According to the convex theory, when and takes equality, the data rate is maximized with
By replacing with , due to , R is convex with respect to . By setting , we can obtain the optimal value of . Substituting and into (10), we can get the maximal data rate.
For HBM, the modulation scheme is formulated as
The algorithm to solve the optimization problem (11) is the same as (9) and thus, it is omitted here for brevity.
4. Adaptive Modulation for the Single User
When the available frequency windows are determined based on the transmission distance, the adaptive modulation problem can be formulated as follows:
The parameters and denote the number of frequency sub-windows and the subcarriers in the m-th sub-window, respectively. Constraint indicates that the sum of all subcarriers cannot exceed the available bandwidth . Constraint stipulates that the sum of subcarriers in each frequency sub-window should be less than the bandwidth of each sub-window. Constraint asserts that the power of any subcarrier cannot exceed the total transmit power. Constraint requires that the modulation order of each subcarrier meets the bit error requirements. Constraints and specify that the bandwidth and power must be positive. Constraint stipulates that the modulation order must be an integer. The problem described is non-convex due to the coupling of variables and in the objective function and constraint , represents the available transmission bandwidth, while represents the bandwidth of the n-th subcarrier in the m-th sub-window at distance d. Consequently, an effective algorithm needs to be proposed to transform this non-convex problem into a convex problem. Through the analysis of the problem structure, we propose the block-coordinated decent (BCD) method to solve it. The principle of the BCD is outlined as follows:
Particularly, a feasible initial solution is firstly determined and then, the variables and are jointly optimized to obtain the initial and . Based on the latest optimized and , the variable is updated to be . The optimization process is repeated until the rate difference between the two iterations is less than the predetermined threshold. According to the principle of the BCD algorithm, the data rate of each iteration will be greater than that of the previous one. Therefore, this algorithm is convergent. According to the BCD method, the prime non-convex optimization problem is decomposed into two sub-problems and as following:
and
The above sub-problems and are convex and can be solved directly using a CVX tool or lagrangian dual method. The details of the BCD algorithm are described in Algorithm 2.
| Algorithm 2 BCD Algorithm |
|
The convergence of the entire method is proven in Appendix A.
Although the convergence speed of the BCD methods cannot be analyzed theoretically [52], the methods typically converge in a few iterations for a moderate number of optimization variables as will be numerically shown in Section 4. Meanwhile, the sub-problems in each iteration of the BCD method are all convex optimization problems, which can be solved in polynomial time. Therefore, the time complexity of the proposed iterative method is polynomial, and it can be practically implemented with fast convergence for a THz wireless communication system with distance-adaptive modulation. The BCD algorithm involves solving two sub-problems and in each iteration. Due to the convexity of and , they can be solved using the CVX tool, which typically employs the interior-point method to obtain the optimal solution. The computational complexity of the interior-point method is polynomial, determined by the number of variables and constraints. Therefore, the arithmetic complexity of solving and is and , respectively. According to the iteration stop condition , the total computation complexity of BCD method is , respectively.
The water-filling power allocation method allocates more power to channels with higher signal-to-noise ratios (SNR) while maintaining a total power constraint. This method involves calculating the SNR for each channel, updating the power allocation, computing the total power, and comparing it with the power constraint. The complexity of calculating the SNR for each channel and updating the power allocation is determined by the number of channels, so the complexity of these operations is . Assuming the number of iterations is m, the total complexity of the water-filling algorithm is . However, the water-filling algorithm is not suitable for scenarios where the channels change frequently. When the channels change frequently, it necessitates frequent recalculations of SNR and updates to the power allocation, increasing the overall computational burden.
In the water-filling power allocation algorithm, the power in the k-th channel is allocated by for ; for otherwise. denotes the noise power, and is the channel power gain of the k-th channel.
5. The Adjustment Probability of Modulation Strategy
When the user moves, the distance between the base station and user changes accordingly. Thus, the distance-dependent available frequency bandwidth varies and the modulation scheme should be adjusted too. Motivated by this, we design the modulation switch rules as shown in Table 2.

Table 2.
Switch Rules of Modulation Schemes.
According to the modulation switch rules, when the user moves, the probability that the SNR difference is not smaller than the threshold , which is usually set to 0.5 dB in engineering practice, is calculated as follows:
By setting
we have . In Equation (16), the parameters and denote the channel power gain at the distance and d, respectively. The channel power gain with the channel error variable , where is the variance of the error variable.
By introducing the auxiliary parameters,
The calculation of and can be classified into several cases under three different scenarios, namely, the user moving farther from the base station with , the user moving closer to the base station with , and the user remaining stationary with .
In the first scenario, where the user moves farther from the base station with , , , and , the calculation of and are classified into two cases, respectively.
The calculation of is shown as following
Case I: when , the probability .
Case II: when , the probability , where represents the cumulative probability distribution function (CDF). denotes the channel power gain of n-th sub-frequency in the m-th sub-window.
The probability is derived as follows:
Case I: when , .
Case II: when , , where the and , and . is thus calculated as
To sum up, the total adjustment probability of modulation scheme is written as
According to Table 2, the adjustment occurs when or and . The probability of the first case is and the probability of the second case is , where we assume the probabilities of the bandwidth difference being no larger and larger than the threshold are equal due to the random mobility of the user.
In the second scenario, where the user moves closer to the base station with , , , , and , the calculation of is classified into four cases.
The is derived as
There are four cases for the calculation of :
Case I: when and , and . Therefore, is calculated as
Case II: when and , .
Case III: when and , and , where and . Therefore, is calculated as
Case IV: when and , .
To sum up, the total adjustment probability of the modulation scheme is given by .
In the third scenario, where the user remains unmoved with , the adjustment probability of the modulation scheme due to the channel time-varying, is calculated as
where with and independent of each other. The detailed derivation process is shown in Appendix A.
6. Simulation Analysis
In this section, we analyze the effectiveness of the proposed modulation scheme and verify the switch probability of the modulation scheme when the user moves. For convenience, we assume there are five available frequency sub-windows for a certain distance, i.e., . Each sub-window is divided into 10 non-overlapped sub-bands, i.e., . The total available THz bandwidth is THz [12]. We use MATLAB software to verify the theoretic analysis. The simulation parameter settings are shown in Table 3 [12].

Table 3.
Simulation Parameters.
On the multiple sub-bands, we adopt different power allocation strategies, i.e., equal power allocation, water-filling power allocation, and the proposed power optimization strategy. The simulation results are shown in Figure 2 and Figure 3.
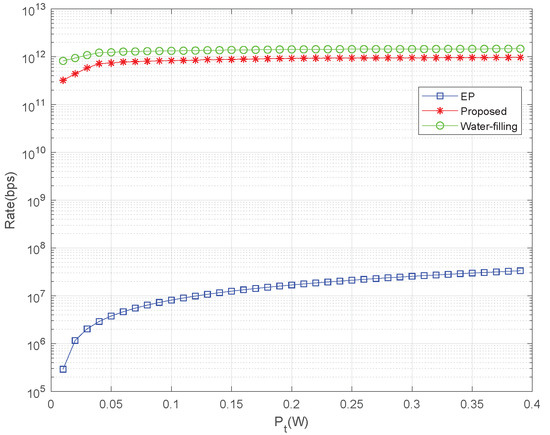
Figure 2.
The data rate comparison of three different power optimization schemes.
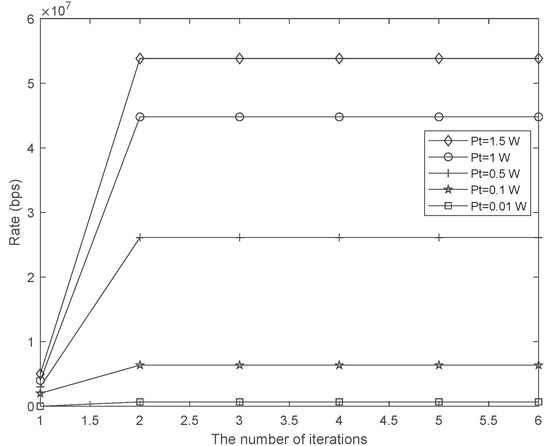
Figure 3.
Complexity vs Pt when Hz.
The data rate of our proposed joint optimization strategy is compared with that of the equal power allocation strategy and water-filling power optimization scheme, as shown in Figure 2. The results show that the data rate of the proposed joint optimization adaptive modulation strategy is close to the upper bound of water-filling strategy. The data rate of equal-power allocation strategy is lowest due to under-utilization of channel varying and distance-dependent frequency characteristics.
Figure 3 illustrates the convergence behavior of the proposed BCD method for different . To speed up the convergence of the BCD method, we initialize the frequency by equally dividing the bandwidth in each frequency sub-window. The time complexities of the two convex sub-problems in each iteration of the BCD method are polynomial. Therefore, from the figure, we can observe that the BCD method needs about 10 iterations to converge, which can also be deduced by the complexity analysis in Algorithm 2, i.e., . Therefore, the proposed method overall has a relatively fast convergence speed.
From Figure 4, when the user moves farther from the base station, the modulation switch probability is higher than in the other two situations. When the user moves closer to the base station, the modulation switch probability is slightly higher than that of not moving as expected. Moreover, when the switch threshold or increases, the modulation switch probability becomes smaller because the range of the satisfying modulation rule threshold enlarges.
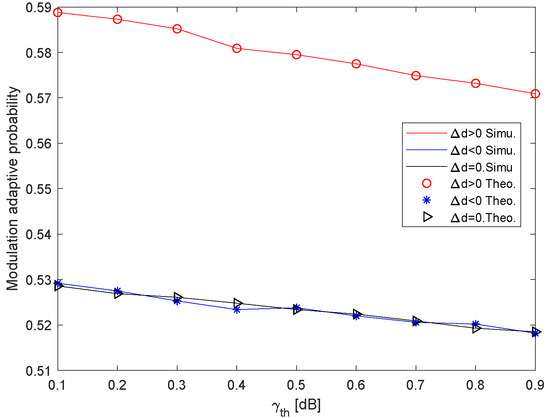
Figure 4.
The modulation adjustment probability with user’s mobility.
From Figure 5, we can see the data rate of the proposed HM-QAM scheme is higher than the other two modulation schemes. The data rate of HBM is higher than HM, as expected. However, we can see from Figure 6 that the bit error rate (BER) of HM-MQAM is higher than that of HBM and HM modulation strategies in low SNR regions. This is because the system trades off the bit error rate for an increase in the data rate. It represents a compromise between reliability and efficiency.
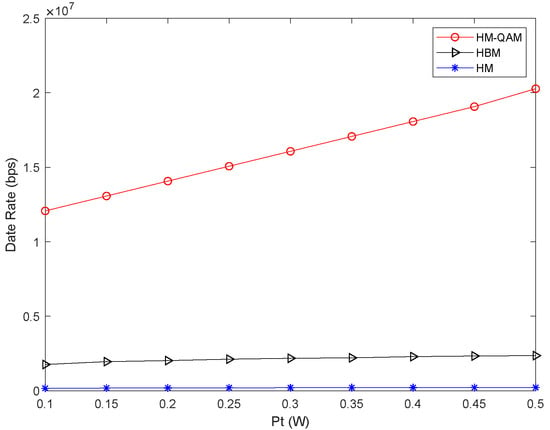
Figure 5.
The data rate of different modulation schemes.
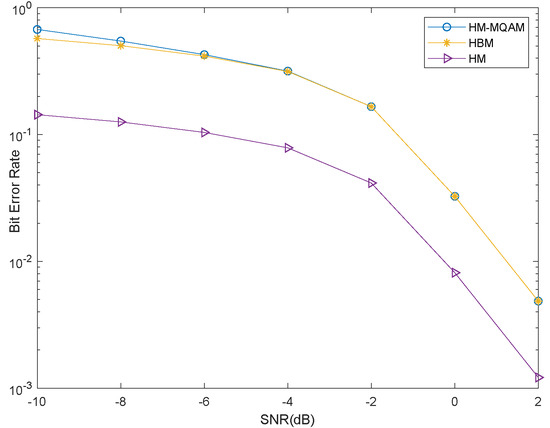
Figure 6.
BER comparison under different modulation schemes.
In Figure 7, we can see the modulation order of the closer user on the common frequency band is higher than the modulation order of the closer user on . The modulation order of the farther user is approximately equal to the modulation order of the closer user on the remaining bandwidth . The modulation order of the closer user is higher than that of the farther user for the HBM and HM schemes. Meanwhile, the modulation order of the HBM scheme is the lowest compared to HM-QAM and HM schemes, thus reducing the required hardware complexity.
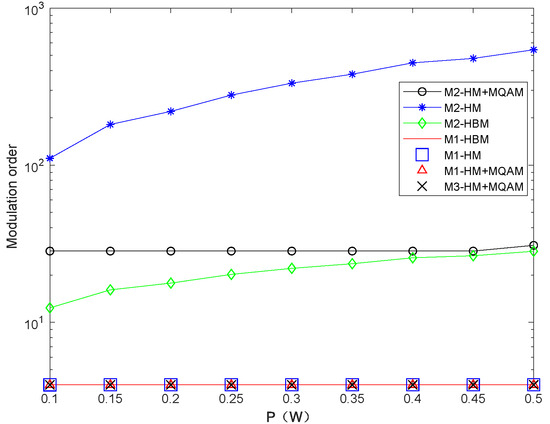
Figure 7.
The modulation order comparison of different modulation schemes.
7. Conclusions
In this paper, we present a multi-carrier-based adaptive modulation optimization strategy by jointly optimizing the subcarrier bandwidth, transmission power and modulation order. We propose the BCD algorithm to solve the non-convex adaptive modulation optimization problem. Furthermore, we consider the user’s mobility and design the adjustment rules of the modulation schemes when the user moves. The adjustment probability is derived for the different situations. Finally, simulations are conducted, and the results show that the data rate of the jointly optimized modulation strategy is higher than that of the equal-power and water-filling strategies. The modulation adjustment probability of the user moving farther from the base station is the highest due to the varying channel and distance-dependent available bandwidth.
Author Contributions
Z.H.: conceptualization, methodology, software, and writing–original draft preparation. Y.X.: conceptualization, software, and writing–review and editing. Y.D.: conceptualization, software, and writing–review and editing. Z.Z.: conceptualization, resources, writing–review and editing, supervision, project administration, and funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by National Natural Science Foundation of China (NSFC) under Grant No. 62101076, in part by National Natural Science Foundation of Sichuan Province (NSFSC) under Grant No. (2022)0920, and in part by Talent Introduction Research Startup Project under Grant No. 376157.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author/s.
Conflicts of Interest
The authors declare no conflicts of interest for publishing in this journal.
Appendix A
Proof of Convergence of Algorithm 2.
From the optimization problem , we have . From optimization problem , we have . After updating by replacing with , from optimization problem , we have . By replacing with , from optimization problem , we have . The process repeats until the convergence condition is satisfied. According to the recursive algorithm, we can obtain that at the -th iteration of the iterative method. Since the solution region is compact due to the bounded , and , the iterative method proposed in Algorithm 2 can finally converge to the optimal point , which completes the proof. □
Proof of Adjustment Probability.
According to the adjustment rules in Table 2, the adjustment probability of modulation scheme is expressed as
By introducing the parameters as (18), and are expressed as
According to the solution existence conditions of the inequalities and , the calculation of and is classified into several cases under three different scenarios: the user moving farther from the base station with , the user moving closer to the base station with , and the user remaining stationary with , as shown in Equations (16)–(23). □
References
- Chaves, A.N.; Cugnasca, P.S.; Jose, J. Adaptive Search Control Applied to Search and Rescue Operations Using Unmanned Aerial Vehicles (UAVs). IEEE Lat. Am. Trans. 2014, 12, 1278–1283. [Google Scholar] [CrossRef]
- Chen, H.; Lan, Y.; Fritz, B.K.; Hoffmann, W.C.; Liu, S. Review of Agricultural Spraying Technologies for Plant Protection Using Unmanned Aerial Vehicle (UAV). Int. J. Agric. Biol. Eng. 2021, 14, 38–49. [Google Scholar]
- Peng Yao, H.W.; Ji, H. Multi-UAVs Tracking Target in Urban Environment by Model Predictive Control and Improved Grey Wolf Optimizer. Aerosp. Sci. Technol. 2016, 55, 131–143. [Google Scholar]
- CISCO. Cisco Annual Internet Report (2018–2023). 2020. Available online: https://www.cisco.com/c/en/us/solutions/collateral/executive-perspectives/annual-internet-report/white-paper-c11-741490.pdf (accessed on 25 December 2020).
- Hossain, Z.; Li, Q.C.; Ying, D.; Wu, G.; Xiong, C. THz Channel Model for 6G Communications. In Proceedings of the 2021 IEEE 32nd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Virtually, 13–16 September 2021; pp. 1–7. [Google Scholar]
- IEEE 802.15 WPAN Terahertz Interest Group (IGthz). 2019. Available online: http://www.ieee802.org/15/pub/TG3d/index_IGthz.html (accessed on 23 July 2019).
- Nagatsuma, T.; Ito, H.; Ishibashi, T. High-power RF Photodiodes and Their Applications. Laser Photonics Rev. 2009, 3, 123–137. [Google Scholar] [CrossRef]
- Huang, K.c.; Wang, Z. Terahertz Terabit Wireless Communication. IEEE Microw. Mag. 2011, 12, 108–116. [Google Scholar] [CrossRef]
- Ojefors, E.; Heinemann, B.; Pfeiffer, U.R. Subharmonic 220- and 320-GHz SiGe HBT Receiver Front-Ends. IEEE Trans. Microw. Theory Tech. 2012, 60, 1397–1404. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Jornet, J.M. Realizing Ultra-Massive MIMO (1024×1024) Communication in the (0.06–10) Terahertz Band. Nano Commun. Netw. 2016, 8, 46–54. [Google Scholar]
- Micovic, M.; Kurdoghlian, A.; Margomenos, A.D.; Brown, D.F.; Shinohara, K.; Burnham, S.D.; Milosavljevic, I.; Bowen, R.L.; Williams, A.J.; Hashimoto, P.; et al. 92–96 GHz GaN Power Amplifiers. In Proceedings of the 2012 IEEE/MTT-S International Microwave Symposium Digest, Montreal, QC, Canada, 17–22 June 2012; pp. 1–3. [Google Scholar]
- Kleine-Ostmann, T.; Nagatsuma, T. A Review on Terahertz Communications Research. J. Infrared Millim. Terahertz Waves 2011, 32, 143–171. [Google Scholar] [CrossRef]
- Tonouchi, M. Cutting-edge Terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Celik, A.; Shihada, B.; Alouini, M.S. Wireless Data Center Networks: Advances, Challenges, and Opportunities. arXiv 2018, arXiv:1811.11717. [Google Scholar]
- Nie, S.; Jornet, J.M.; Akyildiz, I.F. Intelligent Environments Based on Ultra-massive MIMO Platforms for Wireless Communication in Millimeter Wave and Terahertz Bands. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 7849–7853. [Google Scholar]
- Saad, W.; Bennis, M.; Chen, M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 2020, 34, 134–142. [Google Scholar] [CrossRef]
- Wang, C.X.; Wang, J.; Hu, S.; Jiang, Z.H.; Tao, J.; Yan, F. Key Technologies in 6G Terahertz Wireless Communication Systems: A Survey. IEEE Veh. Technol. Mag. 2021, 16, 27–37. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, Q.; He, J.; Habibi, M.A.; Melnyk, S.; El-Absi, M.; Han, B.; Renzo, M.D.; Schotten, H.D.; Luo, F.L.; et al. Terahertz Communications and Sensing for 6G and Beyond: A Comprehensive Review. IEEE Commun. Surv. Tutor. 2024. [Google Scholar] [CrossRef]
- Farrag, S.; Maher, E.; El-Mahdy, A.; Dressler, F. Performance Analysis of UAV Assisted Mobile Communications in THz Channel. IEEE Access 2021, 9, 160104–160115. [Google Scholar] [CrossRef]
- Xu, L.; Chen, M.; Chen, M.; Yang, Z.; Chaccour, C.; Saad, W.; Hong, C.S. Joint Location, Bandwidth and Power Optimization for THz-Enabled UAV Communications. IEEE Commun. Lett. 2021, 25, 1984–1988. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, H.; Liu, X.; Long, K.; Nallanathan, A. Joint UAV Placement Optimization, Resource Allocation, and Computation Offloading for THz Band: A DRL Approach. IEEE Trans. Wirel. Commun. 2023, 22, 4890–4900. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, K.; Pan, C.; Zhu, H.; Wang, J. UAV-Assisted and Intelligent Reflecting Surfaces-Supported Terahertz Communications. IEEE Wirel. Commun. Lett. 2021, 10, 1256–1260. [Google Scholar] [CrossRef]
- Jia, Z.; Sheng, M.; Li, J.; Niyato, D.; Han, Z. LEO-Satellite-Assisted UAV: Joint Trajectory and Data Collection for Internet of Remote Things in 6G Aerial Access Networks. IEEE Internet Things J. 2021, 8, 9814–9826. [Google Scholar] [CrossRef]
- Badarneh, O.S.; Bouanani, F.E.; Almehmadi, F. A General Framework for UAV-Aided THz Communications Subject to Generalized Geometric Loss. IEEE Trans. Veh. Technol. 2023, 72, 14589–14600. [Google Scholar] [CrossRef]
- Termehchi, A.; Syed, A.; Kennedy, W.S.; Erol-Kantarci, M. Distributed Safe Multi-Agent Reinforcement Learning: Joint Design of THz-enabled UAV Trajectory and Channel Allocation. IEEE Trans. Veh. Technol. 2024, 1–16. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, X. IRS/UAV-Based Edge-Computing and Traffic-Offioading Over 6G THz Mobile Wireless Networks. In Proceedings of the ICC 2023—IEEE International Conference on Communications, Dalian, China, 10–12 August 2023; pp. 6480–6485. [Google Scholar]
- Ren, X.; Chen, X.; Jiao, L.; Dong, Z.; Dai, X. Joint Location, Bandwidth and Computation Offloading for Thz-Enabled Hierarchical Multicoalition UAV MEC Networks. In Proceedings of the 2023 IEEE 11th International Conference on Information, Communication and Networks (ICICN), Xi’an, China, 10–13 August 2023; pp. 316–321. [Google Scholar]
- Bhardwaj, P.; Bansal, V.; Biyani, N.; Shukla, S.; Zafaruddin, S.M. Performance of Integrated IoT Network With Hybrid mmWave/FSO/THz Backhaul Link. IEEE Internet Things J. 2024, 11, 3639–3652. [Google Scholar] [CrossRef]
- Farrag, S.; Maher, E.A.; El-Mahdy, A.; Dressler, F. Sum Rate Maximization of Uplink Active RIS and UAV-assisted THz Mobile Communications. In Proceedings of the 2023 19th International Conference on the Design of Reliable Communication Networks (DRCN), Geltru, Spain, 17–20 April 2023; pp. 1–7. [Google Scholar]
- Wang, D.; Wu, M.; Wei, Z.; Yu, K.; Min, L.; Mumtaz, S. Uplink Secrecy Performance of RIS-Based RF/FSO Three-Dimension Heterogeneous Networks. IEEE Trans. Wirel. Commun. 2024, 23, 1798–1809. [Google Scholar] [CrossRef]
- Iradukunda, N.; Pham, Q.V.; Ding, Z.; Hwang, W.J. THz-Enabled UAV Communications Using Non-Orthogonal Multiple Access. IEEE Trans. Veh. Technol. 2023, 72, 10977–10981. [Google Scholar] [CrossRef]
- Castro, C.; Elschner, R.; Merkle, T.; Schubert, C.; Freund, R. Experimental Demonstrations of High-Capacity THz-Wireless Transmission Systems for Beyond 5G. IEEE Commun. Mag. 2020, 58, 41–47. [Google Scholar] [CrossRef]
- Jornet, J.M.; Akyildiz, I.F. Information Capacity of Pulse-based Wireless Nanosensor Networks. In Proceedings of the 2011 8th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, Salt Lake City, UT, USA, 27–30 June 2011; pp. 80–88. [Google Scholar]
- Jornet, J.M.; Akyildiz, I.F. Channel Modeling and Capacity Analysis for Electromagnetic Wireless Nanonetworks in the Terahertz Band. IEEE Trans. Wirel. Commun. 2011, 10, 3211–3221. [Google Scholar] [CrossRef]
- Jornet, J.M.; Akyildiz, I.F. Femtosecond-Long Pulse-Based Modulation for Terahertz Band Communication in Nanonetworks. IEEE Trans. Commun. 2014, 62, 1742–1754. [Google Scholar] [CrossRef]
- Han, C.; Bicen, A.O.; Akyildiz, I.F. Multi-Wideband Waveform Design for Distance-Adaptive Wireless Communications in the Terahertz Band. IEEE Trans. Signal Process. 2016, 64, 910–922. [Google Scholar] [CrossRef]
- Han, C.; Akyildiz, I.F. Distance-aware Multi-carrier (DAMC) Modulation in Terahertz Band communication. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 5461–5467. [Google Scholar]
- Wu, Y.; Han, C.; Yang, T. DFT-Spread Orthogonal Time Frequency Space Modulation Design for Terahertz Communications. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Rio de Janeiro, Brazil, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Boulogeorgos, A.A.A.; Papasotiriou, E.N.; Alexiou, A. A Distance and Bandwidth Dependent Adaptive Modulation Scheme for THz Communications. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; pp. 1–5. [Google Scholar]
- Gao, W.; Chen, Y.; Han, C.; Chen, Z. Distance-Adaptive Absorption Peak Modulation (DA-APM) for Terahertz Covert Communications. IEEE Trans. Wirel. Commun. 2021, 20, 2064–2077. [Google Scholar] [CrossRef]
- Sarieddeen, H.; Alouini, M.-S.; Al-Naffouri, T.Y. Terahertz-band Ultra-massive Spatial Modulation MIMO. IEEE J. Sel. Areas Commun. 2019, 37, 2040–2052. [Google Scholar] [CrossRef]
- Yan, S.; Song, Q.; Lin, X.; Wang, P.; Zhao, C. On the Spatial Modulation for 60 GHz Millimeter Wave Communications based on Characteristics of Variance. In Proceedings of the 16th International Symposium on Communications and Information Technologies (ISCIT), Qingdao, China, 26–28 September 2016; pp. 92–95. [Google Scholar]
- Hadani, R.; Rakib, S.; Molisch, A.F.; Ibars, C.; Monk, A.; Tsatsanis, M.; Delfeld, J.; Goldsmith, A.; Calderbank, R. Orthogonal Time Frequency Space (OTFS) Modulation for Millimeter-wave Communications Systems. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honolulu, HI, USA, 4–9 June 2017; pp. 681–683. [Google Scholar]
- Raviteja, P.; Phan, K.T.; Hong, Y.; Viterbo, E. Interference Cancellation and Iterative Detection for Orthogonal Time Frequency Space Modulation. IEEE Trans. Wirel. Commun. 2018, 17, 6501–6515. [Google Scholar] [CrossRef]
- Surabhi, G.D.; Augustine, R.M.; Chockalingam, A. Peak-to-Average Power Ratio of OTFS Modulation. IEEE Commun. Lett. 2019, 23, 999–1002. [Google Scholar] [CrossRef]
- Bodet, D.; Sen, P.; Hossain, Z.; Thawdar, N.; Jornet, J.M. Hierarchical Bandwidth Modulations for Ultra-Broadband Communications in the Terahertz Band. IEEE Trans. Wirel. Commun. 2023, 22, 1931–1947. [Google Scholar] [CrossRef]
- Hossain, Z.; Jornet, J.M. Hierarchical Bandwidth Modulation for Ultra-Broadband Terahertz Communications. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–7. [Google Scholar]
- Boulogeorgos, A.A.A.; Papasotiriou, E.N.; Alexiou, A. Analytical Performance Assessment of THz Wireless Systems. IEEE Access 2019, 7, 11436–11453. [Google Scholar] [CrossRef]
- Saeed, A.; Gurbuz, O.; Bicen, A.O.; Akkas, M.A. Variable-Bandwidth Model and Capacity Analysis for Aerial Communications in the Terahertz Band. IEEE J. Sel. Areas Commun. 2021, 39, 1768–1784. [Google Scholar] [CrossRef]
- Yacoub, M.D. The α-μ Distribution: A Physical Fading Model for the Stacy Distribution. IEEE Trans. Veh. Technol. 2007, 56, 27–34. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Ngo, D.T.; Khakurel, S.; Le-Ngoc, T. Joint Subchannel Assignment and Power Allocation for OFDMA Femtocell Networks. IEEE Trans. Wirel. Commun. 2014, 13, 342–355. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).